1 Introduction

Uncertainty in the coefficients of a linear program is often handled by probability constraints or, more generally, bounds on a risk measure. The random restrictions are then captured by imposing risk constraints on their violation. Consider the linear program

$$\begin{aligned} {\mathbf c}^\prime {\mathbf x}\longrightarrow \min \quad \hbox {s.t.} \ \tilde{\mathbf A}{\mathbf x}\ge {\mathbf b}\,, \end{aligned}$$
(1)

and assume that \(\tilde{\mathbf A}\) is a stochastic \(m\times d\) matrix and \({\mathbf b}\in \mathbb {R}^m\), \({\mathbf c}\in \mathbb {R}^d\), \({\mathbf x}\in \mathbb {R}^d\). This is a stochastic linear optimization problem. To handle the stochastic restrictions a joint risk constraint,

$$\begin{aligned} \rho ^m(\tilde{\mathbf A}{\mathbf x}-{\mathbf b}) \le {\mathbf 0}\,, \end{aligned}$$
(2)

may be introduced, where \(\rho ^m\) is an \(m\)-variate risk measure. For instance, with \(\rho ^m(Y)=\text {Prob}[Y<0]-\alpha \) the restriction (2) becomes

$$\begin{aligned} \text {Prob}[\tilde{\mathbf A}{\mathbf x}\ge {\mathbf b}] \ge 1 - \alpha \,, \end{aligned}$$
(3)

and a usual chance-constrained linear program is obtained. Alternatively, the restrictions may be subjected to separate risk constraints,

$$\begin{aligned} \rho ^1(\tilde{\mathbf A}_j {\mathbf x}-b_j) \le 0\,, \quad j=1\dots m\,, \end{aligned}$$
(4)

with \(\tilde{\mathbf A}_j\) denoting the \(j\)-th row of \(\tilde{\mathbf A}\). In (4) each restriction is subject to the same bound that limits the risk of violating the condition. A linear program that minimizes \({\mathbf c}'{\mathbf x}\) subject to one of the restrictions, (2) or (4), is called a risk-constrained stochastic linear program.

For stochastic linear programs (SLPs) in general and risk-constrained SLPs in particular, the reader is referred to, e.g., Kall and Mayer (2010). What we call a risk measure here is mentioned in that book as a quality measure, and useful representations of the corresponding constraints are given. As most of the literature, Kall and Mayer (2010) focus on classes of SLPs with chance constraints that lead to convex programming problems, since these have obvious computational advantages; see also Prékopa (1995). Our choice of the quality measure, besides its generality, enjoys a meaningful interpretation and, as it will be seen, enables the use of convex structures in the problem.

In the case of a single constraint (\(m=1\)) notate

$$\begin{aligned} \rho (\tilde{\mathbf a}'{\mathbf x}-b) \le 0. \end{aligned}$$
(5)

A practically important example of an SLP with a single risk constraint (5) is the portfolio selection problem. Let \(\tilde{r}_1, \dots , \tilde{r}_d\) be the return rates on \(d\) assets and notate \(\tilde{\mathbf r}=(\tilde{r}_1, \dots , \tilde{r}_d)'\). A convex combination of the assets’ returns is sought, \(\tilde{\mathbf r}'{\mathbf x}= \sum _{j=1}^d \tilde{r}_j x_j\) that has maximum expectation under a risk constraint and an additional deterministic constraint,

$$\begin{aligned} \max _{{\mathbf x}\in \mathcal{C}}\ E[\tilde{\mathbf r}]'{\mathbf x}, \quad \hbox {s.t.}\ \rho (\tilde{\mathbf r}'{\mathbf x})\le \rho _0,\; {\mathbf x}\in \mathcal{C}\,, \end{aligned}$$
(6)

where \(\rho \) is a risk measure, \(\rho _0\in \mathbb {R}\) is a given upper bound of risk (a nonnegative monetary value), and \(\mathcal{C}\in \mathbb {R}^d\) is a deterministic set that restricts the vector \({\mathbf x}\) of portfolio weights in some way. For example, if short sales are excluded, \(\mathcal{C}\) is the positive orthant in \(\mathbb {R}^d\). The solution \({\mathbf x}^*\) is the optimal investment under the given model. We will see that a solution, if it exists, is, as a rule, finite and unique. In our geometric approach such a solution corresponds to the intersection of some line and some convex body that both contain the point \(E[\tilde{\mathbf r}]\).

Regarding the choice of \(\rho \), two special cases are well known. First, let \(\rho (\tilde{\mathbf r}'{\mathbf x})= \text {Prob}[\tilde{\mathbf r}'{\mathbf x}\le - v_0]\) and \(\rho _0=\alpha \). Then the optimization problem (6) says: maximize the mean return \(E[\tilde{\mathbf r}'{\mathbf x}]\) under the restrictions \({\mathbf x}\in \mathcal{C}\) and

$$\begin{aligned} \text {V@R}_\alpha (\tilde{\mathbf r}'{\mathbf x}) \le v_0. \end{aligned}$$

That is, the value at risk \(\text {V@R}_\alpha \) of the portfolio return must not exceed the bound \(v_0\). Second, let

$$\begin{aligned} \rho (\tilde{\mathbf r}'{\mathbf x})= - \frac{1}{\alpha }\int _0^\alpha Q_{\tilde{\mathbf r}'{\mathbf x}}(t)\,\hbox {d}t, \end{aligned}$$
(7)

where \(Q_Z\) signifies the quantile function of a random variable \(Z\). This means that the measured risk is the expected shortfall of portfolio return and shall stay below \(\rho _0\).

In practice, \(\tilde{\mathbf a}\) has to be obtained from data. If the solution of the SLP is based on \(n\) observed coefficient vectors \({\mathbf a}^1,\dots ,{\mathbf a}^n \in \mathbb {R}^d\), the SLP is mentioned as an empirical risk-constrained SLP. In other words, we assume that \(\tilde{\mathbf a}\) follows an empirical distribution that gives equal mass \(\frac{1}{n}\) to some observed points \({\mathbf a}^1,\dots , {\mathbf a}^n\in \mathbb {R}^d\). Rockafellar and Uryasev (2000) investigate an empirical stochastic program that arises in portfolio choice when the expected shortfall of a portfolio is minimized. They convert the objective into a function that is convex in the decision vector \({\mathbf x}\) and optimize it by standard methods. This approach is commonly used in more recent works of these and other authors on portfolio optimization.

A more complex situation is investigated by Bertsimas and Brown (2009), who discuss the risk-constrained SLP with arbitrary coherent distortion risk measures, which also include expected shortfall. These allow for a sound interpretation in terms of expected utility with distorted probabilities. For the linear restriction an, as it is called, uncertainty set is constructed, consisting of all coefficients satisfying the risk constraint. Bertsimas and Brown (2009) discuss the uncertainty set that turns the SLP into a minimax problem, called robust linear program; however, they provide no optimal solution of this program there. The uncertainty set is a convex body and, as will be made precise below in this paper, comes out to equal a so-called weighted-mean trimmed region. Natarajan et al. (2009), on the reverse, construct similar risk measures from given polyhedral and conic uncertainty sets. As an extension, Ben-Tal et al. (2010) propose the so-called “soft robustness” model, which, as they show, can be regarded as an LP with the feasible set defined by some convex risk measure. Such approaches are also applicable to approximately solving a multi-stage robust convex optimization problem, where the information about the realization of uncertain parameters is adjusted on each stage; see Bertsimas and Goyal (2013).

Pflug (2006) has proposed an iterative algorithm to optimize a portfolio by using distortion functionals; in each step he adds a constraint to the problem and solves it by the simplex method. Meanwhile, many other authors have recently contributed to the development of robust linear programs related to risk-constrained optimization problems: see, e.g., Nemirovski and Shapiro (2006), Ben-Tal et al. (2009) and Chen et al. (2010). For a review of robust linear programs in portfolio optimization the reader is referred to Fabozzi et al. (2010). There are also attempts to solve this problem by means of robust nonlinear models (see, for instance, Kawas and Thiele (2011)), which, however, are substantially less investigated in the literature than the linear ones. Other applications are surveyed in detail in Gabrel et al. (2014).

In this paper we contribute to this discussion in three respects:

  1. 1.

    The uncertainty set of an SLP under a general coherent distortion risk constraint is shown to be a weighted-mean trimmed region, which provides a useful visual and computable characterization of the set.

  2. 2.

    An algorithm is constructed that solves the minimax problem over the uncertainty set, hence the SLP.

  3. 3.

    If the data are i.i.d. from a general probability distribution, the uncertainty set and the solution of the SLP are shown to be consistent estimators of the uncertainty set and the SLP solution.

The paper is organized as follows. In Sect. 2 constraints on distortion risk measures are discussed. They are characterized by uncertainty sets in parameter, which, in turn, are shown to be weighted-mean trimmed regions (Theorem 1). Based on Theorem 1, which is a core result, we formulate a robust linear program, which is investigated in Sect. 3 and by which the SLP with a distortion risk constraint is solved. Section 4 introduces an algorithm for this program and discusses sensitivity issues of its solution. In Sect. 5 we address the SLP and its solution for generally distributed coefficients and investigate the limit behavior of our algorithm if based on an independent sample of coefficients. Section 6 contains first computational results and concludes the article. The Appendix gathers properties of distortion risk measures, a proof of Theorem 1 and a demonstration (Proposition 5) that the weighted-mean trimmed regions have the coherency property.

2 Distortion risk constraints and weighted-mean regions

2.1 Distortion risk measures

A large and versatile subclass of risk measures is the class of distortion risk measures, which have appeared first from ideas in insurance research (Wang et al. 1997). Again, let \(Q_Y\) denote the quantile function of a random variable \(Y\).

Definition 1

(Distortion risk measure) Let \(r\) be an increasing function \([0,1]\rightarrow [0,1]\). The function \(\rho \) given by

$$\begin{aligned} \rho (Y)= - \int _0^1 Q_{Y}(t)\,\hbox {d}r(t) \end{aligned}$$
(8)

is a distortion risk measure with weight generating function \(r\).

Distortion risk measures are essentially the same as spectral risk measures (Acerbi 2002). Their properties are considered in detail in the Appendix. Here, we concentrate on their coherency, as this property is crucial in assessing diversified risks.

A distortion risk measure is coherent if and only if \(r\) is concave. For example, with \(r(t)=0\) if \(t < \alpha \) and \(r(t)=1\) if \(t\ge \alpha \), the value at risk \(\text {V@R}_\alpha (Y)= - Q_{Y}(\alpha )\) is obtained, which is a noncoherent distortion risk measure. A prominent example of a coherent distortion risk measure is the expected shortfall, which is yielded by \(r(t)=t/\alpha \) if \(t < \alpha \) and \(r(t)=1\) otherwise. This measure is defined as (the negative of) the conditional expectation of \(Y\) under the condition that \(Y\) does not exceed its \(\alpha \)-quantile, \(Q_{Y}(\alpha )\). Roughly speaking, it is the mean of the \(\alpha \cdot 100\%\) largest possible losses. Clearly, for a given \(\alpha \), this measure is more conservative than the value at risk, because its value cannot be smaller than \(\text {V@R}_\alpha (Y)\). Also observe that, for \(r(t)=t\), the risk measure (1) becomes the expectation of \(-Y\).

A general distortion risk measure \(\rho (Y)\) can thus be interpreted as the expectation of \(-Y\) with respect to a probability distribution that has been distorted by the function \(r\). In particular, a concave function \(r\) distorts the probabilities of lower outcomes of \(Y\) in the positive direction (the lower the more) and conversely for higher outcomes (the higher the less). In recent empirical applications, coherent distortion risk measures other than expected shortfall have been used by several authors; see, e.g., Adam et al. (2008) for a comparison of various such measures in portfolio choice.

An equivalent characterization of a distortion risk measure is that it is a law-invariant and comonotonic risk measure; see Kusuoka (2011). \(\rho \) is comonotonic if

$$\begin{aligned} \rho (Y+Z) = \rho (Y) + \rho (Z) \;\; \text {for all } Y \hbox { and Z that are comonotonic }, \end{aligned}$$

i.e., that satisfy \(\big (Y(\omega ) - Y(\omega ^\prime )\big )\big (Z(\omega )-Z(\omega ^\prime )\big ) \ge 0\) for every \(\omega , \omega ^{\prime }\in \Omega \). If \(Y\) has an empirical distribution on \(y_1,\dots , y_n\in \mathbb {R}\), the definition (8) of a distortion risk measure specializes to

$$\begin{aligned} \rho (Y) = -\sum _{i=1}^{n}{q_i y_{[i]}}, \end{aligned}$$
(9)

where \(y_{[i]}\) are the values ordered from above and \(q_i\) are nonnegative weights adding up to \(1\). (Observe that \(q_i= r(y_{[\frac{n+1-i}{n}]})-r(y_{[\frac{n-i}{n}]})\).) Then, the distortion risk measure (9) is coherent if and only if the weights are ordered, i.e., \({\mathbf q}\in \Delta ^n_{\le }:= \{{\mathbf q}\in \Delta ^n \,:\, 0\le q_1\le \dots \le q_n\}\).

2.2 Weighted-mean regions as uncertainty sets

If \(\rho \) is a coherent distortion risk measure, the uncertainty set \(\mathcal{U}_\rho \) has a special geometric structure, which will be explored now to visualize the optimization problem and to provide the basis for an algorithm. We will demonstrate that \(\mathcal{U}_\rho \) equals a so-called weighted-mean trimmed region (or, equivalently, WM region) of the distribution of \(\tilde{\mathbf a}\).

Given the probability distribution \(F_Y\) of a random vector \(Y\) in \(\mathbb {R}^d\), WM regions form a nested family of convex compact sets, \(\{D_\alpha (F_Y)\}_{\alpha \in [0,1]}\), which are affine equivariant (that is \(D_\alpha (F_{AY+b})= A\,D_\alpha (F_Y) + b\) for any regular matrix \(A\) and \(b\in \mathbb {R}^d\)). By this, the regions describe the distribution with respect to its location, dispersion and shape. Weighted-mean trimmed regions have been introduced in Dyckerhoff and Mosler (2011) for empirical distributions, and in Dyckerhoff and Mosler (2012) for general ones.

For an empirical distribution on \({\mathbf a}^1, \dots , {\mathbf a}^n\in \mathbb {R}^d\), a weighted-mean trimmed region is a polytope in \(\mathbb {R}^d\) and defined as

$$\begin{aligned} D_{{\mathbf w}_\alpha }({\mathbf a}^1,\dots ,{\mathbf a}^n)={{\mathrm{\,conv}}}\left\{ \sum _{j=1}^n w_{\alpha , j}{\mathbf a}^{\pi (j)}\,:\, \pi \text { permutation of } \{1,\dots ,n\}\,\right\} . \end{aligned}$$
(10)

Here, \({\mathbf w}_\alpha =[w_{\alpha ,1}, \dots , w_{\alpha ,n}]'\) is a vector of ordered weights, i.e., \({\mathbf w}_\alpha \in \Delta ^n_\le \), indexed by \(0\le \alpha \le 1\) that satisfies the implication: if \(\alpha < \beta \), then

$$\begin{aligned} \sum _{j=1}^kw_{\alpha ,j}\le \sum _{j=1}^kw_{\beta ,j}\,,\quad \forall k=1,\dots ,n. \end{aligned}$$
(11)

Any such family of weight vectors \(\{{\mathbf w}_\alpha \}_{0\le \alpha \le 1}\) specifies a particular notion of weighted-mean trimmed regions. There are many types of weighted-mean trimmed regions. They contain well-known trimmed regions like the zonoid regions, the expected convex hull regions and several others. For example,

$$\begin{aligned} w_{\alpha ,j}=\left\{ \begin{array}{l@{\quad }l} \frac{1}{n\alpha }\,&{} \text {if } j>n-\lfloor n\alpha \rfloor ,\\ \frac{n\alpha -\lfloor n\alpha \rfloor }{n\alpha }\,&{}\text {if } j=n-\lfloor n\alpha \rfloor ,\\ 0\,&{}\text {if } j<n-\lfloor n\alpha \rfloor , \end{array}\right. \end{aligned}$$

\(0\le \alpha \le 1\) defines the zonoid regions. However, some popular types of trimmed regions, such as Mahalanobis or halfspace regions, are no weighted-mean trimmed regions.

Now, we are ready to formulate the key theoretical result of this section, which formalizes the relation between coherent distortion risk measures and their uncertainty sets on one side, and weighted-mean trimmed regions on the other side. This is stated in the following Theorem 1, which is proved in the Appendix. Also in the Appendix, the geometrical properties of WM regions leading to such a relation are considered.

Theorem 1

If \({\tilde{{\mathbf a}}}\) has an empirical distribution on \({\mathbf a}^1,\dots ,{\mathbf a}^n\) and \(\rho \) is a coherent distortion risk measure, then it holds that:

$$\begin{aligned} \{{\mathbf x}\in \mathbb {R}^d\,:\, \rho ({\tilde{{\mathbf a}}}^{\prime } {\mathbf x}-b)\le 0\} =\{ {\mathbf x}\in \mathbb {R}^d\,:\, {{\mathbf a}}^{\prime } {\mathbf x}\ge b \forall {\mathbf a}\in D_{{\mathbf w}_\alpha }({\mathbf a}^1,\dots ,{\mathbf a}^n) \}.\quad \quad \end{aligned}$$
(12)

The reader can see that, loosely speaking, Theorem 1 provides a transition from a well-interpreted but hardly manageable risk constraint to an equivalent well-manageable constraint regarding a trimmed region that can be determined by a geometrical algorithm. In fact, note that \(D_{{\mathbf w}_\alpha }({\mathbf a}^1,\dots , {\mathbf a}^n)\) is a \(d\)-dimensional convex polytope, and thus the convex hull of a finite number of points (its vertices) or, equivalently, a bounded nonempty intersection of a finite number of closed halfspaces (that contain its facets). By this the calculation and representation of such a polytope can be done in two ways: either by its vertices or by its facets. A polytope’s boundary includes a finite number of faces having different affine dimensions. Recall that a nonempty intersection of the boundary with a hyperplane is a facet if it has an affine dimension \(d-1\), and a ridge if it has an affine dimension \(d-2\). It is called an edge if it is a line segment, and a vertex if it is a single point. In general, each facet of a polytope in \(\mathbb {R}^d\) is itself a polytope of dimension \(d-1\) and has at least \(d\) vertices. With WM regions the number of a facet’s vertices can vary considerably; it ranges between \(d\) and \(d!\) (Bazovkin and Mosler 2012a). That is why in calculating WM regions a representation by facets is preferable. In the following Sect. 3 we consider the topic in detail.

3 Solving the SLP with distortion risk constraint

3.1 Calculating the uncertainty set

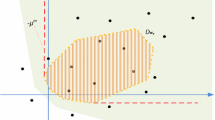
In the previous section we have shown that the uncertainty set \(\mathcal{U}_\rho \) equals the weighted-mean trimmed region \(D_{{\mathbf w}_\alpha }\) for a properly chosen weight vector \({\mathbf w}_\alpha \). Bazovkin and Mosler (2012a) provide an algorithm by which this WM region can be exactly calculated in any dimension \(d\). The results can be visualized in dimensions two and three; for examples, see Fig. 1.

Fig. 1
figure 1

Visualization of WM regions by the R package WMTregions. Left panel facets of a three-dimensional region in \(\mathbb {R}^3\). Right panel vertices of a four-dimensional region projected on a subspace of \(\mathbb {R}^3\)

Full size image

It has been already mentioned that the number of vertices of a facet can be as much as \(d!\). Therefore, the representation of a WM region by its vertices appears to be less efficient than that by its facets. In the sequel, we will use the facet representation for solving the SLP.

3.2 The robust linear program

Using the result of Theorem 1, we can write the robust linear program (1) with distortion risk constraint (5) as

$$\begin{aligned} {\mathbf c}^\prime {\mathbf x}\longrightarrow \min \quad \hbox {s.t.} \ {\mathbf a}'{\mathbf x}\ge b\;\; \text {for all } {\mathbf a}\in \mathcal{U}\,, \end{aligned}$$
(13)

where the subscript \(\rho \) has been dropped for convenience. In simple words, we get a deterministic linear program with a set of constraints whose coefficients are contained in a set \(\mathcal U\) that is, according to Theorem 1, a weighted-mean trimmed region. The restriction in (13) is then rewritten as

$$\begin{aligned} {\mathbf x}\in \mathcal{X}= \bigcap _{{\mathbf a}\in \mathcal{U}} X_{\mathbf a}\,, \quad X_{\mathbf a}= \{{\mathbf x}:{\mathbf a}' {\mathbf x}\ge b\}. \end{aligned}$$
(14)

Note that \(\mathcal{X}\), as an intersection of a finite number of halfspaces, is a convex polyhedron. Therefore, a linear goal function is to be minimized on a convex polyhedron. Obviously, any optimal solution will lie on the boundary of \(\mathcal{X}\).

3.3 Finding the optimum on the uncertainty set

In constructing an algorithm for the robust linear program, we explore the set \(\mathcal{X}\) of feasible solutions and relate it to the uncertainty set \(\mathcal{U}\) in the parameter space. It is shown that the space of solutions \({\mathbf x}\) and the space of coefficients \({\mathbf a}\) are, in some sense, dual to each other. The following two lemmas provide the connection between \(\mathcal{X}\) and \(\mathcal{U}\). First, we demonstrate that \(\mathcal{X}\) is the intersection of those halfspaces whose normals are extreme points of \(\mathcal{U}\).

Lemma 1

It holds that

$$\begin{aligned} \mathcal{X} = \bigcap _{{\mathbf a}\in \mathcal{U}}\{{\mathbf x}\,:\, {\mathbf a}' {\mathbf x}\ge b\} = \bigcap _{{\mathbf a}\in {{{\mathrm{\,ext}}}\mathcal{U}}}\{{\mathbf x}\,:\, {\mathbf a}' {\mathbf x}\ge b\}. \end{aligned}$$

Proof

We show that \(\bigcap _{{\mathbf a}\in {{{\mathrm{\,ext}}}\mathcal{U}}}{X_{\mathbf a}} \subset X_{{\mathbf u}}\) for all \({{\mathbf u}}\in \mathcal{U}\); then \(\bigcap _{{\mathbf a}\in {{{\mathrm{\,ext}}}\mathcal{U}}}{X_{\mathbf a}} \subset \bigcap _{{\mathbf a}\in \mathcal{U}}{X_{\mathbf a}}.\) The opposite inclusion is obvious. Assume \({{\mathbf u}}\in \mathcal{U}\). Then, as \(\mathcal{U}\) is convex and compact, \({{\mathbf u}}\) is a convex combination of some points \({\mathbf a}^1,\dots , {\mathbf a}^\ell \in {{{\mathrm{\,ext}}}\mathcal{U}}\), i.e., \({\mathbf u}=\sum _{i=1}^\ell \lambda _i {\mathbf a}^i\) with \(\lambda _i\ge 0\) and \(\sum _{i=1}^\ell \lambda _i=1\), and for any \({\mathbf x}\in \bigcap _{{\mathbf a}\in {{{\mathrm{\,ext}}}\mathcal{U}}}{X_{\mathbf a}}\) holds as \({\mathbf x}\in X_{{\mathbf a}^j}\) and \({{\mathbf a}^j}'{\mathbf x}\ge b\) for all \(j\); hence, \({{\mathbf u}}'{\mathbf x}=\sum _{i=1}^\ell \lambda _i {{\mathbf a}^i}'{\mathbf x}\ge b\), that is, \({\mathbf x}\in X_{{\mathbf u}}\). \(\square \)

Lemma 1 says that each facet of the set \(\mathcal{X}\) of feasible solutions corresponds to a vertex of the uncertainty set \(\mathcal{U}\). Hence, it is sufficient to consider the extreme points of the uncertainty set.

As a generalization of Lemma 1, we may prove by recursion on \(k\): each \(k\)-dimensional face of the feasible set corresponds to a \((d-k)\)-dimensional face of the uncertainty set in the solution space. This resembles the dual correspondence between convex sets and their polars (cf. Rockafellar 1997). However, in contrast to polars, this correspondence of facets is not reflexive.

From Lemma 1, it is immediately seen how the robust optimization problem contrasts with a deterministic problem, where the empirical distribution of \(\tilde{\mathbf a}\) concentrates at some \({\mathbf a}^0\in \mathcal{U}\). Observe that the deterministic feasible set \(\mathcal{X}\) is just a halfspace, \(\mathcal{X}_{{\mathbf a}^0}=\{{\mathbf x}\,:\,{{\mathbf x}'{\mathbf a}^0}\ge b\}\). In the general robust case, a halfspace is obtained for each \({\mathbf a}\in {{\mathrm{\,ext}}}\mathcal{U}\), and the robust feasible set \(\mathcal{X}\) is their intersection. The halfspaces are bounded by hyperplanes with normals equal to \({\mathbf a}\in {{\mathrm{\,ext}}}\mathcal{U}\), and their intercepts are all the same and equal to \(b\). Consequently, the robust feasible set \(\mathcal{X}\) is always included in the deterministic feasible set \(\mathcal{X}_{{\mathbf a}^0}\),

$$\begin{aligned} \mathcal{X} \subseteq \mathcal{X}_{{\mathbf a}^0} \quad \text {for any}\;\; {{\mathbf a}^0} \in \mathcal{U}. \end{aligned}$$

Moreover, the two feasible sets cannot be equal unless each element of \(\mathcal{U}\) is a scalar multiple of \({{\mathbf a}^0}\) with a factor greater than one, \(\mathcal{U} \subseteq \{{\mathbf a}\,:\,{\mathbf a}= \lambda {{\mathbf a}^0}, \lambda >1\}\). Consequently, the minimum value of the robust stochastic LP cannot be smaller than the value of an LP with any deterministic parameter \({{\mathbf a}^0}\) chosen from the uncertainty set. Fig. 2 (left panel) illustrates how a deterministic feasible set in dimension two compares to a general robust one: the line that bounds the halfspace \(\mathcal{X}_{{\mathbf a}^0}\) ‘folds’ into a piecewise linear curve delimiting \(\mathcal{X}\). In turn, Fig. 2 (right panel) demonstrates the same relation between the uncertainty sets in the parameter space: the deterministic uncertainty set, which is a singleton \({{\mathbf a}^0}\), ‘enlarges’ into a nondegenerate uncertainty set containing \({{\mathbf a}^0}\).

Fig. 2
figure 2

Deterministic and robust cases: feasible set (left panel), uncertainty set (right panel)

Full size image

Let

$$\begin{aligned} {U_{\mathbf x}} = \{{\mathbf a}\in \mathbb {R}^d: {\mathbf a}'{\mathbf x}\ge b\}\,, \quad {\mathbf x}\in \mathbb {R}^d. \end{aligned}$$

Lemma 2

It holds that

$$\begin{aligned} \mathcal{U} \subset \bigcap _{{\mathbf x}\in \mathcal{X}}{U_{\mathbf x}} \subset \bigcap _{{\mathbf x}\in {{\mathrm{\,ext}}}\mathcal{X}}{U_{\mathbf x}}. \end{aligned}$$

Moreover, each vertex \({\mathbf x}\in {{\mathrm{\,ext}}}\mathcal{X}\) corresponds to a facet of \(\mathcal{U}\).

Proof

By Lemma 1, we have \({\mathbf x}\in \mathcal{X} \quad \Leftrightarrow \quad {\mathbf a}'{\mathbf x}\ge b\) for all \({\mathbf a}\in \mathcal{U}\). Now, let \({\mathbf a}\in \mathcal{U}\); then for any \({\mathbf x}\in \mathcal{X}\) it holds that \({\mathbf a}'{\mathbf x}\ge b\); hence, \({\mathbf a}\in U_{\mathbf x}\). Conclude \(\mathcal{U} \subset \bigcap _{{\mathbf x}\in \mathcal{X}}{U_{\mathbf x}}\). Further, it is clear that an extreme point \({\mathbf x}\in {{\mathrm{\,ext}}}\mathcal{X}\) yields a facet of \(\mathcal{U}\). \(\square \)

Remark. While \(\mathcal{U}\) is always compact, \(\mathcal{X}\) is in general not. Therefore, neither inclusion holds with equality.

According to Lemma 1, we could now reformulate the robust LP (13), basing it on the constraints generated by the vertices of \(\mathcal U\):

$$\begin{aligned} {\mathbf c}^\prime {\mathbf x}\longrightarrow \min \quad \hbox {s.t.} \ {\mathbf a}'{\mathbf x}\ge b\;\; \text {for all } {\mathbf a}\in {{\mathrm{\,ext}}}\mathcal{U}\,, \end{aligned}$$

and then apply the ordinary simplex method to it. However, usually WM regions have a very large number of vertices, because even a single facet can have up to \(d!\) ones. Bazovkin and Mosler (2012a) have shown this number to lie between \(\mathcal{O}(n^d)\) and \(\mathcal{O}(\frac{n^{2d}}{2^d})\) depending on the type of the WM region. This obviously makes the basic straightforward approach almost inapplicable here. On the other side, WM regions can be efficiently determined by their facets. In our algorithm, we pursue still another way to find the optimal solution, namely searching it even without explicit construction of \(\mathcal X\) and taking advantage of the facet representation of \(\mathcal U\).

To manage this task let us consider the goal function \({\mathbf c}'{\mathbf x}\). In the solution space the optimization vector \({\mathbf c}\) defines a direction, which can be also determined by a set of hyperplanes orthogonal to this direction. Clearly, all these hyperplanes are parallel and their normals are some multiples of \({\mathbf c}\). For example, in dimension two for \({\mathbf c}=(2.1,1.4)'\) and \(b=5,\) the hyperplanes \(\{{\mathbf x}:(2.1,1.4)'\cdot {\mathbf x}=5\}\) and \(\{{\mathbf x}:(4.2,2.8)'\cdot {\mathbf x}=5\}\) belong to the set. Recall that we have fixed the intercept of all hyperplanes in the solution space at some \(b\), and thus can distinguish them by their normals only. In the parameter space, each of these hyperplane corresponds to the point \({\mathbf c}\) multiplied with a proper scaling factor. Hence, the image of all the hyperplanes in the parameter space is obtained by moving a point along a straight ray \(\varphi \) that starts at the origin and contains \({\mathbf c}\), as shown on Fig. 3.

Fig. 3
figure 3

Duality between spaces

Full size image

One of the hyperplanes touches \(\mathcal X\) at the optimum. All others either intersect the interior of \(\mathcal X\) or do not intersect it at all. This means that the touching hyperplane corresponds to a point lying on the surface of \(\mathcal U\). Therefore, we have to search the intersection of \(\mathcal{U}\) with the ray \(\varphi \). Then, because of Lemma 2, the intersected facet of \(\mathcal{U}\) corresponds to the optimal vertex of \(\mathcal X\).

Note that finding the intersection of a line and a polyhedron in \(\mathbb {R}^3\) is an important problem in computer graphics (cf. Kay and Kajiya 1986). The same principle is employed for a general dimension \(d\). The uncertainty set \(\mathcal{U}\) is the finite intersection of halfspaces \(\mathcal{H}_j\), \(j=1\dots J\), each being defined by a hyperplane \(H_j\) with normal \({\mathbf n}_j\) pointing into \(\mathcal{H}_j\) and intercept \(d_j\).

Consider some point \({\mathbf u}\) on the ray \(\varphi \) that is not in \(\mathcal{U}\). Compute \(\frac{d_j}{{\mathbf u}'{\mathbf n}_j}\) for all halfspaces \(\mathcal{H}_j\) that do not include \({\mathbf u}\), i.e., where \(({\mathbf u}'{\mathbf n}_j - d_j)< 0\) holds. (In other words, \(H_j\) is visible from \({\mathbf u}\).) Find \(j_*\) at which this value is the largest. Recall that moving a point \({\mathbf u}\) along \(\varphi \) is equivalent to multiplying \({\mathbf u}\) by some constant. The farthest move is given by the largest constant. The optimal solution \({\mathbf x}^*\) of the robust SLP has to satisfy \({\mathbf a}'{\mathbf x}^*\ge b\), which is equivalent to

$$\begin{aligned} {\mathbf a}'\left( \frac{d_{j_*}}{b} {\mathbf x}^*\right) \ge d_{j_*}. \end{aligned}$$

Hence, to obtain \({\mathbf x}^*\), the normal \({\mathbf n}_{j_*}\) has to be scaled with the constant \(\frac{b}{d_{j_*}}\),

$$\begin{aligned} {\mathbf x}^* = \frac{b}{d_{j_*}} {\mathbf n}_{j_*}. \end{aligned}$$
(15)

Besides the regular situation described above, two special cases can arise:

  1. 1.

    There is no facet visible from the origin. This means that no solution is obtained.

  2. 2.

    \(\varphi \) does not intersect \(\mathcal U\). Then the whole procedure is repeated with the opposite ray \(- \varphi \). If this still gives no intersection, an infinite solution exists.

Finally, we should point out that not the whole polytope \(\mathcal{U}\) needs to be calculated, but only that part of it that intersects the ray \(\varphi \). In searching for the optimum, not all \(F\) facets need to be checked, but only a subset of the surface where the intersection will happen. Such a filtration makes the procedure more efficient. Next, we show how to select this subset.

Let \({\mathbf x}^*\) be an optimal solution of the robust SLP. A subset \(\mathcal{U}_\text {eff}\) of \(\mathcal{U}\) will be mentioned as an efficient parameter set if

  • \({\mathbf x}^*\) remains the solution for \(\bigcap _{{\mathbf a}\in \mathcal{U}_\text {eff}}\{{\mathbf x}: {\mathbf a}' {\mathbf x}\ge b\ \} \supset \mathcal{X} \quad \text {and}\)

  • \({\mathbf a}, {\mathbf d}\in \mathcal{U}_{\text {eff}}, \ {\mathbf a}'{\mathbf x}\ge b\Rightarrow {\mathbf d}'{\mathbf x}\ge b,\ \forall {\mathbf x}\quad \text {implies} \quad {\mathbf a}={\mathbf d}.\)

That is to say, \(\mathcal{U}_\text {eff}\) is the minimal subset of \(\mathcal U\) containing all facets that can be optimal for some \({\mathbf c}\).

Proposition 1

\(\mathcal{U}_\text {eff}\) is the union of all facets of   \(\mathcal U\) for which \(d_j\ge 0\) holds.

In other words, an efficient parameter set \(\mathcal{U}_\text {eff}\) consists of that part of the surface of \(\mathcal U\) that is visible from the origin \(\mathbf 0\). The proof is obvious.

To visualize the efficient parameter set we use the augmented uncertainty set, which is defined as

$$\begin{aligned} \{{\mathbf a}: {\mathbf a}= \lambda {\mathbf a}^*, \lambda >1,{\mathbf a}^*\in \mathcal{U}_\text {eff}\}. \end{aligned}$$

It includes all parameters that are dominated by \(\mathcal{U}_\text {eff}\); see the shaded area in the right panel of Fig. 4.

Fig. 4
figure 4

Finding the optimal solution on the uncertainty set

Full size image

So far, we have assumed that \(b>0\). It is easy to show that with \(b<0\) we have to construct the intersection of \(\varphi \) with the part of the surface of \(\mathcal U\) that is invisible from the origin \(\mathbf 0\), which is \(\tilde{\mathcal{U}}_\text {eff}\) in this case. In the sense of Proposition 1, \(\tilde{\mathcal{U}}_\text {eff}\) contains all facets of \(\mathcal U\) with \(d_j\le 0\). Obviously, \(\tilde{\mathcal{U}}_\text {eff}\) is always nonempty in this case, which, in turn, means that the existence of a solution is guaranteed. However, the solution can be infinite if \(\varphi \) does not intersect \(\tilde{\mathcal{U}}_\text {eff}\).

By the same approach, a robust linear program of maximum type can be solved. Note that

$$\begin{aligned} {\mathbf c}^\prime {\mathbf x}\longrightarrow \max \quad \hbox {s.t.}. \ {\mathbf a}'{\mathbf x}\le b\;\; \text {for all } {\mathbf a}\in \mathcal{U}\,, \end{aligned}$$
(16)

can be rewritten as

$$\begin{aligned} (-{\mathbf c})^\prime {\mathbf x}\longrightarrow \min \quad \hbox {s.t.} \ (-{\mathbf a})'{\mathbf x}\ge -b\;\; \text {for all } {\mathbf a}\in \mathcal{U}. \end{aligned}$$
(17)

Clearly, (17) is equivalent to (13).

4 The algorithm

In this section, the algorithmic procedure for obtaining an optimal solution to (13) is given in detail.

Input:

  • a vector \({\mathbf c}\in \mathbb {R}^d\) of coefficients of the goal function,

  • \(n\) observations \(\{{\mathbf a}^1,\dots ,{\mathbf a}^n\}\subset \mathbb {R}^d\) of coefficient vectors of the restriction,

  • a right-hand side \(b\in \mathbb {R}\) of the restriction,

  • a distortion risk measure \(\rho \) (defined either by name or by a weight vector).

Output:

  • the uncertainty set \(\mathcal{U}\) of parameters given by

    • facets (i.e., normals and intercepts),

    • vertices,

  • the optimal solution \({\mathbf x}^*\) of the robust LP and its value \({\mathbf c}'{\mathbf x}^*\).

Steps:

  1. A.

    Calculate the subset \(\mathcal{U}_\text {eff}\subset \mathcal{U}\) consisting of facets \(\{({\mathbf n}_j,d_j)\}_{j\in J}\).

  2. B.

    Create a line \(\varphi \) passing through the origin \(\mathbf 0\) and \({\mathbf c}\).

  3. C.

    Search for a facet \(H_{j_*}\) of \(\mathcal{U}_\text {eff}\) that is intersected by \(\varphi \):

    1. a.

      Select a subset \(\mathcal{U}_{sel}\subseteq \mathcal{U}_\text {eff}\) of facets. This may be either \(\mathcal{U}_\text {eff}\) itself or its part where the intersection is expected; \(\mathcal{U}_{sel}=\{ ({\mathbf n}_j,d_j)\,:\,j\in J_{sel}\}\). For example, we can search for the best solution on a pre-given subset of parameters. Another possible filtration consists in iterative transitions to facets having better criterion values.

    2. b.

      Take a point \({\mathbf u}=\lambda {\mathbf c}, \lambda \ge 0\), outside the augmented uncertainty set. Find the \(j_* = \arg \underset{j}{\max }\{\lambda _j=\frac{d_j}{{\mathbf u}'{\mathbf n}_j}:\lambda _j>0\}_{j\in J_{sel}\subseteq J}\). For the case \(b<0,\) just replace \(\arg {\max }\) with \(\arg {\min }\).

      1. I.

        If \(\varphi \) does not intersect \(\mathcal{U}_\text {eff}\), then the solution is infinite. If \(b>0\), then repeat C.b. with the opposite ray \(-\varphi \); else stop.

      2. II.

        If in the case \(b>0\) the inner part of \(\mathcal U\) contains the origin, then no solution exists; stop.

    3. c.

      \({\mathbf x}^* = \frac{b}{d_{j_*}} {\mathbf n}_{j_*}\) is the optimal solution of the robust LP.

In fact, the line \(\varphi \) consists of points that correspond to hyperplanes whose normal is the vector \({\mathbf c}\) in the dual space. One part of \(\varphi \) is dominated by points from \(\mathcal{U}_\text {eff}\), while the other is not (which results from Proposition 1). The crossing point \({\mathbf a}^*\) defines the hyperplane that touches the feasible set at the optimum as its dual.

Moreover, a typical nonnegativity side constraint \({\mathbf x}\ge \mathbf{0}\) can easily be accounted for in the algorithm. In considering this, the search for facets has just to be restricted to those having nonnegative normals.

To solve the portfolio selection problem (6) with the algorithm, we treat the realizations of the vector \(-\tilde{\mathbf r}\) of losses rates as \(\{{\mathbf a}^1,\dots ,{\mathbf a}^n\}\), and minimize \({\mathbf c}' {\mathbf x}\) with \({\mathbf c}= \frac{1}{n}\sum _{i=1}^{n}{{\mathbf a}^i}\). This corresponds to transforming the maximizing SLP by (17) and running the procedure outlined above. Note that both \(\varphi \) and \(\mathcal U\) contain the point \(\frac{1}{n}\sum _{i=1}^{n}{{\mathbf a}^i}\), that is, they always intersect, which, in turn, guarantees the existence of a finite solution. To meet a unit budget constraint, the solution \({\mathbf x}^*\) is finally scaled down to \(\sum _{j=1}^d x^*_j=1\). Recall that the risk measure is, by definition, scale equivariant.

4.1 Sensitivity and complexity issues

Next, we discuss how the robust SLP and its optimal solution behave when the data \(\{{\mathbf a}^1,\dots ,{\mathbf a}^n\}\) on the coefficients are slightly changed. From (18) it is immediately seen that the support function \(h_\mathcal{U}\) of the uncertainty set is continuous in the data \({\mathbf a}^j\) as well as in the weight vector \({\mathbf w}_\alpha \). (Note that the support function \(h_\mathcal{U}\) is even uniformly continuous in \({\mathbf a}^1,\dots ,{\mathbf a}^n\) and \({\mathbf w}_\alpha \), which is tantamount to saying that the uncertainty set \(\mathcal{U}\) is Hausdorff continuous in the data and the risk weights.) Consequently, a slight perturbation of the data will only slightly change the value of the support function of \(\mathcal{U}\), which is a practically useful result regarding the sensitivity of the uncertainty set with respect to the data. The same is true for a small change in the weights of the risk measure.

We conclude that the point \({\mathbf a}^{j_*}\) where the line through the origin and \({\mathbf c}\) cuts \(\mathcal{U}\) depends continuously on the data and the weights. However this is not true for the optimal solution \({\mathbf x}^*\), which may ‘jump’ when the cutting point moves from one facet of \(\mathcal{U}\) to a neighboring one.

The theoretical complexity in time of finding the solution is compounded from the complexity of one transition to the next facet and by the whole number of such transitions until the sought-for facet is achieved. Bazovkin and Mosler (2012a) have shown that the transition has a complexity of \(\mathcal{O}(d^2n)\). In turn, in the same paper the number of facets \(N(n,d)\) of a WM region is shown to lie between \(\mathcal{O}(n^d)\) and \(\mathcal{O}(n^{2d})\) depending on the type of the WM region. Thus, it is easily seen that an average number of facets in a facets chain of a fixed length is defined by the density of facets on the region’s surface, \(\root d \of {N(n,d)}\), and is estimated by a function between \(\mathcal{O}(n)\) and \(\mathcal{O}(n^2)\). The overall complexity is then \(\mathcal{O}(d^2n^2)\) up to \(\mathcal{O}(d^2n^3)\). Notice that the lower complexity is achieved for zonoid regions, namely when the expected shortfall is used for the risk measure.

4.2 Ordered sensitivity analysis

Alternative uncertainty sets that are ordered by inclusion can be also compared. From Lemma 1 it is clear that the respective sets of feasible solutions are then ordered in the reverse direction; see, e.g., Fig. 5. In particular, we can consider the robust LP for two alternative distortion risk measures based on weight vectors \({\mathbf w}_\alpha \) and \({\mathbf w}_\beta \), respectively, that satisfy the monotonicity restriction (11). Then the resulting uncertainty sets are nested, \(\mathcal{U}_\beta \subset \mathcal{U}_\alpha ,\) and so are, conversely, the feasible sets, \(\mathcal{X}_\beta \supset \mathcal{X}_\alpha \). This is a useful approach for visualizing the sensitivity of the robust LP against changes in risk evaluation.

Fig. 5
figure 5

Example of the ‘reversed’ central regions in the dimension 2

Full size image

5 Robust SLP for generally distributed coefficients

So far, an SLP (1) has been considered where the coefficient vector \(\tilde{\mathbf a}\) follows an empirical distribution. It has been solved on the basis of \(n\) observations \(\{{\mathbf a}^1,\dots ,{\mathbf a}^n\}\). In this section the SLP is addressed with a general probability distribution \(P\) of \(\tilde{\mathbf a}\). We formulate the robust SLP in the general case and demonstrate that the solution of this SLP can be consistently estimated by random sampling from \(P\).

Consider a distortion risk measure \(\rho \) (8) that measures the risk of a general random variable \(Y\) and has weight generating function \(r\), \(\rho (Y)= - \int _0^1 Q_{Y}(t) dr(t)\). As in Sect. 2.2, a convex compact \(\mathcal U\) in \(\mathbb {R}^d\) is constructed through its support function \(h_\mathcal{U}\),

$$\begin{aligned} h_\mathcal{U}({\mathbf p}) = \int _0^1 Q_{{\mathbf p}'\tilde{\mathbf a}}(t)\,\hbox {d}r(t). \end{aligned}$$

Now, let a sequence \((\tilde{\mathbf a}^n)_{n\in \mathbb {N}}\) of independent random vectors be given that are identically distributed with \(P\), and consider the sequence of random uncertainty sets \(\mathcal{U}_n\) based on \(\tilde{\mathbf a}^1, \dots , \tilde{\mathbf a}^n\). Dyckerhoff and Mosler (2011) have shown:

Proposition 2

(Dyckerhoff and Mosler 2011) \(\mathcal{U}_n\) converges to \(\mathcal{U}\) almost surely in the Hausdorff sense.

The proposition implies that by drawing an independent sample of \(\tilde{\mathbf a}\) and solving the robust LP based on the observed empirical distribution, a consistent estimate of the uncertainty set \(\mathcal{U}\) is obtained. Moreover, the cutting point \({\mathbf a}^{j_*}\), where the line through the origin and \({\mathbf c}\) hits the uncertainty set, is consistently estimated by our algorithm. If an ambiguous solution is possible, in particular for a discretely distributed \(\tilde{\mathbf a}\), the algorithm calculates one of the available solutions consistently. In fact, the optimal solution \({\mathbf x}^*\) may perform a jump when \({\mathbf a}^{j_*}\) moves from one facet of \(\mathcal{U}\) to a neighboring one; however the algorithm for determining \({\mathbf x}^*\) selects always a unique facet containing \({\mathbf a}^{j_*}\).

6 Concluding remarks

A stochastic linear program (SLP) has been investigated, where the coefficients of the linear restrictions are random. Distortion risk constraints are imposed on the random restrictions and an equivalent robust SLP is modeled, whose worst-case solution is searched over an uncertainty set of coefficients. If the risk is measured by a general coherent distortion risk measure, the uncertainty set of a restriction has been shown to be a weighted-mean trimmed region. This provides a comprehensive visual and computable characterization of the uncertainty set. An algorithm has been developed that solves the robust SLP under a single stochastic constraint, given a set of observations. It is available as an R-package StochaTR (Bazovkin and Mosler 2012b). Moreover, when the data are generated by an infinite i.i.d. sample, the limit behavior of the solution was investigated. The algorithm allows the introduction of additional deterministic constraints, in particular, those regarding nonnegativity.

Table 1 reports simulated running times (in seconds) of the R-package for the 5 %-level expected shortfall and different \(d\) and \(n\). The data are simulated by mixing the uniform distribution on a \(d\)-dimensional parallelogram with a multivariate Gaussian distribution. In light of the table, the complexity seems to grow with \(d\) and \(n\) slower than \(\mathcal{O}(d^2n^2)\).

Table 1 Running times of StochaTR for different \(n\) and \(d\) (in seconds)
Full size table

Besides this, we contrast our new procedure with the seminal approach of Rockafellar and Uryasev (2000), who solve the portfolio problem by optimizing the expected shortfall with a simplex-based method. In illustrating their method, they simulate three-dimensional normal returns having specified expectations and covariance matrices. We have applied our package to likewise simulated data on a 1.73GHz single-core CPU with at most 1.5 gigabytes of memory available. The computational times are exhibited in Table 2. For a comparison, some cells also contain a second value that corresponds to the Rockafellar and Uryasev (2000) procedure and is taken from Table 5 there. Our algorithm usually needs some dozens of iterations only, which are substantially fewer than those of the algorithm of Rockafellar and Uryasev (2000). Also, in contrast to the latter, where the resulting portfolio can vary between \((0.42,0.13,0.45)\) for \(n=1{,}000\) and \((0.64,0.04,0.32)\) for \(n=5{,}000\), we get a stable optimal portfolio. Our solution averages at \((0.36,0.15,0.49)\), which has approximately the same \(\text {V@R}\) and expected shortfall as that in the compared study but yields a better value of the expected return. Note that the computational times reported in Rockafellar and Uryasev (2000) do not differ much from ours.

Table 2 Running times of StochaTR for different \(n\) and \(\alpha \) (in s); in parentheses running times of Rockafellar and Uryasev (2000)
Full size table

Finally, our approach turns out to be very flexible. In particular, nonsample information can be introduced into the procedure in an interactive way by explicitly changing and modifying the uncertainty set. More research is needed in extending the algorithm to solve SLPs with multiple constraints (2). Also, procedures that allow for a stochastic right-hand side in the constraints and random coefficients in the goal function are yet to be explored.