Introduction

Around the world, sustainability has become a focal point of many economic development strategies. Leading companies may even use sustainability as a means of gaining competitive advantage as the growing environmental awareness of customers is changing the marketplace, Mahadevan et al. (2003). From a production viewpoint sustainability covers many aspects of environmental production; green manufacturing, use of natural resources, recycling, material re-use and re-manufacturing. However, managing a reverse supply chain involves coping with many new uncertainties, especially those concerned with the quantity, quality and timing of the returned products, Seitz et al. (2003). In a number of recent papers many issues have been raised, such as how to design a product so that it is easy to be disassembled and reused (Kondo et al. 2003), or how to make decisions on product recovery (van der Laan and Saloman 1999; Teunter and Vlachos 2002), for example reselling, recovery, or disposal. The recovery option may also include repair, refurbishing, remanufacturing, cannibalization and recycling, Thierry et al. (1995).

Here we focus on investigating how a remanufacturing process affects traditional pipelines in terms of the variance of the serviceable inventory and the order rates (the bullwhip phenomena) to produce new products. We consider the scenario where “used” products are pushed through a remanufacturing process as soon as they are returned from the “customer” (or marketplace). There is a lead-time associated with the time to remanufacture a product and also a lead-time associated with the time that a product is “in use” by the customer. Because both these two lead-times are in the reverse loop and their impacts on the system dynamics performance are the same even though their scale is different (Tang and Naim 2004), for convenience, we will join these two lead-times together and called it T r , the Time to Remanufacture. We assume this remanufacturing lead-time is a stationary stochastic variable drawn from an exponential distribution. We use a first order exponential distribution to represent the delay in the remanufacturing process, as it is the simplest known way to represent a delay, Tang and Naim (2004). This has some mathematical advantages and according to Lin et al. (2005), Wang (2004) and Barron et al. (2004), it also represents the life-cycle of many physical components. For example, the process failure rate for mechanical components is often exponentially distributed. Later on we separate out the remanufacturing lead-time from the “in-use” lead-time to investigate the impact of this assumption.

Only a fraction, 0≤k≤1 of demand is returned from the marketplace, the rest we suppose is either unusable or is lost to a landfill as was also assumed by Muckstadt and Isaac (1981).

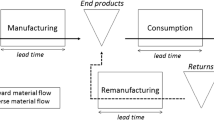
We also assume the remanufactured products are “as good as new” and thus form part of the serviceable stock. Serviceable stock is the finished goods from which customer demand is satisfied. In this study the terms net stock/inventory/serviceable stock are used interchangeably. The recoverable stock is not investigated here because our focus is how the remanufacturing process affects the conventional (forward) supply chain. We assume that the customer demand is a stationary, independently and identically distributed (i.i.d.) random process. Our analysis is independent of the actual distribution of the stochastic customer demand. That is, the demand distribution could be a normal, log normal, exponential or a gamma distribution for example. The manufacture of new products is controlled by a continuous time variant of the Order-Up-To policy known as the APIOBPCS model, Dejonckheere et al. (2003). Figure 1 illustrates the material flow in this manufacturing/remanufacturing supply chain. We note that this system is different to the push/pull system of van der Laan and Saloman (1999), even though their model inspired this investigation.

Fig. 1
figure 1

Material flow in a simple manufacturing/remanufacturing system

Full size image

Much of the literature on reverse logistics has addressed inventory management. Fleischmann et al. (1997) provides a review of quantitative models in reverse logistics. Guide (2000) identifies and describes seven complicating characteristics of production planning and control activities for remanufacturing firms; uncertainty in the timing and the quantity of returns, balancing returns with demands, disassembly, uncertainty in materials recovered, reverse logistics, materials matching requirements, routing uncertainty and processing time uncertainty. Guide (2000) claims these special features require significant changes in production planning and control activities. It is this research opportunity we explore here.

Inderfurth and van der Laan (2001) study a simple four-parameter control rule for an inventory model with remanufacturing. There the remanufacturing lead-time is treated as a decision variable to improve the performance of the policy. Kiesmüller and van der Laan (2001) investigate an inventory model with dependent product demands and returns. In this specific case they conclude that neglecting the dependency between demands and returns of products may increase total average costs. Fleischmann and Kuik (2003) investigate an independent stochastic item returns scenario. Kleber et al. (2002) provide a continuous time inventory model to decide when returns should be used and when returns should be kept in inventory and not be remanufactured or disposed of immediately. van der Laan (2003) analyze the economic consequences in a stochastic inventory system with both manufacturing and remanufacturing from an average cost and net present value viewpoint. Kiesmüller (2003) offers a new approach for a control problem with different lead-times for production and remanufacturing to decide the quantities and timing of manufacturing and remanufacturing respectively. However, almost all quantitative literature is based upon a specified cost function and few papers study dynamic performance. To the date, the only effort that we know of that has been made is by Tang and Naim (2004) and Zhou et al. (2005), in which a hybrid inventory system is studied by considering simple Push and Pull policies. However the analytical analysis of variance ratio issue (e.g. inventory variance and bullwhip) in their papers are left untouched. Our aim here is to contribute to this field by highlighting how the inventory variance and the bullwhip phenomenon are affected by the reverse logistics operations.

The inventory variance determines the stock levels required to meet a given target customer service level. The higher the variance of inventory levels, the more stock will be needed to maintain customer service at the target level, Dejonckheere et al. (2002). The bullwhip effect relates to the order we place to maintain the inventory levels. Both the inventory variance and bullwhip directly affect the economics of a scenario, Disney and Grubbström (2003). We will show that the inventory variance and bullwhip are conflicting phenomenon, that is, when inventory variance increases, the bullwhip often decreases. This leads to a trade-off analysis.

The methodology we use is control theory. Herbert Simon (1952), the Nobel Laureate for Economics in 1978, was the first to show that the production/inventory systems have the properties of a control system. This theory was further developed by Magee (1958) and Towill (1970, 1982a,b), and extended to a conventional supply chain by Wikner et al. (1991). Furthermore, Tang and Naim (2004) and Zhou et al. (2005) apply control theory to the study of a hybrid system with both manufacturing and remanufacturing. Table 1 summarizes the control theory approach by comparison with the Operational Research approach.

Table 1 Comparison of the operational research and control theory approach to supply-chain design (adapted from Towill et al. 2001)
Full size table

The rest of our paper is organized as follows. First, we give a formal definition of our model and derive the corresponding continuous time, Laplace domain transfer function of the remanufacturing supply chain. Section 3 presents a Åström’s method for deriving analytical expressions of the variance ratio. This method is powerful as it can be applied to very complex systems. Section 4 analyzes the variance of the serviceable stock levels.

We then compare the inventory variance performance of the remanufacturing supply chain with the performance of traditional supply chain and draw out some managerial implications. Section 5 addresses the bullwhip phenomena produced by the system. Again we also compare it with a traditional supply chain. Here we find that there is a trade-off to be made between the variance of serviceable stock and bullwhip. In Section 6, we study the trade-off between the variance of the serviceable stock levels and variance of the order rates for the production of new products. Section 7 investigates the impact of explicitly modeling the “in-use” lead-time and the remanufacturing lead-time as two separate lead-times. Section 8 concludes.

Model description

In our analysis we assume that time passes continuously and consequently we exploit the Laplace transform in our analysis. The manufacturers’ replenishment order is placed to produce new product based on a forecast of future demand, the serviceable inventory and the current work in progress at the original equipment factory. The ordering policy that we study here is based upon the APIOBPCS model. APIOBPCS is an acronym for Automatic Pipeline Inventory and Order Based Production Control System (John et al. 1994). The policy can be expressed as; “let the production targets be equal to the sum of forecasted demand, plus a fraction (1/T i ) of the inventory error, plus a fraction (1/T w ) of the WIP error”.

However, the remanufacturing scenario requires a slight modification to the classical APIOBPCS policy as shown in Fig. 2. In words the modified APIOBPCS model is “the order place is equal to the sum of forecasted demand plus a fraction of the discrepancy between the actual and target net stock of serviceable inventory plus a fraction of the discrepancy between the actual and target work-in-process”. Furthermore only a fraction (k) of the demand is returned, brought up to a “good as new” condition and added to the net stock of serviceable inventory after a random delay. This random delay is drawn from an exponential distribution with an average of T r time units. Recall that we are assuming the demand is a stationary i.i.d. stochastic process. This means the minimum mean squared error forecast of all future demands is given by the long-term expected value of demand, the mean.

Fig. 2
figure 2

Block diagram of our re-manufacturing system

Full size image

We may rearrange Fig. 2 using standard techniques (see Nise 1994 for an introduction) to obtain the net stock/inventory and order rate Laplace transfer functions,

$$\frac{{NS}}{D} = \frac{{T_{i} {\left( {k - 1 - sT_{r} } \right)}{\left( {T_{p} + T_{w} + sT_{p} T_{w} } \right)}}}{{{\left( {1 + sT_{r} } \right)}{\left( {T_{w} + sT_{i} {\left( {T_{p} + T_{w} + sT_{p} T_{w} } \right)}} \right)}}}$$
(1)
$$\frac{{OR}}{D} = \frac{{{\left( {1 + sT_{p} } \right)}{\left( {1 - k + sT_{r} } \right)}T_{w} }}{{{\left( {1 + sT_{r} } \right)}{\left( {T_{w} + sT_{i} {\left( {T_{p} + T_{w} + sT_{p} T_{w} } \right)}} \right)}}}$$
(2)

All of the constants in the system may be assumed to be larger than zero, so we have T i ≥0, T p ≥0, T w ≥0, and T r ≥0. Furthermore, 0≤k≤1.

Åström’s method of deriving the variance ratios

Disney and Towill (2003) have explored the relationship between “long-run” variance ratio measures and the system’s transfer function. We adopt their definition for variance amplification as

$$VarAmp = \frac{{\sigma ^{2}_{{output}} }}{{\sigma ^{2}_{{input}} }}$$
(3)

.

It can be shown that the integral of the square of the systems unit impulse response is equal to the variance of the systems output divided by the variance of the systems input when demand is stochastic (Newton et al. 1957, see Eq. (4)). We have sketched this mathematical proof in Appendix A for the reader. Here it is sufficient to present a realisation of the methodology to calculate the variance ratio.

$$VarAmp = \frac{{\sigma ^{2}_{{output}} }}{{\sigma ^{2}_{{input}} }} = I = {\int_0^\infty {{\left[ {L^{{ - 1}} {\left( {G{\left( s \right)}} \right)}} \right]}^{2} } }dt = {\int_0^\infty {{\left[ {g{\left( t \right)}} \right]}} }^{2} dt$$
(4)

where G(s) is the system’s transfer function and g(t) is the corresponding system impulse response in the time domain. It is derived from the inverse Laplace transform of G(s), i.e. g(t)=L −1(G(s)). As our system is linear time invariant, its Laplace transform is a rational expression. However the integral, I, is often difficult to obtain, thus we may exploit Parseval’s Relation as shown in Eq. (5) (Newton et al. 1957).

$$I = {\int_0^\infty {g^{2} {\left( t \right)}} }dt = \frac{1}{{2\pi j}}{\int_{ - j\infty }^{j\infty } {G{\left( { - s} \right)}G{\left( { - s} \right)}ds} }$$
(5)

. As G(s) is a rational function, it can be expressed as

$$G{\left( s \right)} = \frac{{B{\left( s \right)}}}{{A{\left( s \right)}}} = \frac{{b_{1} s^{{n - 1}} + \cdots + b_{{n - 1}} s + b_{n} }}{{a_{0} s^{n} + a_{1} s^{{n - 1}} + \cdots + a_{{n - 1}} s + a_{n} }} = \frac{{{\sum\limits_{i = 1}^n {b_{i} s^{{n - 1}} } }}}{{{\sum\limits_{i = 0}^n {a_{i} s^{{n - 1}} } }}}$$
(6)

, and the integral-square transform function will appear in the form

$$\frac{{\sigma ^{2}_{{output}} }}{{\sigma ^{2}_{{input}} }} = \frac{1}{{2\pi j}}{\int_{ - j\infty }^{j\infty } {\frac{{B{\left( s \right)}B{\left( { - s} \right)}}}{{A{\left( s \right)}A{\left( { - s} \right)}}}ds} }$$
(7)

. The integral (7) will always exist (but may not always be easy to obtain) if the zeros of the polynomial, A(s), do not have positive real components. Note that the polynomial B(s) must be at least one degree less than the polynomial A(s) in order to guarantee that the Laplace transform G(s) is rational. On the basis of Parseval’s theorem, Åström (1970) evaluated the integral I in terms of the coefficients appearing in the polynomials B(s) and A(s) appearing in (6).

We will now exploit Åström’s approach to solving the integral square of signals. We will focus on the application of the method and refer interested readers to Åström (1970) for the rigorous mathematical proof.

The first step of Åström’s method is to build two new polynomials, A m (s) and B m (s) with a lower order than n of A(s) in (6). This is done with

$$\begin{array}{*{20}l} {{A_{m} {\left( s \right)} = a^{m}_{0} s^{m} + a^{m}_{1} s^{{m - 1}} + \cdots + a^{m}_{m} \quad {\text{and}}} \hfill} \\ {{B_{m} {\left( s \right)} = b^{m}_{1} s^{{m - 1}} + b^{m}_{2} s^{{m - 2}} + \cdots + b^{m}_{m} } \hfill} \\ \end{array} $$

, which are defined recursively from the Eqs. (8) and (9),

$$a^{{m - 1}}_{i} = \left\{ {\begin{array}{*{20}l} {{a^{m}_{{i + 1}} } \hfill} & {{i\,even} \hfill} \\ {{a^{m}_{{i + 1}} - \alpha _{m} a^{m}_{{i + 2}} } \hfill} & {{i\,odd,\,and\,\alpha _{m} = a^{m}_{0} /a^{m}_{1} } \hfill} \\ \end{array} \,\forall i = 0, \cdots ,m - 1} \right.$$
(8)
$$b^{{m - 1}}_{i} = \left\{ {\begin{array}{*{20}l} {{b^{m}_{{i + 1}} } \hfill} & {{i\,odd} \hfill} \\ {{b^{m}_{{i + 1}} - \beta _{m} a^{m}_{{i + 2}} } \hfill} & {{i\,even,\,and\,\beta _{m} = b^{m}_{0} /a^{m}_{1} } \hfill} \\ \end{array} \,\forall i = 1, \cdots ,m - 1} \right.$$
(9)

. The polynomials A m−1 and B m−1 can only be defined if a 1 m≠0. Åström (1970) shows these new coefficients may be obtained by the following table.

$$\begin{array}{*{20}c} {{a^{m}_{0} }} & {{a^{m}_{1} }} & {{a^{m}_{2} }} & {{a^{m}_{3} }} & {{a^{m}_{4} }} & { \cdots } & {{b^{m}_{1} }} & {{b^{m}_{2} }} & {{b^{m}_{3} }} & {{b^{m}_{4} }} & {{b^{m}_{5} }} \\ {{}} & {{a^{{m - 1}}_{0} }} & {{a^{{m - 1}}_{1} }} & {{a^{{m - 1}}_{2} }} & {{a^{{m - 1}}_{3} }} & {{}} & {{}} & {{b^{{m - 1}}_{1} }} & {{b^{{m - 1}}_{2} }} & {{b^{{m - 1}}_{3} }} & {{b^{{m - 1}}_{4} }} \\ {{}} & {{}} & {{}} & {{}} & { \vdots } & {{}} & {{}} & {{}} & {{}} & {{}} & { \vdots } \\ {{}} & {{}} & {{}} & {{a^{1}_{0} }} & {{a^{1}_{1} }} & {{}} & {{}} & {{}} & {{}} & {{}} & {{b^{1}_{1} }} \\ \end{array}$$
(10)

Note that the first row in the matrix consists of the original constants from the system’s transfer function. After having obtained the values α m and β m , the value of the integral I is then given by

$$I = {\sum\limits_{m = 1}^n {\beta ^{2}_{m} /{\left( {2\alpha _{m} } \right)} = {\sum\limits_{m = 1}^n {{\left( {b^{m}_{1} } \right)}^{2} /{\left( {2a^{m}_{0} a^{m}_{1} } \right)}} }} }$$
(11)

. Because of its recursive nature, Åström’s method is easy too implement in computer software packages. Let us highlight Åström’s method explicitly here. Rearranging the net stock transfer function (1), we have

$$\begin{aligned} & A{\left( s \right)} = T_{i} T_{p} T_{r} T_{w} s^{3} + {\left( {T_{i} T_{p} T_{r} + T_{i} T_{p} T_{w} + T_{i} T_{r} T_{w} } \right)}s^{2} + {\left( {T_{i} T_{p} + T_{i} T_{w} + T_{r} T_{w} } \right)}s + T_{w} , \\ & B{\left( s \right)} = - T_{i} T_{p} T_{r} T_{w} s^{2} - T_{i} {\left( {T_{p} T_{r} + T_{p} T_{w} - kT_{p} T_{w} + T_{r} T_{w} } \right)}s - T_{i} {\left( {T_{p} - kT_{p} + T_{w} - kT_{w} } \right)} \\ \end{aligned} $$
(12)

Because the denominator is a third order polynomial, see (1), then Åström’s table has three rows,

$$\begin{array}{*{20}c} {{a^{3}_{0} }} & {{a^{3}_{1} }} & {{a^{3}_{2} }} & {{a^{3}_{3} }} & {{}} & {{b^{3}_{1} }} & {{b^{3}_{2} }} & {{b^{3}_{3} }} \\ {{}} & {{a^{2}_{0} }} & {{a^{2}_{1} }} & {{a^{2}_{2} }} & {{}} & {{}} & {{b^{2}_{1} }} & {{b^{2}_{2} }} \\ {{}} & {{}} & {{a^{1}_{0} }} & {{a^{1}_{1} }} & {{}} & {{}} & {{}} & {{b^{1}_{1} }} \\ {{}} & {{}} & {{}} & {{}} & {{}} & {{}} & {{}} & {{}} \\ \end{array} $$
(13)

where;

a03=T i T p T r T w ;

a13=T i T p T r +T i T P T w +T i T r T w ;

a23=T i T p +T i T w +T r T w ;

a33=T w ;

b13=−T i T p T r T w ;

b23=−T i (T p T r +T p T w −kT p T w +T r T w );

b33=−T i (T p −kT p +T w −kT w ).

To complete Åström’s method, a six step approach is taken as follows.

  1. Step 1;

    Use α m =a 0 m/a 1 m and β m =b 1 m/a 1 m to calculate α 3 and β 3

    $$\begin{array}{*{20}l} {{\alpha _{3} = a^{3}_{0} /a^{3}_{1} = } \hfill} & {{\frac{{T_{p} T_{r} T_{w} }}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}};} \hfill} \\ {{\beta _{3} = b^{3}_{1} /a^{3}_{1} = } \hfill} & {\begin{aligned} & - \frac{{T_{p} T_{r} T_{w} }}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}} \\ & \\ \end{aligned} \hfill} \\ \end{array} $$
    (14)
  2. Step 2;

    Using (16) and (17) we translate a 1 to 3 3 into a 0 to 2 2 and b 2 to 3 3 into b 1 to 2 2

    $$\begin{array}{*{20}l} {{a^{2}_{0} = a^{3}_{1} = T_{i} T_{p} T_{r} + T_{i} T_{p} T_{w} + T_{i} T_{r} T_{w} ;} \hfill} \\ {{a^{2}_{1} = a^{3}_{2} - \alpha _{3} a^{3}_{3} = {\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} + \frac{{T_{r} ^{2} T_{w} }}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}}} \right)};} \hfill} \\ {{a^{2}_{2} = a^{3}_{3} = T_{w} ;} \hfill} \\ {{b^{2}_{1} = b^{3}_{2} = - T_{i} {\left( {T_{p} T_{r} + T_{p} T_{w} - kT_{p} T_{w} + T_{r} T_{w} } \right)};} \hfill} \\ {{b^{2}_{2} = b^{3}_{3} - \beta _{3} a^{3}_{3} = \frac{{T_{p} T_{r} T_{w} ^{2} + {\left( { - 1 + k} \right)}T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}}} \hfill} \\ \end{array} $$
    (15)
  3. Step 3;

    Repeat Step 1 to find α 2 and β 2,

    $$\begin{array}{*{20}l} {{\alpha _{2} = a^{2}_{0} /a^{2}_{1} = } \hfill} & {{\frac{{T_{i} {\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}^{2} }}{{{\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}};} \hfill} \\ {{\beta _{2} = b^{2}_{1} /a^{2}_{1} = } \hfill} & {\begin{aligned} & - \frac{{T_{i} {\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}{\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} - kT_{w} } \right)}} \right)}}}{{{\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}} \\ & \\ \end{aligned} \hfill} \\ \end{array} $$
    (16)

    .

  4. Step 4;

    Using (16) and (17) we translate a 1 to 2 2 into a 0 to 1 1 and b 2 2 into b 1 1,

    $$\begin{array}{*{20}l} {{a^{1}_{0} = a^{2}_{1} = } \hfill} & {{{\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} + \frac{{T^{2}_{r} T_{w} }}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}}} \right)};} \hfill} \\ {{a^{1}_{1} = a^{2}_{2} = } \hfill} & {{T_{w} ;} \hfill} \\ {{b^{1}_{1} = b^{2}_{2} = } \hfill} & {{\frac{{T_{p} T_{r} T_{w} + {\left( { - 1 + k} \right)}T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}}{{T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}}}} \hfill} \\ \end{array} $$
    (17)

    .

  5. Step 5;

    Repeat Step 1 to find α 1 and β 1

    $$\begin{array}{*{20}l} {{\alpha _{1} = a^{1}_{0} /a^{1}_{1} = } \hfill} & {{\frac{{{\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}}{{T_{w} {\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}};} \hfill} \\ {{\beta _{1} = b^{1}_{1} /a^{1}_{1} = } \hfill} & {{\frac{{T_{p} T_{r} T_{w} ^{2} + {\left( { - 1 + k} \right)}T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}}{{T_{w} {\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}}} \hfill} \\ \end{array} $$
    (18)

    .

  6. Step 6;

    Finally we may use (11) to reveal the integral I as,

    $$VarAmp_{{NS}} = {\sum\limits_{k = 1}^3 {\beta ^{2}_{k} /(2\alpha _{k} ) = \frac{{{\left[ \begin{aligned} & T_{p} T_{r} ^{2} T_{w} ^{3} + {\left( {k - 1} \right)}^{2} T_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}^{2} {\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)} + \\ & T_{i} T_{w} {\left( \begin{aligned} & T_{r} ^{2} T_{w} ^{2} + T_{p} T_{r} T_{w} {\left( {2T_{r} + T_{w} } \right)} \\ & + T_{p} ^{2} {\left( {T_{r} ^{2} + T_{r} T_{w} + {\left( {k - 1} \right)}^{2} T_{w} ^{2} } \right)} \\ \end{aligned} \right)} \\ \end{aligned} \right]}}}{{2T_{w} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}}} }$$
    (19)

    .

(19) is our desired closed form expression for the inventory variance. This has been further verified via simulation in the Matlab software package. As we assume the demand rate is drawn from an arbitrary i.i.d. distribution we may select a number of typical i.i.d. inputs in this example. We have chosen the normal distribution and the exponential distribution. We have also compared our simulation results with the exact analytical expressions of (19). Our results are shown in Table 2, for various combinations of the parameters in the solution space. Table 2 illustrates that the variance ratio is indeed independent of the distribution of the demand process.

Table 2 The inventory variance in continuous time when end−consumer demand is i.i.d
Full size table

Analysis of the closed form inventory variance expression

The inventory variance had been derived in (19). As it is quite complex, let us first review some special cases. By setting k=0, we may determine the inventory variance in a traditional supply chain. This is shown in (20). Recall, T i and T w are control parameters that we may use to tune the dynamic response of the system and T p is the lead-time associated with the manufacture of new product.

$$VarAmp_{{NS,k = 0}} = \frac{{T_{p} T_{w} ^{2} + T_{i} {\left( {T_{p} + T_{w} } \right)}^{2} }}{{2T_{w} {\left( {T_{p} + T_{w} } \right)}}}$$
(20)

We notice that T i only occurs in the numerator. This means that reducing T i will reduce inventory variance. An important subset of the control parameters occurs when T w =T i . It allows further simplification to (19) and (20) as shown in (21) and (22) respectively.

$$VarAmp_{{NS,T_{w} = T_{i} }} = \frac{{{\left[ \begin{aligned} & {\left( {k - 1} \right)}^{2} T_{i} ^{3} {\left( {T_{p} + T_{r} } \right)} + T_{p} ^{2} T_{r} {\left( {{\left( {k - 1} \right)}^{2} T_{p} + T_{r} } \right)} + T_{i} ^{2} {\left( {T_{p} + T_{r} } \right)} \cdot \\ & {\left( {3{\left( {k - 1} \right)}^{2} T_{p} + T_{r} } \right)} + T_{i} T_{p} {\left( {{\left( {k - 1} \right)}^{2} T_{p} + T_{r} } \right)}{\left( {T_{p} + 3T_{r} } \right)} \\ \end{aligned} \right]}}}{{2{\left( {T_{i} + T_{p} } \right)}{\left( {T_{i} + T_{r} } \right)}{\left( {T_{p} + T_{r} } \right)}}}$$
(21)
$$VarAmp^{{}}_{{NS,k = 0,T_{w} = T_{i} }} = \frac{{T_{i} ^{2} + 3T_{i} T_{p} + T_{p} ^{2} }}{{2{\left( {T_{i} + T_{p} } \right)}}} = \frac{1}{2}{\left( {T_{i} + T_{p} } \right)} + \frac{{T_{i} T_{p} }}{{2{\left( {T_{i} + T_{p} } \right)}}}$$
(22)

In (21), we find that the order of both T i and T p is higher in the numerator than in the denominator. Thus both T p and T i should be reduced in order to dampen inventory variance. This result is more obvious in (22), a supply chain with no returns, as subtracting (21) from (22) results in (23).

$${\left( {21} \right)} - {\left( {22} \right)} = \frac{{{\left( { - 2 + k} \right)}k{\left( {T_{i} T_{p} {\left( {T_{i} ^{2} + 3T_{i} T_{p} + T_{p} ^{2} } \right)} + {\left( {T_{i} + T_{p} } \right)}^{3} T_{r} } \right)}}}{{2{\left( {T_{i} + T_{p} } \right)}{\left( {T_{i} + T_{r} } \right)}{\left( {T_{p} + T_{r} } \right)}}} < 0$$
(23)

Here we can see that when T w =T i , that is, when the two feedback gains are equal, then inventory variance in a remanufacturing supply chain will always be less than in a traditional supply chain. This is because we assume 0≤k≤1, thus (23) is always negative.

When all of the products are returned from the marketplace (after the stochastic exponential delay), k=1. Then (19) reduces to,

$$VarAmp_{{k = 1,T_{w} = T_{i} }} = \frac{{T_{r} {\left( {T_{i} T_{p} {\left( {T_{i} + T_{p} } \right)} + T_{r} {\left( {T_{i} ^{2} + 3T_{i} T_{p} + T_{p} ^{2} } \right)}} \right)}}}{{2{\left( {T_{i} + T_{p} } \right)}{\left( {T_{i} + T_{r} } \right)}{\left( {T_{p} + T_{r} } \right)}}}$$
(24)

Again, compared to inventory variance in a traditional supply chain, we have

$${\left( {24} \right)} - {\left( {22} \right)} = - \frac{{T_{i} T_{p} {\left( {T_{i} ^{2} + 3T_{i} T_{p} + T_{p} ^{2} } \right)} + {\left( {T_{i} + T_{p} } \right)}^{3} T_{r} }}{{2{\left( {T_{i} + T_{p} } \right)}{\left( {T_{i} + T_{r} } \right)}{\left( {T_{p} + T_{r} } \right)}}} < 0$$
(25)

, where we can clearly see the smoothing effect of the reverse flow is maximized when k=1. Returning now to the general case of (19). We may factor this into the following,

$$VarAmp_{{NS}} = \frac{{T_{p} T_{w} ^{2} + T_{i} {\left( {T_{p} + T_{w} } \right)}^{2} }}{{2T_{w} {\left( {T_{p} + T_{w} } \right)}}} + \frac{{{\left( {k - 2} \right)}kT_{i} T_{p} ^{2} T_{w} ^{2} }}{{2{\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}} + \frac{{{\left( {k - 2} \right)}kT_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} T_{w} + T_{p} {\left( {T_{r} + T_{w} } \right)}} \right)}}}{{2T_{w} {\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}}$$
(26)

In (26) the first term on the right hand side is the inventory variance generated by a traditional supply chain. The second and third terms are always negative as 0≤k≤1. This result reveals that the inventory variance with returns, in our specified model, is always less than without returns.

Returning again to (19). Differentiating (19) with respect to k and T r yields

$$\frac{{\partial VarAmp_{{NS}} }}{{\partial k}} = \frac{{{\left( {k - 1} \right)}T_{i} {\left( {T_{p} ^{2} T_{w} ^{3} + T_{i} {\left( {T_{p} + T_{w} } \right)}^{2} {\left( {T_{p} T_{w} + T_{r} {\left( {T_{p} + T_{w} } \right)}} \right)}} \right)}}}{{T_{w} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} ^{2} T_{w} + T_{i} T_{p} T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}}}$$
(27)
$$\frac{{\partial VarAmp_{{NS}} }}{{\partial T_{r} }} = \frac{{{\left( {2 - k} \right)}kT_{i} {\left( {T_{i} T_{p} ^{2} T_{w} ^{2} {\left( {T_{p} + T_{w} } \right)} + T_{r} ^{2} T_{i} {\left( {T_{p} + T_{w} } \right)}^{3} + 2T_{r} T_{p} T_{w} {\left( {T_{p} T_{w} ^{2} + T_{i} {\left( {T_{p} + T_{w} } \right)}^{2} } \right)}} \right)}}}{{2{\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} ^{2} T_{w} + T_{i} T_{p} T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}^{2} }}$$
(28)

The inventory variance (27) is monotone and always negative (or zero when k=1) in the return rate, k. (28) is monotone and positive in the remanufacturing lead-time, T r . The relationship of inventory variance between return rate k and manufacturing lead-times is illustrated in Fig. 3 where we have set T p =3, T i =4, and T w =8.

Fig. 3
figure 3

The effect of return rate and lead-time on inventory variance when T p =3, T w =8 and T i =4

Full size image

Bullwhip in the remanufacturing supply chain

“Bullwhip” is the phenomenon where the orders at the supplier level tend to have a larger variance than sales to the buyer (that is the demand gets distorted), and the distortion propagates upstream in an amplified form (i.e. variance amplification), Dejonckheere et al. (2002). Lee et al. (1997) have summarized the negative impact of bullwhip problem as follows; excessive inventory investments throughout the supply chain to cope with the increased demand variability, reduced customer service due to the inertia of the production/distribution system, lost revenues due to shortages, reduced productivity of capital investment, increased investment in capacity, inefficient use of transport capacity and increased missed production schedules. Thus, avoiding or reducing bullwhip has a real and important impact on the performance of a commercial company.

A mathematical definition of bullwhip that we will adopt here has been proposed by Chen et al. (2000) as,

$$Bullwhip = \frac{{\sigma ^{2}_{{OR}} }}{{\sigma ^{2}_{D} }}$$
(29)

.

From (29), we can see that bullwhip is also a variance ratio problem. After employing the same methods as used in Section 3 we acquire the bullwhip analytical expression as,

$$Bullwhip = \frac{{T_{w} {\left( {T_{r} ^{2} {\left( {T_{i} + T_{p} } \right)}T_{w} + {\left( {k - 1} \right)}^{2} T_{i} T_{p} {\left( {T_{i} + T_{p} } \right)}T_{w} + T_{r} T_{i} {\left( {{\left( {k - 1} \right)}^{2} T_{i} + T_{p} } \right)}{\left( {T_{p} + T_{w} } \right)}} \right)}}}{{2T_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}}$$
(30)

Zhou et al. (2004) have also derived (30) using Parsevel’s Relation. Again we start by setting k=0 to determine the bullwhip in a traditional supply chain as shown in (31).

$$Bullwhip_{{k = 0}} = \frac{{T_{w} {\left( {T_{i} + T_{p} } \right)}}}{{2T_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}}}$$
(31)

Equation (31) shows that in a supply chain with no returns, the bullwhip decreases as T i increases and the lead-time, T p , should be reduced in order to smooth production and reduce the associated capacity on-costs. Again, in the subset of T w =T i , then (30) and (31) further simplifies to (32) and (33) respectively.

$$Bullwhip_{{T_{w} = T_{i} }} = \frac{{{\left( {k - 1} \right)}^{2} T_{i} + T_{r} }}{{2T_{i} {\left( {T_{i} + T_{r} } \right)}}} = \frac{1}{{2T_{i} }} + \frac{{k^{2} - 2k}}{{2{\left( {T_{i} + T_{r} } \right)}}}$$
(32)
$$Bullwhip_{{k = 0,T_{w} = T_{i} }} = \frac{1}{{2T_{i} }}$$
(33)

Here we can see that when T w =T i , then bullwhip in a remanufacturing supply chain will always be less than in a traditional supply chain due to the conditions on the return rate (0≤k≤1), as the last term of (32) is always negative. (32) and (33) show that when T w =T i the lead-time T p drops out of the bullwhip expression.

When all of the products are returned from the marketplace (after the stochastic exponential delay), k=1. Here (30) reduces to,

$$Bullwhip_{{k = 1,T_{w} = T_{i} }} = \frac{1}{{2T_{i} }} - \frac{1}{{2{\left( {T_{i} + T_{r} } \right)}}}$$
(34)

, where we can clearly see that; bullwhip in a remanufacturing supply chain is always less than in a traditional supply chain. However this smoothing effect is reduced with longer remanufacturing lead-times, T r . Returning now to the general case of (30). We may factor this into the following,

$$Bullwhip = \frac{{{\left( {T_{i} + T_{p} } \right)}T_{w} }}{{2T_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}}} + \frac{{{\left( {k - 2} \right)}kT_{w} }}{{2T_{i} {\left( {T_{p} + T_{w} } \right)}}} + \frac{{{\left( {k - 2} \right)}k{\left( {T_{p} ^{2} - T_{r} ^{2} } \right)}T_{w} ^{2} }}{{2T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{i} T_{p} T_{r} + T_{r} ^{2} T_{w} + T_{i} {\left( {T_{p} + T_{r} } \right)}T_{w} } \right)}}}$$
(35)

.

In (35) the first term on the right hand side is the bullwhip generated by a traditional supply chain. The second term is always negative as o≤k≤1. Interestingly, the third term is; zero when T r =T p , negative when T r <T p and positive when T r >T p . The sum of the last two terms is positive only when T p is negative or complex. A complex T p occurs when \(T_{i} < \frac{{4T_{r} T_{w} ^{2} }}{{{\left( {T_{r} + T_{w} } \right)}^{2} }}\), and T p is negative otherwise. As negative or complex lead-times have no meaning in reality, we conclude that the sum of the last two terms is always negative. This means that our supply chain with returns always has less bullwhip than one without returns.

This leads us to investigate bullwhip when the remanufacturing lead-time (this also includes the time the product is in the hands of the user) is the same as the manufacturing lead-time. When T r =T p , (30) becomes,

$$Bullwhip_{{T_{p} = T_{r} }} = \frac{{{\left( {{\left( {k - 1} \right)}^{2} T_{i} + T_{p} } \right)}T_{w} }}{{2T_{i} ^{2} {\left( {T_{p} + T_{w} } \right)}}}$$
(36)

. (36) is always less than (30). Returning again to (30), differentiating (30) with respect to k and T r yields;

$$\frac{{\partial Bullwhip}}{{\partial k}} = \frac{{{\left( {k - 1} \right)}T_{w} {\left( {T_{p} {\left( {T_{i} + T_{p} } \right)}T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}}}{{T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} ^{2} T_{w} + T_{i} T_{p} T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}}}$$
(37)

,

$$\frac{{\partial Bullwhip}}{{\partial T_{r} }} = \frac{{{\left( {1 - k} \right)}T_{w} ^{2} {\left( {2T_{r} T_{p} {\left( {T_{i} + T_{p} } \right)}T_{w} + T_{r} ^{2} T_{i} {\left( {T_{p} + T_{w} } \right)} + T_{i} T_{p} ^{2} {\left( {T_{p} + T_{w} } \right)}} \right)}}}{{T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} ^{2} T_{w} + T_{i} T_{p} T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}^{2} }}$$
(38)

.

We can see that (37) is monotone and always negative (or zero when k=1) in the return rate, k. (38) is monotone and positive (or zero when k=1) in the remanufacturing lead-time, T r . The relationship of the return rate k and the manufacturing lead-times, T r , to bullwhip is illustrated in Fig. 4 where we have set T p =3, T i =4, and T w =8.

Fig. 4
figure 4

The effect of return rate and lead-time on bullwhip when T p =3, T w =8 and T i =4

Full size image

Our analysis broadly supports the results of Wang (2002) who has adapted the beer game (Sterman 1989) to include a reverse logistics scenario. Initial results from Wang (2002) also suggest that remanufacturing reduces bullwhip in a supply chain. We also find that in a remanufacturing supply chain, the inventory variance and bullwhip experienced by the manufacturer of new products is reduced when compared to a traditional supply chain. This means that returns can be used to smooth inventory variance and bullwhip. The higher the return rate and the shorter the remanufacturing lead-time the smoother the order and inventory patterns are.

We notice that our findings are different from Muckstadt and Isaac (1981). In their paper, returns are completely independent of the (Poisson) demand process. Increasing the return rate then increases the total variance of the system. In our paper, the return process is correlated with the demand process (albeit after the exponentially distributed random time delay). Increasing the return rate then actually decreases the variance in net demand and the total variance in system as was shown in van der Laan et al. (1999a) for a special case of their model. However, we have considered a linear system, where we continuously adjust order rates in time. Both Muckstadt and Isaac (1981) and van der Laan et al. (1999b) investigated adapted (r,Q) policies for a reverse logistics scenario. These are non-linear systems that have been solved using Markov Chains.

We also noticed that the parameter T i , has a different impact on the inventory variance and than that on bullwhip. When T i increases the inventory variance increases whilst bullwhip decreases. This leads us to the next section where we investigate the trade-off between inventory variance and bullwhip.

The optimal T i

As discussed in Disney et al. (2004) and Disney and Grubbström (2003), the inventory variance has a direct impact on the expected inventory (holding and shortage/backlog) costs and the order variance (bullwhip) affects the production costs (in normal production mode or via overtime). To obtain exact costs it is necessary to use the variances inside probability density functions as was shown in Disney and Grubbström (2003). However, this is rather complex and would increase our solution space from five to nine dimensions. Furthermore, unless we assumed a very simple distribution, our results would not be amenable for further algebraic analysis and numerical investigations would be needed (as the probability density function of the normal distribution is essentially non-algebraic). Thus, here we simply assume the costs are a linear, equally weighted, function of the inventory and order variance. This is adequate for our purposes here as we wish to illustrate that the proportional controller, T i , is a useful lever to manipulate the balance between bullwhip and inventory variance costs in a supply chain. So setting the objective function (OF) in our trade-off as

$$OF = VarAmp_{{NS}} + Bullwhip$$

, yields, after some manipulation,

$$OF = \frac{{{\left[ \begin{aligned} & T_{r} ^{2} T_{w} {\left( {T_{i} ^{3} T_{p} ^{2} + 2T_{i} ^{3} T_{p} T_{w} + {\left( {1 + T_{i} ^{2} } \right)}{\left( {T_{i} + T_{p} } \right)}T_{w} ^{2} } \right)} + \\ & {\left( {k - 1} \right)}^{2} T_{p} T_{w} {\left( {T_{i} ^{4} T_{p} ^{2} + 2T_{i} ^{4} T_{p} T_{w} + {\left( {T_{i} + T_{i} ^{3} } \right)}{\left( {T_{i} + T_{p} } \right)}T_{w} ^{2} } \right)} + \\ & T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}{\left( {{\left( {k - 1} \right)}^{2} T_{i} T_{w} ^{2} + T_{p} T_{w} ^{2} + T_{i} ^{2} T_{p} T_{w} ^{2} + {\left( {k - 1} \right)}^{2} T_{i} ^{3} {\left( {T_{p} + T_{w} } \right)}^{2} } \right)} \\ \end{aligned} \right]}}}{{2T_{i} ^{2} T_{w} {\left( {T_{p} + T_{w} } \right)}{\left( {T_{r} ^{2} T_{w} + T_{i} T_{p} T_{w} + T_{r} T_{i} {\left( {T_{p} + T_{w} } \right)}} \right)}}}$$
(39)

.

Theoretically, the optimal T i can be derived by solving for zero gradients of (39). However, as (39) is quite complex, we will study the simplified case of T r =T p and T w =T i . There (39) simplifies to (40).

$$OF = \frac{{{\left[ \begin{aligned} & 2{\left( {k - 1} \right)}^{2} T_{i} ^{4} + 2{\left( {4 + 3{\left( {k - 2} \right)}k} \right)}T_{i} ^{3} T_{p} + 2T_{p} ^{2} + {\left( {2 + {\left( {k - 2} \right)}k} \right)}T_{i} T_{p} {\left( {2 + T_{p} ^{2} } \right)} + \\ & 2T_{i} ^{2} {\left( {{\left( {k - 1} \right)}^{2} + 2{\left( {2 + {\left( {k - 2} \right)}k} \right)}T_{p} ^{2} } \right)} \\ \end{aligned} \right]}}}{{4T_{i} {\left( {T_{i} + T_{p} } \right)}^{2} }}$$
(40)

.

Taking the partial derivative we have,

$$\frac{{\partial OF}}{{\partial T_{i} }} = \frac{{{\left[ \begin{aligned} & {\left( {k - 1} \right)}^{2} T_{i} ^{5} + 3{\left( {k - 1} \right)}^{2} T_{i} ^{4} T_{p} - 3T_{i} T_{p} ^{2} - T_{p} ^{3} + {\left( {k - 1} \right)}^{2} T_{i} ^{3} {\left( {4T_{p} ^{2} - 1} \right)} + \\ & T_{i} ^{2} T_{p} {\left( { - 3 + 2T_{p} ^{2} + {\left( {k - 2} \right)}k{\left( {T_{p} ^{2} - 1} \right)}} \right)} \\ \end{aligned} \right]}}}{{2T_{i} ^{2} {\left( {T_{i} + T_{p} } \right)}^{3} }}$$
(41)

.

Obviously, the optimal T i should be the function of T p and k. However, (41) is a fifth order function of T i and it is hard to obtain analytical solutions. But for the special cases; k=0 and k=1, we have

$$T^{ * }_{{i_{{k = 0}} }} = \frac{1}{2}{\left( { - T_{p} + {\sqrt {1 + T_{p} ^{2} } } + {\sqrt {1 + 2T_{p} {\left( { - T_{p} + {\sqrt {1 + T_{p} ^{2} } }} \right)}} }} \right)},$$
(42)
$$T^{ * }_{{i_{{k = 1}} }} = \frac{{T_{p} {\left( {3 + {\sqrt {1 + T_{p} ^{2} } }} \right)}}}{{2{\left( {T_{p} ^{2} - 2} \right)}}}$$
(43)

.

We further illustrate the more general case when k varies from zero to one via numerical investigations. Figure 5 reveals that bullwhip and inventory variance (and their sum) is larger for small k. It verifies our conclusion that the returns can smooth both inventory and order variance. Table 3 provides some numerical results in each case. We notice that with increasing returns, it takes a larger T i to minimize the sum of the variances. Thus greater returns allow smoother production rates to be achieved without unduly increasing inventory requirements.

Fig. 5
figure 5

The optimal sum of variance ratios when T p =T r =3 and T w =T i

Full size image
Table 3 The optimal T i * that minimizes the sum of bullwhip and inventory variance when T p =T r =3 and T w =T i
Full size table

The impact of a re-manufacturing delay

Recall that we assumed that the time the products stay in the marketplace (in hands of the user) plus the time that it takes to remanufacture the product to bring it up to as “good as new” is represented by a single exponential delay. We wish now to investigate the impact of splitting these two lead-times apart. This is easily achieved with the following substitution, \(\frac{k}{{1 + T_{r} s}} \to \frac{k}{{{\left( {1 + T_{r} s} \right)}{\left( {1 + T_{u} s} \right)}}}\), in the block diagram shown in Fig. 2. T u , corresponds to the remanufacturing delay which we have represented as a first order lag, and T r is the exponentially distributed time a product is in the marketplace.

We wish now to understand the question; “for which values of T u (the remanufacturing lead-time), does the remanufacturing supply chain outperform the traditional supply chain?” After running through the math (details omitted, but they follow directly from our procedure outlined earlier) the bullwhip for the remanufacturing system with T w =T i is given by

$$Bullwhip = \frac{{{\left( {k - 1} \right)}^{2} T_{i} ^{2} {\left( {T_{r} + T_{u} } \right)} + T_{r} T_{u} {\left( {T_{r} + T_{u} } \right)} + T_{i} {\left( {T_{r} ^{2} + {\left( {2 + k^{2} } \right)}T_{r} T_{u} + T_{u} ^{2} } \right)}}}{{2T_{i} {\left( {T_{i} + T_{r} } \right)}{\left( {T_{i} + T_{u} } \right)}{\left( {T_{r} + T_{u} } \right)}}}$$
(44)

. It is possible to determine the more general criteria, that is when T w is independent from T i , but we have not presented the results here due to the lengthy algebra. Similarly, the inventory variance expression turns out to be

$$VarAmp_{{NS}} = \frac{1}{2}{\left( \begin{aligned} & \frac{{kT_{i} ^{4} {\left( {T_{i} + 2T_{p} } \right)}{\left( { - 2T_{i} + kT_{i} + 2T_{r} } \right)}}}{{{\left( {T_{i} ^{2} - T_{p} ^{2} } \right)}{\left( {T_{i} ^{2} - T_{r} ^{2} } \right)}{\left( {T_{i} + T_{u} } \right)}}} + \frac{{kT_{p} ^{4} {\left( {2T_{i} + T_{p} } \right)}{\left( { - 2T_{p} + kT_{p} + 2T_{r} } \right)}}}{{{\left( {T_{p} ^{2} - T_{i} ^{2} } \right)}{\left( {T_{p} ^{2} - T_{r} ^{2} } \right)}{\left( {T_{p} + T_{u} } \right)}}} + \\ & \frac{{k^{2} T_{r} ^{2} {\left( { - T_{i} T_{p} + T_{i} T_{r} + T_{p} T_{r} } \right)}{\left( {T_{i} T_{p} + T_{i} T_{r} + T_{p} T_{r} } \right)}}}{{{\left( {T_{i} ^{2} - T_{r} ^{2} } \right)}{\left( {T_{p} ^{2} - T_{r} ^{2} } \right)}{\left( {T_{r} + T_{u} } \right)}}} + \frac{{T_{i} {\left( {T_{i} + 2T_{p} } \right)}}}{{T_{i} + T_{p} }} + T_{p} \\ \end{aligned} \right)}$$
(45)

Subtracting (32) from (44), equating to zero and solving for T u , yields the maximum value of T u for which the bullwhip in the remanufacturing supply chain is less than the bullwhip in the traditional supply chain. It is given by

$$T_{u} < \frac{{{\left( {2 - k} \right)}T_{i} T_{r} }}{{{\left( {k - 2} \right)}T_{i} + kT_{r} }}$$
(46)

It can be seen that higher values of k, T i and T r reduce the maximum remanufacturing lead-time for which the bullwhip is less in a reverse supply chain than a traditional supply chain. We note that when (46) is negative the remanufacturing supply chain is superior to the traditional supply chain for all T u . (46) becomes negative when T r >(T i (k−2))/k. In a like manner (but subtracting (21) from (46)), the maximum value of T u for which the remanufacturing supply chain has less inventory variance than the traditional supply chain is given by

$$T_{u} < \frac{{\begin{array}{*{20}l} {{{\sqrt {\begin{array}{*{20}l} {{ - 4{\left( {k - 2} \right)}T_{i} T_{p} T_{r} {\left( {T_{i} T_{p} {\left( {T^{2}_{i} + 3T_{i} T_{p} + T^{2}_{p} } \right)} + {\left( {T_{i} + T_{p} } \right)}^{3} T_{r} } \right)}} \hfill} \\ {{{\left( {{\left( {k - 2} \right)}T_{i} T_{p} {\left( {T_{i} + T_{p} } \right)}^{3} + T_{r} {\left( {\begin{array}{*{20}l} {{2{\left( {2k - 3} \right)}T^{3}_{i} T_{p} + 6{\left( {k - 1} \right)}T^{2}_{i} T^{2}_{p} + } \hfill} \\ {{2{\left( {2k - 3} \right)}T_{i} T^{3}_{p} + {\left( {k - 2} \right)}T^{4}_{p} + {\left( {k - 2} \right)}T^{4}_{i} } \hfill} \\ \end{array} } \right)} + k{\left( {T_{i} + T_{p} } \right)}^{3} T^{2}_{r} } \right)} + } \hfill} \\ {{{\left( {\begin{array}{*{20}l} {{{\left( {k - 2} \right)}T^{4}_{p} T^{2}_{r} + {\left( {k - 2} \right)}T^{4}_{i} {\left( {T_{p} + T_{r} } \right)}^{2} + T^{3}_{i} T_{p} {\left( {T_{p} + T_{r} } \right)}{\left( {3{\left( {k - 2} \right)}T_{p} - 6T_{r} + 4kT_{r} } \right)} + } \hfill} \\ {{2T_{i} T^{3}_{p} T_{r} {\left( {{\left( {k - 2} \right)}T_{p} + {\left( {2k - 3} \right)}T_{r} } \right)} + T^{2}_{i} T^{2}_{p} {\left( {{\left( {k - 2} \right)}T^{2}_{p} + {\left( {7k - 12} \right)}T_{p} T_{r} + 6{\left( {k - 1} \right)}T^{2}_{r} } \right)}} \hfill} \\ \end{array} } \right)}^{2} } \hfill} \\ \end{array} } }} \hfill} \\ {{ - {\left( {k - 2} \right)}T^{4}_{p} T^{2}_{r} - {\left( {k - 2} \right)}T^{4}_{i} {\left( {T_{p} + T_{r} } \right)}^{2} - T^{3}_{i} T_{p} {\left( {T_{p} + T_{r} } \right)}{\left( {3{\left( {k - 2} \right)}T_{p} - 6T_{r} + 4kT_{r} } \right)} - } \hfill} \\ {{2T_{i} T^{3}_{p} T_{r} {\left( {{\left( {k - 2} \right)}T_{p} + {\left( {2k - 3} \right)}T_{r} } \right)} - T^{2}_{i} T^{2}_{p} {\left( {{\left( {k - 2} \right)}T^{2}_{p} + {\left( {7k - 12} \right)}T_{p} T_{r} + 6{\left( {k - 1} \right)}T^{2}_{r} } \right)}} \hfill} \\ \end{array} }}{{2{\left( {{\left( {k - 2} \right)}T_{i} T_{p} {\left( {T_{i} + T_{p} } \right)}^{3} + k{\left( {T_{i} + T_{p} } \right)}^{3} T^{2}_{r} + T_{r} {\left( {\begin{array}{*{20}l} {{2{\left( {2k - 3} \right)}T^{3}_{i} T_{p} + 6{\left( {k - 1} \right)}T^{2}_{i} T^{2}_{p} + } \hfill} \\ {{{\left( {k - 2} \right)}T^{4}_{i} + 2{\left( {2k - 3} \right)}T_{i} T^{3}_{p} + {\left( {k - 2} \right)}T^{4}_{p} } \hfill} \\ \end{array} } \right)}} \right)}}}$$
(47)

(47) is too complex to study further and we have yet to find any properties that help us gain insights into it structure. However, numerical investigations reveal that the remanufacturing supply chain is superior for low values of T u . Smaller values of T u are required to ensure the inventory variance benefits of the reverse flow are not eliminated when k→1, T p →0, T i →0 and T r →∞. We note our numerical investigations seem to reveal that for most parameters settings our findings remain unaffected (qualitatively) when we include an explicit remanufacturing delay.

Conclusions

We have studied a stylized manufacturing/remanufacturing supply chain that reclaims product to as good as new, as soon as they are available and tops up serviceable inventory by production of new products. We have achieved this using block diagrams, Laplace transforms and Åström’s method of calculating the integral square of a signal. Our findings are summarized in Table 4. It shows that the returned product can be used to reduce the inventory variance and bullwhip effect experienced by the manufacturer of original equipment compared to a manufacturer in a supply chain without remanufacturing or reverse logistics. This means that, in our specified case, a reverse logistics supply chain may be more cost efficient than a traditional one even if variable costs of recovery are higher than for new production. This is in contrast to our intuition and the findings in Seitz et al. (2003) and Fleischmann et al. (1997) for example. Thus, product recovery not only benefits the environment but may also have positive commercial effects. However, longer in-use and remanufacturing lead-times have less impact at reducing bullwhip than shorter in-use and remanufacturing lead-times.

Table 4 Summary managerial insights
Full size table

We have also shown that our replenishment rule that schedules the production of new components is able to make a balance between production/bullwhip costs and inventory costs by tuning the proportional controller, T i . Finally we highlighted the impact of the re-manufacturing lead-time on our findings. Of course, our findings only relate to our specified system and the assumptions we have made. We have yet to determine whether this system is optimal for a given set of cost functions, or to investigate the impact of the structure of the lead-times on our findings. For example, what happens if pure time delays rather than first order lags /exponentially distributed time delays are used to represent the delays? This is challenging as some systems with pure time delays result in differential-difference problems that cannot be studied using the Laplace transform and Åström’s method. However the Lambert W Function appears to be useful in this respect (Warburton and Disney 2005).