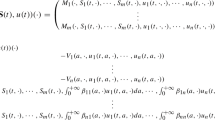A structured population model with diffusion in structure space

Abstract

A structured population model is described and analyzed, in which individual dynamics is stochastic. The model consists of a PDE of advection-diffusion type in the structure variable. The population may represent, for example, the density of infected individuals structured by pathogen density x, $x\ge 0$. The individuals with density $x=0$ are not infected, but rather susceptible or recovered. Their dynamics is described by an ODE with a source term that is the exact flux from the diffusion and advection as $x\rightarrow 0^+$. Infection/reinfection is then modeled moving a fraction of these individuals into the infected class by distributing them in the structure variable through a probability density function. Existence of a global-in-time solution is proven, as well as a classical bifurcation result about equilibrium solutions: a net reproduction number $R_0$ is defined that separates the case of only the trivial equilibrium existing when $R_0<1$ from the existence of another—nontrivial—equilibrium when $R_0>1$. Numerical simulation results are provided to show the stabilization towards the positive equilibrium when $R_0>1$ and towards the trivial one when $R_0<1$, result that is not proven analytically. Simulations are also provided to show the Allee effect that helps boost population sizes at low densities.

1 Introduction

Modeling the dynamics of structured populations (where the structure may be age, size or other physiological indicator) has been an active research area, at least since the book edited by Metz and Diekmann (1986) sparked both relevant biological applications (de Roos and Persson 2013) and interesting mathematical problems (Thieme 1988; Diekmann et al. 1998). In this type of model, one distinguishes between the internal dynamics (i.e. how the structure evolves in an individual) and the overall population dynamics of the number of individuals and of the distribution of the structure in them.

Beyond population dynamics and ecology, this methodology has been applied to immuno-epidemiological models where the infected population is structured through their pathogen load and immune level (Gilchrist and Sasaki 2002; Angulo et al. 2013a, b; Gandolfi et al. 2015; Barbarossa and Röst 2015), and to metapopulation models in which individuals correspond to patches, and the structure represents the population size in the patch (Gyllenberg and Metz 2001; Gyllenberg and Hanski 1992).

Generally, the internal dynamics has been assumed to be described by a system of ordinary differential equations, leading at the population level to a partial differential equation of transport type (Perthame 2007), though different mathematical approaches have been used (Diekmann et al. 1998, 2007).

Hadeler (2010) extended the method to the case in which the underlying individual dynamics includes a stochastic component. Hence, the overall population density is described through a partial differential equation including diffusion in the structure variables, for which appropriate boundary conditions were sought. This approach was followed in recent years by Farkas and Hinow (2011) and Calsina and Farkas (2012) through the introduction of Wentzell boundary conditions.

Restricting ourselves to the case where the stucture variable, x, is one-dimensional and non-negative, we show here how the standard theory of degenerate diffusion (as first proposed by Feller 1951, 1952, 1954) leads to a simple and rather complete analysis.

Although a multi-dimensional internal state may be more realistic in many interesting applications, there are also cases where the assumption of a one-dimensional non-negative structure variable is relevant. We refer mainly to two applications mentioned above. The first one is epidemiological: the individuals being modeled are infectives (infected/infectious), and x describes their pathogen load. Alternatively, we consider a metapopulation model: individuals represent patches, and x describes the population size in that patch.

An interesting feature of both cases is that individuals at $x=0$ are qualitatively different from the others: in the first case corresponding to susceptible (not infected) individuals and in the second case to empty patches. In what follows we will use interchangeably the terms colonization/infection referring to the case when an individual moves from 0 to a positive x-state, and extinction/recovery referring to the case where an individual moves from a positive x-state to 0.

Models based on transport equations in the x-space have serious problems dealing with the special state at $x=0$; for instance in many structured metapopulation models (Gyllenberg and Metz 2001; Gyllenberg and Hanski 1992) there are no empty patches, since, even if they are created by catastrophes that completely wipe out a local population, they get immediately recolonized by a continuous flow of immigrants.

We show in this article how stochastic dynamics at the individual level naturally solves the problem without any special assumption. In the next Section we shall present the model, introducing also some properties of one-dimensional diffusion for which we mainly refer to Karlin and Taylor (1981). In Sect. 3, after stating some properties of the semigroup associated to one-dimensional parabolic equations (Feller 1952), we set the problem in abstract form and prove global existence of solutions (several technical details are relegated to the “Appendix”). In Sect. 4, we find conditions for instability of the trivial equilibrium and observe that they correspond to those for existence of a unique positive equilibrium that is explicitly specified. Section 5 shows some numerical results that illustrate the properties of the solutions, while comments and possible extensions are left to the Discussion Section.

2 The model

2.1 Feller diffusion with logistic growth

We shall assume that the dynamics of pathogen load within each individual (or population in each patch) follows a diffusion process

$$\begin{aligned} dX_t = r (X_t) dt + \sqrt{2 a( X_t)} dw_t \qquad x>0,\ t >0, \end{aligned}$$

(1)

where r(x) represents the infinitesimal drift and 2a(x) the infinitesimal variance. In what follows, we shall generally assume

$$\begin{aligned} r(x) ={\bar{r}} x(1-cx), \qquad a(x) = {\bar{a}} x, \end{aligned}$$

(2)

a process that has been studied in several recent papers (Lambert 2005; Cattiaux et al. 2009; Méléard and Villemonais 2012) and is usually referred as “Feller diffusion with logistic growth” (Feller 1951). All constants are assumed to be strictly positive; moreover, without loss of generality we set ${\bar{a}}=1$, since this just amounts to rescaling the x-axis. Finally, note that $K = 1/c$ can be considered the carrying capacity, to which the system would tend in the absence of stochasticity.

With this choice of r and a, absorption into $x=0$ is certain (Karlin and Taylor 1981; Cattiaux et al. 2009). This means that recovery from infection (local extinction) is certain, although the time required may be extremely long.

In fact, note that the diffusion coefficient (as well as the drift) vanishes at the boundary $x=0$. The overall behavior can be determined, by classifying the boundaries $x=0$ and $x= + \infty$ according to the seminal work by Feller (1954). He identified four possible types of boundaries: a diffusion process can reach a regular boundary and also move inside starting there, with behaviour ranging from absorption to reflection through intermediate behaviors known as sticky boundary; a diffusion process can start from an entrance boundary but cannot reach it from inside; an exit boundary can be reached in finite time but a diffusion process cannot start from it; finally a natural boundary cannot be reached in finite time, nor a process can start from it.

To proceed with the classification, following the terminology by Karlin and Taylor (1981, Sections 15.3 and 15.6), we introduce the scale function

$$\begin{aligned} S(x) = \int _{x_0}^x \exp \left\{ -\int _{x_0}^z \frac{r(\xi )}{a(\xi ) }\,d\xi \right\} \;dz = \int _{x_0}^x e^{-{\bar{r}}(\zeta -x_0) + {\bar{r}}c\left( \zeta ^2 - x_0^2\right) /2}\,d\zeta , \end{aligned}$$

(3)

where $x_0 > 0$ is arbitrary, and the rightmost expression is obtained using (2) and ${\bar{a}} = 1$.

The hitting times $\tau _{a,b}$, for $0< a < b$, are defined as

$$\begin{aligned} \tau _{a,b} = \inf \{t: \ X_t = a \text{ or } X_t = b\ \}. \end{aligned}$$

(4)

A useful property (Karlin and Taylor 1981, formula (15.3.10)) is that, defining

$$\begin{aligned} X_t{\, reaches \, a\, before }\,b \end{aligned}$$

as $X_{\tau _{a,b}} = a$, we have for $0< a< x < b$,

$$\begin{aligned} \mathbb {P}(X_t \text{ reaches } a \text{ before } b\;|\;X_0 = x) = \frac{S(b) - S(x)}{S(b) - S(a) } = \frac{\int _{x}^b e^{-{\bar{r}}\zeta + {\bar{r}}c\zeta ^2 /2}\,d\zeta }{\int _{a}^b e^{-{\bar{r}}\zeta + {\bar{r}}c\zeta ^2 /2}\,d\zeta }. \end{aligned}$$

(5)

Since $\displaystyle \lim _{a \rightarrow 0^+} S(a) > - \infty$, while $\displaystyle \lim _{b \rightarrow + \infty } S(b) = + \infty$, it follows that

$$\begin{aligned} \lim _{b \rightarrow \infty } \mathbb {P}(X_t \text{ reaches } \text{0 } \text{ before } b\;|\;X_0 = x) = 1. \end{aligned}$$

In words, $X_t$ cannot drift to $+ \infty$ while it is certain to reach 0.

Because of this, we define (for $0 \le a < x$) $\tau _a =\displaystyle \lim _{b \rightarrow \infty } \tau _{a,b}$ and when no confusion may arise, $\tau = \tau _0$.

For the classification of the boundaries, it is necessary to introduce a few other functions (Karlin and Taylor 1981):

$$\begin{aligned} m(x)&= \frac{\exp \left\{ \int _{x_0}^x \frac{r(\xi )}{a(\xi ) }\,d\xi \right\} }{2a(x) } = \frac{e^{{\bar{r}}(x-x_0) - {\bar{r}}c\left( x^2 - x_0^2\right) /2}}{ 2x} \end{aligned}$$

(6)

$$\begin{aligned} {\varSigma }(a)&= \int _a^{x_0} [ S(\xi ) - S(a)] m(\xi )\, d\xi = \int _a^{x_0} \int _a^\xi e^{-{\bar{r}}\zeta + {\bar{r}}c\zeta ^2 /2}\,d\zeta \frac{e^{{\bar{r}}\xi - {\bar{r}}c\xi ^2 /2}}{ 2\xi }\, d\xi \end{aligned}$$

(7)

$$\begin{aligned} M(a,x]&= \int _a^x m(\xi )\;d\xi = \int _a^x \frac{e^{{\bar{r}}(\xi -x_0) - {\bar{r}}c\left( \xi ^2 - x_0^2\right) /2}}{ 2\xi }\;d\xi \end{aligned}$$

(8)

$$\begin{aligned} N(a)&= \int _a^{x_0} [S(x_0) - S(\xi )] m(\xi )\,d\xi = \int _a^{x_0} \int _\xi ^{x_0} e^{-{\bar{r}}\zeta + {\bar{r}}c\zeta ^2 /2}\,d\zeta \frac{e^{{\bar{r}}\xi - {\bar{r}}c\xi ^2 /2}}{ 2\xi }\, d\xi . \end{aligned}$$

(9)

The function m(x) is called speed density and is related to the speed at which the process moves. Roughly speaking, ${\varSigma }(a)$ represents the mean time to reach the boundary $x=a$ or an alternative interior state $x=b$ starting from an intermediate $x=x_0$, while N(a) represents the time to reach an internal $x=x_0$ starting from the boundary $x=a$.

It can be checked that

$$\begin{aligned} \lim _{a \rightarrow 0^+} {\varSigma }(a) < + \infty \quad \text{ and }\quad \lim _{a \rightarrow 0^+} M(a,x] = + \infty . \end{aligned}$$

This implies that $x = 0$ is an exit boundary (Karlin and Taylor 1981, Table 15.6.2), while $x =+ \infty$ is an entrance boundary since

$$\begin{aligned} \lim _{a \rightarrow +\infty } S(a) = + \infty \quad \text{ amd }\quad \lim _{a \rightarrow + \infty } N(a) < + \infty . \end{aligned}$$

The entrance boundary at infinity is interpreted to mean (Revuz and Yor 1999, Definition 7.3.9) that there exist ${\bar{x}}$ and $t_0$ such that

$$\begin{aligned} \lim _{x \rightarrow \infty } \mathbb {P}(\tau _{{\bar{x}}} < t_0\ |\ X_0 = x) > 0. \end{aligned}$$

Assuming that the process $X_t$ is absorbed at 0 once it reaches that boundary (other choices are possible; see Feller 1954), one can define the transition function $p_0(t,x;\xi )$ with the property that, for each Borel set $B \subset (0,\infty )$,

$$\begin{aligned} \mathbb {P}(X_t \in B\ |\ X_0 = \xi ) = \int _B p_0(t,x;\xi ) \, dx. \end{aligned}$$

(10)

Because of absorption at 0, $p_0(t,\cdot ;\xi )$ is a defective density, i.e.

$$\begin{aligned} \int _0^\infty p_0(t,x;\xi ) \, dx < 1 = \mathbb {P}(\tau _0 > t\ |\ X_0 = \xi ). \end{aligned}$$

It is clear that most arguments would remain the same with different choices of the functions a and r as long as $x=0$ is an exit boundary, and $x=+\infty$ is unattainable. This fact will be exploited in the numerical examples, where $r(\cdot )$ is modified to allow for an Allee effect.

2.2 The equation at the population level

The forward Kolomogorov equation associated to the process $X_t$ with absorbtion at $x=0$ is

$$\begin{aligned} u_t (t,x) = \partial _x \bigl [(a( x ) u(t,x))_x - r(x) u(t,x) \bigr ],\qquad x,\ t > 0, \end{aligned}$$

with no boundary conditions (Feller 1954).

Feller (1954) also introduced the elementary return process in which particles absorbed at 0 jump (after an exponential waiting time) to some state $x >0$. Assuming, for the sake of simplicity, that the distribution of the jumps has a density q(x), the elementary return process has a density u(t, x) on the positive x-axis that is the (weak) solution of

$$\begin{aligned} u_t (t,x) = \partial _x \bigl [(a( x ) u(t,x))_x - r(x) u(t,x) \bigr ] + \lambda E(t) q(x),\qquad t,\ x >0, \end{aligned}$$

(11)

where E(t) represents the probability that the process is at 0, and $1/\lambda$ is the mean waiting time at 0. E satisfies the equation

$$\begin{aligned} E'(t) = -\lambda E(t) + \lim _{x \rightarrow 0^+} \biggl [\bigl (a( x ) u(t,x)\bigr )_x - r(x) u(t,x)\biggr ]. \end{aligned}$$

(12)

We assume now that the population consists of an infinite number of individuals whose infection level, if infected, is described by Eq. (1). Furthermore, infected individuals produce (at a rate $\beta (x)$) propagules that may infect susceptible (i.e. infection-free) individuals. Analogously, we assume an infinite number of patches characterized by their population size x; propagules produced by each patch may colonize empty patches.

Because of the infinite number of patches, one can equate probabilities with densities (the argument can be made rigorous employing, for example, the methods of Ethier and Kurtz 1986). Then, the function u(t, x), representing the density at time t of individuals in a given state $x > 0$ (i.e. $\int _{x_1}^{x_2} u(t,x) \, dx$ is the fraction of individuals with infection load between $x_1$ and $x_2$ at time t, or the fraction of patches whose population size is between $x_1$ and $x_2$) and E(t), representing the fraction of infection-free individuals (empty patches), will satisfy Eqs. (11) and (12), with the caveat that $\lambda$ will not be a constant but rather will depend on current infection load.

More specifically, we shall assume $\lambda (t) = \int \limits _0^\infty \beta (x) u(t,x)\,dx$, where the function $\beta$ (the rate at which infectives at state x produce infectious propagules) includes also the probability of reaching an individual host.

In summary, for $t>0$, we shall consider the system

$$\begin{aligned} \left\{ \begin{aligned} E'(t)&= -\lambda (t) E(t) + \lim _{x \rightarrow 0^+} \biggl [\bigl (a( x ) u(t,x)\bigr )_x - r(x) u(t,x)\biggr ], \\ u_t (t,x)&= \partial _x \bigl [(a( x ) u(t,x))_x - r(x) u(t,x) \bigr ] + \lambda (t) E(t) q(x),\quad x >0,\\ \lambda (t)&= \int \limits _0^\infty \beta (x) u(t,x)\,dx, \end{aligned}\right. \end{aligned}$$

(13)

where the dynamics of the susceptibles (respectively, empty patches), E, is modeled with a sink represented as the product of the force of infection, $\lambda$, and the susceptible population size (respectively, unit colonization rate times the density of empty patches), and a source representing the rate at which infected individuals recover (respectively, the rate at which colonized patches die out), $\displaystyle \lim _{x \rightarrow 0^+} \bigl [\bigl (a( x ) u(t,x)\bigr )_x- r(x) u(t,x)\bigr ]$—the flux towards 0 of the second equation of (13).

3 Abstract formulation

3.1 Semigroup associated to 1-dimensional parabolic equations

In a series of papers Feller in the 1950s proved some fundamental results about 1-dimensional parabolic equations and their relationship to diffusion processes. In particular we shall use the following result.

Theorem 1

(Theorem 15.2 of Feller 1952) Let $a(\cdot ) > 0$ and $r(\cdot )$ be continuous functions on the (possibly infinite) interval $(r_1,r_2)$. Let ${\varOmega }^*$ be the operator

$$\begin{aligned} ({\varOmega }^* g)(x) = \frac{d}{dx }\biggl [ \frac{d}{dx }\bigl (a(x)g(x)\bigr ) - r(x)g(x)\biggr ], \end{aligned}$$

(14)

defined on the set of functions g smooth enough on $(r_1,r_2)$ that ${\varOmega }^* g \in L^1(r_1,r_2)$. That is,

$$\begin{aligned} \mathscr {D}({\varOmega }^* )=\left\{ g\in L^1(r_1,r_2): ag\in W^{1,1}(r_1,r_2) \text{ and } (ag)' - rg\in W^{1,1}(r_1,r_2)\right\} . \end{aligned}$$

If none of the boundaries are regular, then ${\varOmega }^*$ is the generator of a strongly continuous positive semigroup $T^*_t$ in $L^1(r_1,r_2)$.

Furthermore, if at least one boundary is of exit type, then $T^*_t$ is strictly norm-decreasing.

This semigroup represents the evolution of the measure associated to the diffusion process (1). More precisely, if g represents the distribution of $X_0$, i.e. $\mathbb {P}(X_0 \in A) = \int _A g(x)\, dx$ for each Borel set A, then

$$\begin{aligned} \int _B (T^*_t g)(x)\, dx = \mathbb {P}(X_t \in B) \quad \text{ for } \text{ each } \text{ Borel } \text{ set } B \subset (0,\infty ). \end{aligned}$$

Using the transition density (10), one can write

$$\begin{aligned} (T^*_t g)(\cdot ) = \int _0^\infty p_0(t,\cdot \,;\xi ) g(\xi )\, d\xi . \end{aligned}$$

$T^*_t$ is the (restriction of the) adjoint of the semigroup $T_t$ on $C_0(0,\infty )$ (the space of bounded continuous functions f on $(0,+\infty )$ such that $f(0) = 0$), where

$$\begin{aligned} (T_t f)(x) = \mathbb {E}(f(X_t)\ |\ X_0 = x), \end{aligned}$$

whose generator is ${\varOmega }$ defined by

$$\begin{aligned} {\varOmega }f= af^{\prime \prime } + rf^\prime . \end{aligned}$$

(15)

Note that $T^*_t$ can be extended to the space of Borel measures (and, actually, is naturally defined there).

As stated above, it is well-known that $T^*_t$ is strictly norm-decreasing; it is also well known (see for instance Méléard and Villemonais 2012, Theorem 18) that for each $\xi > 0$, $\displaystyle \lim _{t \rightarrow \infty } \mathbb {P}_\xi ( \tau _0 > t) = 0$. It immediately follows that, for each density function g with compact support,

$$\begin{aligned} \Vert T^*_t g \Vert = \mathbb {P}(\tau _0 > t) \xrightarrow [t \rightarrow \infty ]{} 0. \end{aligned}$$

However, we found no estimates in the literature on the growth bound of the semigroup in $L^1$. Hence here we establish the following

Proposition 1

The growth bound $\omega$ of $T_t^*$ satisifies

$$\begin{aligned} \omega ({\varOmega }^*) = \lim _{t \rightarrow \infty } \frac{\log (\Vert T_t^*\Vert )}{ t} < 0. \end{aligned}$$

The proof, which is extensively based on a sharper result found (Cattiaux et al. 2009) for $T_t$ in a weighted $L^2$ space, is reported in the “Appendix”.

An immediate consequence of the above result is that the essential growth bound (Engel and Nagel 2000) satisfies $\omega _{ess}({\varOmega }^*) \le \omega ({\varOmega }^*) < 0.$

3.2 Semilinear problem

Problem (13) can be written in abstract form as

$$\begin{aligned} \left\{ \begin{aligned} u'(t)&= {\varOmega }^* u(t) + F(u(t)),\\ u(0)&= u_0, \end{aligned} \right. \end{aligned}$$

(16)

where $F: L^1(0,\infty ) \rightarrow L^1(0,\infty )$ is

$$\begin{aligned} \bigl [F(u)\bigr ] (x) = \left( \int \limits _0^\infty \beta (\xi ) u(\xi )\,d\xi \right) \left( 1 - \int \limits _0^\infty u(\xi )\,d\xi \right) q(x). \end{aligned}$$

(17)

Note that in the formulation (16) we avoid considering the dynamics of the boundary accumulation function E explicitly but rather we just define it as $E(t)=1- \int \limits _0^\infty u(t,x)\,dx$.

Indeed, if $u_0 \in \mathscr {D}({\varOmega }^* )$, the solution u(t) of (16) belongs to $\mathscr {D}({\varOmega }^* )$; hence, $u(t)(\cdot )$ is absolutely continuous on $(0,+\infty )$ and we can define $u(t,x) = u(t)(x)$ that will be a classical solution of the second equation of (13) with $1 - \int _0^\infty u(t,x)\, dx$ in place of E(t). Using this definition and computing

$$\begin{aligned} \frac{d}{dt } \int _0^\infty u(t,x)\, dx \end{aligned}$$

we see that E(t) satisfies the first equation of (13).

Conversely, if (E(t), u(t, x)) is a classical solution of (13) such that $E(0) = 1 - \int _0^\infty u(0,x)\, dx$, we see using the same computations that

$$\begin{aligned} E(t)=1- \int \limits _0^\infty u(t,x)\,dx \qquad \forall \ t \le T. \end{aligned}$$

Defining $u(t)(x) = u(t,x)$, we then obtain a classical solution of (16).

In case $u_0 \not \in \mathscr {D}({\varOmega }^* )$, (16) yields only mild solutions, but, given that $T_t^*$ is an analytic semigroup, they will actually be regular solutions for $t > 0$. In any case, we constrain ourselves to the case of regular solutions.

For problem (16)–(17), we have

Proposition 2

Assume that $\beta$ is a continuous and bounded function on $(0,+\infty )$ with $\beta (0) = 0$, and q is a probability density function on $(0,\infty )$.

Then for each $u_0 \in L^1$ there exists a unique (mild) solution of (16) on some interval [0, T].

The result follows easily from standard results (Pazy 1983, Theorem 6.1.4) since, under the assumptions we made, F is a locally Lipschitz operator on $L^1(0,\infty )$.

For the solution of (16) to make sense from the biological point of view, we then need to prove that, starting from non-negative $u_0$ with $\Vert u_0\Vert _1 \le 1$, the solution u of (16) is non-negative and $\Vert u(t,\cdot )\Vert _1 \le 1$ for all $t>0$. Proving this will also ensure that the solution is global. Thus, we prove the following:

Proposition 3

Let $u_0 \ge 0$ with $\Vert u_0\Vert _1 \le 1$ and let u be the solution of (16) on [0, T]. Then, $u \ge 0$ and $\Vert u(t,\cdot )\Vert _1 \le 1$ for all $t \in [0,T]$.

The details of the proof are relegated to the “Appendix”. In it we provide a probabilistic construction of $E(t) = 1 - \int \limits _0^\infty u(t,x)\,dx$ and u(t, x). More specifically, E(t) will be obtained as the series $\displaystyle \sum \nolimits _{i=0}^{\infty } E_i(t)$ where

$$\begin{aligned} E_0(t)= E_0 \exp \left\{ -\int _0^t \lambda (v)\, dv\right\} \end{aligned}$$

is the fraction of individuals that have never been infected in the time interval [0, t]. $E_1(t)$ is the fraction of individuals who are infection-free at time t but who were infectious for a single interval within [0, t) and, similarly, $E_i(t)$ represents the fraction of those who are infection-free at time t but who were infectious in exactly i disjoint intervals within [0, t). The density $u(t,\cdot )$ is then written as an analogous series of corresponding terms.

This method is very similar to the generation expansion employed by Diekmann et al. (2018) in order to characterize the distribution of immune status (see also Breda et al. 2012, in an epidemic model with reinfection).

4 Equilibria and stability

Equation (16) clearly has the trivial equilibrium $u\equiv 0$ (corresponding to $E=1$). Concerning its stability, we shall prove the following threshold property.

Theorem 2

The trivial equilibrium is asymptotically stable (respectively, unstable) for (16) if $R_0 < 1$ (respectively, $R_0 > 1$), where

$$\begin{aligned} \begin{aligned} R_0&= \int _0^\infty \mathbb {E}\left( \int _0^{\tau _0} \beta (X_s)\, ds | X_0 = x \right) q(x)\, dx \\&= \int _0^\infty \int _0^x \int _t^\infty e^{\frac{{\bar{r}}}{K }(t-\xi )\left( \frac{t+\xi }{2 }-K\right) } \frac{\beta (\xi )}{\xi }\,d\xi \;dt\; q(x)\, dx. \end{aligned} \end{aligned}$$

(18)

The definition of $R_0$ on the first line of (18) corresponds to the usual intepretation of the net reproduction number: $R_0$ represents the expected number of propagules produced by an initial colonizing group (starting with size x according to the distribution q) before the patch becomes extinct ($\tau _0$ represents the absorption time). If each new group of colonizers produces on average more than one successful propagule (assuming that all patches are available), then the metapopulation will persist, even though each population will eventually become extinct; otherwise it will not.

The expression on the second line of (18) (valid under (2) and ${\bar{a}} = 1$) comes from standard theory of diffusion processes (Karlin and Taylor 1981) and yields an explicit method to compute $R_0$.

Proof

A central role in the stability of the equilibrium 0 is played by the growth bound of the linearized operator of (16) at $u=0$, ${\varOmega }^* + F'(0)$, where $F'(0)$ is the operator on $L^1$ defined by

$$\begin{aligned} \bigl [F'(0) u \bigr ](x) = q(x) \int _0^\infty \beta (\xi ) u(\xi )\, d\xi . \end{aligned}$$

First of all, note that, since $F'(0)$ is compact (because it has a one-dimensional range) and the growth bound of $T_t^*$ is negative, it follows that

$$\begin{aligned} \omega _{ess} ({\varOmega }^* + F'(0)) = \omega _{ess} ({\varOmega }^*) < 0. \end{aligned}$$

Hence (see for instance Prüß 1981, Theorem E), the equilibrium $u\equiv 0$ is asymptotically stable (respectively, unstable) for (16) if the growth bound of the semigroup generated by ${\varOmega }^* + F'(0)$ is negative (respectively, positive).

As $T_t^*$ is a positive semigroup on $L^1$, its growth bound corresponds to its spectral bound $s({\varOmega }^*)$ (Engel and Nagel 2000, Th. VI.2.5) and the same will hold for the semigroup generated by ${\varOmega }^* + F'(0)$, i.e.

$$\begin{aligned} \omega _0({\varOmega }^* + F'(0)) =\max \left\{ \mathfrak {R}\lambda : \lambda \in \sigma ({\varOmega }^* + F'(0))\right\} . \end{aligned}$$

(19)

As both $F'(0)$ and $T_t^*$ are positive and $T_t^*$ has negative growth bound, it follows (see, for instance, Theorem 3.5 in Thieme 2009 where the assumption on ${\varOmega }^* + F'(0)$ being resolvent positive holds because of Theorem 3.4 since $F'(0)$ is compact) that

$$\begin{aligned}&s\bigl ({\varOmega }^* + F'(0)\bigr )< 0 \, (\text{ respectively },>0) \\&\quad \iff \rho \bigl (F'(0)(-{\varOmega }^*)^{-1} \bigr ) < 1 \, (\text{ respectively, } >1). \end{aligned}$$

Since $F'(0)$ has one-dimensional range, the only eigenvector of $F'(0)(-{\varOmega }^*)^{-1}$ is q. Hence,

$$\begin{aligned} \rho \bigl (F'(0)(-{\varOmega }^*)^{-1} \bigr ) = \int _0^\infty \beta (x) ((-{\varOmega }^*)^{-1}q)(x)\, dx. \end{aligned}$$

We have established that $u = 0$ is asymptotically stable (respectively, unstable) if

$$\begin{aligned} \int _0^\infty \beta (x) ((-{\varOmega }^*)^{-1}q)(x)\, dx < 1 \ (\text{ respectively, }\; > 1\;). \end{aligned}$$

In order to have a criterion that is easier to interpret and evaluate, we look at $\int _0^\infty \beta (x) ((-{\varOmega }^*)^{-1}q)(x)\, dx$ as the linear functional $(-{\varOmega }^*)^{-1}q$ applied to the function $\beta$. By duality, this is equal to the linear functional q applied to the function $(-{\varOmega })^{-1}\beta$. In other words,

$$\begin{aligned}&\int _0^\infty \beta (x) ((-{\varOmega }^*)^{-1}q)(x)\, dx \nonumber \\&\quad = \int _0^\infty q(x) ((-{\varOmega })^{-1} \beta )(x)\, dx = \int _0^\infty q(x) h(x) \, dx \end{aligned}$$

(20)

where $h \in C_0 (0,\infty )$ satisfies ${\varOmega }(h) = - \beta$ or, equivalently,

$$\begin{aligned} a(x) h''(x) + r(x) h'(x) = -\beta (x),\quad x \in (0,\infty ). \end{aligned}$$

(21)

Clearly, (20) can also be obtained directly through appropriate integrations by parts.

The solution to Eq. (21) can be written, using the Green function

$$\begin{aligned} G(x,\xi ) = \frac{1}{\xi } \int _0^{\min \{x,\xi \}} e^{(r/2K)[(t-K)^2 - (\xi -K)^2]}\, dt,\qquad 0 < x,\xi , \end{aligned}$$

(22)

as

$$\begin{aligned} h(x)= & {} \int _0^\infty G(x,\xi ) \beta (\xi )\, d\xi \nonumber \\ \quad= & {} \int _0^x \int _0^\xi e^{(r/2K)[(t-K)^2 - (\xi -K)^2]}\, dt \, \frac{\beta (\xi )}{\xi } \, d\xi \nonumber \\&\quad + \int _x^\infty \int _0^x e^{(r/2K)[(t-K)^2 - (\xi -K)^2]}\, dt \, \frac{\beta (\xi )}{\xi } \, d\xi \nonumber \\ \quad= & {} \int _0^x \int _t^\infty e^{(r/2K)[(t-K)^2 - (\xi -K)^2]} \, \frac{\beta (\xi )}{\xi } \, d\xi \, dt. \end{aligned}$$

(23)

It is immediate now to see that (23) is indeed solution of (21) when $a(x) = x$ and $r(x) ={\bar{r}}x(1-x/K)$. Then, (20) and (23) yield the expression in the second line of $R_0$.

As for its interpretation, note that, recalling the Definition (4) of the hitting times $\tau _{a,b}$, we see that $f_{a,b}(x)= \mathbb {E}\left( \int \limits _0^{\tau _{a,b}} \beta (X_s)\, ds | X_0 = x \right)$ satisfies (Karlin and Taylor 1981, 15.3.3) Eq. (21) in (a, b) with $f_{a,b}(a) = f_{a,b}(b) = 0$. Moreover, $f_{a,b}(x)$ has an explicit expression (Karlin and Taylor 1981, 15.3.11) whose limit for $b \rightarrow +\infty$ and $a \rightarrow 0^+$ is (23).

On the other hand, since

$$\begin{aligned} \mathbb {P}(X_{\tau _{a,b}} = b\ |\ X_0 = x) \rightarrow 0 \text{ as } b \rightarrow +\infty \text{ and } a \rightarrow 0^+, \end{aligned}$$

it follows that

$$\begin{aligned} \displaystyle \lim _{\overset{a \rightarrow 0^+}{b \rightarrow \infty }} \mathbb {E}\left( \int \limits _0^{\tau _{a,b}} \beta (X_s)\, ds\ \bigg |\ X_0 = x \right) = \mathbb {E}(\int _0^{\tau _0} \beta (X_s)\, ds\ \big |\ X_0 = x ). \end{aligned}$$

Hence, the expression on the first line of (18) is equal to that on second line. $\square$

Next we consider positive equilibria. At an equilibrium ${\bar{u}}$ of (16), necessarily

$$\begin{aligned} \lambda = \int _0^\infty \beta (x) {\bar{u}}(x)\, dx \end{aligned}$$

is constant. Then $\bigl ({\bar{E}}, {\bar{u}}(x)\bigr )$ will be the stationary distribution of the elementary return process with holding time rate $\lambda$. Using the explicit form provided by Peng and Li (2013), we obtain

$$\begin{aligned} {\bar{u}}(y) = \frac{\displaystyle \int _0^\infty q(x) G(x,y)\, dx}{\displaystyle \frac{1}{\lambda } + \displaystyle \int _0^\infty q(x) \int _0^\infty G(x,y)\, dy \, dx}. \end{aligned}$$

(24)

Let us define

$$\begin{aligned} {\varPsi }= \int _0^\infty q(x) \int _0^\infty G(x,y)\, dy \, dx = \int _0^\infty q(x) \mathbb {E}(\tau _x) \, dx. \end{aligned}$$

Then, substituting (24) in the definition of $\lambda$, we obtain

$$\begin{aligned} \lambda = \frac{\displaystyle \int _0^\infty \beta (y)\displaystyle \int _0^\infty q(x) G(x,y)\, dx\, dy}{\displaystyle \frac{1}{\lambda } + {\varPsi }}, \end{aligned}$$

and, noting that the numerator is exactly $R_0$, we have

$$\begin{aligned} \lambda = \frac{R_0 - 1}{ {\varPsi }}. \end{aligned}$$

(25)

Of course, this corresponds to a positive solution if, and only if, $R_0 > 1$. We have thus obtained the following result.

Theorem 3

Problem (16) has a positive equilibrium if and only if $R_0 > 1$. It can be written explicitly as

$$\begin{aligned} \begin{aligned} {\bar{u}}(y)&= \frac{R_0 - 1}{R_0 {\varPsi }} \int _0^\infty q(x) G(x,y)\, dx \\&= \frac{R_0 - 1}{R_0 {\varPsi }y} \int _0^y e^{({\bar{r}}/2K)[(t-K)^2 - (y-K)^2]} \int _t^\infty q(x) \, dx\, dt. \end{aligned} \end{aligned}$$

(26)

Correspondingly,

$$\begin{aligned} {\bar{E}} = 1 - \int _0^\infty {\bar{u}}(y)\, dy = 1/R_0. \end{aligned}$$

It is not difficult to check that (26) is indeed a solution of (16).

The characteristic equation at ${\bar{u}}$ can be used in order to analyze local stability of the positive equilibrium, but we shall not perform such analysis here.

5 Numerical results

We approximate the solution of (13) using finite differences in explicit form, that is backward in time with the x-derivatives discretized at the previous time level. Specifically, we let ${\varDelta }x>0$ and ${\varDelta }t>0$ be the discretization parameters (that will have to satisfy a stability condition) and we let the final time of simulation T be an integer multiple of ${\varDelta }t$ and $N=\frac{T}{{\varDelta }t}\in \mathbb {N}$. Similarly, we let $\max \text{ supp }(u_0)$ and $\max \text{ supp }(q)$ be integer multiples of ${\varDelta }x$, and define $N_{q_0}=\displaystyle \frac{\sup \{\text{ supp }(q)\}}{{\varDelta }x}$ and $N_{u_0}=\displaystyle \frac{\sup \{\text{ supp }(u_0)\}}{{\varDelta }x}$. We choose next an integer $M>\max \{N_{q_0}, N_{u_0}\}$ large enough that the practical computational support of u in x for the time span [0, T] will not exceed $M{\varDelta }x$. We introduce the computational time-grid

$$\begin{aligned} t^n=n{\varDelta }t,\quad 0\le n\le N, \end{aligned}$$

and the computational x-grid

$$\begin{aligned} x_j=j{\varDelta }x,\quad 0\le n\le M. \end{aligned}$$

For a function f of the structure variable x we use the notation $f_j=f(x_j)$ and for a function g of time t we use the notation $g^n=g(t^n)$. We want to find approximations $U_j^n$ of $u(t^n,x_j)$ for $0\le n\le N$ and $1\le j\le M$. The support in x of the approximations grows by ${\varDelta }x$ at each time-step ${\varDelta }t$. However, the magnitude of most of the approximate values on the right x-tail are so small that we can actually neglect them without introducing any appreciable errors. The numerical algorithm is

$$\begin{aligned} \left\{ \begin{array}{rl} U^n_0&{}=U^n_{M+1}=0,\qquad 0\le n\le N, \\ I^n&{}=\displaystyle \sum _{j=1}^MU^n_j,\ {\varLambda }^n=\displaystyle \sum _{j=1}^M\beta _jU^n_j,\ E^n=1-I^n,\quad 0\le n\le N, \\ \displaystyle \frac{U^{n+1}_j-U^n_j}{{\varDelta }t}&{}=\displaystyle \frac{a_{j+1}U^n_{j+1}-2a_jU^n_j+a_{j-1}U^n_{j-1}}{({\varDelta }x)^2}-\displaystyle \frac{r_{j+1}U^n_{j+1}-r_{j-1}U^n_{j-1}}{2{\varDelta }x} \\ &{}\qquad \qquad \qquad +{\varLambda }^nE^nq_j,\qquad 1\le j\le M,\,\ 0\le n\le N-1. \end{array}\right. \nonumber \\ \end{aligned}$$

(27)

For our simulations we use for both $u_0$ and q truncated inverted parabolas with support between their zeros at $x=0$ and $x=0.0333$, and at $x=0$ and $x=0.6667$, respectively. Since q must be a probability density function, we multiply the quadratic $x(0.6667-x)$ by the factor that makes its integral exactly equal to 1. For normalization purposes we take ${\bar{a}}=c=1$, and to ensure stability we need ${\varDelta }t<\frac{{\varDelta }x}{2aM}$, where we use $M=\frac{3}{{\varDelta }x}$ to establish the computational x-support of the solution u to be $[0,\frac{3}{c}]$. For the force of infection, $\lambda$, we use the infectivity function $\beta (x)=\dfrac{\alpha x}{\kappa +x}$, a classical Michaelis-Menten type.

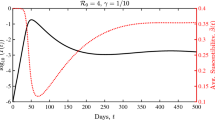
Next we present (Fig. 1) the solution corresponding to $\alpha =4.8$, $\kappa =0.3333$, ${\bar{r}}=9$, $T=50$, ${\varDelta }x=0.001$ and ${\varDelta }t=1.25\times 10^{-7}$, at various values of t, together with the initial condition (left panel). The total infected $I=I(t)$ are plotted on the right panel. The net reproduction number in this case is $R_0\approx 4.5$. We see the density of infected (or patch occupancy) approaching an equilibrium, albeit slowly.

Fig. 1

The case ${\bar{r}}=9$ with logistic growth

We present in Fig. 2 the solution corresponding to ${\bar{r}}=3$, $T=15$, ${\varDelta }x=0.001$ and ${\varDelta }t=1.25\times 10^{-7}$, at various values of t, together with the initial condition (left panel). The total infected $I=I(t)$ are plotted on the right panel. The net reproduction number was kept just above 4 by changing the parameter $\alpha$. We see on the right panel the equilibrium value $\approx 0.75$ being reached quickly (compare the largest time shown on the left panel, $T=15$ in Fig. 2 and $T=50$ in Fig. 1). We also notice a distinct qualitative difference in the equilibrium densities corresponding to ${\bar{r}}=3$ and ${\bar{r}}=9$.

Fig. 2

The case ${\bar{r}}=3$ with logistic growth

We introduce now one more parameter in the simulations, $\eta \ge 0$, to slightly modify the function r into a rational function to allow for an Allee effect: $r(x) = \left( \frac{{\bar{r}}x-\eta }{x+\eta }\right) x(1-cx)$. This function reduces to the logistic when $\eta =0$.We present (Fig. 3) the solution corresponding to the parameters used for Fig. 1, $\alpha =4.8$, $\kappa =0.3333$, ${\bar{r}}=9$, ${\varDelta }x=0.001$ and ${\varDelta }t=1.25\times 10^{-7}$, and choose $\eta =0.1$ (compared to $\eta =0$ in Fig. 1), at $t=20, 40, 60, 80, 100, 120, 140, 160, 180$ to show what seems like stabilization at the positive equilibrium solution. The right panel suggests that I is stabilizing at a value approximately equal to 0.05, albeit extremely slowly.

Fig. 3

Modified drift drastically reducing the equilibrium ($\eta =0.1$)

Finally, we show the Allee effect causing the extinction of the population by just changing the value of $\eta$ in the preceding simulation from 0.1 to 0.12. The CPU time for this simulations is fairly large (approximately 30 hours to arrive at $T=250$) but there is clear evidence of extinction considering the total infected population, I, and using its exponential fitting for $150\le t\le 250$ that is almost perfect, $I\approx 0.0882 e^{-0.0206t}$, with a Pearson coefficient of determination $R=0.99998$.

We show in Fig. 4 the x-density of infected, u, for $150\le t\le 250$ on the left panel, and the total infected population size, $I=I(t)$, (black line) in logarithmic scale, together with the exponential fitting (red dashes) on the right panel.

Fig. 4

Exponential fitting of solutions with Allee effect ($\eta = 0.12$) and the infection going extinct

6 Possible extensions

In the previous sections, we have shown how including stochasticity of internal dynamics leads to a diffusion equation in the structuring variable at the population level. In the case we have examined, the resulting equation can be analysed using the powerful tools developed for one-dimensional (degenerate) diffusion (Karlin and Taylor 1981), and this leads to explicit formulae for the reproduction number $R_0$ and the positive equilibrium.

Undoubtedly, the dynamics at the individual level is extremely simple, and several extensions are needed in order to make the model useful either in the analysis of specific infections or for theoretical investigations.

First, note that all analytical computations have been performed under the assumption that the deterministic growth rate r(x) is such that dynamics at the individual level follows the logistic model. However, in many cases it may be more appropriate to assume that $r(x) < 0$ for $x > 0$ small; in other words, a minimum dose is necessary for infection to take over (if we look at the epidemic interpretation); in the other interpretation, local populations are subject to an Allee effect. Such extension does not pose theoretical problems, but would simply make the expressions for $R_0$ more complex. Here we have examined this case only through numerical simulations.

Another extension that does not pose major mathematical problems, but is biologically relevant is the inclusion of heterogeneity in individuals (or patches) (Gyllenberg and Hanski 1997; Pugliese 2011), for instance by attaching an index $\omega$ to individuals. From the mathematical point of view, this would entail an extra integral in all formulae, as long as there is no correlation between the indexes of the infectious and the newly infected. Certainly, in that case one may reasonably question whether it makes sense to assume an infinite population at all values of $\omega$.

A limitation of the current model is that a fixed set of individuals (or patches) is considered; the model only describes the dynamics of the distribution of pathogen load (or population) in those. While this may be somewhat reasonable for patches in metapopulations, it does not make much sense for individuals. This has routinely been done for macroparasite models (they can be seen as infection models where the internal structure is discrete) without leading to big changes in the structure of equations (see for instance Kretzschmar 1993; Milner and Patton 2003).

An important extension would be to assume a more complex internal dynamics: infections develop but then are controlled by the immune system; populations grow but then exhaust resources. One could attempt to model this by passing to an (at least) two-dimensional state (x, y), or giving an age to new infections (colonizations) and letting parameters change with age. We are currently extending the numerical schemes presented in Sect. 5 to cover this case. The theoretical analysis for that case is out of reach at this time.

The most complex extension would be to introduce reinfections, respectively, colonizations also of occupied patches: one could assume that emigrants into a patch at level y bring it instantaneously to level $y + x$ with probability density q(x). This would make it possible to analyze the effect of reinfections (particularly when a minimum dose of infection is necessary for infection success); in metapopulations, this has been called the rescue effect (Gyllenberg and Hanski 1997). Mathematically, the problem becomes enormously more complex because it can no longer be represented as a semilinear equation (perturbation of a well-understood linear differential operator). Still, as the problem is extremely relevant biologically, simplified approaches are probably necessary: see, for instance de Graaf et al. (2014) who fitted available data on pertussis antibody titers through a model of this type, with a force of infection taken as an external input of the model, instead of dependent on the infection level in the population.

A Appendix

We present here the details of the proofs of Propositions 1 and  3.

Proof

(of Proposition 1) We wish to show that the growth bound of $T_t ^*$ is negative. First of all, note that any $f \in L^1$ can be written as $f = f_+ - f_-$, with $\Vert f \Vert _1 = \Vert f_+\Vert _1 + \Vert f_-\Vert _1$ and $\Vert T_t^* f \Vert _1 \le \Vert T_t^* f_+\Vert _1 + \Vert T_t^*f_-\Vert _1$. Therefore, it suffices to consider only nonnegative functions.

If $f \ge 0$, the norm of $T_t ^*f$ can be written as

$$\begin{aligned} \Vert T_t^* f\Vert _1 = \int _0^\infty \int _0^\infty f(\xi ) p_0(t,x,\xi )\,d\xi \, dx = \int _0^\infty f(\xi ) \mathbb {P}_\xi ( \tau _0 > t)\, d\xi ; \end{aligned}$$

the last term can be interpreted as $\mathbb {P}_f ( \tau _0 > t)$ if f is a probability density that represents the initial distribution.

It is well known (see for instance Méléard and Villemonais 2012, Theorem 18) that for each $\xi > 0$, $\displaystyle \lim _{t \rightarrow \infty } \mathbb {P}_\xi ( \tau _0 > t) = 0$. However, we also need to prove exponential convergence uniformly in $\xi$.

In order to do that, we use the transformation and methods from Cattiaux et al. (2009). Specifically, let $Z_t = 2 \sqrt{X_t}$. Then,

$$\begin{aligned} dZ_t = \left( - \frac{1}{2 Z_t }+ \frac{{\bar{r}} Z_t}{ 2} - \frac{{\bar{r}} Z_t^3}{8K }\right) dt + dW_t. \end{aligned}$$

(28)

It is clear that $\mathbb {P}(X_t> 0) = \mathbb {P}(Z_t > 0)$. Hence, the distribution of the variable $\tau _0$ is the same for either process.

First of all, for the process $Z_t$ Cattiaux et al. (2009) proved (Theorem 5.2) that, for each $z > 0$,

$$\begin{aligned} \lim _{t \rightarrow \infty } e^{\lambda _1 t} \mathbb {P}_z( \tau _0 > t) = \eta _1(z) \langle \eta _1, 1 \rangle _\mu , \end{aligned}$$

(29)

where $\lambda _1 > 0$ is the first eigenvalue of the generator of the process in the space $L^2(\mu )$, $\eta _1$ is the corresponding (positive) eigenfunction and

$$\begin{aligned} \mu (dz) = m(z)\, dz \text{ with } m(z) = C \frac{1}{z }\exp \left\{ \frac{rz^2}{2 }\left( 1 - \frac{z^2}{8K }\right) \right\} . \end{aligned}$$

Note that m(z) is the speed density for the process $Z_t$.

Cattiaux et al. (2009) also proved (Proposition 4.1) that $\eta _1$ is an increasing function. If we could establish that it is also a bounded function, the conclusion would follow immediately. As this is not obvious, we rather prove that $\mathbb {P}_\xi ( \tau _0 > t)$ is uniformly exponentially bounded in $\xi$, by a more direct computation. $\square$

Lemma 1

There exist $\lambda > 0$ and $M \ge 1$ such that for all $z \ge {\bar{z}}$

$$\begin{aligned} \mathbb {P}_z(\tau _0 > t) \le M e^{-\lambda t} \qquad t \ge 0. \end{aligned}$$

Proof

We start by exploiting Theorem 7.3 from (Cattiaux et al. 2009) that shows that the process $Z_t$ comes down from infinity, i.e. there exist ${\bar{z}}$ and $t_0$ such that

$$\begin{aligned} \lim _{z \rightarrow \infty } \mathbb {P}_z (\tau _{{\bar{z}}} < t_0) = p > 0 \end{aligned}$$

where

$$\begin{aligned} \tau _{{\bar{z}}} = \inf \{ t > 0: Z_t \le {\bar{z}}\}. \end{aligned}$$

Hence for all z,

$$\begin{aligned} \mathbb {P}_z ( \tau _{{\bar{z}}} > t_0) \le 1 - p. \end{aligned}$$

(30)

It follows that

$$\begin{aligned}&\mathbb {P}_z( \tau _{{\bar{z}}}> n t_0) = \int _{{\bar{z}}}^\infty \mathbb {P}_z( \tau _{{\bar{z}}}> n t_0 | Z_{(n-1)t_0} = \xi ) \mathbb {P}_z(Z_{(n-1)t_0} = d\xi ) \\&\quad = \int _{{\bar{z}}}^\infty \mathbb {P}_\xi (\tau _{{\bar{z}}}> t_0) \mathbb {P}_z(Z_{(n-1)t_0} = d\xi ) \le (1-p) \\&\quad \int _{{\bar{z}}}^\infty \mathbb {P}_z(Z_{(n-1)t_0} = d\xi ) = (1-p) \mathbb {P}_z ( \tau _{{\bar{z}}} >(n-1) t_0). \end{aligned}$$

Hence, by induction,

$$\begin{aligned} \mathbb {P}_z ( \tau _{{\bar{z}}} > n t_0) \le (1 - p)^n. \end{aligned}$$

(31)

Now take T such that (using 29)

$$\begin{aligned} P_{{\bar{z}}} ( \tau _0> t) \le 2 \eta _1({\bar{z}}) \langle \eta _1, 1 \rangle _\mu e^{-\lambda _1 t}= M_0 e^{-\lambda _1 t} \quad \forall \ t > T. \end{aligned}$$

For $t > T + t_0$ and $z > {\bar{z}}$, let $n = [(t-T)/t_0]$; then, we have

$$\begin{aligned}&\mathbb {P}_z(\tau _0> t) = \int _0^{nt_0} \mathbb {P}_z(\tau _0> t | \tau _{{\bar{z}}} = s) \mathbb {P}_z(\tau _{{\bar{z}}} = ds) + \mathbb {P}_z(\tau _0> t | \tau _{{\bar{z}}}>nt_0) \\&\quad \mathbb {P}_z (\tau _{{\bar{z}}}> n t_0) . \end{aligned}$$

Furthermore,

$$\begin{aligned} \mathbb {P}_z(\tau _0> t | \tau _{{\bar{z}}} = s) = \mathbb {P}_{{\bar{z}}} (\tau _0 > t - s). \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{array}{rl} \mathbb {P}_z(\tau _0> t) &{}\le \int \limits _0^{nt_0} \mathbb {P}_{{\bar{z}}} (\tau _0> t - s) \mathbb {P}(\tau _{{\bar{z}}} = ds) + \mathbb {P}_z (\tau _{{\bar{z}}}> nt_0) \\ &{}\le \sum \limits _{j=0}^{ n-1} \int \limits _{j t_0}^{(j+1) t_0} \mathbb {P}_{{\bar{z}}} (\tau _0> t - s) \mathbb {P}(\tau _{{\bar{z}}} = ds) + (1-p)^n \\ &{}\le \sum \limits _{j=0}^{ n-1} \mathbb {P}_{{\bar{z}}} (\tau _0 > t-(j+1)t_0) \mathbb {P}(j t_0 \le \tau _{{\bar{z}}} \le (j+1)t_0 ) + (1-p)^n \\ &{}\le \sum \limits _{j=0}^{ n-1} M_0 e^{-\lambda _1 (t- (j+1) t_0)}(1-p)^j + (1-p)^n \\ &{}= M_0 e^{-\lambda _1 (t- t_0)}\frac{e^{\lambda _1 t_0 n}(1-p)^n - 1}{e^{\lambda _1 t_0 }(1-p) - 1 } +(1-p)^n, \end{array} \end{aligned}$$

assuming $\lambda _1 \not = - \frac{\log (1-p)}{t_0 }$; otherwise, a simple modification is necessary.

Let

$$\begin{aligned} \lambda _0 = - \frac{\log (1-p)}{t_0 }\qquad \lambda = \min \{\lambda _0,\lambda _1\}. \end{aligned}$$

Then,

$$\begin{aligned} \mathbb {P}_z(\tau _0 > t)\le & {} M_0 e^{-\lambda _1(T-t_0)}e^{-\lambda _1 t_0 n} \frac{e^{(\lambda _1-\lambda _0)t_0 n}-1}{e^{(\lambda _1-\lambda _0)t_0 }-1 } + e^{-\lambda _0 t_0 n} \le M_1 e^{-\lambda t_0 n} \\\le & {} M_1 e^{-\lambda (t-T-t_0)} . \end{aligned}$$

We have then proved the lemma for $t > T+t_0$ with $M = M_1 e^{\lambda (T+t_0)}$. Choosing $M_1 \ge 1$, the lemma obviously holds also for $t \le T+t_0$. $\square$

We can now compute

$$\begin{aligned} \Vert T_t^* f\Vert _1= & {} \int _0^\infty f(\xi ) \mathbb {P}_\xi ( \tau _0> t)\, d\xi = \int _0^{{{\bar{z}}}^2} f(\xi ) \mathbb {P}_\xi ( \tau _0> t)\, d\xi \\&\quad + \int _{{{\bar{z}}}^2}^\infty f(\xi ) \mathbb {P}_\xi ( \tau _0> t)\, d\xi \\&\le \mathbb {P}_{{\bar{z}}} ( \tau _0 (Z_t) > t) \int _0^{{{\bar{z}}}^2} f(\xi ) \, d\xi + M_1 e^{-\lambda t} \int _{{{\bar{z}}}^2}^\infty f(\xi )\, d\xi \\&\le M_0 e^{-\lambda _1 t} \int _0^{{{\bar{z}}}^2} f(\xi ) \, d\xi + M_1 e^{-\lambda t} \int _{{{\bar{z}}}^2}^\infty f(\xi )\, d\xi \le M e^{-\lambda t} \Vert f \Vert . \end{aligned}$$

Hence

$$\begin{aligned} \lim \sup _{t \rightarrow \infty } \log (\Vert T_t^*\Vert _1) \le - \lambda < 0 , \end{aligned}$$

which shows that the growth bound of $T_t^*$ in $L^1(0,\infty )$ is negative. $\square$

Proof

(of Proposition 3) For $t\in [0,T]$, let

$$\begin{aligned} \lambda (t) = \int \limits _0^\infty \beta (x) u(t,x)\,dx. \end{aligned}$$

We shall argue by contradiction. Since $\lambda (0) > 0$, by continuity it follows that $\lambda (t) > 0$ for t small; thus we define

$$\begin{aligned} \tau = \inf \{ t \in [0,T] : \lambda (t) < 0\}. \end{aligned}$$

This is just saying that $\tau$ is the first positive time at which $\lambda$ vanishes. On $[0,\tau ]$ the solution u of (16) can be written probabilistically as the density function of a process $Y_t$, a variation of the elementary return process introduced by Feller (1954). Following the construction used by Peng and Li (2013) (in a much simpler case than the original), we write $u(t,\cdot )$ explicitly as the transition probability function for $Y_t$ using simple ingredients. In fact, although all terms may be interpreted probabilistically, we shall just build the needed ingredients for our construction of the solution.

Let

$$\begin{aligned} A(t,\xi ) = 1 - \int _0^\infty p_0(t,x;\xi )\, dx > 0 \end{aligned}$$

(32)

be the probability that process $X_t$ is absorbed at $x=0$ before time $t > 0$, conditional on $X_0 = \xi$, and let

$$\begin{aligned} {\bar{A}}(t) = \int _0^\infty A(t;\xi ) q(\xi )\, d\xi \end{aligned}$$

represent the absorption probability if the initial distribution is q.

Let

$$\begin{aligned} E_0 = 1- \int _{0}^{\infty } u_0(x)\, dx \ge 0, \end{aligned}$$

and define, for $t>0$,

$$\begin{aligned} F_1(t) = \int _0^\infty A(t;\xi ) u_0 (\xi )\, d\xi + E_0 \int _0^t \lambda (s) e^{-\int _0^s \lambda (u)\, du} {\bar{A}}(t-s) \, ds. \end{aligned}$$

(33)

$F_1$ can be interpreted as the probability that the process $Y_t$ gets absorbed at least once by time t.

As $F_1$ is continuous and increasing, we can consider its derivative $f_1= F_1'$ and—to simplify notation—we assume $F_1(t) = \int \limits _0^t f_1(s)\,ds$; if not, one should simply interpret the following integrals as Stieltjes integrals reading $f_1(t)\, dt$ as $dF_1(t)$ and similarly for $f_n(t)$ defined below.

We then define iteratively the function $F_n, n\ge 1,$ as

$$\begin{aligned} F_n( t) = \int _0^t f_{n-1}(s) \int _s^t \lambda (u) e^{-\int _s^u \lambda (v)\, dv}{\bar{A}}(t-u)\, du \, ds. \end{aligned}$$

(34)

From (34), as ${\bar{A}}$ is a non-decreasing function, we derive the following bound for any $t \le T$:

$$\begin{aligned} \begin{aligned} F_n(t)&\le \int _0^t f_{n-1}(s) \int _s^t \lambda (u) e^{-\int _s^u \lambda (v)\, dv} {\bar{A}}(t-s) \, du \, ds \\&= \int _0^t f_{n-1}(s) \left( 1 - e^{-\int _s^t \lambda (v)\, dv}\right) {\bar{A}}(t-s) \, ds \le \rho F_{n-1}(t) \end{aligned} \end{aligned}$$

(35)

with

$$\begin{aligned} \rho = \left( 1 - e^{-\int _0^T \lambda (v)\, dv} \right) {\bar{A}}(T) < 1. \end{aligned}$$

(36)

This ensures that the series $\sum \limits _{n=1}^\infty F_n$ converges uniformly on [0, T].

Now let us define

$$\begin{aligned} E(t) = E_0 \exp \left\{ -\int _0^t \lambda (v)\, dv\right\} + \sum _{n=1}^{\infty } \int _0^t f_{n}(s) \exp \left\{ -\int _s^t \lambda (v)\, dv\right\} ds, \end{aligned}$$

(37)

and

$$\begin{aligned} \begin{aligned} u(t,x)&= \int _0^\infty u_0(\xi )p_0(t,x;\xi )\, d\xi \\&\quad + E_0 \int _0^t \lambda (s) e^{-\int _0^s \lambda (v)\, dv} \int _0^\infty q(\xi ) p_0 (t-s,x;\xi )\, d\xi \, ds \\&\quad + \sum _{n=1}^{\infty } \int _0^t f_n(s)\int _s^t \lambda (u) e^{-\int _s^u \lambda (v)\, dv} \int _0^\infty q(\xi ) p_0 (t-u,x;\xi )\, d\xi \, du\, ds \\&= \int _0^\infty u_0(\xi )p_0(t,x;\xi )\, d\xi + \int _0^t \lambda (s) E(s) \int _0^\infty q(\xi ) p_0 (t-s,x;\xi )\, d\xi \,ds . \end{aligned} \end{aligned}$$

(38)

We wish to prove that u(t, x) is, in fact, an explicit form of the solution to (16). By construction, it is clear that both E and u are positive. Moreover, we have

$$\begin{aligned} \int _0^\infty u(t,x)= & {} \Vert u_0\Vert _1 - \int _0^\infty u_0(\xi ) A_0(t,\xi )\,d\xi + E_0 \left( 1 - e^{-\int _0^t \lambda (v)\, dv}\right) \\&\quad -\,E_0 \int _0^t \lambda (s)e^{-\int _0^s \lambda (v)\, dv} {\bar{A}} (t-s)\, ds \\&\quad \,+ \sum _{n=1}^{\infty } \int _0^t f_n(s) \left( 1 - e^{-\int _s^t \lambda (v)\, dv}\right) \, ds \\&\quad -\,\sum _{n=1}^{\infty } \int _0^t f_n(s) \int _s^t \lambda (u)e^{-\int _s^u \lambda (v)\, dv} \, du\, ds \\= & {} \Vert u_0\Vert _1 + E_0 - \int _0^t f_1(s)\, ds - E(t) \\&\quad +\,\sum _{n=1}^{\infty } \int _0^t f_n(s)\,ds - \sum _{n=1}^{\infty } \int _0^t f_{n+1}(s)\,ds, \end{aligned}$$

the last step coming from (34). Hence we have obtained

$$\begin{aligned} \Vert u(t)\Vert _1 = 1 - E(t) \qquad \text{ for } \text{ all } t \in [0,\tau ], \end{aligned}$$

where $E(\cdot ) > 0$ is defined in (37). Thus, we have proved $\Vert u(\tau )\Vert _1 < 1$. Finally, from the last line of (38), it is easy to see that

$$\begin{aligned} u_t(t,x) = \partial _x \biggl [ \bigl (a( x ) u(t,x)\bigr )_x - r(x) u(t,x) \biggr ] + \lambda (t) E(t) q(x), \end{aligned}$$

with $E(t) = 1 - \Vert u(t)\Vert _1$, and thus u is indeed the solution of (16).

Since $u(\cdot ) \ge 0$ and $\lambda$ was defined as

$$\begin{aligned} \lambda (t) = \int _0^\infty \beta (x) u(t,x)\, dx, \end{aligned}$$

we have obtained a contradiction with the existence of $\tau = \inf \{ t \in [0,T] : \lambda (t) < 0 \}$, because the set defining it is empty.

Hence (38) holds for all $t \in [0,T]$, and we have established that $u(t) \ge 0$ and $\Vert u(t) \Vert _1 < 1$ on this interval. $\square$