Optimal control approach for establishing wMelPop Wolbachia infection among wild Aedes aegypti populations

Abstract

Wolbachia-based biocontrol has recently emerged as a potential method for prevention and control of dengue and other vector-borne diseases. Major vector species, such as Aedes aegypti females, when deliberately infected with Wolbachia become less capable of getting viral infections and transmitting the virus to human hosts. In this paper, we propose an explicit sex-structured population model that describes an interaction of uninfected (wild) male and female mosquitoes and those deliberately infected with wMelPop strain of Wolbachia in the same locality. This particular strain of Wolbachia is regarded as the best blocker of dengue and other arboviral infections. However, wMelPop strain of Wolbachia also causes the loss of individual fitness in Aedes aegypti mosquitoes. Our model allows for natural introduction of the decision (or control) variable, and we apply the optimal control approach to simulate wMelPop Wolbachia infestation of wild Aedes aegypti populations. The control action consists in continuous periodic releases of mosquitoes previously infected with wMelPop strain of Wolbachia in laboratory conditions. The ultimate purpose of control is to find a tradeoff between reaching the population replacement in minimum time and with minimum cost of the control effort. This approach also allows us to estimate the number of Wolbachia-carrying mosquitoes to be released in day-by-day control action. The proposed method of biological control is safe to human health, does not contaminate the environment, does not make harm to non-target species, and preserves their interaction with mosquitoes in the ecosystem.

1 Introduction

Aedes aegypti is an invasive mosquito species that has colonized all tropical and sub-tropical regions worldwide and its presence and abundance in many tropical countries are strongly correlated with dengue infections (see, e.g., Jansen and Beebe 2010; Brown et al. 2011; references therein).

According to Sinkins (2004) and Hilgenboecker et al. (2008), Wolbachia is a maternally inherited bacterial symbiont which is naturally present in many insects, including some mosquito species. It also induces a particular reproductive phenotype known as cytoplasmic incompatibility (CI, see, e.g., Turelli and Hoffmann 1991; Telschow et al. 2007). Roughly speaking, CI phenotype enables a Wolbachia-infected female to produce viable and Wolbachia-infected offspring as a result of her mating with either infected or uninfected male, while ensuring the absence of viable offspring originated from mating between uninfected females and Wolbachia-infected males.

Ruang-Areerate and Kittayapong (2006) assert that the presence of Wolbachia has never been detected in wild populations of Aedes aegypti mosquitoes; however, there is sufficient evidence that this mosquito species is susceptible to so-called Wolbachia “transinfection”, i.e. a deliberate infection of wild mosquitoes by Wolbachia pathogen taken from other insect species (Xi et al. 2005; Ruang-Areerate and Kittayapong 2006; McMeniman et al. 2009). This process is usually held in laboratory conditions and can be viewed as “cultivation” of Wolbachia-carriers.

Traditional methods aimed at reduction of vector population rely heavily on the larvicide and insecticide spraying, particularly during the dengue outbreaks. However, these chemical substances are rather expensive to be employed as a preventive measure in public health programs. Additionally, they are harmful to other non-target species, contaminate the environment with chemical residuals, and may induce resistance in mosquito populations over time. As an alternative, many scholars suggest various types of biological control of vector populations, including Wolbachia-based biocontrol (Moreira et al. 2009; Hancock et al. 2011a, b; Walker et al. 2011; McGraw and O’Neill 2013; Frentiu et al. 2014a, b), which preserves the natural ecosystems and has a remarkably preventive character. Moreover, this method is completely safe for humans since Wolbachia cannot be transferred to humans through the bite of infected mosquitoes (see Popovici et al. 2010; references therein). The same work provides solid argument on this issue and gives sufficient evidence proving that:

• Wolbachia only invades insect species, as well as spiders, mites, and terrestrial crustaceans;

• Wolbachia is not transferred to plants, water, soil, or earthworms;

• Wolbachia is non-transferrable horizontally through predator-prey interaction¹.

All the above makes Wolbachia-based biocontrol even more attractive in the context of dengue prevention and control given its environmental friendliness, safety to human health and potential cost-effectiveness (Frentiu et al. 2014a). There is enough scientific evidence (McMeniman et al. 2009; Hoffmann et al. 2011; Walker et al. 2011; Bull and Turelli 2013; Sinkins 2013; Frentiu et al. 2014b) that Wolbachia have the potential to spread widely and ultimately thwart the mosquito’s ability to transmit the dengue viruses (DENV1-DENV4) by a combination of three basic mechanisms:

• direct reduction and/or blocking of virus transmission ability;

• shortening the mosquito lifespan so that she cannot mature the viral infection and dies before becoming infectious;

• reduction of wild mosquito populations caused by CI phenotype (inviable eggs produced by uninfected females after mating with Wolbachia-infected males).

In general terms, Wolbachia-based biocontrol basically seeks to replace the wild mosquitoes, which are capable of transmitting dengue and other vector-borne diseases, with Wolbachia-infected ones, whose capacity of disease transmission is very low.

Several mathematical models describing the Wolbachia invasion in wild population of mosquitoes have been proposed, including the simplest frequency-based models consisting of one equation (Turelli 2010; Schraiber et al. 2012), two-state model including only female mosquitoes (Campo-Duarte et al. 2017a, b), stage-structured models (Farkas and Hinow 2010; Hancock et al. 2011a), models with spacial dispersion (Barton and Turelli 2011; Hancock and Godfray 2012), models dealing with fitting of experimental data (Coelho and Codeço 2011; Koiller et al. 2014), models assessing the effect of Wolbachia in dengue dynamics (Hancock et al. 2011b; Hughes and Britton 2013; Ndii et al. 2015), and the model involving a proportional feedback law for Wolbachia infestation (Bliman et al. 2015).

Recently, Farkas et al. (2017) proposed a large-scaled sex-structured model that addresses Wolbachia invasion in wild mosquito population. This advanced model can be adjusted to different mosquito species and Wolbachia strains, since it comprises the possibilities for including imperfect maternal transmission of Wolbachia, incomplete CI phenotype, and male-killing effect.

All these models reveal the bistable nature of Wolbachia dynamics and are characterized by the existence of a threshold in the proportion between wild and Wolbachia-infected mosquitoes² above which the invasion and stabilization of Wolbachia can be achieved.

Depending on the Wolbachia strain and the DENV serotype, a stronger or weaker impact on dengue transmissibility can be expected. In particular, the wMelPop strain of Wolbachia causes complete blockage of the different serotypes of dengue and also acts as an effective blocker of other arboviruses (Moreira et al. 2009; Walker et al. 2011; Ferguson et al. 2015; Dutra et al. 2016). Other Wolbachia strains, such as wMel and wAlbB, are also capable of inhibiting the replication of dengue virus in mosquitoes but to a lesser extent than wMelPop strain (Bian et al. 2010; Walker et al. 2011; Ferguson et al. 2015).

All three Wolbachia strains, which are currently being studied in the context of biocontrol for arboviral infections (wAlbB, wMel and wMelPop), induce maternal transmission rates and CI levels close to 100% in Aedes aegypti mosquitoes³, which facilitates the infection spread among wild mosquito populations (Xi et al. 2005; McMeniman et al. 2009; Walker et al. 2011). However, many scholars point out that wMelPop strain is associated with high “fitness costs” since it reduces the female fecundity, viability of eggs, and the lifespan of infected mosquitoes (McMeniman and O’Neill 2010; Schraiber et al. 2012; Hoffmann 2014; Ross et al. 2014; Ritchie et al. 2015). The latter explains the failure of the 2012 field experiments targeting to establish wMelPop-infected Aedes aegypti in Australia and Vietnam by several abundant releases of mosquitoes infected with wMelPop Wolbachia strain (Yeap et al. 2014; Nguyen et al. 2015). Effectively, the infection frequency started to decline after suspension of these releases and wild mosquitoes may finally supplant all Wolbachia-carriers.

Although the fitness costs of wMel and wAlbB are regarded as low (wMel) and moderate (wAlbB) by different scholars, these two strains induce lower levels of dengue virus inhibition than wMelPop strain, so their effect on the disease transmission would be sufficient to eliminate dengue in low or moderate transmission settings, but may be insufficient to achieve complete control of dengue in hyper-endemic areas (Ferguson et al. 2015).

On the other hand, the life-shortening effect of wMelPop grants another advantage to biocontrol strategies based on this particular strain of Wolbachia. Dengue, as well as other vector-borne pathogens, requires a period of virus incubation⁴ within the mosquito vector before the virus can be transmitted to a new human host. In other words, only older female mosquitoes are able to transmit dengue. The transinfection of mosquitoes with wMelPop strain virtually removes older mosquitoes from the population, thus substantially reducing the pathogen transmission to human hosts.

In summary, despite its high fitness costs and little success in field trials (Yeap et al. 2014; Nguyen et al. 2015), wMelPop strain should not be discharged yet as a candidate for dengue control programs due to its three abilities recapitulated by Woolfit et al. (2013):

• to invade mosquito populations through CI and maternal transmission,

• to reduce the proportion of older mosquitoes in the population responsible for the majority of disease transmission,

• to confer stronger inhibition of dengue virus replication in mosquitoes.

Therefore, our study is focused on the mathematical modeling of wMelPop Wolbachia invasion of wild Aedes aegypti population, which is a challenging task given the reduced fitness of wMelPop and its difficulty in establishing and persisting (McMeniman and O’Neill 2010; Schraiber et al. 2012; Hoffmann 2014; Ross et al. 2014; Ritchie et al. 2015).

In this paper, we propose a sex-structured model that explicitly displays the maternal transmission of Wolbachia from one generation to another together with the reproductive phenotype of cytoplasmic incompatibility (see Sect. 2).⁵ This model has so-called compartmental nature where the total mosquito population is subdivided into four interacting and homogeneously mixed subpopulations (uninfected and Wolbachia-infected males and females) what allows to represent the infection evolution by finite-dimensional ordinary differential equations. It is worthwhile to note that our model can be viewed as an extended continuous-time version of the discrete-time model for sexual insect reproduction without pair formation initially proposed by Lindström and Kokko (1998). Therefore, it differs from the sex-structured model of Farkas et al. (2017) which can be regarded as an extension of continuous-time human demographic model with pair formation attributed to Keyfitz (1972) (see also Remark 1).

Our model also exhibits bistability, which is in line with all previously developed models. The core advantage of our model is its straightforwardness and explicitness that allows for natural introduction of the decision variable (control) in order to simulate continuous (daily) releases of Wolbachia-infected mosquitoes.

Maternal transmission certainly makes the Wolbachia-infected female a “driving force” of Wolbachia infection within wild populations of mosquitoes since Wolbachia spreads and persists when it reaches an infection frequency in the population such that an average infected female has more offspring than an average uninfected female. On the other hand, the presence and abundance of Wolbachia-infected males gives an indirect reproductive advantage to Wolbachia-carrying females due to cytoplasmic incompatibility. As the number of matings between uninfected females and infected males increases, an average uninfected female starts to lose a fraction of her viable offspring.

Therefore, the introduction of Wolbachia into wild Aedes aegypti populations should be performed by releasing Wolbachia-infected males and females, which are previously “cultivated” in laboratory conditions. It is worthwhile to note that some male-biased release strategies have been proved viable (Hancock et al. 2011b). However, such interventions should be more expensive in practice than unbiased releases since they must account for additional costs related to female elimination at larvae, pupae, or adult stages.

In this paper, we design the release programs (or strategies) which can be implemented in practice. These strategies are computed off-line before the beginning of the intervention; therefore, it is feasible to estimate their underlying costs as well as the daily numbers of Wolbachia-carriers to be cultivated for the releases.

Using our model we have shown that the population replacement with wMelPop strain cannot be achieved by a single release (no matter how abundant it is) when the densities of wild mosquitoes are close to equilibrium values.⁶ As an alternative, we have proposed in Sect. 3 two options, namely:

• 1. Multiple continuous releases with constant release rate (see Sect. 3.1); in this case, at each day t we release a certain number of Wolbachia-infected mosquitoes, previously cultivated in laboratory, and this number is defined as a constant fraction of the total number of mosquitoes infected with Wolbachia which are currently present in the locality at the same day t.

• 2. Multiple continuous releases with variable release rate (see Sect. 3.2); in this case, the release rate is a function of time, and the fraction of Wolbachia-infected mosquitoes to be released daily varies from 1 day to another.

Both options guarantee an eventual replacement of the wild Aedes aegypti population with a Wolbachia-infected one. However, first option requires to release huge numbers of Wolbachia-infected mosquitoes and does not account for the costs related to their laboratory cultivation. Under this approach, not all released mosquitoes effectively contribute to the population replacement, a great portion of them may simply die (without producing a Wolbachia-infected offspring!) due to the competition with coevals (both infected and uninfected).

On the other hand, second option seems more reasonable. We formulate it by using the frameworks of optimal control theory and we clearly define the replacement goal that consists in driving the population of wild females towards extinction. Additionally, our setting allows to minimize the costs related to laboratory cultivation of Wolbachia-carriers and to estimate the finite horizon of population replacement.

Section 4 is devoted to the numerical solution of the optimal control problem formulated in the preceding section and focuses on the interpretation of simulation results. All numerical calculations have been carried out using the entomological parameters of wMelPop strain of Wolbachia, which is regarded as the best blocker of dengue and other arboviruses (Moreira et al. 2009; Walker et al. 2011; Ferguson et al. 2015) but possesses a rather high fitness cost (McMeniman and O’Neill 2010; Hoffmann 2014; Ross et al. 2014; Ritchie et al. 2015).

For numerical solution of optimal control problems, we have applied GPOPS-II software package and its brief description is given in the “Appendix B”. Finally, Sect. 5 presents the conclusions and ideas for further research.

2 Modeling framework

2.1 Population dynamics of wild Aedes aegypti mosquitoes

We start by presenting a general framework of sexual reproduction model without pair formation which is applicable to many insect species. This model has been concisely described by Kot (2001) in the following way:

$$\begin{aligned} \left. \begin{array}{rcl} \dfrac{d M}{dt} &{} = &{} \epsilon \varLambda ( F, M ) - \mu M, \\ &{} &{} \\ \dfrac{d F}{dt} &{} = &{} (1- \epsilon ) \varLambda ( F, M ) - \delta F, \\ \end{array} \right\} \end{aligned}$$

(1)

where M(t), F(t) represent the densities of wild male and female mosquitoes at the moment $t \ge 0$, respectively; $\epsilon : (1-\epsilon )$ expresses the primary sex ratio in offspring which is usually supposed to be 1 : 1; $\mu> \delta >0$ are sex-specific mortality rates for males and females [according to Liles (1965), mating females have higher average longevity than mating males]. Function $\varLambda ( F, M)$ in (1) is a so-called “per capita birth function” which expresses the recruitment rate of new individuals (i.e., an average number of viable offsprings per unit time that survive to the adulthood) derived from successful mating between males and females. Caswell and Weeks (1986) claimed that the harmonic form of birth function is considered to be the least flawed choice since it fulfils a number of criteria for sexual reproduction. Namely, it is non-negative and non-decreasing with respect to male and female densities, and vanishes whenever there is a complete lack of either males or females, that is, $\varLambda (0,M)=\varLambda (F,0)=0$.

On the other hand, birth functions should reflect the density-dependent regulation during larval development of Aedes aegypti mosquitoes which was observed yet by Dye (1984) three decades ago. The latter can be modeled using the idea developed by Lindström and Kokko (1998) for discrete-time sex-structured population models; namely, by setting

$$\begin{aligned} \varLambda ( F, M) = \frac{ \rho M F}{M+F} \, e^{-\sigma (M+F)}, \end{aligned}$$

(2)

where $\rho$ stands for the number of viable eggs laid by one female mosquito in average per day, while the exponential term expresses the survival of eggs through larvae and pupae stages and the parameter $\sigma >0$ regulates the larvae development into adults under density dependence and larval competition. Thus, higher values of $\sigma$ imply stronger competition and fewer breeding sites, while its lower values permit that a larger fraction of eggs survive to the adulthood. Regarding the values of $\epsilon , \rho , \mu$, and $\delta$ it is logical to suppose that

$$\begin{aligned} \epsilon \rho> \mu , \quad (1-\epsilon ) \rho> \delta , \quad \text{ and } \quad \rho > \mu + \delta . \end{aligned}$$

(3)

The latter implies that the number of viable eggs laid at each day exceeds the number of adult mosquitoes that die at the same day due to natural causes.

Remark 1

It should be emphasized that birth function $\varLambda ( F, M)$ defined by (2) comprises the competition between all mosquito larvae (i.e. those to be further developed as males and females) at the aquatic stage. On the other hand, Farkas et al. (2017) propose another birth function of the form

$$\begin{aligned} \varLambda (M,F) = \frac{\lambda (F) M F}{M + F}, \end{aligned}$$

(4)

where $\lambda (F)$ is a monotonically decreasing function of the total number of only females effectively present in the locality at the moment t that approaches a positive limit as $F \rightarrow \infty$. Under this definition, $\lambda (F)$ can be viewed as the density-dependent egg-laying rate. However, both birth functions (2) and (4) become compatible if we allow for $\lambda (F)$ to be a monotonically decreasing function of total mosquito population, that is $\lambda (M+F)$.

It is easy to see that our model (1) with the birth function $\varLambda ( F, M)$ defined by (2) fits the definition of Kolmogorov system for obligatory mutualism (Brauer and Castillo-Chávez 2012) and can be written as

$$\begin{aligned} \,\, \dfrac{d M}{dt}= & {} M \, f(M,F), \quad f(M,F) = \frac{ \epsilon \rho F}{M+F} \, e^{-\sigma (M+F)} - \mu , \end{aligned}$$

(5a)

$$\begin{aligned} \dfrac{d F}{dt}= & {} F \, g(M,F), \quad g(M,F)= \frac{ (1- \epsilon ) \rho M}{M+F} \, e^{-\sigma (M+F)} - \delta . \end{aligned}$$

(5b)

Here f(M, F) and g(M, F) express the per capita growth rates of males and females which are strictly negative in the absence of the opposite sex (that is, $f(M,0)<0, g(0,F)<0$) and fulfill the following conditions

$$\begin{aligned} \frac{\partial f}{\partial M}(M,F)<0, \quad \frac{\partial g}{\partial F}(M,F) <0 \end{aligned}$$

(6)

for $M> 0, F > 0$.

Obligatory mutualism requires that both sexes be equitable; therefore, to guarantee the survival and persistence of mosquito population we introduce the quantity

$$\begin{aligned} \mathcal {Q}=\frac{(1-\epsilon ) \epsilon \rho }{\epsilon \delta +(1-\epsilon ) \mu } = \frac{\rho }{\delta /(1-\epsilon ) + \mu /\epsilon } \end{aligned}$$

(7)

which is derived from the conditions (3) and is usually referred to as basic offspring number or mosquito survival threshold.⁷ Thus, condition $\mathcal {Q}<1$ would imply an eventual extinction of the mosquito population due to the lack of one sex (i.e., if $\epsilon \rightarrow 0^{+}$ or $\epsilon \rightarrow 1^{-}$) or other reasons. Since this is not a realistic case, we should suppose further on that $\mathcal {Q}>1$.

Fig. 2

Left: phase portrait of the system (1) and its steady states (0, 0) and $(M_{\sharp }, F_{\sharp })$. Right: vector field of the system (1) with flow streamlines aiming at the attractor $(M_{\sharp }, F_{\sharp })$. Here, blue and red curves denote M-isocline and F-isocline, respectively

Proposition 1

For $\mathcal {Q} >1,$ the dynamical system (5) has two steady states:

• 1. The origin (0, 0), which is unstable (saddle point) and can be reached only if $M(0)=0$ or $F(0)=0$.

• 2. A strictly positive steady state $(M_{\sharp },F_{\sharp })$ with coordinates

  $$\begin{aligned} M_{\sharp }= & {} \frac{\epsilon \delta }{\sigma [\epsilon \delta + (1-\epsilon ) \mu ]} \ln \left[ \frac{(1-\epsilon ) \epsilon \rho }{\epsilon \delta + (1-\epsilon ) \mu } \right] = \frac{\epsilon \delta \ \ln \mathcal {Q} }{\sigma [\epsilon \delta + (1-\epsilon ) \mu ]}, \end{aligned}$$

  (8a)
  $$\begin{aligned} F_{\sharp }= & {} \frac{(1-\epsilon )\mu }{\sigma [\epsilon \delta + (1-\epsilon ) \mu ]} \ln \left[ \frac{(1-\epsilon ) \epsilon \rho }{\epsilon \delta + (1-\epsilon ) \mu } \right] = \frac{(1-\epsilon ) \mu \ \ln \mathcal {Q} }{\sigma [\epsilon \delta + (1-\epsilon ) \mu ]}, \end{aligned}$$

  (8b)

  which is globally asymptotically stable in the interior of $\mathbb {R}^{2}_{+},$ that is, for any $M(0) > 0$ and $F(0)>0$.

Additionally, for any positive initial conditions $M(0)=M_0, F(0)=F_0$ the trajectories of the system (1) are bounded when $t \rightarrow \infty .$

Proof

We should start by recalling that the trajectories of Kolmogorov-type systems originated from the positive quadrant $\mathbb {R}^2_+$ remain in $\mathbb {R}^2_+$ for all $t \ge 0$ (Brauer and Castillo-Chávez 2012; Farkas 2001). In other words, $\mathbb {R}^2_+$ is positively invariant. Additionally, direct application of Dulac criterion (Brauer and Castillo-Chávez 2012, Theorems 4.8 and 4.9) clearly indicates the absence of limit cycles in $\mathbb {R}^2_+$ of any two-dimensional mutualistic system of Kolmogorov type, including our system (5) that satisfies the conditions (6).

Both steady states (0, 0) and $(M_{\sharp },F_{\sharp })$ can be obtained by direct solution of the system

$$\begin{aligned} \left. \begin{array}{rcl} M \, f(M,F) &{} = &{} 0 \\ F \, g(M,F) &{} = &{} 0 \\ \end{array} \right\} \end{aligned}$$

under the condition $\mathcal {Q} > 1.$

To evaluate the Jacobian matrix in the origin (0, 0) and avoid division by zero (cf. formulas (5), we evaluate first

$$\begin{aligned} J(0,F) = \left[ \begin{array}{rccr} \rho \epsilon e^{-\sigma F} - \mu &{} &{} &{} 0 \\ \rho (1-\epsilon ) e^{-\sigma F } &{} &{} &{} -\delta \end{array} \right] , \quad J(M,0) = \left[ \begin{array}{rccr} -\mu &{} &{} &{} \rho \epsilon e^{-\sigma M} \\ 0 &{} &{} &{} \rho (1-\epsilon ) e^{\sigma M} -\delta \end{array} \right] . \end{aligned}$$

It is easy to see that J(0, F) has one negative and one positive eigenvalue when $F \rightarrow 0$ and $\mathcal {Q} > 1$; a similar statement applies to the eigenvalues of J(M, 0) when $M \rightarrow 0$. Therefore, the origin (0, 0) is a saddle point and both axes $M=0, F=0$ constitute together the stable manifold of this saddle point.

On the other hand, the Jacobian matrix evaluated in the steady state (8) is given by

$$\begin{aligned} J(M_{\sharp },F_{\sharp })=\left[ \begin{array}{lll} - \dfrac{\epsilon \mu \delta \left[ \ln \mathcal {Q}+1 \right] }{\epsilon \delta + (1- \epsilon ) \mu } &{} &{} \dfrac{\epsilon \delta \left[ \epsilon \delta + (1-\epsilon ) \mu \ln \mathcal {Q} \right] }{(1-\epsilon ) \left[ \epsilon \delta + (1- \epsilon ) \mu \right] } \\ &{} &{} \\ \dfrac{(1- \epsilon ) \mu \left[ (1-\epsilon ) \mu + \epsilon \delta \ln \mathcal {Q} \right] }{\epsilon \left[ \epsilon \delta +(1-\epsilon ) \mu \right] } &{} &{} - \dfrac{(1-\epsilon )\delta \mu \left[ \ln \mathcal {Q} + 1 \right] }{\epsilon \delta + (1-\epsilon )\mu } \\ \end{array} \right] \end{aligned}$$

and its characteristic polynomial can be written as

$$\begin{aligned} \lambda ^2 + a_1 \lambda + a_0 = \lambda ^2+\frac{\delta \mu [\ln \mathcal {Q} + 1]}{\epsilon \delta + (1- \epsilon )\mu } \lambda + \delta \mu [\ln \mathcal {Q} + 1] = 0. \end{aligned}$$

If $\mathcal {Q}>1$ then both coefficients $a_1, a_0$ of the above polynomial are strictly positive; therefore, both eigenvalues of $J(M_{\sharp },F_{\sharp })$ have negative real parts and the steady state $(M_{\sharp },F_{\sharp })$ is locally asymptotically stable in the interior of $\mathbb {R}^{2}_{+}.$Additionally, due to the absence of limit cycles and positive invariance of $\mathbb {R}^2_+$, the steady state $(M_{\sharp },F_{\sharp })$ is globally stable in the interior of $\mathbb {R}^2_+$, that is, excluding the axes $M=0, F=0$. The latter implies that the trajectories of the system (1) originated from any $M(0)>0, F(0) >0$ move towards $(M_{\sharp },F_{\sharp })$ when $t \rightarrow \infty .$

Figure 1 displays the phase portrait of the system (1) (left chart) and indicates that all phase trajectories in the plane (M, F) are attracted by the point $\left( M_{\sharp },F_{\sharp } \right)$ (right chart). In both charts, the blue curve corresponds to M-isocline ($f(M,F)=0$) while the red curve denotes F-isocline ($g(M,F)=0$), and all arrows point out to the directions of the vector field (f, g).

Finally, to prove the boundedness of the trajectories M(t), F(t) for all $t \ge 0$ we first set $P(t) = M(t) + F(t)$ and, keeping in mind that $\delta = \min \{ \mu , \delta \},$ we obtain that

$$\begin{aligned} P'(t)= & {} M'(t) + F'(t) = \frac{\rho MF e^{-\sigma (M+F)}}{M + F} - \mu M - \delta F \\\le & {} \frac{\rho P^2 e^{-\sigma P}}{P} - \delta P = \left[ \rho e^{-\sigma P} - \delta \right] P, \end{aligned}$$

where $0< e^{-\sigma P} < 1$ is strictly decreasing and $e^{-\sigma P} \rightarrow 0$ as $P \rightarrow \infty$. Therefore, $P(t) \le \max \{ \bar{P}, P_0 \}$ for all $t \ge 0$, where $P_0 = M(0) + F(0)$ is the initial condition and $\bar{P}$ is the (unique) root of the algebraic equation $\rho e^{-\sigma P} - \delta =0$, that is,

$$\begin{aligned} \bar{P} = \dfrac{1}{\sigma } \ln \left( \frac{\rho }{\delta } \right) > 0. \end{aligned}$$

It is worthwhile to note that $\bar{P}$ defines the carrying capacity of Ricker differential equation $P'(t) =\left[ \rho e^{-\sigma P(t)} - \delta \right] P(t)$ [see, e.g., Thieme (2003) or similar textbooks]. This completes the proof of Proposition  1. $\square$

It should be noted that the phase portrait plotted in Fig. 1, as well as other illustrations and simulations throughout this paper, had been done using the numerical values of model’s parameters given in Table  1, Sect. 4.

Fig. 3

Approximations of the trajectories of the system (1), (5) by logistic curves

Remark 2

It is worthwhile to note that M(t) and F(t) in the sex-structured system, as well as their sum $P(t)=M(t)+F(t)$ (i.e., total mosquito population), have almost logistic growth. In other words, they all can be approximated by solutions of the following logistic equations:

$$\begin{aligned} \frac{d M}{dt} = r M \left( 1- \frac{M}{K_M} \right) , \quad \frac{d F}{dt} = r F \left( 1- \frac{F}{K_F} \right) , \quad \frac{d P}{dt} = r P \left( 1- \frac{P}{K_M + K_F} \right) ,\nonumber \\ \end{aligned}$$

(9)

where $K_M=M_{\sharp }, K_F=F_{\sharp },$ and $r=\rho e^{-\sigma (M_{\sharp } + F_{\sharp })}.$ This is displayed in Fig. 2 where the lower (blue), medium (red), and upper (black) solid curves are the plots of M(t), F(t) and of their sum $P(t)=M(t)+F(t)$ from the sex-structured system (1), (5), while the dashed curves are their respective approximations by the corresponding solutions of logistic equations (9). Here we have fixed the same initial conditions $M(0)=0.8 M_{\sharp }, F(0)=0.8 F_{\sharp }, P(0)=0.8 (M_{\sharp } + F_{\sharp } )$ for the system (1), (5) and for logistic equations (9).

It is well-known that only female mosquitoes F(t) are capable of transmitting dengue and other vector-borne diseases, since male mosquitoes do not ingest blood meals. Due to this fact, almost all models that describe transmission of vector-borne diseases between mosquitoes and humans only include (sub)populations of female mosquitoes (such as susceptible, infected, etc.) and completely ignore the population of male mosquitoes. In particular, some of these models propose logistic growth for female mosquito population (see, e.g. Manore et al. 2014; Campo-Duarte et al. 2017a, b) while supposing that there are enough males for their successful mating. The latter is in line with our findings and is clearly illustrated by the striking resemblance between F(t) and its “logistic approximation” in Fig. 2 when both males and females have relatively high initial densities. This resemblance becomes even better as $\left( M(0), F(0) \right) \rightarrow \left( M_{\sharp }, F_{\sharp } \right)$. However, very little resemblance will be observed when one of two sexes (or both) has low initial density.

2.2 Population dynamics involving Wolbachia-infected mosquitoes

Model (5) can be adapted to include Wolbachia-infected mosquitoes whose population dynamics is similar to that of wild (or uninfected with Wolbachia) mosquitoes. Let

$$\begin{aligned} M(t) = M_n(t) + M_w(t) \quad \hbox {and} \quad F(t) = F_n(t) + F_w(t) \end{aligned}$$

where $M_n, F_n$ represent the densities of wild male and female mosquitoes, while $M_w, F_w$ stand for the densities of Wolbachia-infected males and females. Let also

$$\begin{aligned} {\varvec{X}}(t) = \left( M_n(t),F_n(t),M_w(t),F_w(t) \right) ^{\prime }, \quad {\varvec{X}}(0)= {\varvec{X}}_0 = \left( M_n^0,F_n^0,M_w^0,F_w^0 \right) ^{\prime }, \end{aligned}$$

be a vector of mosquito densities and a vector of initial conditions, respectively. Then the population dynamics involving wild and Wolbachia-infected mosquitoes can be described by the following closed-form ODE system:

$$\begin{aligned} \dfrac{d {\varvec{X}}}{dt} = {\varvec{G}}({\varvec{X}}), \qquad {\varvec{X}}(0) = {\varvec{X}}_0, \end{aligned}$$

(10)

where the components of vector field ${\varvec{G}}= \left( G_1,G_2,G_3,G_4 \right) ^{\prime }$ are given by

$$\begin{aligned} G_1 \left( M_n,F_n,M_w,F_w \right)= & {} \frac{\epsilon _n \rho _n F_n M_n}{M_n+F_n+M_w+F_w} \, e^{-\sigma (M_n+F_n+M_w + F_w)} -\mu _n M_n, \nonumber \\\end{aligned}$$

(11a)

$$\begin{aligned} G_2 \left( M_n,F_n,M_w,F_w \right)= & {} \frac{(1-\epsilon _n) \rho _n F_n M_n}{M_n+F_n+M_w+F_w} \, e^{-\sigma (M_n+F_n+ M_w+F_w)}-\delta _n F_n, \nonumber \\\end{aligned}$$

(11b)

$$\begin{aligned} G_3 \left( M_n,F_n,M_w,F_w \right)= & {} \frac{\epsilon _w \rho _w F_w (M_n + M_w) }{M_n+F_n+M_w+F_w} \, e^{-\sigma (M_n+ F_n+M_w+F_w)}-\mu _w M_w, \nonumber \\\end{aligned}$$

(11c)

$$\begin{aligned} G_4 \left( M_n,F_n,M_w,F_w \right)= & {} \frac{(1-\epsilon _w) \rho _w F_w (M_n + M_w)}{M_n+F_n+M_w+F_w} \, e^{-\sigma (M_n + F_n + M_w + F_w)} - \delta _w F_w.\nonumber \\ \end{aligned}$$

(11d)

The birth functions [positive terms in the right-hand sides of (11)] have a form similar to (2) and the exponential term in (11) regulates the density dependence at larval stage and competition between uninfected and Wolbachia-infected individuals for the same food resources and breeding sites. Here $\epsilon _n/(1-\epsilon _n)$ and $\epsilon _w/(1-\epsilon _w)$ express the primary sex ratios for uninfected and Wolbachia-infected mosquitoes;⁸ $(\mu _n, \delta _n)$ and $(\mu _w, \delta _w)$ are mortality rates of uninfected and Wolbachia-infected males and females, and $\rho _n, \rho _w$ are fecundity rates of uninfected and Wolbachia-infected females, respectively.

Bull and Turelli (2013) emphasized that Wolbachia infection reduces the mosquito lifespan. Additionally, McMeniman et al. (2009) and Ritchie et al. (2015) claimed that wMelPop Wolbachia strain reduces the fecundity rate and shortens the lifespan of Aedes aegypti females by up to 50%. In other words, the individual fitness of Wolbachia-carriers (both males and females) is considerably lower than that of wild mosquitoes and it is fair to assume that

$$\begin{aligned} \mu _n< \mu _w, \quad \delta _n < \delta _w, \quad \rho _n > \rho _w. \end{aligned}$$

(12)

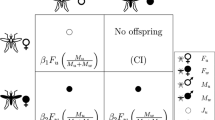
On the other hand, Wolbachia-infected females have more opportunities to produce viable offspring than their uninfected coevals. In effect, the birth function in Eqs. (11c)–(11d) explicitly addresses the maternal transmission of Wolbachia together with the effect of CI phenotype upon mosquito reproduction (see Fig. 3). In particular, system (10)–(11) patently states that there will be no viable offspring when Wolbachia-infected males are mating with uninfected females, while mating between Wolbachia-infected females and uninfected males always results in viable Wolbachia-infected offspring.

Fig. 4

Illustration of the CI reproductive phenotype and maternal transmission of Wolbachia: a no viable offspring is produced after mating between uninfected females and Wolbachia-infected males; b and c viable Wolbachia-infected offspring is produced by a Wolbachia-infected female fecundated by either infected or uninfected male. Public-domain source: http://www.eliminatedengue.com/our-research/wolbachia

Note that system (10)–(11) is also of Kolomogorov type but it is neither strictly mutualistic nor competitive in a general sense. Here, uninfected males $M_n$ and females $F_n$ still exhibit obligatory mutualism [as in two-dimensional system (1), (5)], while the presence of Wolbachia-infected males, $M_w$, is facultative (not obligatory) for persistence of Wolbachia-carriers, both males and females. The latter is attributed to CI-phenotype (see Fig. 3) according to which a Wolbachia-carrying female should produce viable Wolbachia-infected offspring after mating with either infected or uninfected male. However, the presence of males (either $M_n$ or $M_w$) is vital and obligatory for successful reproduction of Wolbachia-carriers.

Actually, wild mosquitoes $M_n, F_n$ compete with Wolbachia-carriers $M_w, F_w$ not only for food and other resources but also for “better mating options”, and the latter is clearly expressed by the model (10)–(11). By direct calculation we can see that

$$\begin{aligned} \frac{\partial G_1}{\partial M_w}< 0, \quad \frac{\partial G_1}{\partial F_w}< 0, \quad \frac{ \partial G_2}{ \partial M_w}< 0, \quad \frac{\partial G_2}{\partial F_w} < 0 \end{aligned}$$

for all positive $M_n, F_n, M_w, F_w$. The above conditions indicate that wild mosquitoes tend to decrease their density for higher densities of Wolbachia-carriers. Additionally, it is worthwhile to note that, despite having reduced fitness, Wolbachia-carriers tend to increase their density for lower densities of wild females in the sense that

$$\begin{aligned} \frac{\partial G_3}{\partial F_n}< 0, \quad \frac{\partial G_4}{\partial F_n} < 0 \end{aligned}$$

for all positive $M_n, F_n, M_w, F_w$. In other words, our model (10)–(11) captures the frequency-dependence, which is in line with other models describing Wolbachia invasion in terms of the infection frequencies (Turelli 2010; Schraiber et al. 2012).

To guarantee the survival and persistence of both mosquito subpopulations, we should impose the following conditions for parameters of the model (10)–(11) that are rather similar to (7), namely:

$$\begin{aligned} \mathcal {Q}_n= & {} \frac{(1-\epsilon _n) \epsilon _n \rho _n}{\epsilon _n \delta _n +(1-\epsilon _n) \mu _n} \,\,\,= \, \frac{\rho _n}{\delta _n/(1-\epsilon _n) + \mu _n/\epsilon _n } \,\,\, > \, 1, \end{aligned}$$

(13a)

$$\begin{aligned} \mathcal {Q}_w= & {} \frac{(1-\epsilon _w) \epsilon _w \rho _w}{\epsilon _w \delta _w +(1-\epsilon _w) \mu _w} \,=\, \frac{\rho _w}{\delta _w/(1-\epsilon _w) + \mu _w/\epsilon _w } \, > \,1, \end{aligned}$$

(13b)

where the quantities $\mathcal {Q}_n$ and $\mathcal {Q}_w$ are referred to as basic offspring numbers of uninfected and Wolbachia-infected mosquitoes, respectively. Conditions (13) are quite natural and simply imply that, in the absence of density dependence, mosquitoes’ birth rates $\rho _n, \rho _w$ are always greater than the sum of their death rates, weighted by a possible sex-ratio distortion. In view of (12) it safe to affirm that $\mathcal {Q}_n > \mathcal {Q}_w$.

Let us establish some basic properties of the solutions of the system (10)–(11) which will be very useful for analyzing stability and persistence of uninfected and Wolbachia-infected mosquito populations.

Proposition 2

For any positive initial condition ${\varvec{X}}_0,$ the ODE system (10)–(11) has a unique nonnegative and bounded solution that exists for all $t \ge 0$.

Proof

We start by recalling that any solution ${\varvec{X}}(t)$ of Kolmogorov-type system (10)–(11) engendered by an initial condition ${\varvec{X}}_0 \in \mathbb {R}_+^4$ remains in $\mathbb {R}_+^4$ (Brauer and Castillo-Chávez 2012; Farkas 2001). Furthermore, uniqueness of solution ${\varvec{X}}(t)$ for an initial condition ${\varvec{X}}_0$ is guaranteed by the local Lipschitz-continuity of the vector field (11) that has continuous partial derivatives.

To prove the boundedness of ${\varvec{X}}(t) = \left( M_n(t),F_n(t),M_w(t),F_w(t) \right)$ we employ the approach already used in the proof of Proposition 1. First we set

$$\begin{aligned} N(t)= & {} \sum \limits _{j=1}^{4} X_j (t) = M_n(t) + F_n (t) + M_w(t) + F_w (t), \\ N(0)= & {} \sum \limits _{j=1}^{4} X_j (0) = M_n^{0} + F_n^{0} + M_w^{0} + F_w^{0} = N_0. \end{aligned}$$

Then, keeping in mind that $\delta _n = \min \left\{ \mu _n, \delta _n, \mu _w, \delta _w \right\}$ and $\rho _n = \max \left\{ \rho _n, \rho _w \right\}$, we obtain

$$\begin{aligned} N'(t)= & {} M_n'(t)+F_n'(t)+M_w'(t)+F_w'(t) \\= & {} \frac{\rho _n M_n F_n e^{-\sigma (M_n +F_n+M_w+F_w)}}{M_n + F_n + M_w + F_w}+\frac{\rho _w F_w( M_w + M_n) e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n + F_n + M_w + F_w} \\&-\mu _n M_n - \delta _n F_n - \mu _w M_w - \delta _w F_w \\\le & {} \frac{\rho _n N^2 e^{-\sigma N}}{N} - \delta _n N = \left[ \rho _n e^{-\sigma N} -\delta _n \right] N. \end{aligned}$$

Therefore, $N(t) \le \max \{ \bar{N}, N_0 \}$ for all $t \ge 0,$ where

$$\begin{aligned} \bar{N} = \dfrac{1}{\sigma } \ln \left( \frac{\rho _n}{\delta _n} \right) > 0. \end{aligned}$$

defines the carrying capacity of Ricker differential equation $N'(t) =\left[ \rho _n e^{-\sigma N(t)} - \delta _n \right] N(t)$ (see, e.g., Thieme (2003) or similar textbooks). $\square$

The positivity and boundedness of all trajectories of the dynamical system (10)–(11) established by the Proposition 2 allows to claim the following property of this sex-strictured compartmental model.

Statement 1

(Property of bistability) Under conditions (12), () the ODE system (10)–() has three nonnegative steady states in $\mathbb {R}_{+}^{4}$ and exhibits bistability in the following sense:

• 1. A strictly positive co-existence equilibrium $E^{c} = \left( M_n^{c}, F_n^{c}, M_w^{c}, F_w^{c} \right)$ is unstable (saddle point).

• 2. Wolbachia-free equilibrium $E_n^{\sharp } = \left( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \right)$ is locally asymptotically stable (nodal attractor) and is reachable at low frequencies of Wolbachia-carriers.

• 3. Wolbachia invasion equilibrium $E_w^{\sharp } = \left( 0, 0, M_w^{\sharp }, F_w^{\sharp } \right)$ is locally asymptotically stable (nodal attractor) and is reachable at high frequencies of Wolbachia-carriers.

To show that Statement  1 is plausible under imposed conditions (12) and (13), we calculate first all possible steady states of the ODE system (10)–(11) by direct solution of the nonlinear system ${\varvec{G}}(M_n,F_n,M_w,F_w) = \mathbf{0},$ where four components of ${\varvec{G}}$ are defined by (11). The trivial equilibrium $E_0=(0,0,0,0)$ is of no interest here (even thought it is a formal solution) since we suppose no sex-ratio distortion, that is, $\mathcal {Q}_n> \mathcal {Q}_w > 1$.

The coordinates of $E_n^{\sharp } = \big ( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \big )$ and $E_w^{\sharp }= \big ( 0, 0, M_w^{\sharp }, F_w^{\sharp } \big ),$ are similar to (8) and can be calculated immediately (cf. Proposition 1):

$$\begin{aligned} M_n^{\sharp } = \frac{\epsilon _n \delta _n \ \ln \mathcal {Q}_n }{\sigma [ \epsilon _n \delta _n+ (1-\epsilon _n) \mu _n]},&F_n^{\sharp } = \frac{(1-\epsilon _n) \mu _n \ \ln \mathcal {Q}_n }{\sigma [\epsilon _n \delta _n + (1-\epsilon _n) \mu _n]}, \end{aligned}$$

(14a)

$$\begin{aligned} M_w^{\sharp } = \frac{\epsilon _w \delta _w \ \ln \mathcal {Q}_w }{\sigma [ \epsilon _w \delta _w+ (1-\epsilon _w) \mu _w]},&F_w^{\sharp } = \frac{(1-\epsilon _w) \mu _w \ \ln \mathcal {Q}_w }{\sigma [\epsilon _w \delta _w + (1-\epsilon _w) \mu _w]}. \end{aligned}$$

(14b)

In order to find the coordinates of the coexistence point $E^c = \big ( M_n^c, F_n^c, M_w^c, F_w^c \big )$ we set first

$$\begin{aligned} N^c = M_n^c + F_n^c + M_w^c + F_w^c. \end{aligned}$$

(15)

From equations $G_1 =0$ and $G_2 =0$ where $G_1, G_2$ are given by (11a), (11b) we obtain

$$\begin{aligned} M_n^c = \frac{\delta _n}{(1-\epsilon _n) \rho _n} N^c e^{\sigma N^c} \quad \hbox {and} \quad F_n^c = \frac{\mu _n}{ \epsilon _n \rho _n} N^c e^{\sigma N^c}. \end{aligned}$$

(16)

Then, from $G_4 =0$ with $G_4$ defined by (11d) we can express

$$\begin{aligned} M_n^c + M_w^c = \frac{\delta _w}{(1-\epsilon _w) \rho _w} N^c e^{\sigma N^c}, \end{aligned}$$

(17)

and using the expression for $M_n^c$ from (16), we have

$$\begin{aligned} M_w^c = \left[ \frac{\delta _w}{(1-\epsilon _w) \rho _w} - \frac{\delta _n}{(1-\epsilon _n) \rho _n} \right] N^c e^{\sigma N^c}. \end{aligned}$$

The above relationship implies that coexistence may take place only if the expression inside the square brackets is positive. The latter occurs when

$$\begin{aligned} \mathcal {R}_0 = \frac{(1-\epsilon _w)\rho _w /\delta _w}{(1-\epsilon _n)\rho _n /\delta _n} < 1, \end{aligned}$$

(18)

which is always true under the conditions (12), (13). Here $0< \mathcal {R}_0 <1$ has an interesting interpretation from the epidemiological standpoint, which is discussed in “Appendix A”.

Further, using the formula (18) for $\mathcal {R}_0$ we can write $M_w^c$ in the following form:

$$\begin{aligned} M_w^c = \frac{\delta _w}{(1-\epsilon _w) \rho _w} (1 - \mathcal {R}_0) N^c e^{\sigma N^c}. \end{aligned}$$

(19)

On the other hand, by substituting (17) into $G_3=0,$ where $G_3$ is given by (11c), we arrive to the proportionality relationship between $M_w^c$ and $F_w^c$:

$$\begin{aligned} F_w^c = \frac{1-\epsilon _w}{\epsilon _w} \cdot \frac{\mu _w}{\delta _w} \cdot M_w^c, \end{aligned}$$

which together with (19) leads us to

$$\begin{aligned} F_w^c = \frac{\mu _w}{\epsilon _w \rho _w} (1 - \mathcal {R}_0) N^c e^{\sigma N^c}. \end{aligned}$$

(20)

By summing up all four Eqs. (16), (19), and (20), the relationship (15) turns into

$$\begin{aligned} \left[ \frac{\delta _n}{(1-\epsilon _n) \rho _n} + \frac{\mu _n}{\epsilon _n \rho _n} + \frac{\delta _w}{(1-\epsilon _w) \rho _w} (1 - \mathcal {R}_0) + \frac{\mu _w}{\epsilon _w \rho _w} (1 - \mathcal {R}_0) \right] N^c e^{\sigma N^c} = N^c. \end{aligned}$$

Additionally, it is worthwhile to recall that two relationships (13) can be also written as

$$\begin{aligned} \frac{1}{\mathcal {Q}_n} = \frac{\delta _n}{(1-\epsilon _n) \rho _n} + \frac{\mu _n}{\epsilon _n \rho _n}, \qquad \frac{1}{\mathcal {Q}_w} = \frac{\delta _w}{(1-\epsilon _w) \rho _w} + \frac{\mu _w}{\epsilon _w \rho _w}. \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{1}{\mathcal {Q}_n} + \frac{1}{\mathcal {Q}_w} (1 - \mathcal {R}_0) = e^{-\sigma N^c} \quad \hbox {and} \quad e^{\sigma N^c} \left[ \mathcal {Q}_w + \mathcal {Q}_n (1 - \mathcal {R}_0) \right] = \mathcal {Q}_n \mathcal {Q}_w, \end{aligned}$$

and $N^c$ can be explicitly expressed in terms of the parameters of the model as

$$\begin{aligned} N^c = \frac{1}{\sigma } \ln \left( \frac{\mathcal {Q}_n \mathcal {Q}_w}{\mathcal {Q}_w + \mathcal {Q}_n (1 - \mathcal {R}_0)} \right) , \end{aligned}$$

where $\mathcal {Q}_n, \mathcal {Q}_w$ are defined by the relationships (13), while $\mathcal {R}_0$ is given by the formula (18).

The coexistence point $E^c = \big ( M_n^c, F_n^c, M_w^c, F_w^c \big )$ is biologically feasible only if

$$\begin{aligned} \mathcal {Q}_0 = \frac{\mathcal {Q}_n \mathcal {Q}_w}{\mathcal {Q}_w + \mathcal {Q}_n (1 - \mathcal {R}_0)} > 1 \end{aligned}$$

(21)

and by using this new quantity $\mathcal {Q}_0$ the coordinates of $E^c$ can be written as

$$\begin{aligned} M_n^{c} = \frac{\delta _n}{\sigma (1-\epsilon _n) \rho _n} \mathcal {Q}_0 \ln \mathcal {Q}_0,&\;\;&F_n^{c} = \frac{ \mu _n }{\sigma \epsilon _n \rho _n} \mathcal {Q}_0 \ln \mathcal {Q}_0, \end{aligned}$$

(22a)

$$\begin{aligned} M_w^{c} = \frac{\delta _w (1-\mathcal {R}_0) }{\sigma (1-\epsilon _w) \rho _w} \mathcal {Q}_0 \ln \mathcal {Q}_0,&\;\;&F_w^{c} = \frac{ \mu _w (1-\mathcal {R}_0) }{\sigma \epsilon _w \rho _w} \mathcal {Q}_0 \ln \mathcal {Q}_0. \end{aligned}$$

(22b)

Fig. 5

The left upper chart displays the value of $\mathcal {Q}_0$ in function of the number of scenario; the right upper chart shows the distribution of eigenvalues (real part) corresponding to the point of coexistence $E_c$, while the lower charts show the eigenvalue distributions (real parts) for Wolbachia-free $E_n$ and Wolbachia invasion $E_w$ steady states, respectively

To analyze local stability of these three equilibria, one may apply a standard technique based on calculation of eigenvalues of the Jacobian evaluated at the steady states. However, this approach looks rather knotty and cumbersome from the computational standpoint. Alternatively, one can use Monte Carlo method (see, e.g. Lawson 2006; Kroese et al. 2011) to repeatedly verify the condition $\mathcal {Q}_0 > 1$ and calculate the eigenvalues of the Jacobian evaluated at each steady state $E_c, E_n,$ and $E_w$. According to (13), (14), (21), and (22) the coordinates of all three steady states can be expressed in terms of nine model’s parameter ($\epsilon _n, \epsilon _w, \rho _n, \rho _w, \mu _n, \mu _w, \delta _n, \delta _w, \sigma$) whose baseline values are given in Table 1. The sampling pool $\mathbb {S}=\prod \nolimits _{i=1}^{9} P_i \in \mathbb {R}^9_+$ was defined by a Cartesian product of nine closed intervals of the form $P_i = [p_i - \theta p_i, p_i + \theta p_i ]$ where each $p_i, i=1, \ldots ,9$ stands for the baseline value of one parameter (see Table 1) and $\theta >0$ defines the variation range. Our sampling comprised $10^{5}$ confounding scenarios $S = (s_1, \ldots , s_9) \in \mathbb {S}$ where each $s_i \in P_i, i=1, \ldots 9$ was randomly chosen for $\theta =0.2$ (that is, 20% deviation from the baseline values) under uniform distribution with no correlation between parameters. Simulation results are presented in Fig. 4, where the left upper chart clearly shows that $\mathcal {Q}_{0} >1$ always holds. Additionally, the right upper chart indicates that coexistence is unstable since one of the eigenvalues is always positive, while the other three have negative real part. Thus, $E_c$ is a saddle point. The lower charts in Fig. 4 point out that both $E_n$ and $E_w$ are attractors since their corresponding eigenvalues always have negative real part.

Fig. 6

Trajectories of the ODE system (10)–(11) engendered by two sets of initial conditions: Left: $M_n(0)> M_n^c, \; F_n(0) > F_n^c, \; M_w(0)< M_w^c, \; F_w(0) < F_w^c$; Right: $M_n(0)< M_n^c, \; F_n(0) < F_n^c, \; M_w(0)> M_w^c, \; F_w(0) > F_w^c,$. Here the dotted lines mark the coordinates of $E_c = \big ( M_n^c, F_n^c, M_w^c, F_w^c \big )$, and the densities of uninfected and Wolbachia-infected mosquitoes are plotted by dashed and solid curves, respectively, with male densities given in blue color and female densities given in red color

From the above numerical experiments, it is plausible to conclude that the coexistence point $E_c$ lays on a hyper-surface that separates the basins of attraction of two stable equilibria $E_n$ and $E_w$. It is not possible to draw a phase portrait of the system (10)–(11) in four dimensions; therefore, we cannot assert much regarding this hyper-surface. However, it is fair to say that all points $\big ( M_n, F_n, M_w, F_w \big ) \in \mathbb {R}^{4}_+$ satisfying the conditions

$$\begin{aligned} M_n> M_n^c, \quad F_n > F_n^c, \quad M_w< M_w^c, \quad F_w < F_w^c \end{aligned}$$

belong to the attraction basin of Wolbachia-free equilibrium $E_n$, while the points satisfying the opposite conditions

$$\begin{aligned} M_n< M_n^c, \quad F_n < F_n^c, \quad M_w> M_w^c, \quad F_w > F_w^c \end{aligned}$$

(23)

belong to the attraction basin of Wolbachia invasion equilibrium $E_w$. The latter is illustrated in Fig. 5 where, depending on selection of the set of initial conditions, either $E_n$ or $E_w$ can be reached when $t \rightarrow \infty$. This type of system behavior is known as bistability.

Many scholars point out that the final outcome of Wolbachia invasion virtually depends on the infection frequency (Turelli 2010; Schraiber et al. 2012), since Wolbachia spreads and persists when an infected female $F_w$ produces, in average, more offspring than an uninfected female $F_n$. At low infection frequencies, Wolbachia-carriers loose the competition with wild mosquitoes due to their reduced fitness (decreased fecundity, shorter lifespan). Therefore, they are driven towards extinction (see Fig. 5, left chart).

On the other hand, at high infection frequencies, Wolbachia-carriers win the competition with wild mosquitoes due to CI reproductive phenotype. Namely, wild females have less chances to mate with wild males (they are scarce!) and to produce viable uninfected offspring, than to encounter with Wolbachia-infected males (they are abundant!) and to produce no viable offspring. The latter should guarantee a greater share of infected offspring at each consequent generation of mosquitoes, which would ultimately results in extinction of wild mosquitoes (see Fig. 5, right chart).

Thus, the competition outcome predicted by Statement  1 agrees with the principle of competitive exclusion attributed to G. F. Gause⁹ according to which only one of two species competing for the same resources should ultimately survive.

Fig. 7

Densities of uninfected (dashed lines) and Wolbachia-infected (solid lines) males (blue color) and females (red color) when $\mathcal {R}_0 < 1$ and $t \rightarrow \infty$

Remark 3

Figure 5 indicates that, despite better fitness, uninfected mosquitoes exhibit so-called critical depensation or Allee effect (see, e.g., Kot 2001; Rockwood 2015 or other similar textbooks) at low frequencies of $M_n(t), F_n(t)$ and high frequencies of $M_w(t), F_w(t)$, i. e., under the conditions (23). In other words, the coordinates of the coexistence equilibrium $E^c = \big ( M_n^c, F_n^c, M_w^c, F_w^c \big )$ mark so-called minimum viable population sizes¹⁰ of uninfected and Wolbachia-infected mosquitoes. The same feature had been observed in other models describing Wolbachia invasion (Turelli 2010; Schraiber et al. 2012; Barton and Turelli 2011; Bliman et al. 2015; Farkas et al. 2017).

Remark 4

It should also be noted that the population replacement may only occur gradually and within the limits of the carrying capacity of the environment. In other words, a single release of vast quantity of Wolbachia-carriers performed at $t=0$ will never induce the Wolbachia invasion if the initial densities of wild mosquitoes are close to equilibrium levels $\big ( M_n^{\sharp }, F_n^{\sharp } \big ).$ The failure of the field experiments targeting to establish wMelPop-infected Aedes aegypti in Australia and Vietnam supports this argument (Yeap et al. 2014; Nguyen et al. 2015). Effectively, the infection frequency, despite being rather high at $t=0$, should decline shortly after the release due to the density dependence and competition between uninfected and infected coevals, where wild mosquitoes will be the winners thanks to their enduring abundance and proximity to equilibrium levels $\big ( M_n^{\sharp }, F_n^{\sharp } \big )$) on the score of better fitness (higher fecundity, longer lifespan). Under this scenario it is reasonable to expect that all released Wolbachia-carriers, as well as their offspring, will ultimately become extinct. This is exactly what our model predicts—see Fig. 6 that shows the population dynamics of uninfected (dashed curves) and Wolbachia-infected (solid curves) mosquitoes supposing that wild mosquitoes have equilibrium densities $\big ( M_n^{\sharp }, F_n^{\sharp } \big )$ at $t=0$ and:

• there was a single release of $4M_n^{\sharp }$ of Wolbachia-infected males and $4F_n^{\sharp }$ of Wolbachia-infected females at the initial time $t=0$ (Fig. 6, left chart);

• there was a single release of $8 M_n^{\sharp }$ of Wolbachia-infected males and $8 F_n^{\sharp }$ of Wolbachia-infected females at the initial time $t=0$ (Fig. 6, right chart).

Thus, no matter how huge is a single release of Wolbachia-carriers, the ultimate goal of population replacement will not be achieved. Therefore, periodical or inoculative releases are indispensable for establishing Wolbachia in wild mosquito populations.

3 Optimal control approach and strategies for inoculative releases

In this section we suppose that wild mosquitoes have equilibrium densities $\big ( M_n^{\sharp }, F_n^{\sharp } \big )$ at $t=0,$ and our goal is to replace the population of wild mosquitoes with Wolbachia-carriers. Even though Wolbachia pathogen is only transmitted maternally from an infected female to her offsprings and infected females act as the driving force of the infection, the presence and abundance of infected males in the environment play an essential role in the spread of Wolbachia in wild populations. When the number of matings between infected males and uninfected females increases, the share of uninfected viable offspring in each generation will decrease by cytoplasmic incompatibility mechanism. Therefore, the spread of Wolbachia can only be expected at high frequencies of infected mosquitoes (both males and females) with respect to their uninfected coevals and within the limits of the carrying capacity of the environment (see Remark 4).

In order to mimic a “synthetical” increase in the fitness of Wolbachia-infected females, one may either to enhance the value of $\rho _w$ or to reduce the value of $\delta _w$, thus pushing the value of $\mathcal {R}_0$ given by (18) above 1.¹¹ The latter can be imitated by releasing periodically a certain amount of Wolbachia-infected females, which have been previously cultivated in laboratory conditions. However, artificial breeding will always supply the cohorts of mosquitoes consisting of both females and males. Knowing that Wolbachia-infected males also play an essential role in Wolbachia invasion, both males and females should be released then.

Remark  4 and Fig. 6 provided sufficient argument against single or inundative releases of vast quantities of Wolbachia-infected mosquitoes, and suggested an alternative option based on periodical or inoculative releases. The open question here is: how many Wolbachia-infected mosquitoes should be released periodically (daily, weekly, etc.) in order to achieve the population replacement?

The number of released mosquitoes can be defined as a fraction of Wolbachia-carriers already present in the locality. In mathematical terms, such fraction may remain constant for each time unit (day) or be variable in time. Below we consider both options.

3.1 Constant release rate

Consider the following variant of ODE system (10)–(11)

$$\begin{aligned} \frac{d M_n}{dt}= & {} \frac{\epsilon _n \rho _n F_n M_n \, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n + F_n + M_w + F_w} -\mu _n M_n, \end{aligned}$$

(24a)

$$\begin{aligned} \frac{d F_n}{dt}= & {} \frac{(1-\epsilon _n) \rho _n F_n M_n \, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n + F_n + M_w + F_w} -\delta _n F_n, \end{aligned}$$

(24b)

$$\begin{aligned} \frac{d M_w}{dt}= & {} \frac{\epsilon _w \rho _w F_w (M_n + M_w) \, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n + F_n + M_w + F_w} -\mu _w M_w + \mathsf {u} M_w, \end{aligned}$$

(24c)

$$\begin{aligned} \frac{d F_w}{dt}= & {} \frac{(1-\epsilon _w) \rho _w F_w (M_n + M_w)\, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n + F_n + M_w + F_w} - \delta _w F_w + \mathsf {u} F_w,\nonumber \\ \end{aligned}$$

(24d)

with the initial conditions

$$\begin{aligned} M_n(0) = M_n^{0}, \quad F_n(0) = F_n^{0}, \quad M_w(0) = M_w^{0}, \quad F_w(0) = F_w^{0}, \end{aligned}$$

(25)

where $\mathsf {u} \in [0,\delta _w)$ is a constant parameter that stands for (daily) release rate and expresses the fraction of Wolbachia-infected mosquitoes to be released each day t as a percentage of Wolbachia-infected mosquitoes, $M_w(t)$ and $F_w(t),$ present in the locality at the same day t. This parameter helps to decrease “synthetically” the mortality rate of Wolbachia-carriers (since they have a shorter lifespan than uninfected ones) from $(\mu _w,\delta _w)$ to $(\mu _w - \mathsf {u},\delta _w - \mathsf {u})$ by virtually replacing the dead ones with those cultivated in laboratory conditions (external input).

Systems (24) and (10)–(11) are quite similar and have the same disease-free equilibrium $E_n^{\sharp } = \big ( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \big )$ given by (14a). The positive terms $\mathsf {u} M_w$ and $\mathsf {u} F_w$ in (24c), (24d) are introduced in order to imitate a “compensation” in the reduced fitness of Wolbachia-carriers by performing the underlying releases. From the mathematical standpoint, we are trying to increase the value of (18) and push it above 1 (see more arguments in “Appendix A”). This action should modify the Wolbachia invasion equilibrium (14b) together with the basic offspring number $\mathcal {Q}_w$ of Wolbachia-infected mosquitoes (13b).

By reanalyzing the dynamical system (24) and applying the next generation operator approach of Diekmann et al. (1990) and Castillo-Chávez et al. (2002) (described in “Appendix A”), we can obtain the following updates

$$\begin{aligned} \mathcal {R}_0^{\mathsf {u}}= & {} \frac{(1-\epsilon _w)\rho _w /(\delta _w - \mathsf {u})}{(1-\epsilon _n)\rho _n /\delta _n}> \mathcal {R}_0, \\ \mathcal {Q}_w^{\mathsf {u}}= & {} \frac{\rho _w}{(\delta _w - \mathsf {u})/(1-\epsilon _w) + (\mu _w - \mathsf {u}) /\epsilon _w }> \mathcal {Q}_w, \\ M_w^{\mathsf {u}}= & {} \frac{\epsilon _w (\delta _w - \mathsf {u}) \ln \mathcal {Q}_w^{\mathsf {u}} }{\sigma [ \epsilon _w (\delta _w - \mathsf {u}) + (1-\epsilon _w) (\mu _w - \mathsf {u})]}> M_w^{\sharp },\\ F_n^{\mathsf {u}}= & {} \frac{(1-\epsilon _w) \mu _w \ln \mathcal {Q}_w^{\mathsf {u}} }{\sigma [\epsilon _w (\delta _w - \mathsf {u}) + (1-\epsilon _w) (\mu _w - \mathsf {u})]} > F_w^{\sharp }, \end{aligned}$$

of the quantities $\mathcal {R}_0, \mathcal {Q}_w, M_w^{\sharp },$ and $F_w^{\sharp },$ respectively.

Thus, the constant release rate $\mathsf {u} >0$ should be chosen to satisfy the condition

$$\begin{aligned} \mathcal {R}_0^{\mathsf {u}} = \frac{(1-\epsilon _w)\rho _w /(\delta _w - \mathsf {u})}{(1-\epsilon _n)\rho _n /\delta _n} > 1, \end{aligned}$$

(26)

while keeping $\mathcal {R}_0^{\mathsf {u}}$ strictly positive. Under this condition, wild mosquitoes $M_n, F_n$ will be gradually driven towards extinction and the population replacement will be eventually reached when $t \rightarrow \infty .$ From the theoretical standpoint, this strategy is feasible and foments the growth of Wolbachia-infected population as shown in Fig. 7 where densities of wild mosquitoes are given by dashed curves while solid curves stand for the densities of Wolbachia-infected mosquitoes. Here, we have taken $\mathsf {u} =0.06$ in order to keep $\mathcal {R}_0 < 1$ and $\mathcal {R}_0^{\mathsf {u}} >1$ while other parameters have the same values as in Table 1. The left chart in Fig. 7 displays the situation when Wolbachia-carriers are released indefinitely as $t \rightarrow \infty$, while the right chart shows what happens when the releases are suspended at a sufficiently large T.

Fig. 8

Densities of uninfected (dashed lines) and Wolbachia-infected (solid lines) males (blue color) and females (red color) of the system (24) with initial conditions $M_n(0)=M_n^{\sharp }, F_n(0)= F_n^{\sharp }, M_w(0)=\mathsf {u} M_n^{\sharp }, F_w(0)= \mathsf {u} F_n^{\sharp }$

Fig. 7 demonstrates that the strategy based on the constant release rate fulfills the goal of reaching the population replacement; however, the cost of such a strategy is very elevated while its effectiveness is rather low. Namely, this strategy insists on uninterrupted production of vast quantities of Wolbachia-carriers in laboratory conditions which are needed for permanent releases. However, not all released Wolbachia-carriers would effectively contribute to the infection spread since a (great) share of them will simply die due to the density-dependent competition with coevals (both infected and uninfected). Additionally, the negative side-effect of this strategy is the forced (temporal) overpopulation of mosquitoes in the target locality (see Fig. 7), which may not be tolerated by human residents of the locality.

As an alternative, we propose another strategy that is based on the variable release rate which is defined by the optimal control approach. In what follows, we demonstrate that this strategy exhibits a better index of cost-effectiveness.

3.2 Variable release rate

In order to formulate the problem of optimal control, we have to introduce the control variable $u(t): [0,T] \mapsto [0, u_{\max }]$ that stands for a time-dependent release rate of Wolbachia-carriers with $0< u_{\max } < \delta _w$ expressing the upper bound of the release rate, which is in line with condition (26). Under these settings, the number of Wolbachia-carriers to be released at the day t is $u(t) \big [ M_w(t) + F_w(t) \big ]$, i. e., this number is a fraction of Wolbachia-infected mosquitoes already present in the target locality at the same day t. At the first sight, this approach does not seem to be credible since it requires a plausible estimation of the current number of Wolbachia-carriers present in the locality. However, it is feasible (and therefore deserves the credibility) since the decision-maker possesses the records regarding the quantities of Wolbachia-carriers released in the target locality at each day t and, therefore, can get a reasonable estimation of the mosquito densities via simulations of the population dynamics model (10)–(11). On the other hand, the densities of wild mosquitoes in the target locality prior to the control action can be estimated by some advanced techniques (see, e. g., Ritchie et al. 2013; Williams et al. 2013; references therein).

Let us suppose that the terminal time of control action $0< T < \infty$ is set free. Our goal is to find an optimal release rate $u^{*}(t) \in [0, u_{\max }], \ t \in [0, T^{*}]$ and the minimum time $T^{*} \in (0,\infty )$ satisfying the terminal endpoint condition

$$\begin{aligned} F_n \left( T^{*} \right) = \varepsilon , \end{aligned}$$

(27)

where $\varepsilon \rightarrow 0^{+}$ is specified by the decision-maker, while minimizing the objective functional

$$\begin{aligned} \min \limits _{\begin{array}{l} 0 \le u(t) \le u_{\max } \\ 0< T< \infty \end{array}} \mathcal {J} (u, T) = \min \limits _{\begin{array}{l} 0 \le u(t) \le u_{\max } \\ 0< T < \infty \end{array}} \int \limits _0^T \left( 1 + \frac{C}{2} \ u^2(t) \ \left[ M_w (t) + F_w(t) \right] \right) dt\nonumber \\ \end{aligned}$$

(28)

over the set of all possible solutions to the dynamical system

$$\begin{aligned} \frac{d M_n}{dt}= & {} \frac{\epsilon _n \rho _n F_n M_n \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+F_w} \, -\mu _n M_n, \end{aligned}$$

(29a)

$$\begin{aligned} \frac{d F_n}{dt}= & {} \frac{(1-\epsilon _n) \rho _n F_n M_n \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+F_w} - \delta _n F_n, \end{aligned}$$

(29b)

$$\begin{aligned} \frac{d M_w}{dt}= & {} \frac{\epsilon _w \rho _w F_w (M_n + M_w) \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+F_w} - \mu _w M_w + u(t) M_w, \end{aligned}$$

(29c)

$$\begin{aligned} \frac{d F_w}{dt}= & {} \frac{(1-\epsilon _w) \rho _w F_w (M_n + M_w) \, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n+F_n+ M_w+F_w} - \delta _w F_w + u(t) F_w,\nonumber \\ \end{aligned}$$

(29d)

with the initial conditions (25).

The terminal endpoint condition (27) implies that, under optimal release rate $u^{*}(t)$, the population of wild females $F_n$ must become virtually extinct¹² at the final (optimal) time $T^{*}$. It is also clear that a protracted reduction in wild female density, $F_n(t)$, will be reflected in inevitable reduction of wild male density, $M_n(t)$, since the wild males may only appear as progenies of mating between wild males and wild females.

Remark 5

Roughly speaking, the terminal endpoint condition (27) may look overly strong here since we know that, in theory, it is sufficient to drive the system (29) into the basin of attraction of the Wolbachia-infected steady state $E_w= \big (0, 0, M_w^{\sharp }, F_w^{\sharp } \big )$ (cf. relationships (23)) and then to suspend the control action. In practice, however, the wild mosquitoes may have an additional input (which is not accounted for in this model) that comes from hatching of uninfected eggs which may have been left in diapause¹³ by previous generations. Therefore, by imposing the terminal endpoint condition (27) we intend to cope with such uncertainties.

The objective functional (28) refers to minimization of the terminal time, $T=\int _0^T dt,$ together with the control effort $\frac{1}{2} u^{2}(t) \left[ M_w(t)+ F_w(t) \right]$ (i. e., cultivation costs of Wolbachia-infected mosquitoes in laboratory conditions) over the period [0, T]. In (28), $C>0$ expresses the (relative) unit cost of control action (i.e., production of one cohort of mosquitoes consisting of a certain number of individuals). By varying the value of C, one can reflect different priorities of the decision-making. Smaller values of C in the objective functional (28) would imply that production costs are (relatively) low in comparison to the time appreciation by the decision-maker, while higher values of C would imply that production costs are (relatively) high.¹⁴

In formulating the control problem we assume that there is no linear relationship between the coverage of control interventions and their respective costs, while the cost related to the strategy implementation span, T, is proportional to time. Therefore, the integrand function in (28) is assumed quadratic with respect to control variable what naturally implies that marginal cost of control action, i. e. $C u(t) \big [ M_w (t) + F_w(t) \big ]$, effectively depends on the control variable at each $t \in [0, T]$ and expresses the number of Wolbachia-carriers ($u (t) \big [ M_w (t) + F_w(t) \big ]$) to be released at the day t in target locality multiplied by the underlying cost $C>0$ of the release. This approach is rather conventional in optimization involving population dynamics and it has been thoroughly justified for models where control functions express different combinations of vector control efforts (Blayneh et al. 2009; Okosun et al. 2011; Moulay et al. 2012; Okosun et al. 2013; Sepúlveda and Vasilieva 2016).¹⁵ Additionally, quadratic form of control in (28) helps to justify the existence of solution of the optimal control problem (27)–(29) allows for rather logical and simple interpretation of the maximum principle (see Remark 7).

To solve the problem of minimizing the objective functional (28) subject to dynamical constraints (29) with initial conditions (25) and terminal condition (27) one may apply the Pontryagin maximum principle. The convexity of the integrand in (28) with respect to control variable u, the linearity of the ODE system (29) in u, and the compactness of the range of state variables in $\mathbb {R}^4_+$ for any finite $0< T < \infty$ should altogether assure the existence of the optimal control (see more details and formal proofs in the book by Fleming and Rishel (1975)). However, uniqueness of optimal control cannot be assured here due to the lack of strick convexity of the objective functional (28) with respect to state variables $M_w(t)$ and $F_w(t)$ (Fleming and Rishel 1975).

In particular, we are interested in the variant of maximum principle applicable to optimal control problems with free terminal time, concisely described by Lenhart and Workman (2007), according to which an optimal pair $(u^{*}, T^{*})$ must always satisfy the necessary conditions that are formulated using the so-called Hamiltonian function:

$$\begin{aligned}&H \left( {\varvec{X}}, u, {\varvec{\lambda }}\right) \nonumber \\&\quad = H \left( M_n, F_n, M_w, F_w, u, \lambda _1, \lambda _2, \lambda _3, \lambda _4 \right) \nonumber \\&\quad = \ - 1 - \ \frac{C}{2} \ u^2 \ \left[ M_w + F_w \right] \nonumber \\&\qquad +\, \lambda _1 \cdot \left[ \frac{\epsilon _n \rho _n F_n M_n \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+F_w} \, - \mu _n M_n \right] \nonumber \\&\qquad +\, \lambda _2 \cdot \left[ \frac{(1-\epsilon _n) \rho _n F_n M_n \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+F_w} -\delta _n F_n \right] \nonumber \\&\qquad +\, \lambda _3 \cdot \left[ \frac{\epsilon _w \rho _w F_w (M_n + M_w) \, e^{-\sigma (M_n+F_n+M_w+F_w)}}{M_n+F_n+M_w+ F_w} -\mu _w M_w + u \ M_w \right] \nonumber \\&\qquad +\, \lambda _4 \cdot \left[ \frac{(1-\epsilon _w) \rho _w F_w (M_n + M_w) \, e^{-\sigma (M_n + F_n + M_w + F_w)}}{M_n +F_n+M_w+F_w} - \delta _w F_w + u \ F_w \right] ,\nonumber \\ \end{aligned}$$

(30)

where ${\varvec{\lambda }}= (\lambda _1, \lambda _2, \lambda _3, \lambda _4)^{\prime }$ can be viewed as Lagrange multipliers.

Let $\big ( u^{*}, T^{*} \big )$ be an optimal pair in the sense that $u^{*}(t)$ is a piecewise continuous real function with domain $[0, T^{*}]$ and range $[0, u_{\max }]$ and $\mathcal {J}(u^{*}, T^{*}) \le \mathcal {J}(u,T)$ for all other controls u and times T. Let ${\varvec{X}}^{*}(t) = {\varvec{X}}\big ( t, u^{*}(t) \big )= \Big ( M_n^{*}(t),F_n^{*}(t),M_w^{*}(t),F_w^{*}(t) \Big )^{\prime }$ be the corresponding state defined for all $t \in [0, T^{*}]$. Then there exists a piecewise differentiable adjoint function ${\varvec{\lambda }}: [0, T^{*}] \mapsto \mathbb {R}^4$ satisfying the adjoint differential equation

$$\begin{aligned} \frac{d {\varvec{\lambda }}}{dt} \ = \ - \ \frac{\partial H \left( {\varvec{X}}^{*}, u^{*}, {\varvec{\lambda }}\right) }{\partial {\varvec{X}}} \end{aligned}$$

(31)

with three transversality conditions

$$\begin{aligned} \lambda _1 (T^{*})= 0, \quad \lambda _3 (T^{*}) = 0, \quad \lambda _4 (T^{*})= 0, \end{aligned}$$

(32)

while $0< T^{*} < \infty$ satisfies the condition (27) and fulfills that

$$\begin{aligned} H \left( {\varvec{X}}^{*}(T^{*}), u^{*}(T^{*}), {\varvec{\lambda }}(T^{*}) \right) = 0. \end{aligned}$$

(33)

Remark 6

It is worthwhile to point out that there are four adjoint variables $\lambda _i, i=1, 2, 3, 4$ (one for each state variable) and only three transversality conditions (32). On the other hand, the state variable $F_n(t)$ has two “end-point” conditions assigned, that is, one initial condition from (25) and the terminal-time condition (27) which can be formally associated with its corresponding adjoint variable $\lambda _2(t)$. For more details regarding the assignment of transversality conditions while dealing with mixed “end-point” conditions for controlled dynamical systems, please refer to the classical textbook by Bryson and Ho (1975).

Moreover, the Hamiltonian (30) has a critical point (maximum¹⁶) at $u=u^{*}(t)$, that is,

$$\begin{aligned} H \left( {\varvec{X}}^{*}(t), u^{*}(t), {\varvec{\lambda }}(t) \right) \ge H \left( {\varvec{X}}^{*}(t), u(t), {\varvec{\lambda }}(t) \right) \end{aligned}$$

for any admissible $u(t): [0, T^{*}] \mapsto [0, u_{\max }]$ and for almost all $t \in [0, T^{*}]$.

The above condition can be written in a more convenient form by following the approach proposed by Lenhart and Workman (2007), namely:

$$\begin{aligned} \left. \begin{array}{ll} u^{*}(t) = 0 &{} \hbox {if} \;\; \dfrac{\partial H }{\partial u}< 0 \\ 0< u^{*}(t) < u_{\max } &{} \hbox {if} \;\; \dfrac{\partial H }{\partial u} = 0 \\ u^{*}(t) = u_{\max } &{} \hbox {if} \;\; \dfrac{\partial H }{\partial u} > 0 \end{array} \right\} \end{aligned}$$

(34)

or, equivalently,

$$\begin{aligned} u^{*}(t) = \max \left\{ 0, \min \left\{ \frac{1}{C} \cdot \frac{\lambda _3(t) M_w(t) + \lambda _4(t) F_w(t)}{M_w (t) + F_w(t)}, u_{\max } \right\} \right\} . \end{aligned}$$

(35)

Remark 7

The Pontryagin maximum principle gives us some interesting insights regarding the costs of control strategies. From the economics standpoint, the condition

$$\begin{aligned} \frac{\partial H}{\partial u} = - C u (M_w + F_w) + \lambda _3 M_w + \lambda _4 F_w = 0 \end{aligned}$$

implies that, under optimal release rate $u^{*}$, the marginal cost of control action (expressed by the term $C u (M_w + F_w)$) should be equal to its marginal benefit (given by the term $\lambda _3 M_w + \lambda _4 F_w$). If the marginal cost of $u^{*}$ is higher than its marginal benefit (that is, $\dfrac{\partial H}{\partial u} < 0$ in (34)) then it is optimal not to employ this strategy at all, i.e., $u^{*}(t)=0$. Alternatively, if the marginal cost of $u^{*}$ is lower than its marginal benefit (that is, $\dfrac{\partial H}{\partial u} > 0$ in (34)) then it is optimal to use all available resources, i.e., $u^{*}(t)=u_{\max }$.

The closed form (35) is usually referred to as characterization of optimal control. Using this form, the original optimal control problem (27)–(29) can be reduced to a two-point boundary value problem. The latter is known as optimality system and is composed by eight differential equations with eight endpoint conditions, namely:

• four direct Eqs. (29) where u(t) is replaced by its characterization (35);

• four adjoint equations (31) where u(t) is replaced by its characterization (35);¹⁷

• four initial conditions (25) specified at $t=0$;

• three transversality conditions (32) and one endpoint condition (27) specified at $t=T^{*}$.

The optimal time $0< T^{*} < \infty$ is then defined by the optimality condition (33).

Due to non-linearity and high dimension of the optimality system described above, it can only be solved numerically. Traditional techniques for solving the optimality systems (as well as boundary value problems for ODE systems in general) include the so-called forward-backward sweep methods outlined by Lenhart and Workman (2007), shooting methods thoroughly described by Roberts and Shipman (1972), and direct collocation methods recapitulated by Ascher et al. (1988). However, when the final time T is not fixed or when additional constraints of the type (27) are imposed, these methods do not guarantee the convergence of the numerical algorithm. Another efficient way to solve numerically this two-point boundary value problem together with necessary optimality condition (33) for terminal time $T^{*}$ is the technique based on direct orthogonal collocation. This method is implemented in the GPOPS-II solver¹⁸ designed for MATLAB platform, which is briefly described in “Appendix B”.

4 Numerical results and discussion

For the sake of numerical simulations, let us assume that major parameters of dynamical system (29) have fixed values given in Table 1. These values are realistic, i.e. they are taken from scientific literature (see exact references in the last column of Table 1); however, this data set is artificial since it was not obtained by the model fitting into real measurements. Here we suppose that Wolbachia does not alter the adult sex ratio in Aedes aegypti (that is, $\epsilon _n = \epsilon _w$) since there is no scientific evidence that proves otherwise. By choosing adequately the value of parameter $\sigma$, one may extend or shrink the carrying capacity of mosquito densities (i.e., the maximum number of mosquitoes sustained by the environment).

Table 1 Reference values of problem’s parameters

It is rather difficult to estimate the mosquito population density (or size) in a particular locality. However, it is possible to estimate an average number of female mosquitoes per one human host using mathematical modeling and data fitting. According to Sepúlveda-Salcedo et al. (2015) and Sepúlveda and Vasilieva (2016), there are usually between 1 and 2 Aedes aegypti females per one human host in dengue-endemic areas. Thus we have chosen the value $\sigma =0.005$ that appear in Table 1 to qualitatively represent the mosquito population (in thousands of individuals) in a medium-sized city with population of about 200.000–300.000 inhabitants.

Our numerical simulations are focused on the “worst scenario”, that is, supposing that wild mosquitoes have almost equilibrium densities at $t=0$. We also assume that the maximum release rate is $u_{\max }=0.06$ meaning 6% per day of the total number of Wolbachia-infected mosquitoes already present in the locality. To get started, we define the initial conditions as follows:

$$\begin{aligned} \begin{array}{lll} M_n(0)= 312, &{} &{} F_n(0)=374, \\ M_w(0)=0.1 M_n (0) = 31.2, &{} &{} F_w(0)=0.1 F_n(0) =37.4, \end{array} \end{aligned}$$

(36)

keeping in mind that, for the numerical values of model parameters from Table 1, we have $M_n^{\sharp }= 312.247$ and $F_n^{\sharp }=374.697$. The two conditions in the lower row of (36) imply that, at $t=0$, there was an abundant initial release of Wolbachia-infected mosquitoes (about 10% of the number of wild males and females initially present in the locality).

We are interested to disclose the optimal release rate $u^{*}$ and to find the number of Wolbachia-carriers males $u^{*}(t) \big [ M_w^{*}(t) + F_w^{*}(t) \big ]$ to be released daily in order to minimize the objective (28). Additionally, we seek to define for how many days $T^{*}$ this release program should be carried on in order to drive the population of wild Aedes aegypti females towards local extinction, that is,

$$\begin{aligned} F_n \left( T^{*} \right) = 10^{-k} \quad \hbox {where} \quad k \in \mathbb {N}. \end{aligned}$$

It is reasonable to expect that $T^{*}$ would increase as k increases. Our numerical calculations have been performed using GPOPS-II software for two reasonable values of k: $k=2$ and $k=4$. We have also considered two alternative priorities in decision-making, namely:

Option A:

Time is far more important than the production cost of Wolbachia-infected mosquitoes ($C=0.02$);

Option B:

Both time and the production cost are equally important ($C=2$);

We have assumed the standard GPOPS-II numerical tolerance of $10^{-5}$ for internal calculations with regards to scaling.¹⁹

Fig. 9

Left column: for $k=2$ the minimum final time is $T^{*}=472$ days. Right column: for $k=4$, the minimum final time is $T^{*}=610$ days . In the middle row, the uninfected populations are plotted by dashed curves, Wolbachia-infected populations are drawn by solid curves, while male and female densities are given by blue and red curves, respectively. Optimal release rates $u^{*}(t)$ for $t \in [0, T^{*}]$. Evolution of mosquito densities $M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t)$ under optimal release rates for $t \in [0, T^{*}]$. Number of Wolbachia-infected mosquitoes to be released daily during $t \in [0, T^{*}]$

Figure 8 presents the results of numerical solutions for Option A. Here, the left column corresponds to numerical solution of the optimal control problem under terminal constraint $F_n(T^{*})=10^{-2}$ (that is, for $k=2$), while the right column provides solutions under terminal constraint $F_n(T^{*})=10^{-4}$ (that is, for $k=4$). Each column contains the graphs of optimal release rate $u^{*}(t)$ (top row), corresponding states $M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t)$²⁰ (middle row), and the optimal number of Wolbachia-carriers to be released daily, that is, $u^{*}(t) \left[ M_w^{*}(t) + F_w^{*}(t) \right]$ (bottom row). The lower charts in Fig. 8 designate the optimal release programs by indicating how many Wolbachia-carriers should be released in the target locality at each day t, while the upper charts for $u^{*}(t)$ just show the daily changes in the release rate which is a technical quantity merely needed to express mathematically the control action.

As expected, the optimal time $T^{*}$ of policy implementation is less in case of $k=2$ ($T^{*}=472$ days) than for $k=4$ ($T^{*}=610$ days).

It is also clearly seen that the release rates $u^{*}(t)$ and the number of Wolbachia-infected mosquitoes $u^{*}(t) \left[ M_w^{*} + F_w^{*}(t) \right]$ to be released daily are quite similar in both cases (see the top and bottom rows of Fig. 8). The number of released Wolbachia-carriers should grow fast during first 252 days (rising from 4 to almost 42 thousands!), and then decline toward low quantities during the following 160 days (from $t=252$ to $t=412$). By the end of this period, the densities of Wolbachia-infected mosquitoes (both males and females, see the middle row of Fig. 8) will clearly prevail in both cases. Additionally, in both cases (Fig. 8) we have that at $t=412$ the optimal states are

$$\begin{aligned} \begin{array}{lll} M_n^{*} (412) \approx 0.012 &{} &{} F_n^{*}(412) \approx 0.073, \\ M_w^{*}(412) \approx 165.728, &{} &{} F_w^{*}(412) \approx 244.102, \end{array} \end{aligned}$$

(37)

(in thousands of individuals) and that the value of control function $u^{*}(t)$ for all $t > 412$ drops below the numerical accuracy ($10^{-5}$); therefore, the control action is suspended, i.e. $u^{*}(t) =0$ and $u^{*}(t) \left[ M_w^{*} + F_w^{*}(t) \right] =0$ when $t \in [412, T^{*}]$.

The optimality condition (33) for final time $T^{*}$ is checked by evaluating the maximized Hamiltonian $H^{*}(t)= H \Big ( M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t), u^{*}(t), {\varvec{\lambda }}(t) \Big )$ over the interval $[0, T^{*}]$ (see the plots given in the top row of Fig. 9). Effectively, $H^{*}(t) < 10^{-5}$ even before arriving to $T^{*}$ in both cases, but the terminal end-point condition $F_n(T^{*})=10^{-k}$ is only met exactly at $t=T^{*}$.

The charts at the bottom row of Fig. 9 display the values of the objective functional (28) with respect to the iteration number. Despite sinking into local minima (at 12-th iteration in both cases), the numerical algorithm is able to jump out and to continue the calculations.

It is worthwhile to recall that Fig. 8 illustrates the solution to the optimal control problem (27)–(29) under Option A, i.e. when time is far more important than the production costs. Under this condition, it is affordable to produce (and then release) huge numbers of Wolbachia-infected mosquitoes. By looking again at the optimal state plots (middle row of Fig. 8) we can clearly see that application of $u^{*}(t)$ leads to a temporal overpopulation of Wolbachia-infected female mosquitoes where the peak of almost 500 thousands (or about 134% of initial wild female density!) is reached at $t=254$. The latter is caused by abundant releases since the mosquito cultivation comes at affordable costs. However, the same graph reveals that the densities of Wolbachia-infected males and females will eventually reach the equilibrium values $M_w^{\sharp }= 186.221$ and $F_w^{\sharp }=223.465$ in accordance with formulas (14b). Thus, the temporal mosquito overpopulation can be regarded as a negative side effect of this decision policy since human residents of the target locality may reject such a policy.

Let us now consider Option B where the decision-making preferences are considerably altered. Namely, the time appreciation has less weight in the decision policy than the production costs of Wolbachia-infected mosquitoes. In other words, mosquito cultivation becomes more expensive but there is more time to implement the program.

Fig. 10

Left column: for $k=2$ and $T^{*}=472$ days, optimal solution was found after 46 iterations. Right column: for $k=4$ and $T^{*}=610$ days, optimal solution was found after 95 iterations. Plots of the maximized Hamiltonian $H^{*}(t)$ for $t \in [0, T^{*}]$. Value of the objective functional $\mathcal {J}(u,T)$ at each iteration

Fig. 11

Left column: for $k=2$ the minimum final time is $T^{*}=499$ days. Right column: for $k=4$, the minimum final time is $T^{*}=637$ days. In the middle row, the uninfected populations are plotted by dashed curves, Wolbachia-infected populations are drawn by solid curves, while male and female densities are given by blue and red curves, respectively. Optimal release rates $u^{*}(t)$ for $t \in [0, T^{*}]$. Evolution of mosquito densities $M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t)$ under optimal release rates for $t \in [0, T^{*}]$. Number of Wolbachia-infected mosquitoes to be released daily during $t \in [0, T^{*}]$

Figure 10 presents the results of numerical solutions for Option B. As before, the left column corresponds to numerical solution of the optimal control problem under terminal constraint $F_n(T^{*})=10^{-2}$ (that is, for $k=2$), while the right column provides solutions under terminal constraint $F_n(T^{*})=10^{-4}$ (that is, for $k=4$). Each column contains the graphs of optimal release rate $u^{*}(t)$ (top row), corresponding states $M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t)$ (middle row), and the optimal number of Wolbachia-infected mosquitoes to be released daily, that is, $u^{*}(t) \left[ M_w^{*}(t) + F_w^{*}(t) \right]$ (bottom row).

The maximized Hamiltonian $H^{*}(t)= H \Big ( M_n^{*}(t), F_n^{*}(t), M_w^{*}(t), F_w^{*}(t), u^{*}(t), {\varvec{\lambda }}(t) \Big )$ is plotted for $k=2$ and $k=4$ in the top row of Fig. 11 over the interval $[0, T^{*}]$ and its value drops below $10^{-5}$ (numerical accuracy) long before $T^{*}$. However, the terminal end-point condition $F_n(T^{*})=10^{-k}$ is only met exactly at $t=T^{*}$.

The charts at the bottom row of Fig. 11 display the values of the objective functional (28) with respect to the iteration number. Again, after sinking into local minima (at 13-th iteration in both cases), the numerical algorithm jumps out and continues the calculations.

Quite expectedly, the optimal time $T^{*}$ of policy implementation is less in case of $k=2$ ($T^{*}=499$ days) than for $k=4$ ($T^{*}=637$ days).

It is also clearly seen that the release rates $u^{*}(t)$ and the number of Wolbachia-carriers $u^{*}(t) \left[ M_w^{*} + F_w^{*}(t) \right]$ to be released daily are quite similar for $k=2$ and $k=4$ (see the top and bottom rows of Fig. 10). The number of released Wolbachia-infected mosquitoes grows fast during first 171 days rising from 4 to almost 24 thousands but without exceeding equilibrium value of wild mosquitoes (in contrast to the strategy obtained for Option A). From this peak, the number of released Wolbachia-infected mosquitoes declines steadily towards lower quantities during the following 203 days (from $t=171$ to $t=373$). By the end of this period, the densities of Wolbachia-infected mosquitoes (both males and females, see the middle row of Fig. 10) will clearly prevail and in both cases we have that at $t=373$ the optimal states are:

$$\begin{aligned} \begin{array}{lll} M_n^{*} (373) \approx 0.206 &{} &{} F_n^{*}(373) \approx 0.672, \\ M_w^{*}(373) \approx 164.989, &{} &{} F_w^{*}(373) \approx 242.067, \end{array} \end{aligned}$$

(38)

(in thousands of individuals) and that the value of control function $u^{*}(t)$ for all $t > 373$ drops below the numerical accuracy ($10^{-5}$); therefore, the control action is suspended, i.e. $u^{*}(t) =0, \ t \in [373, T^{*}]$.

Fig. 12

Left column: for $k=2$ and $T^{*}=499$ days, optimal solution was found after 59 iterations. Right column: for $k=4$ and $T^{*}=637$ days, optimal solution was found after 80 iterations. Plots of the maximized Hamiltonian $H^{*}(t)$ for $t \in [0, T^{*}]$. Value of the objective functional $\mathcal {J}(u,T)$ at each iteration

In contrast to Option A, the optimal strategy $u^{*}(t)$ here does not produce temporal overpopulation of Wolbachia-infected mosquitoes. Thus, by changing the priorities of decision-making from Option A to Option B, we can avoid the negative side effect of temporal overpopulation at the cost of “allegedly” extending the overall period of policy implementation by 27 days, that is, from 472 to 499 days (for $k=2$) and from 610 to 637 days (for $k=4$). In practical term, however, it can be observed that

$$\begin{aligned} u^{*}(t) = 0 \quad \hbox {for} \quad \left\{ \begin{array}{lll} t \in [412, T^{*}] &{} {(\mathbf Option A )}, &{} k=2,4 \\ t \in [373, T^{*}] &{} {(\mathbf Option B )}, &{} k=2,4 \end{array} \right. \end{aligned}$$

(39)

meaning that factual releases are suspended 39 days earlier for Option B than for Option A. Therefore, active control intervention (releases of Wolbachia-carriers) goes on for less time in case of Option B. On the other hand, in case of Option A, one has to wait less for actual fulfilments of the terminal conditions $F_n (T^{*})=10^{-k}, k=2,4$; therefore, the overall time of policy implementation is less.

As shown by (39), when the releases are suspended, the terminal conditions $F_n (T^{*})=10^{-k}, k=2,4$ are not met yet (cf. (37), (38)). Nonetheless, the densities of wild mosquitoes, $M_n^{*}(t)$ and $F_n^{*}(t)$, continue to decrease as $t \rightarrow T^{*}$ and both wild populations are eventually driven towards extinction (see the middle row charts of Figs. 8 and  10). This outcome is quite expected here since, according to Proposition 1, the original ODE system (10)–(11) is bistable, and the control effort u(t) in (29) is applied in order to drive the system states from the attraction basin of Wolbachia-free equilibrium $E_n$ to the attraction basin of Wolbachia invasion equilibrium $E_w$. In other words, inoculative releases of Wolbachia-carriers at the optimal rate $u^{*}(t)$ should gradually change the frequency of Wolbachia infection in the locality either causing a temporal overpopulation of the mosquitoes (Option A) or without exceeding the carrying capacity of the environment (Option B).

Actually, in both cases (i.e. for Options A and B) the optimal states (37) and (38) are already in the attraction basin of $E_w = \big ( 0,0,M_w^{\sharp }, F_w^{\sharp } \big )$ since they satisfy the conditions (23). The latter becomes clear after evaluating the coordinates of the coexistence equilibrium $E_c$ for parameter values given in Table 1:

$$\begin{aligned} M_n^c=46.555, \quad F_n^c = 55.866, \quad M_w^c = 139.665, \quad F_w^c = 167.598. \end{aligned}$$

Thus, meeting the terminal-time constraint $F_n (T^{*})=10^{-k}, k=2,4$ is now a matter of waiting and letting nature take its course. The goal will be reached sooner or later without any additional control effort.

5 Conclusions and further research

In this paper, we have presented an explicit sex-structured model that describes the population dynamics and interaction between two subpopulations of Aedes aegypti mosquitoes: wild (or uninfected) and deliberately infected with wMelPop strain of Wolbachia. Our model captures the principal features of density-dependence and bistability which are present in other models of Wolbachia invasion developed by different scholars (Farkas and Hinow 2010; Turelli 2010; Barton and Turelli 2011; Coelho and Codeço 2011; Hancock et al. 2011a; Hancock and Godfray 2012; Schraiber et al. 2012; Koiller et al. 2014; Bliman et al. 2015) and accords with the larger-scaled sex-structured model developed by Farkas et al. (2017) for different Wolbachia strains and mosquito species. Additionally, it possesses the necessary grade of explicitness that allows for natural introduction of the control variable in order to simulate an external intervention.

Our primary goal was to propose a feasible method for inducing and establishing Wolbachia infection with wMelPop strain among wild (uninfected) local populations of Aedes aegypti mosquitoes and to reach the population replacement in finite time. This particular strain causes complete blockage of the different serotypes of dengue and also acts as an effective blocker of other arboviruses (Moreira et al. 2009; Walker et al. 2011; Ferguson et al. 2015). On the other hand, rather high “fitness costs” of wMelPop strain makes it difficult to establish in wild populations of Aedes aegypti mosquitoes. Nonetheless, we have proposed a feasible release program for spreading this particular Wolbachia strain among wild mosquito populations.

It is too early to speak about practical implementation of our approach, but this paper has made some essential steps towards this goal. First, we have established a general structure of a successful release program (see two lower charts in Figs. 8 and  10), which is “bell-formed” in the following sense. During initial phase of the release program, the number of Wolbachia-carrying mosquitoes released per day is increased gradually from moderate quantities until reaching a “top value”. Further, the number of Wolbachia-carrying mosquitoes released per day declines a bit faster towards total suspension. Second, we have estimated such a “top value” that characterizes the maximum daily production capacity of laboratory where Wolbachia-carrying mosquitoes are artificially bred and cultivated. The latter is an essential datum for practical implementation of releases. Third, we have provided estimation for duration of the release program implementation and population replacement (optimal time $T^{*}$).

It is worthwhile to note that our release policies derived by applying the optimal control framework to sex-structured model concurs with recommendations of Yeap et al. (2014) in the following sense: (i) considerable quantities of Wolbachia-carriers should be released; (ii) releases should take place over a long period of time; (iii) invasion of wMelPop Wolbachia strain is only likely to occur in relatively isolated populations.

Knowing that wMelPop strain of Wolbachia is considered the most beneficial in the context of prevention and control of dengue and other vector-borne infections, our method for establishing wMelPop strain of Wolbachia may become part of integrated measures for vector control. In this paper, we have focused on the “worst scenario” by supposing that wild mosquito densities are close to their equilibrium values at the beginning of control action. However, our method can be even more beneficial as a posterior measure in a two-stage (or multi-stage) vector control interventions. Namely, if the population density of wild mosquitoes is reduced during the initial stage(s) by other actions (such as, insecticide spraying, sterile-insect techniques, etc.), then wMelPop Wolbachia invasion and, ultimately, the population replacement can be achieved faster and cheaper (i.e., by cultivating less overall number Wolbachia-carriers in the laboratory). Additionally, introducing insecticide resistance into the Wolbachia-carriers during their artificial breeding can also be helpful (Hoffmann and Turelli 2013). However, modeling of this approach lays beyond the scope of this paper and is left for further research.

Appendices

Appendix A: Meaning of $\mathcal {R}_0$ in Proposition  1

In order to reveal the meaning of threshold $\mathcal {R}_0$ given by formula (18) in Proposition 1, we propose to follow the next generation operator approach attributed to Diekmann et al. (1990), which was further presented by Castillo-Chávez et al. (2002) in a form of comprehensive tutorial.

In fact, since Wolbachia symbiont is maternally transmitted from a female mosquito to her offspring, the next generation produced by this female will be infected with Wolbachia. Thus, Wolbachia infection can be viewed as a maternally transmitted disease among the mosquito population. The steady state $E_n^{\sharp } = \big ( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \big )$ can be regarded as a disease-free equilibrium in epidemiological terminology. The threshold value $\mathcal {R}_0$ that determines whether the epidemics vanishes or spreads is usually referred to as basic reproductive number.²¹ Diekmann et al. (1990) defined $\mathcal {R}_0$ as the spectral radius of the “next generation operator”, while Castillo-Chávez et al. (2002) provide a method to calculate this spectral radius in case of discrete heterogeneity, i. e. when the population of individuals is subdivided into several groups with fixed characteristics. According to this approach, the ODE system (10)–(11) can be re-written in the following form:

$$\begin{aligned} \frac{d \varvec{Y}}{d t}= & {} \varvec{f}(\varvec{Y},\varvec{Z})=\left( G_1 (\varvec{Y},\varvec{Z}), G_2 (\varvec{Y},\varvec{Z}) \right) ^{\prime },\\ \frac{d \varvec{Z}}{d t}= & {} \varvec{g}(\varvec{Y},\varvec{Z}) = \left( G_3(\varvec{Y},\varvec{Z}), G_4 (\varvec{Y},\varvec{Z}) \right) ^{\prime }, \end{aligned}$$

where $\varvec{Y}= \big ( M_n, F_n \big ) \in \mathbb {R}^2_+$ couples the uninfected individuals, while $\varvec{Z}= \big ( M_w, F_w \big )\in \mathbb {R}^2_+$ engages Wolbachia-infected individuals. Since $E_n^{\sharp } = \big ( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \big )= \big ( \varvec{Y}^{\sharp }, \mathbf{0})$ stands for infection-free equilibrium, we have $\varvec{f}(\varvec{Y}^{\sharp },\mathbf{0}) = \varvec{g}(\varvec{Y}^{\sharp },\mathbf{0}) = \mathbf{0}.$ Let

$$\begin{aligned} A = D_{Z} \left( E_n^{\sharp } \right) = \left[ \begin{array}{ll} \dfrac{\partial G_3}{\partial M_w} &{} \dfrac{\partial G_3}{\partial F_w} \\ \dfrac{\partial G_4}{\partial M_w} &{} \dfrac{\partial G_4}{\partial F_w} \end{array} \right] = \left[ \begin{array}{lll} -\mu _w &{} &{} \dfrac{\epsilon _w \rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n)}}{M^{\sharp }_n + F^{\sharp }_n} \\ 0 &{} &{} \dfrac{(1-\epsilon _w)\rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n)}}{M^{\sharp }_n + F^{\sharp }_n} -\delta _w \\ \end{array} \right] \end{aligned}$$

and further assume that A can be written in the form $A = \mathcal {M} - D$, with $\mathcal {M} \ge 0$ (that is, $m_{ij} \ge 0$) and $D > 0$, a diagonal matrix.²² Under this assumption

$$\begin{aligned} \mathcal {M} = \left[ \begin{array}{lll} 0 &{} &{} \dfrac{\epsilon _w \rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n)}}{M^{\sharp }_n + F^{\sharp }_n } \\ 0 &{} &{} \dfrac{(1-\epsilon _w)\rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n )}}{M^{\sharp }_n + F^{\sharp }_n } \\ \end{array} \right] , \quad D = \left[ \begin{array}{ll} \mu _w &{} 0 \\ 0 &{} \delta _w \end{array} \right] . \end{aligned}$$

Then, according to Castillo-Chávez et al. (2002), $\mathcal {R}_0$ can be defined as the spectral radius of

$$\begin{aligned} \mathcal {M} D^{-1}=\left[ \begin{array}{lll} 0 &{} &{} \dfrac{\epsilon _w \rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n)}}{\delta _w (M^{\sharp }_n + F^{\sharp }_n)} \\ 0 &{} &{} \dfrac{(1-\epsilon _w) \rho _w M^{\sharp }_n e^{ -\sigma (M^{\sharp }_n + F^{\sharp }_n)}}{\delta _w (M^{\sharp }_n + F^{\sharp }_n)} \\ \end{array} \right] . \end{aligned}$$

Namely,

$$\begin{aligned} \mathcal {R}_0 = \varrho \left( \mathcal {M} D^{-1} \right) = \max \left\{ 0,\frac{(1-\epsilon _w) \rho _w M^{\sharp }_n e^{-\sigma (M^{\sharp }_n + F^{\sharp }_n )}}{ \delta _w (M^{\sharp }_n +F^{\sharp }_n )} \right\} \end{aligned}$$

is the dominant eigenvalue of $\mathcal {M} D^{-1}$. By replacing the values of $M_n^{\sharp }$ and $F_n^{\sharp }$ from (14a), we obtain that

$$\begin{aligned} \mathcal {R}_0 = \frac{(1-\epsilon _w)\rho _w /\delta _w}{(1-\epsilon _n)\rho _n /\delta _n} \end{aligned}$$

only depends on female-related parameters. The latter is quite logical since all Wolbachia-infected females are “spreaders” of the disease. In view of conditions (12), we have $\mathcal {R}_0 < 1$ (cf. (18)), that is, the “birth-death ratio” of Wolbachia-infected females (numerator in the right-hand side of (18)) is less than the “birth-death ratio” of uninfected females (denominator in the right-hand side of (18)). In other words, Wolbachia-infected females exhibit reduced individual fitness in comparison to wild females. If we suppose that both infected and uninfected females have the same chances for successful mating that results in viable offspring (i.e., uninfected males and females have sufficiently high frequencies), then at each next generation of mosquitoes there will be a lesser fraction of Wolbachia-infected individuals and a greater fraction of uninfected individuals. Under this scenario, all Wolbachia-carriers will be eventually driven towards extinction, and the disease-free equilibrium $E_n^{\sharp } = \big ( M_n^{\sharp }, F_n^{\sharp }, 0, 0 \big )$ will be reached.

On the other hand, reduced individual fitness of Wolbachia-infected females is recompensed, at high infection frequencies, by their reproductive advantage derived from CI-phenotype. The latter is explained by Proposition 1.

Hypothetically speaking, if we disregard the conditions (12) and suppose that Wolbachia does not alter neither fecundity nor longevity of the host (that is, $\epsilon _n=\epsilon _w, \rho _n=\rho _w, \mu _n = \mu _w, \delta _n=\delta _w$ so that $\mathcal {R}_0 = 1$), then Wolbachia invasion could be induced by a single release of very small number of Wolbachia-carriers, and this “imaginary” scenario also agrees with our model (10)–(11), as well as with the principle of competitive exclusion.

Appendix B: Technical note on GPOPS-II solver for MATLAB platform

Generally speaking, there are two groups of collocation techniques — the direct collocation and the orthogonal collocation. Under the direct collocation approach, the state and adjoint trajectories of the optimality system are discretized at a set of appropriately chosen grid of nodes (that is, collocation points) in the fixed time interval $[t_0, t_f]$. Then the state and adjoint trajectories are iteratively approximated using the same fixed-degree polynomials (usually, cubic splines) at all subinterval of the grid in order to satisfy the differential constraints (i.e., the discretized ODE system), while the boundary constraints are taken into account at each iteration. Convergence of all methods based on direct collocation is usually achieved by increasing the number of collocation points.

On the other hand, the orthogonal collocation is performed over entire time interval $[t_0, t_f]$ where the collocation points are usually associated with Gaussian quadrature, i.e. they are roots of some orthogonal polynomial, or a linear combination of orthogonal polynomials and its derivatives. Under this approach, the state and adjoint variables of the continuous-time optimality system (as well as their derivatives) are approximated by using Lagrange interpolating polynomials over $[t_0, t_f]$ supported by the collocation points. Convergence of this method can be achieved by increasing the degree of the polynomial approximation.

The GPOPS-II solver implements an adaptive combination of two collocation techniques described above which is also known as Radau pseudospectral method. According to Garg et al. (2009), the Radau pseudospectral method is capable of dealing with free initial $t_0$ or final $t_f$ time since the input time interval $t \in [t_0, t_f]$ (which is in our case is $t \in [0,T]$ with T left free) should be transformed into $\tau \in [-1, 1]$ (with fixed endpoints!) using the affine transformation

$$\begin{aligned} \tau = \frac{2 }{t_f - t_0} \ t - \frac{t_f + t_0}{t_f - t_0}. \end{aligned}$$

In particular, this method uses the Legendre-Gauss-Radau set²³ of orthogonal collocation points what basically explains its name.

Another advantage of Radau pseudospectral method, besides its adaptiveness, is that this method (in contrast to other pseudospectral methods) allows to use the exact formulas for first- and second-order partial derivatives of problem entries and, thus, to solve more accurately the nonlinear programming problems resulting from discretization.

The main limitation of GPOPS-II package is that it requires the continuity of the first- and second-order derivatives of the Hamiltonian and endpoint constraints with respect to all variables. However, the models considered in this paper meet this condition.

Further and more detailed information regarding the GPOPS-II package, as well as some comprehensive examples, can be consulted in the paper by Patterson and Rao (2014).