Mathematical model of multivalent virus–antibody complex formation in humans following acute and chronic HIV infections

Abstract

Antibodies that bind viral surface proteins can limit the spread of the infection through neutralizing and non-neutralizing functions. During both acute and chronic Human Immunodeficiency Virus infection, antibody–virion immune complexes are formed, but fail to ensure protection. In this study, we develop a mathematical model of multivalent antibody binding and use it to determine the dynamical interactions that lead to immune complexes formation and the role of complexes with increased numbers of bound antibodies in the pathogenesis of the disease. We compare our predictions with published temporal virus and immune complex data from acute infected patients. Finally, we derive quantitative and qualitative conditions needed for antibody-induced protection.

1 Introduction

The major challenge in designing a vaccine against the Human Immunodeficiency Virus (HIV) infection is the difficulty in inducing the production of broadly neutralizing antibodies that block the infection (Bonsignori et al. 2012; Burton et al. 2012; Kwong and Mascola 2012; Plotkin 2009; Tomaras and Haynes 2010). Tomaras et al. (2008) have shown that, in natural HIV infections, the first antibody responses develop eight days following virus detection, in the form of immune complexes, with free antibodies following five days later. These antibodies primarily bind the immunodominant region of envelope protein gp41 and have weak antiviral functions such as neutralization, antibody-dependent cellular viral inhibition and cellular cytotoxicity (ADCVI and ADCC), activation of complement and opsonization (Liu et al. 2011; Tomaras and Haynes 2009; Tomaras et al. 2008). It has been suggested that antibody and immune complexes change dynamically over time in amount, specificity, and function, with antibody preferentially binding gp120 during chronic infections (Liu et al. 2011) and neutralizing the founder virus (Aasa-Chapman et al. 2004; Gray et al. 2007; Pilgrim et al. 1997; Richman et al. 2003; Tomaras et al. 2008; Wei et al. 2003).

In this study, we use a mathematical model to determine the dynamical interactions between HIV virus and the anti-gp41 monoclonal IgG antibodies. We investigate the mechanisms leading to immune complex formation during acute and chronic HIV infection. We assume that wild-type HIV virion has $14$ surface units called spikes (Zhu et al. 2006) and each envelope spike has three gp41 subunits that are accessible for antibody binding (Zhu et al. 2008; Center et al. 2002; Liu et al. 2008; Tran et al. 2012; Sattentau 2013). Moreover, if the low spike numbers prevents cross-linking between B cell receptors (Mouquet et al. 2010; Sattentau 2013), then immune complexes with at most $42$ numbers of bound antibodies can be formed. Immune complexes with increased number of bound antibodies may have different contributions to infection or protection. To determine whether multiple binding events have a role in HIV pathogenesis, we develop a mathematical model of multivalent immune complex formation and investigate the factors that affect the timing of total immune complexes population’s growth and function. We compare our predictions with published temporal virus and anti-gp41 IgG–virion immune complexes data from six acutely infected HIV patients (Liu et al. 2011).

Lastly, we use the model to predict conditions under which the pre-existing or HIV-induced antibodies contribute to viral protection. Before one can estimate the total level of antibody needed to prevent infection (in vivo), one has to estimate the number of antibody molecules needed to render a single HIV particle noninfectious. Experimental studies have predicted anything from one antibody per virion (Dimmock 1993) to one antibody per functional spike (Klasse and Sattentau 2002; Yang et al. 2005). Mathematical studies have presented combinatorial formulations for the amount of antibodies needed to neutralize an entire virion (Dimmock 1993; McLain and Dimmock 1994) or a single spike (Magnus and Regoes 2010; Magnus et al. 2013; Yang et al. 2005; Magnus and Regoes 2011; Magnus 2013). Here, we assume that the number of binding sites is constant among all virions and that all trimers are bound with the same affinity by monoclonal antibodies. With these assumptions, we determine the dynamics between the plasma virus population and the plasma anti-gp41 antibody population and we quantify the amount and quality of pre-existing antibodies needed for blocking infection when multivalent binding (1) has no antiviral effect, (2) reduces virus infectivity, or (3) increases virus clearance.

2 Mathematical model

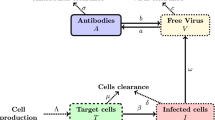
We develop a mathematical model of IgG–virion immune complex formation following HIV infection. We assume that all viral particles have $n=42$ epitopes on their surface and define $V_0$ to be free virus, and $V_i$ ($i=0, 1, \ldots n$) to be IgG–virion immune complexes with $i$ spikes bound by antibodies as follows. When $V_i$ encounters antibody, $A$, there are $n-i$ ways to occupy one of its surface proteins and obtain a virion with $i+1$ occupied sites, $V_{i+i}$. The reaction kinetics can be represented schematically as

(1)

where $k_p$ and $k_m$ are the binding and unbinding rates.

We incorporate this into the standard HIV infection model (Perelson et al. 1996) and assume that uninfected CD4 T cells, $T$, are produced at rate $s$ per ml per day, die at per capita rate $d$, and become infected by free virus or immune complexes, $V_i$, at rates $\beta _i$ ($i=0, 1, \ldots n-1$). The infectivity rates $\beta _i$ are decreasing with the number of bound spikes $i$. Moreover, we assume that virus $V_n$, which has no free spikes, cannot infect. Infected cells, $I$, die through immune killing or cell bursting at a per capita rate $\delta$. Free virus is produced at rate $p$ per infected cells per day and cleared at per capita rate $c_0$.

HIV specific antibody is produced at constant rate, $s_A$, per ml per day, increases due to antigenic stimulation of B cells by viruses with free spikes $V_i$ ($i=0, 1, \ldots n-1$) at rate $\alpha$ per virus per day, and decays at per capita rate $d_A$. IgG–virion immune complexes are cleared at rates $c_i$ dependent on the number of antibodies bound. The system describing the host–virus interaction is

$$\begin{aligned} \frac{\,\mathrm {d}T}{\,\mathrm {d}t}&= s-d T-\sum _{i=0}^{n-1}\beta _i V_i T,\nonumber \\ \frac{\,\mathrm {d}I}{\,\mathrm {d}t}&= \sum _{i=0}^{n-1}\beta _i V_i T-\delta I,\nonumber \\ \frac{\,\mathrm {d}V_0}{\,\mathrm {d}t}&= p I-c_0 V_0- nk_p V_0 A+k_m V_1,\nonumber \\ \frac{\,\mathrm {d}V_i}{\,\mathrm {d}t}&= (i+1)k_m V_{i+1} -(n-i)k_p V_i A -i k_m V_i\nonumber \\&\quad +(n-i+1) k_p V_{i-1} A -c_{i} V_i,\quad i=1,..., n-1\nonumber \\ \frac{\,\mathrm {d}V_n}{\,\mathrm {d}t}&= k_p V_{n-1} A- nk_m V_n -c_{n} V_n,\nonumber \\ \frac{\,\mathrm {d}A}{\,\mathrm {d}t}&= s_A+\alpha \sum _{i=0}^{n-1} V_i A - d_A A +k_m\sum _{i=1}^n iV_i -k_p A\sum _{i=0}^{n-1} (n-i) V_i. \end{aligned}$$

(2)

The initial values are $T(0)=T_0=s/d$, $I(0)=0$, $V_0(0)=v$, $V_i(0)=0$ ($i=1, ... n$), and $A(0)=A_0=s_A/d_A$.

The total virus density is $V_T=V_0+\sum _{i=1}^n V_i$, and the total IgG–virion immune complexes density is $X= \sum _{i=1}^n V_i$. We assume that in the absence of antibody the infections will become chronic. Thus we assume that the basic reproductive number $R_0=\frac{sp\beta _0}{c_0 d\delta }>1$ (Bonhoeffer et al. 1997).

We use this model to determine the relationship between the dynamics of the virus and IgG–virion immune complexes under various assumptions. In particular, we investigate the changes in the model predictions when infectivity and clearance rates $\beta _i$ and $c_i$ are either constant or $i$-dependent. For both scenarios we investigate the virus and IgG–virion immune complexes dynamics when the total number of available spikes (given by $n$), the levels of available HIV-specific antibody (given by $A_0$), and the antibody affinity (given by $K_A=k_p/k_m$) are varied. We will compare the theoretical results with data from six patients with acute HIV infections (Liu et al. 2011).

3 Analytical results

3.1 Asymptotic analysis of the full model

System (2) has an infection free steady-state

$$\begin{aligned} S_0=\left( \frac{s}{d},0,0,\ldots ,0,\frac{s_A}{d_A}\right) , \end{aligned}$$

and $j$ chronic steady-states

$$\begin{aligned} S_j=(\bar{T}, \bar{I}, \bar{V}_0, \ldots , \bar{V}_n, \bar{A})_j, \end{aligned}$$

where the number of non-zero steady-states $j$ is dependent on the model parameters and the number of binding sites, $n$.

Proposition 1

For $n=2$, steady-state $S_0$ is locally asymptotically stable when

$$\begin{aligned} R_0<1+\chi _2, \end{aligned}$$

where $\varPi =K_A A_0=\frac{k_p}{k_m}\frac{s_A}{d_A}$ and

$$\begin{aligned} \chi _2=\frac{2\frac{c_2}{k_m}\varPi ^2+2\varPi \frac{c_1}{k_m}\left( \frac{c_2}{k_m}+2\right) \left( 1-\frac{\beta _1 c_0}{\beta _0 c_1}\right) }{\varPi \frac{c_0}{k_m}\frac{c_2}{k_m}+2\varPi \frac{c_0}{k_m}\left( \frac{c_2}{k_m}+2\right) \frac{\beta _1}{\beta _0}+\frac{c_0}{k_m}\left( \frac{c_1}{k_m}+1\right) \left( \frac{c_2}{k_m}+2\right) }. \end{aligned}$$

(3)

Proof

The Jacobian matrix for system (2) and $n=2$ is

$$\begin{aligned} \begin{bmatrix} -d-\beta _0\bar{V}_0-\beta _1\bar{V}_1&\quad 0&\quad -\beta _0\bar{T}&\quad -\beta _1\bar{T}&\quad 0&\quad 0\\ \beta _0\bar{V}_0+\beta _1\bar{V}_1&\quad -\delta&\quad \beta _0\bar{T}&\quad \beta _1\bar{T}&\quad 0&\quad 0\\ 0&\quad p&\quad -c_0-2k_p\bar{A}&\quad k_m&\quad 0&\quad -2k_p \bar{V}_0\\ 0&\quad 0&\quad 2k_p \bar{A}&\quad -k_m-k_p\bar{A}-c_1&\quad 2k_m&\quad -k_p\bar{V}_1+2k_p\bar{V}_0\\ 0&\quad 0&\quad 0&\quad k_p\bar{A}&\quad -2k_m-c_2&\quad k_p\bar{V}_1\\ 0&\quad 0&\quad (\alpha -2k_p)\bar{A}&\quad (\alpha -k_p)\bar{A}+k_m&\quad 2k_m&\quad \varGamma _1\\ \end{bmatrix} \end{aligned}$$

where $\varGamma _1=\alpha (\bar{V}_0+\bar{V}_1)-d_A-2k_p\bar{V}_0-k_p\bar{V}_1$. The characteristic equation corresponding to $S_0$ is

$$\begin{aligned} (\lambda +d)(\lambda +d_A)(\lambda ^4+M_1\lambda ^3+M_2\lambda ^2+M_3\lambda +M_4)=0, \end{aligned}$$

(4)

where

$$\begin{aligned} M_1&=\sum _{i=0}^2 c_i +\delta +3k_m(\varPi +1),\\ M_2&=c_0\delta (1-R_0)+\varPi \left( \sum _{i=0}^2 (i+1)c_i +2k_m(\varPi +2)+3\delta \right) \\&\quad \ +(c_1+k_m)(c_2+2k_m)+(\delta +c_0)(3k_m+c_1+c_2),\\ M_3&=c_0\delta (c_1+c_2+k_m(\varPi +3))(1-R_0)+2\varPi k_m \delta c_1\left( 1-\frac{\beta _1 c_0}{\beta _0 c_1}R_0\right) \\&\quad \ +\varPi k_m \left( 4k_m(\delta +c_1)+c_2(c_0+3\delta +2c_1)\right) \\&\quad \ +(\delta +c_0)(c_1+k_m)(c_2+2k_m)+2\varPi ^2 k_m^2 (c_2+\delta ),\\ M_4&=\delta \Bigg ((c_0c_2 k_m \varPi +c_0(c_1+k_m)(c_2+2k_m))\left( 1-R_0\right) \\&\quad \ +2\varPi c_1 k_m (c_2+2k_m)\left( 1-\frac{\beta _1 c_0}{\beta _0 c_1} R_0\right) +2\varPi ^2 c_2 k_m^2\Bigg ). \end{aligned}$$

From Routh–Hurwitz conditions, equation (4) has roots with negative real parts if $M_1>0$, $M_4>0$, $M_1 M_2-M_3>0$ and $M_3 (M_1 M_2 - M_3)- M_1^2 M_4>0$. We can show, using Maple, that a sufficient condition for stability is equivalent to $R_0<1+\chi _2$ (computation upon request). $\square$

Proposition 2

For $n=3$, steady-state $S_0$ is locally asymptotically stable when

$$\begin{aligned} R_0<1+\chi _3, \end{aligned}$$

where $\varPi =K_A A_0=\frac{k_p}{k_m}\frac{s_A}{d_A}$ and

$$\begin{aligned} \chi _3\!=\!\frac{6\varPi ^3\frac{c_3}{k_m}\!+\!\left( \!3\frac{c_1}{k_m}\frac{c_3}{k_m}\varPi ^2\!+\!3\varPi \frac{c_1}{k_m}\!\left( \!\frac{c_2}{k_m}\!+\!2\!\right) \!\left( \frac{c_3}{km}\!+\!3\right) \!\right) \!\left( \!1\!-\!\frac{\beta _1 c_0}{\beta _0 c_1}\!\right) \!+\!6\varPi ^2\frac{c_2}{k_m}\!\left( \!\frac{c_3}{k_m}\!+\!3\!\right) \!\left( \!1\!-\!\frac{\beta _2 c_0}{\beta _0 c_2}\!\right) }{X_1\varPi ^2\!+\!X_2\varPi \!+\!X_3}, \end{aligned}$$

(5)

where

$$\begin{aligned} X_1&= \frac{c_0}{k_m}\frac{c_3}{k_m}\left( 2+3\frac{\beta 1}{\beta _0}\right) +6\left( \frac{c_3}{k_m}+3\right) \frac{c_0}{k_m}\frac{\beta _2}{\beta _0},\nonumber \\ X_2&= \frac{c_0}{k_m}\left( 6\frac{c_2}{k_m}+ 2\frac{c_2}{k_m}\frac{c_3}{k_m}+\frac{c_3}{k_m}+\frac{c_1}{k_m}\frac{c_3}{k_m}\right) +3\left( \frac{c_2}{k_m}+2\right) \left( \frac{c_3}{k_m}+3\right) \frac{c_0}{k_m}\frac{\beta _1}{\beta _0},\nonumber \\ X_3&= \frac{c_0}{k_m}\left( \frac{c_1}{k_m}+1\right) \left( \frac{c_2}{k_m}+2\right) \left( \frac{c_3}{k_m}+3\right) . \end{aligned}$$

(6)

Proof

The Jacobian matrix for system (2) and $n=3$ is

$$\begin{aligned} \begin{bmatrix}\! -d\!-\!\sum _{i=0}^2\beta _i \bar{V}_i&\quad 0&\quad -\beta _0\bar{T}&\quad -\beta _1\bar{T}&\quad -\beta _2\bar{T}&\quad 0&\quad 0\!\\\! \sum _{i=0}^2\beta _i\bar{V}_i&\quad -\delta&\quad \beta _0\bar{T}&\quad \beta _1\bar{T}&\quad \beta _2\bar{T}&\quad 0&\quad 0\!\\\! 0&\quad p&\quad -c_0-3k_p\bar{A}&\quad k_m&\quad 0&\quad 0&\quad -3k_p \bar{V}_0\!\\\! 0&\quad 0&\quad 3k_p \bar{A}&\quad -k_m-2k_p\bar{A}-c_1&\quad 2k_m&\quad 0&\quad -2k_p\bar{V}_1+3k_p\bar{V}_0\!\\\! 0&\quad 0&\quad 0&\quad 2k_p\bar{A}&\quad -2k_m-c_2-k_p\bar{A}&\quad 3k_m&\quad 2k_p\bar{V}_1-k_p\bar{V}_2\!\\\! 0&\quad 0&\quad 0&\quad 0&\quad k_p\bar{A}&\quad -3k_m-c_3&\quad k_p\bar{V}_2\!\\\! 0&\quad 0&\quad (\alpha -3k_p)\bar{A}&\quad (\alpha -2k_p)\bar{A}+k_m&\quad (\alpha -k_p)\bar{A}+2k_m&\quad 3k_m&\quad \varGamma _2\!\\\! \end{bmatrix} \end{aligned}$$

where $\varGamma _2=\alpha (\bar{V}_0+\bar{V}_1+\bar{V}_2)-d_A-3k_p\bar{V}_0-2k_p\bar{V}_1-k_p\bar{V}_2$. The characteristic equation corresponding to $S_0$ is

$$\begin{aligned} (\lambda +d)(\lambda +d_A)(\lambda ^5+P_1\lambda ^4+P_2\lambda ^3+P_3\lambda ^2+P_4\lambda +P_5)=0, \end{aligned}$$

where

$$\begin{aligned} M_1&= \sum _{i=0}^3 c_i+\delta +6k_m(\varPi +1),\nonumber \\ M_2&= c_0\delta (1-R_0)+\textit{pos. terms},\nonumber \\ M_3&= c_0 \delta \left( \sum _{i=1}^3 c_i+6k_m+3k_m\varPi \right) (1-R_0)+3\delta c_1 k_m\varPi \left( 1-R_0\frac{\beta _1 c_0}{\beta _0 c_1}\right) \nonumber \\&+\textit{pos. terms},\nonumber \\ M_4&= c_0\delta \left( 2k_m^2 \varPi ^2+k_m\varPi \left( 7 k_m+ \sum _{i=1}^2 ic_i\right) +\sum _{i\ne j=1}^3c_i c_j\right. \nonumber \\&\left. +\,k_m\left( 11k_m+\sum _{i=1}^3 (6-i)c_i\right) \right) (1-R_0)\nonumber \\&+\,c_1\delta k_m \varPi (3 k_m \varPi +15k_m+3c_2 +3c_3)\left( 1-R_0\frac{\beta _1 c_0}{\beta _0 c_1}\right) \nonumber \\&+\,6 c_2\delta k_m^2 \varPi ^2 \left( 1-R_0\frac{\beta _2 c_0}{\beta _0 c_2}\right) +\textit{pos. terms},\nonumber \\ M_5&= \delta \left( 6c_3 k_m^3 \varPi ^3 +\left( 2c_0c_3 k_m^2\varPi ^2+c_0 k_m\varPi (6k_m c_2+2c_2 c_3+k_m c_3+c_1 c_3)\right. \right. \nonumber \\&\left. +c_0(c_1+k_m)(c_2+2k_m)(c_3+3k_m)\right) (1-R_0)\nonumber \\&+3k_m c_1 \varPi (k_m c_3 \varPi +(c_2+2k_m)(c_3+3k_m))\left( 1-\frac{\beta 1 c_0}{\beta _0 c_1}R_0\right) \nonumber \\&\left. +6k_m^2\varPi ^2 c_2(c_3+3k_m)\left( 1-\frac{\beta _2 c_0}{\beta _0 c_2}R_0\right) \right) . \end{aligned}$$

(7)

By the Routh–Hurwitz condition, the characteristic equation has roots with negative real parts if $M_1>0$, $M_5>0$, $M_1 M_2-M_3>0$ and $M_3 (M_1 M_2 - M_3)- M_1^2 M_4-M_1 M_5>0$. We can show, using Maple, that all conditions hold when $M_5>0$ (computations available upon request), which is equivalent to $R_0<1+\chi _3$. $\square$

Analytical results showing the stability of $S_0$ for $n\ge 4$ are tedious. Numerically, we can show that there exists a $\chi _n$ such that $S_0$ is locally asymptotically stable when $1<R_0<1+\chi _n$.

It is interesting to note that, for fixed $R_0$ and fixed antibody parameters $K_A$ and $A_0$, $\chi _n$ decreases as the number of available spikes $n$ increases. Indeed, virions with large numbers of infectious epitopes require binding by larger numbers of antibodies before they can be rendered non-infectious. In particular, for $c_i=c$ and $\beta _i=\beta$ for all $i$, we have that $\chi _2 \approx \varPi /2$ and $\chi _3 \approx \varPi /3$. This trend continues for increased values of $n$. When $R_0$ and $\varPi$ are fixed, large $n$ values lower the chance that the inequality $1<R0<\chi _n$ is preserved. However, allowing for $\varPi$ values to increase with increased $n$ ensures that the clearance condition $1<R_0<1+\chi _n$ holds always. In Sect. 5 we numerically estimate the minimum value of $\varPi =K_A A_0$ needed for clearance as a function of the binding epitopes $n$, when all other parameters are kept constant.

4 Numerical results

4.1 Distribution of immune complexes during acute infections

Studies have shown that the anti-gp41 IgG antibodies formed in response to acute HIV infections lack antiviral functions (Liu et al. 2011; Tomaras et al. 2008). They bind the virus, forming antibody–virion immune complexes without inducing neutralization, opsonization, phagocytosis, antibody-dependent cellular cytotoxicity or antibody-dependent cellular viral inhibition (Tomaras and Haynes 2009). We model this by assuming that the antibody does not affect infectivity rates, i.e. $\beta _i=\beta$ = const. and that removal of IgG–virion immune complexes is not enhanced when multiple binding events occur, i.e., $c_i=c=$const., for $i=0,\ldots ,n$. Under these modeling assumptions, we investigate the dynamics of anti-gp41 IgG–immune complexes and of total virus during the first year of infection as given by model (2) and the parameters in Table 1.

Table 1 Variables and parameter values used for the simulations

When the antibody expansion rate is high such that $\alpha V_T>d_A$ throughout the infection, the antibody population increases to high levels. In particular, for $\alpha >\alpha _c=4\times 10^{-7}$ (which corresponds to antibody expansion to equilibrium values of 0.55 mg per ml) immune complexes with with high number of bound antibodies are formed (see Fig. 1, panel (A)). At the beginning, the total virus consists mostly of free virus, $V_0$, and anti-gp41 IgG–virion immune complexes, $V_i$, with few bound antibodies (see Fig. 1, panel (B), left). By 1 year, however, less than $1\,\%$ of the total virus is free and the anti-gp41 IgG–virion immune complexes with a high number of bound antibodies dominate the total virus population (see Fig. 1, panel (B) right). The delay in the emergence of $V_i$, with large $i$, is due to the delay in antibody production, with free antibody concentration below 2 $\mu$g per ml in the first 4 months, and reaching its equilibrium value 3 year after infection. Earlier dominance by anti-gp41 IgG–virion immune complexes with high number of bound antibodies can be obtained when the antibody expansion rate, $\alpha$, is increased even further.

Fig. 1

a Total virus, $V_T$, (solid black lines), total anti-gp41 IgG–virion immune complexes, $X$, (solid grey lines) and complexes with $i$-spikes bound by antibody, $V_i$, over time. b Change over time in the frequency of $V_i$s for $i=0,\ldots ,n$. The parameters used are $n=42$, $\beta =4\times 10^{-7}$, $p=200$, $\alpha =4 \times 10^{-7} k_p= 10^{-12}$, $A_0=8\times 10^8$ and $s_A= A_0 d_A$. The other parameters are as in Table 1

We investigate the effect of $n$ on the dynamics of $V_T$ and $X$, by assuming that $n=12$, $n=42$ and $n=105$, i.e., a virion has $4$, $14$ and $35$ spikes respectively, corresponding to the boundaries found in Zhu et al. (2006). All other parameters are as in Fig. 1. Total virus concentration $V_T$ is not affected by the change in $n$. The total immune complexes population, however, grows faster for high $n$ (see Fig. 2). The steady state level of the free antibody is increased from $0.17$ mg/ml for $n=12$ to $1.4$ mg/ml for $n=105$, suggesting that high antibody levels are needed for all epitopes to get bound.

Fig. 2

Total virus $V_T$ and immune complexes $X$ as given by model (2) for $n=105$ (solid lines), $n=42$ (dashed lines) and $n=12$ (dotted lines). The other parameters are as in Fig. 1. Note that the $V_T$ curves overlap

In model (2) each epitope can be bound with equal strength $k_p$. Since the binding rate may decreases during multiple binding events due to steric hindrance, we relaxed this by assuming that

and $k_{p_i}=k_p/(i+1)$. Such a decrease in antibody binding has no effect on the total virus population (see Fig. 3, black lines) and a small effect on the immune complexes population (see Fig. 3, gray lines).

Fig. 3

Total virus $V_T$ and immune complexes $X$ as given by model (2) for $k_{p_i}=k_p$ (solid lines) and $k_{p_i}=k_p/(i+1)$ (dashed lines). The other parameters are as in Fig. 1. Note that the $V_T$ curves overlap

Data fitting. We compared the virus and immune complexes theoretical curves to published HIV RNA and anti-gp41 IgG–virion immune complexes data from six acutely infected patients (figure 1 in Liu et al. (2011)). The patients were sampled near the peak of the viral load, which we assume corresponds to $t=7$ days after virus detectability, i.e., $V(0)=100$ copies per ml (Tomaras et al. 2008; Liu et al. 2011). Moreover, we assume that at $t=0$ a negligible number of CD4 T cells are infected and set $T(0)=10^6$ per ml and $I(0)=1$ per ml, as in Tomaras et al. (2008). The uninfected CD4 T cells are produced at rate $s = 10^4$ per ml per day (Sachsenberg et al. 1998) and die at rate $d = 0.01$ per day (Stafford et al. 2000). We use previous estimates for the infected cells death rate, $\delta = 0.39$ per day (Markowitz et al. 2003), and virus clearance rate, $c_0 = 23$ per day (Ramratnam et al. 1999). Since the antibody has no antiviral activity, we assume $c_i=c_0=23$ per day and $\beta _i=\beta$ ml per virion per day, for all $i$.

We start with low levels of pre-existing antibodies which we set at anti-gp41 IgG limit of detection, $0.2$ ng/ml, corresponding to $A_0=8\times 10^{8}$ molecules per ml (Abd 2013; Tomaras et al. 2008; Ciupe et al. 2011), and no anti-gp41 IgG–virion immune complexes $X_i(0)=0$ for all $i$. IgG has a half-life in blood of $9.7$ days, corresponding to an antibody removal rate $d_A=\ln (2)/9.7=0.07$ per day (Zalevsky et al. 2010). Before HIV infection, antibodies are assumed to be at equilibrium. Therefore the antibody production rate is $s_A= d_A A_0= 5.6\times 10^{7}$ per day. The virus–antibody dissociation rate is $k_m=100$ per day (Zhou et al. 2007; Schwesinger et al. 2000; Tabei et al. 2012). Moreover we allow for all $n=42$ viral epitopes to be bound by anti-gp41 antibody.

We fit the remaining parameters $\{\beta , p, k_p, \alpha \}$ to human HIV-1 and anti-gp41 IgG–virion immune complexes from six patients discovered during acute HIv infection (figure 1 in Liu et al. 2011). We use the ‘fminsearch’ routine in Matlab, which uses the Nelder–Mead simplex optimization algorithm (Lagarias et al. 1998). The best parameter estimates are presented in Table 2 and the corresponding best-fit solutions of model (2) are presented in Fig. 4.

We investigated the time-dependent sensitivity of the model (2)’s solutions to parameters variations as follows (Bortz and Nelson 2004; Banks and Bortz 2005). We define the sensitivity functions $X_q=q \partial X (t,q)/\partial q$, where $X (t,q)=\{T,I,V_0, V_1, \ldots ,V_n, A\}(t, q)$ are the variables in model (2) and $q=\{\beta , N, \alpha , k_p\}$ are the parameters used in data fitting. The sensitivity equations are obtained by differentiating both sides of system (2) with respect to $q$ and solving them subject to initial conditions $X_q(0,q)=0$ for all $X_q$. The semi-relative sensitivities are calculated by multiplying the absolute sensitivity by q. The temporal changes of the semi-relative functions

$$\begin{aligned} q V_{T,q}= q\sum _{i=0}^{n} \frac{\partial V_i}{\partial q} \end{aligned}$$

and

$$\begin{aligned} q X_{q}= q\sum _{i=1}^{n} \frac{\partial V_i}{\partial q} \end{aligned}$$

Table 2 Best estimates from fitting model (2) to patients with acute HIV infections

Fig. 4

Total virus $V_T$ (left panel) and immune complexes $X$ (right panel) as given by the fit of the model (2) with $n=42$ to six patient’s data (filled circles). The fixed and estimated parameters are given in Tables 1 and 2

are presented in Fig. 5. Parameters $\beta$ and $N$ exhibit their greatest influence over $V_T$ and $X$ early in the simulations, and the influence levels off to constant positive values when $V_T$ and $X$ are at steady-state (see Fig. 5 top panels, dashed vs solid lines). Moreover, $\beta$ has a higher influence than $N$. The antibody expansion rate, $\alpha$, has a positive influence on $X$ and a negative influence on $V_T$ at the beginning of the simulations. The influence is small, constant and negative when $V_T$ and $X$ are at the steady-state (see Fig. 5 bottom panels, solid lines). Lastly, the antibody binding rate $k_p$ has no influence on the dynamics of $V_T$ and $X$ (seen Fig. 5 bottom panels, dashed lines).

For the best parameter estimates, we calculate the basic reproductive number in the absence of antibodies to be $R_0=\frac{p \beta _0 s}{c_0 d\delta }=14\pm 6$, higher than in Ribeiro et al. (2010); Stafford et al. (2000) but lower that in Little et al. (1999).

Fig. 5

The semi-relative curves $q \frac{d V_t}{d q}$ (left) and $q \frac{d X}{d q}$ (right) over time as given by system (5). The parameters are as in Tables 1 and 2 (average values)

The average predicted antibody affinity is $K_A=k_p/k_m=2.3 \pm 2.6\times 10^{-15}$ ml/molecules, corresponding to $1.4 \pm 1.6 \times 10^6$ M$^{-1}$. The estimate is similar to Liu et al. (2011); Tabei et al. (2012) and lower than in Zhou et al. (2007). The average predicted antibody expansion rate is $\alpha =5.6\pm 4.9 \times 10^{-7}$ ml per virion per day. For these estimates, our model predicts a slow initial grow of antibodies and IgG–virion immune complexes. The total population of immune complexes, $X$, is composed initially of $V_i$s with low $i$, and accounts for a low percentage of the total virus load, as reported experimentally (Liu et al. 2011). By day 112, however, (corresponding to end of the experiment) $V_i$ for all $i=0,\ldots ,n$ can be measured in all patients and the highly bound immune complexes dominate $X$. We therefore predict that following the transient stage and in the absence of antibody-induces antiviral effects the viral load is composed almost exclusively of IgG–virion immune complexes, such that $V_T\approx X$.

We predict high equilibrium levels for the free antibody, ranging between $7.8\times 10^{13}$ and $1.2\times 10^{17}$ molecules per ml (i.e. $0.021$–$33$ mg/ml) among the six patients. In spite of these levels, our model predicts a failure to protect against the infection. Indeed, as shown in Sect. 2, blocking of viral infection is dependent on $K_A$ and $A_0$, which are small, instead of the steady-state antibody levels. Therefore, for antibody-mediated protection, we require an increase in either affinity rates, $K_A$, and/or the levels of pre-existing antibody, $A_0$ (for exact quantities see Sect. 5).

4.2 Distribution of immune complexes during chronic infections

In the previous section, we have assumed that during acute infections all gp41 epitopes must be bound by antibodies to render a virion non-infectious. Therefore $V_n$ is neutralized while any other IgG–virion complexes, $V_i$, $i=0,1,\ldots ,n-1$ had the same infectivity $\beta _i=\beta$ and clearance $c_i=c$ rates. We now relax this and assume that antibody may, in time, acquire antiviral function. First, we consider variable antibody neutralization by assuming that increased bound antibody number leads to decreased infectivity rates. For example, a virion with ten bound antibodies infects with a lower probability than a virion with only two bound antibodies. This could be due to the spatial positioning of the spikes, so that the spike adjacent to a bound spike cannot reach a CD4 T cell receptor (Mulampaka and Dixit 2011) or to more than one spike engagement being needed for virus entry (Kuhmann et al. 2000; Magnus and Regoes 2012; Magnus et al. 2009; Platt et al. 2007). We let

$$\begin{aligned} \beta _i= \beta \frac{n_c^h}{i^h+n_c^h}, \end{aligned}$$

(8)

where $i=1,\ldots , n-1$, $\beta _0=\beta$, and $\beta _n=0$. Parameter $n_c$ is the number of spikes for which the infectivity is reduced by half and the Hill coefficient $h$ accounts for the steepness of decay in infectivity. For $i\le n_c$, $\beta _i \approx \beta$, and for $i\ge n_c$, $\beta _i\approx 0$.

We also consider non-neutralization effects such as antibody-dependent cellular viral inhibition and cellular cytotoxicity. We incorporate these in the model by considering an increased clearance rate of the IgG–virion immune complexes with higher number of bound antibodies

$$\begin{aligned} c_{i}=c + c_A \frac{i^l}{i^l+m_c^l}, \end{aligned}$$

(9)

for $i={0,\ldots n}$. $c_{A}$ is the maximum antibody-mediated clearance per day, $m_c$ the number of spikes at which additional clearance is half-maximal and the Hill coefficient $l$ accounts for steepness of clearance increase.

Under these effects, the overall virus composition changes and the highly bound immune complexes no longer dominate the total virus. We determined the fraction of IgG–virion immune complexes in the total virus population ten years following infection for different hill coefficients. For $n_c=m_c=21$ and $c_A=4c$, model (2) with $\beta _i$ and $c_i$ given by (8) and (9) predicts that immune complexes represent $45\,\%$ of the total virus for $h=l=1$, $91\,\%$ for $h=l=2$ and $99\,\%$ for $h=l=10$. In all cases, the immune complexes with high levels of bound antibody contribute least to the total virus load (see Fig. 6). Experimental measurements in one chronic HIV patients have shown that IgG–virion immune complexes levels represent $50\,\%$ of the total virus (figure 3 in Liu et al. (2011)). We therefore predict that antibody-induced antiviral effects are needed to explain the fraction of IgG–virion immune complexes observed during chronic HIV. However, even these antiviral effects are not strong enough to hinder protection.

Fig. 6

The frequency of $V_i$s ($i=0,\ldots ,n$) 10 years after infection for model (2) with $\beta _i$ and $c_i$ given by (8), (9) with $n_c=m_c=21$, $c_A=4c$, and $h=l=1$ (left), $h=l=2$ (middle), $h=l=10$ (right). The parameters used are $n=42$, $\beta = 4\times 10^{-7}$, $p=200$, $\alpha =4\times 10^{-7}$ $k_p=10^{-12}$, $A_0=8\times 10^8$ and $s_A= A_0 d_A$. The other parameters are as in Table 1

5 Estimates of antibody levels needed for protection

As showed in Sect. 2, virus infection is blocked when $1<R_0<1+\chi _n$, where $\chi _n=f_n(\varPi , \beta _i, \frac{c_i}{k_m})$, $\varPi =K_A A_0$ and $K_A=k_p/k_m$. In particular, $\chi _2$ and $\chi _3$ are given by Eqs. (3) and (5).

We first looked at the conditions needed for blocking viral spread during acute infections, modeled as $\beta _i=\beta$ and $c_i=c$, for all $i$. The virus infection will be blocked when $1<R_0<1+\chi _n^0$, where

$$\begin{aligned} \chi _2^0=\frac{2\varPi ^2}{\varPi \left( 3\frac{c}{k_m}+4\right) +\left( \frac{c}{k_m}+1\right) \left( \frac{c}{k_m}+2\right) }, \end{aligned}$$

and

$$\begin{aligned} \chi _3^0=\frac{6\varPi ^3}{\varPi ^2 \left( 18+11\frac{c}{k_m}\right) +\varPi \left( 18 +22 \frac{c}{k_m} +6\frac{c^2}{k_m^2}\right) +\left( \frac{c}{k_m}+1\right) \left( \frac{c}{k_m}+2\right) \left( \frac{c}{k_m}+3\right) }. \end{aligned}$$

Finding analytical forms for $\chi _n^0$ is tedious. However, we can show numerically that $\chi _2^0>\chi _3^0> \cdots >\chi _n^0$, suggesting that an increase in the binding sites $n$ leads to a decrease in the protection capacity of the antibodies. This happens because the limited pre-existing antibodies, $A_0$, get distributed to an increasing number of binding sites. We estimate the minimum value of $\varPi$ needed for immune protection as a function of the binding sites $n$ (see Fig. 7). We found that an increase in $n$ requires an increase in $\varPi$ for protection to be preserved. This suggests that when IgG–virion immune complexes with a large number of bound antibody are formed either the pre-existing antibody, $A_0$, or the antibody affinity, $K_A$, need to be increased to ensure protection. If we assume that the antibody affinity is the average among the six patients, i.e., $K_A=1.3\times 10^6$ M$^{-1}$ and the other parameters are as in Fig. 1, then the pre-existing antibody levels needed for blocking infection range between $6\times 10^{14}$ molecules/ml for $n=1$ and $1.1\times 10^{16}$ molecules/ml for $n=42$. This corresponds 0.16–3 mg/ml of anti-gp41 IgG. Since the total levels of IgG in the body is 7–17 mg/ml (Dati et al. 1996; Gonzalez-Quintela et al. 2007), blocking virus infection in the absence of antiviral effects is unlikely. However, virus clearance might occur under affinity maturation leading to higher $K_A$, and/or vaccination, and/or antibody infusion, leading to higher $A_0$.

Since a large number of initial antibodies are needed for protection in the absence of antiviral effects and the induction of such levels may not be biologically feasible, it is important to determine whether one can insure protection by inducing a smaller number of antibodies which have neutralizing and/or non-neutralizing properties. To address this question, we next consider variable antiviral events, in particular increased virus clearance and decreased viral infectivity, and estimate the level of $\varPi$ needed for protection.

Fig. 7

Minimum $\varPi =K_A A_0$ needed for virus clearance as a function of binding sites $n$ for model (2) with $\beta _i=\beta$, $c_i=c$ and parameters in Table 1. The other parameters are $\beta =4\times 10^{-7}$, $p=200$, $\alpha =4\times 10^{-7}$ and $s_A=A_0 d_A$

If we assume that antibody binding causes virus neutralization, such that $\beta _i<\beta _j$ for $i>j$ and $c_i=c$ for all $i$ and $j$, then the virus infection will be blocked when $1<R_0<1+\chi _n^\beta$, where $\chi _n^\beta =f_n(\varPi , \beta _i, \frac{c}{k_m})$. In particular,

$$\begin{aligned} \chi _2^\beta =\frac{2\varPi ^2+2\varPi \left( \frac{c}{k_m}+2\right) \left( 1-\frac{\beta _1}{\beta _0}\right) }{\varPi \frac{c}{k_m}+2\varPi \left( \frac{c}{k_m}+2\right) \frac{\beta _1}{\beta _0}+\left( \frac{c}{k_m}+1\right) \left( \frac{c}{k_m}+2\right) }, \end{aligned}$$

and

$$\begin{aligned} \chi _3^\beta \!=\!\frac{6\varPi ^3 \!+\!\left( \!3\frac{c}{k_m}\varPi ^2\!+\!3\varPi \left( \!\frac{c}{k_m}\!+\!2\!\right) \left( \!\frac{c}{k_m}\!+\!3\!\right) \!\right) \left( \!1\!-\!\frac{\beta _1}{\beta _0}\!\right) \!+\!6\varPi ^2 \left( \!\frac{c}{k_m}\!+\!3\!\right) \left( \!1\!-\!\frac{\beta _2}{\beta _0}\!\right) }{\left( \!\frac{c}{k_m}\left( \!2\!+\!3\frac{\beta _1}{\beta _0}\!\right) \!+\!6\left( \!\frac{c}{k_m}\!+\!3\!\right) \frac{\beta _2}{\beta _0}\!\right) \varPi ^2\!+\!\left( \! \frac{c}{k_m}\!\left( \!7\!+\!3\frac{c}{k_m}\!\right) \!+\!3\left( \!\frac{c}{k_m}\!+\!2\!\right) \left( \! \frac{c}{k_m}\!+\!3\!\right) \frac{\beta _1}{\beta _0}\!\right) \varPi \!+\!\left( \!\frac{c}{k_m}\!+\!1\!\right) \left( \!\frac{c}{k_m}\!+\!2\!\right) \left( \!\frac{c}{k_m}\!+\!3\!\right) }. \end{aligned}$$

Since $\chi _n^\beta >\chi _n^0$, fewer pre-existing antibodies are needed for protection. Indeed, for $\beta _i$ given by equation (8), $h=1$, $n=42$, $K_A=1.3\times 10^6$ M$^{-1}$ and the other parameters as in Fig. 1, the initial antibody concentration needed for blocking the infection decays from $1.4$ mg/ml when $n_c=42$ to $0.88$ mg/ml for $n_c=21$ to $0.038$ mg/ml for $n_c=1$. The antibody densities are $53$, $70$ and $98.7\,\%$ lower than the ones needed in the absence of neutralization effects. These concentrations decrease further if we assume that antibody bind fewer spikes per virion (not shown).

If we assume that antibody binding is followed by increases viral clearance through antibody non-neutralizing antiviral effects such as antibody-dependent cellular viral inhibition and cellular cytotoxicity, i.e., $c_i> c_j$ for $i>j$ and $\beta _i=\beta$ for all $i\ne j$, then virus infection will be blocked when $1<R_0<1+\chi _n^c$, where $\chi _n^c=f_n(\varPi , \frac{c_i}{k_m})$. In particular,

$$\begin{aligned} \chi _2^c=\frac{2\frac{c_2}{k_m}\varPi ^2+2\varPi \frac{c_1}{k_m}\left( \frac{c_2}{k_m}+2\right) \left( 1-\frac{ c_0}{c_1}\right) }{\varPi \frac{c_0}{k_m}\left( 3\frac{c_2}{k_m}+4\right) +\frac{c_0}{k_m}\left( \frac{c_1}{k_m}+1\right) \left( \frac{c_2}{k_m}+2\right) }, \end{aligned}$$

and

$$\begin{aligned} \chi _3^c\!=\!\frac{6\varPi ^3 \frac{c_3}{k_m}\!+\!\left( \!3\frac{c_1}{k_m}\frac{c_3}{k_m}\varPi ^2\!+\!3\varPi \frac{c_1}{k_m}\left( \!\frac{c_2}{k_m}\!+\!2\!\right) \left( \frac{c_3}{km}\!+\!3\right) \!\right) \left( \!1\!-\!\frac{c_0}{c_1}\!\right) \!+\!6\varPi ^2\frac{c_2}{k_m}\left( \!\frac{c_3}{k_m}\!+\!3\!\right) \left( \!1\!-\!\frac{c_0}{c_2}\!\right) }{\frac{c_0}{k_M}\left( \!11\frac{c_3}{k_m}\!+\!18\!\right) \! \varPi ^2\!+\!\frac{c_0}{k_m}\!\left( \!\left( \!5\frac{c_2}{k_m}\!+\!\frac{c_1}{k_m}\!\right) \frac{c_3}{k_m}\!+\!15\frac{c_2}{k_m}\!+\!7\frac{c_3}{k_m}\!+\!18\!\right) \!\varPi \!+\!\frac{c_0}{k_m}\left( \!\frac{c_1}{k_m}\!+\!1\!\right) \left( \!\frac{c_2}{k_m}\!+\!2\!\right) \left( \!\frac{c_3}{k_m}\!+\!3\!\right) }. \end{aligned}$$

It can be shown that $\chi _n^c>\chi _n^0$. Therefore, fewer pre-existing antibodies are needed for protection. Indeed, for $l=1$, $n=42$, $K_A=1.3\times 10^6$ M$^{-1}$, the other parameters as in Eq. (1) and $c_A=4c=92$ d$^{-1}$ (Igarashi et al. 1999), the initial antibody concentrations needed for protection are $0.92$ mg/ml for $m_c=42$, $0.73$ mg/ml for $m_c=21$, and $0.48$ mg/ml for $m_c =1$. The antibody densities are $69$, $75$ and $84\,\%$ smaller than the ones needed in the absence of increased virus clearance. To obtain protection against the virus for the initial concentration $A_0=0.038$ mg/ml (obtained for $n_c=1$ in the antibody-induced neutralization case) the antibody mediated clearance $c_A$ must increase to $c_A=8.5c$ for $m_c=1$, $c_A=18.2c$ for $m_c=15.7$ and $c_A=22.7c$ for $m_c=42$.

Finally, if we combine the neutralization and non-neutralization antiviral effects given by Eqs. (8) and (9), the pre-existing antibody value needed for protection decays from $0.88$ mg/ml in the neutralization alone case to $0.07$ mg/ml for the dual effects and $n_c=m_c=21$, $h=l=1$ and $c_A=4c$.

6 Discussion

In this study we developed a mathematical model of multivalent antibody binding that accounts for the formation of anti-gp41 IgG–virion immune complexes with different numbers of bound antibodies. The model is used to explain the levels and dynamics of virus and immune complexes observed in data from acute infected patients. We report that when the antibody population expands above the limit of detection but does not induce antiviral effects, the total virus population contains free virus only transiently before becoming populated exclusively by immune complexes. The immune complexes with a high number of bound antibodies dominates the virus load. Experimental studies have predicted immune complexes levels that range between 5–60 % of total virus during the first $112$ days of acute infection (Liu et al. 2011). We show that low pre-existing antibody levels, followed by a slow antibody expansion can explain these low initial levels. However, once the antibody concentration reaches high levels, the total virus load will be dominated by immune complexes. If the pre-existing antibody concentration or the antibody production is increased, we predict binding of all free virus, with preference for complexes with high numbers of bound antibodies.

When the antibody–virus binding results in antibody-induced antiviral effects, which decrease infectivity and enhance virus removal but are not sufficient for blocking infection, the total virus population contains high levels of free virus throughout the infection. The relatively constant 1:2 ratio of immune complexes to total virus observed in a chronic patient (Liu et al. 2011) can be explained by our model only when antiviral effects lead to removal of highly bound immune complexes. The free virus and low bound immune complexes are the only populations contributing to the total virus load.

In our model antibodies grow proportionally to the present antigen, and their delayed expansion is due to low initial conditions and low expansion rate. Further investigation is needed to determine whether this delayed expansion can be reproduced by a more complex model that considers B cells activation, expansions, somatic hypermutation inside germinal centers, and maturation into antibody-producing plasma cells.

We used our model to investigate the conditions under which virus infection can be prevented and found that protection against infection requires the presence of high levels of pre-existing antibodies, with high affinity to the virus. An important question is whether there exists a threshold in the multivalent immune complex formation that renders complexes non-infectious or exposes them to accelerated removal by phagocytes. We have shown that antibody-induced antiviral effects reduce the number of pre-existing antibody needed for protection, with neutralization effects having higher contributions than the non-neutralizing effects. Moreover, lowering the threshold at which the antiviral activity emerges is beneficial to the patient. Once the infection occurs, however, the virus cannot be cleared regardless of the degree of binding, the maximum induced antibody or the antibody-induced antiviral effects.

We assumed that the virus population is homogeneous in the total number of spikes and studied the conditions for protection against infection when this number is varied. We found that a population with high number of available spikes will require higher pre-existing antibody levels for protection to occur. Further work is needed assess the changes in our results when we incorporate frequencies of virions with different spike numbers as in Magnus and Regoes (2010, 2011); Magnus (2013). Moreover, we considered that only the infectious spikes are bound by antibody. Several studies have reported the ability of IgG to bind both infectious and noninfectious virions (Burrer et al. 2005; Liu et al. 2011; Moore et al. 2006). When we incorporate the non-infectious virions into our model, an even higher level of pre-existing antibodies are needed for protection to compensate for the absorption of higher numbers of antibodies by one virion.

In conclusion, we have developed a model of multivalent antibody–virion binding during HIV infection and we used it to investigate the levels, antiviral effects and roles in anti-viral protection of IgG–virion immune complexes with increasing numbers of bound antibodies during acute and chronic infection. Our results provide insight into the virus–antibody interactions that can be useful for the design of an antibody-mediated vaccine against HIV.