Method of conditional moments (MCM) for the Chemical Master Equation

Abstract

The time-evolution of continuous-time discrete-state biochemical processes is governed by the Chemical Master Equation (CME), which describes the probability of the molecular counts of each chemical species. As the corresponding number of discrete states is, for most processes, large, a direct numerical simulation of the CME is in general infeasible. In this paper we introduce the method of conditional moments (MCM), a novel approximation method for the solution of the CME. The MCM employs a discrete stochastic description for low-copy number species and a moment-based description for medium/high-copy number species. The moments of the medium/high-copy number species are conditioned on the state of the low abundance species, which allows us to capture complex correlation structures arising, e.g., for multi-attractor and oscillatory systems. We prove that the MCM provides a generalization of previous approximations of the CME based on hybrid modeling and moment-based methods. Furthermore, it improves upon these existing methods, as we illustrate using a model for the dynamics of stochastic single-gene expression. This application example shows that due to the more general structure, the MCM allows for the approximation of multi-modal distributions.

1 Introduction

Modeling of single cell dynamics has been a field of active research for several decades, starting with the groundbreaking work of   Hodgkin and Huxley (1952), who mathematically described the dynamics of individual neurons. In the course of time, modeling entered other fields, e.g., metabolism, signal transduction, and gene regulation (Klipp et al. 2005). Nowadays, there exists a variety of different modeling approaches which all share two essential elements, namely, chemical species ($S_1, S_2, \ldots , S_{n_{s}}$) and chemical reactions ($R_1, R_2, \ldots , R_{n_{r}}$). A chemical species is an ensemble of chemically identical molecular entities, such as proteins and RNA molecules, while a process, which results in the interconversion of chemical species, is referred to as chemical reaction (McNaught and Wilkinson 1997), e.g., synthesis, degradation, and phosphorylation. Accordingly, chemical reactions relate reactants and products, and can be written as:

$$\begin{aligned} R_j: \quad \sum _{i=1}^{n_{s}} \nu _{ij,x}^{-} S_i \rightarrow \sum _{i=1}^{n_{s}} \nu _{ij,x}^{+} S_i, \quad j = 1,\ldots ,{n_{r}}. \end{aligned}$$

Thereby, $\nu _{ij,x}^{-} \ (\nu _{ij,x}^{+}) \in \mathbb{N }_0$ denotes the stoichiometric coefficient of species $i$ in reaction $j$, defined as the number of molecules consumed (produced) when the reaction takes place (Klipp et al. 2005). The net interconversion of species $i$ in reaction $j$ is $\nu _{ij,x}= \nu _{ij,x}^{+} - \nu _{ij,x}^{-}$. Accordingly, the stoichiometry of the $j\hbox {-th}$ reaction is defined by the vectors $\nu _{j,x}^{-} = (\nu _{1j,x}^{-},\ldots ,\nu _{{n_{s}}j,x}^{-}) \in \mathbb{N }_0^{{n_{s}}}, \nu _{j,x}^{+} = (\nu _{1j,x}^{+},\ldots ,\nu _{{n_{s}}j,x}^{+}) \in \mathbb{N }_0^{{n_{s}}}$, and $\nu _{j,x}= (\nu _{1j,x},\ldots ,\nu _{{n_{s}}j,x}) \in \mathbb{N }_0^{{n_{s}}}$. In the following we assume that all reactions are at most bimolecular, hence, for all $j, \sum _{i=1}^{{n_{s}}} \nu _{ij,x}^{-} \le 2$. Reactions with at most two educts cover essentially all reactions found in nature (Gillespie 1992).

The time-evolution of the number of molecules in the chemical processes can be modeled using different model classes. In particular models based upon the reaction rate equation, the chemical Langevin equation and discrete-state continuous-time Markov chains (CTMCs) are frequently used. Among these model classes, CTMCs allow for the most precise description of the underlying physical process as the discrete nature of molecules and reaction events is captured (Gillespie 1977). The state, $X_t \in \mathbb{N }_{0}^{{n_{s}}}$, of a CTMC at time $t$ is the collection of the ensemble sizes $[S_i]$ of the individual chemical species at time $t, X_t = (X_{1,t}:=[S_1],\ldots ,X_{{n_{s}},t}:=[S_{n_{s}}])$. The state of a CTMC remains constant as long as no reaction takes place. If the $j\hbox {-th}$ chemical reaction, $R_j$, takes place the ensemble sizes change according to the stoichiometry of the reaction, $X_{t} \rightarrow X_{t} + \nu _{j,x}$. The index $j$ of the next reaction as well as the time to the next reaction are randomly distributed with statistics determined by the propensity functions $a_j:\mathbb{N }_0^{{n_{s}}} \rightarrow \mathbb{R }_+$ (Feller 1940). In this work we assume the propensities $a_j(X_t)$ follow the law of mass action with reaction rate parameters $c_j > 0$, as provided in Table 1. Note that the associated propensities are “proper”, hence $a_{j}(X_t) = 0$ whenever $\exists i \in \{1,\ldots ,{n_{s}}\}: X_{i,t} \ngeq \nu _{ij,x}^{-}$. For the latter component-wise inequality we write in the following $X_t \ngeq \nu _{j,x}^-$.

Table 1 Propensity functions for reactions following mass action kinetics (Gillespie 1977) for $i, i_1, i_2 \in \{1,\ldots ,{n_{s}}\}$ and $i_1 \ne i_2$.

A single realization of the CTMC provides one possible time-course of the stochastic process $X_t$. The statistics of these time-courses, the probabilities $p(x|t) = P(X_t=x)$ that an individual cell $X_t$ occupies a certain state $x=(x_{1},\ldots ,x_{n_{s}}) \in \mathbb{N }_0^{{n_{s}}}$ at time $t$, are described by the CME (Kampen 2007),

$$\begin{aligned} \frac{\partial }{\partial t}p(x|t) = \sum _{\begin{array}{c} j=1 \\ x \ge \nu _{j,x}^{+} \end{array}}^{n_{r}} a_j(x-\nu _{j,x})p(x-\nu _{j,x}|t) - \sum _{j=1}^{n_{r}} a_j(x)p(x|t), \end{aligned}$$

(1)

in which the inequality constraint $x \ge \nu _{j,x}^{+}$ is required to ensure positivity.

For some CMEs closed-form solutions can be derived, e.g., for CMEs including only monomolecular reactions (Jahnke and Huisinga 2007), however, in general, merely a numerical approximation of the solution is feasible. Unfortunately, such numerical approximations are difficult as the number of reachable states $x$ is, even for systems with only few state variables, often large or even infinite. To determine the probability mass function $p(x|t)$ despite the large number of states, different approximation schemes have been introduced. In particular the finite state projection (Munsky and Khammash 2006, 2008), the product approximation (Jahnke 2011), the approximation of the CME by the Fokker-Planck equation (Gardiner 2011; Kampen 2007), and inexact integration methods (Mateescu et al. 2010; Sidje et al. 2007) are frequently used. Unfortunately, these methods mostly fail if the system contains species with low-copy numbers and species with medium/high-copy numbers. In this case, hybrid modeling approaches have been proven to be more efficient (Hellander and Lötstedt 2007; Henzinger et al. 2010; Jahnke 2011; Menz et al. 2012).

Hybrid methods (HMs) are based on the observation that the abundance of medium/high-copy number species often evolves almost deterministically for a given state of the low-copy number species. Accordingly, HMs employ a stochastic description for species with low-copy numbers and a deterministic description for species with medium/high-copy numbers. Based upon this intuitive concept, Hellander and Lötstedt (2007), Jahnke (2011) and Menz et al. (2012) introduced alternative hybrid modeling approaches. The hybrid models proposed by Menz et al. and Jahnke basically describe the expected values of the abundance of the medium/high-copy number species conditioned on the low-copy number species. Hellander and Lötstedt reduce the complexity of this model further by using merely the expected value of the abundance of the medium/high-copy number species, instead of the conditional expectation. While both methods reduce the computational complexity tremendously, they rely on the assumption that the abundance of the medium/high-copy number species evolve deterministically or has at least negligible variance. Apparently, these methods are not applicable if all states show a significant degree of stochasticity which manifests in non-zero second- and higher-order moments.

Aside from methods which approximate the solution of the CME, there exists a class of methods which merely approximate the moments of the solution of the CME. These methods are known as methods of moments (MMs) (Engblom 2006; Lee et al. 2009) and describe the moments using a set of ordinary differential equations (ODEs). If the system contains at most monomolecular reactions, the moment equations provide the exact moments at a significantly reduced computational cost. For systems involving bimolecular reactions the moment equations are not closed but contain higher-order moments. These higher-order moments can be approximated using moment closure techniques (Engblom 2006; Hespanha 2007; Lee et al. 2009; Ruess et al. 2011; Singh and Hespanha 2011). It has been shown that the moment equations provide a good approximation of the moment of the CME solution, independent of the mean molecule numbers, if enough moments are considered and if the moment closure is accurate (Engblom 2006). Unfortunately, if the solution of the CME possesses several modes, the moment closure often becomes inaccurate. The discrete decomposition into modes cannot be well represented by the moment closures.

In this work, we propose the method of conditional moments (MCM) which combines ideas from hybrid methods and the method of moments, thereby overcoming the individual shortcomings of the existing approaches. The MCM is derived in Sect. 2. It employs a fully stochastic description for the low-copy number species and a moment-based description for the medium/high-copy number species. The moments of the medium/high-copy number species are conditioned on the state of the low-copy number species. The evolution equation for the marginal probabilities and for the conditional moments are derived from the CME, without the need for employing a multi-scale expansion approach (Menz et al. 2012) or van Kampen’s $\varOmega$-expansion (Kampen 2007). As the MCM is in case of bimolecular reactions not closed, like the MM, we discuss different moment closure techniques and the numerical simulation in general. The relation to existing models, the CME, the hybrid models by Jahnke (2011) and Menz et al. (2012), the moment equation, and the reaction rate equation is outlined in Sect. 3.2. In Sect. 4, we discuss the numerical properties of the conditional moment equation and propose an approach to compute consistent initial conditions. Using the numerical methods, in Sect. 5 we compare the MCM with the MM, the HM by Jahnke, and solution of the CME (computed using the finite state projection). The paper is concluded in Sect. 6.

Example

In the following, we illustrate our results using a model for stochastic gene expression (Fig. 1a). This model describes the transcription and translation of a transcription factor which increases its own synthesis via a positive regulatory feedback, a well known motif occurring in many gene regulatory networks. The coding DNA segment can be present in an open conformation and a closed conformation. To the open conformation we refer as on-state ($\hbox {D}_{\mathrm{on}}$) and to the closed conformation as off-state (${\hbox {D}}_{\mathrm{off}}$). As we assume that the coding DNA segment is only present once in the DNA strand, it holds that $[\hbox {D}_{\mathrm{on}}] + [{\hbox {D}}_{\mathrm{off}}]= 1$. In the on-state, RNA polymerase can bind to the DNA and synthesize mRNA ($\hbox {R}$). Accordingly, in the off-state no RNA polymerase can bind. The produced mRNA can be translated into proteins ($\hbox {P}$). Proteins and mRNA can be degraded. Furthermore, the proteins $\hbox {P}$ induce the activation of the corresponding DNA sequence and establish a positive feedback loop. The corresponding system of reactions is:

$$\begin{aligned} \begin{array}{llll} R_1: &{} {{\hbox {D}}_{\mathrm{off}}} &{}\overset{\tau _{\mathrm{on}}}{\rightarrow } {\hbox {D}_{\mathrm{on}}} &{} \hbox {(DNA opening)}\\ R_2: &{} {\hbox {D}_{\mathrm{on}}} &{}\overset{\tau _{\mathrm{off}}}{\rightarrow } {{\hbox {D}}_{\mathrm{off}}} &{} \hbox {(DNA closing)}\\ R_3: &{} {\hbox {D}_{\mathrm{on}}} &{}\overset{k_{\mathrm{r}}}{\rightarrow } {\hbox {D}_{\mathrm{on}}} + {\hbox {R}} &{} \hbox {(mRNA synthesis)}\\ R_4: &{} {\hbox {R}} &{} \overset{\gamma _{\mathrm{r}}}{\rightarrow } \emptyset &{} \hbox {(mRNA degradation)}\\ R_5: &{} {\hbox {R}} &{} \overset{k_{\mathrm{p}}}{\rightarrow } {\hbox {R}} + \hbox {P}&{} \hbox {(protein synthesis)}\\ R_6: &{} \hbox {P}&{} \overset{\gamma _{\mathrm{p}}}{\rightarrow } \emptyset &{} \hbox {(protein degradation)}\\ R_7: &{} \hbox {P}+ {{\hbox {D}}_{\mathrm{off}}} &{} \overset{\tau _{\mathrm{on}}^{\mathrm{p}}}{\rightarrow } \hbox {P}+ {\hbox {D}_{\mathrm{on}}} &{} \hbox {(protein-induced DNA opening)} \end{array} \end{aligned}$$

(2)

This simple model is a combination of the well-known Golding model (Golding et al. 2005) with protein synthesis, as modeled by Munsky et al. (2009), and an additional feedback loop, similar to the model by Kepler and Elston (2001). It comprises several gene expression models as special cases, e.g., (Friedman et al. 2006; Golding et al. 2005; Peccoud and Ycart 1995; Shahrezaei and Swain 2008), and can therefore be used in a series of applications, e.g., (Munsky et al. 2012, 2009; Raser and O’Shea 2004). Furthermore, this systems is well suited to evaluate hybrid modeling approaches, the $\hbox {D}_{\mathrm{on}}$ and ${\hbox {D}}_{\mathrm{off}}$ are clearly low-copy number species, while $\hbox {R}$ and $\hbox {P}$ can be medium/high-copy number species depending on the parameter values. The rich dynamics of the process, which allows for bimodal probability distributions and strong correlation of mRNA and protein number with the DNA states, is illustrated in Fig. 1b.

Fig. 1

Illustration of a the gene expression model with positive feedback loop and b the dynamics of the process. The trajectories and the steady state distribution reveal the number of mRNA and proteins correlates strongly with the DNA state. For slow switching rates $\tau _{\mathrm{on}}, \tau _{\mathrm{off}}$ and $\tau _{\mathrm{on}}^{\mathrm{p}}$, probability distributions become bimodal. a Schematic of stochastic gene expression model showing conversion reactions (continuous arrows), production processes (dashed arrows) and regulatory interactions (dotted arrows). b Stochastic simulation of the gene expression model (left) and steady state distribution of the stochastic process (right) for parameters $\theta = (\tau _{\mathrm{on}},\tau _{\mathrm{off}},k_{\mathrm{r}},\gamma _{\mathrm{r}},k_{\mathrm{p}},\gamma _{\mathrm{p}},\tau _{\mathrm{on}}^{\mathrm{p}}) = (0.05, 0.05, 10, 1, 4, 1, 0.015)$. The contributions of the on-state (red) and the off-state (blue) to the steady state distribution are color-coded

Notation

The space of $n$-dimensional vectors of non-negative integers is denoted by $\mathbb{N }_0^n$. The space of $n$-dimensional vectors of non-negative real numbers is denoted by $\mathbb{R }_+^n$. The vectorial inequality $a \ge b$ is interpreted component-wise, $\forall i: a_i \ge b_i$. Furthermore, $a \ngeq b$ implies that $\exists i: a_i \ngeq b_i$.

2 Method of conditional moments

2.1 Decomposition of state space

We divide the chemical species into two classes, low- and medium/high-copy number species. Accordingly, we decompose the Markov process $X_t=(Y_t,Z_t)$ and the state vector $x = (y,z)$. The vectors $y = (y_1,\ldots ,y_{n_{s,y}}) \in \mathbb{N }_0^{n_{s,y}}$ and $z =(z_1,\ldots ,z_{n_{s,z}}) \in \mathbb{N }_0^{{n_{s,z}}}$ contain the molecule number of low- and medium/high-copy number species, respectively. Using the multiplication axiom, the probability mass function of the CME can be restated as

$$\begin{aligned} p(x|t) = p(y,z|t) = p(z|y,t) p(y|t), \end{aligned}$$

(3)

where $p(y|t)$ is the probability $P(Y_t=y)$ and $p(z|y,t)$ is the conditional probability of $Z_t=z$ given $Y_t=y$. This formulation of $p(y,z|t)$ as product of $p(z|y,t)$ and $p(y|t)$ is essential and will be used throughout the paper.

For the abundance of the low-copy number species $Y_t$ we employ a fully stochastic description. Hence, we consider the marginal probability

$$\begin{aligned} p(y|t) = \sum _{z \ge 0} p(y,z|t). \end{aligned}$$

(4)

The distribution of $Z_t$ will be modeled also stochastically but using the time-dependent conditional means and higher-order centered conditional moments,

$$\begin{aligned} \mu _{i,z}(y,t)&= \mathbb E _{z}\left. \left[ Z_i\right| y,t\right] = \sum _{z \ge 0} z_i p(z|y,t), \end{aligned}$$

(5)

$$\begin{aligned} C_{I,z}(y,t)&= \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I\right| y,t\right] = \sum _{z \ge 0} (z - \mu _{z}(y,t))^I p(z|y,t). \end{aligned}$$

(6)

Here we employ the product notation

$$\begin{aligned} (Z-\mu _{z}(y,t))^{I} := \prod _{i=1}^{{n_{s,z}}} (Z_i-\mu _{i,z}(y,t))^{I_i}, \end{aligned}$$

(7)

with $I=(I_1,\ldots ,I_{n_{s,z}})$ being a vector of non-negative integers. Moreover, let $F:\mathbb{N }_0^{n_{s,z}} \times \mathbb{R }_+ \rightarrow \mathbb{R }$ be a polynomial function in the first argument, $Z$. We write $\mathbb E _{z}\left. \left[ F(Z,t)\right| y,t\right]$ for the conditional expectation $\mathbb E \left[ F(Z,t)| Y_t=y\right]$,

$$\begin{aligned} \mathbb E _{z}\left. \left[ F(Z,t)\right| y,t\right] = \sum _{z \ge 0} F(z,t) p(z|y,t). \end{aligned}$$

(8)

Note that we assume here and throughout the manuscript that the solution of the CME is sufficiently regular in the sense that all moments, conditional moments and conditional expectations of the considered polynomial function exist. This is indeed the case for most CMEs used to model (bio-)chemical processes.

The description of $p(z|y,t)$ in terms of its moments does obviously result in a loss of information, however, the information content can be increased by increasing the order of the employed moments.

Example

For example (2) the DNA states ${\hbox {D}}_{\mathrm{off}}$ and $\hbox {D}_{\mathrm{on}}$ might be considered as low-copy number species, $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}])$, while mRNA and protein are medium/high-copy number species, $z = ([\hbox {R}],[\hbox {P}])$, respectively. Such natural decompositions are available for many systems, in particular for gene regulatory networks.

In the following, we derive the evolution equation for $p(y|t), \mu _{i,z}(y,t)$, and $C_{I,z}(y,t)$. Therefore, we decompose the stoichiometric vectors, $\nu _{j,x}^- \!=\! (\nu _{j,y}^-,\nu _{j,z}^-), \nu _{j,x}^{+}$ $= (\nu _{j,y}^{+},\nu _{j,z}^{+})$ and $\nu _{j,x}= (\nu _{j,y},\nu _{j,z})$, as well as the reaction propensities,

$$\begin{aligned} a_j(X_t) = c_j g_{j}(Y_t) h_{j}(Z_t), \end{aligned}$$

in accordance with the species assignment. This decomposition is possible for any reaction propensities following mass action kinetics. Using the decomposed stoichiometry and reaction propensities, the CME (1) can be reformulated as follows:

$$\begin{aligned} \frac{\partial }{\partial t}p(y,z|t)&= \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \\ z \ge \nu _{j,z}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) h_{j}(z-\nu _{j,z}) p(y-\nu _{j,y},z-\nu _{j,z}|t)\nonumber \\&-\sum _{j=1}^{n_{r}} c_j g_{j}(y) h_{j}(z) p(y,z|t). \end{aligned}$$

(9)

2.2 Evolution equation for the marginal probability $p(y|t)$

To derive the evolution equations for the marginal probability and the conditional moments, we repeatedly need the following result.

Lemma 1

Let $p(y,z|t) = p(z|y,t) p(y|t)$ satisfy a proper CME (9) $(\forall x \ngeq \nu _{j,x}^-: a_j(x) = 0)$, then

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ T(Z,t) h_{j}(Z)\right| y,t\right] p(y|t) + \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] p(y|t)\nonumber \\ \end{aligned}$$

(10)

for any polynomial test-function $T: \mathbb{N }_0^{n_{s,z}} \times \mathbb{R }_+ \rightarrow \mathbb R$.

This Lemma generalizes a result by (Engblom (2006), Lemma 2.1). The proof is provided in Appendix A.

Given Lemma 1, we obtain for the test function $T(z,t) = 1$ the evolution equation for $p(y|t)$.

Proposition 1

$$\begin{aligned} \frac{\partial }{\partial t}p(y|t)&= \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t) \nonumber \\&- \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] p(y|t). \end{aligned}$$

(11)

For any proper CME the evolution equation (11) describes the dynamics of the marginal probabilities exactly. Thus, this evolution equation describes the transition process of the CTMC in $y$. It can be shown that (11) possesses all key properties of a CME: conservation of the probability mass and positivity of the solution. Note that $p(y|t)$ is only influenced by reactions which actually change $y$, as for all other reactions the former and the latter terms are identical but possess opposite signs.

The evolution of $p(y|t)$ depends on the conditional expectation of the partial reaction propensities, $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right]$. These conditional expectations are in general unknown, however, for the mass action kinetics, they can be expressed in terms of the conditional mean and the centered conditional moments. For reactions which are at most bimolecular, the Taylor series representation of $h_{j}(z)$ at $\mu _{z}(y,t)$ is

$$\begin{aligned} h_{j}(z)&= h_{j}(\mu _{z}(y,t)) + \sum _{k=1}^{n_{s,z}} \frac{\partial h_{j}(\mu _{z}(y,t))}{\partial z_k} (z_k-\mu _{k,z}(y,t)) \nonumber \\&+ \frac{1}{2} \sum _{k,l=1}^{n_{s,z}} \frac{\partial ^2 h_{j}(\mu _{z}(y,t))}{\partial z_k \partial z_l} (z_k-\mu _{k,z}(y,t))(z_l-\mu _{l,z}(y,t)). \end{aligned}$$

(12)

This representation is exact as third and higher-order derivatives of $h_{j}(z)$ are zero. Given (12), the conditional expectation of $h_{j}(z)$ becomes

$$\begin{aligned} \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] = h_{j}(\mu _{z}(y,t)) + \frac{1}{2} \sum _{k,l=1}^{n_{s,z}} \frac{\partial ^2 h_{j}(\mu _{z}(y,t))}{\partial z_k \partial z_l} C_{e_k + e_l,z}(y,t), \end{aligned}$$

(13)

in which $e_k$ denotes the $k$-th unit vector. The second summand in (12) vanishes as $\mathbb E _{z}\left. \left[ Z_k-\mu _{k,z}(y,t)\right| y,t\right] =0$. In case of linear propensities or vanishing higher-order moments, we obtain $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] = h_{j}(\mu _{z}(y,t))$.

Given this Taylor series representation (13), the evolution equation for the marginal probability (11) can be formulated in terms of the conditional means and the centered conditional moments. Therefore, we substitute the conditional expectation $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right]$ by (13) into (11). This yields the time-evolution of the state probability $p(y|t)$ as a function of the conditional moments.

Example

For example (2), the marginal probability of the DNA being in the off-state is $p_{\mathrm{off}}(t) := p(\hbox {off}|t)$, with $\hbox {off}= (1,0)$, and the marginal probability of the DNA being in the on-state is $p_{\mathrm{on}}(t) := p(\hbox {on}|t)$, with $\hbox {on}= (0,1)$. According to (11) and (13), the evolution equations for these probabilities are

$$\begin{aligned} \frac{\partial p_{\mathrm{off}}}{\partial t}&= - \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\mu _{\mathrm{p},\mathrm{off}}\right) p_{\mathrm{off}}+ \tau _{\mathrm{off}}p_{\mathrm{on}}, \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial p_{\mathrm{on}}}{\partial t}&= \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\mu _{\mathrm{p},\mathrm{off}}\right) p_{\mathrm{off}}- \tau _{\mathrm{off}}p_{\mathrm{on}}, \end{aligned}$$

(15)

in which $\mu _{\mathrm{p},\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ [\hbox {P}]\right| \hbox {off},t\right]$ is the conditional expectation of the protein number given that the DNA is in the off-state.

2.3 Evolution equation for the conditional mean $\mu _{z}(y,t)$

As the time-derivative (11) of the marginal probability depends on the conditional means and the conditional covariances, the corresponding evolution equations are needed. In this section, we consider the conditional mean for which we obtain the following result.

Proposition 2

$$\begin{aligned}&p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \left( \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y-\nu _{j,y},t))^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] \right. \nonumber \\&\qquad \left. + \left( \mu _{i,z}(y-\nu _{j,y},t) + \nu _{ij,z}\right) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y-\nu _{j,y},t\right] \right) p(y-\nu _{j,y}|t) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) (\mathbb E _{z}\left. \left[ (Z - \mu _{z}(y,t))^{e_i} h_{j}(Z)\right| y,t\right] + \mu _{i,z}(y,t) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] ) p(y|t) \nonumber \\&\qquad - \mu _{i,z}(y,t) \frac{\partial }{\partial t} p(y|t). \end{aligned}$$

(16)

Proposition 2, whose proof is stated in Appendix B, provides a description of the dynamics of $\mu _{i,z}(y,t)$ via a differential algebraic equation (DAE). This DAE (16) cannot be restated as an ODE because a division by $p(y|t)$ is not possible as $p(y|t)$ may become zero. The treatment of the DAE is addressed in Sect. 4.

The dynamics of $\mu _{i,z}(y,t)$ are determined by two types of reaction fluxes: fluxes associated to reactions conserving and changing $y$, respectively. The former results only in a net change of the abundance of medium/high-copy number species. These reactions contribute the reaction flux $+ \nu _{ij,z}c_j g_{j}(y) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] p(y|t)$, which are similar to fluxes found when using the MMs (Engblom (2006), Proposition 2.2). For reactions which change $y$, the reaction flux takes the general form found on the right-hand side of (16). The complexity arises from the balance between influx and outflux which results in a net change of the conditional expectation $\mu _{i,z}(y,t)$.

The evolution equation (16) reveals that the dynamics of $\mu _{i,z}(y,t)$ depend as we expect on conditional moments of $h_{j}(z)$. This dependency can be avoided by employing the Taylor series representation of $h_{j}(z)$. Using (12), the conditional moment $\mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right]$ can, for any $I \ge 0$, be expressed in terms of the conditional mean and the centered conditional moments.

Lemma 2

$$\begin{aligned} \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right]&= h_{j}(\mu _{z}(y,t)) C_{I,z}(y,t) \nonumber \\&+ \sum _{k=1}^{n_{s,z}} \frac{\partial h_{j}(\mu _{z}(y,t))}{\partial z_k} C_{I + e_k,z}(y,t) \nonumber \\&+ \frac{1}{2} \sum _{k,l=1}^{n_{s,z}} \frac{\partial ^2 h_{j}(\mu _{z}(y,t))}{\partial z_k \partial z_l} C_{I + e_k + e_l,z}(y,t). \nonumber \\ \end{aligned}$$

(17)

By substituting (17) into the evolution equation (16) for $\mu _{i,z}(y,t)$, we obtain an equation which depends merely on $p(y|t), \mu _{i,z}(y,t)$ and $C_{I,z}(y,t)$. Still, $C_{I,z}(y,t)$ is unknown, therefore, we study in the next section the dynamics of $C_{I,z}(y,t)$.

Example

For example (2), the conditional means are the mean mRNA number in the off-state, $\mu _{\mathrm{r},\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ [\hbox {R}]\right| \hbox {off},t\right]$, the mean protein number in the off-state, $\mu _{\mathrm{p},\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ [\hbox {P}]\right| \hbox {off},t\right]$, the mean mRNA number in the on-state, $\mu _{\mathrm{r},\mathrm{on}}(t) = \mathbb E _{z}\left. \left[ [\hbox {R}]\right| \hbox {on},t\right]$, and the mean protein number in the on-state, $\mu _{\mathrm{p},\mathrm{on}}(t) = \mathbb E _{z}\left. \left[ [\hbox {P}]\right| \hbox {on},t\right]$. Following Proposition 2, we obtain the evolution equations

$$\begin{aligned} p_{\mathrm{off}}\frac{\partial \mu _{\mathrm{r},\mathrm{off}}}{\partial t}&= \left( \mu _{\mathrm{r},\mathrm{on}}- \mu _{\mathrm{r},\mathrm{off}}\right) \tau _{\mathrm{off}}p_{\mathrm{on}}- \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{rp},\mathrm{off}\,}p_{\mathrm{off}}- \gamma _{\mathrm{r}}\mu _{\mathrm{r},\mathrm{off}}p_{\mathrm{off}}, \end{aligned}$$

(18)

$$\begin{aligned} p_{\mathrm{off}}\frac{\partial \mu _{\mathrm{p},\mathrm{off}}}{\partial t}&= \left( \mu _{\mathrm{p},\mathrm{on}}- \mu _{\mathrm{p},\mathrm{off}}\right) \tau _{\mathrm{off}}p_{\mathrm{on}}- \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{p}^2,\mathrm{off}}p_{\mathrm{off}}\nonumber \\&+\left( k_{\mathrm{p}}\mu _{\mathrm{r},\mathrm{off}}- \gamma _{\mathrm{p}}\mu _{\mathrm{p},\mathrm{off}}\right) p_{\mathrm{off}}, \end{aligned}$$

(19)

$$\begin{aligned} p_{\mathrm{on}}\frac{\partial \mu _{\mathrm{r},\mathrm{on}}}{\partial t}&= \left( \mu _{\mathrm{r},\mathrm{off}}- \mu _{\mathrm{r},\mathrm{on}}\right) \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\mu _{\mathrm{p},\mathrm{off}}\right) p_{\mathrm{off}}+ \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{rp},\mathrm{off}\,}p_{\mathrm{off}}\nonumber \\&+ \left( k_{\mathrm{r}}- \gamma _{\mathrm{r}}\mu _{\mathrm{r},\mathrm{on}}\right) p_{\mathrm{on}}, \end{aligned}$$

(20)

$$\begin{aligned} p_{\mathrm{on}}\frac{\partial \mu _{\mathrm{p},\mathrm{on}}}{\partial t}&= \left( \mu _{\mathrm{p},\mathrm{off}}- \mu _{\mathrm{p},\mathrm{on}}\right) \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\mu _{\mathrm{p},\mathrm{off}}\right) p_{\mathrm{off}}+ \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{p}^2,\mathrm{off}}p_{\mathrm{off}}\nonumber \\&+ \left( k_{\mathrm{p}}\mu _{\mathrm{r},\mathrm{on}}- \gamma _{\mathrm{p}}\mu _{\mathrm{p},\mathrm{on}}\right) p_{\mathrm{on}}, \end{aligned}$$

(21)

in which $C_{\mathrm{p}^2,\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ ([\hbox {P}]-\mu _{\mathrm{p},\mathrm{off}})^2\right| \hbox {off},t\right]$ is the variance of the protein number in the off-state and $C_{\mathrm{rp},\mathrm{off}\,}(t) = \mathbb E _{z}\left. \left[ ([\hbox {R}]-\mu _{\mathrm{r},\mathrm{off}})([\hbox {P}]-\mu _{\mathrm{p},\mathrm{off}})\right| \hbox {off},t\right]$ is the covariance of protein number and mRNA number in the off-state. To obtain (18)–(21) we substituted the term $\frac{\partial }{\partial t} p(y|t)$ in (16) by (14) or (15), depending on the equation.

We note that the evolution Eqs. (18)–(21) possess similar structures. To elucidate the structure, we considered the right-hand side of $p_{\mathrm{off}}\frac{\partial \mu _{\mathrm{r},\mathrm{off}}}{\partial t}$ which possesses the summands $(\mu _{\mathrm{r},\mathrm{on}}- \mu _{\mathrm{r},\mathrm{off}}) \tau _{\mathrm{off}}p_{\mathrm{on}}, - \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{rp},\mathrm{off}\,}p_{\mathrm{off}}$, and $- \gamma _{\mathrm{r}}\mu _{\mathrm{r},\mathrm{off}}p_{\mathrm{off}}$. The first two summands describe the change of $\mu _{\mathrm{r},\mathrm{off}}$ due to transitions between different DNA states. For zeroth and first order reactions (here $R_1$ and $R_2$) merely the influxes into the node change the mean. This change is the influx rate, $\tau _{\mathrm{off}}p_{\mathrm{on}}$, times the difference in the means of the mRNA amounts in the two DNA states, $\mu _{\mathrm{r},\mathrm{on}}- \mu _{\mathrm{r},\mathrm{off}}$. For higher-order reactions which result in transition of $y$ (here $R_7$), higher-order terms are necessary to describe the changes in the mean, $- \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{rp},\mathrm{off}\,}p_{\mathrm{off}}$. The third summand, $- \gamma _{\mathrm{r}}\mu _{\mathrm{r},\mathrm{off}}p_{\mathrm{off}}$, describes the dynamics caused by reactions which preserve the DNA state. We emphasize that this structure is similar for all evolution equations.

2.4 Evolution equation for the centered conditional moments $C_{I,z}(y,t)$

To derive the centered conditional moments $C_{I,z}(y,t)$, where $I$ encodes which centered moment we considered (7), we introduce the vectorial binomial coefficient,

$$\begin{aligned} \begin{pmatrix} I \\ k \end{pmatrix} := \prod _{i=1}^{n_{s,z}} \begin{pmatrix} I_i \\ k_i \end{pmatrix} = \prod _{i=1}^{n_{s,z}} \frac{I_i!}{(I_i-k_i)! k_i!} \end{aligned}$$

and the product $\nu _{j,z}^I = \prod _{i=1}^{n_{s,z}} \nu _{ij,z}^{I_i}$. $I \in \mathbb{N }_0^{n_{s,z}}$ and $k \in \mathbb N _0^{n_{s,z}}$ denote integer-valued vectors. Using these notations, we state our result for the centered conditional moments $C_{I,z}(y,t)$.

Proposition 3

$$\begin{aligned}&p(y|t) \frac{\partial }{\partial t} C_{I,z}(y,t) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z\!+\!\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] p(y|t) \nonumber \\&\qquad - \sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i C_{I-e_i,z}(y,t) p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t) - C_{I,z}(y,t) \frac{\partial }{\partial t} p(y|t), \end{aligned}$$

(22)

with

$$\begin{aligned}&\mathbb E _{z}\left. \left[ (Z+\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] \nonumber \\&\quad =\sum _{0 \le k \le I} \begin{pmatrix} I \\ k \end{pmatrix} \left( \mu _{z}(y-\nu _{j,y},t)-\mu _{z}(y,t)+\nu _{j,z}\right) ^{I-k} \nonumber \\&\qquad \cdot \, \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y-\nu _{j,y},t))^{k} h_{j}(Z)\right| y-\nu _{j,y},t\right] . \end{aligned}$$

(23)

The proof of this proposition is provided in Appendix C.

Proposition (3) provides an evolution equation for $C_{I,z}(y,t)$. To state these dynamics in terms of the marginal probabilities, the conditional means and the centered conditional moments, the expectations $\mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(z)\right| y,t\right]$ and $\mathbb E _{z}\left. \left[ (Z-\mu _{z}(y-\nu _{j,y},t))^{k} h_{j}(Z)\right| y-\nu _{j,y},t\right]$ can be substituted with corresponding Taylor series representation (17). Furthermore, $\frac{\partial }{\partial t} p(y|t)$ can replaced by (11).

Example

To illustrate the structure of the evolution equation (22), we return to example (2). As the equations are lengthy, we state merely the evolution equation for the variance in the mRNA abundance in the off-state, $C_{\mathrm{r}^2,\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ ([\hbox {R}]-\mu _{\mathrm{r},\mathrm{off}})^2\right| \hbox {off},t\right]$,

$$\begin{aligned} p_{\mathrm{off}}\frac{\partial C_{\mathrm{r}^2,\mathrm{off}}}{\partial t}&= \left( C_{\mathrm{r}^2,\mathrm{on}}- C_{\mathrm{r}^2,\mathrm{off}}+ \left( \mu _{\mathrm{r},\mathrm{on}}- \mu _{\mathrm{r},\mathrm{off}}\right) ^2\right) \tau _{\mathrm{off}}p_{\mathrm{on}}\nonumber \\&- \tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{r}^2\mathrm{p},\mathrm{off}}p_{\mathrm{off}}+ \gamma _{\mathrm{r}}\left( \mu _{\mathrm{r},\mathrm{off}}- 2 C_{\mathrm{r}^2,\mathrm{off}}\right) p_{\mathrm{off}}, \end{aligned}$$

in which $C_{\mathrm{r}^2\mathrm{p},\mathrm{off}}(t) = \mathbb E _{z}\left. \left[ ([\hbox {R}]-\mu _{\mathrm{r},\mathrm{off}})^2 ([\hbox {P}]-\mu _{\mathrm{p},\mathrm{off}})\right| \hbox {off},t\right]$. The first summand describes the first order approximation of the influx in the off-state, $\tau _{\mathrm{off}}p_{\mathrm{on}}$, times the changes of the variance due to differences, $C_{\mathrm{r}^2,\mathrm{on}}(t) - C_{\mathrm{r}^2,\mathrm{off}}(t)$, and due to differences in the means, $\left( \mu _{\mathrm{r},\mathrm{on}}(t) - \mu _{\mathrm{r},\mathrm{off}}(t)\right) ^2$, in the two discrete states. The second summand describes additional changes of the variance due to transitions resulting from second order reactions. The last summand describes the dynamics of the variance within the considered mode.

2.5 Conditional moment equation

In the previous sections we derived evolution equations for the marginal probabilities, the conditional means and the centered conditional moments. By combining these equations we obtain the conditional moment equation.

Theorem 1

(Conditional moment equation) Let $p(y,z|t) = p(z|y,t) p(y|t)$ satisfy a proper CME (9), an exact evolution equation for the marginal probabilities $p(y|t)$ and the conditional moments $\mu _{i,z}(y,t) = \sum _{z \ge 0} z_i p(z|y,t)$ and $C_{I,z}(y,t) = \sum _{z \ge 0} (z - \mu _{z}(y,t))^I p(z|y,t)$ is given by the system

$$\begin{aligned} \frac{\partial }{\partial t}p(y|t)&= \sum _{j=1, y \ge \nu _{j,y}^{+}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t) \nonumber \\&- \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] p(y|t)\nonumber \\ p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t)&= \sum _{j=1, y \ge \nu _{j,y}^{+}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y-\nu _{j,y},t))^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t) \nonumber \\&+ \sum _{j=1, y \ge \nu _{j,y}^{+}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) (\mu _{i,z}(y-\nu _{j,y},t)+ \nu _{ij,z})\nonumber \\&\,\cdot \,\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&- \sum _{j=1}^{n_{r}} c_j g_{j}(y) \Big (\mathbb E _{z}\left. \left[ (Z - \mu _{z}(y,t))^{e_i} h_{j}(Z)\right| y,t\right] \nonumber \\&+ \mu _{i,z}(y,t) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] \Big ) p(y|t) - \mu _{i,z}(y,t) \frac{\partial }{\partial t} p(y|t) \nonumber \\ p(y|t) \frac{\partial }{\partial t} C_{I,z}(y,t)&= \sum _{j=1,y \ge \nu _{j,y}^{+}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \sum _{0 \le k \le I} \begin{pmatrix} I \\ k \end{pmatrix} \left( \mu _{z}(y-\nu _{j,y},t)\right. \nonumber \\&\left. -\mu _{z}(y,t)+\nu _{j,z}\right) ^{I-k} \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y-\nu _{j,y},t))^{k} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&-\sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] p(y|t) \nonumber \\&-\sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i C_{I-e_i,z}(y,t) p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t) - C_{I,z}(y,t) \frac{\partial }{\partial t} p(y|t),\nonumber \\ \end{aligned}$$

(24)

with $\displaystyle \mathbb E _{z}\left. \left[ (Z\!-\!\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] \!=\! h_{j}(\mu _{z}(y,t)) C_{I,z}(y,t) \!+\! \sum \nolimits _{k=1}^{n_{s,z}} \frac{\partial h_{j}(\mu _{z}(y,t))}{\partial z_k}$ $C_{I + e_k,z}(y,t) + \frac{1}{2} \sum _{k,l=1}^{n_{s,z}} \frac{\partial ^2 h_{j}(\mu _{z}(y,t))}{\partial z_k \partial z_l}C_{I + e_k + e_l,z}(y,t)$.

The conditional moment equation follows directly from the Propositions 1, 2 and 3. It provides an exact description for the stochastic evolution of $Y_t$ and the moments of $Z_t$.

As we expected, the conditional moment equation is in general not closed. The evolution equations for moments of order $m$ depend on moments of order $> m$. For the moment equation by Engblom (2006), closure could be shown for processes which contain only reactions with affine propensities (Engblom (2006), Proposition 2.10), i.e. zero and first order reactions. A careful study reveals that this is different for the conditional moment equation. The conditional moment equation is closed if all reactions possess mass action kinetics and belong to one of the following reaction classes:

• Class 1 Reactions which have only low-copy number species ($S_{i,y}, i = 1,\ldots ,{n_{s,y}}$) as educts,

  $$\begin{aligned} R_j: \quad \sum _{i=1}^{n_{s,y}} \nu _{ij,y}^- S_{i,y} \rightarrow \sum _{i=1}^{n_{s,y}} \nu _{ij,y}^{+} S_{i,y} + \sum _{i=1}^{n_{s,z}} \nu _{ij,z}^{+} S_{i,z}. \end{aligned}$$

• Class 2 First order reactions of high-copy number species ($S_{i,z}, i = 1,\ldots ,{n_{s,z}}$) producing only high-copy number species,

  $$\begin{aligned} R_j: \quad S_{i',z} \rightarrow \sum _{i=1}^{n_{s,z}} \nu _{ij,z}^{+} S_{i,z}. \end{aligned}$$

For reactions $R_j$ of class 1 it holds that $h_{j}(Z) = 1, \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] = 1$ and $\mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] = \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I\right| y,t\right]$, thus the moment order is conserved. For reactions of class 2 we have $h_{j}(Z) = Z_i'$ and moments of order $m+1$ appear in the evolution equations for $p(y,t), \mu _{i,z}(y,t)$ and $C_{I,z}(y,t)$. Indeed, the same moment of order $m+1$ enters in each evolution equation twice, in the first and in the second summation over the reactions ($j$). As these moments of order $m+1$ possess opposite signs and are conditioned on the same low-copy number state $y$, since $\nu _{ij,y}=0$ for reactions of class 2, they cancel. This is similar to the effect observed for the moment equation (Engblom 2006).

For all reactions not belonging to class 1 and 2 we can construct simple examples for which the conditional moment equation is not closed. One class of such reactions are first order reactions which convert a high-copy number species into one or more low-copy number species. For this class of reactions the moment equation is closed but the conditional moment equation is not closed. On the other hand, for any bimolecular reactions belonging to class 1, the conditional moment equation is closed while the moment equation is not closed.

For processes that include arbitrarily zero, first and second order reactions, the moment equation contains moments of order $\le m+1$. For the conditional moment equation (17) indicates that also moments of order $m+2$ appear. This is indeed the case if low-copy number species can be produced from high-copy number species via bimolecular reactions, e.g., $S_{i_1,z} + S_{i_2,z} \rightarrow \sum _{i=1}^{n_{s,y}} \nu _{ij,y}^{+} S_{i,y}$. In this case the covariance $C_{I + e_{i_1} + e_{i_2},z}$ enters in the evolution equation for $C_{I,z}$. This is different for the MM (Engblom 2006), which contains for truncation index $m$ moments of at most order $m+1$.

Example

The conditional moment equation for example (2) is not closed because reaction $R_7$ does not belong to any of the above mentioned classes. If the reaction $R_7$ is removed, the system is closed and the conditional moment equation is exact.

2.6 Moment closure techniques

The dependence of the evolution equations for moments of order $m$ on moments of order $m + 1$ and $m + 2$ prohibits the numerical simulation and establishes the need for approximation methods. In the context of the MM, these approximation methods are known as moment closures. The basic idea is to truncate the moments at order $m$, and to express the moments of order $> m$ as a function of the lower-order moments (Hespanha 2008).

For the uncentered moment equation a variety of different closure schemes have been proposed. Most of these schemes employ distributional assumptions, e.g., that the underlying probability distribution is normal (Whittle 1957), log-normal (Singh and Hespanha 2006), beta-binomial (Krishnarajah et al. 2005), and a mixture of distributions (Krishnarajah et al. 2005). Other approaches employ assumptions about the cumulants of the distribution (Matis and Kiffe 1999, 2002) or perform derivative matching (Hespanha 2007; Singh and Hespanha 2011). In a recent study a stochastic closure method has been introduced, which is based on a combination of SSA simulations and Kalman filtering (Ruess et al. 2011).

All moment closure methods developed for uncentered moment equations can in principle also be applied to centered moment equations. Nevertheless, we find that for centered moment equations (Engblom 2006; Lee et al. 2009) mostly the low dispersion closure (Hespanha 2008) is employed. Here the assumption is that the distribution is tightly clustered around the mean, thus the higher-order centered moments are close to zero. Thus, if only centered moments up to order $m$ are included ($C_{I,z}(y,t)$ for all $I$ with $\sum _{i=1}^{n_{s,z}} I_i \le m$), the moments of order $m+1$ and $m+2$ are replaced by zero (Engblom 2006; Lee et al. 2009). Hence, for $m=1$ the variances and covariances are replaced by zero. For $m = 2$ the third-order moments, that describe the skewness of the distribution, are replaced by zero, which is similar to an approximation using the (multivariate) normal distribution.

As the conditional moment equations have been expressed in terms of the centered moments, in the following we also use the low dispersion closure. For any $C_{I,z}$ with $\sum _{i=1}^{n_{s,z}} I_i > m$ we employ the approximation

$$\begin{aligned} \forall y,t: \, C_{I,z}(y,t) = 0. \end{aligned}$$

(25)

Clearly, by increasing the truncation order $m$, the approximation quality can be increased as the underlying distribution is described more precisely. However, this increase comes at the cost of an increased computational effort. The number of conditional moments for a given state $y$ is

$$\begin{aligned} \sum _{k=1}^m \begin{pmatrix} {n_{s,z}}+k-1 \\ k \end{pmatrix}, \end{aligned}$$

(26)

with ${n_{s,z}}$ being the number of medium/high-copy number species. Thus, the number of equations increases rapidly with $m$. Additional assumptions about the co-dependence of elements of $z$ might be employed to eliminate conditional moments and to slow down this increase (Menz et al. 2012). We also experienced numerical problems for $m \gg 1$, establishing an additional limitation.

Example

In example (2), the low dispersion closure with $m = 1$ yields the approximation $C_{\mathrm{rp},\mathrm{off}\,}= C_{\mathrm{p}^2,\mathrm{off}}= 0$. For $m = 2$ we get $C_{\mathrm{r}^2\mathrm{p},\mathrm{off}}= C_{\mathrm{rp}^2,\mathrm{off}}= C_{\mathrm{p}^3,\mathrm{off}}= 0$.

For bi- and multi-modal distributions $p(x|t)$, moment closure methods often provide only unsatisfactory approximations of the higher-order moments. This is due to the complex structure which does in general not allow for a reliable estimation of the moments of order $> m$ using moments of order $\le m$. This problem can be partially circumvented using the conditional moment equation, if the full distribution $p(x|t)$ is bi- or multi-modal but the conditional distribution $p(z|y,t)$ is not. In this case, the modes of $p(x|t)$ are associated with different low-copy number states. As for the conditional moment equation the approximation of the moments of the unimodal conditional distribution $p(z|y,t)$ is sufficient, and also low-order closure schemes are often appropriate.

Despite this improvement, moment closures merely approximate the moments of the CME solution. For the moment equation it is well-known that these approximations can cause divergence (Singh and Hespanha 2011). Similar problems can also occur for the conditional moment equation. For truncation orders $m \ge 2$, the non-negativity of the conditional means ${\mu }_z(y,t)$ and the higher-order conditional moments $C_{I,z}(y,t)$ cannot be guaranteed as $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right]$ and $\mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right]$ may become negative. If the non-negativity of molecule numbers (e.g., ${\mu }_z(y,t)$) or probabilities (e.g., $p(y|t)$) is violated, the approximation of the CME solution is implausible and the state of the conditional moment equation often diverges.

To avoid negativity of solutions and divergence, the moment closure has to be chosen carefully and specifically according to the problem. In this work we merely use the low dispersion moment closure, however, any closure schemes developed for the moment equation are appropriate. The use of more sophisticated closure methods can avoid divergence problems and further improve the approximation achieved by the conditional moment equation.

3 Comparison of the method of conditional moments with the method of moments and hybrid methods

In the last sections we introduced the conditional moment equation and outlined moment closure methods. The former provides a hybrid stochastic moment description for the time-evolution of the CME solution. The question which remains open is how the conditional moment equation relates to existing hybrid approximations and moment-based descriptions of the CME. In the following, we compare our method to the hybrid methods introduced by Menz et al. (2012), Jahnke (2011), Henzinger et al. (2010) and Mikeev and Wolf (2012). Moreover, we analyze the relationship to the centered moment equations by Engblom (2006), whose derivations have been restated by Lee et al. (2009). Our analysis reveals that the MCM essentially provides a generalization to these approaches.

3.1 Relation between the conditional moment equation and moment equation

As discussed earlier, the moment equation describes the evolution of the statistical moments of the solution of the CME. In contrast to the conditional moment equation, the moment equation by Engblom (2006) does not decompose the species into two different classes. Instead, the distribution of all species is described using the corresponding moments. In terms of the conditional moment equation this means that ${n_{s,y}}=0$ and ${n_{s,z}}={n_{s}}$. Thus, $z = x, \nu _{j,y}= \emptyset , \nu _{j,z}= \nu _{j,x}$, and $g_{j}(y) = 1$. Furthermore, the marginal probability is one, $p(y|t) = 1$, the conditional moments are equal to the (unconditional) moments, $\mu _{i,z}(y,t) = \bar{\mu }_{i}(t)$ and $C_{I,z}(y,t) = {\bar{C}}_{I}(t)$, and the conditional expectation $\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right]$ becomes the expectation $\mathbb E \left[ T(Z,t)|t\right]$. When inserting all this in the evolution equation (24), we obtain

$$\begin{aligned} \frac{\partial }{\partial t} \bar{\mu }_{i}(t) = \sum _{j=1}^{n_{r}} c_j \nu _{ij,x}\mathbb E \left[ h_{j}(Z)|t\right] \end{aligned}$$

(27)

and

$$\begin{aligned} \frac{\partial }{\partial t} {\bar{C}}_{I}(t)&= \sum _{j=1}^{n_{r}} c_j \sum _{0 \le k < I} \begin{pmatrix} I \\ k \end{pmatrix} \nu _{j,x}^{I-k} \mathbb E \left[ (Z-\bar{\mu }_{}(t))^{k} h_{j}(Z)|t\right] \nonumber \\&- \sum _{i=1}^{n_{s}} I_i \mathbb E \left[ (Z-\bar{\mu }_{}(t))^{I-e_i}|t\right] \frac{\partial }{\partial t}\bar{\mu }_{i}(t) \end{aligned}$$

(28)

with

$$\begin{aligned} \mathbb E \left[ (Z-\bar{\mu }_{}(t))^I h_{j}(Z)|t\right]&= h_{j}(\bar{\mu }_{}(t)) {\bar{C}}_{I}(t) + \sum _{k=1}^{n_{s}} \frac{\partial h_{j}(\bar{\mu }_{}(t))}{\partial z_k} {\bar{C}}_{I + e_k}(t)\nonumber \\&+ \frac{1}{2} \sum _{k,l=1}^{n_{s}} \frac{\partial ^2 h_{j}(\bar{\mu }_{}(t))}{\partial z_k \partial z_l} {\bar{C}}_{I + e_k + e_l}(t). \end{aligned}$$

This result is equivalent to the result of (Lee et al. (2009), Equation (6) and (8)), which is a reformulation of the result by (Engblom (2006), Equation (2.46)).

Beyond the expected result that the moment equation is a special case of the conditional moment equation, the means $\bar{\mu }_{i}(t) = \mathbb E \left[ x_i|t\right]$ and the centered moments ${\bar{C}}_{I}(t) = \mathbb E \left[ (X - \bar{\mu }_{}(t))^I|t\right]$ can be computed from the conditional moments for any assignment to low- and medium/high-copy number species, $X_t = (Y_t,Z_t)$.

Proposition 4

For $X_t = (Y_t,Z_t)$, the conditional moment equation (24) describes the evolution of the population mean,

$$\begin{aligned} \bar{\mu }_{i}(t) = {\left\{ \begin{array}{ll} \displaystyle \bar{\mu }_{i,y}(t) = \sum _{y\ge 0} y_i p(y|t) &{} \hbox {for } i \in \{1,\ldots ,{n_{s,y}}\} \\ \displaystyle \bar{\mu }_{j,z}(t) = \sum _{y\ge 0} \mu _{j,z}(y,t) p(y|t) &{} \hbox {for } i \in \{{n_{s,y}}+1,\ldots ,{n_{s}}\}, \end{array}\right. } \end{aligned}$$

(29)

where $j = i-{n_{s,y}}$, and the centered moments,

$$\begin{aligned} {\bar{C}}_{I}(t) = \sum _{y\ge 0} (y - \bar{\mu }_{y}(t))^{I_y} \sum _{0 \le k \le I_z} \begin{pmatrix} I_z \\ k \end{pmatrix} (\mu _z (y,t)-\bar{\mu }_z(t))^{I_z-k} C_{k,z}(y,t) p(y|t)\nonumber \\ \end{aligned}$$

(30)

with $I = (I_y,I_z)$ and $\bar{\mu }_{y}(t) = \left( \bar{\mu }_{1}(t),\ldots ,\bar{\mu }_{{n_{s,y}}}(t)\right)$.

To determine the statistical moments (29) and (30) we assess the overall statistics of the mixture defined by the discrete states and the corresponding conditional moments. The derivation of Proposition (4) can be found in Appendix D.

Example

For the gene expression model (2), Proposition 4 states that the means are $\bar{\mu }_{\mathrm{off}}(t) = p_{\mathrm{off}}(t), \bar{\mu }_{\mathrm{on}}(t) = p_{\mathrm{on}}(t), \bar{\mu }_{\mathrm{r}}(t) = \mu _{\mathrm{r},\mathrm{off}}(t) p_{\mathrm{off}}(t) + \mu _{\mathrm{r},\mathrm{on}}(t) p_{\mathrm{on}}(t)$ and $\bar{\mu }_{\mathrm{p}}(t) = \mu _{\mathrm{p},\mathrm{off}}(t) p_{\mathrm{off}}(t) + \mu _{\mathrm{p},\mathrm{on}}(t) p_{\mathrm{on}}(t)$. For the variances and covariances we obtain, for instance,

$$\begin{aligned} \bar{C}_{\mathrm{r}^2}(t)&= \left( \left( \mu _{\mathrm{r},\mathrm{off}}(t) - \bar{\mu }_{\mathrm{r}}(t)\right) ^2 + C_{\mathrm{r}^2,\mathrm{off}}(t) \right) p_{\mathrm{off}}(t)\nonumber \\&+ \left( \left( \mu _{\mathrm{r},\mathrm{on}}(t) - \bar{\mu }_{\mathrm{r}}(t)\right) ^2 + C_{\mathrm{r}^2,\mathrm{on}}(t) \right) p_{\mathrm{on}}(t). \end{aligned}$$

(31)

3.2 Relation between the conditional moment equation and hybrid methods

Similar to the conditional moment equation, the hybrid methods by Menz et al. (2012), Jahnke (2011), Henzinger et al. (2010), and Mikeev and Wolf (2012) rely on the assignment of species to two groups. Low-copy number species are modeled stochastically, while medium/high-copy number species are modeled deterministically but conditioned on the state of the low-copy number species. This deterministic modeling considers merely the mean concentration and relies on the assumption that the variance in the abundance of the medium/high-copy number species is zero. Indeed, if we use the truncation index $m = 1$ and the trivial moment closure $C_I(y,t) = 0$, the conditional moment equation simplifies to

$$\begin{aligned} \frac{\partial }{\partial t}p(y|t)&= \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) h_{j}(\mu _{z}(y-\nu _{j,y},t)) p(y-\nu _{j,y}|t) \nonumber \\&- \sum _{j=1}^{n_{r}} c_j g_{j}(y) h_{j}(\mu _{z}(y,t)) p(y|t) \end{aligned}$$

(32)

and

$$\begin{aligned} p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t)&= \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j \left( \mu _{i,z}(y-\nu _{j,y},t) + \nu _{ij,z}\right) \nonumber \\&\cdot g_{j}(y-\nu _{j,y}) h_{j}(\mu _{z}(y-\nu _{j,y},t)) p(y-\nu _{j,y}|t) \nonumber \\&- \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mu _{i,z}(y,t) h_{j}(\mu _{z}(y,t)) p(y|t) \nonumber \\&- \mu _{i,z}(y,t) \frac{\partial }{\partial t} p(y|t), \end{aligned}$$

(33)

which corresponds to the hybrid model by (Jahnke (2011), Equation (5.8) and (5.9)). The conditional moment equation with $m = 1$ (32)–(33) is also closely related to the hybrid model by (Menz et al. (2012), Equation (3.46) and (3.47)). Indeed, we can establish equivalence if (1) the partial means used by Menz et al. are expressed as product of conditional means and marginal probabilities and (2) the “discrete reactions” defined by Menz et al. do not change medium/high-copy number species.

We note that (32)–(33) is not equivalent to the hybrid simulation methods used by (Henzinger et al. (2010), Equation (11)–(15)) and by (Mikeev and Wolf (2012), Equation (6) and (7)). These methods rely on an ad hoc derivation which results in a slightly different description of the coupling of discrete states $y$. The coupling terms are similar to the exact coupling terms derived here, but they are not identical.

Example

Note that for example (2), the corresponding hybrid model by Jahnke (2011) is given by (14)–(15), (18)–(21) with $C_{\mathrm{p}^2,\mathrm{off}}(t) \equiv C_{\mathrm{rp},\mathrm{off}\,}(t) \equiv 0$.

3.3 The conditional moment equation as a unifying modeling framework

The findings of the previous sections imply that the moment equation (Engblom 2006; Lee et al. 2009) and the hybrid systems (Jahnke 2011; Menz et al. 2012) are special cases of the conditional moment equation. For $m = 1$ in combination with a low dispersion closure (25) we obtain the hybrid models (Jahnke 2011; Menz et al. 2012). The moment equation (Engblom 2006; Lee et al. 2009) arises when $y = \emptyset , z = x$ and $m \in \mathbb N$. For $y = \emptyset , z = x, m = 1$ and a low dispersion moment closure we even get the reaction rate equation. Thus, these three model classes are subsets of the conditional moment equation (24).

Indeed, if we choose $y = x$, we even recapture the CME. Strictly speaking, the class of CMEs is therefore a subset of the class of conditional moment equations. In this work the conditional moment equation is however merely used to approximate the statistical properties of a given CME. An overview about the different model classes and the dependencies is provided in Fig. 2.

Fig. 2

Illustration of the properties of five model classes, Chemical Master Equation, conditional moment equation, moment equation, hybrid models, and reaction rate equation, in terms of the set of discrete states $y$ and the truncation order $m$. The vector $x$ contains all species, while $y$ and $z$ contain those defined as low-copy number species and the medium/high-copy number species, respectively

4 Simulation of the conditional moment equation

To analyze the conditional moment equation, its properties, and to compare it with existing methods, we employ in the following simulation-based methods. As the conditional moment equation is a DAE, the numerical treatment is however non-trivial (Ascher and Petzold 1998). DAEs allow for a much richer dynamic behavior than ODEs, including discontinuities. While general purpose solvers are available for DAEs with arbitrary DAE indexes, e.g., Hindmarsh et al. (2005), all of them require initial values for the state variables and their time-derivatives (Brown et al. 1998). Hence, we have to compute $p(y|0), \dot{p}(y|0), \mu _{i,z}(y,0), \dot{\mu }_{i,z}(y,0), C_{I,z}(y|0)$, and $\dot{C}_{I,z}(y|0)$ from the initial distribution $p(x|0) = p(y,z|0)$.

4.1 Construction of initial conditions

At a first glance, the assignment of initial conditions might seem to be straight forward, but it is indeed challenging. We face the problem that for $y$ with $p(y|0) = 0$ the conditional probabilities $p(z|y,0)$ are not determined as

$$\begin{aligned} \forall y \hbox { with } p(y|0) = 0:\quad p(y,z|0) = p(z|y,0) p(y|0) = p(z|y,0) \cdot 0 = 0. \end{aligned}$$

This indeterminacy of $p(z|y,0)$ complicates the calculation of initial moments and their derivatives. However, this indeterminacy is no disadvantage of the conditional moment equation as these state do not contribute to the distribution. Furthermore, we will present a method to construct a consistent initialization.

To elucidate the problem and the solution procedure, we first have a look at our example.

Example

To illustrate the calculation of initial conditions for states $y$ with $p(y|0) = 0$, we consider example (2). At $t=0$ we assume that the DNA is with probability $\xi _{\mathrm{off}}$ in the off-state and with probability $(1-\xi _{\mathrm{off}})$ in the on-state. In both, on- and off-state, mRNA and protein numbers follow independent Poisson distributions. This yields the initial condition

$$\begin{aligned} p(y,z|0) = \left\{ \begin{array}{rl} \xi _{\mathrm{off}}\,\, \mathrm Pois (z_1|\lambda _{\mathrm{r},\mathrm{off}}\,) \mathrm Pois (z_2|\lambda _{\mathrm{p},\mathrm{off}}\,) &{} \hbox {for } y = \hbox {off}, \\ (1 - \xi _{\mathrm{off}}) \mathrm Pois (z_1|\lambda _{\mathrm{r},\mathrm{on}}) \mathrm Pois (z_2|\lambda _{\mathrm{p},\mathrm{on}}) &{} \hbox {for } y = \hbox {on}, \\ \end{array} \right. \end{aligned}$$

(34)

with distribution parameters $\lambda _{\mathrm{r},\mathrm{off}}, \lambda _{\mathrm{r},\mathrm{on}}, \lambda _{\mathrm{p},\mathrm{off}}$ and $\lambda _{\mathrm{p},\mathrm{on}}$. $\mathrm Pois (z_i|\lambda ) = \frac{\lambda ^{z_i} e^{-\lambda }}{z_i!}$ denotes the Poisson distribution which possesses mean and variance $\lambda$.

Given $p(y,z|0)$ we calculate now the initial conditions. Thereby we distinguish two cases: $\xi _{\mathrm{off}}\in (0,1)$ (Case 1) and $\xi _{\mathrm{off}}\in \{0,1\}$ (Case 2). To keep the example brief we merely provide equations for the marginal probabilities and the conditional means.

• Case 1: For $\xi _{\mathrm{off}}\in (0,1)$ the initial marginal probabilities are $p_{\mathrm{off}}(0) = \xi _{\mathrm{off}}$ and $p_{\mathrm{on}}(0) = 1 - \xi _{\mathrm{off}}$. This yields the conditional probabilities

  $$\begin{aligned} p(z|\hbox {off},0)&= \frac{p(\hbox {off},z|0)}{\xi _{\mathrm{off}}} = \mathrm Pois (z_1|\lambda _{\mathrm{r},\mathrm{off}}\,) \mathrm Pois (z_2|\lambda _{\mathrm{p},\mathrm{off}}\,),\\ p(z|\hbox {on},0)&= \frac{p(\hbox {on},z|0)}{1 - \xi _{\mathrm{off}}} = \mathrm Pois (z_1|\lambda _{\mathrm{r},\mathrm{on}}) \mathrm Pois (z_2|\lambda _{\mathrm{p},\mathrm{on}}), \end{aligned}$$

  from which we deduce via (5) that $\mu _{\mathrm{r},\mathrm{off}}(0) = \lambda _{\mathrm{r},\mathrm{off}}, \mu _{\mathrm{r},\mathrm{on}}(0) = \lambda _{\mathrm{r},\mathrm{on}}, \mu _{\mathrm{p},\mathrm{off}}(0) = \lambda _{\mathrm{p},\mathrm{off}}$ and $\mu _{\mathrm{p},\mathrm{on}}(0) = \lambda _{\mathrm{p},\mathrm{on}}$. To determine the initial derivatives we evaluate the evolution equations at $t = 0$. From (14) and (15) it follows that ${\dot{p}}_{\mathrm{off}}(0) = - \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{off}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\lambda _{\mathrm{p},\mathrm{off}}\right) \xi _{\mathrm{off}}+ \tau _{\mathrm{off}}$ and ${\dot{p}}_{\mathrm{on}}(0) = \left( \tau _{\mathrm{on}}+ \tau _{\mathrm{off}}+ \tau _{\mathrm{on}}^{\mathrm{p}}\lambda _{\mathrm{p},\mathrm{off}}\right) \xi _{\mathrm{off}}- \tau _{\mathrm{off}}$, while (18)-(21) yield $\dot{\mu }_{\mathrm{r},\mathrm{off}}(0) = (\lambda _{\mathrm{r},\mathrm{on}}- \lambda _{\mathrm{r},\mathrm{off}}) \tau _{\mathrm{off}}\frac{1 - \xi _{\mathrm{off}}}{\xi _{\mathrm{off}}} - \gamma _{\mathrm{r}}\lambda _{\mathrm{r},\mathrm{off}}$, et cetera. The initial conditions for the higher-order moments can be computed accordingly.

• Case 2: For $\xi _{\mathrm{off}}\in \{0,1\}$, the initialization is more difficult. To illustrate the problem and a solution we consider $\xi _{\mathrm{off}}= 0$. In this case, the initial marginal probabilities are $p_{\mathrm{off}}(0) = 0$ and $p_{\mathrm{on}}(0) = 1$. Their derivatives ${\dot{p}}_{\mathrm{off}}(0) = \tau _{\mathrm{off}}$ and ${\dot{p}}_{\mathrm{on}}(0) = - \tau _{\mathrm{off}}$ are found by evaluating (14) and (15), respectively. Furthermore, the initial conditions for the on-state can be assessed as before, yielding $\mu _{\mathrm{r},\mathrm{on}}(0) = \lambda _{\mathrm{r},\mathrm{on}}, \mu _{\mathrm{p},\mathrm{on}}(0) = \lambda _{\mathrm{p},\mathrm{on}}, \dot{\mu }_{\mathrm{r},\mathrm{on}}(0) = k_{\mathrm{r}}- \gamma _{\mathrm{r}}\lambda _{\mathrm{r},\mathrm{on}}$, and $\dot{\mu }_{\mathrm{p},\mathrm{on}}(0) = k_{\mathrm{p}}\lambda _{\mathrm{r},\mathrm{on}}- \gamma _{\mathrm{p}}\lambda _{\mathrm{p},\mathrm{on}}$. The conditional moments in the off-state pose problems as we cannot solve $p([1,0],z|0) = p(z|[1,0],0) p([1,0]|0)$ for $p(z|[1,0],0)$ because $p([1,0]|0) = 0$. Thus, we can neither evaluate (5) to get a $\mu _{\mathrm{r},\mathrm{off}}$ and $\mu _{\mathrm{p},\mathrm{off}}$, nor use (18) and (19) to determine the initial derivatives. To circumvent these problems we note that the evolution equation for $\mu _{\mathrm{r},\mathrm{off}}$ (18) evaluated at $t = 0$ is $0 = \left( \mu _{\mathrm{r},\mathrm{on}}(0) - \mu _{\mathrm{r},\mathrm{off}}(0)\right) \tau _{\mathrm{off}}$. Thus, the evolution equation does not define the initial derivative of $\mu _{\mathrm{r},\mathrm{off}}, \dot{\mu }_{\mathrm{r},\mathrm{off}}(0)$, but the initial value $\mu _{\mathrm{r},\mathrm{off}}(0) = \mu _{\mathrm{r},\mathrm{on}}(0) = \lambda _{\mathrm{r},\mathrm{on}}$. Similarly we evaluate the evolution equation for $\mu _{\mathrm{p},\mathrm{off}}$ (19) at $t = 0$ to find $\mu _{\mathrm{p},\mathrm{off}}(0) = \mu _{\mathrm{p},\mathrm{on}}(0) = \lambda _{\mathrm{p},\mathrm{on}}$. To determine the initial derivative of $\mu _{\mathrm{r},\mathrm{off}}$ and $\mu _{\mathrm{p},\mathrm{off}}$ we compute the partial derivative of the corresponding evolution equations with respect to $t$ and evaluate it at $t = 0$. For $\mu _{\mathrm{r},\mathrm{off}}$ the partial derivative of the evolution equation is

  $$\begin{aligned}&\frac{\partial p_{\mathrm{off}}}{\partial t} \frac{\partial \mu _{\mathrm{r},\mathrm{off}}}{\partial t} + p_{\mathrm{off}}\frac{\partial ^2 \mu _{\mathrm{r},\mathrm{off}}}{\partial t^2} \\&\quad =\tau _{\mathrm{off}}\left( \left( \frac{\partial \mu _{\mathrm{r},\mathrm{on}}}{\partial t} - \frac{\partial \mu _{\mathrm{r},\mathrm{off}}}{\partial t}\right) p_{\mathrm{on}}+ \left( \mu _{\mathrm{r},\mathrm{on}}- \mu _{\mathrm{r},\mathrm{off}}\right) \frac{\partial p_{\mathrm{on}}}{\partial t}\right) \\&\qquad - \tau _{\mathrm{on}}^{\mathrm{p}}\left( \frac{\partial C_{\mathrm{rp},\mathrm{off}\,}}{\partial t} p_{\mathrm{off}}+ C_{\mathrm{rp},\mathrm{off}\,}\frac{\partial p_{\mathrm{off}}}{\partial t} \right) - \gamma _{\mathrm{r}}\left( \frac{\partial \mu _{\mathrm{r},\mathrm{off}}}{\partial t} p_{\mathrm{off}}+ \mu _{\mathrm{r},\mathrm{off}}\frac{\partial p_{\mathrm{off}}}{\partial t}\right) , \end{aligned}$$

  which for $t = 0$ simplifies to

  $$\begin{aligned} \tau _{\mathrm{off}}\dot{\mu }_{\mathrm{r},\mathrm{off}}(0) = \tau _{\mathrm{off}}\left( k_{\mathrm{r}}- \gamma _{\mathrm{r}}\lambda _{\mathrm{r},\mathrm{on}}- \dot{\mu }_{\mathrm{r},\mathrm{off}}(0)\right) - \tau _{\mathrm{off}}\tau _{\mathrm{on}}^{\mathrm{p}}C_{\mathrm{rp},\mathrm{off}\,}(0) - \tau _{\mathrm{off}}\gamma _{\mathrm{r}}\lambda _{\mathrm{r},\mathrm{on}}. \end{aligned}$$

  When solving the latter equation for $\dot{\mu }_{\mathrm{r},\mathrm{off}}(0)$ we obtain

  $$\begin{aligned} \dot{\mu }_{\mathrm{r},\mathrm{off}}(0) = \frac{k_{\mathrm{r}}}{2} - \gamma _{\mathrm{r}}\lambda _{\mathrm{r},\mathrm{on}}- \frac{\tau _{\mathrm{on}}^{\mathrm{p}}}{2} C_{\mathrm{rp},\mathrm{off}\,}(0). \end{aligned}$$

  Thus, using the first derivative of the evolution equation, we can determine the initial derivative $\dot{\mu }_{\mathrm{r},\mathrm{off}}(0)$. The unknown $C_{\mathrm{rp},\mathrm{off}\,}(0)$ can be computed from the evolution equation for $C_{\mathrm{rp},\mathrm{off}\,}$ or might, for truncation index $m = 1$, be set to zero. By applying the same procedure to (19), we obtain

  $$\begin{aligned} \dot{\mu }_{\mathrm{p},\mathrm{off}}(0) = k_{\mathrm{p}}\lambda _{\mathrm{r},\mathrm{on}}- \gamma _{\mathrm{p}}\lambda _{\mathrm{p},\mathrm{on}}- \frac{\tau _{\mathrm{on}}^{\mathrm{p}}}{2} C_{\mathrm{p}^2,\mathrm{off}}(0), \end{aligned}$$

  with $C_{\mathrm{p}^2,\mathrm{off}}(0)$ being determined by the evolution equation of $C_{\mathrm{p}^2,\mathrm{off}}$. The derivation of $\mu _{\mathrm{r},\mathrm{off}}(0), \mu _{\mathrm{p},\mathrm{off}}(0), \dot{\mu }_{\mathrm{r},\mathrm{off}}(0)$ and $\dot{\mu }_{\mathrm{p},\mathrm{off}}(0)$ concludes Case 2. A similar procedure can be used to determine the initial conditions for $\xi _{\mathrm{off}}= 1$.

The example shows that the calculation of the initial condition might be non-trivial for some setups, however, the partial derivatives of the evolution equation define the initial conditional moments and their initial derivatives. In the following, we introduce an initialization scheme for the conditional moment equation. Given an initial probability distribution $p(y,z|0)$, we first state the initial condition for all states $y$ with $p(y|0) = \sum _{z \ge 0} p(y,z|0) > 0$. Afterwards, we propose an initialization scheme for states $y$ with $p(y|0) = 0$.

States $y$ with $p(y|0) > 0$: For states $y$ with $p(y|0) > 0$ the initial conditions for the conditional moments follow from (5) and (6), yielding

$$\begin{aligned} \mu _{i,z}(y,0)&= \sum _{z \ge 0} z_i p(z|y,0) = \sum _{z \ge 0} z_i \frac{p(y,z|0)}{p(y|0)}, \end{aligned}$$

(35)

$$\begin{aligned} C_{I,z}(y,0)&= \sum _{z \ge 0} (z - \mu _{z}(y,t))^I p(z|y,0) = \sum _{z \ge 0} (z - \mu _{z}(y,t))^I \frac{p(y,z|0)}{p(y|0)}. \nonumber \\ \end{aligned}$$

(36)

The initial derivatives are defined by the evolution equations (11), (16), and (22) evaluated for $t = 0$.

States $y$ with $p(y|0) = 0$: For states $y$ with $p(y|0) = 0$, the initial conditional probability $p(z|y,0)$ is undetermined. Thus, (35) and (36) cannot be evaluated. In addition, the derivative $\dot{\mu }_{i,z}(y,0)$ remains undefined as at time $t = 0$ it is, in (16), multiplied by $p(y|0) = 0$ and vanishes. The same holds true for $\dot{C}_{I,z}(y,0)$. Merely, $\dot{p}(y|0)$ can be computed directly by evaluating (11), yielding

$$\begin{aligned} \dot{p}(y|0) = \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y-\nu _{j,y},0\right] p(y-\nu _{j,y}|0), \end{aligned}$$

(37)

with $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y\!-\!\nu _{j,y},0\right]$ defined according to (13). Fortunately, $\dot{p}(y|0)$ only depends on states with non-zero marginal probabilities for which $\mathbb E _{z}\left. \left[ h_{j}(Z)\right| y\!-\!\nu _{j,y},0\right]$ is known.

To determine $\mu _{i,z}(y|0), \dot{\mu }_{i,z}(y,0), C_{I,z}(y|0)$, and $\dot{C}_{I,z}(y,0)$, we employ derivatives of the evolution equations (16) and (22). The differentiation order depends on the system structure, the state $y$, and the initial condition $p(y,z|0)$. In Appendix E (Proposition 5) we show that the $(K_y-1)$-th derivative of the evolution equations (16) and (22), with

$$\begin{aligned} \forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0 \quad \hbox {and} \quad \partial _{t}^{K_y}p(y|0) \ne 0, \end{aligned}$$

(38)

is necessary to determine $\mu _{i,z}(y|0)$ and $C_{I,z}(y|0)$. To assess $\dot{\mu }_{i,z}(y,0)$ and $\dot{C}_{I,z}(y,0)$, we need the $K_y$-th derivative. In favor of readability we skip the precise formulae for the initial conditional moments and their derivatives. Therefore we refer to Appendix E, which provides the detailed derivation.

Note that from (38) it follows that $K_y$ is the minimal number of reactions which have to take place to reach state $y$ from a state $\tilde{y}$ with $p(\tilde{y}|0)>0$. If there does not exist a reaction path with non-zero probability which leads from a state $\tilde{y}$ with $p(\tilde{y}|0)$ to $y, K_y$ does not exist as all derivatives of the marginal probability $p(y|t)$ are zero. Thus, for certain tuples of systems and initial conditions, the initial condition of the conditional moment equations remains partially undefined.

States $y$ with zero marginal probability for all $t$ do not influence and are not influenced by other states. Thus, these states $y$ can be eliminated from the system for the given initial condition. This represents an exact model reduction for this initial condition. We emphasize that for altered initial conditions the differentiation order $K_y$ has to be reevaluated and a reduction might not be possible.

4.2 Numerical simulation of DAE systems

Given consistent initial conditions, available DAE methods can be used to simulate the conditional moment equation. The most common methods rely on the Taylor series expansion (Pryce 1998) or on sophisticated, adaptive discretization schemes paired with solvers for nonlinear algebraic equations (Brown et al. 1994).

Taylor series based solvers employ the expansion of the DAE solution at each integration step (Nedialkov and Pryce 2007). Therefore, symbolic differentiation is employed. Existing solvers such as DAETS can handle “moderate stiffness well, but is unsuitable for highly stiff problems” (Nedialkov and Pryce 2007). Because of this stiffness constraint and the need for symbolic differentiation, we employed in this work the SUNDIALS toolbox IDAS (Hindmarsh et al. 2005) which employs variable-order, variable-coefficient backward differentiation formulas (Byrne and Hindmarsh 1975). The resulting nonlinear algebraic system is solved using Newton iterations, e.g., based on Krylov methods (Brown et al. 1994). The SUNDIALS toolbox IDAS (Hindmarsh et al. 2005) and the alternative implementation DASPK (Brown et al. 1994) have been assessed using a variety of nonlinear DAEs. They are applicable to stiff problems with arbitrary DAE index.

We emphasize that the combination of IDAS with a consistent initialization scheme allows for consistent numerical treatment and has advantages compared to the methods proposed by Menz et al. (2012) and Jahnke (2011). The formulation of the hybrid stochastic-deterministic model introduced by (Menz et al. (2012), Equation (3.46) and (3.47)) requires the division by $p(y|t)$. As this division is numerically unstable for $p(y|t) \approx 0$ and impossible for $p(y|t) = 0$, the authors instead divide by $p(y|t) + \delta$, with $\delta$ being a small positive number. This alters the dynamics as we illustrate in Appendix F for example (2). Also Jahnke (2011) chose an ODE formulation but circumvented the division by $p(y|t)$ using a dynamic state truncation. Merely the time evolution of states with $p(y|t) > \epsilon$ is considered, which generates the need for extrapolating the solution. While these methods provide good results for the example considered by Menz et al. (2012) and Jahnke (2011), we are not aware of general convergence results. Furthermore, the DAE solvers implemented in IDAS have been proven appropriate in many different situations and we show in the following section that they work well in situations where $p(y|t) \approx 0$ and $p(y|t) = 0$, and, for different truncation orders $m$. The regime $m \ge 2$ has not been entered by existing hybrid models.

5 Application examples: Stochastic gene expression

In the previous sections, we illustrated our theoretical findings using the gene expression model described by (2). In this section, we will compare the properties of the conditional moment equation with the moment equation and the hybrid model by Jahnke (2011) for this model using numerical simulations.

5.1 Model and scenarios

We consider two different scenarios:

• fast switching between DNA states, $\tau _{\mathrm{on}}= \tau _{\mathrm{off}}= 1 \, \text {h}^{-1}$, and

• slow switching between DNA states, $\tau _{\mathrm{on}}= \tau _{\mathrm{off}}= 0.05\, \text {h}^{-1}$.

For both scenarios we assume mRNA and proteins half-life times of roughly 45 min, thus $\gamma _{\mathrm{r}}= \gamma _{\mathrm{p}}= 1\, \hbox {h}^{-1}$. Furthermore, we choose $k_{\mathrm{r}}= 10\, \hbox {h}^{-1}, k_{\mathrm{p}}= 4\, \hbox {h}^{-1}$ and $\tau _{\mathrm{on}}^{\mathrm{p}}= 0.015\, \hbox {h}^{-1}$. This yields on average $\approx 7$ mRNAs and $\approx 25$ proteins in the stationary distribution. These parameters are within the biologically plausible range, see, e.g., (Munsky et al. 2012; Shahrezaei and Swain 2008; Taniguchi et al. 2010) and references therein.

To simulate the process for the two parameterizations,

• $\theta ^{(1)} = (1, 1, 10, 1, 4, 1, 0.015)$ (fast switching) and

• $\theta ^{(2)} = (0.05, 0.05, 10, 1, 4, 1, 0.015)$ (slow switching),

we employ the finite state projection (Munsky and Khammash 2006). As state space of the FSP we use

$$\begin{aligned} \varOmega _{\mathrm{FSP}}=\left\{ x \in \mathbb N ^4_0| x_1, x_2 \in \{0,1\} \wedge x_3 \in \{0,\ldots ,40\} \wedge x_4 \in \{0,\ldots ,200\} \right\} . \end{aligned}$$

For the initial conditions (34) we use in the remainder,

$$\begin{aligned} \xi _{\mathrm{off}}= 0.7, \, \lambda _{\mathrm{r},\mathrm{off}}= \lambda _{\mathrm{r},\mathrm{on}}= 4, \hbox {and} \, \lambda _{\mathrm{p},\mathrm{off}}= \lambda _{\mathrm{p},\mathrm{on}}= 10, \end{aligned}$$

the chosen state space $\varOmega _{\mathrm{FSP}}$ ensures a projection error $< 10^{-6}$ for $t \in [0,100]$ h. For our purposes, this error is negligible and the time interval is sufficiently long as for $t=100$ h the process almost reaches its steady state. We chose here the FSP instead of extensive Gillespie simulations, as for this system the FSP simulation is computationally more efficient.

Simulation results for $\theta ^{(1)}$ and $\theta ^{(2)}$ are shown in Fig. 3. While for $\theta ^{(1)}$, mRNA and proteins distributions in off- and on-state are alike, for $\theta ^{(2)}$ we observe a separation in state space. In the off-state, mRNA and protein numbers are low, while in the on-state mRNA and proteins numbers are relatively high. This yields bimodal distributions as discussed by Munsky et al. (2012) and experimentally observed by Gandhi et al. (2011). The qualitative differences observed for $\theta ^{(1)}$ and $\theta ^{(2)}$ render the parameter vectors suited for a comparison of hybrid models, the method of moments and the method of conditional moments. For this comparison we employ the low dispersion moment closure (MM and MCM) and $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}])$ (HM and MCM). While different hybrid models exist, we restrict ourself to the model introduced by Jahnke (2011), which is equivalent to the conditional moment equation of order $m = 1$.

Fig. 3

Probability distribution of mRNA and protein numbers for parameters $\theta ^{(1)}$ and $\theta ^{(2)}$. The contribution of the off-state (blue area) and the on-state (red area) to the overall distribution (solid black line) is color-coded. a For fast switching between DNA states, $\theta ^{(1)}$, the mRNA and protein distributions in off- and on-state are quite similar. b In case of slow switching rates, $\theta ^{(2)}$, the distributions associated to off- and on-state are different. In this case the number of mRNA and proteins found in the off-state are on average much smaller than those found in the on-state. a mRNA distribution and protein distribution for $\theta ^{(1)}$. Total probability distribution (solid black line), and conditional probability distributions in the on-state (red area) and in the off-state (blue area) are shown. b mRNA distribution and protein distribution for $\theta ^{(2)}$. Total probability distribution (solid black line), and conditional probability distributions in the on-state (red area) and in the off-state (blue area) are shown (color figure online)

For the simulation of the different models we employed sophisticated numerical solvers contained in the SUNDIALS package. The FSP and the moment equation are simulated using CVODES. For the hybrid model and the conditional moment equation we employed IDAS. Relative and absolute error tolerances are set to $10^{-6}$ to ensure small numerical errors. All other options are set to the default values.

5.2 DNA states as low-copy number species

In the first part of this example we consider only the DNA states, ${\hbox {D}}_{\mathrm{off}}$ and $\hbox {D}_{\mathrm{on}}$, as low copy number species, yielding $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}])$ and $z = ([\hbox {R}],[\hbox {P}])$. This is the case for which the conditional moment equations have been provided in the previous sections. For this setting we analyze the approximation quality and the convergence properties with respect to the truncation order $m$.

5.2.1 Comparison of hybrid model, moment equation (order 2) and conditional moment equation (order 2)

To assess the approximation properties of the different methods we study the short-time dynamics, $t \in [0,10]$, and the long-term dynamics, $t \in [90,100]$. For both time intervals, we compute the overall moments $\bar{\mu }_{i}(t)$ and ${\bar{C}}_{I}(t)$, whose evolution is described by the MM and which can also be evaluated using the HM and MCM using Proposition (4). To evaluate the variances and covariances ${\bar{C}}_{I}(t)$ for HM we employ the moment closure and set all second order centered moments to zero.

Figure 4 depicts the moments computed using the moment equation for $m = 2$, the hybrid model by Jahnke (2011), and the conditional moment equation for $m = 2$. As reference solution we plot the moments computed from the FSP solution, which are assumed to be exact. We find that for $\theta ^{(1)}$ all three methods provide a good description of the means. Concerning second order moments, here illustrated using the time-dependent 1-$\sigma$ interval (mean $\pm$ standard deviation), the MM and the MCM perform much better than the HM. In particular for mRNA and protein, the HM underestimates the variances significantly. This is a result of the moment closure for $m = 1$, which assumes the conditional variances in on- and off-state to be zero, a very rough approximation (Fig. 5a, b). The non-zero overall variance follows from (31) and is a result of the differences in the means of the on- and off-state.

Fig. 4

Time courses of the statistics of $p_{\mathrm{on}}, p_{\mathrm{off}}$, [R], and [P] computed using the finite state projection (grey solid line), the method of moments (green solid line), the hybrid stochastic-deterministic model proposed by Jahnke (2011) (red solid line), and the method of conditional moments (blue solid line). Solid lines provide mean and dashed lines indicate the 1-$\sigma$ interval (mean $\pm$ standard deviation). For the selected truncation level, the FSP error is $<10^{-6}$. Therefore, the mean and the 1-$\sigma$ interval (gray shading) computed from the FSP is employed as reference solution to evaluate the approximation quality of the other methods. Simulation results are depicted for a $\theta ^{(1)}$ and b $\theta ^{(2)}$. For $\theta ^{(1)}$ all methods perform well, providing a good approximation of the means. All variances are described well by the method of moments and the method of conditional moments while the hybrid method fails to describe the variance in [R] and [P]. For $\theta ^{(2)}$ the method of conditional moments outperforms the method of moments and the hybrid method in particular for $t \gg 1$. a Time-dependent means and 1-$\sigma$ intervals for $\theta ^{(1)}$. b Time-dependent means and 1-$\sigma$ intervals for $\theta ^{(2)}$ (color figure online)

Fig. 5

Joint probability of mRNA and protein numbers at time $t=5$ h conditioned on the DNA state. Probability distributions for parameters $\theta ^{(1)}$ in a off-state and b on-state exhibit a pronounced but similar correlation structure. For parameters $\theta ^{(2)}$ the correlation structure in c off-state and d on-state is also pronounced and depends strongly on the DNA state. a Conditional probability of mRNA and protein numbers in off-state for $\theta ^{(1)}$. b Conditional probability of mRNA and protein numbers in on-state for $\theta ^{(1)}$. c Conditional probability of mRNA and protein numbers in off-state for $\theta ^{(2)}$. d Conditional probability of mRNA and protein numbers in on-state for $\theta ^{(2)}$

For the slow switching scenario, $\theta ^{(2)}$, an accurate approximation is more difficult to achieve. The MM of order 2 and the HM fail to capture the long-term behavior of means and variances. The reason for the non-satisfying performance of the MM and the HM is the complex distribution arising from the CME for this parameterization. Figure 3b shows that the underlying distributions are multi-modal, posing severe problems for any moment closure scheme and thus limiting the accuracy of the MM. In addition, the correlation structures between mRNA and protein number is pronounced and different for the two DNA states (Fig. 5c, d), causing problems for the HM.

Both methods, the MM and the HM, are outperformed by the MCM for $\theta ^{(2)}$. The conditional moment equation can better resolve the structure of the solution, as it combines the discreteness of the DNA state, causing the bimodality, with information about moments of the high-copy species conditioned on the discrete states. This allows a better approximation of the overall distribution. In that respect, the conditional moment equation can also be interpreted as a sophisticated closure scheme.

Note that the improved approximation of the conditional moment equation compared to the moment equation can be achieved by a minor increase in the model size. Employing the conservation law for the DNA states, the moment equation of order 2 possesses 9 state variables (3 means, 3 variances and 3 covariances). The conditional moment equation of order 2 possesses 12 state variables (for each of the two discrete states 1 marginal probability, 2 means, 2 variances and 1 covariances). Hence, merely 3 states have to be added to achieve a better resolution of the distribution.

5.2.2 Convergence with respect to truncation order

As mentioned earlier, the conditional moment equation outperforms for $\theta ^{(2)}$ and $m = 2$ the other methods. However, for the overall moments, $\bar{\mu }_{i}(t)$ and ${\bar{C}}_{I}(t)$ (Fig. 4b), as well as for the conditional moments, $\mu _{i,z}(y,t)$ and $C_{I,z}(y,t)$, and the marginal probabilities, $p(y|t)$ (Fig. 6a) there are still significant discrepancies between the solution of the conditional moment equation and the FSP. The main sources of these discrepancies are the skewness of the distribution of mRNA and proteins number in the off-state (Fig. 3b) and the nonlinear correlation of mRNA and proteins number (Fig. 6b). These third and higher-order effects can already be described well with a conditional moment equation of order 3. Figure 6b shows that for $m=3$ the conditional moment method closely matches the FSP solution.

Fig. 6

Marginal probabilities and conditional moments computed using the method of conditional moments for parameters $\theta ^{(2)}$ with a truncation order $m = 2$ and b truncation order $m = 3$. For $m=2$ we find small errors in the trajectories of the marginal probabilities and the protein distributions. These errors significantly decrease for $m = 3$, indicating that the skewness of mRNA and protein distribution is non-negligible. a Marginal probabilities and conditional moments for $\theta ^{(2)}$ and truncation order $m = 2$. b Marginal probabilities and conditional moments for $\theta ^{(2)}$ and truncation order $m = 3$

To evaluate the convergence with respect to the truncation order $m$ more carefully we evaluate the relative error of the means,

$$\begin{aligned} e_{\mu }^{\mathrm{MCM}}(T) = \sum _{i=1}^n \left| \frac{\bar{\mu }_{i}^{\mathrm{MCM}}(T)-\bar{\mu }_{i}^{\mathrm{FSP}}(T)}{\bar{\mu }_{i}^{\mathrm{FSP}}(T)}\right| , \end{aligned}$$

and of the variances and covariances,

$$\begin{aligned} e_{C,2}^{\mathrm{MCM}}(T) = \sum _{i_1=1}^n \sum _{i_2=1}^{i_1} \left| \frac{{\bar{C}}_{e_{i_1}+e_{i_2}}^{\mathrm{MCM}}(T)-{\bar{C}}_{e_{i_1}+e_{i_2}}^{\mathrm{FSP}}(T)}{{\bar{C}}_{e_{i_1}+e_{i_2}}^{\mathrm{FSP}}(T)}\right| , \end{aligned}$$

for $T = 100$ h. $\bar{\mu }_{i}^{\mathrm{MCM}}(T)$ (${\bar{C}}_{e_{i_1}+e_{i_2}}^{\mathrm{MCM}}(T)$) and $\bar{\mu }_{i}^{\mathrm{FSP}}(T)$ (${\bar{C}}_{e_{i_1}+e_{i_2}}^{\mathrm{FSP}}(T)$) denote the means (variances) at time $T$ determined using the MCM and the FSP, respectively. The same errors, namely $e_{\mu }^{\mathrm{MM}}(T)$ and $e_{C,2}^{\mathrm{MM}}(T)$, can of course be defined for the MM.

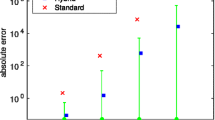
The error measures $e_{\mu }(T)$ and $e_{C,2}(T)$ allow for a quantitative assessment of the approximation performances for large times. Figure 7 depicts $e_{\mu }(T)$ and $e_{C,2}(T)$ for the moment equations and the conditional moment equations with truncation orders $m \in \{1,\ldots ,6\}$, for $\theta ^{(2)}$. Apparently, the error in the first and second order moments strongly depends on the truncation order $m$. The error in the mean, $e_{\mu }(T)$, for the hybrid stochastic-deterministic model (MCM with $m=1$) is roughly twice the error for the MCM with $m=2$, and roughly six times the error for the MCM with $m=3$. Furthermore, for all truncation orders $m$, the MCM outperforms the MM. The error $e_{\mu }(T)$ for $m = 1$ is 1.5 times smaller and the error decreases more rapidly for increasing moment orders $m$. For the moment equation the error decreases exponentially with an exponent of $\approx -0.1$, whereas for the conditional moment equation the exponent is $\approx -0.55$. Comparing MM and MCM, we find that even for $m = 6$, the error for the MM is approximately 0.1, a level which we reach with the MCM already for $m = 2$.

Fig. 7

Relative errors in means and second order central moments computed using the method of moments (green), the hybrid stochastic-deterministic model proposed by Jahnke (2011) (red), and the method of conditional moments (blue). The relative errors $e_{\mu }(T)$ and $e_{C,2}(T)$ are shown for parameters $\theta ^{(2)}$ and for $T = 100$ h, a time point at which the state of the system is numerically indistinguishable from the steady state. As the HM is a special case of the MCM for the considered selection of $Y_t$ and $Z_t$, the relative error can be reduced by increasing the truncation order $m$. Compared to the MM, the MCM has a smaller offset at $m = 1$ and a steeper slope ($\hbox {MM} \,\approx -0.1$; $\hbox {MCM}\,\approx -0.55$). In log-scale the approximation quality of means and second order central moments shows a similar behavior, but differs roughly by a factor of 6 (color figure online)

The errors in the variances and covariances, $e_{C,2}^{\mathrm{MCM}}(T)$ behave similar to the errors in the means $e_{\mu }(T)$. An increase of $m$ results in a decrease of the error, and, MCM outperforms the MM by far. The key difference is that the improvement when going from hybrid stochastic-deterministic model (MCM with $m=1$) to the MCM with $m=2$ is more pronounced. This more significant improvement is expected as for $m=1$ the variances and covariances are merely computed from the means of the individual low-copy number states (mixture of delta-distributions), while for $m=2$ the model also accounts for the variance within the low-copy number states.

The size of the moment equation and the conditional moment equation for different truncation orders $m$ is shown in Table 2. For $m < 4$ the moment equations has fewer states than the conditional moment equation, however, this turns around for $m \ge 4$. If we assume that the cardinality of the set of low-copy number states is finite it can actually be shown that there exists a truncation level above which the moment equation has more states than the conditional moment equation. This is due to the faster growth of the number of moments in the MM compared to the MCM. Apparently, for low truncation orders $m$, the moment equation will always posses fewer states than the conditional moment equation.

Table 2 Number of state variables of the moment equation and the conditional moment equation for different truncation orders $m$ for the 3-stage gene expression example, with DNA states as low-copy number species

5.3 DNA states and mRNA as low-copy number species

The treatment of the DNA states as low-copy number species allows for the assessment of the statistics of mRNA and protein numbers, however, the precise distribution remains hidden. For this reason, we consider now in addition to ${\hbox {D}}_{\mathrm{off}}$ and $\hbox {D}_{\mathrm{on}}$ also the mRNA, $\hbox {R}$, as low-copy number species. This is in particular interesting because the mean mRNA number is low ($\approx 7$). Furthermore, for $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}],[\hbox {R}])$ and $z = [\hbox {P}]$ the set of low-copy number states is no longer finite. Hence, the numerics of the DAE can be assessed for $p(y|t) \approx 0$.

In the following we consider only scenario 2 (slow switching, $\theta ^{(2)}$) as for this case the dynamics of the system are more involved and the probability distributions are more complex. Similar to the CME, we use a finite state projection for the conditional moment equation with

$$\begin{aligned} \varOmega _{\mathrm{MCM}}=\left\{ y \in \mathbb N ^3_0| y_1, y_2 \in \{0,1\} \wedge y_3 \in \{0,\ldots ,40\}\right\} \!. \end{aligned}$$

The marginal probabilities of states $y \notin \varOmega _{\mathrm{MCM}}$ are set to zero. For the simulation we employ as before the IDAS solver of the SUNDIALS package. Although the marginal probabilities $p(y|t)$ quickly approach zero for $y_3 > 20$—some marginal probabilities are actually below $10^{-25}$—the solver yields numerically stable results. Thus, approximations of the dynamical systems as proposed by Menz et al. (2012) are, at least for this example, not necessary. An assessment of different numerical schemes can be found in Appendix F.

Figures 8, 9, 10, 11 and 12 depict different aspects of the simulation results for the MCM, the approximation properties of the hybrid model by Jahnke (2011) (MCM with $m = 1$) and the MCM with $m = 2$. Figure 8 shows that both, the HM and the MCM with $m = 2$, yield visually similar results for the marginal probabilities of the mRNA numbers $p([\hbox {R}]|t)$. When comparing the marginal probabilities, $p_{\mathrm{HM}}([\hbox {R}]|t)$ and $p_{\mathrm{MCM}}([\hbox {R}]|t)$, with the marginal probabilities computed using the FSP, $p_{\mathrm{FSP}}([\hbox {R}]|t)$, we however find that the error of the HM,

$$\begin{aligned} \left| p_{\mathrm{HM}}([\hbox {R}]|t) - p_{\mathrm{FSP}}([\hbox {R}]|t)\right| , \end{aligned}$$

is much larger than the error of the MCM with $m = 2$,

$$\begin{aligned} \left| p_{\mathrm{MCM}}([\hbox {R}]|t) - p_{\mathrm{FSP}}([\hbox {R}]|t)\right| . \end{aligned}$$

This is shown in Fig. 9. Thus, taking the second-order moments of high-copy number species into account improves the approximation of the marginal probabilities of low-copy number states.

Fig. 8

Probability distribution of mRNA numbers for scenario 2, $\theta ^{(2)}$, computed using a the HM by Jahnke (2011) and b the MCM with $m=2$. The contribution of the off-state (blue area) and the on-state (red area) to the overall distribution (black solid line) is color-coded. a HM by Jahnke (2011) (MCM with $m=1$). b MCM with $m=2$ (color figure online)

Fig. 9

Error of the marginal probabilities for scenario 2, $\theta ^{(2)}$, computed using a the HM by Jahnke (2011) and b the MCM with $m=2$. The error is evaluated with respect to the FSP solution of the CME, which is assumed to be exact. The individual lines represent the errors in the marginal probabilities in the off-state (blue solid line), in the on-state (red solid line), and in the overall marginal probabilities (solid line). a HM by Jahnke (2011) (MCM with $m=1$). b MCM with $m=2$ (color figure online)

Fig. 10

Conditional mean of protein number for scenario 2, $\theta ^{(2)}$, computed using a the HM by Jahnke (2011) and b the MCM with $m=2$. The individual lines represent the conditional means in the off-state (blue solid line), in the on-state (red solid line), and the overall conditional mean (black solid line). a HM by Jahnke (2011) (MCM with $m=1$). b MCM with $m=2$ (color figure online)

Fig. 11

Error of the conditional mean of protein number for scenario 2, $\theta ^{(2)}$, computed using a the HM by Jahnke (2011) and b the MCM with $m=2$. As ground truth we considered the solution of the FSP of the CME. The individual lines represent the errors in the conditional means in the off-state (blue solid line), in the on-state (red solid line), and in the overall marginal probabilities (black solid line). a HM by Jahnke (2011) (MCM with $m=1$). b MCM with $m=2$ (color figure online)

Fig. 12

Mean and variance of the protein abundance for different DNA states, mRNA numbers, and time points computed using the MCM with truncation order $m = 2$. a Conditional moments of protein number for the different low-copy number states at time $t = 5$. b Time-dependence of conditional moments of protein number in off-state and on-state for the stationary mean of the mRNA number, $[\hbox {R}] = 7$. The solid lines show the mean concentration, and the dashed lines correspond to 1-$\sigma$ intervals (mean $\pm$ standard deviation). Gray shaded area represents the 1-$\sigma$ intervals according to FSP simulation. The conditional moments for the off-state (left, blue) and on-state (right, red) are plotted individually. a Mean and variance of protein number for different mRNA numbers in off-state (left) and on-state (right) at $t = 5$ h. b Time-dependent mean and variance of protein number for mRNA number $[\hbox {R}] = 7$ in off-state (left) and on-state (right) (color figure online)

The analysis of the mean protein number for a given mRNA number establishes a similar picture. The simulation results for HM and MCM with $m = 2$ are shown in Fig. 10a, b, respectively. A visual assessment reveals no obvious differences between both simulations. The evaluation of the error with respect to the FSP simulation same definition as above shows however that the error for the HM (Fig. 11a) is more than one order of magnitude larger than the error for the MCM with $m = 2$ (Fig. 11b).

In addition to the accurate approximation of the marginal probabilities and the conditional mean of the protein number, the MCM with $m=2$ also provides an accurate approximation of the conditional variances of the protein number. This is shown in Fig. 12, which depicts mean and 1-$\sigma$ interval of the protein numbers, $[\hbox {P}]$, in off- and on-state for (a) different mRNA numbers at time $t = 5$ h and (b) the mean mRNA number in the steady state ($[\hbox {R}] = 7$) at different time points. The gray shaded areas represent values computed using the FSP, while the lines represent the results for the MCM with $m = 2$. As shown earlier in Figs. 8, 9, 10, and 11, already the hybrid method provides a reasonable approximation of the mean, however, the variances are underestimated (results not shown) and the consideration of the variances improves the result further.

Beyond the comparison of HM and MCM with $m=2$, we also studied the distribution of mRNA and protein numbers. The most surprising finding was that the conditional mean of the protein number for a given mRNA number is higher in the off-state than in the on-state, $\forall [\hbox {R}]: \mu _{\mathrm{p},\mathrm{off}}([\hbox {R}],t) \ge \mu _{\mathrm{p},\mathrm{on}}([\hbox {R}],t)$ (Fig. 10). We actually expected a higher-conditional mean in the on-state, as observed in Fig. 6 for $\mu _{\mathrm{p},\mathrm{off}}(t)$ and $\mu _{\mathrm{p},\mathrm{on}}(t)$. This expectation is not met because when a transition from the on-state to the off-state occurs the mRNA synthesis is switched off but the high protein numbers are still likely even for states with low mRNA values. On the other hand, a transition from the off-state to the on-state causes an mRNA number increase but the protein number might still be low. Both phenomena are due to the delay between changes in the mRNA number and changes in the protein number. Marginalizing over the mRNA number, we find here that $\mu _{\mathrm{p},\mathrm{off}}(t) \le \mu _{\mathrm{p},\mathrm{on}}(t)$ because the marginal probability distributions of off- and on-states are different, resulting in a different weighting of $\mu _{\mathrm{p},\mathrm{off}}([\hbox {R}],t)$ and $\mu _{\mathrm{p},\mathrm{on}}([\hbox {R}],t)$, respectively.

To summarize the example, the MCM can improve upon the MM and the HM if the probability distribution possesses a complex shape. To achieve this improvement, the MCM requires often more states. For low truncation orders $m$ the MM has the smallest number of states, followed by the HM and the MCM. All three models have in general fewer states than the CME.

6 Summary and conclusion

In this paper we introduced the method of conditional moments. The MCM provides an approximation of the statistics (mean, variances and higher-order centered moments) of the solution of the CME based on a hybrid modeling framework. Low-copy number species are modeled as discrete stochastic entities, whereas the distribution of medium/high-copy number species is modeled using statistical moments. The conditional moment equation shares many properties with the moment equation and with similar equations for hybrid stochastic-deterministic models. Indeed, we proved that it generalizes the moment equation (Engblom 2006; Lee et al. 2009) and hybrid stochastic-deterministic methods (Jahnke 2011; Menz et al. 2012). Due to its generality, the conditional moment equation overcomes shortcomings of these previous methods. In particular it allows for the accurate statistical modeling of multi-modal distributions with complex correlation structures. This is illustrated using a model of stochastic gene expression which exhibits a bimodal distribution. In future work this has to be assessed for multi-attractor models (Strasser et al. 2012).

In addition to the better approximation of multi-modal distributions, the approximation of marginal probabilities and conditional moments is often improved compared to standard methods. This is achieved by introducing higher-order moments, however, these higher-order moments are more than auxiliary variables. There are many biological applications in which not only the mean but also the population heterogeneity is of interest [see, e.g., (Munsky et al. 2012, 2009; Zechner et al. 2012) and references therein]. In these manuscripts the authors show that information about higher-order moments are often helpful or even necessary to infer the parameters and/or the structure of stochastic biochemical processes.

In this manuscript we formulated the MCM for reactions with zero, one, or two educts whose reaction propensities follow the law of mass action. The restriction to this class of reactions and reaction propensities can probably be relaxed, e.g., by avoiding the assumption that the propensities can be separated, $a_j(Y_t,Z_t)= c_j g_{j}(Y_t) h_{j}(Z_t)$. The problem of generalizing the MCM has to be approached in future work.

The conditional moment equation is, like the moment equation, not closed if the reaction system contains nonlinear propensity functions. For this case we propose the low dispersion moment closure, which is easily applied as we formulated the conditional moment equation in terms of conditional means and higher-order centered conditional moments. In the future we are going to study more sophisticated closure methods based upon the log-normality assumption (Singh and Hespanha 2006) or derivative matching (Singh and Hespanha 2011). This is necessary as the approximation properties of the MCM strongly depend on the appropriateness of the moment closure schemes. An unfortunate choice can actually cause the divergence of the conditional moment equation, as it is also the case for the moment equation (Singh and Hespanha 2011). Beyond the evaluation of different moment closures, we will evaluate the convergence properties for increasing truncation order $m$.

The closed version of the conditional moment equation is a DAE system, whose initial conditions cannot be determined easily. In this paper we introduce a scheme for the consistent initialization of this DAE, which can also be used for the hybrid models introduced by Jahnke (2011). Furthermore, we discuss different solution schemes for the resulting DAE. We remark that this numerical scheme cannot be directly applied to the hybrid model by Menz et al. (2012), which is formulated in terms of partial moments. However, we think that the formulation in terms of the conditional moments is nevertheless favorable. This formulation does, in contrast to the formulation by Menz et al. (2012), not require the division by $p(y|t)$, and hence no substitution of $p(y|t)$ by $p(y|t)+\delta , \delta \in \mathbb R _+$ with $\delta \ll 1$, which clearly alters the solution as we show in Appendix F, is necessary for the numerical simulation.

An important question for the application of any hybrid modeling approach is clearly how the species should be assigned to the different groups. Unfortunately, this question is difficult and the answer has to be expected to be highly problem-specific. Our example revealed that even the distribution of species with in average seven copies, the mRNA, can be modelled successfully using conditional moments. This will however not hold in general. To ensure a certain approximation accuracy a priori or a posteriori error estimators would be necessary. For the product approximation and the Hellander-Lötstedt model a posteriori error estimators already exist (Jahnke 2011), and a generalization to hybrid models would be of general interest. Besides the verification of a certain approximation quality, an error estimator would enable the development of guaranteed parameter estimation and optimization methods (Hasenauer et al. 2012).

Even though no error estimates exist, hybrid models and moment equations have been proven to be valuable tools for parameter estimation of stochastic processes. Milner et al. (2012) and Zechner et al. (2012) showed recently that parameters of stochastic processes can be inferred using the moment equation. For hybrid systems the same has been shown by Mikeev and Wolf (2012). As the MCM allows for a better description of stochastic dynamics than the HM and the MM, also parameter estimation methods employing the conditional moment equation are promising. The resulting parameter estimates are potentially more precise, as the model is closer to the CME, and allows for the consideration of discrete copy-number information for low abundance species. By extending the MCM to allow for parameter variability, similar to (Hasenauer et al. 2011a, b; Koeppl et al. 2012; Zechner et al. 2012), also the parameter estimation procedures for heterogeneous cell populations can be improved.

Summing up, the method of conditional moments that we introduced in this manuscript provides a unifying framework for the approximation of the Chemical Master Equation. Due to its generality the MCM is of great interest in several fields beyond mathematical, computational and systems biology and for a variety of applications.

Appendices

Appendix A: Proof of Lemma 1

The differentiation of $\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)$ results in

$$\begin{aligned} \frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) = \sum _{z\ge 0}T(z,t) \frac{\partial }{\partial t} p(y,z|t) + \sum _{z\ge 0} p(y,z|t) \frac{\partial }{\partial t} T(z,t), \end{aligned}$$

which we reformulate as

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad \!=\!\sum _{z\ge 0}T(z,t) \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+}\\ z \!\ge \! \nu _{j,z}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) h_{j}(z\!-\!\nu _{j,z}) p(z\!-\!\nu _{j,z}|y-\nu _{j,y},t) p(y-\nu _{j,y}|t)\nonumber \\&\quad - \sum _{z\ge 0}T(z,t) \sum _{j=1}^{n_{r}} c_j g_{j}(y) h_{j}(z) p(z|y,t) p(y|t)+ p(y|t) \sum _{z\ge 0} p(z|y,t) \frac{\partial }{\partial t} T(z,t) \end{aligned}$$

by substitution of $\frac{\partial }{\partial t} p(y,z|t)$ with (9) and the use of the multiplication axiom (3). Next we change the order of summation and substituting in the first sum $z \rightarrow z + \nu _{j,z}$, yielding

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \sum _{z \ge \nu _{j,z}^-} T(z+\nu _{j,z},t) h_{j}(z) p(z|y-\nu _{j,y},t) p(y-\nu _{j,y}|t) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \sum _{z \ge 0} T(z,t) h_{j}(z) p(z|y,t) p(y|t) + p(y|t) \sum _{z\ge 0} p(z|y,t) \frac{\partial }{\partial t} T(z,t) \end{aligned}$$

This equation can be reformulated further by exploiting the fact that the CME is proper, meaning that $h_{j}(z) = 0$ whenever $z \ngeq \nu _{j,z}^-$. Accordingly, the limit of the first summation over $z, z \ge \nu _{j,z}^-$, can be set to zero, $z \ge 0$. Using the definition of the conditional expectation (8) we obtain (10) which concludes the proof. $\square$

Note that the manipulations of infinite sums are allowed under absolute convergence, which holds for any test-function $T(z,t)$ which is polynomial in $z$ if for all $t$ sufficiently many moments of $p(y,z|t)$ with respect to $z$ exist (Engblom 2006). Note that Lemma 1 is a generalization of a result by Engblom (2006, Lemma 2.1).

Appendix B: Proof of Proposition 2

We consider the conditional mean weighted by the corresponding probability, $\mu _{i,z}(y,t) p(y|t) = \sum _{z \ge 0} z_i p(y,z|t)$. By differentiating this product with respect to $t$ we readily obtain

$$\begin{aligned} p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t) = \frac{\partial }{\partial t} \left( \mu _{i,z}(y,t) p(y|t)\right) - \mu _{i,z}(y,t) \frac{\partial }{\partial t} p(y|t). \end{aligned}$$

(39)

The unknown derivative $\frac{\partial }{\partial t} \left( \mu _{i,z}(y,t) p(y|t)\right)$ follows from Lemma 1 by choosing the test function $T(Z,t) = Z_i$,

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \mu _{i,z}(y,t) p(y|t)\right) \nonumber \\&\quad = \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right] p(y|t). \end{aligned}$$

(40)

This derivative depends on $\mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right]$ and $\mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right]$. By adding and subtracting the conditional means we can reformulate these conditional expectations to

$$\begin{aligned} \mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right]&= \mathbb E _{z}\left. \left[ (Z_i - \mu _{i,z}(y,t) + \mu _{i,z}(y,t)) h_{j}(Z)\right| y,t\right] \nonumber \\&= \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y,t))^{e_i} h_{j}(Z)\right| y,t\right] \nonumber \\&+ \mu _{i,z}(y,t) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] \end{aligned}$$

(41)

and

$$\begin{aligned}&\mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right] \nonumber \\&\quad = \mathbb E _{z}\left. \left[ (Z_i- \mu _{i,z}(y-\nu _{j,y},t) + \mu _{i,z}(y-\nu _{j,y},t)+\nu _{ij,z}) h_{j}(Z)\right| y - \nu _{j,y},t\right] \nonumber \\&\quad = \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y-\nu _{j,y},t))^{e_i} h_{j}(Z)\right| y - \nu _{j,y},t\right] \nonumber \\&\qquad + (\mu _{i,z}(y-\nu _{j,y},t)+\nu _{ij,z}) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y - \nu _{j,y},t\right] . \end{aligned}$$

(42)

Substitution of these reformulated conditional expectations into (40) followed by the insertion of (40) into (39) yields the evolution equation for the conditional mean (16), which concludes the proof of Proposition 2. $\square$

Appendix C: Proof of Proposition 3

We consider the product $C_{I,z}(y,t) p(y|t)$ and differentiate it with respect to time, which readily yields

$$\begin{aligned} p(y|t) \frac{\partial }{\partial t} C_{I,z}(y,t) = \frac{\partial }{\partial t} \left( C_{I,z}(y,t) p(y|t)\right) - C_{I,z}(y,t) \frac{\partial }{\partial t} p(y|t). \end{aligned}$$

(43)

Using Lemma 1 with $T(Z,t) = (Z-\mu _{z}(y,t))^I$, we obtain

$$\begin{aligned}&\frac{\partial }{\partial t}\left( C_{I,z}(y,t) p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z\!+\!\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] p(y|t)\nonumber \\&\qquad - \sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^{I-e_i}\right| y,t\right] p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t), \end{aligned}$$

(44)

where the third sum corresponds to the term $\mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] p(y|t)$ in (10) and

$$\begin{aligned} \forall i \in \{1,\ldots ,{n_{s,z}}\} \hbox { with } I_i \ge 1: \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^{I-e_i}\right| y,t\right] = C_{I-e_i,z}(y,t).\qquad \end{aligned}$$

(45)

After substituting (43) and (45) into (44), it remains for us to prove that (23) holds. Therefore, we add and subtract $\mu _{z}(y-\nu _{j,y},t)$ in $(Z+\nu _{j,z}-\mu _{z}(y-\nu _{j,y},t))^I$ and apply the multinomial theorem, yielding

$$\begin{aligned}&(Z+\nu _{j,z}-\mu _{z}(y,t))^I \nonumber \\&\quad = (Z-\mu _{z}(y-\nu _{j,y},t)+\mu _{z}(y-\nu _{j,y},t)-\mu _{z}(y,t)+\nu _{j,z})^I\nonumber \\&\quad = \sum _{0 \le k \le I} \begin{pmatrix} I \\ k \end{pmatrix} \left( \mu _{z}(y-\nu _{j,y},t)-\mu _{z}(y,t)+\nu _{j,z}\right) ^{I-k} (Z-\mu _{z}(y-\nu _{j,y},t))^{k}, \nonumber \\ \end{aligned}$$

(46)

where the summation runs over all vectors $k \in \mathbb N _0^{n_{s,z}}$ for which $k_i \in [0,I_i]$ for all $i$. By substituting (46) into $\mathbb E _{z}\left. \left[ (Z+\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right]$ and employing that the expectation of a sum is the sum of the expectations, we arrive at (23), which concludes the proof. $\square$

Appendix D: Proof of Proposition 4

For $i \in \{1,{n_{s,y}}\}$ Eq. (29) states merely the definition of the mean. The result for ${n_{s,y}} < i \le {n_{s}}$ follows from

$$\begin{aligned} \bar{\mu }_i(t) = \sum _{y\ge 0} \sum _{z\ge 0} z_{j} p(y,z|t) = \sum _{y\ge 0} \underbrace{\sum _{z\ge 0} z_{j} p(z|y,t)}_{\displaystyle = \mu _{j,z}(y,t)} p(y|t), \hbox { with } j = i-{n_{s,y}}, \end{aligned}$$

which concludes the proof of (29). The result for the centered moment ${\bar{C}}_{I}(t)$ is obtained by a reordering of the sums and the application of the multiplication axiom (3):

$$\begin{aligned} {\bar{C}}_{I}(t)&= \sum _{y\ge 0} \sum _{z\ge 0} (y - \bar{\mu }_{y}(t))^{I_y} (z - \bar{\mu }_{z}(t))^{I_z} p(y,z|t) \\&= \sum _{y\ge 0} (y - \bar{\mu }_{y}(t))^{I_y} \sum _{z\ge 0} (z - \bar{\mu }_{z}(t))^{I_z} p(z|y,t)p(y|t). \end{aligned}$$

In order to arrive at the term $(z - \mu _{z}(y,t))^{I_z}$, we add and subtract $\mu _{z}(y,t)$. This yields $(z - \mu _{z}(y,t) + \mu _{z}(y,t) - \bar{\mu }_{z}(t))^{I_z}$ and reformulation in terms of $(\mu _{z}(y,t)- \bar{\mu }_z(t))$ and $(z - \mu _{z}(y,t))$ using the multinomial theorem gives

$$\begin{aligned} {\bar{C}}_{I}(t)&= \sum _{y \ge 0}{(y - {\bar{\mu }}_{y}(t))}^{I_y} \sum _{z \ge 0} \sum _{0 \le k \le I_z} \begin{pmatrix} I_z \\ k \end{pmatrix} (\mu _{z}(y,t)\nonumber \\&- {{\bar{\mu }}_z(t))}^{I_z-k} \cdot (z - \mu _{z}(y,t))^{k} p(z|y,t)p(y|t). \end{aligned}$$

Finally, we exchange the two inner sums and substitute $\sum _{z\ge 0} (z - \mu _{z}(y,t))^{k} p(z|y,t)$ by $C_{k,z}(y,t)$. The modified equation for ${\bar{C}}_{I}(t)$ becomes (30) which concludes the proof. $\square$

Appendix E: Initial conditions for states $y$ with $p(y|0) = 0$

Proposition 5

Given an initial distribution $p(y,z|0)$, a state $y$ with $p(y|0) = 0$, and the differentiation index $K_y$ with $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$ and $\partial _{t}^{K_y}p(y|0) \ne 0$, the initial conditional moments for (24) are

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) \mu _{i,z}(y,0) \nonumber \\&\quad = \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}}\left( \mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0} \nonumber \\ \end{aligned}$$

(47)

and

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) C_{I,z}(y,0) \nonumber \\&\quad \!=\!\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^+ \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}}\left( \mathbb E _{z}\left. \left[ (Z + \nu _{j,z}\!-\! \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y\!-\!\nu _{j,y}|t)\right) \right| _{t=0},\nonumber \\ \end{aligned}$$

(48)

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{\mu }_{i,z}(y,0) + \partial _{t}^{K_y+1}p(y|0) \mu _{i,z}(y,0) \nonumber \\&\quad ={\mathop {\mathop {\mathop {\sum }\limits _{j=1}}\limits _{y \ge \nu _{j,y}^{+}}}\limits ^{n_{r}}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ Z^{e_i} h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0), \end{aligned}$$

(49)

and

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{C}_{I,z}(y,0) + \partial _{t}^{K_y+1}p(y|0) C_{I,z}(y,0)\nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ (Z \!+\! \nu _{j,z}- \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,0))^{I} h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0)\nonumber \\&\qquad - \sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i C_{I-e_i,z}(y,0) \dot{\mu }_{i,z}(y,0) \partial _{t}^{K_y}p(y|0). \end{aligned}$$

(50)

Proof

To prove Proposition 5, we consider a general test function $T(Z,t)$ and its conditional expectation $\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right]$. It can be shown using Leibniz rule that for any $L \in \mathbb N$,

$$\begin{aligned} \frac{\partial ^{L}}{\partial t^{L}}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) = \sum _{k=0}^L \begin{pmatrix} L \\ k \end{pmatrix} \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) \left( \frac{\partial ^{L-k}}{\partial t^{L-k}}\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] \right) . \nonumber \\ \end{aligned}$$

(51)

Furthermore, by applying the differentiation operator $\frac{\partial ^{L-1}}{\partial t^{L-1}}$ to (10) it follows from Lemma 1 that

$$\begin{aligned}&\frac{\partial ^L}{\partial t^L}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \frac{\partial ^{L-1}}{\partial t^{L-1}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \frac{\partial ^{L-1}}{\partial t^{L-1}}\left( \mathbb E _{z}\left. \left[ T(Z,t) h_{j}(Z)\right| y,t\right] p(y|t)\right) \nonumber \\&\qquad + \frac{\partial ^{L-1}}{\partial t^{L-1}}\left( \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] p(y|t)\right) . \end{aligned}$$

Using the general Leibniz rule this equation can be reformulated to

$$\begin{aligned}&\frac{\partial ^L}{\partial t^L}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \frac{\partial ^{L-1}}{\partial t^{L-1}} \left( \mathbb E _{z}\left. \left[ T(Z\!+\!\nu _{j,z},t) h_{j}(Z)\right| y\!-\!\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \sum _{k=0}^{L-1} \begin{pmatrix} L-1 \\ k \end{pmatrix} \left( \frac{\partial ^{L-k-1}}{\partial t^{L-k-1}} \mathbb E _{z}\left. \left[ T(Z,t) h_{j}(Z)\right| y,t\right] \right) \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) \nonumber \\&\qquad + \sum _{k=0}^{L-1} \begin{pmatrix} L-1 \\ k \end{pmatrix} \left( \frac{\partial ^{L-k-1}}{\partial t^{L-k-1}} \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] \right) \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) . \end{aligned}$$

(52)

By evaluating (51) and (52) at $t = 0$ for $L = K_y$ and employing that $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$ we obtain

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) \mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right] \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}. \nonumber \\ \end{aligned}$$

(53)

As $\partial _{t}^{K_y}p(y|t)$ is non-zero, (53) defines the initial values $\mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right]$. The Eqs. (47) and (48) for the initial conditions $\mu _{i,z}(y,0)$ and $C_{I,z}(y,0)$ follow for $T(Z,t) = Z_i$ and $T(Z,t) = (Z - \mu _{z}(y,t))^I$, respectively.

To derive equations for the initial derivatives $\dot{\mu }_{i,z}(y,0)$ and $\dot{C}_{I,z}(y,0)$ we evaluate (51) and (52) at $t = 0$ for $L = K_y+1$. Employing $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$, this yields

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{\mathbb{E }}_{z}\left. \left[ T(Z,0)\right| y,0\right] + \partial _{t}^{K_y+1}p(y|0) \mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right] \nonumber \\&\quad ={\mathop {\mathop {\sum }\limits _{j=1}}\limits _{y \ge \nu _{j,y}^{+}}^{n_{r}}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0} \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ T(Z,0) h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0) \nonumber \\&\qquad + \left. \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,0)\right| y,t\right] \right| _{t=0} \partial _{t}^{K_y}p(y|0). \end{aligned}$$

(54)

As $\partial _{t}^{K_y}p(y|t)$ is non-zero, (54) defines the initial derivative $\dot{\mathbb{E }}_{z}\left. \left[ T(Z,0)\right| y,0\right]$. Thus, by selecting $T(Z,t) = Z_i$ we obtain (49) which allows for the calculation of $\dot{\mu }_{i,z}(y,0)$. To obtain (50), we finally choose $T(Z,t) = (Z - \mu _{z}(y,t))^I$.

To determine the initial values using (47)-(50) we evaluate the $(K_y-1)$-th derivatives of $\mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)$ and $\mathbb E _{z}\left. \left[ (Z + \nu _{j,z}- \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)$ at $t=0$. Therefore, we merely employ (52) with the appropriate test function $T(Z,t), L = K_y-1$, and the substitution $y \rightarrow y-\nu _{j,y}$. The resulting derivatives are replaced using the same approach and all other conditional expectations are expressed in terms of centered moments using a Taylor series representation similar to (17). While the resulting equation is extremely lengthy, and therefore not stated here, it is straight forward to construct them for any problem using a simple recursion. Employing the structure of (52), it can be shown that the derivatives merely depend on the marginal probabilities and the initial conditional moments of states $\tilde{y}$ with $p(\tilde{y}|0) > 0$. These conditional moments can be computed directly from $p(y,z|0)$, hence, the right-hand sides of (47)–(50) can be evaluated which concludes the proof. $\square$

Some numerical schemes, e.g., DAE solvers based on Taylor series methods, might require higher-order derivatives at the initial time point. These higher-order derivatives can also be constructed using the results of Proposition 5. Therefore, one merely employs (52) with the required order $L$.

Appendix F: Comparison of DAE and approximative ODE formulation of the conditional moment equation

The conditional moment equation is a DAE, $M(\xi ) \dot{\xi } = F(\xi )$, with the state vector $\xi \in \mathbb R ^{n_{\xi }}$ and mass matrix $M(\xi ) \in \mathbb R ^{{n_{\xi }}\times {n_{\xi }}}$. The state vector contains the marginal probabilities, the conditional means and higher-order conditional moments (for $m\ge 2$). The class of DAEs is more general than the class of ODEs, $\dot{\xi } = f(\xi )$. Only if $M(\xi )$ is invertible for all $\xi$ the DAE can be reformulated to an ODE, namely $f(\xi ) = M^{-1}(\xi )F(\xi )$. This invertibility is not ensured for the conditional moment equation. Thus, the conditional moment equation is not an ODE and can also not be simply restated as one.

Different approaches exist to approximate DAEs with ODEs. The most common approximation is probably $\dot{\xi } = (M(\xi ) + \delta I)^{-1}F(\xi )$ where $I$ is the identity matrix. The constant $\delta \in \mathbb R _+$ should be as small as possible to achieve a good approximation, but large enough to ensure invertibility. Clearly, even for small $\delta$, the ODE solution is merely an approximation of the DAE solution. To illustrate this we depict in Fig. 13 the error of different methods for the three-stage gene expression model with $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}],[\hbox {R}])$ and $z = [\hbox {P}]$ (see Sect. 5.3). The error is evaluated with respect to the FSP solution which we consider as a gold standard. Figure 13a depicts the error between the FSP solution and the solution of the conditional moment equation computed using a DAE solver. Figure 13b, c depict the error between the FSP solution and the solution of the approximated conditional moment equation, $\dot{\xi } = (M(\xi ) + \delta I)^{-1}F(\xi )$, computed using an ODE solver for $\delta = 10^{-6}$ and $\delta = 10^{-10}$, respectively. It can be seen that the error in the marginal probabilities is small for all three methods, but the error in the conditional moments is indeed very large for the ODE approximations. Interestingly, a smaller $\delta$ results only in a shift of the error into large mRNA numbers, thus small marginal probabilities, but does not decrease the maximal error.

Fig. 13

Error in the marginal probabilities (left) and in the conditional mean of protein number (right) for scenario 2, $\theta ^{(2)}$. The subplots depict the error between the solution of the MCM with $m=2$ computed using different numerical methods and the FSP solution of the CME. The individual lines represent the errors in the conditional means in the off-state (blue solid line), in the on-state (red solid line), and in the overall marginal probabilities (black solid line). (Remark The y-axis scales of the different plots are different.) a DAE solver. b ODE solver with $\delta = 10^{-6}$. c ODE solver with $\delta = 10^{-10}$. d DAE solver with approximated initial conditions ($\delta = 10^{-6}$) (color figure online)

Besides the error introduced by the approximation of the DAE with an ODE, we would like to mention that the reformulation in terms of an ODE might not always be numerically advantageous. DAEs can also be solved for $p(y|t) = 0$, when the corresponding equations provide equality constraints for the dynamic variables. In case of $p(y|t) \ll 1$, the DAE has the advantage that the multiplication by a small value is numerically more stable than the division by a small value. Beyond the simulation of the dynamics, also the treatment of the initial conditions might be critical. For small marginal probabilities $p(y|t)$ the evaluation of (35) and (36) might become numerically unstable. In this situation it can be advantageous to accept a small error in the initial conditions and to use

$$\begin{aligned} \mu _{i,z}(y,0)&= \sum _{z \ge 0} z_i \frac{p(y,z|0)}{p(y|0) + \delta },\\ C_{I,z}(y,0)&= \sum _{z \ge 0} (z - \mu _{z}(y,t))^I \frac{p(y,z|0)}{p(y|0) + \delta }. \end{aligned}$$

As the states for which the error is introduced possess very low marginal probabilities, in our experience the error decays quickly. This is also shown in Fig. 13d, which shows the simulation results obtained using a DAE solver with an approximation of the initial conditions with $\delta = 10^{-6}$.

To sum up, in our experience the simulation of the conditional moment equation using a DAE solver is superior to the approximation of the conditional moment equation by an ODE followed by the simulation of the ODE using ODE solvers. Furthermore, errors introduced in the initial conditional moments of states with lower marginal probabilities in general decay quickly.