Introduction

The spatial structure of available habitat can have enormous influences on the success of populations living within a landscape. Fragmentation and the connections between patches are key aspects of that spatial structure. River systems can be viewed as a landscape in which a set of patches forms a “dendritic” structure, which is arranged in an explicitly spatial manner that is neither linear nor fully two-dimensional (Charles et al. 2000; Fagan 2002; Lowe 2002; Grant et al. 2007; Muneepeerakul et al. 2007b; Labonne et al. 2008; Fagan et al. 2009).

The defining feature of a dendritic network is its hierarchical branching structure. In river networks, the branching structure arises from the confluences of streams running downhill: looking upstream, a large branch can split into smaller branches, which can themselves split. An overall sketch of a watershed therefore has a tree-like shape, with many more small branches than large ones. (Reticulate patterns are, however, also possible in a river system if the local topography is such that a stream splits and then merges.) The directional flow of water in the river network means that, for any two patches that are connected, one is downstream from the other. Individuals are therefore likely to move differently in the two directions, though the means and speed by which they move (e.g., active swimming or passive drift) may change with season, location, and life stage.

Previous work has incorporated both hierarchical branching and biased dispersal in investigating the effects of river network structures on the populations within them. Particular foci include the effect of dendritic structure on the time to and probability of extinction (Fagan 2002; Lowe 2002; Labonne et al. 2008; Fagan et al. 2009), expected fragment sizes (Fagan 2002; Labonne et al. 2008), asymptotic population growth rates (Charles et al. 1998, 2000), independence of patches (Schick and Lindley 2007), genetic distance between populations (Labonne et al. 2008), and community composition (Muneepeerakul et al. 2007a, b, 2008). Several of these studies have considered the effects of alterations on the branching structure, in the form of disrupted connections or out-of-network dispersal (Charles et al. 1998, 2000; Fagan 2002; Fagan et al. 2009). Nearly all of this work has been carried out in metapopulation frameworks that use varying degrees of explicit spatial structure. Grant et al. (2007) provide a more detailed review of studies on the ecological effects of dendritic networks.

Metapopulation models have also been used in the context of river networks without explicitly considering the branching structure (e.g., Dunham and Rieman 1999; Gotelli and Taylor 1999; Hill et al. 2002; Koizumi and Maekawa 2004). The evolution and consequences of diadromy, or migration between fresh and salt waters, are common applications, notably in salmon (Rieman and Dunham 2000; Schtickzelle and Quinn 2007) (and see also Schick and Lindley 2007, who use graph theory). In these models, branches suitable for spawning (typically upstream) are the patches, and other segments of the river are not incorporated in the model. Dispersal therefore means reproduction by an individual in a branch other than that in which it was born. The metapopulation thus includes the dendritic aspect of the river network only implicitly (but see Schick and Lindley 2007, where dispersal probabilities are tied to distance traveled).

Biased or asymmetric dispersal has also been considered in non-dendritic systems. Metapopulation models have been applied to examine the effects of such dispersal on community composition, spatial synchrony, total population size, and population persistence (e.g., Levine 2003; Roy et al. 2005; Vuilleumier and Possingham 2006). Models of advection and diffusion have been used to investigate how populations can persist and spread in the presence of unidirectional currents, incorporating patch size, variability in flow, environmental disturbances, behavior of individuals, and competition (e.g., Speirs and Gurney 2001; Anderson et al. 2005; Pachepsky 2005; Lutscher et al. 2007).

Here, we use the established dendritic metapopulation approach to examine the effects of branching spatial structure and life history on the asymptotic growth rate of a resident population. We cover a range of system sizes, and also the consequences of random changes to the dendritic structure. We consider several life history strategies, defined in the context of hierarchical branching structure with asymmetric dispersal. Matrix methods allow numeric computation of the long-term growth rate and sensitivities to model parameters. We find that system size and shape, in conjunction with the demography and dispersal patterns of the population, can have substantial effects on the population’s growth rate and, hence, on its ability to persist.

Methods

Matrix framework

In the dendritic metapopulation, we let each patch represent a segment of the river system (Fig. 1a; rather than a confluence, Grant et al. (2007)). To incorporate stage-structure, we use the matrix formulation of Hunter and Caswell (2005), described in more detail in the section “Projection matrices.” Briefly, the state of the population is described by a vector, n, whose elements are the abundances of each life stage in each habitat patch. A propagation matrix, A, summarizes the changes in the system over one time step, i.e., n(t + 1) = A n(t).

Fig. 1
figure 1

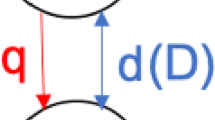
The fork geometry, with parameter definitions. Here, we assume that all segments within a level are equivalent, so parameter values depend only on level l. Dispersal probabilities \(d^{(k)}_l\) out of level l and \(u^{(k)}_l\) into level l may differ between juveniles (k = 0) and adults (k = 1). Survival and maturation rates for juveniles and adults in level l are g l , p l , and q l , and the number of offspring per adult per breeding episode is f l . a Segments and levels. b Two life stages. c Downstream dispersal. d Upstream dispersal

Full size image

The size of the propagation matrix is the product of the number of spatial patches and the number of life stages. Separate, smaller matrices can be written for dispersal for each life stage, and for survival and reproduction for each spatial patch, and then combined (described in the section “Projection matrices”). The aggregation technique employed by Charles et al. (1998, 2000) is based on a similar matrix structure, but it uses two very different time scales such that survival and reproduction are assumed to apply to distributions at equilibrium under dispersal.

We begin by considering the “fork” geometry. The river segments are arranged into levels, determined by the number of confluences separating them from the outlet. We focus on a symmetrically bifurcating structure (Fig. 1a), so L levels correspond to R = 2L − 1 segments. We assume that the properties of a branch are determined entirely by its level in the hierarchical structure, which is reasonable to the extent that segments at the same distance upstream have similar physical attributes (e.g., elevation, gradient, volumetric flow rate, length). Real rivers can, of course, be much more idiosyncratic, but these assumptions capture the essential aspects of a dendritic structure that distinguish it from a linear or lattice arrangement. Although we describe our methods in the context of the fork structure, this approach works for any network of patches, and we later relax the fork assumptions.

We model two life stages: juveniles and adults (Fig. 1b). This allows incorporation of basic biological differences in dispersal abilities and preferences between, say, tadpoles and adult frogs, or hatchlings and mature fish. We consider several life history scenarios, described in the section “Life history.”

For patches in level l over one time unit, fecundity for each adult is f l (this quantity contains the number of eggs and the probability of each hatching), juveniles survive with probability g l or mature with probability p l , and adult survival is with probability q l . Dispersal for life stage k is at rates \(d^{(k)}_l\) downstream from a segment in level l and \(u^{(k)}_l\) upstream to a segment in level l; allowable dispersal paths are shown in Fig. 1c, d. For some species, dispersal out either end of the system may be possible (getting flushed out of the outlet, or wandering out of headwater tributaries), often leading to death. We look at only the effects of loss out of the lowest level of the system, at rate \(d^{(k)}_0\); there is no dispersal in from the outlet, \(u^{(k)}_0 = 0\). (This is similar in spirit to the boundary conditions used in advection–diffusion models of the drift paradox (e.g., Speirs and Gurney 2001). See Muneepeerakul et al. (2007b) for a different approach to handling dispersal loss from the system.)

Notation follows Hunter and Caswell (2005) to the extent possible. Numbering of the segments, the levels, and the matrix elements starts with 0.

Projection matrices

Let M k be the dispersal matrix for stage k. Let \(m^{(k)}_{ij}\) be the matrix element that corresponds to the probability of dispersal from segment j to segment i in a single time unit for life stage k. The segments are numbered from downstream to upstream, as shown in Fig. 1a. For the bifurcating fork geometry with L levels, the elements of M k are

$$ m^{(k)}_{ij} = \begin{cases} 1-d^{(k)}_{l(j)}-2u^{(k)}_{l(i)+1} & \text{if $i = j$ and $l(i) < L-1$} \\ 1-d^{(k)}_{l(j)} & \text{if $i = j$ and $l(i) = L-1$} \\ d^{(k)}_{l(j)} & \text{if $0 \le i < 2^{L-1} - 1$, and} \\ & {\kern6pt}\text{$j = 2i+1$ or $j = 2i+2$} \\ u^{(k)}_{l(i)} & \text{if $0 \le j < 2^{L-1} - 1$, and} \\ & {\kern6pt}\text{$i = 2j+1$ or $i = 2j+2$} \\ 0 & \text{otherwise}, \end{cases} $$
(1)

where \(l(s) = \lfloor \log_2(s+1) \rfloor\) is the level to which segment s belongs (\(\lfloor .\rfloor\) denotes the floor function). As an example, for a river system with three levels and, hence, seven segments, the dispersal matrix for stage k is

$${\bf M}_k = \begin{pmatrix} 1-d^{(k)}_0-2u^{(k)}_1 & d^{(k)}_1 & d^{(k)}_1 & 0 & 0 & 0 & 0 \\ u^{(k)}_1 & 1-d^{(k)}_1-2u^{(k)}_2 & 0 & d^{(k)}_2 & d^{(k)}_2 & 0 & 0 \\ u^{(k)}_1 & 0 & 1-d^{(k)}_1-2u^{(k)}_2 & 0 & 0 & d^{(k)}_2 & d^{(k)}_2 \\ 0 & u^{(k)}_2 & 0 & 1-d^{(k)}_2 & 0 & 0 & 0 \\ 0 & u^{(k)}_2 & 0 & 0 & 1-d^{(k)}_2 & 0 & 0 \\ 0 & 0 & u^{(k)}_2 & 0 & 0 & 1-d^{(k)}_2 & 0 \\ 0 & 0 & u^{(k)}_2 & 0 & 0 & 0 & 1-d^{(k)}_2 \end{pmatrix}. $$
(2)

The full dispersal matrix is block diagonal, with one block for each life stage (k = 0 for juveniles, and k = 1 for adults):

$$ \mathbb{M} = \begin{pmatrix} {\bf M}_0 & 0 \\ 0 & {\bf M}_1 \\ \end{pmatrix}. $$
(3)

For two life stages, the demographic matrix for a segment in level l is

$${\bf B}_l = \begin{pmatrix} g_l & f_l \\ p_l & q_l \\ \end{pmatrix}. $$
(4)

The full demographic matrix \(\mathbb{B}\) has the blocks B l on the diagonal (one block per segment) and 0 elsewhere, i.e.,

$$ \mathbb{B} = \begin{pmatrix} {\bf B}_0 & 0 & 0 & 0 & \dots \\ 0 & {\bf B}_1 & 0 & 0 & \dots \\ 0 & 0 & {\bf B}_1 & 0 & \dots \\ 0 & 0 & 0 & {\bf B}_2 & \dots \\ \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{pmatrix}. $$
(5)

Note that, when all segments within a level have identical properties, one matrix element per level is sufficient, provided that dispersal rates are multiplied by the appropriate number of source segments. We do not use such level-based matrices here because the fork degradation procedure (described in the section “Geometry”) requires individual treatment of segments.

Ordering the system by segment and having demography act before dispersal, the overall population projection matrix is

$$ {\bf A} = {\bf P}^\mathsf{T} \mathbb{M} \, {\bf P} \, \mathbb{B} $$
(6)

(see Hunter and Caswell (2005, Table 1a); P is the vec-permutation matrix that transforms the matrix organization from by-patch to by-stage). The asymptotic growth rate for the population, λ, is the dominant eigenvalue of A.

The above framework can be easily expanded to incorporate periodic temporal variation in demography and dispersal. For example, ignore year-to-year variation but suppose that behavior during the year can be broken into Y discrete phases, each expressed with dispersal and demographic matrices \(\mathbb{M}_y\) and \(\mathbb{B}_y\), y = 1, 2 ...Y. The projection matrix for each phase is \({\bf A}_y = {\bf P}^\mathsf{T} \mathbb{M}_y \, {\bf P} \, \mathbb{B}_y\), and so, the annual projection matrix is

$$ {\bf A} = {\bf A}_Y {\bf A}_{Y-1} \ldots {\bf A}_2 {\bf A}_1. $$
(7)

Sensitivities

The sensitivity matrix of A, S A , is obtained from its dominant eigenvectors (e.g., Hunter and Caswell 2005, Eq. 12). The elements of this matrix are \(\partial \lambda / \partial a_{ij}\). What we want, however, is the sensitivity of the asymptotic growth rate to the dispersal and demographic parameters.

For the projection matrix A in Eq. 6, the sensitivity of the asymptotic growth rate λ to the elements of the dispersal matrix \(\mathbb{M}\) is \({\bf S}_\mathbb{M} = {\bf P} {\bf S_A} \mathbb{B}^\mathsf{T} {\bf P}^\mathsf{T}\) (Hunter and Caswell 2005, Table 1a). Break \({\bf S}_\mathbb{M}\) into four R ×R blocks and call the two diagonal blocks \({\bf S}^{(k)}_\mathbb{M}\); their elements are \(\partial \lambda / \partial m^{(k)}_{ij}\).

To obtain the sensitivity of the growth rate to the parameters \(d^{(k)}_l\) and \(u^{(k)}_l\), apply the chain rule:

$$\frac{\partial \lambda}{\partial d^{(k)}_l} = \sum\limits_{i,j} \frac{\partial \lambda}{\partial m^{(k)}_{ij}} \frac{\partial m^{(k)}_{ij}}{\partial d^{(k)}_l} $$
(8)
$$ \frac{\partial \lambda}{\partial u^{(k)}_l} = \sum\limits_{i,j} \frac{\partial \lambda}{\partial m^{(k)}_{ij}} \frac{\partial m^{(k)}_{ij}}{\partial u^{(k)}_l} $$
(9)

The second factor in each term is the derivative of an element in \(\mathbb{M}\) with respect to the parameter of interest. Looking at \(\mathbb{M}\), we see that \(\partial m^{(k)}_{ij} / \partial d^{(k)}_l = 0\) unless segment j is in level l, and \(\partial m^{(k)}_{ij} / \partial u^{(k)}_l = 0\) unless segment j is in level l − 1. Moreover, the symmetry of the system means that \(\sum_i \left(\partial \lambda / \partial m^{(k)}_{ij}\right) \left(\partial m^{(k)}_{ij} / \partial d^{(k)}_l\right)\) (and likewise for u) is the same for each segment j in level l. Level l has 2l segments, the first of which has index 2l − 1. Inspection of M k or \(m^{(k)}_{ij}\) (Eq. 1) yields

$$\begin{array}{rll} \frac{\partial \lambda}{\partial d^{(k)}_l} &= & \begin{cases} -\dfrac{\partial \lambda}{\partial m^{(k)}_{00}} & \text{for $l = 0$} \\ 2^l \left ( \dfrac{\partial \lambda}{\partial m^{(k)}_{s' s}} - \dfrac{\partial \lambda}{\partial m^{(k)}_{s s}} \right ) & \text{for $0 < l < L$} \end{cases} \\ && \text{where $s = 2^l - 1$ and $s' = (s-1)/2$} \end{array}$$
(10)
$$\begin{array}{rll} \frac{\partial \lambda}{\partial u^{(k)}_l} &= & \ 2^l \left ( \dfrac{\partial \lambda}{\partial m^{(k)}_{s' s}} - \dfrac{\partial \lambda}{\partial m^{(k)}_{s s}} \right ) \quad \text{for $0 < l \le L-1$} \\ && \text{where $s = 2^{l-1}-1$ and $s' = 2s + 1$.} \end{array}$$
(11)

So there are two components to the sensitivity of level-specific dispersal rates. One is the number of segments in each level, which always increases with level. The other is the sensitivity within each segment (which is the same for all segments within a level, under the symmetry of the system we are using). If segment sensitivity increases with level, then the asymptotic growth rate is always more sensitive to dispersal (in either upstream or downstream directions) happening further upstream. But if segment sensitivity decreases with level, then further details must be considered to determine where the greatest sensitivity to dispersal lies.

The sensitivity of the asymptotic growth rate λ to the elements of the demography matrix \(\mathbb{B}\) is \({\bf S}_\mathbb{B} = {\bf P}^\mathsf{T} \mathbb{M}^\mathsf{T} {\bf P} {\bf S_A}\) (Hunter and Caswell 2005, Table 1a). Break \({\bf S}_\mathbb{B}\) into 2 × 2 blocks, and call the diagonal ones \({\bf S}^{(s)}_\mathbb{B}\); their elements are \(\partial \lambda / \partial b^{(s)}_{ij}\), where \(b^{(s)}_{ij}\) are the elements of B l(s).

Again applying the chain rule and summing sensitivities over all segments within a level, we have (with s = 2l − 1 − 1):

$$\begin{array}{rll} \frac{\partial \lambda}{\partial g_l} &=& 2^l \left ( \frac{\partial \lambda}{\partial b^{(s)}_{00}} \right ) \qquad \qquad\, \frac{\partial \lambda}{\partial f_l} = 2^l \left ( \frac{\partial \lambda}{\partial b^{(s)}_{01}} \right ) \\ \frac{\partial \lambda}{\partial p_l} &=& 2^l \left ( \frac{\partial \lambda}{\partial b^{(s)}_{10}} \right ) \qquad\qquad \frac{\partial \lambda}{\partial q_l} = 2^l \left ( \frac{\partial \lambda}{\partial b^{(s)}_{11}} \right ). \end{array}$$
(12)

The sensitivity to each parameter is again determined by the number of segments in the level and the sensitivity within each segment, and hence could either increase or decrease with level.

In the case of periodic variations (Eq. 7), the sensitivity of λ to the entries of \(\mathbb{M}_y\) and \(\mathbb{B}_y\) can be obtained by application of Hunter and Caswell (2005, Eqs. 12–15) and the logic just outlined. We do not show the details here.

Scenarios considered

The matrix-based framework described in the section “Matrix framework” is quite flexible and can handle many combinations of patch-based and stage-based assumptions about dispersal and life history, and also sets of rates that change periodically with time. Here, we restrict our analysis to a few generalized scenarios. We consider life histories that combine constant dispersal or seasonal migration with upstream or downstream breeding habits. In addition to the fork structure described in Fig. 1 and Section “Matrix framework”, we also consider perturbations of the dispersal pathways.

Life history

We concentrate on populations in which individuals remain within the river system, rather than spending a portion of their life in the ocean or undergoing overland migrations to terrestrial areas. Such species, which include some fish, herptiles, invertebrates, and plants, encompass a wide range of life history strategies. Depending on the species and life stage, individuals may disperse passively with the currents (e.g., propagules of riparian plants, larvae of some invertebrates) or actively with or against the currents (e.g., fish and amphibians).

We choose life histories in the context of the branching, “fork” geometry (Fig. 1), so values of any parameter are the same for all segments in a given level, and some quantities change continuously with level. We cannot possibly consider all combinations of dispersal, survival, and reproduction, but we choose six generalized scenarios that capture distinct life history modes.

The first three scenarios we use here take all processes to be constant over time and allow reproduction in all levels of the system. This constant-rates framework is appropriate for species without strongly seasonal behavior, such as non-migratory species that reproduce wherever they happen to be. Many stream invertebrates likely fall into this realm, as they have been found both to drift downstream and to swim upstream throughout the year (Williams and Williams 1993; Elliott 2003). These scenarios may also be adequate for non-migratory freshwater fish, and potentially for plants whose propagules drift downstream and are carried upstream by animals that remain in the stream corridors. The constant-rates method can also be applied whenever the net annual effects can be directly placed into a single yearly propagation matrix. Within this framework, the suitability of breeding habitat may vary with level, e.g., tied to flow rate, depth, substrate, or resource availability. If the resources and physical conditions necessary for reproduction are spatially separated from those needed for maturation, adults and juveniles may be expected to disperse in opposite directions.

The C scenarios: constant rates throughout the year.

C-all: :

Equal reproduction in all levels. Reproductive potential is equal in all levels: per-capita fecundity is independent of level. Upstream dispersal is the same for adults and juveniles, as is downstream dispersal. Downstream dispersal is somewhat more rapid than upstream dispersal.

C-up: :

More reproduction upstream. Reproduction is biased towards upstream areas: fecundity increases linearly with level. Juveniles disperse more rapidly downstream, and adults disperse more rapidly upstream.

C-down: :

More reproduction downstream. Reproduction is biased towards downstream areas: fecundity decreases linearly with level. Juveniles disperse more rapidly upstream, and adults disperse more rapidly downstream.

In each of these cases, we hold each of juvenile maturation (p), adult survival (q), juvenile upstream dispersal (u (0)), juvenile downstream dispersal (d (0)), adult upstream dispersal (u (1)), and adult downstream dispersal (d (1)) constant across the system. The downstream dispersal parameters also apply to loss from the outlet. We additionally set g = 0 so that juveniles die if they do not mature after a single time unit, e.g., 1 year. For C-up and C-down, fecundity varies linearly with level, from 0 to f max. Because the number of segments increases with level, per capita fecundity averaged over all segments increases with system size for C-up and decreases with system size for C-down. The actual amount of reproduction, however, will depend on the abundance at each level. Parameter values used for the results in the section “Results” are shown in Table 1.

Table 1 Parameter values used for the results presented here
Full size table

The second set of life histories we consider is more appropriate for species showing seasonal differences in dispersal and reproduction. Freshwater fish with well-defined migration routes (potamodromous species or populations) span a wide taxonomic range and show great variety of movement patterns (McKeown 1984). Likewise, amphibians may move along stream courses to avoid high temperatures or freezing, to seek better food or shelter, and to return to the same breeding sites year after year (Russell et al. 2005). Spawning migrations (generally upstream, but occasionally downstream) allow eggs to be laid in segments with lower predation and more appropriate food supplies, temperatures, and oxygenation for juveniles (McKeown 1984). These areas may not be suitable for breeding year-round, and they may not have sufficient food or cover for adults. Dispersal outside of the spawning season allows individuals to reach habitats far from their breeding locations. In both fish and amphibians, adults and juveniles may migrate at different times (McKeown 1984; Russell et al. 2005). We divide the year into four categories of behavior and apply each of those seasonal matrices three times successively to create an annual projection matrix (Eq. 7, with Y = 12).

The S scenarios: seasonal rate variation.

S-all: :

Equal reproduction in all levels. Per-capita fecundity is the same in all levels, but breeding only occurs in one season. Upstream dispersal is the same for adults and juveniles, as is downstream dispersal. Downstream dispersal is somewhat more rapid than upstream dispersal.

S-up: :

Upstream breeders. Adults swim upstream in the breeding season (season 1) and the period preceding it (season 4); they swim downstream in seasons 2 and 3. Juveniles move only downstream, slowly when they are very small (season 1) and more rapidly when they are larger. Juveniles mature in seasons 3 and 4. Fecundity is nonzero only in the highest level in season 1.

S-down: :

Downstream breeders. Adults swim downstream in the breeding season (season 1) and the period preceding it (season 4); they swim upstream in seasons 2 and 3. Juveniles move primarily upstream, but with a little downstream drift. Juveniles mature in seasons 3 and 4. Fecundity is nonzero only in the lowest level in season 1.

For S-up and S-down, juvenile survival in the breeding season is greatest near the favorable breeding segments. Other parameter constraints within each season are as for the Cs, and values are given in Table 1. S-up bears a resemblance to anadromy (and S-down to catadromy), but it allows adults to survive after reproducing and potentially live for many breeding seasons; additionally, juveniles mature in 1 year, and individuals do not leave freshwater.

The C-all scenario is like a less-detailed representation of S-all, except for the difference in dispersal potential: individuals can disperse up to 12 times as far per year in S-all. The C-up and S-up scenarios (and also the C-down and S-down scenarios) differ in dispersal potential as well, and also in the level-dependence of juvenile survival and fecundity.

These six scenarios were chosen to allow comparisons of the essence of various life history strategies. Although they do not mimic any species exactly, examples of species that are approximated by the above assumptions may be of interest. (For many of the vertebrate species, one could include additional life stages to account for the variable number of years for juvenile maturation.) The S-up scenario applies to many potamodromous fish, including kokanee salmon (Burgner 1991), Colorado pikeminnow (Minckley and Marsh 2009), razorback sucker (Minckley and Marsh 2009), Murray cod (Humphries 2005), silver and golden perch (Reynolds 1983), and the brook lamprey (Maitland 2003). The S-down scenario is less common, but it would be appropriate for some sculpin (Goto 1986) and a flannel-mouthed characin (Planquette et al. 1996, obtained via Froese and Pauly 2000). Considering the lowest level to be an estuary would make it applicable to many more species. S-all would be appropriate for many non-migratory freshwater fish in seasonal environments, and also map turtles (Pluto and Bellis 1988). The C scenarios apply most directly to species, often tropical, that reproduce aseasonally, but even species breeding once per year can be reasonably approximated with a single annual transition matrix if dispersal is not coordinated to change direction with season. The C-all scenario could apply to some rainbowfish (Pusey et al. 2001), guppies (Reznick et al. 1993), freshwater snails (Schneider and Lyons 1993), and painted turtles (MacCulloch and Secoy 1983). Many invertebrates (mayflies, copepods, ostracods, springtails; (Williams and Williams 1993; Bilton et al. 2001)) may have dispersal patterns approximating C-up, though reproduction is probably not limited to the uppermost segments of the river system.

Geometry

The bifurcating “fork” geometry (Fig. 1a) can be generalized to any number of levels. To look at the effects of system size on population growth rate, we consider between two and eight levels, corresponding to systems with three to 255 segments.

To assess the effect of the branching structure itself, we use an iterative process to “degrade” the fork structure (Fig. 2). Beginning with the fork’s dispersal connections, we randomly remove one of the existing dispersal pathways and reassign it to a connection that did not previously exist (i.e., to a zero in the dispersal matrix); λ is then recalculated for this new geometry. From this new configuration, another dispersal pathway is then chosen and reassigned, and so on, gradually washing out the original fork structure. An exception to random changes in dispersal connections is for level 0, from which downstream dispersal out of the system always occurs. Additionally, the sum of all dispersal probabilities out of a segment cannot exceed one, and the system cannot be divided into completely disconnected parts (i.e., the dispersal matrix must remain irreducible). All connections except \(d^{(k)}_0\) remain two-way—each pair of patches connected one way by \(d^{(k)}_l\) is connected in the other direction by \(u^{(k)}_l\). Through all these processes, the segments retain their identities, including survival and fecundity rates.

Fig. 2
figure 2

Fork degradation procedure. For each step in the sequence, an existing dispersal pathway is removed and placed between two previously unconnected patches. Each pathway is two-way: the large arrowheads indicate downstream dispersal and the small arrowheads indicate upstream dispersal. Two example reassignments are shown in the upper panels. The lower panels show the dispersal matrix for one life stage corresponding to each configuration (compare with Eq. 2). Black squares represent non-zero elements, and white squares represent zero elements. The shaded, diagonal elements are adjusted so that the sum of each column is one (except the first, which sums to 1 – \(d_0^{(k)}\)). Squares marked “a” show the first pathway reassignment, squares marked “b” show the second, and squares marked “c” show the one that will be third. This graphical matrix representation does not distinguish between the upstream and downstream components of each dispersal pathway, but the repositioned pathways are oriented randomly

Full size image

After each step of degradation, we count the number of connections by which the current geometry differs from the original fork, i.e., half the number of elements by which the two dispersal matrices differ, considering only a single life stage and disregarding diagonal elements. The number of differing connections may be less than the number of degrading steps taken if a step happens to restore a fork-like connection. Enough replicates of the sequential degradation procedure were performed to obtain 100 samples at each number of connection differences from two to 20.

Repositioning a connection corresponds physically to placing a dam or other barrier between two previously connected segments and simultaneously placing a canal or other watercourse (or removing an existing dam) between two previously unconnected segments. Anthropogenic changes in connectivity between segments of river systems are not constrained to be so symmetric, but our intent with this degradation process is to isolate the effects of the branching structure itself while controlling for system size and the total potential for dispersal, mortality, and reproduction. This idea of degrading or “rewiring” a heavily structured arrangement of dispersal pathways was used by Holland and Hastings (2008) in the context of predator–prey dynamics, and it has been applied extensively in the study of “small world” networks (Watts 1998).

Results

Fork

First, we consider the effect of system size and fecundity or dispersal on the asymptotic growth rate, λ, for the fork geometry alone (Fig. 3). Sensitivities are shown in Table 2, but they can also be visualized with the plots. Elasticities are less visually apparent but are easily computed from the sensitivities.

Fig. 3
figure 3

Effect of system size, fecundity (a–c), and dispersal (d–f) on asymptotic growth rate λ. Parameter values are those in Table 1 for a–c, except as noted in the legends, and for “full” dispersal in d–f; for “half” dispersal, all dispersal rates are reduced by 50%

Full size image
Table 2 Example eigenvectors and sensitivities for the constant-rates life histories, for parameter values given in Table 1 and five levels
Full size table

For most of the life histories, λ increases with system size because proportionally fewer individuals are in the lowest level, where they can be lost from the system. (Without loss from the outlet, smaller systems have equal or greater growth rates than larger ones because proportionally more of the segments have high fecundity (results not shown).) The exception is for S-down, in which there is a trade-off between upstream safety from the outlet and not being able to reproduce outside the lowest level. For all life histories, the population growth rate asymptotes quickly with system size because larger systems have proportionally fewer individuals in downstream segments. The rate of change of λ with system size is greater for the Ss than the Cs because there are more reproductive episodes (three rather than one) and dispersal opportunities (12 rather than one) per year for the Ss.

Figure 3a–c shows the effects on λ of system size and fecundity. Unsurprisingly, λ is always larger for larger f. For C-all and S-all, the change in λ for a given change in f is larger for larger values of λ, but the proportional change in λ (the elasticity of λ with respect to f) does not change with the size of the system because all segments have the same fecundity. For C-up and C-down, λ is very slightly more elastic with respect to f in larger systems because fecundity changes more slowly with level. For S-up and S-down, λ is less elastic with respect to f in larger systems because more segments have zero fecundity.

Figure 3d–f shows the effects on λ of system size and dispersal magnitude. The growth rate is always larger for scenarios with less dispersal because there is less loss from the outlet. This effect is diminished in larger systems (except for S-down) because more individuals disperse to and breed in segments farther from level 0, i.e., away from where loss from the outlet occurs. The trade-off between loss from the outlet and breeding only in the lowest level is evident for S-down with high dispersal, but for low dispersal, not going far from the breeding level is more important.

In small systems, increases to λ can come through changes to fecundity, survival, or dispersal. In large systems, changes to dispersal generally have much smaller effects on λ because the distances between substantially different patches are greater. If dispersal occurs over larger distances than just nearest neighbors, as here, dispersal is more likely to remain important in larger systems. Figure 3 also shows that, when all other parameters are fixed, the growth rate is greater for upstream than downstream breeders. This is because there are more segments of higher fecundity when fecundity increases with level.

The combined effects of fecundity and dispersal on λ are illustrated in Fig. 4. For C-all, S-all, C-up, and S-up, when adult upstream dispersal is small, increasing it increases λ. For C-down and particularly S-down, the trade-off between upstream safety and downstream breeding is apparent, since increasing upstream dispersal only increases λ when fecundity is low. Changing fecundity clearly has a much larger effect on λ than changing dispersal. For S-up, however, increasing fecundity has little effect on λ unless there is enough upstream dispersal for individuals to take advantage of the upstream breeding sites. The Ss are more sensitive to fecundity than the Cs are because reproduction occurs during 3 months, rather than once per year. This is particularly evident for S-all and S-up, for which many segments contribute to population growth.

Fig. 4
figure 4

Population growth rate for five levels. Contour plots illustrate the combined effects of fecundity, f, and adult upstream dispersal, u (1), on λ. Other parameter values are given in Table 1. The thick contour lines mark λ = 1, to show the threshold between deterministic population growth and decline

Full size image

Table 2 shows the equilibrium proportions of abundance and the sensitivities for a five-level system with constant annual rates. Abundance for any level l is the sum of the abundances of the 2l segments within that level. Despite the downstream dispersal bias, abundances are higher in upstream levels under C-all because of loss from the outlet below level 0. Under C-up, juveniles are most abundant in the most productive uppermost level; adults are slightly more abundant in the level below that because many juveniles disperse one level downstream before maturing. Under C-down, despite fecundity being greatest in the lowermost level, abundances are greater in level 1 because of loss from level 0 and the ability of juveniles to swim upstream. In general, λ is more sensitive to each process when it occurs in levels where the species is more abundant. Downstream dispersal only increases λ when it moves individuals into levels with higher fecundity (d (k) for l > 1 under C-down), and upstream dispersal only decreases λ when it moves individuals into levels with lower fecundity (u (k) for l > 1 under C-down). Growth rate is more sensitive to dispersal for C-down than C-up, and it is more sensitive to fecundity and survival for C-up than C-down.

Eigenvectors for the seasonal life histories are shown in Fig. 5. The distribution of individuals within the system varies over the course of the year, but equilibrium proportions exist for each month. Since S-all has constant dispersal throughout the year, changes within the year effectively consist simply of juveniles maturing to adults. Abundances are higher at the higher levels because of reduced probability of loss from the outlet. For S-up and S-down, juvenile maturation is also evident, as is seasonal dispersal of both juveniles and adults. In all cases, there are no juveniles in the fourth season because those that do not mature die.

Fig. 5
figure 5

Eigenvectors for the seasonal life histories, for parameter values given in Table 1 and five levels. The thick gray lines represent juveniles in each level, and the thick black lines represent adults in each level. The length of each line shows the proportion of the population in that life stage and location at that time. The abundances of all segments within the same level are summed for this display, as in Table 2

Full size image

Degraded fork

To assess the effect on asymptotic growth rate of disruptions to the dendritic structure, we “degraded” the fork geometry (Fig. 2). Stepping away from the original fork structure by repeatedly repositioning dispersal connections, we found that even a small number of changes (due to, say, flooding or diverting a channel or sustained active transplanting) can cause substantial changes in λ (Fig. 6). The expected magnitude and direction of this effect, as well as its sensitivity to the particular spatial arrangement, depends markedly on system size and life history.

Fig. 6
figure 6

Step-by-step degradation of the fork geometry (Fig. 2), for each life history and three system sizes. Each dot indicates λ for a particular set of dispersal connections, and the thick lines show the median λ over all the randomly adjusted geometries at each distance from the fork. Initial parameter values are given in Table 1. Note the difference in vertical axis scale between the constant rates (Cs) and seasonal rates (Ss)

Full size image

Because there are more upstream than downstream segments, the average effect of degrading the fork structure is to enhance the connections among upstream segments and correspondingly decrease the connections of downstream segments, subject to the constraint that no subgroup of segments becomes isolated. This effect is less pronounced in larger systems, where the connectivity rearrangements are more likely to occur among the numerous, equivalent upstream segments. This geometric result of degrading the branching structure has different consequences for the different life histories.

For species that breed in all segments, reducing connectivity with the lower segments reduces loss through the outlet for upstream segments, thereby increasing λ. This is only slightly apparent for C-all, where changing the spatial structure of the system has very little effect on the population growth rate (Fig. 6a–c). Segments in all levels are identical except for their distance from the outlet, but even that matters little when the dispersal distance is as most one level per generation and reproduction occurs everywhere. For S-all, λ is substantially more sensitive to changes in connectivity (Fig. 6d–f) because of the opportunities for more likely and more distant dispersal within a generation.

For species that breed mostly upstream, reducing connectivity with the lower segments would also be expected to reduce loss through the outlet and increase λ. This is not evident for C-up, however (Fig. 6g–i), because few individuals are found in downstream segments (see the equilibrium proportions in Table 2, for example). The C-up life history is more sensitive to changes in structure than C-all because there is more variability among the segments in reproductive potential, though less so in larger systems where fecundity changes more gradually with level. The S-up life history strongly shows the effect of reduced connectivity with lower segments (Fig. 6j–l) because the dispersal modes lead to substantial abundance in the lower segments for at least part of the year (Fig. 5). S-up also shows the most sensitivity of λ to changes in connectivity. There is not only the potential for increased and more distant dispersal, but also seasonal dispersal, so that the population’s distribution changes throughout the course of the year (Fig. 5). Additionally, the fecundity difference between segments in high and low levels is sharper for S-up than C-up. These factors create more variation among the segments, leading to greater variability in the response of λ to spatial structure.

For downstream breeders, reducing connectivity with the lower segments leads to a trade-off between less loss through the outlet for upstream segments and less escape of juveniles from the downstream breeding grounds to the safer upstream areas. For the C-down life history, there is not much net effect on λ on average, but there is substantial variability in the response of λ to particular spatial arrangements (Fig. 6m–o). The S-down life history shows a more consistent reduction in λ with degradation of the fork structure, likely because breeding is only in the lowest level and reduced escape of juveniles is therefore more detrimental. In this instance, loss of the branching structure makes the population likely to decline deterministically (λ < 1).

Overall, we find that although the symmetrically bifurcating geometry is a very special case in terms of connectivity, the asymptotic population growth rate in a dendritic network typically falls within the range of values possible among a set of otherwise-similar patches with different connectivities. In general, λ is less sensitive to connectivity in larger systems because the between-segment variance is less: the higher levels in a large system have many identical segments, making connection changes less likely to have an effect. The variation in λ is generally much greater for the seasonal than the constant-rates life histories due to differences in dispersal (the Ss have more total, distant, and varied dispersal over the course of a year) and among-patch variation in fecundity.

Discussion

We have demonstrated how matrix models can be applied to stage-structured life histories within a network of patches forming a river system. This is a flexible framework that can incorporate spatial and temporal variation in survival, fecundity, and dispersal. We illustrated a few representative life history scenarios, intended to be biologically relevant without being excessively detailed or organism-specific, and found that system size, connectivity, and demographic parameters can have quite variable effects on the asymptotic growth rate of the population.

For a symmetrically branching arrangement of habitat patches, we found that system size can have a substantial effect on the asymptotic population growth rate. This is most pronounced for life histories in which the number of segments that support breeding increases with system size (Fig. 3a, b, d, e), but it is also apparent with a single breeding segment (Fig. 3c, f). Under many circumstances, system size alone can make the difference between a deterministically viable population (λ > 1) and a doomed one (λ < 1).

An interesting feature of the downstream-breeder life history is that the segment furthest downstream is both the best for reproduction and the most endangered by loss out the outlet. This trade-off can lead to population persistence for only intermediate values of upstream dispersal (for moderate values of fecundity; Fig. 4): too little upstream dispersal yields heavy loss out the outlet, and too much upstream dispersal allows insufficient time in the breeding grounds. An analogous result is obtained for downstream dispersal (results not shown).

By altering the connections in the heavily structured dendritic network, we found that, for any of the life histories we considered, changes to the fork structure can either increase or decrease λ (Fig. 6). The largest decreases are generally larger than the largest increases, but the median change over all randomly adjusted geometries depends on life history. We conclude that even a small number of unplanned or poorly investigated alterations to connectivity have the potential to substantially change a population’s asymptotic growth rate, and the direction and magnitude of this change will not necessarily be intuitively obvious.

We modeled disruptions to dendritic structure in a generic manner by adding or removing connections between segments. In natural river systems, anthropogenic changes increasingly affect connections within the network, for example through building or tearing down dams (Nilsson et al. 2005; Graf 2001) or constructing extensive canals (Johnson 1977; Fairless 2008). The hydrological and ecological effects of any such large-scale alteration will be complex, but the general strategy of representing its consequences through the dispersal parameters in population-level models may nevertheless be useful when attempting to quantify the impact of proposed or ongoing landscape changes.

The model we present here makes many simplifying assumptions about the ecology and environment of the species considered. Matrix population and metapopulation models can, however, incorporate a wide range of circumstances, such as demographic and environmental stochasticity, density dependence, plasticity, temporal autocorrelation, community dynamics, and species interactions (e.g., Caswell 1983; Barbeau and Caswell 1999; Hill et al. 2004; Roy et al. 2005; Smith et al. 2005; Vindenes et al. 2008), and such techniques could certainly be applied within river network models such as ours. Our focus on asymptotic behavior disregards transient effects, which may show substantially different dynamics (Hastings 2004); these could, however, be investigated in the same framework simply by tracking the population’s distribution over time. These models do not include adaptation and, hence, apply to ecological rather than evolutionary time scales.

Even with the many simplifications we make in the structure of our modeling framework, it can easily be customized in a variety of ways to particular populations and river systems of interest. Any spatial arrangement of patches can be accommodated, and dispersal can additionally be made dependent on the distances between patches, as in many metapopulation models (Hanski 1994). The connections between patches could also change deterministically through the course of the year due to seasonal drought or flooding (though stochastic changes in patch connectivity (e.g., Fortuna et al. 2006) would be somewhat trickier to deal with). Periodic disturbances that affect connectivity and productivity in the system, such as decadal floods, could also be included. For either constant or variable connectivity patterns, the dispersal probabilities could more explicitly incorporate the hydrological features of the segments, such as elevation, volumetric flow rate, or length. The life history of the species in question can be described in more detail with additional life stages or sex-specific differences in migration (common in amphibians, at least; Russell et al. 2005) with only some additional bookkeeping. Our model framework does not explicitly distinguish between dispersal and migration, but migration can be represented by high dispersal rates in one direction and little dispersal in the other direction. The upstream and downstream dispersal rates might be expected to switch half a year later for migration in the reverse direction.

We considered here only species confined to freshwater. One means of extending this model to diadromous fish is to add one or more habitat patches for the ocean, located below level zero. Oceanic patches would likely have substantially different population dynamics from the rest of the system. Such extensions could prove useful as a spatially explicit framework for studying the combined consequences of freshwater connectivity changes, estuarine habitat degradation, and oceanic temperature cycles, all factors that affect salmon population dynamics (McClure et al. 2003).

In our life history scenarios, we emphasized loss of individuals from the lowest level. We incorporated this by dispersal through an outlet and out of the system, though similar results are expected from high mortality in the lowest level, caused by, for example, pollution in coastal cities (Mallin et al. 2000). Indeed, incorporating dispersal consequences into survival probabilities is an established method for dealing with spatial structure implicitly (Kareiva et al. 2000; Wilson 2003). The same approach could apply to the portion of a river network that is upstream from an inhospitable or impassable area. In fact, any sharp change in habitat can have a similar draining effect if species are ill-suited to the conditions beyond the boundary. The spatial scale of the consequences of pollution or other perturbations further upstream could also be investigated in this context; comparison with other theoretical treatments (e.g., Anderson et al. 2005) could prove interesting.

Our work here has had a theoretical focus, but these matrix models are amenable to parameterization using field data when information on habitat geometry, demographic rates, and dispersal probabilities are available. This seems like a tall order, but in fact, the necessary mark–recapture methods have been shown to be feasible for stream invertebrates, amphibians, and fish (e.g., Skalski and Gilliam 2000; Elliott 2003; Lowe 2003; Perry et al. 2009). Once the essential details of a system have been encapsulated, the consequences of proposed modifications to connectivity, survival, or reproduction can then be examined.