1 Introduction

West Nile virus (WNv) was first isolated from the blood of a febrile woman in the West Nile province of Uganda in 1937 (Smithburn et al. 1940). This mosquito-borne virus has been recognized as the cause of epidemics of febrile illness and sporadic encephalitis in Africa, the Mediterranean Basin, Europe, India, and Australia (Russell and Dwyer 2000). WNv was detected for the first time in North America in 1999, during an encephalitis outbreak in New York City (Center for Disease Control and Prevention (CDC) 1999). Since then, WNv activity has been reported in 46 additional states in the United States (Center for Disease Control and Prevention (CDC) 2001). The first reports of WNv activity in Canada came in 2001 when the virus was found in dead birds and mosquito pools in southern Ontario (Center for Disease Control and Prevention (CDC) 2001).

When an infected mosquito bites a bird, it transmits the virus; the bird may then develop sufficiently high viral titers during the next 3–5 days to infect another mosquito. The WNv is different from other mosquito-born diseases since it involves a cross-infection between the host birds and mosquitoes and those birds could travel with no natural (spatial) boundaries. During its life cycle, the virus circulates between mosquitoes and birds. The virus can also be passed via vertical transmission from a mosquito to its offspring which increases the survival of WNv in nature (Swayne et al. 2000). It has been found that birds from certain species may become infected by WNv after ingesting it from an infected dead animal or infected mosquitoes, which are both natural food items of some species (Komar et al. 2003). Although mosquitoes can transmit the virus to humans and many other species of animals (e.g. horses, cats, bats, and squirrels), it cannot be transmitted back to mosquitoes.

Mathematical modeling studies for WNv among mosquitoes and avian species appeared shortly after WNv first arrived in North America in 1999. Thomas and Urena (2001) applied a discrete time system to model the interactions between the virus life cycle and the consequent effects on humans. Wonham et al. (2004) presented a single-season model with a system of differential equations for WNv transmission in the mosquito–bird population. Their work, using local stability results and simulations, showed that while mosquito control decreases WNv outbreak threshold, controlling birds increases it. Cruz-Pacheco et al. (2005) presented and analyzed a mathematical model for the transmission of WNv infection between mosquito and avian populations and by using experimental and field data as well as numerical simulations, they found the phenomena of damped oscillations of the infected bird population. Lewis et al. (2006) studied the spatial spread of the virus, established the existence of traveling waves and computed the spatial spreading speed of the infection. In 2006, Lewis et al. also made a comparative study of the discrete-time model (Thomas and Urena 2001) and the continuous-time model (Wonham et al. 2004). Kenkre et al. (2005) provided a theoretical framework for the analysis of the WNv epidemic and for dealing with mosquito diffusion and birds migration. Bowman et al. (2005) proposed a model system incorporating mosquito–bird–human population for assessing control strategies against WNv. Moreover, many other works on the transmission dynamics of WNv have been published recently (Blayneh et al. 2010; Gourley et al. 2007; Jang 2007; Wan and Zhu 2010).

In North America, the virus has been found in more than 300 species of birds (Kurt et al. 2003). In a modeling study of WNv by Cruz-Pacheco et al. (2005), the authors use experimental and field data and the same model to estimate the basic reproduction number for several specific species of birds, respectively. From the study of Hamer et al. (2009), the dynamics of WNv transmission are influenced strongly by a few key super spreader bird species, and their results showed that the WNv mosquitoes fed predominantly (83 %) on birds with a high diversity of species used as hosts (25 species), and WNv mosquitoes also fed on mammals (19 %; 7 species with humans representing 16 %). Their study indicated that approximately 66 % of WNv-infectious mosquitoes became infected from feeding on just a few species of birds. Yet, as far as we know, the past modeling effects to understand the transmission dynamics of WNv have treated the avian species as one family. The study by Hamer et al. (2009) suggested that it is essential to consider the impact of avian species diversity in one system to understand the transmission dynamics of WNv.

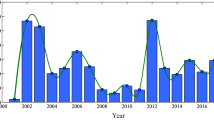
However, it is not realistic to consider over 300 species of birds in one model. Note that of those many bird species, corvids are the most susceptible to infection and comprise an auspicious component of the mortality (Peterson and Marfin 2002). The surveillance data for WNv in southern Ontario, Canada, suggest that the corvids and non-corvids have different disease-induced mortality rates. In Fig. 1, we present the percentages of dead birds from corvids and other bird species in Peel region, Ontario from 2003 to 2005 (Patrick 2005). From Fig. 1, one can see that corvids account up to \(80\,\%\) in 2003, \(90\,\%\) in 2004 and \(75\,\%\) in 2005 of the total of deaths due to WNv.

Fig. 1
figure 1

Percentages of WNv positive dead corvids and non-corvids in Peel region, Ontario, Canada from 2003 to 2005. Data from the surveillance program of Ontario Ministry of Health and Long-Term Care

Full size image

In this paper, we propose a system of ordinary differential equations to model the role of corvids and non-corvids in the transmission of WNv in the mosquito–bird cycle in a single season. The system of eight differential equations can have up to two positive equilibria. The analysis of the model including a backward bifurcation gives a further sub-threshold condition beyond the reproduction number for the control of the virus. The existence of the backward bifurcation also suggests that the long term WNv activity in a given region depends on the initial population sizes of birds and density of mosquitoes. The result of this study suggests that even though dead corvids (American crow) may not be seen in a given region, like in the early years of the endemic of the virus, there might be still a possibility of an outbreak due to the existence of the non-corvids as reservoirs. This study also suggests that it is essential to consider the diversity of the avian species when modeling WNv in an area.

The paper is organized as follows: We formulate the model, with birds being classified as corvids and non-corvids, in Sect. 2; and in the next section, we find and analyze the equilibrium points of the model. The backward bifurcation analysis is given in Sect. 4 with more details in the appendix. Our numerical simulations and discussion are presented in Sect. 5.

2 Model formulation

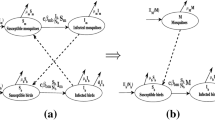
According to the transmission cycle of the virus, we plot the flow chart in Fig. 2. In the flow chart, \( M_{s}(t) \) and \( M_{i}(t) \) are the number of susceptible and infectious mosquitoes at time \( t \) respectively. The total number of mosquitoes is \( N_{m}(t)=M_{s}(t)+M_{i}(t).\) Due to its short life span, a mosquito never recovers from the infection and we do not consider the recovered class in the mosquitoes (Gubler 1989). The number of susceptible, infected and recovered corvid birds at time \( t \) are denoted by \( B_{1s}(t)\), \(B_{1i}(t)\) and \(B_{1r}(t),\) respectively. Similarly, the number of susceptible, infected and recovered non-corvid birds at time \(t\) are denoted by \( B_{2s}(t)\), \(B_{2i}(t)\) and \( B_{2r}(t).\) Thus, \( N_{b1}=B_{1s}+B_{1i}+B_{1r} \) and \( N_{b2}=B_{2s}+B_{2i}+B_{2r}\) are the total number of corvid and non-corvid birds, and the total number of birds will be \( N_{b}=N_{b1}+N_{b2}.\) Moreover, the number of infected birds at time \(t\) is denoted by \(B_{i}(t)=B_{1i}(t)+B_{2i}(t).\) According to Hamer et al. (2009), WNv mosquitoes also feed on mammals (humans, horses, cats, bats, and squirrels, etc.); hence, we let \( A \) be the total of mammals that mosquitoes will bite for blood meals. Since the death due to infection among individuals in these other categories can be ignored, we assume that \( A \) is constant.

Fig. 2
figure 2

Flow chart of the WNv among vector mosquitoes and corvids and non-corvids, host birds

Full size image

Let us define the biting rate \(b_{m}\) of mosquitoes as the average number of bites per mosquito per day. The transmission probability is the probability when an infectious bite produces a new case in a susceptible member of the other species. The probability that a mosquito chooses a particular bird or other animal to bite can be assumed as \(\frac{1}{N_{b}+A}\). Thus, a bird receives in average \( b_{m} \left( \frac{N_{m}}{N_{b}+A}\right) \) bites per unit of time. Then, the infection rate per susceptible bird (corvids or non-corvids) is given by \(\beta _{b} b_{m} \left( \frac{N_{m}}{N_{b}+A}\right) \frac{M_{i}}{N_{m}} =\beta _{b}b_{m}\frac{M_{i}}{N_{b}+A},\) where \( \beta _{b}\) is the WNv transmission probability from mosquitoes to birds. Similarly, the infection rate per susceptible mosquito is \(\beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}\), where \( \beta _{m}\) is the WNv transmission probability from birds to mosquitoes. As was mentioned in the introduction, mosquitoes can transmit WNv vertically (Swayne et al. 2000), and the fraction of progeny of infectious mosquitoes that is infectious is denoted by \(q\), with \(0 \le q <1\).

For the corvid and non-corvid bird populations, we assume constant recruitment rates \(\gamma _{b1}\) and \(\gamma _{b2}\) respectively due to birth and immigration. Usually the bird population remains unchanged over years if there are no avian diseases or environmental changes. For simplicity in this paper, we assume that the natural death rate of non-corvid birds is the same as that of corvid birds \(d_{b}\). Another assumption is that infected corvid and non-corvid birds recover at constant rates of \(\nu _{1}\) and \(\nu _{2},\) respectively. The specific death rates associated with WNv infection in the corvid and non-corvid birds population are \(\mu _{1}\) and \(\mu _{2}\), respectively. The corvids family is more competent than the non-corvids family of birds, i.e, the number of secondary infections produced by individuals of those species is greater than the corresponding number produced by the non-corvids (Komar et al. 2003). Moreover, from Fig. 1, we noticed that the disease mortality rates of the corvids family are significantly greater than the corresponding ones for the non-corvids family (Komar et al. 2003). So we can assume that \(\mu _{1} > \mu _{2}\).

Based on the above assumptions, and extending the ideas in Buck et al. (2009), Cruz-Pacheco et al. (2005) and Wonham et al. (2004), our WNv model is given by

$$\begin{aligned} \left\{ \begin{array}{lcl} \displaystyle \frac{dM_{s}}{dt} &{}=&{} \left( r_{m}M_{s}+(1-q)r_{m}M_{i}\right) \left( 1-\frac{N_{m}}{K_{m}}\right) -d_{m}M_{s} - \beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}M_{s}, \\ \displaystyle \frac{dM_{i}}{dt}&{}=&{} qr_{m}M_{i}\left( 1-\frac{N_{m}}{K_{m}}\right) - d_{m}M_{i}+\beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}M_{s}, \\ \displaystyle \frac{dB_{1s}}{dt}&{}=&{} \gamma _{b1}-d_{b}B_{1s}-\beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}M_{i},\\ \displaystyle \frac{dB_{1i}}{dt}&{}=&{} -(d_{b}+\mu _{1}+\nu _{1})B_{1i}+\beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}M_{i},\\ \displaystyle \frac{dB_{1r}}{dt}&{}=&{} -d_{b}B_{1r}+\nu _{1}B_{1i},\\ \displaystyle \frac{dB_{2s}}{dt}&{}=&{} \gamma _{b2}-d_{b}B_{2s}-\beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}M_{i},\\ \displaystyle \frac{dB_{2i}}{dt}&{}=&{} -(d_{b}+\mu _{2}+\nu _{2})B_{2i}+\beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}M_{i},\\ \displaystyle \frac{dB_{2r}}{dt}&{}=&{} -d_{b}B_{2r}+\nu _{2}B_{2i}, \end{array} \right. \end{aligned}$$
(2.1)

where the definitions and values of the parameters used in the model (2.1) are summarized in Table 1.

Table 1 Parameters in the model for the transmission dynamics of WNv
Full size table

Adding the first two equations of (2.1), the total number of mosquitoes \( N_{m} \) satisfies

$$\begin{aligned} \frac{dN_{m}}{dt}=r_{m}N_{m}\left( 1-\frac{N_{m}}{K_{m}}\right) -d_{m}N_{m}. \end{aligned}$$
(2.2)

For any given positive initial condition \( N_{m}(0)>0 \), the total number of mosquitoes approaches a steady value \(\tilde{M} =\left( 1-\frac{d_{m}}{r_{m}}\right) K_{m}\).

The Eq. (2.2) indicates that the mosquito population will die out if \(d_{m} \ge r_{m},\) while the mosquito population will eventually stabilize at a positive equilibrium \(\tilde{M}\) if \(d_{m}<r_{m}.\) That is why in our work we are assuming the latter case.

For the two species of birds, their totals satisfy

$$\begin{aligned} \frac{dN_{bj}}{dt}=\gamma _{bj}-d_{b}N_{b_{j}}-\mu _{i}B_{ji}, \quad j=1,2, \end{aligned}$$
(2.3)

respectively. From (2.3), one can see that if there is no virus involved (\(B_{ji}=0\)), the total populations of corvids and non-corvids will approach \( \tilde{B_{j}} = \frac{\gamma _{bj}}{d_{b}} \), \( j=1,2 \), respectively.

To better organize the analysis, we denote \( \delta _{j} = d_{b}+\mu _{j}+\nu _{j}\), \(j=1,2\). From the definition of \(\mu _{j} \) and \(\nu _{j} \) we can define \( \frac{1}{\delta _{1}}\) and \( \frac{1}{\delta _{2}} \) as the adjusted infectious period taking into account the mortality rates of corvid and non-corvid birds respectively. Let \(\tilde{B} = \tilde{B_{1}} +\tilde{B_{2}}+A,\) which is the total number of birds and other mammals.

3 Equilibrium points and reproduction number

The model (2.1) has two disease free equilibrium (DFE) points, \( E_{0}\!=\!(0,0,\tilde{B_{1}},0,0,\tilde{B_{2}},0,0) \) and \( E_{1}= (\tilde{M},0,\tilde{B_{1}},0,0,\tilde{B_{2}},0,0)\).

For the DFE \( E_{0} \), one can verify that its Jacobian matrix has eigenvalues \(\lambda _{1}=\lambda _{2}=\lambda _{3}=\lambda _{4}=-d_{b}\), \( \lambda _{5}=-\delta _{1} , \, \lambda _{6}=-\delta _{2} \), \( \lambda _{7}=(qr_{m}-d_{m}) \) and \( \lambda _{8}=(r_{m}-d_{m})>0 \), so \( E_{0} \) is a hyperbolic saddle point.

The local stability of \( E_{1} \) is governed by the basic reproduction number \( R_{0} \) which can be calculated from the next generation matrix for the system (2.1). Note that the model has five infected groups, namely \( M_{i}, B_{1i}, B_{1r}, B_{2i} \) and \( B_{2r}. \) Using the notation of van den Driessche and Watmough (2002), the new infection terms and the remaining transfer terms for those five groups are given below, in partitioned form. In the following, let

$$\begin{aligned} \mathfrak I = \left( \begin{array}{c} qr_{m}M_{i}\left( 1-\frac{N_{m}}{K_{m}}\right) +\beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}M_{s}\\ \beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}M_{i}\\ 0 \\ \beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}M_{i}\\ 0 \end{array} \right) , \quad \upsilon = \left( \begin{array}{c} d_{m}M_{i}\\ \delta _{1}B_{1i} \\ d_{b}B_{1r}-\nu _{1}B_{1i}\\ \delta _{2}B_{2i}\\ d_{b}B_{2r}-\nu _{2}B_{2i} \end{array} \right) . \end{aligned}$$

Thus, at point \( E_{1} \), the Jacobian matrices of \(\mathfrak I \) and \(\upsilon \) with respect to the five groups leads to

$$\begin{aligned} F(E_{1})= \left( \begin{array}{ccccc} qd_{m} &{} \frac{\beta _{m}b_{m}\tilde{M}}{\tilde{B}}&{}0&{} \frac{\beta _{m}b_{m}\tilde{M}}{\tilde{B}} &{} 0 \\ \frac{\beta _{b}b_{m}\tilde{B_{1}}}{\tilde{B}}&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0 \\ \frac{\beta _{b}b_{m}\tilde{B_{2}}}{\tilde{B}}&{}0&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}0 \end{array} \right) , \quad V^{-1}(E_{1}) = \left( \begin{array}{ccccc} \frac{1}{d_{m}} &{} 0&{}0&{} 0&{}0 \\ 0&{}\frac{1}{\delta _{1}}&{}0&{}0&{}0 \\ 0&{}\frac{\nu _{1}}{d_{b}\delta _{1}}&{}\frac{1}{d_{b}}&{}0&{}0 \\ 0&{}0&{}0&{}\frac{1}{\delta _{2}}&{}0 \\ 0&{}0&{}0&{}\frac{\nu _{2}}{d_{b}\delta _{2}}&{}\frac{1}{d_{b}} \end{array}\right) , \end{aligned}$$

where \( F \) is a non-negative matrix and \( V \) is non-singular. It is not difficult to find the basic reproduction number defined by \( R_{0}=\rho (FV^{-1}) \), the spectral radius of the matrix \(FV^{-1}\). If we denote

$$\begin{aligned} \mathfrak R = \sqrt{ \beta _{m}\beta _{b}b_{m}^{2}\frac{\tilde{M}}{d_{m}\tilde{B}^{2}} \left( \frac{\tilde{B}_{1}}{\delta _{1}}+\frac{\tilde{B}_{2}}{\delta _{2}}\right) }, \end{aligned}$$
(3.1)

then the basic reproduction number

$$\begin{aligned} R_{0} =\frac{q}{2} + \frac{1}{2}\sqrt{q^{2}+4\mathfrak R ^{2}}. \end{aligned}$$
(3.2)

Note that for the WNv infection, the number of infections produced by a single corvid or non-corvid bird during its infectious period in a completely susceptible mosquito population is given by \( \beta _{m}b_{m}\frac{\tilde{M}}{\tilde{B}^{2}} \left( \frac{\tilde{B}_{1}}{\delta _{1}}+\frac{\tilde{B}_{2}}{\delta _{2}}\right) \). In the same way, the number of infections in a completely susceptible avian population produced by a single infectious mosquito is given by \(\frac{\beta _{b}b_{m}}{d_{m}}. \) Then \(\mathfrak R \) is the basic reproductive number in the absence of vertical transmission.

The following proposition is a consequence from Theorem 2 of van den Driessche and Watmough (2002):

Proposition 3.1

For system (2.1), the disease-free equilibrium \( E_{1} \) is locally asymptotically stable if \( R_{0}<1 \) and unstable if \( R_{0}>1 \).

The epidemiological implication of Proposition (3.1) is that, in general, when \(R_{0}<1\), a small influx of infected mosquitoes into the community would not generate a large outbreak, and the disease dies out in time. However, we show in the next subsection that the disease may still persist even when \(R_{0} < 1\).

3.1 Endemic equilibrium points

To obtain all the endemic equilibrium points (EEP), or the positive equilibrium points, first we set the right hand sides in Eq. (2.1) equal to zero:

$$\begin{aligned} \left( r_{m}M_{s}+(1-q)r_{m}M_{i}\right) \left( 1-\frac{N_{m}}{K_{m}}\right) -d_{m}M_{s} - \beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}M_{s}&= 0,\quad \end{aligned}$$
(3.3)
$$\begin{aligned} qr_{m}M_{i}\left( 1-\frac{N_{m}}{K_{m}}\right) - d_{m}M_{i}+\beta _{m}b_{m}\frac{B_{1i}+B_{2i}}{N_{b}+A}M_{s}&= 0,\quad \end{aligned}$$
(3.4)
$$\begin{aligned} \gamma _{b}-d_{b}B_{1s}-\beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}M_{i}&= 0,\quad \end{aligned}$$
(3.5)
$$\begin{aligned} -(d_{b}+\mu _{1})B_{1i}-\nu _{1} B_{1i}+\beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}M_{i}&= 0,\quad \end{aligned}$$
(3.6)
$$\begin{aligned} -d_{b}B_{1r}+\nu _{1}B_{1i}&= 0,\quad \end{aligned}$$
(3.7)
$$\begin{aligned} \gamma _{b2}-d_{b}B_{2s}-\beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}M_{i}&= 0,\quad \end{aligned}$$
(3.8)
$$\begin{aligned} -(d_{b}+\mu _{2})B_{2i}-\nu _{2} B_{2i}+\beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}M_{i}&= 0,\quad \end{aligned}$$
(3.9)
$$\begin{aligned} -d_{b}B_{2r}+\nu _{2}B_{2i}&= 0.\quad \end{aligned}$$
(3.10)

Then we write the susceptible and recovered bird variables in terms of \( B_{1i} \) and \( B_{2i} \)

$$\begin{aligned} \begin{array}{l} B_{1s}=\tilde{B_{1}} - \frac{\delta _{1}}{d_{b}}B_{1i}, \\ B_{2s}=\tilde{B_{2}} - \frac{\delta _{2}}{d_{b}}B_{2i}, \\ B_{1r} = \frac{\nu _{1}}{d_{b}}B_{1i}, \\ B_{2r} = \frac{\nu _{2}}{d_{b}}B_{2i}. \end{array} \end{aligned}$$
(3.11)

By adding (3.3) and (3.4), we have \(N_{m} \left( N_{m}-K_{m}\left( 1-\frac{d_{m}}{r_{m}}\right) \right) =0 \). At any positive equilibrium, we have \( N_{m} = M_{s}+M_{i}=K_{m}\left( 1-\frac{d_{m}}{r_{m}}\right) = \tilde{M} \).

In case \( M_{s}+M_{i}=\tilde{M} \), it follows from (3.6), (3.9) and (3.11) that one can verify

$$\begin{aligned} B_{2i} = \frac{\delta _{1}\tilde{B_{2}}}{\delta _{2}\tilde{B_{1}}}B_{1i}. \end{aligned}$$
(3.12)

From Eq. (3.4), we have \( (1-q)d_{m}M_{i}=\beta _{m}b_{m}M_{s}\frac{B_{1i}+B_{2i}}{N_{b}+A} \), and then

$$\begin{aligned} M_{i}=\frac{\beta _{m}b_{m}\tilde{M}(B_{1i}+B_{2i})}{(1-q)d_{m}(N_{b}+A) +\beta _{m}b_{m}(B_{1i}+B_{2i})}. \end{aligned}$$
(3.13)

Equations (3.6) and (3.9) imply that

$$\begin{aligned} B_{1i}+B_{2i} =\left( \frac{\beta _{b}b_{m}M_{i}}{N_{b}+A}\right) \left( \frac{\tilde{B_{1}}}{\delta _{1}}+\frac{\tilde{B_{2}}}{\delta _{2}} -\frac{B_{1i}}{d_{b}}-\frac{B_{2i}}{d_{b}}\right) . \end{aligned}$$
(3.14)

Eliminating \( M_{i} \) from Eqs. (3.13) and (3.14), a straight forward calculation gives that if an endemic equilibrium exists, its \(B_{i}\)-coordinates should satisfy the following quadratic equation:

$$\begin{aligned} c_{20}B_{1i}^{2}+c_{11}B_{1i}B_{2i}+c_{02}B_{2i}^{2}+c_{10}B_{1i} +c_{01}B_{2i}+c_{00}=0, \end{aligned}$$
(3.15)

where

$$\begin{aligned} \begin{array}{lcl} c_{20} &{}=&{} (1-q)d_{m}\left( \frac{\mu _{1}}{d_{b}}\right) ^{2}-\beta _{m}b_{m}\frac{\mu _{1}}{d_{b}},\\ c_{11} &{}=&{} 2(1-q)d_{m} \frac{\mu _{1}}{d_{b}} \frac{\mu _{2}}{d_{b}}-\beta _{m}b_{m}(\frac{\mu _{1}}{d_{b}} +\frac{\mu _{2}}{d_{b}}),\\ c_{02} &{}=&{} (1-q)d_{m}\left( \frac{\mu _{2}}{d_{b}}\right) ^{2}-\beta _{m}b_{m}\frac{\mu _{2}}{d_{b}},\\ c_{10} &{}=&{}\beta _{m}b_{m}\tilde{B}-2(1-q)d_{m}\tilde{B}\frac{\mu _{1}}{d_{b}} +\beta _{m}\beta _{b}b_{m}^{2}\frac{\tilde{M}}{d_{b}},\\ c_{01} &{}=&{} \beta _{m}b_{m}\tilde{B}-2(1-q)d_{m}\tilde{B}\frac{\mu _{2}}{d_{b}} + \beta _{m}\beta _{b}b_{m}^{2}\frac{\tilde{M}}{d_{b}},\\ c_{00} &{}=&{} (1-q)d_{m}\tilde{B}^{2}-\tilde{M}\beta _{m}\beta _{b}b_{m}^{2}\left( \frac{\tilde{B_{1}}}{\delta _{1}}+\frac{\tilde{B_{2}}}{\delta _{2}}\right) .\end{array} \end{aligned}$$
(3.16)

Using the expression for \(R_{0}\) in (3.2) we can write

$$\begin{aligned} \beta _{b}\beta _{m}b_{m}^{2}\frac{\tilde{M}}{\tilde{B}^{2}}\left( \frac{\tilde{B_{1}}}{\delta _{1}}+\frac{\tilde{B_{2}}}{\delta _{2}}\right) = d_{m}(R_{0}^{2}-qR_{0}), \end{aligned}$$

so we can rewrite \( c_{00} \) in (3.16) as

$$\begin{aligned} c_{00}= \tilde{B}^{2} d_{m}\left( 1-q+R_{0}\right) (1-R_{0}). \end{aligned}$$
(3.17)

To obtain the positive equilibrium points, we find the intersection of the line (3.12) with the quadratic curve (3.15).

For the curve defined by (3.15), let \(D=c_{02} c_{20} - \frac{1}{4}c_{11}^{2}.\) One can verify that \( D = - \frac{\beta _{m}^{2}b_{m}^{2}}{4d_{b}^{2}}\left( \mu _{1}- \mu _{2}\right) ^{2} <0.\) Therefore, the quadratic curve (3.15) is a hyperbola. In order to better understand the intersection of this hyperbola with line (3.12), we make the following rotation of \( B_{1i} \) and \( B_{2i} \) axes by letting

$$\begin{aligned} \begin{array}{lcl} x &{}=&{} \left[ (1-q)d_{m}\frac{\mu _{1}}{d_{b}}-\beta _{m}b_{m}\right] B_{1i} +\left[ (1-q)d_{m}\frac{\mu _{2}}{d_{b}}-\beta _{m}b_{m}\right] B_{2i},\\ y &{}=&{} \frac{\mu _{1}}{d_{b}}B_{1i} + \frac{\mu _{2}}{d_{b}}B_{2i}. \end{array} \end{aligned}$$
(3.18)

The inverse of the rotation operator is given by

$$\begin{aligned} \begin{array}{lcl} B_{1i}&{}=&{}\frac{1}{\beta _{m}b_{m} ( \mu _{1}-\mu _{2} ) } ( \mu _{2}x - [(1-q)d_{m}\mu _{2}-\beta _{m}b_{m}d_{b} ]y ), \\ B_{2i}&{}=&{}\frac{1}{\beta _{m}b_{m} ( \mu _{1}-\mu _{2} ) } ( -\mu _{1}x + [(1-q)d_{m}\mu _{1}-\beta _{m}b_{m}d_{b} ]y ), \end{array} \end{aligned}$$
(3.19)

provided \( \mu _{1} \ne \mu _{2} \). By using this transformation we can conclude that,

$$\begin{aligned} N_{b}+A = \tilde{B}- \frac{\mu _{1}}{d_{b}}B_{1i}-\frac{\mu _{2}}{d_{b}}B_{2i} = \tilde{B}-y. \end{aligned}$$
(3.20)

Using the new coordinates, it follows from (3.18) that the line (3.12) and the hyperbola (3.15) become

$$\begin{aligned}&L {:} \,\,\, y = \frac{x}{k},\end{aligned}$$
(3.21)
$$\begin{aligned}&C {:} \,\,\, y =\left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) \frac{ x-x_{0} }{x-x_{1}}, \end{aligned}$$
(3.22)

where

$$\begin{aligned} \begin{array}{lcl}k &{}=&{} (1-q)d_{m}-\frac{ \beta _{m}b_{m}d_{b}\left( \frac{\tilde{B_{1}}}{\delta _{1}} +\frac{\tilde{B_{2}}}{\delta _{2}}\right) }{\mu _{1} \frac{\tilde{B_{1}}}{\delta _{1}} + \mu _{2} \frac{\tilde{B_{2}}}{\delta _{2}}}, \\ x_{0} &{}=&{} \frac{c_{00}}{ \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}}, \\ x_{1} &{}=&{} (1-q)d_{m}\left( \tilde{B}-\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) . \end{array} \end{aligned}$$
(3.23)

Since \( 1>\mu _{1}>\mu _{2}>0 \), \( q\in (0,1) \), and from the Table 1, we have \( (1-q)d_{m}\mu _{2}-\beta _{m}b_{m}d_{b} > 0, \) then \((1-q)d_{m}\mu _{1}-\beta _{m}d_{b} > 0\), and then \(0<k<1 \). For the equation of a hyperbola (3.22) whose (mutually orthogonal) asymptotes are \(x= x_{1}\) and \(y= \tilde{B} + \beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\) respectively, the horizontal asymptote intersects the \(y\)-axis at a positive point while the intersection of the vertical asymptote with the \(x\)-axis depends on the sign of \( x_{1}.\)

To obtain the intersection between the hyperbola (3.22) and the line (3.21), we have to find the roots of the following equation:

$$\begin{aligned} x^{2}- \left[ x_{1} + \left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) k \right] x + c_{00} k =0. \end{aligned}$$
(3.24)

The discriminant \(\Delta \) for the quadratic equation (3.24) satisfies,

$$\begin{aligned} \Delta =\left[ ((1-q)d_{m}+k)\tilde{B}- ((1-q)d_{m}-k) \beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right] ^{2}-4kc_{00}. \end{aligned}$$

Depending on the sign of \(\Delta \), we can have up to two positive equilibria. Let \(E=(M_{s}^{*},\) \(M_{i}^{*},\) \(B_{1s}^{*},\) \(B_{1i}^{*},\) \(B_{1r}^{*},\) \(B_{2s}^{*}, B_{2i}^{*}, B_{2r}^{*})\) be any one of the arbitrary endemic equilibrium of the model (2.1), represented as

$$\begin{aligned} B_{1i}^{*}&= \frac{\frac{d_{b}}{\delta _{1}}\tilde{B_{1}}x}{k\left( \mu _{1} \frac{\tilde{B_{1}}}{\delta _{1}}+\mu _{2}\frac{\tilde{B_{2}}}{\delta _{2}}\right) }, \ \ \ B_{2i}^{*}=\frac{\delta _{1}\tilde{B_{2}}}{\delta _{2}\tilde{B_{1}}}B_{1i}^{*},\\ B_{1s}^{*}&= \tilde{B_{1}} - \frac{\delta _{1}}{d_{b}}B_{1i}^{*}, \ \ \ B_{2s}^{*}=\tilde{B_{2}} - \frac{\delta _{2}}{d_{b}}B_{2i}^{*}, \ \ \ B_{1r}^{*} = \frac{\nu _{1}}{d_{b}}B_{1i}^{*}, \ \ \ B_{2r}^{*} = \frac{\nu _{2}}{d_{b}}B_{2i}^{*},\\ M_{i}^{*}&= \frac{\beta _{m}b_{m}\tilde{M}(B_{1i}^{*}+B_{2i}^{*})}{(1-q)d_{m}\left( \tilde{B} - \frac{\mu _{1}}{d_{b}}B_{1i}^{*}-\frac{\mu _{2}}{d_{b}}B_{2i}^{*}\right) +\beta _{m}b_{m}(B_{1i}^{*}+B_{2i}^{*})}, \ \ \ M_{s}^{*}=\tilde{M} - M_{i}^{*}. \end{aligned}$$

If \( R_{0} > 1 \), then \( c_{00} < 0 \) and we always have only one positive root,

$$\begin{aligned} x_{E_{2}}=\frac{\left[ x_{1} + \left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) k \right] +\sqrt{\Delta }}{2}, \end{aligned}$$

and we denote the corresponding equilibrium by \(E_{2}\).

If \( R_{0} =1,\) then \( c_{00}=0 \); subsequently, we have one positive root if

$$\begin{aligned} x_{1} + \left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) k >0. \end{aligned}$$

This condition can be written in another form as:

$$\begin{aligned} \frac{\beta _{b}b_{m}}{d_{b}}\frac{\tilde{M}}{\tilde{B}} <\left( \frac{(1-q)d_{m}+k}{(1-q)d_{m}-k}\right) . \end{aligned}$$
(3.25)

Now we consider the case \( R_{0} < 1 \). Since \( c_{00} > 0 \), we always have one or two positive roots if \( \Delta \ge 0 \).

First if \( x_{1}>x_{0} \), then

$$\begin{aligned} \frac{(1-q)d_{m}}{d_{b}}\tilde{B} > \beta _{m}b_{m}\left( \frac{\tilde{B_{1}}}{\delta _{1}} + \frac{\tilde{B_{2}}}{\delta _{2}}\right) > (1-q)d_{m}\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}^{2}}, \end{aligned}$$

which implies \( \tilde{B}>\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} \). Since \( c_{00}>0 \), then \( x_{0}>0 \) and \( R_{0}<1 \). Moreover, the hyperbolic curve \( C \) will intersect the \(x, y\) axes at positive points as shown in Fig. 3a.

Fig. 3
figure 3

If \(x_{1} \ge x_{0} \), system does not have any endemic equilibrium point (EEP). a \(x_{1}>x_{0} \ \ \ (R_{0}<1)\), no EEP. b \(x_{1}=x_{0} \ \ \ (R_{0}<1)\), no EEP

Full size image

So the line \(L\) has two positive intersection points with the hyperbola \(C\) as shown in Fig. 3a, with one being above the line \(y=\tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\). Let x-coordinates of \(L\) and \(C\) with \(y=\tilde{B}\) be denoted by \(x_{10}\) and \(x_{11}\), then (3.21) and (3.22) give,

$$\begin{aligned} x_{10} = k\tilde{B}= \left( (1-q)d_{m}-\frac{ \beta _{m}b_{m}d_{b}\left( \frac{\tilde{B_{1}}}{\delta _{1}} +\frac{\tilde{B_{2}}}{\delta _{2}}\right) }{\mu _{1} \frac{\tilde{B_{1}}}{\delta _{1}} + \mu _{2} \frac{\tilde{B_{2}}}{\delta _{2}}}\right) \tilde{B}, \end{aligned}$$

and

$$\begin{aligned} x_{11}=\left( (1-q)d_{m}-\frac{ \beta _{m}b_{m}d_{b}\left( \frac{\tilde{B_{1}}}{\delta _{1}} +\frac{\tilde{B_{2}}}{\delta _{2}}\right) }{\tilde{B}}\right) \tilde{B}. \end{aligned}$$

As shown in Fig. 3a, one can verify that \(x_{10}<x_{11}\) which means the other intersection of \(L\) with \(C\) is also above the line \(y=\tilde{B}\). Thus, from (3.20) that total number of birds would be negative, so this case does not occur biologically.

If \( x_{1}=x_{0} \), then \( c_{00}=(1-q)d_{m}\left( \tilde{B^{2}}-\beta _{b}^{2}b_{m}^{2}\frac{\tilde{M}^{2}}{d_{b}^{2}}\right) >0 \), which implies \( R_{0}<1 \). Note in this case the hyperbola \(C\) will be reduced to a line \( y= \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\), as shown in Fig. 3b. Thus, we have one positive equilibrium point that satisfies \( y = \tilde{B} + \beta _{b}b_{m}\frac{M_{i}}{d_{b}} \). Again, from (3.20) the total number of birds would be negative, and this case has no positive equilibrium. Hence, there is no positive equilibria if \(x_{1} \ge x_{0}\). Now we consider the case \( x_{1}<x_{0}.\) Here we need to consider the following five cases.

Case 1

If \( x_{1}<0\) with \(x_{0}<0 \), then \( R_{0}>1 \), and therefore \( c_{00}<0 \) which leads to \( \Delta >0 \). Consequently, the hyperbolic curve \(C\) intersects the x-axis with one negative component. So there is one intersecting point as shown in Fig. 4. From the case \( x_{1}>x_{0} \) we proved that \(x_{10}<x_{11}\) which leads to the intersection between \(L \) and \(C\) at point below the line \(y=\tilde{B}\). Thus, it follows from (3.20) that the total number of birds would be positive, so if \( R_{0}>1 \) there exists a unique endemic equilibrium.

Fig. 4
figure 4

Case 1 \(x_{1}<x_{0} \) and \( x_{0}<0,\) \((R_{0}>1),\) system always has a unique EEP

Full size image

Case 2

If \( x_{1}<0\) with \( x_{0}=0 \), then \( R_{0}=1 \). Therefore, the hyperbolic curve \(C\) passes through the origin, and we have \( \Delta =\left( x_{1} + \left( \tilde{B}+\beta _{b}\frac{\tilde{M}}{d_{b}}\right) k\right) ^{2} \). In this case and under condition (3.25) we have one positive intersection point; otherwise, we will not have any positive intersection point. These subcases are shown in Fig. 5a, b. Also by the same way as in Case 1, this intersection point is below the line \(y=\tilde{B}\).

Fig. 5
figure 5

Case 2 \(x_{1}<x_{0} \) with \( x_{0}=0,\) \((R_{0}=1),\) we have at most one EEP. a No EEP. b One EEP

Full size image

Case 3

If \( x_{1}<0\) with \( x_{0}>0 \), then \( \tilde{B}<\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} \) and \( R_{0}<1\). Therefore, under condition (3.25), we can see that we do not have any positive intersection points if \( \Delta <0 \) and we have one or two intersection points if and only if \( \Delta \ge 0 \). Moreover, from the definition of \(c_{00}\) in Eq. (3.16), we can conclude that \( c_{00}<k\tilde{B}\left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} \right) \) which means \(\frac{1}{k} x_{0}<\tilde{B} \) and then \(x_{0}<x_{10}<x_{11}\). Then any intersection between \(L\) and \(C\) occurs at a point below the line \( y=\tilde{B} \). It is important to note here that if \( \Delta = 0 \), then we denote the basic reproduction number by \( R_{0}=R_{0}^{1}.\) Case 3 is shown in Fig. 6.

Fig. 6
figure 6

Case 3 \(x_{1}<x_{0} \), \( x_{1} <0\) with \( x_{0}>0,\) \((R_{0}<1),\) we have at most two EEPs. a \(\Delta <0\) no EEP. b \(\Delta =0\) one EEP. c \(\Delta >0\) two EEP

Full size image

Case 4

If \( x_{1}=0\) then \( \tilde{B}=\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} \) and

$$\begin{aligned} \Delta = - 4 k \tilde{B} \beta _{m}b_{m}\left( \tilde{B}-\left( \frac{\mu _{1}}{\delta _{1}}\tilde{B_{1}} +\frac{\mu _{2}}{\delta _{2}}\tilde{B_{2}}\right) \right) < 0. \end{aligned}$$

So we do not have any real intersection points.

Case 5

If \( x_{1}>0\) with \( x_{0}>0 \), then \( R_{0}<1 \) and

$$\begin{aligned} \frac{\beta _{m}b_{m}d_{b}}{(1-q)d_{m}}\left( \frac{\tilde{B_{1}}}{\delta _{1}} + \frac{\tilde{B_{2}}}{\delta _{2}}\right) < \beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} < \tilde{B}. \end{aligned}$$

By the same way in Case 3, we can have a maximum of two positive intersection points. However, in the case that we have positive intersection points, we can conclude that \( c_{00}>k\tilde{B}\left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}} \right) \) which means \(\frac{1}{k} x_{0}>\tilde{B} \) and then \(x_{11}>x_{0}\). This leads to the intersection between \(L\) and \(C\) at a point above the line \( y=\tilde{B} \). Hence, from (3.20) the total number of birds is negative, and this case does not occur biologically. Case 5 is shown in Fig. 7.

Fig. 7
figure 7

Case 5. If \(x_{1} < x_{0}\) with \(x_{1} >0,\) \((R_{0}<1)\), no EEP. a \(\Delta <0\). b \(\Delta =0\). c \(\Delta >0\)

Full size image

Now, if we use \(x_{E_{2}}\) and \(x_{E_{3}}\) to define equilibrium points \(E_{2} \) and \(E_{3}\) we are able to state the principal results about the existence and number of the equilibrium points.

Proposition 3.2

If we suppose that \((1-q)d_{m}\mu _{2}-\beta _{m}b_{m}d_{b} > 0,\) the system (2.1) can have up to two positive equilibrium. More precisely,

  1. 1.

    If \( R_{0}>1 \), there exists a unique endemic equilibrium \(E_{2}.\)

  2. 2.

    If \( R_{0}<1 \), then

    1. (a)

      If \(\frac{d_{b}}{\beta _{b}b_{m}}<\frac{\tilde{M}}{\tilde{B}} < \frac{d_{b}}{\beta _{b}b_{m}}\left( \frac{(1-q)d_{m}+k}{(1-q)d_{m}-k}\right) \) and \(\Delta > 0 \), there exists two endemic equilibria \(E_{2}\) and \(E_{3}\).

    2. (b)

      If \(\frac{d_{b}}{\beta _{b}b_{m}}<\frac{\tilde{M}}{\tilde{B}} < \frac{d_{b}}{\beta _{b}b_{m}}\left( \frac{(1-q)d_{m}+k}{(1-q)d_{m}-k}\right) \) and \( \Delta = 0, \) these two equilibria coalesce.

    3. (c)

      Otherwise, there is no endemic equilibrium.

  3. 3.

    If \( R_{0}=1 \), then

    1. (a)

      If \(\frac{\tilde{M}}{\tilde{B}} < \frac{d_{b}}{\beta _{b}b_{m}}\left( \frac{(1-q)d_{m}+k}{(1-q)d_{m}-k}\right) ,\) there exists a unique endemic equilibrium \(E_{2}.\)

    2. (b)

      Otherwise, there is no endemic equilibrium.

The epidemiological implication of Proposition (3.2) is that when \(R_{0}<1\) the virus may or may not become endemic (at any region) depending on the ratio between the quantity of mosquitoes on one hand and that of birds and other mammals on the other hand.

3.2 Local stability of \( E_{2}\) and \( E_{3} \)

In this section, we study the local stability of the EEP in the system (2.1). By using the Jacobian matrix, at any equilibrium point, the eigenvalues satisfy: the first \( -(r_{m}-d_{m})\), the second \( -d_{b} \) that is repeated four times, as well as the eigenvalues from the matrix \( W \) with

$$\begin{aligned} W=\left( \!\begin{array}{c@{\quad }c@{\quad }c} -(1-q)d_{m}\frac{\tilde{M}}{M_{s}}&{} \frac{\left( (1-q)d_{m}\frac{\mu _{1}}{d_{b}}-\beta _{m}b_{m}\right) M_{i} +\beta _{m}b_{m}\tilde{M}}{N_{b}+A} &{}\frac{\left( (1-q)d_{m}\frac{\mu _{2}}{d_{b}}-\beta _{m}b_{m}\right) M_{i} +\beta _{m}b_{m}\tilde{M}}{N_{b}+A} \\ \beta _{b}b_{m}\frac{B_{1s}}{N_{b}+A}&{} -\left( \delta _{1} + \delta _{1} \frac{\left( \beta _{b}b_{m}\frac{M_{i}}{d_{b}} - \frac{\mu _{1}}{d_{b}}B_{1i} \right) }{N_{b}+A} \right) &{} \delta _{1} \frac{\frac{\mu _{2}}{d_{b}}B_{1i}}{N_{b}+A} \\ \beta _{b}b_{m}\frac{B_{2s}}{N_{b}+A}&{} \delta _{2} \frac{\frac{\mu _{1}}{d_{b}}B_{2i}}{N_{b}+A}&{} - \left( \delta _{2} + \delta _{2} \frac{\left( \beta _{b}b_{m}\frac{M_{i}}{d_{b}} - \frac{\mu _{2}}{d_{b}}B_{2i} \right) }{N_{b}+A}\right) \end{array}\!\right) \!. \end{aligned}$$

We can find the eigenvalues of \( W \) by finding the roots of the cubic equation

$$\begin{aligned} \lambda ^{3}+A_{2}\lambda ^{2}+A_{1}\lambda + A_{0}=0, \end{aligned}$$
(3.26)

where

$$\begin{aligned} A_{2}&= \displaystyle (1-q)d_{m}\frac{\tilde{M}}{M_{s}} +(\delta _{1}+\delta _{2})+ \delta _{1}\left( \frac{\frac{\beta _{b}b_{m}M_{i}}{d_{b}} -\frac{\mu _{1}}{d_{b}}B_{1i}}{N_{b}+A}\right) +\delta _{2}\left( \frac{\frac{\beta _{b}b_{m}M_{i}}{d_{b}}-\frac{\mu _{2}}{d_{b}}B_{2i}}{N_{b}+A}\right) ,\\ A_{1}&= \displaystyle (1-q)d_{m} \frac{\tilde{M}}{M_{s}} (\delta _{1}+\delta _{2}) + \delta _{1}\delta _{2} \left( 1+ \frac{\frac{\beta _{b}b_{m}M_{i}}{d_{b}}}{N_{b}+A}\right) \left( 1+ \frac{\frac{\beta _{b}b_{m}M_{i}}{d_{b}}-\frac{\mu _{1}}{d_{b}}B_{1i} -\frac{\mu _{2}}{d_{b}}B_{2i}}{N_{b}+A} \right) \\&\displaystyle +(1\!-\!q)d_{m} \frac{\tilde{M}}{M_{s}} \left( \frac{\delta _{1}\left( \frac{\beta _{b}b_{m}M_{i}}{d_{b}} \!-\!\frac{\mu _{1}}{d_{b}}B_{1i}\right) +\delta _{2}\left( \frac{\beta _{b}b_{m}M_{i}}{d_{b}} \!-\!\frac{\mu _{2}}{d_{b}}B_{1i}\right) }{N_{b}+A} \right) \!-\!\beta _{m}b_{m} \frac{\tilde{M}}{M_{i}}\frac{\delta _{1} B_{1i}\!+\!\delta _{2}B_{2i}}{N_{b}\!+\!A}\\&\displaystyle -\frac{\delta _{1}\left( (1-q)d_{m}\frac{\mu _{1}}{d_{b}} -\beta _{m}b_{m}\right) B_{1i} +\delta _{2}\left( (1-q)d_{m}\frac{\mu _{2}}{d_{b}} -\beta _{m}b_{m}\right) B_{2i}}{N_{b}+A},\\ A_{0}&= \displaystyle \delta _{1}\delta _{2} (1-q)d_{m}\left( 1+\frac{\beta _{b}b_{m}\frac{M_{i}}{d_{b}}}{N_{b}+A}\right) \frac{\tilde{M}}{M_{s}}\left( \frac{\frac{\beta _{b}b_{m}M_{i}}{d_{b}}-\frac{\mu _{1}}{d_{b}}B_{1i} - \frac{\mu _{2}}{d_{b}}B_{2i}}{N_{b}+A}\right) \\&-\delta _{1}\delta _{2} \left( 1+\frac{\beta _{b}b_{m}\frac{M_{i}}{d_{b}}}{N_{b}+A}\right) \frac{\left( (1-q)d_{m}\frac{\mu _{1}}{d_{b}}-\beta _{m}b_{m}\right) B_{1i} +\left( (1-q)d_{m}\frac{\mu _{2}}{d_{b}} -\beta _{m}b_{m}\right) B_{2i}}{N_{b}+A}. \end{aligned}$$

For any endemic equilibrium point \(E=(M_{s}^{*},M_{i}^{*},B_{1s}^{*},B_{1i}^{*},B_{1r}^{*}, B_{2s}^{*},B_{2i}^{*},B_{2r}^{*})\) of the system (2.1), we have the following proposition to determine the sign of the eigenvalues and the roots for the characteristic equation (3.26).

Proposition 3.3

For the system (2.1), \(E_{2}\) is stable while \( E_{3}\) is unstable when they exist.

Proof

For both \(E_{2}\) and \(E_{3}\), from Eq. (3.6) we have \( \beta _{b}b_{m}\frac{M_{i}^{*}}{d_{b}} > \frac{\delta _{1}}{d_{b}}B_{1i}^{*} > \frac{\mu _{1}}{d_{b}}B_{1i}^{*}.\) Similarly by (3.9) we have \( \beta _{b}b_{m}\frac{M_{i}^{*}}{d_{b}} > \frac{\mu _{2}}{d_{b}}B_{2i}^{*} \). Hence, \( A_{2}>0 \) (in (3.26)) for both \(E_{2}\) and \(E_{3}.\)

By using Eqs. (3.3) to (3.10) and (3.13) we can conclude that, for any positive equilibrium with \( M_{s}^{*}=\frac{\tilde{M}(1-q)d_{m}(\tilde{B}-y_{E})}{(1-q)d_{m}\tilde{B}-x_{E}} \) and \(M_{i}^{*}=\frac{\tilde{M}((1-q)d_{m}y_{E}-x_{E})}{(1-q)d_{m}\tilde{B}-x_{E}},\) we can rewrite \(A_{0}\) as

$$\begin{aligned} A_{0} \!=\! \frac{\delta _{1}\delta _{2}}{k(\tilde{B} \!-\! y_{E})^{2}} \left( 1\!+\!\frac{\beta _{b}b_{m}\frac{M_{i}^{*}}{d_{b}}}{\tilde{B} - y_{E}}\right) \left( 2x_{E}^{2}\!-\!x_{E}\left[ ((1\!-\!q)d_{m}\!+\!k)\tilde{B}\!-\!((1\!-\!q)d_{m}\!-\!k)\beta _{b}\frac{\tilde{M}}{d_{b}}\right] \right) . \end{aligned}$$

If \( R_{0}<1 \) and case 3(a) of Proposition (3.2) holds, then we have two positive equilibrium points denoted by \( (x_{E_{2}},y_{E_{2}})\) and \((x_{E_{3}},y_{E_{3}})\). For \(E_{3}\) from (3.24) we can see that

$$\begin{aligned} x_{E_{3}}<\frac{1}{2}\left[ ((1-q)d_{m}+k)\tilde{B}-((1-q)d_{m}-k)\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right] , \end{aligned}$$

therefore \( A_{0} < 0,\) the roots of (3.26) will have different signs, and \(E_{3}\) is unstable. While for \(E_{2}\), from (3.24) we have \(x_{E_{2}}>\frac{1}{2}\left[ ((1\!-\!q)d_{m}\!+\!k)\tilde{B}\!-\!((1\!-\!q)d_{m}\!-\!k)\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right] . \) Hence, we conclude that \(A_{0}>0.\)

In the same way, if \(R_{0}>1,\) from Proposition (3.2), we have one positive equilibrium point denoted by \( (x_{E_{2}},y_{E_{2}}) \) and from (3.24),

$$\begin{aligned} x_{E_{2}}>\frac{1}{2}\left[ ((1-q)d_{m}+k)\tilde{B}-((1-q)d_{m}-k)\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right] \end{aligned}$$

and \( A_{0}>0.\)

Finally, to prove that all roots of Eq. (3.26) are negative at \(E_{2}\), in the two cases \(R_{0}<1\) and \(R_{0}>1\), we need to prove that if \( A_{0}>0 \) then \( A_{1}A_{2} - A_{0}>0.\)

By (3.4) we conclude that at \(E_{2}\), \((1-q)d_{m}M_{i}^{*}>\beta _{m}b_{m}M_{s}^{*}\frac{B_{1i}^{*}}{N_{b}^{*}+A},\) so this leads to \( (1-q)d_{m} \frac{\tilde{M}}{M_{s}^{*}}> \beta _{m}b_{m} \frac{\tilde{M}}{M_{i}^{*}}\frac{B_{1i}^{*}}{N_{b}^{*}+A},\) and in the same way, \( (1-q)d_{m} \frac{\tilde{M}}{M_{s}^{*}} > \beta _{m}b_{m} \frac{\tilde{M}}{M_{i}^{*}}\frac{B_{2i}^{*}}{N_{b}^{*}+A} \). Therefore,

$$\begin{aligned} \delta _{1} \left[ (1\!-\!q)d_{m} \frac{\tilde{M}}{M_{s}^{*}} \!-\! \beta _{m}b_{m} \frac{\tilde{M}}{M_{i}^{*}}\frac{B_{1i}^{*}}{N_{b}^{*}\!+\!A}\right] \!+\! \delta _{2}\left[ (1\!-\!q)d_{m} \frac{\tilde{M}}{M_{s}^{*}} \!-\! \beta _{m}b_{m} \frac{\tilde{M}}{M_{i}^{*}}\frac{B_{2i}^{*}}{N_{b}^{*}\!+\!A}\right] > 0.\nonumber \\ \end{aligned}$$
(3.27)

From (3.6) at \(E_{2}\) we can conclude that \( \frac{\beta _{b}b_{m}M_{i}^{*}}{d_{b}} > \frac{\mu _{1}}{d_{b}}B_{1i}^{*} + \frac{\mu _{2}}{d_{b}}B_{2i}^{*} \). Then we have

$$\begin{aligned} \delta _{1}\delta _{2} \left( 1+ \frac{\frac{\beta _{b}b_{m}M_{i}^{*}}{d_{b}}}{N_{b}^{*}+A}\right) \left( 1+ \frac{\frac{\beta _{b}b_{m}M_{i}^{*}}{d_{b}} -\frac{\mu _{1}}{d_{b}}B_{1i}^{*}-\frac{\mu _{2}}{d_{b}}B_{2i}^{*}}{N_{b}^{*}+A} \right) > 0. \end{aligned}$$
(3.28)

It follows from (3.27) and (3.28) that \( A_{0} > 0 \) implies that \( A_{1}>0 \) and

$$\begin{aligned}&A_{1}A_{2} - A_{0}\\&\quad = \displaystyle \left( (1-q)^{2}d_{m}^{2} \frac{\tilde{M}}{M_{s}^{*}} +A_{1}\right) \left[ (\delta _{1}+\delta _{2})+ \frac{\delta _{1}\left( \frac{\beta _{b}b_{m}M_{i}^{*}}{d_{b}} -\frac{\mu _{1}}{d_{b}}B_{1i}^{*}\right) +\delta _{2}\left( \frac{\beta _{b}b_{m}M_{i}^{*}}{d_{b}} -\frac{\mu _{2}}{d_{b}}B_{1i}^{*}\right) }{N_{b}^{*}+A} \right] \\&\qquad \displaystyle + \delta _{1}\delta _{2} \left[ 1+\frac{\beta _{b}b_{m}\frac{M_{i}^{*}}{d_{b}}}{N_{b}^{*}+A}\right] \frac{\left( (1-q)d_{m}\frac{\mu _{1}}{d_{b}}-\beta _{m}b_{m}\right) B_{1i}^{*} +\left( (1-q)d_{m}\frac{\mu _{2}}{d_{b}}-\beta _{m}b_{m}\right) B_{2i}^{*}}{N_{b}^{*}+A}\\&\qquad -(1-q)d_{m}\frac{\tilde{M}}{M_{s}^{*}} \left( \frac{\delta _{1}\left( (1-q)d_{m}\frac{\mu _{1}}{d_{b}} -\beta _{m}b_{m}\right) B_{1i}^{*}+\delta _{2}\left( (1-q)d_{m}\frac{\mu _{2}}{d_{b}} -\beta _{m}b_{m}\right) B_{2i}^{*}}{N_{b}^{*}+A}\right) . \end{aligned}$$

Thus \(A_{1}A_{2}-A_{0}>0,\) and the proof is complete.\(\square \)

4 Backward bifurcation

To discuss the backward bifurcation, we choose \( \delta _{1}= \mu _{1} + \nu _{1} +d_{b}\) and \(\delta _{2}= \mu _{2} + \nu _{2} +d_{b} \) as the bifurcation parameters. We will express the two conditions \( R_{0}=1 \) and \(\Delta = 0\) in terms of the parameters \( \delta _{1} \) and \( \delta _{2} \) \((\delta _{1}>\delta _{2})\), and then present the bifurcation diagram in \(( \delta _{1}, \delta _{2})\) plane.

First, with \( R_{0}=1 \), Eq. (3.2) can be rewritten as,

$$\begin{aligned} \delta _{1}= \alpha \tilde{B_{1}} + \frac{\alpha ^{2} \tilde{B_{1}} \tilde{B_{2}}}{\delta _{2}-\alpha \tilde{B_{2}}} \end{aligned}$$
(4.1)

where \( \alpha = \frac{\beta _{b}\beta _{m}b_{m}^{2}\tilde{M}}{(1-q)d_{m}\tilde{B}^{2}}.\)

The second curve can be obtained by letting \(\Delta =0 \) in Eq. (3.24). Solving \(\Delta =0 \) in terms of \(\delta _{1}\) one can get

$$\begin{aligned} \delta _{1}= \rho \tilde{B_{1}} +\frac{\rho ^{2} \tilde{B_{1}} \tilde{B_{2}}}{\delta _{2}-\rho \tilde{B_{2}}}, \end{aligned}$$
(4.2)

where

$$\begin{aligned} \rho = \frac{\beta _{b}\beta _{m}b_{m}^{2}\tilde{M}}{(1-q)d_{m}\tilde{B}^{2}-\frac{1}{4k}\left( ((1-q)d_{m}+k)\tilde{B} -((1-q)d_{m}-k)\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) ^{2} }. \end{aligned}$$

In the positive quadrant of the parameters plane \((\delta _{1}, \delta _{2}),\) Eq. (4.1) is a hyperbola, whose (mutually orthogonal) asymptotes are \( \delta _{1}=\alpha \tilde{B_{1}} \) and \( \delta _{2}=\alpha \tilde{B_{2}} \). Similarly, Eq. (4.2) represents a hyperbola with (mutually orthogonal) asymptotes, \(\delta _{1}=\rho \tilde{B_{1}} \) and \( \delta _{2}=\rho \tilde{B_{2}}.\) From the above we can conclude that if \( ((1-q)d_{m}+k)\tilde{B}=((1-q)d_{m}-k)\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}, \) then the two hyperbolas (4.1) and (4.2) are the same, and \(x_{1} + \left( \tilde{B}+\beta _{b}b_{m}\frac{\tilde{M}}{d_{b}}\right) k =0 \) in Eq. (3.24). Then when \(\frac{\tilde{M}}{\tilde{B}} = \frac{d_{b}}{\beta _{b}b_{m}}\left( \frac{(1-q)d_{m}+k}{(1-q)d_{m}-k}\right) ,\) we do not have any positive equilibrium points if \( R_{0}\le 1,\) while if \( R_{0}>1,\) we have one positive equilibrium point, where \( \rho >\alpha > 0.\)

One can verify that the two hyperbolas (4.1) and (4.2) do not intersect in the positive quadrant, and a region for the existence of two endemic equilibria to occur is well defined in the shadow area as shown in Fig. 8.

Fig. 8
figure 8

In the plane \( (\delta _{1},\delta _{2}),\) when \( R_{0}<1 \) we have two EEPs in the dashed area

Full size image

Then from the above and from Proposition (3.2), if the discriminant \(\Delta \) is set to zero and solved for the critical value of \(R_{0},\) which we denote by \(R_{0}^{1},\) then we have

$$\begin{aligned} R_{0}^{1}= \frac{q+\sqrt{q^{2}+\frac{((1-q)d_{m}+k)^{2}}{kd_{m}}\left( \frac{4k(1-q)d_{m}}{((1-q)d_{m}+k)^{2}} - \left( 1- \frac{(1-q)d_{m}-k}{(1-q)d_{m}+k}\frac{\beta _{b}b_{m}}{d_{b}} \frac{\tilde{M}}{\tilde{B}}\right) ^{2}\right) }}{2}. \end{aligned}$$
(4.3)

Thus, the backward bifurcation scenario involves the existence of a subcritical transcritical bifurcation at \(R_{0}=1\) and of a saddle-node bifurcation at \(R_{0}=R_{0}^{1}<1\). The qualitative bifurcation diagrams describing two types of bifurcation at \(R_{0}=1\) are depicted in Fig.9a, b.

Fig. 9
figure 9

Basic reproduction number and bifurcation diagram. a Backward bifurcation. b Forward bifurcation

Full size image

Theorem 4.1

Consider model (2.1) with positive parameters. If

$$\begin{aligned} A<\left( \mu _{1}\!-\! (\nu _{1} \!+\! d_{b}(1\!+\!\frac{\beta _{m}b_{m}}{(1\!-\!q)d_{m}}))\right) \frac{\tilde{B_{1}}}{\delta _{1}} \!+\!\left( \mu _{2} \!-\! (\nu _{2} \!+\! d_{b}(1\!+\!\frac{\beta _{m}b_{m}}{(1\!-\!q)d_{m}}))\right) \frac{\tilde{B_{2}}}{\delta _{2}},\nonumber \\ \end{aligned}$$
(4.4)

then system (2.1) undergoes a backward bifurcation when \(R_{0}=1.\)

Proof

See the Appendix.\(\square \)

The parameter \(A\) measuring the effects of other animals bitten by mosquitoes to take blood meals is usually ignored in many compartment models for mosquito-borne diseases. So if we assume that all the birds as one family and \(A=0\), then the condition for occurrence of the backward bifurcation in the Theorem 4.1 can be simplified as

$$\begin{aligned} \mu > \nu + d_{b}\left( 1+\frac{\beta _{m}b_{m}}{(1-q)d_{m}}\right) \end{aligned}$$
(4.5)

which is consistent with the results on backward bifurcation in Jiang et al. (2009) and Wan and Zhu (2010).

The epidemiological significance of the phenomenon of backward bifurcation is that if \(R_{0}\) is nearly below unity, then the disease control strongly depends on the initial sizes of the various sub-populations of the model. On the other hand, reducing \(R_{0}\) below the saddle-node bifurcation value \(R_{0}^{1}\) will help to eradicate the disease.

5 Simulations and discussions

In this section, we carry out some numerical simulations to illustrate the effects and role of two avian species, corvids and non-corvids, on the transmission of WNv and its dynamics. Numerical results are obtained using values for parameters given in Table 1.

5.1 The basic reproduction number in case of corvid and non-corvid populations

Let \(h \in [0,1]\) be the percentage of corvids in new recruitment of birds. If \(\gamma _{b}\) is the recruitment rate, then in the model (2.1) we have \(\gamma _{b1}=h\gamma _{b}\) and \(\gamma _{b2}=(1-h)\gamma _{b}\). If \(h=0\), then all birds are non-corvid, and if \(h=1\), all birds are corvids.

It follows from (3.2) that we can rewrite the basic reproduction number as

$$\begin{aligned} R_{0} \!=\!\frac{q}{2} \!+\! \frac{1}{2}\sqrt{q^{2}\!+\!4\mathfrak R ^{2}} \ \ \ \text{ with } \ \ \ \mathfrak R \!=\! \sqrt{ \beta _{m}b_{m}^{2}\frac{\gamma _{b}}{d_{b}}\frac{\tilde{M}}{d_{m} \left( \frac{\gamma _{b}}{d_{b}}\!+\!A\right) ^{2}} \left( \frac{\beta _{b1}h}{\delta _{1}}\!+\!\frac{\beta _{b2}(1\!-\!h)}{\delta _{2}}\right) }.\nonumber \\ \end{aligned}$$
(5.1)

For the case of \(h=1\) and \(h=0\), if we denote

$$\begin{aligned} R_{0j} = \frac{q}{2} + \frac{1}{2}\sqrt{q^{2}+4\beta _{m}b_{m}^{2}\frac{\gamma _{b}}{d_{b}} \frac{\tilde{M}}{d_{m}\left( \frac{\gamma _{bj}}{d_{b}}+A\right) ^{2}} \left( \frac{\beta _{bj}}{\delta _{j}}\right) }, \ \ \ j=1, 2, \end{aligned}$$
(5.2)

then \(R_{01}\) and \(R_{02}\) are the basic reproduction numbers in the case that all birds are corvids (\(j=1\)) and non-corvids (\(j=2\)), respectively. One can verify that we have

$$\begin{aligned} \left( R_{0}-\frac{q}{2}\right) ^{2} = h\left( R_{01}-\frac{q}{2}\right) ^{2}+(1-h)\left( R_{02}-\frac{q}{2}\right) ^{2}, \ \ \ h\in [0,1]. \end{aligned}$$
(5.3)

Since corvids are more competent in transmitting the virus as the primary host for the virus (Komar et al. 2003), therefore we have \(\frac{\beta _{b1}}{\delta _{1}} > \frac{\beta _{b2}}{\delta _{2}}.\) So from (5.2), we have \(R_{01}>R_{02}\). One can further verify that \(R_{02}<R_{0}<R_{01}.\)

For the reproduction number as a function of the percentage \(h\in [0,1],\) it follows from (5.3) that we have

$$\begin{aligned} R_{0}=\frac{q}{2} + \sqrt{\left( R_{02}-\frac{q}{2}\right) ^{2}+h(R_{01}+R_{02}-q)(R_{01}-R_{02})}, \ \ \ h\in [0,1]. \end{aligned}$$
(5.4)

Since \(R_{01}>R_{02},\) so for the case with a small vertical transmission rate \(q\), as shown in Fig. 10, the basic reproduction number \(R_0\) is an increasing function of \(h\) which defines a segment of a parabola (5.4) for \(h\in [0,1].\)

Another important observation is that if we do not distinguish the birds as corvids and non-corvids, and take the bird population as only one species (using corvid parameters), just like what have been done in available modeling for WNv, we have \(R_{0}<R_{01}\), resulting in over estimation of the epidemic of the virus in the birds population. This observation suggests that it will be essential to further classify the birds into more species according to their responses, or death rates due to the infection of the virus. We leave this for our future work.

Fig. 10
figure 10

The basic reproduction number \(R_{0}\) as a function of \(h\)

Full size image

As shown in Fig. 10, one can see that \(R_{0}\) is an increasing function of \(h\in [0,1]\). This means that in regions with high percentage of corvids, the virus becomes epidemic with higher basic reproduction number. This is consistent with the observation in Peel region, Ontario, Canada in early years when the virus first arrived and caused the outbreak, (see Fig. 1). It is well known that a large number of corvid birds died due to the infection and thus, leading to the decrease of their numbers. Yet in regions with a lower percentage, the epidemic either did not occur or was not as severe as regions with higher percentages of corvid birds. In later years after the virus had established in the region, when \(R_{0} < 1\) the outbreak of the virus may still occur (inspite of the lower number of corvid birds) due to existence of the backward bifurcation.

5.2 Backward bifurcation

By Theorem 4.1, the backward bifurcation will occur when \(R_{0}=1\) and the condition (4.4) is satisfied. The existence of the backward bifurcation is illustrated by simulating the model (2.1) with the values of the parameters from Table 1 and \(A=\frac{\tilde{B_{1}}}{20}\). We keep \( \mu _{1}, \mu _{2}\) as bifurcation parameters and we plot the two curves (4.1) and (4.2) in the \( ( \mu _{1}, \mu _{2}) \) planes. As shown in Fig. 11, we note that the two positive equilibria exist only in a small area \( S \) between the two hyperbola curves.

Fig. 11
figure 11

Bifurcation curves for the model (2.1) in the plane \( (\mu _{1},\mu _{2})\)

Full size image

By taking \( ( \mu _{1}, \mu _{2}) = (0.24, 0.07)\in S\), a time series of \(B_{i}\) is plotted in Fig. 12 showing the DFE and two endemic equilibria. Also using (3.2) and (4.3), we can find \(R_{0}^{1}=0.9922<R_{0}=0.9962<1.\) Moreover, the value of the right hand side of condition (4.4) can be calculated as \(0.2386\times \tilde{B_{1}};\) subsequently, the value of \(A=\frac{\tilde{B_{1}}}{20}\) satisfies the condition (4.4). Therefore, the backward bifurcation will occur (when \(R_{0}\) is nearly below unity). We can then find \(B_{1i}\) in the two endemic equilibria \( E_{2}\) and \( E_{3} \) as \( B^{2}_{1i}=1,779 \) and \( B^{3}_{1i}= 409,\) respectively.

Further, Fig. 12 shows that one of the endemic equilibria \( E_{2} \) is stable, the other \( E_{3} \) is unstable (saddle), and the DFE is stable. This clearly shows the co-existence of two locally-asymptotically stable equilibria when \(R_{0}<1.\)

Fig. 12
figure 12

The trajectories of infected corvid birds in (2.1) with \( (\mu _{1}, \mu _{2}) = (0.24, 0.07)\in S\) for different selection of initial values

Full size image

5.3 The impact of other mammals \( A \)

From the expression in (3.2) and (5.3), we can conclude that the basic reproduction number increases as \(A\) decreases.

Fig. 13
figure 13

Total number of infected bird population with different values of \(A=0\), \(\frac{B_{s}^{*}}{2}\), \(B_{s}^{*}\) and \(2B_{s}^{*}\)

Full size image

In Fig. 13, we simulate and present the total number of infected birds with different sizes of \(A\). We compare the cases when \(A=0,\) \(\frac{B_{s}^{*}}{2}\), \(B_{s}^{*}\) and \(2B_{s}^{*}\), where \(B_{s}^{*}\) is the initial number of birds and we also assume that all birds are of one family. One can see that the peak value of infected bird population increases and the peak time occurs earlier when \(A\) decreases. This is due to the fact that some of the mosquito bites are shared by other mammals which causes the decrease of the incidence of the birds.

5.4 The impact of bird species diversity

In Sect. 5.1, we see that the basic reproduction number is an increasing function of \(h\) (the percentage of corvids of the total birds population). By using the same parameters as in Table 1, in Fig. 14 we present the total number of infected birds (\(B_{i}\)) for \(h\in [0, 1]\).

Fig. 14
figure 14

Total of all infected birds with different values of \(h\)

Full size image

Usually, registers of WNv cases in the avian population are based on the number of dead birds found. Thus, epidemiological reports indicate high WNv prevalence in avian species with high disease mortality rate. In Fig. 15, using the parameters given in Table 1, we present the corvids and non-corvid birds population with initial total bird population \(15,000\). We can observe in Fig. 15a that the peak time of the infected mosquitoes appears earlier with higher percentage of corvid birds. It suggests that if we ignore the weather and environmental factors for a region with higher percentage of corvids, the peak time of the total infected mosquitoes (correspondingly the risk of WNv risk) in the region arrives earlier.

From Fig. 15b, we can observe that the peak time of the infected non-corvid subpopulation occurs later with the increase of its percentage that ranges between \(40\) and \(80\,\%.\) On the other hand, the peak time of the infected corvid subpopulation occurs earlier with the increase of its percentage. This observation together with the simulations in Fig. 15a suggests that for a region with more corvids, usually one would observe a large amount of dead corvids, the virus first causes the outbreak in the bird populations, and is followed with the peak of infected mosquitoes which can potentially induce the outbreak in the human population. But for a region with less corvids, it takes longer time for the epidemic of the virus to reach a peak in the birds population which would postpone the peak of infection in mosquito population. In this case if the cold wind arrives earlier in the region, it can blow away the epidemic of the virus in human population. The above! observation is consistent with the endemic of the virus in regions in Southern Ontario (Public Health Agency of Canada Public Health Agency of Canada). The first year Ontario had more cases of WNv was in 2002, a total of 394 human cases reported.

Fig. 15
figure 15

Comparison of the peak time of total infected mosquitoes, and infected corvids and non-corvids. Corvid is \(20,\) \(40\) and \(60\,\%\) of the total population. a Infected mosquitoes. b Peak time for infected corvids and non-corvids for different \(h\)

Full size image

Yet, if warmer weather promotes the abundance of total mosquitoes to reach a peak earlier, it can still cause outbreak in humans even if there are fewer number of corvids in the region. Recent outbreak of WNv in regions like Durham, Ontario verifies our observation. This year, the early and hot summer in Southern Ontario allows mosquitoes to breed more quickly, which allows the WNv in infected mosquitoes, and therefore in birds, to replicate faster. As of September 25, 2012, a total of 220 cases of human infection were reported (Public Health Agency of Canada Public Health Agency of Canada). For the risk assessment and forecasting of WNv, it will be very important and interesting to study and estimate the peak times for the mosquito abundance, total infected birds and human cases. We will consider this in a future work when the related data can be available.

This paper presents a deterministic model for the transmission dynamics of WNv, by classifying avian populations as corvids and non-corvids. A detailed analysis of the model shows the presence of the locally stable disease free equilibrium whenever the associated reproduction number is less than unity. The model undergoes backward bifurcation where the stable disease free equilibrium co-exists with a stable endemic equilibrium. The existence of the backward bifurcation indicates that the spread of the virus when \(R_{0}\) is nearly below unity could be dependent on the initial sizes of the sub-population of the model. This paper generalizes the results of backward bifurcation in previous work (Jiang et al. 2009; Wan and Zhu 2010).

Thus, in this work, we analyzed the effects of two avian populations, corvid and non-corvid family of birds with different responses to the virus, and we found that the level of incidence (measured by the peak) and the basic reproduction number are completely different when assuming one family of bird population. We also discussed the impact of other mammals on the transition of WNv. Thus, from the above, we can conclude that if we do not classify the bird population into different species and if we do not include other mammals, any epidemic calculations will be overestimated.