1 Introduction

In this article we consider population models of the form

$$\begin{aligned} p(t+1)=X(t)p(t),\quad X(t)=A(t)+B(t),\quad t=0,1,\ldots \end{aligned}$$

with \(p(0)\) given in \(\mathbb R ^m\). \(p(t)\) is the population vector while \(A(t)\) and \(B(t)\) are nonnegative square matrices of size \(m\) for all \(t\): \(A(t)\) is a birth matrix, while \(B(t)\) is a survival matrix. For simplicity, we assume that the nonnegative matrices \((A(t),B(t))\) are chosen in a finite list of environments \((A^{(k)},B^{(k)})_{1\le k\le K}\), there being a probability \(M_{i,j}\) that an environment of type \(i\) is followed by an environment of type \(j\) \((1\le i,j\le K)\). There is also a probability \(\mu _i\) that \((A(0),B(0))\) is of type \(i\). The matrix \(M=(M_{i,j})\) of this Markov chain is supposed to be irreducible. For the survival matrices to make sense biologically, we assume that \(\sum _i B_{i,j}^{(k)}\le 1\) for all \(j\) and all \(k\). We also assume: (H1) there exists \(\kappa \) such that \(\Vert B^{(\kappa )}\Vert _1=\max _j \sum _i B_{i,j}^{(\kappa )}< 1\); (H2) the projection matrices \(A^{(k)}+B^{(k)}\) form an ergodic set (see e.g. Caswell 2001). For example, primitive matrices with a common incidence matrix form an ergodic set. Some of the assumptions above may be relaxed.

A large literature exists concerning such population models in a random environment (Lewontin and Cohen 1969; Tuljapurkar 1990 and references therein). In particular, writing \(|p(t)|=\sum _i p_i(t)\) and \(\Vert \cdot \Vert \) for any matrix norm, it is known that with the assumptions above the almost sure limit

$$\begin{aligned} r=\lim _{t\rightarrow +\infty } (\log |p(t)|)/t=\lim _{t\rightarrow +\infty } (\log \Vert X(t-1)X(t-2)\cdots X(0)\Vert )/t \end{aligned}$$
(1)

exists and is independent of \(p(0)\) and of the particular sequence of environments randomly chosen following the Markov chain ((Tuljapurkar 1990, p. 26)). To stress the dependence of the growth rate \(r\) on the matrices \(A(t)\) and \(B(t)\), we shall write \(r=r(A,B)\). If for example the population vector is a scalar and if \(M_{i,j}=m_j\) for all \(i\) and \(j\), which means that the environments are independent and identically distributed (i.i.d.), then it is known that

$$\begin{aligned} r(A,B)=\sum _k m_k \log (A^{(k)}+B^{(k)}) \end{aligned}$$
(2)

(see, e.g., (Haccou et al. 2005, § 2.9.2)).

The classical concept of basic reproduction number (also called net reproductive rate) \(R_0\) has been extended from constant environments to periodic environments by Bacaër and Guernaoui (2006). This \(R_0\) is an asymptotic per generation growth rate (Bacaër and Ait Dads 2011, 2012). The case of nonperiodic continuous-time deterministic environments was considered by Thieme (2009, § 5.1) and Inaba (2012). In a recent article, Hernandez-Suarez et al. (2012) suggested an adaptation of \(R_0\) to models with random environments. It seems however that the position of their “\(R_0\)” with respect to 1 does not always decide between population growth and population decay (a counter-example will be given below). In the present article, we explain how \(R_0\) should be computed so that it gives the right threshold: it is the unique solution of the equation

$$\begin{aligned} r(A/R_0,B)=0. \end{aligned}$$
(3)

In other words, \(R_0\) is the number by which all birth rates should be divided to bring the population to the critical situation where neither exponential growth nor exponential decay occurs. Such a characterization of \(R_0\) was emphasized for constant environments by Li and Schneider (2002, Theor.  3.1) and for periodic environments either in a continuous-time or discrete-time setting by Bacaër (2007, Sect. 3.4, 2009, Sect. 4).

In Sect.  2, \(R_0\) is defined as the spectral radius of a “next-generation operator” following the terminology of Diekmann and Heesterbeek (2000). Proposition  1 shows that \(R_0>1\) if and only if \(r>0\). Proposition  2 shows that \(R_0\) may be computed using Eq. (3). The formula for \(R_0\) obtained for periodic environments by Bacaër (2009) is in fact a special case of the approach of the present article. Section  3 shows that the parameter recently introduced by Hernandez-Suarez et al. (2012) determines growth or decay of the population’s expectation. Section  4 focuses on the scalar case, for which \(R_0\) is easily computed. Some numerical examples are presented in Sect.  5. Continuous-time models are briefly discussed in Sect.  6 in order to make the link with a recent article by Artalejo et al. (2012). The conclusion explains that the difference between our \(R_0\) and the “\(R_0\)” of Hernandez-Suarez et al. (2012) is the same as the difference between the expected growth rate of the population and the growth rate of the expected population, which has often been discussed (Lewontin and Cohen 1969; Tuljapurkar 1990).

2 Definition and properties of \(R_0\)

As in the periodic case (Bacaër and Ait Dads 2011, 2012), let us split the population in generations. Let \(q(n,t)\) be the population vector belonging to generation \(n\) at time \(t\): for all \(t\ge 0\) and \(n\ge 0\),

$$\begin{aligned} q(0,0)&= p(0),\quad q(0,t+1)=B(t) q(0,t)\nonumber \\ q(n+1,0)&= 0,\quad q(n+1,t+1)=A(t) q(n,t)+B(t)q(n+1,t). \end{aligned}$$
(4)

Note that the zero on the right side of the equation \(q(n+1,0)=0\) stands for the zero vector in \(\mathbb R ^m\). Then \(p(t)=\sum _{n\ge 0} q(n,t)\) satisfies \(p(t+1)=(A(t)+B(t))p(t)\) for all \(t\ge 0\). Let \(L=\ell ^1(\mathbb N ,\mathbb R ^m)\) be the vector space of sequences \((x(0),x(1),\ldots )\) with \(x(t)\in \mathbb R ^m\) for all \(t\ge 0\) such that \(\Vert x\Vert =\sum _{t\ge 0} \sum _{i=1}^m |x_i(t)|<+\infty \). Then \(L\) is a Banach space. Notice that (4) may be written as

$$\begin{aligned} q(n+1,0)=0,\quad -B(t)q(n+1,t)+q(n+1,t+1)=A(t)q(n,t). \end{aligned}$$
(5)

Let us introduce the operators \(\mathcal A :L\rightarrow L\), \(\mathcal B :L\rightarrow L\), and the identity operator \(\mathcal I :L\rightarrow L\) such that for all \(x\in L\) and \(t\ge 0\),

$$\begin{aligned} (\mathcal A x)(0)&= 0,\quad (\mathcal A x)(t+1)=A(t)x(t), \\ (\mathcal B x)(0)&= 0,\quad (\mathcal B x)(t+1)=B(t)x(t),\\ (\mathcal I x)(t)&= x(t). \end{aligned}$$

Since \(A(t)\) and \(B(t)\) are chosen among a finite set of matrices, it is clear that \(\mathcal A x\in L\) and \(\mathcal B x\in L\) if \(x\in L\). Moreover \(\mathcal A \) and \(\mathcal B \) are bounded linear operators.

Lemma 1

The spectral radius \(\rho (\mathcal A +\mathcal B )\) is equal to \(e^{r(A,B)}\).

Proof

Set \(\mathcal X =\mathcal A +\mathcal B \). For all \(x\in L\) and \(\tau \ge 1\), we have \((\mathcal X ^\tau x)(t)=0\) for \(0\le t\le \tau -1\) and \((\mathcal X ^\tau x)(t)=X(t-1)X(t-2)\cdots X(t-\tau ) x(t-\tau )\) if \(t\ge \tau \). From (1) and from the spectral radius formula we see that

$$\begin{aligned} \rho (\mathcal X )=\lim _{\tau \rightarrow +\infty } \Vert \mathcal X ^\tau \Vert ^{1/\tau } = e^{r(A,B)}, \end{aligned}$$

where \(\Vert \cdot \Vert \) is the operator norm associated with the vector norm in \(L\). \(\square \)

Lemma 2

\(r(0,B)<0\): the population dies out if there are no births.

Proof

We have \(\Vert B^{(k)}\Vert _1 \le 1\) for all \(k\) and \(\Vert B^{(\kappa )}\Vert _1<1\). The environment \(\kappa \) occurs (as \(t \rightarrow +\infty )\) in a positive fraction \(\pi _\kappa \) of the \(t\) terms of the matrix product of Eq. (1) because the Markov chain is assumed irreducible. But \(\Vert \cdot \Vert _1\) is a sub-multiplicative norm. So we get \(r(0,B)\le \pi _{\kappa } \log \Vert B^{(\kappa )}\Vert _1<0\). \(\square \)

Since \(r(0,B)<0\), Lemma 1 shows that \(\rho (\mathcal B )<1\). So \(\mathcal I -\mathcal B \) is invertible: if \(y=(\mathcal I -\mathcal B )x\), then \(x=(\mathcal I -\mathcal B )^{-1}y=y+\mathcal B y+\mathcal B ^2y+\cdots \), i.e.,

$$\begin{aligned} x(t)=\sum _{\tau =0}^{t} B(t-1)B(t-2)\cdots B(\tau ) y(\tau ) \end{aligned}$$

for all \(t\ge 0\). For all \(n\ge 0\), set \(q_n=(q(n,t))_{t\ge 0}\). Equation (5) is equivalent to \((\mathcal I -\mathcal B )q_{n+1}=\mathcal A q_n\), i.e., \(q_{n+1}=(\mathcal I -\mathcal B )^{-1}\mathcal A q_n\). Since \(q_0\in L\), we have \(q_n\in L\) for all \(n\ge 1\). Now set \(g_n=\mathcal A q_n\). In this way \(g_n(t+1)=A(t)q(n,t)\) is the birth vector due to generation \(n\) between time \(t\) and \(t+1\). We arrive at the following conclusion:

$$\begin{aligned} g_{n+1}=\mathcal A q_{n+1}=\mathcal A (\mathcal I -\mathcal B )^{-1}g_n. \end{aligned}$$

More explicitly, we have \(g_{n+1}(0)=0\) and the renewal equation for the births

$$\begin{aligned} g_{n+1}(t+1)=\sum _{\tau =0}^t A(t) B(t-1) B(t-2)\cdots B(\tau ) g_n(\tau ) \end{aligned}$$
(6)

for all \(t\ge 0\) and \(n\ge 0\).

Definition 1

The spectral radius of the next-generation operator \(\mathcal A (\mathcal I -\mathcal B )^{-1}\) is called \(R_0\).

Notice the analogy between Definition  1 and the presentation of \(R_0\) for continuous-time models in time-heterogeneous environments by Thieme (2009, § 5.1) and Inaba (2012). As for the growth rate \(r(A,B)\) in Sect.  1, we shall write \(R_0(A,B)\) to stress the dependence with respect to the sequence of matrices \(A(t)\) and \(B(t)\).

Proposition 1

\(R_0(A,B)>1\) if \(r(A,B)>0\), \(R_0(A,B)=1\) if \(r(A,B)=0\), and \(R_0(A,B)<1\) if \(r(A,B)<0\).

Proof

Applying a result by Thieme (2009, Theor. 3.10), we know that \(R_0(A,B)-1\) has the same sign as \(\rho (\mathcal A +\mathcal B )-1\). But Lemma 1 showed that \(\rho (\mathcal A +\mathcal B )=e^{r(A,B)}\). So \(R_0(A,B)-1\) has the same sign as \(r(A,B)\). \(\square \)

Proposition 2

Assume that \(R_0(A,B)>0\). Then \(R_0(A,B)\) is the unique solution of the equation \(r(A/R,B)=0\) on the interval \(R\in (0,+\infty )\).

Proof

Since the basic reproduction number depends linearly on the set of birth rates, we have \(R_0(A/R_0(A,B),B)=1\). So \(r(A/R_0(A,B),B)=0\) because of Proposition  1. Hence the equation \(r(A/R,B)=0\) has at least one solution. Given Eq. (1), the mapping \(R \mapsto r(A/R,B)\) is obviously nonincreasing on the interval \(R\in (0,+\infty )\). It is easily checked, by taking the second derivative, that for every \((i,j)\) the mapping \(R\mapsto A_{i,j}(t)/R+B_{i,j}(t)\) is either identically zero or log-convex [this point was already used by Bacaër and Ait Dads (2012, Appendix C)]. It follows from the results of Cohen (1980, Theor. 1) that the mapping \(R\mapsto r(A/R,B)\) is convex. So the equation \(r(A/R,B)=0\) cannot have more than one solution. Indeed if it had two distinct solutions \(R_1\) and \(R_2\) with \(R_1<R_2\), the nonincreasing and convex function \(R\mapsto r(A/R,B)\) would be constant equal to 0 not only on the interval \((R_1,R_2)\), but for all \(R\ge R_1\). This function from \((0,+\infty )\) to \(\mathbb R \) being convex, it is also continuous. So \(r(A/R,B)\rightarrow r(0,B)<0\) as \(R\rightarrow +\infty \). We have thus reached a contradiction. \(\square \)

Remark 1

Proposition  2 shows that, in general, computing \(R_0\) is as difficult as computing \(r\), and requires slightly more computer time because a dichotomy method has to be used.

Remark 2

For periodic environments where the sequence is \((1,2,\ldots ,K)\), Bacaër (2009) showed that \(R_0\) was the spectral radius of

$$\begin{aligned} \left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} A^{(1)}&0&\cdots&0\\ 0&A^{(2)}&\,&\vdots \\ \vdots&\ddots&\ddots&0\\ 0&\cdots&0&A^{(K)} \end{array} \right) \left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -B^{(1)}&I&0&\cdots&0 \\ 0&-B^{(2)}&I&\,&0\\ 0&\ddots&\ddots&\,&\vdots \\ \vdots&\ddots&\ddots&0&I\\ I&\cdots&0&0&-B^{(K)} \end{array} \right)^{-1} \end{aligned}$$
(7)

Bacaër and Ait Dads (2012, Prop. 3) emphasized that this \(R_0\) is the unique solution of the equation

$$\begin{aligned} \rho \left(\left(\frac{A^{(K)}}{R}+B^{(K)}\right)\cdots \left(\frac{A^{(1)}}{R}+B^{(1)}\right) \right)=1. \end{aligned}$$

Given Eq. (1), the left side above is obviously equal to \(e^{r(A/R,B)}\). So we can conclude from Proposition  2 that the \(R_0\) of Bacaër (2009) is the same as the \(R_0\) of Definition  1 in the special case of periodic environments (\(M_{i,j}=1\) if \(j=i+1\) and \(1\le i\le K-1\), \(M_{K,1}=1\), and \(M_{i,j}=0\) otherwise). To emphasize this, it is convenient to present \(R_0\) in a periodic environment as the spectral radius of

$$\begin{aligned} \left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0&0&\cdots&0&A^{(K)}\\ A^{(1)}&0&\,&0\\ 0&\ddots&\ddots&\,&\vdots \\ \vdots&\ddots&\ddots&0&0\\ 0&\cdots&0&A^{(K-1)}&0 \end{array} \right) \left(\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} I&0&\cdots&0&-B^{(K)}\\ -B^{(1)}&I&\,&0\\ 0&\ddots&\ddots&\,&\vdots \\ \vdots&\ddots&\ddots&I&0\\ 0&\cdots&0&-B^{(K-1)}&I \end{array} \right)^{-1},\nonumber \\ \end{aligned}$$
(8)

which is easily shown to be the same as the spectral radius of (7) (see Hernandez-Suarez et al. 2012, Sect. 5). The fact that this spectral radius coincides with the spectral radius of \(A(I-B)^{-1}\) (Cushing and Zhou 1994; Caswell 2001) when the environment is constant (with \(A^{(k)}=A\) and \(B^{(k)}=B\) for all \(k\)) was already shown by Bacaër and Ait Dads (2012).

Proposition 3

The definition of \(R_0\) above is independent of the particular random sequence \((A(t),B(t))_{t\ge 0}\) of environments following the Markov chain with matrix \(M\). So \(R_0\) may be called the basic reproduction number of the model.

Proof

Let \((A(t),B(t))\) and \((A^{\prime }(t),B^{\prime }(t))\) be two sequences of environments following the Markov chain with matrix \(M\). Let \(R_0(A,B)\) and \(R_0(A^{\prime },B^{\prime })\) be the corresponding basic reproduction numbers. We wish to show that \(R_0(A,B)=R_0(A^{\prime },B^{\prime })\). From Proposition  2, we know that \(r(A/R_0(A,B),B)\!=\!0\) and that \(r(A^{\prime }/R_0(A^{\prime },B^{\prime }),B^{\prime })\!=\!0\). But growth rates are independent of the particular sequence of environments (Tuljapurkar 1990). So \(0=r(A/R_0(A,B),B)=r(A^{\prime }/R_0(A,B),B^{\prime })\). We see that both \(R_0(A,B)\) and \(R_0(A^{\prime },B^{\prime })\) are solutions of \(r(A^{\prime }/R,B^{\prime })=0\). Proposition  2 implies that \(R_0(A,B)=R_0(A^{\prime },B^{\prime })\). \(\square \)

3 Another parameter

In a recent article, Hernandez-Suarez et al. (2012) suggested to call “\(R_0\)” the spectral radius of

$$\begin{aligned} \left(\begin{array}{ccc} M_{1,1} A^{(1)}&\cdots&M_{K,1} A^{(K)}\\ \vdots&\,&\vdots \\ M_{1,K} A^{(1)}&\cdots&M_{K,K} A^{(K)}\end{array} \right) \left[ I - \left(\begin{array}{ccc} M_{1,1} B^{(1)}&\cdots&M_{K,1} B^{(K)}\\ \vdots&\,&\vdots \\ M_{1,K} B^{(1)}&\cdots&M_{K,K} B^{(K)}\end{array} \right) \right]^{-1}, \end{aligned}$$
(9)

where \(I\) is an identity matrix of suitable size. To avoid any confusion, we shall call this spectral radius \(R_*\).

In the literature on Markovian environments, it is known that

$$\begin{aligned} \log \mu = \lim _{t\rightarrow +\infty } \frac{\log \mathbb E [|p(t)|]}{t} \end{aligned}$$
(10)

exists (recall that \(|\cdot |\) stands for the sum of components). Moreover \(\mu \) is the spectral radius of \(D(M^{\prime }\otimes I)\), where \(D\) is the block-diagonal matrix \(D=\mathrm diag (A^{(1)}+B^{(1)},\cdots ,A^{(K)}+B^{(K)})\), \(M^{\prime }\) is the transpose of \(M\), and \(I\) is the identity matrix (see Tuljapurkar 1990, p. 45, where it is called Bharucha’s formula).

Proposition 4

\(R_*>1\) if \(\log \mu >0\), \(R_*=1\) if \(\log \mu =0\), and \(R^*<1\) if \(\log \mu <0\).

Proof

Notice that the matrix \(D(M^{\prime }\otimes I)\) is equal to

$$\begin{aligned} \left(\begin{array}{ccc} M_{1,1} (A^{(1)}+B^{(1)})&\cdots&M_{K,1} (A^{(K)}+B^{(K)})\\ \vdots&\,&\vdots \\ M_{1,K} (A^{(1)}+B^{(1)})&\cdots&M_{K,K} (A^{(K)}+B^{(K)})\end{array} \right). \end{aligned}$$

This matrix is equal to \(A^*+B^*\), where

$$\begin{aligned} A^*=\left(\begin{array}{ccc} M_{1,1} A^{(1)}&\cdots&M_{K,1} A^{(K)}\\ \vdots&\,&\vdots \\ M_{1,K} A^{(1)}&\cdots&M_{K,K} A^{(K)}\end{array} \right), \end{aligned}$$

and \(B^*\) is defined similarly by replacing \(A\) by \(B\). Applying the result given by Thieme (2009, Theor. 3.10), we know that \(\rho (A^*+B^*)-1\) and \(\rho (A^*(I-B^*)^{-1})-1\) have the same sign. But \(\mu =\rho (A^*+B^*)\) and \(R_*=\rho (A^*(I-B^*)^{-1})\). \(\square \)

Remark 3

In a periodic environment we have \(R_0=R_*\), as can be seen by comparing the matrices (8) and (9).

4 The scalar case

If the matrices \(A(t)\) and \(B(t)\) are scalars, and if the environments are i.i.d., then it follows immediately from Eq. (2) and Proposition  2 that

$$\begin{aligned} \sum _{k=1}^K m_k \log \left(\frac{A^{(k)}}{R_0}+B^{(k)}\right)=0, \end{aligned}$$

or equivalently that

$$\begin{aligned} \prod _{k=1}^K \left(\frac{A^{(k)}}{R_0}+B^{(k)}\right)^{m_k}=1. \end{aligned}$$

Consider now the more general case of Markov dependence between successive environments. Recall that \(M=(M_{i,j})\) is the matrix of transition probabilities. The chain being irreducible, let \(\pi \) be the positive stationary distribution of the time spent in the different environments: \(\pi _j = \sum _i \pi _i M_{i,j}\) for all \(j\) and \(\sum _j \pi _j=1\). As mentioned by Haccou et al. (2005, § 2.9.2) the growth rate is

$$\begin{aligned} r(A,B)=\sum _k \pi _k \log (A^{(k)}+B^{(k)}) \end{aligned}$$

[for a proof, simply notice that \(\log p(t)=\sum _{\tau =0}^{t-1} \log X(\tau ) + \log p(0)\) and that, as \(t\rightarrow +\infty \), the number of terms equal to \(\log (A^{(k)}+B^{(k)})\) in the sum over \(\tau \) is \(\pi _k\, t+o(t)\)]. So Proposition  2 shows that \(R_0\) is the solution of

$$\begin{aligned} \prod _{k=1}^K \left(\frac{A^{(k)}}{R_0}+B^{(k)}\right)^{\pi _k}=1. \end{aligned}$$
(11)

Thus \(R_0\) can be easily computed, e.g., using a dichotomy method.

5 Examples

As a first example, consider a scalar population (\(m=1\)) and suppose that there are two environments (\(K=2\)):

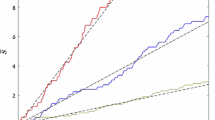
$$\begin{aligned} (A^{(1)},B^{(1)})=(1,0.5),\quad (A^{(2)},B^{(2)})=(0.1,0.58),\quad M=\left(\begin{array}{c@{\quad }c} 0.3&0.7\\ 0.6&0.4 \end{array}\right). \end{aligned}$$

The stationary distribution is \((\pi _1,\pi _2)=(6/13,7/13)\). Equation (11) gives \(R_0\simeq 0.949<1\): the population goes extinct almost surely. For such an example, Eq. (9) gives \(R_*\simeq 1.050>1\). For illustration we made several simulations of the model starting from \(p(0)=1\). Fig.  1 suggests that the process is indeed subcritical. The parameter values were chosen precisely so that \(R_0<1\) while \(R_*>1\). However it seems that in many other cases both parameters are on the same side of \(1\) and differ only very slightly, the difference often being less than 1 %. Although such a difference may appear as biologically insignificant, it does have its importance for establishing threshold results mathematically.

Fig. 1
figure 1

\(\log p(t)\) as a function of \(t\). Here \(R_0<1\) while \(R_*>1\)

Full size image

As a second example, let us consider a model with two stages and two environments:

$$\begin{aligned} \begin{aligned} A^{(1)}&=\left(\begin{array}{c@{\quad }c} 0.1&2\\ 0&0 \end{array}\right),&\quad B^{(1)}&=\left(\begin{array}{c@{\quad }c} 0&0\\ 0.1&0 \end{array}\right),\\ A^{(2)}=\left(\begin{array}{c@{\quad }c} 1&0.3\\ 0&0 \end{array}\right),\quad B^{(2)}&=\left(\begin{array}{c@{\quad }c} 0&0\\ 0.7&0 \end{array} \right),&\quad M&=\left(\begin{array}{c@{\quad }c} 0.5&0.5\\ 0.5&0.5 \end{array}\right). \end{aligned} \end{aligned}$$

Notice that the matrices \(A^{(k)}+B^{(k)}\) for \(k=1,2\) are Leslie matrices and that the environments are independent and identically distributed. Formula (9) gives \(R_*=1.01>1\). If we run simulations starting for example from \(p(0)=(1\, 1)^{\prime }\), if we estimate the growth rate \(r\) by \(\frac{1}{t} \log (|p(t)|/|p(0)|)\) with \(t=5000\), and if we iterate the process 1000 times, we find that the expected growth rate is \(-0.1021\) with a sample standard error of 0.0074. This suggests that \(r<0\) and therefore that \(R_0<1\). To estimate \(R_0\) numerically, we use Proposition  2: we divide \(A^{(k)}\) for \(k=1,2\) by \(R\) and estimate the new growth rate. With \(R=0.84\), we find \(r\simeq 0.0135\) with a sample standard error of \(0.0072\), suggesting that \(r>0\). With \(R=0.88\), we find \(r\simeq -0.0168\) with a sample standard error of \(0.0071\), suggesting that \(r<0\). So it seems that \(0.84<R_0<0.88\).

For the same example, one can also directly use the definition of \(R_0\) as the spectral radius of the operator \(\Omega =\mathcal A (\mathcal I -\mathcal B )^{-1}\). Beware that this operator does not have any nonzero eigenvalue, as the continuous-time case studied by Inaba (2012, Lemma 9). But we can compute \(g_n\) for \(n\) large and estimate \(R_0\) from \(\root n \of {\Vert g_n\Vert /\Vert g_0\Vert }\). In our example notice that \(B^{(k)}B^{(k^{\prime })}=0\) for all \(k,k^{\prime }=1,2\) and that \(g_0(t)=0\) for all \(t\ge 3\). It follows from the renewal equation (6) that \(g_{n}(t)=0\) for all \(t\ge \tau \) implies \(g_{n+1}(t)=0\) for all \(t\ge \tau +2\). So \(g_n(t)=0\) for all \(t\ge 2n+3\). To compute \(g_n\), it is therefore enough to consider the operator \(\Omega \) on the finite dimensional subspace \(\ell ^1(\{0,1,\ldots ,2n+2\},\mathbb R ^2)\). For \(n=1,000\), we chose 10 random sequences of environments and found estimates of \(R_0\) with a mean of 0.86 and a sample standard error of 0.015, in line with the estimate already obtained.

6 Continuous-time models

Let us now briefly sketch how a similar theory can be developed for linear continuous-time population models in a random ergodic environment. For example let us take a model of the form

$$\begin{aligned} dp/dt = (A(t)-B(t))p(t), \end{aligned}$$
(12)

where \(p(t)\) is a vector, \(A(t)\) a nonnegative square matrix function of size \(m\), and \(B(t)\) a matrix function of the same size with nonnegative off-diagonal coefficients. We assume for simplicity that \((A(t),B(t))\) belongs to a finite list of environments \(((A^{(k)},B^{(k)}))_{1\le k\le K}\) and that the transition between the environments follows an inhomogeneous continuous-time Markov chain (see, e.g., Ge et al. 2006): the probability \(\Pi _k(t)\) to be in state \(k\) at time \(t\) satisfies \(d\Pi /dt=Q(t)\Pi \), where \(Q(t)\) is irreducible, \(T\)-periodic, with nonnegative off-diagonal coefficients, piecewise continuous, and such that \(Q_{jj}(t)=-\sum _{i\ne j} Q_{ij}(t)\). The matrix \(Q(t)\) is allowed to be periodic because many populations experience a mixture of seasonal and random effects (for discrete-time models such a mixture can be incorporated in the transition matrix \(M\) of Sect.  1). Let \(\lambda _1(A,B)\) be the largest Lyapunov exponent (see, e.g., Arnold and Wihstutz 1986) of (12). We shall assume that \(\lambda _1(0,B)<0\): the population tends to 0 without births.

The basic reproduction number \(R_0\) can be defined as the spectral radius of the renewal operator \(\mathcal K \) on \(L^1((0,\infty ),\mathbb R ^m)\) given by \((\mathcal K u)(t)= \int _0^t K(t,x) u(t-x)\, dx\), where the kernel is given by \(K(t,x)=A(t) C(t,x)\) and \(C(t,x)\) is the survival matrix from time \(t-x\) to time \(t\): \(C(t,x)=Z(t)\), \(dZ/ds = -B(s)Z(s)\) for \(t-x<s<t\) and \(Z(t-x)=I\) (the identity matrix). Indeed it is known (Bacaër and Ait Dads 2011, Lemma 2) that the birth vector per unit of time due to generation \(n\) satisfies a recurrence relation involving the operator \(\mathcal K \), which is similar to Eq. (6). For a discussion of the link between the spectral radius of this operator and \(R_0\) but for deterministic models, see Inaba (2012, Sect. 4). If \(R_0>0\) then \(R_0\) may once again be characterized by the fact that \(\lambda _1(A/R_0,B)=0\), as in Proposition  2. The spectral radius \(R_0\) of \(\mathcal K \) is almost surely independent of the particular random sequence of environments, as in Proposition  3.

If \(p(t)\) is a scalar population then \(\lambda _1(A,B)=\langle A \rangle - \langle B \rangle \), where for instance \(\langle A \rangle = \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t A(s)\, ds\). So \(R_0 = \langle A \rangle / \langle B \rangle \) as, e.g., in the work of Córdova-Lepe et al. (2012) on a model with almost periodic coefficients. The row vector \(v=(1\ 1 \ldots 1)\) satifies \(dv/dt=0=v Q(t)\). So it can be shown, following Perthame (2007, § 6.3.2), that there is a unique \(T\)-periodic positive solution \(u(t)\) of \(du/dt = Q(t) u(t)\) such that \(\sum _i u_i(t)=1\). The law of large numbers for Markov chains shows that \(\langle A \rangle = \frac{1}{T}\int _0^T \sum _k u_k(s) A^{(k)}\, ds\). So

$$\begin{aligned} R_0=\frac{\int _0^T \sum _k u_k(s) A^{(k)}\, ds}{\int _0^T \sum _k u_k(s) B^{(k)}\, ds}. \end{aligned}$$

If moreover \(Q(t)\) does not depend on \(t\) then there is a unique vector \(u\) such that \(Qu=0\) and \(\sum _i u_i=1\). So \(R_0=(\sum _k u_k A^{(k)})/(\sum _k u_k B^{(k)})\). This formula for \(R_0\) is the same as the one for “\(R_0^{ARA}\)” by Artalejo et al. (2012, § 4.1).

7 Conclusion

The difference between the \(R_0\) in the present paper and the “\(R_0\)” (which we call \(R_*\)) of Hernandez-Suarez et al. (2012) is similar to the difference between on one side the “stochastic” growth rate (1), which is also equal to the expected growth rate of the population

$$\begin{aligned} r=\lim _{t\rightarrow +\infty } \mathbb E \left[\frac{\log |p(t)|}{t}\right], \end{aligned}$$

and on the other side the growth rate of the expected population (10) (Lewontin and Cohen 1969; Tuljapurkar 1990). It is the position of \(r\) with respect to 0 or of our \(R_0\) with respect to 1, which decides whether the population is sub- or supercritical in simulations. However \(\log \mu \) and \(R_*\) are much easier to compute in Markovian environments with structured (non-scalar) populations: they are given by the spectral radii of simple matrices.