Introduction

In oncology, one of the most important steps for screening compounds is the evaluation of their in vitro anticancer activity. Generally, after a first test on pure enzymatic systems, the most active moieties are compared on the basis of their capability to inhibit tumor cell proliferation in vitro. In these kinds of experiments, tumor cell cultures are exposed to different concentrations of the compound for a given time. For a given drug concentration C and exposure time T, drug efficacy (E) is measured as the ratio of the number of surviving cells to the number of cells observed in the control arm, in which cells are grown without anticancer agents. The design of the experiments is tailored to the specific phase of development and the corresponding needs. In the screening phase, for example, the cells are usually exposed only to a limited number of concentration levels for a unique fixed period of time [10, 11, 13], whilst, in case of further investigation on a specific compound, a wider range of concentration levels and exposure times is adopted. In the latter case, drug efficacy is typically summarized by a two-entry table (E vs. c and t) and, in case of sufficient data, also by a three-dimensional response surface [1, 8, 9, 12, 17]. This bivariate relationship \( E = f(c,t) \) may be characterized by descriptive and empirical methodologies. These approaches, however, do not provide a unique drug specific estimate of the anticancer activity. For example, the EC50 values may change significantly when calculated at different exposure times, showing that the experimental design and conditions may strongly influence the assessment of drug activity.

An alternative and more ambitious approach would be to develop a pharmacodynamic (PD) model of the time course of observed data. Along this direction, a first attempt has been made in [14], where a PD model of the in vitro effects of methotrexate is developed. In order to account for the substantial delay of the observed drug effect, the authors resorted to transit compartment models, which are emerging as a simple and robust approach to describe physiological time delays [6, 15].

In this paper, a new PD model describing the effect of drug concentration on cell proliferation rate is investigated. Differently from [14], where attention is focused on a single drug, our aim is to have a model describing the behaviour of a variety of drugs so as to enable comparative potency ranking. A major difference with respect to [14] is that the transit compartments are used to model the damage process of the tumor cells instead of describing delayed drug action. The proposed model describes the in vitro cell growth by means of few physiologically relevant parameters. In particular, it is possible to obtain a unique drug-specific index of efficacy on which candidate ranking can be based.

Materials and methods

Chemical supplies

All drugs and compounds used were either obtained from Nerviano Medical Sciences (Nerviano, Milan, Italy) or commercially available.

Cell culture conditions

A2780 human ovarian cancer cells were seeded at 20,000 cell/cm2 in complete medium (RPMI 1640 plus 10% Foetal Bovine Serum). 24 h after seeding, cells were treated with compounds dissolved in 0.1% DMSO, at different concentrations.

The cells were incubated at 37°C and 5% CO2 and at the end of the exposure time the plates were processed using CellTiter-Glo assay (Promega) following the manufacturer’s instruction. CellTiter-Glo is a homogenous method based on the quantification of the ATP present, an indicator of metabolically active cells [5]. ATP is quantified using a system based on luciferase and d-luciferin resulting into light generation. Briefly, 25 ml reagent solution is added to each well and, after 5-min shaking microplates are read by Envision (PerkinElmer) luminometer. The luminescent signal is proportional to the number of active cells present in culture. Dead cells do not affect cell counts because they do not contribute to the ATP content. As a consequence, the number of metabolically active cells can be directly derived from the luminescent signal using a specific calibration curve [5, 7].

Inhibitory activity was evaluated comparing treated versus control data using Assay Explorer (MDL) program.

Experimental

Two different experimental sessions were considered; in the first one, commercial anticancer drugs were investigated: 5-fluorouacil (5-FU), cisplatin, docetaxel, doxorubicin, etoposide, gemcitabine, SN38 (the active metabolite of irinotecan), paclitaxel, vinblastine and vincristine. In the second session, four compounds in early discovery phase, namely compounds A, B, C, and D, were tested. In both cases, at each concentration level, cell counts were replicated using four wells. Replicates of controls (cells without treatment) were also included, eight wells in the first session and fourteen wells in the second one.

A twofold concentration range was considered; in particular, the different compounds were used at the following concentrations: doxorubicin from 9.77 nM to 10 µM, paclitaxel from 0.244 nM to 0.25 µM, 5-FU, cisplatin and etoposide from 97.6 nM to 100 µM, vincristine, vinblastine and docetaxel from 24.4 pM to 25 nM, SN38 from 19.5 nM to 20 μM, gemcitabine from 2.44 nM to 2.5 μM, compound A and compound C from 78.1 nM to 40 μM, compound B and compound D from 97.7 nM to 50 μM. The following exposure times were tested for the drugs of the first session: 4, 8, 12, 24, 48, and 72 h; the exposure times for the compounds of the second session were: 4, 8, 24, 48, and 72 h, except for the compounds A and C for which the measurement at 48 h was not taken. For each concentration level (and for controls), cell counts evaluated at different exposure times and averaged over replicates were gathered to obtain the average growth time course.

The experiments were carried out using a 96-well plate format. Each plate, associated with a specific exposure time, included wells treated with two drugs at different concentrations together with untreated wells used as control reference. As a whole, in the first session 30 plates (corresponding to six exposure times and five pair of drugs) yielded the growth curves of ten drugs at different concentrations and five controls. In the second session, nine plates (corresponding to five exposure times for a pair of compounds and four exposure times for another pair) yielded the growth curves of four drug candidates at different concentrations and two controls.

Pharmacodynamic model

Unperturbed growth model (untreated cells)

Tumor proliferation of untreated cells was described by an exponential growth model \( N_{u} \left( t \right) = N_{0} {\text{e}}^{{\lambda _{0} t}} \) or, in terms of differential equations:

$$ \begin{aligned} &{\frac{{{\text{d}}N_{u} \left( t \right)}}{{{\text{d}}t}} = \lambda _{0} N_{u} \left( t \right)} \hfill \\&{N_{u} \left( 0 \right) = N_{0} } \hfill \\ \end{aligned} $$

where N u (t) is the number of proliferating tumor cells at time t, λ0 is the rate of exponential growth, and N 0 is the number of proliferating cells at time t = 0. The origin of the time axis is 24 h after seeding, which also corresponds to the start of the treatment.

Perturbed growth model (treated cells)

In the proposed model, the antitumor drug, whose concentration is assumed constant and is denoted by c, makes some cells non-proliferating, eventually bringing them to death. It is assumed that the rate of transformation of proliferating cells into non-proliferating ones is proportional to the number of proliferating ones through the constant parameter k 2, which acts as an index of drug potency. The time which is elapsed from the instant when the cell is hit by the drug to the cell death is called time-to-death. The death process has been described by a chain of transit compartments that can be thought of as progressive stages of damage. A three-compartment model has been adopted here. In terms of differential equations, the overall in vitro tumor growth inhibition model (TGI model A, Eq. (1)) is:

$$ \left\{ {\begin{aligned}& {\frac{{{\text{d}}N_{p} \left( t \right)}}{{{\text{d}}t}} = \lambda _{0} N_{p} \left( t \right) - k_{2} cN_{p} \left( t \right)} \hfill \\ &{\frac{{{\text{d}}N_{1} \left( t \right)}}{{{\text{d}}t}} = k_{2} cN_{p} \left( t \right) - k_{1} N_{1} \left( t \right)} \hfill \\& {\frac{{{\text{d}}N_{2} \left( t \right)}}{{{\text{d}}t}} = k_{1} N_{1} \left( t \right) - k_{1} N_{2} \left( t \right)} \hfill \\ &{\frac{{{\text{d}}N_{3} \left( t \right)}}{{{\text{d}}t}} = k_{1} N_{2} \left( t \right) - k_{1} N_{3} \left( t \right)} \hfill \\ \end{aligned} } \right. $$
(1)
$$ \begin{array}{*{20}c} {N_{t} \left( t \right) = N_{p} \left( t \right) + N_{1} \left( t \right) + N_{2} \left( t \right) + N_{3} \left( t \right)} \hfill \\ {N_{p} \left( 0 \right) = N_{0} , N_{1} \left( 0 \right) = N_{2} \left( 0 \right) = N_{3} \left( 0 \right) = 0} \hfill \\ \end{array} $$

where N p (t) denotes the number of proliferating cells at time t and \( N_{i} \left( t \right), i = 1, 2, 3 \) the number of cells in the ith damage stage. In the above equations, k 1 is the rate of transition from a damage compartment to the next one (the average time-to-death corresponding to \( {3 \mathord{\left/ {\vphantom {3 {k_{1} }}} \right. \kern-\nulldelimiterspace} {k_{1} }} \)).

If the (average) death time exceeds the last observation of the time-course, cell death cannot be observed so that, for practical purposes, the damage compartments can be merged together, obtaining the following reduced model (TGI model B, Eq. (2)):

$$ \left\{ {\begin{aligned}&{\frac{{{\text{d}}N_{p} \left( t \right)}}{{{\text{d}}t}} = \lambda _{0} N_{p} \left( t \right) - k_{2} cN_{p} \left( t \right)} \hfill \\ &{\frac{{{\text{d}}N_{{{\text{np}}}} \left( t \right)}}{{{\text{d}}t}} = k_{2} cN_{p} \left( t \right)} \hfill \\ \end{aligned} } \right. $$
(2)
$$ \begin{gathered} N_{t} \left( t \right) = N_{p} \left( t \right) + N_{{{\text{np}}}} \left( t \right) \hfill \\ N_{p} \left( 0 \right) = N_{0} , N_{{{\text{np}}}} \left( 0 \right) = 0 \hfill \\ \end{gathered} $$

where \( N_{{{\text{np}}}} \left( t \right) \) is the total number of non-proliferating cells regardless of their degree of damage. It has to be noticed that this implies that in TGI model B no cells are lost during the observation time period (i.e., 72 h) and, as a consequence, the number of observed cells may never show a decrease even at the highest drug concentration levels. As such, this model can be considered representative of the effect of the drug on the cells only in this transient phase and, differently from TGI model A, cannot be extrapolated outside this time interval.

The analytic expression of the total number \( N_{t} \left( t \right) \) of tumor cells is reported in Appendix for both models.

Threshold concentration

From Eq. (1) it is seen that the derivative of the proliferating cells is negative if and only if \( c > {{\lambda _{0} } \mathord{\left/ {\vphantom {{\lambda _{0} } {k_{2} }}} \right. \kern-\nulldelimiterspace} {k_{2} }}. \) The concentration \( C_{T} = {{\lambda _{0} } \mathord{\left/ {\vphantom {{\lambda _{0} } {k_{2} }}} \right. \kern-\nulldelimiterspace} {k_{2} }}, \) called threshold concentration, is the minimal drug concentration that stops the increase of the number of proliferating cells. If \( c > C_{T} , \) the number of cells asymptotically tends to zero.

Inhibition surfaces

The results of in vitro cell-growth studies can be represented as inhibition surfaces, which show the effect \( E\left( {c,t} \right) \) as a function of concentration c and exposure time t. The usual approach is to estimate such surfaces from experimental data collected on a grid of values in the plane (c, t), using either parametric [9, 17] or nonparametric [8] methods. Using the new TGI model, an analytic expression for the whole inhibition surface can be derived from the parameters N 0, λ 0, k 1, k 2. More precisely:

$$ E\left( {c,t} \right) = 100\left( {1 - \frac{{N_{t} \left( {t,c} \right)}}{{N_{u} \left( t \right)}}} \right) $$

where \( N_{t} \left( {t,c} \right) \) is the total number \( N_{t} \left( t \right) \) of tumor cells (see Appendix for its analytic expression) at drug concentration c.

EC50 calculation

For a given exposure time T, \( {\text{EC}}_{x} \left( T \right) \) is defined as the concentration \( \overline c \) such that \( E\left( {\overline c ,T} \right) = x. \) In particular, EC50 is commonly used to characterize the potency of the compounds. EC50 can be estimated from the following three-parameter Hill’s model:

$$ E(c,T) = E_{0} (T) + \frac{{\left( {100 - E_{0} (T)} \right)c^{m} }}{{{\text{EC}}_{{50}}^{m} (T) + c^{m} }} $$

where m is a shape factor and \( E_{0} (T) \) is the baseline effect.

Note that for some values of t, EC50 may not exist. In fact, if t is too small, no concentration can achieve a 50% effect due to the non-null time-to-death. In the following, t min denotes the minimal time such that EC50 exists for all t > t min.

According to the proposed TGI model, t min is the minimal time t such that \( {{N_{t} \left( {t,\infty } \right)} \mathord{\left/ {\vphantom {{N_{t} \left( {t,\infty } \right)} {N_{u} \left( t \right) = 0.5}}} \right. \kern-\nulldelimiterspace} {N_{u} \left( t \right) = 0.5}}, \) where \( N\left( {t,\infty } \right) \) is the total number of tumor cells at time t when drug concentration tends to infinity. From Appendix, it follows that for TGI model A

$$ {\text{e}}^{{ - k_{1} t_{{\min }} }} \left( {1 + k_{1} t_{{\min }} + k_{1}^{2} \frac{{t_{{\min }}^{2} }}{2}} \right) - \frac{1}{2}{\text{e}}^{{\lambda _{0} t_{{\min }} }} = 0 $$
(3)

so that t min can be numerically computed by finding the zeros of the Eq. (3).

Note that for TGI model B, corresponding to \( k_{1} = 0 \) in Eq. (3), the minimal time admits the simple expression \( t_{{\min }} = {{\ln \left( 2 \right)} \mathord{\left/ {\vphantom {{\ln \left( 2 \right)} {\lambda _{0} }}} \right. \kern-\nulldelimiterspace} {\lambda _{0} }}, \) which coincides with the cell doubling time.

Data analysis

The PD model was implemented using Winnonlin (version 3.1, Pharsight, CA, USA). Parameters were estimated using weighted nonlinear least squares. Different weighting strategies (uniform, 1/y observed, 1/y 2observed ) were applied and chosen based on the analysis of residuals and the coefficient of variation of the estimated parameters. The pharmacodynamic model was fitted to the cell counts averaged over replicates. For each experiment, the unperturbed and perturbed growth models were fitted simultaneously to the data of control and treated groups.

Results

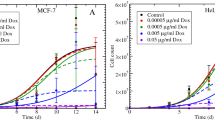
Both experimental sessions were analyzed using the proposed in vitro TGI model. According to such model, the unperturbed growth can be considered a particular case of the perturbed one for c = 0, so that for each drug simultaneous fitting of both control and treated arms is possible. The activity of different compounds (ten commercial anticancer drugs and four compounds still in discovery phase) was analyzed. As an example Fig. 1 shows the observed and model-fitted growth for both controls and cells exposed to different concentrations of three representative compounds, namely doxorubicin (Root Mean Square Error RMSE = 945.8), 5-FU (RMSE = 771.9), and compound C (RMSE = 667.4). In case of 5-FU the use of model B (Eq. 2) was suggested by the lack of any decrease in the observed number of cells also at the highest concentration level of 100 μM. It appears that the model was able to adequately describe cell growth for all three compounds. Similar results were obtained for the other eleven compounds, with RMSE ranging in the interval [616.9, 1322.9] and [235.1, 667.4] for the first and second experimental session, respectively. Fitted versus observed number of cells are plotted in Fig. 2 for all the fourteen compounds.

Fig. 1
figure 1

Observed data (black circles) and fitted growth curves (continuous lines) for both untreated and treated A2780 human ovarian cancer cells exposed to different concentrations of doxorubicin (Panel A), 5-FU (Panel B) and compound C (Panel C). Data of each panel were simultaneously fitted by using TGI model A (doxorubicin and compound C) or TGI model B (5-FU)

Full size image
Fig. 2
figure 2

Regression plot of fitted versus observed number of cells for all the fourteen compounds

Full size image

Parameter values estimated for all the tested compounds together with the corresponding coefficient of variation (CV%) are reported in Table 1. The parameters related to the growth of untreated cells (N 0 and λ 0) were always well determined with CV% below 5% in all the investigated cases. The exponential rate λ 0 had an average value of 3.06 × 10−2 h−1 with a very limited range of variability [2.58 × 10−2, 3.39 × 10−2]. The corresponding doubling time ln(2)/λ0 = 22.7 h was in optimal agreement with the biological knowledge on the A2780 cell line. The values of N 0 clustered in two groups according to the different experimental sessions; for the first session, the average initial number of cells resulted to be 2279, whilst for the other session (candidate compounds) lower values were estimated (average value of 1164).

Table 1 Pharmacodynamic parameters (λ0, N 0, k 1, k 2) and their coefficient of variation (%) obtained fitting TGI model A or B to the cell counts for each investigated compound
Full size table

The estimated values of the potency parameter k 2 ranged from 6.34 × 10−4 µM−1 h−1 for 5-FU to 21.8 μM−1 h−1 for vinblastine; the CV% were always less than 15% indicating a very good precision of the estimates. For cisplatin, doxorubicin, etoposide, gemcitabine and the four compounds in discovery phase, the estimated values of k 1 ranged from 0.033 to 0.416 h−1 with CV% always less than 42%. For the other drugs (paclitaxel, SN38, vinblastine, 5-FU, vincristine and docetaxel), the k 1 parameter (transition rate through the mortality chain) was not significantly different from zero (t test, P > 0.05) indicating that 72 h are not enough to observe cell death. For this reason, these drugs were analyzed using the TGI model B.

From the model parameters λ 0 and k 2, the threshold concentration C T (which, as previously defined, is the minimum concentration that stops the increase of proliferating cells) was computed (see Table 1). For a given cell line, the C T parameter can be also used to rank the compounds according to their potency with lower C T values corresponding to greater potency. The computed values of C T ranged from 1.55 × 10−3 µM for vinblastine to 48.4 µM for 5-FU.

The robustness of the proposed approach when the number of plates is very limited as usually happens in screening experiments was also investigated. For this purpose, a reduced data set consisting of only the data collected at 4 and 72 h (first and last exposure time) was considered. The parameters λ 0, N 0, k 1, and k 2 obtained from these reduced data sets were still identifiable, with values and CV% comparable to those previously obtained from the full time courses (see Table 1). In particular, the Spearman’s correlation between k 2 estimated on the full data set and its estimate on the reduced data set was equal to 0.9747 (0.9912 for C T ) indicating consistency in the drug potency ranking.

From the analytic expression of \( E\left( {c,t} \right), \) see “Materials and methods”, inhibition surfaces providing the effect E as a function of concentration c and exposure time t for all compounds were computed and are reported in Fig. 3. The different profiles of EC50 versus exposure time of all the analyzed compounds are plotted in Fig. 4. It is apparent that EC50 exhibits a strongly nonlinear time dependence passing from vertical asymptotes to slow decays. The vertical asymptotes occur in correspondence of t min, the minimal time at which EC50 is defined. The values of t min computed as explained previously (see “Materials and methods”) are reported in Table 1. Recall that for the six drugs whose k 1 was not significantly different from zero, t min coincides with the cell doubling time. When k 1 was identifiable, a linear dependence of t min on the logarithm of k 1 was observed (see Fig. 5).

Fig. 3
figure 3

Inhibition surfaces providing the effect E as a function of concentration c and exposure time t. A refers to the first experimental session: a 5-FU; b cisplatin; c docetaxel; d doxorubicin; e etoposide; f gemcitabine; g SN38; h paclitaxel; i vinblastine; l vincristine. B refers to the second experimental session: a compound A; b compound B; c compound C; d compound D

Full size image
Fig. 4
figure 4

Relationship between EC50 and exposure time t for all the analyzed compounds. Note the nonlinear dependence of EC50 upon t and the existence of a minimum time t min, specific for each compound, below which EC50 is not defined

Full size image
Fig. 5
figure 5

Relationship between the minimal time t min needs for EC50 to exist and the model parameter k 1 (transit rate through mortality chain compartments). The circles are associated to compounds whose parameter k 1 is significantly different from zero. Regression performed on semi-log scale: \( t_{{\min }} = - 0.2714 - 15.818 \cdot \log _{{10}} (k_{1} ), \) r 2 = 0.961. Doubling time computed considering the average value of λ 0 estimated for all compounds corresponds to k 1 = 0.0353 on that regression

Full size image

The shape of the curves in Fig. 4 suggests that robust estimates of EC50 can be obtained only exposing the cells for a sufficiently long period of time, e.g. 48 or 72 h as in these experiments. In fact, for exposure times close to t min, EC50 is extremely time sensitive.

The C T values and the EC50 at 72 h, the longest exposure time, showed a tight log–log correlation (r 2 = 0.983) with the exponential coefficient equal to 1.05, see Fig. 6.

Fig. 6
figure 6

Relationship between the newly proposed potency parameter C T (threshold concentration) and EC50 at 72 h calculated for all the tested compounds. The drawback of EC50 is that it depends on the exposure time, see Fig. 4. Conversely, the threshold concentration C T is time-independent. Regression performed on log–log scale: \( \log _{{10}} \left( {C_{T} } \right) = 0.371 + 1.05 \cdot \log _{{10}} \left( {{\text{EC}}_{{50}} } \right), \) r 2 = 0.983

Full size image

Discussion

Ten commercial anticancer drugs and four new generation compounds still in discovery phase were tested in vitro using A2780 tumor cell line in two different experimental sessions. A new PD approach to the analysis of the response curves was proposed and tested. The model was able to adequately describe the time course of the cell growth in control and treated cells showing the appropriateness and suitability of the model assumptions. As a result, for each compound, four physiologically meaningful pharmacodynamic parameters could be estimated: N 0 and λ 0, the starting number of cells and the rate of cell growth in the control plates, are mainly related to the experimental conditions and to the adopted cell line, whereas k 1 and k 2, the cell rate-to-death and the drug potency may be considered as drug-specific parameters. For each of the 14 tested compounds a simultaneous fitting of all the data was successfully performed. The estimates of N 0 were homogeneous within each of the two experimental sessions. The different values observed between the two sessions reflected the number of seeded cells that may vary from session to session. On the contrary, the estimates of λ 0 were remarkably stable also across sessions with an average doubling time value of 22.5 h, in good agreement with the doubling time expected for the A2780 cell line. For six drugs, the k 1 parameter was not significantly different from zero because the time-to-death was comparable or longer than the observation period (72 h in our experimental setting). This may be a possible indication of analogies among the mechanisms of action within this group of drugs. In these cases, the simplified TGI model B was considered and successfully identified.

The in vitro experiments considered in the present paper are mainly used for screening purposes during the early phase of drug development. In this context, it is particularly important to optimize the experimental setting and procedures. It has been shown that the model parameters can be reliably estimated also from a reduced data set consisting of data collected only at two times (4 and 72 h).

So far, the in vitro anticancer activity of candidate drugs has been analyzed mainly by means of descriptive and empirical approaches, where the results are presented under the form of inhibition surfaces and summarized by means of the EC50 at selected exposure times. This empirical approach suffers from several drawbacks. First of all, the time dependence of EC50 hampers its use both as a latency index and a ranking criterion. Second, the point-to-point reconstruction of the inhibition surface requires a large number of evaluations in order to cover the widest range of concentrations and exposure times, resulting expensive and time consuming. Finally, from a purely empirical description of the inhibition it is difficult to predict the effect of changes in experimental conditions.

By contrast, this paper describes a model-based approach, which relies on a simple dynamic model of the drug effect on the cell growth. This approach has several advantages with respect to the empirical one. Few evaluations are sufficient to estimate the model parameters, yielding time-independent potency indices, k 2 and C T , that can be used to rank the candidate compounds under analysis. The inhibition surface and the relative EC50 value can be easily derived and the minimal time t min, needed for the EC50 to be observable, is obtained from a specific formula. From the graphs presented in Fig. 4 it can be recognized that also cell exposure times of 48 h, commonly used in many laboratories including the NCI60 [2, 3, 19], may suffice to obtain a first estimate of EC50 for screening purposes. An interesting open question regards the generality of the proposed model. Although no claim of general validity is made, in the present paper the model was shown to be able to satisfactorily explain tumor growth inhibition for 14 compounds with known different mechanisms of action. The structure of the proposed in vitro model is very similar to that of the so called TGI in vivo model [16, 18], which has been successfully applied to even more compounds including new targeted candidates [4]. Although no immediate relationship exists between the parameters of the two models, there is motivation for investigating the possible prediction of the in vivo parameters from the in vitro ones.