Introduction

Dislocations are linear topological defects in a crystal lattice that act as carriers of plastic strain. The stress required to move a dislocation by glide is lower than the ideal shear strength of a crystal, and glide-controlled creep can be a significant contributor to deformation, especially under conditions of moderate to high stress or low temperature. Dislocations can also act as reservoirs for point defects, as the strain fields around the core induce elastic and inelastic interactions between point defects and dislocations that cause segregation of point defects to dislocation cores. This can diminish dislocation mobility through the phenomenon of solute drag, whereby the additional energy required to either pull a solute cloud along with a translating dislocation or break free from it altogether increases the stress required for dislocation creep (Cottrell and Bilby 1949). Alternatively, in the glide-creep regime, point defects can enhance dislocation mobility, by reducing the stress required to initiate glide at 0 K (the Peierls stress, σp).

Vacancies have been found to reduce stacking fault energies and lubricate dislocation glide in a variety of metals, including fcc Al (Lauzier et al. 1989; Lu and Kaxiras 2002), Ni, Cu, Fe (Asadi et al. 2014). Vacancies can also reduce the Peierls stress in non-metals, such as the superconductor MgB2 (Shen et al. 2015). Theoretical calculations show that hydrogen can lubricate dislocation glide in fcc metals such Al (Lu et al. 2001) and Fe (Taketomi et al. 2008), which may explain the ubiquitous phenomenon of hydrogen induced local plasticity in these metals. Chemical impurities, in the form of interstitial oxygen defects, can also lubricate dislocation glide in oxides such as UO2, decreasing the critical resolved shear stress and changing the relative strength of its major slip systems (Keller et al. 1988). This is attributed to interactions between dislocation cores and the interstitial oxygen ions reducing the Peierls barrier to glide (Ashbee and Yust 1982).

(Mg, Fe)O is thought to be the second most abundant mineral in the Earth’s lower mantle, after the perovskite-structured mineral (Mg, Fe)SiO3 bridgmanite, comprising slightly less than 20% of the region’s volume (e.g. Lee et al. 2004). Despite being less abundant than bridgmanite, the relatively low strength of (Mg, Fe)O means that it may accommodate the majority of the strain in lower-mantle rocks (Girard et al. 2016). Along a mantle geotherm, MgO deforms athermally to ~ 2000 km depth, with dislocation–dislocation interactions governing flow rates. At greater depths, the rheology is in the thermally activated regime and the Peierls stress becomes important for determining strain rates (Cordier et al. 2012). In MgO, the dominant slip system at ambient pressure is 1/2<110>{110}, with a modest additional contribution from the 1/2<110>{100} slip system. High pressure creep experiments show that the relative activity of the 1/2<110>{100} slip system in MgO gradually increases with pressure and, above ~ 23 GPa, this slip system comes to dominate over the 1/2<110>{110} slip system (Girard et al. 2012).

In some mantle silicates and oxides, dissolved water-related defects, in the form of chemically bound hydroxyl, may enhance strain rates by reducing the Peierls stress. For instance, under dry conditions the measured Peierls stress of olivine, the most abundant mineral in the Earth’s upper mantle, is between 3.8 GPa (Idrissi et al. 2016) and ~ 15 GPa (Demouchy et al. 2013), although more typical values are in the range 5–10 GPa (e.g. Evans and Goetze 1979; Kranjc et al. 2016; Proietti et al. 2016). In contrast, high-stress, low-temperature deformation experiments designed to measure the Peierls stress of hydrated olivine report its value to be in the range 1.6–2.9 GPa (Katayama and Karato 2008), significantly below the range of Peierls stresses measured for dry olivine. These experiments have measured only an average Peierls stress for olivine, which does not correspond to any individual slip system. However, changes in the deformation fabric with water content suggest that some slip systems are more sensitive to water content than others (Jung and Karato 2001; Katayama et al. 2004).

In pure MgO, hydrogen is incorporated via the charge-neutral substitution of an Mg2+ ion by a pair of protons, represented in the Kroger–Vink notation as {2HMg}X (Kröger and Vink 1956). Analogous defects, in which a divalent cation (typically Mg or Fe) is replaced with two protons are also found in (Mg, Fe)-silicates in the mantle, including olivine (Bai and Kohlstedt 1993; Kohlstedt et al. 1996). The solubility of hydrogen in MgO is very low, and under conditions of ambient pressure and water saturation, the concentration of hydrated Mg vacancies is < 10 wt ppm H2O (Joachim et al. 2012). However, concentrations of hydrated vacancies may be much higher in regions of the crystal under compressional strain, as is the case directly above the glide plane of an edge dislocation. This is certainly the case for bare Mg vacancies (i.e. vacancies without protons present), which in cluster-based simulations segregate strongly to 1/2<110>{110} edge dislocation cores in MgO, with a segregation energy of − 1.7 eV for the tightest binding site (Zhang et al. 2010). Ab initio calculations show that {2HMg}X defects in MgO bind to {310} tilt grain boundaries, which can be modeled as an array of dislocation, with minimum segregation energies on the order of − 1 eV at 0 GPa (Karki et al. 2015).

A number of different methods exist for calculating Peierls stresses from atomistic simulations. While fully atomistic calculations are possible, one approach that has seen considerable use in materials science is the Peierls–Nabarro (PN) method (Peierls 1940; Nabarro 1947). This model uses a hybrid continuum-elastic approach in which a dislocation is represented as a discrete distribution of dislocation density which interact with each other elastically, held together by inelastic restoring forces representing the shear strength of the crystal. These restoring forces can be calculated using atomistic simulations by introducing the concept of a generalized stacking fault (GSF), which is a translational discontinuity across the glide plane of the crystal, whose energy can be calculated using any one of the numerous atomic simulation techniques available (Christian and Vítek 1970).

The PN approach has been applied to calculation of dislocation properties, including Peierls stresses, of dislocations in pure MgO, and is able to reproduce experimentally observed dislocation properties with some accuracy. Carrez et al. (2009) used an ab initio parameterized continuous PN model of relative slip strength in MgO, predicting that the 1/2<110>{110} slip system is approximately an order of magnitude weaker than the 1/2<110>{100} slip system, consistent with experimental observations (e.g. Foitzik et al. 1989). Ab initio parameterised Peierls–Nabarro–Galerkin (PNG; Denoual 2004) simulations show that Peierls stress of the 1/2<110>{110} slip system is lower than that of the 1/2<110>{100} slip system at low pressure, but that the strengths of the two slip systems converge at lower mantle pressures (Amodeo et al. 2012). This approach was used as the basis for simulations of dislocation mobility by kink-nucleation in MgO (Cordier et al. 2012).

In this study, we use the PN model to compare Peierls-stresses in MgO with and without dissolved {2HMg}X defects, in order to determine whether hydrous defects can reduce the Peierls stress in mantle minerals, and to determine the possible significance of this for deformation of MgO. To do this, we use density functional theory (DFT; Hohenberg and Kohn 1964; Kohn and Sham 1965) to calculate generalized stacking fault energies are calculated for slip in the 1/2<110> direction on the {100} and {110} planes, with and without {2HMg}X defects present at the slip plane. These GSF energies, together with elastic constants calculated ab initio are used to parameterize PN models for 1/2<110>{100} and 1/2<110>{100} dislocations in both hydrous and anhydrous MgO.

Computational details

Ab initio calculations

All atomistic calculations performed in this study use plane-wave density functional theory (DFT), as implemented in version 5.2.0 of Quantum Espresso (Giannozzi et al. 2009). Core and semi-core electrons were represented using the planar augmented wave (PAW) method (Blöchl 1994), while the exchange correlation (xc) energy was treated using the PBEsol xc-functional (Perdew et al. 2008). This xc-functional, which was developed to correct biases in earlier parameterizations towards isolated systems, was chosen for its ability to accurately predict the structure and properties of crystalline solids (see e.g. Ropo et al. 2008; Demichelis et al. 2010). The PAW data sets for Mg, H, and O atoms are from version 1.0.0 of pslibrary (Dal Corso 2014); details of their generation parameters can found therein. The kinetic energy cutoff and spacing of the Monkhorst–Pack grid used to sample reciprocal space (Monkhorst and Pack 1976) were chosen to ensure convergence of the total energy to with < 5 meV/atom. This required a kinetic energy cutoff of 80 Ry (~ 1090 eV) and a Monkhorst–Pack grid spacing that corresponds to a 4 × 4 × 4 grid for the 8-atom rock salt unit cell. In all calculations, free parameters (atomic positions and, where applicable, cell parameters) were relaxed using the BFGS quasi-Newton scheme (Pfrommer et al. 1997).

In the bulk crystal, the lowest energy configuration of {2HMg}X defect is one in which the two hydrogen ions are bonded to opposing oxygen ions within the M-site octahedron, with the O–H bonds in each defect parallel and pointing towards the center of the site. This is consistent with the DFT calculations of Hernández et al. (2013), who similarly found the linear hydrogen configuration to be the most stable. There are three possible arrangements and all possible configurations of this defect are symmetry equivalent in a perfect crystal. However, as discussed below, the insertion of a topological defect such as a dislocation or generalized stacking fault breaks the symmetry of the crystal, leading to multiple symmetry-inequivalent configurations of the {2HMg}X defect.

The elastic constants Cij determine the strength of the repulsive elastic interactions between components of the dislocation density in the PN model. These were calculated using the finite strain approach, in which a small strain is applied to the simulation cell and the internal coordinates (i.e. atomic positions) are relaxed. The elastic constants can then be extracted by fitting the residual stress to the Hooke’s law relation \({\sigma _i}={C_{ij}}{\epsilon _j}\). Linear elasticity breaks down at large strain amplitudes whereas, if the strain amplitude is too small, the numerical error due to the use of finite convergence criteria may be of the same order as the residual stresses, leading to high uncertainties in the fitted values of the Cij. The number of distinct imposed strains depends on the symmetry of the crystal; for MgO, which has cubic symmetry, a single strain was sufficient to determine all ofhe Cij. In addition to the elastic constants of anhydrous MgO, we also calculated elastic constants for 1 × 1 × 1 and 2 × 2 × 2 supercells, each containing a single {2HMg}X defect, to assess the possible influence of hydrated defects on the elastic self-interaction of a Peierls–Nabarro dislocation.

Peierls–Nabarro calculations

The Peierls–Nabarro (PN) model represents a planar dislocation with finite core-width as a distribution of dislocation density ρ along the glide plane. This distribution may be continuous or discrete. The core shape is determined by the balance between the repulsive elastic interactions between components of the dislocation density distribution at different points in the crystal and the inelastic restoring forces caused by the presence of a disregistry u in the material at the glide plane. The core energy ECORE of a dislocation in the PN model is

$${E_{{\text{CORE}}}}={E_{{\text{ELASTIC}}}}+{E_{{\text{MISFIT}}}}+{E_{{\text{WORK}}}}$$
(1)

where EMISFIT is the inelastic energy due to displacement of atoms across the glide plane, \({E_{{\text{WORK}}}}=-\sigma \mathop \smallint \nolimits^{} u\left( x \right){\text{d}}x\) is the work done on the dislocation by an applied stress σ, and EELASTIC is

$${E_{{\text{ELASTIC}}}}\left[ {\rho (x)} \right]= - K\mathop \iint \nolimits^{} \rho \left( {x'} \right)\rho \left( x \right){\text{ln}}\left| {x - x'} \right|{\text{d}}x'{\text{d}}x$$
(2)

which is the energy due to the elastic self-interaction of the dislocation density distribution. The static core structure of the dislocation can be determined by minimizing ECORE with σ = 0. The Peierls stress is calculated by gradually increasing σ until Eq. (1) no longer has a minimum energy solution, as the dislocation is able to glide freely.

In the classical formulation of the Peierls–Nabarro model, a dislocation core is represented as continuous distribution of infinitesimal dislocation density. However, such a distribution is translationally invariant, meaning that there no energy barrier to glide of the dislocation. The dislocation can alternatively be represented as a distribution of dislocation density on a discrete lattice (Bulatov and Kaxiras 1997). In this approach, the dislocation density takes finite values and the inelastic misfit energy becomes a sum over the lattice points, i.e.

$${E_{{\text{MISFIT}}}}=\mathop \sum \limits_{n} \gamma ({\bf u}(n{a_p})){a_p}$$
(3)

where ap is the lattice spacing and γ(u) (called the γ-line in 1D and the γ-surface in 2D) gives the inelastic energy of a crystal lattice offset across the glide plane by u, the disregistry. In this work the γ-line is calculated from energies recovered from generalized stacking fault calculations (Christian and Vítek 1970) with the energies calculated using density functional theory.

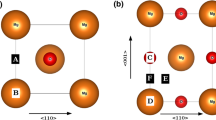
A GSF is a planar defect in a crystal across which the crystal is offset by some vector u, perpendicular to the normal of the GSF plane. In an atomistic simulation, a GSF is inserted by cutting an appropriately oriented simulation cell and displacing one-half with respect to the other by u. The atomic coordinates are then to relaxed to their minimum energy configuration, subject to the constraint Mg2+ and O2− ions can only move in the direction of the stacking fault normal. It is common to incorporate a vacuum layer into the simulation cell, to prevent direct interactions between stacking faults along the slab axis. In all GSF calculations described here, the vacuum layer was 15 Å thick, and the coordinates of all atoms within 2.5 Å of the vacuum layer were fixed during relaxation. For {100} and {110} oriented simulation cells, the energies of the γ-line maxima to within 10 meV/Å2 by the use of a slab cell whose thickness (in units of the fault normal vector) was n = 6. GSF cell geometries for simulating slip on {100} and {110} are shown in Fig. 1.

Fig. 1
figure 1

Simulation cells containing 1/4<110 > generalized stacking faults on the a {100} and b {110} planes

Full size image

To calculate the effect of protonated Mg vacancies on GSF energies, all γ-line calculations were repeated with simulation cells containing a single {2HMg}X defect at the slip plane, with the cell dimensions in the x- and y-directions doubled to reduce interactions between the defect and its periodic images. Consistent with the fact that the strain field induced by a point defect decays more quickly with distance than that of an unstable stacking fault, the slab cell thickness used in calculations of GSF energies without adsorbed point defects were sufficient to ensure convergence of those with {2HMg}X defects present at the slip plane. For the {100} GSF calculations, this corresponds to a cross-sectional area of √2a × √2a, where a is the unit cell parameter of MgO, while the cross-sectional area of the cell used in the {110} GSF calculations was √2a × 2a. However, although the differently oriented simulation cells have different cross-sectional areas, the number of defects per lattice site at the slip plane is the same for the {100} and {110} oriented simulation cells, permitting a direct comparison of the effects of protonated Mg vacancies on glide of 1/2<110>{100} and 1/2<110>{110} dislocations.

Parameterizing the inelastic restoring force using calculations of GSF energies in which a point defect has been inserted allows us to investigate the potential influence that point defect might have on the core structure and mobility of a particular dislocation. The dislocation properties calculated using this represent only an approximation to the true effect that the point may have, as the point defect is effectively spread out across the entire dislocation core. This is less of a problem for dislocations in MgO, which have narrow, undissociated cores, than it would be for dislocations with widely dissociated cores, for example [001] dislocations in olivine (Durinck et al. 2007) and [010] dislocations in wadsleyite (Metsue et al. 2010). Additionally, because the PN model does not simulate an individual point defect, it is impossible to calculate the binding energy between the point defect and a dislocation. However, the PN model has some advantages over fully atomistic calculations, the most important of which is that GSF simulation cells contain fewer atoms than those used in fully atomistic simulations of dislocations, so that it is possible to use DFT instead of empirical potentials, which may be inaccurate for highly deformed regions of a crystal, such as in the vicinity of a dislocation core.

Results and discussion

Elastic constants

The shape and mobility of a Peierls–Nabarro dislocation are controlled by the balance between the repulsive elastic interactions between components of the dislocation density and the inelastic restoring parameterized using GSF calculations. Before addressing the effects of adsorbed {2HMg}X defects on GSF energies, we will address the question of how sensitive the elastic constants Cij—and through them the elastic prefactor K in Eq. (2)—are to the concentration of these defects.

Compared with the experimental measurements (taken from Sinogeikin and Bass 1999), the PBEsol xc-functional predicts modestly lower elastic stiffness, with the calculated 0 GPa elastic constants less than their experimental values by 1.6% (C11) and 6.9% (C44). To determine the effect of water on the elastic constants of MgO, we compare the Cij calculated for anhydrous MgO above with those calculated using 1 × 1 × 1 and 2 × 2 × 2 supercells, each containing a single {2HMg}X defect (Table 1). In the 1 × 1 × 1 supercell, one quarter of the Mg sites are replaced with {2HMg}X, while the 2 × 2 × 2 supercell contains one {2HMg}X per 32 Mg sites. The Voigt–Reuss–Hill average of the isotropic shear modulus, GVRH, for the 1 × 1 × 1 cell is ~ 18% softer than the dry shear modulus at 0 GPa, compared with a ~ 4% shear modulus relaxation of the shear modulus for the 2 × 2 × 2 simulation cell. Pressure increases the relative shear modulus deficit of the 1 × 1 × 1 simulation cell slightly, to ~ 19.5%, while that of the 2 × 2 × 2 simulation cell is essentially pressure invariant. However, while the effect of water on the isotropic shear modulus is relatively pressure insensitive, this is not the case for the individual elastic constants. For instance, the value of C12 for the 1 × 1 × 1 simulation cell is ~ 34.7% lower than that of dry MgO at 0 GPa, but only 18.7% lower at 100 GPa.

Table 1 Calculated elastic constants (in GPa) of anhydrous MgO, compared with those of 1 × 1 × 1 and 2 × 2 × 2 supercells containing a single {2HMg}X defect
Full size table

For a more rigorous quantification of the effect of defect chemistry on the elasticity of a material, we can compute the Euclidean distance between the elasticity tensors of the pure material and the supercells containing protonated vacancies. To do this, the elasticity tensor is represented as a 21-dimensional vector, corresponding to the number of linearly independent elastic constants Cij for a triclinic crystal, with appropriate prefactors to maintain invariance under coordinate transformations (Browaeys and Chevrot 2004). The distance between two elasticity tensors is then ||C1–C2||, where C1 and C2 are the vector representations of the two tensors, and the relative deviation of C1 from C2 is ||C1–C2||/||C2||. For MgO, which has cubic symmetry, only the first 9 components of the vectorial representation of the elasticity tensor are non-zero, with components 1–3 equal to C11, components 4–6 equal to √2C12, and components 7–9 equal to 2C44. This technique has been used to calculate the effect of chemistry and order on the elasticity of metal alloys (e.g. Xie et al. 2012; Zhou et al. 2013). Using the elastic constants reported in Table 1, we calculate the normalized distance between the elasticity tensor of dry MgO and a 1 × 1 × 1 supercell to be 0.239 at 0 GPa, decreasing to 0.15 at 125 GPa. The elasticity tensor of the 2 × 2 × 2 supercell is even closer to that of dry MgO, reflecting the eightfold reduction in the defect concentration, with a normalized distance between the dry and wet C of just 0.046 at ambient pressure, decreasing only slightly with pressure to 0.043 at 125 GPa.

Crystal elasticity affects the core properties of a dislocation through the elastic energy coefficient K in Eq. (2), which depends both on the elastic constants Cij and the dislocation geometry. Elastic energy coefficients for the 1/2<110>{100} and 1/2<110>{110} edge dislocations, and for the 1/2<110> screw dislocation (whose coefficient is the same for glide on {100} and {110}) calculated from the elastic constants of dry and protonated vacancy-containing MgO. As expected, the elastic energy coefficients calculated from the elastic constants of supercells containing a {2HMg}X defect are systematically lower than those calculated for dislocations in dry MgO (Table 1). At 0 GPa, Ke for the 1/2<110>{100} slip system is 22.2% lower when calculated using the elastic constants for the 1 × 1 × 1 supercell. However, the Ke for this slip system computed using the elastic constants of the 2 × 2 × 2 supercell differs form the dry value by only − 4.6%, comparable to the difference between the DFT and experimental values. The value of Ke calculated for the 1/2<110>{110} slip system at ambient pressure is even less sensitive to the concentration of {2HMg}X defects, with the values calculated using the elastic constants of the 1 × 1 × 1 and 2 × 2 × 2 supercells differing from the dry Ke by − 13.2 and − 3.9%, respectively. However, the deficit increases modestly with pressure, reaching − 18.1 and − 4.3% at 125 GPa. The effect of {2HMg}X concentration on Ks, the elastic energy coefficient of the 1/2<110 > screw dislocation, is similar to that reported for Ke.

For MgO, as for magnesian silicates such as forsterite (Liu et al. 2009) and wadsleyite (Mao et al. 2008; Chang et al. 2015), the incorporation of water as protonated vacancies softens the elasticity tensor. However, this effect decreases rapidly with decreasing water content. Consequently, since the simulation cells used for GSF calculations in this study have relatively large cross-sections and bulk water solubilities are extremely low in both MgO (< 10 ppmw; Joachim et al. 2012) and (Mg, Fe)O (< 100 ppmw; Bolfan-Casanova et al. 2003), the elastic energy coefficients for all PN simulations in this study were calculated using the elastic constants of dry MgO.

Generalized stacking fault energies

To determine the effect of {2HMg}X defects on inelastic stacking faults in MgO, it is first necessary to calculate the energies of these stacking faults in the absence of adsorbed point defects (shown in Fig. 2). At 0 GPa, the maximum energy computed along the 1/2<110> γ-line is associated with the 1/4<110> stacking fault vector for slip on both the {110} and {100} families of of planes, with values of 0.0691 and 0.1434 eV/Å2, comparable to the values of 0.0655 and 0.1361 eV/Å2 calculated for these GSFs using the PBE xc-functional in a previous study (Carrez et al. 2009). However, {110} GSF energies are more pressure sensitive than {100} GSF energies. Comparing the energies of the 1/4<110 > stacking fault vector on {110} and {100} as functions of pressure (Fig. 3), it can be seen that, in the former case, the calculated GSF energy increases almost six-fold over the pressure range 0–125 GPa, reaching 0.3907 eV/Å2 at the highest pressure, whereas the energy of the 1/4<110> stacking vector on {100} is roughly doubled, reaching 0.2605 eV/Å2 at 125 GPa. This causes a reversal of the relative heights of the 1/2<110>{110} and 1/2<110>{100} γ-lines, which occurs at ~ 54 GPa. Since the γ-line functions influence the dislocation energy (Eq. 1) through the inelastic misfit energy (Eq. 3), this means that the relative strengths for dislocation glide on {110} and {100} will invert at high pressure.

Fig. 2
figure 2

Pressure evolution of wet and dry 1/2<110>{110} (top) and 1/2<110>{100} (bottom) γ-lines in MgO

Full size image
Fig. 3
figure 3

Pressure dependence of the γ-line maximum for slip along 1/2<110> on the {100} (diamonds) and {110} (squares) planes, with dry and wet values plotted with full and empty symbols, respectively. For wet γ-lines, values are shown only for the lowest energy {2HMg}X configuration for each slip plane

Full size image

Due to the high symmetry of MgO, there are three possible symmetry equivalent—and thus energy degenerate—configurations of the {2HMg}X defect in the bulk crystal. However, this energy degeneracy is lifted by the insertion of a stacking fault. There are two distinct configurations of the {2HMg}X defect for GSFs on {110}. In one, the O–H bonds lie within the stacking fault plane, but are normal to the stacking fault vector (Fig. 4a). For the other, the O–H bonds intersect the glide plane with an angle of 45° (Fig. 4b). There are likewise two symmetrically distinct configurations for a protonated vacancy located near the {100} plane: one with the O–H bonds in the fault plane and inclined 45° with respect to the GSF vector (Fig. 4c), and the other with O–H bonds normal to the fault plane (Fig. 4d). For both {100} and {110} oriented fault planes, the configuration whose O–H bonds are make an angle of 45° with respect to 1/2<110> is doubly degenerate.

Fig. 4
figure 4

The symmetrically distinct configurations of the {2HMg}X defect relative to the {110} stacking fault plane correspond to the cases when the O–H bonds are either (a) in the slip plane and parallel to b, or b crossing the slip plane. For a {2HMg}X defect on a {100} stacking fault, the two symmetrically distinct configurations are those with c the O–H bond in the slip plane and d normal to the slip plane

Full size image

The orientation of the O-H bonds in the {2HMg}X defect, relative to the slip plane, influences the calculated GSF energy, as can be seen by comparing the wet and dry γ-lines (Fig. 2). For slip on {110}, the defect configuration in which the O–H bonds cross the slip plane has a γ-line maximum of 0.0923 eV/Å2, higher than the calculated γ-line maximum for dry MgO. In contrast, the γ-line maximum is reduced by the presence of the defect with the O–H bonds within the {110} plane, to just 0.0529 eV/Å2. At 125 GPa applied pressure, the corresponding values for the two defect configurations are 0.3572 and 0.3423 eV/Å2. For slip on {100}, meanwhile, the γ-line maximum at 0 GPa is 0.1447 eV/Å2 when O–H bonds are aligned normal to the glide plane compared with 0.1214 eV/Å2 when the O–H bonds are parallel to it. At 125 GPa, the corresponding energies are 0.2378 and 0.2194 eV/Å2 so that, while the absolute and relative differences in energy are reduced, the defect with O–H bonds in the slip plane remains lower in energy. In summary, for slip along 1/2<110> on {110} and {100}, it is clear that the orientation of the O–H bonds relative to the slip plane influences the degree of water weakening, with lower energies when the configuration of the adsorbed {2HMg}X defect has O–H bonds parallel to the slip plane. In the following section, where we calculate Peierls stresses for dislocations in hydrous MgO, we will use the γ-lines calculated for these {2HMg}X defects.

One way to quantify the impact of a protonated vacancy on a generalized stacking fault is to consider the relative reduction of the γ-line maximum by the addition of a single defect at the stacking fault plane. For the 1/2<110>{110} γ-line, the energy maximum at 0 GPa is reduced by 23% by the addition of a {2HMg}X defect, the deficit decreasing steadily with pressure to 12% at 125 GPa. In contrast, the 1/2<110>{100} γ-line is less affected by the presence of a protonated defect at 0 GPa, and the maximum energy decreases by 15%. However, the relative magnitude of the γ-line relaxation increases slightly with pressure, to 16% at 125 GPa.

As mentioned at the end of “Peierls–Nabarro calculations”, it is impossible to calculate the binding energy between a point defect and a dislocation with the PN formalism. However, by taking the difference between dry and wet GSF energies with the same stacking fault vector u, it possible to determine the segregation energy Eseg of a protonated vacancy from the bulk to a generalized stacking fault. For the 1/4<110>{100} GSF, the segregation energy at 0 GPa is − 0.78 eV, rising to − 1.14 eV at 125 GPa. At 0 GPa, the segregation energy to a 1/4<110>{110} GSF is − 0.81 eV, but rises more quickly with pressure, reaching − 1.90 eV at 125 GPa. While a direct quantitative comparison with the results of Karki et al. (2015) for {2HMg}X segregation to {310} tilt boundaries is not possible, the magnitudes of the segregation energies reported at 0 GPa in that study are comparable to those found here (approximately − 1 eV), and increase with pressure.

Peierls–Nabarro dislocations

Using the γ-lines calculated in “Generalized stacking fault energies”, Peierls–Nabarro dislocation core structures can be obtained by minimizing Eq. (1) with applied stress σ = 0. A static dislocation can be characterized by its core width ξ, which is defined to be the width of the region within which |b|/4 < |u(x)| < 3|b|/4, and its maximum dislocation density, ρmax. In anhydrous MgO, both of these parameters are nearly constant for the 1/2<110>{100} edge dislocation and the 1/2<110> screw dislocation spreading on {100}, whereas ξ and ρmax respectively decrease and increase for the 1/2<110>{110} edge dislocation and the 1/2<110> screw dislocation spreading on {110} (Fig. 5). Relaxing the static dislocation core structure using the wet γ-lines increases core spreading, particularly on the {110} plane, with a corresponding decrease in the value ρmax. However, this hydrogen-induced dislocation core spreading has no significant effect on the pressure derivatives of either ξ or ρmax.

Fig. 5
figure 5

Pressure dependence of the dislocation core width, as a fraction of the Burger’s vector magnitude |b| (top) and maximum dislocation density along the glide plane (bottom). Results for the 1/2<110>{110} and 1/2<110>{100} slip systems are shown with square and diamond symbols, respectively, while values for hydrous MgO are indicated with hollow symbols

Full size image

From these static dislocation core structures, Peierls stresses for the different slip systems can be obtained by minimizing Eq. (1) with |σ| > 0, using the static disregistry profile u(x) as input. Within the 1/2<110>{110} slip system, the Peierls stress of the 1/2<110>{110} edge dislocation is lower than that of the 1/2<110> screw dislocation gliding on {100}, which controls mobility in this slip system. The Peierls stress of the edge dislocation at ambient pressure is 0.06 GPa, similar to the 0.02 GPa (Carrez et al. 2009) and 0.04 GPa (Liu et al. 2012) calculated for this dislocation in previous studies. For the 1/2<110> screw dislocation, σp for glide on {110} is 0.26 GPa at ambient pressure. Previous computational studies have found values for this slip system ranging from 0.04 GPa (Carrez et al. 2009) to 0.16 GPa (Liu et al. 2012). For the 1/2<110>{100} slip system we find that, across the entire pressure range 0–125 GPa, a 1/2<110> screw dislocation gliding on {100} has lower Peierls stress than 1/2<110>{100} edge dislocation. At 0 GPa, the screw dislocation has σp = 1.7 GPa for the screw dislocation, comparable to the value of 1.53 GPa calculated by Carrez et al. (2009) using a continuous 1D PN model. Carrez et al. determined the Peierls stress of the 1/2<110>{100} edge dislocation at ambient pressure to be 1.16 GPa, markedly lower than the 2.8 GPa computed in this study.

The 0 GPa Peierls stresses are thus comparable with those found in previous studies, albeit modestly higher for all dislocations studied. This difference can be attributed to the choice of xc-functional as Carrez et al. (2009) and Liu et al. (2012) used the PBE-GGA xc-functional (Perdew et al. 1996), which is known to significantly overestimate the cell volume, due to under-binding of the exchange–correlation energy. For MgO, the elastic constants Cij increase with decreasing cell volume (i.e. increasing pressure) which means that, at a given pressure the PBE xc-functional underestimates the elastic constants. Consequently, PN simulations parameterized using the results of DFT calculations performed using the PBE xc-functional should consistently predict lower Peierls stresses than those parameterized using the PBEsol xc-functional, as is the case here.

In “Generalized stacking fault energies”, it was shown that adsorption of {2HMg}X defects to the fault plane lowers GSF energies along the 1/2<110>{110} γ-line. When these γ-lines are used to parameterize PN calculations of dislocation glide, this translates into lower Peierls stresses for glide on the 1/2<110>{110} slip system. Although the edge and screw dislocations in this slip have comparable Peierls stresses at ambient pressure, above 0 GPa the Peierls stress of the 1/2<110 > screw dislocation gliding on {110} is greater than that of the 1/2<110>{110} edge dislocation, and screw dislocation controls the mobility of this slip system. At 0 GPa, the Peierls stress of a 1/2<110>{110} edge dislocation is 0.06 GPa, indistinguishable from the Peierls stress for this slip system in dry MgO. However, as can be seen in Fig. 6a, the pressure derivative dσp/dP is lowered by {2HMg}X defects and, at 125 GPa pressure, the σp calculated using the wet γ-line is 1.7 GPa, < 50% of the value for this dislocation in dry MgO (3.6 GPa). For glide of 1/2<110> screw dislocations on {110}, the Peierls stress is 0.06 GPa when the wet γ-line is used, compared with 0.26 GPa under dry conditions; at 125 GPa the corresponding wet and dry values are 10.6 and 23.0 GPa.

Fig. 6
figure 6

Pressure dependence of the Peierls stresses calculated for a glide of edge dislocation, and b screw dislocations. Square and diamond symbols correspond to the {110} and {100} glide planes, while filled and hollow symbols are used to represent σp in anhydrous and hydrous MgO

Full size image

The effect of protonated vacancies on the qualitative pressure dependence of dislocations gliding on {100} is more pronounced. Whereas, in dry MgO, the Peierls stress of 1/2<110>{100} edge dislocations increases monotonically with pressure, the addition of water leads to a pronounced negative curvature of σp(P). This effect is sufficiently great that σp actually decreases above 75 GPa. The Peierls stress for glide of 1/2<110> screw dislocations on {100} is similar for anhydrous and hydrous MgO at ambient pressure (~ 1.7 GPa). However, the adsorption of protonated vacancies to the glide plane greatly reduces the pressure dependence of σp, which in hydrous MgO is just 2.7 GPa at 125 GPa, compared with 4.2 GPa for dry MgO. As was found for dry MgO, the Peierls stress of the 1/2<110>{100} dislocation is greater than that of the 1/2<110> screw dislocation gliding on {100} at all pressures, although in wet MgO the Peierls stress for the edge and screw dislocation begin to converge at high pressure.

For 1/2<110> screw dislocations in dry MgO, the relatively rapid increase in σp for glide on {110} with pressure means that glide on {100} becomes easier at high pressure. This results in a cross-over of the relative strengths of the two glide planes at high pressure. Using the Peierls stresses calculated for dry MgO, we that this occurs at a pressure of 24.8 GPa, comparable to the ~ 23 GPa measured in creep experiments (Girard et al. 2012). However, glide of 1/2<110> screw dislocations on {110} is preferentially enhanced by the presence of protonated vacancies over glide on {100}. While this effect is not sufficient to prevent the preferred glide plane from changing at mantle pressures, the slip system cross-over is shifted to higher pressures (Fig. 7b). For the {2HMg}X defect concentrations used in this study, the cross-over pressure at which glide of 1/2<110> screw dislocation on {110} increases to 32.1 GPa. Assuming linear dependence of the Peierls stress on {2HMg}X defect, this implies that the cross-over pressure is shifted by ~ 29 GPa multiplied by the fraction of protonated cation sites at the glide plane. In anhydrous MgO, the 1/2<110>{110} edge dislocation slip system is weaker than the 1/2<110>{100} edge dislocation slip system at all mantle-relevant pressures (Fig. 7a), and this is not changed by the incorporation of {2HMg}X defects at the glide plane. However, the pressure at which the Peierls stress of 1/2<110 > screw dislocation on {110} exceeds that of the 1/2<110>{100} edge dislocation increases from 30.6 GPa in dry MgO to 46.2 GPa for hydrous MgO with {2HMg}X present at the concentrations used in this study, giving a dependence of the cross-over pressure on {2HMg}X concentration of ~ 62 GPa times the fraction of occupied sites.

Fig. 7
figure 7

Ratio of σp for glide on {100} and {110} for a edge and b screw dislocations, with (filled symbols) and without (hollow symbols) {2HMg}X defects present. The horizontal dashed line for the screw dislocations represents a Peierls stress ratio of 1

Full size image

The hydrolytic weakening of the Peierls stress found here is a direct result of the reduction of the γ-line maximum by the insertion of suitably oriented {2HMg}X defects at the slip plane. This reduces the inelastic restoring force that balances the repulsive elastic interaction between components of the dislocation density distribution ρ at different lattice planes. What cannot be determined, however, is whether the reduction of the γ-line energies is due to the presence of hydrogen, or the vacancy generated when creating a {2HMg}X defect. Given that the 1/2<110> γ-line maxima on both {110} and {100} correspond to the points of closest approach between Mg atoms on either side of the stacking fault plane, it is likely that the mechanism by which protonated vacancies reduce the Peierls stress is by minimizing the repulsive interactions between adjacent Mg ions across the glide plane. In this case, the role of the H atoms is solely to charge-balance the creation of an Mg vacancy.

Creation of protonated defects is not the only mechanism by which vacancies can be generated in MgO or its iron-bearing analogue (Mg, Fe)O. Insertion of trivalent cations, such as Al3+ and Fe3+ into MgO/(Mg, Fe)O leads to the creation of M-site vacancies to maintain overall charge neutrality. Extrinsic vacancies associated with trivalent cations can vastly outnumber intrinsic vacancies, such as those associated with Schottky defects (Van Orman et al. 2009). In the case of MgO, doping with trivalent cations at the 100–200 ppm level decreases dislocation mobility and increases its critical resolved shear stress (Singh and Coble 1974a, b). The increase in yield strength is nearly identical for Cr3+, Al3+, and Fe3+, despite their different ionic radii, which suggests that this pinning is not caused by attractive elastic interactions between the trivalent cation and the dislocation core but the substantial change in the electrostatic energy of this complex when it is sheared by a passing dislocation (Ahlquist 1975). However, Otsuka et al. (2010) have suggested that under lower mantle conditions, ferric iron and {□M}″ vacancies dissociate. It is thus possible that, under oxidized conditions, there will be free vacancies, capable of inducing Peierls stress reductions comparable to those predicted here for protonated vacancies to dislocation cores, with similar geophysical implications. More work needs to be done to investigate the effects of Fe3+ on the deformation of (Mg, Fe)O with realistic Fe contents.

Iron-bearing (Mg, Fe)O is the weakest major phase in the Earth’s lower mantle. In both numerical simulations of two-phase creep (Madi et al. 2005) and high-pressure deformation experiments on magnesiowustite + bridgmanite aggregates (Girard et al. 2016) the bulk of the strain in multi-phase lower mantle materials is accommodated by (Mg, Fe)O. When deformed under moderate stress conditions, (Mg, Fe)O polycrystals develop pronounced lattice preferred orientation (LPO) (Yamazaki and Karato 2002), although a recent deformation experiment of a magnesiowustite + bridgmanite at 61 GPa found no evidence for the development of a coherent deformation fabric (Miyagi and Wenk 2016). MgO is highly elastically anisotropic over the entire pressure range of the Earth’s mantle (Karki et al. 1999). (Mg, Fe)O is even more anisotropic than pure MgO and probably accounts for the majority of the observed seismic wave anisotropy in the Earth’s lower mantle (Marquardt et al. 2009), especially as (Mg, Fe)SiO3 bridgmanite, the other major component of the lower mantle, does not develop any significant LPO when deformed under mantle-relevant conditions (Merkel et al. 2003). At high pressure, the 1/2<110> screw dislocations experience more lattice friction for glide on {110} than on {100}, which results in a change in the LPO for a give pattern of mantle strain. Lattice preferred orientation of (Mg, Fe)O has also been invoked to explain seismic anisotropy in the D″ region of the lowermost mantle, on the assumption that the dominant slip system is 1/2<110>{100} (Karato 2014). In hydrous MgO, the greatest Peierls stress reduction was found for the 1/2<110>{110} slip system, so that the pressure at which {100} becomes the dominant slip for the 1/2<110> screw dislocations is displaced to higher pressures under hydrous conditions. At pressures representative of the deep lower mantle, the preferred slip system is the same for both hydrous and anhydrous MgO. However, {2HMg}X defects preferentially enhance 1/2<110>{110} slip by {2HMg}X defects, thereby altering the relative activities of the two major slip systems in MgO and changing its LPO, and potentially the observed pattern of seismic anisotropy.

Conclusions

In this study, we have used the PN model, parameterized using ab initio calculated GSF energies to determine the effect of a common variety of protonated vacancy, {2HMg}X, on the Peierls stress of MgO. Using DFT, 1/2<110> γ-lines were calculated for slip on the {110} and {100} families of planes, representing the most important slip systems in MgO, and these were used to parameterize Peierls–Nabarro calculations of edge and screw dislocation core structures and Peierls stresses. Calculations were performed using stoichiometric MgO simulation cells, in addition to simulation cells containing {2HMg}X defects, and it was found that the latter produced wider dislocation cores and lower Peierls stresses over the entire pressure range of the Earth’s mantle. Although σp is decreased by the presence of protonated vacancies at the glide plane for slip on both {100} and {110}, we find that the Peierls stress reduction is greatest for 1/2<110>{110} slip (for both edge and screw dislocations). In the case of 1/2<110> screw dislocations, this leads to an increase in the pressure at which glide on {100} becomes easiest, meaning that the presence of water may influence the deformation fabric.

These calculations show that the presence of protonated defects near a dislocation core in MgO can reduce its Peierls stress. However, although we have considered only MgO, the results have implications for the glide controlled creep of other mantle minerals such as olivine or pyroxene. The easy glide planes of the dominant slip systems for dislocation are parallel to sheets of MO6 octahedra (where M is typically Mg or Fe), for which MgO may be considered a structurally simple analogue. Glide lubrication by protonated defects may provide an explanation for the lower yield strength and different LPO of hydrous versus anhydrous olivine, and this possibility warrants further exploration using atomistic simulations.