Introduction

The term illite was introduced by Grim et al. (1937) to refer to very little mica-like mineral, commonly found in argillaceous sediments. A more restrictive definition was given by Środoń and Eberl (1984) who referred to an Al–K mica-like, non-expanding, dioctahedral mineral, occurring in the clay fraction. Together with kaolinite, chlorite and smectite, illite is in fact one of the four major constituents of argillaceous sedimentary rocks. Yates and Rosenberg (1997) were the first to use the term “K-deficient mica”. Illite crystallizes in the monoclinic system and its structure is very similar to that of 2:1 mica where two tetrahedral sheets sandwich an octahedral one to build up the T-O-T sheet (Brigatti and Guggenheim 2002; Wenk and Bulak 2004). The general chemical formula of a mica can be written as: AM2–3T4O10X2 where in natural micas A = interlayer cations: K, Na, Ca, Ba; M = octahedral cations: Mg, Fe2+, Al, Fe3+; T = tetrahedral cations: Si, Al, Fe3+; X = (OH), F, Cl, O. In accordance with the recent International Mineralogical Association (IMA) protocol on micas nomenclature (Rieder et al. 1998), dioctahedral K-micas with an interlayer cation content between 0.85 and 1 per half-cell are defined muscovites, whereas dioctahedral K-micas with an interlayer cation content between 0.6 and 0.85 per half-cell are defined illites. Compositional overlaps and inconsistencies have been observed (Yates and Rosenberg 1996, 1997). This is why a more suitable term for illite would be K-deficient mica at least until relations between the two phases are definitely resolved. An approximate formula for illite can be written as (Rosenberg 2002): K0.88Al2(Si3.12Al0.88)O10(OH)2 deduced both by experimental studies (Yates and Rosenberg 1996, 1997), and by studies of natural materials (Inoue et al. 1987). Illite seems to contain more water with respect to micas. Norrish and Pickering (1983) showed that the H2O content is inversely related to K2O in illites.

Illite polytypes 1M and 2M1 are major components of clays used for the production of traditional ceramics such as cooking pots, plates, tiles and bricks. Illite clays are called Ball Clays, after the method of their early extraction (by hand spade) in Devon (England), and differ from China Clays where illite is absent. For industrial applications, the understanding of the high temperature transformations of illite is of paramount importance for the knowledge of the structural and microstructural properties of the fired ceramic bodies.

To our knowledge, there are no data on illite dehydroxylation kinetics in the literature so far. DTA curves of four illitic samples (MacKenzie 1970) invariably show the presence of a first endothermic peak at 100–150 °C due to dehydration, followed by a second endothermic peak at about 550 °C due to dehydroxylation. A third additional peak is present at about 900 °C and is due to a later stage of dehydroxylation. This peak is less intense than the one at 550 °C. In addition, its intensity and shape depend upon the composition of the sample. Since illite has a muscovite-like structure, the discussion on the dehydroxylation mechanism will necessarily include a comparison of the results with the muscovite dehydroxylation kinetics. Sanchez-Navas (1999) analyzed the transformation of muscovite in a gneiss rock and studied the transformation reaction of muscovite into andalusite and K-feldspar. The author proposed a reaction mechanism involving a topotactic substitution during the early stages of the process. Because this mechanism alone cannot describe the advanced stages of the process, Sanchez-Navas proposed an additional diffusion of K and H2O throughout the interlayer volume, shear zones and other surfaces parallel to muscovite (001). Rodriguez-Navarro et al. (2003) studied the formation and growth of mullite after the decomposition of muscovite at high temperature. They postulated a three steps process which starts at temperatures higher than 900 °C. The first step is the dehydroxylation sensu strictu of the muscovite together with partial melting. The process produces pseudo-rectangular boxes filled with melted material and dispersed nano-crystals of mullite. The second step is the substitution of the muscovite pseudo-morphs by mullite aggregates, with bigger and longer crystal, compared to the ones formed during the former step. The third step is the complete substitution of the muscovite by mullite multiple fibres. The authors postulated that dehydroxylation is determined by the release of water molecules through the lattice planes of muscovite with potassium to prompt melting and formation of bubbles. When the melt contained in the pockets is oversaturated with Al and Si, nucleation and growth of mullite begins. The newly-formed crystals of mullite are oriented with the (001) planes coincident with the (001) plane of muscovite. In the final step, the result is a mosaic assemblage where the crystals are also randomly oriented, due to the high rate of formation and growing of the crystals while the fuse is cooling down.

For the first time, this work attempts to investigate the reaction mechanism of dehydroxylation of illite. Several methods of classical kinetic analysis were used to achieve a clear conclusive picture of the dehydroxylation mechanism.

Experimental

The investigated sample is from a mine located in the Tokaj Mountains (North-Eastern Hungary), nearby the towns of Sátoralijaújhely and Füzérradvány.

To concentrate the illite phase present in the original material, separation in sedimentation tubes and application of the Stokes law was attempted. Using this method, the fraction with an average particle size < 1.5 μm was collected after 70 h. To separate finer fractions, centrifuges were also used. They are based on modified Stokes law introduced by Svedberg and Nichols (1923), and modified by Jackson (1969). With this method, the fraction between 1.5 and 0.5 μm was separated using a Beckman (Model J-6B) centrifuge working at 2,000 rpm. To concentrate the finer fraction with an average size < 0.5 μm, an High Speed IEC International Centrifuge (Model HT) working at 7,500 rpm was used.

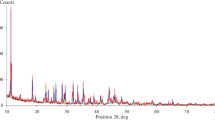
The XRPD patterns of the separated illite fractions were collected using a Philips PW1729 diffractometer, with Bragg–Brentano geometry, Cu Kα radiation, and graphite crystal monochromator. Phase identification was possible using the ICDD database Powder Diffraction File, Release 2002 (PDF-2). To check the purity of the separated clay fraction, 1 h long data collections were used with the following experimental conditions: sample side-loading technique, 3–40°2θ, 0.02°2θ step, 2 s per step, 40 kV and 30 mA, 1/2° divergence, 0.2 mm receiving and 1/2° antiscatter slits.

X-ray fluorescence (XRF) chemical analyses were performed with a Philips PW2480 spectrometer. The separated Hungarian illite was prepared following the technique described in Arletti (2005). The sample preparation is the same, except for the quantity of powder (300 mg instead of 3 g) and glue (1 drop instead of 3).

DTA, TG, and DTG measurements were possible using a Seiko SSC 5200 thermal analyser with TG/DTA 320U module. The sample was heated up to 1,100 °C with a constant rate of 10 °C/min.

Transmission electron microscopy (TEM) measurements were performed with a Jeol JEM 2010 microscope, equipped with a Slow Scan CCD Gatan 694 camera. A few particles of illite were dispersed in acetone. A drop of suspension was then placed on a sample holder and carbon-coated to avoid particle movements during the analysis. TEM images were also collected using a HRTEM FEI Tecnai F20 G2 equipped with a N2 cooled system stage to hold the sample at the temperature of −180 °C. In this case, specimen were prepared by embedding in resin for ultramicrotoming and ion-milling thinning. The softwares used for the image analysis were the Gatan Digital Micrograph (Rasband 1997–2005) and the freeware ImageJ (Abramoff et al. 2004).

The illite dehydroxylation kinetics were studied using a Panalytical X’Pert Pro diffractometer equipped with an Anton Paar HTK16 heating chamber. The sample powder was diluted in acetone and placed upon the Pt strip, which is at the same time heating element and sample holder. The fast RTMS detector allowed to monitor the phase decomposition in a wide angular range (7–30 °2θ) in short time span (about 4 min per measurement). This angular range allowed to follow the evolution of a series of Bragg peaks: (001), (002), (020), (−112), (003) and (112). The temperature calibration of the heating chamber was performed using known phase transitions/transformations of different materials. The isothermal temperatures used for this sample were: 875, 910, 935, 945, 960, 975, 980, 1,010 and 1,050 °C.

For all the peaks present in the patterns collected during the various isothermal runs, the calculated integrated area was normalized and transformed into the conversion factor α according to:

$$ \alpha = {\sum\limits_i {\frac{{A_{{i,T_{J} }} }} {{A_{{i,\max }} }}} }, $$

where A i  = integrated area of ith peak at temperature T J , A i,max = maximum value of the integrated area of ith peak. Plots of α versus time (min) were drawn for the peaks at each isothermal temperature. The plots are the basis of the kinetic analysis performed using the following methods:

Isoconversional method

Following the formalism described in Friedman (1964) and Baitalow et al. (1999), the logarithmic form of the general equation:

$$ \frac{{{\text{d}}\alpha }} {{{\text{d}}t}} = A\exp {\left( { - \frac{{E_{{\text{a}}} }} {{RT}}} \right)}f(\alpha ) $$

with A = the frequency factor, E a = the apparent activation energy, R = gas constant (8.316 kJ/mol), T = temperature (K), f(α) = differential form of the general kinetic expression, is:

$$ \ln t = A\exp {\left( {\frac{{E_{{\text{a}}} }} {{RT}}} \right)} - \ln {\left( {\frac{A} {{g(\alpha )}}} \right)}. $$

From different isothermal runs for which same values of α were reached, linear plots ln(t ik ) versus 1/T ik with slope proportional to E a can be drawn. This method may give a model-independent value of activation energy. If all the curves have the same slope, only one mechanism with one activation energy is inferred. Any variation of the slope of the curves is an indication that at least two different mechanisms with distinct activation energies are involved. Since: (1) some data points were missing at the extremes, only the values in the range 0.3 < α < 0.7 were used, (2) because it is known that the Friedman plots provide correct values of E a when the slope does not change (Koga and Criado 1998), the E a values obtained from these plots are only indicative and should only be used only to say whether a single or multiple reaction steps are in action.

The Avrami method

This is the classical method of analysis performed using the model for heterogeneous solid state reactions described by the general expression of the Avrami–Erofe’ev equation (Hancock and Sharp 1972; Bamford and Tipper 1980):

$$ \alpha = 1 - \exp {\left[ {( - kt)^{n} } \right]} $$

The logarithmic transform of this equation is used to build a graph of ln[−ln(1−α)] versus ln(t) (the so-called ln–ln plot) in which isothermal experimental data are linearized. The reaction order (n), also known as Avrami–Erofe’ev coefficient, related to the reaction mechanism involved, is calculated from the slope of the regression line. k, the rate constant, is calculated from the intercept. When possible, the plots were built in the range 0.1 < α < 0.9.

Direct application of kinetic equations

To confirm the reaction mechanism, different integral forms of the kinetic expressions g(α) were tested in the general equation g(α) = k(t−t 0), where t is the total time, t 0 is the time needed to reach the isothermal temperature + induction time. Each kinetic expression has a physical meaning. In this study, the following kinetic equations (Bamford and Tipper 1980) were used:

  1. 1.

    Avrami–Erofe’ev (An) → g(α) = [−ln(1−α)]1/n

  2. 2.

    Contracting area (R2) → g(α) = 1–(1−α)1/2

  3. 3.

    Contracting volume (R3) → g(α) = 1–(1−α)1/3

  4. 4.

    Monodimensional diffusion (D1) → g(α) = α 2

  5. 5.

    Bidimensional diffusion (D2) → g(α) = (1−α)ln(1−α) + α

  6. 6.

    Tridimensional diffusion (D3) → g(α) = [1–(1−α)1/3]2

  7. 7.

    Ginstling–Brounshtein (D4) → g(α) = 1–(2α/3)–(1−α)2/3.

The kinetic equations were used to draw the g(α) versus (t−t 0) plots whose linearity is an indication of the correctness of the applied kinetic model. The method allows the determination of k.

The Arrhenius plot

The logarithmic form of the Arrhenius law:

$$ k{\text{ }} = {\text{ }}A{\text{exp}}{\left[ {\frac{{ - E_{{\text{a}}} }} {{RT}}} \right]} $$

is:

$$ {\text{ln}}(k) - {\text{ln}}(A) = \frac{{ - E_{{\text{a}}} }} {{RT}} \to {\text{ln}}(k) = {\left( {\frac{{E_{{\text{a}}} }} {R}} \right)}{\left( {\frac{{ - 1}} {T}} \right)} + {\text{ln}}(A) $$

(E a /R) is the angular coefficient, ln(A) the intercept of the linear plot ln(k) versus (−1/T). The linear fit provides the values of E a and A.

Determination of the kinetic model-independent activation energy

Since, at a constant temperature, k = g(α)/g(0.5), a relationship between t 0.5 and temperature is written as (Bamford and Tipper 1980):

$$ {\text{ln}}{\left( {\frac{{\text{1}}} {{t_{{0.5}} }}} \right)}{\text{ }} = {\text{ }}{\left( {\frac{{E_{a} }} {R}} \right)}{\left( -{\frac{{1}} {T}} \right)}{\text{ }} + {\text{ ln}}(A) - {\text{ln}}[g(0.5)]. $$

For each isothermal run, the values of time (t) to reach α = 0.5 were calculated. It is important to notice that the induction time (the time between the beginning of the experiment and the actual beginning of the reaction) must be subtracted to t 0.5. The slope of the linear curve provides the value of E a. The advantage of the method is that is not dependent upon the kinetic model and hence that the obtained value of E a is not influenced by the selection of the reaction mechanism.

Results

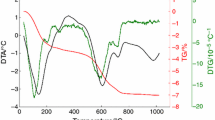
Figure 1 reports the powder pattern of the separated pure fraction of illite and Fig. 2 reports the DTA and TG traces of the pure illite sample. Table 1 reports the chemical analysis and Fig. 3 shows a selection of HRTEM images of the sample. The complete mineralogical and microstructural characterization attempted with the simulation programs Wildfire (Reynolds 1993, 1994), Newmod (Reynolds 1985) and Mud Muster (Eberl et al. 1996) is reported in Ferrari et al. (2006). The outcome of that work showed that the investigated illite sample is the 1M-polytype (likely a disordered 1Md-polytype) with cis–trans-vacant mixed-layers (percentage of cis-vacant layers = 30%), expandability percentage of 10%, nearly no iron and K = 0.8 in the interlayer region, and about ten cells stacked along the c direction.

Fig. 1
figure 1

XRD patterns of the < 1.5 μm fraction separated from the Hungarian clay

Full size image
Fig. 2
figure 2

Results of the TG (dashed line) and DTA (solid line) analysis of the separated illite

Full size image
Table 1 The chemical analyses of the investigated illite sample
Full size table
Fig. 3
figure 3

Selected HRTEM images of the investigated illite

Full size image

Figure 4 shows the α-time plots. The quality of the data made possible the distinction between two families of peaks: the basal peaks, 001 and 002, and the non-basal 020 peak. The analysis was performed on the two distinct families of peaks (Fig. 4a, b), and the sum of them (Fig. 4c), obtained by merging of the results of the basal peaks and non basal 020 peak was done. The intensity of the non basal peak was doubled to give the same weight to both families. The isoconversional plot is shown in Fig. 5. Figure 6a–c report the Avrami plots. Table 2 contains the values of n, k and r 2 obtained for each isothermal run. As previously described, a series of different kinetic equations were applied to identify the reaction mechanism. Here, as an example, only the graph using the Avrami–Erofe’ev equation (An) is shown (Fig. 7a–c). Table 3 summarizes the results obtained only using the models with r 2 ≥ 0.90.

Fig. 4
figure 4

α-time plots of the illite dehydroxylation reaction using the basal peaks (a), the 020 peak (b), and merged peaks (c). Legend: empty triangle up 875 °C, empty square 910 °C, full circle 935 °C, empty triangle down 945 °C, full triangle up 960 °C, empty circle 975 °C, full square 980 °C, full triangle down 1,010 °C, empty hexagon 1,050 °C

Full size image
Fig. 5
figure 5

Isoconversional plots using the basal peaks. Legend: empty squares 30% α, full circles 40% α, full triangles 50% α, empty circles 60% α, full squares 70% α

Full size image
Fig. 6
figure 6

Avrami plots using the basal peaks (a), the 020 peak (b), and merged peaks (c). Legend: empty triangle up 875 °C, empty square 910 °C, full circle 935 °C, empty triangle down 945 °C, full triangle up 960 °C, empty circle 975 °C, full square 980 °C, full triangle down 1,010 °C, empty hexagon 1,050 °C

Full size image
Table 2 The calculated values of n and r 2 obtained by the application of the Avrami method
Full size table
Fig. 7
figure 7

Results of the fit with the Avrami–Erofe’ev kinetic equation (An) using the basal peaks (a), the 020 peak (b), and merged peaks (c). Legend: empty triangle up 875 °C, empty square 910 °C, full circle 935 °C, empty triangle down 945 °C, full triangle up 960 °C, empty circle 975 °C, full square 980 °C, full triangle down 1,010 °C, empty hexagon 1,050°C

Full size image
Table 3 The values of r 2 obtained by the application of the kinetic equations to the raw data. Only the models with r 2 ≥ 0.90 are considered statistically meaningful
Full size table

Figure 8a–c show the Arrhenius plot for the determination of the activation energy, applied to the An model. Figure 9a–c show instead the plots for the determination of the model-independent E a and Table 4 reports all the calculated E a and A (and r 2) values.

Fig. 8
figure 8

Arrhenius plots using the basal peaks (a), the 020 peak (b), and merged peaks (c). Full circles and empty circles represent the data for the two different slopes of the curve. The errors associated to each data point are smaller than the size of the data point itself

Full size image
Fig. 9
figure 9

Plots for the determination of the activation energy calculated using the basal peaks (a), the 020 peak (b), and merged peaks (c). Full circles and empty circles represent the data for the two different slopes of the curve (see text for details). The errors associated to each data point are smaller than the size of the data point itself

Full size image
Table 4 The calculated Arrhenius parameters (E a and A) and relative r 2 from the kinetic analysis of both illites
Full size table

Discussion

In this work, several different methods were applied to investigate the reaction mechanism and to cross-check the results of the kinetic analysis. The isoconversional method allowed the determination of the steps of the reaction mechanism. The plot in Fig. 5 shows that the curves progressively change their slope (a variation of activation energy) with α. This indicates the existence of at least two steps in the dehydroxylation reaction, namely a low temperature step and a high temperature step. The existence of at least two steps is confirmed by the DTA curve in the thermal analyses, where two distinct peaks are visible in the 600–700 °C interval (Fig. 2).

The Avrami method (Fig. 6) yields the value of n. This method is empirical and the information on the nucleation + crystal growth and rate limiting step may not be univocally determined. Hence, other complementary methods are recommended to confirm the reaction mechanism. The calculated mean Avrami coefficient is 0.494 in the low temperature range (875–960 °C) and 1.283 in the high temperature range (975–980 °C). The existence of two families of Avrami is in concert with the outcome of the isoconversional method, showing at least two-step reaction with two distinct rate limiting steps. If the interpretative tables of Hulbert (1969) are used, for the low temperature rate limiting step, n = 0.5 indicates a one-dimensional diffusion controlled reaction with instantaneous nucleation rate. Assuming an instantaneous nucleation rate, the value of 1 may indicate two different mechanisms: (1) one-dimensional interface controlled reaction; (2) two-dimensional diffusion controlled reaction.

The direct application of the kinetic equations (see Table 3) did not allow the determination of a unique reaction mechanism revealing to be a rather insensitive method. The regression analysis of each isothermal run indicated many possible mechanisms: (1) Avrami–Erofeev model with n = 1; (2) Ginstling–Brounshtein model of diffusion (D4); (3) model D2, two-dimensional diffusion controlled reaction; (4) model R2, interface controlled two-dimensional reaction. Comparing this information with the previous ones, it is still not possible to reach a unique definition of the reaction mechanism for the high temperature rate limiting step. Hence, this method was of little help for the understanding of the reaction mechanism.

The Arrhenius plot (Fig. 8) was used to calculate the apparent activation energy and frequency factor (the Arrhenius parameters: see Table 4). A cross-check of the calculated activation energies can also be obtained by applying the model-independent method of analysis (Fig. 9).

Both the Arrhenius plot and the plot for the calculation of the model-independent activation energy showed a two step-curve (two slopes) with calculated values of 697 and 231 kJ/mol and 676 and 230 kJ/mol (Figs. 8a, 9a), respectively. Taking into account the results of the isoconversional analysis, the reaction sequence can be divided in at least two steps, with the first step at lower temperature characterized by a higher activation energy (676 kJ/mol) and the second step at higher temperature with a lower activation energy (230 kJ/mol). The values calculated with other kinetic models gave intermediate values. In fact, the distinction of the two steps was not observed and the values should be considered only apparent mean values.

The kinetic analysis was performed on both the basal and non-basal peaks. If the determination of the activation energy independent from the kinetic model is considered, an important remark should be made. The E a values of the two step in the case of the basal peaks are 656 and 275 kJ/mol (Fig. 9a), whereas the values for the 020 peak are 407 and 233 kJ/mol (Fig. 9b and Table 4). Therefore, it seems that a different kinetic behaviour is displayed by the basal and non-basal peaks, with a much faster reaction (lower activation energy) in the direction perpendicular to the TOT units (basal sheets). However, this should be an artefact. The intensity of the basal and non-basal peaks are very different. As a matter of fact, illite shows a very high intensity for the basal peaks and very low for the others due to preferred orientation effects. This problem is emphasized by the sample loading technique as the powder was front loaded on the Pt strip. Thus, during the reaction in temperature, the intensity of the non-basal peaks decreases much faster than that of the basal peaks as the original peak to background ratio of the former was already very low compared to that of the latter. Because the intensity (integrated area) is proportional to the conversion factor α, the anticipated disappearance of the non-basal peak with respect to the basal peaks is erroneously interpreted as faster reaction rate.

With the results of the kinetic analysis, it is possible to describe a model for the dehydroxylation reaction consistent with those present in the literature for muscovite and 2:1 phyllosilicates. Rouxhet (1970) and Mazzuccato et al. (1999) who studied the dehydroxylation kinetic of a 2M1 muscovite in vacuum in the low temperature range 760–860 °C, described the reaction as a multi-step model composed by: (1) condensation of the water molecules in the octahedral layer; (2) one-dimensional diffusion of the water molecules through the tetrahedral ring enlarged by thermal expansion (the observed rate limiting step of the reaction); (3) two-dimensional diffusion of the water molecules through the interlayer region. The activation energy determined by these authors in vacuum conditions is 197 and 251 kJ/mol, respectively. Other authors (Kodama and Brydon 1968) found a similar value (226 kJ/mol).

The general postulated kinetic model can be described as a multi-step reaction sequence with:

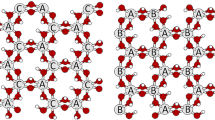
(1) Condensation of the water molecule in the octahedral layer according to the reaction 2(OH) ⇒ H2O(↑) + O (Fig. 10a) with the residual oxygen atom that moves to the same Z coordinate as that of Al and adapts itself midway between two closest Al cations to complete their fivefold coordination (Drits et al. 1995). The structural modification takes place in slightly different ways for cis-vacant and trans-vacant layers with both distorted but intact tetrahedral layers (Drits et al. 1995; Muller et al. 2000). The structure model of this dehydroxylated phase is similar to the intermediate product of dehydroxylation of muscovite (Guggenheim et al. 1987) and pyrophyllite. For the latter, Sainz-Díaz et al. (2004) clearly stated that the dehydroxylate·2H2O has the water molecules inside the hexagonal cavity of tetrahedral. This stage is not the rate limiting step of the reaction. Thus, the Avrami coefficient bear no information about this fast process but the calculated apparent activation energy likely includes both the condensation of water and the next step of the reaction, its migration away from the octahedral layer throughout the hexagonal tetrahedral cavities (step 2). It should be remarked that the existence of this first step is masked by the detection limits of our kinetic analysis. In fact, because no significant differences in the pattern of original and semihydroxylate or dehydroxylate derivative are observed in the XRPD patterns of illite and pyrophyllite (see Drits et al. 1995; Muller et al. 2000; Sainz-Díaz et al. 2004), such details cannot be revealed by our experimental powder patterns collected in situ.

Fig. 10
figure 10

a The octahedral layer of illite during the first step of dehydroxylation. The oxygen atom from the OH- group shifts to the centre of the line connecting two H atoms to form a water molecule. Al gains a fivefold coordination; b the water molecules formed at the centre of the octahedral cavity escape throughout the tetrahedral rings; c water molecules are released through the interlayer region, thanks to the K atoms defects

Full size image

(2) One-dimensional diffusion of the water molecules throughout the tetrahedral ring enlarged by thermal expansion (Fig. 10b). This is the second stage and rate limiting step of the reaction represented by the Avrami coefficient equal to 0.5. Although part of the energy is spent for the Al–O bond breaking (step 1), the large apparent E a of 676 kJ/mol mainly refers to this process. The effect of thermal expansion of the tetrahedral hexagonal cavity is certainly crucial to allow migration of the water molecules in the interlayer region. At room temperature, the migration would be inhibited because the minimum van der Waals diameter of the water molecule is 2.917 Å (Webster et al. 1998) and the effective aperture of the tetrahedral ditrigonal cavity of muscovite is only about 2.91 Å (Guggenheim et al. 1987). At high temperature the effective aperture increases (for muscovite the calculated value is 2.97 Å at 800 and 3.02 Å at 1,000 °C: Guggenheim et al. 1987) and the passage is possible. Moreover, the hexagonalization of the ditrigonal cavity in temperature further increases the effective aperture diameter. It would be interesting to understand whether the kinetic energy of the trapped water molecule due to the enormous accumulated water vapour pressure induces a further local distortion of the ring to ease the passage. This phenomenon has been observed during the dehydration of some zeolite species such as analcime where the release of water molecules takes place via local deformation of the framework cavities (Cruciani and Gualtieri (1999).

Although K+ ions present in the interlayer region under the tetrahedral ring should inhibit the passage of the water molecules, the passage is made possible thanks to the K+ ions vacancy defects of illite which allow such migration (Fig. 10b). The defects are likely filled with water molecules at low temperature (see the section on the structure model of illite) and lost during the dehydration stage.

(3) Two-dimensional diffusion of the water molecules through the interlayer region. This is the third stage and rate limiting step of the reaction represented by the Avrami coefficient equal to 1. The calculated activation energy of this process is 230 kJ/mol. The migration is favoured by the existence of point defects in the interlayer (the K+ ion vacancies) which trace preferred migration pathways (Fig. 10c).

The distinction of two or more steps with different activation energies was not recognized by Mazzuccato et al. (1999). In concert with our results, the kinetic analysis of Mazzuccato et al. (1999) using an Avrami-type model yielded values for the reaction order (n = 0.5) compatible with a reaction mechanism limited by a one-dimensional diffusion step. Using the Avrami method alone, only a single value of apparent activation energy of 251 kJ/mol was determined. Although the temperature range of the study was limited to a low temperature region, it is likely that the use of isoconversional methods may have revealed the presence of at least one additional step. Considering the results obtained in this work, n = 0.5 determined by Mazzuccato et al. could only correspond to the second (low temperature) step of the reaction. On the other hand, the value of the activation energy is probably a mean value of all the three postulated steps which would be about 350–400 kJ/mol in air and remarkably lower in vacuum (250–300 kJ/mol). Large differences in the values of activation energies have already been reported for illite decomposition under vacuum and water vapour pressure (Bamford and Tipper 1980). In concert, the apparent activation energy of dehydroxylation of muscovite was reported in the range 325–400 kJ/mol (Nicol 1964).

A final remark regards the comparison of the dehydroxylation of illite with that of other dioctahedral sheet silicates. Albeit the experimental conditions and methods of analysis may be rather different, the literature reports values of apparent activation energies (E a) of dehydroxylation and indication about the reaction mechanism for kaolinite (Bellotto et al. 1995), halloysite (Földvári 1997), muscovite (Mazzucato et al. 1999), pyrophyllite (Brindley 1975), and montmorillonite (Bray and Redfern 2000). Table 5 reports a schematic summary of the most relevant literature data and shows that E a increases from kaolinite to illite according to the following sequence: E a,kaolinite ≈ E a,halloysite < E a,montmorillonite < E a,pyrophyllite ≈ E a,muscovite < E a,illite. The lowest E a (109–192 kJ/mol) values are found for the TO sheet silicates kaolinite and halloysite because, following to the breaking of the Al–OH bonding, the condensation of the water molecule occurs right in the interlayer space and the reaction is governed by the diffusion of the formed molecules in the interlayer region. Higher Ea (ca. 250–600 kJ/mol) is required for the TOT structures because the water molecule formed in the octahedral sheet need to cross the tetrahedral ring opening (first rate limiting step) and migrate along the interlayer region (second rate limiting step). Unfortunately distinction of the two reaction steps was not observed in the literature and an overall value of E a has been reported together with a general indication of a diffusion controlled reaction. As a matter of fact, the values of 325–400 kJ/mol likely represent a mean value between the high E a of the first step and the lower E a of the second step. Notwithstanding, other factors must play a role in tuning the energetics of the reaction. Otherwise, it would be difficult to explain the lower E a of montmorillonite with respect to that of the other TOT sheet silicates. At a speculative level it is possible to say that such factors could be: (1) the population of the compensating cation at the window of the tetrahedral rings which acts as a barrier to diffusion of the water molecules is very low in montmorillonite and consequently migration is favoured; (2) large degree of tetrahedral and octahedral substitutions and defects which may favour both the condensation of the water molecule and the distortion of the tetrahedral ring; (3) the high density of stacking defects in montmorillonite with a turbostratic structure and the nanometer-scale crystals determine an extremely large specific surface and reactivity. This has the consequence to significantly shorten or annul the mean free path of the water molecule in the interlayer region (very low or null Ea spent to overcome the second reaction limiting step).

Table 5 Relevant literature values of E a for the dehydroxylation reaction of sheet silicates
Full size table

Conclusions

This work reports for the first time the kinetic study of the dehydroxylation reaction of a pure natural 1M-illite using in situ X-ray powder diffraction (XRPD). Different methods of kinetic analysis were used to obtain a full picture of the dehydroxylation mechanism. In general, it is important to say that the application of the Avrami method alone may lead to misleading interpretations for multi-step reactions because the different reaction steps may not be revealed if only an overall value of the activation energy is determined. Cases which are typically at risk of misinterpretation are multi-step reactions with similar or equal kinetic steps (e.g., two subsequent one-dimensional diffusion rate limiting steps) or different kinetic steps with similar or equal activation energy. The combination of various methods permits to fully disclose the reaction mechanism and the rate limiting steps. The isoconversional method and the model-independent determination of E a in combination with the classical Avrami method have certainly contributed to the drawing of a clear picture of mechanism of illite dehydroxylation.

The comparison of the kinetic of dehydroxylation of illite with that of other dioctahedral sheet silicates remains an open issue. It requires further accurate specific kinetic studies (especially on montmorillonite and pyrophyllite, and other trioctahedral sheet silicates) to assess the actual rate limiting steps of the reaction, calculate the relative values of E a, and to build a general consistent model of the kinetics of dehydroxylation of sheet silicates.