Introduction

A central goal of behavioral ecology is to measure and explain the variability of animal behavior within levels of organizations, from individuals to species and higher taxonomic levels. As researchers, we usually do so by conducting analyses that investigate differences in mean behavior across groups, such as sex or species, or treatments, such as the presence or absence of predators. Such analyses statistically account for the variability within groups or treatments to estimate their effects and allow inferences to a larger population (e.g., Carrete and Tella 2011, more generally, see Bart et al. 1999; Martin and Bateson 2007). Direct comparisons of variability across groups or treatments are generally evaluated by calculating a coefficient of variation or similar statistic (e.g., Carrete and Tella 2011). A shortcoming of this traditional approach is that it fails to address the actual location (i.e., the actual values) of the distribution, which is of interest in many cases.

Thus, another approach is to treat the distribution of the response variable, or a specific portion of the distribution, as the object of interest. How edges of the distribution (i.e., the most extreme behaviors) change across groups or treatments may, for instance, be particularly informative. These bounds could provide insights into the costs of expressing behaviors because very costly behaviors should be rare in populations. For instance, only the minimum intensity of an anti-predator behavior may increase with predation risk because the highest intensity may already be constrained by the costs associated with a trade-off with foraging (or other) activities. Other portions of the distribution may also be of interest. For instance, conservation biologists and wildlife managers may be most interested in identifying thresholds beyond which some behavior of interest [e.g., flight initiation distance (FID)] is expressed (Blumstein and Fernández-Juricic 2010).

Quantile regression is a method to study change in one or several portion(s) of a response variables’ distribution. Technically, it allows the estimation of the rate of change in conditional quantiles of a response variable in a linear model (see below). For instance, it can be used to study how edges of data cloud, approximated, for instance, by the 0.1st and 0.9th quantile, change across groups or along a continuous explanatory variable. Importantly, and powerfully, other quantiles of interest can be estimated. Quantile regression overcomes problems with the estimation of regression models that have nonconstant variance (i.e., heteroscedasticity), and the method is robust to response outliers.

Quantile regression is strikingly absent from the toolbox of behavioral ecologists: a February 2012 GoogleScholar search for “quantile regression” in articles published in Animal Behaviour, Behavioral Ecology, and Behavioral Ecology and Sociobiology returned only two hits, whereas it is increasingly used in other domains of ecology (over 50 hits returned in Ecology, Journal of Animal Ecology, and Journal of Ecology). Our intention here is to introduce behavioral ecologists to this method in the context of a specific case study. Quantile regression might help us better understand how animals adjust their FID—the distance at which an animal flees an approaching predator or threat (Ydenberg and Dill 1986). Blumstein (2003) reported that FID increased with the starting distance (SD) of the experimenter in 64 out of 68 bird species. He suggested that animals flee earlier to avoid the increasing cost of monitoring the approaching threat when the distance at which the threat has been detected increases (Blumstein et al. 2003). Since then, a positive relationship between SD and FID has been found in many other studies and taxa (e.g., Cooper 2005; Geist et al. 2005; Stankowich and Coss 2006; Cooper et al. 2009). This finding suggests that SD must be incorporated in analyses of FID and that a general rule of anti-predator behavior might be “flush early and avoid the rush” (Blumstein 2010).

This generality can, however, be questioned (Dumont, Pasquaretta, Réale, Bogliani, and von Hardenberg, unpublished manuscript). A draw of FID values from, for instance, a random uniform distribution subject to the constraint that FID ≤ SD (because, by definition, escape cannot occur before the experiment starts) will almost invariably produce higher FID values at higher SD and generate a spurious positive relationship between FID and SD (Fig. 1). Thus, evidence for a positive statistical relationship between FID and SD should not lead one to assume a direct influence of SD on FID. Also, nonrandom distribution of FID values with SD may have SD–FID regression slopes that may not differ from those produced by some random model (an example is shown Fig. 1). Quantile regression is a method that can solve this problem by comparing slopes of specific quantiles (Fig. 1). It also allows the direct testing of the hypothesis that if flushing early is beneficial (lowering monitoring costs and increasing the likelihood of success of escape), we predict that the distance at which most individuals have fled (such as the 0.1st FID quantile) would increase with SD more than if the FID data were drawn from a null model not including an effect of SD on FID.

Fig. 1
figure 1

Examples of hypothetical relationships between starting distance (SD) and flight initiation distance (FID). Black squares represent FID data drawn from a random uniform distribution, under the constraint that FID ≤ SD. White dots represent nonrandom FID data. Sample size is 80 for both random and nonrandom data. The slopes of the SD–FID relationships estimated by ordinary least-square regression were almost identical for both random and nonrandom FID data (continuous and dotted line, respectively). However, 0.1st and 0.9th quantile regression lines differ widely between random and nonrandom FID data (continuous and dotted lines, respectively). The 1:1 line is shown (continuous, bold)

Full size image

Here, we first present a model for FID which can serves as a null model to test hypotheses about the SD–FID relationship, then discuss how quantile regression may ease such testing, and finally conduct a quantile regression analyses on real SD–FID data to demonstrate its use in this specific context. We conclude by discussing the overlooked opportunities that quantile regression offers to behavioral ecologists.

Methods

Quantile regressions

Classical ordinary least-squares (OLS) regression estimates the rate of change in the mean of a response variable, conditional on one or several predictor variables. It is usually expressed as E(y|X), which means that the expectation of y is conditional on predictor X (see Sokal and Rohlf 1995). Quantile regression extends this estimation to any part of the response distribution, expressed formally as any conditional quantile Q y (τ|X). This conditional quantile is defined so that a proportion τ (or equally 100τ %) of the values of the response variable are less or equal to the regression quantile estimate at the X value. Because of this definition, quantile regression is insensitive to outliers as long as they remain above or below a regression quantile estimate. An important property of quantile regression is that it does not require any assumptions about the distribution of the regression residuals. The regression quantiles are estimated by minimizing the sum of weighted absolute values of residuals (Koenker 2005).

Quantiles are ordered quantities and thus quantile regression lines should logically not cross over the range of values of the independent variable, but this is not always enforced by the most common estimation process [the Koenker–Bassett algorithm (Koenker 2005)]. Crossing, however, does not always occur, and if quantiles are not poorly estimated, crossing is rarely severe and is often restricted to near the extreme values of the range of the predictor (see Neocleous and Portnoy 2008 for further discussion). Recently, algorithms ensuring no-crossing have been developed (Wu and Liu 2009; Bondell et al. 2010), but they may have drawbacks. For instance, quantile estimates may change slightly depending on how many quantiles are estimated. Thus, in most applications the stable estimations—with regard to the number of quantiles used—provided by the Koenker–Bassett algorithm might be favored, whereas noncrossing algorithms may be particularly important when estimating the predicted quantiles of the response variable at a specific value of the predictor. More formal mathematical treatments of quantile regression are provided by Koenker (2005) and by Lingxin and Naiman (2007). Cade and Noon (2003) make special efforts to present this method in the context of ecological research and particularly focus on studies designed to identify limiting factors.

Developing a model of FID

In order to better understand how to test for the existence of a SD–FID relationship, we first developed a simple model of FID, which encompasses two rules underlying the behavior of the targeted animals. First, they escape when the distance between the experimenter and the animal is reduced to a distance d at which safety is compromised (see Bonenfant and Kramer 1996; Cárdenas et al. 2005) and/or monitoring costs are considered too high to bear (Blumstein et al. 2003; Blumstein 2010). This distance can be fixed or dynamically adjusted to the early detection of a threat (i.e., increase with SD). For simplicity, we here assumed that individual distances d are drawn from a log-normal distribution—which ensures that all values are positive—with mean d = d min + βSD and with a variance σ, right-truncated at SD because, by definition, the experiment censors the observed distribution of FID values at SD. This distribution is written TLN(d min + βSD, σ, SD). Second, until the experimenter reaches distance d, animals leave the place they are at following a random Poisson process of constant average rate λ (originally in s-1, but can be expressed in m-1 assuming a constant speed during the FID experimental approach). The distribution of the distances traveled by the experimenter before these natural departures occur therefore follows an exponential distribution of rate λ, right-truncated at SD for the reason described above. This distribution is written TEXP(λ, SD). The rate λ accounts for the natural mobility of the animal when conducting its activities undisturbed. It is later referred to as the natural rate of leaving and enters FID if escape is mistakenly recorded as such, but is actually a leaving decision unrelated to the presence of the experimenter. We can imagine that there is variation in the likelihood of an animal naturally leaving: a roosting animal may be unlikely to leave without disturbance, while an actively foraging animal may indeed move away on its own.

Our approach therefore defines two potential distances at which the animal leaves, one when the animal only reacts to the experimental approach and one when it does not react to the experimental approach but leave naturally. FID equals whichever distance is the largest:

$$ {\hbox{FID}} = { \max }\left[ {{\hbox{TLN}}\left( {{d_{{ \min }}} + \beta {\hbox{SD}},\sigma, {\hbox{SD}}} \right),{\hbox{SD}} - {\hbox{TEXP}}\left( {\lambda, {\hbox{SD}}} \right)} \right] $$

Note that TEXP(λ, SD) is undefined for λ = 0 (i.e., when the animal leave during the time of the experiment approach only because of the threat), and under such conditions, FID is simply FID = max(TLN(d min + βSD, σ, SD).

An important aspect of this model is that all data for which SD < d min lie on the 1:1 line (FID equals SD), which generates a nonlinearity in the SD–FID relationship, while simultaneously providing no information on the effect of SD on FID, because it occurs for any value of β. Although nonlinear (e.g., piecewise) regressions could be used, this approach is beyond the scope of this paper and we here simply studied the slope of SD–FID relationship on data for which SD > d min.

Using this model, we used simulations to explore the expectations for the slopes of the SD–FID relationship when assessed using OLS and quantile regression. We studied increasing values of λ and β. Note that when β = 0, the model produces slopes of the SD–FID under the null hypothesis that SD does not affect FID. We then suggest the best way to test observed values against this null model and conducted these analyses on FID data collected on four bird species.

FID data

Here, we present a quantile regression analysis of the FIDs of four species of birds—California thrasher (Toxostoma redivivum), western scrub jay (Aphelocoma californica), California towee (Melozone crissalis), and silver gull (Chroicocephalus novaehollandiae). Gulls were studied around Botany Bay, near Sydney, Australia, while the other three species were studied in southern California chaparral habitats. Following Blumstein (2003), individuals were directly approached by a solitary human observer walking at 0.5 m/s until they flew or walked off. Birds on nests were not disturbed, and by design, we focused on individuals that were initially resting or foraging. For these analyses, we focus on the distance the experimental approach was initiated (SD—the distance at which the bird was first detected by the observer) and the distance flight was first initiated (FID). We acknowledge (as do Blumstein 2010; Dumont et al. unpublished manuscript) that using the alert distance—the distance an animal becomes alert to the approaching human—would be better so as to reduce the likelihood of including movements unrelated to escape behavior (see also Cooper 2008). However, using alert distance rather than SD does not completely eliminate the possibility that animals became aware of the approaching human (by looking only, which may be unnoticeable by the experimenter) before they actually displayed an obvious alert behavior. For instance, habituated animals may be aware of approaching humans while maintaining their current foraging activities and may only engage in escape behavior when the human is quite close. Furthermore, identifying alert behavior may be difficult, prone to error, or impossible in some species, and it might be more prudent, in some cases, to rely on the better-measured SD.

Statistical analyses

For each species’ FID dataset, we first estimated d min, the threshold distance at which animals always escape. In real-world data, d min is unlikely to be exactly defined and thus needs to be approximated. We estimated d min as the distance below which FID was always at least 90 % of SD. Our results were qualitatively robust to the choice of this threshold. Using data for which SD > d min, we then estimated the change in the mean FID value with increasing SD by fitting classical OLS regression. The 95 % confidence intervals (95 % CI) were based on standard errors accounting for heteroscedasticity in the data based on HC3 correction for covariance matrices (Long and Ervin 2000). We also fitted quantile regressions using both the traditional Koenker–Bassett algorithm (Koenker 2005) and a recent noncrossing algorithm (Bondell et al. 2010). They produced similar quantitative results, and those from the Koenker–Bassett algorithm are presented here. Slopes were constrained to be between 0 and 1. We obtained 95 % CI for quantile slope estimates using a bootstrap approach. In our datasets, FID was always lower than SD, and therefore FID estimates were not censored by SD. As noted by a reviewer, if this is not the case, one could benefit from using censored quantile regression.

Tools to perform quantile regressions are readily available in many statistical packages; we used the quantreg package (v. 4.67; Koenker 2011) for the R statistical software (v. 2.14.0; R Core Development Team 2011).

Results and discussion

Figure 2 shows how the natural rate of leaving (λ) is a critical determinant of the slope of the FID–SD relationship. As animals become more likely to leave while being experimentally approached, FID values become closer to SD values and thus the slope increases toward the value of 1. This supports the intuitive idea that conducting FID experiments is difficult on species that do not remain in place because many false escapes will be recorded. We note that this potential confounding effect, even independently of any effect of SD, in across-species SD–FID comparisons has so far been overlooked. The figure also shows that when there is no effect of SD on FID, the slope estimates from OLS regression are zero only under two conditions: First, there is no variability in d. This occurs because introducing variability in d via a log normal distribution creates a left-skewed distribution of FID values, generating positive slope of the SD–FID relationship. Second, and more importantly, animals only leave when disturbed by the experimental approach. Only when this is ascertained one could use standard inference from OLS regression (i.e., test against the null hypothesis of a slope of 0) to analyze the FID–SD relationship. Even minor departures from these conditions quickly lead to significant slopes. Finally, and most importantly, the figure shows that for both OLS and quantile regressions, similar slopes may arise from two situations. The first is when SD does not affect the distance d at which animal escape and the animal leaves at a given rate lambda. The second is when d increases with SD, but until the experimenter reaches this distance, the animal has a lower likelihood of leaving. Thus, without prior information on the natural rate of leaving, one cannot properly quantify the relationship between SD on FID.

Fig. 2
figure 2

An example of how the SD–FID slopes estimated by ordinary least-square (dotted) and 0.05th, 0.1st and 0.9th quantile regressions (continuous) change with the natural rate of leaving (λ) and the increasing effect of SD on FID. FID is modeled as FID = max[d = TLN(d min + βSD, σ, SD), TEXP(λ, SD)]. See “Developing a model of FID” for details. Panel a: FID is not affected by SD (β = 0), and there is no variability in d (σ = 0). Panel b: FID increases with SD (β = 0.3), and there is no variability in d (σ = 0). Panel c: FID is not affected by SD (β = 0), and there is variability in d [σ = log(2)]. Panel d FID increases with SD (β = 0.3), and there is variability in d [σ = log(2)]. Slopes shown are averages of 20 simulation replicates

Full size image

When the value of λ is exactly known and the distribution of d min known, it is possible to test the null hypothesis that SD does not affect FID by checking whether or not the 95 % confidence interval of the OLS slope estimate from the data includes the expected value of the slope from the null model. It will, however, be complex (and costly) to conduct these estimations reliably, and this approach is therefore likely to be impractical and error-prone.

When the value of λ is not exactly known, one needs to first assume that the likelihood of the animal leaving before the experimenter reach distance d min is negligible. Under this assumption, the more robust test appears to be testing whether the slope estimated on the lowest quantiles differs significantly from zero. Indeed, the SD–FID slope estimated on the lowest quantiles increase with λ more slowly than the OLS slope and is not sensitive to the variability of d min. Lowest quantiles will provide more robust test—their SD–FID slope remains zero for higher λ (Fig. 2). The accuracy of their estimation is however lower (see below), and as a rule-of-thumb, we would recommend using the 0.1st quantile. Interestingly, both for OLS and quantile regression on any quantile, a SD–FID slope not significantly different from zero always allows us to reject the hypothesis of an effect of SD on FID.

Note that using alert distance rather than SD does not solve the above problems. Animals may well have detected a potential threat at a reasonable distance without triggering an escape decision, and the movement observed by the experimenter may be linked to a leaving decision unrelated to the experiment (e.g., naturally changing foraging patches). Using only FID data for which departure was undoubtedly related to the approaching experimenter (for instance, when the animal runs away in the direction opposite to the experimenter) is likely to be too conservative: an animal may decide to flee the approaching threat without engaging at first in such costly escape behavior. This will bias the analysis toward understanding the effect of SD on extreme escape behavior only.

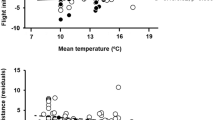
In our bird data, the OLS slopes of SD–FID relationships differed significantly from 0 for all species [California towhee: 0.34 (95 %CI: 0.43–0.52); silver gull: 0.07 (95 %CI: 0.11–0.15); California thrasher: 0.54 (95 %CI: 0.68–0.83)]; western scrub jay: 0.27 (95 %CI: 0.44–0.61); see also Fig. 3]. However, we have no prior information on λ and thus cannot know the expected value of these slopes under the null hypothesis that SD does not affect FID. Thus, we are strictly unable to test against a proper null model that includes the probability of leaving. If, however, we assume that individuals left for no other reason than because we approached them, the 0.1st FID quantile slope estimated for California towhees and for silver gulls was almost zero [0.11 (95 %CI: 0.07–0.20) and 0.04 (95 %CI: 0.02–0.07), respectively; Fig. 3c, d, g, h], and we did not reject the null hypothesis that SD did not affect FID for these species. By contrast, the 0.1st FID quantile slope was positive for California thrashers [0.33 (95 %: 0.15–0.55); Fig. 3a, e] and western scrub jays [0.29 (95 %: 0.19–0.37); Fig. 3b, f], which were characterized by a lack of small FID values at large SD.

Fig. 3
figure 3

Relationships between starting distance (SD) and flight initiation distance (FID) in four bird species [a, e California thrasher (n = 61); b, f western scrub jay (n = 123); c, g California towhee (n = 374); d, h silver gull (n = 272)]. Panels a, b, c, d show the data, the 1:1 line (continuous, bold), the OLS regression line (dotted), and the quantile regression lines for the 0.05, 0.1, …, 0.95th quantiles. Panels e, f, g, h show how the slopes of the regression lines and their associated 95 % confidence intervals vary across the 0.05, 0.1, …., 0.95th quantiles (continuous line: slope, dotted lines: confidence interval)

Full size image

The use of quantile regressions on upper quantiles also brings additional valuable information. For instance, Fig. 2 suggests that when the value of the 0.9th quantile slope is significantly below 1.0 λ has a low value. In our data, the slope of the 0.9th FID quantile was low for silver gulls, which suggested a low natural rate of leaving. This is not surprising given that approximately 90 % of the gulls tested were roosting at the start of the experimental FID approach, and thus had little motivation to engage in moves unrelated to escape.

This work shows that investigating changes across the entire distribution of the response variable, rather than the mean only, is important. First, quantile regression allowed the detection of nonrandomness in the FID data distribution when OLS regression would have failed. Second, the use of quantile regression is more consistent with the prediction that to detect if individuals flush early, the lowest part (i.e., the lowest quantiles) of the FID distribution is the most informative. As stated in the introduction, OLS regression may not be able to differentiate between FID data that may differ in the changes of the lowest quantiles (note, for instance, that the OLS slopes were almost identical for scrub jays and California towhees, whereas their 0.1st FID quantile slopes clearly differ).

Quantile regression, however, has limitations. Similar to OLS regression, the accuracy of a quantile’s estimate is affected by sample size (Cade and Noon 2003), but unfortunately, power analysis cannot be easily conducted. Additionally, accuracy of the estimation varies across quantiles, with the most extreme quantiles (closest to zero or one) less well estimated than quantiles closer to the median (Cade and Noon 2003). Thus, although this ultimately depends on the regression models and the distribution of the data, correct estimation of many and/or extreme quantiles will generally require larger sample size than usually needed for OLS regression. This data requirement is the main drawback of quantile regression, but knowing about this ahead of time should permit sufficient data to be collected. Analyses conducted using increasingly larger subsamples of the datasets used in this study suggested that a sample size of 50 or more was usually required to achieve consistent results using linear regressions and even when all data were used lower sample size at higher SD values prevented us to meaningfully test for nonlinearity of the SD–FID relationship using quantile regressions (not shown). We also suggest estimating regression slopes for many quantiles, as presented in Fig. 3, to help assess the stability of estimation of the quantile regression slopes.

Beyond the data requirements, our work suggests that future FID studies would benefit from obtaining independent estimates of λ, for instance, by monitoring undisturbed behavior of the studied species, or from artificially decreasing λ by, for instance, providing attractive food patches where experiment would be conducted. One can also imagine conducting experimental approaches at a high speed to reduce the likelihood of the animal naturally leaving the location. This may, however, affect the global perception of risk and would also make it difficult to compare data between species. More generally, we urge behavioral ecologists studying flight initiation distance to account for the natural rate of leaving and collect the necessary data to develop better null models.

We see an additional benefit to using quantile regression in the context of FID studies. The great variability observed in FID data (Fig. 3) may question if sensitivity to threat is a species-specific trait or is overwhelmed by individual differences and/or plasticity. Blumstein et al. (2003) showed that mean FID could be consistently different between species across various environmental contexts, and a number of studies have identified phylogenetic signal in FID data (e.g., Blumstein 2006; Møller 2008, 2009). However, amount of overlap could be wide, which may decrease the ecological relevance of such differences. Comparing profiles as such produced in Fig. 3 will help in understanding species differences. FID data are also widely used to design buffer zones between wildlife and humans (Rodgers and Schwikert 2002; Fernández-Juricic et al. 2005), and quantile regression could clarify the effect of relying, even conservatively, on species-specific mean FID values to design these buffer zones (Blumstein et al. 2003).

The SD–FID relationship provides a case study in which both theoretical predictions and experimental design interact to define what portion of the response data are informative and, furthermore, highlights the utility of quantile regression. Quantile regression, however, should be valuable to many other questions that behavioral ecologists ask. The method is commonly used by ecologists to investigate limiting factors that shape the edges of data cloud (Scharf et al. 1998; Cade et al. 1999), and it could be applied similarly in behavioral ecology. For instance, Korstjens et al. (2010) found that temperature was an important factor limiting the active time of primates, providing a rare use of quantile regression in behavioral ecology studies. Quantile regression may thus shed light on the constraints imposed on behavioral adjustments. We also suggest that quantile regression may be particularly useful to investigate changes in intraspecific variability, quantified as the differences between quantiles. Ultimately, we invite behavioral ecologists to consider quantile regression as an important tool for their statistical toolbox.