On the motion of magnetotactic bacteria: theoretical predictions and experimental observations

Abstract

The movement of magnetotactic bacteria is done in a viscous media in the low Reynolds number regime. In the present research, the simple model for magnetotactic bacteria motion, proposed by Nogueira and Lins de Barros (Eur Biophys J 24:13–21, 1995), was used to numerically simulate their trajectory. The model was done considering a spherical bacterium with a single flagellum and a magnetic moment positioned in the sphere center and parallel to the flagella. The numerical solution shows that the trajectory is a cylindrical helix and that the body Euler angles have linear dependencies on time. Using that information, analytical expressions were obtained for the first time for the center-of-mass coordinates, showing that the trajectories are helixes oriented to the magnetic field direction. They also show that the magnetic moment does not align to the magnetic field, but it precesses around it, being fully oriented only for very high magnetic fields. The analytical solution obtained permits to relate for the first time the flagellar force to the axial velocity and helical radius. Trajectories of uncultivated magnetotactic bacteria were registered in video and the coordinates were obtained for several bacteria in different magnetic fields. The trajectories showed to be a complex mixture of two oscillating functions: one with frequency lower than 5 Hz and the other one with frequency higher than 10 Hz. The simple model of Nogueira and Lins de Barros shows to be incomplete, because is unable to explain the trajectories composed of two oscillating functions observed in uncultivated magnetotactic bacteria.

Introduction

Magnetotactic bacteria (MTB) are prokaryotes that passively interact with the geomagnetic field through biomineralized magnetic nanoparticles arranged in a chain inside the bacterial cytoplasm (Yan et al. 2012). Each magnetic nanoparticle is involved by a lipid membrane and the nanoparticle + membrane set is known as magnetosome. MTB move using their flagella in a viscous fluid in the low Reynolds number regime (Klumpp et al. 2019), where viscous forces are stronger than inertial forces. In that case, the net force and torque acting on the bacteria are null. Optical microscopy observations have shown that the 2D trajectory of MTB under the influence of external magnetic fields is undulatory, similar to the 2D projection of helical trajectories (see, for example, references Nogueira and Lins de Barros 1995; Lefevre et al. 2009; Zhang et al. 2012; Chen et al. 2015). For the multicellular magnetotactic prokaryote Candidatus Magnetoglobus multicellularis has been assumed that the trajectory is a cylindrical helix and the velocity, helix radius, and frequency were obtained from the trajectory coordinates (Almeida et al. 2013; Keim et al. 2018). To study the motion of MTB in the low Reynolds number regime is necessary to know all the forces and torques acting on the bacteria (Klumpp et al. 2019). Nogueira and Lins de Barros (1995) developed a simple model using that approach, considering a spherical MTB with a single flagellum and a magnetosome chain aligned to the flagellum action line. With that model, they were able to calculate numerically the temporal evolution of the center of mass coordinates (x, y, z), being the trajectory similar to a cylindrical helix. On the other hand, Cui et al. (2012), Yang et al. (2012), and Kong et al. (2014) studied the motion of non-spherical MTB, to include the effect of the bacterial body geometry on the viscous forces. To do that, they numerically simulated the motion using the second Newton’s law, considering all the forces and torques and calculating the appropriate inertial terms for the geometrical body form. They also included a relative inclination λ between the magnetosome chain and the flagellar action line. Yang et al. (2012) observed that when λ ≠ 0, the velocity decreases when the magnetic field increases, effect also observed experimentally by Pan et al. (2009). Anyway, in any of those studies was obtained an analytical expression for the MTB motion trajectory, associating the force parameters to the trajectory parameters. An analytical solution for the motion of micro-organisms in terms of the applied forces and torques is important, because it permits to understand how those parameters influence the observed trajectory. In the present paper, the motion of MTB is numerically simulated using the model of Nogueira and Lins de Barros (1995), the numerical solution for the center of mass coordinates (x, y, z) and for the Euler’s angles (θ, ϕ, ψ) is obtained and discussed and for the first time is shown that an analytical solution can be found for the trajectory, relating the flagellar and drag force parameters to the trajectory parameters. Those results were compared to experimental measurements of the motion of uncultured MTB under different magnetic fields, showing that the analytical solution for the simple model of Nogueira and Lins de Barros (1995) is incomplete.

Motion model in the low Reynolds number regime

Nogueira and Lins de Barros (1995) considered the following relations valid in the low Reynolds number regime:

$${\mathbf{F}}_{\text{flagella}} + {\mathbf{F}}_{\text{Hidro}} = 0,$$

(1a)

$${\varvec{\uptau}}_{\text{flagella}} + {\varvec{\uptau}}_{\text{Hidro}} + {\varvec{\uptau}}_{\text{magnetic}} + {\varvec{\uptau}}_{\text{body}} = 0.$$

(1b)

It is defined a system fixed to the body (e₁, e₂, e₃) with origin in the center-of-mass located in the center of the spherical body. e₃ is in the direction of the diameter parallel to the flagella. It is also defined a system fixed to the laboratory (e_X, e_Y, e_Z) (Fig. 1). In the system fixed to the body, F_flagella can be written as follows:

$${\mathbf{F}}_{\text{flagella}} = {\text{F}}_{12} \left( {\cos \omega t\;{\mathbf{e}}_{1} + \sin \omega t\;{\mathbf{e}}_{2} } \right)+ F_{3} \;{\mathbf{e}}_{3} ,$$

(2)

where ω is the flagellar angular velocity, also calculated as 2πf being f the rotation frequency. Assuming that the magnetotactic bacteria are a coccus; the hydrodynamic force F_Hidro can be written as follows:

$${\mathbf{F}}_{\text{Hidro}} = - 6\pi \eta R{\mathbf{v,}}$$

(3)

where η is the fluid viscosity, R is the bacterial radius, and v is the relative velocity. Thus:

$${\mathbf{v}} = V_{12} \left( {\cos \omega t\;{\mathbf{e}}_{1} + \sin \omega t\;{\mathbf{e}}_{2} } \right)+ V_{3} \;{\mathbf{e}}_{3} ,$$

(4)

where $V_{3} = F_{3} /6\pi \eta R$ and $V_{12} = F_{12} /6\pi \eta R.$

Fig. 1

Schematic representation of the reference system used in the theoretical model for MTB motion. The magnetotactic bacterium is assumed to be spheroidal with a single flagellum rotating with angular velocity ω and a magnetic moment m fixed in the center of the bacterial body and oriented parallel to the flagellum. e₁, e₂, and e₃ are orthonormal vectors fixed to the bacterial body. e_x, e_y, and e_z are orthonormal vectors fixed to the laboratory. The applied magnetic field B is directed in the − e_z direction. The Euler angle θ is the angle among e₃ and e_z

In Eq. (1b) τ_body denotes the reaction torque due to the torque that generates the rotation of the flagellum. As ω is constant, we can consider that τ_body is also constant:

$$\varvec{\tau}_{\text{body}} = - \tau_{\text{body}} {\mathbf{e}}_{3} .$$

(5)

The flagellar torque is calculated directly as follows:

$$\tau_{\text{flagella}} = R {\mathbf{e}}_{3} \times {\mathbf{ F}} = N_{12} ( - \sin \omega t\; {\mathbf{e}}_{1} + \cos \omega t\;{\mathbf{e}}_{2} ),$$

(6)

where $N_{12} = RF_{12}$. The hydrodynamic torque τ_Hidro is calculated considering a spherical body rotating in a viscous medium:

$$\varvec{\tau}_{\text{Hidro}} { = - 8}\pi \eta {\text{R}}^{ 3} {\mathbf{\varOmega ,}}$$

(7)

Ω is the angular velocity of the body and can be written in terms of the Euler angles (ϕ, θ, ψ) in the body system:

$$\varOmega_{1} = \phi^{'} \sin \theta \sin \psi + \theta^{'} \cos \psi ,$$

(8a)

$$\varOmega_{2} = \phi^{'} \sin \theta \sin \psi - \theta^{'} \cos \psi ,$$

(8b)

$$\varOmega_{3} = \phi^{'} \cos \psi + \psi^{'} ,$$

(8c)

and in the laboratory system:

$$\varOmega_{x} = \psi^{'} \sin \theta \sin \phi + \theta^{'} \cos \phi ,$$

(8d)

$$\varOmega_{y} = - \psi^{'} \sin \theta \cos \phi + \theta^{'} \sin \phi ,$$

(8e)

$$\varOmega_{z} = \psi^{'} \cos \theta + \phi^{'} ,$$

(8f)

where ′ means total time derivative.

To calculate the magnetic torque, we consider that the magnetosome chain is collinear to the e₃ direction producing a magnetic moment m = me₃. To write the magnetic field B, we consider the system fixed to the laboratory, and without loss of generality, we consider B collinear to e_z: B = − Be_z. In this case:

$$\tau_{\text{magnetic }} { = }{\mathbf{m}} \times {\mathbf{B}} {\text{ = mB sin}}\theta ( {\text{cos}}\psi {\mathbf{e}}_{ 1} {\text{ - sin}}\psi {\mathbf{e}}_{ 2} ).$$

(9)

The model of Nogueira and Lins de Barros (1995) considers B constant, and for t > 0, B is antiparallel to e_Z. Adding Eqs. (5–7, 9) to Eq. (1b), it is possible find an expression for Ω, and using Eqs. (8a–8c), it is possible to find the following equations for the Euler angles:

$$\phi^{'} = \alpha \csc \theta \cos (\omega t + \psi ),$$

(10a)

$$\theta^{'} = \beta \sin \theta - \alpha \sin (\omega t + \psi ),$$

(10b)

$$\psi^{'} = - \gamma - \alpha \cot \theta \cos (\omega t + \psi ).$$

(10c)

The movement of the center of mass can be written relative to the system fixed to the laboratory from Eq. (4) and the proper transformation between the laboratory and body systems. The result is as follows:

$$x' = V_{12} [\cos \phi \cos (\omega t + \psi ) - \sin \phi \cos \theta \sin (\omega t + \psi )] + V_{3} \sin \phi \sin \theta ,$$

(11a)

$$y' = V_{12} [\sin \phi \cos (\omega t + \psi ) + \cos \phi \cos \theta \sin (\omega t + \psi )] - V_{3} \cos \phi \sin \theta ,$$

(11b)

$$z' = V_{12} \sin \theta \sin (\omega t + \psi ) + V_{3} \cos \theta .$$

(11c)

In Eqs. (10) and (11), the following is valid: $\alpha = (N_{12} /8\pi \eta R^{3} ), \beta = (mB/8\pi \eta R^{3} ), \gamma = (\tau_{\text{body}} /8\pi \eta R^{3} )$, and V₁₂ can be written as (4/3)αR. Observe that in the system fixed to the laboratory, if the fluid has null velocity, the relative velocity in Eq. (3) becomes the center of mass velocity.

Numerical solution

Equations (10) and (11) are coupled. To solve them numerically was used the numerical integrator LSODA from ODEPACK library, available in Python language (Hindmarsh 1983). The parameters used were: η = 1 × 10⁻³ Pa·s, R = 1 μm, m = 1.5 × 10⁻¹⁵ A·m², F₃ = F₁₂ = 4 × 10⁻¹² N, ω = 250 rad/s, τ_body = 2 × 10⁻¹⁸ N·m, α = 159 rad/s, γ = 79 rad/s, V₃ = V₁₂ = 212 μm/s, and B = (0.1, 0.6, 1, 2, 4, 8, 16, 20, 30, 40, 50, 60, 100, 200, 300, 400, 500) Oe. The results for x, y, z, ϕ, θ, and ψ for B = 60 Oe are shown in Figs. 2 and 3. It is observed that after a while, the coordinates x and y oscillate as sinusoidal waves and the coordinate z varies linearly (Fig. 2). Those are characteristics of a helical trajectory with coordinates $x(t) = R \cdot \cos (2\pi ft), \;y(t) = R\cdot\sin (2\pi ft)\; {\text{and}}\; z(t) = V_{Z} \cdot t$, where V_Z is the axial velocity and R is the radius of the helix. It is observed that the Euler angle θ after a while gets a constant value θ_E. At t = 0, the value of θ is zero, and after the inversion of the magnetic field, the magnetic moment tends to align to the magnetic field. Figure 3 shows that θ does not attain 180°, meaning that the bacterial body and the magnetic moment are precessing around the magnetic field vector. Angles ϕ and ψ after some time vary linearly. That behavior is observed for all the magnetic field values used in the numerical analysis. It can be stated that, after some time, the trajectory gets a stationary state, where the center-of-mass coordinates vary as a cylindrical helix with axis parallel to the magnetic field, and the angles can be written as follows:

$$\phi = \phi_{0 } - \omega_{1} \cdot t,$$

(12a)

$$\psi = \psi_{0} - \omega_{2} \cdot t,$$

(12b)

$$\theta = \theta_{\text{E}} .$$

(12c)

Fig. 2

Numerical results for the center of mass coordinates as function of time for a magnetic field of 60 Oe. a Coordinate x. b Coordinate y. c Coordinate z

Fig. 3

Numerical results for the Euler angles as a function of time for a magnetic field of 60 Oe. a Angle ϕ. b Angle ψ. c Angle θ. Observe that after some time, θ becomes constant in an equilibrium value θ_E, whose value is not equal to 0, π, or 2π, meaning that the magnetosome chain is not aligned to the magnetic field

From the numerical solutions, it is observed that ω₂ does not depend on the magnetic field and $\omega_{2} = \omega$. From Eqs. (8d, e, f), it can be calculated the angular velocity of the body Ω:

$$\varOmega_{\text{x}} = - \omega \cdot\sin (\theta_{\text{E}} )\cdot\sin (\phi_{0} - \omega_{1} \cdot t) ,$$

(13a)

$$\varOmega_{\text{y}} = \omega \cdot\sin (\theta_{\text{E}} ) \cdot \cos (\phi_{0} - \omega_{1} \cdot t) ,$$

(13b)

$$\varOmega_{\text{z}} = - \omega \cdot\cos (\theta_{\text{E}} ) - \omega_{1} ,$$

(13c)

$$\varOmega = \left[ {\omega_{1}^{2} + \omega^{2} + 2 \cdot \omega \cdot \omega_{1} \cdot \cos (\theta_{\text{E}} )} \right]^{1/2} .$$

(13d)

It can be observed that the body angular velocity is a vector that precesses around the axis e_z that is the magnetic field direction. As the magnetic moment is fixed to the body (Fig. 1), it precesses around the magnetic field with angular velocity ω₁. The body spins around the e_z axis with angular velocity $- \omega_{1} - \omega \cdot\cos (\theta_{\text{E}} ).$

The trajectory radius R and axial velocity V_z (Fig. 4), θ_E and ω₁ (Fig. 5), and ϕ₀ and ψ₀ (Fig. 6) are shown as function of the magnetic field B. It is observed that the axial velocity decreases initially, gets a minimum value, and growths to get a stable value. It has been assumed in the literature (Pan et al. 2009; Yang et al. 2012) that a decrease of the velocity when the magnetic field increases is associated to an intrinsic inclination of the magnetosome chain relative to the flagellar bundle. Here, our results show that the velocity decreases even when the magnetosome chain is aligned to the flagella.

Fig. 4

a Axial velocity V_Z as function of the magnetic field B obtained from the derivative of z(t) (Fig. 1c). The insert shows − dθ_E/dB as function of B, calculated from the θ_E curve (Fig.  5a). Observed that V_Z and − dθ_E/dB have a minimum value in the same magnetic field of about 30 Oe. b Radius of the cylindrical helix as function of the magnetic field B. It was obtained directly from x(t) or y(t) (Fig. 1a, b), assuming that they represent the coordinates of an helix

Fig. 5

a Equilibrium angle θ_E as function of the magnetic field B. b Angular velocity ω₁ as function of the magnetic field B. Each value corresponds with the inclination of angle ϕ as function of time (Fig. 2a)

Fig. 6

a Phase constant ψ₀ as function of the magnetic field B. Insert shows its decay for higher magnetic fields. b Phase constant ϕ₀ as function of the magnetic field B. Insert shows its decay for higher magnetic fields

Analytical solution

Equation (12) permits to find a solution for the coordinates of the center of mass (x, y, z) solving (Eq. 11). If Eq. (12) is used in Eq. (10), the following expressions are found:

$$- \omega_{1} = \alpha \csc (\theta_{\text{E}} ) \cos (\psi_{0} ),$$

(14a)

$$0 = \beta \sin (\theta_{\text{E}} ) - \alpha \sin (\psi_{0} ),$$

(14b)

$$- \omega_{2} = - \gamma - \alpha \cot (\theta_{\text{E}} )\cos (\psi_{0} ) = - \omega .$$

(14c)

After some algebra, the following can be shown:

$$\left[ {\alpha^{2} /\left( {\omega_{1}^{2} + \beta^{2} } \right)} \right] + \left[ {(\gamma - \omega )^{2} /\omega_{1}^{2} } \right] = 1,$$

(15a)

$$\tan (\psi_{0} ) = - \beta /\omega_{1} ,$$

(15b)

$$\tan (\theta_{\text{E}} ) = \alpha \cos (\psi_{0} )/(\omega - \gamma ) .$$

(15c)

If the magnetic field is null $(\beta = 0)$, Eq. (15) transforms into:

$$\omega_{1} = \left( {\alpha^{2} + (\gamma - \omega )^{2} } \right)^{1/2} ,$$

(16a)

$$\psi_{0} = 0 \quad {\text{or}}\quad \pi ,$$

(16b)

$$\tan (\theta_{\text{E}} ) = \alpha /(\gamma - \omega ).$$

(16c)

For high magnetic fields $(\beta \to \infty )$, Eq. (15) transforms into:

$$\omega_{1} = \gamma - \omega ,$$

(17a)

$$\psi_{0} = \pi /2,$$

(17b)

$$\theta_{\text{E}} = \pi .$$

(17c)

Using Eq. (12) in Eq. (11), and after simple integration, the following solution for the center-of-mass coordinates is found:

$$x = x_{0} - (R_{12} \sin (\psi_{0} ) \cos (\theta_{\text{E}} ) \cos (\phi_{0} - \omega_{1} t)) + [(R_{3} \sin (\theta_{\text{E}} ) \cos (\phi_{0} - \omega_{1} t) - R_{12} \cos (\psi _{0}) \sin (\phi_{0} - \omega_{1} t))],$$

(18a)

$$y = y_{0} - (R_{12} \sin (\psi_{0} ) \cos (\theta_{\text{E}} ) \sin (\phi_{0} - \omega_{1} t)) + [(R_{3} \sin (\theta_{\text{E}} ) \sin (\phi_{0} - \omega_{1} t) + R_{12} \cos (\psi _{0}) \cos (\phi_{0} - \omega_{1} t))],$$

(18b)

$$z = z_{0 } + (V_{3} \cos (\theta_{\text{E}} ) + V_{12} \sin (\theta_{\text{E}} ) \sin (\psi 0)) t,$$

(18c)

where $R_{12} = V_{12} /\omega_{1}$ and $R_{3} = V_{3} /\omega_{1}$. Equation 18 represents a cylindrical helix, because the projection of the trajectory in the XY plane is a circle of radius:

$$r = \left[ {\left( {R_{3} \sin (\theta_{\text{E}} ) - R_{12 } \sin (\psi_{0} ) \cos (\theta_{\text{E}} )} \right)^{2} + R_{12}^{2} \cos^{2} (\psi_{0} )} \right]^{1/2} .$$

(19)

From Eq. (18c), the axial velocity is identified as follows:

$$V_{z } = V_{3} \cos (\theta_{\text{E}} ) + V_{12} \sin (\theta_{\text{E}} ) \sin (\psi_{0} ),$$

(20)

where θ_E and ψ₀ are functions of β.

In the limit of higher magnetic fields $(\beta \to \infty )$, the trajectory becomes the following:

$$x = x_{0} + R^{'}_{12} \cos (\phi_{0} + (\omega - \gamma )t),$$

(21a)

$$y = y_{0} + R^{'}_{12} \sin (\phi _{0} + (\omega - \gamma )t),$$

(21b)

$$z = z_{0} + V_{3} t,$$

(21c)

where $R^{'}_{12} = V_{12} /(\omega - \gamma )$. In this case, the trajectory corresponds with the classical expression for a cylindrical helix.

For null magnetic fields $(\beta = 0)$, the trajectory is as follows:

$$x = x_{0} + R_{3} \sin (\theta_{\text{E}} ) \cos (\phi_{0} - \omega_{1} t) - R_{12} \sin (\phi_{0} - \omega_{1} t),$$

(22a)

$$y = y_{0} + R_{3} \sin (\theta_{\text{E}} ) \sin (\phi_{0} - \omega_{1} t) + R_{12} \cos (\phi_{0} - \omega_{1} t),$$

(22b)

$$z = z_{0} + V_{3} \cos (\theta_{\text{E}} ) t.$$

(22c)

Equation (22) show that the trajectory for normal non-magnetic micro-organisms is a helix with parameters:

$$r = \left[ {R_{3}^{2} \cdot \left[ {\alpha^{2} /\omega_{1}^{2} } \right] + R_{12}^{2} } \right]^{1/2} ,$$

(23a)

$$\omega_{1} = \left[ {\alpha^{2} + (\gamma - \omega )^{2} } \right]^{1/2} ,$$

(23b)

$$V_{z} = V_{3} \cdot [(\gamma - \omega )/\omega_{1} ].$$

(23c)

Equation (22) shows for the first time that non-magnetotactic bacteria, while maintaining a constant swimming direction, must swim following helical trajectories with parameters described by Eq. (23). Interestingly, Eq. (22) represents a trajectory that is a particular case for the chiral ribbon that has been observed for the trajectory of sperm cells (Su et al. 2012, 2013):

$$x = r_{\text{h}} \cos (\omega_{\text{h}} t + \theta_{\text{h}} ) + A_{\text{b}} \cos (\omega_{\text{b}} t + \theta_{\text{b}} )\sin (\omega_{\text{h}} t + \theta_{\text{h}} ),$$

(24a)

$$y = r_{\text{h}} \sin (\omega_{\text{h}} t + \theta_{\text{h}} ) - A_{\text{b}} \cos (\omega_{\text{b}} t + \theta_{\text{b}} )\cos (\omega_{\text{h}} t + \theta_{\text{h}} ),$$

(24b)

$$z = \text{v}_{z} t + A_{\text{b}} (\omega_{\text{h}} r_{h} /\text{v}_{z} )\cos (\omega_{\text{b}} t + \theta_{\text{b}} ),$$

(24c)

where $A_{b } = r_{b} \text{v}_{z} (\text{v}_{z}^{2} + \omega_{h}^{2} r_{h}^{2} )^{ - 1/2}$. r_h, ω_h, and θ_h are, respectively, the chiral ribbon radius, angular velocity, and phase constant, and r_b, ω_b, and θ_b are, respectively, the beating waveform radius, beating angular velocity, and beating phase constant and v_z is the forward velocity along the z axis. It is observed that Eqs. (18) and (22) are a particular case of Eq. (24) for ω_b = 0, where the chiral ribbon becomes a cylindrical helix.

Experimental MTB trajectories

Uncultured MTB were collected at Ubatiba River, Marica, Rio de Janeiro, Brazil. They were maintained in the laboratory in plastic jars near to the window and at ambient conditions in our lab in Rio de Janeiro city. The local geomagnetic parameters are: horizontal component = 18 μT, vertical component = − 15 μT, and total intensity = 23 μT.

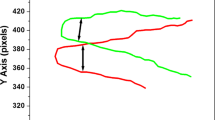
To isolate MTBs for the experiments, a sub-sample was transferred to a specially designed flask containing a lateral capillary aperture and a small magnet generate a magnetic field aligned to the capillary aperture (Lins et al. 2003). The studied uncultured MTB are South-seeking and swam towards the capillary facing the North Pole of a magnet. After 5 min, samples were collected with a micropipette and put on a glass slide for observation in an inverted microscope. On the stage of the inverted microscope (Nikon Eclipse TS100) was set a pair of coils connected to a DC power supply and fixed to a glass microscope slide where the collected drop with MTB was placed. The used lens had magnification of 40×. The magnetic fields generated by the coils were 2.1 Oe, 2.9 Oe, 3.8 Oe, and 4.6 Oe. The MTB motion was recorded in the inverted microscope with a digital camera (Lumera Infinity 1) in a rate of 82 fps. Experimentally for the video microscopy, the camera position was adjusted in such a way that the horizontal axis of the frames was aligned to the applied magnetic field B. The coordinates of the trajectories were obtained using the software ImageJ (NIH–USA). The coordinates were in pixel units and the conversion to μm was done using a calibration ruler, which consists in a 1 mm line divided in 100 parts. In the experimental set-up, the external magnetic field is applied in the horizontal direction, meaning that the trajectory horizontal coordinate, as function of time, must be a straight line (Fig. 7c). As Fig. 7a shows, the 2D trajectory observed does not correspond with the projection of a single cylindrical helix but with a complex mixture of two cylindrical helixes, being one with low-frequency value and the other one with higher frequency value.

Fig. 7

Example of an MTB trajectory for a magnetic field of 4.6 Oe. a The trajectory as seen in a video of 640 × 460 pixels. The insert shows a zoom of the same trajectory. b The vertical coordinate of the trajectory as function of time. c The horizontal coordinate of the trajectory as function of time. As the magnetic field is oriented in the horizontal direction the horizontal coordinated is similar to a straight line, as must be for a helix whose axis is oriented to the magnetic field. However, observe that there are present small oscillations over the straight line. d The vertical coordinate corrected after the rotation in the angle θ_m as explained in the text. This correction permits the correct FFT analysis. e FFT of the curve shown in d. It is observed the presence of two frequencies: one at 1.3 Hz and another at 14 Hz

Let us consider the horizontal coordinate as the Z axis and the vertical coordinate as the X axis. If the helix axis is parallel to the Z axis and located on the focal plane together with the X axis, the observed trajectory must be similar to a sinusoidal function parallel to the Z axis. However, that is not the case, because all the curves have a little inclination relative to the magnetic field direction. It is known that MTB trajectories are misaligned to the magnetic field by an angle θ_m due to thermal noise (Kalmijn 1981) and this noise is not included in the simple model used in the present study. In that case, the Z and X coordinates must be rotated as follows:

$$Z^{'} = Z\cos \theta_{\text{m}} + X\sin \theta_{\text{m}}$$

(25a)

$$X^{'} = - Z\sin \theta_{\text{m}} + X\cos \theta_{\text{m}} ,$$

(25b)

being Z′ and X′ the coordinates observed in the experiment. To recover the coordinates Z and X, the angle θ_m in relation to the Z coordinate was calculated directly in the graph and both coordinates X′ and Z′ where rotated by that angle. The coordinates Z and X were fitted to the following expressions:

$$X = R_{1} \cos (\omega_{1} t + \theta_{\text{ph1}} ) + A_{2} \cos (\omega_{2} t + \theta_{\text{ph2}} )\sin (\omega_{1} t + \theta_{\text{ph1}} ),$$

(26a)

$$Z = \text{v}_{\text{z}} t + A_{2} (\omega_{1} R_{1} /\text{v}_{\text{z}} )\cos (\omega_{2} t + \theta_{\text{ph2}} ),$$

(26b)

where $A_{2} = R_{2} \text{v}_{z} (\text{v}_{z}^{2} + \omega_{1}^{2} R_{1}^{2} )^{ - 1/2}$. They are similar to Eq. (24a) and (24c) that have been suggested for other micro-organisms swimming in the low Reynolds number regime showing two frequencies.

As Fig. 7 and Table 1 show, the trajectories are composed of two oscillating functions, one with frequency lower than 5 Hz and other with frequency higher than 10 Hz. As can be seen in Table 1, the axial velocity has a tendency to decrease (ANOVA test p = 0.06) when the magnetic field increases and the radii for higher frequencies do not depend on the magnetic field. For the lower frequencies, the radius increases and the frequency decreases when the magnetic field increases. Interestingly the axial velocity decreases and R₁ increases when the magnetic field increases as predicted by the model and shown in Fig. 4. For the higher frequencies, only the frequency decreases when the magnetic field increases. The oscillating function with lower frequency shows the higher radius and vice versa (Table 1). Qualitatively, the axial velocity and the higher frequency decrease as predicted by the model (Figs. 4a, 5b). One interesting problem to be considered here is the effect of the glass slide or wall effect in the motion parameters. Edwards et al. (2013) analyzed the motion of spherical microbeds driven by bacteria near and far walls. They observed that far from walls the beds move in helical trajectories, meaning that their kinematics is related to near-constant forces and torques. Near wall motion is more stochastic. As Fig. 7a shows, MTB trajectories are well fitted with two helical trajectories, meaning that they must be swimming in a far-wall regime. Khalil et al. (2017) study the movement of Magnetospirillum gryphiswaldense near and far the glass surface, and observed that drag forces and torques increase near to the glass surface, decreasing the velocity and angular velocity of the bacteria. However, wall effects must be independent of the magnetic field. In that regard, the decrease in the trajectory frequencies f₁ and f₂ (Table 1) when the magnetic field increases must be related to the interaction of the bacteria with the magnetic field and not with the glass surface. The component with lower frequency is not predicted by the model proposed by Nogueira and Lins de Barros (1995) (see Fig. 5). Our theoretical results predict a helical trajectory with only one frequency ω₁, but our experimental results show that it is not the case. The experimental results show that the model of Nogueira and Lins de Barros (1995) is incomplete, because it is unable to predict the oscillations with lower frequencies and only predicts the oscillations with higher frequencies. That can be observed also in Fig. 8 of Cui et al. (2012) and Figs. 3 and 7 of Nogueira and Lins de Barros (1995) where similar models were used and the fit to experimental results only reproduce the higher frequencies. However, Yang et al. (2012) analyzed numerically the movement of ovoid MTB with two lateral flagellar bundle and observed that in some conditions for higher fields (2.5 mT), the MTB trajectory is composed of two superimposed helixes, and they justified the large one with low frequency as being produced by the noncoincidence between the translation and rotating axes, mainly because the magnetosome chain axis does not overlap with the flagella propulsion axis, assuming an inclination angle for the magnetosome chain. That noncoincidence is also predicted by the simple model of Nogueira and Lins de Barros (1995), as can be observed in Fig. 5a, producing also a decrease in the velocity until the angle θ_E starts to approach to the stability (Fig. 4a). Yang et al. (2012) shows that while the velocity decreases, the low-frequency helix increases its radius, and that is observed in Table 1 for the low-frequency radius R₁. That can be an indication that the magnetosome chains in the analyzed uncultured MTB have some inclination relative to the flagellar bundles.

Table 1 Experimental parameters for the trajectories of uncultured MTB from Ubatiba River, Marica, Rio de Janeiro, Brazil

Discussion

The observation of the motion of micro-organisms using optical microscopes produces 2D images that had been identified as the projections of helical trajectories in the focal plane (Fenchel 2001; Keim et al. 2018). Here for the first time is shown that, from first principles, the MTB trajectory in the low Reynolds number regime corresponds with a cylindrical helix, whose axis is perfectly aligned to the magnetic field, and at the same time, the bacterial magnetic moment is not aligned to the magnetic field but precesses around it with angular velocity equal to the trajectory angular velocity ω₁. Our simulation shows that the MTB trajectory has a stable regime after some time, being characterized for a constant value of the Euler angle θ and for linear functions of time for angles ϕ and ψ. Equation (18) represents the coordinates of the trajectory in the stable regime. The angular velocity of the trajectory is identified as ω₁ that is the solution of Eq. (15a). That equation can be transformed into the following algebraic equation:

$$\omega_{1}^{4} + (\beta^{2} - (\gamma - \omega )^{2} - \alpha^{2} )\omega_{1}^{2} - \beta^{2} (\gamma - \omega )^{2} = 0,$$

(27)

whose solution for ω²₁ is:

$$\omega_{1}^{2} = - (1/2)(\beta^{2} - (\gamma - \omega )^{2} - \alpha^{2} ) \pm [(1/4) (\beta^{2} - (\gamma - \omega )^{2} - \alpha^{2} )^{2} + \beta^{2} (\gamma - \omega )^{2} ]^{1/2} .$$

(28)

As can be seen, ω₁ is function of the magnetic torque, body torque, flagellum torque, and the flagellum angular velocity. Equation (28) shows that ω₁ has real and imaginary solutions. Only the real solutions produce oscillatory solutions in Eqs. (18).

From Eq. (18c) is identified the axial velocity as follows:

$$V_{\text{z}} = V_{3} \cos (\theta_{\text{E}} ) + V_{12} \sin (\theta_{\text{E}} ) \sin (\psi_{0} ).$$

(29)

As $\beta \sin (\theta_{\text{E}} ) = \alpha \sin (\psi_{0} )$, the last equation can be written as follows:

$$V_{\text{z}} = V_{3} \cos (\theta_{\text{E}} ) + V_{12} (\beta /\alpha )\sin^{2} (\theta_{\text{E}} ).$$

(30)

As can be seen in Figs. 4a and 5a, θ_E is function of β and V_z has a minimum for certain value of β. The minimum occurs, because the angle θ_E increase from an initial value to π rads, and in that process $\cos (\theta_{\text{E}} )$ and ${ \sin }^{ 2} (\theta_{\text{E}} )$ decrease and increase, respectively, to later invert their tendencies. A closer analysis shows that the minimum in V_z corresponds with the minimum of $- {\text{d}}\theta_{\text{E}} /{\text{d}}B$ (insert Fig. 4a). Equation (30) also shows that V_z increases or decreases depending on the dominance of F₃ over F₁₂.

As θ_E is function of β is difficult to calculate the value of β where ${\text{d}}V_{\text{z}} / {\text{d}}\beta { = 0}$. Interestingly, the coefficient of ${ \sin }^{ 2} (\theta_{\text{E}} )$ in Eq. (29) can be rewritten as $V_{12} \cdot\beta /\alpha = ({\text{mB}})/(6\pi \eta R^{2} )$. Therefore, in V_z, the term $\cos (\theta_{\text{E}} )$ depends directly on the longitudinal flagellar force F₃ and inversely on the fluid viscosity η and on the micro-organism radius R (as $V_{3} = F_{3 } / 6\pi \eta R$), and the term ${ \sin }^{ 2} (\theta_{\text{E}} )$ depends directly on the magnetic energy mB and inversely on the fluid viscosity η and on the micro-organism square radius R². The dependence on R makes the coefficient of ${ \sin }^{ 2} (\theta_{\text{E}} )$ be lower than that of $\cos (\theta_{\text{E}} )$ and even low values for the magnetic moment can make the coefficient of ${ \sin }^{ 2} (\theta_{\text{E}} )$ to be negligible. Numerical simulations done with F₃ = 100·F₁₂ show that the minimum in velocity goes a magnetic field of about 5 Oe and is practically negligible when compared to the velocity for higher magnetic fields (data not shown). Perhaps that is the reason why in the measurement of MTB velocity Kalmijn (1981) did not observe that decrease: F₃ ≫ F₁₂. The present study does not reject the fact that MTB velocity decreases as the magnetic field increases when the magnetic moment has an inclination relative to the flagellum (Pan et al. 2009; Yang et al. 2012). Our results reinforce the fact that the velocity decreases because of the noncoincidence between the translation and rotating axes during the MTB motion (see Fig. 4).

The analytical solution obtained in the present paper shows a helical trajectory with only one angular velocity, because $\psi^{'} = - \omega_{2} = - \omega$, but Eqs. 11 and 12 show that if $\omega_{2} \ne \omega$, then the trajectory must present two frequencies: ω₁ and ω − ω₂. $\psi^{'} = - \omega$, because it represents a rotation around the e₃ axis and the flagella is rotating around the same axis. Perhaps, different conditions in the model can be able to produce ω₂ ≠ ω as a magnetosome chain positioned in the cellular wall and not in the center, or even a non-homogeneous mass distribution locating the center of mass not in the geometrical center (as suggested for sperm by Su et al. 2013), or a more than one flagellar bundle rotating in the MTB body (as done by Yang et al. 2012).

Conclusions

The present research shows new characteristics for MTB motion trajectories obtained from numerical solutions to the motion equations based on the simple model of Nogueira and Lins de Barros (1995). An analytical solution for MTB trajectories was obtained based on the numerical solutions, showing for the first time that the trajectories are in fact cylindrical helixes with axis parallel to the magnetic field. The numerical and analytical solution also shows that the magnetic moment is not fully oriented to the magnetic field, but precesses around it with the same angular velocity of the trajectory. The parameters of the helix where obtained for the general case and in the particular case of null magnetic field and very high magnetic fields. On the other hand, trajectories for uncultured MTB were registered and analyzed. They are the mixture of two oscillating functions with different frequencies. The simple model used in the present study showed to be incomplete, because it is unable to explain the low frequencies observed in the trajectories of uncultured MTB. The trajectory composed by two oscillating functions must be the result of the forces and torques acting on the bacteria, perhaps associated with an inclination between the magnetosome chain and the applied magnetic field, as showed by Yang et al. (2012). New modification to the simple model of Nogueira and Lins de Barros (1995) must be done in the future by the consideration of a center-of-mass located out of the geometrical center, a magnetosome chain with an inclination relative to the flagellum or positioned in the cellular wall, two flagellar bundles oscillating with different frequencies, and different expressions for the flagellar force.