The Role of Complex Formation and Deleterious Mutations for the Stability of RNA-Like Replicator Systems

Abstract

In the RNA world hypothesis, RNA(-like) self-replicators are suggested as the central player of prebiotic evolution. However, there is a serious problem in the evolution of complexity in such replicators, i.e., the problem of parasites. Parasites, which are replicated by catalytic replicators (catalysts), but do not replicate the others, can destroy a whole replicator system by exploitation. Recently, a theoretical study underlined complex formation between replicators—an often neglected but realistic process—as a stabilizing factor in a replicator system by demonstrating that complex formation can shift the viable range of diffusion intensity to higher values. In the current study, we extend the previous study of complex formation. Firstly, by investigating a well-mixed replicator system, we establish that complex formation gives parasites an implicit advantage over catalysts, which makes the system significantly more vulnerable to parasites. Secondly, by investigating a spatially extended replicator system, we show that the formation of traveling wave patterns plays a crucial role in the stability of the system against parasites, and that because of this the effect of complex formation is not straightforward; i.e., whether complex formation stabilizes or destabilizes the spatial system is a complex function of other parameters. We give a detailed analysis of the spatial system by considering the pattern dynamics of waves. Furthermore, we investigate the effect of deleterious mutations. Surprisingly, high mutation rates can weaken the exploitation of the catalyst by the parasite.

Introduction

In the so-called RNA world hypothesis (Gilbert 1986; Gesteland et al. 2006), an RNA self-replicator (Pace and Marsh 1985; Sharp 1985; Cesh 1986) has been suggested as the central player of prebiotic evolution both in genetic and functional aspects, preceding a system involving protein translation. The hypothesis is based on the fact that RNA molecules are capable of replication through complementary base-paring (Joyce 1987; Orgel 2004) and can also have catalytic activity for various chemical reactions (Joyce 1998) through various catalytic strategies (Ke and Doudna 2006). The hypothesis is also supported by strong circumstantial evidence such as the essential role ribozyme plays in protein translation (Steitz and Moore 2003), and, a large number of roles played by RNA cofactors in metabolism (White 1976). If an RNA molecule—or any alternatives (Joyce et al. 1987; Joyce and Orgel 2006)—can indeed replicate itself with variation in its progeny through mutation, it will be the simplest system capable of Darwinian evolution in a self-sustained manner (Muller 1966; Crick 1968; but see also Segré et al. 2000).

A question naturally arises with respect to this hypothesis: can such an RNA(-like) replicator exist? Many experimental efforts have been made in attempt to synthesize RNA replicators in the laboratory (Bartel 1998; Chen et al. 2006; Joyce and Orgel 2006, for review). Although no complete RNA replicator has been synthesized yet, progress has been made that has significant implications; e.g., Johnston et al. (2001) succeeded in producing a ribozyme that can polymerize a short stretch of RNA on RNA templates, which was recently improved by Zaher and Unrau (2007) to polymerize a little more.

If we suppose such replicators exist, another question arises, with which the current study is concerned. How can a system of RNA-like replicators increase its complexity through evolution, approaching a current form of life? In more general terms, what are the potential dynamics of the ecology and evolution of RNA-like replicators? Theoretical research has been conducted to examine these questions (Stadler and Stadler 2004; Szathmáry 2006, for review). Interestingly, these studies showed that the evolution of complexity in a system of simple replicators is not expected to happen with ease. Firstly, the evolution of complexity through the accumulation of information contained in the genome of a single replicator (quasi-)species is limited by too a high mutation rate¹, which is naturally assumed in RNA-based replication (Eigen 1971; Küppers 1983; Eigen et al. 1989). Secondly, the evolution of complexity via the cooperation of several replicator species—e.g., via the hypercycle (Eigen and Schuster 1979)—is hindered by parasitic replicators, which do not contribute to the replication of the other replicators but still benefit from (or exploit) cooperative replicators (Maynard Smith 1979; Bresch et al. 1980).

Solutions to these problems—and problems in these solutions—have been suggested in the literature (e.g., Michod 1983; Szathmáry and Demeter 1987; Károlyi et al. 2000; Hogeweg and Takeuchi 2003; Lehman 2003; Scheuring et al. 2003; Altmeyer et al. 2004; Santos et al. 2004; Takeuchi et al. 2005; Kun et al. 2005; and the references therein). The result that is especially relevant here is the consideration of a spatially extended system: in a spatial system, local interactions and/or spatial pattern formation can greatly circumvent the exploitation by parasites (Boerlijst and Hogeweg 1991a,b; McCaskill et al. 2001; Szabó et al. 2002; Hogeweg and Takeuchi 2003). This point illustrates that the consideration of a spatially extended system is crucial in prebiotic evolution. In this context, Füchslin et al. (2004) recently underlined the importance of the formation of reaction complexes between replicators—an often-neglected, but natural, process in RNA-like replicators—from a chemical point of view. They found that complex formation shifts the range of diffusion intensity for which a replicator system is viable to higher values in the presence of moderate parasites that are mutated from catalysts, and thereby it was argued that complex formation enhances the stability of a spatial replicator system for greater diffusion intensity. The current study aims to extend this research.

With respect to the problem of parasites, the crucial aspect of complex formation is its effect on the resistance of catalysts against parasites. We focus on this point and ask what effect complex formation has on the stability of replicator systems under strong exploitation by parasites. We firstly investigate a well-mixed system and then extend the study to a spatial system. It might seem odd to study a well-mixed system, since the consideration of a spatial system is crucial in prebiotic evolution. Nevertheless, we study a well-mixed system to simplify the elucidation of one of the principles involved in the general dynamics of replicators with complex formation. We then examine the (more complex) effect of complex formation on a spatial system, taking local interactions and spatial pattern formation into consideration.

In the latter part of this study, we shift our focus to the effect of deleterious mutations, which has not been paid a great deal of attention in this context. We report that deleterious mutations can alleviate the problem of parasites.

Simple Trans-Acting Replicators

This section summarizes some well-known results of the dynamics of a replicator system without complex formation under the mean-field assumption (Joyce 1983, footnote; McCaskill et al. 2001).

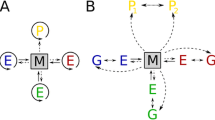
The model is formulated as follows. The simplest reaction scheme of trans-acting replicators is

$$ {\eqalign{ & {\rm{2X}}\dynrightarrow{{k_{x} }}{} {\rm{3X,}} \cr & {\rm{X}}\,{\rm{ + }}\,{\rm{Y}}\dynrightarrow{{k_{y} }}{} {\rm{X}}\,{\rm{ + }}\,{\rm{2Y,}} \cr} } $$

(1)

where X is the catalyst, and Y is the parasite, and k _x and k _y are the reaction rate constants. For simplicity, the substrate for replication (active monomer) is not explicitly designated. Furthermore, it is assumed that the system contains only one type of catalyst and one type of parasite. A simple ordinary differential equation (ODE) model of the population dynamics with the above scheme is

$$ \eqalign{ & \dot{x} = \,k_{x} x^{2} \theta \, - \,dx, \cr & \dot{y}\, = \,k_{y} xy\theta \, - \,dy,} $$

(2)

where x and y are the concentration of X and that of Y respectively ($\ifmmode\expandafter\dot\else\expandafter\.\fi{x}$ and $\ifmmode\expandafter\dot\else\expandafter\.\fi{y}$ are the time derivatives); θ = 1 − (x + y)/Θ, which phenomenologically represents limited multiplication (e.g. due to the finite supply of substrates); Θ is a parameter representing the capacity of the system (Θ > 0); and d is the decay rate, which, for simplicity, is assumed to be the same for X and Y. Note that Eq. (2) is valid only for x, y ≥ 0, and 0 ≤ θ ≤ 1. This completes the formulation of the model.

It can be shown through a stability analysis that Eq. (2) has an asymptotically stable equilibrium in which the catalyst survives—i.e., $\ifmmode\expandafter\bar\else\expandafter\=\fi{x}$ > 0 where the bar denotes the equilibrium value—if and only if k _x Θ > 4d and k _x > k _y . If these two conditions are not satisfied, the only stable equilibrium is $(\ifmmode\expandafter\bar\else\expandafter\=\fi{x},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{y})$ = (0, 0), i.e., the replicators die out. This equilibrium is present and stable for all relevant parameter values because of the Allee effect (Allee 1931). The first condition for the survival of the catalyst, k _x Θ > 4d, means that the replication activity of the catalyst, k _x , and the capacity of a system, Θ, must be high enough to compensate for the decay, d. The second condition, k _x > k _y , means that the catalyst must be a better template for replication than the parasite. This condition can be understood as follows: from Eq. (2), the replication rate per unit amount of catalysts and that of parasites are k _x x and k _y x, respectively, so if k _x < k _y (and also y > 0 and k _x Θ > 4d), the parasite outgrows the catalyst indefinitely. This results in a decrease of the total concentration to zero, because the parasite does not replicate the other molecules. In consequence, if k _y > k _x , the system collapses. If, however, k _x > k _y , then the catalyst can outgrow the parasite indefinitely; the parasite goes extinct. If k _x = k _y , coexistence between the catalyst and the parasite is possible; however, coexistence is a pathological case, for the exact equivalence between the two rate constants is unrealistic.

It is natural to conceive that a parasite can be a better template than the catalyst (Maynard Smith 1979; Bresch et al. 1980). Thus, the parasite poses a problem in prebiotic evolution: it impedes the origin and persistence of a cooperative replicator system (but see Hanczyc and Dorit 1998, for an interesting discussion). However, it is well known that the problem of parasites is alleviated in a spatial system, where local interaction and/or spatial pattern formation can enable catalysts to persist even if parasites are better templates than the catalysts (Boerlijst and Hogeweg 1991a,b; McCaskill et al. 2001; Szabó et al. 2002; Hogeweg and Takeuchi 2003). As is clear from this, the consideration of a spatial system is crucial in prebiotic evolution, and in fact Füchslin et al. (2004) underlined the importance of the effect of complex formation in a spatial system. Nonetheless, we next study the effect complex formation in a well-mixed system to make a clearer elucidation of a principle involved in the replicator dynamics.

Replicators with Complex Formation in a Well-Mixed System

Model

We consider the following reaction scheme for replicators with complex formation (Stadler et al. 2000; Füchslin et al. 2004):

$$ \eqalign{ 2{\rm X} {\mathop{{\rightleftharpoons}}\limits^{a_{x}}_{b_{x}}} &C_{xx} {\mathop\rightarrow\limits^{k_x}} 3{\rm X}, \cr {\rm X + Y} {\mathop{{\rightleftharpoons}}\limits^{a_{y}}_{b_{y}}} &C_{xy} {\mathop\rightarrow\limits^{k_y}} {\rm X+2Y},}$$

(3)

where C _xx and C _xy are the complexes formed by an X-X pair and an X-Y pair, respectively; and a _i , b _i , and k _i (i = x, y) are reaction rate constants. A simple ODE model to describe the population dynamics with this scheme is

$$ \eqalign{ \dot{x}\, &= \, - 2a_{x} x^{2} \, + \,(2b_{x}\, + \,3k_{x} \theta )c_{{xx}} \, - \,a_{y} xy\, + \,(b_{y} \, + \,k_{y} \theta )c_{{xy}} \, - \,dx, \cr \dot {y}\, &= \, - a_{y} xy\, + \,(b_{y} \, + \,2k_{y} \theta )c_{{xy}} \, - \,dy, \cr \dot {c}_{{xx}} \, &= \,a_{x} x^{2} \, - \,(b_{x} \, + \,k_{x} \theta )c_{{xx}} \, - \,dc_{{xx}} , \cr \dot {c}_{{xy}} \, &= \,a_{y} xy\, - \,(b_{y} \, + \,k_{y} \theta )c_{{xy}} \, - \,dc_{{xy}} .} $$

(4)

To reduce the number of parameters, we assume the following: a _x = 1 − exp(G) and b _x = 1 − a _x ; a _y = 1 − exp(βG), and b _y = 1 − a _y , where G ≤ 0 and β ≥ 0. The parameter G represents a sort of binding energy between X and X. The parameter β represents the binding energy between X and Y relative to that between X and X; thus, if β > 1, then Y is recognized as a template by X better than X is. This assumption is motivated by the fact that the affinity constant of the reaction ${\rm{2X}}{{\rightleftharpoons}}{\rm{C}}_{{xx}}$ is calculated as an exponential function of the binding energy, as K _x = a _x /b _x = exp(−G) − 1 [for ${\rm{X}}\,{\rm{ + }}\,{\rm{Y}}{{\rightleftharpoons}}{\rm{C}}_{{xy}},$ as K _y = exp(−βG) − 1]. Besides the above simplification, we make the important assumption that β and G are independent of each other (we come back to this point later). Moreover, it is assumed that κ _x = κ _y for simplicity, which means that the rate of polymerization is the same for X and Y, once a catalyst has recognized a template (this does not affect our results).

Bifurcation Analysis

In Eq. (4), if β > 1, then the stable equilibrium is only $(\ifmmode\expandafter\bar\else\expandafter\=\fi{x},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{y},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{c}_{{xx}} ,\,\ifmmode\expandafter\bar\else\expandafter\=\fi{c}_{{xy}} )$ = (0, 0, 0, 0) (see below; cf. Füchslin et al. 2004, Appendix A). This result parallels the result from Eq. (2) that if k _y > k _x , the stable equilibrium is only $(\ifmmode\expandafter\bar\else\expandafter\=\fi{x},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{y})$ = (0, 0). Also, as in Eq. (2), this equilibrium is always present and stable due to the Allee effect, and it can be reached if the initial value of x is too small or that of y is too large (this equilibrium is not depicted in Fig. 1).

Fig. 1

The stable and unstable equilibria of Eq. (4) are plotted against β (bifurcation diagram). The coordinate of the left graph is the equilibrium value of x ($\ifmmode\expandafter\bar\else\expandafter\=\fi{x}$); that of the right graph is the equilibrium value of y ($\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$). The solid lines represent the stable equilibria; the broken lines represent the unstable equilibria; and the dotted lines represent the maximum/minimum of stable oscillatory solutions (limit cycle). The lines in the two graphs correspond to each other. A thinned solid line above (resp. below) the point T in the left (resp. right) graph is not relevant because $\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$ < 0. The points F (fold bifurcation), T (trans-critical bifurcation), H (Hopf bifurcation) and h (homoclinic bifurcation is suspected) designate critical points at which the system’s behavior qualitatively changes. An apparent crossing of the lines in the right graph is due to the projection in two-dimensions. The parameters are as follows: G = −5, Θ = 1, d = 0.02, κ _x = κ _y = 1. Note that some equilibria are not depicted in the graphs (see text). One can see from this figure that X and Y can coexist for β _F < β < β _h, but the system inevitably collapses for β > β _h (β _h < 1)

In contrast, if β ≤ 1, Eq. (4) exhibits various behavior different from that of Eq. (2) depending on the value of β. For various values of β, we numerically calculated the stable/unstable equilibria of Eq. (4), as shown in Fig. 1 (see the Methods section for the details of calculation). As seen from Fig. 1, the behavior of the system qualitatively changes when β crosses some critical values (bifurcation points) designated by F, T, H, and h. Let us denote these critical values by β _F, β _T, β _H, and β _h, respectively. In the following, we explain the behavior of Eq. (4) for each parameter region divided by these critical β values, from a small to large value (β _F < β _T < β _H < β _h).

For β < β _F, the catalyst always out-competes the parasite. This result parallels the result from Eq. (2) for k _y < k _x . If, however, β becomes greater than β _F, a stable equilibrium in which the catalyst and the parasite coexists (i.e., $\ifmmode\expandafter\bar\else\expandafter\=\fi{x},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$ > 0) emerges (via fold bifurcation), as shown by the F-H line in Fig. 1. This means that the coexistence is possible although the parasite is a worse template than the catalyst in this region of β (note that β _F < 1). However, for a system to reach this equilibrium, the initial value of y must be sufficiently large. This can be seen by noticing that the equilibrium in which the catalyst out-competes the parasite (i.e., $\ifmmode\expandafter\bar\else\expandafter\=\fi{x}$ > 0 and $\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$ = 0) is also stable in the same region of β (the solid horizontal line left of T in Fig. 1). If β becomes greater than β _T, the latter equilibrium, however, becomes unstable (via transcritical bifurcation). Thus, the parasite can now always invade the catalyst as long as initially y > 0. In other words, the equilibrium in which the catalyst and the parasite coexist can be reached even if the initial value of y is very small.

The above results are in sharp contrast with those from Eq. (2): if complex formation is taken into account, the catalyst and the parasite can coexist even in a well-mixed system. The coexistence is possible because of the advantage of the parasite, which originates from the fact that: (i) complexes are formed, and that (ii) the parasite does not replicate other molecules. The details are explained in the following.

If the total concentration of the catalyst and parasite is sufficiently high, the parasite can outgrow the catalyst: firstly, the multiplication rate of the catalyst per unit amount of molecules is proportional to c _xx /x _t (the subscript t denotes the total concentration), and that of the parasite is proportional to c _xy /y _t. Secondly, to make one molecule of C _xx , two molecules of the catalyst are required, whereas to make one molecule of C _xy , one molecule of the catalyst and one molecule of the parasite are required. This means that to form an equal amount of the two complexes, the amount of catalysts required is three times more than that of parasites. Therefore, the parasite has an advantage over the catalyst; hence, the parasite can outgrow the catalyst.

If the total concentration of the catalyst and parasite is sufficiently low, the catalyst can outgrow the parasite. Firstly, if x _t and y _t are sufficiently small, it holds that x _t ≈ x and y _t ≈ y because x $\gg$ c _xx , c _xy and y $\gg$ c _xy . Secondly, under the quasi-steady state assumption (e.g., see Segel 1984), the values of c _xx and of c _xy are calculated as c _xx = a _x x ² _t /(b _x + κθ + d) and c _xy = a _x x _t y _t/(b _y + κθ + d) respectively, where κ = κ _x = κ _y . Then, c _xx /x _t can be greater than c _xy /y _t if a _x /b _x > a _y /b _y (i.e., β < 1). Thus, the catalyst can outgrow the parasite.

In summary, if the concentrations of the replicators are sufficiently high, the parasite outgrows the catalyst, which results in a decrease in the total concentration. If the concentrations are low, the system behaves as if there is no complex, and thus the catalyst will increase its concentration because β < 1. In essence, the coexistence is possible because of the frequency-dependent selection between the catalyst and the parasite.

For a yet-greater value of β, such that β > β _H, a stable oscillatory solution (limit cycle) appears (via Hopf bifurcation) accompanied by the destabilization of the equilibrium in which the catalyst and the parasite stationary coexist, as shown by H in Fig. 1. As β increases, the amplitude of the oscillation increases till its lower bound of y reaches zero at β = β _h, and then the oscillatory solution disappears. After the disappearance of the oscillatory solution (β > β _h), the stable equilibrium is only $(\ifmmode\expandafter\bar\else\expandafter\=\fi{x},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{y},\,\ifmmode\expandafter\bar\else\expandafter\=\fi{c}_{{xx}} ,\,\ifmmode\expandafter\bar\else\expandafter\=\fi{c}_{{xy}} )$ = (0, 0, 0, 0). Thus, β _h is the maximal severity of the parasite the catalyst can tolerate (denoted by β _max hereafter). The fact that β _max is smaller than one means that the parasite kills the catalyst by exploitation, even if the parasite is a worse template than the catalyst. This makes a sharp contrast with the result from Eq. (2).

How Does Complex Formation Affect a Replicator System?

We give here a more detailed account of the effect of complex formation on the replicator system. For simplicity, let us assume that C _xx and C _xy do not decay. Under the quasi-steady state assumption on $\ifmmode\expandafter\dot\else\expandafter\.\fi{c}_{{xx}}$ and $\ifmmode\expandafter\dot\else\expandafter\.\fi{c}_{{xy}},$ c _xx and c _xy are determined from the equations

$$ {\eqalign{ & 0\, = \,a_{x} \,(x_{{\rm{t}}} \, - \,2c_{{xx}} \, - \,c_{{xy}} )^{2} \, - \,(b_{x} \, + \,\kappa _{x} \theta )c_{{xx}} , \cr & 0\, = \,a_{y} \,(x_{{\rm{t}}} \, - \,2c_{{xx}} \, - \,c_{{xy}} )(y_{{{\rm{t}}\,}} \, - \,c_{{xy}} )\, - \,(b_{y} \, + \,\kappa _{y} \theta )c_{{xy}} , \cr} } $$

(5)

where x _t = x + 2c _xx + c _xy ; and y _t = y + c _xy .

For simplicity, let us assume that b _i ${ \gg }$ κ _i (i = x or y) for a moment—we will come back to this point later. On one hand, if b _i $\gg$ a _i (i.e., K _i $\ll$ 1), the solutions of Eq. (5) can be approximated by c _xx = K _x x ² _t and c _xy = K _y x _t y _t. Since the growth of x _t and y _t is calculated as κc _xx θ and κc _xy θ, respectively, one obtains the equations

$$ \eqalign{ & \dot {x}_{{\rm{t}}} \, = \,\kappa _{x} K_{x} x_{{\rm{t}}} ^{2} \theta \, - \,dx_{{\rm{t}}} , \cr & \dot {y}_{{\rm{t}}} \, = \,\kappa _{y} K_{y} x_{{\rm{t}}} y_{{\rm{t}}} \theta \, - \,dy_{{\rm{t}}} , } $$

which are, in fact, identical to Eq. (2); i.e., the current system can be approximated by the system without complex formation if b _i $\gg$ a _i . On the other hand, if b _i $\ll$ a _i (i.e., K _i $\gg$ 1), one can similarly obtain the equations

$$ {\eqalign{ & \dot{x}_{{\rm{t}}} \, = \,{1 \over 2}\kappa _{x} {{x_{{\rm{t}}} } \over {x_{{\rm{t}}} \, + \,y_{{\rm{t}}} }}x_{{\rm{t}}} \theta \, - \,dx_{{\rm{t}}} , \cr & \dot{y}_{{\rm{t}}} \, = \,\kappa_{y} {{x_{{\rm{t}}} } \over {x_{{\rm{t}}} \, + \,y_{{\rm{t}}} }}y_{{\rm{t}}} \theta \, - \,dy_{{\rm{t}}} . } } $$

In this system, Y always out-competes X unless κ _x > 2κ _y . This factor of 2 originates from the advantage of the parasite discussed before. It is now easy to see that if K _x $\ll$ 1 (and κ _x = κ _y ), then β _max ≈ 1 (the former equations), but if K _x $\gg$ 1, then β _max ≈ 0 (the latter equations). When K _x increases from 0 to infinity, β _max decreases from 1 to 0 (but note that K _x cannot be too close to zero, because the system collapses if the growth is too slow to compensate the decay). In other words, as the equilibrium of $2{\rm X} \rightleftharpoons {\rm{C}}_{xx}$ is shifted more to the right side, the catalyst will be killed more easily by the parasite.

The above argument is confirmed by numerical calculation (without assuming b _i $\gg$ κ). In Fig. 2, three measures of the maximal tolerable strength of parasites are plotted as a function of G: the maximal relative binding energy β _max; the maximal absolute binding energy β _max G; the maximal relative association constant K _y /K _x , where β = β _max. As shown in Fig. 2(i), decreasing G decreases β _max. Furthermore, as shown in Fig. 2(ii), decreasing G decreases log(K _y /K _x ), without saturation. In addition, we note that the above result holds when other parameters (Θ, d, κ _x , and κ _y ) are different or when κ _x ≠ κ _y , provided that X is viable when y = 0 (data not shown).

Fig. 2

(i) β _T and β _max (i.e., β _h) as a function of G (the continuation of bifurcation points). The solid line represents β _max; the broken line represents β _T. The parameters are the same as in Fig. 1 except for G, which is the abscissa. In the region designated by A, Y cannot invade X (unless the initial value of y is sufficiently large). In region B, Y can invade X if initially y > 0. In region C, the system collapses ($\ifmmode\expandafter\bar\else\expandafter\=\fi{x}\, = \,\ifmmode\expandafter\bar\else\expandafter\=\fi{y}\,\, = 0$). Numerical calculation suggests that the two lines collide at a large value of G (≈ −0.133), above which X is not viable even in the absence of Y. The inset shows β _T G and β _max G as a function of G. The notations are the same as before. One can see from these graphs that as G decreases (i.e., as the binding affinity becomes stronger), the catalyst becomes more vulnerable to the parasite. (ii) The ratio of affinity constants, K _y /K _x , as a function of G when β = β _max (solid line) or β = β _T (broken line). K _y /K _x = [exp(βG) − 1]/[exp(G) − 1]. The parameters are the same as in (i). One can see from this graph that decreasing G steadily decreases log(K _y /K _x ).

The above results mean that under the mean-field assumption (i.e., in a well-mixed system), the replicator system becomes increasingly unstable as the binding affinity between the catalysts increases. This point can be further elaborated as follows. It is natural to conceive that trans-acting molecular replicators have (or had) some kind of motifs—whether a structure or a sequence—that function either to recognize other molecules to replicate (recognizing motif) or to be recognized by other molecules to be replicated (tag motif²). Some mutations can destroy the recognizing motif while preserving the tag motif, giving rise to a parasite of which tag motif has an activity comparable to that of the original catalyst (see also Altmeyer et al. 2004). Then, the binding affinity between the catalyst and a so created parasite is likely to be positively correlated to the binding affinity between the catalysts. Therefore, from the result that β _max decreases as G decreases, it can be concluded that the greater becomes the binding affinity between the catalysts, the more vulnerable the catalyst becomes to the parasite.

Finally, if κ _i $\gg$ b _i , from Eq. (5) one can obtain the approximation as follows:

$$ \eqalign{ & c_{{xx}} \, = \,{{a_{x} x_{{\rm{t}}} ^{{\rm{2}}} } \over \theta }, \cr & c_{{xy}} \, = \,{{a_{y} x_{{\rm{t}}} y_{{\rm{t}}} } \over \theta }. \cr} $$

Although this approximation cannot be used to obtain the population dynamics of the replicators³, it tells that the advantage of Y disappears in the limit of κ → ∞ irrespective of the value of K _x . This can also be numerically confirmed as shown in Fig. 3.

Fig. 3

β _max from Eq. (4) as a function of κ. The parameters are the same as in Fig. 1 except for G, which is designated in the graph. One can see from this figure that β _max approaches to 1 when κ→∞. This means that, in the limit of κ→∞, β _max approaches to that of the system without complex formation; i.e., the catalyst can tolerate the parasite of which template activity is less than or equal to that of the catalyst

Dynamics in a Spatially Extended System

In a spatial system, pattern formation of populations plays an important role in the survival of catalysts under strong exploitation by parasites (Boerlijst and Hogeweg 1991a). Thus, we next ask whether the advantage of parasites due to complex formation still plays any significant role in a spatial system with respect to the survival of catalysts.

Cellular Automata Model

We have constructed a stochastic cellular automata (CA) model for a replicator system with complex formation. The model is a spatially extended, individual-based, Monte Carlo simulation model. It consists of a two-dimensional square grid and replicators (X or Y) located on the grid. One square in the grid, called a ‘cell’ hereafter, holds at most one replicator. The complex C _xx is represented by two molecules of X’ located in two contiguous cells, where a prime designates a molecule forming a complex (respectively, C _xy is represented by one of X’ and one of Y’). The size of the grid is 512 × 512 cells, and the boundary of the grid is toroidal.

The state of the model system is fully specified by the type and location of all replicators. The temporal dynamics of the model are run by the consecutive application of an algorithm representing the five types of reaction: complex formation, complex dissociation, replication, decay as in Reaction (3); and diffusion.

The algorithm runs as follows:

• 1. Randomly choose one cell. According to the content of the cell, a subset of the reactions can happen.

• 2. Choose a type of reaction according to certain probabilities, which are calculated from the rate constants of the possible reactions. These probabilities are referred to as the probabilities of reactions (see below).

• 3. If the chosen reaction is first order (i.e. complex dissociation or decay), it happens. If it is second-order, then randomly choose one of the eight cells neighboring to the cell chosen first (Moore neighborhood). If the cell chosen second contains a molecule of the right type for the chosen reaction to happen⁴ (the order of choices does not matter), then the reaction happens.

The diffusion is implemented as a simple random walk, and it is a second-order reaction in the model, where one of the two chosen cells must be empty. When a complex molecule diffuses, the two replicators composing the complex tag along with each other so that they do not dissociate.

The parameters specifying the rate constants are denoted by a _i , b _i (i = x or y) and κ as in Reaction (3) and by D for the diffusion intensity. It is assumed that a _x + b _x = c, where c is some constant (in contrast to the ODE model, c is not necessarily 1). Furthermore, a _x is calculated as c[1 − exp(G)], where G has the same meaning as in the ODE model (similarly, a _y = c[1 − exp(βG)]). The probabilities of reactions are calculated from the rate constants such that in the limit of D → ∞ the CA model behaves, on average, identical to Eq. (4), with the same rate constants and Θ scaled to one.⁵ The details of the algorithm is described in the Methods section.

For comparison’s sake, another CA model was constructed for a replicator system without complex formation as in Reaction (1). The difference from the previous model lies in the fact that replication reaction is third order here (i.e., the third cell is chosen from the seven cells that are the neighbors of the cell chosen second, excluding the cell chosen first). In other words, replication does not involve complexes.

To compare the above two models, it is important to note the following. In a well-mixed system, we observed that whether the catalyst survives in the system without complex formation depends only on the ratio between k _x and k _y (given k _x Θ > 4d), whereas in a spatial system, as we shall see later, the absolute value of the rate constants also play an important role for the survival of the catalyst. Then, to compare the two systems (with/without complex formation), one must somehow normalize k _i (i.e., the replication rate constant of the system without complex formation) with respect to G, a _x + b _x , κ, and β. As a means of normalization, we employ k _i = κa _i /(b _i +κ) here, which would be the overall rate of replication without competition between replicators. In addition, we have also examined two other normalization methods: k _i = a _i and k _i = a _i κ/b _i : the results were consistent with those presented in this study (not shown).

Effect of Complex Formation on β_max as a Function of Diffusion Intensity D

The results of Füchslin et al. (2004) showed that complex formation shifts, to higher values, the region of diffusion intensity D for which R _C > 0, where R _C is the maximum tolerable mutation rate from catalysts to moderately strong parasites.⁶ In other words, complex formation stabilizes the system for greater diffusion intensity (while destabilizing it for smaller diffusion intensity). From this result, one may expect that a similar result should hold with respect to β _max. However, from the results of the ODE model we can also expect that for a very large value of D, complex formation should destabilize the system by decreasing β _max. In this section, we examine how complex formation affects the stability of the system as a function of D, taking β _max as a measure.

We measured β _max as a function of D for the system with and without complex formation (see the Methods section for details). In so doing, we introduced mutation to the parasite, i.e., the reaction ${{\rm{C}}_{{xx}} {\rm{ }}\dynrightarrow{{{R\kappa }}}{} {\rm{ 2X + Y}}},$ to prevent the extinction of the parasite due to the finiteness of the population. The mutation rate R was set to a very small value (R = 10⁻⁴).⁷ The results of the measurements are shown in Fig. 4, where β _max is plotted as a function of D for various parameter sets. The results show that whether complex formation increases or decreases β _max depends not only on D, but also on the other parameters such as a _x + b _x and d, except for very large values of D, for which complex formation is always a destabilizing factor. In particular, complex formation does not necessarily increase β _max for greater values of D (= 0.1, 1) in contrast to the implication from the results of Füchslin et al. (2004). Thus, we conclude that the effect of complex formation on β _max depends on the parameters. Before discussing this result, let us first look at particular simulation runs in more detail.

Fig. 4

β _max as a function of D in the spatial systems. The solid lines with circles are for the system with complex formation. The dashed lines with triangles are for the system without complex formation [k _i = a _i κ/(b _i + κ)]. The parameters are as follows: κ = 1; G = −0.5; R = 10^–4 (the rest are indicated in the graphs). A dotted line is placed at β _max = 1 for convenience. One can see from this figure that β _max depends heavily on D, and the effect of complex formation on β _max depends on the other parameters

Figure 5 shows snapshots of the simulations of the model with complex formation for various values of D. From this, one can see that spatial patterns form in the system, in particular, traveling wave patterns. The front of a wave is composed of catalysts and its back is composed of parasites. In the wave front, the catalysts propagate into an empty area, while in the wave back the parasites outgrow the catalysts and leave an empty area behind by local extinction (this will be referred to as parasite propagation). In this way, a wave travels and rotates. It turns out that β _max depends heavily on the possibility and stability of wave patterns, which makes it necessary to consider the dynamics of spatial patterns in order to understand the effect of complex formation in more detail. Thus, we next take a closer look at the wave patterns.

Fig. 5

Snapshots of the simulations of the system with complex formation for various values of D. β is set to β _max for each simulation. The parameters are as follows: κ = 1; G = –0.5; a _i + b _i = 1; d = 0.015; and R = 10⁻⁴ (the values of β and D are indicated above each snapshot). The color coding is as follows: the catalyst is white; the parasite is black; empty cells are gray. The snapshots depict the whole CA field

Dynamics of Wave Patterns

The wave patterns observed in the simulations are dynamic:

• (i) The size of a wave can grow due to an asymmetry between the propagation speed of the wave front and that of the wave back. For this to happen, a wave pattern must travel a sufficiently long distance before colliding to form other patterns.

• (ii) A wave can be annihilated when the catalysts are completely outgrown by the parasites. This happens more often if the wave is smaller, or the parasite is stronger (i.e., β is greater), or the propagation of the catalyst is slower.

• (iii) A wave can be split into two (or more) waves when the catalysts are partially outgrown by the parasites. This split is promoted by the rotation of the wave and by the mutation of the catalyst to the parasite (i.e., R > 0).⁸

Moreover, upon the collision of multiple waves, the interactions between them give rise to various outcomes:

• (i) The parasites can completely enclose the catalysts, which can results in wave annihilation.

• (ii) Waves can merge into one.

• (iii) Waves can be split. This happens often when two colliding waves greatly differ in their size (while annihilated, the smaller wave splits the larger one into two).

In order to understand the behavior of the current system, it turns out to be crucial to consider the population dynamics of wave patterns (see also Savill et al. 1997). Let us explain how the birth and death of waves is manifested in our model system:

• (i) The death of a wave can happen when the catalysts are completely enclosed by parasites. This enclosing occurs when the parasites at the back of the wave catch up with the catalyst at the wavefront or when multiple waves collide.

• (ii) The birth of a wave happens mainly via the splitting of waves, but it can also happen via the escape of the catalyst, as explained in Fig. 6.

The relative frequency of the birth and death of waves determines the number of individual waves in the system, and the size thereof. This greatly affects the stability of the system and thus β _max. For instance, if the birth of waves happens more frequently, the number of waves becomes greater, and their spatial size becomes smaller. In this case, the annihilation of a single wave has a smaller effect on the whole system, and thus the system becomes more stable, and hence β _max will be greater.

Fig. 6

Consecutive snapshots of the simulation of the system with complex formation. Time goes from left to right. The parameters are as follows: κ = 1, G = −0.5, a _i + b _i = 1, d = 0.015, D = 0.01, and R = 10⁻⁴. The color coding is the same as in Fig. 5. The snapshots depict only a part of the whole CA field (75 × 75 cells) at the same position. One can see from this figure how the birth of a wave can happen via the escape of catalysts: a small number of catalysts are left behind a propagating layer of parasites, and then the catalysts left behind can develop a new wave. The Allee effect plays an important role for this to happen

The stability of the system depends heavily on the possibility and stability of wave patterns, which depend on the two properties of the system: (1) the relationship between the size of the patterns (or D as explained soon) and the size of the grid; and (2) the relationship between the speed of catalyst propagation and the speed of parasite propagation—the former corresponds to the propagation of wave fronts, and the latter to the contraction of wave backs. With respect to the first point, Fig. 4 shows that increasing D decreases β _max (this is a very general result as it holds for all the cases examined). To understand this, one must consider the relationship between the size of the patterns and the size of the grid. As shown in Fig. 5, increasing D increases the spatial size of the wave patterns relative to the grid, and as a result, the system becomes less stable. Therefore, β _max decreases as D increases. The second point will be developed further in the following section.

β_max and the Dynamics of Spatial Patterns

In this section, we study β _max as a function of various parameters (d, κ, and G) to understand the dynamics of the spatial system in more detail. Although the combinations of the parameter sets and the systems (with or without complex formation) investigated here are by no means exhaustive, it will become clear that the method of analysis developed here is generally applicable to the current replicator system.

β_max as a Function of Decay Rate d

β _max was measured as a function of d. As shown in Fig. 7, the results show that β _max is a non-monotonic function of d. Fig. 8 depicts snapshots of the simulations of the system without complex formation for various values of d. The most noticeable observation from these is that wave patterns do not form for d = 0.01, for which β _max is the lowest. Furthermore, if wave patterns form (d ≥ 0.015), then increasing d decreases their width. These observations can be understood as follows. Firstly, increasing d slows down the propagation of the catalyst as easily expected. Secondly, increasing d speeds up the propagation of the parasite, because it increases the turn-over rate of populations. It is worth noting that the speed of parasite propagation is, in fact, mostly determined by d as long as β is sufficiently large. This is because the parasite does not directly kill the catalyst in the current system.⁹ If the width of waves decreases, the waves become destabilized. Consequently, increasing d decreases β _max for d for which wave patterns form. However, if d is too small (d ≤ 0.01), the speed of parasite propagation is so much slower than that of catalyst propagation that the wave patterns do not form anymore (Fig. 8). In other words, because of too large an asymmetry between the two propagation speeds, the wave pattern becomes too large to fit to the grid. In this case, it is easy for parasites to surround catalysts as it can be seen from Fig. 8. Hence, if d becomes too small to form wave patterns, then β _max decreases. In fact, this decrease of β _max is quite abrupt, and this shows the importance of wave pattern formation to the stability of the system.

Fig. 7

β _max as a function of d in the spatial systems. The solid line with circles is for the system with complex formation. The dashed line with triangles is for the system without complex formation. The parameters are as follows: κ = 1; G = −0.5, a _i + b _i = 2.5, d = 0.015, D = 0.01, and R = 10⁻⁴. One can see from this figure that there is an optimal d maximizing β _max

Fig. 8

Snapshots of simulations of the system without complex formation for various values of d. D = 0.01; the other parameters are the same as in Fig. 7 (the values of d and β are indicated above each snapshot). The snapshots depict the whole grid

β_max as a Function of Replication Rate κ

β _max was measured as a function of κ for the system with complex formation as shown in Fig. 9. Interestingly, the result shows that increasing κ can decrease β _max if D is sufficiently small (≤1), which is the opposite of the results from the ODE model (cf. Fig. 3). To explain this result, snapshots of the simulations are shown in Fig. 10 for various values of κ. As seen from this, the wave patterns form only for a moderate range of κ. If κ is too small, the propagation speed of the catalyst is much too slow compared to that of the parasite; thus, no sooner are waves formed than they disappear. If κ is too great, the propagation speed of the catalyst is too much faster than that of the parasite; thus, waves are too large to fit to the grid. Since wave patterns do not form for extreme values of κ, β _max becomes low for such cases.

Fig. 9

β _max as a function of κ for the spatial system with complex formation. The parameters are as follows: G = −0.5, a _i +b _i = 1, and d = 0.015, and R = 10⁻⁴ (the value of D is indicated in the graph)

Fig. 10

Snapshots of the simulations in Fig. 9 for various values of κ. D = 0.01; the other parameters are the same as in Fig. 9 (the values of κ and β are indicated above each snapshot). The color coding is the same as in Fig. 5. The snapshots depict the whole grid.

The above situation is, however, reversed if the diffusion intensity is sufficiently great: For a sufficiently large D, increasing κ increases β _max (Fig. 9, D = 1 and 10). For D = 10, the result is easily understood: spatial patterns do not form for D = 10 and κ = 0.3, as shown in Fig. 11. Then, the result must be the same as that of the ODE model. For D = 1, however, wave patterns do form as shown in Fig. 11. However, the size of the waves is so large and the distance between them is so small that the asymmetry in the two propagation speeds does not have a significant effect. What is more, increasing κ apparently increases the chance of the catalyst escape (Fig. 6) because of a reduction in the Allee effect. Because of these two reasons, increasing κ increases β _max for D = 1.

Fig. 11

Snapshots of the simulations of the system with complex formation for various values of κ for higher values of D. The parameters are the same as in Fig. 10 (the values of κ, D, and β are indicated above each snapshot). The color coding is the same as in Fig. 5. The snapshots depict the whole grid

β_max as a Function of Binding Energy G

β _max is measured as a function of G as shown in Fig. 12. The result shows that as the affinity between the catalysts increases (i.e., as G decreases), β _max decreases for a very large value of D (= 10), whereas β _max increases for sufficiently small values of D (≤ 1). Note that the latter result is opposite to the result from the ODE model (cf. Fig. 2). These results are explained as follows. For a great value of D (= 10), pattern formation does not play a significant role, and hence β _max behaves in the same way as in the well-mixed system. For D = 1, however, spatial patterns do form, but the patterns are so large that the asymmetry in the two propagation speeds, which could be enhanced by decreasing G, does not have a significant effect. Moreover, decreasing G increases the chance of catalyst escape by reducing the Allee effect (see the previous section). In consequence, β _max increases as G decreases. Furthermore, the result showed that, for D = 0.01, decreasing G still increases β _max, although patterns forming in the system are clearly traveling waves (for G = −1, β _max becomes greater than 9.99; data not shown in Fig. 12). This is because although decreasing G does increase the asymmetry in the two propagation speeds, its extent is much less than that of increasing κ. This can be understood by realizing that the effect of decreasing G quickly saturates as seen from the approximation

$$ {\kappa {\rm{c}}_{{xx}} \, \approx \,\kappa x^{2} _{{\rm{t}}} {\rm{/(4}}x_{{\rm{t}}} \,\, + \,{{b_{x} \, + \,\kappa \theta } \over {a_{x} }})}, $$

Fig. 12

β _max as a function of G for the spatial system with complex formation. The parameters are as follows: κ = 1, a _i + b _i = 1, and d = 0.015, R = 10⁻⁴ (the value of D is indicated in the graph). For D = 1 and G = −2.5, β _max is greater than 9.99. This means that β can take an arbitrary large value, because whether β is 9.99 or more does not have any significant difference in the CA model (for, a _x ≈ 1 and b _x ≈ 0, anyway)

where the quasi-steady state assumption and y _t = 0 is assumed. Thus, decreasing G does not increase the asymmetry to the extent that it can destroy the wave patterns. Moreover, decreasing G reduces the possible difference between the overall replication rate of the parasite and that of the catalyst (for a very small G, a _x ≈ 1, and b _x ≈ 0). In consequence, decreasing G increases β _max for D = 0.01.

Effect of Complex Formation on the Stability of the Spatial System

With the notion of pattern dynamics developed above, we can now analyze the effect of complex formation on the stability of the spatial replicator system under strong exploitation by parasites by considering how complex formation affects the speed of catalyst propagation and that of parasite propagation. In general:

• If the asymmetry between the two speeds plays a significant role in the system’s stability (i.e., the wave patterns travel a sufficiently long distance before colliding with the other patterns), and if complex formation decreases/increases the asymmetry, then complex formation will stabilize/destabilize the system.

• If the asymmetry does not play a significant role (i.e., wave patterns do not form, or they do not travel a long distance), and if complex formation decreases/increases the Allee effect by increasing/decreasing the overall rate of replication, then complex formation can stabilize/destabilize the system.

Moreover,

• With respect to the speed of catalyst propagation, it turns out that, under the current normalization method k _x = κa _x /(b _x + κ), if a _x + b _x > κ, then complex formation decreases the speed of catalyst propagation (i.e., the overall rate of replication), but if a _x + b _x < κ, then it increases the speed of catalyst propagation.

• With respect to the speed of parasite propagation, although complex formation can increase the speed (since it gives the parasite a replication advantage), it has much less effect than the decay rate d, as long as β is large enough to ensure local extinction. (But note that complex formation does decrease the value of β for which the parasite causes local extinction, which illustrates that complex formation does strengthen the parasite in a spatial system).

In summary, complex formation is one out of many other factors affecting the dynamics of spatial patterns, and its effect on the stability of the spatial replicator system is not as straightforward as in the well-mixed system.

Comparison with the previous study

Our result, that complex formation does not necessarily increase β _max for greater values of D, may seem contradictory to the results of Füchslin et al. (2004) who found that complex formation increases the maximal tolerable mutation rate from the catalyst to the parasite (R _C ) for greater values of D. To understand the gap between these two results, we investigated the model of Füchslin et al. (2004).

The model was implemented with a square grid of two different sizes (60 × 60 or 300 × 300 cells) with toroidal boundary. The value of R _C was measured with the parameters for which Füchslin et al. (2004) found that complex formation enables a system to have a greater R _C than the case otherwise.¹⁰ The results were as follows: if the size of the grid was 60 × 60 cells, complex formation increased R _C , as is consistent with the result of Füchslin et al. (2004), who used a cubic grid of 60 × 60 × 60 cells. However, if the size of the grid was increased to 300 × 300 cells, complex formation actually decreased R _C . This can be understood as follows. Firstly, the size of wave patterns forming in this system was typically about 50 × 50 cells or larger. Secondly, under the normalization of the rate constants employed by Füchslin et al. (2004), complex formation greatly decreases the overall replication rate, which decreases the concentration of replicators in the system. From these two points, one can see the following. On one hand, if the grid is too small to hold wave patterns, complex formation stabilizes the system because it decreases the concentration of replicators, which can weaken the exploitation by parasites under a limited diffusibility by making it difficult for parasites to gain access to catalysts. On the other hand, if the grid is large enough to hold a sufficiently large population of waves, complex formation destabilizes the system because it increases the asymmetry between the two propagation speeds by reducing the speed of catalyst propagation. In conclusion, if the population dynamics of wave patterns can be established, complex formation does not stabilize the replicator system for the parameters reported by Füchslin et al. (2004) with respect to R _C . (The same domain dependency also holds for the effect of complex formation on the maximal strength of parasites the system can tolerate).

Although we have not examined a three-dimensional system, it seems highly likely that the size of the grid Füchslin et al. (2004) used was indeed too small to hold a sufficiently large population of wave patterns. This can also explain why their simulation results agreed with their results for an infinite-dimensional system, where the formation of spatial patterns is, by definition, impossible. In contrast, the current study showed that the consideration of spatial pattern formation is important to understand the stability of a replicator system.

Alleviating Effect of Mutation

So far, we have investigated the effect of complex formation on the stability of replicator systems. We now shift our focus to the effect of mutation; in particular, the mutation that destroys both replication and template activity of replicators. The purpose of this section is to show that high rates of such mutation weaken the exploitation by the parasite, and therewith it can stabilize the replicator system to a certain extent. For shortness’ sake, this type of mutation is referred to as a deleterious mutation (it should be distinguished from the mutation converting a catalyst to a parasite mentioned earlier). It seems likely that deleterious mutations happen frequently in RNA-like replicators (see also Altmeyer et al. 2004). Thus, the alleviating effect of deleterious mutations should be a relevant factor in the replicator dynamics.

The reaction scheme considered here is

$$ \eqalign{ 2{\rm X} {\mathop{{\rightleftharpoons}}\limits^{a_{x}}_{b_{x}}} &C_{xx} {\mathop\rightarrow\limits^{k(1-M)}} 3{\rm X}, \cr {2\rm X} {\mathop{{\rightleftharpoons}}\limits^{a_{x}}_{b_{y}}} &C_{xx} {\mathop\rightarrow\limits^{kM}} {\rm 2X+Z}, \cr{\rm X+Y} {\mathop{{\rightleftharpoons}}\limits^{a_{y}}_{b_{y}}} &C_{xy} {\mathop\rightarrow\limits^{k(1-M)}} {\rm X+2Y}, \cr{\rm X+Y} {\mathop{{\rightleftharpoons}}\limits^{a_{y}}_{b_{y}}} &C_{xy} {\mathop\rightarrow\limits^{kM}} {\rm X+Y+Z}, \cr{\rm Z+X} {\mathop{{\rightleftharpoons}}\limits^{e_{x}}_{f_{x}}} &C_{zx}, \cr{\rm Z+Y} {\mathop{{\rightleftharpoons}}\limits^{e_{y}}_{f_{y}}} &C_{zy},} $$

where M represents the probability of deleterious mutation per replication [M must be distinguished from R defined in the model of Füchslin et al. (2004)]. Z denotes the molecule that arises through the deleterious mutations, which is referred to as a junk molecule for shortness’ sake. It is assumed that all molecules decay at a constant rate d (not designated above). In the following sections, we first investigate the effect of deleterious mutations in a well-mixed system, and then examine it in a spatial system.

Well-Mixed System with Deleterious Mutations

The ODE model was constructed by taking deleterious mutations into account. In this model, two parameters were newly introduced: G _z , the binding energy between X and Z; and M, the deleterious mutation rate (the details of the model are explained in the Methods section). β _max was numerically calculated as a function of M for various values of G _z and G as shown in Fig. 13 (see the Methods section for details of the calculation). As Fig. 13 shows, if the binding affinity between the junk molecule and the other molecules is sufficiently weak (i.e., G _z is sufficiently large), increasing M increases β _max for all values of G examined until M reaches a certain limit. This can be understood as follows: increasing M produces more Z and reduces the amount of X in the system, so that the system is effectively diluted. Thus, the complexes are formed less, and consequently the advantage of Y is reduced.

Fig. 13

β _max as a function of M for various values of G _z and G in the well-mixed system. From top to down, the thin solid lines are for G = −1.5; the broken lines are for G = −3; and the thick solid lines are for G = −5. Among the lines with the same G value, from top to down, the value of G _z is 0, 0.25G, 0.5G, 0.75G and G. For G = −1.5 (the thin solid lines), however, the lines for G _z = 0, 0.25G and 0.5G are almost on top of each other (but the same trend as the other plots holds such that the greater is G _z , the greater is β _max at a certain value of M). The parameters are as follows: Θ = 1, d = 0.02, κ = 1. The graph shows that the increase of M can increase β _max if G _z is sufficiently small. In addition, all lines suddenly stop at a certain large value of M (denoted by M _max in text), above which the catalyst cannot survive even in the absence of the parasite

In addition, if M becomes greater than the critical value (denoted by M _max)¹¹, X goes extinct even in the absence of Y (García-Tejedor et al. 1987; Nuño et al. 1993; Campos et al. 2000), as indicated by the discontinuity of the lines in Fig. 13, Thus, it can be said that the catalyst in a well-mixed system is the most resistant against parasites when M is just below M _max. (However, it must be noted that the system cannot have M too close to M _max in reality because the stochasticity, which is ignored in the current model, would drive the system to extinction).

If the binding affinity between the junk molecule and the other molecules is too strong (i.e., G _z is too small), the increase of M does not increase β _max anymore (Fig. 13). This can be understood as follows: decreasing the amount of X reduces the advantage of Y. However, this mechanism is nullified if there is too great an amount of C _zx and C _zy because these complexes act as a sort of a reservoir for X and Y through the buffering effect of the reactions ${\rm{Z}}\,{\rm{ + }}\,{\rm{Y}}\,\rightleftharpoons{{}}{} {\rm{C}}_{{zy}}$ and ${\rm{Z}}\,{\rm{ + }}\,{\rm{Y}}\,\rightleftharpoons{{}}{} {\rm{C}}_{{zy}}.$ This can be seen from the fact that if the decay rate of C _zx and C _zy is increased sufficiently, increasing M can increase β _max (data not shown).

In contrast to the system with complex formation, deleterious mutations do not weaken the parasite in the system without complex formation. This is because deleterious mutations weaken the parasite by reducing the amount of complexes.

Spatial System with Deleterious Mutations

The CA model with complex formation was extended by taking deleterious mutations into account. β _max was measured as a function of M, where G _z = 0 and R = 10⁻⁴, as shown in Fig. 14. The results show that the effect of deleterious mutations in the spatial system is more complex than in the well-mixed system. The general behavior of the model can be seen from snapshots of simulations depicted in Fig. 15. As M increases, the wave patterns become thinner, and if M becomes too great, wave patterns do not form anymore. This can be understood as follows. Firstly, increasing M slows down the speed of catalyst propagation. Secondly, increasing M weakens the parasite (see the previous section and also the next paragraph). This can slow down the speed of parasite propagation, but its effect is a minor one, as we saw previously that the speed of local extinction is mostly determined by d if β is sufficiently large. Therefore, increasing M increases the asymmetry in the two propagation speeds, which results in thinning the waves. For a small value of M, the effect of weakening the parasite apparently overcompensates for the effect of thinning the waves, since the wave patterns become more stable than the case of M = 0. Consequently, β _max becomes greater. For a moderate value of M, however, the waves become so narrow that they become less stable (see Fig. 15); hence, β _max becomes smaller. These are the common behaviors for different values of D. However, for a large value of M the results depend on D: for a sufficiently large D (≥0.1), β _max continues to decrease as M increases. However, for a small D (= 0.01), β _max increases if M is sufficiently increased. This result is explained as follows. If D is sufficiently small, the population of the catalyst is subdivided into small patches due to a large production of junk molecules. The subdivision localizes the exploitation by the parasite as shown in Fig. 16. This makes it possible for the system to tolerate a quite large value of β, but if D is sufficiently great, the subdivision of the population does not happen (at least not in the current grid size).

Fig. 14

β _max as a function of M in the spatial system with complex formation. The parameters are as follows: κ = 1, G = −0.5, G _z = 0, a _i +b _i = 1, d = 0.015, and R = 10⁻⁴ (the value of D is indicated in the graph). β _max for D = 0.01 and M = 0.4 is outside of the figure, and its value is 8.19, as indicated in the graph

Fig. 15

Snapshots of the simulations in Fig. 14 for various values of M. The color coding is as follows: the catalyst is white; the parasite is black; junk molecules are dark gray; the empty cell is light gray. D = 0.01; the other parameters are the same as in Fig. 14. The values of β and M are indicated above each snapshot. The snapshots depict the whole grid

Fig. 16

Consecutive snapshots of the simulation of the system with complex formation for a high value of M. The parameters are as follows: β = 8.17, M = 0.4, and the others are the same as in Fig. 14. The time goes from left to right. The color coding is the same as in Fig. 15. The snapshots depict a part of the grid (65 × 65) at the same position. The figure shows how the exploitation by parasites is localized by the subdivision of catalyst populations due to a large production of junk molecules and a small value of D

Although deleterious mutations do not necessarily increase β _max in the spatial system, we show here that they do always weaken the parasite. So far, β _max has been used as a measure of a system’s resistance against parasites, but we next examine a system’s resistance by measuring the minimum value of β (β _min) for which the parasite can invade and sustain its population without any mutational influx from the catalyst (i.e., R = 0). β _min was measured in the system with complex formation as shown in Fig. 17. The result shows that β _min increases consistently as M increases. Moreover, the same result also holds for the system without complex formation (data not shown). This is in contrast with the results from the well-mixed system, where the effect of deleterious mutations is valid only in conjunction with complex formation. This difference is explained by the spatial structure of populations. Because replication happens locally in a spatial system, the distribution of replicators is inhomogeneous (wave patterns do not form for β as small as β _min). This inhomogeneity reduces the chance that a parasite ‘meets’ a catalyst, relative to the chance that a catalyst meets a catalyst. Hence, the production of junk molecules, which reduces the chance that a molecule meets a catalyst, has a greater effect on the survival of the parasite than on that of the catalyst.

Fig. 17

β _min as a function of M in the spatial system with complex formation. β _min is defined as the minimum β for which the parasite can invade and sustain its population (β _max > β _min in all the cases examined). The parameters are as follows: κ = 1, G = −0.5, a _i + b _i = 1, and d = 0.015. The value of D is indicated in the graph. β _min for D = 0.01 and M = 0.4 is outside of the figure, and its value is 2.51, as indicated in the graph

In conclusion, deleterious mutations weaken the parasite in a spatial system not only by reducing complex formation but also by inhibiting the contact between parasites and catalysts.

Discussion

The current study has established that complex formation gives an advantage to parasites, while deleterious mutations disadvantage them. Moreover, the study showed that the effects of these two processes on the stability of a replicator system are significantly dependent on whether the system is well-mixed or not. In a well-mixed system, complex formation makes the system more vulnerable against parasites, whereas deleterious mutations make a replicator system with complex formation more resistant against parasites. However, in a spatial system, complex formation does not necessarily destabilize the system, nor do deleterious mutations necessarily stabilize the system. This is because it is the dynamics of spatial patterns that is crucial to the stability of the spatial system, on which complex formation and deleterious mutations can have various effects depending on the parameters. In fact, the dynamics of spatial patterns can reverse the behavior of the system in many ways relative to expectation based on a well-mixed system.

Our result with respect to deleterious mutations reveals an interesting relationship between the two problems of prebiotic evolution, i.e., the error-threshold and parasites (see the Introduction). On one hand, as the error-threshold indicates, high mutation rates are disadvantageous for the maintenance and accumulation of information. On the other hand, as our study showed, high mutation rates are actually advantageous for the protection against parasites. Hence, high rates of mutation have an opposing effect on the stability of a replicator system with respect to the error-threshold and to parasites.

In addition, we mention important aspects of a replicator system that was not covered in the current study. In the current models, a replicator system was simplified by the assumption that there are only a few predefined categories of replicators (labeled X or Y), while the population of replicators is actually composed of a collection of genetically diverse sequences (quasi-species). Our assumption greatly simplifies mutation processes in the model, which on one hand helps us to investigate the system with ease, but on the other hand, ignores some of the significant aspects of mutations. One such aspect is that high mutation rates increase the diversity of catalysts, which can constrict the exploitation by parasites to the subset of the catalysts (Kaneko and Ikegami 1992; Huynen and Hogeweg 1994; Hogeweg and Takeuchi 2003). Thus, high mutation rates can alleviate the problem of parasites in yet another way. Considering the evolution toward a target instead of the maintenance of the system, there is yet another advantage of high mutation rates: it can speed up evolution to a certain extent (e.g., Eigen and Schuster 1979; Orr HA 2000; Van Nimwegen and Crutchfield 2001).

Finally, we note that spatial pattern formation and the dynamics of mesoscale patterns are the recurrent theme of the spatial population dynamics in general (e.g., Boerlijst and Hogeweg 1991a,b; Savill et al. 1997; Pagie and Hogeweg 1999, 2000; Van Ballegooijen and Boerlijst 2004).

Methods

The ODE model with deleterious mutations

$$ \eqalign{ \dot {x}\, &= \, - 2a_{x} x^{2} \, + \,\{ 2b_{x} \, + \,(3 - M)\kappa \theta \} c_{{xx}} \, - \,a_{y} xy\, + \,\{ b_{{y\,}} \, + \,\kappa \theta \} c_{{xy}} \cr &\,\,\,- e_{x} zx\, + \,f_{x} c_{{zx}} \, - \,dx, \cr \dot {y}\, &= \, - a_{y} xy\, + \,\{ b_{y} \, + \,(2 - M)\kappa \theta \} c_{{xy}} \, - \,x_{y} zy\, + \,f_{y} c_{{zy}} \,\, - \,dy, \cr \dot {z}\,\, &= \,M\kappa c_{{xx}} \theta \, + \,M\kappa c_{{xy}} \theta \cr &\,\,\,- e_{x} zx\, + \,f_{x} c_{{zx}} \, - \,e_{y} zy\, + \,f_{y} c_{{zy}} \, - \,dz, \cr \dot {c}_{{xx}} \, &= \, - a_{x} x^{2} \, + \,(b_{x} \, + \,\kappa \theta )c_{{xx}} \, - \,dc_{{xx}} , \cr \dot {c}_{{xy}} \, &= \, - a_{y} xy\, + \,(b_{y} \, + \,\,\kappa \theta )c_{{xy}} \, - \,dc_{{xy}} , \cr \dot {c}_{{zx}} \, &= \,e_{x} zx\, - \,f_{x} c_{{zx}} - \,dc_{{zx}} , \cr \dot {c}_{{zy}} \, &= \,e_{y} zy\, - \,f_{y} c_{{zy}} - \,dc_{{zy}} , } $$

(6)

where θ = 1−(x + y + z + c _xx + c _xy + c _zx + c _zy )/Θ, and M is the mutation rate to the junk molecule per replication. It is assumed that a _x = 1 − exp(G), a _y = 1 − exp(βG) e _x = 1 − exp(G _z ) and e _y = 1 − exp(βG _z ), where G _z (≤0) represents the binding energy between X and Z. Moreover, it is assumed that b _x = 1 − a _x , b _y = 1 − a _y , f _x = 1 − e _x and f _y = 1 − e _y .

Methods of Calculating Equilibria in the ODE Models

For Fig. 1, the bifurcation diagram was obtained by using CONTENT (Kuznetsov 1999).

For Fig. 2, β _T as a function of G was obtained as follows: Firstly, for a value of G, an equilibrium with $\ifmmode\expandafter\bar\else\expandafter\=\fi{x}$ > 0 and $\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$ = 0 was obtained by numerically integrating Eq. (4) with x = 0.9 and c _xx = 0.1, y = c _xy = 0 as the initial condition. Secondly, the minimum value of β for which the largest eigenvalue of Jacobian at the equilibrium is positive was obtained by conducting a binary search within 0 < β < 1 (this value is β _T). Thirdly, the above process was repeated for various values of G. On the other hand, β _h as a function of G was calculated as follows: firstly, for a value of G, an equilibrium with $\ifmmode\expandafter\bar\else\expandafter\=\fi{x}$ > 0 and $\ifmmode\expandafter\bar\else\expandafter\=\fi{y}$ = 0 was obtained in the same way as above. Secondly, Eq. (4) is numerically integrated for a value of β (>β _H) for the duration of t to record the value of x(t) after initially setting y to y ₀ (inoculating the parasite) while initially setting the other variables at the previously obtained equilibrium. Thirdly, through gradually increasing β, the minimum value of β for which x(t) < x _min, which is the criteria of the collapse of the system, is obtained (this value is β _h). Fourthly, the above process was repeated for various values of G. The parameters used in the figure were as follows: t = 10⁷, x _min = 10⁻⁷, y ₀ = 10⁻⁵. Several sets of t, y ₀, and x _min were used, and the results did not change as long as t ⁻¹, x _min, and y ₀ were sufficiently small. The computation was done by using GRIND (De Boer and Pagie 2005) modified by the authors for the above calculation.

For Fig. 13, β _max is calculated by almost the same method as that of calculating β _h in Fig. 2. The difference is that the binary search for β _max was conducted within the range of 0 < β < 1. The parameters (t, y ₀, and x _min) were the same as the previous paragraph.

Details of the CA Model

The algorithm has been already described in the main text. Here we explain how the rate constants of the ODE models are related to the probabilities of reactions in the CA models. For a first-order reaction, its rate constant was used as the probability of the reaction after dividing by a common normalizing factor denoted by α. For a second-order reaction, say ${\rm{X}}\,{\rm{ + }}\,Y\dynrightarrow{k}{},$ the reaction rate is calculated as k[X][Y] in the ODE model, where the square brackets denote concentrations. In the CA model, there are two possibilities: A is chosen first and B is chosen second, or vise versa. To make the rate constant k have the same meaning as in the ODE model, the probability of reaction is calculated as α(k/2). If the reaction is ${\rm{X}}\,{\rm{ + }}\,{\rm{X}}\dynrightarrow{k}{},$ then the probability of reaction is similarly calculated as αk. [In a similar manner, the probability of a third-order reaction, such as ${\rm{X}}\,{\rm{ + }}\,{\rm{Y + }}\,{\rm{Z}}\dynrightarrow{k}{},$ is calculated as α(k/6)]. Moreover, since a complex molecule in the CA model is represented by two molecules occupying two cells, the chance that a complex molecule is chosen for reaction is twice as much as a single molecule. To cancel this effect, the factor 0.5 is multiplied to the probability of all reactions involving a complex molecule. By defining the probabilities of reactions in the above way, they have the same magnitude relationship as the rate constants in the ODE model (see also Gillespie 1976).

The current algorithm is closely related to the Gillespie algorithm (Gillespie 1976) in the following sense. For simplicity, let us assume that there are two cells, c ₁ and c ₂, in the system, and two possible reactions, r ₁ and r ₂. Let ${p_{r_{x},c_{i}}}$ denote the probability that r _x happens in c _i given that c _i is chosen for reaction. In the current algorithm, the probability that c ₁ is chosen is 1/2, and that c ₂ is chosen is 1/2. The probability P(r ₁, c ₁, i + 1) that r ₁ happens in c ₁ at the (i + 1)-th choice of the cells and no other reactions have not happened is calculated as

$$ {\eqalign{ P{({r_1} ,{c_1}} ,i\, + \,1)\, &= \,{\rm{Prob}}(c_{1} \,{\rm{is}}\,{\rm{chosen,}}\,{\rm{and}}\,r_{1} \,{\rm{happens)}} \cr & \,\,\times \,{\rm{Prob(nothing}}\,{\rm{happens}}\,{\rm{till}}\,{\rm{the}}\,i{\rm{ - th}}\,{\rm{choice)}} \cr & = {1 \over 2}p_{r_1 ,c_1} \, \times \,{\sum\limits_{r = 0}^i {\left(\eqalign{&{i}\cr&{r}} \right)} }\{ {1 \over 2}(1 - p_{r_{1} ,c_{1}} \, - \,p_{r_{2} ,c_{1}} )\} ^{r} \{ {1 \over 2}(1 - p_{r_{1} ,c_{2}} \, - \,p_{r_{2} c_{2}} )\} ^{{i - r}} \cr & = {1 \over 2}p_{r_{1} ,c_{1}} (1 - {1 \over 2}{\sum\limits_{j,k} {p_{r_j , c_k }})^{i}} \, } } $$

The probability P(r ₁, c ₁) that the first reaction happening in the system is r ₁ that occurs in c ₁ is

$$ {\eqalign{ P(r_{1} ,c_{1} )\, &= \,\,{\mathop {\lim }\limits_{n \to \infty } }\,{\sum\limits_{i = 0}^n {P(r_{1} ,c_{1} ,\,i\, + \,1)} } \cr & = \,{\mathop {\lim }\limits_{n \to \infty } }\,{1 \over 2}{p_{r_1 ,c_1}} \,{\sum\limits_{i = 0}^n {(1 - {1 \over 2}{\sum\limits_{j,k} {p_{r_j ,c_k }} })^{i} } } \cr & = \,{{p_{r_1 ,c_1 }} \over {{\sum\nolimits_{j,k} {p_{r_j ,c_k} } }}}. } } $$

Therefore, the current algorithm is similar to the Gillespie algorithm.

Furthermore, under the mean-field assumption (i.e., in the limit of D → ∞), the current algorithm becomes the same as the Gillespie algorithm. Let us calculate the probability P(r ₁) that the first reaction happening in the system is r ₁ under the mean-field assumption. Let us assume that the system has now a lot of cells. Suppose r ₁ represents the reaction ${\rm{X}}\,{\rm{ + }}\,{\rm{Y}}\dynrightarrow{{a_{y} }}{} C_{{xy}},$ then ${p_{r_{1} ,c_i }}$ is calculated as 2 × α(a _y /2)[X][Y], where the square brackets denote the number of the focal molecules divided by the total number of cells in the grid, which equals the probability that the randomly chosen cell contains that molecule; the multiplying factor 2 comes from the two possibilities in the order of choices (X and then Y, or Y and then X); the dividing factor 2 is explained in the first paragraph of this section. Suppose r ₂ represents the reaction ${\rm{X}}\,{\rm{ + }}\,{\rm{X}}\dynrightarrow{{a_{x} }}{} C_{{xx}},$ then one similarly obtains ${p_{r_{2} ,c_i }}$ = αa _x [X]². Under the mean-field assumption, the diffusion process can be excluded from the consideration, and moreover, ${p_{r_{x} ,c_i }}$ = ${p_{r_{x} ,c_j }}$ holds. Thus, P(r ₁) is calculated as

$$ {\eqalign{ P(r_{1} )\, &= \,{\sum\limits_i {P(r_{1} ,c_{i} )} } \cr & = \,{{a_{y} {\rm{[X][Y]}}} \over {a_{y} {\rm{[X][Y]}}\, + \,a_{x} {\rm{[X]}}^{2} }}, \cr} } $$

which is the same as in the Gillespie algorithm.

Finally, α is set so as to make Σ _x p(r _x , c _i ) smaller than one, which is required to make the algorithm behave in the desired manner. (The source code of the above algorithm is available upon request.)

Method of Measuring β_max and β_min in the CA Models

β _max in Figs. 7, 9, 12, and 14 is defined as the maximum value of β for which the system is viable. β _max was measured by a binary search method on a predefined range of β with an interval of 0.01. A system was considered viable if it survived for sufficiently long time steps (typically, in the order of 10¹¹ choices of cells for α = 0.5). The initial condition of the first run of a measurement was set such that a half-circle with radius of 10 cells was filled by X, and the other half was filled by Y, which should promote the formation of wave patterns. When a system was viable with a certain value of β, then the initial condition to examine the next value of β—which would be greater than the previous β—was taken from the final state of the system with the previous β (unless Y had gone extinct). When the system was not viable, then the initial condition for the next β—which would be smaller than the previous β—was the same as the previous initial condition. Thus, the initial conditions were presumably stable at least for a value of β smaller than the current value (except for the very first simulation). Furthermore, after binary search has stopped, the system is reexamined by incrementally increasing β in order to reduce the effect of mismatch between the initial condition and the value of β.¹² Such care with respect to initial condition is necessary to examine the resistance of the system against the parasite. This is because the formation of wave patterns is critical for the stability of a system, and it depends on the initial condition.

β _min in Fig. 17 is defined as the maximum value of β for which Y can invade the system and sustain its population. β _min is measured by binary search method as before. However, since the formation of wave patterns does not happen with β close to β _min, the initial condition here is always set such that the grid is filled with X except for a circle of radius 40 cells, which is filled with Y. Y is considered to be able to invade if it survives for sufficiently many time steps (typically on the order of 10¹¹ choices of cells for α = 0.5). If extinction of a whole system happens, then it is considered that Y can invade.