Abstract
We complete the characterization of finite bands admitting a natural duality, by showing that every finite normal band admits a natural duality. In particular we show that every finite normal band is finitely related.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A general notion of natural duality for a quasi-variety was initiated by Davey and Werner [9], generalizing well-known dualities such as Stone duality for Boolean algebras, Priestley duality for distributive lattices and Hofmann-Mislove-Stralka duality for semilattices. A natural duality for a quasi-variety gives a uniform method to represent each algebra in the quasi-variety as the algebra of all continuous homomorphisms over some structured Boolean space. There has been some work on dualisability of semigroups, especially bands and groups. As a part of Pontryagin duality, it is known that every finite abelian group is dualisable. Davey and Quackenbush [8] proved that the finite dihedral groups D n , for odd n, are dualisable. Moreover, Quackenbush and Szabó [24] showed that a finite group with cyclic Sylow subgroups is dualisable. In the other direction, they proved that finite non-abelian nilpotent groups are not dualisable [23]. Sporadic examples of finite bands allowing such a duality have appeared as examples in several places. Hobby [15] has studied an infinite family of finite semigroups including some instances of bands and has shown that most of them do not admit a natural duality. Davey and Knox worked on dualisability of bands and they proved that finite rectangular bands are dualisable [7]. In addition, in [6] they gave dualities for the quasi-varieties of left normal, right normal and normal bands. Dualities for semilattices, left-zero and right-zero semigroups are covered by Hofmann-Mislove-Stralka [16] and Banaschewski [2]. Jackson [18] has shown that a quasi-variety of bands cannot admit a natural duality if it does not consist of normal bands. We complete the classification of the dualisability of finite bands by showing that all remaining quasi-varieties of normal bands admit a natural duality. In particular we show that every finite normal band is finitely related.
2 Background
Normal bands were first studied by McLean [22]. Kimura [19] determined all identities on idempotent semigroups up to three variables, but a complete classification of band varieties was given independently in the early 1970s by Fennemore [12], Gerhard [13] and Biryukov [3]. In the following description, we refer to Howie’s text [17]. The lattice of subvarieties of the variety \(\mathcal{N}\) of normal bands is composed of eight varieties as shown in Fig. 1. The atoms are the varieties \(\mathcal{L},\mathcal{S},\mathcal{R}\) of left-zero semigroups, semilattices and right-zero semigroups, respectively. The varieties left normal bands \(\mathcal{L}^{0}\), right normal bands \(\mathcal{R}^{0}\) and rectangular bands \(\mathcal{RB}\) are the remaining nontrivial, proper subvarieties.
Shafaat [26] showed that the lattices of varieties and quasi-varieties have the same set of atoms which is the set of varieties \(\{\mathcal{L},\mathcal{S},\mathcal{R}\}\). He described the lattice of quasi-varieties by the following theorem.
Theorem 2.1
[26, Theorem 4]
The following is a complete list of quasi-varieties of normal bands (and implications defining them within \(\mathcal {N}\) ):
-
(1)
\(\mathcal{T}\): [x=y];
-
(2)
\(\mathcal{L}\): [xy=x];
-
(3)
\(\mathcal{S}\): [xy=yx];
-
(4)
\(\mathcal{R}\): [xy=y];
-
(5)
\(\mathcal{L}\vee\mathcal{S}\): [xz=yz→xy=yx];
-
(6)
\(\mathcal{RB}\): [xyx=x];
-
(7)
\(\mathcal{S}\vee\mathcal{R}\): [zx=zy→xy=yx];
-
(8)
\(\mathcal{RB}\vee\mathcal{S}\): [xzy=yzx→xy=yx];
-
(9)
\(\mathcal{L}^{0}\): [xyz=xzy];
-
(10)
\(\mathcal{R}^{0}\): [xyz=yxz];
-
(11)
\(\mathcal{L}^{0}\vee\mathcal{R}\): [zx=zy→uxy=uyx];
-
(12)
\(\mathcal{R}^{0}\vee\mathcal{L}\): [xz=yz→xyu=yxu];
-
(13)
\(\mathcal{N}\): [xyzx=xzyx].
The lattice is depicted in Fig. 2 where solid points depict varieties. Throughout this paper, we denote algebras by bold Latin letters, for example: A,B and their underlying sets by A,B. Observe that the above quasi-varieties are generated by basic semigroups as follows:
-
\(\mathcal{L}=\operatorname {\mathbb {ISP}}({\mathbf{L}})\);
-
\(\mathcal{S}=\operatorname {\mathbb {ISP}}({\mathbf{S}})\);
-
\(\mathcal{R}=\operatorname {\mathbb {ISP}}({\mathbf{R}})\);
-
\(\mathcal{RB}=\operatorname {\mathbb {ISP}}({\mathbf{L}}\times {\mathbf{R}})\);
-
\(\mathcal{L}^{0}=\operatorname {\mathbb {ISP}}({\mathbf{L}}^{0})\);
-
\(\mathcal{L}\vee\mathcal{S}=\operatorname {\mathbb {ISP}}({\mathbf{L}}\times {\mathbf{S}})\);
-
\(\mathcal{RB}\vee\mathcal{S}=\operatorname {\mathbb {ISP}}(\mathbf{RB}\times {\mathbf{S}})\);
-
\(\mathcal{L}^{0}\vee\mathcal{R}=\operatorname {\mathbb {ISP}}({\mathbf{L}}^{0}\times {\mathbf{R}})\);
where L, S, R, L 0, RB are the 2-element left-zero semigroup, the 2-element semilattice, the 2-element right-zero semigroup, the 3-element left normal semigroup obtained by adjoining a zero to L, and the 4-element rectangular band isomorphic to product of L and R, respectively.
3 Some dualities for Bands
For details on the following definitions and preliminary steps concerning natural dualities, see Clark and Davey [4]. Let M be a finite algebra. We say M admits a natural duality or M is dualisable if there is some discrete topological structure \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) such that every algebra \({\mathbf{A}}\in \operatorname {\mathbb {ISP}}({\mathbf{M}})\) is represented as an algebra of morphisms \(\operatorname {hom}({\mathbf{X}},{ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}})\) for some \({\mathbf{X}}\in \operatorname {\mathbb {IS}_{\mathrm{c}}\mathbb {P}^{+}}{ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) where \({{\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}=\langle M; G, H, R, \mathcal{T}\rangle\) such that
-
(1)
G is a set of total operations on M such that (for g∈G of arity n≥1) g:M n→M is a homomorphism;
-
(2)
H is a set of partial operations on M such that if h∈H is n-ary then the domain, \(\operatorname {dom}(h)\), of h is a (non-empty) subalgebra of M n and \(h\colon \operatorname {dom}(h)\to {\mathbf{M}}\) is a homomorphism;
-
(3)
R is a set of finitary relations on M such that if r∈R is n-ary then r forms a subalgebra of M n;
-
(4)
\(\mathcal{T}\) is the discrete topology on M.
Under these conditions, there is a naturally defined dual adjunction between the quasi-variety \(\mathcal{A}=\operatorname {\mathbb {ISP}}({\mathbf{M}})\) and the topological quasi-variety \(\mathcal{X}= \operatorname {\mathbb {IS}_{\mathrm{c}}\mathbb {P}^{+}}{ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) consisting of isomorphic copies of topologically closed substructures of non-zero powers of \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\). On the other hand, if \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) fails to yield a natural duality on \(\mathcal {A}\) then M is said to be non-dualisable.
We will establish dualisability for various bands by way of the following “Interpolation Condition” (IC).
IC Duality Theorem 3.1
[4]
Suppose G∪H∪R is finite. Then \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) dualises M provided the following interpolation condition (IC) is satisfied: for each \(n\in\mathbb{N}\) and each substructure X of \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}^{n}\), every morphism \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) extends to term function t:M n→M of the algebra M.
Our dualities will be built upon five existing dualities namely the dualities for the quasi-varieties generated by the 2-element semilattice S, the 2-element left-zero semigroup L, the 2-element right-zero semigroup R, the 4-element rectangular band RB and the 3-element left normal band L 0. (Throughout this article associativity and idempotence are assumed)
-
The variety \(\mathcal{S}\) of semilattices satisfies the identity xy≈yx. The meet semilattice with 1, S=〈{0,1};∧,1〉 was proved to be dualisable by Hofmann, Mislove and Stralka [16] (for more details we also refer the reader to Davey and Werner [9]) and its alter ego is obtained by taking the existing operations and adding the discrete topology, so
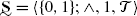 . A simple modification of the proof shows that 〈{0,1};∧〉, 〈{0,1};∧,0〉, 〈{0,1};∧,0,1〉 are also dualisable.
. A simple modification of the proof shows that 〈{0,1};∧〉, 〈{0,1};∧,0〉, 〈{0,1};∧,0,1〉 are also dualisable. -
The variety \(\mathcal{L}\) of left-zero semigroups satisfies the identity xy≈x and the variety \(\mathcal{R}\) of right-zero semigroups satisfies the dual identity. As these are term-equivalent to sets, duality for these two varieties is covered by the duality for sets given by Banaschewski [2] (for details see [9]).
-
The variety \(\mathcal{RB}\) of rectangular bands satisfies the identity xyx≈x or equivalently the anti-commutative quasi-identity xy≈yx→x≈y. Clark and Davey [4] gave a natural duality for the variety of rectangular bands while Davey and Knox [7] gave a new proof that every finite rectangular band is naturally dualisable.
-
Davey and Knox [6] gave a sufficient condition for the dualisability of the quasi-variety generated by a finite dualisable algebra with zero added. As a result, the variety of left normal bands is naturally dualisable by [6, Theorem 3.6].
4 Dualities for Quasi-varieties of Normal Bands
In this section we will prove that the five nonvariety quasi-varieties of normal bands are dualisable by showing that they possess alter egos that satisfying (IC). Shafaat [26] showed that every quasi-variety of normal bands is generated by a direct product of some of the bands L,S,R,L 0 and R 0. Hence, each of these quasi-varieties is generated by the direct product of two dualisable algebras from two different varieties. However, it is not always true that the direct product of dualisable algebras is dualisable. For example, let I=〈{0,1};→〉 denote the 2-element implication algebra. For a,b∈{0,1}, define I a,b =〈{0,1};→,a,b〉. Then I 0,1 and I 1,0 are term-equivalent to the 2-element Boolean algebra, whence dualisable by Stone duality, but I 0,1×I 1,0 is not, as shown in [5]. We modify this example in the last section of this article by showing the product of a dualisable groupiod with constant with a dualisable 2-element right-zero semigroup with constant is non-dualisable.
Saramago [25] and Davey and Willard [10] showed that if two algebras generate the same quasi-variety and one of them is dualisable then the other is dualisable. In all proofs, we consider an algebra D that generates the specified quasi-variety of normal bands, and show that D is dualisable. Moreover, in each case the alter ego of the algebra D is of finite type, hence it is sufficient to show that (IC) holds. We end this subsection with three lemmas that will be used often below. The first is general and the second and third refer to the 2-element semilattice and the 2-element left- or right-zero semigroup, respectively.
Definition 4.1
A family of maps {φ i :X→Y i ∣i∈I} is separating if for all x≠y in X, there is i∈I with φ i (x)≠φ i (y).
Lemma 4.2
Let D be a finite algebra, let M and N be subalgebras of D and g M :D→M, g N :D→N be homomorphisms onto M and N, respectively with {g M ,g N } separating. Assume \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) is an alter ego of D that includes the unary homomorphisms g M , g N . Consider \({\mathbf{X}}\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}^{n}\), for some \(n \in\mathbb{N}\) and assume that \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) is a morphism such that there is a term t(x 1,…,x n ) with
Then φ(x)=t(x), for every x∈X.
Proof
Let x∈X. As g M (x)∈X∩M n, we have φ(g M (x))=t(g M (x)) which implies that g M (φ(x))=g M (t(x)). Similarly, g N (x)∈X∩N n implies φ(g N (x))=t(g N (x)). Then we have g N (φ(x))=g N (t(x)). Since g M , g N are separating homomorphisms and φ is a morphism, therefore φ(x)=t(x), for every x∈X. □
The following two basic lemmas will essentially establish (IC) for S and L (whence R); we need the precise details for our proofs later.
Lemma 4.3
Let \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {S}}}\vphantom {\underline {\mathbf {S}}}}}=\langle\{a,b\}; \ast, a, b\rangle\) be the 2-element bounded semilattice with ∗ the semilattice operation and a∗b=b. For \({\mathbf{X}}\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {S}}}\vphantom {\underline {\mathbf {S}}}}}^{n}\), let \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {S}}}\vphantom {\underline {\mathbf {S}}}}}\) be a morphism. Let \(\widehat{a}\) be the ∗-product of all elements of the set {x∈X∣φ(x)=a} and \(I=\{i\leq n\mid(\widehat {a})_{i}=a\}\). Then the set I≠∅ and for all x∈X, we have \(\varphi(x)=x_{i_{1}}\ast\dots\ast x_{i_{m}}\) where {i 1,…,i m }=I.
Proof
First, \(\widehat{a}\) is well defined as \(\varphi(\underline{a})=a\). Since the constant tuple \(\underline{b}\neq\widehat{a}\), it follows that the set I is nonempty. We will prove that for x∈X, we have φ(x)=a if and only if x i =a for all i∈I. By the definition of \(\widehat{a}\) and I, it follows that for x∈X with φ(x)=a we have x i =a for all i∈I. Conversely, if for all i∈I we have x i =a then \(x\ast\widehat{a}=\widehat{a}\). It follows that \(a=\varphi(\widehat{a})=\varphi(x)\ast\varphi (\widehat {a})=\varphi(x)\ast a=\varphi(x)\).
Equivalently, for x∈X, we have φ(x)=b if and only if there exists j∈I with x j =b. Hence for all x∈X we have \(\varphi (x)=x_{i_{1}}\ast\dots\ast x_{i_{m}}\) where {i 1,…,i m }=I. □
Lemma 4.4
Let \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {L}}}\vphantom {\underline {\mathbf {L}}}}}=\langle\{a,c\};\ast, \vee,\wedge, '\rangle\) be an algebra where 〈{a,c};∨,∧,′〉 is a Boolean algebra with a<c and 〈{a,c};∗〉 is a 2-element left-zero or right-zero semigroup. For \({\mathbf{X}}\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {L}}}\vphantom {\underline {\mathbf {L}}}}}^{n}\), let \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {L}}}\vphantom {\underline {\mathbf {L}}}}}\) be a homomorphism. Let J={j≤n∣(∀x∈X)φ(x)=x j } and define \(\check{a}=\bigvee \varphi^{-1}(a)\). Then the set J≠∅ and we have \((\check {a})_{j}=a\) if and only if j∈J .
Proof
Let X≠∅. Since \(\varphi(\underline{a})=a\), then φ −1(a)≠∅. Hence, \(\check{a}\) is well defined. Suppose that \((\check{a})_{j}=a\). We shall prove that φ(x)=x j for every x∈X. Either φ(x)=a or φ(x)=c, let’s suppose the first case. Hence x∈φ −1(a) and \(\check {a}\vee x = \check{a}\). However, \(\check{a}_{j}\vee x_{j} = \check {a}_{j}=a\). Therefore, x j =a=φ(x). In the second case, if φ(x)=c, then φ(x′)=a. Applying the above argument proves that (x′) j =a, whence x j =c=φ(x).
To prove that J≠∅, it is enough to show that \(\check {a}\neq\underline{c}\). Suppose by way of contradiction that \(\check {a}= \underline{c}\), then \((\check{a})'= \underline{a}\). However, \(\check{a}=\check{a}\vee(\check{a})'\) which implies that \(\varphi (\check{a})=\varphi(\check{a})\vee\varphi((\check{a})')= a\vee c=c\), a contradiction. □
We introduce the following notation which will be required in the coming proofs.
Notation 4.5
Let M={x,y} and N={x,y,z}. Define the binary operations ∨ x,y :M 2→M, ∧ x,y :M 2→M, ∨ x,y,z :N 2→N and ∧ x,y,z :N 2→N as follows:
Note that ∨ x,y (∧ x,y ) is the join (meet) in the chain x<y and ∨ x,y,z (∧ x,y,z ) is the join (meet) in the chain x<y<z.
4.1 \(\mathcal{L}\vee\mathcal{S}\) duality
We will show that the quasi-variety generated by the product of the left-zero semigroup L with the 2-element semilattice S is dualisable by finding an alter ego satisfying (IC). By symmetry, the quasi-variety generated by the product of the 2-element semilattice S with the 2-element right-zero semigroup R is also dualisable. Consider the semigroup D on {(i,s)∣i,s∈{0,1}} with the multiplication ∗ given by
It is easy to check that D is isomorphic to L×S. Note that for k∈{0,1},
form 2-element left-zero subsemigroups and 2-element subsemilattices, respectively, under ∗. Let ρ k :D→D, κ l :D→D and λ 0:D→D be endomorphisms defined as follows:
where ′ is the complement operation on {0,1} such that 0′=1 and 1′=0. We will not notationally distinguish between an endomorphism and its restriction to a subset of its domain. To make the proof notationally easier to read, let
Let ∨ a,b , ∧ a,b be binary operations on L 1 as defined in Notation 4.5. Similarly, define the binary operations ∨ c,d , ∧ c,d on L 0.
By Lemma 4.4, 〈L 1;∗,∨ a,b ,∧ a,b ,κ l ,a,b,𝒯〉 and 〈L 0;∗,∨ c,d ,∧ c,d ,κ l ,c,d,𝒯〉 dualise 〈L 1;∗〉 and 〈L 0;∗〉, respectively. By Lemma 4.3, 〈S 0;∗,a,c,𝒯〉 and 〈S 1;∗,b,d,𝒯〉 dualise 〈S 0;∗〉 and 〈S 1;∗〉, respectively. Observe that ∨ c,d =ρ 0∘∨ a,b ∘(ρ 1×ρ 1) and similarly ∧ c,d =ρ 0∘∧ a,b ∘(ρ 1×ρ 1). Finally, the set ▷={b,c,d} forms a subsemigroup of D. Let
and
Theorem 4.6
The alter ego

dualises D and hence \(\mathcal{L}\vee\mathcal{S}\) has a natural duality.
Proof
Since \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) is of finite type, by the IC Duality Theorem 3.1, it suffices to prove that \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) satisfies (IC). Let \(n \in\mathbb {N}\) and \({\mathbf{X}}\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}^{n}\). Let \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) be a morphism. We will apply Lemma 4.2 on D with subalgebra M chosen to be L 1 and subalgebra N chosen to be S 0.
Now we consider first L 1. As every term function of L k is a projection, for all \(x\in X\cap L^{n}_{k}\), we have φ(x)=x j , for some j∈{1,…,n}. Let
Define \(\check{a}=\bigvee_{a,b} \rho_{1}(\varphi^{-1}(a))\). Hence we have \(\check{a}\in X\cap L^{n}_{1} \) and \(\varphi(\check{a})=a\). Applying Lemma 4.4 on 〈L 1;∗,∨ a,b ,∧ a,b ,κ l 〉, we have \((\check{a})_{j}=a\), for \(j\in I_{L_{1}}\), and \((\check{a})_{k}=b\), for \(k\notin I_{L_{1}}\).
We now consider S 0. Define \(\widehat{a}\) to be the ∗-product of all elements of the set λ 0(φ −1(a)) and let
Applying Lemma 4.3 on 〈S 0;∗,a,c〉, for every \(x\in X\cap S_{0}^{n}\) we have \(\varphi (x)=x_{i_{1}}\ast\dots\ast x_{i_{m}}\), where \(\{i_{1},\dots, i_{m}\} = I_{S_{1}}\), and \((\widehat{a})_{i}=a\), for \(i\in I_{S_{0}}\), and \((\widehat{a})_{l}=c\), for \(l\notin I_{S_{0}}\).
Now we claim that \(I_{S_{0}}\cap I_{L_{1}}\neq\varnothing\). Suppose to the contrary that \(I_{S_{0}}\) and \(I_{L_{1}}\) are disjoint. Without loss of generality, we may assume that \(I_{S_{0}}=\{1,\dots,m\} \) and \(I_{L_{1}}=\{m+1, \dots, m+| I_{L_{1}}|\}\) . The following table will give a contradiction to the assumption \(I_{S_{0}}\cap I_{L_{1}}= \varnothing\).
The last line shows that φ does not preserve the subsemigroup ▷, a contradiction. Hence \(I_{S_{0}}\cap I_{L_{1}}\neq \varnothing\).
We are now in a position to apply Lemma 4.2. Let \(j\in I_{S_{0}}\cap I_{L_{1}}\) and t:D n→D be a term function given by
For all \(x\in X\cap S_{0}^{n} \), we have \(\varphi(x)= x_{i_{1}}\ast \dots \ast x_{i_{m}}\), which is equal to t(x 1,…,x n ) on S 0, and for all \(x\in X\cap L_{1}^{n} \), we have φ(x)=x j , for some \(j\in I_{L_{1}}\), which is equal to t(x 1,…,x n ) on L 1. Since ρ 1 and λ 0 are separating retracts onto L 1 and S 0, respectively, Lemma 4.2 shows that φ(x)=t(x), for all x∈X. □
4.2 \(\mathcal{RB}\vee\mathcal{S}\) duality
Let M be a finite rectangular band. Then by Davey and Knox [7] M is dualisable by some alter ego \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {M}}}\vphantom {\underline {\mathbf {M}}}}}\) of finite type. Let S be a 2-element semilattice. Then by Hofmann, Mislove and Stralka [16], S is dualisable by some alter ego \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {S}}}\vphantom {\underline {\mathbf {S}}}}}\) of finite type. Consider the semigroup D on {(i,s,j)∣i,s,j∈{0,1}} with the multiplication ∗ given by
It is clear that D≅L×S×R. Note that for k∈{0,1}, M k ={(i,k,j)∣i,j∈{0,1}} form rectangular bands under ∗. Notice that for fixed coordinates i,j, the sets S ij ={(i,s,j)∣s∈{0,1}} form 2-element subsemilattices under ∗. We define the sets
which form right-zero subsemigroups and left-zero subsemigroups under ∗, respectively. Observe that D generates the quasi-variety join \(\mathcal{RB}\vee\mathcal{S}\). (See Fig. 2.)
Let σ k :D→D, ρ k :D→D, λ k :D→D, κ l :D→D and κ r :D→D be the endomorphisms defined as follows:
where ′ is the complement operation on the set {0,1} such that 0′=1,1′=0.
To make the proof notationally easier, let
be the elements of the set D. Let ∨ a,b , ∧ a,b be binary operations on R 01={a,b} as defined in Notation 4.5. Similarly, we define the remaining binary operations ∨ Z ,∧ Z on Z∈{L sj ,R is }.
Observe that ∨ c,d =κ l ∘∨ a,b ∘(κ l ×κ l ), ∨ e,f =σ 0∘∨ a,b ∘(σ 1×σ 1) and ∨ g,h =σ 0∘κ l ∘∨ a,b ∘((κ l ∘σ 1)×(κ l ∘σ 1)), and similarly, the remaining partial operations ∧ Z and ∨ Z can be expressed in terms of ∧ a,b , ∧ a,c , ∨ a,c and some endomorphisms. Let
and let
Finally, the sets ▷1={e,c,g} and ▷2={e,b,f} form subsemigroups of D. Notice that by Lemma 4.3,

dualises S 00. We will show in the proof of Theorem 4.7 that

dualises the rectangular band M 1.
Theorem 4.7
The alter ego

dualises D and hence \(\mathcal{RB}\vee\mathcal{S}\) has a natural duality.
Proof
We can apply the IC Duality Theorem 3.1 since the alter ego \({{\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) is of finite type. Let \(n \in\mathbb{N}\) and \({\mathbf{X}}\leqslant {{\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}^{n}\). Let \(\varphi\colon {\mathbf{X}}\to { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\) be a morphism. We will apply Lemma 4.2 on D with M chosen to be the subsemigroup M 1 and N chosen to be the subsemigroup S 00.
First, we consider the rectangular band M 1. It is easy to check that M 1≅L 10×R 01. Let
Now define \((\check{a})^{L}=\bigvee_{a, c} \rho_{0}(\sigma _{1}(\varphi ^{-1}(a)))\); then \((\check{a})^{L}\in X\cap L_{1 0}^{n}\) and \({\varphi ((\check{a})^{L})=a}\). Applying Lemma 4.4 on 〈L 10;∗,∨ a,c ,∧ a,c ,κ l 〉, we have \((\check {a})^{L}_{k}=a\), for \(k\in I_{L_{1 0}}\), and \((\check{a})^{L}_{l}=c\), for \(l\notin I_{L_{1 0}}\). Let
Define \((\check{a})^{R}=\bigvee_{a, b} \lambda_{0}(\sigma _{1}(\varphi ^{-1}(a)))\); then \((\check{a})^{R}\in X\cap R_{0 1}^{n}\) and \(\varphi ((\check{a})^{R})=a\). Then by applying Lemma 4.4 on 〈R 01;∗,∨ a,b ,∧ a,b ,κ r 〉, we have \((\check{a})^{R}_{j}=a\), for \(j\in I_{R_{0 1}}\), and \((\check {a})^{R}_{q}=b\), for \(q\notin I_{R_{0 1}}\).
We now consider S 00. Define \(\widehat{a}\) to be ∗-product of all elements of the set λ 0∘ρ 0(φ −1(a)) and let
Applying Lemma 4.3 on 〈S 00;∗,a,e〉, for every \(x\in X\cap S_{0 0}^{n}\) we have \(\varphi(x)= x_{i_{1}}\ast \dots\ast x_{i_{m}}\), for \(\{i_{1},\dots, i_{m}\}= I_{S_{0 0}}\). Moreover, we have \((\widehat{a})_{i}=a\), for \(i\in I_{S_{0 0}}\) and \((\widehat{a})_{s}=e\), for \(s\notin I_{S_{0 0}}\).
We claim that \(I_{S_{0 0}}\cap I_{L_{1 0}}\neq\varnothing\) and \(I_{S_{0 0}}\cap I_{R_{0 1}}\neq\varnothing\). Suppose by way of contradiction that \(I_{S_{0 0}}\cap I_{L_{1 0}}= \varnothing\). Without loss of generality, we may assume that \(I_{S_{0 0}}=\{1, \dots , m\}\), \(I_{L_{1 0}}=\{m +1, \dots, |I_{L_{1 0}}| + m\}\). The table below will give us a contradiction to the assumption that \(I_{S_{0 0}}\cap I_{L_{1 0}}= \varnothing\).
The last line shows that φ does not preserve the relation ▷1, hence \(I_{S_{0 0}}\cap I_{L_{1 0}}\neq \varnothing \). By symmetry, we have \(I_{S_{0 0}}\cap I_{R_{0 1}}\neq\varnothing\).
We are now in a position to apply Lemma 4.2. Let \(i_{L}\in I_{S_{0 0}}\cap I_{L_{1 0}}\) and \(i_{R}\in I_{S_{0 0}}\cap I_{R_{0 1}}\). Let t:D n→D be the term function given by
Then, for all \(x\in X\cap M_{1}^{n} \), we have \(\varphi (x)=x_{i_{L}}\ast x_{i_{R}}\) which is equal to t(x 1,…,x n ) on M 1, and for all \(x\in X\cap S_{0 0}^{n} \), we have \(\varphi (x)= x_{i_{1}}\ast\dots\ast x_{i_{m}}\), which is equal to t(x 1,…,x n ) on S 00. Since σ 1 and λ 0∘ρ 0 are separating retracts onto M 1 and S 00, respectively, Lemma 4.2 shows that φ(x)=t(x), for all x∈X. □
4.3 \(\mathcal{L}^{0}\vee\mathcal{R}\) duality
We will show that the quasi-variety generated by the product of the left normal band L 0 and right-zero semigroup R is dualisable (and by symmetry we conclude that the quasi-variety generated by the product of right normal band and left-zero semigroup is dualisable) by showing that it has an alter ego that satisfies (IC). Let D be the semigroup on
with multiplication ∗ defined by:
Note that for l∈{0,1,2}, k∈{0,1}, the sets R l ={(l,j)∣j∈{0,1}} form 2-element right-zero subsemigroups and M k ={(i,k)∣i∈{0,1,2}} form left normal idempotent subsemigroups under ∗. For k∈{0,1}, the sets L k ={(i,k)∣i∈{1,2}} form 2-element left-zero subsemigroups and
form 2-element subsemilattices under ∗. Observe that D generates the quasi-variety \({\mathcal{L}^{0}\vee\mathcal{R}}\). Let ρ k :D→D, λ l :D→D, κ r :D→D and ♯:D→D be endomorphisms defined as follows:
and
where ′ is the complement on the set {0,1}. To make it notationally easier for the reader, we let
Let ∨ a,c ,∧ a,c be binary operations on R 1={a,c} as defined in Notation 4.5. We define the following operations ∨ b,d ,∧ b,d ,∨0,0′,∧0,0′,∨ a,b,0,∧0,a,b ,∨ c,d,0′ and ∧0′,c,d similarly.
Observe that ρ 0=κ r ∘ ρ 1, λ 2=♯ ∘ λ 1, ∨ b,d =♯ ∘∨ a,c ∘ (♯×♯), ∧ b,d =♯ ∘∧ a,c ∘ (♯×♯), ∨ c,d,0′=ρ 0∘∨ a,b,0∘(ρ 1×ρ 1) and ∧0′,c,d =ρ 0∘∧0,a,b ∘(ρ 1×ρ 1). We define ∨ a,b to be the binary operation ∨ a,b,0 restricted to the set L 1, and similarly for ∧ a,b , ∨ c,d and ∧ c,d . Let
and let
Finally, the set ▷={0,0′,c,d} forms a subsemigroup of D. Notice that by using Lemma 4.4, the alter ego  dualises L
1 and
dualises L
1 and  dualises R
1. We will show in the proof of Theorem 4.8 that
dualises R
1. We will show in the proof of Theorem 4.8 that

dualises the left normal band M 1.
Theorem 4.8
The alter ego

dualises D and hence \(\mathcal{L}^{0}\vee\mathcal{R}\) has a natural duality.
Proof
We apply the IC Duality Theorem 3.1. Let \(n \in\mathbb{N}\) and \({\mathbf{X}}\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}^{n}\). Consider a morphism \(\varphi\colon {\mathbf{X}}\to {{\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {D}}}\vphantom {\underline {\mathbf {D}}}}}\). We will apply Lemma 4.2 on D with the subalgebra M chosen to be the subsemigroup M 1 and the subalgebra N to be the subsemigroup R 1.
First, we consider M 1. Let \(A=\{x\in X\cap M_{1}^{n}\mid\varphi (x)\neq0\}\) and define \(\widehat{x}\) to be the ∗-product of all elements of A relative to some fixed ordering, with the constant \(\underline{a}\) first. Let \(I_{A}=\{i\leq n\mid\widehat{x}_{i}\neq 0\} \). Hence by definition of \(\widehat{x}\) and I A , we have for all x∈A, x i ≠0 for all i∈I A . Conversely, let \(x\in X\cap M_{1}^{n}\) with x i ≠0, for all i∈I A . Then \(\widehat{x}\ast x=\widehat{x}\), showing φ(x)≠0 and x∈A. Therefore, for all \(x\in X \cap M_{1}^{n}\), we have φ(x)≠0 if and only if x i ≠0 for all i∈I A . Equivalently, for all \(x\in X \cap M_{1}^{n}\), we have φ(x)=0 if and only if there exists i∈I A such that x i =0. Let \(\pi_{I_{A}}\colon D^{n}\to D^{I_{A}}\) be the restriction to I A . It is clear that \(\pi _{I_{A}}(A)\subseteq L_{1}^{I_{A}}\). As ∨ a,b,0,∧0,a,b ,♯ are total operations on M 1, L 1 is subuniverse of 〈M 1;∗,∨ a,b,0,∧0,a,b ,♯,a,b,0〉 and \(\underline{a}, \underline{b}\in\pi_{I_{A}}(A)\), then \(\pi _{I_{A}}(A)\leqslant { {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {L}}}\vphantom {\underline {\mathbf {L}}}}}_{1}^{I_{A}}\).
Let \(\psi\colon\pi_{I_{A}}(A)\to L_{1}\) be given for all \(z\in\pi _{I_{A}}(A)\) by ψ(z)=φ(x), where x∈A and \(\pi _{I_{A}}(x)=z\). Then ψ is well defined if and only if \({\operatorname {ker}(\pi _{I_{A}})\subseteq \operatorname {ker}(\varphi)}\). We will argue that ψ is well defined, that is, for x,y∈A with \(\pi_{I_{A}}(x)= \pi_{I_{A}}(y)\) we show that φ(x)=φ(y). Since \(x\ast\widehat{x}=y\ast \widehat{x}\) and φ preserves ∗, we know that \(\varphi (x)=\varphi(x\ast\widehat{x})=\varphi( y\ast\widehat{x})= \varphi(y)\). Hence \(\operatorname {ker}(\pi_{I_{A}})\subseteq \operatorname {ker}(\varphi)\), that is, ψ is a unique morphism such that \(\psi\circ\pi_{I_{A}}=\varphi\). Since \({ {\smash {\underset {\raise .4ex\hbox {$\smash \sim $}}{\mathbf {L}}}\vphantom {\underline {\mathbf {L}}}}}_{1}\) dualises L 1 with (IC), the morphism ψ extends to the term t=x i for some i∈I A . Define the term function s to be \(s= x_{i}\ast x_{i_{1}}\dots\ast x_{i_{m}}\) where I A ={i 1,…,i m } and m≤n. It easy to see that t is equivalent to s on L 1. If \(x\in(X\cap M_{1}^{n})\backslash A\) then φ(x)=0 and there exists l∈I A such that x l =0. Hence s(x)=0=φ(x). Thus for all \(x\in X\cap M_{1}^{n}\), we have φ(x)=s(x).
We now consider the subsemigroup R 1. Let
and define \(\check{a}=\bigvee_{a, c} \lambda_{1}(\varphi^{-1}(a))\). Applying Lemma 4.4 on
we have \(I_{R_{1}}\neq\varnothing\). Moreover, we have \((\check {a})_{j}=a\), for \(j\in I_{R_{1}}\) and \((\check{a})_{k}=c\), for \(k\notin I_{R_{1}}\).
We will argue that \(I_{R_{1}}\cap I_{A}\neq\varnothing\). Suppose by way of contradiction that \({I_{R_{1}}\cap I_{A}= \varnothing}\). Without loss of generality we may assume that \(I_{R_{1}}= \{1,\dots, | I_{R_{1}} |\}\) and \(I_{A}=\{ | I_{R_{1}} |+1,\dots, | I_{R_{1}} |+ m\}\). Then the following table will give us a contradiction to the assumption \(I_{R_{1}}\cap I_{A}= \varnothing\).
The last line shows that φ does not preserve the relation ▷, a contradiction. We are now in a position to apply Lemma 4.2. Let \(j\in I_{A}\cap I_{R_{1}}\) and t:D n→D be a term function given by
For all \(x\in X\cap M_{1}^{n} \) we have φ(x)=s(x) which is equal to t(x 1,…,x n ) on M 1, and for all \(x\in X\cap R_{1}^{n} \) we have φ(x)=x j , for some \(j\in I_{A}\cap I_{R_{1}}\), which is equal to t(x 1,…,x n ) on R 1. Since ρ 1 and λ 1 are separating retracts onto M 1 and R 1, respectively, Lemma 4.2 shows that φ(x)=t(x), for all x∈X. □
We conclude this section with a brief discussion about dualisability of a semigroup and the residual character of the variety it generates. In addition, we give the definition of finite degree and two corollaries to the main results in this article. A variety is residually finite if and only if all of its subdirectly irreducible members are finite. Golubov and Sapir [14] gave a description of all residually finite semigroups. McKenzie [21] classified (independently of [14]) residually finite varieties of semigroups. He showed that if a semigroup is not a group or not very close to being union of groups, then it generates a residually large variety.
There is no obvious connection between dualisability of an algebra and the residual character of the variety it generates, however it has been noticed that all known dualisable semigroups generate residually finite varieties. This article continues to reinforce this theme. However, it is not true that algebras that generate residually finite varieties are dualisable. For example, the two element implication algebra is non-dualisable, although it generates residually small variety.
Corollary 4.9
For a finite band M, the following are equivalent:
-
(1)
M is dualisable;
-
(2)
M is a normal band;
-
(3)
M is not inherently non-dualisable;
-
(4)
The variety \(\operatorname {\mathbb {HSP}}({\mathbf{M}})\) has a finite residual bound.
For a fixed number n, the set of all term functions on a semigroup M forms a subsemigroup F M (n) of \({\mathbf{M}}^{M^{n}}\). The clone of M is the set of all term functions of M,
Definition 4.10
An algebra M has finite degree if there is a finite set \(\mathcal{R}\) of finitary relations on the set M, such that \(\operatorname {Clo}({\mathbf{M}})\) is the family of all operations preserving the relations in \(\mathcal {R}\). Algebras with finite degree are also known as finitely related.
Aichinger, Mayr and McKenzie [1] showed that every finite group has the finite degree property, while finite commutative semigroups and nilpotent semigroups were shown to have finite degree in [5]. Dualisability by an alter ego of finite type implies finite degree: it is the property CLO in [4] for example. Thus we obtain the following corollary to the main results of this article.
Corollary 4.11
Every finite normal band has finite degree.
After the submission of this article, two independent articles have appeared which extend this corollary to cover the class of regular bands: Dolinka [11] and Mayr [20].
5 An inherently non-dualisable algebra
Each of the algebras shown to be dualisable in the previous sections are of the form D×L or D×R, where D is some dualisable semigroup. The semigroups L and R are projection algebras in the sense that all fundamental operations are projections, and one might be led to speculate that the direct product of a dualisable algebra with a projection algebra is always dualisable. We do not resolve this in the present article, however in this section we show that it is possible to obtain a nondualisable algebra from the direct product of a dualisable algebra with a dualisable projection algebra with constants.
A finite algebra D is called inherently non-dualisable (abbreviated to IND) provided M is non-dualisable wherever M is a finite algebra with \({\mathbf{D}}\in \operatorname {\mathbb {ISP}}({\mathbf{M}})\). In this section, we will show that the direct product of a dualisable algebra with a 2-element right-zero semigroup with constant can be inherently non-dualisable. The 2-element implication algebra 〈{0,1};→,0〉 with 0 as added constant is dualisable as it is a term equivalent to the 2-element Boolean algebra [4, Exercise 10.6], while the 2-element right-zero algebra with a constant is dualisable as it is a pointed set and so is covered by Banaschewski [2]. We show that the direct product is IND. First we recall the Inherently Non-dualisable Algebra Lemma [4].
IND Lemma 5.1
Let D be a finite algebra. Assume there exists an infinite set S, a subalgebra A of D S and an infinite subset A 0 of A and a function \(u\colon\mathbb{N}\to\mathbb{N}\) such that
-
(i)
if θ is a congruence on A of finite index at most n, then \(\mathrel{\theta}\upharpoonright_{A_{0}}\) has only one class with more than u(n) elements,
-
(ii)
g∉A where g is the element of D S such that g(s):=ρ s (b), for each s∈S, with b any element of the block of \(\operatorname {ker}(\rho_{s}){\upharpoonright_{A_{0}}}\) which has size greater than u(|D|).
The element g described in (ii) is often referred to as the ghost element.
Example 5.2
Let I 0=〈{0,1};→,0〉 be the implication algebra with added constant and let R 0=〈{0,1};⋅,0〉 be a right-zero semigroup with 0 as added constant. The direct product I 0×R 0 is inherently non-dualisable.
Proof
The direct product I 0×R 0 is isomorphic to the algebra D=〈{a,b,c,d};∗,a〉 with ∗ defined as follows.
We apply Lemma 5.1 to show that D is inherently non-dualisable. Let S be an infinite set and let A be the subalgebra of D S with underlying set \(D^{S}\backslash\{ \underline {c}\}\). (We will leave it to the reader to check that A is indeed subalgebra.) Let \(A_{0}=\{ c_{j}^{d}\mid j\in S\}\) where \(c_{j}^{d}\) is defined to be the constant element \(\underline{c}\) except with d in the jth coordinate. Let \(u\colon\mathbb{N\to\mathbb{N}}\) be the function with u(n)=1, for all n and let θ be a congruence on A with the index n. Assume that \(c_{i}^{d}\mathrel {\theta}c_{j}^{d}\) and \(c_{k}^{d}\mathrel{\theta}c_{l}^{d}\) with i,j,k,l pairwise unequal. Now we have \(c_{k}^{d}=(c_{i}^{d}\ast c_{i}^{d})\ast c_{k}^{d} \mathrel{\theta} (c_{j}^{d}\ast c_{i}^{d})\ast c_{k}^{d}= c_{j\ k}^{d\ d}\). By symmetry we get \(c_{j}^{d}\mathrel {\theta} c_{j\ k}^{d\ d}\mathrel{\theta}c_{k}^{d}\mathrel{\theta }c_{l}^{d}\). Hence \(\mathrel{\theta}\upharpoonright_{A_{0}}\) has a unique block with more than u(n) elements. It is easily checked that the constant \(\underline{c}\) is the ghost element. Since \(\underline {c}\notin A\), we are done. □
References
Aichinger, E., Mayr, P., McKenzie, R.: On the number of finite algebraic structures. To appear in J. Eur. Math. Soc.
Banaschewski, B.: Projective covers in categories of topological spaces and topological algebras. In: General Topology and Its Relation to Modern Analysis and Algebra, Proc. Conf., Kanpur, 1968, pp. 63–91. Academia, Prague (1971)
Biryukov, A.P.: Varieties of idempotent semigroups. Algebra Log. 9, 153–164 (1970)
Clark, D.M., Davey, B.A.: Natural Dualities for the Working Algebraist. Cambridge University Press, Cambridge (1998)
Davey, B.A., Jackson, M., Pitkethly, J., Szabó, Cs.: Finite degree: algebras in general and semigroups in particular. Semigroup Forum 83, 89–110 (2011)
Davey, B.A., Knox, B.J.: Regularising natural dualities. Acta Math. Univ. Comen. 68, 295–318 (1999)
Davey, B.A., Knox, B.J.: From rectangular bands to k-primal algebras. Semigroup Forum 64, 29–54 (2002)
Davey, B.A., Quackenbush, R.W.: Natural duality for dihedral varieties. J. Aust. Math. Soc. A 61, 216–228 (1996)
Davey, B.A., Werner, H.: Dualities and equivalences for varieties of algebras. In: Contributions to Lattice Theory, Szeged, 1980. Colloquia Mathematica Societatis János Bolyai, vol. 33, pp. 101–275. North-Holland, Amsterdam (1983)
Davey, B.A., Willard, R.: The dualisability of a quasi-variety is independent of the generating algebra. Algebra Univers. 45, 103–106 (2001)
Dolinka, I.: Finite regular bands are finitely related. Bull. Aust. Math. Soc. 87, 1–9 (2013)
Fennemore, C.: All varieties of bands. Math. Nachr. 48, 237–262 (1971)
Gerhard, J.A.: The lattice of equational classes of idempotent semigroups. J. Algebra 15, 195–224 (1970)
Golubov, E.A., Sapir, M.V.: Varieties of finitely approximable semigroups. Sov. Math. Dokl. 20(4), 828–832 (1979)
Hobby, D.: Nondualisable semigroups. Bull. Aust. Math. Soc. 65, 491–502 (2002)
Hofmann, K.H., Mislove, M., Stralka, A.: The Pontryagin Duality of Compact 0-Dimensional Semi-Lattices and Its Applications. Lecture Notes in Mathematics, vol. 396. Springer, Berlin (1974)
Howie, J.M.: Fundamentals of Semigroups Theory. Oxford University Press, Oxford (1995)
Jackson, M.: Dualisability of finite semigroups. Int. J. Algebra Comput. 13, 481–497 (2003)
Kimura, N.: Note on idempotent semigroups, IV. Proc. Jpn. Acad. 34, 121–123 (1958)
Mayr, P.: On finitely related semigroups. Semigroup Forum 86, 613–633 (2013)
McKenzie, R.: Residually small varieties of semigroups. Algebra Univers. 13, 171–201 (1981)
McLean, D.: Idempotent semigroups. Am. Math. Mon. 61, 110–113 (1954)
Quackenbush, R.W., Szabó, Cs.: Nilpotent groups are not dualisable. J. Aust. Math. Soc. 72, 173–179 (2002)
Quackenbush, R.W., Szabó, Cs.: Strong duality for metacyclic groups. J. Aust. Math. Soc. 73, 377–392 (2002)
Saramago, M.J.: Some remarks on dualisability and endodualisability. Algebra Univers. 43, 197–212 (2000)
Shafaat, A.: On the structure of certain idempotent semigroups. Trans. Am. Math. Soc. 149, 371–378 (1970)
Acknowledgements
The author would like to thank the referee of this paper for his helpful suggestions. This paper contains a part of the author’s doctoral thesis written under supervision of Professor Brian Davey and Dr. Marcel Jackson. The author would like to thank them for their excellent guidance.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mikhail Volkov.
Rights and permissions
About this article
Cite this article
AlDhamri, N. Dualities for quasi-varieties of bands. Semigroup Forum 88, 417–432 (2014). https://doi.org/10.1007/s00233-013-9541-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00233-013-9541-4





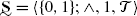 . A simple modification of the proof shows that 〈{0,1};∧〉, 〈{0,1};∧,0〉, 〈{0,1};∧,0,1〉 are also dualisable.
. A simple modification of the proof shows that 〈{0,1};∧〉, 〈{0,1};∧,0〉, 〈{0,1};∧,0,1〉 are also dualisable.