Abstract
In this paper we investigate the ascending chain conditions on principal left and right ideals for semidirect products of semigroups and show how this is connected to the corresponding problem for rings of skew generalized power series. Let S be a left cancellative semigroup with a unique idempotent e, T a right cancellative semigroup with an idempotent f and \(\omega: T \to \operatorname {End}(S)\) a semigroup homomorphism such that ω(f)=id S . We show that in this case the semidirect product S⋊ ω T satisfies the ascending chain condition for principal left ideals (resp. right ideals) if and only if S and T satisfy the ascending chain condition for principal left ideals (resp. right ideals and \(\operatorname {Im}\omega(t)\) is closed for complete inverses for all t∈T). We also give several examples to show that for more general semigroups these implications may not hold.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The aim of this article is to investigate how ascending chain conditions for principal left and right ideals behave in regard to semidirect products of semigroups. The motivation comes from the following theorem for rings.
Theorem 1.1
[5, Theorem 3.3]
Let R be a ring, (S,⋅,≤) a strictly totally ordered monoid and \(\omega: S \to \operatorname {End}(R)\) a monoid homomorphism.
-
(i)
R[[S,ω]] is an ACCPL-domain if and only if R is an ACCPL-domain, S is an ACCPL-monoid and ω s is injective for any s∈S.
-
(ii)
R[[S,ω]] is an ACCPR-domain if and only if R is an ACCPR-domain, S is an ACCPR-monoid and ω s is injective and preserves nonunits of R for any s∈S.
We are able to prove a similar result for semidirect products of semigroups (see Theorem 3.11 and Corollary 3.12) from where the main parts of the above theorem follow as a corollary.
Let S be a semigroup. If S is not a monoid we may adjoint an identity 1 to form a monoid which will be denoted by S 1. If S is already a monoid we define S 1=S. Recall that a left ideal of S is any nonempty subset of S that is closed under multiplication from the left with elements of S. Right ideals are defined analogously. A principal left (resp. right) ideal of S generated by an element a∈S is given by S 1 a (resp. aS 1).
An element b∈S is an inverse of a∈S if aba=a and bab=b. If such an element b exists then a is said to be a regular element of S. If there exists an inverse b of a such that ab=ba then a is completely regular and we shall say that b is a complete inverse of a. If such b exists then it is unique. The set of all regular elements of S will be denoted by \(\operatorname {Reg}(S)\).
A semigroup S is said to satisfy the ascending chain condition on principal left ideals (ACCPL) if there does not exist an infinite strictly ascending chain of principal left ideals of S. The ascending chain condition on principal right ideals (ACCPR) if defined analogously. Semigroups that satisfy the ACCPL (resp. ACCPR) are sometimes called ACCPL-semigroups (resp. ACCPR-semigroups). It has been shown in [5, Example 2.6] that these two conditions are independent. For any undefined concepts on semigroups we refer the reader to [1].
In Sect. 2 we present some results involving cancellativity that we need later on. In particular in the class of all left cancellative semigroups we give a characterization of those semigroups that contain at most one idempotent. The main results are contained is Sect. 3 where we study in detail under what conditions the semidirect product of semigroups will satisfy ACCPL and ACCPR. We divide the proof of the main theorem into several lemmas and give numerous examples to demonstrate that the conditions involved are essential. At the end of Sect. 3 we show how our results are connected to the skew generalized power series rings. We postpone the more technical proofs of our examples to Sect. 4.
2 Cancellativity and chain conditions
Ascending chain conditions for principal one-sided ideals are essentially conditions on sequences of elements. We put this simple fact into a lemma since we will use it throughout this paper. The point of this lemma is also that even though one-sided ideals are given via S 1 we need only work with sequences in S.
Lemma 2.1
For an arbitrary semigroup S the following are equivalent:
-
(1)
S is an ACCPR-semigroup.
-
(2)
For any sequences (a n ) n∈ℕ and (b n ) n∈ℕ in S such that a n =a n+1 b n for all n∈ℕ, there exists N∈ℕ and a sequence (c n ) n∈ℕ in S such that a n+1=a n c n for all n≥N.
-
(3)
For any sequences (a n ) n∈ℕ and (b n ) n∈ℕ in S such that a n =a n+1 b n for all n∈ℕ, there exists N∈ℕ and c N ∈S such that a N+1=a N c N .
Proof
\(\mathrm{(1)} \Rightarrow \mathrm{(2)}\): If (a n ) n∈ℕ and (b n ) n∈ℕ are as in (2) then we have a chain a 1 S 1⊆a 2 S 1⊆a 3 S 1⊆⋯ of principal right ideals, which must stabilize say at N. Hence there exists a sequence (c n ) n∈ℕ⊆S 1 such that a n+1=a n c n for all n≥N. If c n =1 for some n, then a n+1=a n and hence a n+1=a n =a n+1 b n =a n b n . So we may take c n =b n instead of c n =1. The new sequence (c n ) n∈ℕ then lies in S.
\(\mathrm{(2)} \Rightarrow \mathrm{(3)}\): This is obvious.
\(\mathrm{(3)} \Rightarrow \mathrm{(1)}\): Suppose there exists a strictly increasing chain a 1 S 1⊊a 2 S 1⊊a 3 S 1⊊⋯ of principal right ideals of S. Then there is a sequence (b n ) n∈ℕ⊆S 1 such that a n =a n+1 b n for all n∈ℕ. Infact b n must lie in S since the inclusions in the chain are strict. By assumption a N+1=a N c N ∈a N S 1 for some N and c N ∈S, which is a contradiction. □
Of course with obvious changes we also get a version of the above lemma for ACCPL.
Left and right cancellativity of semigroups is often very helpful when considering ACCPR and ACCPL. Recall that a semigroup S is left (resp. right) cancellative if ax=ay (resp. xa=ya) implies x=y for all a,x,y∈S. The following is a generalization of [5, Proposition 2.1] to semigroups and only one-sided cancellativity is assumed.
Proposition 2.2
For a left cancellative semigroup S the following are equivalent:
-
(1)
S is an ACCPR-semigroup.
-
(2)
For any sequences (a n ) n∈ℕ and (b n ) n∈ℕ in S such that a n =a n+1 b n for all n∈ℕ, there exists N∈ℕ such that b n is regular and a n ∈a n S for all n≥N.
-
(3)
For any sequences (a n ) n∈ℕ and (b n ) n∈ℕ in S such that a n =a n+1 b n for all n∈ℕ, there exists N∈ℕ such that b N is regular and a N+1∈a N+1 S.
Proof
\(\mathrm{(1)} \Rightarrow \mathrm{(2)}\): Let (a n ) n∈ℕ and (b n ) n∈ℕ be as in (2). Then by Lemma 2.1 a n+1=a n c n for some c n ∈S for all n≥N. Choose any n≥N. Then a n =a n+1 b n =a n c n b n ∈a n S, which implies a n c n =a n c n b n c n and by left cancellativity c n =c n b n c n . From this we get c n b n =c n b n c n b n and again by left cancellativity b n =b n c n b n . This shows that b n is regular.
\(\mathrm{(2)} \Rightarrow \mathrm{(3)}\): This is obvious.
\(\mathrm{(3)} \Rightarrow \mathrm{(1)}\): Let (a n ) n∈ℕ,(b n ) n∈ℕ⊆S be sequences such that a n =a n+1 b n for all n∈ℕ. By assumption there exists N∈ℕ such that b N is regular and a N+1=a N+1 x for some x∈S. Let c be an inverse of b N . Then cb N cx=cx and by left cancellativity b N cx=x. Hence a N+1=a N+1 x=a N+1 b N cx=a N cx. By Lemma 2.1 S satisfies ACCPR. □
Next we characterize left cancellative semigroups in which at most one idempotent exists.
Proposition 2.3
For a left cancellative semigroup S the following are equivalent:
-
(1)
S has at most one left identity.
-
(2)
S has at most one idempotent.
-
(3)
Every inverse in S is complete.
-
(4)
Each element in S has at most one inverse.
-
(5)
If s=sab for some elements a,b,s in S then a is a complete inverse of b.
-
(6)
\(\operatorname {Reg}(S)\) is either empty or a subgroup of S.
Proof
Let s and x be elements of S such that s=sx. Then for all a∈S we have sa=sxa and left cancellativity implies a=xa. So x is a left identity.
\(\mathrm{(1)} \Leftrightarrow \mathrm{(2)}\): Any left identity is an idempotent and any idempotent e=e 2 is a left identity by the above.
\(\mathrm{(2)} \Rightarrow \mathrm{(3)}\): Let a′ be an inverse of a. Then aa′ and a′a are idempotents, hence they are equal.
\(\mathrm{(3)} \Rightarrow \mathrm{(4)}\): This is obvious since complete inverses are unique.
\(\mathrm{(4)} \Rightarrow \mathrm{(1)}\): Let e and f be two left identities of S. Then efe=e and fef=f and also eee=e. So e and f are both inverses of e, hence e=f.
\(\mathrm{(1)} \Rightarrow \mathrm{(5)}\): If s=sab then also sa=saba, so by the above ab and ba are left identities. This implies aba=a, bab=b and by assumption ab=ba.
\(\mathrm{(5)} \Rightarrow \mathrm{(1)}\): Let e and f be two left identities of S. Then e=efe so by assumption e and f are each others complete inverses. In particular they commute, hence e=fe=ef=f.
\(\mathrm{(2)} \Rightarrow \mathrm{(6)}\): Every regular element is L-related to some idempotent and R-related to some idempotent. So either \(\operatorname {Reg}(S)\) is empty or every element in \(\operatorname {Reg}(S)\) is H-related to a unique idempotent of S. In the second case \(\operatorname {Reg}(S)\) is an H-class, because every element that is related to an idempotent is automatically regular. Since this H-class contains an idempotent it is a subgroup of S.
\(\mathrm{(6)} \Rightarrow \mathrm{(2)}\): This follows from the fact that all idempotents lie in \(\operatorname {Reg}(S)\) and a group has only one idempotent. □
Observe that conditions (2) and (6) are equivalent in any semigroup. Note also that in a left cancellative monoid S the identity element 1 is a unique left identity and regular elements are exactly the invertible elements of S in the group sense. The following example shows that a left cancellative semigroup with a unique left identity need not be a left cancellative monoid.
Example 2.4
Let ℕ denote the set of positive integers. Define multiplication on S=ℕ×ℕ by
It is easy to see that (S,⋅) is a left cancellative semigroup with a unique left identity (1,1). Since (1,1) is not a right identity, (S,⋅) is not a monoid. This is an example with trivial group \(\operatorname {Reg}(S)\). However if G is any group then S×G is an example with \(\operatorname {Reg}(S \times G)\) isomorphic to G.
Proposition 2.2 has a simple corollary (cf. [5, Corollary 2.2] for part (2)).
Corollary 2.5
Let T be a left cancellative ACCPR-semigroup with at most one idempotent.
-
(1)
Let ψ:S→T be a semigroup homomorphism such that \(\psi^{-1}(\operatorname {Reg}(T)) \subseteq \operatorname {Reg}(S)\). If ψ is injective or if S is a left cancellative monoid then S is an ACCPR-semigroup as well.
-
(2)
If S is a subsemigroup of T such that \(\operatorname {Reg}{S}=\operatorname {Reg}{T} \cap S\) then S is an ACCPR-semigroup as well.
Proof
(1): If ψ is injective then S is also a left cancellative semigroup. So in both cases we may use Proposition 2.2. Let (a n ) n∈ℕ and (b n ) n∈ℕ be sequences in S such that a n =a n+1 b n for all n∈ℕ. Since ψ(a n )=ψ(a n+1)ψ(b n ) for all n∈ℕ there exists N∈ℕ and t∈T such that ψ(b N ) is regular and ψ(a N+1)=ψ(a N+1)t. By assumption b N is also regular. Let c be an inverse of b N . Then ψ(c) is an inverse of ψ(b N ). As in the proof of Proposition 2.3 this implies that t and ψ(b N )ψ(c) are idempotents in T, so they are equal. Hence ψ(a N+1)=ψ(a N+1)ψ(b N )ψ(c)=ψ(a N+1 b N c). If ψ is injective then a N+1=a N+1 b N c and so a N+1∈a N+1 S. If S is a monoid then we also have a N+1∈a N+1 S. So S satisfies condition (3) of Proposition 2.2 hence it is an ACCPR-semigroup.
(2): In this case the inclusion of S into T is an injective homomorphism that satisfies the condition in (1). □
3 Semidirect product of semigroups
Let S and T be two semigroups and \(\omega: T \to \operatorname {End}(S)\) a semigroup homomorphism where \(\operatorname {End}(S)\) is the monoid of all endomorphisms of S. The image of an element t∈T under ω will be denoted by ω t . Now define multiplication on the Cartesian product S×T by
Then the set S×T together with this multiplication becomes a semigroup called the semidirect product of semigroups S and T over ω. This semigroup will be denoted by S⋊ ω T.
The following lemma is easy to verify. Some parts of it can be found in [2, Lemmas 3.1 and 3.2].
Lemma 3.1
Let S and T be semigroups and \(\omega: T \to \operatorname {End}{S}\) a semigroup homomorphism. Then the following holds.
-
(1)
If S and T are right cancellative then S⋊ ω T is right cancellative.
-
(2)
If S and T are left cancellative and ω t is injective for all t∈T then S⋊ ω T is left cancellative.
If there exists u∈T such that ω u is surjective then the implications go the other way as well.
If we take ω t =id S for all t∈T then S⋊ ω T is the direct product of S and T. It is known that for cancellative monoids S and T the direct product S×T satisfies ACCPL if and only if S and T satisfy ACCPL (this is true also if S and T are not cancellative, see Theorem 3.13). The same holds even for infinite direct sums of cancellative monoids (see [3] and [5]). The aim of this section is to investigate how ACCPL and ACCPR behave in regard to semidirect products of semigroups.
For the rest of this section, let S and T be semigroups and \(\omega : T \to \operatorname {End}(S)\) a semigroup homomorphism. First we consider when the fact that the semidirect product satisfies ACCPL or ACCPR implies the same for each factor.
Lemma 3.2
If S⋊ ω T satisfies ACCPL (ACCPR) and there exists f∈T such that f 2=f and ω f =id S then S satisfies ACCPL (ACCPR) as well.
Proof
Denote Q=S⋊ ω T and let s 1,s 2∈S. If s 1=ss 2 for some s∈S then (s 1,f)=(s,f)(s 2,f). If (s 1,f)=(s,t)(s 2,f) for some s∈S and t∈T then f=tf and s 1=sω t (s 2). Hence ω t =ω t ω f =ω tf =ω f =id S and so s 1=ss 2. This shows that
If s 1=s 2 s for some s∈S then (s 1,f)=(s 2,f)(s,f). If (s 1,f)=(s 2,f)(s,t) for some s∈S and t∈T then s 1=s 2 ω f (s)=s 2 s. This shows that
The conclusion of the lemma follows easily from (1) and (2). □
Note that the existence of an idempotent f as in Lemma 3.2 gives us an inclusion S↪S⋊ ω T defined by s↦(s,f). As the next example demonstrates the existence of an idempotent alone does not suffice for the conclusion of the lemma, not even if there are other elements in T that act on S as the identity map.
Example 3.3
Let S=(0,1]×(0,∞) be equipped with multiplication and T=ℕ∪{∞} be equipped with addition (here n+∞=∞+n=∞ and ∞+∞=∞). Define \(\omega: T \to \operatorname {End}(S)\) by

So ∞ is an idempotent in T but ω ∞≠id S . The commutativity of multiplication in (0,∞) ensures that ω ∞ is an endomorphism of S. Obviously ω is a homomorphism. Simple calculations show that for all (a,b)∈S and all n∈ℕ we have

and

Suppose there is a strictly increasing chain of principal left or right ideals in S⋊ ω T generated by ((a k ,b k ),t k ). Then t k =∞ for at most one k and from this k on the sequence t k must be decreasing and hence finite. So S⋊ ω T satisfies ACCPL and ACCPR (and so does T). However S does not satisfy ACCPL nor ACCPR, since (0,1] does not (see Theorem 3.13).
Lemma 3.4
If S⋊ ω T satisfies ACCPL (ACCPR) and there exists e∈S such that e 2=e then T satisfies ACCPL (ACCPR) as well.
Proof
Let S⋊ ω T be an ACCPL-semigroup. Let t n and u n be elements of T such that t n =u n t n+1 for all n∈ℕ. Define \(x_{n}=(\omega_{t_{n}}(e),t_{n}) \in S \rtimes_{\omega}T\) and \(y_{n}=(\omega_{t_{n}}(e),u_{n}) \in S \rtimes_{\omega}T\). Then

for all n∈ℕ. Since S⋊ ω T is an ACCPL-semigroup there exist N∈ℕ and (s,t)∈S⋊ ω T such that x N+1=(s,t)x N . In particular t N+1=tt N . Therefore T is an ACCPL-semigroup.
Now let S⋊ ω T be an ACCPR-semigroup. Let t n and v n be elements of T such that t n =t n+1 v n for all n∈ℕ. Define \(x_{n}=(\omega_{t_{1}}(e),t_{n}) \in S \rtimes_{\omega}T\) and \(y_{n}=(\omega_{v_{n}v_{n-1} \ldots v_{1}}(e),v_{n}) \in S \rtimes_{\omega}T\). Then

for all n∈ℕ. As above this implies t N+1=t N t for some N∈ℕ and t∈T. Hence T is an ACCPR-semigroup. □
The following example shows that the lemma does not hold if S has no idempotent.
Example 3.5
Let S=ℕ be equipped with addition and T=(0,1] with multiplication. Let ω be trivial, so S⋊ ω T=S×T. For all (n,t)∈S×T we have
From this it is obvious that S×T satisfies ACCPL and ACCPR (and so does S), however T does not satisfy ACCPL nor ACCPR.
Now we investigate when the semidirect product inherits the property of satisfying ACCPL and ACCPR from its factors. As it turns out these two conditions for semidirect products are very different, so we treat them separately.
Lemma 3.6
If S and T satisfy ACCPL and for all t,u∈T with ut=t there exists v∈T with vt=t such that ω v ω u =ω u ω v =id S then S⋊ ω T satisfies ACCPL as well.
Proof
Suppose s n ,r n ∈S and t n ,u n ∈T are such that we have (s n ,t n )=(r n ,u n )(s n+1,t n+1) in S⋊ ω T for all n∈ℕ. So \(s_{n}=r_{n}\omega_{u_{n}}(s_{n+1})\) and t n =u n t n+1 for all n∈ℕ. Since T is an ACCPL-semigroup there exists m∈ℕ such that t n+1=v n t n for some v n ∈T for all n≥m. For n>m define \(s_{n}'=\omega_{u_{m}u_{m+1} \ldots u_{n-1}}(s_{n}) \in S\). Then
and since S is an ACCPL-semigroup there exists k>m and s∈S such that \(s_{k+1}'=ss_{k}'\). Since t n+1=v n u n t n+1 for all n≥m by assumption there exist w n ∈T with w n t n+1=t n+1 such that \(\omega_{w_{n}}\omega_{v_{n}u_{n}}=\mathit{id}_{S}\) for all n≥m. If we denote z n =w n v n then \(\omega_{z_{n}}\) is a left inverse of \(\omega_{u_{n}}\) for all n≥m. Hence
where \(s'=\omega_{z_{k}z_{k-1} \ldots z_{m}}(s)\). In addition z k t k =w k v k t k =w k t k+1=t k+1, so (s k+1,t k+1)=(s′,z k )(s k ,t k ). This shows that S⋊ ω T is an ACCPL-semigroup. □
Without additional assumptions about elements of T the conclusion of the lemma may not hold. In fact even if we only exclude the assumption vt=t the semidirect product may not satisfy ACCPL.
Example 3.7
Let S=〈…,x −2,x −1,x 0,x 1,x 2…〉 be the free monoid over the set {…,x −2,x −1,x 0,x 1,x 2,…}, 〈v〉 the free monoid over {v} and T 1 a monoid with representation T 1=〈t,u | tu=ut=t〉. Define the monoid T by T=T 1×〈v〉=〈t,u,v | tu=ut=t,tv=vt,uv=vu〉. First note that T 1={1,u,u 2,u 3,…}∪{t,t 2,t 3,…} and

So it is obvious that T 1 satisfies ACCPL. Since any free monoid satisfies ACCPL, both S and T (by Theorem 3.13) satisfy ACCPL. Now define endomorphisms of S by

Since ω t ω u =ω u ω t =ω t , ω t ω v =ω v ω t and ω u ω v =ω v ω u =id S , these endomorphisms induce a homomorphism \(\omega: T \to \operatorname {End}(S)\). If \(\overline{u}\overline{t}=\overline{t}\) in T then \(\overline{u}=u^{n}\) for some n∈ℕ∪{0} and for \(\overline{v}=v^{n}\) we have \(\omega_{\overline{v}}\omega_{\overline{u}}=\omega_{\overline{u}}\omega_{\overline{v}}=\mathit{id}_{S}\). The semigroup S⋊ ω T does not satisfy ACCPL since the sequence of principal left ideals generated by elements (x n ,t) is an infinite strictly increasing chain. This is because (x n ,t)=(1,u)(x n+1,t) for all n∈ℤ. However if (x n+1,t)=(s,a)(x n ,t)=(sω a (x n ),at) then at=t implies a=u k for some k∈ℕ∪{0} and hence sω a (x n )=sx n−k ≠x n+1 which is a contradiction.
Lemma 3.8
If S and T satisfy ACCPR and for all p,r,s∈S and t,u∈T srω t (p)=s and t=tu imply \(r \in \operatorname {Im}\omega_{t}\) then S⋊ ω T satisfies ACCPR as well.
Proof
Let s n ,r n ∈S and t n ,u n ∈T be such that (s n ,t n )=(s n+1,t n+1)(r n ,u n ) for all n∈ℕ. So \(s_{n}=s_{n+1}\omega_{t_{n+1}}(r_{n})\) and t n =t n+1 u n for all n∈ℕ. Since S and T are ACCPR-semigroups there exist k∈ℕ, s∈S and t∈T such that s k+1=s k s and t k+1=t k t. Then \(s_{k}=s_{k}s\omega_{t_{k+1}}(r_{k})\) and t k+1=t k+1 u k t, hence by assumption there exists r∈S such that \(s=\omega_{t_{k+1}}(r)\). This implies
which means that S⋊ ω T satisfies ACCPR. □
We will say that a subset M of a semigroup S is closed for complete inverses if r∈M whenever r is a complete inverse of some element of M. In the main theorem the above lemma will be used in the following way. Let S and T satisfy ACCPR and suppose in addition that for all p,r,s∈S and t,u∈T srω t (p)=s and t=tu imply that r is a complete inverse of ω t (p). If \(\operatorname {Im}\omega_{t}\) is closed for complete inverses for all t∈T with t=tu for some u∈T then by the above lemma S⋊ ω T satisfies ACCPR. The next lemma shows that the inverse implication holds as well.
Lemma 3.9
If S⋊ ω T satisfies ACCPR and for all p,r,s∈S and t,u∈T srω t (p)=s and t=tu imply that r is a complete inverse of ω t (p) then \(\operatorname {Im}\omega_{t}\) is closed for complete inverses for all t∈T with t=tu for some u∈T.
Proof
Let t=tu in T and let r∈S be a complete inverse of ω t (p) for some p∈S. Define x n =(r n,t)∈S⋊ ω T and y=(p,u)∈S⋊ ω T. Then
for all n∈ℕ and since S⋊ ω T is an ACCPR-semigroup there exists k∈ℕ, q∈S and v∈T such that x k+1=x k ⋅(q,v) in S⋊ ω T. The first component of this equation gives us r k+1=r k ω t (q). If we multiply this by ω t (p) from the right side and use the fact that r is a complete inverse of ω t (p) we get
By assumption this means that ω t (q) in a complete inverse of ω t (p). So r=ω t (q), since complete inverses are unique. □
Observe that in the paragraph before this lemma we could exchange the term “complete inverse” with term “unique inverse” or even “inverse” and the implications would still hold. However in this case the inverse implication would fail to hold. Namely, the following example shows that we can not replace “complete inverse” with “unique inverse” in the above lemma. Since the proof of the example is rather technical we will present it in the last section.
Example 3.10
Let S=S 1×S 2 where S 1 and S 2 are semigroups with representations S 1=〈z,w | w 2=w〉 and S 2=〈x,y | xyx=x, yxy=y〉. Let T={0,1,2} be a submonoid of the multiplicative monoid (ℤ4,⋅). Define a homomorphism \(\omega: T \to \operatorname {End}(S)\) by

It is clear that the above induces an endomorphism ω 2. It is easy to check that ω is indeed a homomorphism. As it turns out (see last section) the semigroup S⋊ ω T satisfies ACCPR and for all s,r,p∈S srp=s implies that r is a unique inverse of p (in particular all inverses in S are unique). However even though 2=2⋅1 in T, \(\operatorname {Im}\omega_{2}\) is not closed for unique inverses since \((w,y) \notin \operatorname {Im}\omega_{2}\) is a unique inverse of \((w,x) \in \operatorname {Im}\omega_{2}\).
Now we assemble everything into our main theorem.
Theorem 3.11
Let S and T be semigroups with idempotents e and f respectively and \(\omega: T \to \operatorname {End}{S}\) a semigroup homomorphism.
-
(1)
Suppose that for all t,u∈T with ut=t there exists v∈T with vt=t such that ω v ω u =ω u ω v =id S . Then S⋊ ω T satisfies ACCPL if and only if S and T satisfy ACCPL.
-
(2)
Suppose that ω f =id S and that for all p,r,s∈S and t,u∈T srω t (p)=s and t=tu imply that r is a complete inverse of ω t (p). Then S⋊ ω T satisfies ACCPR if and only if S and T satisfy ACCPR and \(\operatorname {Im}\omega_{t}\) is closed for complete inverses for all t∈T with t=tu for some u∈T.
Proof
(1): Since f 2=f by assumption ω f is invertible. But ω f ω f =ω f , hence ω f =id S . The rest follows directly from Lemmas 3.2, 3.4 and 3.6.
(2): This follows from Lemmas 3.2, 3.4, 3.8 and 3.9. □
Assuming some cancellativity simplifies the formulation of the above theorem.
Corollary 3.12
Let S be a left cancellative semigroup with a unique idempotent e and T a right cancellative semigroup with an idempotent f such that ω f =id S . Then the following holds.
-
(1)
S⋊ ω T satisfies ACCPL if and only if S and T satisfy ACCPL.
-
(2)
S⋊ ω T satisfies ACCPR if and only if S and T satisfy ACCPR and \(\operatorname {Im}\omega_{t}\) is closed for complete inverses for all t in T.
Proof
(1): If ut=t in T then fut=ft and right cancellativity implies fu=f. Using ω on this we get ω u =id S . Now apply Theorem 3.11.
(2): Proposition 2.3 ensures that the assumptions of Theorem 3.11 are satisfied. Since T is right cancellative the idempotent f is a right identity. So t=tf for all t∈T. Now apply Theorem 3.11. □
For a semigroup S we will denote by \(\operatorname {SEnd}(S)\) the monoid of all surjective endomorphisms of S.
Theorem 3.13
Let S and T be semigroups with idempotents and let \(\omega: T \to \operatorname {SEnd}(S)\) be a semigroup homomorphism. Then S⋊ ω T satisfies ACCPL (ACCPR) if and only if S and T satisfy ACCPL (ACCPR).
Proof
If ut=t in T then ω u =id S since ω t is surjective. In particular ω f =id s for any idempotent f∈T. Also \(\operatorname {Im}\omega_{t}=S\) for all t∈T. Now the theorem follows from Lemmas 3.2, 3.4, 3.6 and 3.8. □
In particular the theorem states that for semigroups S and T with idempotents S×T satisfies ACCPL (ACCPR) if and only if S and T satisfy ACCPL (ACCPR).
In [4] the ring of skew generalized power series was introduced. The construction is as follows. Let (S,⋅,≤) be a strictly ordered monoid, R a ring with identity and \(\omega: S \to \operatorname {End}{R}\) a monoid homomorphism where \(\operatorname {End}(R)\) is the monoid of all ring endomorphisms of R that preserve the identity. Let R[[S,ω,≤]] be the set of all maps f:S→R whose support \(\operatorname {supp}(f)=\{s \in S ; \ f(s) \neq0\}\) is artinian and narrow (for details see [4]). For two such maps f and g the set X s (f,g)={(x,y)∈S×S; xy=s, f(x)≠0, g(y)≠0} turns out to be finite for all s∈S. Thus one can define a multiplication on R[[S,ω,≤]] by
if X s (f,g)≠∅ and (fg)(s)=0 otherwise. Then R[[S,ω,≤]] together with pointwise addition and above multiplication becomes a ring called the ring of skew generalized power series with coefficients in R and exponents in S.
Conditions ACCPL and ACCPR can be defined for rings analogously to those for semigroups. In fact a ring (R,+,⋅) satisfies ACCPL (ACCPR) if and only if the multiplicative monoid (R,⋅) does. A domain R satisfies ACCPL (ACCPR) if and only if the cancellative monoid R ∗=(R∖{0},⋅) does. In [5, Theorem 3.3] the authors have characterized skew generalized power series rings with exponents in a strictly totally ordered monoid that are domains satisfying ACCPL (resp. ACCPR). Now we show how part of this result can be derived from the above. In fact this was the motivation for our considerations (compare Corollary 3.12 with [5, Theorem 3.3]).
Let R be a domain with identity, S a strictly totally ordered monoid and \(\omega: S \to \operatorname {End}(R)\) a monoid homomorphism such that ω s is injective for all s∈S. Then by [5, Proposition 3.1(ii)] R[[S,ω,≤]] is a domain, hence R[[S,ω,≤]]∗ is a cancellative monoid. For any f∈R[[S,ω,≤]]∗ the set \(\operatorname {supp}(f) \subseteq S\) is well ordered and so it has a smallest element that we denote by π(f). By [5, Proposition 3.1(i)] the map

is a monoid homomorphism. Since S is strictly totally ordered, it is cancellative. Lemma 3.1 then implies that R ∗⋊ ω S is a cancellative monoid. If f is in \(\psi^{-1}(\operatorname {Reg}(R^{\ast}\rtimes_{\omega}S))\) then (f(π(f)),π(f)) is invertible in R ∗⋊ ω S. It is easy to see that this implies that both π(f) and f(π(f)) are invertible, so by [5, Proposition 3.2] f is invertible in R[[S,ω,≤]]∗. Thus \(\psi^{-1}(\operatorname {Reg}(R^{\ast}\rtimes_{\omega}S)) \subseteq \operatorname {Reg}(R[[S,\omega,\leq]]^{\ast})\). If S and R satisfy ACCPL then by Corollary 3.12 so does R ∗⋊ ω S. Similarly if S and R satisfy ACCPR and ω s preserves nonunits of R for all s∈S (that is \(\operatorname {Im}\omega_{s}\) is closed for complete inverses, since R ∗ is cancellative monoid) then by Corollary 3.12 R ∗⋊ ω S satisfies ACCPR as well. Corollary 2.5 now implies that R[[S,ω,≤]]∗ satisfies ACCPL, respectively ACCPR, hence so does the ring R[[S,ω,≤]].
4 Some proofs
In this section we present the proofs needed for Example 3.10. Assume that all the notations are as in the example. By definition S 2=F/∼, where F is the free semigroup over the set {x,y} and ∼ is the least congruence relation on F such that xyx∼x and yxy∼y. First we need a more explicit description of the relation ∼.
A word in F is called alternating if it does not contain xx or yy as a subword (u is a subword of v if v∈F 1 uF 1). For an alternating word a define
Note that \(\bar{a}\) is again an alternating word that starts and ends with the same letters as a and \(\bar{\bar{a}}=\bar{a}\). An arbitrary word in F is a unique product of its maximal alternating subwords. If u=u 1 u 2…u n , where u i are the maximal alternating subwords of u then define
Note that \(\bar{u}_{i}\) are exactly the maximal alternating subwords of \(\bar{u}\), since \(\bar{\phantom{u}}\) does not change the beginning or the end of the word. So \(\bar{\bar{u}}=\bar{u}\).
Step 1
For u,v∈F we have u∼v if and only if \(\bar{u}=\bar{v}\).
For an arbitrary word u∈F assume the following notations
- \(\operatorname {b}(u)\) :
-
the first letter of u,
- \(\operatorname {e}(u)\) :
-
the last letter of u,
- \(\operatorname {B}(u)\) :
-
the first maximal alternating subword of u,
- \(\operatorname {E}(u)\) :
-
the last maximal alternating subword of u,
- |u|:
-
the length of u,
-
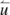 :
: -
the word \(\bar{u}\) without the first letter,
-
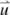 :
: -
the word \(\bar{u}\) without the last letter,
where we allow  and
and  to be empty. By considering all possible cases it can be seen that for two alternating words a and c we have \(\overline{ac}=\overline{\bar{a}\bar{c}}\). Since we only have four possibilities for \(\bar{a}\) and \(\bar{c}\) it is easy to check that
to be empty. By considering all possible cases it can be seen that for two alternating words a and c we have \(\overline{ac}=\overline{\bar{a}\bar{c}}\). Since we only have four possibilities for \(\bar{a}\) and \(\bar{c}\) it is easy to check that

Let u=u 1 u 2…u n and v=v 1 v 2…v m be arbitrary words in F, where u i and v i are maximal alternating subwords. Then all u i and v i except perhaps u n and v 1 are maximal alternating subwords of uv, thus
and hence by the above

Now define a relation ≈ in F by u 1≈u 2 if and only if \(\bar{u}_{1}=\bar{u}_{2}\). Clearly this is an equivalence relation. If u 1≈u 2 then \(\operatorname {b}(u_{1})=\operatorname {b}(u_{2})\), \(\operatorname {e}(u_{1})=\operatorname {e}(u_{2})\), \(\operatorname {B}(\bar{u}_{1})=\operatorname {B}(\bar{u}_{2})\) and \(\operatorname {E}(\bar{u}_{1})=\operatorname {E}(\bar {u}_{2})\). So \(\overline{u_{1}v}\) and \(\overline{u_{2}v}\) (resp. \(\overline {vu_{1}}\) and \(\overline{vu_{2}}\)) will calculate in the same way. Hence u 1 v≈u 2 v (resp. vu 1≈vu 2). Thus ≈ is in fact a congruence. For arbitrary u∈F we have \(\bar{u} \sim u\) (for alternating words this is clear, for arbitrary words this is a consequences of ∼ being a congruence), so the relation ≈ is contained in the relation ∼. Since xyx≈x and yxy≈y, the minimality of ∼ implies that relations ∼ and ≈ are the same.
Step 2
If srp∼s in F then one of the following holds: (r∼x and p∼y) or (r∼y and p∼x) or (r∼xy∼p) or (r∼yx∼p).
If we denote e=rp then \(\overline{se}=\bar{s}\). Since \(\overline {se}=\bar{s}\bar{e}\) would lead to a contradiction e=∅ we must have  . This means that
. This means that  , hence \(\bar{e}=\operatorname {b}(e)\operatorname {e}(s)\), where \(\operatorname {b}(e) \neq \operatorname {e}(s)\) by (3). This implies e∼xy or e∼yx. By symmetry we may assume e∼xy, so \(\overline{rp}=xy\). If \(\overline {rp}=\bar{r}\bar{p}\) then \(\bar{r}=x\) and \(\bar{p}=y\). Now let
, hence \(\bar{e}=\operatorname {b}(e)\operatorname {e}(s)\), where \(\operatorname {b}(e) \neq \operatorname {e}(s)\) by (3). This implies e∼xy or e∼yx. By symmetry we may assume e∼xy, so \(\overline{rp}=xy\). If \(\overline {rp}=\bar{r}\bar{p}\) then \(\bar{r}=x\) and \(\bar{p}=y\). Now let  , hence by (3) \(\operatorname {e}(r) \neq \operatorname {b}(p)\) and \(|\operatorname {E}(\bar{r})||\operatorname {B}(\bar{p})| \neq1\). If
, hence by (3) \(\operatorname {e}(r) \neq \operatorname {b}(p)\) and \(|\operatorname {E}(\bar{r})||\operatorname {B}(\bar{p})| \neq1\). If  and
and  then \(|\operatorname {E}(\bar{r})|=1\), which implies \(|\operatorname {B}(\bar{p})|>1\) and so \(\bar{p}=yxy\). This leads to a contradiction \(\bar{p}=\bar{\bar{p}}=y\). Similarly
then \(|\operatorname {E}(\bar{r})|=1\), which implies \(|\operatorname {B}(\bar{p})|>1\) and so \(\bar{p}=yxy\). This leads to a contradiction \(\bar{p}=\bar{\bar{p}}=y\). Similarly  and
and  would lead to a contradiction. Thus
would lead to a contradiction. Thus  and
and  . Now \(\bar{r}=xx\) and \(\bar{p}=yy\) would imply \(|\operatorname {E}(\bar {r})||\operatorname {B}(\bar{p})|=1\), which is not true. Therefore \(\bar{r}=xy\) and \(\bar{p}=xy\), since \(\operatorname {e}(r) \neq \operatorname {b}(p)\).
. Now \(\bar{r}=xx\) and \(\bar{p}=yy\) would imply \(|\operatorname {E}(\bar {r})||\operatorname {B}(\bar{p})|=1\), which is not true. Therefore \(\bar{r}=xy\) and \(\bar{p}=xy\), since \(\operatorname {e}(r) \neq \operatorname {b}(p)\).
Step 3
If srp=s in S then r is a unique inverse of p.
Suppose (s 1,s 2)(r 1,r 2)(p 1,p 2)=(s 1,s 2) is S. Then s 1 r 1 p 1=s 1 in S 1 and s 2 r 2 p 2=s 2 in S 2. By Step 2 clearly r 2 is an inverse of p 2 in S 2. Step 2 also shows that inverses in S 2 are unique, so r 2 is a unique inverse of p 2. Since in S 1 length in z (the number of letters z occurring in the element) is clearly well defined, r 1 and p 1 can not contain any z, so r 1=p 1=w. Since w is a unique inverse of w in S 1, (r 1,r 2) is a unique inverse of (p 1,p 2) in S.
Step 4
Semigroup S⋊ ω T satisfies ACCPR.
Suppose s n =s n+1 q n in S 2, that is \(\bar{s}_{n}=\overline {s_{n+1}q}_{n}\) in F. Closer examination of (3) shows that we have the following possible cases:
-
(1)
\(\bar{s}_{n}=\bar{s}_{n+1}\bar{q}_{n}\), hence \(|\bar {s}_{n+1}|<|\bar{s}_{n}|\),
-
(2)
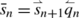 and \(|\bar{q}_{n}| \geq 3\), hence \(|\bar{s}_{n+1}|<|\bar{s}_{n}|\),
and \(|\bar{q}_{n}| \geq 3\), hence \(|\bar{s}_{n+1}|<|\bar{s}_{n}|\), -
(3)
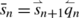 and \(|\bar{q}_{n}|=2\), hence \(|\bar{s}_{n+1}|=|\bar{s}_{n}|\) and one of the following holds:
and \(|\bar{q}_{n}|=2\), hence \(|\bar{s}_{n+1}|=|\bar{s}_{n}|\) and one of the following holds: -
(3.1)
\(\bar{q}_{n}=xx\), \(\ \bar{s}_{n+1}=axy\), \(\ \bar{s}_{n}=axx\) for some a∈F 1,
-
(3.2)
\(\bar{q}_{n}=yy\), \(\ \bar{s}_{n+1}=ayx\), \(\ \bar{s}_{n}=ayy\) for some a∈F 1,
-
(3.3)
\(\bar{q}_{n}=xy\), \(\ \bar{s}_{n+1}=ay\), \(\ \bar{s}_{n}=ay\) for some a∈F 1,
-
(3.4)
\(\bar{q}_{n}=yx\), \(\ \bar{s}_{n+1}=ax\), \(\ \bar{s}_{n}=ax\) for some a∈F 1,
-
(3.1)
-
(4)
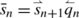 and \(|\bar{q}_{n}|=1\) and one of the following holds:
and \(|\bar{q}_{n}|=1\) and one of the following holds: -
(4.1)
\(\bar{q}_{n}=x\), \(\ \bar{s}_{n+1}=axy\), \(\ \bar{s}_{n}=ax\) for some a∈F 1,
-
(4.2)
\(\bar{q}_{n}=y\), \(\ \bar{s}_{n+1}=ayx\), \(\ \bar{s}_{n}=ay\) for some a∈F 1.
-
(4.1)
To prove that S⋊ ω T satisfies ACCPR let (r n ) n ,(p n ) n ⊆S 1, (s n ) n ,(q n ) n ⊆S 2 and (t n ) n ,(u n ) n ⊆T be sequences such that
for all n∈ℕ. Then \((r_{n},s_{n})=(r_{n+1},s_{n+1})\omega_{t_{n+1}}(p_{n},q_{n})\) and t n =t n+1 u n . If 1 appears in (t n ) n then all consequent terms must be 1. If 1 does not appear in (t n ) n but 2 does then all consequent terms must be 2. If 1 and 2 do not appear in (t n ) n then all terms are 0. So t n must be constant from some term on.
Let first t n =0 for all n∈ℕ big enough. Then for these n we get (r n ,s n )=(r n+1,s n+1)(w,xy). But (w,xy) is an idempotent in S, so (r n+1,s n+1)=(r n+2,s n+2)(w,xy)=(r n+2,s n+2)(w,xy)3=(r n ,s n )(w,xy). This implies
for all n big enough.
Now let t n =1 for all n∈ℕ big enough. Then for these n we have (r n ,s n )=(r n+1,s n+1)(p n ,q n )=(r n+1 p n ,s n+1 q n ). For a∈S 1 let |a| z denote the number of letters z in a (this is well defined). Then for n big enough |r n | z =|r n+1 p n | z =|r n+1| z +|p n | z ≥|r n+1| z . Thus the sequence |r n | z is nonincreasing, hence it must be constant from some n on. Therefore |p n | z =0 and so p n =w for n big enough. Then r n =r n+1 w and as above (w is an idempotent in S 1) this implies r n+1=r n w for n big enough. Now for these n consider what can happen with s n =s n+1 q n (see the cases above). If (3.3), (3.4), (4.1) and (4.2) never happen then the sequence \(|\bar{s}_{n}|\) is nonincreasing and hence constant from some n on. So for n big enough only (3.1) and (3.2) can happen, but this is impossible since on one hand all s n should end with two equal letters on the other hand all s n should end with two different letters. So for some n one of the (3.3), (3.4), (4.1) and (4.2) happens. In any case there exists s∈S 2 such that s n+1=s n s (s=xy in case (3.3), s=yx in case (3.4), s=y in case (4.1) and s=x in case (4.2)). For this n we have (r n+1,s n+1)=(r n ,s n )(w,s), thus
Now let t
n
=2 for all n∈ℕ big enough. Then for these n we have (r
n
,s
n
)=(r
n+1,s
n+1)(w,a
n
), where \(\bar{a}_{n}\) is of the form x
m or x
m
y for some m∈ℕ (see the definition of ω
2). As above r
n
=r
n+1
w implies r
n+1=r
n
w for n big enough. Now as above consider what can happen with s
n
=s
n+1
a
n
for these n (a
n
takes the place of q
n
). Since a
n
starts with x, cases (3.2), (3.4) and (4.2) can never happen. Suppose that (3.3) never happens. For u∈F let |u|
x
denote the number of letters x in u. In case (1) we have \(|\bar{s}_{n+1}|_{x}<|\bar {s}_{n}|_{x}\), since \(\bar{a}_{n}\) contains at least one x. In case (2) element  contains at least one x and since \(\bar{a}\) starts with x, \(\bar{s}_{n+1}\) has to end with y. Hence in this case we also have \(|\bar{s}_{n+1}|_{x}<|\bar{s}_{n}|_{x}\). In case (3.1) we also have \(|\bar{s}_{n+1}|_{x}<|\bar{s}_{n}|_{x}\) and in case (4.1) we have \(|\bar{s}_{n+1} |_{x}=|\bar{s}_{n}|_{x}\). Thus the sequence \(|\bar{s}_{n}|_{x}\) is nonincreasing, so it must be constant from some term on. So for n big enough only (4.1) can happen, but this is impossible since on one hand all s
n
should end with x on the other hand all s
n
should end with y. So for some n big enough (3.3) must happen. For this n we have s
n+1=s
n
xy and (r
n+1,s
n+1)=(r
n
,s
n
)(w,xy), thus
contains at least one x and since \(\bar{a}\) starts with x, \(\bar{s}_{n+1}\) has to end with y. Hence in this case we also have \(|\bar{s}_{n+1}|_{x}<|\bar{s}_{n}|_{x}\). In case (3.1) we also have \(|\bar{s}_{n+1}|_{x}<|\bar{s}_{n}|_{x}\) and in case (4.1) we have \(|\bar{s}_{n+1} |_{x}=|\bar{s}_{n}|_{x}\). Thus the sequence \(|\bar{s}_{n}|_{x}\) is nonincreasing, so it must be constant from some term on. So for n big enough only (4.1) can happen, but this is impossible since on one hand all s
n
should end with x on the other hand all s
n
should end with y. So for some n big enough (3.3) must happen. For this n we have s
n+1=s
n
xy and (r
n+1,s
n+1)=(r
n
,s
n
)(w,xy), thus
We have shown that in any case there exists n∈ℕ and ((r,s),t)∈S⋊ ω T such that ((r n+1,s n+1),t n+1)=((r n ,s n ),t n )((r,s),t). So S⋊ ω T satisfies ACCPR.
References
Higgins, P.M.: Techniques of Semigroup Theory. Oxford University Press, Oxford (1992)
Klawe, M.: Semidirect product of semigroups in relation to amenability, cancellation properties, and strong Følner conditions. Pac. J. Math. 73 (1997)
Liu, Z.: The ascending chain condition for principal ideals of rings of generalized power series. Commun. Algebra 32, 3305–3314 (2004)
Mazurek, R., Ziembowski, M.: On von Neumann regular rings of skew generalized power series. Commun. Algebra 36, 1855–1868 (2008)
Mazurek, R., Ziembowski, M.: The ascending chain condition for principal left or right ideals of skew generalized power series rings. J. Algebra 322, 983–994 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mark V. Lawson.
Rights and permissions
About this article
Cite this article
Stopar, N. Ascending chain conditions on principal left and right ideals for semidirect products of semigroups. Semigroup Forum 85, 322–336 (2012). https://doi.org/10.1007/s00233-012-9415-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00233-012-9415-1



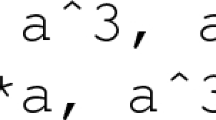
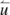 :
: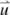 :
: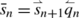 and
and 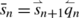 and
and 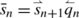 and
and