Assessment of the inclination surface on the microlayer behavior during nucleate boiling, a numerical study

Abstract

Nucleate boiling is an important part of pool boiling process. Heat transfer from the microlayer plays a considerable role in heat transfer to the fluid. The axisymmetric assumption of the microlayer for a horizontal surface needs to be evaluated for an inclined one. In this study, the effect of surface orientation on the microlayer thickness and the heat transfer rate are investigated numerically. The governing equations are simplified employing scaling analysis. The results for the microlayer thickness, the heat flux and the total heat transfer rate for the heated surface are obtained and presented. The asymmetry of the microlayer increases as the surface inclination angle varies from horizontal to vertical. Even though, the driving force due to gravity in the microlayer is negligible, however its effect on the macro region changes the microlayer parameters. The results show that the maximum microlayer heat transfer rate for the vertical surface increases by 28.8% compared to that for a horizontal surface. The proposed model, which is capable of evaluating the microlayer thickness and its surface heat transfer rate, can be employed as a surface boundary condition in the macro region simulations of the nucleate boiling.

1 Introduction

Boiling heat transfer occurs in a variety of industrial processes such as those occurring in chemical processing plants, boilers, and heat exchangers. Complete understanding of the boiling phenomenon and the parameters which affect its efficiency and the heat transfer rate will be helpful for optimal design of the heat exchangers. In the pool boiling process, the heating surface is immersed into a quiescent fluid. The bubbles nucleate at the active sites on the surface. The nucleated bubbles get detached from the surface when the buoyancy force becomes dominant. The detachment process induces a recirculation zone behind the bubbles. After the bubble detaches from the surface, the superheated liquid fills the remaining cavity. Consequently, the local heat transfer rate increases due to the higher heat capacity and thermal conductivity of the superheated liquid compared to those of the vapor. The liquid flow traps the remnants of the vapor in the cavity which act as a new bubble embryo [1, 2]. By increasing the wall superheat, the nucleation, transition, and film boiling modes occur along the boiling curve [3]. Recently, Marcel et al. [4, 5] studied the pool boiling on a horizontal surface employing the automata model. Their results showed excellent agreement with the experimental data.

Different heat transfer mechanisms, such as the microlayer evaporation [6], the contact line heat transfer [7], evaporation of the superheated liquid around the bubble [8], convective heat transfer due to the bubble rising motion and transient heat conduction in the liquid on the surface after the bubble departure [9] have been proposed to demonstrate the bubble growth phenomenon at active nucleation sites.

Formation of the microlayer underneath the bubble during the bubble nucleation and growth was confirmed experimentally by Moore and Mesler [10] and Hsu and Schmidt [11]. Their results showed a rapid reduction of the surface temperature underneath the bubble during the first stages of the bubble growth. The temperature reduction indicates a rapid extraction of heat during a short period of time. The first theory for the microlayer was introduced by Cooper and Lloyd [6]. They measured the surface temperature underneath a bubble of toluene and isopropyl-alcohol during nucleate boiling. The results showed that at the early stages of the boiling process, a rapid reduction of the surface temperature underneath the bubble occurs. Subsequently, with the growth of the bubble, the surface temperature increases. They stated that the rapid growth of the bubble results in the entrapment of a thin liquid layer underneath of it which forms the microlayer. A large heat flux occurs in the microlayer due to difference between temperature of the upper and the lower surfaces of the heating plate which are equal to the saturation or vapor temperature and the heated surface temperature, respectively. The microlayer evaporation drops the surface temperature rapidly. After the complete evaporation of the microlayer and drying out the heated surface, the temperature of the upper surface begins to increase slowly. The theory of Cooper and Lloyd were also confirmed by the experimental studies of Jawurek [12], Voutsinos and Judd [13] and Koffman and Plesset [14]. They reported different microlayer thicknesses in the order of few micrometers. Moreover, Voutsinos and Judd [11] indicated that 25% of the total heat transfer to the bubble was due to the microlayer evaporation. The experimental study of Koffman and Plesset [14] for nucleate boiling of water and ethanol showed that the radial flow of liquid into the microlayer is negligible. Therefore, without significant mass transfer from the superheated liquid, the microlayer vanishes due to evaporation.

As far as recent experimental studies on the bubble growth using infrared thermometry, total reflection and laser interferometry techniques and MEMS sensors are concerned, Jung and Kim [15] investigated growth dynamics and heat transfer of a single bubble during nucleate boiling on a horizontal surface. The results showed that the microlayer thickness and the length underneath the bubble vary during the bubble growth. At early stages of the bubble formation, the microlayer thickness and its length increase with time. However, during the final stages of the evaporation, while the bubble equivalent diameter increases, these parameters decrease and the microlayer evaporates completely. Their results showed that 17% of the total heat transfer to a single bubble is due to the microlayer evaporation. However, they did not address the reasons behind variation of the microlayer thickness and its length during the bubble formation.

An experimental study conducted by Yabuki and Nakabeppu [9] on an isolated bubble during boiling of saturated water indicated that at the beginning of the bubble formation, the temperature of the surface underneath the bubble drops rapidly due to the microlayer evaporation, and during the later stages of the bubble growth, as the surface temperature is increasing, it drops again. They noted that rewetting of the surface by the superheated liquid flowing near the bubble base is the reason of the surface temperature drop, and proposed that the microlayer is connected to the superheated liquid near the bubble base at the three-phase contact point. The results also showed that about 50% of the total heat transfer occurs in the microlayer, and that the local heat flux due to the microlayer evaporation exceeds 1 MW/m² [9]. Even though, the aforementioned investigations have increased our knowledge of the microlayer and its effect on the nucleate boiling, further research is required to understand the physics of the microlayer.

As far as analytical approaches for analyzing the microlayer are concerned, no analytical model exists which incorporates all of the microlayer characteristics. A simplified analytical model for the microlayer underneath the bubble is introduced by Stephan and Busse [16] and Lay and Dhir [17]. They divided the bubble nucleation zone to macro and micro regions. The macro region contains the superheated liquid surrounding the vapor as well as the liquid-vapor interface; while, the micro region includes the microlayer that is connected to the macro region at the three-phase contact point. The forces due to the interface curvature, the disjoining pressure, the hydrostatic head, and the liquid drag were considered in the model. Solving an equation proposed in their model for microlayer thickness, the pressure gradient, the heat transfer and the microlayer evaporation rate were obtained. Numerical investigations conducted using the Lay and Dhir model [18,19,20], show that the model predicts the bubble growth dynamic proposed by but fails to determine the surface temperature variation. Moreover, the model is applicable only to the horizontal surfaces. In addition to the Lay and Dhir model, some other numerical models have also been proposed for the microlayer [21, 22]. The available experimental data for the microlayer thickness and its length are employed as boundary conditions in these models. Therefore, the errors due to the experimental measurements are clearly transferred to these numerical simulations.

The contact angle between the bubble and the heated surface is an important boundary condition which couples the micro and the macro regions. During early stages of the nucleate boiling on a horizontal surface, the bubble projected area on the heated surface increases; and the bubble contact angle decreases with respect to time. As the bubble grows symmetrically on the heated horizontal surface, the buoyancy force tries to lift it vertically. Eventually, a bubble neck forms near the surface, and the bubble contact angle increases until the buoyancy force overcomes the surface tension and the adhesive forces and the bubble breaks off. The circumferential contact angle of the bubble remains constant during the entire growth process for a horizontal surface. However, the bubble nucleation, growth and departure occur differently for an inclined surface. The angle between the surface and the buoyant force, which is less than 90° in this case, results in sliding of the bubble along the surface. Experimental results [23] show that the contact angle varies linearly from 40 deg. for an upward-facing to 5 deg. for a downward-facing heated surface. Therefore, the bubble growth is asymmetric for this case, and the contact angle varies circumferentially which, in turn, affects the micro region formation, the heat transfer rate and the microlayer thickness. Experimental studies of boiling conducted on inclined surfaces previously show that the surface angle indeed affects the bubble formation [24], the critical heat flux [25,26,27,28,29] and the heat transfer rate [30, 31]. Therefore, the microlayer is certainly influenced by the inclination of the surface. However, the model of lay and Dhir is applicable to the horizontal heated surfaces only, and it cannot be employed to model bubble growth on an inclined surface where the variation of the circumferential contact angle creates a three-dimensional microlayer.

Hence, the main objective of the present study is to develop a three-dimensional model of the microlayer for the bubble growth on an inclined surface based on the Lay and Dhir [17] model. The proposed model is employed to simulate the bubble growth during nucleate boiling on inclined surfaces. The effects of the macro region on the microlayer are considered as boundary conditions. The effects of the surface angle on the microlayer heat transfer rate, the heat flux and the microlayer thickness during nucleate boiling on an inclined heated surface are investigated. Moreover, the effect of the gravity on the microlayer structure is also investigated.

2 Problem formulation

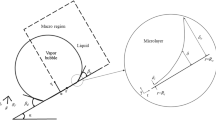
In this study, a model is presented for the growth and detachment of a vapor bubble nucleated on an inclined heated surface. Subsequently, the model is employed to investigate the effect of surface inclination on the bubble growth during the nucleate boiling phenomena. A schematic of the vapor bubble and the inclined heated surface are shown in Fig. 1. The solution domain is divided into the micro and macro regions. The macro region consists of the bubble and its surroundings liquid; while, the micro region encompasses the microlayer (Fig. 1).

Fig. 1

A schematic of a vapor bubble growing on an inclined surface during nucleate boiling showing the macro region and the microlayer

In order to model the micro region, the following assumptions are made:

• The ratio of the microlayer thickness (δ) to the microlayer length (R_l) is small (δ/R_l < <1), and the Reynolds number in the micro region is less than unity. Due to this assumption, the inertia, the radial heat conduction and the viscous dissipations in the governing equations are ignored [17].

• The dominant pressure gradient in the microlayer is in the radial direction [17].

• The lubrication theory is applicable for the microlayer. The lubrication approximation assumption for the microlayer has been validated by previous investigators [17, 32].

• Due to the dominant radial pressure gradient and small thickness of the microlayer, the driving pressure force in the tangential direction is negligible. Therefore, the tangential velocity is negligible (u_θ ≈ 0). Furthermore, the variation of the radial velocity component in the tangential direction is neglected.

• The axial liquid velocity in the microlayer is negligible (u_z ≈ 0). This assumption is based on employing the continuity equation at the interface between the liquid and the vapor and recognizing that the liquid density is much larger than that of the vapor.

• The convection term as well as the radial and tangential conduction terms in the energy equation are negligible.

• The heat transfer across the microlayer is assumed to be one-dimensional.

2.1 Heat and mass transfer coupling in the microlayer

An energy balance for a differential element of the microlayer is written as follows:

$$ -{h}_{fg}\kern0.24em d{\dot{m}}_r=d{\dot{Q}}_{microlayer}, $$

(1)

where ${\dot{m}}_r$ and ${\dot{Q}}_{microlayer}$, which are the fluid mass flow rate and the heat transfer rate in the microlayer, respectively. As shown in Fig. 1, $d{\dot{m}}_r$ and $d{\dot{Q}}_{microlayer}$ can be calculated as follows:

$$ d{\dot{m}}_r=\frac{d}{dr}\left(2\pi r{\rho}_l{\overline{u}}_r\delta \right) dr, $$

(2)

$$ d{\dot{Q}}_{microlayer}={q}_{con}2\pi r\; dr. $$

(3)

where δ, ${\overline{u}}_r$ and q_conare the microlayer thickness, the average liquid velocity and the conduction heat transfer rate across the microlayer, respectively. $d{\dot{m}}_r$ is the amount of mass flow rate that is vaporized in a differential element of the microlayer. Similarly, in Eq. (3), $d{\dot{Q}}_{microlayer}$ is the heat transfer rate in a differential element of the microlayer. The conduction heat transfer rate across the microlayer is written as

$$ {q}_{con}={k}_l\frac{\left({T}_w-{T}_{int}\right)}{\delta }, $$

(4)

where T_w and T_int are the wall and the interface temperatures, respectively. It is to be noted that, based on the stated assumptions, convection heat transfer in the microlayer is negligible.

2.2 Flow field in the microlayer

The Navier-Stokes equations in the cylindrical coordinate system for the steady, laminar and incompressible flow in the microlayer are written as

$$ \frac{1}{r}\frac{\partial }{\partial r}\left(r{u}_r\right)+\frac{1}{r}\frac{\partial {u}_{\theta }}{\partial \theta }+\frac{\partial {u}_z}{\partial z}=0, $$

(5)

$$ {\displaystyle \begin{array}{l}{\rho}_l\left({u}_r\frac{\partial {u}_r}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial {u}_r}{\partial \theta }+{u}_z\frac{\partial {u}_r}{\partial z}-\frac{u_{\theta}^2}{r}\right)=\\ {}\kern2.4em -\frac{\partial {p}_l}{\partial r}+{\mu}_l\left(\frac{\partial^2{u}_r}{\partial {r}^2}+\frac{1}{r}\frac{\partial {u}_r}{\partial r}-\frac{u_r}{r^2}+\frac{1}{r^2}\frac{\partial^2{u}_r}{\partial {\theta}^2}+\frac{\partial^2{u}_r}{\partial {z}^2}-\frac{2}{r^2}\frac{\partial {u}_{\theta }}{\partial \theta}\right)+{\rho}_l{g}_r,\end{array}} $$

(6)

$$ {\displaystyle \begin{array}{l}{\rho}_l\left({u}_r\frac{\partial {u}_{\theta }}{\partial r}+\frac{u_r{u}_{\theta }}{r}+\frac{u_{\theta }}{r}\frac{\partial {u}_{\theta }}{\partial \theta }+{u}_z\frac{\partial {u}_{\theta }}{\partial z}\right)=\\ {}-\frac{1}{r}\frac{\partial {p}_1}{\partial \theta }+{\mu}_l\left(\frac{\partial^2{u}_{\theta }}{\partial {r}^2}+\frac{1}{r}\frac{\partial {u}_{\theta }}{\partial r}-\frac{u_{\theta }}{r^2}+\frac{1}{r^2}\frac{\partial^2{u}_{\theta }}{\partial {\theta}^2}+\frac{\partial^2{u}_{\theta }}{\partial {z}^2}+\frac{2}{r^2}\frac{\partial {u}_r}{\partial \theta}\right)+{\rho}_l{g}_{\theta },\end{array}} $$

(7)

$$ {\displaystyle \begin{array}{l}{\rho}_l\left({u}_r\frac{\partial {u}_z}{\partial r}+\frac{u_{\theta }}{r}\frac{\partial {u}_z}{\partial \theta }+{u}_z\frac{\partial {u}_z}{\partial z}\right)=\\ {}-\frac{\partial {p}_l}{\partial z}+{\mu}_l\left(\frac{\partial^2{u}_z}{\partial {r}^2}+\frac{1}{r}\frac{\partial {u}_z}{\partial r}+\frac{1}{r^2}\frac{\partial^2{u}_z}{\partial {\theta}^2}+\frac{\partial^2{u}_z}{\partial {z}^2}\right)+{\rho}_l{g}_z,\end{array}} $$

(8)

where u_r, u_θ and u_z are the radial, the tangential and the axial liquid velocity components in the microlayer, respectively. Using the stated assumptions, the continuity equation is simplified to

$$ \frac{1}{r}\frac{\partial }{\partial r}\left(r{u}_r\right)=0. $$

(9)

Solving Eq. (9) yields the following expression for the radial velocity component

$$ {u}_r=\frac{f\left(\theta, z\right)}{r}, $$

(10)

where f (θ,z) is obtained employing the momentum equation in the radial direction.

Moreover, based on the assumptions, the only remaining terms in the axial and tangential components of the momentum equation, are the pressure gradient and the gravity terms. Consequently, the pressure change in the tangential and axial directions is due to the gravity only.

Considering the assumptions, the radial component of the momentum equation (Eq. (6)) can be written as follows:

(11)

Equation (11) can be simplified further using the following scaling analysis. At any point in the microlayer, the characteristic lengths in the radial and axial directions are selected as R_l and δ, respectively. Hence, the scales of the terms denoted by (I), (II) and (III) in Eq. (11) are as follows:

$$ {\displaystyle \begin{array}{l}\mathrm{I}:{\mu}_l\frac{\partial^2{u}_r}{\partial {r}^2}\sim {\mu}_l\frac{u_r}{r^2}\sim {\mu}_l\frac{u_r}{R_l^2},\\ {}\mathrm{I}\mathrm{I}:{\mu}_l\frac{\partial^2{u}_r}{\partial {z}^2}\sim {\mu}_l\frac{u_r}{\delta^2},\\ {}\mathrm{I}\mathrm{I}\mathrm{I}:{\rho}_l\left({u}_r\frac{\partial {u}_r}{\partial r}\right)\sim {\rho}_l\frac{u_r^2}{R_l}.\end{array}} $$

(12)

The ratio of the microlayer thickness (δ) to the microlayer length (R_l) is much smaller than unity. Therefore, according to Eq. (12), the velocity gradients in radial direction in Eq. (11) can be omitted compared to the velocity gradient along the z-axis.

The terms (II) and (III) are the dominant viscous and inertial terms, respectively. The Reynolds number (ρ_lu_rR_l/μ_l) as well as the ratio of microlayer thickness to the microlayer length (δ/R_l) are very less than unity in the microlayer region. Therefore, comparing the scales of the terms shows that the inertial terms can be neglected according to Eq. (13).

(13)

Consequently, the final form of the momentum equation in the radial direction is

$$ 0=-\frac{\partial {p}_l}{\partial r}+{\mu}_l\left(\frac{\partial^2{u}_r}{\partial {z}^2}\right)+{\rho}_l{g}_r, $$

(14)

where g_r = g sinα sinθ (Fig. 1). The boundary conditions for Eq. (14) are given by

$$ {\displaystyle \begin{array}{lll}{u}_r=0& \mathrm{at}& z=0,\\ {}\frac{\partial {u}_r}{\partial z}=0& \mathrm{at}& z=\delta .\end{array}} $$

(15)

Integrating Eq. (14) and applying the above boundary conditions yield the following expression for the radial velocity component

$$ {u}_r=-\frac{1}{\mu_l\;}\left(\frac{d{p}_l}{dr}-\rho {g}_r\right)\left(\delta z-\frac{z^2}{2}\right). $$

(16)

Using Eq. (16) for the radial velocity component, the average radial liquid velocity${\overline{u}}_r$ is written as

$$ {\overline{u}}_r=-\frac{1}{3{\mu}_l}\left(\frac{d{p}_l}{dr}-\rho {g}_r\right){\delta}^2. $$

(17)

2.3 Pressure variation calculation

The pressure difference between the liquid and the vapor is due to the gravity, the capillary effect, the disjoining pressure and the momentum exchange across the liquid-vapor interface. This pressure difference can be written as [17].

$$ {p}_l-{p}_v=\left({\rho}_v{v}_v^2-{\rho}_l{v}_l^2\right)-\sigma K+{\rho}_l{g}_z\left(\delta -{\delta}_0\right)-\frac{A}{\delta^3}, $$

(18)

where σ is the surface tension, and K is the curvature of the interface which is given by

$$ K=\frac{1}{r}\frac{\partial }{\partial r}\left[r\frac{\partial \delta }{\partial r}/\sqrt{1+{\left(\frac{d\delta}{d r}\right)}^2}\right]. $$

(19)

The conservation of mass at the liquid-vapor interface yields

$$ {\rho}_{\upsilon }{v}_{\upsilon }={\rho}_l{v}_l. $$

(20)

Using Eq. (20) and considering that the liquid density is much larger than that of the vapor, it is concluded that${\rho}_l{v}_l^2<<{\rho}_{\upsilon }{v}_{\upsilon}^2$. Therefore, the liquid momentum exchange in Eq. (18) can be neglected in comparison to the momentum exchange of the vapor. Moreover, the vapor velocity is defined in terms of the evaporative heat flux as follows [8]:

$$ {v}_v=\frac{q_e}{\rho_v\;{h}_{fg}}. $$

(21)

The evaporative heat flux is obtained from the expression proposed by Wayner [32] and Lay and Dhir [17] which has been modified here to incorporate the effect of the surface inclination.

$$ {q}_e={a}_1{\left(\frac{M}{2\pi \tilde{R}{T}_{sat}^3}\right)}^{1/2}\left\{{\rho}_{\upsilon }{h}_{fg}\left({T}_{int}-{T}_v\right)+\frac{\upsilon_l{p}_{\upsilon }}{\tilde{R}}\left[-\sigma K-\frac{A}{\delta^3}+\left({\rho}_l-{\rho}_{\upsilon}\right)g\cos \alpha \left(\delta -{\delta}_o\right)\right]\right\}{h}_{fg}, $$

(22)

where M, $\tilde{R}$ and υ_l are the molecular weight, the gas constant and the specific volume of the fluid, respectively. T_v, T_sat and T_int are the vapor, the saturation and the interface temperatures, respectively. The constant ɑ₁ in Eq. (22) is equal to unity [17, 33].

Equations (19), (21) and (22) are substituted into Eq. (18) to calculate the liquid pressure variation inside the microlayer. Subsequently, the radial derivative of the liquid pressure is employed in Eq. (16) to calculate the liquid velocity.

Substituting Eqs. (2), (3), (4) and (17) into Eq. (1), yields the following fourth-order, non-linear ordinary differential equation for the microlayer thickness:

$$ {{{\delta^{\prime}}^{\prime}}^{\prime}}^{\prime }=\frac{r{\delta}^3\left(2{C}_2{h}_{ev}^2{A}_{36}{A}_6+{A}_1{A}_4\sigma \left({A}_{34}+{A}_{35}\right)+{A}_1\left(3{A}_{17}+2{A}_{22}+2{A}_{23}+2{A}_{28}\right)\right)-6{A}_1{\mu}_l\left(r{A}_{30}+{A}_{31}+{A}_{32}\right)}{r{\delta}^3\sigma \left(2{C}_1{C}_2{h}_{ev}^2{A}_3{A}_6\left(-{C}_3{h}_{ev}+{A}_1\right)-{A}_1{A}_4\left({\delta^{\prime}}^4+2{\delta^{\prime}}^2+1\right)+3{A}_1{A}_3\right)}. $$

(23)

The constants in Eq. (23) are given in the appendix. The boundary conditions for Eq. (23) are

$$ {\displaystyle \begin{array}{lllll}\delta ={\delta}_i,& {\delta}^{\prime }=0,& {{\delta^{\prime}}^{\prime}}^{\prime }=0& \mathrm{at}& r={r}_i,\\ {}{\delta}^{\prime }={\tan}^{-1}\beta & & & \mathrm{at}& r={r}_o.\end{array}} $$

(24)

To simulate the microlayer on the inclined heated surface, Eq. (23) together with the boundary conditions (24) should be solved. Subsequent to calculating the microlayer thickness, other microlayer parameters such as the radial velocity component, the liquid-vapor interface temperature, the evaporative heat flux, the heat transfer rate and the pressure gradient components can be determined.

The coupling of the micro and the macro regions solutions is through the macro region contact angle (specifying the microlayer slope at the contact point), the bubble radius and the location of the contact point. As stated previously, the main objective of the present study is to develop a three-dimensional model for the microlayer formed underneath the bubble growing on an inclined heated surface during nucleate boiling. Therefore, instead of solving the governing equations of the macro simultaneously, the microlayer equations are solved only using the interfacial conditions obtained from the experimental data of Jung and Kim [15].

3 Solution method

Equation (23) with the boundary conditions (24) is the governing equation of the microlayer. A computer code written in MATLAB is employed to integrate this equation. To begin with, the fourth-order ordinary differential equation of the microlayer thickness (Eq. (23)) is transformed to a system of first-order ordinary differential equations. The resulting system of ordinary differential equations is subsequently integrated using the Euler method. As shown previously, three of the boundary conditions (24) are given at r = r_i while the other is specified at the contact point of the macro and the micro regions, i.e., at r = r_o. The shooting method is employed to solve the system of ordinary differential equations in this case. The solution procedure begins with an initial guess for the second derivative of microlayer thickness (δ”) at r = r_i. The equations are then integrated and the first derivative of the microlayer thickness at the contact point, i.e., δ^’ at r = r_o, is calculated.

The computer code is employed to simulate the growth of a vapor bubble on a horizontal heated surface for ∆T_sup = 20 K. An integration interval independent study is performed and the effect of varying the number of integration points on the bubble growth is investigated. Three different integration intervals having 2 × 10⁴, 2 × 10⁵ and 2 × 10⁶ integration points are employed for this purpose. The simulation results for the bubble contact angle and the heat flux for these cases are presented in Table 1. As it is observed from this table, 2 × 10⁵ integration points is fine enough to capture the details of the heat and mass transfer in the microlayer. Therefore, this number of integration points is employed to perform all of the subsequent numerical integrations.

Table 1 Results of the integration interval independence study

4 Model validation

There is not any experimental data available for validating the proposed model. Hence, to validate the model, the simulation of nucleate boiling of water on a horizontal heated surface is performed using the macro region equations given in appendix 2. The results for the variation of the bubble equivalent diameter with respect to t/t_d during the nucleate boiling are compared with the experimental results reported by Son et al. [18]. They investigated the growth of a single bubble during the nucleate boiling of saturated water on a horizontal heated surface with the contact angle φ = 50° under atmospheric pressure.

Fig. 2 shows a comparison between the experimental results of Son et al. [18] and the results of the present model for the bubble equivalent diameter during nucleate boiling with respect to t/t_d where t_d is the total time of bubble growth and departure from the heated surface. As it is observed from Fig. 2, a relatively good agreement exists between the experimental results and the results of the present model. Although, the validation is performed for a horizontal surface; nevertheless, it gives some confidence in the performance of the model for an inclined surface.

Fig. 2

Comparisons between the results of the present model for the bubble equivalent diameter with respect to time with the experimental results of Son et al. [18] for saturated water and φ = 50°

5 Results and discussion

The developed model is employed to simulate the microlayer during the growth of a vapor bubble on an inclined heated surface. The effects of gravity and the circumferential variation of the contact angle on the microlayer and the bubble growth are investigated. The working fluids are saturated water and steam, which are considered to be at the atmospheric pressure. The wall superheat temperature is 20K(T_w = T_sat + 20 K). The thermophysical properties of the liquid and vapor phases are presented in Table 2.

Table 2 Thermophysical properties of water and its vapor

The contact angle between the vapor and the heated surface is given by

$$ \beta ={\tan}^{-1}\frac{\delta_o}{\left({r}_o-{r}_i\right)}, $$

(25)

where δ_o is the maximum thickness of the microlayer at the contact point of the micro and the macro regions [18]. For nucleate boiling on a horizontal heated surface, at any time during the bubble growth, the contact angle around the bubble base circumference is constant and the microlayer is axisymmetric. However, when the surface is inclined, the contact angle around the bubble base circumference varies from a minimum value β_u (at the upper contact point θ = π/2) to a maximum value β_d (at the lower contact point θ = −π/2) (Fig. 1). The circumferential variation of the bubble base contact angle is obtained from the following expression:

$$ \beta =\Big\{{\displaystyle \begin{array}{ll}{\beta}_0-\varDelta \beta \left(\frac{\theta }{\pi /2}\right),& -\pi /2\le \theta <\pi /2\\ {}{\beta}_u+\varDelta \beta \left(\frac{\theta }{\pi /2}-1\right),& \pi /2\le \theta <3\pi /2\end{array}} $$

(26)

where β₀ is equal to horizontal surface contact angle and can be determined from the heated surface properties. The value of β₀ is considered to be 50° and Δβ = (β_d- β_u)/2.

According to the experimental results of Stephan [23], Δβ varies from 5° to 40° while changing the surface inclination from 0° (an upward-facing surface) to 180° (a downward-facing surface). Therefore, the maximum variation of the bubble base contact angle with respect to α is Δβ = 35°. Using the experimental results of Stephan [23] and assuming that the difference between the contact angles at the upper and the lower contact points varies linearly with respect to the surface inclination, the following expresion is proposed for Δβ:

$$ \varDelta \beta =\frac{70\alpha }{\pi },\kern0.5em 0\le \alpha \le \pi /2. $$

(27)

Using Δβ from Eq. (27), the contact angle is calculated from Eq. (26) and is employed as the boundary condition at the contact line between the micro and macro regions.

5.1 Variation of the liquid pressure in the microlayer

Variations of the capillary pressure gradient, dP_c/dr, the gravity pressure gradient, dP_g/dr, the disjoining pressure gradient dP_d/dr, the vapor recoil pressure gradient dP_qe/dr, and the total pressure gradient dP_l/dr with respect to the bubble radius for the bubble growth on an inclined heated surface are shown in Fig. 3. The results in this figure are for the bubble base radius of 0.02 mm, the maximum thickness of the microlayer equal to δ_o = 3.5 μm, and for different values of α.

Fig. 3

Variations of the various liquid pressure gradients in the microlayer with respect to the bubble radius for the horizontal and inclined surfaces, a at the upstream contact angle θ = π/2, b at the downstream contact angle θ = −π/2

The capillary pressure is proportional to the second derivative of the microlayer thickness which itself decreases rapidly along the microlayer. The second derivative of the microlayer thickness has its maximum value near the inner region; while it tends to zero near the macro contact point. Moreover, the slope of the microlayer increases as the microlayer grows. Therefore, according to Eq. (19), the effect of capillary pressure diminishes as the microlayer grows. The capillary pressure gradient is in the flow direction over most of the microlayer length. However, when the thickness of the microlayer increases, the slope of the capillary pressure gradient becomes negative which opposes the liquid flow. The vapor recoil pressure gradient, which opposes the liquid flow toward the micro region, is proportional to the evaporation rate at the vapor-liquid interface. The evaporation rate as well as the vapor recoil pressure decrease as the microlayer thickness increases. Therefore, the vapor recoil pressure gradient decreases with increasing the microlayer thickness.

The disjoining pressure gradient is inversely proportional to the fourth power of the microlayer thickness and decreases with increasing the microlayer thickness. During the initial stages of the bubble growth, the thickness of the microlayer is small. Therefore, the disjoining pressure gradient is important and should be considered only during the initial stages of the bubble growth.

The gravity pressure gradient, which is due to the hydrostatic head, increases as the microlayer thickness grows. The thickness of the microlayer is of the order of 10⁻⁶ m. Hence, the gravity pressure gradient can be neglected in comparison to the capillary pressure gradient. Comparisons between different pressure gradient terms shows that the capillary pressure gradient is much greater than the other considered pressure gradients, and it plays a dominant role on the liquid flow into the microlayer.

The upstream bubble contact angle (β at θ = π/2) decreases by increasing the surface inclination angle. The upstream contact angle affects the microlayer thickness and the slope of the pressure variation in the microlayer. As Fig. 3a shows, the rate of decrease of the capillary, disjoining and recoil pressure gradients with respect to the radius decreases as the surface inclination angle increases. Therefore, the net pressure gradient is positive and is in the direction of the liquid flow.

Consequently, the microlayer length increases by increasing the surface inclination in the upper part of the bubble (0 < θ < π). The opposite effect occurs for the downstream bubble contact angle (β at θ = −π/2). The variations of the pressure gradients in the microlayer for the inclined and horizontal surfaces at θ = −π/2 are shown in Fig. 3b. As it is observed from this figure, an increase in the surface inclination angle reduces the microlayer length as well as the net pressure gradient. Therefore, the microlayer length decreases rapidly by increasing the surface inclination angle.

5.2 Microlayer thickness

As stated in the previous section, the circumferential variation of bubble contact angle changes the microlayer thickness and its length as well as the total heat flux across the liquid film. The variation of the microlayer thickness with respect to the radius for different inclination angles at θ = π/2 and θ = −π/2 is shown in Fig. 4a. The results in this figure are for the bubble base radius equal to 0.02 mm. The microlayer is symmetric for a horizontal surface. For the circumferential angle 0 < θ < π, increasing the surface inclination angle reduces the contact angle and the rate of pressure gradient reduction. The larger pressure gradient in comparison to that for a horizontal surface, ensures more liquid flow toward the microlayer. The variation of the microlayer thickness for the circumferential angle π < θ < 2π is opposite to that for 0 < θ < π. For π < θ < 2π increasing the surface inclination angle reduces the microlayer thickness (Fig. 4a). To gain a better understanding of the microlayer behavior, the iso-thickness contour lines for the microlayer for a vertical surface (α = π/2) are shown in Fig. 4b. The asymmetry of the liquid film is clearly demonstrated in the figure.

Fig. 4

Variations of the microlayer thickness on an inclined heated surface a variations of the microlayer thickness with respect to the radius for (0 ≤ α ≤ π/2) at θ = π/2 and θ = −π/2 b isothickness contours lines on a vertical heated surface

5.3 Vapor-liquid interface temperature

Fig. 5a shows the variation of vapor-liquid interface temperature with respect to the radius for different surface inclination angles at θ = π/2 and θ = −π/2. The interface temperature is obtained by equating the conductive and the evaporative heat fluxes through the liquid layer. The maximum interface temperature occurs at the minimum thickness of the microlayer. With the growth of the microlayer, the heat transfer rate as well as the temperature difference between the interface and the vapor decrease. At the outer region of microlayer, the temperature tends to the water saturation temperature. Increasing the surface inclination angle reduces the interface temperature gradient for the circumferential angle 0 < θ < π; while, the opposite trend is observed for the circumferential angle π < θ < 2π. The isotherms for a vertical surface are also shown in Fig. 5b. The results show that for 0 < θ < π, the temperature gradient along the microlayer is less than that for π < θ < 2π. Hence, the interface temperature of the microlayer becomes asymmetrical. Comparisons of the interface temperature gradient for the horizontal and vertical heated surfaces shows 74.7% reduction and 140% increase of the temperature gradient for θ = π/2 and θ = −π/2 compared to that of the horizontal surface, respectively.

Fig. 5

Variations of the liquid-vapor interface temperature on an inclined heated surface a temperature variation with respect to the radius for (0 ≤ α ≤ π/2) at θ = π/2 and θ = −π/2 b isotherms on a vertical heated surface

5.4 Heat flux in the microlayer

Due to the small thickness of the microlayer, the temperature gradient and the heat flux are quite large there. The heat flux variation along the radial direction for (0 ≤ α ≤ π/2) and for the circumferential contact angles θ = π/2 and θ = −π/2 are shown in Fig. 6a. The overall trend of heat flux variation is similar to that of the vapor-liquid interface temperature. The maximum heat flux occurs at the minimum thickness of the liquid layer. Moreover, the heat flux decreases in the radial direction for all of the considered cases (Fig. 6a).

Fig. 6

Variations of the heat flux in the microlayer a on an inclined heated surface for (0 ≤ α ≤ π/2) at θ = π/2 and θ = −π/2 b isoheat flux contour lines on a vertical heated surface

Increasing the surface inclination angle decreases the rate of heat flux reduction along the microlayer length for the circumferential angle 0 < θ < π, and increases it for π < θ < 2π. The variation of the heat flux is directly related to the vapor-liquid interface temperature and the microlayer thickness. The isoheat flux contour lines around the bubble growing on a vertical heated surface are also shown in Fig. 6b. The asymmetry of the microlayer around the bubble is clearly observed from this figure. The microlayer heat transfer rates for the vertical and the horizontal heated surfaces are 1.95 × 10⁻² W and 1.89 × 10⁻² W, respectively, which shows 3.17% enhancement of the heat transfer for the vertical surface compared to that of the horizontal one.

5.5 The overall heat transfer rate from the microlayer

The variations of the microlayer heat transfer rate for horizontal and vertical heated surfaces during the bubble growth period are shown in Fig. 7. For the results presented in this figure, the variation of the bubble base radius with respect to time is considered to follow the experimental results of Jung and Kim [15]. As it is observed from this figure, the microlayer heat transfer rate for the vertical heated surface is, generally, larger than that of the horizontal surface especially at the middle of the bubble growth period when the bubble base radius is large. The maximum enhancement of the heat transfer rate by changing the surface from horizontal to vertical is about 28.8% (Fig. 7). It is to be noted that the total microlayer area is larger for an inclined surface compared to that of a horizontal surface. The larger microlayer area results in the heat transfer enhancement on the inclined surfaces.

Fig. 7

Variations of the microlayer heat transfer rate for the horizontal and vertical heated surfaces during the bubble growth

5.6 Effect of surface inclination angle on the microlayer heat transfer rate

To investigate the effect of the surface inclination on the microlayer heat transfer rate, simulations are performed for a range of α between 0° and 90° for three different test cases. The considered test cases, which are based on the experimental results of Jung and Kim [15], are shown in Table 3. Fig. 8 shows the microlayer heat transfer rate for different surface inclination angles during the bubble growth period for the three test cases. The results indicate that for all the considered test cases, increasing the surface angle from α = 0 to α = π/2 results in the enhancement of the heat transfer in the microlayer. This heat transfer enhancement is due to the increase of the microlayer surface area with increasing α.

Table 3 The considered test cases from the experimental of Jung and Kim [15] used for investigating the effect of the surface inclination

Fig. 8

Variations of the microlayer heat transfer rate with respect to the inclination angle for the three considered test cases presented in Table 3

6 Conclusions

A model for the microlayer underneath the bubble during nucleate pool boiling on an inclined heated surface is presented. The effects of the surface inclination on the microlayer thickness, the vapor-liquid interface temperature and the heat transfer rate are investigated. The main conclusions are as follows:

• 1. On the inclined surfaces, the pressure gradients due to the capillary and recoil pressures are dominant. Although, the gravity pressure gradient is negligible in comparison to the other pressure gradients, the effect of the gravity on the macro region which is applied through the boundary conditions of the micro region, changes the variation of the dominant pressure gradients within the microlayer.

• 2. For the circumferential angle 0 < θ < π, increasing the surface inclination angle results in increasing the microlayer length, in decreasing the vapor-liquid temperature gradient and in intensifying the heat transfer rate from the microlayer. The opposite trends are observed for the circumferential angle π < θ < 2π. The maximum enhancement of the heat transfer rate by changing the surface from horizontal to vertical is about 28.8%.

• 3. The symmetry assumption generally used for simulating the microlayer on a horizontal heated surface is not valid for the bubble growing on the inclined surfaces. Therefore, to obtain the correct results for the bubble growth on an inclined heated surface, three-dimensional simulations should be performed for a whole range of θ between 0 and 2π.

• 4. The proposed model has the capability of modeling the microlayer for the inclined surfaces as well as for the horizontal one. The model can be employed to determine wall boundary conditions when simulating the bubble growth during nucleate pool boiling on various inclined surfaces. This issue will be addressed in future works.

Appendices

Appendix 1

$$ {A}_1={h}_{ev}{\rho}_v{h}_{fg}+\frac{k_l}{\delta}\kern0.5em {P}_1={\rho}_v{h}_{fg}{T}_v\kern0.5em {K}_1=\frac{\sigma {\delta}^{{\prime\prime} }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}} $$

$$ {A}_2=3\sigma {\delta^{{\prime\prime}}}^2\frac{\delta^{\prime }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}}\kern0.5em {p}_g=g\sin \alpha \left({\rho}_l-{\rho}_v\right)\left(\delta -{\delta}_e\right)\kern0.5em {h}_{ev}={a}_1{h}_{fg}\sqrt{\frac{M}{2\pi R{T}_{sat}^3}} $$

$$ {A}_3=\frac{1}{{\left({\delta^{\prime}}^2+1\right)}^{3/2}}\kern0.5em {p}_d=\frac{A}{\delta^3}\kern0.5em {P}_1={\rho}_v{h}_{fg}{T}_v $$

$$ {A}_4=\frac{1}{{\left({\delta^{\prime}}^2+1\right)}^{7/2}}\kern0.5em {C}_1=\frac{\mu_l{p}_v}{\rho_vR}\kern0.5em {P}_2=g{p}_1-{K}_1-{p}_d $$

$$ {A}_5=\frac{h_{ev}\left(-{C}_1{P}_2+{P}_1\right)+\frac{k_l{T}_w}{\delta }}{A_1}\kern0.5em {C}_2=\frac{1}{\rho_v{h}_{fg}^2}\kern0.5em {C}_3={\rho}_v{h}_{fg} $$

$$ {A}_6={\rho}_v{h}_{fg}\left({A}_5-{T}_v\right)+{C}_1{P}_1\kern0.5em {A}_7={h}_{ev}\left(-{C}_1{P}_2+{P}_1\right)+\frac{k_l{T}_w}{\delta}\kern0.5em {A}_8=\frac{9\sigma {\delta}^{{\prime\prime\prime} }{\delta}^{{\prime\prime} }{\delta}^{\prime }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}} $$

$$ {A}_9=-\frac{15\sigma {\delta^{{\prime\prime}}}^3{\delta^{\prime}}^2}{{\left({\delta^{\prime}}^2+1\right)}^{7/2}}\kern0.5em {A}_{10}=\frac{3\sigma {\delta^{{\prime\prime}}}^3}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}}\kern0.5em {A}_{11}=g\left({\rho}_l-{\rho}_v\right){\delta}^{{\prime\prime} } $$

$$ {A}_{12}=-\frac{12A{\delta^{{\prime\prime}}}^2}{\delta^5}\kern0.5em {A}_{13}=\frac{3A{\delta}^{{\prime\prime} }}{\delta^4}\kern0.5em {A}_{14}=g\left({\rho}_l-{\rho}_v\right){\delta}^{\prime } $$

$$ {A}_{15}=\frac{3A{\delta}^{\prime }}{\delta^4}\kern0.5em {A}_{16}=-\frac{\sigma {\delta}^{{\prime\prime\prime} }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}}+{A}_2+{A}_{14}+{A}_{15} $$

$$ {A}_{17}={A}_8+{A}_9+{A}_{10}+{A}_{11}+{A}_{12}+{A}_{13}\kern0.5em {A}_{18}=-{h}_{ev}{C}_1{A}_{16}-\frac{k_l{T}_w{\delta}^{\prime }}{\delta^2} $$

$$ {A}_{19}=\frac{h_{ev}^2{A}_6\Big({\rho}_v{h}_{fg}\left(\frac{A_{18}}{A_1}+\frac{\delta^{\prime }{k}_l{A}_7}{\delta^2{A}_1^2}+{C}_1{A}_{16}\right)}{\rho_v{h}_{fg}^2} $$

$$ {A}_{20}=\frac{1}{2}\left({A}_2-{A}_{19}+{A}_{15}-{A}_{16}\right)-\frac{3}{2}\left(\frac{\sigma {\delta^{{\prime\prime}}}^3{\delta}^{\prime }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}}+\frac{A{\delta}^{\prime }}{\delta^4}\right)+\frac{1}{2}{\rho}_lg\sin \alpha \cos \varphi $$

$$ {A}_{21}=\frac{2{\delta}^{\prime }{k}_l}{\delta^2{A}_1^2}\left({A}_{18}+\frac{\delta^{\prime }{k}_l{A}_7}{\delta^2{A}_1}-\frac{\delta^{\prime }{A}_7}{\delta }+{\delta}^{{\prime\prime} }{A}_7\right) $$

$$ {A}_{22}=\frac{6A{\delta^{\prime}}^2}{\delta^5}-\frac{3}{2}\frac{A{\delta}^{{\prime\prime} }}{\delta^4}-\frac{1}{2}{A}_{11}\kern0.5em {\mathrm{A}}_{23}=-\frac{9}{2}\frac{\sigma {\delta}^{{\prime\prime} }{\delta}^{{\prime\prime} }{\delta}^{\prime }}{{\left({\delta^{\prime}}^2+1\right)}^{5/2}}\kern0.5em {\mathrm{A}}_{24}=\frac{2{k}_l{\mathrm{T}}_{\mathrm{w}}{\delta^{\prime}}^2}{\delta^3} $$

$$ {\mathrm{A}}_{25}=-\frac{k_l{\mathrm{T}}_{\mathrm{w}}{\delta}^{{\prime\prime} }}{\delta^2}\kern0.5em {\mathrm{A}}_{26}=3\left({\mathrm{A}}_{16}+{\mathrm{A}}_{19}\right)+{2\mathrm{A}}_{20}-3{\rho}_lg\sin \alpha \cos \varphi $$

$$ {A}_{27}=\frac{1}{3}\frac{C_1{A}_1^2{A}_{26}{\delta}^2+3{\rho}_v{h}_{fg}{A}_1{A}_{18}{\delta}^2+3{\rho}_v{h}_{fg}{k}_l{A}_7{\delta}^{\prime }}{A_1^2{\delta}^2} $$

$$ {A}_{28}=\frac{h_{ev}^2\Big({\rho}_v{h}_{fg}{\left(\frac{A_{18}}{A_1}+\frac{\delta^{\prime }{k}_l{A}_7}{\delta^2{A}_1^2}+{C}_1{A}_{16}\right)}^2}{\rho_v{h}_{fg}^2} $$

$$ {A}_{29}={A}_{17}{\left({\delta^{\prime}}^2+1\right)}^{3/2}\kern0.5em {A}_{30}=-\frac{1}{2}\frac{A_{26}{\delta}^2{\delta}^{\prime }}{\mu_l}\kern0.5em {A}_{31}=-\frac{1}{6}\frac{A_{26}{\delta}^3}{\mu_l} $$

$$ {A}_{32}=-\frac{r\left({A}_5-{T}_w\right){k}_l}{\rho_l{h}_{fg}\delta}\kern0.5em {A}_{33}={A}_1{A}_{21}+{A}_{24}+{A}_{25}-{A}_{29}{A}_3{C}_1{h}_{ev} $$

$$ {A}_{34}=-3{\delta^{{\prime\prime}}}^3\left({\delta^{\prime}}^2+1\right)\kern0.5em {A}_{35}=15{\delta^{{\prime\prime}}}^3{\delta^{\prime}}^2\kern0.5em {A}_{36}={C}_1{A}_1{A}_{29}{A}_3+{C}_3{A}_{35} $$

Appendix 2

Macro region equations:

The macro region equations including continuity, momentum and energy equations are defined as follows:

$$ \frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho u\right)={\dot{m}}_{masstransfer}, $$

(1)

$$ \frac{\partial \left(\rho u\right)}{\partial t}+\nabla \cdot \left(\rho\;u\;u\right)=-\nabla p+\nabla \cdot \left[\mu \left(\nabla u+\nabla {u}^T\right)\right]+\rho g+{F}_{\sigma }, $$

(2)

$$ \frac{\partial \left(\rho E\right)}{\partial t}+\nabla \cdot \left(u\left(\rho E+p\right)\right)=\nabla \cdot \left[{k}_{eff}\left(\nabla T\right)\right]+{S}_h, $$

(3)

The additional equation for tracking the interphase between the phases is the continuity equation for the volume fraction of one of the phases.

$$ \frac{\partial \left(\rho \alpha \right)}{\partial t}+\nabla \cdot \left(\rho u\;\alpha \right)={\dot{m}}_{mass\kern0.17em transfer}, $$

(4)

The mass transfer between phases has two parts. The first part is due to the overall mass transfer of vaporization around the bubble perimeter. The second part is due to the effect of microlayer. The first part is accounted by the employed boiling model automatically, while the second part should be added to the model. Following the method introduced by Son et al. [18], the additional mass transfer due to the microlayer ($\rho {\dot{V}}_{micro}$) is defined as follows:

$$ {\dot{V}}_{micro}=\underset{R_0}{\overset{R_l}{\int }}\frac{k_1\left({T}_w-{T}_{\mathrm{int}}\right)}{\rho_v{h}_{fg}\delta \varDelta {V}_{micro}} rdr. $$

(5)

Equation (5) is considered as a source term in the continuity equation of vapor phase.