1 Introduction

Boiling phenomenon occurs in a variety of industrial apparatus. Steam generating boilers, chemical processing plants and nuclear reactors are a few examples where the boiling phenomenon occurs when heat is transferred from the heated surfaces to the relatively colder surrounding fluids. Nucleate boiling, which is the first stage of the boiling phenomenon, plays a significant role in transferring heat from the heated surfaces to the surrounding fluids due to the large latent heat of evaporation. The main causes of a high heat transfer rate in the nucleate boiling are the bubble formation at low temperatures, the high frequency of the bubble formation and its large growth rate. Complete understanding of the bubble growth dynamics and the parameters which effect it are essential for the optimal design of heat transferring apparatus.

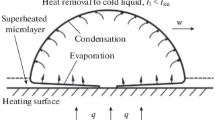
During the boiling process in a liquid, there is not any bubble formation on the heated surface as long as the temperature of the liquid in contact with the surface is below its saturation temperature. The nucleation phenomenon begins with increasing the temperature of the heated surface. However, the nucleated bubbles condense before being released into the liquid. As the liquid temperature increases and gets close to the saturation temperature due to the heat transfer from the surface, the nucleated bubbles grow and are detached from the surface. However, they condense while rising in the cold liquid. With continuing the heat transfer from the surface, the liquid temperature reaches its saturation temperature away from the surface. Under such circumestances, the bubbles that are nucleated on the surface do not condense in the liquid while rising to the free surface [1].

One of the parameters that affect the bubble growth dynamics, as pointed out by many researchers and proved in the recent experimental studies [2, 3], is the microlayer. In the initial stage of the nucleate boiling, the bubble embryo grows rapidly, and pushes the superheated liquid away from the heated surface. Under this circumstance, a thin layer of the liquid with a few micrometers thickness develops on the heated surface underneath the bubble. The thin liquid layer is called the microlayer. Formation of the microlayer underneath the bubble during the bubble nucleation and growth was confirmed experimentally by Moore and Mesler [4] and Hsu and Schmidt [5]. Furthermore, numerous studies conducted by various researchers, including Cooper and Lloyd [6], Jawurek and Jude [7], Voutsinos and Judd [8], Kaufman and Kim [9], Jung and Kim [2] and Yabuki and Nakabeppu [3], on the role of the microlayer in the nucleate boiling process indicate that the contribution of the microlayer to the total heat transfer to the bubble varies between 17 to 50%. It is noteworthly that the local heat flux due to the microlayer evaporation exceeds 1 MW/m2 [2]. These studies attest to the important role of the microlayer in the nucleate boiling. However, due to the complexity of the microlayer, a comprehensive analytical model has not been developed for this layer yet. Employing a few significant assumptions, an analytical model for the microlayer underneath the bubble has been introduced by Lay and Dhir [10]. The proposed model for the microlayer predicts the growth of the bubble rather accurately, nevertheless, it is unable to predict the temperature distribution on the heated surface.

Generally, the bubble growth dynamics is investigated under two different circumstances, namely, injecting a gas into an isothermal liquid or heating a surface and subsequent nucleation of vapor bubbles in its surrounding liquid. Some researchers have investigated the bubble growth dynamics experimentally, analytically or numerically by injecting a gas into liquids on horizontal [11,12,13,14] or inclined surfaces [15]. Other researchers have studied the bubble growth dynamics during the nucleate boiling process. In these studies, the impacts of different pertinent parameters, such as the gravity [16,17,18,19,20], the material and quality of the surface [21, 22], the surface geometry [23, 24], the surface wettability, its thermophysical properties [25,26,27] and the heat transfer rate [28,29,30], on the bubble growth dynamics have been investigated experimentally or numerically.

These studies attest to versatility of the parameters which affect the bubble growth dynamics. Dhir et al. [19] showed that decrease of the gravity intensity increases the diameter of the bubble when its growth rate is low; whereas, it has no effect on a bubble with a high growth rate. Rousselet [27] showed that increasing the surface wettability results in filling the cavities on the surface and, hence, reducing the number of vapor production centers. Coating the heated surfaces with nano-particles affects their roughnesses as well as their the chemical properties; therefore, increasing the number of active cavities and enhancing the heat transfer from them. However, increasing the surface roughness beyond a certain limit does not affect the heat transfer rate from the surface. Recent experimental studies by Jung and Kim [2] and Yabuki and Nakabeppu [3] have demonstrated that the rapid growth rate during the early stages of the bubble growth is due to the evaporation of the microlayer which results in a simultaneous sharp drop of the surface temperature. When the evaporation of the microlayer is completed, the bubble growth rate becomes slower and the surface temperature begins to increase.

A parameter that significantly affects the structure of the microlayer, the heat transfer rate from it, and the bubble growth dynamics is the contact angle between the heated surface and the liquid-vapor interface. The results presented by Son et al. [31] for the nucleate boiling on a horizontal surface indicate that by increasing the contact angle from 25° to 30°, the bubble equivalent diameter increases by 22.2%. More than being affected by the heated surface quality and the fluid properties, the contact angle is influenced by the variation of the heated surface inclination.

In most of the numerical studies performed on the nucleate boiling, the heated surface is considered to be horizontal and the microlayer underneath the bubble is assumed to be symmetric. Nevertheless, one of the parameters that can affect the microlayer and the bubble growth dynamics during the nucleate boiling is the inclination of the heated surface. Lay and Dhir [10], in their proposed model for the microlayer, assumed a symmetrical microlayer around the bubble base. This assumption is reasonable on a horizontal heated surface. However, in the nucleate boiling on an inclined heated surface, the symmetry assumption for microlayer is not valid anymore, and employing this assumption yields erroneous results. Abdoli et al. [32] modified the model proposed by Lay and Dhir for the microlayer to be able to include the effect of the surface inclination on the bubble growth dynamics.

The pool boiling phenomenon on the inclined heated surfaces is investigated by some researchers such as Mei et al. [33, 34], Dadjoo et al. [35], Kim et al. [36, 37], Sadaghiani et al. [38], Kibar et al. [39], Tanjung and Jo [40] and others [41,42,43,44]. The collective result of their studies is that by increasing the surface inclination, the critical heat flux (CHF(decreases and the pool boiling heat transfer increases. However, nearly all of these studies are concerned with the heat transfer coefficient and the critical heat transfer rate during the pool boiling and do not consider the details of the bubble growth dynamics on the inclined surfaces. Therefore, the purpose of the present study is to employ the modified model for the bubble growth on an inclined heated surface presented by the current authers in [32] to conduct a comprehensive numerical inveatigation of the bubble growth dynamics on the inclined heated surfaces.

In this regards, the effects of changing the surface inclination on the contact angle around the bubble base, the length of the bubble base, the bubble slippage on the surface before detachment, the bubble shape, the bubble equivalent diameter and the heat transfer from the surface are analyzed and the results are presented. Based on the results of the present study, the optimum surface inclination for the maximum heat transfer from the surface is determined.

2 Mathematical modeling

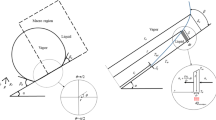
A vapor bubble during nucleate boiling on an inclined heated surface is shown in Fig. 1. The solution domain in this figure is divided into two parts, namely, the micro and the macro regions. The macro region consists of the bubble and its surrounding superheated liquid; while, the micro region is a thin liquid layer underneath the bubble between the heated surface and the liquid-bubble interface whose thickness varies from the diameters of a few molecules to a few micrometers.

Fig. 1
figure 1

A schematic diagram showing the micro and the macro regions during the nucleate boiling on an inclined heated surface

Full size image

In the macro region, where the liquid and the vapor phases coexist, the equations for the conservations of mass, momentum, and energy should be solved for the fluid. Coupling between the micro and the macro regions is through the appropriate boundary conditions. In the modified model for the microlayer, similar to the model of Lay and Dhir [10], the microlayer is located at the triple point and moves with the movement of the triple point during the growth and collapse of the bubble.

2.1 Governing equations of the macro region

The conservation laws for mass, momentum, and energy in the macro region are, respectively, given by the following equations:

$$ \frac{\partial \rho }{\partial t}+\nabla .\left(\rho \overrightarrow{u}\right)=0 $$
(1)
$$ \rho \left(\frac{\partial \overrightarrow{u}}{\partial t}+\overrightarrow{u}.\overrightarrow{\nabla}\overrightarrow{u}\right)=-\overrightarrow{\nabla}p+\nabla .\left[\mu \left(\overrightarrow{\nabla}\overrightarrow{u}+\overrightarrow{\nabla}{\overrightarrow{u}}^T\right)\right]+\rho \overrightarrow{g}+\overrightarrow{F} $$
(2)
$$ {\rho c}_p\left(\frac{\partial T}{\partial t}+\overrightarrow{u}.\overrightarrow{\nabla}T\right)=\nabla .k\overrightarrow{\nabla}T $$
(3)

Employing the method proposed by Wu and Dhir [45], the equation for the mass conservation (Eq. 1) can be written in the following form:

$$ \nabla .\overrightarrow{u}=\frac{\overrightarrow{m}}{\rho^2}.\nabla \rho +{\dot{V}}_{micro}=\frac{k\nabla \mathrm{T}}{h_{fg}{\rho}^2}.\nabla \rho +{\dot{V}}_{micro} $$
(4)

where hfg is the enthalpy of vaporization and \( {\dot{V}}_{micro} \), which is obtained by the solving microlayer equations, is given by.

$$ {\dot{V}}_{micro}=\underset{0}{\overset{2\pi }{\int }}\underset{R_i}{\overset{R_0}{\int }}\frac{k_l\left({T}_W-{T}_{int}\right)}{\rho_m{h}_{fg}{\delta \Delta V}_{micro}} rdrd\theta $$
(5)

where Tw and Tint are the heated surface and the fluid-vapor interface temperatures, respectively, and ΔVmicro is the volume of the vapor in each of the computational cells which encompass the microlayer during the process.

To capture the interface between the vapor and the liquid phases in the macro region, the volume of fluid method (VOF) is employed. In this method, a volume fraction is defined for each of the phases existing in a computational cell which shows how much of the cell volume is occupied by each phase. The sum of the volume fractions of the phases existing in the cell is equal to unity.

$$ \sum \limits_{i=1}^n{\alpha}_i=1 $$
(6)

where αi is the volume fraction of the phase i and n is the total number of phases in the computational cell. In this method, the average thermophysical properties [10] which are employed in the governing equations, are obtained based on the respective volume fractions of the different phases existing in the computational cell, according to the following equation:

$$ \varnothing =\sum \limits_{i=1}^n{\alpha}_i{\varnothing}_i $$
(7)

where ϕi is the thermophysical property of the phase i and ϕ is the corresponding average thermophysical property.

2.2 Governing equation of the microlayer

The balance of energy for an element of the fluid in the microlayer is written as [10].

$$ -{h}_{fg}d{\dot{m}}_r={\dot{Q}}_{microlayer} $$
(8)

where \( {\dot{m}}_r \)and \( {\dot{Q}}_{microlayer} \), which are the mass flow rate and the rate of heat transfer in the microlayer, respectively, are given by.

$$ d{\dot{m}}_r=2\pi r{\rho}_l{\overline{u}}_r\delta $$
(9)
$$ {\dot{Q}}_{microlayer}=2\pi rqdr $$
(10)

where ρl is the liquid density, \( {\overline{u}}_r \)is the radial component of the average liquid velocity in the microlayer, δ is the microlayer thickness, and q is the rate of heat transfer to the microlayer through the inclined heated surface. In order to determine ur, the following momentum equation together with its boundary conditions should be solved in the microlayer;

$$ \frac{\partial {p}_l}{\partial r}={\mu}_l\left(\frac{\partial^2{u}_r}{{\partial y}^2}\right)+{\rho}_l{g}_r $$
(11)
$$ {\displaystyle \begin{array}{ccc}{u}_r=0& at& y=0\\ {}\frac{{\partial u}_r}{\partial y}& at& y=\delta \end{array}} $$
(12)

where gr = g sinα.

The pressure difference between the fluid and the vapor depends on the gravity and the momentum difference at the liquid-vapor interface. The pressure difference can be expressed as follows [10]:

$$ {p}_l-{p}_v=\left({\rho}_v{v}_v^2-{\rho}_l{v}_l^2\right)-\sigma K+{\rho}_l{g}_y\left(\delta -{\delta}_0\right)-\frac{A}{\delta^3} $$
(13)

where σ is the surface tension, A is the Hamaker constant which is equal to 10−20 j and K is the curvature of the liquid-vapor interface which is given by:

$$ K=\frac{1}{r}\frac{\partial }{\partial r}\left[r\frac{\partial \delta }{\partial r}/\sqrt{1+{\left(\frac{d\delta}{d r}\right)}^2}\right] $$
(14)

The equation of the conservation of energy in the microlayer is

$$ q={k}_l\frac{\left({T}_w-{T}_{int}\right)}{\delta }={h}_{ev}\left[{T}_v-{T}_v+\left({p}_l-{p}_v\right)\frac{T_V}{\rho_l{h}_{fg}}\right] $$
(15)

where Tv is the vapor temperature, pv is the vapor pressure, pl is the fluid pressure and hev denotes the heat transfer coefficient due to evaporation which is given by [46].

$$ {h}_{ev}={\left(\frac{a_1M}{2\pi \overline{R}{T}_v}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{\rho_v{h}_{fg}^2}{T_V} $$
(16)

where M and \( \overline{R} \) are the molecular weight of the vapor and the universal gas constant, respectively. Moreover, Tv = Tsat (pv) where Tsat is the saturation temperature corresponding to the vapor pressure. According to Hicman [47] and Lay and Dhir [10] the constant ɑ1 in Eq. (16) is equal to unity.

Employing Eq. (11) and Eqs. (13) through (16) makes it possible to write Eq. (12) as the following fourth-order nonlinear ordinary differential equation for the microlayer thickness:

$$ {\delta}^{{\prime\prime\prime} \prime }=f\left(\delta, {\delta}^{\prime },{\delta}^{\prime \prime },\delta^{\prime\prime\prime}\right) $$
(17)

At the inner radius, r = Ri, the microlayer thickness has its minimum value which is of the order of nanometer (Fig. 1). Moreover, the microlayer profile is parallel to the heated surface here and, hence, the slope of the thickness profile is zero. At the outer radius, r = Ro, the slope of the microlayer thickness profile is equal to the tangent of the contact angle of the liquid-vapor interface with the heated surface. Therefore, the boundary conditions for Eq. (17) are as follows:

$$ {\displaystyle \begin{array}{l}\delta ={\delta}_i\kern0.75em ,\kern0.75em {\delta}^{\prime }=0\kern1em ,\kern1em {{\delta^{\prime}}^{\prime}}^{\prime }=0\kern3.25em \mathrm{at}\kern2.25em r={R}_i\ \\ {}{\delta}^{\prime }={\tan}^{-1}\beta \kern10.5em \mathrm{at}\kern2.25em r={R}_o\ \end{array}} $$
(18)

where β, which is the contact angle between the liquid-vapor interface and the heated surface, is given by [31].

$$ \beta ={\tan}^{-1}\frac{\delta_0}{\left({R}_o{R}_i\right)} $$
(19)

where δ is the microlayer thickness at the contact point between the microlayer and the macro region, and Ri and Ro are the inner and outer radii of the microlayer with respect to the bubble center, respectively (Fig. 1). The details of Eq. (17) are given by Abdoli et al. [32].

To determine the microlayer thickness during the nucleate boiling on the inclined heated surface, Eq. (17) is solved numerically employing the boundary conditions (18). Subsequently, other parameters associated with the microlayer, such as, the radial velocity, the evaporation rate (Eq. 5) and the contact angle between the liquid-vapor interface and the heated surface (Eq. 19) are calculated. Having obtained these parameters, the governing equations of the macro region are solved. The coupling between the micro and the macro regions is through the contact angle, the bubble base radius, the location of the contact point and the microlayer evaporation rate.

3 Numerical method

To simulate the bubble growth during the nucleate boiling on the inclined heated surface, the coupled system of governing differential equations for the micro and macro regions should be solved simultaneously. In the present study, a computer code written in MATLAB, based on the Euler method, is employed to solve the ordinary differential equation and its boundary condations (Eqs. 17 and 18) for the microlayer thickness. Having obtained the thickness of the microlayer, the microlayer evaporation rate, which acts as a source term in the continuity equation of the macro region, is calculated. Subsequently, the governing equations for the macro region are solved numerically using the finite volume method and the FLUENT software yielding new values for the inner and outer radii of the microlayer, and the contact angle between the liquid-vapor interface and the heated surface. Using the new values of Ri, Ro and β, the microlayer equation is solved for the next time step, \( {\dot{V}}_{micro} \) is calculated, and the equations of the macro region are solved again. This procedure is repeated until the bubble gets detached from the heated surface. The details of the numerical procedures for simulating the micro and the macro regions as well as of the scheme employed to couple them are presented in the following subsection. The working fluid in this study is water at atmospheric pressure. The thermophysical properties of water and its vapor are given in Table 1.

Table 1 Thermophysical properties of water and its vapor at atmospheric pressure [1]
Full size table

3.1 Three-dimensional simulation of the macro region

The transient partial differential equations governing the non-isothermal fluid flow in the macro region are solved numerically using the finite volume method and the FLUENT software. The three-dimensional computational domain employed to perform the simulation is shown in Fig. 2. The heated surface comprises the bottom boundary of the domain. At the center of the surface is an active cavity whose diameter and depth are 100 μm and 150 μm, respectively [48]. Since the fluid flow in the macro region is due to the bubble growth, far from the bubble, the fluid is considered to be stagnant. Therefore, the sides and top boundaries of the domain are selected far enough from the nucleation site to insure that the assumption of stagnant fluid there is reasonably accurate. To make it possible for the nucleated bubble to eventually leave the computational domain, its top boundary is considered to be a free surface with constant pressure. As far as the flow boundary conditions are concerned, the no-slip and the impermeable wall boundary conditions are imposed on the heated surface. Along the side boundaries, the velocity components of the fluid are considered to be zero. Moreover, the fluid is initially stagnant. As far as the thermal boundary conditions are concerned, all of the domain boundaries, except the heated surface, are considered to be insulated. The temperature of the heated surface is considered to be constant and equal to ΔTsup = 10.2°c. The initial temperature of the fluid is ΔTsub = 3°c. Generaly, when the temperature of the heated surface at the nucleation site reaches the temperature required for the bubble nucleation, which according to the experimental results is ΔTsup ≈ 8°c [48], a semi-spherical bubble nucleus is formed at the center of the heated sufrace (Fig. 2).

Fig. 2
figure 2

Computational domain for the three-dimensional simulation of the nucleate boiling

Full size image

A typical structured grid employed for the numerical simulation is depicted in Fig. 3. According to the experimental studies conducted by Jung and Kim [2] and Yabuki and Nakabeppu [3], the thickness of the microlayer for 8°c < ΔTsup < 12°c is at most 3 μm, and its length for the same temperature range varies from 0.5 mm to 0.8 mm. Using these data, the mesh is refined in the microlayer underneath the bubble to insure that the microlayer is always located within three computational cells in the radial direction along the heated surface around the circumference of the bubble base (Fig. 4). Furthermore, the smallest size of the computational cell is chosen to be equal to the radius of the bubble nucleus [48]. The time step for the numerical simulation is Δt = 5 × 10−8 s.

Fig. 3
figure 3

A three-dimensional nonuniform structured grid with 5 × 106 cells employed for the numerical simulation

Full size image
Fig. 4
figure 4

A cross section of the bubble and its surrounding liquid showing the computational cells at the contact points where the microlayer is located

Full size image

As far as the size of the computational domain in Fig. 2 is concerned, it should be chosen large enough to guarantee that its size dose not affect the simulation results. A study conducted by the authors, whose results are presented in the subsection 3.4, as well as the studies performed by other investigators [30, 31] show that choosing the size of the computational domain equal to five times of the maximum bubble diameter fulfills this requirement. Hence, the results presented in the following are for a computaional domain meeting this criterion.

The volume of fluid method is employed to keep track of the moving boundaries during the simulation. In this method, a fixed mesh is employed during the entire simulation time. A volume fraction is associated with the liquid and the vapor phases existing in a computational cell, which is defined as the ratio of the volume of the considered phase to the total volume of the cell. The liquid-vapor interface passes through the cells whose volume fractions are between zero and unity. Having calculated the interface velocity, the location of the liquid-vapor interface is updated at each time step during the simulation.

The coupling between the governing equations of the macro region and that of the microlayer is through the volume of the vapor resulting from the evaporation of the microlayer which appears as the source term in the continuity equation for the macro region. To couple the microlayer and the macro region, the cells encompassing the microlayer (Fig. 4), are identified at each time step during the simulation, and the volume of the vapor generated in them is calculated. Using this volume, \( {\dot{V}}_{micro} \)is obtained from Eq. (5) and employed as the source term in Eq. (4).

3.2 Simulation of the microlayer

In order to simulate the development of the microlayer during the nucleate boiling on an inclined heated surface, its governing eq. (17) and the boundary conditions (18) are solved numerically at each time step during the simulation of the bubble growth. A computer code written in MATLAB, based on the Euler method, is employed for this purpose. To implement the numerical method, the fourth-order ordinary differential eq. (17) is converted to a set of four first-order ordinary differential equations. The resulting equations are, subsequently, solved for the microlayer region underneath the bubble aroud the circumference of the bubble base. Since the first three boundary conditions (18) are prescribed at r = Ri, and the fourth one is imposed at r = Ro, the shooting method is employed in the solution procedure. Having solved the microlayer equation, new values of δ and β for the microlayer around the circumference of the bubble base are determined. Subsequently, \( {\dot{V}}_{micro} \), which acts on the source term in the continuity equation for the macro region, is calculated, and the equations for the macro region are solved for the next time step.

3.3 Grid independence study

A grid independence study is performed in order to guarantee that the simulation results are independent of the grid size. For this purpose, the proposed numerical scheme is employed to simulate the growth and detachment of a vapor bubble nucleated on a horizontal heated surface. A cubic computational domain whose dimensions are the same as those of the domain shown in Fig. 2 and its bottom boundary is the horizontal heated surface is utilized to conduct the simulations. Three different nonuniform grids with the total number of cells equal to 5 × 104, 4 × 105 and 5 × 106 are employed to perform the numerical simulation. The results for the equivalent diameter of the bubble at the instant of detachment from the heated surface, Dd, the time required for the bubble nucleus to grow and to get detached from the surface, td, and the total heat transfer from the surface during this time, Qd, for the considered grids are presented in Table 2. As it is observed from this table, Dd, td and Qd approach constant values with refining the mesh. The results show that the differences between the values of Dd, td and Qd obtained for the grid with 5 × 106 cells and those obtained for the grid with 4 × 104 cels are 0.17%, 0.5% and 0.45%, respectively.

Table 2 Effect of the mesh refinement on the bubble diameter at the detachment moment, the time required for the detachment and the total heat transfer from the surface during this time for the nucleate boiling on the horizontal surface
Full size table

Therefore, the nonuniform grid with 5 × 106 cells is fine enough to perform the simulation of the nucleate boiling, and to capture the details of the microlayer underneath the bubble. Furthermore, the difference between the experimental results of Yabuki and Nakabeppu [3] for the equivalent bubble diameter for the nucleate boiling on a horizontal heated surface and the results of the present simulation for Dd employing the grid with 5 × 106 cells is 0.58%. Based on the above results, the nonuniform grid with 5 × 106 cells is employed to obtain the simulation results presented in the following.

3.4 Effects of the computational domain walls on the bubble hydrodynamics

A crucial issue when selecting the computational domain is to assure that the effect of its walls on the bubble hydrodynamics is negligible. The results of the studies conducted by other investigators on the nucleate boiling on a horizontal heated surface indicate that when the ratio of the length (width) of the squared bottom boundary of the domain, L, to the bubble diameter at the moment of detachment from the surface, Dd, is greater than 3, the effect of the domain walls on the bubble hydrodynamics becomes negligible [30, 31].

To investigate the effect of the dimensions of the domain on the nucleate boiling in the current study, three different cubic computational domains shown in Fig. 5 are employed for the simulation. The ratio of the length (width) of the square bottom boundary of the domain to the bubble diameter at the moment of detachment from the surface, L/Dd, for these domains are 2, 3, and 5 (Fig. 5). The height of the domain for all of the considered cases is equal to 5 times of the bubble diameter at the detachment moment. To perform the numerical simulation, a nonuniform mesh with 5 × 106 cells is employed for each of the considered domains. Table 3 shows the simulation results for the bubble diameter at the detachment moment, Dd, and the time it takes for the nucleus to grow and get detached from the surface, td, for the considered cases. Apart from the dimensions of the heated surface, other conditions are the same for the simulations presented in Table 3 . The results for the bubble diameter and the time presented in Table 3 approach constant values with increasing L/Dd. This indicates that the dimensions of the computational domain in Fig. (5-c) are large enough so that the effect of its walls on the bubble hydrodynamics be negligible. Therefore, this computational domain is used to obtain all of the simulation results presented in the following.

Fig. 5
figure 5

The computational domains used to investigate the wall effect on the bubble hydrodynamics

Full size image
Table 3 Effect of the dimensions of the computational domain on the bubble hydrodynamics
Full size table

3.5 Validation of the model

Due to lack of experimental results for the nucleate boiling on an inclined heated surface, to validate the proposed numerical procedure, the experimental results of Yabuki and Nakabeppu [3] for the nucleate boiling of a vapor bubble in saturated water at atmospheric pressure on a horizontal surface are used. They conducted their experiments for a range of superheat temperature of the heated surface ΔTsup = 8–15°c, and presented the bubble radius during the nucleate boiling phenomenon. To compare the results of the present simulation with their experimental results, the superheat temperature of the surface is considered to be equal to ΔTsub = 8.1°c.

Figure 6 shows comparisons between the results of the present simulation with the experimented results of Yabuki and Nakabeppu [3] for the variation of the bubble radius during the nucleate boiling on a horizontal surface. The simulation results presented are for two different cases, namely, with and without considering the microlayer. td in this figure represents the bubble detachment time. As it is observed from this figure, good concordance exists between the results of the present simulation obtained with considering the effect of the microlayer with the experimental results of the Yabuki and Nakabeppu for the bubble radius. However, the difference between the simulation results without considering the effect of the microlayer and the experimental results are significant.

Fig. 6
figure 6

Comparisons of the results of the present simulation for the bubble growth on a horizontal heated surface with the experimental results of Yabuki and Nakabeppu [3]

Full size image

Initially, the growth of the bubble is mainly due to the evaporation of the microlayer, which occurs quite rapidly. This causes high bubble growth rates initially. However, after completion of the microlater evaporation, the bubble growth is due to the evaporation at the liquid-bubble interface resulting in small growth rates (Fig. 6). The above observations indicate that the microlayer plays a significant role in the growth of the vapor bubble particularly during the early stage of the growth period. Therefore, the effect of the microlayer should be considered while simulating the nucleate boiling phenomenon. The discripancy between the experimental and the numerical results in Fig. 6 is mainly attributed to not considering the microlayer effect.

4 Results and discussion

Having completed the grid independence study and the model validation, the proposed numerical simulation is employed to investigate the impact of the heated surface inclination on the nucleate boiling of a vapor bubble in stagnant water at atmospheric pressure considering the effect of the microlayer. The dimensions of the computational domain employed to perform the simulations are the same as those in Fig. (5-c). The nonuniform mesh with 5 × 106 cells, which is used for the simulations, is the same as that shown in Fig. 3. The time step for the numerical simulations is 5 × 10−8 s. The thermophysical properties of water and its vapor are given in Table 1. In the following, the superheat temperature of the heated surface is considered to be ΔTsup = 10.2°c.

Figure 7 shows the variation of the equivalent bubble radius with respect to time for an inclined heated surface with different inclinations. α = 0 in this figure corresponds to the horizontal heated surface. The results in Fig. 7 are for t ≤ td, where td is the time required for the bubble to get detached from the heated surface. As it is observed from this figure, α = 30° corresponds to the largest bubble radius during the growth time, i.e., for t ≤ td. With increasing α from 30° to 60°, the bubble radius decreases continuously and approaches the bubble radius for the horizontal heated surface.

Fig. 7
figure 7

Variations of the equivalent bubble radius with respect to time during the nucleate boiling and before detachment from the inclined heated surface for different inclinations

Full size image

Figure 8 shows cross sections of the bubble in the r-y plane passing through the bubble base center (Fig. 1) at selected times during the growth period before detachment from the heated surface. The results are presented for the horizontal surface as well as for three inclined surfaces with the inclinations of 30°, 45°, and 60°. The asymmetrical growth of the vapor bubble on the inclined heated surface as opposed to its symmetrical growth on the horizontal surface is clearly observed from this figure.

Fig. 8
figure 8

Effect of the inclination of the heated surface on the bubble cross section during the growth period before detachment from the surface, (a) α = 0, (b) α = 30°, (c) α = 45° and (d) α = 60°

Full size image

For the horizontal heated surface, the upward movement of the bubble results in a symmetrical flow pattern in the surrounding fluid. However, for the inclined heated surface, this movement results in a relatively large vortex in the surrounding fluid as a consequence of which a drag force is imposed on the bubble surface, contrary to the case of the horizontal surface for which the forces due to the buoyancy and the surface tension act perpendicular to the surface in the upward and downward directions, respectively. Therefore, on the inclined surface, The bubble is detached from the surface finally as a result of the interaction between the buoyancy, the surface tention and the drag forces which results in an elliptical bubble shape (Figs. 8(b), 8(c) and 8(d)).

Moreover, for the inclined heated surface, the buoyancy force has two components, along and perpendicular to the surface. The component of the buoyancy force along the surface, which causes the bubble to slip along the surface, does not affect the bubble detachment from the surface. On the other hand, with increasing the length of the bubble base on the inclined surface, the surface tension force increases. Decreasing the perpendicular component of the buoyancy force and increasing the force due to the surface tension compared to the corresponding ones on the horizontal surface result in a larger bubble radius before detachment for the inclined surface compared to that for the horizontal one (Figs. 8(b), 8(c) and 8(d)). Furthermore, inclining the heated surface may result in intensifying the natural convection and increasing the heat transfer to the bubble. Hence, the equivalent bubble radius increases compared to that of the bubble growing on a horizontal heated surface. Increasing the surface inclination beyond α = 30° intensifies the natural convection heat transfer in the domain. Consequently, more heat is transferred to the liquid than to the bubble. Therefore, the bubble volume decreases with increasing α beyond a certain value.

Figure 9 shows three-dimensional pictures of the bubble at two different times during the simulation of the nucleate boiling on the heated surface with different inclinations. As it is observed from this figure, on the horizontal heated surface, the bubble grows symmetrically and the contact angle is the same around the circumference of the bubble base. However, on the inclined heated surface, the bubble growth is asymmetrical, and the contact angle, the microlayer thickness and its profile vary around the circumference of the bubble base. The contact angles in the upper half of the circumference of the bubble base, with respect to the line passing through the bubble base center and being perpendicular to the r-y plane, are smaller compared to those in the lower half of the circumference.

Fig. 9
figure 9

Three-dimensional pictures of the bubble at two different times during the growth period before detachment from the surface, (a) α = 0, (b) α = 30°, (c) α = 45° and (d) α = 60°

Full size image

Figure 10 shows the effect of inclination of the heated surface on the uppermost and lowermost contact angles and the bubble cross section at the moment of detachment from the heated surface. The uppermost and lowermost contact angles are those at the points of intersection of the r-y plane which passes through the bubble base center with the upper and lower parts of the bubble base circumference, respectively. The results presented in this figure are for α = 0 (the horizontal surface), α = 30°, 45°, and 60°. The bubble grows symmetrically on a horizontal heated surface, and the contact angle of the bubble with the heated surface is the same around the bubble base (Fig. 10(a)). Clearly, this angle will change during the bubble growth period. For an inclined heated surface, the components of the buoyancy and the surface tension forces acting on the bubble are different from the corresponding magnitudes for the horizontal surface. Hence, the bubble grows asymmetrically and gets closer to the surface around the upper half of the circumference of the bubble base with respect to the line passing through the bubble base center and being perpendicular to the r-y plane (Figs. 10 (b), 10 (c) and 10 (d)).

Fig. 10
figure 10

Impact of the surface inclination on the uppermost and lowermost contact angles and the bubble cross section at the moment of detachment from the heated surface, (a) α = 0, (b) α = 30°, (c) α = 45° and (d) α = 60°

Full size image

With increasing the surface inclination, the asymmetry of the contact angle of the bubble with the heated surface around the bubble base increases. During the bubble growth on the inclined surface, the component of the surface tension force which is parallel to the surface prevents the bubble from sliding on the surface. On the other hand, the resultant of the buoyancy and the drag forces drives the bubble along the surface. The interaction between these forces causes the bubble to move toward the surface around the upper half of the circumference of the bubble base. For α = 30°, the bubble volume, as well as the resultant of the buoyancy and the drag forces are larger than the corresponding magnitudes for the other surface inclinations, resulting in a smaller contact angle in the upper half of the bubble base circumference compared to those for α = 45° and α = 60°. With increasing the surface inclination from 30° to 45° and 60°, the bubble volume decreases constantly, resulting in the larger uppermost contact angles (Fig. 10 (c) and 10(d)). The contact angle directly affects the microlayer and the bubble growth.

A key parameter in designing a heat exchanger is the rate of heat transfer from the heated surfaces. Therefore, the effect of the inclination of the heated surface on the rate of heat transfer between the surface and its surrounding fluid is quite important. The time required for the bubble to grow and get detached from the heated surface, the frequency of the bubble nucleation, the equivalent bubble diameter at the detachment moment, and the total heat transfer from the surface during the growth period of the bubble for different inclinations of the surface are given in Table 4. As it is observed from Table 4, the equivalent bubble diameter is larger for the considered inclined heated surfaces than that for the horizontal heated surface. Moreover, the time required for the bubble to grow and get detached from the surface for the inclined surfaces is larger than that for the horizontal surface. Hence, the frequency of the bubble formation on the inclined surfaces is lower than that on the horizontal surface.

Table 4 Effect of the surface inclination on the equivalent bubble diameter, the frequency of the bubble formation, the growth period of the bubble, and the total heat transfer from the surface
Full size table

Figures 11 and 12 show the velocity vectors and the dynamic pressure distribution in the cross section of the computational domain in the r-y plane passing through the bubble base center (Fig. 1) at two different times during the bubble growth on the heated surface with different inclinations, respectively. As it is observed from Fig. 11, the magnitudes of the velocity vectors inside the bubble and close to the interface are quite large. However, by moving away from the interface, the magnitudes of the velocity vectors in the fluid surrounding the bubble drop significantly. Moreover, the two symmetric clockwise and counterclockwise vortices, which exist in the cross section of the computational domain for the case of the bubble growth on a horizontal surface (Fig. 11-a) change to a single clockwise vortex (Figs. (11-b), (11-c) and (11-d)). This vortex is attributed to the large magnitudes of the velocity vectors and large dynamic pressure in the region where the bubble gets close to the inclined surface during its asymmetrical growth. Figure 12 shows that, except inside the bubble and its immediate vicinity, the pressure is constant and equal to the atmospheric pressure inside the fluid. These observations indicate that the effect of the computational domain walls on the bubble growth dynamics is indeed negligible, and the boundary conditions are applied correctly.

Fig. 11
figure 11

Velocity vectors in the cross section of the computational domain at two different times during the bubble growth on the heated surface with different inclinations, (a) α = 0, (b) α = 30°, (c) α = 45° and (d) α = 60°

Full size image
Fig. 12
figure 12

Dynamic pressure distribution in the cross section of the computational domain at two different times during the bubble growth on the heated surface with different inclinations, (a) α = 0, (b) α = 30°, (c) α = 45° and (d) α = 60°

Full size image

Figure 13 shows the variations of the frequency of the bubble formation, the equivalent bubble diameter, and the total heat transfer from the surface with respect to the surface inclination. As observed from this figure, the maximum equivalent bubble radius and the minimum frequency of the bubble formation occur at α = 30°. Moreover, for the steady state nucleate boiling, the minimum heat transfer occurs for a horizontal heated surface. With increasing the surface inclination, the heat transfer increases initially and reaches its maximum value for α = 30°. Further increase of the surface inclination results in the reduction of the heat transfer from the surface (Fig. 13). For the inclined heated surface with α = 30°, 32% increase of the heat transfer compared to that for the horizontal surface is observed.

Fig. 13
figure 13

Impact of the heated surface inclination on the frequency of the bubble formation, the equivalent bubble diameters, and the total heat transfer from the surface

Full size image

Table 5 shows the effect of the surface inclination on the bubble slippage length and the bubble base length before its detachment from the surface. As it was stated before, with increasing the bubble equivalent diameter, the components of the buoyancy and the drag forces parallel to the surface increase, and their resultant force becomes larger than the component of the surface tension force along the surface. Under the effect of these forces, the bubble slips upwards along the heated surface. With increasing the surface inclination, the components of the buoyancy and drag forces along the surface increases resulting in a larger slippage of the bubble along the surface before its detachment. On the horizontal surface, necking of the bubble base before detachment from the surface results in reduction of the contact area with the heated surface. This results in the reduction of the surface tension force, and, as a consequence, the bubble gets detached from the surface under the influence of a smaller buoyancy force. Therefore, its equivalent diameter will be smaller compared to that of the bubble growing on the inclined surface. For the inclined surface, the larger equivalent bubble diameter together with the larger buoyancy and drag forces result in the larger contact area between the bubble and the heated surface. With increasing the surface inclination, the length of the bubble base increases. For α = 60°, the length of the bubble base is 7 times larger than that for a horizontal surface (Table 5).

Table 5 Effect of the surface inclination on the bubble slippage length and the bubble base length before its detachment from the surface
Full size table

5 Conclusions

The model proposed by Lay and Dhir for the microlayer on a horizontal heated surface is modified in order to be able to use it for both the horizontal and inclined heated surfaces. By simulating the bubble formation and growth processes on the horizontal and inclined surfaces using the modified microlayer model, the effects of the surface inclination on the contact angle variation around the bubble base, heat transfer during the nucleate boiling, final shape of the bubble, bubble base length, bubble slippage on the surface, and variation of the equivalent radius of the bubble during nucleate boiling are investigated. The main conclusions are as follows:

  1. 1.

    The contact angle of the liquid-vapor interface with the heated surface at the bubble base around the bubble during the nucleate boiling on the horizontal surface is always symmetric. However, on the inclined surface, the contact angle varies around the bubble base. Moreover, its range of variation around the bubble base increases by increasing the surface inclination.

  2. 2.

    The heat transfer from the heated surface depends on the size of the bubble and the frequency of bubble formation on the surface. Comparisons between the heat transfer for the horizontal surface with those of the inclined surfaces with different inclinations indicates that the horizontal surface has the lowest and the inclined surface with α = 30°, has the highest heat transfer among the investigated cases.

  3. 3.

    On the horizontal surface, the bubble base is necked before detachment from the surface. On the inclined surface, the resulting parallel components of the buoyancy and the surface tension forces increase the bubble contact area and the bubble base length on the surface. Furthermore, by increasing the surface inclination, the bubble base length increases.

  4. 4.

    With increasing the bubble size, the drag and the component of the buoyancy forces parallel to the surface increase overcoming the component of the surface tension parallel to the surface. Hence, the bubble moves upward on the heated surface under these conditions. Moreover, with increasing the surface inclination, the drag and the parallel components of the buoyancy forces increase causing the bubble to slips on the surface before detachment.

  5. 5.

    For the horizontal heated surface, the bubble at the final stage of its growth is detached from the surface as a result of the interaction between the buoyancy and the surface tension forces. This results in an elliptical bubble shape. However, on an inclined heated surface, the component of the surface tension parallel to the surface acts at the bubble base, and prevents its necking, whereas, the drag and the component of the buoyancy force parallel to the surface act on the bubble surface in the opposite direction. This causes the bubble shape to be far from the elliptical shape of the bubble growing on the horizontal surface.