1 Introduction

Thermal behavior of porous ceramic insulators made of closed cell pores has been studied in recent years. Reduction in thermal conductivity of closed cell ceramics or insulators leads to higher energy efficiency and better reactor performance. Insulators sustain very high temperature, so they must have particular thermo-physical properties which can be used in high-temperature industrial furnaces. In the petrochemical industry in which most reactions are exothermic, usage of insulators at walls is essential in order to prevent energy loss and improving reaction yields. Thermal conductivity is the most important factor in selecting the appropriate insulator. Due to complexity in the experimental measurement of thermal conductivity, use of theoretical models is very useful and common. The thermal conductivity of the porous medium depends on the geometry as well as thermal conductivity of solid and gas phases [1]. Numerical methods, such as the finite element method, finite difference method and the Boltzmann lattice method [2] have been widely used to investigate the effective thermal conductivity of porous media. Also, several analytical models are used for prediction of thermal conductivity of porous media, and the results agree well with existing experimental data [3]. A porous media are considered as a continuous phase and the confined air in cavities plays as a disperse phase. This approach has been proposed by Hashin–Shtrikman [4]. The restrictive limits of the effective thermal conductivity of porous medium are defined [1, 2]. The upper bound refers to a continuous solid phase, including uniformly dispersed fluid filled porous media that is defined by Eq. (4). Also, the lower bound refers to a continuous fluid phase, including uniformly dispersed solid spheres as described by Eq. (5) [4]. Maxwell–Eucken considered a random distribution of pores with different diameters in porous media [4–7]. In fact the Maxwell–Eucken (Eq. 7) is arithmetically equivalent to Eq. (1). Landauer developed a model to predict effective thermal conductivity of porous media which is defined as a mixture of two phases [4–7]. The percolation model assumes a completely random distribution of solid and gas that is equivalent to an Effective Medium Theory (EMT) [8–10]. Kou et al. [3] proposed a self-similar fractal model. This is a descriptive statistical model based on numerous continuous pores in which the pore size is identified. The pores are assumed as capillary tubes that are parallel to the matrix. Capillary resistance was calculated by Capillary length and pore size and with similar electrical, porous media total resistance was obtained [11, 12]. A review of effective thermal conductivity models were given in Table 1.

Table 1 Review of effective thermal conductivity models
Full size table

The aim of this research is proposing a theoretical model to predict effective thermal conductivity of closed cell insulators, which is compatible with the experimental data. Also, experimental data are measured for insulators of Maroon petrochemical Olefin cracking unit. Meanwhile, two dimensionless numbers are also proposed which are very helpful in predicting the Nusselt number in future studies. As the proposed model demonstrates good agreement with experimental data, it can be used for thermal modeling of high temperature reactors.

2 Theory and calculation

Among various models, the self-consistent model is the only one providing a reasonable estimation of the effective thermal conductivity and is hence a very effective model for homogeneous porous media [15]. This model predicts interaction between dispersed and continuous phases with a unit volumetric element which consist of a sphere inscribed in a bigger concentric sphere in an infinite environment. Porous medium is constituted of conjunct matrixes. For this selected element the governing equations should be solved together. Self-consistent model was given in Fig. 1 schematically.

Fig. 1
figure 1

A schematic presentation of the domain used in the self-consistent model

Full size image

The governing equations are represented for a representative matrix element as follows [16–18]:

Continuity equation:

$$ \nabla \cdot {\vec{\text{v}}} = 0 $$
(11)

Momentum equation:

$$ \nabla {\text{P}} =\uprho_{\text{g}} {\text{g}} -\uprho_{\text{g}} {\text{g }}\upbeta\left( {{\text{T}}_{\text{g}} - {\text{T}}_{\text{avg}} } \right) $$
(12)

Energy equation under steady state conditions:

$$ \nabla^{2} T = 0 $$
(13)

The model is assumed steady state and heat transfer rate in the radial direction is uniform in an isotropic geometry. Due to the very low velocity of confined gas, local thermal equilibrium assumption is valid [19–22]. Energy balance is derived on a spherical matrix phase using the following simplifying assumptions:

$$ \frac{{\partial \left( {\rho E} \right)}}{\partial t} + \nabla \cdot \rho vE = - \nabla \cdot q - \left( {\nabla \cdot pv} \right) - \left( {\nabla \cdot \left[ {\tau \cdot v} \right]} \right) + \rho \left( {v \cdot g} \right) $$
(14)

at constant heat transfer rate this equation can be rewritten as Eq. 15.

$$ \rho C_{V} \frac{DT}{Dt} = - \nabla \cdot q_{i} - T\left( {\frac{\partial p}{\partial T}} \right)_{V} \nabla \vartheta + \tau :\nabla \vartheta $$
(15)

In which subscript m represents the matrix. With the same assumptions for gas (subscript g) and extremely effective environment (subscript eff) similar relationships may be derived. Based on these assumptions the energy balance equation can be simplified in the entire element as Eqs. 16–18. The energy equations are written for confined gas and continuous ceramic phase separately.

$$ \nabla^{2} T_{g} = 0\quad 0 \le r \le a $$
(16)
$$ \nabla^{2} T_{m} = 0\quad a \le r \le b $$
(17)
$$ \nabla^{2} T_{eff} = 0\quad b \le r \le \infty $$
(18)

Using the continuity of the heat flux and temperature jump conditions between the matrix and gas on the energy conservation equation, following boundary conditions are valid at the interface between the two phases.

$$ T_{g} = T_{m} + \frac{{k_{m} }}{h}\left( {\frac{{\partial T_{m} }}{\partial r}} \right)_{r = a} \quad {\text{at}}\;r = a $$
(19)
$$ k_{m} \left( {\frac{{\partial T_{m} }}{\partial r}} \right)_{r = a} = k_{g} \left( {\frac{{\partial T_{g} }}{\partial r}} \right)_{r = a} \, \quad {\text{ at}}\; \, r = a $$
(20)
$$ T_{eff} = T_{m} \quad {\text{at }}\; \, r = b $$
(21)
$$ k_{m} \left( {\frac{{\partial T_{m} }}{\partial r}} \right)_{r = b} = k_{eff} \left( {\frac{{\partial T_{eff} }}{\partial r}} \right)_{r = b} \quad {\text{at }}\; \, r = b $$
(22)

The aforementioned equations are simplified only in r direction as Eqs. 23–25.

$$ T_{g} = A_{g} rCos\theta \quad 0 \le r \le a $$
(23)
$$ T_{m} = \left( {A_{m} r + \frac{{B_{m} }}{{r^{2} }}} \right)Cos\theta \quad a \le r \le b $$
(24)
$$ T_{eff} = \left( {A_{eff} r + \frac{{B_{eff} }}{{r^{2} }}} \right)Cos\theta \quad b \le r \le \infty $$
(25)
$$ A_{g} a^{3} - A_{m} a^{3} \left( {1 - \frac{{k_{m} }}{h \cdot a}} \right) - B_{m} \left( {1 + \frac{{2k_{m} }}{h \cdot a}} \right) = 0 $$
(26)
$$ A_{m} b^{3} + B_{m} - B_{eff} = A_{eff} b^{3} $$
(27)
$$ k_{m} A_{m} b^{3} - 2B_{m} k_{m} + 2B_{eff} k_{eff} = k_{eff} A_{eff} b^{3} $$
(28)

Temperatures at a and b boundaries are equal. Also, it is assumed that effective thermal conductivity of unit cell can be developed for the whole the object.

$$ U = \frac{1}{V}\left\{ {\int\limits_{{V_{m} - V_{c} }} {k\nabla T \cdot \nabla T} dV + \int\limits_{{V_{g} - V_{c} }}^{{V_{g} + V_{c} }} {k\nabla T \cdot \nabla TdV} + \int\limits_{{V_{g} - V_{c} }} {k\nabla T \cdot \nabla TdV} } \right\} $$
(29)
$$ \nabla \left( {T\left( {k\nabla T} \right)} \right) = Tk\nabla^{2} T + k\nabla T \cdot \nabla T \Rightarrow \nabla \left( {T\left( {k\nabla T} \right)} \right) = k\nabla T \cdot \nabla T $$
(30)
$$ \begin{aligned} U & = \frac{1}{V}\left( {\int\limits_{{S_{mo} }} {T_{m} k_{m} \nabla T_{m} \cdot \vec{n} \cdot dS} + \int\limits_{{S_{mi} }} {T_{m} k_{m} \nabla T_{m} \cdot - \vec{n} \cdot dS} } \right. \\ & \quad \left. { + \int\limits_{{S_{go} }} {T_{m} k_{m} \nabla T_{m} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} \cdot dS + \int\limits_{{S_{gi} }} {T_{g} k_{g} \nabla T_{g} \cdot - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} \cdot dS + } \int\limits_{{S_{gi} }} {T_{g} k_{g} \nabla T_{g} \cdot \vec{n} \cdot dS} } } \right) \\ \end{aligned} $$
(31)
$$ U = \frac{{k_{eff} }}{V}\left[ {A_{eff} \cdot b - \frac{{2A_{eff} B_{eff} }}{{b^{3} }} + \frac{{A_{eff} B_{eff} }}{{b^{2} }} - \frac{{2B_{eff} }}{{b^{5} }}} \right] $$
(32)

By solving energy equation with considering the porosity of the object as being \( \varphi = (\frac{a}{b})^{3} \), effective thermal conductivity of insulators can be represented by Eq. 33.

$$ k_{eff} = k_{m} \left[ {1 + \frac{{3\varphi + \left( {\frac{{k_{m} }}{{k_{g} - k_{m} }}} \right)\left( {\frac{{k_{g} }}{h \cdot a}} \right)3\varphi }}{{1 - \varphi + \left( {\frac{{3k_{m} }}{{k_{g} - k_{m} }}} \right) - \left( {\frac{{k_{m} }}{{k_{g} - k_{m} }}} \right)\left( {\frac{{k_{g} }}{h \cdot a}} \right)\left( {2 + \varphi } \right)}}} \right] $$
(33)

Two dimensionless numbers, \( {\text{P}}_{\text{lt}} \) (ratio of heat transfer coefficient in local thermal equilibrium to the difference between heat transfer coefficients in local thermal Non-equilibrium) and \( {\text{R}}_{\text{nu}} \) (Reverse Nusselt Number) are defined as follows.

$$ P_{lt} = \frac{{k_{m} }}{{k_{g} - k_{m} }} = \frac{heat\;transfer\; coefficient\; in \;LTE}{diffrence\; between \;heat\; transfer\; cofficients\; in\; LTNE} $$
(34)
$$ R_{nu} = \frac{{k_{g} }}{h \cdot a} = \frac{1}{Nu} $$
(35)

Then, final equation for keff is obtained as Eq. 36.

$$ k_{eff} = k_{m} \left[ {1 + \frac{{3\varphi \left( {1 + P_{lt} *R_{nu} } \right)}}{{1 - \varphi + 3P_{lt} - \left( {P_{lt} *R_{nu} } \right)\left( {2 + \varphi } \right)}}} \right] $$
(36)

3 Results and discussion

The results of the proposed model are validated in comparisons against theoretical and experimental data. Initially the present model results are compared against published experimental data [23–25]. Effective thermal conductivity of porous media like mineral polymer IPM and IPMT alumino silicates are reported on the furnace condition with different porosities [24]. It was found that the chemical composition of porous media affects the microstructure characteristics such as size and spatial arrangement of pores, homogeneity and thermal behavior of porous matrix. In particular, homogeneity of inorganic polymer improves thermal insulation specifications. The relation between effective thermal conductivity and porosity is consistent with analytical models that were described by Maxwell–Eucken and Landauer [24]. To prepare porous geopolymers, two different compositions of metakaolin were tested with a specific Si/Al molar ratio. This was achieved by mixing different proportions of the standard and sand-rich alumino silicates. Alkaline solution was added to each powder with a solid/liquid ratio of 1.66. Finally IPM and IPMT were obtained with Si/Al molar ratios of 1.23 and 1.79 respectively. Na/Al ratio was close to 1 to achieve homogeneous slurry and balance the negative charge of alumina oligomers. The porosity and size distribution was evaluated carefully [23, 24]. Thermal conductivity is measured at different conditions using the Heat Flow Meter (ASTM C518, ISO8301). Homogeneous samples with parallel flat faces are selected. The apparatus works based on Fourier’s law under steady state conditions. A thermal gradient is imposed across the sample width which is maintained between two copper plates, the upper plate is a heat source [24].

The ASTM standard C177, ‘‘Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus,’’ is used as a template and modified to accommodate the additional requirements for operation in a cryogenic environment. A single-sided guarded-hot-plate with only one cold plate and one specimen is used. The effective thermal conductivity of the samples was measured by recording the temperature on either side of the sample for a specific heater power after steady state was achieved [25–27]. Standard deviation (SD) which was calculated by following formula shows good agreement with experimental results.

$$ {\text{Standard }}\;{\text{deviation}} = \sqrt {\sum\nolimits_{{{\text{i}} = 1}}^{\text{n}} {\frac{{\left[ {{\text{k}}_{{{\text{eff}},{\text{i}}}}^{ \exp } - {\text{k}}_{{{\text{eff}},{\text{i}}}}^{\text{cal}} } \right]^{2} }}{{{\text{n}} - 1}}} } $$
(37)

The results show good agreement and high accuracy between experimental effective thermal conductivity and results of the model as shown in Table 2. Porosity plays a key role in effective thermal conductivity of porous media. Figures 2 and 3 show \( k_{eff}^{\exp } \) and \( k_{eff}^{cal} \) versus porosity for synthetic polymers IPM and IPMT.

Table 2 Thermal conductivity of matrix km (W/mK) [24], effective thermal conductivity of insulator resulted from experimental studies \( k_{eff}^{\exp } \)(W/mK) [24] and calculated effective thermal conductivity of insulator through the developed model Eq. 33
Full size table
Fig. 2
figure 2

Variation of effective thermal conductivities for IPM porous media against porosity (experimental and predicted)

Full size image
Fig. 3
figure 3

Variation of effective thermal conductivities for IPMT porous media against porosity (experimental and predicted)

Full size image

In Table 3 experimental and computed keff by Eq. 33 are compared together. Polyurethane foam with 97 % porosity, 25 mm thickness and temperature gradient of 10 K are considered.

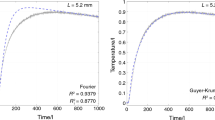
Table 3 Thermal conductivity of matrix km (W/mK) [25], effective thermal conductivity of insulator resulted from experimental studies \( k_{eff}^{\exp } \)(W/mK) [25], calculated effective thermal conductivity of insulator through the developed model Eq. 33 for polyurethane foam
Full size table

Figure 4 and Table 3 show the comparison of model predictions of polyurethane foam versus temperature and experimental data. The results are very compatible and SD is very low.

Fig. 4
figure 4

Predicted and experimental results [25] for effective thermal conductivity of polyurethane foam versus temperature

Full size image

Further on, different insulators are assessed and experimental data are measured. The refractory pieces of Amol Carborundom Co. products are employed in Maroon petrochemical olefin cracking unit furnaces called K26_AC4-A which is shown in Fig. 5.

Fig. 5
figure 5

Refractory ceramic blocks used in the Maroon Petrochemical Economic Zone Mahshahr-Iran (plates 1–8 olefin unit)

Full size image

Refractory insulator bricks contain different molar ratios of metal oxides such as Al2O3, SiO2 and Fe2O3. The products are named as K28-AC5, K26-AC4_B, K26-AC4_A, K25-AC3 and K23-AC2. The overall density of bricks varies between 0.6 to 0.95 g/cm3 and maximum operating temperature between 1260 °C for K23 and 1540 °C for K28. Thermodynamic properties of air and the insulator material have been extracted from the literatures and have been reported in Table 4 [26–31].

Table 4 Properties of refractory ceramic blocks used in the Maroon Petrochemical Economic Zone Mahshahr-Iran (olefin unit furnace 1–8)
Full size table

Figure 6 shows SEM image of an insulator brick (taken by Cambridge Stereio Scan-S360 equipped with spot analysis, EDX).

Fig. 6
figure 6

SEM image of refractory ceramic blocks used in the Maroon Petrochemical Economic Zone Mahshahr-Iran (olefin unit furnace 1–8)

Full size image

The SDs of different models relative to the experimental results are reported in Table 5. The SD of the proposed model from experimental results is about 0.5 %, which is lower than previous models demonstrating that the proposed model can be predicted effective thermal conductivity of closed cell porous media more accurately compared to previously reported theoretical models.

Table 5 Comparing the experimental results and theoretical effective thermal conductivities estimated by different models for refractory K26_AC4-A product Amol Carborundom, used in Maroon petrochemical olefin cracking unit
Full size table

In Figs. 7, 8, 9, 10 and 11, experimental results were compared to the proposed model as well as the previous models for different insulators in the temperature range 600–1300 °C. The results of keff of K26_AC4-A were plotted against operating temperature in Fig. 7. These data were reported in Table 5 too. Although the SD of the proposed model is lower than the other models, but at a temperature lower than 950 °C, Assad’s model shows better agreement. Also, for temperature higher than 950 °C, the proposed model shows the best agreement with experimental data.

Fig. 7
figure 7

Comparison of predicted effective thermal conductivity for insulator K26_AC4-A by different models and the experimental measurements

Full size image
Fig. 8
figure 8

Comparison of predicted effective thermal conductivity for insulator K28_AC5 by different models and the experimental measurements

Full size image
Fig. 9
figure 9

Comparison of predicted effective thermal conductivity for insulator K26_AC4-B by different models and the experimental measurements

Full size image
Fig. 10
figure 10

Comparison of predicted effective thermal conductivity for insulator K26_AC3 by different models and the experimental measurements

Full size image
Fig. 11
figure 11

Comparison of predicted effective thermal conductivity for insulator K26_AC2 by different models and the experimental measurements

Full size image

The keff values of K28_AC5 insulator were calculated and plotted against temperature in Fig. 8. All models showed the same behavior against temperature change. Keff decreased against temperature with a mild slope from 600 to 900 °C and then increased with temperature enhancement. Landauer’s model showed the most deviation from experimental data. The obtained model was predicted effective thermal conductivity better than the other developed models.

The accuracy of different models were compared together in Fig. 9 for K26_AC4-B sample. Thermal behavior of this sample is very similar to K26_AC4-A type. This is due to the similar structure of the ceramics.

The K26_AC3 and K26_AC2 were studied in this research too. The experimental data were measured at different temperatures and were compared with different theoretical models same as other samples. Figures 10 and 11 showed the good agreement between developed model’s results and experimental data. SDs of different models confirm the accuracy of developed model.

4 Conclusions

The present study focuses on the heat transfer in ceramic thermal insulator porous media. A self-consistent method is developed to achieve effective thermal conductivity for the porous medium used. The porous matrix is divided into continuous and discrete phases. This method leads to an equation for effective heat transfer coefficient containing terms of matrix and air conductivity heat transfer coefficients and porosity. In this study, two dimensionless numbers, \( {\text{P}}_{\text{lt}} \) (ratio of heat transfer coefficient in local thermal equilibrium to the difference between heat transfer coefficients in local thermal Non-equilibrium) and \( {\text{R}}_{\text{nu}} \) (Reverse Nusselt Number) were introduced. These two numbers indirectly considers effect of various parameters such as size and shape of the pores, temperature gradient, thermophysical properties, components of the dispersed phase and arrangement of dispersed phase. The model thus developed was examined against experimental data and was at the same time compared to other similar models previously developed over a wide range of insulator properties. The comparisons show good agreement over the whole of the wide range examined using SD as a criterion resulting in SD of around 0.5 % compared to more than 1 % at times for other models.