Modeling of mass and charge transport in a solid oxide fuel cell anode structure by a 3D lattice Boltzmann approach

Abstract

A 3D model at microscale by the lattice Boltzmann method (LBM) is proposed for part of an anode of a solid oxide fuel cell (SOFC) to analyze the interaction between the transport and reaction processes and structural parameters. The equations of charge, momentum, heat and mass transport are simulated in the model. The modeling geometry is created with randomly placed spheres to resemble the part of the anode structure close to the electrolyte. The electrochemical reaction processes are captured at specific sites where spheres representing Ni and YSZ materials are present with void space. This work focuses on analyzing the effect of structural parameters such as porosity, and percentage of active reaction sites on the ionic current density and concentration of H₂ using LBM. It is shown that LBM can be used to simulate an SOFC anode at microscale and evaluate the effect of structural parameters on the transport processes to improve the performance of the SOFC anode. It was found that increasing the porosity from 30 to 50 % decreased the ionic current density due to a reduction in the number of reaction sites. Also the consumption of H₂ decreased with increasing porosity. When the percentage of active reaction sites was increased while the porosity was kept constant, the ionic current density increased. However, the H₂ concentration was slightly reduced when the percentage of active reaction sites was increased. The gas flow tortuosity decreased with increasing porosity.

1 Introduction

Solid oxide fuel cells (SOFCs), which are the subject of this study, offer a number of advantages for sustainable and efficient electricity generation, such as high conversion efficiency, high-quality exhaust heat and flexible fuel input [1]. If the performance is improved and the cost is decreased, SOFC can stand as a viable sustainable power generating device for a broad range of applications from mobile phones to power stations. SOFCs are interesting for two main reasons as a power generating device. Firstly, they can convert fuel to electricity directly without any mechanically moving parts and are therefore highly efficient as power generating devices. Secondly, they can function with a variety of different fuels due to their high operating temperature (600–1100 °C) [1].

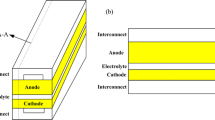
SOFCs with a supportive anode structure is usually built up by nickel/yttria stabilized zirconia (Ni/YSZ) cermet with high electrochemical performance and good chemical stability [1, 2]. The porous anode plays an important role in this type of configuration, both as a main actor for the active transport processes and as a support for the cell. The performance of an SOFC depends on many parameters but among the critical ones are the functionality of the porous anode microstructure, kinetics and availability of active reaction sites. The materials have become increasingly sophisticated in structure and composition. For the purpose of computational modeling of SOFCs, the transport processes within the anode must be captured at the microscopic scale, and their role included in macroscale physical processes. There is a need for a better understanding of the details of the microscopic physical processes in the porous structure of the anode with the reaction sites. In order to be able to explore the complexities of the SOFC, it is important to model the physical processes on their correct length and time scales, and to combine the information from the different scales in a numerical model.

The microstructure presented in the macroscale models are basically described by a few empirical parameters (e.g., porosity and tortuosity). Not only are these parameters difficult to measure but they cannot properly describe the microscopic physical behavior [3, 4]. These parameters are obtained through experimental studies or detailed numerical studies of the microscopic material and can often only be described three-dimensionally. With this said, microscale modeling for the porous electrodes with the electrochemical and chemical reactions is essential for the progress of fuel cells. Functional electrode structures are known to work in favor of electrochemical reactions, reforming reactions and transport processes [5, 6]. In the real SOFC porous samples, the structures are highly distributed and the active TPB density may vary considerably within the porous sample [3]. However, these porous structures are hard to regenerate in a computational model. In this study, the geometry is built up by homogeneous spherical particles and randomly placed reactive sites where a three-phase-boundary (TPB) exists.

A considerable amount of research has been conducted on SOFCs to date, and the various computational methods used vary from macroscale to nanoscale, as discussed in the previous section. Some studies on the interaction of charge and mass transport with chemical and electrochemical reactions will be discussed below. The effects of electrode microstructure on activation and concentration polarization (losses) in SOFCs have been studied by Virkar et al. [7] considering only a steady-state, one-dimensional model for gas diffusion. It was shown that polarization losses can be minimized by optimization of the electrode micro structure. Detailed multi-dimensional modeling of the transport processes inside fuel cells is very useful in design and research studies.

Suzue et al. [8] reconstructed the porous media of an SOFC anode by a stochastic model to evaluate the structural parameters and developed a 3D model by LBM to analyze the charge and mass transport of the SOFC anode. It was concluded that when the temperature was increased, the reaction zone in the anode became thinner and the current concentration appeared closer to the electrolyte interface. Iwai et al. [9] also reconstructed the anode of an SOFC by the Focused Ion Beam Scanning Electron Microscopy (FIB-SEM) method and developed a 3D LBM model to evaluate the mass and charge transport. Iwai et al. [9] focused on quantification of microstructural parameters such as tortuosity, TPB length and volume fraction by two different methods. It was concluded that the methods only differed by less than 3 %. Kanno et al. [10] also reconstructed the porous anode of an SOFC by FIB-SEM. The reconstructed anode was used as the geometry of a 3D LBM model to analyze the charge and mass transport to evaluate the losses of the anode. It was concluded that a smaller sample of the reconstructed porous media led to an under-prediction of the overpotential.

Several previous studies have been conducted on SOFC. However, there exist a limited number of studies analyzing the performance of the SOFC anode at microscale with the momentum, charge, heat and mass transport processes coupled. In this study all these transport processes are coupled and the equations for these processes are solved simultaneously. The aim of this study is to determine the interaction between the transport and reaction processes in the anode of an SOFC through simulations carried out using LBM. The microscale model simulates charge, momentum, heat and mass transport with electrochemical reactions in the porous anode structure of an SOFC in 3D for a geometry built up with randomly placed spheres as a replica of a porous anode. The modeling domain includes specific active reaction sites where all three phases of Ni, YSZ and void space are present. The use of homogeneous spheres for building the model geometry is chosen to more easily control the porosity and the number of specific reaction sites. The focus is on the effect of structural parameters such as porosity and percentage of reaction sites on the ionic current density and concentration of H₂. Some of the inlet and boundary conditions for the microscale model are obtained from our previous macroscale model [1]. This is a first step towards coupling the microscale model in this study with the previously developed macroscale model.

2 Governing equations

There are two general electrochemical reactions if the fuel cell is fed with hydrogen and the reactions are handled in a global scheme manner. The active species involved in this case are hydrogen and oxygen. The species reactive transport is initiated with a hydrogen (H₂) molecule diffusing through the pores in the anode combined with a negatively charged oxygen ion (O²⁻) traveling through the solid electrolyte from the cathode side. H₂ forms a molecule of H₂O during this oxidation reaction and releases a pair of electrons. The H₂O molecule formed at the TPB then diffuses back through the pores in the anode while the electrons generated at the anode TPB are conducted through the anode material to the current collector, and finally flow through an external circuit. The electrons enter the cathode and are conducted through the cathode material to the cathode TPB. Here, the electrons combine with oxygen that has diffused from the air through pores in the cathode to create oxygen ions as indicated in Eq. (2). These ions are conducted through the electrolyte and the cycle is completed [2, 6].

$$H_{2} + O^{2 - } \to H_{2} O + 2e^{ - }$$

(1)

$$\frac{1}{2}O_{2} + 2e^{ - } \to O^{2 - }$$

(2)

Note that only Eq. (1) is modeled in this study. Both Eqs. (1) and (2) provide the needed reactions for the SOFCs functionality with H₂ as fuel and the closed loop for the transport of the electrons.

The physical processes for the modeling domain are represented by four main equations in this study. First, the reaction–advection–diffusion equation can be written in general form as [11, 12]:

$$\frac{{\partial C_{j} }}{\partial t} + (\varvec{u} \cdot \nabla ) C_{j} - D_{jk} \nabla^{2} C_{j} = R_{j}$$

(3)

where C _j is the concentration of species j, D _jk is the diffusion coefficient between the two species j and k, R _j the reaction rate for reaction with the specific species j, u the velocity vector and t is time. The electrochemical reactions are implemented by source terms as:

$$R_{{H_{2} }} = \frac{ - i}{{2 \cdot {\text{F}}}}$$

(4)

$$R_{{H_{2} O}} = \frac{i}{{2 \cdot {\text{F}}}}$$

(5)

where i is the current density and F the Faraday constant. Second, the Navier–Stokes equations for conservation of momentum and the conservation of mass are presented as:

$$\frac{{\partial \varvec{u}}}{\partial t} + (\varvec{u} \cdot \nabla )\varvec{u} +\Delta p - \upsilon \nabla^{2} \varvec{u} = 0$$

(6)

$$\nabla \cdot \varvec{u} = 0$$

(7)

where p is the pressure for the fluid and $\nu$ is the kinematic viscosity. The third equation concerns heat transfer and is presented below in terms of temperature.

$$\frac{\partial T}{\partial t} + (\varvec{u} \cdot \nabla )T - \upalpha \nabla^{2} T = Q$$

(8)

where T is the temperature, $\upalpha$ the thermal diffusivity and Q the heat flux. The heat flux is based on heat generation by the electrochemical reactions and on the losses through the activation, the concentration and the ohmic polarizations,

$$Q = i \cdot \left( {\frac{{T \cdot\Delta S_{r} }}{{n_{e} \cdot {\text{F}}}} + \eta_{act} + \eta_{conc} } \right) + \sum {\frac{{i^{2} }}{\sigma }}$$

(9)

where ΔS _r is the entropy change of the reaction (−50.2 J/(K mol) [1, 13, 14]) and σ the ionic or electronic conductivity. Whereas the above mentioned equations represent the transport processes, the fourth and fifth equations are the charge transport in terms of the electronic and ionic potential. The ion and electron transport is presented as [3, 10, 15]:

$$\sigma_{io} \nabla^{2} \phi_{\text{io}} = i_{io} \cdot AV_{e}$$

(10)

$$\sigma_{e} \nabla^{2} \phi_{\text{e}} = - i_{e} \frac{{i^{2} }}{\sigma }AV_{e}$$

(11)

where $\sigma$ is the ionic or electronic conductivity, ϕ the ionic or electronic potential and AV _e the surface area to volume for the electrochemical reaction. The subscripts io and e represents ionic and electronic, respectively. The influence of different potentials/polarizations varies depending on cell operating conditions and design/structure. The local potentials vary between different positions (in 3D) within the cell and they are affected by, for example, the local hydrogen and oxygen concentrations, the local temperature as well as the ion and electron transport path.

Further, the following equations below are described to clarify a number of parameters in the main equations in the 3D model. The current density can be obtained through the Butler–Volmer equation [2, 4, 15]. If the transfer coefficient is assumed to be 0.5, the Butler–Volmer equation is reduced to Eq. (12) which is based on the assumption of symmetric electron transfer in the Butler–Volmer equation and the activation overpotential is mainly important at small currents. This often agrees well with experimental Tafel plots [15].

$$i = 2 \cdot i_{0} \cdot sinh\left( {\frac{{n_{e} \cdot {\text{F}} \cdot \eta_{act} }}{{2 \cdot {\text{R}} \cdot T}}} \right)$$

(12)

$$\eta_{act} = \phi_{e} - \phi_{i} - E_{eq}$$

(13)

$$i_{0} = \frac{{{\text{R}} \cdot T}}{{n_{e} \cdot {\text{F}}}} \cdot k_{e}^{{\prime \prime }} \cdot exp\left( {\frac{ - E}{R \cdot T}} \right)$$

(14)

$$E^{OCV} = E_{0} - \frac{{{\text{R}} \cdot T}}{{2{\text{F}}}}ln\left( {\frac{{p_{H2O} }}{{p_{{H_{2} }} \cdot \left( {p_{{O_{2} }} } \right)^{0.5} }}} \right)$$

(15)

$$\eta_{conc} = \frac{{{\text{R}} \cdot T}}{{n_{e} \cdot {\text{F}}}}\ln \left( {\frac{{p_{{H_{2} ,TPB}} \cdot p_{{H_{2} O,b}} }}{{p_{{H_{2} ,b}} \cdot p_{{H_{2} O,TPB}} }}} \right)$$

(16)

where k _e ″ the pre-exponential factor which is $6.54 \times 10^{11} \,\Omega ^{ - 1} \,{\text{m}}^{ - 2}$ [13], i ₀ the exchange current density, n _e the number of electrons transferred per reaction, η _act,e the electrode activation polarization over-potential, R the ideal gas constant, E ^eq the equilibrium voltage, E the activation energy (140 kJ/mol [13]), and p is the partial pressure for the H₂ and H₂O at the TPB or b (bulk fluid). Note that E ₀ is the theoretical voltage. Equation (16) is valid for equilibrium conditions. If the detailed charge transfer carriers and pathways are neglected, the overpotential at the TPB sites can be held constant. Due to internal resistance and polarizations (overpotential losses), the actual voltage (E) becomes less than the open-circuit voltage. The actual voltage can be expressed as:

$$E = E^{OCV} - \eta_{act} - \eta_{ohm} - \eta_{conc}$$

(17)

where η is the polarization due to activation, concentration and ohmic losses, respectively.

In this study, an averaged effective diffusivity is used to take into account both the ordinary and Knudsen diffusivity. The mass transport at the microscale range is analyzed for the diffusion within the SOFC anode and the Knudsen diffusion is considered in the calculations. Including the Knudsen diffusion for SOFCs is commonly done in the literature, see [5, 7, 8, 10, 13].

The effective diffusivity by Knudsen diffusion is defined as [16, 17]:

$$D_{Keff} = \frac{{d_{p} }}{3} \cdot \sqrt {\frac{8 \cdot R \cdot T}{{\pi \cdot M_{jk} }}}$$

(18)

where d _p is the particle diameter and M _jk is the average molecular weight of species j and k defined as [16, 17]:

$$M_{jk} = 2 \cdot \left[ {\frac{1}{{M_{j} }} + \frac{1}{{M_{k} }}} \right]^{ - 1}$$

(19)

The effective diffusivity which is based on the ordinary diffusion is defined here as [16, 17]:

$$D_{e} = \frac{{0.0026 \cdot T^{3/2} }}{{P \cdot M_{jk}^{1/2} \cdot \sigma_{jk}^{2} \cdot\Omega _{D} }}$$

(20)

where, besides the parameters mentioned above which remain the same, σ _jk is the characteristic length between the colliding molecules which depends on the choice of the intermolecular force law and Ω _D the dimensionless collision integral. Note that the pressure P is 1 bar in Eq. (20) and that the parameters in this equation are not all in SI units. The ones which differ from the SI unit standard are M _jk (g/mol) and σ _jk (Å). The effective diffusivities are then averaged as below [16, 17]:

$$D_{eff} = 2 \cdot \left[ {\frac{1}{{D_{Keff} }} + \frac{1}{{D_{e} }}} \right]^{ - 1}$$

(21)

3 Lattice Boltzmann modeling

LBM is based on the Boltzmann equation and is perceived as an alternative to the traditional CFD based on the Navier–Stokes equation. LBM keeps track of the movements of molecule ensembles and the evolution of the distribution functions and recovers the different transport equations by recovering the macroscopic parameters. LBM has shown promising simulation results of fluid flows and mass diffusion through complex geometries. Conventional CFD methods use fluid density, velocity and pressure as the primary variables, while the LBM uses a more fundamental approach with the so-called particle velocity distribution function (PDF) [18–20]. Despite LBM’s simplicity, it has a disadvantage of taking up more memory than a traditional CFD approach. For this case parallel computing offers the opportunity to include several physical processes in the model with success. LBM is comparable to conventional methods such as Finite Element Method (FEM), Finite Volume Method (FVM) and Finite Difference Method (FDM) in terms of functionality, accuracy and computational time for physical problems, especially on component level or at microscale. Some of the main advantages of LBM over the conventional methods are computational efficiency and easy implementation of parallelization. Also LBM offers the ability to handle a geometry as complex as desired, because the method does not need to create a volume mesh while the conventional methods need to generate a volume mesh and may fail when the geometry becomes too complex. Kandhai et al. [21] and also Geller et al. [22] have conducted comparative studies on LBM with FEM and FVM on mixer reactors and laminar flows, respectively. LBM has also been used as a numerical method for transport processes in SOFCs and it has been compared with conventional methods such as FDM, FEM and FVM [20].

LBM’s main function, PDF, is defined as the number of particles of the same species travelling along a particular direction with a particular velocity. LBM is built up on lattice points which are given locations placed all over the regularized solution domain. The LBM is described by two different actions taking part at each lattice point (site); namely streaming and collision [18, 19]. Streaming describes the movement of the particles of each species and collision describes interactions between the particles of the same or different species. In this study, the number of directions is 19 for the PDF which recovers the conservation of momentum and mass. To recover the other equations the number of directions is 7. The theory shows it is sufficient with 7 lattice directions to capture the phenomena for the continuum equations. For more information regarding the functionality of the scheme of D3Q7, the reader is referred to [23–25]. The collision operator used in all the particle distribution functions is the Bhatnagar, Gross and Krook (BGK) [26] collision operator which is the most simple collision operator in LBM. There are other possible choices besides the BGK, e.g., the Multi-Relaxation-Time. This is often chosen because it is numerically more stable but on the other hand the computations are slower. In this model, stability is not an issue mainly because the low Reynolds number of the flow. For BGK, it is assumed that the particle distribution function relaxes to an equilibrium state after the collision at a single relaxation time [26]. For small enough dt and dx and, small Mach numbers, it can be shown by the Chapman–Enskog expansion analysis that this numerical scheme solves the equation of an incompressible fluid flow at the limit of weak compressibility with second order accuracy. The method has been developed to handle more than the momentum transport. By applying the Chapman–Enskog expansion it is possible to derive a correct LB model for other physical processes such as heat or charge transport. LBM-BGK schemes similar to that for advection and diffusion have been used for a scalar field for example temperature (heat/enthalpy) by the LB community (Shan and Doolen [27]; Huber et al. [28]) or chemical transport processes (Kang et al. [29]). The PDF is combined by the streaming and collision in the LB equation and is here presented for species j [4, 18, 19, 30–32].

$$f_{\upalpha }^{j} \left( {x + e_{\upalpha }^{j} \cdot t, t + \Delta t} \right) = f_{\upalpha }^{j} \left( {x, t} \right) + \Omega_{\upalpha }^{j} \left( {x,t} \right) + F_{\upalpha }^{j} \left( {x,t} \right)$$

(22)

where $f_{\upalpha }^{j}$ is the PDF, $e_{\upalpha }^{j}$ the velocity, $\Omega_{\upalpha }^{j}$ the collision term, $\Delta t$ the simulation time step and $F_{\upalpha }^{j}$ the source term at any spatial location $x$ and time $t$ along the direction α. The collision term and the equilibrium function are specified as:

$$\Omega_{\upalpha }^{j} \left( {x,t} \right) = - \left( {\frac{{f_{\upalpha }^{j} \left( {x, t} \right) - f_{\upalpha }^{j, eq} \left( {x, t} \right)}}{{\tau_{j} }}} \right)$$

(23)

$$f_{\upalpha }^{j, eq} = w_{\upalpha } \cdot C_{j} \left[ {1 + 3 \cdot e_{\upalpha } \cdot u_{j} } \right]$$

(24)

$$u_{j} = \frac{{\sum\nolimits_{j} {\frac{1}{{\tau_{j} }}} \cdot \sum\nolimits_{\upalpha } {f_{\upalpha }^{j} e_{\upalpha } } }}{{\sum\nolimits_{j} {\frac{1}{{\tau_{j} }}C_{j} } }}$$

(25)

where $w_{a}$ is the weight factor due to the placement of the particles in the grid, u _j is the specific velocity contribution and $\tau_{j}$ is the relaxation time for the specific species j. When the mass diffusion is modeled in LBM, two approaches are often used; pure diffusion or advection–diffusion (also called convection–diffusion). Pure diffusion and advection–diffusion are simulated with different equilibrium distributions f ^eq _σ,α . The equilibrium distribution for advection diffusion is presented in Eq. (24) but for the case of pure diffusion u = 0 in Eq. (24). There is no need for a higher order of terms in the equilibrium distribution for the propagation of species. This can be obtained by Chapman–Enskog analysis on the advection–diffusion equation. The reader is referred to Latt [31] for detailed information. In this case for the simulation of mass transport, the force term includes the effect of the chemical reactions and is shown below [10, 27, 33]:

$$F_{\upalpha }^{j} \left( {x,t} \right) = w_{\upalpha } \cdot \Delta t \cdot R_{j}$$

(26)

where $w_{\upalpha }$ is the weight function along the direction α, and R _j the reaction rate in lattice units for species j. Δt and Δx are the time step and length step in the simulation, respectively. These are defined in real units, (s) seconds and (m) meters, respectively. The concentration $C$ is obtained directly in (mol/m³) which has been shown by several authors [12, 19, 33, 34]. The concentration is obtained by Eq. (26) [12, 18, 19, 27].

$$C_{j} = \mathop \sum \limits_{\upalpha = 0}^{6} f_{\upalpha }^{j} \left( {x, t} \right)$$

(27)

To recover the equation for conservation of momentum, a PDF, named $g_{a}$, is applied as:

$$g_{\upalpha } \left( {x + \Delta x, t + \Delta t} \right) = g_{\upalpha } \left( {x, t} \right) + \Omega_{\upalpha ,g} \left( {x,t} \right)$$

(28)

$$\rho = \mathop \sum \limits_{\upalpha = 0}^{18} g_{\upalpha }$$

(29)

$$g_{\upalpha }^{eq} \left( x \right) = w_{\upalpha } \cdot \rho \left[ {1 + 3\frac{{e_{\upalpha } \cdot v}}{{c^{2} }} + \frac{9}{2}\frac{{\left( {e_{\upalpha } \cdot v} \right)^{2} }}{{c^{4} }} - \frac{3}{2}\frac{{\varvec{v}^{2} }}{{c^{2} }}} \right]$$

(30)

$$\varvec{v} = \frac{1}{\rho } \cdot \mathop \sum \limits_{\upalpha = 0}^{18} g_{\upalpha } \varvec{e}_{\upalpha }$$

(31)

where $g_{\upalpha }$ is the PDF for momentum, $e_{\upalpha }$ the velocity, $\Omega_{\upalpha }$ the collision term, $\rho$ is the density of the fluid and $v$ the fluid velocity. Two different PDFs are used to recover the ion and electron transport. For simplicity and due to similarities between the equations, it is only written out here once. The ion or electron transport uses a PDF, named $b_{a}$, which is applied as [34]:

$$b_{\upalpha } \left( {x + \Delta x, t + \Delta t} \right) = b_{\upalpha } \left( {x, t} \right) + \Omega_{\upalpha ,h} \left( {x,t} \right) + B_{\upalpha } \left( {x,t} \right)$$

(32)

$$B_{\upalpha } \left( {x,t} \right) = w_{\upalpha } \cdot \Delta t \cdot i$$

(33)

$$b_{\upalpha }^{j, eq} = w_{\upalpha } \cdot \phi_{j} \left[ {1 + 3 \cdot e_{\upalpha } \cdot u_{j} } \right]$$

(34)

$$\phi = \mathop \sum \limits_{\upalpha = 0}^{6} b_{\upalpha }$$

(35)

where $b_{\upalpha }^{{}}$ is the PDF for ionic or electronic potential, $B_{\upalpha }$ the source term at any spatial location $x$ and time $t$ along the direction α and ϕ the ionic or electronic potential depending on which equation being simulated. A BGK collision operator is used for the PDF recovering of the ion/electron transport. In a similar manner as for the mass diffusion, a particle distribution function is set up for the temperature [27, 28]:

$$h_{\upalpha } \left( {x + \Delta x, t + \Delta t} \right) = h_{\upalpha } \left( {x, t} \right) + \Omega_{\upalpha ,h} \left( {x,t} \right) + H_{\upalpha } \left( {x,t} \right)$$

(36)

$$H_{\upalpha } \left( {x,t} \right) = w_{\upalpha } \cdot \Delta t \cdot Q$$

(37)

$$h_{\upalpha }^{j, eq} = w_{\upalpha } \cdot T_{j} \left[ {1 + 3 \cdot e_{\upalpha } \cdot u_{j} } \right]$$

(38)

$$T = \mathop \sum \limits_{\upalpha = 0}^{6} h_{\upalpha }$$

(39)

where $h_{\upalpha }^{{}}$ is the PDF for temperature, $H_{\upalpha }^{{}}$ the source term for the heat transport equation at any spatial location $x$ and time $t$ along the direction and T the temperature. Q is defined in Eq. (9). A BGK collision operator is used for the PDF recovering the heat transport. The temperature is not explicitly illustrated in the results of this article because it is in general rather constant with a temperature difference of only 5 K along the main flow direction (x-direction) in this study.

The relation between the SI units and the lattice units is formed by using the parameters Δx and Δt, which are the discrete space step and time step, respectively [31]. The relation is handled through the equations given below:

$$\Delta x = \frac{{L_{P} }}{N}$$

(40)

$$\Delta t_{fluid} = \frac{{\upsilon_{LB} }}{{\upsilon_{P} }} \cdot\Delta x^{2}$$

(41)

$$\upsilon_{LB} = \frac{1}{3} \cdot \left( {\tau_{fluid} - 0.5} \right)$$

(42)

where L _p is the physical length in one length direction and N the number of grid points in the same length direction. Further, υ is the kinematic viscosity in physical units and υ _LB is the lattice Boltzmann viscosity. τ is the relaxation time and is usually set to a value around 1 [31].

In a similar manner this can be done for the species, potential and temperature. Here it is only shown for the temperature and H₂:

$$\Delta t_{ T} = \frac{{\upalpha_{LB} }}{{\upalpha_{P} }} \cdot\Delta x^{2}$$

(43)

$$\upalpha_{LB} = \frac{1}{3} \cdot \left( {\tau_{T} - 0.5} \right)$$

(44)

$$\Delta t_{ H2} = \frac{{D_{H2} }}{{\Delta x^{2} }} \cdot\Delta t_{T}$$

(45)

where α is the thermal diffusivity in SI units and α _LB is the lattice Boltzmann thermal diffusivity based on the thermal relaxation time [31].

The values of the boundary conditions for the LB model are extracted from a previously developed FEM model [1, 35] namely inlet velocity, interface conditions for the potential distributions and inlet concentration for the gas species. The parameters concerning the cell structure and transport processes for the calculations are presented in Table 1 and the inlet and operating conditions are presented in Table 2. The boundary condition at $x = L$ is specified for the concentration of H₂ and at $x = 0$ the mole flux is specified for the H₂. For the planes at $y = 0$ and at $y = L$ as well as $z = 0$ and at $z = H$ periodic boundary conditions are used. A small amount of water is set as an inlet condition (x = 0) to enable the transport and reaction processes. Note that L and H are length and height dimension constants, respectively. The reactions are implemented at the anode/electrolyte interface and at specific reaction sites. In this study the x-direction is along the main flow direction, whereas the y-direction is perpendicular to the main flow direction. Initially, the velocity in the x-direction is set to a constant value of 0.015 m/s and set to zero in the y- and z-directions to replica the situation for the transport processes in a whole SOFC as in the macroscale model. The electronic potential is set to zero at x = 0, specified as a constant value at x = L and all other boundaries are set to be periodic. The ionic potential is set to zero at x = L, specified to a constant value at x = 0 and all other boundaries are set as periodic. The boundary condition for the temperature at x = 0 is set as a constant value and the outlet is defined as a convective flux boundary condition. All other boundaries for the temperature distribution are specified as periodic boundary conditions.

Table 1 Parameters in the SOFC analysis

Table 2 Inlet and operating conditions [1]

To treat the electrode structure realistically, there will be obstacles treated like impermeable solid surfaces for the gas species [12, 31]. The obstacles are suited for no-slip reflection which is simply a bounce-back definition where the particles are reflected back in the same direction as they arrived. However, the ions and electrons will travel through the solid particles in the porous domain.

The tortuosity is also calculated in during the simulation as it is an important parameter in macroscale models for SOFCs. A common definition of the tortuosity, which is used in this study, is the ratio of the length of the actual path of the fluid particles to the shortest path length in the direction of the flow [36]. However, the definition of tortuosity may vary; in some models it represents the effect of additional pathways, while in others it is simply a numerical parameter adjusted to fit the experimental data [36]. It should also be mentioned that the tortuosity differs for gas-phase transport and ion and electron transport. The tracking of the fluid particles is one of the main features of the LBM, which makes it fairly easy to obtain the tortuosity based on the streamlines or velocity field when the transport processes are simulated. However, the value of the tortuosity obtained is specific to the porous medium considered in the simulation, and will be different for other porous media.

Some of the physical parameters are taken from our previously developed macroscale two-dimensional CFD model covering an intermediate temperature anode-supported SOFC [1, 35]. The significant parameters concerning the cell structure and transport processes for the calculations are presented in Table 1 and the inlet and operating conditions are presented in Table 2.

To visualize the flow in the complex geometry, the 3D porous domain is created through randomly placed spherical obstacles which can be viewed in Fig. 1. In Fig. 1 the modeling geometry is presented with placement of the boundary conditions and the size of the modeling domain. The space before the inlet represents an electrolyte interface and the outlet without any spheres is used to check the flow for an undisturbed domain. The modeling domain in this study represents only a small part of the anode close to the electrolyte to capture the electrochemical activity. The modeling geometry consists of specific active reaction sites throughout the domain. These specific sites are simulated to represent the TPB locations. There are two different sizes of the spherical particles to represent Ni and YSZ. When one Ni and one YSZ sphere, that is to say one sphere of each size, are close enough to each other and connected with a pore space, an active reaction site is created. Note that the two different sizes of spheres are not connected specifically to the phases Ni or YSZ but are used to identify the active sites where one sphere of each size is needed. The ions and electrons will travel through the solid particles and will not be specifically connected to YSZ or Ni. Both ions and electrons are able to travel through both types of spheres. In Fig. 1, the blue randomly placed spheres of two different sizes represent the particles of Ni and YSZ. A grey coverage is placed on top of the blue spheres to visualize where the reactions take place. The grey coverage in Fig. 1 represents a coating to illustrate that the reactions only take place on the surface of the particles where the active site is located. Note that Fig. 1 is not to scale in size and porosity but is just presented to visualize the geometry and the placement of the reaction sites.

Fig. 1

Schematic figure of the modeling domain with descriptive boundary conditions and size of the domain

Reynolds number (Re) varies throughout the modeling domain as it is a porous media. In this study, throughout the porous domain, the Reynolds number is Re ≤ 0.01. The inlet velocity of 0.015 m/s leads to Re ≈ 5 × 10⁻⁵ based on the pore diameter. The average velocity is extracted from our previous macroscale model in COMSOL Multiphysics [1, 35]. The production and consumption of species are included by implementing the reaction rate of the electrochemical reaction, shown in Eq. (3), in the mass diffusion equation.

4 Results and evaluation

For the simulations, a computer cluster provided by Lunarc at Lund University is used. The modeling studies are performed in Palabos and part of it in MATLAB to compare the standard of the in-house codes to a commercial program.

In Fig. 2, the velocity field is presented to illustrate that LBM can easily handle the obstacles in a porous domain by the bounce-back effect for the particles at the obstacle wall. The velocity distribution is presented for part of the modeling domain with the enlarged particles (dark blue) to provide an understanding of the bounce-back theory which most easily is viewed for the fluid flow process in the porous media. The velocity in the porous domain is low and it is fully laminar throughout the whole model. As seen in Fig. 2, the local velocity is increased when the passages between the particles are narrow and the local velocity is decreased when the passages are broad.

Fig. 2

Velocity distribution (m/s) in the modeled porous domain

Figure 3 shows the concentration distribution of H₂ for the porous domain with spherical obstacles of the entire modeling domain. The inlet concentration is specified at x = L as 10 mol/m³ (which can be converted into a mole fraction of $x_{{H_{2} }}$ = 0.9) and the concentration flux is specified to zero at x = 0 normal to the boundary interface in the flow direction. The mass diffusion of H₂ predicts a continuous reduction of H₂ in the opposite flow direction. H₂O increases throughout the modeling domain from x = 0 to x = L.

Fig. 3

Concentration distribution of H₂ (mol/m³)

Figure 4 presents the ionic current density distribution at the center of the porous modeling domain along the main flow direction. The ionic current densities are plotted for cases with different porosities ranging from 30 to 50 %. Note that the ionic current density is only plotted for the region closest to the electrolyte from 0 to 15 μm. Most activity occurs at the interface to the electrolyte and the anode structure has an active reaction zone of about 15 μm. The ionic current density decreases along the main flow direction. The decreased ionic current density (along the main flow direction) can be explained by an increased temperature and a decreased concentration of the electrochemical reactants. An increase in porosity decreases the ionic current density slightly. In contrast to the effect of temperature, the difference in magnitude between the ionic current density lines for various porosity is larger closer to x = L which can be explained as an effect of the number of reaction sites and because the reacting species decreases as the porosity increases. The percentage of reaction sites remains the same but the number of particles decreases which decreases the number of reaction sites. The decrease in ionic current density along the main flow direction can be explained due to the influence of the charge transfer losses, η _ohm , depends mostly on the ion conductivity. Higher current density due to less available concentration of the reacting species will decrease the open-circuit voltage (along the main flow direction).

Fig. 4

Ionic current density along the center of the modeling domain for porosities of 30, 40 and 50 %, respectively

Figure 5 presents the concentration distribution of H₂ along the center of the porous modeling domain along the main flow direction, for the three porosities studied. The percentage of active reaction sites was 10 %. The H₂ concentration distributions were similar for all porosities. As the porosity increases the H₂ consumption decreases, and is more visible towards x = 0, as most of the H₂ is consumed. This can be explained by the fact that less reaction sites are available as there is more pore space between the solid particles. The H₂ consumption will also decrease with increasing porosity, as fewer active reaction sites come into contact with the gas species. If the porosity is decreased to the point where the fluid flow pathways are compressed, the H₂O production will decrease rapidly.

Fig. 5

Concentration distribution of H₂ along the center of the domain for porosities of 30, 40 and 50 %, respectively

Figure 6 shows the ionic current density distribution at the center of the porous modeling domain from x = 0 to x = 15 μm, with percentages of active sites ranging from 5 to 15 %. Note that the specific active reaction sites are described by the volume percentage of the total volume of the particles. The reaction layer is assumed to be located at the anode–electrolyte interface. The ionic current density decreases rapidly with distance from the inlet, which indicates resistance by diffusion. Decreasing the percentage of active sites decreases the ionic current density slightly along the flow direction. Values of active sites greater than 15 % were also simulated, but the increase in ionic current density was less significant above 20 %, where it appears that less reacting species are available. In future studies it might be of interest to investigate the effect on the transport processes and current density by gradients in the percentage of active sites, by linearly decreasing the number of active sites starting from the electrolyte boundary.

Fig. 6

Ionic current density along the center of the domain for three different percentages of reaction sites: 5, 10 and 15 %

Figure 7 presents the concentration distribution of H₂ at the center of the porous modeling domain from x = 0 to x = 150 μm, as a function of the percentage of reaction sites. The porosity was kept constant at 40 %, as well as the number of particles. It can be seen that the concentration distributions of H₂ are similar in all cases. However, as the percentage of reaction sites increases, the H₂ consumption increases. This is more visible towards x = 0 as most of the H₂ has been consumed.

Fig. 7

Concentration distribution of H₂ along the center of the domain for different percentages of reaction sites of 5, 10 and 15 %, respectively

The tortuosity was evaluated by measuring the lengths of all the streamlines, and calculating the average length divided by the length of the cell. The values of different tortuosities for the gas species are presented in Fig. 8. Three cases were studied for each porosity using different randomly placed spheres throughout the modeling domain. The trend visible in Fig. 8 shows a decrease in tortuosity as the porosity is increased. These results are in good agreement with those presented by Ghassemi et al. [36]. However, a more comprehensive study is required to confirm these results. The results concerning tortuosity in this study are limited, but provide at least an indication of the values of tortuosity for the gas species and the trend over the small range studied here.

Fig. 8

Tortuosity in the anode for porosities of 30, 40 and 50 %, using three random reconstructions of the porous medium

Some of the results are compared to experimental work in the literature. However, the experimental studies are conducted on a whole unit cell of an SOFC and therefore some of the results obtained from this numerical study may differ slightly from the experimental results. The maximum ionic current density is compared in the voltage–current density curves found in the literature for the same operating conditions. The ionic current densities obtained from the case studies in this work are slightly higher than several numerical and experimental studies found in the literature for an inlet temperature of 1000 K and operating voltage of 0.7 V. Yang et al. [37] conducted experimental work on an anode-supported SOFC for operating temperatures between 1023 and 1123 K and the current density obtained for 0.7 V was around 6500 A/m². However, there are a number of studies that confirm the high ionic current density such as Rogers et al. [38]. They obtained a current density around 13 000 A/m² for 1073 K and 0.7 V.

The relatively high ionic current density might be explained by an under-prediction of the overpotential for a small sample of the porous volume which was found by Kanno et al. [10]. Also the high ionic current density is affected by the fact that only the anode is included in this study and not the entire SOFC. The trend and change of the ionic current density due to temperature is supported by Suzue et al. [8] both in magnitude of the maximum ionic current density and the development of the ionic current density in the x-direction. The curve trend can be explained by low ion transport resistance as the porous media in the model is treated as a mixed ionic and electronic conducting material where the ions and electrons are able to travel through all the solid particles.

By comparing the results with previous results [35] it can be shown that a larger H₂ concentration variation is obtained when the charge transfer, the electrochemical properties and their structural properties are described parallel to each other. This is due to the inter-dependence of the process paths and changes in geometric and kinetic transport properties. The studies in Palabos are compared with standard in-house codes with good agreement.