1 Introduction

The boundary layer flow over a moving continuous solid surface is an important type of flow, which occurs in several engineering processes. For example, in industry the heat-treated materials travel between a feed roll and a wind-up roll while they are subject to heat transfer with a fluid. Another example is the materials manufactured by extrusion of plastic sheets [1]. These engineering processes can be modeled as a stretching sheet. The stretching sheet phenomena occur in many other applications such as: paper production, glass blowing, metal spinning [2], polymer engineering [3], cooling of metallic sheets and crystal growing [1, 3]. In the mentioned applications, the heat transfer rate in the boundary layer over stretching sheet is important because the quality of the final product depends on the heat transfer rate between the stretching surface and the fluid during the cooling or heating process [4]. Therefore, the choice of a suitable cooling/heating liquid is essential as it has a direct impact on the rate of heat transfer.

In recent years, the heat transfer enhancement of nanofluid has been proposed as a route for surpassing the performance of heat transfer rate in liquids currently available [5]. Nanofluid is described as a fluid in which the solid nanoparticles with the length scales of nanometers are suspended in a conventional heat transfer fluid. It has been demonstrated that the addition of highly conductive particles can significantly enhance the thermal conductivity of the pure base fluid. For example, it was reported that the effective thermal conductivity of an ethylene–glycol-based nanofluid which contains nano size copper particles with diameters less than 10 nm increased by up to 40 at 0.3 % vol. of dispersed particles [6]. An excellent review of nanofluid physics and developments can be found in [7, 8] and the book of Das et al. [9]. The current experimental data shows that the force-convection enhances in the presence of nanoparticles [10], and the enhancement increases with the increase of nanoparticle volume fraction [11].

Currently, there are two main approaches in the modeling of heat transfer convection in nanofluids. In the first approach, the nanofluid can be modeled as the common pure fluid where the conventional equations of mass, momentum and energy can be used. In the mentioned models, it is assumed that the enhancement of convective heat transfer is just because of the enhancement in thermophysical properties, which are affected by nanoparticle volume fraction and nanoparticle properties. In these models, the nanoparticles are in thermal equilibrium with fluid molecules, and there is not any slip velocity between the nanoparticles and fluid molecules. Thus, a uniform mixture of nanoparticles is considered for the nanofluid [5, 11–13].

In the second approach, it is believed that in the convection of nanofluids there are several slip mechanisms, so the volume fraction of nanoparticles in the nanofluid may not be uniform. A comprehensive survey in the field of convective transport in nanofluids has been done by Buongiorno [14]. He demonstrated that the high heat transfer coefficients in the nanofluids cannot be explained adequately by thermal dispersion [15], nanoparticle rotation [16] or increase in turbulence intensity of nanoparticles [17] as proposed in the literatures. Buongiorno considered seven slip mechanisms which can produce a relative velocity between the nanoparticles and the base fluid. Of all of these seven mechanisms, only thermophoresis and Brownian diffusion were found to be important. Later, Buongiorno [14] developed an analytical model for convective transport in nanofluids in which Brownian motion and thermophoresis effect were considered.

Sakiadis [18] studied the boundary layer behavior for the sheet moving with a constant velocity in a viscous fluid. The analytical solution for steady stretching of the surface was given by Crane [19]. After this pioneering work, various aspects of the problem including magneto hydrodynamic flows [20], non-Newtonian fluids [21], nanofluids [22–24], flows with chemical reactions [25], and also different hydrodynamic and thermal boundary conditions have been investigated.

Some of the researchers considered different idealized thermal boundary conditions for the sheet surface. Gupta and Gupta [26] analyzed heat and mass transfer over a stretching sheet with constant surface temperature. Different thermal boundary conditions such as power-law surface temperature and power-law surface heat flux were discussed by Fang [27]. Cortell [28] investigated the viscous flow and heat transfer over a stretching sheet prescribed power law surface temperature. However, when the sheet is prescribed to a convective fluid from below, the consideration of constant or variable temperature/heat flux is not a realistic boundary condition in many engineering applications of stretching sheet. In this case, the convective boundary condition is a more realistic thermal boundary condition. Recently, number of researchers examined the convective boundary condition. Aziz [29] considered the classical problem of hydrodynamic and thermal boundary layers over a flat plate in a uniform stream of fluid. Aziz obtained a similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Later, Magyari [30] introduced an analytical approach for heat equation which has been implemented in the work of Aziz [29]. Hamad et al. [31] investigated the heat and mass transfer of boundary layer stagnation-point flow over a stretching sheet in a porous medium saturated by a nanofluid using a lie group analysis. Ishak [32] obtained a similarity solution of flow and heat transfer over a permeable surface with a convective boundary condition. The forced convection of a uniform stream flow over a flat surface with a convective surface boundary condition has been theoretically analyzed by Merkin and Pop [33]. Yao et al. [34] studied heat transfer in the stretching sheet problem with convective boundary condition, and they obtained an exact solution in the form of an incomplete Gamma function. They reported that the convective boundary condition results in temperature slip at the wall, which it is greatly affected by the Prandtl number and the wall stretching parameters. They found that the temperature profiles are quite different from the prescribed wall temperature cases.

Beyond the temperature boundary conditions, many researchers studied the different aspects of hydrodynamic boundary conditions including permeable stretching sheet and partial slip velocity on the sheet surface. The slip flow problem of laminar boundary layer is of considerable practical interest. Microchannels which are at the forefront of today’s turbomachinery technologies, are widely being considered for cooling of electronic devices, micro heat exchanger systems, etc. If the characteristic size of the flow system is small or the flow pressure is very low, slip flow happens [35]. Wang [36] reported that the partial slip between the fluid and the moving surface may occur in situations that the fluid is particulate such as emulsions, suspensions, foams and polymer solutions. Wang [37], Andersson [38] and Ariel [39] employed a partial slip boundary condition to study the flow of a pure fluid over a stretching sheet. The effects of partial slip on the steady flow of an incompressible, electrically conducting third grade fluid past a stretching sheet has been examined by Sahoo and Do [40]. Hayat et al. [41] analyzed the effect of the slip boundary condition on the magneto hydrodynamic flow and heat transfer over a stretching sheet. The influence of partial slip, thermal radiation and temperature dependent fluid properties on the hydro-magnetic fluid flow and heat transfer over a flat plate with heat generation has been analyzed by Das [42].

Bocquet and Barrat [43] examined the effect of flow boundary conditions from nano to micro scales near the solid interfaces. They briefly discussed the mechanisms of surface slip and heat transfer on the interface. Bachok et al. [44] extended the Blasius and Sakiadis problems in nanofluids. Yacob et al. [5] investigated boundary layer flow past a stretching sheet with a convective boundary condition at the surface for two types of nanofluids, namely, Cu–water and Ag–water. They discussed the effect of the convective parameter on the heat transfer characteristics, but they did not consider the effect of Brownian motion and thermophoresis in their study. They found that the heat transfer rate at the surface increases with the increase of the nanoparticle volume fraction while it decreases with the increase of the convective parameter.

Recently, the Buongiorno’s model [14] has been used by Kuznetsov and Nield [45] to study the influence of nanoparticles on the natural convection boundary layer flow past a vertical plate. Khan and Pop [22] analyzed the boundary-layer flow of a nanofluid past a stretching sheet in a model in which the Brownian motion and thermophoresis effects have been taken into account. Hassani et al. [46] analytically examined the work of Khan and Pop [22]. Makinde and Aziz [47] examined the effect of a convective boundary condition on the boundary layer flow of nanofluids past a linear stretching sheet in order to obtain the more realistic solution where non-isothermal conditions at the flat sheet are present. They found that the local concentration of nanoparticles increases as the convection Biot number increases. The entropy generation [48] and magnetic effects [49] also are analyzed for nanofluid flow and heat transfer over stretching sheets. Rana and Bhargava [50] considered a nonlinear velocity for the sheet, and they analyzed the flow and heat transfer of a nanofluid over it.

To the best of authors’ knowledge, there is not any investigation to address the effect of the slip boundary condition on the heat transfer characteristics of nanofluid flow over stretching sheet prescribed convective boundary conditions in a model in which the dynamic effects of nanoparticles are taken into account. The present study aims to examine the effect of the slip boundary condition on the heat transfer characteristics of stretching sheet which is subjected to convective heat transfer on its surface in the presence of nanoparticles and their dynamic effects.

2 Governing equations

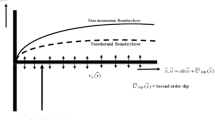
Consider a two-dimensional incompressible and steady state viscous flow of a nanofluid over a continuously stretching surface. The velocity of surface is linear, and is taken as U w(x) = c.x where c is a constant, and x is the coordinate component measured along the stretching surface. A flow with the convective heat transfer coefficient of h f and temperature of T f is flowing below the stretching sheet. The scheme of physical configuration is depicted in Fig. 1. It is worth mentioning that there are three distinct boundary layers, namely, hydrodynamic boundary layer (velocity), thermal boundary layer (temperature) and concentration boundary layer (nano particle volume fraction) over the sheet. However, in the Fig. 1 only single boundary layer is plotted to avoid congestion. Here, the nanofluid flows at y = 0 where y is the coordinate measured normal to the stretching surface.

Fig. 1
figure 1

Scheme of physical configuration of stretching sheet

Full size image

In the continuum modeling of fluidic transport no-slip boundary condition is sometimes assumed, which means that the fluid velocity component is assumed to be zero relative to the solid boundary [51]. For nanofluids, however, this assumption no longer holds [51], and a certain degree of tangential slip must be allowed [51, 52]. Considering the Navier’s condition, the velocity slip is assumed to be proportional to the local shear stress at the sheet surface [37]. The fraction of nanoparticles ø w is assumed constant at the stretching surface. The stretching sheet surface temperature T w , which will be evaluated later, is the result of a convective heating process depending to temperature of hot convective fluid below the stretching sheet (T f ) and convective heat transfer coefficient (h f ).

When y attends to infinity, the values of the temperature and nanoparticle fraction attend to the constant values of T ∞ and ø ∞ in the quiescent part of the nanofluid, respectively. ø and T indicate the fraction of nanoparticles and the temperature of flow, respectively. For nanofluids, by considering the dynamic effects of the nano particles and applying the boundary layer approximations the Boungiorno’s [14] convective transport equations in the Cartesian coordinate system of x and y can be written as follows [22, 47]:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{{\rho_{f} }}\frac{\partial p}{\partial x} + \nu \nabla^{2} u $$
(2)
$$ u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{1}{{\rho_{f} }}\frac{\partial p}{\partial y} + \nu \nabla^{2} v $$
(3)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \nabla^{2} T + \tau \left\{ {D_{B} \nabla \phi \cdot \nabla T + \frac{{D_{T} }}{{T_{\infty } }}\nabla T \cdot \nabla T} \right\} $$
(4)
$$ u\frac{\partial \phi }{\partial x} + v\frac{\partial \phi }{\partial y} = D_{B} \nabla^{2} \phi + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\nabla^{2} T $$
(5)

subject to the following boundary conditions at the sheet,

$$ v = 0,\quad u = U_{W} (x) - U_{S} ,\quad - k\left( {\frac{\partial T}{\partial y}} \right) = h_{f} (T_{f} - T),\quad \phi = \phi_{W} ,\quad at\,y = 0 $$
(6)

and the following boundary conditions at the far field (i.e. y→∞),

$$ v = u = 0,\quad T = T_{\infty } ,\quad \phi = \phi_{\infty } , $$
(7)

Here, u and v are the velocity components along the axis x and y respectively. p is the fluid pressure, α is the thermal diffusivity, k is the thermal conductivity of fluid, v is the kinematic viscosity, ρ f is the density of the base fluid, ρ p is the density of the particles, U s is the velocity slip at the wall, D B is the Brownian diffusion coefficient, and D T is the thermophoresis diffusion coefficient. τ = (ρc) p /(ρc) f is the ratio of the effective heat capacity of the nanoparticle material and heat capacity of the fluid, ρ is the density and ø is rescaled nanoparticle volume fraction and ∇ 2 is the Laplace operator in Cartesian coordinates.

In order to obtain similarity solution for Eqs. (1)–(5), the stream function and dimensionless variables can be introduced in the following form,

$$ \psi = \sqrt {cv} \,f(\eta ),\quad \eta = y\sqrt {c/v} $$
(8a)
$$ \beta (\eta ) = \frac{{\phi - \phi_{\infty } }}{{\phi_{W} - \phi_{\infty } }},\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }} $$
(8b)

The stream function ψ can be defined as \( u = {{\partial \,\psi } \mathord{\left/ {\vphantom {{\partial \,\psi } {\partial \,y}}} \right. \kern-0pt} {\partial \,y}} \), \( v = - {{\partial \,\psi } \mathord{\left/ {\vphantom {{\partial \,\psi } {\partial \,x}}} \right. \kern-0pt} {\partial \,x}} \), so that Eq. (1) is satisfied identically. The pressure outside the boundary layer in quiescent part of flow is constant; and the flow occurs only due to the stretching of the sheet; and hence, the pressure gradient can be neglected. Considering the usual boundary layer approximations, \( u > > v \), \( \frac{\partial u}{\partial y} > > \frac{\partial u}{\partial x},\frac{\partial v}{\partial x},\frac{\partial v}{\partial y} \), the momentum equation in y direction reduces to \( \frac{\partial P}{\partial y} = 0 \). By applying the introduced similarity transforms, Eq. (8a, b), on the remaining governing Eqs. (2), (4), (5) the following set of ordinary differential equations are obtained,

$$ f^{\prime \prime \prime } + f\,f^{\prime \prime } - f^{\prime 2} = 0, $$
(9)
$$ \frac{1}{pr}\theta^{\prime \prime } + f\theta^{\prime } + Nb\beta^{\prime } \theta^{\prime } + Nt\theta^{\prime 2} = 0, $$
(10)
$$ \beta^{\prime \prime } + \frac{Nt}{Nb}\theta^{\prime \prime } + Le\,f\,\beta^{\prime } = 0, $$
(11)

Here, by using the boundary layer approximations and introducing the Navier’s condition one may obtain,

$$ u - U_{W} (x) = N\rho \nu \frac{\partial u}{\partial y} = U_{S} $$
(12)

where ρ is the density and N is a slip constant. By applying the similarity transforms, the Eq. (12) is reduced to,

$$ f^{\prime}(0) - 1 = \lambda f^{\prime\prime}(0), $$
(13)

where \( \lambda = N\,\rho (cv)^{1/2} \) is the dimensionless slip factor. Performing introduced similarity transforms (i.e. Eq. (8)) on the remaining boundary conditions Eqs. (6), (7) the transformed boundary conditions are obtained which can be summarized as below,

$$ At\,\eta = 0:\quad f = 0,\quad f^{\prime} = 1 + \lambda f^{\prime\prime},\quad \theta^{\prime} = Bi(\theta - 1),\quad \beta = 1 $$
(14)
$$ At\,\eta \to \infty :\quad f^{\prime} = 0,\quad \theta = 0,\quad \beta = 0 $$
(15)

In the above equations, primes denote differentiation with respect to η. The parameters of Pr, Le, Nb, Nt and Bi are defined by,

$$ Pr = \frac{\nu }{\alpha },Le = \frac{\nu }{{D_{B} }},Nb = \frac{{(\rho c)_{P} D_{B} (\phi_{W} - \phi_{\infty } )}}{{(\rho c)_{f} \nu }},Nt = \frac{{(\rho c)_{P} D_{T} (T_{f} - T_{\infty } )}}{{(\rho c)_{f} \nu T_{\infty } }},Bi = \frac{{h_{f} \sqrt {v/c} }}{k} $$
(16)

where Pr, Le, Nb, Nt and Bi denote the Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter and Biot number, respectively. Consider a case which Nb and Nt are equal to zero and Biot number attends to infinity. The problem reduces to the classical problem of flow and heat transfer due to a stretching surface in a viscous fluid with constant wall temperature [36, 37, 40]. In this case, the boundary value problem for β becomes ill-posed without physical meaning.

The quantities of local Nusselt number (Nu x ) and Sherwood number (Sh x ) as important parameters in heat and mass transfer can be introduced as,

$$ Nu_{x} = \frac{{xq_{W} }}{{k(T_{W} - T_{\infty } )}},\quad Sh_{x} = \frac{{xq_{m} }}{{D_{B} (\phi_{W} - \phi_{\infty } )}} $$
(17)

where q w is the wall heat flux and q m is the wall mass flux. Using the similarity transforms introduced in Eq. (8), one may obtain,

$$ Re_{x}^{ - 1/2} Nu_{x} = - \theta^{\prime}(0),\quad Re_{x}^{ - 1/2} Sh_{x} = - \beta^{\prime}(0) $$
(18)

where Re x  = u w (x)x/ν is the local Reynolds number based on the stretching surface velocity, u w (x). Kuznetsov and Nield referred the value of \( Re_{x}^{ - 1/2} Nu_{x} \) as the reduced Nusselt number, and the value of \( Re_{x}^{ - 1/2} Sh_{x} \) as reduced Sherwood number [45]. Also, Khan and Pop [22] and Makinde and Aziz [47] used these names in their papers. It is worth mentioning that Wang [36] and Andersson [38] obtained an exact solution for Eq. (9) subject to the boundary conditions Eqs. (14) and (15).

3 Results and discussion

The exact solution of momentum equation, Eq. (9), subject to the boundary conditions of Eqs. (14) and (15) is proposed by Andersson [38] as follow:

$$ f\left( \eta \right) = \gamma \left( {1 - \exp ( - \gamma \eta )} \right) $$
(19)

where γ is the real and positive root of \( \lambda \gamma^{3} + \gamma^{2} - 1 = 0 \).

Using the exact solution (Eq. (19)), the set of ordinary differential equations (Eqs. (10) and (11)) subject to the boundary conditions (Eqs. (14) and (15)) are solved numerically for various ranges of the slip boundary condition and for different values of the Prandtl number, Lewis number, Brownian motion parameter, thermophoresis parameter and Biot number. Numerical results are obtained using Runge–Kutta–Fehlberg method [53, 54]. The most crucial factor of the solution is to choose the appropriate finite value of η ∞ . Thus, to estimate the value of η ∞ , it increased from initial value of 15 to the evaluated values of θ′(0) and β′(0) which they differ only after desired significant digit.

The values of Biot number (Bi) are chosen as less than unit, higher than unit (Bi = 10) and very high (Bi = 1,000). The results of increase of the Biot number from very low to very high values show that the value of Bi = 1,000 can accurately simulate the isothermal boundary condition which has been previously considered by Khan and Pop [22] with no slip boundary condition. Therefore, Bi = 1,000 is considered as the physical infinity of the problem where the wall temperature is very close to the hot fluid temperature T f . The values of slip factor (λ) are chosen as zero (no slip), between zero and unit and a value larger than unit (λ = 1.5). This selected range of the slip parameters is in good agreement with works of Hamad et al. [55], Wang [36, 37]. Since most nanofluids examined to date have large values for the Lewis number Le > 1 [56], the values of Le = 5 and 10 have been examined in the present study. The choice of the values for Nb and Nt was dictated by the fact that these values were used by Khan and Pop [22] and Makinde and Aziz [47] for the flow of nanofluid over an stretching sheet.

Table 1 shows the variation of the reduced Nusselt number (Nur) for different values of Nb, Nt, Le and λ when Pr = 1.0 and Pr = 10. Table 2 shows the variation of reduced Sherwood number for the same parameters as Table 1. Results of Table 1 demonstrate that increase of Biot number increases the reduced Nusselt number while the increase of either thermophoresis parameter or slip factor decreases the reduced Nusselt number for the selected range of Prandtl and Lewis numbers. The results of Table 2 show that the increase of the slip factor decreases the reduced Sherwood number, but the variation of other remaining parameters has different effects on reduced Sherwood number.

Table 1 Variation of reduced Nusselt number—θ′(0) with Nb, Nt, Le, Pr, Bi and λ
Full size table
Table 2 Variation of reduced Sherwood number—β′(0) with Nb, Nt, Le, Pr, Bi and λ
Full size table

Profiles of θ(η) and β(η) for selected values of the slip factor (λ), Nb and Nt are shown in Figs. 2 and 3, respectively, when Pr = 5, Le = 5 and Bi = 0.1. These figures show the effect of the slip boundary condition on the non-dimensional temperature and concentration distribution profiles. These figures also show that increase of the slip factor increases the magnitude of non-dimensional temperature and concentration distribution. The Brownian motion tends to uniform the concentration of nanoparticles, and the thermophoresis force tends to move nanoparticles from hot to cold areas. Increase of Nb and Nt increases the movement of nanoparticles away from the sheet surface and consequently increases the magnitude of temperature profiles and concentration distribution profiles (as seen in Figs. 2, 3). Increase of slip factor increases the magnitude of both thermal and concentration boundary layer thickness.

Fig. 2
figure 2

Effect of slip factor, Nt and Nb on temperature profiles for Pr = 5, Le = 5, Bi = 0.1

Full size image
Fig. 3
figure 3

Effect of slip factor, Nt and Nb on concentration profiles for Pr = 5, Le = 5, Bi = 0.1

Full size image

For a typical case with Pr = 5, Le = 5 and Bi = 0.1, the dependent similarity variables θ(η) and β(η) are plotted for different values of slip factors λ and Biot number parameter Bi in the Figs. 4 and 5, respectively. Figure 4 shows that increase of the slip factor λ or Biot number Bi increases the magnitude of non-dimensional temperature profiles. The stronger convection (higher Biot number) results in higher surface temperatures and consequently the higher values of temperature profiles. Increase of the slip factor decreases the tendency of the nanofluid to remove the heat away from the plate and consequently causes the higher values of temperature profiles. Figure 4 also depicts that for the small (Bi = 0.1) and large (Bi = 10) values of Biot number the effect of the slip factor λ on the wall values of non-dimensional temperature profiles θ(0) is less than it for middle values of Biot number (Bi = 1). Increase of the Biot number or slip factor increases the thermal boundary layer thickness and wall temperature values θ(0). Increase of thermal boundary layer thickness with the increase of the slip factor is due to the fact that the flow of fluid in the boundary layer is in results of the stretching of the sheet. Therefore, increase of the slip factor decreases the flow motion and consequently increases the thickness of thermal and concentration boundary layers. Figure 5 reveals that profiles of β(η) for all selected values of Biot number and slip factor take value of one on the sheet surface, and they tends to zero as η tends to infinity. This figure depicts that increase of Biot number or increase of the slip factor increases the values of β(η). It is worth noticing that in the case of (λ → 0) the present study reduces to the work of Makinde and Aziz [47]. In the Figs. 2 and 4, the non-dimensioanl temperature profiles (in the case of λ → 0) are compared with the results reported by Makinde and Aziz [47]. Similarly, in the Fig. 5, the non-dimensioanl concentration profiles (in the cases of λ → 0) are compared with the results reported by Makinde and Aziz [47]. These figures show that the results of present study are in good agreement with the previous study.

Fig. 4
figure 4

Effect of slip factor and Bi on temperature profiles for Nb = Nt = 0.1, Pr = Le = 5

Full size image
Fig. 5
figure 5

Effect of slip factor and Bi on concentration profiles for Nb = Nt = 0.1, Pr = 5, Le = 5

Full size image

The variation of dimensionless heat transfer rate (i.e. reduced Nusselt number) and dimensionless mass transfer rate (i.e. reduced Sherwood number) respect to thermophoresis parameter for different values of Biot number and slip factor when Pr = 10, Le = 10 and Nb = 0.1 are shown in Figs. 6 and 7. According to Fig. 6 the dimensionless heat transfer rate, reduced Nusselt number, increases with decrease of the thermophoresis parameter, increase of the Biot number and decrease of the slip factor. Figure 7 depicts that increase of thermophoresis parameter decreases the reduced Sherwood number for small values of Biot number (i.e. Bi ≈ 0.1), but for comparatively large values of the Biot number (i.e. Bi ≈ 0.5) increase of thermophoresis parameter first decreases the reduced Sherwood number and then increases it. In addition, from the Fig. 7 it is clear that increase of the slip factor decreases the reduced Sherwood number. The wall temperature values θ(0) as a function of Prandtl number for selected values of Biot number and slip factor parameter are plotted in Fig. 8 when Nb = Nt = 0.1 and Le = 5. This figure depicts that the dimensionless wall temperature increases with increase of Biot number or slip parameter, but it first decreases and then slowly increases with the increase of Prandtl number. Therefore, for each comparatively large value of Biot number there is an optimum Prandtl number which minimizes the dimensionless wall temperature θ(0).

Fig. 6
figure 6

Effects of slip factor, biot number and thermophoresis parameter on the dimensionless heat transfer rates for Pr = 10, Le = 10 and Nb = 0.1

Full size image
Fig. 7
figure 7

Effects of slip factor, biot number and thermophoresis parameter on the dimensionless concentration rates for Pr = 10, Le = 10 and Nb = 0.1

Full size image
Fig. 8
figure 8

Effects of slip factor, biot number and Prandtl number on the dimensionless wall temperature for Le = 5 and Nb = 0.1 and Nt = 0.1

Full size image

4 Conclusion

The effect of partial slip (i.e. Navier’s condition) on the boundary layer flow and heat transfer of nanofluids past stretching sheet prescribed convective heat transfer is theoretically investigated. The boundary layer equations governing the flow, heat and nanoparticle are reduced to a set of nonlinear ordinary differential equations using the similarity transformations. The obtained differential equations are solved numerically for different combinations of nanofluid parameters. Effect of slip factor (λ), Biot number (Bi) and nanofluid parameters including Lewis number (Le), Brownian motion parameter (Nb) and thermophoresis parameter (Nt) on the nanoparticle and thermal boundary layers are discussed using tables and figures. It is observed that by the increase in the slip factor λ and Biot number Bi the thermal boundary layer thickness increased. The reduced Nusselt number and reduced Sherwood number on the stretching sheet are strongly influenced by the slip factor and Biot number. In all cases, the reduced Nusselt number and reduced Sherwood number are decreased with the increase of slip factor λ. The reduced Nusselt number increased with the increase of Biot number and decreased with the increase of thermophoresis parameter for comparatively large values of Prandtl and Lewis numbers. The dimensionless wall temperature increased with increase of the Biot number or slip factor. Finally, it is found that for small values of the Biot number, increase of the thermophoresis parameter decreases the reduced Sherwood number (for comparatively small values of thermophoresis), but when the thermophoresis parameter is comparatively large, the increase of thermophoresis parameter increases the reduced Sherwood number. Therefore, for each value of slip factor and comparatively large values of Biot number (i.e. Bi ≈ 0.5) and small values of Nb (i.e. Nb = 0.1) there is an Nt which minimizes the Sherwood number. In addition, when Nb and Nt are comparatively small, for each comparatively large value of Biot number there is an optimum Prandtl number which minimizes the dimensionless wall temperature θ(0).