1 Introduction

In the literature concerning thermal effects in continuum mechanics there are developed several parabolic and hyperbolic theories for describing the heat conduction. The hyperbolic theories are also called theories of second sound and there the flow of heat is modeled with finite propagation speed, in contrast to the classical model based on the Fourier’s law leading to infinite propagation speed of heat signals. A review of these theories is presented in the articles by Chandrasekharaiah [2] and Hetnarski and Ignaczak [3].

Differential equations of fractional order have been the focus of many studies due to their frequent appearance in various applications in fluid mechanics, viscoelasticity, biology, physics and engineering. The most important advantage of using fractional differential equations in these and other applications is their non-local property. It is well known that the integer order differential operator is a local operator but the fractional order differential operator is non-local. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. This is more realistic and it is one reason why fractional calculus has become more and more popular [4–6].

Fractional calculus has been used successfully to modify many existing models of physical processes. The first application of fractional derivatives was given by Abel who applied fractional calculus in the solution of an integral equation that arises in the formulation of the tautochrone problem. One can state that the whole theory of fractional derivatives and integrals was established in the 2nd half of the nineteenth century. Caputo and Mainardi [7, 8] and Caputo [9] found good agreement with experimental results when using fractional derivatives for description of viscoelastic materials and established the connection between fractional derivatives and the theory of linear viscoelasticity. One can refer to Padlubny [5] for a survey of applications of fractional calculus.

Among the few works devoted to applications of fractional calculus to thermoelasticity we can refer to the works of Povstenko [10, 11], who introduced a fractional heat conduction law, found the associated thermal stresses, and established the fundamental solutions to the Cauchy problem in the case of spherical symmetry and investigated stresses, due to the fractional heat conduction law, in an infinite body with a circular cylindrical hole. Sherief et al. [12] introduced new model of thermoelasticity using fractional calculus, proved a uniqueness theorem and derived a reciprocity relation and a variational principle. Youssef [13] introduced another new model of fractional heat conduction equation, proved a uniqueness theorem and presented one-dimensional application. Some applications of fractional calculus to various problems of mechanics of fluid are reviewed in the literature [14–18]. In most of these investigations the effect of the thermal state in a fluid is not considered.

In this work we construct a mathematical model for heat equation with fractional derivatives and thermoelectric properties. The governing coupled equations in the frame of the boundary layer are applied to a problem of a layer medium in the presence of a transverse magnetic field. Laplace transforms and state space approach techniques are used to get the solution. Numerical results for the temperature, the velocity component and heat flux are represented graphically. The effect of thermoelectric figure-of-merit on fluid flow is studied for different values of fraction order.

2 Fourier heat conduction law with time-fraction order

Thermoelectric devices have many attractive features compared with the conventional fluid-based refrigerators and power generation technologies, such as long life, no moving part, no noise, easy maintenance and high reliability. However, their use has been limited by the relatively low performance of present thermoelectric materials. The efficiency of a thermoelectric material is related to the so-called dimensionless thermoelectric figure-of-merit ZT. The thermoelectric figure of merit provides a measure of the quality of such materials for applications and is defined in [19]:

$$ ZT = \frac{{\sigma_{o} S^{2}}}{\kappa}T. $$
(1)

The best thermoelectric materials that are currently in devices have a value of \( ZT \gg 1 \).

A related effect (the Peltier effect) was discovered a few years later by Peltier, who observed that if an electrical current is passed through the junction of two dissimilar materials, heat is either absorbed or rejected at the junction depending on the direction of the current. This effect is due to the difference in Fermi energies of the two materials. The absolute temperature T, the Seebeck coefficient S and the Peltier coefficient Π are related by the first Thomson relation as in [20]:

$$ \Uppi = ST.$$
(2)

Cattaneo [21] was the first to offer an explicit mathematical correction of the propagation speed defect inherent in Fourier’s heat conduction law. Cattaneo’s theory allows for the existence of thermal waves, which propagate at finite speeds. Starting from Maxwell’s idea [22] and from paper by Cattaneo [21], an extensive amount of literature [23–26] has contributed to elimination of the paradox of instantaneous propagation of thermal disturbances. The approach is known as extend irreversible thermodynamics, which introduces time derivative of the heat flux vector, Cauchy stress tensor and its trace into the classical Fourier law by preserving the entropy principle. Josef and Preziosi [25] give a detailed history of heat conduction theory. In addition to discussing various other models of heat conduction, these authors’s state that Cattaneo’s equation is the most obvious and simple generalized of Fourier’s law that gives rise to a finite speed of propagation. Pure and Kythe [26] investigated the effects of using the (Maxwell–Cattaneo) model in Stoke’s second problem for a viscous fluid. They also studied the effects of discontinuous boundary data on the velocity gradients temperature fields occurring in Stoke’s first problem for a viscous fluid. They also note that in the theory of generalized thermofluid, the non-dimensional thermal relaxation time τ o defined as τ o  = C p P r , where C p and P r are the Cattaneo and Prandtl numbers respectively, is of order (10)−2.

The Fourier law, modified in this way, established an impact equation relating heat flux vector, velocity, and temperature.

The energy equation in terms of the heat conduction vector q is

$$ \rho C_{p} \frac{\text{D}}{{\text{D}}t}T = - \nabla \cdot {\user2{q}} + Q, $$
(3)

where ρ is the density of the fluid and C p is the specific heat at constant pressure and

$$ \begin{aligned} Q =& \mu \;\left[ {2 \left( {\frac{\partial u}{\partial x}} \right)^{2} + 2\left( {\frac{\partial v}{\partial y}} \right)^{2} + 2\left( {\frac{\partial w}{\partial z}} \right)^{2} + \left( {\frac{\partial w}{\partial y} + \frac{\partial \,v}{\partial z}} \right)^{2} } \right. \hfill \\ &\quad \left. { + \left( {\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right)^{2} } \right], \hfill \\ \end{aligned} $$
(4)

is the internal heat due to viscous stresses and the operator \(\frac{\text{D}}{{{\text{D}}t}} \) is the material derivative defined as

$$ \frac{{\rm D}}{{{\rm D}t}} = \frac{\partial }{{\partial t}} + \left({{\user2{V}} \cdot \nabla } \right) $$
(5)

The generalized Fourier’s and Ohm’s laws in MHD for a thermoelectric medium are given by Shercliff [27]

$$ {\user2{q}} = - \kappa \nabla T + \Uppi {\user2{J}}, $$
(6)
$$ {\user2{J}} = \sigma_{o} \left({\user2{E}} + {\user2{V}} \times{\user2{B}} -S\nabla T \right), $$
(7)

where J is the conduction current density vector, E and B are respectively, the electric density and the magnetic flux density vectors and \( {\user2{V} }= \left( {U,V,W} \right) \) is the vector velocity of the fluid. Substituting (6) in (3) we shall obtain the well-known energy equation

$$ \rho C_{p} \frac{\text{D}}{{{\text{D}} t}} T = \kappa \nabla^{2} T - \nabla \cdot \Uppi \, {\user2{J}} + Q . $$
(8)

Theoretically, Fourier’s heat-conduction equation leads to solutions exhibiting infinite propagation speed of thermal signals. It was shown in Cattaneo [21] and Lebon and Rubi [23] that it is more reasonable physically to replace (6) by the following generalized Fourier’s law of heat conduction including the current density effect to obtain [28]

$$ {\user2{q}} + \tau_{o} \frac{\partial {\user2{q}}}{\partial t} = - \kappa \nabla T + \Uppi\, {\user2{J}} .$$
(9)

In this paper, we consider the theory developed by taking a new fractional Taylor’s series of time-fractional order α [29], to expand \( {\user2{q}}(x, t + \tau_{o}) \) and retaining terms up to order α in the thermal relaxation time τ o . One then obtains a non-Fourier formula of heat conduction including the current density effect in which the evolution equation contains a fractional order derivative with respect to time. That is

$$ {\user2{q}} + \;\frac{{{{\uptau}}_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } \,{\user2{q}}}}{{\partial \,t^{\alpha } }} = - k \nabla T + \Uppi\, {\user2{J}} \quad 0 < \alpha \le 1, $$
(10)

taking into consideration

$$ \frac{{\partial^{\alpha} }}{{\partial t^{\alpha } }}f(y,t) = \left\{ \begin{array}{ll} f(y,t) - f(y,0)& \alpha \to 0 \\ {\user2{I}}^{\alpha -1} \,\frac{\partial f(y,t)}{\partial t}& 0 < \alpha < 1 \hfill \\ \frac{\partial f(y,t)}{\partial t}& \alpha = 1 \hfill \\ \end{array}\right., $$

where the notion I α is the Riemann–Liouville fractional integral is introduced as a natural generalization of the well-known n-fold repeated integral I n f(t) written in a convolution-type form as in [30]:

$$ \left. \begin{array}{l} I^{\alpha } f(t) = \int\limits_{o}^{t} {\frac{{(t - \varsigma )^{\alpha-1} }}{\Upgamma (\alpha )}\;f(\varsigma )\;d\varsigma } \hfill \\ I^{0} f(t) = f(t) \hfill \\ \end{array} \right\}\quad \alpha > 0. $$

In the limit as α tends to one, (9) reduces to the well known Cattaneo law used by Lord and Shulman [31] to derive the equation of the generalized theory of thermoelasticity with one relaxation time. It is known that Lebon et al. [32] and Jou et al. [33] that the classical entropy derived using this law instead of being monotonically increasing behaves in an oscillatory way. Strictly speaking, this result is not incompatible with the Clausius’ formulation of the second law, which states that the entropy of the final equilibrium state must be higher than the entropy of the initial equilibrium state. However, the non-monotonic behavior of the entropy is in contradiction with the local equilibrium formulation of the second law, which requires that the entropy production must be positive everywhere at any time (Lebon et al. [32]). During the last two decades, this became the subject of many research papers and resulted in the introduction of what is known now as extended irreversible thermodynamics. A review can be found in Jou et al. [33].

Now taking the partial time derivative of fraction order α of (3), we get [34]

$$ \rho C_{p} \frac{\text{D}}{{{\text{D}} t}}\,\left( {\frac{{\partial^{\alpha } T}}{{\partial t^{\alpha } }}} \right) = - \nabla \, \cdot \;\left( {\frac{{\partial^{\alpha } {\user2{q}}}}{{\partial {\kern 1pt} t^{\alpha } }}} \right)\;+ \;\frac{{\partial^{\alpha } Q}}{{\partial t^{\alpha } }}. $$
(11)

Multiplying (11) by \( \frac{{\tau_{{_{o} }}^{\alpha } }}{\alpha !} \) and adding to (3) we obtain

$$ \rho \,C_{p} \,\frac{\text{D}}{{{\text{D}}t}}\, \left( {T + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\, \frac{{\partial^{\alpha } \,T}}{{\partial \,t^{\alpha } }}} \right) = - \;\nabla \cdot \;\left({\user2{q}} + \frac{{\tau_{o}^{\alpha } }} {\alpha !} \frac{{\partial^{\alpha } \,{\user2{q}}}} {{\partial \,t^{\alpha } }} \right)\; + \;\left( {Q + \frac{{\tau_{o}^{\alpha } }} {\alpha !}\frac{{\partial^{\alpha } Q}}{{\partial \,t^{\alpha } }}} \right).$$
(12)

Using (10), we get

$$ \rho \,C_{p} \,\frac{\text{D}}{{{\text{D}}t}}\,\left( {T + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\,\frac{{\partial^{\alpha } \,T}}{{\partial \,t^{\alpha } }}} \right) = \kappa \;\nabla^{2} T\,\, - \;\nabla \cdot \,\,\Uppi \,{\user2{J}}\; + \;\left( {Q + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } \,Q}}{{\partial \,t^{\alpha } }}} \right). $$
(13)

Taking into account the definition of \( \frac{\text{D}}{{{\text{D}}t}}\) from (5), we arrive at

$$ \left[ {\frac{\partial }{\partial \,t} + \left( {\user2{V}} \cdot \,\nabla \right)} \right]\,\left[ {T + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\,\frac{{\partial^{\alpha } \,T}}{{\partial \,t^{\alpha } }}} \right] = \frac{\kappa }{{\rho \,C_{p} }}\;\nabla^{2} \,T\, - \;\frac{1}{{\rho \,C_{p} }}\,\nabla .\,\,\Uppi \,{\user2{J}}\; + \frac{1}{{\rho \,C_{p} }}\;\left( {Q + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } Q}}{{\partial \,t^{\alpha } }}} \right) . $$
(14)

Equation (14) is the energy equation with fractional time derivatives of order α(0 < α ≤ 1), taking into account the relaxation time τ o .

The heat (14) in the limiting case α = 1 transforms to

$$ \left[ {\frac{\partial }{\partial \,t} + \left( {\user2{V}} \cdot \,\nabla \right)} \right]\,\left[ {T + \tau_{o}\,\frac{\partial \,T}{\partial \,t}} \right] = \frac{k}{{\rho\,C_{p} }}\;\nabla^{2} \, T- \frac{1}{{\rho \,C_{p} }}\,\nabla \cdot\,\,\Uppi \,\,{\user2{J}}\; + \frac{1}{{\rho \,C_{p} }}\; \left( {Q+ \tau_{o} \frac{\partial \,Q}{\partial \,t}} \right) , $$
(15)

which is the same equation obtained by Ezzat and Youssef [28] in the generalized theory of thermoelectric fluid.

In the limiting case and using homogenous initial condition α = 0, (14) reduces to

$$ \left[{\frac{\partial }{\partial \,t} + \left({\user2{V}}\,\cdot\,\nabla \right)} \right]\,\,T = \frac{k}{{\rho\,C_{p} }}\;\nabla^{2} \,T\, - \;\frac{1}{{\rho \,C_{p} }}\,\nabla\cdot\,\,\Uppi\, {\user2{J}} + \frac{1}{{\rho \,C_{p} }}\;Q , $$
(16)

which is the same equation obtained by the coupled theory of thermoelectric MHD [27].

3 Governing equations and sate space approach

Consider the laminar flow of an infinite incompressible thermoelectric fluid above the non conducting half-space y > 0. Taking the positive y-axis of the Cartesian coordinate system in the upward direction and the fluid flows through half-space y > 0 above and in contact with the plane surface occupying xz-plane. A constant magnetic field of strength H o acts in the z direction. The induced electric current due to the motion of the fluid that is caused by the buoyancy forces does not distort the applied magnetic field. The previous assumption is reasonably true if the magnetic Reynolds number of the flow (R m  = UL σ o μ o ) is assumed to be small, which is the case in many aerodynamic applications where rather low velocities and electrical conductivities are involved. Under these conditions, no flow occurs in the y and z directions and all the considered functions at a given point in the half-space depend only on its y-coordinate and time t. The velocity field is of the form, \( {\user2{V}} \equiv \left( {u, \, 0, \, 0} \right). \)

Given the above assumptions the governing one-dimensional unsteady boundary layer equations for momentum and heat transfer in such flow situations [35], in the usual form, are

  1. 1.

    The figure-of-merit ZT at some reference temperature, T o  = T w  – T ∞ is defined as

    $$ ZT_{o} = \frac{{\sigma_{o} k_{o}^{2} }}{\kappa }T_{o} , $$
    (17)

    where k o is the Seebeck coefficient at T o .

  2. 2.

    The first Thomson relation at room temperature is

    $$ \uppi_{o} = k_{o} T_{o} , $$
    (18)

    where π o is the Peltier coefficient at T o .

  3. 3.

    The magnetic induction has one non-vanishing component:

    $$ {\user2{B}}_{z} = \;\mu_{o} \,H_{o} = \;{\user2{B}}_{o} \,({\text{constant}}) $$
  4. 4.

    The Lorentz force F = J ∧ B, has one component in x-direction is

    $$ {\user2{F}}_{x} = - \sigma_{\text{o}} \,{\user2{B}}_{\text{o}}^{ 2} \,u\; - \sigma_{\text{o}} \,k_{\text{o}} \,{\user2{B}}_{\text{o}} \,\frac{\partial \,T}{\partial \,y} . $$
    (19)
  5. 5.

    The equation of motion with modified Ohm’s law

    $$ \frac{{\partial u}}{\partial \,t}\,= \upsilon \frac{{\partial^{ 2} u}}{{\partial \,y^{ 2} }} \; - \;\;\frac{{\sigma_{\text{o}} \,{\user2{B}}_{\text{o}}^{ 2} }}{\rho }\,\,u\; - \frac{{\sigma_{\text{o}} k_{\text{o}} {\user2{B}}_{o} }}{\rho }\,\frac{\partial \,T}{\partial \,y} . $$
    (20)
  6. 6.

    The energy equation with modified Fourier’s law

    $$ \rho \,C_{p} \frac{\partial }{\partial \,t\,}\,\left( {T + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\,\frac{{\partial^{\alpha } \,T}}{{\partial \,t^{\alpha } }}} \right) = \left( {\kappa \, + \,\sigma_{o} \uppi_{o} k_{o} } \right)\;\frac{{\partial^{ 2} T}}{{\partial \,y^{2} }}\;\, + \;\uppi_{o} \sigma_{o} \,B_{o} \,\;\frac{\partial \,u}{\partial \,y} + \;Q + \;{{\uptau}}_{o} \,\frac{\partial \,Q}{\partial \,t}. $$
    (21)

Let us introduce the following non-dimensional variables:

$$ \begin{aligned} &y^{*} \; = \;\frac{\,U}{\upsilon }y\,,\quad \;t^{*} \; = \;\frac{{\,\,U^{2} }}{\upsilon }t\,,\quad \;\tau_{o}^{*} = \;\frac{{\,\,U^{2} }}{\upsilon }\tau_{o} ,\quad \;u^{*} \; = \;\frac{u}{U},\;\quad \Uptheta = \frac{{T - T_{\infty } }}{{T_{o} }},\quad q^{*} \; = \;\frac{\upsilon }{{\kappa \,T_{o} \,U}}\;q \hfill \\ &Q^{*} = \frac{{\upsilon^{2} {\kern 1pt} Q}}{{\kappa {\kern 1pt} {\kern 1pt} U^{2} {\kern 1pt} {\kern 1pt} T_{o} }},\quad p_{r} = \;\frac{{C_{p} \mu }}{\kappa },\quad M\; = \;\frac{{\upsilon \,\sigma_{o} {\user2{B}}_{o}^{2} }}{{\rho \,U^{2} }},\quad K_{o}\; = \;\frac{{k_{o} \sigma_{o} {\user2{B}}_{o} T_{o} }}{{\rho \,U^{2} }},\quad \;\Uppi_{o}\; = \;\frac{{\uppi_{o} \upsilon \,\sigma_{o} {\user2{B}}_{o} }}{{\kappa \,T_{o} }} \hfill \\ \end{aligned} $$
(22)

Equations (20) and (21) are reduce to the non-dimensional equations (dropping the asterisks for convenience)

$$ \frac{{\partial \,{\kern 1pt} u}}{\partial \,t} = \frac{{\partial^{2} u}}{{\partial {\kern 1pt} \,y^{2} }} - Mu - \;K_{o} \,\frac{\partial \,\Uptheta }{\partial \,y} , $$
(23)
$$ p_{r} \,\left( {\frac{\partial }{\partial \,t} + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha + 1} }}{{\partial \,t^{\alpha + 1} }}} \right)\,\Uptheta = \,(1 + ZT_{o} )\,\frac{{\partial^{2} \,\Uptheta }}{{\partial \,y^{2} }}\; + \;\Uppi_{o} \,\frac{\partial \,u}{\partial \,y}\, + \,Q + {{\uptau}}_{o} \frac{\partial \,Q}{\partial \,t}. $$
(24)

To simplify the algebra, only problems with zero initial conditions are considered. Appling the Laplace transform defined by the formulas [10]

$$ \left. \begin{aligned} L\{ g(t)\} =&\, \bar{g}(s) = \int\limits_{0}^{\infty } {\hbox{e}^{ - st} g(t)\;dt} \hfill \\ L\{ D^{n} g(t)\} =&\, s^{n} \,L\{ g(t)\} \quad \quad n > 0 \hfill \\ \end{aligned} \right\}, $$
(25)

on both sides of  (23) and (24) and writing the resulting equations in matrix form results in

$$ \frac{{\rm d}}{{{\rm d}y}}\left\{ {\begin{array}{*{20}c} {\bar{\Uptheta }(y,s)} \\ {{{\bar{\rm u}}}(y,s)}\\ {\bar{\Uptheta }^{\prime } (y,s)} \\ {{{\bar{\rm u}}}^{\prime } (y,s)} \\ \end{array}} \right\} = \left\{ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ a & 0 & 0 & { - b} \\ 0 & {s + M} & {K_{o} } & 0 \\ \end{array}} \right\}\left\{ {\begin{array}{*{20}c}{\bar{\Uptheta }(y,s)} \\ {{{\bar{\rm u}}}(y,s)} \\ {\bar{\Uptheta }^{\prime } (y,s)} \\ {{{\bar{\rm u}}}^{\prime } (y,s)} \\ \end{array}} \right\} - \beta \bar{Q}(y,s)\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ 0 \\ \end{array}} \right], $$
(26)

where

$$ a = \frac{{sp_{r} }}{{1 + ZT_{o} }}\left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}s^{\alpha } } \right) ,\quad b = \frac{{\Uppi_{o} }}{{1 + ZT_{o} }},\quad\beta = \frac{1}{{1 + ZT_{o} }}\left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}s^{\alpha } } \right). $$

The formal solution of (26) can be expressed as

$$ {\bar{\user2{G}}}(y,s) = \exp \, \left[ {\user2{A}}(y,s)\,y \right]\left({\bar{\user2{G}}}(0,s) +\int \limits_{0}^{y} \exp \, \left[ { - \, {\user2{A}}(s)z} \right]B\,(z,s) \, dz \right). $$
(27)

In the special case when there is no heat source acting inside the medium, (25) simplifies to

$$ \bar{\user2{G}}(y,s) = \exp \left[ {\user2{A}}(y,s)\,y \right]\,\;\bar{\user2{G}}(0,s). $$
(28)

The characteristic equation of the matrix A(s) has the form

$$ k^{4} - \, \left( {s\, + M + a - K_{o} b} \right) \, k^{2} \, + \, (s + M)a = 0, $$
(29)

where k is a characteristic root. The Cayley–Hamilton theorem states that the matrix A satisfies its own characteristic equation in the matrix sense. Therefore, it follows that

$$ {\user2{A}}^{4} -\left( {s + M + a-K_{o} b} \right) \, {\user2{A}}^{2} + a(s + M)\,{\user2{I}} = 0. $$
(30)

Equation (30) shows that A 4 and all higher powers of A can be expressed in terms of A 3, A 2, A and I, the unit matrix of order 4. The matrix exponential can now be written in the form

$$ {\text{exp}}[{\user2{A}}(s)y] = a_{0} (y,s){\user2{I}} + a_{1} (y,s)\,{\user2{A}}(s) + a_{2} (y,s)\,\mathop {\user2{A}}\nolimits^{2} (s) + a_{3} (y,s)\mathop {\user2{A}}\nolimits^{3} \, (s).$$
(31)

The scalar coefficients of (31) are now evaluated by replacing the matrix A by its characteristic roots ±k 1 and ±k 2, which are the roots of the biquadratic (29), satisfying the relations

$$ \,k_{1}^{2} + k_{2}^{2} = s + M + a-K_{o} b, $$
(32a)
$$ k_{1}^{2} k_{2}^{2} = (s + M)a. $$
(32b)

This leads to the system of equations

$$ \exp ( \pm k_{1} x) = a_{o} \pm a_{1} k_{1} + a_{2} k_{1}^{2} \pm a_{3} k_{1}^{3} , $$
(33a)
$$ \exp ( \pm k_{2} x) = a{}_{o} \pm a_{1} k_{2} + a_{2} k_{2}^{2} \pm a_{3} k_{2}^{3} . $$
(33b)

The solution of the above system of linear equations is given by

$$ \begin{aligned} &a_{o} = \frac{{\,k_{1}^{2} \cosh \,k_{2} \,y-k_{2}^{2} \cosh k_{1} y}}{{k_{1}^{2}-k_{2}^{2} }},\quad a_{1} = \frac{{k_{1}^{3} \sinh k_{2} \,y-k_{2}^{3} \sinh k_{1} y}}{{k_{1} k_{2} (k_{1}^{2}-k_{2}^{2} )}}, \hfill \\ &a_{2} = \frac{{\cosh k_{1} y-\cosh k_{2} y}}{{k_{1}^{2}-k_{2}^{2} }},\quad a_{3} = \frac{{k_{2} \sinh k_{1} y-k_{1} \sinh k_{2} \,y}}{{k_{1} k_{2} (k_{1}^{2}-k_{2}^{2} )}} \hfill \\ \end{aligned} .$$
(34)

Substituting the expression (34) into (31) and computing A 2, and A 3, we obtain after some lengthy algebraic manipulations,

$$ { \exp}\left[ {\user2{A}}\left(s \right) \cdot y \right] = L\left({y, s} \right) = \left[\ell_{ij} \left({y,s} \right)\right],\quad i,j = 1, 2, 3, 4. $$
(35)

where the elements ℓ ij (y, s) are given in Appendix.

It is now possible to solve a broad class of one-dimensional problems of thermoelectric fluid flow with fractional order heat transfer in the presence of a constant magnetic field.

4 Applications

Problem I: A thermal shock semi-space problem

We consider a semi-space homogeneous thermoelectric medium occupying the region y ≥ 0 with quiescent initial state. A thermal shock is applied to the boundary plane y = 0 in the form

$$ \Uptheta (0, t) = \Uptheta_{o} \,H(t), $$
(36)

where, \( \Uptheta_{o} \) is a constant and the boundary plane y = 0 is taken to be a fixed plane, i.e.

$$ u (0,t) = 0. $$
(37)

Since the solution is unbounded at infinity, the initial conditions should be so adjusted that the infinite terms are eliminated.

We now apply the state space approach described above to this problem. The two components of the transformed initial state (0, s) are known, namely,

$$ \bar{\Uptheta} (0,s) = \frac{{\Uptheta_{o}}}{s},$$
(38)

which follows from (35) and

$$ \bar{u} (0,s) = 0, $$
(39)

which follows from (36).

To obtain the two remaining components \( \bar{u}^{\prime } (0,s) \) and \( \bar{\theta}^{\prime } (0,s)\) we substitute y = 0 in both sides of (28) and in performing the necessary matrix operations, we obtain a system of linear algebraic equations in the two unknowns \( \bar{u}^{\prime } (0,s) \) and \( \bar{\Uptheta }^{\prime } (0,s) , \) whose solution gives

$$ \bar{u}^{\prime } (0,s) = \frac{{aK_{o} \Uptheta_{o} }}{{s\left( {k_{1} k_{2} + a} \right)}}, $$
(40)
$$ \bar{\Uptheta }^{\prime } (0,s) =-\frac{{\Uptheta_{o} k_{1} k_{2} \left( {k_{1}+ k_{2} } \right)}}{{s\left( {k_{1} k_{2} + s + M} \right)}}. $$
(41)

Inserting the values from (38) to (41) into the right-hand side of (28), we obtain upon using (32)

$$ \bar{\Uptheta }\,({\kern 1pt} y,s{\kern 1pt} )\, = \,\frac{{\Uptheta _{o} }}{{s\,}}\left[ {\frac{{k_{2} {\kern 1pt} \left( {k_{1}^{2} \; - s - M} \right)\,{\text{e}}^{{ - k_{1} y}} \; - \;k_{1} \;\left( {k_{2}^{2} \; - s - M\,} \right)\,{\text{e}}^{{ - k_{2} y}} }}{{{\kern 1pt} \left( {k_{1} \, - \,k_{2} {\kern 1pt} } \right)\left( {k_{1} k_{2} + s + M} \right)}}} \right] $$
(42)
$$ \bar{u}(y,s) =-\frac{{a\,K_{o} \Uptheta_{o} }}{{s \left({k_{1}-k_{2} } \right)\left( {k_{1} k_{2} + a} \right)}}\left[{{\text{e}}^{{-k_{1} y}}-{\hbox{e}}^{-k_{2} y}} \right].$$
(43)

In non-dimensional form, the expression for the skin-friction component τ in the main flow is:

$$ \bar{\tau} = \left( {\frac{{\partial \bar{u}}}{{\partial y}}} \right)_{y = 0} = \frac{{a K_{o} \Uptheta_{o} }}{{s\left( {k_{1} k_{2} + a} \right)}} .$$
(44)

Problem II: A problem of a layer media

We consider a thermoelectric fluid occupying the region 0 ≤ y ≤ Y bounded by two parallel walls in the presence of a transverse magnetic field applied externally. Initially both the plates and fluid are assumed to be at rest. Let us suddenly impart a constant velocity U to the lower plate in its own plane in the presence of magnetic field.

The mechanical boundary conditions can be written as

$$ u(0, t) = U,\quad {\text{or}}\quad \bar{u}(0,s) = \frac{1}{s}, $$
(45)
$$ u(Y,t) = 0,\quad {\text{or}}\quad \bar{u}(Y,s) = 0. $$
(46)

The thermal boundary conditions are assumed to be

$$ \Uptheta (0,t) = \Uptheta_{o} H(t)\quad{\text{or}}\quad \bar{\Uptheta } (0,s) = \frac{{\mathop \Uptheta_{o} }}{s}, $$
(47)
$$ \frac{{\partial \Uptheta (Y,t)}}{\partial y} = 0\quad {\text{or}}\quad \frac{{\partial \bar{\Uptheta}(Y,s)}}{\partial y} = 0. $$
(48)

Condition (47) means that the plate y = 0, is acted on by a constant thermal shock at time t = 0, while condition (48) signifies that the plate y = Y, is thermally insulated.

Equations (44) and (47) give two components of the initial state vector \( \bar{\user2{G}} \)(0, s). To obtain the remaining two components, we use (28) between y = 0 and y = Y to obtain the following two simultaneous linear equations:

$$ l_{23} (Y,s)\,\,\,\bar{\Uptheta }^{\prime } (0,s)\,\, + l_{24} (Y,s)\,\,\,\bar{u}^{\prime } (0,s)\, = \,-\frac{{\Uptheta_{o} }}{s}l_{21} (Y,s)\,\,- \,\frac{1}{s}l_{22} (Y,s), $$
$$ {\user2{l}}_{33} (Y,s)\bar{\Uptheta }^{\prime } (0,s)\ + {\user2{l}}_{34} (Y,s)\bar{u}^{\prime } (0,s)=-\frac{{\Uptheta_{o} }}{s}{\user2{l}}_{31} (Y,s)-\,\frac{1}{s}{\user2{l}}_{32} (Y,s). $$

The solution of these equations gives

$$ \begin{aligned} \bar{\Uptheta }^{\prime } (0,s)\, =& \frac{{\Uptheta_{o} a(k_{1}^{2}-k_{2}^{2} )}}{\Upgamma s}\left( {\sinh k_{1} Y\sinh k_{2} Y} \right) \hfill \\ &+ \frac{{k_{1} k_{2} b}}{\Upgamma s} \times \left( {k_{1} \cosh k_{2} Y \sinh k_{1} Y-k_{2} \cosh k_{1} Y \sinh k_{2} Y} \right) \hfill \\ \end{aligned} $$
(49)
$$ \begin{aligned} \,\bar{u}^{\prime } (0,s) =& \frac{{\Uptheta_{o} a K_{o} }}{\Upgamma s} \left( {k_{2} \sinh k_{1} Y \cosh k_{2} Y-k_{1} \sinh k_{2} Y\,\cosh k_{1} Y} \right) \hfill \\ &+ \frac{{k_{1} k_{2} (k_{1}^{2}-k_{2}^{2} )}}{\Upgamma \,s}\,\left( {\cosh k_{1} Y\cosh k_{2} Y} \right) \hfill \\ \end{aligned} $$
(50)
$$ \Upgamma = k_{1} \left( {k_{2}^{2}-a} \right)\,\cosh k_{1} Y\,\sinh k_{2} Y\,-\,k_{2} \left( {k_{1}^{2}-a} \right)\,\cosh k_{2} Y\,\sinh k_{1} Y. $$

Inserting the values from (45) to (50) into the right-hand side of (28), we obtain upon using (32)

$$ \begin{aligned} \overline{\Uptheta } (y,s)\, =& \,\left( {\frac{{\Uptheta_{o} k_{1} \left( {k_{2}^{2}-a} \right)}}{\Upgamma \,s}\sinh k_{2} Y-\frac{{k_{1} k_{2} b}}{\Upgamma \,s}\,\,\,\,\cosh \,k_{2} Y} \right)\,\,\,\,\times \cosh \,k{}_{1}(Y - y) \\ &- \,\,\,\left( {\frac{{\Uptheta_{o} k_{2} \left( {k_{1}^{2} - a} \right)}}{\Upgamma \,s}\,\,\,\,\sinh k_{1} Y -\frac{{k_{1} k_{2} b}}{\Upgamma \,s}\,\,\cosh \,k_{1} Y} \right)\times \cosh \,k{}_{2}(Y - y), \\ \end{aligned} $$
(51)
$$ \begin{aligned} \bar{u}(y,s)\, =& \,\left( {\frac{{aK_{o} \,\Uptheta_{o} \,}}{\Upgamma \,s}\,\,\sinh k_{2} Y\,\,\, - \,\,\,\,\frac{{k_{2} \left( {k_{1}^{2} - a} \right)}}{\Upgamma \,s}\,\,\cosh k_{2} Y} \right)\,\,\,\times \sinh k_{1} \,(Y - y) \\ &- \,\,\,\,\left( {\frac{{aK_{o} \,\Uptheta_{o} \,}}{\Upgamma \,s}\,\,\sinh k_{1} Y\,\,\,-\,\,\,\,\frac{{k_{1} \left( {k_{2}^{2} - a} \right)}}{\Upgamma \,s}\,\,\cosh k_{1} Y} \right)\,\,\,\times \sinh k_{2} \,(Y-y). \\ \end{aligned} $$
(52)

Problem (III): Plane distribution of heat sources

We assume that there is a plane distribution of continuous heat sources located at the plate y = 0. The intensity of the heat sources is thus given by

$$ Q(y,t) = Q_{o} \,H(t)\delta (y), $$

where Q o is a constant and δ(y) is Dirac’s delta function. Taking Laplace transform, we obtain

$$ \bar{Q}(y,s) = Q_{o} \frac{\delta (y)}{s}. $$
(53)

We shall now proceed to obtain the solution of the problem for the region y ≥ 0. The solution for the other region is obtained by replacing each y by –y.

Evaluating the integral in  (27) using the integral properties of the Dirac delta function, we obtain

$$ \bar{\user2{G}}(y,s) = \;L(y,s)\,[\bar{\user2{G}}(0,s)\; + \;H(s)], $$
(54)

where

$$ {\user2{B}}(y,s) = - \frac{{Q_{o} \beta }}{4s}\, \, \,\left[ \begin{array}{l} \frac{{k_{1} k_{2} + s + M}}{{k_{1} + k_{2} }} \hfill \\ 0 \hfill \\ 1 \hfill \\ \frac{{K_{o} }}{{k_{1} + k_{2} }} \hfill \\ \end{array} \right]. $$

Equation (54) expresses the solution of the problem in the Laplace transform domain in terms of the vector H(s) representing the applied heat source and the vector \( \bar{\user2{G}}(0,s) \) representing the conditions at the plane source of heat. In order to evaluate the components of this vector, we note first that due to the symmetry of the problem, the temperature is a symmetric of y while the velocity is anti-symmetric. It thus follows that

$$ u\,(0, t) = 0\quad {\text{or}}\quad \bar{u} \, (0,s)\;\, = 0. $$
(55)

Gauss’s divergence theorem will now be used to obtain the thermal condition at the plane source. We consider a short cylinder of unit base whose axis is perpendicular to the plane source of heat and whose bases lie on opposite sides of it. Taking limits as the height of the cylinder tends to zero and noting that there is no heat flux through the lateral surface, upon using the symmetry of the temperature field we get

$$ {\user2{q}}\,(0,t) = \;\frac{{Q_{o} }}{2}\,H(t)\,\quad \;{\text{or}}\quad \, \bar{\user2{q}}(0,s) = \;\frac{{Q_{o} }}{2s}. $$
(56)

Using Fourier’s law of heat conduction in the non-dimensional form, namely

$$ \bar{\user2{q}} = -\frac{{\left( {\left[ {1 + ZT_{o} } \right]\;\bar{\Uptheta }^{\prime } \; + \Uppi_{o} \;\bar{u}} \right)}}{{1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}s^{\alpha } }} $$
(57)

we obtain the condition

$$ \Uptheta^{\prime } (0,s) = -\frac{{\beta \,Q_{o} }}{2s}.\; $$
(58)

Equations (55) and (58) give two components of the vector \( \bar{\user2{G}}\left( {0, s} \right) \). In order to obtain the remaining two components, we substitute y = 0 on both sides of  (54) obtaining a system of linear equations whose solution gives

$$ \bar{\Uptheta }(0,s) = \;\frac{{\beta {\kern 1pt} Q_{o} (k_{1} k_{2} + s + M)}}{{2{\kern 1pt} s{\kern 1pt} k_{1} k_{2} (k_{1} + k_{2} )}}, $$
(59)
$$ \bar{u}^{\prime } (0,s) = \;\frac{{\beta {\kern 1pt} {\kern 1pt} K_{o} {\kern 1pt} {\kern 1pt} Q_{o} }}{{2{\kern 1pt} s{\kern 1pt} \left( {k_{1} + k_{2} } \right)}}. $$
(60)

As before, we have suppressed the positive exponential terms appearing in the entries of L(y, s). Substituting the above values in the right-hand side of (54), we obtain

$$ \bar{\Uptheta }\,({\kern 1pt} y,s{\kern 1pt} )\, = \,\frac{{\beta {\kern 1pt} {\kern 1pt} Q_{o} }}{{2{\kern 1pt} s({\kern 1pt} k_{1}^{2} \,-\,k_{2}^{2} {\kern 1pt} )\,}}\times \left[ {\frac{{k_{1}^{2} \;-s-M}}{{k_{1} }}\,{\hbox{e}}^{{ \pm k_{1} y}}-\frac{{k_{2}^{2} \;-s-M}}{{k_{2} }}\,{\hbox{e}}^{{ \pm k_{2} y}} } \right]\;, $$
(61)
$$ \bar{u}\,({\kern 1pt} y,s{\kern 1pt} )\, = \,\frac{{ \pm \,\beta {\kern 1pt} {\kern 1pt} K_{o} {\kern 1pt} {\kern 1pt} Q_{o} }}{{2{\kern 1pt} s{\kern 1pt} \times \left( {k_{1}^{2} \,-\,k_{2}^{2} } \right)\,}}\left[ {\,{\hbox{e}}^{{ \pm k_{1} y}}-{\hbox{e}}^{{ \pm k_{2} y}} } \right].\; $$
(62)

In the above equations the upper (plus) sign indicates the solution in the region y < 0, while the lower (minus) sign indicates the region y ≥ 0, respectively.

5 Numerical inversion of the Laplace transforms

In order to invert the Laplace transform in the above equations, we adopt a numerical inversion method based on a Fourier series expansion [36]. In this method, the inverse g(t) of the Laplace transform \( \bar{g}\,\left( s \right) \) is approximated by the relation

$$ g\,(t) = \frac{{{\hbox{e}}^{{c^{*}t}} }}{{t_{1} }}\,\,\;\left[ {\frac{1}{2}\bar{g}\,\left( {c^{*} } \right) + \text{Re} \,\,\left( {\;\sum\limits_{k = 1}^{N} {\exp \left( {\frac{{i\,k{\kern 1pt} \Uppi t}}{{t_{1} }}\,} \right)} \;\times\bar{g}\,\left( {c^{*} + \frac{{i\,k{\kern 1pt} \Uppi }}{{t_{1} }}\,} \right)} \right)} \right]\,,\quad \quad 0 \le t \le 2{\kern 1pt} t_{1} \,, $$
(63)

where c * is an arbitrary constant greater than all the real parts of the singularities of g(t) and N is sufficiently large integer chosen such that,

$$ {\hbox{e}}^{{c^{*} t}} \text{Re} \;\left[ {\exp \left( {\frac{{i\,N\pi t}}{{t_{1} }}\,} \right)\;\bar{g}\,\left( {c^{*} + \frac{{i\,N \pi }}{{t_{1} }}} \right)\,\;} \right] \le \,\;\varepsilon , $$
(64)

where ε is a prescribed small positive number that corresponds to the degree of accuracy required.

Using the numerical procedure cited, to invert the expressions of temperature, velocity and microrotaion, fields in Laplace transform domain.

6 Numerical results and discussion

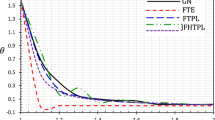
The investigation of the effect of the fractional derivative parameter α (0 < α < 1) and the thermoelectric coefficients are named for Seebeck coefficient K o and Peltier coefficient Π o as well as the efficiency of a thermoelectric figure of merit ZT o on the flow of thermoelectric fluid over the boundaries, in the presence of magnetic field has been carried out in the preceding sections. The computations were performed for a value of time, namely, t = 1. This enables us to represent the typical numerical results in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, for the temperature Θ, velocity component u and heat flux for various values of the parameters. The graphs show curves predicted by the different theories of thermoelectric MHD. In these figures, continues lines represent the solution corresponding to using the classical Fourier equation of heat conduction F-Law, (\( \, \alpha = 0,\;\tau_{o} = 0 \)) and dotted lines represent the solution corresponding to Cattaneo theory GF-Law, \( \alpha = 1.0,\;\tau_{o} = 0.02 \), while broken lines represent the solution corresponding to using fractional Fourier equation of heat conduction FF-Law, (\( 0 < \alpha < 1,\;\tau_{o} = 0.02 \)).

Fig. 1
figure 1

Dependence of temperature on distance for different theories in problem

Full size image
Fig. 2
figure 2

Dependence of temperature on distance for different values of fractional order in problem I

Full size image
Fig. 3
figure 3

A plot of the temperature as a function of the figure-of-merit for several thermoelectric fluids in problem I

Full size image
Fig. 4
figure 4

A plot of the temperature as a function of the Seebeck coefficient for different values of Peltier coefficient in Problem I

Full size image
Fig. 5
figure 5

A plot of the temperature as a function of the Peltier coefficient for different values of thermoelectric figure-of-merit in problem I

Full size image
Fig. 6
figure 6

A plot of the temperature as a function of fractional order α for several thermoelectric fluids

Full size image
Fig. 7
figure 7

Dependence of velocity on distance for different theories in problem II

Full size image
Fig. 8
figure 8

A plot of the temperature for different values of thermoelectric figure-of-merit in problem III

Full size image
Fig. 9
figure 9

Dependence of velocity on distance for different theories in problem III

Full size image
Fig. 10
figure 10

A plot of the heat flux for several thermoelectric fluids with different values of thermoelectric figure of merit in problem III

Full size image

Hence we conclude with following points:

  1. i.

    In all figures, it is noticed that the fractional order α has a significant effect on all fields.

  2. ii.

    It is noticed that all the waves reach the steady state depending on the value the fractional order α.

  3. iii

    The important phenomenon observed in all computations is that the solution of any of the considered functions vanishes identically outside a bounded region of space surrounding the heat source at a distance from it equal to y *(t); say y*(t) is a particular value of y depending only on the choice of t and is the location of the wave front. This demonstrates clearly the difference between the solution corresponding to using classical Fourier heat equation F-Law, (\( \alpha = 0,\;\tau_{o} = 0 \)) and to using the generalized Fourier case GF-Law, (\( \alpha = 1.0,\;\tau_{o} = 0.02 \)). In the first and older theory the waves propagate with infinite speeds, so the value of any of the functions is not identically zero (though it may be very small) for any large value of y. In non-Fourier theory the response to the thermal and mechanical effects does not reach infinity instantaneously but remains in a bounded region of space given by 0 < y < y *(t) for the semi space problem and by \( {\rm Min}\left( {0,y^{*} (t) - c} \right) < y < y + y^{*} (t)\) for the whole space problem.

  4. iv

    In Figs. 1 and 2, we notice that the temperature increment in the fractional order theory FF-Law, (\( 0 < \alpha < 1,\;\tau_{o} = 0.02 \)) is continuous function, which means that the particles transport the heat to the other particles easily and this makes the decreasing rate of the temperature greater than the other ones. In the generalized theory GF-Law, (\( \alpha = 1.0,\;\tau_{o} = 0.02 . \)) the thermal waves exhibit a jump discontinuity at y = 3.75, but cut the y-axis rapidly than the other ones [37] as in Figs. 1 and 8.

  5. V.

    Figure 3 presents some data on the temperature as a function of figure-of- merit of various thermoelectric fluids. We notice that the efficiency of a thermoelectric material figure-of-merit is proportional to the temperature of the fluid particles [38, 39].

  6. Vi.

    The Seebeck and Peltier effects are shown to be closely related within the new thermodynamic model applied recently to the quantitative theory of the Seebeck coefficient. In this work, the model was developed for the evaluation of the Seebeck and Peltier coefficients. The gradual decrease of temperature with Seebeck coefficients as shown in Fig. 4 has also been reported by Huston [40], Ambia et al. [41] and Patankar et al. [42]. In Fig. 5 we observe that the Peltier coefficient is proportional to the temperature at constant value of Seebeck coefficient. These results agree with the expectation by the first Thomson relation Π = ST [20].

  7. Vii.

    Figure 6 presents some data on the temperature as a function of fractional order α of various thermoelectric fluids.

  8. vii.

    The velocity distributions for the layer medium and the infinite space in the presence of heat sources are represented graphically in Figs. 7 and 9 for different values of fractional order α. From these figures we learn that the velocity of the fluid particles increase with the decrease of the fractional order α. This means that the boundary layer region around the surface dependence on the fractional order α.

  9. iX.

    Investigation of heat transfer involves measuring a heat flux on a surface along which a liquid moves [39]. It is notice from Fig. 10 that heat flux increases with decreasing the Prandtl number.

  10. X.

    The flow of fluids over the boundaries has many applications such as boundary-layer control. The study of unsteady boundary layers owes its importance to the fact that all boundary layers that occur in real life are, in a sense, unsteady. In recent years, the requirements of modern technology have stimulated interest in fluid-flow studies, which involve the intersection of several phenomena. One such study is related to the effects of free convection flow through a porous medium, which play an important role in agriculture, engineering, petroleum industries, and heat transfer [43].

7 Conclusions

  1. (i)

    The main goal of this work is to introduce a new mathematical model for Fourier law of heat conduction with time-fractional order and includes the thermoelectric figure-of-merit. According to this new theory, we have to construct a new classification for materials according to their fractional parameter α where this parameter becomes a new indicator of its ability to conduct heat in conducting medium. This model enables us to improve the efficiency of a thermoelectric material figure-of-merit according to the choice of suitable values of fractional derivative order α. The result provides a motivation to investigate conducting thermoelectric materials as a new class of applicable thermoelectric fluids.

  2. (ii)

    The importance of state-space analysis is recognized in fields where the time behavior of any physical process is of interest [1]. The state-space approach is more general than the classical Laplace and Fourier transform techniques. Consequently, state space is applicable to all systems that can be analyzed by integral transforms in time, and is applicable to many systems for which transform theory breaks down [44].

  3. (iii)

    The flow of fluids over the boundaries has many applications such as boundary-layer control. The study of unsteady boundary layers owes its importance to the fact that all boundary layers that occur in real life are, in a sense, unsteady. In recent years, the requirements of modern technology have stimulated interest in fluid-flow studies, which involve the intersection of several phenomena. One such study is related to the effects of free convection flow through a porous medium, which play an important role in agriculture, engineering, petroleum industries, and heat transfer.

  4. (iv)

    Experimental studies confirmed that the one-dimensional model could be used for heat calculation in fluids over the boundaries.