1 Introduction

Thermophoresis is a phenomenon by which sub micrometer sized particles suspended in a non isothermal gas acquires a mean speed relative to the gas in the direction of decreasing temperature. It is a mechanism for the capture of particles on cold surfaces, being especially important for submicron particles since the thermophoretic velocity is relatively independent of particle size. This pheomenon has got outstanding importance in vast number of applications. A few of them are: in determining exhaust gas particle trajectories from combustion devices, in studying the particulate material deposition on turbine blades. Also this has been sited as a cause for the deposition of particulate matter on heat exchange surfaces with the attendant reduction of the heat transfer coefficient. It is an established fact that thermophoresis is the dominant mass transfer mechanism in the modified chemical vapor deposition (MCVD) process used in the fabrication of optical fiber performs. Thermophoresis is also significant in view of its relevance to postulated accidents by radioactive particle deposition in nuclear reactors.

When an impure gas is bounded by a solid surface, a boundary layer will develop, and energy and momentum transfer gives rise to temperature and velocity gradients. Mass transfer caused by gravitation, molecular diffusion, eddy diffusion and inertial impact results in deposition of suspended components onto the surface.

Transport phenomenon involving the motion of small particles suspended in gaseous media and their deposition on immersed or containment solid surfaces occur often in industry and in nature. In variety of applications, there is a need to predict the transport rates of aerosol particles. The thermophoretic velocity is relatively independent of particle size, hence this phenomenon is used in air cleaning and aerosol sampling devices. The detailed study regarding practical applications of thermophoretic phenomenon can be found in [8, 10].

Derjaguin et al. [7] studied measurement of the coefficient of thermal slip of gases and thermophoresis velocity of large sized aerosol particles. Further, experimental verification of the theory, ‘Thermophoresis of aerosol particles’ was reported by Derjaguin et al. [6]. A paper by Epstein et al. [9] deal with thermophoretic deposition in natural convection flow from a vertical plate. But the analysis was considered for the cold surface. Garg and Jayaraj [11] analyzed numerically the thermophoretic deposition of small particles due to impingement of a laminar slot jet on an inclined plate using an implicit finite difference scheme more discussions and applications of thermophoresis can be found in [12, 13]. The analysis was done for the cold, hot and adiabatic plate conditions. The study of thermophoresis particle deposition on a vertical plate was extended to porous medium by Chamkha and Pop [4]. Chamkha et al. [5] studied thermophoresis free convection from a vertical cylinder embedded in a porous medium. The governing partial differential equations are transformed into a set of non similar equations and they are solved using an implicit finite difference method.

Study of convective transport in porous media has become an interesting topic due to its enormous applications in geothermal reservoirs, thermal insulation engineering, packed bed catalytic reactors and heat storage beds. The book by Nield and Bejan [15] provides more discussions and applications of convective transport in porous media. Mixing and recirculation of local fluid streams occur as the fluid moves through tortuous paths in packed beds. This hydrodynamic mixing of fluid at pore level causes thermal and solutal dispersion in porous medium. This becomes more considerable for moderate and fast flows. Detailed discussion and literature survey is available in Murthy [14].

In industrial and chemical engineering processes which involves multi component fluid, concentrations vary from point to point resulting in mass transfer. Energy flux can be generated not only by temperature gradient but also by concentration gradient as well. The energy flux caused by concentration gradient is called the Dufour effect and the same by temperature gradient is called the Soret effect. These effects are very significant when the temperature and the concentration gradients are high. The importance of these effects in convective transport in clear fluids has been studied by Bergaman and Srinivasan [2], Zimmerman et al. [19].

Heated jets or diffusion flames created by blowing combustible gas from a vertical pipe are controlled by forced convection in the initial region and by buoyancy forces far from the jet or pipe exist. Industrial smokestacks usually have a significant momentum flux to assist the initial rise of the contaminant plume. The simplest physical model of such a flow is two-dimensional laminar flow along a vertical flat plate. Recent applications of this model can be found in the area of reactor safety, combustion flames and solar collectors as well as building energy conservation.

Bourich et al. [3] studied analytically and numerically the Soret effect on the onset of convection in a vertical porous layer subjected to uniform heat flux. The influence of Soret and Dufour effects on flow field in free convection boundary layer from a vertical surface embedded in a Darcian porous medium has been studied by Postelinicu [16], Anghel et al. [1]. Mixed convection in a fluid saturated porous medium under the influence of viscous dissipation and thermophoresis has been discussed by Seddeek [18]. Recently, Postelnicu [17] has analyzed the effect of thermophoresis particle deposition in free convection boundary layer from a horizontal flat plate embedded in a porous medium. But, the influence of Soret and Dufour effects were not considered. The Soret, Dufour effects and thermophoresis particle deposition becomes more significant when the concentration gradients, temperature gradients are high. Also, the inertial effect, dispersion effects has a significant effect on convective transport in porous medium. Certainly, the combined effect of these parameters have large impact on heat and mass transfer rates. Hence in this paper we aim at analyzing thermophoresis particle deposition in free convection from a vertical plate embedded in a fluid saturated non-Darcy porous medium under the influence of Soret, Dufour, and dispersion effects.

2 Governing equations

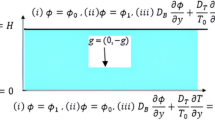
Free convection heat and mass transfer from a vertical plate embedded in a fluid saturated non-Darcy porous medium has been considered. The wall is maintained at constant temperature and concentration T w and C w , respectively. The ambient medium temperature and concentration are T ∞ and C ∞, respectively. The X-axis is taken along the plate and the Y-axis is normal to it. We assume that the fluid and the porous medium have constant physical properties. The fluid flow is moderate and the permeability of the medium is low so that the Forchheimer flow model is applicable. With the Boussinesq approximation, the governing equations for the boundary layer flow from the wall to the fluid saturated porous medium can be written as:

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0 $$
(1)
$$ U + \frac{c\sqrt{K}}{\nu}U^{2} = \frac{Kg}{\nu}[\beta_{T} (T - T_{\infty}) + \beta_{C} (C - C_{\infty})] $$
(2)
$$ U\frac{\partial T}{\partial X} + V\frac{\partial T}{\partial Y} = \frac{\partial}{\partial Y}\left(\alpha_{e} \frac{\partial T}{\partial Y}\right) + \frac{Dk_{T}}{C_{s} C_{P}}\frac{\partial^{2} C}{\partial Y^{2}} $$
(3)
$$ U\frac{\partial C}{\partial X} + V\frac{\partial C}{\partial Y} + \frac{\partial}{\partial Y}(Cv_{t}) = \frac{\partial}{\partial Y}{\left(D_{e} \frac{\partial C}{\partial Y} \right)} + \frac{Dk_{T}}{C_{s} C_{P}}\frac{\partial^{2} T}{\partial Y^{2}} $$
(4)

along with the boundary conditions

$$ Y = 0, \quad V = 0, \quad T = T_{w}, \quad C = C_{w} $$
(5)
$$ Y \to \infty, \quad U \to 0, \quad T \to T_{\infty}, \quad C \to C_{\infty} $$
(6)

Here U and V are the velocity components along X and Y directions, T is the temperature, C is concentration, c is the inertial coefficient, K is the permeability constant, β T , β C are the coefficients of thermal and solutal expansions, ν is the kinematic viscosity, ρ is the density, g is the acceleration due to gravity, α e is the effective thermal diffusivity and D e is the solutal diffusivity. The thermal and solutal dispersion diffusivities can be written as α e = α + γdU, D e = D + ξdU where γ and ξ are coefficients of thermal and solutal dispersions, respectively, α and D are constant thermal and molecular diffusivities, respectively. k T is the thermal diffusion ratio, C s is concentration susceptibility, C P is the specific heat at constant pressure.

The temperature gradient established in the thermal boundary layer drives the particle either towards the plate where they get deposited or away from the plate thereby forming a critical layer adjacent to the plate. The velocity acquired by the small particles relative to the gas velocity is related to the temperature gradient in the flow field is given by

$$ {v}_{t} = - k(\nu /T)\nabla T $$
(7)

The thermophoretic constant k in the expression of the thermophoretic velocity v t depends upon the regime of the flow. In most of the cases the value of this constant k lies between 0.25 and 1.25. Here we assume that the thermophoretic constant k is independent of temperature. Due to the boundary layer behavior the temperature gradient \(\frac{\partial T}{\partial Y}\) is much larger than \(\frac{\partial T}{\partial X}.\) From Eq. (7) it follows that the component of v t normal to the plate is given by \({v}_{t} = - k(\nu /T)\frac{\partial T}{\partial Y}.\) It is assumed that in the absence of thermophoresis the particles move with the fluid at the local fluid velocity. The Eqs. (1–4) are transformed into ordinary differential equations (8–10) with the dimensionless numbers and similarity parameters defined in the paper by Chamkha and Pop [4].

$$ f^{\prime\prime} + 2Ff^{\prime} f^{\prime\prime} = \left(\theta^{\prime} + N\phi^{\prime} \right) $$
(8)
$$ \theta^{\prime\prime} + \frac{1}{2}f\theta^{\prime} + Ra_{\gamma} (f^{\prime} \theta^{\prime\prime} + f^{\prime\prime} \theta^{\prime}) + D_{f} \phi^{\prime\prime} = 0 $$
(9)
$$ \begin{aligned} & \phi^{\prime\prime} + \frac{Le}{2}f\phi^{\prime} + LeRa_{\xi} (f^{\prime} \phi^{\prime\prime} + f^{\prime\prime} \phi^{\prime}) + \frac{Lek\Pr}{N_{t} + \theta}[\theta^{\prime} \phi^{\prime} + \phi \theta^{\prime\prime} - \frac{\phi}{N_{t} + \theta}\theta^{\prime 2} ] + S_{r} Le\theta^{\prime\prime} = 0 \end{aligned} $$
(10)

The boundary conditions are

$$ \eta = 0:f = 0,\quad \theta = 1,\quad \phi =1 $$
(11)
$$ \eta \to \infty :\theta \to 0,\quad \phi \to 0,\quad f^{\prime} \to 0 $$
(12)

In the above \(F = \left(\frac{c{\sqrt K}\,Kg\beta_{T} \theta_{w}}{\nu^{2}}\right)\) is the inertial Parameter, Ra γ = γRa d , Ra ξ = ξRa d represents thermal and solutal dispersion, respectively, \(Ra_{d} = \frac{Kg\beta_{T} \theta_{w} d}{\alpha \nu}\) is the pore diameter dependent Rayleigh number, \(Le = \frac{\alpha}{D}\) is the diffusivity ratio (Lewis number), \(N = \frac{\beta_{C} \phi_{w}}{\beta_{T} \theta_{w}}\) is the buoyancy ratio, \(V_{t} = (\frac{- k\Pr}{N_{t} + \theta})\frac{\partial \theta}{\partial y}\) is the thermophoretic velocity, \(N_{t} = \frac{T_{w} - T_{\infty}}{T_{\infty}}.\) HereD f , S r are the non-dimensional parameters representing Dufour and Soret effect given by \(D_{f} = \frac{Dk_{T} \phi_{w}}{C_{s} C_{p} \alpha \theta_{w}}, \quad S_{r} = \frac{Dk_{T} \theta_{w}}{C_{s} C_{p} \alpha \phi_{w}}.\)

The parameter N > 0 represents the aiding buoyancy and N < 0 represents the opposing buoyancy. The heat transfer and mass transfer coefficient in their non-dimensional form are written as

$$ Nu_{x} /Ra_{x}^{1/2} = - [1 + Ra_{\gamma} f^{\prime} (0)]\theta^{\prime} (0) $$
(13)
$$ Sh_{x} /Ra_{x}^{1/2} = - [1 + Ra_{\xi} f^{\prime} (0)]\phi^{\prime} (0) $$
(14)

3 Results and discussion

The ordinary differential Eqs. (8–10) along with the boundary conditions (11, 12) are integrated by giving appropriate initial guess values for f′(0), θ′(0) and ϕ′(0) to match the values with the corresponding boundary conditions f′(∞), θ′(∞) and ϕ′(∞), respectively. Nag software (DO2HAEF routine) is used for integrating the corresponding first order system of equations and for shooting and matching the initial boundary conditions. The integration length η∞ varies with parameter values and it has been chosen suitably every time such that the boundary conditions at the outer edge of the boundary layer are satisfied. The results obtained here are accurate up to fourth decimal place. Extensive calculations have been performed with different values of parameters to obtain the flow, temperature, concentration fields inside the boundary layer. With Ra γ = 0, Ra ξ = 0, F = 0, D f = 0, S r = 0 the present problem reduces to effect of thermophoresis particle deposition in free convection boundary layer from a vertical plate embedded in a Darcy porous medium’ studied by Chamkha [4].

Of interest in this problem are the non-dimensional concentration profiles ϕ(η) and wall thermophoretic deposition velocity V tw given by \(V_{tw} = \frac{- k\Pr}{1 + N_{t}}\theta^{\prime} (0).\) Hence the effect of the parameters D f  and  S r on, the concentration distribution, wall thermophoretic deposition velocity V tw , non-dimensional heat transfer coefficient and non-dimensional mass transfer coefficient is studied in detail for different values of the parameters in both aiding as well as opposing buoyancies.

The concentration distribution for fixed values of D f , S r , Le are plotted in the Figs. 2 and 3. In Fig. 2, we observe that the concentration distribution is more when S r = 10 than when S r = 3. This shows that the concentration distribution is more for higher values of S r . Also it clearly indicates that the concentration distribution is more when S r  = 10 than when D f = 10. Hence it implies that the concentration distribution is weakly dependent on the parameter D f . Figure 3 highlights the significance of Le and S r on concentration distribution. We notice that there is a relative rise in the concentration profile near the wall for the case Le = 100, S r = 15. This will give rise to a large wall concentration gradient, causing a high deposition on the surface. Also, it is seen that when Le = 0.3 the concentration distribution is greater, than when Le = 100. This reflects the combined effect of S r and Le on concentration distribution.

Fig. 1
figure 1

Schematic drawing of the problem

Full size image
Fig. 2
figure 2

Concentration distribution inside the boundary layer for different values of D f , S r

Full size image
Fig. 3
figure 3

Concentration distribution inside the boundary layer for different values of D f , S r , Le

Full size image

The influence of the parameters D f and S r on the wall thermophoretic deposition velocity V tw are well exhibited in Figs. 4 and 5. Even though the effect of these parameters is to increase the wall thermophoretic deposition velocity, the rate of increase depends on magnitude of several parameters. This is comprehensible from the figures [Fig. 4 (Le = 100, Ra γ = 3.2,Ra ξ = 0); Fig. 5 (Le = 100, Ra ξ = Ra γ = 0)] and Table 1. Also from both the figures it can be distinguished that the magnitude of V tw is more for lesser values of Le. Thus it makes certain that the wall thermophoretic deposition velocity is more sensitive to Le. For fixed values of Ra γ = 0, Ra ξ = 0, increase in F (Table 1) increases V tw . The same occurs when F = 0, Ra ξ = 0 and Ra γ is increased. But V tw decreases with increase in Ra ξ for F = 0, Ra γ = 0. Rate of change of thermophoretic velocity depends not only on D f , S r , Ra γ, Ra ξ, F but also on thermophoretic coefficient k. This is evident from Fig. 6 that with the increase of k, there is significant increase in thermophoretic velocity .

Fig. 4
figure 4

Effect of D f on wall thermophoretic deposition velocity for different values of Ra γ, Ra ξ, Le

Full size image
Fig. 5
figure 5

Effect of S r on wall thermophoretic deposition velocity for different values of Ra γ, Ra ξ, Le

Full size image
Table 1 Effect of F, Ra γ,Ra ξ on wall thermophoretic deposition velocity
Full size table
Fig. 6
figure 6

Effect of thermophoretic coefficient k on wall thermophoretic deposition velocity for different values of Ra γ, Ra ξ, Le

Full size image

The effect of k, D f and S r on heat and mass transfer is shown graphically in Figs. 7, 8, 9, 10, 11, and 12 and in Table 2. Even though increase in heat transfer and decrease in mass transfer with the increase of k is not evident from Figs. 7 to 8 except in the case Le = 100, Ra γ = 3.2, Ra ξ = 0, D f = 1.0, S r = 0 (Fig. 7), it is verified from the data (Table 2) that the non-dimensional heat transfer coefficient increases and non-dimensional mass transfer decreases. Therefore it is remarkable that for a particular combination Le, Ra γ, Ra ξ, D f , S r the effect of k is more pronounced. Transport phenomenon involving the motion of small particles suspended in gaseous media and their deposition on immersed or containment solid surfaces occur often in industry and in nature. The thermophoretic coefficient k is different for different fluids. It also varies as the properties of the fluids change. Hence the concentration distribution, heat and mass transfer rates changes. Also, it is seen that, the non-dimensional heat transfer coefficient reduces with the increase of N t where as the mass transfer coefficient increases (figure not enclosed).

Table 2 Effect of of D f , S r , k on non-dimensional heat transfer and mass transfer coefficient
Full size table
Fig. 7
figure 7

Variation of non-dimensional heat transfer coefficient with the variation of k

Full size image
Fig. 8
figure 8

Variation of non-dimensional mass transfer coefficient with the variation of k

Full size image

Heat transfer profiles increase with the increase of D f and S r (Figs. 9, 10; Table 2) and the amount of heat transfer from the plate to the medium is found to be notably higher for the case Le = 0.3 compared to that of the cases Le = 3 and Le = 100. Also, for all values of Le the magnitude of heat transfer is more when Ra γ = 3.2 in contrast with Ra ξ = 3.2. This shows the significance of Ra γ on heat transfer. From Fig. 11 marginal decrease in mass transfer with the increase of D f is clearly visible. Also it is observed that the magnitude of mass transfer is more when Le = 0.3, Ra ξ = 3.2, Ra γ = 0 compared to Le = 0.3, Ra ξ = 0, Ra γ = 3.2. But the circumstances happen to be different with the increase of S r , as evident from the Fig. 12. Mass transfer decreases in all the cases except in that of the case Le = 100, Ra γ = 3.2, Ra ξ = 0. Thus the analysis of the Figs. 7, 8, 9, 10, 11, and 12 reveal that the rate of heat transfer and mass transfer varies due to the complex interaction among several parameters.

Fig. 9
figure 9

Variation of non-dimensional heat transfer coefficient with the variation of D f

Full size image
Fig. 10
figure 10

Variation of non-dimensional heat transfer coefficient with the variation of S r

Full size image
Fig. 11
figure 11

Variation of non-dimensional mass transfer coefficient with the variation of D f

Full size image
Fig. 12
figure 12

Variation of non-dimensional mass transfer coefficient with the variation of S r

Full size image

Thus the rate of change of heat transfer, mass transfer and wall thermophoretic deposition velocity varies depending on Soret, Dufour, dispersion parameters and also according to the different values of k and N t . Thus the combined effect of all parameters is more important in determining more accurately the heat transfer and mass transfer rates.

4 Opposing buoyancy

The influence of the parameters D f  and  S r on concentration distribution and effect of D f on heat and mass transfer in the opposing buoyancy remains the same as in the case of aiding buoyancy. Increasing the opposing buoyancy decreases the concentration distribution and this is depicted in Fig. 13. Heat transfer decreases with the increase of S r and the same increases with D f (Fig. 14). But mass transfer decreases with the increase of both D f   and  S r (Fig. 15).

Fig. 13
figure 13

Concentration distribution inside the boundary layer for different values of S r in the opposing buoyancy

Full size image
Fig. 14
figure 14

Variation of non-dimensional heat transfer coefficient with the variation of D f , S r

Full size image
Fig. 15
figure 15

Variation of non dimensional mass transfer coefficient with the variation of D f , S r

Full size image

5 Conclusion

Similarity solution technique is used to analyze the thermophoresis effect on a vertical plate embedded in a non-Darcy porous medium under the influence of Dufour, Soret effects. The effect of the parameters D f   and  S r on concentration distribution, thermophoretic wall deposition velocity, heat transfer and mass transfer is analyzed for different values of dispersion parameters and Lewis number. It is worth mentioning that the parameter S r is more influential than the parameter D f in increasing the concentration distribution.

The effect of the parameters D f , S r N t and k is to increase the wall thermophoretic deposition velocity and this rate of increase depends on magnitude of several parameters. Wall thermophoretic deposition velocity increases with the increase of F, Ra ξ. But it decreases with the increase of Ra γ. This shows the considerable effect of F, Ra ξ, Ra γ on V tw .

The non-dimensional heat transfer coefficient decreases with the increase of N t where as the non-dimensional mass transfer coefficient increases. But this is different with the increase of k. That is the non-dimensional heat transfer coefficient increases and non-dimensional mass transfer decreases with the increase of k.

Rate of change of heat transfer, mass transfer and wall thermophoretic deposition velocity changes corresponding to different values of k, N t , D f , S r , F, Ra ξ, Ra γ. Thus the combined effect is of immense importance while determining accurately the heat transfer and mass transfer rates.