1 Introduction

Design of efficient thermal control systems is crucial in the development of advanced electronic equipment. However, heat transfer analysis of such systems is highly challenging to researchers in this area due to many constraints like limitations in space, reliability, power consumption, noise level, exposed area available for heat transfer, dielectric properties of cooling fluid and so on. The principal objective of the thermal control system of any electronic component is to maintain a relatively constant temperature, which should be below the maximum service temperature specified by the manufacturer. In spite of its many advantages, natural convection air-cooling can become inadequate for many applications due to the low heat transfer coefficient value and forced convection air-cooling may be required to maintain the desired temperatures and this is routinely done in many applications, as for example, in desk top computers.

The presence of temperature gradients in a fluid under the action of gravitational field always gives rise to natural convection currents and hence heat transfer by natural convection. For high values of heat flux transferred within the devices, there is a need to resort to forced convection heat transfer with the help of a fan or pump. The relative magnitudes of the inertia and buoyancy forces divide the mixed convection flow into three regimes, viz., forced convection dominant, mixed convection and free convection dominant regimes.

The convection heat transfer coefficient whether natural or forced, is a strong function of the fluid velocity. Heat transfer coefficients encountered in forced convection are much higher than those encountered in natural convection, because of higher fluid velocity. As a result, there is a general tendency to ignore natural convection in heat transfer analysis that involves forced convection, although natural convection always accompanies forced convection. The error involved in ignoring natural convection is negligible at high velocities, but it may be considerable when forced convection occurs at low velocities. The convection heat transfer coefficient is a strong function of Reynolds number in forced convection and Grashof number in natural convection and the importance of natural convection relative to the forced convection is given by Richardson number.

A forced or free convective flow can be either laminar or turbulent. Turbulent flow is highly irregular and exhibits random fluctuations in the flow quantities. The irregularity in the flow is manifested through complex variations of velocity, temperature and pressure with space as well as time. The occurrence of random fluctuations tends to increase the rates of mass, momentum and energy transport in turbulent flow. Improved turbulent mixing increases temperature gradients near the solid surface and thereby results in a higher heat transfer. High transfer rates of momentum, heat and species are practically the most important features of turbulent flows. It is in this context that studies on turbulent mixed convection heat transfer are becoming increasingly relevant. In this study, a numerical investigation has been carried out in the context of electronic equipment cooling. The study focuses on turbulent mixed convective flow and heat transfer around electronic components. An isothermal or constant heat flux approximation without considering wall thickness and thermal conductivity differences between the wall material (substrate) and heat sources, will not predict the temperature fields accurately. Hence, in the present study, uniform volumetric heat generation is considered in some portions of the wall with finite thickness, to make the analysis more realistic. A vertical plate or vertical parallel plate channel is a commonly encountered geometry in the analysis pertaining to electronic applications, since it closely simulates the cooling passages of a series of printed circuit boards (PCBs). Closely packed electronic components can be approximated as uniformly distributed heat sources attached to PCBs. With a two-dimensional analysis, it is possible to capture most of the thermal and flow characteristics, reasonably accurately, with less computational effort. Hence, a two-dimensional analysis is carried out in the present study, for the sake of simplicity.

Kuyper et al. [1], numerically, simulated natural convective flow of air in a differentially heated, inclined square cavity for both laminar and turbulent flows, in the range of Rayleigh numbers 104–1010. Velusamy et al. [2] numerically studied the interaction of surface radiation with turbulent natural convection of a transparent medium in a rectangular enclosure, covering a wide range of Rayleigh numbers and aspects ratios. They used the standard k-ɛ model to obtain the numerical results of Kuyper et al. [1] for turbulent equations. They used the boundary conditions of k = 0 and ɛ→∞ at the walls. Many investigators presented experimental results for mixed convection turbulent flows in various geometries [3–5]). Nakajima et al. [6] studied experimentally and numerically, the effect of buoyancy on turbulent heat transfer in combined free and forced flow. Inagaki and Komori [7] investigated the transport mechanism of turbulent mixed convection heat transfer between two uniformly heated vertical parallel plates. Anand et al. [8] numerically predicted the effect of wall conduction on free convection between asymmetrically heated vertical plates, for the case of uniform wall temperature. Their study revealed the effect of wall conduction on heat transfer, particularly at high Grashof numbers, low conductivity ratios, and high wall thickness to channel width ratios. A similar problem was numerically studied by Kim et al. [9] for the case of uniform heat flux. Lee et al. [10] used the fin approximation to solve for combined, conjugate convection with surface radiation. Gururaja Rao et al. [11] carried out a numerical investigation of conjugate laminar mixed convection with surface radiation from a vertical channel for symmetric and uniform volumetric heat generation.

Herwig [12], Balaji and Herwig [13] and Premachandran and Balaji [14] successfully employed the approach of asymptotic computational fluid dynamics (ACFD) to multimode heat transfer problems and concluded that it is an attractive option in the analysis of such problems in heat transfer. The studies of Gururaja Rao et al. [11] and Premachandran and Balaji [14] clearly demonstrated the effect of conjugate heat transfer from a vertical channel and horizontal channel, respectively, in the laminar regime. The present study intends to explore the effect of conjugate mixed convection heat transfer from a vertical channel with flush-mounted discrete heat sources in the turbulent regime and to obtain a correlation for T *max , for a wide range of parameters. The parameters that influence a conjugate heat transfer problem are Re s, Ri +, ratio of the thermal conductivities (k c/k f and k s/k f) and the aspect ratio (AR). When one looks at the literature on conjugate heat transfer, we can see that a dimensionless parameter that involves two scales, with one being the ratio of thermal conductivities and the other being the ratio of length scales characterizing conduction and convection, is usually used (see for example [15–18]). However, in this study, the thickness δ is fixed and whenever the spacing “S” changes, the Reynolds number also changes. Hence, in this work the ratio of thermal conductivities has been directly used as the parameter that characterizes conjugate convection. The number of parameters that influence the heat transfer rate is large and a full scale parametric study to develop a correlation for the maximum temperature of the heat sources will be extremely time consuming, for the turbulent flow regime. Hence, in this study ACFD is used to develop a correlation for T *max .

2 Mathematical formulation

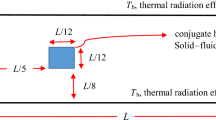
The geometry for the problem under consideration, along with the system of coordinates used, is shown in Fig. 1. The heat sources are equi-spaced along the left wall of the channel. The cooling medium considered is air. The outer boundaries of the channel walls are assumed to be perfectly insulated. The assumptions made are (1) the flow is incompressible and turbulent (2) fluid properties are constant except for density for which Boussinesq approximation is assumed to be valid and (3) conduction along the walls is one dimensional. As shown in Fig. 1, the flow enters the channel with uniform velocity and temperature profiles. The standard k-ɛ model is adopted for the prediction of turbulent fluxes due to its simplicity and successful application in turbulent buoyant flows [1, 2].

Fig. 1
figure 1

Schematic of the vertical channel with four flush-mounted discrete heat sources on left wall

Full size image

2.1 Governing equations

The Reynolds averaged Navier–Stokes (RANS) equations along with the energy equation in non-dimensional form are given by

  • continuity:

    $$ \frac{{\partial u^{*}}}{{\partial x^{*}}} + \frac{{\partial v^{*}}}{{\partial y^{*}}} = 0 $$
    (1)

  • x-momentum:

    $$ \frac{{\partial u^{*}}}{{\partial t^{*}}} + u^{*} \frac{{\partial u^{*}}}{{\partial x^{*}}} + v^{*} \frac{{\partial u^{*}}}{{\partial y^{*}}} = - \frac{{\partial p^{*}}}{{\partial x^{*}}} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial x^{*}}}{\left[ {2{\left({1 + \upsilon_{t}^{*}} \right)}{\left({\frac{{\partial u^{*}}}{{\partial x^{*}}}} \right)}} \right]} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial y^{*}}}{\left[ {{\left({1 + \upsilon_{t}^{*}} \right)}{\left({\frac{{\partial u^{*}}}{{\partial y^{*}}} + \frac{{\partial v^{*}}}{{\partial x^{*}}}} \right)}} \right]} $$
    (2)

  • y-momentum:

    $$ \frac{{\partial v^{*}}}{{\partial t^{*}}} + u^{*} \frac{{\partial v^{*}}}{{\partial x^{*}}} + v^{*} \frac{{\partial v^{*}}}{{\partial y^{*}}} = - \frac{{\partial p^{*}}}{{\partial y^{*}}} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial x^{*}}}{\left[ {{\left({1 + \upsilon_{t}^{*}} \right)}{\left({\frac{{\partial u^{*}}}{{\partial y^{*}}} + \frac{{\partial v^{*}}}{{\partial x^{*}}}} \right)}} \right]} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial y^{*}}}{\left[ {2{\left({1 + \upsilon_{t}^{*}} \right)}{\left({\frac{{\partial v^{*}}}{{\partial y^{*}}}} \right)}} \right]} + Ri^{+} T^{*} $$
    (3)

  • energy:

    $$ \frac{{\partial T^{*}}}{{\partial t^{*}}} + u^{*} \frac{{\partial T^{*}}}{{\partial x^{*}}} + v^{*} \frac{{\partial T^{*}}}{{\partial y^{*}}} = \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial x^{*}}}{\left[ {{\left({\frac{1}{{Pr}} + \frac{{\upsilon^{*}_{t}}}{{\sigma_{T}}}} \right)}{\left({\frac{{\partial T^{*}}}{{\partial x^{*}}}} \right)}} \right]} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial y^{*}}}{\left[ {{\left({\frac{1}{{Pr}} + \frac{{\upsilon_{t}^{*}}}{{\sigma_{T}}}} \right)}{\left({\frac{{\partial T^{*}}}{{\partial y^{*}}}} \right)}} \right]} $$
    (4)

  • Equation for turbulent kinetic energy

    $$ \frac{{\partial k^{*}}}{{\partial t^{*}}} + u^{*} \frac{{\partial k^{*}}}{{\partial x^{*}}} + v^{*} \frac{{\partial k^{*}}}{{\partial y^{*}}} = \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial x^{*}}}{\left[ {{\left({1 + \frac{{\upsilon_{t}^{*}}}{{\sigma_{k}}}} \right)}{\left({\frac{{\partial k^{*}}}{{\partial x^{*}}}} \right)}} \right]} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial y^{*}}}{\left[ {{\left({1 + \frac{{\upsilon_{t}^{*}}}{{\sigma_{k}}}} \right)}{\left({\frac{{\partial k^{*}}}{{\partial y^{*}}}} \right)}} \right]} + P_{k}^{*} + G_{k}^{*} - \varepsilon^{*} $$
    (5)

  • Equation for dissipation rate of turbulent kinetic energy

    $$ \begin{aligned} \frac{{\partial \varepsilon^{*}}}{{\partial t^{*}}} + u^{*} \frac{{\partial \varepsilon^{*}}}{{\partial x^{*}}} + v^{*} \frac{{\partial \varepsilon^{*}}}{{\partial y^{*}}}& = \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial x^{*}}}{\left[ {{\left({1 + \frac{{\upsilon_{t}^{*}}}{{\sigma_{\varepsilon}}}} \right)}{\left({\frac{{\partial \varepsilon^{*}}}{{\partial x^{*}}}} \right)}} \right]} + \frac{1}{{{Re}_{\rm s}}}\frac{\partial}{{\partial y^{*}}}{\left[ {{\left({1 + \frac{{\upsilon_{t}^{*}}}{{\sigma_{\varepsilon}}}} \right)}{\left({\frac{{\partial \varepsilon^{*}}}{{\partial y^{*}}}} \right)}} \right]}&\quad + {\left[ {C_{{\varepsilon 1}} {\left({P^{*}_{k} + C_{{\varepsilon 3}} G_{k}^{*}} \right)} - C_{{\varepsilon 2}} \varepsilon^{*}} \right]}\frac{{\varepsilon^{*}}}{{k^{*}}} \end{aligned} $$
    (6)

Where the functions P * k , G * k , υ * t and C ɛ3 are defined by the following relationships.

$$ \begin{aligned} P_{k}^{*} & = \frac{{\upsilon_{t}^{*}}}{{{Re}_{\rm s}}}{\left[ {2{\left({\frac{{\partial u^{*}}}{{\partial x^{*}}}} \right)}^{2} + 2{\left({\frac{{\partial v^{*}}}{{\partial y^{*}}}} \right)}^{2} + {\left({\frac{{\partial u^{*}}}{{\partial y^{*}}} + \frac{{\partial v^{*}}}{{\partial x^{*}}}} \right)}^{2}} \right]}, \quad G_{k}^{*} = - \frac{{\upsilon_{t}^{*}}}{{\sigma_{T}}}\frac{{Ri^{+}}}{{{Re }_{\rm s}}}{\left({\frac{{\partial T^{*}}}{{\partial x^{*}}} + \frac{{\partial T^{*}}}{{\partial y^{*}}}} \right)}, \\ \upsilon_{t}^{*} &= {Re}_{\rm s} C_{\mu} \frac{{k^{{*^{2}}}}}{{\varepsilon^{*}}}, \quad C_{{\varepsilon 3}} = \tanh {\left({\frac{{v^{*}}}{{u^{*}}}} \right)} \end{aligned} $$

The x-derivative of temperature appearing in G * k term has been neglected by many researchers. However, this term has been taken into account in the present study. The constants appearing in the turbulence model are assigned the following values [19] C μ = 0.09, C ɛ1 = 1.44, C ɛ2 = 1.92, σ T  = 1.0, σ k  = 1.0, σɛ = 1.314.

2.2 Boundary conditions

2.2.1 Inlet boundary conditions

The fluid is assumed to be entering the channel with a uniform velocity (V ∞) and uniform temperature (T ∞). The appropriate dimensionless boundary conditions in this case would be

$$ u^{*} = 0, \quad v^{*} = 1, \quad T^{*} = 0 $$

The turbulent kinetic energy and its dissipation rate at the inlet are calculated from a prescribed turbulence intensity of 5%.

2.2.2 Outlet boundary conditions

At the exit of the computational domain, the following boundary conditions are used for any variable ϕ

$$ \frac{{\partial \phi}}{{\partial y}} = 0 \quad \hbox{for} \ \phi = u^{*}, {{v}}^{*}, {{T}}^{*}, {{k}}^{*} {\text{and}}\varepsilon^{*} $$

This corresponds to the fully developed flow condition, which is justified consequent upon high aspect ratios in this study (6  ≤  AR  ≤  15). The boundary condition of \(\frac{{\partial^{2} \phi}}{{\partial y^{2}}} = 0\) was also used but the changes in the results were not significant. Furthermore, the higher order boundary condition resulted in a slower convergence. In view of these, the condition \(\frac{{\partial \phi}}{{\partial y}} = 0\) was used for subsequent computations.

2.2.3 Wall boundary conditions

Adiabatic boundary conditions are imposed at the outer surfaces of the walls. The temperature along the wall varies continuously due to volumetric heat generation (either in full or in a discrete portion) and also due to subsequent conduction along the wall and convection to the fluid. Hence, the wall boundary condition is derived based on an energy balance. While performing an energy balance, the temperature gradient across the wall is neglected since the thickness of the wall is relatively “thin”. This is known as the thermally thin limit [15–18]. For all the problems considered, the outer surface, the bottom and the top ends of the wall are assumed to be perfectly insulated. Hence, in the energy balance, the wall element may belong to any one of the following types:

  1. 1.

    A portion of the wall with uniform volumetric heat generation with the top and bottom ends heat conducting.

  2. 2.

    A portion of the wall without any heat generation with the top and bottom ends heat conducting (for problems with flush mounted discrete heat source).

  3. 3.

    A portion of the wall with one end insulated (for the top and bottom ends of the wall).

Now, doing an energy balance for the heat generating portion results in

$$ {Q}_{{\rm cond}, y^{*}}+{\dot{q}}^{\prime\prime\prime}\delta\Delta y^{*}={Q}_{{\rm cond}, y^{*}+\Delta y^{*}}+{Q}_{\rm conv} $$

Using Taylor series expansion and neglecting higher order terms, this can be modified as

$$ {Q}_{{\rm cond}, y}+{\dot{q}}^{\prime\prime\prime}\delta\Delta y={Q}_{{\rm cond}, y}+\frac{\partial {Q}_{{\rm cond}, y}}{\partial y}+{Q}_{\rm conv} $$

Now substituting for Q cond, y and Q conv and rearranging the final equation in non-dimensional form is

  • For the heat generating part of the wall

    $$ \frac{{\partial^{2} T^{*}_{C}}}{{\partial^{2} y^{{*2}}}} + \frac{{k_{\rm f}}}{{k_{\rm c}}}\frac{S}{\delta}\frac{{\partial T_{C}^{*}}}{{\partial x^{*}}} + \frac{{k_{\rm f}}}{{k_{\rm c}}}\frac{S}{{4H_{1}}}\frac{S}{\delta} = 0 $$
    (7)

  • For that part of the wall that does not generate heat

    $$ \frac{{\partial^{2} T_{C}^{*}}}{{\partial^{2} y^{*2}}} + \frac{{k_{\rm f}}}{{k_{\rm c}}}\frac{S}{\delta}\frac{{\partial T_{C}^{*}}}{{\partial x^{*}}} = 0 $$
    (8)

The same procedure can be extended to all the cases given above.

At the interface between the fluid and the wall, continuity of temperature and heat flux apply. These are

$$ T_{C}^{*} (0,y^{*}) = T^{*} (0,y^{*}) $$
(9)
$$ k_{\rm c} \left. {\frac{{\partial T_{C}^{*}}}{{\partial x^{*}}}} \right|_{{x^{*} = 0}} = k_{\rm f} \left. {\frac{{\partial T^{*}}}{{\partial x^{*}}}} \right|_{{x^{*} = 0}} $$
(10)

The boundary conditions for all other variables are

$$ u^{*} = 0; v^{*} = 0; k^{*} = 0 $$

ɛ* → ∞ (for numerical implementation it has been set as 1015)

2.3 Solution procedure

The two dimensional governing equations are discretised on a semi staggered, non-uniform, grid using a finite volume method. The velocities and pressures are iteratively calculated based on the SIMPLE algorithm. The discretised equations are then solved using an explicit pseudo-time marching technique. Wall functions are not used in the study and sufficiently fine grids have been employed in the inner layer to enable integration up to the walls [1, 2]. The grids in the x direction are generated using a geometric progression. The smallest non-dimensional grid size used close to the wall is 5 × 10−6. Finer grids are also needed at the entrance to the channel and also along the wall where the temperature gradients are high (at the intersections between the heat generating and the non-heat generating portions). For this, separate cosine grids are employed along the y direction for both the non-heat generating portion and the heat generating portion. Comparatively, more number of grids is used along the heat generating part. Based on a detailed grid sensitivity test, a 91 ×  225 grid is used.

2.4 Validation

The turbulent code has been validated for;

  1. 1.

    Natural convection heat transfer inside a square enclosure for the laminar and turbulent regimes by comparing the values of average Nusselt number with the published results of Elsherbiny et al. [20], Velusamy et al. [2], Markatos and Pericleous [19] and De Vahl Davis [21].

  2. 2.

    Laminar mixed convection in a vertical channel by comparing the temperature and velocity distributions at the exit of the channel with the results of Aung and Worku [22].

  3. 3.

    Turbulent mixed convection between vertical parallel plates by comparing the vertical velocity and temperature distribution at the channel exit with the results of Nakajima et al. [6] for Re=5870 and Ri = 2.2 × 10−3.

The validation of the code has been discussed in detail in an earlier paper [23] and so the comparisons are not repeated here.

3 Results and discussion

Numerical results have been obtained for a wide range of Re s, Ri +, ratio of conductivity of the discrete heat source to the fluid (k c/k f), ratio of conductivity of the substrate to the fluid (k s/k f) and AR. For the present study, air is considered as the coolant and the heat generating electronic components are modeled as discrete heat sources, flush mounted to the PCB. The geometry under consideration is, shown in Fig. 1. The geometric parameters are the height of the channel (H) = 0.3 m, thickness (δ) = 1.5 × 10−3 m, height of the heat source (H 1) = 0.03 m and the spacing between the walls (S) that varies according to the AR. The range of parameters used in the present study, to obtain the correlation, is given in Table 1. For the parametric study, with a view to develop the correlation, only one parameter is allowed to change at a time and all other parameters are kept at the reference values. The reference values chosen for the parameters are Re s = 10,000, Ri + = 0.25, AR=10, k c/k f = 417 and k s/k f = 125.

Table 1 Range of parameters used in present study (T ∞ = 300 K)
Full size table

3.1 Features of the flow and temperature fields in mixed convection

Figures 2, 3, 4, 5, 6 and 7 present the detailed features of mixed convection flow and thermal fields, within the vertical channel. For this study, all the variables except Ri + are kept at their reference values. At high Richardson number values, the maximum mid velocity in the channel is low (Fig. 2). Ri + represents the relative strength of the buoyancy driven flow as compared to the forced convection flow. It is evident from the mean velocity distributions shown in Figs. 2a and b that the effect of buoyancy is predominant only when the forced convection velocities are smaller in magnitude. It is also observed that the velocity or momentum boundary layer thickness is larger (i.e. diffusion effects penetrate deeper into the channel flow) at higher Ri + values, due to the smaller magnitudes of the mean velocity. The turbulent kinetic energy profiles shown in Fig. 3a, b indicate that turbulence is suppressed, when the influence of buoyancy increases, in other words, the buoyancy force tries to suppress turbulence. It is seen that k values are smaller for higher Ri + and this can be attributed to the flow expression term G * k in Eq. 5. Similarly, in Fig. 3b, it is observed that the suppression of turbulence is slightly more near the left wall which has flush-mounted heat sources. With respect to vertical distance, the variation in turbulent kinetic energy profile for the forced convection dominated (Ri + = 0.01) case is opposite to that observed for the buoyancy dominated (Ri + = 5) case. In the natural convection dominated case, (Fig. 3b), the existence of significant velocity gradients (due to thicker boundary layer) in the mid-portion of the channel, results in kinetic energy production in the central region also. Hence, k increases with vertical distance (y). In the forced convection dominated case (Fig. 3a); turbulent kinetic energy is generated only close to the wall. Thus, if the specified inlet value of k is too high, due to the dissipation of kinetic energy (at the Kolmogorov scale), the k values decrease in the central part of the channel with y. The variation of turbulent viscosity (μ t ) across the channel exit is shown in Fig. 4 for Ri + = 5. The turbulent viscosity increases approximately in a linear manner up to the centre line of the channel and attains a value which is about 20 times of the value corresponding to the laminar viscosity. The temperature profiles depicted in Fig. 5a, b illustrate that high Ri + (buoyancy-dominated) cases correspond to larger temperature differentials, in addition to the lower mean velocity values observed in Fig. 2. The higher temperature differentials, in turn, will be achieved in the situations with larger levels of heat generation from the heat sources. For the forced convection dominated as well as buoyancy dominated cases, the wall temperature at the channel exit is less than those shown at the interior sections, this can be attributed to the fact that the three sections corresponding to y = H/4, H/2 and 3H/4 fall in regions close to the heating elements, while the exit section is in the unheated zone. The thermal boundary layer thickness also increases with Ri +, for reasons as discussed in reference to Fig. 2a, b. The temperature contours shown in Fig. 6a, b also confirm the trends discussed above. The heat transfer coefficient (h) values, based on the ΔT between wall temperature and T ∞, along the left wall, are shown in Fig. 7. In general, h decreases with vertical distance due to the thickening of the thermal boundary layer. However, a slight increase in h is observed towards the end of each heat sources. This can be attributed to the local increase in vertical velocity due to buoyancy, as the air receives heat from the heat source.

Fig. 2
figure 2

a Velocity distribution at different locations of the channel for Ri + = 0.01. b Velocity distribution at different locations of the channel for Ri + = 5

Full size image
Fig. 3
figure 3

a Turbulent kinetic energy distribution at different locations of the channel for Ri + = 0.01. b Turbulent kinetic energy distribution at different locations of the channel for Ri + = 5

Full size image
Fig. 4
figure 4

Distribution of turbulent viscosity at exit of the channel for Ri + = 5

Full size image
Fig. 5
figure 5

a Temperature distribution at different locations of the channel for Ri + = 0.01. b Temperature distribution at different locations of the channel for Ri + = 5

Full size image
Fig. 6
figure 6

a Temperature contour plot for Ri + = 1.48. b Temperature contour plot for Ri + = 5

Full size image
Fig. 7
figure 7

Distribution of heat transfer coefficient along the chips for Ri + = 1.5

Full size image

3.2 Parametric study

3.2.1 Effect of the thermal conductivity ratio k c/k f

Figure 8 shows the effect of the thermal conductivity ratio k c/k f on the dimensional maximum temperature, when all other parameters remain constant at their reference values. When the thermal conductivity ratio is low, the maximum temperature is high and it decreases sharply as the conductivity ratio is increased to around 200. This indicates that more heat is conducted along the substrate, to be transferred to the cooling air in the unheated regions. For a further increase in conductivity ratio, the decrease in maximum temperature is marginal as shown in Fig. 8. Figure 9 shows the temperature distribution along the wall for three different thermal conductivities. As the thermal conductivity of the chip material increases, the temperature is found to be distributed more uniformly along the chip, implying that the direct heat transfer from the chip to air decreases while the indirect heat transfer through the unheated wall region increases.

Fig. 8
figure 8

Variation of the maximum temperature with conductivity ratio k c/k f

Full size image
Fig. 9
figure 9

Distribution of T max along the channel wall for different thermal conductivities of the heat source

Full size image

3.2.2 Effect of the thermal conductivity ratio k s/k f

Figure 10 shows the influence of the thermal conductivity ratio k s/k f on the dimensional maximum temperature. Here also, as expected, the non-dimensional maximum temperature decreases when k s/k f is increased. The decrease in temperature is more pronounced for increase in k s/k f up to around 150. It is observed that the effect of thermal conductivity ratio k s/k f on the maximum temperature is almost similar to that of the conductivity ratio k c/k f. Figure 11 shows the effect of the conductivity ratio k s/k f on the temperature distribution along the channel wall. With increase in k s, the temperature gradient at the interface shows a decreasing trend as expected, and temperature distributes more uniformly along the channel wall. The effect of the thermal conductivity of the substrate on the maximum temperature and its position can be seen from the figure. When k S/k f is increased from 10 to 150, the decrease in maximum temperature is significant. For a further increase in this ratio (or the thermal conductivity of the solid), the change in wall temperature is not as large as in the previous case.

Fig. 10
figure 10

Variation of the maximum temperature with conductivity ratio k s/k f

Full size image
Fig. 11
figure 11

Distribution of T max along the channel wall for different thermal conductivities of the substrate

Full size image

3.2.3 Effect of aspect ratio, AR

An analysis was also carried out by keeping the height of the channel constant and varying the AR by changing the width of the channel. Figure 12 shows that as the AR increases, the non-dimensional maximum temperature decreases non-linearly. However, with respect to aspect ratio, the dimensional temperature increases due to a decrease in spacing and poorer heat transfer as shown in Fig. 13. Since the values of Re s and Ri + are kept constant, a decrease in spacing effectively increases the heat flux correspondingly to keep the Grashof number constant. The variation of the dimensional temperature along the left channel wall with aspect ratio is shown in Fig. 14. It is evident from this figure that the wall temperature rises sharply in the heated zone and decreases in the un-heated zone due to heat transfer to the cooling air. However, there is a general increase of wall temperature in the vertical direction because of the increase in the cooling air temperature and hence its reduced capacity to carry away the heat.

Fig. 12
figure 12

Variation of non-dimensional maximum temperature with aspect ratio AR

Full size image
Fig. 13
figure 13

Variation of the maximum temperature with aspect ratio AR

Full size image
Fig. 14
figure 14

Temperature variation along the channel wall for different channel aspect ratios

Full size image

3.2.4 Effect of Reynolds number, Re s

As the Reynolds number increases, the non-dimensional maximum temperature decreases non-linearly as shown in Fig. 15. The dimensional maximum temperature increases almost linearly with increase in Reynolds number. This is because; as the Re s increases the Grashof number also increases to keep the Ri + constant. Since the geometric parameters are held constant this means an increase in heat flux and the velocity of flow. The overall effect is to increase the maximum temperature.

Fig. 15
figure 15

Variation of the non-dimensional maximum temperature with Reynolds number Re s

Full size image

3.2.5 Effect of modified Richardson number, Ri +

The value of Ri + is varied by modifying \({\dot{q}}^{\prime\prime\prime}\) while all other parameters are held constant at the reference values. The maximum temperature increases linearly with Ri +. This is in view of the fact that both the temperature and the Richardson number scales vary linearly with the rate of heat generation \({\dot{q}}^{\prime\prime\prime}.\)

3.3 Correlation for the maximum temperature

A correlation is obtained for maximum non-dimensional temperature for a wide range of parameters using ACFD technique. For the present problem, the maximum non-dimensional temperature remains constant with Ri +; therefore, this parameter is not included in the correlation developed. The independent variables that influence the maximum temperature, identified for the present study are AR, Re s, k c/k f and k s/k f. The reference values selected for these variables are AR=10, Re s = 10,000, k c/k f = 417 and k s/k f = 125.The T *max, ref obtained with these values assigned to independent variables is 0.00306. A preliminary study suggested that T *max can be expanded linearly with respect to a new set of variables. For example, the variation of T *max with respect to Re s is non-linear. However, it is possible to introduce a new variable ɛ1 equal to (Re s/Re s ref )0.1 so that the variation of T *max with ɛ1 is now linear.

A correlation can now be expressed in the vicinity of T *max, ref as,

$$ T_{{\max}}^{*} = T_{{\max, {\rm ref}}}^{*} + \frac{{\partial T_{{\max}}^{*}}}{{\partial \varepsilon_{1}}}{\left({\varepsilon_{1} - \varepsilon_{{1,{\rm ref}}}} \right)} + \frac{{\partial T_{{\max}}^{*}}}{{\partial \varepsilon_{2}}}{\left({\varepsilon_{2} - \varepsilon_{{2,{\rm ref}}}} \right)} + \frac{{\partial T_{{\max}}^{*}}}{{\partial \varepsilon_{3}}}{\left({\varepsilon_{3} - \varepsilon_{{3,{\rm ref}}}} \right)} + \frac{{\partial T_{{\max}}^{*}}}{{\partial \varepsilon_{4}}}{\left({\varepsilon_{4} - \varepsilon_{{4,{\rm ref}}}} \right)} $$
(11)

Where \(\varepsilon_{1} = {\left({{Re}_{\rm s} /{Re}_{{\rm s ref}}} \right)}^{{0.1}}, \ \varepsilon _{{\rm 1,ref}} = 1.0, \ \varepsilon_{2} = {\left({A{R} /A{R}_{{\rm ref}}} \right)}^{{0.1}}, \ \varepsilon_{{\rm 2,ref}} = 1.0, \ \varepsilon_{3} = {\left({{\left({k_{\rm c}/k_{\rm f}} \right)}/{\left({k_{\rm c}/k_{\rm f}} \right)}_{{\rm ref}}} \right)}^{{0.2}}, \ \varepsilon_{{\rm 3,ref}} = 1.0, \ \varepsilon_{4} = {\left({{\left({k_{\rm s}/k_{\rm f}} \right)}/{\left({k_{\rm s}/k_{\rm f}} \right)}_{{\rm ref}}} \right)}^{{0.2}}, \ \varepsilon_{{\rm 4,ref}} = 1.0\). The coefficients of the above equation are evaluated using the procedure described in [13]. The evaluated coefficients are now substituted and the correlation is derived as,

$$ T^{*}_{{\max}} = 0.00306 - 0.02554(\varepsilon_{1} - 1) - 0.02049(\varepsilon_{2} - 1) - 0.00122(\varepsilon_{3} - 1) - 0.00095(\varepsilon_{4} - 1) $$
(12)

This equation is valid for the range of parameters shown in Table 1, when air is used as cooling medium. A parity plot (Fig. 16) shows that the maximum temperature, T *max obtained from the numerical solution and T *max obtained from the above correlation compare very well, the maximum error being 7.5%. For comparison, additional numerical results are also used with randomly selected values for the variables.

Fig. 16
figure 16

Parity plot showing agreement of T *max (correlation) with T *max

Full size image

4 Conclusions

In the present work, a numerical study of conjugate turbulent mixed convection heat transfer in a vertical channel with four flush mounted heat sources on the left wall has been carried out. The ACFD approach has been applied to the above mentioned problem to obtain a correlation for the maximum temperature. The main conclusions of the study are:

  1. 1.

    The velocity boundary layer thickness decreases as the mean velocity of flow increases.

  2. 2.

    The dimensional maximum temperature increases linearly with Ri +. However the non-dimensional maximum temperature remains constant.

  3. 3.

    The maximum temperature of electronic components can be reduced significantly by increasing the conductivity ratio k S/k f up to around 150. Increasing thermal conductivity ratio beyond this value does not have much effect on the maximum temperature, when air is used as the cooling medium.

  4. 4.

    For the range of parameters tested, the maximum temperature can be reduced by increasing the thermal conductivity ratio k c/k f up to around 200. Increasing the conductivity ratio beyond 200 does not significantly affect the maximum temperature.

  5. 5.

    The correlation developed using ACFD approach gives fairly accurate predictions for the maximum temperature in the channel over a wide range of parameters that are of engineering interest.