1 Introduction

Heat always conducts from warmer objects to cooler ones. Empirically, the heat conduction rate is related to the spatial temperature difference and the composition of material. Fourier (1,768–1,830) pondered this phenomenon and proposed the well-known and later widely used Fourier’s law of heat conduction,

$${\mathbf{q}}{\left({\mathbf{r}},t \right)} = - \lambda \nabla T{\left({\mathbf{r}}, t\right)},$$
(1)

which states that heat flux q is directly proportional to the temperature gradient ∇ T. The proportionality λ is the thermal conductivity of material. The negative sign ahead of λ indicates that the two vectors, heat flux and temperature gradient take opposite directions.

There is a broad experimental basis for the Fourier’s law, and in this sense it is just a phenomenological description of regular thermal processes where the thermal time scale is comparatively long and the heat flux density is not very large. Fourier’s law elucidates such a thermal case in which temperature difference (∇ T) and heat propagation (q) take place concurrently, thus itself implies an infinite speed of propagation of a thermal disturbance, indicating that a local change of temperature causes an instantaneous perturbation at each point in the medium. This is physically unreasonable.

Substituting the Fourier’s law into the law of conservation of energy, the change rate in the amount of heat in a spatial infinitesimal can be determined by finding the summation of the net flow-in heat flux and the heat generation (S), illustrated as,

$$\nabla^{2} T{\left({\mathbf{r}},t\right)} + \frac{1}{\lambda}S {\left({\mathbf{r}},t\right)} = \frac{1}{a}\frac{{\partial T{\left({\mathbf{r}},t\right)}}}{{\partial t}}.$$
(2)

This is the traditional parabolic heat conduction model, which describes the diffusion way of thermal propagation.

Although the Fourier’s law may still be sufficiently accurate for engineering problems under regular conditions, the fundamental assumptions of an instantaneous response and a quasi-equilibrium thermodynamic transition behind the model need to be carefully examined when extended to problems involving a high heat flux or a sudden temperature change, and/or a micro (even nano) temporal/spatial scale. An equilibrium state in thermodynamic transitions, first of all, needs time to be established. For a physical process occurring in a much shorter time interval than that required for attaining equilibrium, the equilibrium concept becomes an approximate description of the physical process, and in this case, the diffusion theory based on a local equilibrium hypothesis becomes invalid. For example, when applied to the problem of reflectivity change resulting from short-pulse laser heating on a multi-layer metal film [1], diffusion theory predicts a reversed trend for the surface reflectivity when compared to the experimental data. The response time in this particular problem is of the order of a picosecond, comparable to the phonon–electron thermal relaxation time. The metal lattice and the hot electron gas simply cannot reach thermodynamic equilibrium in such a short period of time, which is the main cause for the failure of the diffusion theory. In some nanoscale systems, such as semiconductor devices based on the GaAs MESFETs or Si MOSFETs, the characteristic size of the device is of the order of nanometer, which is comparable to or even smaller than the mean free path of the energy carriers. The validity of the classic Fourier law needs carefully examining therein.

The earliest experimental evidences of the existence of non-Fourier heat conduction were obtained in some special materials at extremely low temperature. Peshkov [2] experimentally studied non-Fourier heat conduction in liquid helium II and measured a thermal propagation speed of about 19 m/s at a temperature of 1.4 K, an order of magnitude smaller than the speed of sound under the same condition. Non-Fourier heat conduction phenomena in some other materials at low temperature have also been verified, such as in NaF crystals (10–20 K) by Jackson and Walker [3] and in Bismuth (1.2–4.0 K) by Narayanmurti and Dynes [4].

Accounting for the lagging response in time between the heat flux vector and the temperature gradient, Tzou [5] provided a macroscopic formulation to describe the non-equilibrium thermodynamic transition which can be expressed by,

$${\mathbf{q}} {\left({\mathbf{r}},t + \tau\right)} = - \lambda \nabla T {\left({\mathbf{r}},t\right)},$$
(3)

with τ being the phase-lag in time, i.e. the thermal relaxation time, an intrinsic thermal property of the medium. Equation 3 indicates that due to insufficient time of response, the temperature gradient established at time t yields a heat flux vector at a later time t+τ. By applying a Taylor’s series expansion and ignoring the second and higher order derivatives, a hyperbolic energy equation reads as,

$$\nabla^{2} T{\left({\mathbf{r}},t\right)} + \frac{1}{\lambda} {\left[{S{\left({\mathbf{r}},t\right)} + \tau \frac{{\partial S{\left({\mathbf{r}},t\right)}}}{{\partial t}}} \right]} = \frac{1}{a}{\left[{\frac{{\partial T{\left({\mathbf{r}},t\right)}}}{{\partial t}} + \tau \frac{{\partial^{2}T{\left({\mathbf{r}},t\right)}}}{{\partial t^{2}}}} \right]}.$$
(4)

This is the so-called hyperbolic non-Fourier heat conduction model [6] from which the thermal propagation is deduced to have a wave nature.

Much effort has been spent to obtain solutions of the hyperbolic heat conduction equation under different conditions, and to develop mathematical and numerical techniques that would accurately predict the non-Fourier temperature profiles for a wide range of physical, geometric and boundary conditions. The related works are listed as follows: (1) Mikic [7], Baumeister and Hamill [8], Amos and Chen [9] obtained the temperature distribution due to a step change in temperature at the boundary of a semi-infinite medium bounded by a plane surface. (2) Glass et al. [10], Orlande and Özisik [11], Maurer and Thompson [12] found solutions of the hyperbolic heat conduction equation in a semi-infinite solid bounded by a plane surface with subjection of time-dependent heat fluxes. (3) Vick and Özisik [13] provided an analytical solution in a semi-infinite planar medium with thermal disturbance generated by a time-dependent heat source. (4) Taitel [14] gave an analytical solution for a thin layer subjected to a step change of temperature on its both sides. (5) Özisik and Vick [15] gave an analytical solution in a finite slab with insulated boundaries where a volumetric energy source was used. (6) Frankel et al. [16] and Hector et al. [17] studied hyperbolic propagation of thermal signals in an infinite plane slab. In their treatments, no heat generation occurred within the slab and one of the surfaces was insulated. On the other surface, a time-dependent heat flux was prescribed, which was either a uniform rectangular [16] or non-uniform and axisymmetric [17] heat pulse. (7) Gembarovic and Majernik [18] gave an analytical solution for a finite slab under a heat pulse boundary condition. (8) Tang and Araki [19] presented an analytical solution to the hyperbolic heat conduction equation in a finite medium under periodic surface heating. (9) Carey and Tsai [20] gave a numerical solution for a thin layer subjected to a step change of temperature on one side. Glass et al. [21, 22] gave numerical solutions for a finite medium with surface radiation and temperature-dependent conductivity, respectively. (10) Barletta [23], Barletta and Pulvirenti [24], Wilhelm and Choi [25] reported analytical solutions of 1-D radial hyperbolic thermal propagation in infinite solid medium. The analytical model that Barletta [23] considered is an infinite solid medium bounded internally by a circular cylindrical surface subject to a time-dependent heat flux, while an infinite long solid cylinder with outer boundary surface prescribed by a time-dependent heat flux was considered by Barletta and Pulvirenti [24]. Wilhelm and Choi [25] studied hyperbolic thermal propagation caused by a linear heat source in a very long cylinder. (11) Kim et al. [26] and Hector et al. [17] solved the 2-D hyperbolic heat conduction equation in a cylinder of finite length. (12) Zhang and Liu [27] studied non-Fourier effects in a spherical solid medium with either a sudden temperature change or a time-dependent pulsed heat flux prescribed on the boundary surface. (13) Frankel et al. [28] analytically studied the hyperbolic thermal propagation process in a planar multi-layer solid medium. (14) Tzou [29–32] obtained 3-D analytical solutions of hyperbolic heat conduction problems with thermal disturbances produced by moving heat source or moving crack. (15) Sadd and Didlake [33], Lebon and Casas-Vazquez [34], Mullis [35] handled some relatively more complicated hyperbolic thermal cases in which phase transition processes were assumed. (16) Barletta and Zanchini [36] analytically studied the 3-D hyperbolic propagation in a solid bar with rectangular cross sections. Thermal disturbances originated from the time-dependent heat fluxes prescribed on its boundary surfaces. A compresensive understanding about the hyperbolic heat conduction can be gotten from the review articles made by Joseph and Preziosi [37, 38].

The pursuit of analytical solutions for the hyperbolic heat conduction equations is of intrinsic scientific interests. In the present study, an analytical expression of the temperature profile in a hollow sphere with sudden temperature changes on its free surfaces is derived. According to this expression, hyperbolic heat propagation behaviors in hollow spherical objects are analyzed and discussed.

2 Model description

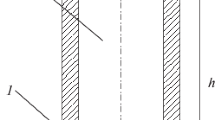
A radial one-dimensional heat conduction process is considered for a hollow sphere (as shown in Fig. 1) with an inner radius r i and outer radius r o and with constant thermal properties and uniform initial temperature distribution T 0. The thermal disturbance is caused by sudden temperature changes on its inner surface (from T 0 to T wi) and outer surface (from T 0 to T w0); no heat source is involved and heat convection and radiation are disregarded (solid medium or fluid medium restricted in a narrow space). The hyperbolic heat conduction equation is employed as the governing equation and the following formulation (in dimensionless form) yields,

$$\frac{{\partial ^{2} \theta {\left({\eta, \xi} \right)}}}{{\partial \eta ^{2}}} + \frac{2}{\eta}\frac{{\partial \theta {\left({\eta, \xi} \right)}}}{{\partial \eta}} = \frac{{\partial \theta {\left({\eta, \xi} \right)}}}{{\partial \xi}} + \varepsilon \frac{{\partial ^{2} \theta {\left({\eta, \xi} \right)}}}{{\partial \xi ^{2}}},$$
(5)

with initial conditions,

$$\theta {\left({\eta, 0} \right)} = 0, \; \left. {\frac{{\partial \theta}}{{\partial \xi}}} \right|_{{\xi = 0}} = 0, \quad {\left({r_{\gamma} \leq \eta \leq 1} \right)},$$
(6)

and boundary conditions,

$$\theta {\left({r_{\gamma}, \xi} \right)} = T_{\gamma},\quad \theta {\left({{\text{1}},\xi} \right)} = 1,\quad\quad {\left({\xi > {\text{0}}} \right)},$$
(7)

where

$$\theta = \frac{{T - T_{\rm o}}}{{T_{{\rm w0}} - T_{\rm o}}},\quad \eta = \frac{r}{{r_{\rm o}}},\quad \xi = \frac{{at}}{{r^{2}_{\rm o}}},\quad \varepsilon = \frac{{a\tau}}{{r^{2}_{\rm o}}},\quad r_{\gamma} = \frac{{r_{\rm i}}}{{r_{\rm o}}}\quad {\text{and}}\quad T_{\gamma} = \frac{{T_{\rm wi} - T_{0}}}{{T_{\rm w0} - T_{0}}}.$$

The thermal relaxation time τ can be expressed as, τ=3a/v 2=a/c 2. Because the velocity v of phonon or electron equals to l/τ, where l is the mean free path of molecule, the dimensionless parameter ɛ can also be defined as ɛ=l 2/3r 20 , i.e. the ratio of thermal length scale to the characteristic physical length scale.

Fig. 1
figure 1

Computational model

Full size image

3 Analytical solution

Applying the Laplace transformation to Eq. 5 with respect to the variable ξ and taking into account initial conditions Eq. 6, a subsidiary equation yields,

$$\frac{{\partial ^{2} \tilde{\theta}{\left({\eta, s} \right)}}}{{\partial \eta ^{2}}} + \frac{2}{\eta}\frac{{\partial \tilde{\theta}{\left({\eta, s} \right)}}}{{\partial \eta}} - {\left({s + \varepsilon s^{2}} \right)} \tilde{\theta}{\left({\eta, s} \right)} = 0,$$
(8)

with boundary conditions,

$$\tilde{\theta}\left(r_{\gamma}, s \right) = \frac{{T_{\gamma}}}{s}{\text{}}, \tilde{\theta}{\left({{\text{1}},s} \right)} = \frac{1}{s}.$$
(9)

After a series of manipulations, the solution of Eq. 8 restricted by the conditions shown in Eq. 9 is easily obtained,

$$\begin{aligned} \eta \tilde{\theta}{\left({\eta, s} \right)} =& \frac{1}{s} {\left\{{\frac{{\exp {\left[ {{\sqrt {s + \varepsilon s^{2}}}{\left({\eta - 1} \right)}} \right]} - T_{\gamma} r_{\gamma} \exp {\left[ {{\sqrt {s + \varepsilon s^{2}}}{\left({\eta + r_{\gamma} - 2} \right)}} \right]}}}{{1 - \exp {\left[ {- 2{\sqrt {s + \varepsilon s^{2}}}{\left({1 - r_{\gamma}} \right)}} \right]}}}} \right\}}\\ & + \frac{1}{s} {\left\{{\frac{{T_{\gamma} r_{\gamma} \exp {\left[ {{\sqrt {s + \varepsilon s^{2}}}{\left({r_{\gamma} - \eta} \right)}} \right]} - \exp {\left[ {{\sqrt {s + \varepsilon s^{2}}}{\left({2r_{\gamma} - \eta - 1} \right)}} \right]}}}{{1 - \exp {\left[ {- 2{\sqrt {s + \varepsilon s^{2}}}{\left({1 - r_{\gamma}} \right)}} \right]}}}} \right\}} \\ \end{aligned}.$$
(10)

Replacing the denominators inside the braces of Eq. 10 with a series of \({\sqrt {s + \varepsilon s^{2}}}\) as,

$$\frac{1}{{1 - \exp {\left[ {- 2{\sqrt {s + \varepsilon s^{2}}}{\left({1 - r_{\gamma}} \right)}} \right]}}} = {\sum\limits_{n = 0}^\infty {\exp {\left[ {- 2n{\sqrt {s + \varepsilon s^{2}}}{\left({1 - r_{\gamma}} \right)}} \right]}}},$$
(11)

it yields,

$$\begin{aligned} \eta \tilde{\theta}{\left({\eta, s} \right)} = \frac{1}{s} \sum\limits_{n = 0}^{\infty} & \left\{\exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n - 2nr_{\gamma} - \eta + 1} \right)}} \right]}\right.\\ &\quad - T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + 2 - \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]}\\ &\quad + T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]} \\ &\quad \left. -\exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta + 1 - 2{\left({n + 1} \right)}r_{\gamma}} \right)}} \right]} \right\}.\\ \end{aligned}$$
(12)

The inverse Laplace transform gives for the temperature response in the hollow sphere the following expression,

$$\eta \theta {\left({\eta, \xi} \right)} = L^{{- 1}} {\left[ {\eta \tilde{\theta}{\left({\eta, s} \right)}} \right]} = L^{{- 1}} {\left[ {s \tilde{\beta}{\left({\eta, s} \right)}} \right]} = \frac{{\partial \beta {\left({\eta, \xi} \right)}}}{{\partial \xi}},$$
(13)

where,

$$\begin{aligned} \tilde{\beta}{\left({\eta, s} \right)} = \frac{1}{{s^{2}}} \sum\limits_{n = 0}^\infty & \left\{\exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n - 2nr_{\gamma} - \eta + 1} \right)}} \right]}\right.\\ &\quad - T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + 2 - \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]} \\ &\quad + T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]} \\ &\quad \left. -\exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta + 1 - 2{\left({n + 1} \right)}r_{\gamma}} \right)}} \right]}\right\}. \\ \end{aligned}$$
(14)

The source function β (η,ξ) is determined from,

$$\beta {\left({\eta, \xi} \right)} = L^{{- 1}} {\left[ {\tilde{\beta}{\left({\eta, s} \right)}} \right]} = L^{{- 1}} {\left[ {F_{1} {\left({\eta, s} \right)}F_{2} {\left(s \right)}} \right]} = f_{1} {\left({\eta, \xi} \right)}*f_{2} {\left(\xi \right)} = {\int\limits_{0}^{\xi} {f_{1} {\left(\eta, \xi' \right)}f_{2} {\left(\xi - \xi' \right)}}}\hbox{d}\xi' $$
(15)

with,

$$\begin{aligned} F_{1} {\left({\eta, s} \right)} = \frac{1}{{{\sqrt {s + \varepsilon s^{2}}}}} \times \sum\limits_{n = 0}^\infty & \left\{ \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n - 2nr_{\gamma} - \eta + 1} \right)}} \right]}\right. \\ &\quad - T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + 2 - \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]} \\ &\quad + T_{\gamma} r_{\gamma} \exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta - {\left({2n + 1} \right)}r_{\gamma}} \right)}} \right]} \\ &\quad - \left .\exp {\left[ {- {\sqrt {s + \varepsilon s^{2}}}{\left({2n + \eta + 1 - 2{\left({n + 1} \right)}r_{\gamma}} \right)}} \right]}\right\},\\ \end{aligned}$$
(16)
$$F_{2} {\left(s \right)} = \frac{\sqrt{s + \varepsilon s^{2}}}{s^{2}}.$$
(17)

Since the source functions f 1 (η, ξ) and f 2(ξ) can be determined from a table of inverse Laplace transforms, finally, the expression for the hyperbolic temperature propagation in the hollow sphere yields,

$$\begin{aligned} \eta \theta {\left({\eta, \xi} \right)} =& \hbox{e}^{\frac{-\xi}{2\varepsilon}} \sum\limits_{n = 0}^{\infty} \left\{ I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - {\left({2n - 2nr_{\gamma} - \eta + 1} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi - {\sqrt \varepsilon}{\left({2n - 2nr_{\gamma} - \eta + 1} \right)}} \right]}\right. \\ &\quad\quad - T_{\gamma} r_{\gamma} I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - {\left({2n - (2n + 1)r_{\gamma} - \eta + 2} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} - \eta + 2} \right)}} \right]} \\ &\quad\quad + T_{\gamma} r_{\gamma} I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - {\left({2n - (2n + 1)r_{\gamma} + \eta} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} + \eta} \right)}} \right]}\\ &\quad\quad -\left. I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - {\left({2n - 2(n + 1)r_{\gamma} + \eta + 1} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} + \eta + 1} \right)}} \right]} \right\} \\ &+ \frac{1}{{2\varepsilon}}\hbox{e}^{\frac{-\xi}{2\varepsilon}}\sum\limits_{n = 0}^{\infty}\int\limits_{0}^{\xi}\left\{I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {{\xi'}^{2} - {\left({2n - 2nr_{\gamma} - \eta + 1} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi' - {\sqrt \varepsilon}{\left({2n - 2nr_{\gamma} - \eta + 1} \right)}} \right]}\right. \\ &\quad\quad - T_{\gamma} r_{\gamma} I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {{\xi'}^{2} - {\left({2n - (2n + 1)r_{\gamma} - \eta + 2} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi' - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} - \eta + 2} \right)}} \right]}\\ &\quad\quad + T_{\gamma} r_{\gamma} I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {{\xi'}^{2} - {\left({2n - (2n + 1)r_{\gamma} + \eta} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi' - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} + \eta} \right)}} \right]} \\ &\quad\quad -\left. I_{0} {\left[ {\frac{1}{{2\varepsilon}}{\sqrt {{\xi'}^{2} - {\left({2n - 2(n + 1)r_{\gamma} + \eta + 1} \right)}^{2} \varepsilon}}} \right]}H{\left[ {\xi' - {\sqrt \varepsilon}{\left({2n - (2n + 1)r_{\gamma} + \eta + 1} \right)}} \right]} \right\}\\ &\times{\left[ {I_{0} {\left({\frac{{\xi - \xi'}}{{2\varepsilon}}} \right)} + I_{1} {\left({\frac{{\xi - \xi'}}{{2\varepsilon}}} \right)}} \right]}\hbox{d}\xi'\\ \end{aligned}$$
(18)

Taking the limiting situation: r γ → 0, i.e. r i → 0 or r o → ∞, the above expression goes back to the form of the temperature solution for a solid sphere [27]. The reliability of this solution is further examined by considering another limit situation, τ → 0, i.e. ɛ → 0. In this situation, the hyperbolic heat conduction should degenerate to be the corresponding parabolic one.

Replacing the Bessel functions in Eq. 18 with the following series,

$$I_{0} (z) = \frac{{\hbox{e}^{z}}}{{{\sqrt {2\pi z}}}}{\left[ {1 + \frac{1}{{8z}} + \frac{9}{{2!(8z)^{2}}} + \cdots} \right]},$$
(19)
$$I_{1} (z) = \frac{{\hbox{e}^{z}}}{{{\sqrt {2\pi z}}}}{\left[ {1 - \frac{3}{{8z}} - \frac{{15}}{{2!(8z)^{2}}} - \cdots} \right]},$$
(20)

and taking into account the approximation equalities below as well as the original limit condition ɛ → 0,

$$\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - (2n - 2nr_{\gamma} - \eta + 1)^{2} \varepsilon}} = \frac{\xi}{{2\varepsilon}} - \frac{{(2n - 2nr_{\gamma} - \eta + 1)^{2}}}{{4\xi}} + O(\varepsilon),$$
(21)
$$\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - (2n - {\left({2n + 1} \right)}r_{\gamma} - \eta + 2)^{2} \varepsilon}} = \frac{\xi}{{2\varepsilon}} - \frac{{(2n - {\left({2n + 1} \right)}r_{\gamma} - \eta + 2)^{2}}}{{4\xi}} + O(\varepsilon),$$
(22)
$$\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - (2n - {\left({2n + 1} \right)}r_{\gamma} + \eta)^{2} \varepsilon}} = \frac{\xi}{{2\varepsilon}} - \frac{{(2n - {\left({2n + 1} \right)}r_{\gamma} + \eta)^{2}}}{{4\xi}} + O(\varepsilon),$$
(23)
$$\frac{1}{{2\varepsilon}}{\sqrt {\xi ^{2} - (2n - 2{\left({n + 1} \right)}r_{\gamma} + \eta + 1)^{2} \varepsilon}} = \frac{\xi}{{2\varepsilon}} - \frac{{(2n - 2{\left({n + 1} \right)}r_{\gamma} + \eta + 1)^{2}}}{{4\xi}} + O(\varepsilon),$$
(24)

it yields,

$$\begin{aligned} \eta \theta (\eta, \xi) = \sum\limits_{n = 0}^{\infty} \int\limits_{0}^{\xi} \frac{1}{{\pi {\sqrt {\xi'(\xi - \xi')}}}} & \left[\hbox{e}^{-(2n - 2nr_{\gamma} - \eta + 1)^{2}/4{\xi}'} - T_{\gamma} r_{\gamma} \hbox{e}^{-(2n - {\left({2n + 1} \right)}r_{\gamma} - \eta + 2)^{2}/4 \xi'}\right. \\ & \quad + \left. T_{\gamma} r_{\gamma} \hbox{e}^{-(2n - {\left({2n + 1} \right)}r_{\gamma} + \eta)^{2}/4{\xi}'} - \hbox{e}^{-(2n - 2{\left({n + 1} \right)}r_{\gamma} + \eta + 1)^{2}/4 \xi'} \right] \hbox{d} \xi',\\ \end{aligned}$$
(25)

Equation 25 is consistent to the analytical expression, obtained in the work by Carslaw and Jaeger [39], for the Fourier heat conduction in hollow spherical medium.

4 Hyperbolic heat propagation behaviors

Utilizing Eq. 18, numerical calculations were performed to display the temperature profile induced by the sudden temperature changes on the boundary surfaces of this hollow sphere. Hyperbolic heat propagation behaviors are to be explored in two ways: temperature wave and time-delay phenomenon of heat propagation.

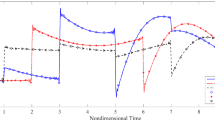
According to Eq. 18, the dimensionless temperature θ is dependent on five parameters: η (position), ξ (time), ɛ (property of material), T γ (thermal disturbance) and r γ (geometry). Keeping T γ=1 and r γ=0.6, several groups of temperature variation curves at different positions (η=0.9, 0.7, 0.8) for different materials (ɛ=0.01, 0.1, 0.35) are plotted, as shown in Fig. 2. For the material of ɛ=0.01, the temperature in the hollow sphere gradually approaches the final thermal equilibrium value (1.0) and no very evident wave characteristic is detected. However, for the temperature curves of ɛ=0.1 and 0.35, a complete different temperature variation trace is displayed. The temperature variations in the hollow spherical medium take on very pronounced characteristic of heat wave. The two heat waves, originated from the inner and outer boundary surfaces respectively, interact each other in the interior of the hollow sphere: at the central plane of the hollow sphere (η=0.8), the two heat waves arrive simultaneously, a temperature jump or drop is caused by the interaction of the two heat waves, as shown in Fig. 2c; while at the positions of η=0.7 or η=0.9, one heat wave arrives earlier than the other, the temperature increases or decreases owing to the earlier arriving heat wave, then further increases or decreases by the later arriving one, as Fig. 2a, b signify.

Fig. 2
figure 2

Dimensionless temperature θ versus dimensionless time ξ for T γ=1 and r γ=0.6 (a η=0.9; b η=0.7; c η=0.8)

Full size image

Also from Fig. 2, if one pays attention to the temporal variation of temperature in the hollow sphere, it can be discovered that the temperature wave rapidly attenuates along with the advance of time evolution. After ξ>4.0 or so, no evident temperature wave can be detected any more and all the curves gradually approach the final thermal equilibrium value (1.0). Accordingly, the hyperbolic heat propagation is an instantaneous behavior, i.e., heat wave only exist in a short time instant after a thermal disturbance.

Comparing the temperature curves shown in Fig. 2a, b, it can be found out that the temperature waves have similar appearance, whereas the amplitudes of temperature variation are clearly different. At the position of η=0.7 (close to the inner boundary surfaces), relatively larger temperature wave amplitudes are exhibited than the temperature curves at the position of η=0.9 (near the outer boundary surface). Closer to the inner boundary surface, smaller is the cross sectional area and larger is the heat flux.

Figure 3 shows the temperature variations at position of η=0.8 in the hollow spheres of three different materials (ɛ=0.01, 0.1, 0.35, respectively) with r γ=0.6 still. In contrast to Fig. 2c in which T γ=1, here T γ = −1, i.e., the two boundary surfaces have opposite temperature changes. Thus the two temperature disturbance signals, to some extent, offset each other in the hollow sphere and the temperature wave takes much smaller amplitude.

Fig. 3
figure 3

Dimensionless temperature θ versus dimensionless time ξ for T γ = −1 and r γ=0.6 at position of η=0.8

Full size image

From Eq. 18, the time-delay amount of hyperbolic temperature propagation is deduced to be directly proportional to ɛ1/2. The time-delay phenomenon of the hyperbolic heat propagation can be extracted from Fig. 4, in which a group of curves display the temperature distributions in the hollow sphere at several time instants (ξ=0.04, 0.1, 0.3 and 0.46). Again, T γ and r γ are kept as 1.0 and 0.6 respectively. A relaxation time τ is specified to give ɛ=0.2. During the early time of this thermal case (ξ=0.04), although temperatures at the regions close to the two boundary surfaces have increased, in some interior region of the hollow sphere it still sticks at the initial value (0.0). The existence of this kind of thermal static region indicates the time-delaying propagation of thermal disturbance. With the time advance, the two heat waves, respectively originated from the two boundary surfaces encounter and interfere each other.

Fig. 4
figure 4

Temperature distribution in the hollow sphere of ɛ=0.2 and r γ=0.6 with T γ=1

Full size image

In order to check the influence of r γ on the hyperbolic heat propagation in the hollow sphere, a few calculations for hollow spheres of different wall thicknesses have been carried out with respect to two different materials (ɛ=0.5, 0.1). The temperature observation point is set at the central plane of the hollow sphere. Various r γ values (r γ=0.1 or 0.9) are realized by varying r i while keeping r o as a constant. The two boundary surfaces are subject to a same amount of temperature jump (T γ =1). Results are shown in Fig. 5. Larger r γ is, i.e., the wall of the hollow sphere is thinner, stronger and faster (high frequency) temperature fluctuation is observed. More evident or more lasting hyperbolic thermal propagation behavior can be detected in the hollow spherical medium of thinner wall.

Fig. 5
figure 5

Temperature variation at the central plane of hollow spheres with different wall thicknesses and with T γ=1 (a r γ =0.9; b r γ =0.1)

Full size image

Figures 2, 4 and 5 all designate a temperature overshooting phenomenon: during some time instant at certain parts in the interior of the hollow sphere, the temperature is unusual high, even higher than the temperature of the heated boundary. For awhile, this unusual phenomenon was ascribed to the extreme non-equilibrium heat transmission in the hyperbolic heat propagation regime. The work by Haji-Sheikh et al. [40] was the first one to point out certain anomalies may exist in the hyperbolic solutions themselves. In order to facilitate the following discussions, a dimensionless quantity p is defined as

$$p = \frac{{ct}}{{r_{\rm o} - r_{\rm i}}} = \frac{\xi}{{{\left({1 - r_{\gamma}} \right)}{\sqrt \varepsilon}}},$$
(26)

which is used to indicate the position of the heat wave front. With respect to Fig. 4 (similar treatment can be addressed to Figs. 2, 5 also), ξ=0.04, 0.1, 0.3 and 0.46 give a value of p=0.224, 0.559, 1.677 and 2.57, respectively. For ξ=0.04, the two heat waves do not yet encounter, there is a thermal static region existing in the central part of the hollow sphere. When ξ=0.46, the heat waves already travel a round trip in the hollow sphere—they hit the inner and outer boundary surface each one time and meet each other at the central plane inside the hollow sphere three times. According to the work by Haji-Sheikh et al. [40], every time, the wave hits the boundary wall, an energy pulse is produced and the Dirichlet boundary condition may be violated; when the two heat waves encounter, an energy pulse is produced too and the overshooting temperature appears. Haji-Sheikh et al. [40] argued that the hyperbolic heat conduction equation, Eq. 4 has some defects, which implicitly lead to those additional energy pulses mathematically and then form some hyperbolic heat conduction anomalies, for instance, (1) extremely high temperature in the heat transfer medium interior; (2) tightly close to the heated outer boundary surface, often the temperature gradient is negative whereas the heat is transported inside from this boundary; (3) close to the inner boundary surface, where the temperature gradient is, when ξ=0.3, slightly positive, whereas the heat is moving inward.

Haji-Sheikh et al. [40] proposed a general method to deal with an anomaly by replacing the temperature discontinuity with an equivalent volumetric heat source for inclusion in the temperature solution. Chen [41, 42] derived a new type of equations and named them ballistic-diffusive equations, which has the potential of giving more reasonable non-Fourier temperature representations relative to the hyperbolic heat conduction equation, for the transient heat conduction in nanostructures. The procedure required to handle the hyperbolic heat conduction anomalies is lengthy and is not included in this work.

5 Concluding remarks

An analytical expression of the hyperbolic heat propagation in a hollow sphere with boundary surfaces subject to sudden temperature changes is obtained. Hyperbolic heat propagation behaviors exhibited in the medium are analyzed. The key factor to determine the significance of non-Fourier effects is the property of material itself, ɛ=a τ/r 2o =l 2/3 r 2o . Generally, the hyperbolic heat conduction is easier to happen in smaller object (or hollow sphere of thinner wall) made of material of longer thermal relaxation time. One expression of the hyperbolic heat propagation is the heat wave, which attenuates with the advance of time and propagation distance, and is only an instantaneous behavior—the wave behaviors diminish along with the time advances. Besides heat wave, another manifestation way of the hyperbolic heat propagation is the time-delay phenomenon. For the presently investigated hollow sphere, the time-delay amount of the hyperbolic temperature propagation is directly proportional to ɛ1/2. The temperature overshooting phenomenon observed in the hyperbolic heat conduction may be certain anomaly, which is caused by the hyperbolic heat conduction model itself.