1 Introduction

The problem of solute dispersion during underground water movement has attracted interest from the early days of this century [131], but it was only since the 1950s that the general topic of hydrodynamic dispersion or miscible displacement became the subject of more systematic study. This topic has interested hydrologists, geophysicists, petroleum and chemical engineers, among others, and for some time now it is treated at length in books on flow through porous media [11, 121]. Some books on chemical reaction engineering [25, 53, 147] treat the topic of dispersion (longitudinal and lateral) in detail and it is generally observed that the data for liquids and gases do not overlap, even in the “appropriate” dimensionless representation.

Since the early experiments of Slichter [131] and particularly since the analysis of dispersion during solute transport in capillary tubes, developed by Taylor [139] and Aris [3, 4], a lot of work has been done on the description of the principles of solute transport in porous media of inert particles (e.g. soils) and in packed bed reactors [11, 45].

Gray [58], Bear [11] and Whitaker [149] derived the proper form of the transport equation for the average concentration of solute in a porous medium, by using the method of volume or spatial averaging, developed by Slattery [130].

Brenner [20] developed a general theory for determining the transport properties in spatially periodic porous media in the presence of convection, and showed that dispersion models are valid asymptotically in time for the case of dispersion in spatially periodic porous media, while Carbonell and Whitaker [27] demonstrated that this should be the case for any porous medium. These authors presented a volume-average approach for calculating the dispersion coefficient and carried out specific calculations for a two-dimensional spatially periodic porous medium. Eidsath et al. [49] have computed axial and lateral dispersion coefficients in packed beds based on these spatially periodic models, and have compared the results to available experimental data. The longitudinal dispersion coefficient calculated by Eidsath et al. shows a Peclet number dependence that is too strong, while their transverse dispersion. However, in soils or underground reservoirs, large-scale nonuniformities lead to values of dispersion coefficients that differ much from those measured in packed beds, and for these cases spatially periodic models cannot be expected to provide excellent results without modifications.

There have been other attempts at correlating and predicting dispersion coefficients based on a probabilistic approach [39, 59, 70, 120] where the network of pores in the porous medium is regarded as an array of cylindrical capillaries with parameters governed by probability distribution functions.

Dispersion in porous media has been studied by a significant number of investigators using various experimental techniques (see Tables in Appendix). However, measurements of longitudinal and lateral dispersion are normally carried out separately, and it is generally recognised that ‘experiments on lateral dispersion are much more difficult to perform than those on longitudinal dispersion’ [121].

When a fluid is flowing through a bed of inert particles, one observes the dispersion of the fluid in consequence of the combined effects of molecular diffusion and convection in the spaces between particles. Generally, the dispersion coefficient in longitudinal direction is superior to the dispersion coefficient in radial direction by a factor of 5, for values of Reynolds number larger than 10. For low values of the Reynolds number (say, Re<1), the two dispersion coefficients are approximately the same and equal to molecular diffusion coefficient.

The detailed structure of a porous medium is greatly irregular and just some statistical properties are known. An exact solution to characterize the flowing fluid through one of these structures is basically impossible. However, by the method of volume or spatial averaging, it is possible to obtain the transport equation for the average concentration of solute in a porous medium [11, 149].

At a “macroscopic” level, the quantitative treatment of dispersion is currently based on Fick’s law, with the appropriate dispersion coefficients; cross-stream dispersion is related to the transverse dispersion coefficient, D T, whereas streamwise dispersion is related to the longitudinal dispersion coefficient, D L.

If a small control volume is considered, a mass balance on the solute, without chemical reaction, leads to

$$D_{{\text{L}}} \frac{{\partial ^{2} C}}{{\partial z^{2}}} + \frac{1}{r}\frac{\partial}{{\partial r}}{\left({D_{{\text{T}}} r\frac{{\partial C}}{{\partial r}}} \right)} - u\frac{{\partial C}}{{\partial z}} = \frac{{\partial C}}{{\partial t}} .$$
(1)

2 Longitudinal dispersion

Over the past five decades, longitudinal dispersion in porous media has been measured and correlated extensively for liquid and gaseous systems. Many publications are available for a variety of applications including, packed bed reactors [30, 48, 64, 96, 141] and soil column systems [11, 106, 110, 111].

One of the first results published about longitudinal dispersion in packed beds of inertial particles was in the 1950s by Danckwerts [37], who published his celebrated paper on residence time distribution in continuous contacting vessels, including chemical reactors, and thus provided methods for measuring axial dispersion rates. The author studied dispersion along the direction of flow for a step input in solute concentration (C S) in a bed of Raschig rings (with length L), crossed by water (C 0) with a value of Re(=ρ Ud/μ) approximately equal to 25 and obtained a PeL(=ud/D L) value of 0.52.

Kramers and Alberda [91] followed Danckwerts’s study with a theoretical and experimental investigation by the response to a sinusoidal input signal. These authors proposed that packed beds could be represented as consecutive regions of well-mixing rather than a sequence of stirred tanks (mixing-cell model) and suggested a PeL ≅ 1, for Re → ∞. McHenry and Wilhelm [100] assumed the axial distance between the mixing-cells in a packing to be equal to particle diameter and showed that PeL must be about 2 for high Reynolds number. The difference in the two results may be explained on the basis of experimental results of Kramers and Alberda [91] that are obtained with L/D ≈ 4.6, a value significantly less than L/D > 20 [63]. Klinkenberg et al. [87] and Bruinzeel et al. [23] show that transverse dispersion can be neglected for a small ratio of column diameter to length and large fluid velocity.

Brenner [19] presented the solution of a mathematical model of dispersion for a bed with finite length, L, and the most relevant conclusion of his work was that for Pea(=uL/D L) ≥ 10, the equations obtained by Danckwerts [37] for an input step in solute concentration and Levenspiel and Smith [96] for a pulse in solute concentration, that assumed an infinite bed, are corrected.

Hiby [78] proposed a better empirical correlation to cover the range of Reynolds numbers to 100. The author reported experimental results with the aid of photographs to compare the two dispersion mechanisms presented above—diffusional model in turbulent flow and the mixing-cell model.

Sinclair and Potter [128] used a frequency–response technique applied to the flow of air through beds of glass ballotini in a Reynolds number range between 0.1 and 20. A further investigation in the intermediate Reynolds number region has been carried out by Evans and Kenney [51] who used a pulse response technique in beds of glass spheres and Raschig rings.

Experiments reported by Gunn and Pryce [68] showed that longitudinal dispersion coefficients given by the theoretical equation for the diffusional model and the theoretical equation for the mixing-cell model are very similar. The authors also showed that neither the mixing-cell model nor the axially dispersed plug-flow model could describe axial dispersion phenomena.

As it may verify, the description of solute transport in packed beds by dispersion models has been studied since the 1950s and has long attracted the attention of engineers and scientists (see Tables 1 and 2).

Typically, the boundary conditions adopted by the vast majority of the investigators reported above have corresponded to the semi-infinite bed, i.e. L is sufficiently large (L/D > 20). Dispersion of the given tracer was measured at two points in the outlet and the distortion of a tracer forced by a pulse input [13, 26, 132], frequency response [40, 46, 91, 100, 135] and step input [37, 78, 101, 108]. Figure 1 illustrates some experimental data points for longitudinal dispersion in liquid and gaseous systems.

Fig. 1
figure 1

Some experimental data points for axial dispersion in liquid and gaseous systems

Full size image

2.1 Experimental techniques

Since the development of the dispersion approximation for the study of solute transport in capillary tubes by Taylor [139], the flow of the tracer is described by dispersion due to molecular diffusion and radial velocity variations. In packed beds, with D/d > 15, the assumption of flat velocity profiles and porosity is reasonable as pointed out by Akehata and Sato [2] and Gunn [63] and later showed by the experimental studies of Stephenson and Stewart [133] and Gunn and Pryce [68], that suggested D/d > 10.

Imagine a packed bed of uniform porosity (ɛ), contained in a long column of length L along which the liquid flows at a superficial velocity U (the interstitial velocity is then u=U/ɛ) and initial concentration of solute C 0, in which a tracer with continuously injection and concentration of solute C S, is dispersed in radial and axial direction. Taking a small control volume inside this boundary layer, a material balance on the solute, with length d z and width d r, leads to differential Eq. 1 [63]. Klinkenberg et al. [87] and Bruinzeel et al. [23] show that transverse dispersion can be neglected in comparison with axial dispersion for a small ratio of column diameter to length (D/L) and large fluid velocity. The partial differential equation describing tracer transport in the bed reduces to

$$D_{{\text{L}}} \frac{{\partial ^{2} C}}{{\partial z^{2}}} - u\frac{{\partial C}}{{\partial z}} = \frac{{\partial C}}{{\partial t}} ,$$
(2)

where z measures length along the bed, and if L is sufficiently large (semi-infinite bed), the appropriate boundary conditions are

$$ C = C_{0} \quad 0 \leq z \leq L\quad t = 0, $$
(3a)
$$uC_{{\text{S}}} = uC - D_{{\text{L}}} \frac{{\partial C}}{{\partial z}} \quad z = 0 \quad t > 0 ,$$
(3b)
$$\frac{{\partial C}}{{\partial z}} = 0 \quad z = L \quad t > 0 .$$
(3c)

For a step input, the concentration at the outlet of the bed (z=L) can be obtained by Carslaw and Jaeger [28], who give the exact solution of the equivalent heat-transfer problem. However, a study developed by Harrison et al. [73] showed that the boundary conditions developed by Danckwerts [37], for an infinite system, hold adequately for a finite system provided uL/D L ≥ 10. So, for a step input (from C 0 to C S), the concentration at the outlet of the bed (z=L) is known [37] to be given if L is sufficiently large, by

$$F (\theta) = \frac{1}{2}{\left[{{\text{1}} - {\text{erf}}{\left({{\sqrt {\frac{{L{\text{Pe}}_{{\text{L}}}}}{{\theta d}}}}\frac{{(1 - \theta )}}{2}} \right)}} \right]}$$
(4)

or for a pulse response by

$$E (\theta) = \frac{1}{2}{\left({\frac{{L{\text{Pe}}_{{\text{L}}}}}{{\pi \theta d}}} \right)}^{{1/2}} \times \exp {\left[{\frac{{- L{\text{Pe}}_{{\text{L}}} (1 - \theta)^{2}}}{{4 \theta d}}} \right]} .$$
(5)

Rifai et al. [115] and Ogata and Banks [107] showed that the solution of Eq. 2 with the boundary conditions and initial condition given by Eq. 3a–c is

$$F (\theta ) = \frac{1}{2}{\left[{ 1 - {\text{erf}}{\left({{\sqrt {\frac{{L{\text{Pe}}_{{\text{L}}}}}{{ \theta d}}}}\frac{{(1 - \theta )}}{2}} \right)}} \right]} + \frac{1}{2}{\left[ {1 - {\text{erf}}{\left({{\sqrt {\frac{{L{\text{Pe}}_{{\text{L}}}}}{{ \theta d}}}}\frac{{(1 + \theta )}}{2}} \right)}} \right]}\exp {\left({\frac{L}{d}{\text{Pe}}_{{\text{L}}}} \right)} .$$
(6)

However, Ogata and Banks [107] showed that for large molecular Peclet numbers (say, uL/D L > 100), the advection dominates and the second term in the right-hand side can be neglected, with an error lesser than 5%, and Eq. 6 reduces to Eq. 4.

2.2 Parameters influencing longitudinal dispersion—Porous medium

Perkins and Johnston [110] in their article review showed some of the variables that influence longitudinal and radial dispersion. However, before attempting in the parameters influencing dispersion, it is important to consider the effect of the packing of the bed on dispersion coefficients. Gunn and Pryce [68] and Roemer et al. [118] showed that when particles in packed beds are not well-packed, the dispersion coefficient is increased. Experimental results of Gunn and Pryce [68] showed that different re-packing of the bed gave deviations of 15% in transverse Peclet values. These experiments confirm that fluid mechanical characteristics are not only defined by the values of the porosity and tortuosity (easy to reproduce), but depend on the quality of packing in the bed.

The effect of radial variations of porosity and velocity on axial and radial transport of mass in packed beds was analytically quantified by Choudhary et al. [31], Lerou and Froment [95], Vortmeyer and Winter [146] and Delmas and Froment [42].

A rigorous measurement of the porosity in a packed bed is fundamental to minimize the errors in the experimental measurements, because the porosity between the inert particles of the bed helps the diffusion of a tracer and gradually increases dispersion.

A more coherent interpretation of the experimental data may be obtained through the use of dimensional analysis. As a starting point, it is reasonable to accept the functional dependence

$$D_{{\text{L}}} = \phi {\left({L,D,u,d,\rho, \mu, D_{{\text{m}}}} \right)}$$
(7)

for randomly packed beds of mono-sized particles with diameter d, where ρ and μ are the density and viscosity of the liquid, respectively, and D m is the coefficient of molecular diffusion of the solute. Making use of Buckingham’s π theorem, Eq. 7 may be rearranged to give

$$\frac{{D_{{\text{L}}}}}{{D_{{\text{m}}}}} \quad {\text{or}} \quad {\text{Pe}}_{{\text{L}}} = \Phi {\left({\frac{L}{D},\frac{D}{d},\frac{{ud}}{{D_{{\text{m}}}}},\frac{\mu}{{\rho D_{{\text{m}}}}}} \right)}$$
(8)

and it is useful to define Pem=ud/D m and Sc =μ/ρ D m. This result suggests that experimental data be plotted as (D L/D m) versus Pem.

2.2.1 Effect of column length

One first aspect to be considered, as a check on the experimental method (infinite medium), is the influence of the length of the bed (L) on the measured value of longitudinal dispersion. In reality, if an experimental method is valid, values of the dispersion coefficient measured with different column lengths, under otherwise similar conditions, should be equal, within the reproducibility limits.

The dependence of the axial dispersion coefficient on the position in packed beds was first examined by Taylor [139]. The author showed that, in laminar flow, dispersion approximation would be valid if the following equation is satisfied,

$$ \theta = \frac{{D_{{\text{m}}} t}}{{R^{2}}} > > 0.14 ,$$
(9)

where R is the tube radius. Carbonell and Whitaker [27] concluded that the axial dispersion coefficient becomes constant if the following expression is satisfied

$$ \theta = {\left({\frac{{1 - \varepsilon}}{\varepsilon}} \right)}^{2} \frac{{D_{{\text{m}}} t}}{{d^{2}}} > > 1 .$$
(10)

Han et al. [69], see Fig. 2, showed that values of the longitudinal dispersion coefficient, for uniform-size packed beds, measured at different positions in the bed are function of bed location unless the approximate criterion

$$\frac{L}{d}\frac{1}{{{\text{Pe}}_{{\text{m}}}}}{\left({\frac{{1 - \varepsilon}}{\varepsilon}} \right)}^{2} \geq 0.3 \quad {\text{or}} \quad \theta = \frac{{D_{{\text{m}}} t}}{{d^{2}}} \geq 0.15 $$
(11)

is satisfied. The authors showed that for Pem < 700, longitudinal dispersion coefficients were nearly identical for all values of x=L, and for Pem > 700 observed an increase in the value of dispersion coefficients with increasing distance down the column.

Fig. 2
figure 2

Effect of bed length on D L

Full size image

2.2.2 Ratio of column diameter to particle diameter

It is well-known (e.g. [145]) that the voidage of a packed bed (and therefore, the fluid velocity) is higher near a containing flat wall. The effects of radial variations of porosity and velocity on axial and radial transport of mass in packed beds were analytically quantified by several investigators like Choudhary et al. [31], Lerou and Froment [95], Vortmeyer and Winter [146] and Delmas and Froment [42].

Schwartz and Smith [123] were the first to present experimental data showing zones of high porosity extending two or three particle diameters from the containing flat wall. The results indicated that unless D/d > 30 important velocity variations exist across the packed bed. Other studies showed that the packed bed velocity profiles significantly differ from flows with large diameter particles in small diameter tubes [24, 35].

Hiby [78] showed that the effect of D/d is not significant in the measured longitudinal dispersion coefficient when the ratio is greater than 12.

Stephenson and Stewart [133] showed that the area of high fluid velocities limits to the area of high porosities, and this area does not extend more than a particle diameter of the wall and the assumption of a flat velocity profile is reasonable. This work confirms the earlier experiments reported by Roblee et al. [117], Schuster and Vortmeyer [122] and Vortmeyer and Schuster [145].

A similar effect was observed in measuring pressure drops across packings, so an empirical rule can be considered that the variations, in radial position, of the fluid velocity, porosity and dispersion coefficient can be negligible, if D/d > 15 [2, 63].

2.2.3 Ratio of column length to particle diameter

Strang and Geankoplis (1958) and Liles and Geankoplis (1960) make much of the effect of L/d but the evidence from fluid mechanical studies [67] was that the effect is confined to a dozen layers of particles and is not very important.

Experimental results of Guedes de Carvalho and Delgado [62] presented in Fig. 3 with two different spherical particles diameter and the same length of the packed bed showed that longitudinal dispersion coefficient does not increased with particle diameter as long as the condition D/d > 15 is satisfied (see Vortmeyer and Schuster [145] and Ahn et al. [1], for wall effects).

Fig. 3
figure 3

Effect of particle size distribution on D L

Full size image

2.2.4 Particle size distribution

Another aspect of dispersion in packed beds that needs to receive attention is the effect of porous medium structure. In a packed bed of different particle sizes, the small particles accumulate in the interstices between large particles, and porosity tends to decrease.

Raimondi et al. [114] and Niemann [105] studied the effect of particle size distribution on longitudinal dispersion and concluded that D L increases with a wide particle size distribution. Eidsath et al. [49] indicated a strong effect of particle size distribution on dispersion. As the ratio of particle diameters went from a value of 2 to 5, the axial dispersion increased by a factor of 1.5, and radial dispersion decreased by about the same factor.

Han et al. [69] showed that for a size distribution with a ratio of maximum to minimum particle diameter equal to 7.3, longitudinal dispersion coefficient are 2 to 3 times larger than the uniform-size particles (see Fig. 3).

Wronski and Molga [152] studied the effect of particle size non-uniformities on axial dispersion coefficients during laminar liquid flow through packed beds (with a ratio of maximum to minimum particle diameter equal to 2.13) and proposed a generalized function to determine the increase of the axial dispersion coefficients in non-uniform beds relative to those obtained in uniform beds.

Guedes de Carvalho and Delgado [62] obtained the same conclusion in their experiments, with ballotini and a ratio of maximum to minimum particle diameter equal to 3.5 in comparison with glass ballotini that have the same size.

2.2.5 Particle shape

The effect of particle shape on longitudinal dispersion has been studied by several investigators, like Bernard and Wilhelm [14], Ebach and White [46], Carberry and Bretton [26], Strang and Geankopolis [135], Hiby [78], Klotz [88] and more recently, Guedes de Carvalho and Delgado [62]. The authors have used beds of spheres, cubes, Raschig rings, sand, saddles and other granular materials, and have concluded that generally longitudinal dispersion coefficient tend to be greater with packs of nonspherical particles than with packs of spherical particles of the same size.

Figure 4 shows that particle shape is a significant parameter, with higher values of D L (i.e. lower PeL) being observed in packed beds of sand and Raschig rings comparatively with the results obtained with spherical beds. Therefore, increased particle sphericity correlates with decreased dispersion, with a sphericity defined as the surface area of a particle divided by the surface area of a sphere of volume equal to the particle.

Fig. 4
figure 4

Effect of particle shape on axial dispersion

Full size image

2.3 Parameters influencing longitudinal dispersion—Fluid properties

2.3.1 Viscosity and density of the fluid

Some investigators, like Hennico et al. [77], used glycerol and obtained significant effect of viscosity, at large Reynolds number, on axial dispersion coefficient. In vertical miscible displacements, if a less viscous fluid displaced another fluid, viscous fingers will be formed [110]. However, if a more viscous fluid displaced a different fluid, the dispersion mechanisms are unaffected but the situation tends to reduce convective dispersion. This leads to increased dispersion relative to the more viscous fluid displacing a less viscous one.

The importance of density gradients has recently been investigated by Benneker et al. [12] and their experiments showed that axial dispersion coefficient is considerably affected by fluids with different densities due the action of gravity forces. Fluid density creates similar effects to fluid viscosity. In a displacement with a denser fluid above the less-dense fluid, gravity forces cause redistribution of the fluids. However, if a denser fluid is on the bottom, usually, a stable displacement occurs.

2.3.2 Fluid velocity

The first two groups of Eq. 8 have importance only when D/d is less than 15 and L/D is so small that the characteristics of dispersion are affected by changing velocity distributions. So, for packed beds, we will usually have D L/D m=Φ (Pem, Sc).

In order to understand the influence of fluid velocity on the dispersion coefficient, it is important to consider the limiting case where u → 0. If D L was defined based on the area open to diffusion (see Eq. 2), in the limit u → 0, solute dispersion is determined by molecular diffusion, with D L=D′m=D m/τ (τ being the tortuosity factor for diffusion and it is equal to \({\sqrt{2}}\) as suggested by 125].

As the velocity of the fluid is increased, the contribution of convective dispersion becomes dominant over that of molecular diffusion [150] and D L=ud/PeL (∞), where u is the interstitial fluid velocity and PeL (∞) ≅ 2 for gas or liquid flow through beds of (approximately) isometric particles, with diameter d [24, 85].

Assuming that the diffusive and convective components of dispersion are additive, the same authors suggest that D L=D′m+ud/PeL (∞), which may be written in dimensionless form [63] as

$$\frac{{D_{{\text{L}}}}}{{D_{{\text{m}}}}} = \frac{1}{\tau}+\frac{1}{2}\frac{{ud}}{{D_{{\text{m}}}}} \quad {\text{or}} \quad \frac{1}{{{\text{Pe}}_{{\text{L}}}}} = \frac{1}{\tau}\frac{\varepsilon}{{{\text{ReSc}}}} + \frac{1}{2} .$$
(12)

This equation is expected to give the correct asymptotic behaviour, in gas and liquid flow through packed beds, at high and low values of Pem(=ud/D m). For gases, this is confirmed in Fig. 5, but for liquids (Fig. 6), the data do not cover the extreme conditions.

Fig. 5
figure 5

Data on axial dispersion in gas flow

Full size image
Fig. 6
figure 6

Data on axial dispersion in liquid flow

Full size image

But these figures show that Eq. 12 is inaccurate over part of the intermediate range of Pem. In the case of gas flow, shown in Fig. 6, significant deviations are observed only in the range 0.6 < Pem < 60, as pointed out by several of the authors [48, 63, 78, 142]. The experimental values of PeL (=ud/D L) are generally higher than predicted by Eq. 12. Several equations have been proposed to represent the data in this intermediate range and the equations of Hiby [78], Edwards and Richardson [48], Evans and Kenney [51], Scott et al. [124], Langer et al. [93] and Johnson and Kapner [86] are shown to fit the data points reasonably well (see Fig. 5).

With liquids, deviations from Eq. 12 occur over the much wider range 2 < Pem < 106, the experimental values of PeL being significantly lower than predicted by that equation. The difference in the behaviour between gases and liquids has to be ascribed to the dependence of PeL on Sc(=μ/ρ D m).

2.3.3 Fluid temperature (or Schmidt number)

The coefficient of longitudinal dispersion for gas flow (Sc ≅ 1) is predicted with good accuracy by Eq. 12, except in the approximate range 0.5 < Pem < 100, where experimental values may be more than twice those given by the equation, as confirmed by Fig. 5.

For liquid flow, a large number of data are available, that were obtained with different solutes in water at near ambient temperature, corresponding to the values of Sc in the range 500 < Sc < 2,000. Most of the data reported in the literature, for this range of Sc, are shown in Fig. 6, and they form a “thick cloud” running parallel to the line defined by Eq. 12, though somewhat below it (at approximately, 0.3 < PeL < 2).

In recent years, data on longitudinal dispersion have been made available for values of Sc between the two extremes of near ideal gas (Sc ≅ 1) and cold water (Sc > 550). Such data were obtained with either supercritical carbon dioxide (1.5 < Sc < 20) or heated water (55 < Sc < 550) and they are displayed in Fig. 7.

Fig. 7
figure 7

Dependence of PeL on Pem for different values of Sc

Full size image

Figure 7 shows a consistent increase in PeL with a decrease in Sc and it may be seen that the dependence is slight for the higher values of Sc (say for Sc of order 750 and above). At the lower end of the range of Pem investigated, there seems to be a tendency for PeL to become independent of Sc, even if the values of D L are still significantly above D m. In the intermediate range, 100 < Pem < 5,000, values of PeL are very nearly constant, for each value of Sc. The convergence of the different series of points at about Pem ≅ 20 seems to suggest that PeL is insensitive to Sc below this value of Pem, for the range of Sc presented.

A good additional test of the consistency of the data of Guedes de Carvalho and Delgado [62] is supplied by the plot in Fig. 8, where it may be seen that all the series of points converge at high Re, as would be expected for turbulent flow. The agreement with the data of Jacques and Vermeulen [85] and Miller and King [101], for cold water, is worth stressing.

Fig. 8
figure 8

Dependence of PeL on Re for different values of Sc

Full size image

Recently, some workers have measured axial dispersion for the flow of supercritical carbon dioxide through fixed beds and this provides important new data in the range 1.5 < Sc < 20. However, the various authors fail to recognize the direct dependence of PeL on Sc. Catchpole et al. [29] represent their data and those of Tan and Liou [138] in a single plot (their Fig. 3) of PeL vs. Re. The majority of points are in the range 1 < Re < 30 and the data of both groups, together, define a horizontal cloud with mid line at about PeL ≅ 0.8, spreading over the approximate range 0.3 < PeL < 1.1.

The data of Yu et al. [153] are for 0.01 < Re < 2 and 2 < Sc < 9. It is worth referring here that the modelling work of Coelho et al. [34] gives theoretical support to experimental findings for low Re, both for spherical and non-spherical particles. No influence of Sc on PeL is detected; but unfortunately, the results are not very consistent, particularly in the range 1 < Pem < 20, where the scatter is high and the values of PeL are much too low.

Figure 9 shows that for low values of Pem (Stokes flow regime), there seems to be a tendency for PeL to become independent of Sc. The values of PeL reported by Miller and King [101], for 6 < Pem < 100, are much too low; this may be because the particles used in most experiments are too small (particle sizes of 55 μm and 99 μm) and this is known to yield enhanced dispersion coefficients, possibly due to particle agglomeration [65, 78]. The data reported by Miyauchi and Kikuchi [102] and plotted in Fig. 9, for 6 < Pem < 300, are higher than our experimental data.

Fig. 9
figure 9

Dependence of PeL on Pem for Stokes flow regime

Full size image

There are considerable experimental difficulties in the measurement of longitudinal dispersion in the liquid phase at small Reynolds number, because the usual method of obtaining low Reynolds number is to reduce particle size and this is known to yield enhanced dispersion coefficients.

2.4 Correlations

It is worth considering here the predicting accuracy of alternative correlations (see Fig. 10). Gunn [64] admitted the existence of two regions in the packing, one of fast flowing and the other of nearly stagnant fluid, to deduce the following expression for the longitudinal dispersion coefficient in terms of probability theory

$$\frac{1}{{{\text{Pe}}_{{\text{L}}}}} = \frac{{\varepsilon {\text{Pe}}_{{\text{m}}}}}{{4\alpha ^{2}_{1} (1 - \varepsilon)}}(1 - p)^{2} + {\left[ {\frac{{\varepsilon {\text{Pe}}_{{\text{m}}}}}{{4\alpha ^{2}_{1} (1 - \varepsilon)}}} \right]}^{2} p(1 - p)^{3} {\left\{{{\text{exp}}{\left[ {- \frac{{4(1 - \varepsilon)\alpha ^{2}_{1}}}{{p(1 - p)\varepsilon {\text{Pe}}_{{\text{m}}}}}} \right]} - 1} \right\}} + \frac{1}{{\tau {\text{Pe}}_{{\text{m}}}}} ,$$
(13)

where α 1 is the first zero of equation J 0 (U)=0 and p is defined, for a packing of spherical particles, by

$$ p = 0.17 + 0.33 \times \exp {\left({- \frac{{24}}{{\text{Re}}}} \right)} \quad {\text{for spheres}}, \; \tau = {\sqrt 2} ,$$
(14a)
$$ p = 0.17 + 0.29 \times \exp {\left({- \frac{{24}}{{\text{Re}}}} \right)} \quad {\text{for solid cylinders}},\; \tau = 1.93 ,$$
(14b)
$$ p = 0.17 + 0.20 \times \exp {\left({- \frac{{24}}{{\text{Re}}}} \right)} \quad {\text{for hollow cylinders}},\; \tau = 1.8. $$
(14c)

Tsotsas and Schlunder [141] deduced an alternative correlation for the prediction of PeL. The authors defining two zones in a simple flow model consisting of a fast stream (central zone in the model capillary) and a stagnant fluid, but the mathematical expressions associated with it are a little cumbersome,

$$\frac{1}{{{\text{Pe}}_{{\text{L}}}}} = \frac{1}{\tau}{\left[ {\frac{1}{{{\text{Pe}}_{{{\text{z,1}}}}}} + \frac{1}{{{\text{Pe}}'_{{\text{m}}}}}{\left({1 - \xi ^{{\text{2}}}_{{\text{c}}}} \right)}} \right]} + \frac{1}{{32}}{\left({\frac{{D_{{\text{c}}}}}{d}} \right)}^{2} {\left[ {{\text{Pe}}_{{{\text{r, 1}}}} \xi _{{\text{c}}} ^{2} f_{1} (\xi _{{\text{c}}}) + {\text{Pe}}'_{{\text{m}}} f_{2}(\xi _{{\text{c}}})} \right]} ,$$
(15)

where the longitudinal and radial Peclet number of the fast stream is

$$\frac{1}{{{\text{Pe}}_{{{\text{z,1}}}}}} = \frac{1}{{{\text{Pe}}'_{1}}} + \frac{1}{{1.14 (1 + 10/{\text{Pe}}'_{1})}} $$
(16a)
$$\frac{1}{{{\text{Pe}}_{{{\text{r,1}}}}}} = \frac{1}{{{\text{Pe}}'_{1}}} + \frac{1}{8}$$
(16b)
$${\text{Pe}}'_{1} = \frac{{u_{1} d}}{{D'_{{\text{m}}}}}$$
(16c)

and u 1=u/ξ 2c is the interstitial velocity of the fast stream, with ξ c (the dimensionless position of the velocity jump, i.e. the ratio between the radius of the zone of high velocities and the radius of packed bed) equal to

$${\text{Re}} \leq 0.1 \to \xi_{{\text{c}}} = 0.2 + 0.21 \exp (2.81 y)$$
(17a)
$${\text{Re}} \geq 0.1 \to \xi_{{\text{c}}} = 1 - 0.59 \exp[ - f(y)] $$
(17b)

with

$$y = \log {\left({{\text{Re}}} \right)} + 1 , $$
(17c)
$$f(y) = y{\left({1 - 0.274y + 0.086y^{2}} \right)} .$$
(17d)

Finally, the distributions functions f 1 (ξ c) and f 2 (ξc) are defined by:

$$f_{1} (\xi_{{\text{c}}}) = {\left({1 -\xi_{{\text{c}}} ^{2}} \right)}^{2} ,$$
(17e)
$$f_{2} (\xi_{{\text{c}}}) = 4\xi_{{\text{c}}} ^{2} - 3 - 4 \ln(\xi_{{\text{c}}}) - \xi_{{\text{c}}} ^{4} .$$
(17f)
Fig. 10
figure 10

Comparison between data and correlations presented in literature

Full size image

In Fig. 11, the lines corresponding to the correlations of Gunn [64] and of Tsotsas and Schlunder [141] are represented, for the higher and lower values of Sc in our experiments (Sc = 57 and Sc = 1930), as well as for gas flow (Sc = 1). It may be seen that the correlation of Gunn [64] is not sensitive to changes in Sc, for Pem < 103, and the correlation of Tsotsas and Schlunder [141] is much too sensitive to variations in Sc; however, this correlation describes dispersion in gas flow with good accuracy.

Fig. 11
figure 11

Comparison between experimental data and Eqs. 18 and 19

Full size image

Figure 11 shows Guedes de Carvalho and Delgado [62] experimental data, at different Schmidt numbers, the experimental data of Jacques and Vermeulen [85] and representative data of experimental points with gas flow, together with the fitted curve

$$\frac{1}{{{\text{Pe}}_{{\text{L}}}}} = \frac{{{\text{Pe}}_{{\text{m}}}}}{5}(1 - p)^{2} + \frac{{{\text{Pe}}_{{\text{m}}} ^{2}}}{{25}}p(1 - p)^{3} {\left\{{{\text{exp}}{\left[ {- \frac{5}{{p(1 - p){\text{Pe}}_{{\text{m}}}}}} \right]} - 1} \right\}} + \frac{1}{{\tau {\text{Pe}}_{{\text{m}}}}}$$
(18)

with

$$p = \frac{{0.48}}{{{\text{Sc}}^{{0.15}}}} + {\left({\frac{1}{2} - \frac{{0.48}}{{{\text{Sc}}^{{0.15}}}}} \right)}{\text{exp}}{\left({- \frac{{{\text{75Sc}}}}{{{\text{Pe}}_{{\text{m}}}}}} \right)} .$$
(19)

It will be clear to the reader that Eq. 18 was closely inspired by Eq. 13, but the dependence of p on Sc was modified. As will be obvious from the plots, each curve is not a “best fit” for the points it tries to represent, but nevertheless, the values of PeL given by Eqs. 18 and 19 will seldom differ by more than 20% from those determined experimentally. It is important to bear in mind that Eqs. 18 and 19 is recommended only for random packings of “isometric” spherical particles which are well-packed.

2.5 Dispersion in packed beds flowing by non-Newtonian fluids

Hilal et al. [81], Edwards and Helail [47], Payne and Paker [109] and Wen and Yin [148] reported results of axial dispersion coefficients for the flow of two polymer solutions through a packed bed and their results were similar to the corresponding Newtonian results. Wen and Fan (1973) correlate the previous results for packed beds with the following expression:

$${\text{Pe}}{\left({= \frac{{Ud}}{{D_{{\text{L}}}}}} \right)} = 0.2 + 0.011 {\text{Re}}_{n}^{{0.48}} \quad {\text{with}} \; {\text{Re}}_{n} = \frac{{\rho d^{n} U^{{2 - n}}}}{m} ,$$
(20)

where m is the power law consistency coefficient. Note that Eq. 26 for n=1 (Newtonian fluids) reduces to the correlation obtained by Chung and Wen [32], for Newtonian fluid through packed beds.

3 Transverse dispersion

Generally, transverse dispersion coefficients are measured in non-reactive conditions, because the rate of mass transfer, observed experimentally, is directly related to the coefficient of transverse dispersion in the bed.

The most popular technique for the measurement of transverse dispersion consists in feeding a continuous stream of tracer from a “point” source somewhere in the bed (usually along the axis, if there is one) and measuring the radial variation of tracer concentration at one or more downstream locations.

The first study of mass transfer by radial dispersion in gaseous systems was carried out by Towle and Sherwood [140]. The results presented were very important for packed bed dispersion because they showed that dispersion was not influenced by the tracer molecular weight.

Bernard and Wilhelm [14] reported the first measurements, in liquid systems, of experimental values of transverse dispersion coefficients in packed beds of inerts by a Fickian model. The authors took into account the wall-effect condition and their experiments suggested that for high values of Reynolds number, the value of PeT is constant and between 11 and 13.

Baron [8] proposed a new model of radial dispersion in which a particle of tracer executes a simple random-walk displacement of ±1/2 particle diameter to give a transversal Peclet number between 5 and 13, when Re → ∞. The basis for this prediction is the random-walk theory, in which a statistical approach is employed. This method does not take into account the effects of radial variations in velocity and void space. Latinen [94] has extended the random-walk concept to three dimensions and predicted a value of 11.3, for PeT (∞).

Klinkenberg et al. [87] solved Eq. 2 for anisotropic dispersion, but considered that dispersion occurs in an infinite medium. In the same work were considered the particulate cases of isotropic dispersion (D T=D L) and longitudinal dispersion neglected.

Plautz and Johnstone [112] used the equation derived by Wilson [151], for heat transfer, and suggested a PeT between 11 and 13, for Re → ∞. Fahien and Smith [52] assumed that for Reynolds numbers in the range between 40 and 100, the Peclet number is independent of fluid velocity and equal to 8. The authors were the first to consider that the tracer pipe can be of significant diameter compared to the diameter of the bed.

Dorweiler and Fahien [44] used the equation derived by Fahien and Smith [52] to study the mass transfer in laminar and transient flows. The results showed that for Re < 200, the Peclet number based on the transverse dispersion coefficient is a linear function of the fluid velocity; and for Re > 200, at room temperature, the Peclet number is constant as also shown by Bernard and Wilhelm [14], Plautz and Johnstone [112] and Fahien and Smith [52]. The authors have demonstrated a difference in the Peclet number with radial position. The transversal Peclet number is constant from the axis to 0.8 times the radius and then rises near the wall.

Hiby and Schummer [79], and later Roemer et al. [118], presented the solution of the mass balance equation (Eq. 1), considering the tracer pipe to be of significant diameter compared to the diameter of the packed bed.

Saffman [120] considered the packed bed as a network of capillary tubes randomly orientated with respect to the main flow. At high Peclet number and at very long time, Saffman found that the dispersion never becomes truly mechanical, with zero velocity of the fluid at the capillary walls, the time required for a tracer particle to leave a capillary would become infinite as its distance from the walls goes to zero. The author proposed that D T=(3/16) ud when Re → ∞, but this prevision of transverse dispersion coefficient is higher than observed experimentally.

Hiby [78] and Blackwell [16] presented an experimental technique in which they divided the sampling region into two annular regions and calculated the transversal dispersion coefficient from the averaged concentrations of each of the two samples.

The experimental data points of Wilhelm [150] suggested that PeT (∞)=12, for beds of closely sized particles, and this value is accepted for the majority of the investigators [15, 33, 63, 78, 150].

Roemer et al. [118] studied radial mass transfer in packed beds at low flow rates, Re < 100. The authors considered the tracer pipe to be of significant diameter compared to the diameter of the bed (“finite source” model) and longitudinal and transverse dispersion are equal. In this work, the authors compared the values of PeT obtained with two methods (“instantaneous finite source” and “point source”) and concluded that the values of PeT obtained with the “point source” method were 10% less that the values obtained with the “instantaneous finite source” method. The authors estimated that neglecting the longitudinal dispersion in calculations of D T, for low values of Reynolds numbers, can cause errors of 10%.

Coelho and Guedes de Carvalho [33] developed a new experimental technique, based on the measurement of the rate of dissolution of planar or cylindrical surfaces, buried in the bed of inert particles and aligned with the flow direction. This alternative technique is simple to use, allows the determination of the coefficient of transverse dispersion in packed beds over a wide range of flow rates, and it is easily adaptable to work over a range of temperatures above ambient, as shown by Guedes de Carvalho and Delgado [60] and Delgado and Guedes de Carvalho [41].

In recent years, nuclear magnetic resonance has been used to determine both diffusion and dispersion coefficients [9, 55], with significant advantages, but this technique were limited to low fluid velocities.

It is important to remember that, at high Reynolds numbers, the main mechanism of transverse dispersion is the fluid deflection caused by deviations in the flow path caused by the particles in the bed (axial dispersion is caused by differences in fluid velocity in the flow), i.e. dispersion is caused by hydrodynamic mechanisms (macroscopic scale) and not by molecular diffusion (Brownian motion).

The result is a poor mixture at the “microscopic scale”. In fact, there are detected different values of solute concentration over a distance of the order of a particle diameter or less, what explains the convenience of use of an efficient averaging procedure [63]. This is probably one of the reasons that explain the difference observed in some experimental results of dispersion (see Fig. 12). Gunn and Pryce [68] showed that the standard deviation without repacking in the measurement of PeT was 5%, while when the bed was repacked each time of measurement, the standard deviation found was 15%.

Fig. 12
figure 12

Some experimental data points for transverse dispersion in liquid and gaseous systems

Full size image

3.1 Experimental techniques

The transverse dispersion coefficient can be determined by plotting (% composition: C 10 and C 90) versus (distance from 50% composition) on arithmetic-probability paper (Perkins and Johnston, 110]. The dispersion coefficient can be calculated by

$$D_{{\text{T}}} = \frac{u}{L}{\left({\frac{{C_{{90}} - C_{{10}}}}{{3.625}}} \right)}^{2} .$$
(21)

The most widely used techniques for the measurement of lateral dispersion are the continuous point source and the instantaneous finite source methods [116], which rely on the injection of tracer in a flowing liquid, followed by tracer detection at several points, downstream of the injection point. If at time t=0, a tracer is injected into the porous medium from an injector for the continuous point source method, the tip of the injector is taken as the tracer origin. For the instantaneous finite source method, the origin lays just down-gradient of the tracer injector.

Several authors like Roemer et al. [118] and Gunn and Pryce [68] used the solution of Eq. 1 when the axial dispersion coefficient is taken equal to radial dispersion coefficient. However, in this paper, we only consider experimental techniques where longitudinal dispersion is neglected.

3.1.1 “Instantaneous finite source” method

The method adopted by some authors like Dorweiler and Fahien [44] and Fahien and Smith [52] is based that the tracer is fed into the main stream at a point on the axis on the column.

The analytical model for an instantaneous finite source in one dimension is first presented by Crank [36]. Baetsle [5] extended the model to three-dimensional dispersion. Hunt [84] and Sun [136] provided the three-dimensional solution to the advection–dispersion equation [5] using different mathematical analysis. Van Genuchten and Alves [143] presented a number of analytical solutions of the one-dimensional convective–dispersive solute transport equation.

Tracer concentration should be low enough to avoid density-induced flow effects. The tracer should be conserved (i.e. not destroyed) in the experiment and the distribution of flow rates at the outlet must be the same as in the feed so as not to induce complications in the flow field.

Radial dispersion may be evaluated by injecting a steady flow of a tracer at a point of a test section column. For a boundary layer, which is thin in comparison with the length of the axial distance (L), longitudinal dispersion will be negligible. Taking a radial co-ordinate, r, to measure the distance to the axis of the bed and a co-ordinate z, to measure the distance along the average flow direction, the differential mass balance on the solute reads

$$\frac{{D_{{\text{T}}}}}{r}\frac{\partial}{{\partial r}}{\left({r\frac{{\partial C}}{{\partial r}}} \right)} = u\frac{{\partial C}}{{\partial z}} ,$$
(22)

where D T is the radial dispersion coefficient. Fahien and Smith [52] solved the differential dispersion Eq. 22 with

$$z = 0\quad 0 < r < R_{{\text{i}}} \quad C = C_{0} ,$$
(23a)
$$z = 0\quad R_{{\text{i}}} < r < R\quad C = 0,$$
(23b)
$${\text{all}}\;z\quad r = R;{\enspace}r = R_{{\text{i}}} \quad \frac{{\partial C}}{{\partial r}} = 0$$
(23c)

and the solution of Eq. 22 with the boundary conditions of (23a–c) is

$$\frac{C}{{C_{0}}} = 1 + \frac{{2R}}{{R_{{\text{i}}}}}{\sum\limits_{n = 1}^\infty {\frac{{J_{1} {\left({\beta _{n} R_{{\text{i}}}/R} \right)}J_{0} {\left({\beta_{n} r/R} \right)}}}{{\beta _{n} J^{2}_{0} {\left({\beta _{n}} \right)}}}\frac{z}{R}{\text{exp}}{\left[ {- \frac{{\beta ^{2}_{n}}}{{{\text{Pe}}_{{\text{T}}}}}\frac{z}{R}} \right]}}} ,$$
(24)

where J 0 and J 1 are the Bessel functions of the first kind, of order 0 and 1, respectively, and the β n are the positive roots of the Bessel function of the first kind, of order 1.

3.1.2 “Continuous point source” method

This method is based on the measurement of radial mass exchange between two coaxial portions of a packed bed, along which liquid flows, parallel to the axis; the feed to the central portion is water containing a small amount of sodium chloride and that too the outer portion is pure water.

Klinkenberg et al. [87] derived an analytical solution for Eq. 22, neglecting the effect of injector radius (see Fig. 13), with the boundary conditions given by

$$z = + \infty \quad {\text{all}}\;R\quad C = C_{0} ,$$
(24a)
$$z = - \infty \quad {\text{all}}\;R\quad C = 0, $$
(24b)
$${\text{all}}\;z\quad r = R;{\enspace}r = 0\quad \frac{{\partial C}}{{\partial r}} = 0$$
(24c)

and the solution of Eq. 22 with the boundary conditions (24a–c) is

$$\frac{C}{{C_{0}}} = 1 + {\sum\limits_{n = 1}^\infty {\frac{{J_{0} {\left({\beta _{n} r/R} \right)}}}{{J^{2}_{0} {\left({\beta _{n}} \right)}}}{\text{exp}}{\left[ {- \frac{{\beta ^{2}_{n} D_{{\text{T}}} z}}{{R^{2} u}}} \right]}}} ,$$
(25)

where J 0 is the Bessel function of the first kind, of order 0, and the β n are the positive roots of the Bessel function of the first kind, of order 1.

Fig. 13
figure 13

Schematic diagram of test section for radial dispersion

Full size image

Plautz and Johnstone [112] and Sinclair and Potter [128] used Eq. 22 for an infinite case, where no boundary is present, of mass diffusion from a point source. The result with axial dispersion neglected was given by Carslaw and Jaeger [28]

$$\frac{C}{{C_{0}}} = \frac{{R^{2} u}}{{4D_{{\text{T}}} z}}\exp {\left({- \frac{{r^{2} u}}{{4D_{{\text{T}}} z}}} \right)} .$$
(26)

This solution includes a simplification possible when z/r > 5 (axial dispersion neglected).

Blackwell [16] assumes the effect of radius injector and gives the analytical solution to the differential equation describing transverse dispersion in the absence of longitudinal dispersion. Hiby and Schummer [79] presented a solution of Eq. 22 that considered the tracer pipe to be of significant diameter compared to the diameter of the bed (see Fig. 14), and the boundary conditions adopted were

$$z > 0\quad r = R\quad \frac{{\partial C}}{{\partial r}} = 0,$$
(27a)
$$z = 0\quad r < R_{{\text{i}}} \quad C = C_{0} ,$$
(27b)
$$z = 0\quad R_{{\text{i}}} < r < R\quad C = 0.$$
(27c)
Fig. 14
figure 14

Sketch of boundary conditions proposed by Hiby and Schummer [79]

Full size image

On the assumption that D T and u are independent of position, the solution of Eq. 22 following Hiby and Schummer [79] gives, for the resulting outlet average concentration in the inner stream of liquid,

$$\frac{{\bar{C}}}{C_{0}} = 4{\sum\limits_{n = 0}^\infty {\frac{{J_{1}^{2} {\left({\beta_{n} R_{{\text{i}}}/R}\right)}}}{{\beta_{n}^{2} J_{0}^{2} {\left({\beta _{n}} \right)}}}{\text{exp}}{\left[ {- \frac{{Ld}}{{{\text{Pe}}_{{\text{T}}}}}{\left({\frac{{\beta _{n}}}{R}} \right)}^{2}} \right]}}} ,$$
(28)

where J 0 and J 1 are the Bessel function of the first kind, of orders 0 and 1, respectively, and the β n are the positive roots of the Bessel functions of the first kind, of order 1. The measurement of \({\bar{C}}\) and C 0 provides a method for the determination of PeT (and therefore of D T), since all other parameters in the equation are known.

Harleman and Rumer [71] and Han et al. [69] consider a steady-state experiment in a rectangular column. The authors solved the differential equation with the boundary conditions,

$$C = C_{0} \quad x = 0\quad 0 < y < + \infty , $$
(29a)
$$C = 0\quad x = 0\quad - \infty < y < 0, $$
(29b)
$$\frac{{\partial C}}{{\partial y}} = 0\quad {\text{all}}\;x\quad y \to \pm \infty $$
(29c)

and the solution obtained for a step input in concentration, is

$$\frac{C}{{C_{0}}} = \frac{1}{2}{\left[{1 - {\text{erf}}{\left({{\sqrt {\frac{{{\text{Pe}}_{{\text{T}}}}}{{Ld}}}}\frac{y}{2}} \right)}} \right]} .$$
(30)

3.1.3 Mass transfer from a flat surface aligned with the flow

Coelho and Guedes de Carvalho [33] developed a new experimental technique, based on the measurement of the rate of dissolution of planar or cylindrical surfaces, buried in the bed of inert particles and aligned with the flow direction.

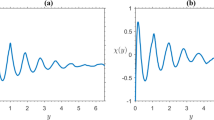
Figure 15a sketches a section through a packed bed along which liquid is flowing, close to a flat wall, part of which (0 < x < L) is slightly soluble. Liquid flow will be taken to be steady, with uniform average interstitial velocity u, and if the concentration of solute in the liquid fed to the bed is C 0 and the solubility of the solid in the wall is C *, a mass transfer boundary layer will develop, across which the solute concentration drops from C C *, at y=0, to C→ C 0, for large y.

Fig. 15
figure 15

a Flow along soluble slab; b Mass transfer boundary layer

Full size image

The question of how large is meant by a “large y” needs some clarification. Obviously, if L were only of the order of a few particle diameters, and u were large, the concentration of solute would fall to C 0 over a distance of less than one particle diameter. In that case, flow in the bulk of the packed bed would have little influence on the mass transfer process, which would be dominated by diffusion in a thin layer of liquid, adjacent to the soluble surface. Already for large L and low u, the thickness of the mass transfer boundary layer will grow from zero, at x = 0, to a value of several particle diameters, at x = L and the process of mass transfer will then be determined by a competition between advection and dispersion in the bulk of the bed. Now it is well-known [145] that the voidage of a packed bed (and therefore the fluid velocity) is higher near a containing flat wall, but in the case of Guedes de Carvalho and Delgado [60] experiments, it may be considered that such a non-uniformity will have negligible effect. For one thing, we work with bed particles of between 0.2 and 0.5 mm and therefore the region of increased voidage will be very thin. Furthermore, because the inert particles making up the bed indent the soluble surface slightly, as dissolution takes place (and this slight indentation is easily confirmed when the piece of soluble solid is removed from within the bed), there is in fact virtually no near wall region of higher voidage. Confirmation of these assumptions is given by the results of the experiments described below.

Taking a small control volume inside this boundary layer (see Fig. 15b), with side lengths δ x, δ y and unity (perpendicular to the figure), it is possible to perform a mass balance on the solute, for the steady state. If the boundary layer is thin, compared to the length of the soluble slab, longitudinal dispersion is likely to be negligible, since the surface y=0, 0 < x < L, is a surface of constant concentration (C C *).

Noting that the surface y=0, 0 < x < L, is a surface of constant concentration, along which ∂2 C/∂x 2=0 and axial dispersion will be negligible, for a boundary layer which is thin in comparison with the length of the soluble slab. (A conservative criterion for this approximation to be valid is L/d > 20). For a slab, the equation of diffusion in one dimension is

$$u\frac{{\partial C}}{{\partial x}} = D_{{\text{T}}} \frac{{\partial ^{2} C}}{{\partial y^{2}}}$$
(31)

to be solved with

$$C = C_{0} \quad x = 0\quad y > 0,$$
(32a)
$$C = C^{*} \quad x > 0\quad y = 0,$$
(32b)
$$C \to C_{0} \quad x > 0\quad y \to \infty .$$
(32c)

The solution is

$$\frac{{C - C_{0}}}{{C^{*} - C_{0}}} = {\text{erfc}}{\left({\frac{y}{{2{\sqrt {D_{{\text{T}}} x/u}}}}} \right)}$$
(33)

and the flux of dissolution at any point on the slab surface may be obtained from (33) as

$$N = - D_{{\text{T}}} \varepsilon {\left({\frac{{\partial C}}{{\partial y}}} \right)}_{{y = 0}} = {\left({C^{*} - C_{0}} \right)}\varepsilon {\left({\frac{{D_{{\text{T}}}}}{{\pi x/u}}} \right)}^{{1/2}} .$$
(34)

The instant rate of solid dissolution over the whole slab surface may now be calculated by integration of the local flux; taking a width b along the surface of the solid, perpendicular to the flow direction, there results

$$n = {\int\limits_0^L {Nb{\text{d}}x}} = {\left({C^{*} - C_{0}} \right)} \varepsilon bL{\left({\frac{{4D_{{\text{T}}}}}{{\pi L/u}}} \right)}^{{1/2}} $$
(35)

and it is useful to define the coefficient

$$k = \frac{n}{{(bL) (C^{*} - C_{0} )}} = \varepsilon {\left({\frac{{4D_{{\text{T}}}}}{{\pi L/u}}} \right)}^{{1/2}} . $$
(36)

This result shows how the measurement of the rate of dissolution of the solid, which is directly related to the average mass transfer coefficient, may be used to determine the coefficient of transverse dispersion in the bed.

A simple way of checking the result in Eq. 36 is afforded by the predicted proportionality between k and the inverse square root of L. Experiments performed by Coelho and Guedes de Carvalho [33] with a wide range of slab lengths, both for the dissolution of benzoic acid in water and the sublimation of naphthalene in air, confirm the general validity of the above theory, provided that the approximate criterion

$$\frac{L}{d} \geq 0.62 {\left({\frac{{ud}}{{D_{{\text{m}}}}}} \right)}$$
(37)

is observed, where D m is the molecular diffusion coefficient of the solute. When the above criterion is not observed, the near wall film resistance to diffusion will have to be taken into account and approximate ways of doing this are described by Coelho and Guedes de Carvalho [33].

The similarity between the result given by Eq. 36 and that obtained by Higbie [80], for gas–liquid mass transfer by surface renewal, is striking. Equation 36 simply states that the average mass transfer coefficient, for the soluble wall, is that corresponding to surface renewal with a time of contact t c=L/u and an apparent diffusion coefficient D T.

3.1.4 Mass transfer from a cylinder aligned with the flow

For practical reasons, it proves simpler to perform experiments in which the dissolving solid is a cylinder, aligned with the flow direction and it is important to know the theoretical expressions relating the average mass transfer coefficient with the coefficient of dispersion, D T, for that situation.

Fortunately, under appropriate conditions, easy to reproduce in the laboratory, the thickness of the mass transfer boundary layer is small in comparison with the radius of the dissolving cylinder and under such circumstances, the analysis presented above, for dissolution from a flat surface, is still applicable with good accuracy.

However, there are instances in which this simplification is not valid and an exact solution may be worked out in cylindrical co-ordinates, as shown by Coelho and Guedes de Carvalho [33].

The resulting expression for k is cumbersome to evaluate, but for small values of the parameter θc=D T t c/a 2, where t c=L/u is the time of contact between liquid and solid, a good approximation is

$$k = \varepsilon {\left({\frac{{4D_{{\text{T}}}}}{{\pi t_{{\text{c}}}}}} \right)}^{1/2}{\left({1 + \frac{{{\sqrt \pi}}}{4}\theta ^{1/2}_{{\text{c}}} - \frac{1}{{12}}\theta _{{\text{c}}} + \frac{{{\sqrt \pi}}}{{32}}\theta^{3/2}_{{\text{c}}} - \cdots} \right)} .$$
(38)

For higher values of θc, up to θc =0.4, the first four terms may be used, instead of the infinite series on the right-hand side of Eq. 38, with an error of less than 1% in k.

3.2 Parameters influencing transverse dispersion—Porous medium

3.2.1 Length of the packed column

Han et al. [69] showed that values of the radial dispersion coefficient, for uniform-size packed beds, measured at different positions in the bed are not function of bed location, i.e. they observed no time-dependent behaviour for radial dispersion, because transverse dispersion is caused by mechanical mechanism alone.

An important aspect to be considered, as a check on the experimental method of Coelho and Guedes de Carvalho [33], is the influence of the length of the test cylinder on the measured value of D T. In reality, the two variables are independent, provided that the criterion given by Eq. 37 is satisfied (see Fig. 16).

Fig. 16
figure 16

Effect of length of soluble cylinder on the measurement of D T

Full size image

3.2.2 Ratio of column diameter to particle diameter

Several investigators, like Fahien and Smith [52], Latinen [94] and Singer and Wilhelm [129], have studied the wall effect on transverse dispersion coefficient. The experiments suggested that in a packing structure characterized by significant variations of void fraction in radial direction, up to a distance of about two particle diameters from the wall, a non-uniform radial velocity profile is induced, with a maximum just near the wall. As a result, the wall effects occur due to large voidage fluctuations near the wall. The above investigators, also showed, that the increase in radial dispersion in the laminar region would be the same order of magnitude as in the turbulent region.

3.2.3 Particle size distribution

Eidsath et al. [49] studied the effect of particle size distribution on dispersion. As the ratio of particle diameter went from a value of 2 to 5, the radial dispersion decreased by a factor of 3, but perhaps the results were a cause of the simple geometry employed in these computations (packed bed of cylinders). Steady-state measurements of radial dispersion reported by Han et al. [69], with same void fraction and the same mean particle diameter, but different particle size range (ratio of maximum to minimum particle diameter equal to 2.2 and 7.3), showed that there was no evidence to indicate a change in radial dispersion with particle size distribution (see Fig. 17a).

Fig. 17
figure 17

Effect of particle size distribution on radial dispersion. a D T/D m versus Pem; b D T/D m versus u

Full size image

The effect of a distribution of particle sizes within the bed, on the radial dispersion coefficient, may be assessed from Guedes de Carvalho and Delgado [60]. In particular, lot D was prepared by carefully blending lots B and E in a proportion of 1:1 (by weight). In Fig. 17b, dispersion data obtained with the mixed lot are seen to fall in between the data for the original separate lots, as might be expected. Figure 17a shows that in a plot of D T/D m vs. Pem, the data for the three lots fall along the same line, when d (in Pem) is taken to represent the average particle size in the bed.

3.2.4 Particle shape

Several investigators paid attention to the effect of particle shape on the radial dispersion coefficient both for liquid and gaseous systems. England and Gunn [50] measured the dispersion of argon in beds of solid cylinders and beds of hollow cylinders and have concluded that D T tend to be greater with packs of hollow cylinders than with packs of solid cylinders, and these results were greater than obtained with packs of spherical particles (see Fig. 18).

Fig. 18
figure 18

Effect of particle shape on transverse dispersion

Full size image

The same conclusion, in liquid systems, has been obtained by Hiby [78], who used packed beds of glass spheres and Raschig rings, and Bernard and Wilhem (1950), who used packed beds of cubes, cylinders and glass spheres. Figure 18 shows that the radial dispersion coefficient tends to be greater in packed beds of non-spherical particles.

However, Blackwell [16], List [99], Guedes de Carvalho and Delgado [60] and others reported experiments with packed beds of sand and showed that D T obtained with “glass ballotini” are very close to those for sand (not pebble or gravel) and the conclusion seems to be that particle shape has only a small influence on lateral dispersion, for random packings of “isometric” particles.

3.3 Parameters influencing transverse dispersion—Fluid properties

3.3.1 Viscosity and density of the fluid

An effect of fluid densities and viscous forces on transverse dispersion has been studied by Grane and Garner [57] and Pozzi and Blackwell [113] and the authors concluded that when a fluid is displaced from a packed bed by a less viscous fluid, the viscous forces create an unstable pressure distribution and the less viscous fluid will penetrate the medium in the form of fingers, unless the density has an opposing effect.

3.3.2 Fluid velocity

For very low fluid velocities, u, dispersion is the direct result of molecular diffusion, with D T=D′m. As the velocity of the fluid is increased, the contribution of convective dispersion becomes dominant over that of molecular diffusion and D T becomes less sensitive to temperature. According to several authors [15, 33, 63, 78, 150] D T → ud/PeT(∞), for high enough values of u, where d is particle size and PeT (∞) ≅ 12 for beds of closely sized particles. Assuming that the diffusive and convective components of dispersion are additive, the same authors suggest that D T=D′m+ud/K, which may be written in dimensionless form as

$$\frac{{D_{{\text{T}}}}}{{D_{{\text{m}}}}} = \frac{1}{\tau} + \frac{1}{{12}}\frac{{ud}}{{D_{{\text{m}}}}} \quad {\text{or}} \quad \frac{1}{{{\text{Pe}}_{{\text{T}}}}} = \frac{1}{\tau}\frac{\varepsilon}{{{\text{ReSc}}}} + \frac{1}{{12}} .$$
(39)

This equation has been shown [33] to give a fairly accurate description of transverse dispersion in gas flow through packed beds, but it is not appropriate for the description of dispersion in liquids, over an intermediate range of values of ud/D m, as pointed out by several of the authors mentioned above.

Figure 19(a–b) shows that the value of the transverse dispersion coefficient is seen to increase with fluid velocity and comparison between the two plots shows that D T also increases with particle size.

Fig. 19
figure 19

Variation of D T with fluid velocity. a sand size d=0.297 mm; b sand size d=0.496 mm

Full size image

Data on dispersion in randomly packed beds of closely sized, near spherical particles, lend themselves to simple correlation by means of dimensional analysis. Making use of Buckingham’s theorem it may therefore be concluded that

$$\frac{{D_{{\text{T}}}}}{{D_{{\text{m}}}}} = \Phi {\left({\frac{{ud}}{{D_{m}}} , \frac{\mu}{{\rho D_{m}}}} \right)} \quad {\text{or}} \quad {\text{Pe}}_{{\text{L}}} = \Phi {\left({{\text{Re, Sc}}} \right)}$$
(40)

and it is useful to make Pem=ud/D m and Sc =μ/ρ D m.

3.3.3 Fluid temperature (or Schmidt number)

The dependence of D T on liquid properties and velocity is best given in plots of PeT vs. Pem, for different values of Sc. Not surprisingly, Fig. 20 shows that the variation of PeT with Pem gets closer to that for gas flow as the value of Sc is decreased. For the lowest Sc tested (Sc = 54; T=373 K), PeT does not differ by more than 30% from the value given by Eq. 39, with PeT (∞)=12, over the entire range of Pem. But for the higher values of Sc, the experimental values of PeT may be up to four times the values given by Eq. 39.

Fig. 20
figure 20

Dependence of PeT on Pem for different values of Sc

Full size image

Delgado and Guedes de Carvalho [41] had studied the dependence of D T/D m on Sc, up to Pem ≅ 1350, and they reported a smooth increase in D T/D m with Pem, for all values of Sc. But the data in Fig. 20 show that there is a sudden change in the trend of variation of PeT with Pem, somewhere above Pem ≅ 1350, a maximum being reached in the approximate range 1400 < Pem < 1800 (depending on Sc). The fact that the change in trend corresponds to a much enhanced increase in D T (i.e. a decrease in PeT), in response to a small increase in u (i.e. in Pem), strongly suggests a connection with the transition from laminar to turbulent flow in the interstices of the packing. The plot of PeT vs. Re, shown in Fig. 21, seems to support this view, since the maxima in PeT are reached for 0.3 < Re < 10 (depending on Sc) and this is the approximate range of values of Re for the transition from laminar to turbulent flow. The range 1 < Re < 10 is often indicated for that transition (e.g. 11], but Scheidegger [121] as giving Re = 0.1 for the lower limit of that transition.

Fig. 21
figure 21

Dependence of PeT on Re for different values of Sc

Full size image

The plot in Fig. 21 also suggests that “purely mechanical” fluid dispersion will be observed above about Re = 100; this value is estimated as the convergence of the data points for liquids with the line representing Eq. 39. Figure 22 shows the data reported by most other authors (all for Sc ≥ 540) in a plot of PeT vs. Pem. With the exception of the data of Hoopes and Harleman [82] and some of the points of Grane and Gardner [57] and Bernard and Wilhelm [14], general agreement is observed with Guedes de Carvalho and Delgado [61] data for high Sc.

Fig. 22
figure 22

Comparison between our data points and the results of other authors for Sc ≥ 540

Full size image

3.4 Correlations

In this context, it is interesting to consider the predicting accuracy of some alternative empirical correlations that have been proposed to represent the experimental data in liquid flow, as the equation of Gunn [64]:

$$\frac{1}{{{\text{Pe}}_{{\text{T}}}}} = \frac{1}{{{\text{Pe}}_{{\text{f}}}}} + \frac{1}{\tau}\frac{\varepsilon}{{{\text{ReSc}}}} ,$$
(41)

where the fluid-mechanical Peclet number, Pef, is defined by,

$${\text{Pe}}_{{\text{f}}} = 40 - 29{\text{e}}^{{- 7/{\text{Re}}}} \quad {\text{for spheres}},\; \tau = {\sqrt 2} ,$$
(42a)
$${\text{Pe}}_{{\text{f}}} = 11 - 4{\text{e}}^{{- 7/{\text{Re}}}} \quad {\text{for solid cylinders}},\; \tau = 1.93, $$
(42b)
$${\text{Pe}}_{{\text{f}}} = 9 - 3.3{\text{e}}^{{- 7/{\text{Re}}}} \quad {\text{for hollow cylinders}},\; \tau = 1.8 .$$
(42c)

And the empirical equation proposed by Wen and Fan [147],

$${\text{Pe}}_{{\text{T}}} = \frac{{17.5}}{{{\text{Re}}^{{0.75}}}} + 11.4 \quad ({\text{for high values of }}{\text{Pe}}_{{\text{m}}}). $$
(43)

In Fig. 23, the solid line corresponding to Eq. 39, with PeT (∞)=12, is again represented and so are two dashed lines corresponding to a correlation proposed by Gunn [64] for the extreme values of Schmidt number obtained in Guedes de Carvalho and Delgado [61] experiments. Comparison with the experimental points shows that the correlation does not account for the influence of Sc on PeT, for Pem < 600, and it may seem to be very inadequate at low values of Sc, for 600 < Pem < 105. The empirical correlation proposed by Wen and Fan [147], for high values of Pem and Sc, is also very inadequate, because it is only based in the experimental data of Bernard and Wilhelm [14] and on the Hartman et al. [74].

Fig. 23
figure 23

Comparison between data and correlations of other investigators

Full size image

Figure 24 represents the experimental points obtained by Guedes de Carvalho and Delgado [61], together with the solid lines represented by Eqs. 44–45, for the values of Sc indicated in the figure, and which are seen to represent the data very well, with a maximum deviation of 20%. For Sc ≤ 550, experiment shows (see Fig. 24) that PeT depends both on Pem and Sc and the following expressions are suggested

$$\frac{1}{{{\text{Pe}}_{{\text{T}}}}} = \frac{1}{\tau}\frac{1}{{{\text{Pe}}_{{\text{m}}}}} + \frac{1}{{12}} - {\left({\frac{{{\text{Sc}}}}{{1500}}} \right)}^{{4.8}} {\left({\tau {\text{Pe}}_{{\text{m}}}} \right)}^{{3.83 - 1.3{\text{log}}_{{10}} {\text{(Sc)}}}} \quad ({\text{for}}\; {\text{Pe}}_{{\text{m}}} \leq 1,600), $$
(44a)
$${\text{Pe}}_{{\text{T}}} = (0.058{\text{Sc}} + 14) - (0.058{\text{Sc}} + 2) \exp {\left({- \frac{{352{\text{Sc}}^{{0.5}}}}{{{\text{Pe}}_{{\text{m}}}}}} \right)} \quad ({\text{for}}; {\text{Pe}}_{{\text{m}}} > 1,600) . $$
(44b)
Fig. 24
figure 24

Comparison between experimental data and Eqs. 44a,b and 45a,b

Full size image

The dividing line between the ascending curves (44a) and the descending curves (44b) is quoted as Pem ≅ 1600, since the exact value of Pem at the point of intersection of (44a) and (44b) depends on Sc. For Sc < 550, the two lines always meet in the interval 1400 < Pem < 1750; for any given value of Pem in this interval, the lower value of PeT (from those given by Eqs. 44a and 44b) should be adopted in the representation of PeT vs. Pem. However, if the line of division between the range of application of Eq. 44a and that of Eq. 44b is taken, rigidly, at exactly Pem = 1600, for all Sc < 550, a small discontinuity will result in the lines PeT vs. Pem at that point, which is nevertheless negligible in comparison with experimental uncertainty.

For Sc > 550, the equations representing the data must take into account that PeT is only dependent on Pem, in the ascending part of the curve PeT vs. Pem and that PeT only depends on Re (=ɛ Pem/Sc), in the descending part of the same curve. The following equations give a good representation of the data for Sc > 550

$$\frac{1}{{{\text{Pe}}_{{\text{T}}}}} = \frac{1}{\tau}\frac{1}{{{\text{Pe}}_{{\text{m}}}}} + \frac{1}{{12}} - 8.1 \times 10^{{- 3}} {\left({\tau {\text{Pe}}_{{\text{m}}}} \right)}^{{0.268}} \quad ({\text{for}}\; {\text{Pe}}_{{\text{m}}} \leq 1,600) , $$
(45a)
$${\text{Pe}}_{{\text{T}}} = 45.9 - 33.9 \times {\text{exp}}{\left({- \frac{{{\text{15Sc}}}}{{{\text{Pe}}_{{\text{m}}}}}} \right)} \quad ({\text{for}}\; {\text{Pe}}_{{\text{m}}} > 1,600) .$$
(45b)

3.5 Dispersion in packed beds flowing by non-Newtonian fluids

The only study of the influence of non-Newtonian fluid in radial dispersion coefficients is reported by Hassell and Bondi [75]. The authors showed that the quality of mixing deteriorate with increasing viscosity.

4 Conclusions

The present work increases our knowledge about dispersion in packed beds by providing a critical analysis on the effect of fluid properties and porous medium on the values of axial and radial dispersion coefficients.

Different experimental techniques are presented in full detail and the data obtained from these techniques are very similar. An improved technique for the determination of the coefficient of transverse dispersion in fluid flow through packed beds is described in more detail, which is based on the measurement of the rate of dissolution of buried flat or cylindrical surfaces.

A large number of experimental data on dispersion available in the literature for packed beds were examined to pave the way for the formulation of new correlations for the prediction of PeT and PeL. The correlations proposed are shown to be more accurate than previous correlations and they cover the entire range of values of Pem and Sc. The longitudinal dispersion coefficient can be calculated by Eqs. 18 and 19 and the transverse dispersion coefficient by Eqs. 44 and 45.