A :

Aspect ratio

C p :

Specific heat at constant pressure (J kg–1 K–1)

Da :

Darcy parameter

g :

Gravitational acceleration (m/sec)

Gr :

Grashof number

H :

Enclosure height (m)

K :

Permeability of the porous medium (m2)

p :

Fluid pressure (Pa)

Pr :

Prandtl number

t :

Time (s)

T :

Temperature (°C)

T 0, T 1 :

Boundary temperatures

u, v :

Velocity in the x- and y-directions (m/s)

U, V :

Dimensionless velocities

x, y, z :

Cartesian coordinates (L)

X, Y :

Dimensionless co-ordinates

α:

Thermal diffusivity

β:

Coefficient of thermal expansion of fluid (K–1)

θ:

Dimensionless temperature

ν:

Effective kinematic viscosity (μ/ρ)

ρ:

Fluid density at reference temperature (T c )

τ:

Dimensionless time

ψ:

Streamfunction (m2/s)

γ:

Inverse Darcy number

Ω:

Dimensionless vorticity

1 Introduction

Bénard convection in cavities filled with a porous medium is a mathematically interesting but practically relevant problem because of its application to geothermal phenomena and the safe disposal of nuclear waste, for example. There now exist a very large number of papers which are devoted to this topic, and many of these have been reviewed recently by Rees [1]. Part of the reason for this voluminous literature lies with the fact that there are many models describing different types of porous medium. For example He and Georgiadis [2] and Rees [3], by bringing into account the quadratic inertia terms in the momentum equation, have investigated the effect of inertia on the onset and weakly nonlinear development of convection. Kladius and Prasad [4] have studied the influence of Darcy and Prandtl numbers for fluid flow in a porous medium. Lage et al. [5, 6] conducted a series of numerical investigations on the effect of Prandtl number on Benard convection in an infinite porous fluid layer. Recently, Jue [7] considered enclosures of various aspect ratios filled with a porous medium and examined the effect of Brinkman resistance in detail for the aspect ratios 1, 2, and 4. Khanafer and Chamkha [8] have also investigated numerically the Brinkman-extended Darcy unsteady mixed convection flow in an enclosure, but with the addition of internal heat generation and the inclusion of the convective terms in the governing equations. Finally the problem of natural convection flow of a fluid in a square cavity filled with porous medium and subject to internal heat generation and non-uniformly heated side-walls has been investigated by Hossain and Wilson [9].

In this paper we follow the analysis of Jue [7] but with different boundary conditions. It is frequently the case that the vertical sidewalls of a convecting cavity are taken to be insulating. This has the effect that at sufficiently low Darcy-Rayleigh numbers the basic state is one of conduction through the porous medium with no flow. In the present paper the lower surface is held at a uniform but relatively hot temperature, but the other three surfaces are maintained at the same relatively cold temperature. The presence of the cold sidewalls causes flow to exist at all nonzero Rayleigh numbers. The present work is a preliminary investigation of the effect of such a boundary condition on the ensuing flow and heat transfer.

2 Mathematical formalism

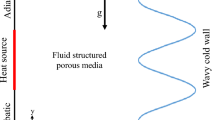
We consider the two-dimensional natural convective flow of a viscous incompressible fluid in an isotropic and rigid porous cavity contained between two horizontal plates at y = 0 and y = H and two vertical sidewalls at x = 0 and x = 2AH, where 2A is the aspect ratio of the cavity. The fluid is taken to have the uniform temperature, T 0 at time t = 0. The temperature of the lower plate is then raised suddenly to T 1 and thereafter maintained uniform. Figure 1a represents the physical model along with the boundary conditions.

Fig. 1.
figure 1

(a) The flow configuration and the coordinate system. (b) Schematic representation of the cavity depicting the mesh used in the numerical simulations and the boundary conditions

Full size image

Under the above assumptions the governing equations for the two-dimensional flow of a viscous incompressible fluid for natural convection flow in a rectangular porous cavity are as follows:

$$ {\partial u \over \partial x} + {\partial v \over \partial y} = 0 $$
(1)
$$ {\partial u \over \partial t} + u{\partial u \over \partial x} + \upsilon {\partial u \over \partial y} = - {1 \over \rho} {\partial p \over \partial x} + \nu \left({\partial ^2 u \over \partial x^2} + {\partial ^2 u \over \partial y^2} \right) - {\nu \over K}u $$
(2)
$$ {\partial v \over \partial t} + u{\partial v \over \partial x} + \upsilon {\partial \upsilon \over \partial y} = - {1 \over \rho} {\partial p \over \partial y} + \nu \left({\partial ^2 \upsilon \over \partial x^2} + {\partial ^2 \upsilon \over \partial y^2} \right) - {\nu \over K} \upsilon + g\beta _T (T - T_0 ) $$
(3)
$$ {\partial T \over \partial t} + u {\partial T \over \partial x} + \upsilon {\partial T \over \partial y} = \alpha \left({\partial ^2 T \over \partial x^2} + {\partial ^2 T \over \partial y^2} \right) $$
(4)

where u and v are the x- and y-components of the velocity field, respectively, K is the permeability of the porous medium, g is the acceleration due to gravity, β T is the volumetric expansion coefficients for temperature and α is the thermal diffusivity. Further, T is the temperature of the fluid flow and the time is t. In this study we have neglected stratification, viscous dissipation and other additional effects such as local thermal nonequilibrium.

In equations (2) and (3) K is the measure of permeability of the porous medium, H is a reference length, ν/H is reference velocity, and T 1 – T 0 is a reference temperature difference. Based on these reference quantities, the following dimensionless variables are constructed:

$$ \eqalign{& X = {x \over H} \quad Y = {y \over H} \quad \tau = {t \over H^2/\nu} \cr & U = {u \over \nu/H} \quad V = {v \over \nu /H} \quad \theta = {T - T_0 \over T_1 - T_0}} $$
(5)

By introducing the above dimensionless dependent and independent variables in the governing equations the following equations are obtained

$$ {\partial \Omega \over \partial \tau} + {\partial (U\Omega ) \over \partial X} + {\partial (V\Omega ) \over \partial Y} = \left({\partial ^2 \over \partial X^2} + {\partial ^2 \over \partial Y^2} \right) \Omega + \gamma \left({\partial U \over \partial Y} - {\partial V \over \partial X} \right) - Gr{\partial \theta \over \partial X} $$
(6)
$$ {\partial T \over \partial \tau} + {\partial (U\theta ) \over \partial X} + {\partial (V\theta ) \over \partial Y} = {1 \over \hbox{Pr}} \left({\partial ^2 \over \partial X^2} + {\partial ^2 \over \partial Y^2} \right)\theta $$
(7)

where

$$ \Omega = - \left({\partial ^2 \over \partial X^2} + {\partial ^2 \over \partial Y^2} \right)\psi $$
(8)

is the vorticity directed in the z direction, and ψ is the stream function defined by

$$ U = {\partial \psi \over \partial Y}, \quad V = - {\partial \psi \over \partial X} $$
(9)

In the above equations

$$ Gr = {g\beta _T (T_1 - T_0 )H^3 \over \nu ^2}, \quad \gamma = 1/\hbox{Da}, \quad \hbox{Pr} = {\nu \over \alpha} $$
(10)

are, respectively, the Grashof number due to thermal diffusion, the inverse of the Darcy number, and the Prandtl number.

The cavity we study is symmetric above the vertical mid-plane and therefore we consider only the left half of the flow region shown in Fig. 1a in order to reduce computational time. However, we note that some computations over the whole fluid domain were undertaken in a deliberate attempt to find solutions which break this symmetry, but were unsuccessful, and therefore we are confident that the solutions given here are realisable in practice. We note that the computations of Banu et al. [10] have yielded asymmetric flows, but in that case all four boundaries were held at the same temperature; in the present configuration the cold sidewalls seem to act to impose symmetry artificially.

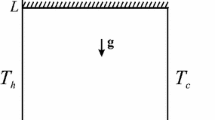
At time τ = 0, the temperature satisfies θ = 0 everywhere except for θ = 1 on the lower plate. As time increases the temperature field develops but the values on the horizontal and vertical bounding surfaces are maintained at their initial values. We apply the boundary conditions ψ = 0 and ∂θ/∂X = 0 on X = AH as required by the symmetry of the cavity. The other boundary conditions are shown in Fig. 1b.

An upwind finite-difference method, together with successive over relaxation iteration technique has been employed to integrate the model equations (6) to (8) governing the flow. Except for the non-linear terms, all spatial dervatives in the governing differential equations are approximated at the interior grid points using second order central difference approximations. In the present computations convergence was assumed when the maximum absolute point-wise change over one iteration was less than 0.0001.

Meshes of size h × h were chosen for the numerical work, and the computational region uses m vertical and n horizontal grid lines as shown in Fig. 1b above. Since the dimensionless distance between the parallel plates is H, the grid size h has the value H/(n – 1) as we use H = 3 and n = 31 equally spaced intervals. In the present computations we consider the aspect ratios A = 1, 2, 3, 4 and 5 and therefore the meshes were taken to be 31 × 31, 61 × 31, 91× 31, 121× 31 and 151× 31, respectively. To see the effect of mesh size on the numerical results, computations were carried out till the steady-state reached for the flow in a rectangular cavity with Gr = 200, Pr = 0.7 and 1/Da = 0.0 using three mesh sizes: 51× 26, 61× 31 and 81× 41 with H =3. The results in terms of maximum and minimum values of ψ are entered in Table 1, which shows the differences due to grid size are no more than 1 percent. Thus all the results reported here are based on the mesh sizes mentioned above.

Table 1. Gr = 200, Pr = 0.7, τ = 10.0, H = 3.0, h = H/(n – 1)
Full size table

Finally, the numerical code was run until the flow attained a steady state. Some of the solutions obtained are presented below in terms of streamlines and isotherms. We have allowed the Grashof number to vary up to 200 and the aspect ratio to take unit values between 1 and 5. The Darcy parameter, γ (= 1/Da), takes values between 0 and 20.

3 Results and discussion

We now present a selection of our computational results in Figs. 2, 3, 4, 5, 6, 7. In Fig. 2 we show how the streamlines and isotherms vary with Grashof number for a square cavity. Here we have taken γ = 0, which corresponds to a pure fluid, rather than a porous medium with Brinkman effects. There is flow at all nonzero Grashof numbers due to the fact that the temperature field cannot consist of horizontal isotherms because of the boundary conditions. As Gr increases the one-cell flow (i.e. two cells in the full-cavity) which is characteristic of the near-zero Gr situation and which is caused by fluid being forced to flow down the sidewalls, gradually gives way to a two-cell flow where fluid flows down the middle of the cavity. The associated variation in the isotherms near X = 0.6 shows not only this developing second cell but its increasing strength. The left hand cell always remains slightly stronger than the right hand cell as it is assisted by the downward buoyancy forced from the cold sidewall.

Fig. 2.
figure 2

(a) Streamlines and (b) isotherms for different Gr: Gr = 20, 50, 100 and 200 while Pr = 0.71 at steady state situation that reached at τ = 3 with aspect ratio 2. Throughout 1/Da = 0.0 (Pure fluid)

Full size image
Fig. 3.
figure 3figure 3

(a) Streamlines and (b) isotherms with aspect ratio A = 1, 2, 3, 4 and 5 at steady state situation that reached at τ = 5 while Gr = 200 and Pr = 0.71. Throughout 1/Da = 0.0 (pure fluid)

Full size image
Fig. 4.
figure 4

Streamlines and isotherms for different values of 1/Da: (a) 1/Da = 1.0, (b) 1/Da = 10.0 (c) 1/Da = 20.0 while Pr = 0.7, Gr = 200 at the steady state siltuation that reaches at τ = 5 with A = 2

Full size image
Fig. 5.
figure 5

Local heat transfer against X/A for different Gr at the bottom surface while A = 2, Pr = 0.7 and 1/Da = 0.0

Full size image
Fig. 6.
figure 6

Local heat transfer against X/A for different 1/Da at the bottom surface while A = 2, Pr = 0.7 and Gr = 200.0

Full size image
Fig. 7.
figure 7

Local heat transfer against X/A for different A at the bottom surface while Gr = 200, Pr = 0.7 and 1/Da = 0.0

Full size image

The aiding effect of the cold sidewall is also seen clearly in Fig. 3 where we concentrate on how the flow varies with increasing cavity aspect for Gr = 200, again for the pure fluid case. In all these cases the number of cells in the half-cavity is precisely the same as the value of A. It is important to emphasise that it is possible to obtain different numbers of cells in many cases, but only by modifying substantially the initial conditions to ones resembling closely the desired solution, such as a 4-cell flow in the A = 5 cavity. The overall strength of the left-hand cell increases slightly as A increases, reflecting the fact that the cavity is becoming less restrictive. We also see the beginnings of a sixth cell in the A = 5 cavity.

We turn now to Darcy-Brinkman convection where the presence of a solid matrix begins to make its presence felt. In Fig. 4 we show how increasing values of γ affect the flow when Gr = 200, and these subfigures may be supplemented by the A = 2 subfigure in Fig. 3 for which γ = 0. The main effect is that the overall strength of the induced fluid motion is reduced due to the increasing resistance of the porous matrix. This causes the isotherms to become more like the low Gr case shown in Fig. 2, and also causes the 2-cell structure shown in Fig. 3 to transform gradually back to a 1-cell flow.

Finally, local Nusselt number or the heat transfer has been calculated at the bottom heated surface from the following non-dimensional expression:

$$ Nu = - \left({\partial \theta \over \partial Y} \right)_{Y = 0} $$
(11)

where Nu is the Nusselt number. In Figs. 5 to 7, we show the surface rate of heat transfer along the lower surface of the cavity; these figures correspond to the detailed streamline and isotherm plots given in Figs. 2, 3, 4, respectively. Figure 5 shows how increasing values of the Grashof number affects the heat transfer. Over the range of Gr considered the local heat transfer increases only slightly with Gr although the induced flow increases in strength quite markedly (see Fig. 2). The reason for this is that the temperature profile is still dominated by conductive temperature profile, as shown in Fig. 2a, and although the flow increases greatly in strength, it is not yet sufficiently strong to achieve a large change in the temperature profile near the lower surface.

Figure 6 gives the heat transfer curves for A = 2 for various values of 1/Da. As 1/Da increases, the resistance to flow also increases, which means that the temperature field approximates more closely to the equivalent conductive state. Therefore we see from this figure that we require 1/Da to be somewhat less than about 10 in order for convective effects to make their presence felt in terms of the lower surface rate of heat transfer.

Figure 7 shows the lower surface rate of heat transfer corresponding to the detailed flow-field and isotherms shown in Fig. 3 for the various aspect ratios considered there. In the region X < 0.1, there is little difference between the various curves, which suggests that the temperature field remains dominated by the presence of the cold sidewall. As the aspect ratio increases the heat transfer curves oscillate with increasing number of maxima and minima. Once there are two cells in the cavity, each new cell which is added as A increases by 1 adds a new extremum to the heat transfer curve. However, each new maximum (or minimum) corresponds to a rate of heat transfer which is almost exactly the same as the previous one, and this indicates that the effect of the cold sidewall is quite local to that sidewall.

4 Conclusions

This has been very much a preliminary study of the effect of cold sidewalls on convection in a internally heated porous cavity heated from below. The main difference between this case and those of the standard Darcy-Bénard problem (which has insulated sidewalls) and the infinitely-conducting case considered by Rees and Lage [11], is that there remains flow at all nonzero values of the Grashof number (or equivalently the Rayleigh number). Thus the resulting flow field is dominated by the presence of this sidewall, and especially so for the range of Grashof numbers considered here. As the aspect ratio of the cavity increases the interior cells become much less affected by the sidewall boundary conditions.

Although we have studied two-dimensional flow in this paper, there is no guarantee at this stage that the flow will remain two-dimensional at fairly large values of the Grashof number. In other contexts, namely those involving thermal ’imperfections’ of the upper and lower surfaces (see, for example [12] and [13]) also give rise to two-dimensional flows at low Rayleigh numbers, but these patterns give way to strongly three-dimensional steady convection at moderate Rayleigh numbers. It will therefore be important to investigate the physical realisability of the present flows.