Abstract
Linear extended top-down tree transducers (or synchronous tree-substitution grammars) are popular formal models of tree transformations that are extensively used in syntax-based statistical machine translation. The expressive power of compositions of such transducers with and without regular look-ahead is investigated. In particular, the restrictions of ε-freeness, strictness, and nondeletion are considered. The composition hierarchy turns out to be finite for all ε-free (all rules consume input) variants of these transducers except for the nondeleting ε-free transducers. The least number of transducers needed for the full expressive power of arbitrary compositions is presented. In all remaining cases (incl. the nondeleting ε-free transducers) the composition hierarchy does not collapse.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Top-down tree transducers are simple formal models that encode tree transformations (i.e., relations between trees). They were introduced in [23, 24] and intensively studied thereafter (see [14–16] for an overview). Roughly speaking, a top-down tree transducer processes the input tree symbol-by-symbol, and specifies in its rules how to translate an input symbol into an output tree fragment together with instructions on how to process the subtrees of the input symbol. This asymmetry between input and output (single symbol vs. tree fragment) was removed in extended top-down tree transducers (xt), which were introduced and studied in [1, 2]. In such a transducer the input side of a rule can now also contain a tree fragment, in which each variable can occur at most once as a placeholder for a subtree. In particular, the tree fragment can even be just a variable, which matches every input tree, and such rules are called ε-rules because they do not process any part of the input tree. In this contribution we only consider linear xt (l-xt), in which the output side of each rule contains each variable at most once as well. Restricted variants of l-xt are used in most approaches to syntax-based machine translation [18, 19].
We also add regular look-ahead [7] (i.e., the ability to check a regular property for the subtrees in an input tree fragment) to l-xt, so our most expressive model is the linear extended top-down tree transducer with regular look-ahead (l- xtR). Contrary to most of the literature [7, 17] we present our models as synchronous grammars [4] because we sometimes use the auxiliary link structure in our proofs. Instead of variables in the input side and a state-variable combination in the output side of a rule, we immediately only use states with the restriction that all states that occur in the output side must also occur in the input side. Moreover, each state that occurs in both sides, must occur exactly once in the input side and exactly once in the output side, which corresponds to the classical linearity condition. In this way, for each rule the states establish links (a state links its occurrence in the output side with its occurrence in the input side), which form an injection from the state occurrences in the output side to the state occurrences in the input side. Regular look-ahead is specified only for the state occurrences (in the input side) that do not participate in the injection (i.e., those states that exclusively occur in the input side). A derivation of the grammar simultaneously generates an input tree and an output tree, which can contain states that are (possibly) linked by explicit links. A rule application expands two linked state occurrences at the same time, thus generating new input and output fragments with new (linked) state occurrences. Moreover, every unlinked state (in the input tree) is expanded into a tree from its regular look-ahead. Example 2 shows an l- xtR, for which we illustrate a few derivation steps in Fig. 2. The tree transformation computed by the example l- xtR is described in Example 8. In the following, we use l- XTR and l-XT to denote the class of all tree transformations computed by l- xtR and l-xt, respectively.
The expressive power of the various subclasses of l- XTR is already well understood [13, 17]. However, in practice complex systems are often specified with the help of compositions of tree transformations [22] because it is much easier to develop (or train) small components that manage a part of the overall transformation. Consequently, [19] and others declare that closure under composition is a very desirable property for classes of tree transformations (especially in the area of natural language processing). If a class \(\mathcal {C}\) of tree transformations is closed under composition, then any composition chain τ 1 ;⋯ ;τ n of tree transformations τ 1,…, τ n of \(\mathcal {C}\) can be replaced by a single tree transformation \(\tau \in \mathcal {C}\). If \(\mathcal {C}\) represents the class of all tree transformations computable by a device, then closure under composition means that we can replace any composition chain specified by several devices by just a single device, which enables an efficient modular development. Unfortunately, neither l- XTR nor l-XT is closed under composition [2, 3, 17].
In general, for a class \(\mathcal {C}\) of tree transformations (that contains the identity transformations) we obtain a composition hierarchy \(\mathcal {C} \subseteq \mathcal {C}^{2} \subseteq \mathcal {C}^{3} \subseteq \dotsb \), where \(\mathcal {C}^{n}\) denotes the class of n-fold compositions of transformations from \(\mathcal {C}\). The class \(\mathcal {C}\) might be closed under composition at power n (i.e., \(\mathcal {C}^{n} = \mathcal {C}^{n+1}\)) or its composition hierarchy might be infinite (i.e., \(\mathcal {C}^{n} \subsetneq \mathcal {C}^{n+1}\) for all n). The former case yields that \(\mathcal {C}^{n} = \mathcal {C}^{m}\) for all m ≥ n, which means that the composition hierarchy of \(\mathcal {C}\) collapses at power n. In particular, \(\mathcal {C}\) is closed under composition if its composition hierarchy collapses at power 1. We note that in practice (e.g., in statistical machine translation) the classes that are closed under composition at a small power are also important because for such classes we can limit the length of composition chains [22]. In this contribution, we investigate the composition hierarchy of the classes l- XTR and l-XT together with their subclasses determined by any combination of the properties: ε-freeness, strictness, and nondeletion, which are abbreviated by ‘
 ’, ‘s’, and ‘n’, respectively. Roughly speaking, ε-freeness requires that there are no ε-rules, strictness guarantees that the output side of each rule contains at least one output symbol, and nondeletion requires that for each rule exactly the same states occur in the input and output side. We use the property abbreviations in front of l- XTR and l-XT to obtain the class of all tree transformations computable by such restricted l- xtR and l-xt, respectively. For instance,
’, ‘s’, and ‘n’, respectively. Roughly speaking, ε-freeness requires that there are no ε-rules, strictness guarantees that the output side of each rule contains at least one output symbol, and nondeletion requires that for each rule exactly the same states occur in the input and output side. We use the property abbreviations in front of l- XTR and l-XT to obtain the class of all tree transformations computable by such restricted l- xtR and l-xt, respectively. For instance,
 denotes the class of all tree transformations computed by ε-free and strict l- xtR.
denotes the class of all tree transformations computed by ε-free and strict l- xtR.
It is known that none of our considered classes is closed under composition [3, Section 3.4]. In addition, it is known [3, Theorem 6.2] that the class
 is closed at power 2. We complete the picture as follows. For each of the remaining classes, we either provide the least power at which the class is closed under composition or show that the composition hierarchy of the class is infinite (denoted by ∞). Our results (together with the mentioned existing result) are presented in Table 1.
is closed at power 2. We complete the picture as follows. For each of the remaining classes, we either provide the least power at which the class is closed under composition or show that the composition hierarchy of the class is infinite (denoted by ∞). Our results (together with the mentioned existing result) are presented in Table 1.
Our contribution is organized as follows. Section 2 recalls the necessary concepts and introduces our notation. We continue in Section 3 with the formal introduction of our main model (l- xtR) including its syntax and semantics and the restrictions that we consider later. In addition, we recall some known equalities between certain fundamental classes of tree transformations in preparation for our first main results. In Section 4 we give a power at which the classes
 ,
,
 ,
,
 , and
, and
 of tree transformations are closed under composition (see Table 1). This is completed in Section 5, where we conclude that these powers are minimal. In Section 6 we prove that the composition hierarchy of each of the remaining classes is infinite. Finally, we present the Hasse diagram of all the ε-free classes in Section 7.
of tree transformations are closed under composition (see Table 1). This is completed in Section 5, where we conclude that these powers are minimal. In Section 6 we prove that the composition hierarchy of each of the remaining classes is infinite. Finally, we present the Hasse diagram of all the ε-free classes in Section 7.
2 Preliminaries
We denote the set of all nonnegative integers by \(\mathbb {N}\). In the following, let S be a set. The power set of S is the set \(\mathcal P(S) = \{S^{\prime } \mid S^{\prime } \subseteq S\}\) of all subsets of S. For an element s of S, we identify the singleton set {s} with s, whenever convenient; this should not lead to confusion. The cardinality of S is denoted by |S|. The set of all words (finite sequences) over S is \(S^{\ast } = \bigcup _{n \in \mathbb {N}} S^{n}\), where S 0 = {ε} contains only the empty word ε. The length of a word w ∈ S ∗ is the unique \(n \in \mathbb {N}\) such that w ∈ S n. We write |w| for the length of w. The concatenation of two words v, w ∈ S ∗ is denoted by v.w or simply vw.
For sets S and T, every subset of S×T is a relation from S to T. Given relations R 1 ⊆ S×T and R 2 ⊆ T×U, the inverse of R 1 is the relation \(R_{1}^{-1} = \{ (t, s) \mid (s, t) \in R_{1}\}\), the domain of R 1 is
and the composition of R 1 and R 2 is the relation
Given a relation R⊆S×S, the powers of R are defined by R 0={(s, s)∣s ∈ S} and R n+1 = R n ;R for \(n \in \mathbb {N}\). The reflexive and transitive closure of R is \(R^{\ast } = \bigcup _{n \in \mathbb {N}} R^{n}\). These notions and notations are lifted to classes \(\mathcal {C}_{1}\) and \(\mathcal {C}_{2}\) of relations in the usual manner. Namely, we let \(\mathcal {C}_{1}^{-1} = \{ R_{1}^{-1}\mid R_{1} \in \mathcal {C}_{1}\}\) and \(\mathcal {C}_{1} \ ; \mathcal {C}_{2} = \{R_{1} \ ; R_{2} \mid R_{1} \in \mathcal {C}_{1},~R_{2} \in \mathcal {C}_{2}\}\). Moreover, the powers of a class \(\mathcal {C}\) are defined by \(\mathcal {C}^{1} = \mathcal {C}\) and \(\mathcal {C}^{n+1} =\mathcal {C}^{n} \ ; \mathcal {C}\) for n ≥ 1. Note that we do not consider the 0-th power for classes. The composition hierarchy [resp. composition closure] of \(\mathcal {C}\) is the family \((\mathcal {C}^{n} \mid n \geq 1)\) [resp. the class \(\bigcup _{n \geq 1} \mathcal {C}^{n}\)]. The classes \(\mathcal {C}\) of tree transformations that we will discuss always contain the identity relations. For such a class, \(\mathcal {C}^{n} \subseteq \mathcal {C}^{n+1}\) for all n ≥ 1. If \(\mathcal {C}^{n}=\mathcal {C}^{n+1}\), then \(\mathcal {C}\) is closed under composition at power n. For n = 1 we shorten this to just \(\mathcal {C}\) is closed under composition. If \(\mathcal {C}\) is closed under composition at power n, then \(\mathcal {C}^{n}\) is the composition closure of \(\mathcal {C}\).
An alphabet Σ is a nonempty and finite set, of which the elements are called symbols. The alphabet Σ is ranked if there additionally is a mapping rk\( : {\Sigma } \to \mathbb {N}\) that assigns a rank to each symbol. We let
for every \(k \in \mathbb {N}\). Often the mapping ‘rk’ is obvious from the context, so we typically denote ranked alphabets by Σ alone. If it is not obvious, then we use the notation σ (k) to indicate that the symbol σ has rank k. For the rest of this paper, Σ, Δ, and Γ will denote arbitrary ranked alphabets if not specified otherwise.
For every set T, let \({\Sigma }(T) = \{\sigma ({t_{1}, \dotsc , t_{k}} ) \mid k \in \mathbb {N},~ \sigma \in {\Sigma }_{k},~ t_{1}, \dotsc , t_{k} \in T\}\). Instead of σ() with σ ∈Σ0 we will simply write σ. Let S be a set of “states” with S∩Σ = ∅, to be used as additional leaf labels. The set T Σ(S) of Σ-trees with states in S is the smallest set U such that S⊆U and Σ(U)⊆U. We write T Σ for T Σ(∅), and any subset of T Σ(S) is a tree language. Given a unary symbol γ ∈Σ1 and a tree t ∈ T Σ(S), we write γ k(t) for the tree γ(⋯γ(t)⋯ ), in which γ occurs k times on top of t.
The set \(\text {pos}(t) \subseteq \mathbb {N}^{\ast }\) of positions of t ∈ T Σ(S) is inductively defined by pos(s) = {ε} for every s ∈ S and
for every \(k \in \mathbb {N}\), σ ∈Σ k , and t 1,…, t k ∈ T Σ(S). The positions of t are partially ordered by the prefix order ≼ on \(\mathbb {N}^{\ast }\); i.e., for words \(w_{1}, w_{2} \in \mathbb {N}^{\ast }\), we have w 1≼w 2 if and only if there exists \(w^{\prime }_{1} \in \mathbb {N}^{\ast }\) such that \(w_{1}w^{\prime }_{1} = w_{2}\). As usual we write w 1≺w 2 if w 1 is a proper prefix of w 2; i.e., w 1≼w 2 and w 1≠w 2. For words \(w_{1}, w_{2} \in \mathbb {N}^{\ast }\), we denote the longest common prefix of w 1 and w 2 by lcp (w 1, w 2). Note that lcp (w 1, w 2) ∈pos(t) for all w 1, w 2∈pos(t) because pos(t) is prefix-closed. The size |t| of a tree t ∈ T Σ(S) is |pos(t)|; i.e., the number of its positions. Its height ht(t) is max{|w|∣w ∈pos(t)}; i.e., the maximal length of its positions. Let t, u ∈ T Σ(S) and w ∈pos(t). The label of t at w is t(w), the subtree of t rooted at w is t| w , and the tree that is obtained from t by replacing the subtree t| w at w by u is denoted by t[w←u]. Formally, s(ε) = s| ε = s and s[ε←u] = u for every s ∈ S, and for all \(k \in \mathbb {N}\), σ ∈Σ k , and t 1,…, t k ∈ T Σ(S) we have
-
(i)
if w = ε, then
$$\begin{array}{@{}rcl@{}} \left( \sigma({t_{1}, \dotsc, t_{k}} ) \right)(w) &=& \sigma \\ \left( \sigma({t_{1}, \dotsc, t_{k}}) \right)|_{w} &=& \sigma({t_{1}, \dotsc, t_{k}}) \\ \left( \sigma({t_{1}, \dotsc, t_{k}}) \right)[w \gets u] &=& u \end{array} $$ -
(ii)
if w = i v with 1 ≤ i ≤ k and v ∈pos(t i ), then
$$\begin{array}{@{}rcl@{}} \left( \sigma({t_{1}, \dotsc, t_{k}}) \right)(w) &= &t_{i}(v) \\ \left( \sigma({t_{1}, \dotsc, t_{k}}) \right)|_{w} &=& t_{i}|_{v} \\ \left( \sigma({t_{1}, \dotsc, t_{k}}) \right)[w \gets u] &=& \sigma({t_{1}, \dotsc, t_{i-1}} , t_{i}[v \gets u], {t_{i+1}, \dotsc, t_{k}} ). \end{array} $$
For 1 ≤ i≤rk(t(w)), the tree t| w i is the i-th direct subtree below w in t. For every subset Δ⊆Σ∪S, we let posΔ(t) = {w ∈pos(t)∣t(w)∈Δ}. A tree t ∈ T Σ(S) is linear (resp. nondeleting) in a subset Q⊆S of states if |pos q (t)|≤1 (resp. |pos q (t)|≥1) for every q ∈ Q. Moreover,
is the set of states that occur in t. For every selection W⊆pos S (t) of leaves and mapping \(\theta : W \to \mathcal P(T_{\Sigma }(S))\) assigning a tree language to each selected leaf, we define the tree language
where W = {w 1,…, w n }. Similarly, given a selection Q⊆S of states and a mapping \(\theta : Q \to \mathcal P(T_{\Sigma }(S))\) assigning a tree language to each selected state, we define the tree language
where \(\theta ^{\prime } : \text {pos}_{Q}(t) \to \mathcal P(T_{\Sigma }(S))\) is given by θ ′(w) = θ(t(w)) for all w ∈pos Q (t). The latter operation is also called OI-substitution [10] of θ in t. To simplify the notation, we fix the set X = {x 1, x 2, x 3,…} of variables, which we assume to be disjoint with all ranked alphabets considered in the paper. For every \(k \in \mathbb {N}\), we let X k = {x i ∣1 ≤ i ≤ k}. Given t ∈ T Σ(X) and θ:X k →T Σ(X), we simply write t[θ(x 1),…, θ(x k )] for t[x←θ(x)∣x ∈ X k ].
A tree homomorphism from Σ to Δ is a mapping φ:Σ→T Δ(X) such that φ(σ)∈ T Δ(X k ) for every \(k \in \mathbb {N}\) and σ ∈Σ k . It is
-
linear (resp. nondeleting) if for every \(k \in \mathbb {N}\) and σ ∈Σ k the tree φ(σ) is linear (resp. nondeleting) in X k , and
-
strict (resp. delabeling) if φ(σ)∉X (resp. φ(σ)∈ X∪Δ(X)) for every σ ∈Σ.
We abbreviate the above restrictions by ‘l’, ‘n’, ‘s’, and ‘d’, respectively. The tree homomorphism φ induces a mapping φ ∗:T Σ→T Δ defined inductively by φ ∗(σ(t 1,…, t k )) = φ(σ)[φ ∗(t 1),…, φ ∗(t k )] for all \(k \in \mathbb {N}\), σ ∈Σ k , and t 1,…, t k ∈ T Σ. As usual, we will from now on denote the induced mapping φ ∗ by φ, and we will also call it a tree homomorphism. We denote by H the class of all tree homomorphisms, and for any combination w of ‘l’, ‘n’, ‘s’, and ‘d’ we denote by w-H the class of all tree homomorphisms of type w. For instance, snl-H is the class of all strict, nondeleting and linear tree homomorphisms.
In the following, we need the class of regular tree languages [15, 16] and some basic properties of that class. The set Reg(Σ) contains all regular tree languages T⊆T Σ over the ranked alphabet Σ. A well-known folklore result states that t[s ← θ(s) ∣ s ∈ S] ∈Reg(Σ) for every finite S, tree t ∈ T Σ(S), and θ : S→Reg(Σ).
A bimorphism is a triple B = (ψ, T, φ) consisting of a regular tree language T ∈Reg(Γ), an input tree homomorphism ψ:T Γ→T Σ, and an output tree homomorphism φ:T Γ→T Δ. The tree transformation τ(B)⊆T Σ×T Δ computed by the bimorphism B is the relation τ(B) = {(ψ(t), φ(t))∣t ∈ T}, which will also be called a bimorphism. Given two combinations v and w of restrictions for tree homomorphisms, we let \(\mathcal {B}(v, w)\) denote the class of all tree transformations computed by bimorphisms B = (ψ, T, φ) such that ψ and φ are tree homomorphisms of type v and w, respectively.
3 Linear Extended Top-down Tree Transducers
Our main model is the linear extended top-down tree transducer [1, 2, 18, 19] with regular look-ahead (l- xtR), which is based on the classical linear top-down tree transducer without [23, 24] and with regular look-ahead [7]. We will present it as a synchronous grammar [4] because we will use an auxiliary structure, called the links, in later proofs. In synchronous grammars, occurrences of equal states in the left- and right-hand side of a rule (representing the input and output side, respectively) are (implicitly) linked and these links are made explicit in a derivation. Each derivation step replaces such a pair of linked state occurrences (at the same time) by the left- and right-hand side of a rule for that state. In a rule of an l- xtR, the (implicit) links form an injection from the state occurrences in the right-hand side to the state occurrences in the left-hand side. Thus, some states might exclusively occur in the left-hand side. Such states can be used to implement regular look-ahead, which restricts the subtrees that are acceptable at these occurrences. It should be clear (see [17, Theorem 4.4]) that there is no need to have regular look-ahead for the other states in the left-hand side, as that can be incorporated into the (nondeterministic) state behavior of the transducer.
Definition 1 ([17, Section 2.2])
A linear extended top-down tree transducer with regular look-ahead (l- xtR) is a tuple M = (Q,Σ,Δ, Q 0, R, c), where
-
Q is a finite set of states and Q 0 ⊆ Q is a set of initial states,
-
Σ and Δ are ranked alphabets of input and output symbols that are both disjoint with Q,
-
R⊆T Σ(Q)×Q×T Δ(Q) is a finite set of rules such that for every (ℓ, q, r)∈ R
-
states(r)⊆states(ℓ), i.e., all states that occur in r must occur in ℓ, and
-
ℓ and r are linear in states(r),
-
-
c:Q la→Reg(Σ) is a mapping that assigns regular look-ahead to each (potentially) deleted state, where \(Q^{\text {la}} = \bigcup _{(\ell , q, r) \in R} \left ( \text {states}(\ell ) \setminus \text {states}(r) \right )\). Formally, the set Q la depends on R (or M), but we prefer the simpler notation and hope that it does not lead to confusion.
For a rule (ℓ, q, r)∈ R we say that ℓ and r are its left- and right-hand side. In contrast to other definitions [13, 17], we do not allow the same state to occur several times in the right-hand side. However, with the help of a simple renaming, each traditional linear extended top-down tree transducer can be written in our slightly more restrictive format. Next, we recall some important syntactic properties of our model. To this end, let M = (Q,Σ,Δ, Q 0, R, c) be an l- xtR in the following. It is
-
a linear extended top-down tree transducer (without look-ahead) [l-xt], if c(q) = T Σ for every q ∈ Q la,
-
a linear top-down tree transducer with regular look ahead [l- tR] if ℓ ∈Σ(Q) for every (ℓ, q, r)∈ R,
-
a linear top-down tree transducer (without look ahead) [l-t] if it is both an l-xt and an l- tR,
-
ε-free (resp. strict) if ℓ∉Q (resp. r∉Q) for every (ℓ, q, r)∈ R,
-
delabeling if ℓ ∈Σ(Q) and r ∈ Q∪Δ(Q) for every (ℓ, q, r)∈ R,
-
nondeleting if states(r) = states(ℓ) for every (ℓ, q, r)∈ R (i.e., Q la = ∅), and
-
a finite-state relabeling [qr] if every rule of R is of the form
$$\left( \sigma({q_{1}, \dotsc, q_{k}} ), q, \delta({q_{1}, \dotsc, q_{k}}) \right) $$with \(k \in \mathbb {N}\), σ ∈Σ k , δ ∈Δ k , and q, q 1,…, q k ∈ Q.
Since the look-ahead component c is trivial for all l-xt, we simply omit it from their representation. We note that every nondeleting l- xtR is an l-xt. Moreover, all l- tR are automatically ε-free. Note also that every qr [finite-state relabeling] is a strict nondeleting delabeling l-t. For clearness’ sake, we sometimes write rules as \(\ell \overset {q}{\longrightarrow } r\) instead of (ℓ, q, r) and, to simplify the notation in examples and illustrations, we write
 as a shorthand for the k rules \(\ell \overset {q_{1}}{\longrightarrow } r, \dotsc , \ell \overset {q_{k}}{\longrightarrow } r\). Note that for every \((\ell \overset {q}{\longrightarrow } r) \in R\) the trees ℓ and r are linear in states(r). Hence for every state p ∈states(r) the sets pos
p
(ℓ) and pos
p
(r) are singletons that we identify with their unique element.
as a shorthand for the k rules \(\ell \overset {q_{1}}{\longrightarrow } r, \dotsc , \ell \overset {q_{k}}{\longrightarrow } r\). Note that for every \((\ell \overset {q}{\longrightarrow } r) \in R\) the trees ℓ and r are linear in states(r). Hence for every state p ∈states(r) the sets pos
p
(ℓ) and pos
p
(r) are singletons that we identify with their unique element.
Example 2
Let us consider the l- xtR M 1=(Q,Σ,Δ, Q 0, R, c) given by
-
Q = {⋆, p, q, q la,id,id′} and Q 0={⋆},
-
\({\Sigma } = \{ \sigma ^{(2)}, \gamma _{1}^{(1)}, \gamma _{2}^{(1)} \} \cup {\Delta }\) and \({\Delta } = \{ \sigma _{1}^{(2)}, \sigma _{2}^{(2)}, \gamma ^{(1)}, \alpha ^{(0)}\}\),
-
R consists of the following rules
$$\begin{array}{lll} \sigma_{1}(p, q) \;\overset{\star,p}{\longrightarrow} \sigma_{1}(p, q)\quad \sigma_{2}(\text{id}, {\text{id}^{\prime}}) \overset{p,q}{\longrightarrow} \sigma_{2}(\text{id}, \text{id}^{\prime})\quad \gamma_{1}(p) \overset{p}{\longrightarrow} p \\ \sigma(q, q^{\text{la}}) \overset{q}{\longrightarrow} q \;\quad\quad\quad\quad\sigma(q^{\text{la}}, q) \overset{q}{\longrightarrow} q\quad\quad\quad\quad\;\; \gamma_{2}(q) \overset{q}{\longrightarrow} q \\ \quad\;\;\gamma(\text{id}) \overset{\text{id}, \text{id}^{\prime}}{\longrightarrow} \gamma(\text{id})\quad\quad\quad\quad\quad\;\; \alpha \overset{\text{id}, \text{id}^{\prime}}{\longrightarrow} \alpha & \end{array} $$ -
c:Q la→Reg(Σ) is given by \(c(q^{\text {la}}) = T_{\{\gamma _{2}, \alpha \}}\) because Q la = {q la}.
Obviously, c(q la) is a regular tree language. Additionally, we note that the state id′ is essentially just a renaming of the state id (and both realize the identity on T {γ, α}). The l- xtR M 1 is an ε-free, delabeling, linear top-down tree transducer with regular look-ahead. It is not strict and not nondeleting.
Next, we recall the semantics of the l- xtR M = (Q,Σ,Δ, Q 0, R, c), which is (mostly) given by synchronous substitution. Formally, a link is just an element \((v, w) \in \mathbb {N}^{\ast } \times \mathbb {N}^{\ast }\). While the links in a rule are implicit and established due to occurrences of equal states, we need an explicit representation of the links in the sentential forms computed by M. These links together with the trees into which they point will form a dependency that is used in proofs later on. Our derivation relation is thus defined over structures consisting of an input tree, an output tree, and a set of links relating positions of those trees. Let us formalize this notion, which we call form.
Definition 3 ([12, Section 3])
A form (over Q, Σ, and Δ) is a triple 〈ξ, L, ζ〉 consisting of an input tree ξ ∈ T Σ(Q), an output tree ζ ∈ T Δ(Q), and a set L⊆pos(ξ)×pos(ζ) of links relating positions in the two trees.
Next, we formalize the links in a rule ρ ∈ R. These links are added to the links of a form whenever the rule ρ is applied in the derivation process. Since these links are relative to the positions at which the rule is applied, two parameters \(v, w \in \mathbb {N}^{\ast }\) indicate those two positions.
Definition 4
Let \((\ell \overset {q}{\longrightarrow } r) \in R\) and \(v, w \in \mathbb {N}^{\ast }\). The set of links of \(\ell \overset {q}{\longrightarrow } r\) for the positions v and w is
Example 5
Let us compute two such sets of links. Whenever it is clear that the relevant positions are in {1,…,9}∗, we write positions without separating dots; e.g., 211 stands for the position 2.1.1 of length 3.
We use grayed splines to indicate links in illustrations. The rules ρ 1 and ρ 2 above and their links, which are those of links ε, ε (ρ 1)={(1,1),(2,2)} and links ε, ε (ρ 2)={(2, ε)}, are displayed in Fig. 1.
The derivation process is started with a simple form 〈q 0,{(ε, ε)}, q 0〉 consisting of an initial state q 0∈ Q 0 as input and output tree and the trivial link relating both occurrences of q 0 (i.e., the roots of the trees). The current form can evolve in two ways. Either (i) we apply a rule (ℓ, q, r)∈ R to a pair (v, w) of linked occurrences of the state q or (ii) we apply the look-ahead. In the former case, such a rule application replaces the linked occurrences of q in the input and output tree by the left- and right-hand side of the rule to obtain the new input and output trees, respectively. The links of the derived form are obtained by adding the links of the rule (ℓ, q, r) for v and w to the current links. Since we are interested in the links used during the derivation, we preserve all links [in particular also the link (v, w) just used] and never remove a link. In the latter case, in which we want to apply the look-ahead, we require an occurrence of a state q at position v of the input tree that does not take part in any link with an occurrence of q in the output tree. It turns out that such a state q must be in Q la, and we can replace that occurrence of q by any tree of the regular look-ahead tree language c(q). Note that such replacements are independent, so different occurrences of q can be replaced by different look-ahead trees of c(q). We can (potentially) continue these replacements until the form is an element of \(T_{\Sigma } \times \mathcal P(\mathbb {N}^{\ast } \times \mathbb {N}^{\ast }) \times T_{\Delta }\).
Definition 6 ([12, Section 3])
Given two forms 〈ξ, L, ζ〉 and 〈ξ ′, L ′, ζ ′〉 over Q, Σ, and Δ, we write 〈ξ, L, ζ〉⇒ M 〈ξ ′, L ′, ζ ′〉 if one of the following two conditions holds:
-
there exist a rule \((\ell \overset {q}{\longrightarrow } r) \in R\) and a link (v, w)∈ L∩(pos q (ξ)×pos q (ζ)) such that
$$\xi^{\prime} = \xi[v \gets \ell] \qquad \zeta^{\prime} = \zeta[w \gets r] \quad \text{and} \quad L^{\prime} = L \cup \text{links}_{v, w}(\ell\overset{q}{\longrightarrow} r), $$ -
there exist a state q ∈ Q la, a position v ∈pos q (ξ) with w∉pos q (ζ) for all links (v, w)∈ L, and a tree t ∈ c(q) such that
$$\xi^{\prime} = \xi[v \gets t]\qquad \zeta^{\prime} = \zeta \quad \text{and} \quad L^{\prime} = L ~. $$
A form 〈ξ, L, ζ〉 is a sentential form (of M) if \(\left \langle q_{0}, \{(\varepsilon , \varepsilon )\}, q_{0} \right \rangle \Rightarrow ^{\ast }_{M} \langle \xi , L, \zeta \rangle \) holds for some q 0∈ Q 0. The set of all sentential forms is denoted by \(\mathcal {S}\mathcal {F}(M)\).
A few derivation steps using the l- xtR M 1 of Example 2 are illustrated in Fig. 2. Next, we define the tree transformation computed by an l- xtR.
Definition 7
The l- xtR M computes the set \(\mathcal {D}(M)\) of dependencies, which are the sentential forms with state-free input and output trees. Hence
Moreover, it computes the tree transformation τ(M), which is given by
Two l- xtR M 1 and M 2 are equivalent if τ(M 1) = τ(M 2).
Example 8
Let M 1 be the l- xtR of Example 2. Then
where
which corresponds to the final sentential form of the derivation displayed in Fig. 2. To describe the tree transformation computed by M 1 in general, we first need some terminology. A tree t ∈ T Σ is “special” if there exist a tree \(c \in T_{\{\sigma , \gamma _{2}, \alpha \}}(X_{1})\) and two trees t 1, t 2∈ T {γ, α} such that (i) t = c[σ 2(t 1, t 2)], (ii) c is linear and nondeleting in X 1, and (iii) for all w ∈pos(c) we have c(w) = σ only if \(w \prec \text {pos}_{x_{1}}(c)\). For such a special tree, the subtree σ 2(t 1, t 2) is the “anchor” of t. Furthermore, the “left spine” of a tree t ∈ T Σ is the set pos(t)∩{1}∗ of positions. For every i ∈{1,2} and position v on the left spine, if t(v) = σ i , then the subtree t| v2 is a “ σ i -rib” of t.
The domain of τ(M 1) consists of all trees t ∈ T Σ such that (i) the sequence of labels of (the positions on) the left spine of t (from root to leaf) is in σ 1{σ 1, γ 1}∗ σ 2 γ ∗ α, (ii) each σ 1-rib of t is special, and (iii) the unique σ 2-rib of t is in T {γ, α}. Such a tree t is only related to u in the transformation τ(M 1), where u is obtained from t by (i) removing all γ 1-symbols on the left spine and (ii) replacing each σ 1-rib by its anchor. Consequently, τ(M 1) is actually a partial function.
Since every pair (t, u)∈ τ(M) is ultimately created by (at least) one successful derivation, leading to a dependency 〈t, L, u〉, we can inspect the links in L, which associate subtrees of t with subtrees of u. Roughly speaking, the links establish which parts of the output tree u were generated due to a particular part of the input tree t. Variants of this correspondence are called contribution in [9] and origin in [20]. Occasionally, we are not interested in the links. In those cases we also write \(q \Rightarrow _{M}^{\ast } (t, u)\) provided that \(\langle q,\{(\varepsilon , \varepsilon )\}, q \rangle \Rightarrow _{M}^{\ast } \langle t, L, u\rangle \) for some \(L \subseteq \mathbb {N}^{\ast } \times \mathbb {N}^{\ast }\). The next, basic lemma expresses the fact that the replacements in the derivations of an l- xtR are context-free.
Lemma 9 (context-freeness)
For every state q ∈ Q, input tree t ∈ T Σ and output tree u∈T Δ , we have \(q \Rightarrow _{M}^{\ast } (t, u)\) if and only if there exists a rule (ℓ,q,r) ∈ R with pos(ℓ) ⊆ pos(t) and pos(r) ⊆ pos(u) such that
-
t(v) = ℓ(v) for all v ∈ pos Σ(ℓ) and u(w) = r(w) for all w ∈ pos Δ (r),
-
\(\ell (v) \Rightarrow _{M}^{\ast } (t|_{v}, u|_{w})\) for every \((v, w) \in \text {links}_{\varepsilon , \varepsilon }(\ell \overset {q}{\longrightarrow } r)\) , and
-
t| v ∈ c(ℓ(v)) for all v ∈ pos(ℓ) with ℓ(v) ∈ states(ℓ)∖states(r).
This lemma can be used in proofs by induction on the length of a derivation because the derivations \(\ell (v) \Rightarrow _{M}^{\ast } (t|_{v}, u|_{w})\) are shorter than the derivation \(q \Rightarrow _{M}^{\ast } (t, u)\).
Notation 10
To allow concise statements, we introduce the following shorthands, which mirror those already defined for tree homomorphisms:

We use these abbreviations in conjunction with l- xtR to restrict to transducers with the indicated properties. For example, snl-xt stands for “strict and nondeleting linear extended top-down tree transducer” (without look-ahead). We use the same abbreviations with the stem (i.e., the material behind the hyphen) in capital letters for the corresponding classes of computed tree transformations. For instance, snl-XT stands for the class of all tree transformations computable by snl-xt, and QR denotes the class of all tree transformations computable by qr. We already remarked that every nondeleting l- xtR is an l-xt, so we have nl-XTR = nl-XT and similarly for the non-extended case and for all defined subclasses. To write such statements concisely, we also use sets of restrictions containing ‘
 ’, ‘s’, ‘n’, and ‘d’ in front of the (potentially already restricted) stems. For instance, for every
’, ‘s’, ‘n’, and ‘d’ in front of the (potentially already restricted) stems. For instance, for every
 , we denote by
, we denote by
 the class of all tree transformations computed by l- xtR that obey all restrictions in
the class of all tree transformations computed by l- xtR that obey all restrictions in
 . In particular, ∅l-XTR = l-XTR. In this manner we can simply state
. In particular, ∅l-XTR = l-XTR. In this manner we can simply state
 for all
for all
 .
.
We observe that
 for every
for every
 ; i.e., every linear tree homomorphism is a linear top-down tree transformation (with the same properties: ‘s’, ‘n’, ‘d’). In fact, if φ:T
Σ → T
Δ is a linear tree homomorphism, then an equivalent l-t M
φ
has the set Q = X
m
∪{⋆} of states, where m is the maximal rank of an element of Σ, the initial state ⋆, and all rules (σ(x
1,…, x
k
), q, φ(σ)) with σ ∈ Σ
k
, \(k\in \mathbb {N}\), and q ∈ Q. It should be clear that τ(M
φ
) = φ.
; i.e., every linear tree homomorphism is a linear top-down tree transformation (with the same properties: ‘s’, ‘n’, ‘d’). In fact, if φ:T
Σ → T
Δ is a linear tree homomorphism, then an equivalent l-t M
φ
has the set Q = X
m
∪{⋆} of states, where m is the maximal rank of an element of Σ, the initial state ⋆, and all rules (σ(x
1,…, x
k
), q, φ(σ)) with σ ∈ Σ
k
, \(k\in \mathbb {N}\), and q ∈ Q. It should be clear that τ(M
φ
) = φ.
Next, we recall some results that relate l-xtR to bimorphisms. In [2] the class \(\mathcal {B}(\text {snl}, \text {snl})\) is denoted by BI, and in [21] the class \(\mathcal {B}(\text {snl}, \text {nl})\) is denoted by B(LCE,LC).
Proposition 11 ([2] and [21, Theorems 17 and 4])

Thus, every tree transformation in l- XTR is the composition of an inverse tree homomorphism, the identity on a regular tree language, and a tree homomorphism. We will need a similar, but simpler result that tells us how to emulate an l- xtR by the composition of an inverse homomorphism and an l- tR.
Proposition 12 ([13, Lemma 4.1 and Corollary 4.1])
For every


Proof
We prove both inclusions starting with ( ⊇). Let φ be a nondeleting and linear tree homomorphism from Γ to Σ, and let M = (Q,Γ,Δ, Q 0, R, c) be an l-tR. We construct the l- xtR M ′ = (Q,Σ,Δ, Q 0, R ′, c ′) such that for each rule (γ(q 1,…, q k ), q, r) in R (with \(k \in \mathbb {N}\), γ ∈Γ k , and q 1,…, q k ∈ Q) the rule (φ(γ)[q 1,…, q k ], q, r) is in R ′. No further rules are in R ′. Note that since φ is nondeleting, we have states(φ(γ)[q 1,…, q k ]) = {q 1,…, q k } and thus Q la is the same for M ′ and M. For every q ∈ Q la we set c ′(q) = φ(c(q)), which is regular because, as is well known, the class of regular tree languages is closed under linear tree homomorphisms. Using Lemma 9, it is straightforward to show that \(q \Rightarrow ^{\ast }_{M^{\prime }} (t,u)\) if and only if there exists s ∈ T Γ with t = φ(s) and \(q \Rightarrow ^{\ast }_{M} (s, u)\). Thus τ(M ′)={(φ(s), u)∣(s, u)∈ τ(M)} = φ −1 ;τ(M).
For the remaining inclusion ( ⊆), let M = (Q,Σ,Δ, Q 0, R, c) be an l-xtR. We turn R into a ranked alphabet such that \(\textnormal {rk}(\ell \overset {q}{\longrightarrow } r) = \left |{\text {pos}_{Q}(\ell )}\right |\) for every \((\ell \overset {q}{\longrightarrow } r) \in R\). Using this ranked alphabet R we now construct the l-tR M ′ = (Q, R∪Σ,Δ, Q 0, R ′, c) and the nondeleting and linear tree homomorphism φ from R∪Σ to Σ as follows. For every \(k \in \mathbb {N}\) and rule ρ = (ℓ, q, r) in R k with pos Q (ℓ) = {v 1,…, v k } the rule \(\rho \left (\ell (v_{1}), \dotsc , \ell (v_{k}) \right ) \overset {q}{\longrightarrow } r\) is in R ′ and φ(ρ) = ℓ[v i ←x i ∣1 ≤ i ≤ k]. No further rules are in R ′. Additionally, φ(σ) = σ(x 1,…, x k ) for every \(k \in \mathbb {N}\) and σ ∈Σ k , which yields that φ(t) = t for every t ∈ T Σ. This latter part is needed for the look-ahead c. Clearly, if we apply the construction in the above proof of the first inclusion to φ and M ′, then we reobtain M. Hence φ −1 ;τ(M ′) = τ(M). □
We use this proposition to establish our first composition result, which extends the classical composition result of [7] for linear top-down tree transducers with regular look-ahead. The only difference is that our first transducer has extended left-hand sides (i.e., it is an l- xtR instead of just an l- tR).
Lemma 13 (composition on the right)
For every


Proof
Immediate from Proposition 12 and the composition closure result (l-TR)2 ⊆ l-TR for linear top-down tree transducers with regular look-ahead; it is straightforward to check that the proof of this result in [7, Theorem 2.11] preserves the properties ‘s’ and ‘n’. □
We conclude this section by discussing two results on regular look-ahead. First, we recall that when deletion is allowed, regular look-ahead adds expressive power.
Proposition 14 ([17, Lemma 4.3])

Proof
The counter-example presented in the proof of [17, Lemma 4.3], which shows l-TR⫅̸l-XT, is in sl-TR. □
Second, we recall from [7, Theorem 2.6] that an l- tR (with look-ahead) can be decomposed into two l-t (without look-ahead), of which the first is a finite-state relabeling. This result can easily be generalized to extended top-down tree transducers and their compositions.
Lemma 15 (look-ahead decomposition)

for every n≥1 and
 .
.
Proof
The second inclusion is immediate because
 . We prove the first inclusion by induction on n. For n = 1 an obvious generalization of the construction in the proof of [7, Theorem 2.6], which preserves ‘s’ and ‘n’, can be used. For n ≥ 1, we have
. We prove the first inclusion by induction on n. For n = 1 an obvious generalization of the construction in the proof of [7, Theorem 2.6], which preserves ‘s’ and ‘n’, can be used. For n ≥ 1, we have

where the case n = 1 is used in the first step, Lemma 13 in the second step, and the induction hypothesis in the last step. □
Lemma 15 implies that

for every n ≥ 1 and
 , so the classes
, so the classes
 and
and
 have the same composition closure. However, this closure is potentially achieved at different powers.
have the same composition closure. However, this closure is potentially achieved at different powers.
4 Four Classes that are Closed at a Finite Power
In this section, we show that the four classes
 ,
,
 ,
,
 , and
, and
 are closed under composition at a finite power. We first recall a central result of [3], which shows that none of them is closed under composition.
are closed under composition at a finite power. We first recall a central result of [3], which shows that none of them is closed under composition.
Proposition 16 ([3, Section 3.4])

We note that [3] states the even stronger result that the class \(\mathcal {B}(\text {snl}, \text {snl})^{2}\) is not contained in the class of all bimorphisms, which implies the above result by Proposition 11. In [3] the class \(\mathcal {B}(\text {snl}, \text {snl})\) is denoted by \(\mathcal {B}(\text {s}, \text {c})\). The proof of Theorem 31 in Section 5 implies Proposition 16 for
 instead of l-XTR, which is all we need; for the implication see non-inclusion (ii) in the proof of Theorem 47.
instead of l-XTR, which is all we need; for the implication see non-inclusion (ii) in the proof of Theorem 47.
Next we recall another central result of [3]: the (very restricted) class
 is not closed under composition (by the previous proposition), but is closed under composition at power 2.
is not closed under composition (by the previous proposition), but is closed under composition at power 2.
Proposition 17 ([3, Theorem 6.2])
 for every n≥3.
for every n≥3.
As we will show now, the (strict) classes
 and
and
 are also closed under composition already at the second power. We start with a lemma that decomposes an
are also closed under composition already at the second power. We start with a lemma that decomposes an
 into two transducers of which one is an
into two transducers of which one is an
 , for which we have the composition closure result of Proposition 17. For the benefit of Section 6, we make ε-freeness optional in the next two lemmas.
, for which we have the composition closure result of Proposition 17. For the benefit of Section 6, we make ε-freeness optional in the next two lemmas.
Lemma 18 (decomposition on the right)
 sdl-H for every
sdl-H for every
 .
.
Proof
This is proved for strict tree homomorphisms in [5, Section I-2-1-3-5]. The proof can be generalized to
 as follows. Let M = (Q,Σ,Δ, Q
0, R) be an sl-xt. Clearly, we may assume a separation of the states into deleted and non-deleted states. More precisely, we assume m ≥ max{rk(σ)∣σ ∈Σ} such that Q = Q
1∪{1,…, m} with \(Q_{1} \cap \mathbb {N} = \emptyset \) and for every rule (ℓ, q, r)∈ R the following three conditions hold: (i) q ∈ Q
1 and states(r)⊆Q
1, (ii) ℓ is linear in Q, and (iii) states(ℓ)∖states(r)⊆{1,…, m}. Let Δ′ be the ranked alphabet {δ
n
∣δ ∈Δ, 0 ≤ n ≤ m} with rk(δ
n
)=rk(δ) + n. In addition, let \(\overline {\Sigma } = \{\overline \sigma \mid \sigma \in {\Sigma }\}\) be the ranked alphabet with \(\textnormal {rk}(\overline \sigma ) = \textnormal {rk}(\sigma )\). We suppose that Δ, Δ′, and \(\overline {\Sigma }\) are pairwise disjoint. As intermediate alphabet we take \({\Gamma } = {\Delta } \cup {\Delta }^{\prime } \cup \overline {\Sigma }\), and let α ∈Δ0 be an arbitrary nullary output symbol. Now we first construct the strict delabeling tree homomorphism φ from Γ to Δ such that (i) φ(δ
n
) = φ(δ) = δ(x
1,…, x
k
) for every δ ∈Δ
k
and 0 ≤ n ≤ m and (ii) \(\varphi (\overline \sigma ) = \alpha \) for every σ ∈Σ. Thus, φ turns every δ
n
into δ and deletes its last n arguments.
as follows. Let M = (Q,Σ,Δ, Q
0, R) be an sl-xt. Clearly, we may assume a separation of the states into deleted and non-deleted states. More precisely, we assume m ≥ max{rk(σ)∣σ ∈Σ} such that Q = Q
1∪{1,…, m} with \(Q_{1} \cap \mathbb {N} = \emptyset \) and for every rule (ℓ, q, r)∈ R the following three conditions hold: (i) q ∈ Q
1 and states(r)⊆Q
1, (ii) ℓ is linear in Q, and (iii) states(ℓ)∖states(r)⊆{1,…, m}. Let Δ′ be the ranked alphabet {δ
n
∣δ ∈Δ, 0 ≤ n ≤ m} with rk(δ
n
)=rk(δ) + n. In addition, let \(\overline {\Sigma } = \{\overline \sigma \mid \sigma \in {\Sigma }\}\) be the ranked alphabet with \(\textnormal {rk}(\overline \sigma ) = \textnormal {rk}(\sigma )\). We suppose that Δ, Δ′, and \(\overline {\Sigma }\) are pairwise disjoint. As intermediate alphabet we take \({\Gamma } = {\Delta } \cup {\Delta }^{\prime } \cup \overline {\Sigma }\), and let α ∈Δ0 be an arbitrary nullary output symbol. Now we first construct the strict delabeling tree homomorphism φ from Γ to Δ such that (i) φ(δ
n
) = φ(δ) = δ(x
1,…, x
k
) for every δ ∈Δ
k
and 0 ≤ n ≤ m and (ii) \(\varphi (\overline \sigma ) = \alpha \) for every σ ∈Σ. Thus, φ turns every δ
n
into δ and deletes its last n arguments.
For every rule (ℓ, q, r)∈ R there exist \(k \in \mathbb {N}\), δ ∈Δ, and r 1,…, r k ∈ T Δ(Q) such that r = δ(r 1,…, r k ) because M is strict. We construct the nondeleting sl-xt M ′=(Q,Σ,Γ, Q 0, R ′) such that R ′ contains the rule
for every rule (ℓ, q, δ(r 1,…, r k ))∈ R, where states(ℓ)∖states(r) = {i 1,…, i n } with i 1<⋯ < i n . This is a proper rule because ℓ is linear in Q. Moreover, R ′ contains the rules \(\left (\sigma (1, \dotsc , k), i, \overline \sigma (1, \dotsc , k)\right )\) for all \(k \in \mathbb {N}\), σ ∈Σ k , and i ∈{1,…, m}. The set R ′ contains no further rules. Thus, M ′ simulates M but attaches the subtrees that are deleted by M to the root of the right-hand side of each rule. It is straightforward to show that τ(M ′) ;φ = τ(M). Clearly, if M is ε-free, then so is M ′. □
The next lemma is our second composition result, which is more restricted than the first, which is Lemma 13, but sufficiently powerful in combination with Lemma 18.
Lemma 19 (composition on the left)
sdl-H;
 for every
for every
 .
.
Proof
Let φ:T Σ→T Γ be a strict delabeling linear tree homomorphism, and let M = (Q,Γ,Δ, Q 0, R) be a strict l-xt. Moreover, let Q ′ = Q∪{⋆} for a new state ⋆∉Q. We extend φ to a tree transformation φ ′:T Σ(Q ′)→T Γ(Q ′) such that φ ′(q ′) = q ′ for every q ′∈ Q ′ and
for every \(k \in \mathbb {N}\), σ ∈Σ k , and t 1,…, t k ∈ T Σ(Q ′). We construct the l-xt M ′=(Q ′,Σ,Δ, Q 0, R ′) such that for each rule (ℓ, q, r)∈ R we have all rules (ℓ ′, q, r) in R ′ for which (i) ℓ ′∈ T Σ(Q ′) is linear in Q, (ii) φ ′(ℓ ′) = ℓ, and (iii) |posΣ(ℓ ′)|=|posΓ(ℓ)|. No further rules are in R ′.
Let us quickly consider a small example. Suppose that R contains the rule \(\gamma \left (\alpha , \gamma ^{\prime }(q) \right ) \overset {q}{\longrightarrow } \delta (q)\) and we have (i) φ(σ) = γ(x 3, x 2), (ii) φ(σ ′) = γ ′(x 1), and (iii) φ(α) = α with {α (0),(σ ′)(2), σ (3)}⊆Σ. Then R ′ contains the rule \(\sigma \left (\star , \sigma ^{\prime }(q, \star ), \alpha \right ) \overset {q}{\longrightarrow } \delta (q)\).
It should be clear that τ(M ′) = φ ;τ(M). Finally, we observe that M ′ is strict because it has the same right-hand sides of rules as M, and it is ε-free if M is ε-free because φ is strict. □
The previous two lemmas are now used to prove that
 and
and
 are closed under composition at power 2.
are closed under composition at power 2.
Theorem 20
 ;
;
 for every n≥1.
for every n≥1.
Proof
The second inclusion is trivial because
 . For the first inclusion, we first prove that
. For the first inclusion, we first prove that
 ;sdl-H. The idea of this inclusion is that the first
;sdl-H. The idea of this inclusion is that the first
 splits off a tree homomorphism of type ‘sdl’ on the right (using Lemma 18), which is then absorbed on the left by the second
splits off a tree homomorphism of type ‘sdl’ on the right (using Lemma 18), which is then absorbed on the left by the second
 (using Lemma 19). This auxiliary statement is proved by induction. For n = 1, we have to prove
(using Lemma 19). This auxiliary statement is proved by induction. For n = 1, we have to prove
 ;sdl-H, which is the statement of Lemma 18. For n ≥ 1 we obtain that
;sdl-H, which is the statement of Lemma 18. For n ≥ 1 we obtain that


where we used Lemma 18 in the second step, Lemma 19 in the third step, and the induction hypothesis in the last step. From Lemma 15 and the above inclusion we now conclude that

Since
 , this implies that
, this implies that

where the second inclusion is due to Proposition 17. Since sdl-H⊆sl-T we can apply Lemma 13 to obtain that

Applying Lemmas 15 and 13 once more, we obtain

Since
 we have proved the statement. □
we have proved the statement. □
Up to now, we have shown that the (strict) classes
 and
and
 are closed under composition at the second power. In the rest of this section, we will show that the classes
are closed under composition at the second power. In the rest of this section, we will show that the classes
 and
and
 are closed under composition at the third and fourth power, respectively. We start with a normal form for
are closed under composition at the third and fourth power, respectively. We start with a normal form for
 , in which every rule that violates the strictness condition is simulated by a chain of rules for a (non-extended) l-tR.
, in which every rule that violates the strictness condition is simulated by a chain of rules for a (non-extended) l-tR.
Lemma 21 (non-strict normal form)
For every
 there exists an equivalent
there exists an equivalent
 such that ℓ ∈ Σ (Q
′) for every rule (ℓ,q,r) ∈ R
′
with r∈Q
′.
such that ℓ ∈ Σ (Q
′) for every rule (ℓ,q,r) ∈ R
′
with r∈Q
′.
Proof
Let M = (Q,Σ,Δ, Q 0, R, c) and M ′=(Q ′,Σ,Δ, Q 0, R ′, c ′). Every (non-strict) rule ρ = (ℓ, q, r) in R with r ∈ Q can be simulated by a finite set \(R^{\prime }_{\rho }\) of l-tR rules as follows. We consider new states of the form 〈ρ, v〉 where v ∈pos(ℓ)∖{ε,poss r (ℓ)}. Moreover, we let 〈ρ, ε〉 = q and 〈ρ,poss r (ℓ)〉 = r. For every position v ∈pos(ℓ) such that v≺poss r (ℓ), we have the following rule in \(R^{\prime }_{\rho }\):
where k = rk(ℓ(v)) and \(i \in \mathbb {N}\) is the unique integer such that v i≼poss r (ℓ). The look-ahead for every new state 〈ρ, v j〉 with j≠i is defined by
We note that states(ℓ| v j )⊆Q la. The tree language c ′(〈ρ, v j〉) is regular by the folklore result stating that OI-substitution preserves regularity, which we mentioned at the end of Section 2. Recall that in OI-substitution, different occurrences of the same state q ′ can be replaced by different trees of c(q ′). The rules in \(R^{\prime }_{\rho }\) simulate the rule ρ by consuming the left-hand side ℓ position by position, following the path from the root to the unique occurrence of r. Thus, we define the set Q ′ of states of M ′ to consist of Q together with all the mentioned new states. The set R ′ of rules consists of all strict rules in R together with the rules in \(R^{\prime }_{\rho }\) for all non-strict rules ρ in R. The look-ahead c ′ equals c on the states in Q la, and is defined as above for the new states. Then τ(M ′) = τ(M) and M ′ satisfies the requirements. □
Example 22
We illustrate the construction on the example rule
for which p, q, r ∈ Q and the relevant look-ahead is c(p) = T. Corresponding to this rule, M ′ has the following two rules in \(R^{\prime }_{\rho }\):
because q = 〈ρ, ε〉 and r = 〈ρ,22〉. Moreover, we have
and c ′(〈ρ,21〉) = {α} for the look-ahead c ′ of M ′.
The next lemma is similar to Lemma 18, in that it demonstrates how to decompose an
 into a delabeling l-tR and an
into a delabeling l-tR and an
 , for which we now have the composition closure result of Theorem 20. The proof is, however, more complicated than the one of Lemma 18. Since the delabeling property is not essential in the following, we actually state a weaker variant.
, for which we now have the composition closure result of Theorem 20. The proof is, however, more complicated than the one of Lemma 18. Since the delabeling property is not essential in the following, we actually state a weaker variant.
Lemma 23 (decomposition on the left)

Proof
Let M = (Q,Σ,Δ, Q
0, R, c) be an ε-free l-xtR such that ℓ ∈Σ(Q) for every rule (ℓ, q, r)∈ R with r ∈ Q. We can assume this normal form without loss of generality by Lemma 21. Additionally, we may assume that |Q|≥m, where m = max{rk(σ)∣σ ∈Σ}. We will construct an l-tR
M
1 and a strict
 such that τ(M
1);τ(M
2) = τ(M). Intuitively speaking, the transducer M
1 processes the input by nondeterministically executing a number of non-strict rules of M. Whenever it executes two consecutive non-strict rules, M
1 simulates the state behavior of M. Moreover, M
1 marks the positions in the (processed) input where it has applied a sequence of consecutive non-strict rules by indicating the corresponding state transition of M. The transducer M
2 then uses these markings to execute the missing strict rules of M.
such that τ(M
1);τ(M
2) = τ(M). Intuitively speaking, the transducer M
1 processes the input by nondeterministically executing a number of non-strict rules of M. Whenever it executes two consecutive non-strict rules, M
1 simulates the state behavior of M. Moreover, M
1 marks the positions in the (processed) input where it has applied a sequence of consecutive non-strict rules by indicating the corresponding state transition of M. The transducer M
2 then uses these markings to execute the missing strict rules of M.
As intermediate ranked alphabet we use Γ=Σ∪(Σ×Q×Q), where each triple 〈σ, q ′, q〉∈Σ×Q×Q has the same rank as σ. We fix m pairwise different states p 1,…, p m ∈ Q. We construct the l-tR M 1=(Q 1,Σ,Γ,{p 1}, R 1, c 1) with states Q 1 = Q∪(Q×Q) and the set R 1 of rules consists of:
-
(i)
the rule \(\sigma ({p_{1}, \dotsc , p_{k}} ) \overset {p}{\longrightarrow } \sigma ({p_{1}, \dotsc , p_{k}})\) for every \(k \in \mathbb {N}\), σ ∈Σ k , and p ∈ Q,
-
(ii)
the two rules

for every non-strict rule \(\sigma ({q_{1}, \dotsc , q_{k}}) \overset {q}{\longrightarrow } q_{i}\) in R with 1 ≤ i ≤ k and every p, q ′∈ Q, and
-
(iii)
the rule

for every \(k \in \mathbb {N}\), σ ∈ Σ k , and q ′, q ∈ Q.
We note that \(Q_{1}^{\text {la}} \subseteq Q^{\text {la}}\). The look-ahead mapping \(c_{1} : Q_{1}^{\text {la}} \to \text {Reg}({\Sigma })\) is given by c 1(q) = c(q) for every \(q \in Q_{1}^{\text {la}}\). Actually, M 1 is delabeling.
Next, we construct the

with the set Q 2 = Q of states, the set R ′={(ℓ, q, r)∈ R∣r∉Q} of strict rules of M, and the set
Again, \(Q_{2}^{\text {la}} \subseteq Q^{\text {la}}\), where \(Q_{2}^{\text {la}}\) contains the look-ahead states of M 2, so we just set the look-ahead mapping \(c_{2} : Q_{2}^{\text {la}} \to \text {Reg}({\Gamma })\) to c 2(q) = c(q) for every \(q \in Q_{2}^{\text {la}}\).
Intuitively, it should be clear that τ(M 1) ;τ(M 2) = τ(M). Whenever M 2 arrives in state q ′ at an input position with label 〈σ, q ′, q〉, it knows that M 1 has applied a sequence of non-strict rules of M that led from state q ′ to state q, and thus M 2 can continue acting as if it is already in state q. Formally, it can be proved that, for every state q ∈ Q, input tree t ∈ T Σ, and output tree u ∈ T Δ, we have \(q \Rightarrow _{M}^{\ast } (t, u)\) if and only if there exists s ∈ T Γ such that \(p_{1} \Rightarrow _{M_{1}}^{\ast } (t, s)\) and \(q \Rightarrow _{M_{2}}^{\ast } (s, u)\). The proof is by induction on the length of the derivations using Lemma 9. It uses several elementary properties of the derivations of M 1 and M 2 such as (for all p, q, q ′, q ″∈ Q):
-
if \(p_{1} \Rightarrow _{M_{1}}^{\ast } (t, s)\), then \(p \Rightarrow _{M_{1}}^{\ast } (t, s)\),
-
if \(p_{1} \Rightarrow _{M_{1}}^{\ast } \left (t, \sigma (s_{1}, \dotsc , s_{k}) \right )\), then \(\langle q^{\prime }, q\rangle \Rightarrow _{M_{1}}^{\ast } \left (t, \langle \sigma , q^{\prime }, q\rangle (s_{1}, \dotsc , s_{k}) \right )\),
-
\(p_{1} \Rightarrow _{M_{1}}^{\ast } \left (t, \langle \sigma , q^{\prime }, q\rangle (s_{1}, \dotsc , s_{k}) \right )\) if and only if \(\langle q^{\prime \prime }, q^{\prime }\rangle \Rightarrow _{M_{1}}^{\ast } \left (t, \langle \sigma , q^{\prime \prime }, q \rangle (s_{1}, \dotsc , s_{k}) \right )\), and
-
\(q \Rightarrow _{M_{2}}^{\ast } \left (\sigma (s_{1}, \dotsc , s_{k}), u\right )\) if and only if \(q^{\prime } \Rightarrow _{M_{2}}^{\ast } \left (\langle \sigma , q^{\prime }, q\rangle (s_{1}, \dotsc , s_{k}), u \right )\).
□
Lemmas 23 and 13 now enable us to prove that the class
 is closed under composition at power 3. The proof is similar to, but easier than, the one of Theorem 20.
is closed under composition at power 3. The proof is similar to, but easier than, the one of Theorem 20.
Theorem 24
 for every n≥1.
for every n≥1.
Proof
Again, the second inclusion is trivial because l-TR and
 are
subclasses of
are
subclasses of
 . Similar to the proof of Theorem 20, the idea of the first inclusion is that the last
. Similar to the proof of Theorem 20, the idea of the first inclusion is that the last
 splits off an l-tR on the left (using Lemma 23), which is then absorbed on the right by the penultimate
splits off an l-tR on the left (using Lemma 23), which is then absorbed on the right by the penultimate
 (using Lemma 13). Formally we prove by induction on n that
(using Lemma 13). Formally we prove by induction on n that

which suffices by Theorem 20. For n = 1 we obtain
 , which is stated in Lemma 23. In the induction step for n ≥ 1, we obtain
, which is stated in Lemma 23. In the induction step for n ≥ 1, we obtain

where we use Lemma 23 in the second step, Lemma 13 in the third step, and the induction hypothesis in the last step. □
It is immediate from Theorem 24 and Lemma 15 that the class
 is closed under composition at power 4. Thus, in contrast to Theorem 20, look-ahead influences the power of closedness in the non-strict case, as will be proved in the next section.
is closed under composition at power 4. Thus, in contrast to Theorem 20, look-ahead influences the power of closedness in the non-strict case, as will be proved in the next section.
Corollary 25
 for every n≥1.
for every n≥1.
A summary of our results concerning the powers at which the considered classes are closed under composition is provided in Table 2. In the next section, we will demonstrate that these powers are indeed the least ones with this property.
5 Least Power of Closedness
In this section, we will determine the least power at which the composition closure is achieved for the classes
 ,
,
 ,
,
 , and
, and
 , which are all computed by certain ε-free l-xtR. For the strict classes the least power is 2, as stated in the next theorem. In the remainder of this section we consider the non-strict classes.
, which are all computed by certain ε-free l-xtR. For the strict classes the least power is 2, as stated in the next theorem. In the remainder of this section we consider the non-strict classes.
Theorem 26

for every n≥3.
Proof
The first inclusion is trivial and its strictness follows from Proposition 14. The second inclusion is also trivial and its strictness follows from Proposition 16, which shows that the class
 is not closed under composition. The three equalities are proved in Theorem 20. □
is not closed under composition. The three equalities are proved in Theorem 20. □
In the following, we will use the computed dependencies in \(\mathcal {D}(M)\), for which we recall some important properties from [11]. Let \(L \subseteq \mathbb {N}^{\ast } \times \mathbb {N}^{\ast }\) be a set of links [e.g., the set L of links in a dependency \(\langle t, L, u\rangle \in \mathcal {D}(M)\)]. The elements of dom(L) are also called link origins of L. For the next definition, proposition and lemma, let M = (Q,Σ,Δ, Q 0, R, c) be the considered ε-free l-xtR.
Definition 27 ([11, Definitions 4 and 5])
A set \(L \subseteq \mathbb {N}^{\ast } \times \mathbb {N}^{\ast }\) of links is
-
strictly input hierarchical if for all links (v 1, w 1),(v 2, w 2) ∈ L
-
v 1≺v 2 implies w 1≼w 2 and
-
v 1 = v 2 implies w 1≼w 2 or w 2≼w 1,
-
-
input link-distance bounded by \(b \in \mathbb {N}\) if for all link origins v 1, v 2∈dom(L) with v 1≺v 2 and |v 2|−|v 1|>b there exists a link origin v ∈dom(L) such that v 1≺v≺v 2 and |v|−|v 1| ≤ b.
The set \(\mathcal {D}(M)\) of dependencies has those properties if for each dependency \(\langle t, L, u\rangle \in \mathcal {D}(M)\) the set L of links has them. We also say that \(\mathcal {D}(M)\) is input link-distance bounded if there exists an integer \(b \in \mathbb {N}\) such that it is input link-distance bounded by b.
We assume that the corresponding properties are defined for the output side, using L −1 instead of L. For example, L is strictly output hierarchical if L −1 is strictly input hierarchical. The set \(\mathcal {D}(M)\) computed by the ε-free l-xtR M always has these properties as shown in [11].
Proposition 28 ([11, Corollary 1 and Theorem 2])
The set \(\mathcal {D}(M)\) of dependencies is strictly input and output hierarchical, and it is input and output link-distance bounded.
These properties should be intuitively clear. They are discussed in more detail in [11]. Roughly speaking, the set L of links of a sentential form of M is strictly input and output hierarchical because links cannot cross each other. In addition, if b is the maximal height of the left-hand (resp. right-hand) side of a rule of M, then L is obviously input (resp. output) link-distance bounded by b. Next, we observe some simple consequences of Proposition 28, which we will use later. Whenever we mention ‘(in)comparable’ in the following, we refer to the partial prefix order ≼.
Lemma 29
Let \(\langle t, L, u \rangle \in \mathcal {D}(M)\) be a dependency, and let \(\mathcal {D}(M)\) be input link-distance bounded by b.
-
(i)
For all links (v, w),(v ′, w ′) ∈ L, v and v ′ are incomparable if and only if w and w ′ are incomparable.
-
(ii)
For all positions v 1, v 2 ∈pos(t) and link origins v 0, v 3∈ d o m(L) with v 0≼v 1≺v 2≼v 3 and |v 2|−|v 1|>b, there exists a link origin v ∈ d o m(L) such that v 1≺v≺v 2 and |v|−|v 1| ≤ b.
Proof
We start with the if-direction in the first item. Without loss of generality, suppose that v≼v ′. Then by the definition of strictly input hierarchical, we know that w and w ′ are comparable. The other direction is similarly true by the definition of strictly output hierarchical. We prove the second item by induction on |v 3|−|v 0| as follows. Since v 0≼v 1≺v 2≼v 3 and |v 3|−|v 0|≥|v 2|−|v 1|>b, there exists a link origin v ∈dom(L) such that v 0≺v≺v 3 and |v|−|v 0| ≤ b. Consequently, v≺v 2. Now we distinguish two cases: (a) If v 1≺v, then v 1≺v≺v 2 and |v|−|v 1|≤|v|−|v 0| ≤ b proving the second item. (b) Otherwise, we have v 0≺v≼v 1≺v 2≼v 3 with v, v 3∈dom(L) and |v 2|−|v 1|>b. Since |v 3|−|v|<|v 3|−|v 0|, we can apply the induction hypothesis to v≼v 1≺v 2≼v 3 to prove the statement. □
In the proofs of Theorems 31 and 33 we will see applications of these properties and the following linking theorem, which we also recall from [11].
Proposition 30 ([11, Theorem 4])
Let Ω and Ψ be ranked alphabets with Ψ0 ≠ ∅ and
Ψ
1 ≠ ∅. Let k,n≥1, and let m
1,…, m
k
be
 such that
such that
where c ′ ,c ′′ ∈T Ω (X n ) are linear and nondeleting in X n . There exist trees t 1 ,…,t n ∈T Ψ , dependencies
with u 0 =c ′[t 1 ,…,t n ] and u k =c ′′[t 1 ,…,t n ], and a family (v ij ,w ij )∈L j of links for 1≤i≤n and 1≤j≤k, such that for all 1≤i≤n:
-
(i)
\(\text {pos}_{x_{i}}(c^{\prime \prime }) \preceq w_{ik}\),
-
(ii)
v i(j+1) ≼w ij for all 1≤j≤k−1, and
-
(iii)
\(\text {pos}_{x_{i}}(c^{\prime }) \preceq v_{i1}\).
Intuitively, the items mean that (i) position w i k is in the subtree t i of the output tree u k = c ″[t 1,…, t n ], (ii) position w i j has prefix v i(j+1) in the intermediate tree u j , and (iii) position v i1 is in the subtree t i of the input tree u 0 = c ′[t 1,…, t n ].
To show that an integer k > 1 is the least power at which the closure under composition is achieved for a class \(\mathcal {C}\), we present a tree transformation \(\tau \in \mathcal {C}^{k}\) that is not in \(\mathcal {C}^{k-1}\). Roughly speaking, this is achieved by deducing certain links given the tree transformation with the help of Proposition 30. These links are necessary in the dependency for the determined input-output tree pairs. Thus, we obtain a partial specification of several dependencies in the sense that we know some of its links, but not necessarily all of them. Then we consider whether these partial specifications can be implemented by a composition of
 . It can be seen from Proposition 30 that we will often not be able to identify both positions of a link exactly, but rather determine that one of its positions has a certain other prominent position as prefix. In such cases, we graphically display the link using a spline with an inverted arrow head that points to the subtree rooted at that prominent position (instead of to the actual position). For example, the splines in Fig. 3 indicate that a position of t on the left (resp. u on the right) is linked to position 2 on the right (resp. on the left).
. It can be seen from Proposition 30 that we will often not be able to identify both positions of a link exactly, but rather determine that one of its positions has a certain other prominent position as prefix. In such cases, we graphically display the link using a spline with an inverted arrow head that points to the subtree rooted at that prominent position (instead of to the actual position). For example, the splines in Fig. 3 indicate that a position of t on the left (resp. u on the right) is linked to position 2 on the right (resp. on the left).
We now prove that 3 is the least power at which the class
 is closed under composition.
is closed under composition.
Theorem 31

Proof
The inclusion follows from Lemma 15. To prove the strictness, let \(M_{1}^{\prime } = (Q^{\prime }, {\Sigma }, {\Delta }, \{\star \}, R^{\prime })\) be the
 that is obtained from the
that is obtained from the
 of Example 2 by removing the state q
la and all rules for the input symbol σ; i.e., the rules \(\sigma (q, q^{\text {la}}) \overset {q}{\longrightarrow } q\) and \(\sigma (q^{\text {la}}, q) \overset {q}{\longrightarrow } q\). Thus, \(\tau (M^{\prime }_{1})\) is the restriction of τ(M
1) to input trees that do not contain any occurrence of σ. In addition, we use the two bimorphisms \(B_{2}, B_{3}\in \mathcal {B}(\text {snl}, \text {snl})\) of [5, Section II-2-2-3-1], where strictness is denoted by ‘e’ and nondeletion by ‘c’. These bimorphisms are similar to the two bimorphisms that are used in [3, Section 3.4] to prove Proposition 16. By Proposition 11,
of Example 2 by removing the state q
la and all rules for the input symbol σ; i.e., the rules \(\sigma (q, q^{\text {la}}) \overset {q}{\longrightarrow } q\) and \(\sigma (q^{\text {la}}, q) \overset {q}{\longrightarrow } q\). Thus, \(\tau (M^{\prime }_{1})\) is the restriction of τ(M
1) to input trees that do not contain any occurrence of σ. In addition, we use the two bimorphisms \(B_{2}, B_{3}\in \mathcal {B}(\text {snl}, \text {snl})\) of [5, Section II-2-2-3-1], where strictness is denoted by ‘e’ and nondeletion by ‘c’. These bimorphisms are similar to the two bimorphisms that are used in [3, Section 3.4] to prove Proposition 16. By Proposition 11,
 , hence B
2 and B
3 can also be defined by
, hence B
2 and B
3 can also be defined by
 and M
3, respectively. For convenience, we present M
2 and M
3 explicitly before we show that \(\tau = \tau (M_{1}^{\prime }) \ ; \tau (M_{2}) \ ; \tau (M_{3})\) cannot be computed by a composition of two
and M
3, respectively. For convenience, we present M
2 and M
3 explicitly before we show that \(\tau = \tau (M_{1}^{\prime }) \ ; \tau (M_{2}) \ ; \tau (M_{3})\) cannot be computed by a composition of two
 .
.
Let M
2=(Q
2,Δ,Γ,{⋆}, R
2) be the
 with Q
2={⋆,id,id′}, the ranked alphabet Γ = {σ
(2), γ
(1), α
(0)}, and the set R
2 consisting of the rules
with Q
2={⋆,id,id′}, the ranked alphabet Γ = {σ
(2), γ
(1), α
(0)}, and the set R
2 consisting of the rules
Moreover, let M
3=(Q
3,Γ,Δ,{⋆}, R
3) be the
 with Q
3={⋆, p,id,id′} and the set R
3 consisting of the rules
with Q
3={⋆, p,id,id′} and the set R
3 consisting of the rules

Note that both τ(M 2) and τ(M 3) are partial functions.
We present a proof by contradiction, so we assume that τ = τ(N
1);τ(N
2) for some
 and N
2. By Proposition 28 there exist a
1, a
2, b
1, b
2≥1 such that \(\mathcal {D}(N_{1})\) and \(\mathcal {D}(N_{2})\) are strictly input and output hierarchical, input link-distance bounded by a
1 and a
2, respectively, and output link-distance bounded by b
1 and b
2, respectively. Let n = 2⋅ max(a
1, a
2, b
1, b
2)+2. We select the trees
and N
2. By Proposition 28 there exist a
1, a
2, b
1, b
2≥1 such that \(\mathcal {D}(N_{1})\) and \(\mathcal {D}(N_{2})\) are strictly input and output hierarchical, input link-distance bounded by a
1 and a
2, respectively, and output link-distance bounded by b
1 and b
2, respectively. Let n = 2⋅ max(a
1, a
2, b
1, b
2)+2. We select the trees
of which c ′ and c ″ are linear and nondeleting in X n (see Fig. 4). To be completely formal, c ′ and c ″ are defined inductively as follows: First, \(c^{\prime } = c^{\prime }_{1}\) with \(c^{\prime }_{n-1} = \sigma _{2}(x_{n}, x_{n-1})\) and \(c^{\prime }_{i-1} = \sigma _{1}(c^{\prime }_{i+1}, c[\sigma _{2}(x_{i}, x_{i-1})])\) for every even integer 2 ≤ i ≤ n−2. Second, we let \(c^{\prime \prime } = \sigma _{1}(c^{\prime \prime }_{2}, x_{1})\) with \(c^{\prime \prime }_{n} = x_{n}\) and \(c^{\prime \prime }_{i-2} = \sigma _{1}(c^{\prime \prime }_{i}, \sigma _{2}(x_{i-1},x_{i-2}))\) for every even 4 ≤ i ≤ n.
It is straightforward to check that
for all t 1,…, t n ∈ T Ψ with Ψ = {γ (1), α (0)}. Note that, according to Example 8, every σ 1-rib \(c[\sigma _{2}(t_{i},t_{i-1})] = {\gamma _{2}^{n}} \left (\sigma _{2}(t_{i},t_{i-1}) \right )\) is transformed into σ 2(t i , t i−1) by \(\tau (M^{\prime }_{1})\). Consequently, we can apply Proposition 30 to obtain that there exist trees t 1,…, t n ∈ T Ψ , dependencies \(\langle c^{\prime }[t_{1}, \dotsc , t_{n}], L_{1}, u_{1}\rangle \in \mathcal {D}(N_{1})\) and \(\langle u_{1}, L_{2}, c^{\prime \prime }[t_{1}, \dotsc , t_{n}] \rangle \in \mathcal {D}(N_{2})\), and links (v i1, w i1) ∈ L 1 and (v i2, w i2) ∈ L 2 for 1 ≤ i ≤ n such that
-
\(\text {pos}_{x_{i}}(c^{\prime \prime }) \preceq w_{i2}\),
-
v i2≼w i1, and
-
\(\text {pos}_{x_{i}}(c^{\prime }) \preceq v_{i1}\).
The splines with the inverted arrow heads indicate some of those links in Fig. 4.
Now, let us consider the obtained (partial) dependencies, which are depicted in Fig. 4. We clearly have (ε, ε),(v n2, w n2) ∈ L 2 and
Thus \(\left |{w_{n2}}\right | \geq \frac {n}{2} > b_{2}\). Since \(\mathcal {D}(N_{2})\) is output link-distance bounded by b 2, there exists a link (v ′, w ′) ∈ L 2 with ε≺w ′≺w n2 and |w ′| ≤ b 2. Consequently, the position w ′ has label σ 1 in u 2 = c ″[t 1,…, t n ] as indicated in Fig. 4. Formally, w ′=1m for some \(1 \leq m\leq b_{2} \leq \frac n2 - 1\). Let i = 2m, which yields 2 ≤ i ≤ n−2. Then w ′≺w (i+1)2 and w ′≺w i2 because \(w^{\prime } \prec \text {pos}_{x_{i+1}}(c^{\prime \prime }) \preceq w_{(i+1)2}\) and \(w^{\prime } \prec \text {pos}_{x_{i}}(c^{\prime \prime }) \preceq w_{i2}\). Since \(\mathcal {D}(N_{2})\) is strictly output hierarchical, we can conclude that v ′≼v (i+1)2≼w (i+1)1 and v ′≼v i2≼w i1. Additionally, w ′ and \(\text {pos}_{x_{i-1}}(c^{\prime \prime })\) are incomparable and \(\text {pos}_{x_{i-1}}(c^{\prime \prime }) \preceq w_{(i-1)2}\), so also the positions w ′ and w (i−1)2 are incomparable (see Lemma 32(i) for a proof of this and similarly straightforward arguments). Consequently, Lemma 29(i) shows that v ′ and v (i−1)2 are also incomparable. Using v (i−1)2≼w (i−1)1, we obtain that v ′ and w (i−1)1 are incomparable, and in particular that v ′ ≰ w (i−1)1.
Next, we inspect the input tree u 0 = c ′[t 1,…, t n ] and the links (ε, ε), (v i1, w i1), and (v (i−1)1, w (i−1)1) in L 1. We already know that \(\text {pos}_{x_{i}}(c^{\prime }) \preceq v_{i1}\) and \(\text {pos}_{x_{i-1}}(c^{\prime }) \preceq v_{(i-1)1}\). Let
be the set of positions of c ′ (and hence of u 0) that are in an occurrence of the tree c and are prefixes of \(\text {pos}_{x_{i}}(c^{\prime })\). Since |V| = n > a 1, it follows from Lemma 29(ii) that there exists a link (v ″, w ″) ∈ L 1 such that v ″∈ V, which also yields v ″≺v i1 and v ″≺v (i−1)1. Since \(\mathcal {D}(N_{1})\) is strictly input hierarchical, we obtain that w ″≼w i1 and w ″≼w (i−1)1. Since v ″ and v (i+1)1 are incomparable, Lemma 29(i) implies that w ″ and w (i+1)1 are incomparable, and in particular that w ″≰w (i+1)1.
Summing up, we have
Since v
′≼w
i1 and w
″≼w
i1, we must have v
′≼w
″ or w
″≼v
′. In the former case, we obtain v
′≼w
″≼w
(i−1)1 contradicting the last statement of (1). Similarly, in the second case, we obtain w
″≼v
′≼w
(i+1)1 contradicting the first statement of (2). Since both cases are contradictory, the assumption that we can compute τ with two
 is wrong. □
is wrong. □
Fortunately, we can reuse the ideas used in the proof of Theorem 31 to conclude that 4 is the least power at which the class
 is closed under composition. The slightly more elaborate proof first establishes that a deleting rule, which is a rule \(\ell \overset {q}{\longrightarrow } r\) such that \(\text {states}(r) \subsetneq \text {states}(\ell )\), must be used at a certain position and then employs the classical cut-and-paste technique to establish that this deletion (without look-ahead) enables undesired translations.
is closed under composition. The slightly more elaborate proof first establishes that a deleting rule, which is a rule \(\ell \overset {q}{\longrightarrow } r\) such that \(\text {states}(r) \subsetneq \text {states}(\ell )\), must be used at a certain position and then employs the classical cut-and-paste technique to establish that this deletion (without look-ahead) enables undesired translations.
We will use some well-known elementary properties of the prefix order, which we state in the next lemma.
Lemma 32
Let \(v, v_{1}, v_{2}, v^{\prime }_{1}, v^{\prime }_{2} \in \mathbb {N}^{\ast }\) be positions with \(v_{1} \preceq v^{\prime }_{1}\) and \(v_{2} \preceq v^{\prime }_{2}\).
-
(i)
If v 1 and v 2 are incomparable, then so are \(v^{\prime }_{1}\) and \(v^{\prime }_{2}\).
-
(ii)
If v 1 and v 2 are incomparable, \(v \preceq v_{1}^{\prime }\) , and \(v\preceq v_{2}^{\prime }\) , then v≼v 1 and v≼v 2.
-
(iii)
If v 1 and \(v^{\prime }_{2}\) are incomparable and \(v^{\prime }_{1}\) and v 2 are incomparable, then v 1 and v 2 are incomparable.
Proof
If v 1 and v 2 are incomparable, then lcp (v 1, v 2) is a proper prefix of both v 1 and v 2. Hence lcp\((v^{\prime }_{1}, v^{\prime }_{2}) = \textnormal {lcp}(v_{1}, v_{2})\), which implies the first two items. For the third item we note that if v 1≼v 2 then \(v_{1} \preceq v^{\prime }_{2}\), and symmetrically, if v 2≼v 1 then \(v_{2} \preceq v^{\prime }_{1}\). □
Theorem 33

Proof
Since the inclusion is trivial, it remains to prove its strictness. Let M
1 be the
 of Example 2, and let M
2 and M
3 be the bimorphisms defined as
of Example 2, and let M
2 and M
3 be the bimorphisms defined as
 in the proof of Theorem 31. We will show that the tree transformation τ = τ(M
1);τ(M
2);τ(M
3) cannot be computed by a composition of three
in the proof of Theorem 31. We will show that the tree transformation τ = τ(M
1);τ(M
2);τ(M
3) cannot be computed by a composition of three
 .
.
We again present a proof by contradiction, hence we assume that
for some
 , N
2, and N
3. By Proposition 28 there exist integers a
1, a
2, a
3, b
1, b
2, b
3≥1 such that \(\mathcal {D}(N_{1})\), \(\mathcal {D}(N_{2})\), and \(\mathcal {D}(N_{3})\) are strictly input and output hierarchical, input link-distance bounded by a
1, a
2, and a
3, respectively, and output link-distance bounded by b
1, b
2, and b
3, respectively. As before, let n = 2⋅ max(a
1, a
2, a
3, b
1, b
2, b
3)+2. Moreover, let \(m \in \mathbb {N}\) be such that m > ht(ℓ) for all rules (ℓ, p, r)∈ R
1. This time, we select the trees
, N
2, and N
3. By Proposition 28 there exist integers a
1, a
2, a
3, b
1, b
2, b
3≥1 such that \(\mathcal {D}(N_{1})\), \(\mathcal {D}(N_{2})\), and \(\mathcal {D}(N_{3})\) are strictly input and output hierarchical, input link-distance bounded by a
1, a
2, and a
3, respectively, and output link-distance bounded by b
1, b
2, and b
3, respectively. As before, let n = 2⋅ max(a
1, a
2, a
3, b
1, b
2, b
3)+2. Moreover, let \(m \in \mathbb {N}\) be such that m > ht(ℓ) for all rules (ℓ, p, r)∈ R
1. This time, we select the trees
We note that c ′ and c ″ are the same as in the proof of Theorem 31 (see Fig. 4), except that we selected a more complicated tree c; thus, c ′ and c ″ are again linear and nondeleting in X n , and can be defined formally as in that proof. Clearly (c ′[t 1,…, t n ], c ″[t 1,…, t n ])∈ τ for all t 1,…, t n ∈ T Ψ with Ψ = {γ (1), α (0)}. This time, every σ 1-rib c[σ 2(t i , t i−1)] is of the form
It is transformed into σ 2(t i , t i−1) by τ(M 1) as before (see Example 8). So we can apply Proposition 30 once again to obtain that there exist t 1,…, t n ∈ T Ψ , dependencies
and links (v i1, w i1) ∈ L 1, (v i2, w i2) ∈ L 2, and (v i3, w i3) ∈ L 3 for 1 ≤ i ≤ n such that
-
\(\text {pos}_{x_{i}}(c^{\prime \prime }) \preceq w_{i3}\),
-
v i3≼w i2 and v i2≼w i1, and
-
\(\text {pos}_{x_{i}}(c^{\prime }) \preceq v_{i1}\).
We first observe that for every j ∈{1,2,3}, the positions v 1j ,…, v n j are pairwise incomparable (as also shown in the proof of Proposition 30 in [11, Theorem 4]). In fact, since \(\text {pos}_{x_{1}}(c^{\prime \prime }), \dotsc , \text {pos}_{x_{n}}(c^{\prime \prime })\) are pairwise incomparable, so are w 13,…, w n3 by the first item above and Lemma 32(i). Hence the corresponding link origins v 13,…, v n3 are pairwise incomparable by Lemma 29(i). This implies that w 12,…, w n2 are pairwise incomparable by the second item above, and hence so are the corresponding link origins v 12,…, v n2 using again Lemma 29(i). This argument can be repeated once more to show the observation.
We now start the analysis of the given dependencies in the same way as in the proof of Theorem 31 by considering the output tree u 3 = c ″[t 1,…, t n ]. Entirely similar to that proof, we obtain a position v ′∈pos(u 2) such that v ′≼w (i+1)2, v ′≼w i2, and v ′≰w (i−1)2.
Next we move to the input tree u 0 = c ′[t 1,…, t n ], where the analysis will be slightly different. As before, we consider the links (ε, ε), (v i1, w i1), and (v (i−1)1, w (i−1)1) in L 1, for which we already know that \(pos_{x_{i}}(c^{\prime }) \preceq v_{i1}\) and \(\text {pos}_{x_{i-1}}(c^{\prime }) \preceq v_{(i-1)1}\). Let
Clearly, |V| = n 2>n⋅a 1. Thus, since \(\mathcal {D}(N_{1})\) is input link-distance bounded by a 1, the set \(V^{\prime } = \{v \in V \mid \exists w \in \mathbb {N}^{\ast }: (v, w) \in L_{1} \}\) of link origins in V contains at least n elements by Lemma 29(ii). Let W ′ = {w∣∃v ∈ V ′:(v, w)∈ L 1} be the set of corresponding link targets. Since the elements of V ′ are pairwise comparable, the elements of W ′ are also pairwise comparable by Lemma 29(i). For every w ∈ W ′, we have w≼w i1 and w≼w (i−1)1 because v≺v i1 and v≺v (i−1)1 for every v ∈ V ′ and \(\mathcal {D}(N_{1})\) is strictly input hierarchical. Additionally, for every w ∈ W ′, the positions w and w (i+1)1 are incomparable because v and v (i+1)1 are incomparable for every v ∈ V ′. Since v i2 and v (i−1)2 are incomparable by the above observation, and v i2≼w i1 and v (i−1)2≼w (i−1)1, we obtain from Lemma 32(ii) that w≼v i2 and w≼v (i−1)2 for every w ∈ W ′. Moreover, for every w ∈ W ′, since v (i+1)2≼w (i+1)1, w≼v i2, v (i+1)2 and v i2 are incomparable, and w and w (i+1)1 are incomparable, Lemma 32(iii) shows that w and v (i+1)2 are incomparable.
Now we distinguish two cases. First, let us assume that |W ′|≥n. In this case, we can continue to derive a contradiction in much the same way as in the proof of Theorem 31. Since the positions in W ′ are pairwise comparable, there are positions w min , w max ∈ W ′ of minimal and maximal length, respectively, with w min ≺w max . Clearly, |w max |−|w min |≥n−1>a 2. Since (ε, ε),(v i2, w i2) ∈ L 2 and w min ≼v i2, there must be a link (v ″, w ″) ∈ L 2 such that w min ≺v ″≺w max by Lemma 29(ii). This implies that v ″≺v i2, v ″≺v (i−1)2, and v ″ and v (i+1)2 are incomparable. Since \(\mathcal {D}(N_{2})\) is strictly input hierarchical, we obtain that w ″≼w i2, w ″≼w (i−1)2, and from Lemma 29(i) we obtain that w ″ and w (i+1)2 are incomparable, which takes us to the situation
which is the analogue of (1) and (2) [in the proof of Theorem 31] and thus contradictory for the same reasons.
In the remaining case, we have |W ′| < n. Together with |V ′|≥n, we obtain by the pigeonhole principle that several input positions of V ′ are linked in L 1 to the same output position \(\overline w\) of W ′. We choose \((\overline v, \overline w) \in L_{1}\) such that \(\overline v\in V^{\prime }\) and \(\left |{\overline v}\right |\) is minimal. Consequently, a rule (ℓ, p, r)∈ R 1 with a state r ∈ P as right-hand side must have been applied at position \(\overline v\) of u 0 = c ′[t 1,…, t n ].
Since \(\overline {v} \in V\), the subtree \(t|_{\overline v}\) is of the form
where \(s\! = {\gamma _{2}^{m}}(\alpha )\). Hence, since N
1 is ε-free, the root of the left-hand side ℓ has label σ. Moreover, \(\ell |_{1} = {\gamma _{2}^{k}}(p^{\prime })\) for some 0 ≤ k < m and p
′∈ P. By the choice of \(\overline v\), the state r occurs in ℓ|2 and so the state p
′ is deleted [i.e., p
′∉states(r)] in this rule. Therefore, the subtree \(u_{0}|_{{\overline v}.1^{k+1}} = \gamma _{2}^{m-k}(\alpha )\) has been created using the second item of Definition 6. Since N
1 is an
 , its look-ahead mapping is trivial, and thus any tree can be created instead of \(u_{0}|_{{\overline v}.1^{k+1}}\); e.g., the tree σ
2(α, α). This shows that also \(\langle u^{\prime }_{0}, L_{1}, u_{1}\rangle \in \mathcal {D}(N_{1})\), where \(u^{\prime }_{0} = u_{0}[\overline v.1^{k+1} \gets \sigma _{2}(\alpha , \alpha )]\), and so \((u^{\prime }_{0}, c^{\prime \prime }[t_{1}, \dotsc , t_{n}]) \in \tau (N_{1}); \tau (N_{2}) ; \tau (N_{3})\). However, since \(u^{\prime }_{0}|_{\overline v}\) is of the form
, its look-ahead mapping is trivial, and thus any tree can be created instead of \(u_{0}|_{{\overline v}.1^{k+1}}\); e.g., the tree σ
2(α, α). This shows that also \(\langle u^{\prime }_{0}, L_{1}, u_{1}\rangle \in \mathcal {D}(N_{1})\), where \(u^{\prime }_{0} = u_{0}[\overline v.1^{k+1} \gets \sigma _{2}(\alpha , \alpha )]\), and so \((u^{\prime }_{0}, c^{\prime \prime }[t_{1}, \dotsc , t_{n}]) \in \tau (N_{1}); \tau (N_{2}) ; \tau (N_{3})\). However, since \(u^{\prime }_{0}|_{\overline v}\) is of the form
the σ 1-rib \(u^{\prime }_{0}|_{1^{h}2}\) of \(u^{\prime }_{0}\) with \(1^{h}2 \preceq \overline v\) (i.e., \(h = \frac {i}{2}-1\)) has two occurrences of σ 2. Hence \(u^{\prime }_{0}\) is not in the domain of τ(M 1) [see Example 8]. This implies that \(u^{\prime }_{0}\) is not in the domain of τ = τ(M 1);τ(M 2);τ(M 3), but
which is a contradiction.
Since both cases are contradictory, τ cannot be computed by a composition of three
 . □
. □
Thus, we have shown that the least power, at which the composition closure is achieved for the classes
 and
and
 , is 3 and 4, respectively. This is stated in the next theorem.
, is 3 and 4, respectively. This is stated in the next theorem.
Theorem 34
For every n≥4,

Proof
We have
 for all n ≥ 1 by Lemma 15. The equalities follow from Theorem 24. The fourth and fifth inclusions are strict by Theorems 31 and 33, respectively. The strictness of the second and third inclusion follows from that of the fourth and fifth, respectively. The strictness of the first inclusion is a consequence of Proposition 14; it also follows from that of the third. □
for all n ≥ 1 by Lemma 15. The equalities follow from Theorem 24. The fourth and fifth inclusions are strict by Theorems 31 and 33, respectively. The strictness of the second and third inclusion follows from that of the fourth and fifth, respectively. The strictness of the first inclusion is a consequence of Proposition 14; it also follows from that of the third. □
In Table 3 we summarize the main results of this and the previous section, which allow us to present the least power at which the closure of the considered composition hierarchies is achieved. For the sake of completeness, we also present the corresponding results for the classes
 and \(\mathcal {B}(\textnormal {l,l})\) that were obtained in [3, 5]. Recall that \(\mathcal {B}\)(l,l) is the class of all tree transformations computable by bimorphisms, in which both tree homomorphisms are linear.
and \(\mathcal {B}(\textnormal {l,l})\) that were obtained in [3, 5]. Recall that \(\mathcal {B}\)(l,l) is the class of all tree transformations computable by bimorphisms, in which both tree homomorphisms are linear.
6 Infinite Composition Hierarchies
To complete the picture, we will need one further result showing the infiniteness of the composition hierarchy for a large number of classes. In order to obtain a result that is as general as possible, we use bimorphisms [3] instead of l-xtR in this section; cf. Proposition 11. We conclude several results for various tree transducer classes from the result for bimorphisms.
To handle bimorphisms properly, we need to define links for tree homomorphisms. As observed after Notation 10, every linear tree homomorphism φ:T Σ→T Δ can be viewed as a linear top-down tree transducer M φ . In particular, for every t ∈ T Σ there is a (unique) set L φ (t)⊆pos(t)×pos(φ(t)) of links such that \(\langle t, L_{\varphi }(t), \varphi (t) \rangle \in \mathcal {D}(M_{\varphi })\). We now generalize this notion to arbitrary tree homomorphisms.
Definition 35
Let φ:T Σ→T Δ be a tree homomorphism and t ∈ T Σ. The set of t-links of φ, denoted by L φ (t), is the smallest subset of pos(t)×pos(φ(t)) such that
-
(ε, ε)∈ L φ (t) and
-
(v i, w w ′) ∈ L φ (t) for all links (v, w)∈ L φ (t), integers 1 ≤ i≤rk(t(v)), and positions \(w^{\prime } \in \text {pos}_{x_{i}} \left (\varphi (t(v)) \right )\).
Intuitively, (v, w)∈ L φ (t) means that φ translates the subtree of t rooted at v into the subtree of φ(t) rooted at w. Note that for a given position v there can be several such positions w (which are, of course, pairwise incomparable), since φ is not necessarily linear, or there may be no such w, since φ is not necessarily nondeleting. We will need the following elementary properties of L φ (t).
Lemma 36
Let φ:T Σ →T Δ be a tree homomorphism, and let t∈T Σ , u=φ(t), and L=L φ (t).
-
(i)
If (v,w)∈L, then φ(t| v )=u| w .
-
(ii)
If (v,w)∈L, then L φ (t| v )={(v ′ ,w ′ )∣(vv ′ ,ww ′ )∈L}.
-
(iii)
If φ is nondeleting, then for all (v 1 ,w 1 )∈L and all v 1 ≼v∈pos(t) there exists a position w 1 ≼w such that (v,w)∈L.
-
(iv)
For all links (v 1 ,w 1 ),(v 2 ,w 2 )∈L with v 1 ≼v 2 and w 1 ≼w 2 , and all v 1 ≼v≼v 2 there exists a unique position w 1 ≼w≼w 2 such that (v,w)∈L.
-
(v)
For all (v 1 ,w 1 )∈L and all w 1 ≼w∈pos(u) there exist unique positions \(v, w^{\prime }, w^{\prime \prime } \in \mathbb {N}^{\ast }\) such that v 1 ≼v, w 1 ≼w ′ , w=w ′ w ′′ , (v,w ′ )∈L, and w ′′ ∈pos Δ (φ(t(v))).
Proof
The proofs of statements (i) and (ii) are straightforward, and hence left to the reader. It is also straightforward to prove the following three statements, which are the special case of statements (iii)–(v), in which we have (v 1, w 1)=(ε, ε). We also leave their proofs to the reader.
-
(iii)′
If φ is nondeleting, then dom(L) = pos(t).
-
(iv)′
For all (v 2, w 2) ∈ L and all v≼v 2 there exists a unique position w≼w 2 such that (v, w)∈ L.
-
(v)′
For every w ∈pos(u) there exist unique positions \(v, w^{\prime }, w^{\prime \prime } \in \mathbb {N}^{\ast }\) such that w = w ′ w ″, (v, w ′) ∈ L, and w ″∈posΔ(φ(t(v))).
Each non-primed statement can now easily be obtained from the corresponding primed statement with the help of (i) and (ii). We start with statement (iii). Let (v 1, w 1) ∈ L and v 1≼v ∈pos(t). Since v 1≼v, let \(\widehat v\) be such that \(v_{1}\widehat v = v\). Obviously \(\widehat {v} \in \text {pos}(t|_{v_{1}})\), and consequently, by statement (iii)′, there exists \(\widehat w\) such that \((\widehat v,\widehat w) \in L_{\varphi }(t|_{v_{1}})\). Together with (v 1, w 1) ∈ L and statement (ii) we conclude that \((v_{1}\widehat v, w_{1}\widehat w) \in L\). Thus, (v, w)∈ L where \(w_{1} \preceq w = w_{1}\widehat w\).
For statement (iv), let (v 1, w 1),(v 2, w 2) ∈ L with v 1≼v 2 and w 1≼w 2, and let v 1≼v≼v 2. Since w 1≼w 2, let \(\widehat w_{2}\) be such that \(w_{1}\widehat w_{2} = w_{2}\). Similarly, since v 1≼v≼v 2, let \(\widehat v \preceq \widehat v_{2}\) such that \(v_{1}\widehat v = v\) and \(v_{1}\widehat v_{2} = v_{2}\). Since (v 1, w 1) ∈ L, statement (ii) implies that \((\widehat v_{2}, \widehat w_{2}) \in L_{\varphi }(t|_{v_{1}})\). Thus, since also \(\widehat v \preceq \widehat v_{2}\), statement (iv)′ implies that there exists \(\widehat w \preceq \widehat w_{2}\) such that \((\widehat v, \widehat w) \in L_{\varphi }(t|_{v_{1}})\). Using statement (ii) again, we have \((v_{1}\widehat v, w_{1}\widehat w) \in L\). Hence the requirements are fulfilled by \(w = w_{1} \widehat w\); note that \(w_{1} \preceq w_{1}\widehat w \preceq w_{1}\widehat w_{2} = w_{2}\). The uniqueness of w follows immediately from the uniqueness condition in statement (iv)′.
Finally, for statement (v), let (v 1, w 1) ∈ L and w 1≼w ∈pos(u). By statement (i) we have \(\varphi (t|_{v_{1}}) = u|_{w_{1}}\). Since w 1≼w, let \(\widehat w\) be such that \(w_{1}\widehat w = w\). Obviously, \(\widehat w \in \text {pos}(u|_{w_{1}})\). By statement (v)′ applied to \(\widehat w\), there exist \(\widehat v, \widehat w^{\prime }, \widehat w^{\prime \prime }\) such that \(\widehat w = \widehat w^{\prime } \widehat w^{\prime \prime }\), \((\widehat v, \widehat w^{\prime }) \in L_{\varphi }(t|_{v_{1}})\), and \(\widehat w^{\prime \prime }\in \text {pos}_{\Delta } \left (\varphi (t|_{v_{1}}(\widehat v)) \right )\). Since (v 1, w 1) ∈ L we can use statement (ii) applied to \((\widehat v, \widehat w^{\prime }) \in L_{\varphi }(t|_{v_{1}})\) to conclude that \((v_{1}\widehat v, w_{1} \widehat w^{\prime }) \in L\). Hence the requirements are fulfilled by \(v = v_{1} \widehat v\), \(w^{\prime } = w_{1}\widehat w^{\prime }\), and \(w^{\prime \prime } = \widehat w^{\prime \prime }\). The uniqueness of v, w ′, and w ″ follows immediately from the uniqueness condition in statement (v)′. □
The unique position v ∈pos(t) corresponding to the position w ∈pos(u) in Lemma 36(v) is informally called the position in t that creates the symbol u(w) at w. Since item (v) holds in particular for (v 1, w 1)=(ε, ε), that position does not depend on the link (v 1, w 1) ∈ L. Similarly, the unique position w in item (iv) does not depend on the link (v 1, w 1).
We now turn to the proof of the infiniteness of the composition hierarchies. The main auxiliary notion used in that proof is the assignment of levels to positions in a tree. Let t ∈ T Σ. Since the branching positions of t (i.e., those that are labeled by symbols of rank at least 2) will play an essential role, we define the set of branching positions of t, the set of branching positions of t together with two different successor indices, and the set of branching positions along a given path, as follows:
and for every v 1, v 2∈pos(t) with v 1≼v 2 we let
Let ℓ ≥ 2 be arbitrary (called distance in the sequel). We inductively define the sets \(\text {PI}^{\ell }_{n}(t) \subseteq \text {pos}(t) \times \mathbb {N} \times \mathbb {N}\) of special positions of level n and distance ℓ with successor indices and the sets \(\text {P}^{\ell }_{n}(t) \subseteq \text {pos}(t)\) for the same special positions without successor indices for every \(n \in \mathbb {N}\) as follows:
Intuitively, each branching position is a special position of level 0 (for any distance ℓ) and a branching position v is a special position of level n+1 if there are two paths in different direct subtrees below v that both have at least ℓ n+1 special positions of level n along the path. Clearly, \(\text {PI}^{\ell }_{n+1}(t)\subseteq \text {PI}^{\ell }_{n}(t)\) and \(\text {P}^{\ell }_{n+1}(t) \subseteq \text {P}^{\ell }_{n}(t)\) for all \(n \in \mathbb {N}\). Note that in the definition of \(\text {PI}^{\ell }_{n+1}(t)\), the condition that \(v_{1}, v_{2} \in \text {P}^{\ell }_{n}(t)\) is superfluous, but technically convenient.
Example 37
Let t be the tree depicted in Fig. 5. Then
Lemma 38
Let t∈T Σ and \(\ell , n \in \mathbb {N}\) with ℓ≥2. Moreover, let \(v, v^{\prime } \in \mathbb {N}^{\ast }\) and \(i, j \in \mathbb {N}\).
-
(i)
\(\langle v^{\prime }, i, j\rangle \in \textnormal {PI}^{\ell }_{n}(t|_{v})\) if and only if \(\langle vv^{\prime }, i, j\rangle \in \textnormal {PI}^{\ell }_{n}(t)\) , and \(v^{\prime } \in \textnormal {P}^{\ell }_{n}(t|_{v})\) if and only if \(vv^{\prime } \in \textnormal {P}^{\ell }_{n}(t)\).
-
(ii)
If \(v, viv^{\prime } \in \textnormal {P}^{\ell }_{n}(t)\) , then there exists \(m \in \mathbb {N}\) such that \(\langle v, i, m\rangle \in \textnormal {PI}^{\ell }_{n}(t)\).
Proof
We prove the items individually. We start with (i), which is obvious because whether or not 〈v, i, j〉 is in \(\text {PI}^{\ell }_{n}(t)\) only depends on the positions of which v is a prefix. Statement (ii) is also trivial for n = 0, hence we only prove it for n+1. Let \(v, viv^{\prime } \in \text {P}^{\ell }_{n+1}(t)\). Since \(v \in \text {P}^{\ell }_{n+1}(t)\) there exist integers i 1, i 2 such that \(\langle v, i_{1}, i_{2}\rangle \in \text {PI}^{\ell }_{n+1}(t)\). If i ∈{i 1, i 2}, then the statement is obviously true. In the remaining case, let i∉{i 1, i 2}. There exists a position \(v_{2} \in \text {P}^{\ell }_{n}(t)\) such that v i 2≼v 2 and \(\left |{\text {br}_{t}(vi_{2}, v_{2}) \cap \text {P}^{\ell }_{n}(t)}\right | \geq \ell ^{n+1}\). Since \(viv^{\prime } \in \text {P}^{\ell }_{n}(t)\), there exist \(i^{\prime } \in \mathbb {N}\) and \(v_{1} \in \text {P}^{\ell }_{n}(t)\) such that v i v ′ i ′≼v 1 and \(\left |{\text {br}_{t}(viv^{\prime }i^{\prime }, v_{1}) \cap \text {P}^{\ell }_{n}(t)}\right | \geq \ell ^{n+1}\). Hence v i≼v 1 and \(\left |{\text {br}_{t}(vi, v_{1}) \cap \text {P}^{\ell }_{n}(t)}\right | \geq \ell ^{n+1}\), which shows that \(\langle v, i, i_{2}\rangle \in \text {PI}^{\ell }_{n+1}(t)\). □
We now prove that a nondeleting tree homomorphism preserves the maximal level of the special positions of a tree.
Lemma 39
Let φ:T Γ →T Δ be a nondeleting tree homomorphism, and let t=γ(t 1 ,…,t k ) for some \(k \in \mathbb {N}\) , γ∈Γ k , and t 1 ,…,t k ∈T Γ . Moreover, let \(\ell , n, i, j \in \mathbb {N}\) be such that ℓ≥2 and \(\langle \varepsilon , i, j\rangle \in \textnormal {PI}^{\ell }_{n}(t)\) . Then for every \(z_{1} \in \text {pos}_{x_{i}}(\varphi (\gamma ))\) and \(z_{2} \in \text {pos}_{x_{j}} (\varphi (\gamma ))\) there exists \(\langle w, i^{\prime }, j^{\prime }\rangle \in \textnormal {PI}^{\ell }_{n}(\varphi (t))\) such that w∈pos(φ(γ)) and wi ′ ≼z 1 and wj ′ ≼z 2.
Proof
Let u = φ(t) = φ(γ)[φ(t 1),…, φ(t k )] and L = L φ (t). We prove the statement by induction on n. In the induction base, we have n = 0 and \(\langle \varepsilon , i, j\rangle \in \text {PI}^{\ell }_{0}(t) = \text {bri}_{t}\). Consider \(z_{1} \in \text {pos}_{x_{i}}(\varphi (\gamma ))\) and \(z_{2} \in \text {pos}_{x_{j}}(\varphi (\gamma ))\), which are occurrences of the variables x i ≠x j in φ(γ). Let w = lcp(z 1, z 2) be their longest common prefix. Since x i ≠x j , we have w≺z 1 and w≺z 2, so let \(i^{\prime }, j^{\prime } \in \mathbb {N}\) be the unique (and necessarily distinct) integers such that w i ′≼z 1 and w j ′≼z 2. Clearly, w ∈pos(φ(γ)) and \(\langle w, i^{\prime }, j^{\prime }\rangle \in \text {bri}_{u} = \text {PI}^{\ell }_{0}(u)\). This completes the induction base.
In the induction step, let \(\langle \varepsilon , i, j\rangle \in \text {PI}^{\ell }_{n+1}(t)\), and suppose that \(v_{1}\in \text {P}^{\ell }_{n}(t)\) and \(v_{2} \in \text {P}^{\ell }_{n}(t)\) are the required special positions of level n such that i≼v 1 and j≼v 2 and
Now, we follow a similar approach as in the induction base. Figure 6 illustrates the used positions and their relations. Consider positions \(z_{1} \in \text {pos}_{x_{i}}(\varphi (\gamma ))\) and \(z_{2} \in \text {pos}_{x_{j}}(\varphi (\gamma ))\). As before, we let
be their longest common prefix, and let w i ′≼z 1 and w j ′≼z 2. Clearly, i ′≠j ′ and so 〈w, i ′, j ′〉∈bri u . It remains to show that \(\langle w, i^{\prime }, j^{\prime }\rangle \in \text {PI}^{\ell }_{n+1}(u)\).
By Definition 35, we have (ε, ε)∈ L and (i, z 1) ∈ L. Since φ is nondeleting and (i, z 1) ∈ L and i≼v 1, it follows from Lemma 36(iii) that there exists \(w^{\prime }_{1}\) such that \(z_{1} \preceq w^{\prime }_{1}\) and \((v_{1}, w^{\prime }_{1}) \in L\). Thus, Lemma 36(i) shows that \(u|_{w^{\prime }_{1}} = \varphi (t|_{v_{1}})\). By assumption we have \(v_{1} \in \text {P}^{\ell }_{n}(t)\), which yields \(\varepsilon \in \text {P}^{\ell }_{n}(t|_{v_{1}})\) by Lemma 38(i); i.e., \(\langle \varepsilon , i^{\prime \prime }, j^{\prime \prime }\rangle \in \text {PI}^{\ell }_{n}(t|_{v_{1}})\) for some i ″, j ″. Since φ is nondeleting, the sets \(\text {pos}_{x_{i^{\prime \prime }}}\left (\varphi (t(v_{1}))\right )\) and \(\text {pos}_{x_{j^{\prime \prime }}} \left (\varphi (t(v_{1})) \right )\) are nonempty. Consequently, the induction hypothesis implies the existence of \(w^{\prime \prime }_{1} \in \text {P}^{\ell }_{n}(\varphi (t|_{v_{1}})) = \text {P}^{\ell }_{n}(u|_{w^{\prime }_{1}})\). Hence \(w^{\prime }_{1}w^{\prime \prime }_{1} \in \text {P}^{\ell }_{n}(u)\) by Lemma 38(i). Let \(w_{1} = w^{\prime }_{1}w^{\prime \prime }_{1}\), and let w 2 be determined in an analogous way. We claim that w 1 and w 2 are the special positions of level n that are required to show that \(\langle w, i^{\prime }, j^{\prime }\rangle \in \text {PI}^{\ell }_{n+1}(u)\). We will only verify the condition
because the proof for w 2 works analogously. Due to w i ′≼z 1, we obtain that \(w_{1} \in \text {br}_{u}(wi^{\prime }, w_{1}) \cap \text {P}^{\ell }_{n}(u)\) .
Let \(\bar {v}_{1} \in \text {br}_{t}(i, v_{1}) \cap \text {P}^{\ell }_{n}(t)\) be any position of level n along the path from i to v 1 such that \(\bar {v}_{1} \prec v_{1}\). Hence there exists a unique integer \(i_{1} \in \mathbb {N}\) such that \(\bar {v}_{1}i_{1} \preceq v_{1}\). Since \((i, z_{1}), (v_{1}, w^{\prime }_{1}) \in L\) together with \(i \preceq \bar {v}_{1}i_{1} \preceq v_{1}\) we can use Lemma 36(iv) to conclude that there exists \(z_{1} \preceq \widehat {w}^{\prime }_{1} \preceq w^{\prime }_{1}\) such that \((\bar {v}_{1}i_{1}, \widehat {w}^{\prime }_{1}) \in L\). Applied once more to \(i \preceq \bar {v}_{1} \preceq \bar {v}_{1}i_{1}\) and the links \((i, z_{1}), (\bar {v}_{1}i_{1}, \widehat {w}^{\prime }_{1}) \in L\), there exists \(z_{1} \preceq \bar {w}^{\prime }_{1} \preceq \widehat {w}^{\prime }_{1}\) with \((\bar {v}_{1}, \bar {w}^{\prime }_{1}) \in L\). Let \(z \in \mathbb {N}^{\ast }\) be such that \(\bar {w}^{\prime }_{1} z = \widehat {w}^{\prime }_{1}\). By Definition 35 we have \(z \in \text {pos}_{x_{i_{1}}} \left (\varphi (t(\bar {v}_{1})) \right )\). Since \(\bar {v}_{1}, v_{1} \in \text {P}^{\ell }_{n}(t)\), we conclude from Lemma 38(ii) that there exists \(j_{1} \in \mathbb {N}\) such that \(\langle \bar {v}_{1}, i_{1}, j_{1}\rangle \in \text {PI}^{\ell }_{n}(t)\). Hence \(\langle \varepsilon , i_{1}, j_{1}\rangle \in \text {PI}^{\ell }_{n}(t|_{\bar {v}_{1}})\) by Lemma 38(i) and \(u|_{\bar {w}^{\prime }_{1}} = \varphi (t|_{\bar {v}_{1}})\) by Lemma 36(i). Now we can apply the induction hypothesis to obtain that there exists \(\langle \bar {w}^{\prime \prime }_{1}, i^{\prime }_{1}, j^{\prime }_{1} \rangle \in \text {PI}^{\ell }_{n}(\varphi (t|_{\bar {v}_{1}}))\) such that \(\bar {w}^{\prime \prime }_{1}i^{\prime }_{1} \preceq z\). Hence \(\langle \bar {w}^{\prime \prime }_{1}, i^{\prime }_{1}, j^{\prime }_{1} \rangle \in \text {PI}^{\ell }_{n}(u|_{\bar {w}^{\prime }_{1}})\) and so \(\langle \bar {w}^{\prime }_{1}\bar {w}^{\prime \prime }_{1}, i^{\prime }_{1}, j^{\prime }_{1} \rangle \in \text {PI}^{\ell }_{n}(u)\) by Lemma 38(i).Consequently, \(\bar {w}_{1} \in \text {P}^{\ell }_{n}(u)\), where \(\bar {w}_{1} = \bar {w}^{\prime }_{1}\bar {w}^{\prime \prime }_{1}\). In addition, \(wi^{\prime } \preceq \bar {w}_{1} \prec w_{1}\) because
In other words, we have shown that \(\bar {w}_{1} \in \text {br}_{u}(wi^{\prime }, w_{1}) \cap \text {P}^{\ell }_{n}(u)\). Moreover, since \(\bar {w}^{\prime \prime }_{1}i^{\prime }_{1} \preceq z\), we have that \(\bar {w}^{\prime \prime }_{1} \in \text {pos}_{\Delta } \left (\varphi (t(\bar {v}_{1})) \right )\). Since also \((\bar {v}_{1}, \bar {w}^{\prime }_{1}) \in L\), we can say that \(\bar {v}_{1}\) is the position in t that creates the symbol \(u(\bar {w}_{1}) = u(\bar {w}^{\prime }_{1} \bar {w}^{\prime \prime }_{1})\) at \(\bar {w}_{1}\). Hence, the uniqueness condition in Lemma 36(v) guarantees that for each selection of \(\bar {v}_{1}\) we obtain a different position \(\bar {w}_{1} \in \text {br}_{u}(wi^{\prime }, w_{1}) \cap \text {P}^{\ell }_{n}(u)\). This verifies (3) because \(w_{1} \in \text {br}_{u}(wi^{\prime }, w_{1}) \cap \text {P}^{\ell }_{n}(u)\) and there are at least ℓ n+1−1 possible selections of \(\bar {v}_{1}\) (and each position \(\bar {w}_{1}\) differs from w 1 because \(\bar {w}_{1} \prec w_{1}\) as shown above). □
The next lemma shows that an inverse linear tree homomorphism reduces the maximal level of the special positions of a tree by at most 1 (for a sufficiently large distance ℓ).
Lemma 40
Let ψ:T Γ →T Σ be a linear tree homomorphism. Moreover, let t∈T Γ and \(\ell , n \in \mathbb {N}\) be such that ℓ>ht(ψ(γ ′ )) for all symbols γ ′ ∈Γ. If there exists \(w \in \textnormal {P}^{\ell }_{n+1}(\psi (t))\) with w∈pos Σ (ψ(t(ε))), then \(\varepsilon \in \textnormal {P}^{\ell }_{n}(t)\).
Proof
The proof is similar to the one of Lemma 39. Let t = γ(t 1,…, t k ) with \(k \in \mathbb {N}\), γ ∈Γ k , and t 1,…, t k ∈ T Γ, and let u = ψ(t) = φ(γ)[φ(t 1),…, φ(t k )]. Moreover, let \(\langle w, i^{\prime }, j^{\prime }\rangle \in \text {PI}^{\ell }_{n+1}(u)\) with w ∈posΣ(ψ(γ)). By the definition of \(\text {PI}^{\ell }_{n+1}(u)\), there exist positions \(w_{1} \in \text {P}^{\ell }_{n}(u)\) and \(w_{2} \in \text {P}^{\ell }_{n}(u)\) such that w i ′≼w 1 and w j ′≼w 2 and
The paths in u from w to w 1 and from w to w 2 contain strictly more than ℓ n+1 positions, so they are longer than any path in ψ(γ). Together with w ∈posΣ(ψ(γ)) we conclude that there must exist 1 ≤ i, j ≤ k and positions \(z_{1} \in \text {pos}_{x_{i}}(\psi (\gamma ))\) and \(z_{2} \in \text {pos}_{x_{j}}(\psi (\gamma ))\) such that w i ′≼z 1≼w 1 and w j ′≼z 2≼w 2. Since ψ is linear and i ′≠j ′, we have i≠j, which yields 〈ε, i, j〉∈bri t . It remains to prove that \(\langle \varepsilon , i, j\rangle \in \text {PI}^{\ell }_{n}(t)\), which we prove by induction on n. In the induction base we have n = 0 and thus \(\langle \varepsilon , i, j\rangle \in \text {bri}_{t} = \text {PI}^{\ell }_{0}(t)\).
We proceed with the induction step. Again, Fig. 6 illustrates the used positions and their relations. Clearly, we have (i, z 1) ∈ L. Let v 1 be the position of t i that creates the symbol u(w 1) at w 1. More precisely, by Lemma 36(v), there exist unique positions \(v_{1}, w^{\prime }_{1}, w^{\prime \prime }_{1}\) such that i≼v 1, \(z_{1} \preceq w^{\prime }_{1}\), \(w_{1} = w^{\prime }_{1} w^{\prime \prime }_{1}\), \((v_{1}, w^{\prime }_{1}) \in L\), and \(w^{\prime \prime }_{1} \in \text {pos}_{\Sigma } \left (\psi (t(v_{1})) \right )\). Similarly, let v 2∈ pos(t) be the position that creates the symbol u(w 2) at w 2. We claim that the property required to prove that \(\langle \varepsilon , i, j\rangle \in \text {PI}^{\ell }_{n}(t)\), and hence \(\varepsilon \in \text {P}^{\ell }_{n}(t)\), holds for br t (i, v 1) and br t (j, v 2), i.e.,
We only prove this property for v 1 because the proof for v 2 is analogous. Since \(w_{1} = w^{\prime }_{1}w^{\prime \prime }_{1} \in \text {P}^{\ell }_{n}(u)\), it follows from Lemma 38(i) that \(w^{\prime \prime }_{1} \in \text {P}^{\ell }_{n}(u|_{w^{\prime }_{1}})\). Moreover, \((v_{1}, w^{\prime }_{1}) \in L\) and Lemma 36(i) yield that \(u|_{w^{\prime }_{1}} = \psi (t|_{v_{1}})\) and thus \(\text {P}^{\ell }_{n}(u|_{w^{\prime }_{1}}) = \text {P}^{\ell }_{n}(\psi (t|_{v_{1}}))\). Together with \(w^{\prime \prime }_{1} \in \text {pos}_{\Sigma } \left (\psi (t(v_{1})) \right )\), we can conclude that \(\varepsilon \in \text {P}^{\ell }_{n-1}(t|_{v_{1}})\) from the induction hypothesis, and hence \(v_{1} \in \text {P}^{\ell }_{n-1}(t)\) by Lemma 38(i).
Next, we consider any position \(\bar {w}_{1} \in \text {br}_{u}(z_{1}, w_{1}) \cap \text {P}^{\ell }_{n}(u)\). We follow the same approach as in the beginning of the induction step. Let \(\bar {v}_{1}\) be the position of t i that creates the symbol \(u(\bar {w}_{1})\) at \(\bar {w}_{1}\). More precisely, we apply Lemma 36(v) to \(\bar {w}_{1}\) to obtain that there exist positions \(\bar {v}_{1}, \bar {w}^{\prime }_{1}, \bar {w}^{\prime \prime }_{1}\) such that \(i \preceq \bar {v}_{1}\), \(z_{1} \preceq \bar {w}^{\prime }_{1}\), \(\bar {w}_{1} = \bar {w}^{\prime }_{1}\bar {w}^{\prime \prime }_{1}\), \((\bar {v}_{1}, \bar {w}^{\prime }_{1}) \in L\), and \(\bar {w}^{\prime \prime }_{1} \in \text {pos}_{\Sigma } \left (\psi (t(\bar {v}_{1})) \right )\). By the same reasoning as in the previous paragraph, we obtain that \(\bar {v}_{1} \in \text {P}^{\ell }_{n-1}(t)\). Also, since \(\bar {w}_{1}\preceq w_{1}\), we clearly have that \(\bar {w}^{\prime }_{1} \preceq w^{\prime }_{1}\) because \(w_{1}^{\prime }\) (resp. \(\bar {w}^{\prime }_{1}\)) is the first position on the path from w 1 (resp. \(\bar {w}_{1}\)) to ε that occurs in a link of L. Now note that L is strictly output hierarchical by Proposition 28 because \(\langle t, L, u\rangle \in \mathcal {D}(M_{\psi })\), where M ψ is the l-t defined after Notation 10. Hence \(\bar {v}_{1} \preceq v_{1}\) because either \(\bar {w}_{1}^{\prime } \prec w_{1}^{\prime }\), which directly yields \(\bar {v}_{1} \preceq v_{1}\), or \(\bar {w}_{1}^{\prime } = w_{1}^{\prime }\), which yields \(\bar {v}_{1} = v_{1}\) because of the uniqueness of \(\bar {v}_{1}\). Thus we have shown that
If two different selections of \(\bar {w}_{1}\) correspond to the same position \(\bar {v}_{1}\), then (since \((\bar {v}_{1}, \bar {w}^{\prime }_{1}), (v_{1}, w^{\prime }_{1}) \in L\) with \(\bar {v}_{1} \preceq v_{1}\) and \(\bar {w}^{\prime }_{1} \preceq w^{\prime }_{1}\)) they also correspond to the same \(\bar {w}^{\prime }_{1}\) by the uniqueness condition in Lemma 36(iv), and hence, since \(\bar {w}^{\prime \prime }_{1} \in \text {pos}_{\Sigma } \left (\psi (t(\bar {v}_{1})) \right )\), their distance is at most \(\text {ht} \left (\psi (t(\bar {v}_{1})) \right ) \leq \ell -1\). In summary, a single position \(\bar {v}_{1}\) can create the symbols of at most ℓ positions of br u (z 1, w 1). Since there are at most ℓ−2 positions between w and z 1 we have
Consequently, \(\left |{\text {br}_{t}(i, v_{1}) \cap \text {P}^{\ell }_{n-1}(t)}\right | \geq \ell ^{n}\) as required since
would imply \(\left |{\text {br}_{u}(z_{1}, w_{1}) \cap \text {P}^{\ell }_{n}(u)}\right | \leq \ell (\ell ^{n}-1) < \ell ^{n+1} - \ell + 2\). This completes the induction step and the proof. □
Next, we combine the previous two lemmas into the main result of this section that will be used to prove the infinity of several composition hierarchies. We show that a bimorphism in \(\mathcal {B}\)( l, n) can reduce the maximal level of the special positions by at most 1 (for a sufficiently large distance ℓ).
Theorem 41
Let B=(ψ,T,φ) be a bimorphism such that ψ:T Γ →T Σ is linear and φ:T Γ →T Δ is nondeleting. Moreover, let (s,u)∈τ(B), and let \(\ell \in \mathbb {N}\) be such that ℓ>ht(ψ(γ)) for every γ∈Γ. For every \(n \in \mathbb {N}\) , if \(\textnormal {P}^{\ell }_{n+1}(s) \neq \emptyset \) , then \(\textnormal {P}^{\ell }_{n}(u) \neq \emptyset \).
Proof
Since (s, u)∈ τ(B), there exists t ∈ T such that ψ(t) = s and φ(t) = u. By assumption, we have that \(\text {P}^{\ell }_{n+1}(\psi (t)) \neq \emptyset \), so let \(w \in \text {P}^{\ell }_{n+1}(\psi (t))\). By Lemma 36(v) there exist v, w ′, w ″ such that w = w ′ w ″, (v, w ′) ∈ L ψ (t), and w ″∈posΣ(ψ(t(v))). Moreover, \(\psi (t)|_{w^{\prime }} = \psi (t|_{v})\) by Lemma 36(i). Since \(w^{\prime }w^{\prime \prime } \in \text {P}^{\ell }_{n+1}(\psi (t))\), Lemma 38(i) implies that
Hence, by Lemma 40, \(\varepsilon \in \text {P}^{\ell }_{n}(t|_{v})\). Since φ is nondeleting, \(\text {pos}_{x_{i}} \left (\varphi (t(v)) \right )\) is nonempty for every 1 ≤ i≤rk(t(v)). Consequently, Lemma 39 implies that \(\text {P}^{\ell }_{n}(\varphi (t|_{v})) \neq \emptyset \). By Lemma 36(iii) there exists \(\bar {w}\) such that \((v, \bar {w}) \in L_{\varphi }(t)\), and moreover, \(\varphi (t|_{v}) = u|_{\bar {w}}\) by Lemma 36(i). Hence \(\text {P}^{\ell }_{n}(u|_{\bar {w}}) = \text {P}^{\ell }_{n}(\varphi (t|_{v})) \neq \emptyset \), which proves that \(\text {P}^{\ell }_{n}(u) \neq \emptyset \) by Lemma 38(i), as desired. □
Now we can simply chain Theorem 41 to show that an n-fold composition of tree transformations in \(\mathcal {B}\)( l, n) can decrease the maximal level by at most n (for a suitable distance ℓ).
Corollary 42 (of Theorem 41)
Let n≥1, and for every 1≤i≤n let B i =(ψ i ,T i ,φ i ) be a bimorphism such that ψ i is linear and φ i is nondeleting. Moreover, let \(\varphi _{i} : T_{{\Gamma }_{i}} \to T_{{\Delta }_{i}}\) and \(\psi _{i+1} : T_{{\Gamma }_{i+1}} \to T_{{\Delta }_{i}}\) for every 1≤i<n. Finally, let \(\ell \in \mathbb {N}\) be such that ℓ>ht(ψ i (γ)) for every 1≤i≤n and γ∈Γ i , and let (t,u)∈τ(B 1 );⋯ ;τ(B n ). If \(\textnormal {P}^{\ell }_{n+1}(t) \neq \emptyset \) , then \(\textnormal {P}^{\ell }_{1}(u) \neq \emptyset \).
It remains to demonstrate a tree transformation that can be computed by
 and that reduces the maximal level of special positions from n+1 to 0. Clearly, this tree transformation cannot be computed by an n-fold composition of tree transformations from \(\mathcal {B}\)(l, n) because the output tree should contain a special position of level 1 by Corollary 42. We make sure that the assumptions of Corollary 42 are satisfied.
and that reduces the maximal level of special positions from n+1 to 0. Clearly, this tree transformation cannot be computed by an n-fold composition of tree transformations from \(\mathcal {B}\)(l, n) because the output tree should contain a special position of level 1 by Corollary 42. We make sure that the assumptions of Corollary 42 are satisfied.
Example 43
Let
-
M = (Q,Σ,Σ,{⋆}, R) be the
 with
with -
Q = {⋆, q} and Σ = {σ (2), α (0)}, and
-
the set R consisting of the following rules
$$\sigma(\star, \alpha)\overset{\star,q}{\longrightarrow} \star \qquad \quad\sigma(\star, q) \overset{\star,q}{\longrightarrow} \sigma(\star, q) \qquad \quad\alpha \overset{\star}{ \longrightarrow} \alpha ~. $$
It is easy to see that τ(M) is a total function. Intuitively, for an input tree t, it removes all positions v and v2 of t such that t(v) = σ and t(v2) = α. Figure 7 shows the repeated application of τ(M), where one application is indicated by ↦. Assuming that each dashed line contains at least three more positions, it is easy to check that, for distance ℓ = 2, the root of the first tree has level 2 (because positions 1, 11, 111, 1111, 2, 21, 211, and 2111 all have level 1). The penultimate tree, which is obtained from the first tree by the application of τ(M)2, only has special positions of level 0.
We use the
 of Example 43, and show that n transformations from \(\mathcal {B}\)(l, n) cannot compute the tree transformation τ(M)n+1.
of Example 43, and show that n transformations from \(\mathcal {B}\)(l, n) cannot compute the tree transformation τ(M)n+1.
Lemma 44
 for every n≥1.
for every n≥1.
Proof
Let Σ = {σ (2), α (0)}. The powers of a tree c ∈ T Σ({x 1}) are defined by c 1 = c and c k+1 = c[c k] for every k ≥ 1. Let T −1 = {α}. For every \(n \in \mathbb {N}\), we define the tree languages C n ⊆ T Σ({x 1}) and T n ⊆ T Σ inductively by C n = {σ(x 1, t)k∣t ∈ T n−1, k ≥ 1} and T n = {c[α]∣c ∈ C n }.
Let M be the
 of Example 43. We have already remarked that τ(M):T
Σ→T
Σ is a total function. It is easy to see that τ(M)(t
n
) ∈ T
n−1 for every \(n \in \mathbb {N}\) and t
n
∈ T
n
. Consequently, τ(M)n+1(t
n+1) ∈ T
0 for every t
n+1∈ T
n+1 (see Fig. 7 that shows trees in T
2, T
1, T
0, and
T−1). Obviously, \(\text {P}^{\ell }_{1}(u) = \emptyset \) for every u ∈ T
0 and ℓ ≥ 2. Thus, with the help of Corollary 42, we can complete the proof by showing that for every ℓ ≥ 2 there exists t ∈ T
n+1 such that \(\text {P}^{\ell }_{n+1}(t) \neq \emptyset \).
of Example 43. We have already remarked that τ(M):T
Σ→T
Σ is a total function. It is easy to see that τ(M)(t
n
) ∈ T
n−1 for every \(n \in \mathbb {N}\) and t
n
∈ T
n
. Consequently, τ(M)n+1(t
n+1) ∈ T
0 for every t
n+1∈ T
n+1 (see Fig. 7 that shows trees in T
2, T
1, T
0, and
T−1). Obviously, \(\text {P}^{\ell }_{1}(u) = \emptyset \) for every u ∈ T
0 and ℓ ≥ 2. Thus, with the help of Corollary 42, we can complete the proof by showing that for every ℓ ≥ 2 there exists t ∈ T
n+1 such that \(\text {P}^{\ell }_{n+1}(t) \neq \emptyset \).
Let ℓ ≥ 2 be fixed. We now prove that for every \(n \in \mathbb {N}\) there exists t ∈ T n such that \(\text {P}^{\ell }_{n}(t) \neq \emptyset \) by induction on n. In fact, we prove the stronger statement that there exists t ∈ T n and \(v \in \text {P}^{\ell }_{n}(t)\) such that \(\left |{\text {br}_{t}(\varepsilon , v) \cap \text {P}^{\ell }_{n}(t)}\right | \geq \ell ^{n+1}\). For n = 0, we select the tree t = c ℓ[α]∈ T 0, where c = σ(x 1, α), and the position v = 1ℓ−1. Since \(\text {P}^{\ell }_{0}(t) = \text {br}_{t}(\varepsilon , v)\), this selection of t and v fulfills the requirements. In the induction step, there exist a tree t ∈ T n and \(v \in \text {P}^{\ell }_{n}(t)\) such that \(\left |{\text {br}_{t}(\varepsilon , v) \cap \text {P}^{\ell }_{n}(t)}\right | \geq \ell ^{n+1}\). We consider the tree \(t^{\prime } = c^{(\ell ^{n+2}+1)}[\alpha ]\) with c = σ(x 1, t) and the position \(v^{\prime } = 1^{\ell ^{n+2}-1}\). Obviously, t ′∈ T n+1 and \(v^{\prime \prime } \in \text {P}^{\ell }_{n+1}(t^{\prime })\) for every v ″≼v ′ because \(\langle v^{\prime \prime },1, 2\rangle \in \text {PI}^{\ell }_{n+1}(t^{\prime })\) via the positions v 1 = v ″12v and v 2 = v ″2v using Lemma 38(i). This completes our induction and proof. □
Now we are able to prove that the composition hierarchy of
 and several other classes is infinite.
and several other classes is infinite.
Theorem 45
For every n≥1 and


Proof
Since all inclusions are trivial, we only need to prove their strictness. By Proposition 11 we have
 , hence
, hence
 and
and
 . Together with Lemma 44 these two statements imply the strictness of the two inclusions on the left. To prove the strictness of the other two inclusions, we prove that snl-XTn+1⫅̸(l-XTR)n. Using simple symmetry, we observe that
. Together with Lemma 44 these two statements imply the strictness of the two inclusions on the left. To prove the strictness of the other two inclusions, we prove that snl-XTn+1⫅̸(l-XTR)n. Using simple symmetry, we observe that
 , which together with the symmetric version of Lemma 44 yields \(\text {snl-XT}^{n+1} \not \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\). Furthermore, \(\text {l-XT}^{\text {R}} =\mathcal {B}(\text {nl}, \text {l})\) by Proposition 11, which yields \(\left (\text {l-XT}^{\text R}\right )^{n} \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\). Together with \(\text {snl-XT}^{n+1} \not \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\) we obtain snl-XTn+1⫅̸(l-XTR)n as desired. □
, which together with the symmetric version of Lemma 44 yields \(\text {snl-XT}^{n+1} \not \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\). Furthermore, \(\text {l-XT}^{\text {R}} =\mathcal {B}(\text {nl}, \text {l})\) by Proposition 11, which yields \(\left (\text {l-XT}^{\text R}\right )^{n} \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\). Together with \(\text {snl-XT}^{n+1} \not \subseteq \mathcal {B}(\text {n}, \text {l})^{n}\) we obtain snl-XTn+1⫅̸(l-XTR)n as desired. □
For the classes
 and
and
 with
with
 we can make more precise statements, which are similar to those in Theorems 26 and 34.
we can make more precise statements, which are similar to those in Theorems 26 and 34.
Theorem 46
For every n≥2,
Proof
The inclusions from left to right are trivial or follow from Lemma 15. The first strict inclusion on each line follows from Proposition 15. The other strict inclusions follow from snl-XTm+1⫅̸(l-XTR)m, which was shown in the proof of Theorem 45 for every m ≥ 1.
It remains to prove that (sl-XTR)n ⊆ sl-XTn. Clearly, it suffices to prove this for n = 2. We first observe that QR ;snl-XT⊆snl-XT. In fact, since
 (as mentioned in the proof of Theorem 45) and, obviously, QR−1=QR, we obtain that
(as mentioned in the proof of Theorem 45) and, obviously, QR−1=QR, we obtain that

where the inclusion follows from Lemma 13. Thus,
where the first step is by Lemma 15, the second step by Lemma 18, the third step by Lemma 19 and the last step by the above observation. □
The authors do not know whether, but guess that \(\text {l-XT}^{n} \subsetneq (\text {l-XT}^{\text {R}})^{n}\) for all n ≥ 2. Table Table 4 summarizes the main results of this section. For the sake of completeness, we mention some additional results from the literature, where T stands for the class of all tree transformations computable by top-down tree transducers [6], and
 stands for the class of tree transformations computable by ε-free extended top-down tree transducers [17]. The result
stands for the class of tree transformations computable by ε-free extended top-down tree transducers [17]. The result
 mentioned in Table 4 can be concluded from [17, Theorem 4.8].
mentioned in Table 4 can be concluded from [17, Theorem 4.8].

7 Hasse Diagram for the ε-Free Classes
Finally, let us compare the six classes of Theorem 34 with the three classes of Theorem 26 and the two classes of Proposition 17. Additionally, we consider the composition hierarchy for the class
 for which we established the infiniteness in Theorem 45. Thus, we compare all ε-free classes considered in this paper.
for which we established the infiniteness in Theorem 45. Thus, we compare all ε-free classes considered in this paper.
Theorem 47
Figure 8 is the Hasse diagram of the displayed classes of tree transformations for all n≥4.
Proof
The equalities are proved in Theorems 20 and 34, and all the inclusions are trivial or hold by either Lemma 15 or Corollary 25. The strictness of the vertical inclusions is proven in Proposition 17 and Theorems 26, 34, and 45. For the remaining strictness and incomparability results (with respect to ⊆) we have to prove the following six results.
-
(i)
 : This is a consequence of Proposition 14.
: This is a consequence of Proposition 14. -
(ii)
 : This follows from Proposition 16. It is also a consequence of the proof of Theorem 31 as follows. Consider the
: This follows from Proposition 16. It is also a consequence of the proof of Theorem 31 as follows. Consider the
 and the
and the
 and M
3 in that proof. If
and M
3 in that proof. If
 then
then
 contradicting the proof of Theorem 31.
contradicting the proof of Theorem 31. -
(iii)
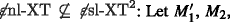 and M
3 be as in the proof of Theorem 31. Note that
and M
3 be as in the proof of Theorem 31. Note that
 and τ(M
2),
and τ(M
2),
 Now suppose that
Now suppose that
 . Then \(\tau (M^{\prime }_{1}) ; \tau (M_{2}) ; \tau (M_{3})\) is in
. Then \(\tau (M^{\prime }_{1}) ; \tau (M_{2}) ; \tau (M_{3})\) is in

where the first equality is due to Theorem 20. However, this contradicts the proof of Theorem 31.
-
(iv)
 : The translation τ = {(t, α)∣t ∈ T
Σ} with Σ = {σ
(2), α
(0)} can obviously be computed by an
: The translation τ = {(t, α)∣t ∈ T
Σ} with Σ = {σ
(2), α
(0)} can obviously be computed by an
 with the rules \(\sigma (q, q^{\prime }) \overset {q_{0}}{\longrightarrow } \alpha \) and \(\alpha \overset {q_{0}}{\longrightarrow } \alpha \), but
with the rules \(\sigma (q, q^{\prime }) \overset {q_{0}}{\longrightarrow } \alpha \) and \(\alpha \overset {q_{0}}{\longrightarrow } \alpha \), but
 for all k ≥ 1 by Corollary 42 because there exists a tree t ∈ T
Σ such that \(\text {P}^{\ell }_{k+1}(t) \neq \emptyset \) as demonstrated in the proof of Lemma 44.
for all k ≥ 1 by Corollary 42 because there exists a tree t ∈ T
Σ such that \(\text {P}^{\ell }_{k+1}(t) \neq \emptyset \) as demonstrated in the proof of Lemma 44. -
(v)
 This follows from the proof of Theorem 31 because the
This follows from the proof of Theorem 31 because the
 , M
2, and M
3 in that proof are nondeleting.
, M
2, and M
3 in that proof are nondeleting. -
(vi)
 : This result follows from the proof of Theorem 33, so let M
1, M
2, and M
3 be the
: This result follows from the proof of Theorem 33, so let M
1, M
2, and M
3 be the
 of that proof. We note that τ(M
2),
of that proof. We note that τ(M
2),
 . It is easy to show that
. It is easy to show that
 , which can be achieved by the decomposition τ(M
1) = τ(N
1);τ(N
2), where N
1 is obtained from M
1 by replacing the two rules involving q
la by \(\sigma (q, q^{\text {la}}) \overset {q}{\longrightarrow } \sigma (q, q^{\text {la}})\) and \(\sigma (q^{\text {la}}, q) \overset {q}{\longrightarrow } \sigma (q^{\text {la}}, q)\) and adding the two rules \(\gamma _{2}(q^{\text {la}}) \overset {q^{\text {la}}}{\longrightarrow } q^{\text {la}}\) and \(\alpha \overset {q^{\text {la}}}{\longrightarrow } \alpha \). Then N
1 is nondeleting. Similarly, we obtain N
2 from M
1 by replacing the two rules involving q
la by \(\sigma (q, \alpha ) \overset {q}{\longrightarrow } q\) and \(\sigma (\alpha , q) \overset {q}{\longrightarrow } q\) (and removing the two rules \(\gamma _{1}(p)\overset {p}{\longrightarrow } p\) and \(\gamma _{2}(q) \overset {q}\longrightarrow q\) because the symbols γ
1 and γ
2 have already been removed by N
1). Note that also N
2 is nondeleting. The decomposition yields that τ(M
1);τ(M
2);τ(M
3) is in
, which can be achieved by the decomposition τ(M
1) = τ(N
1);τ(N
2), where N
1 is obtained from M
1 by replacing the two rules involving q
la by \(\sigma (q, q^{\text {la}}) \overset {q}{\longrightarrow } \sigma (q, q^{\text {la}})\) and \(\sigma (q^{\text {la}}, q) \overset {q}{\longrightarrow } \sigma (q^{\text {la}}, q)\) and adding the two rules \(\gamma _{2}(q^{\text {la}}) \overset {q^{\text {la}}}{\longrightarrow } q^{\text {la}}\) and \(\alpha \overset {q^{\text {la}}}{\longrightarrow } \alpha \). Then N
1 is nondeleting. Similarly, we obtain N
2 from M
1 by replacing the two rules involving q
la by \(\sigma (q, \alpha ) \overset {q}{\longrightarrow } q\) and \(\sigma (\alpha , q) \overset {q}{\longrightarrow } q\) (and removing the two rules \(\gamma _{1}(p)\overset {p}{\longrightarrow } p\) and \(\gamma _{2}(q) \overset {q}\longrightarrow q\) because the symbols γ
1 and γ
2 have already been removed by N
1). Note that also N
2 is nondeleting. The decomposition yields that τ(M
1);τ(M
2);τ(M
3) is in
 . However, as demonstrated in the proof of Theorem 33, we have that τ(M
1);τ(M
2);τ(M
3) is not in
. However, as demonstrated in the proof of Theorem 33, we have that τ(M
1);τ(M
2);τ(M
3) is not in
 .
.
□
The authors did not attempt to present a Hasse diagram that contains all the classes (including the non- ε-free classes) discussed in this paper, but consider this a worthwhile effort.
8 Conclusion
Linear extended top-down tree transducers (with or without regular look-ahead) are formal models of syntax-based statistical machine translation. They have several good properties [19]. In particular, most of them can be presented as bimorphisms in the sense of [3], which yields that a result of [3] implies that ε-free, strict, and nondeleting l-xt are not closed under composition and that their composition hierarchy collapses at power 2. We extended their investigation to the composition hierarchy of the classes obtained by dropping some of the restrictions ε-freeness, strictness, and nondeletion. We showed in Theorem 34 that the composition hierarchy of ε-free l-xtR collapses at power 3 and that of ε-free l-xt collapses at power 4. In fact, the powers 3 and 4 are the least powers with that property. To complete the picture, we showed in Theorem 45 that the composition hierarchies of l-xt, l-xtR, and ε-free and nondeleting l-xt are infinite. Finally, we presented the Hasse-diagram of the powers of the considered ε-free classes in Theorem 47. In the future, the authors would like to investigate the composition hierarchy of weighted linear extended top-down tree transducers.
References
Arnold, A., Dauchet, M.: Transductions inversibles de forêts. Thèse 3ème cycle M. Dauchet, Université de Lille (1975)
Arnold, A., Dauchet, M.: Bi-transductions de forêts. In: ICALP, pp 74–86. Edinburgh University Press (1976)
Arnold, A., Dauchet, M.: Morphismes et bimorphismes d’arbres. Theoret. Comput. Sci. 20(1), 33–93 (1982)
Chiang, D.: An introduction to synchronous grammars. In: ACL. ACL. Part of a tutorial given with K. Knight (2006)
Dauchet, M.: Transductions de forêts — bimorphismes de magmoïdes. Première thèse, Université de Lille (1977)
Engelfriet, J.: Bottom-up and top-down tree transformations — a comparison. Math. Systems Theory 9(3), 198–231 (1975)
Engelfriet, J.: Top-down tree transducers with regular look-ahead. Math. Systems Theory 10(1), 289–303 (1977)
Engelfriet, J.: Three hierarchies of transducers. Math. Systems Theory 15(2), 95–125 (1982)
Engelfriet, J., Maneth, S.: Macro tree translations of linear size increase are MSO definable. SIAM J. Comput. 32(4), 950–1006 (2003)
Engelfriet, J., Schmidt, E.M.: IO and OI I. J. Comput. System Sci. 15(3), 328–353 (1977)
Fülöp, Z., Maletti, A.: Linking theorems for tree transducers. Submitted manuscript; available at: http://www.inf.u-szeged.hu/fulop/publ/linking.pdf (2014)
Fülöp, Z., Maletti, A., Vogler, H.: Preservation of recognizability for synchronous tree substitution grammars. In: ATANLP. ACL, pp 1–9 (2010)
Fülöp, Z., Maletti, A., Vogler, H.: Weighted extended tree transducers. Fundam. Inform. 111(2), 163–202 (2011)
Fülöp, Z., Vogler, H.: Syntax-Directed Semantics—Formal Models Based on Tree Transducers. EATCS Monographs on Theoret. Comput. Sci. Springer (1998)
Gécseg, F., Steinby, M.: Tree Automata. Akadémiai Kiadó, Budapest (1984) 2nd edition availble at. arXiv:1509.06233
Gécseg, F., Steinby, M.: Tree languages. In: Rozenberg, G., Salomaa, A. (eds.) Handbook of Formal Languages. chap. 1, vol. 3, pp 1–68. Springer (1997)
Graehl, J., Hopkins, M., Knight, K., Maletti, A.: The power of extended top-down tree transducers. SIAM J. Comput. 39(2), 410–430 (2009)
Graehl, J., Knight, K., May, J.: Training tree transducers. Comput. Linguist. 34(3), 391–427 (2008)
Knight, K., Graehl, J.: An overview of probabilistic tree transducers for natural language processing. In: CICLing, LNCS, vol. 3406, pp 1–24, Springer (2005)
Lemay, A., Maneth, S., Niehren, J.: A learning algorithm for top-down XML transformations. In: PODS. ACM, pp 285–296 (2010)
Maletti, A.: Compositions of extended top-down tree transducers. Inf. Comput. 206(9–10), 1187–1196 (2008)
May, J., Knight, K., Vogler, H.: Efficient inference through cascades of weighted tree transducers. In: ACL, pp 1058–1066 (2010)
Rounds, W.C.: Mappings and grammars on trees. Math. Systems Theory 4 (3), 257–287 (1970)
Thatcher, J.W.: Generalized2 sequential machine maps. J. Comput. System Sci. 4(4), 339–367 (1970)
Author information
Authors and Affiliations
Corresponding author
Additional information
This is a revised and extended version of [Z. Fülöp and A. Maletti: Composition closure of ε -free linear extended top-down tree transducers. In Proc. 17th DLT, volume 7907 of LNCS, pages 239–251. Springer-Verlag, 2013].
This work was partially supported by the exchange project 55 657 of the German Academic Exchange Service (DAAD) and Hungarian Scholarship Board Office (MÖB). Z. Fülöp was partially supported by the NKFI grant K 108 448, and A. Maletti was partially supported by the German Research Foundation (DFG) grant MA / 4959 / 1-1.
Rights and permissions
About this article
Cite this article
Engelfriet, J., Fülöp, Z. & Maletti, A. Composition Closure of Linear Extended Top-down Tree Transducers. Theory Comput Syst 60, 129–171 (2017). https://doi.org/10.1007/s00224-015-9660-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-015-9660-2













 with
with

 : This is a consequence of Proposition 14.
: This is a consequence of Proposition 14. : This follows from Proposition 16. It is also a consequence of the proof of Theorem 31 as follows. Consider the
: This follows from Proposition 16. It is also a consequence of the proof of Theorem 31 as follows. Consider the
 and the
and the
 and M
3 in that proof. If
and M
3 in that proof. If
 then
then
 contradicting the proof of Theorem 31.
contradicting the proof of Theorem 31.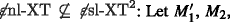 and M
3 be as in the proof of Theorem 31. Note that
and M
3 be as in the proof of Theorem 31. Note that
 and τ(M
2),
and τ(M
2),
 Now suppose that
Now suppose that
 . Then
. Then 
 : The translation τ = {(t, α)∣t ∈ T
Σ} with Σ = {σ
(2), α
(0)} can obviously be computed by an
: The translation τ = {(t, α)∣t ∈ T
Σ} with Σ = {σ
(2), α
(0)} can obviously be computed by an
 with the rules
with the rules  for all k ≥ 1 by Corollary 42 because there exists a tree t ∈ T
Σ such that
for all k ≥ 1 by Corollary 42 because there exists a tree t ∈ T
Σ such that  This follows from the proof of Theorem 31 because the
This follows from the proof of Theorem 31 because the
 , M
2, and M
3 in that proof are nondeleting.
, M
2, and M
3 in that proof are nondeleting. : This result follows from the proof of Theorem 33, so let M
1, M
2, and M
3 be the
: This result follows from the proof of Theorem 33, so let M
1, M
2, and M
3 be the
 of that proof. We note that τ(M
2),
of that proof. We note that τ(M
2),
 . It is easy to show that
. It is easy to show that
 , which can be achieved by the decomposition τ(M
1) = τ(N
1);τ(N
2), where N
1 is obtained from M
1 by replacing the two rules involving q
la by
, which can be achieved by the decomposition τ(M
1) = τ(N
1);τ(N
2), where N
1 is obtained from M
1 by replacing the two rules involving q
la by  . However, as demonstrated in the proof of Theorem 33, we have that τ(M
1);τ(M
2);τ(M
3) is not in
. However, as demonstrated in the proof of Theorem 33, we have that τ(M
1);τ(M
2);τ(M
3) is not in
 .
.