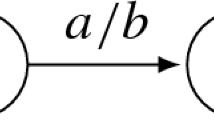Automaton Semigroups: The Two-state Case

Abstract

We prove that semigroups generated by reversible two-state Mealy automata have remarkable growth properties: they are either finite or free. We give an effective procedure to decide finiteness or freeness of such semigroups when the generating automaton is also invertible.

1 Introduction

Automaton (semi)groups — short for semigroups generated by Mealy automata and groups generated by invertible Mealy automata — were formally introduced half a century ago (for details, see [9, 17] and references therein). Over the years, important results have started revealing their full potential, by contributing to important conjectures in group theory, as the Milnor problem (the first example of a group of intermediate growth) or the Burnside problem (an example of a very simple Mealy automaton generating an infinite torsion group).

In a way, semigroups can be classified according to their growth function: at one end stand finite semigroups and at the other one free semigroups. Finiteness of automaton semigroups is an undecidable problem in general [13], and it is therefore valuable to find special classes of Mealy automata for which the finiteness problem is decidable. Beside this undecidability result, several sufficient or necessary criteria for finiteness have been developped [2, 4, 8, 9, 18, 20, 21, 25, 26] . Regarding the decidability of freeness, it has been and it is still a challenge: only some particular invertible Mealy automata, possibly parametrized, have been shown to generate free groups [14, 23, 27–29]; and some Cayley automaton semigroups have been shown to be free [26]. Very recently, [10] presents a decidable sufficient condition to have free semigroups in an automaton group, but in a very different context, since the considered Mealy automata cannot be reversible.

In this paper, we link both issues for semigroups generated by reversible two-state Mealy automata, indirectly giving a classification of the growth of automata semigroups [17, Problem 7.1.1] for this particular case: we prove that such semigroups are either finite or free, in this latter case the states of the generating Mealy automaton being free generators of the semigroup, answering a conjecture stated in [18]. In particular we prove that in the free case the generated semigroup is spherically transitive [17, Problem 7.2.1(f)].

On the basis of this dichotomy between finite and free semigroups, we prove that finiteness and freeness of the semigroup are decidable if the generating reversible two-state Mealy automaton is also invertible. Decidability of finiteness extends by duality to groups generated by two-letter invertible-reversible Mealy automata. The problems of deciding finiteness or freeness of automaton semigroups was raised by Grigorchuk, Nekrashevych, and Sushchanskii [17, Problem 7.2.1(b)].

Specializing to two letters or states may seem to be a strong restriction, but most of the significant examples in literature have faced this restriction: the first example of a finitely generated group of intermediate growth, the Grigorchuk group [16, 17], is generated by a two-letter Mealy automaton while the very smallest Mealy automaton with intermediate growth [6] has two letters and two states; the lamplighter group [15] is generated by a two-letter and two-state Mealy automaton; the Aleshin automaton [3, 28] gives the simplest example of a free automaton group and has two letters. The article [7] is entirely devoted to the study of groups generated by 3-state 2-letter invertible Mealy automata.

This paper is organized as follows. In Section 2 we define Mealy automata and automaton (semi)groups. Basic tools to manipulate them are introduced in Section 3. Section 4 is devoted to the dichotomy between free and finite semigroups. The decidability results are proved in Section 5. The final section explores possible and impossible extensions of our results. The cornerstone of our proofs and constructions is the very classical Nerode equivalence used to minimize automata.

2 (Semi) Groups Generated by Mealy Automata

2.1 Mealy Automata

If one forgets initial and final states, a (finite, deterministic, and complete) automaton ${\mathcal A}$ is a triple $(A,{\Sigma },\delta = (\delta _{i}: A\rightarrow A )_{i\in {\Sigma }})$, where the stateset A and the alphabet Σ are non-empty finite sets, and where the δ _i are functions.

A Mealy automaton is a quadruple

$$\left( A, {\Sigma}, \delta = (\delta_{i}: A\rightarrow A )_{i\in {\Sigma}}, \rho = (\rho_{x}: {\Sigma}\rightarrow {\Sigma} )_{x\in A} \right)\:, $$

such that both (A,Σ,δ) and (Σ,A,ρ) are automata. In other terms, a Mealy automaton is a letter-to-letter transducer with the same input and output alphabet.

The graphical representation of a Mealy automaton is standard, see Fig. 1.

Fig. 1

Examples of Mealy automata: the Aleshin automaton generates the rank 3 free group [3, 28], the Baby-Aleshin automaton generates the free product ${\mathbb {Z}}_{2}^{*3}={\mathbb {Z}}_{2}*{\mathbb {Z}}_{2}*{\mathbb {Z}}_{2}$ [23]

A Mealy automaton ${\mathcal A}=(A,{\Sigma },\delta , \rho )$ is invertible if the functions ρ _x are permutations of Σ and reversible if the functions δ _i are permutations of A.

In a Mealy automaton ${\mathcal A}=(A,{\Sigma }, \delta , \rho )$, the sets A and Σ play dual roles. So we may consider the dual (Mealy) automaton defined by $\mathfrak d({\mathcal {A}}) = ({\Sigma },A, \rho , \delta )$. Obviously, a Mealy automaton is reversible if and only if its dual is invertible.

Considering the underlying graph of a Mealy automaton, it makes sense to look at the connected components of a Mealy automaton. Note that a connected component of a reversible Mealy automaton is always strongly connected: its (δ _i :A→A) _i∈Σ are permutations of a finite set and in particular they are surjective.

2.2 Automaton (semi) Groups

Let ${\mathcal A} = (A,{\Sigma }, \delta ,\rho )$ be a Mealy automaton. We view ${\mathcal A}$ as an automaton with an input and an output tape, thus defining mappings from input words over Σ to output words over Σ. Formally, for x∈A, the map $\rho _{x} : {\Sigma }^{*} \rightarrow {\Sigma }^{*}$, extending $\rho _{x} : {\Sigma } \rightarrow {\Sigma }$, is defined by:

$$\forall i \in {\Sigma}, \ \forall {\mathbf{s}} \in {\Sigma}^{*}, \qquad \rho_{x}(i{\mathbf{s}}) = \rho_{x}(i)\rho_{\delta_{i}(x)}({\mathbf{s}}) \:. $$

By convention, the image of the empty word is itself. The mapping ρ _x is length-preserving and prefix-preserving. We say that ρ _x is the production function associated with $({\mathcal A},x)$ or more briefly, if there is no ambiguity, the production function of x. For x=x ₁⋯x _n ∈A ⁿ with n>0, set $\rho _{{\mathbf {x}}}: {\Sigma }^{*} \rightarrow {\Sigma }^{*}, \rho _{{\mathbf {x}}} = \rho _{x_{n}} \circ {\cdots } \circ \rho _{x_{1}} \:$.

Denote dually by $\delta _{i}:A^{*}\rightarrow A^{*}, i\in {\Sigma }$, the production functions associated with the dual automaton ${\mathfrak {d}}({\mathcal {A}})$. For ${\mathbf {s}}=s_{1}{\cdots } s_{n} \in {\Sigma }^{n}$ with n>0, set $\delta _{{\mathbf {s}}}: A^{*} \rightarrow A^{*}, \ \delta _{{\mathbf {s}}} = \delta _{s_{n}}\circ {\cdots } \circ \delta _{s_{1}}$.

The semigroup of mappings from Σ^∗ to Σ^∗ generated by ρ _x ,x∈A, is called the semigroup generated by ${\mathcal A}$ and is denoted by $\langle {{{\mathcal {A}}}\rangle }_{+}$. When ${\mathcal {A}}$ is invertible, its production functions are permutations on words of the same length and thus we may consider the group of mappings from Σ^∗ to Σ^∗ generated by ρ _x ,x∈A; it is called the group generated by ${\mathcal {A}}$ and is denoted by $\langle {{\mathcal {A}}}\rangle$.

An invertible Mealy automaton generates a finite group if and only if it generates a finite semigroup [2]. A Mealy automaton generates a finite semigroup if and only if so does its dual [2, 23, 24].

3 Basic Tools

In this section, we present basic tools to manipulate Mealy automata: Nerode equivalence and minimization of automata (Section 3.1) are classic constructions from automata theory, ${\mathfrak {m}}{\mathfrak {d}}$-reduction and ${\mathfrak {m}}{\mathfrak {d}}$-triviality (Section 3.2) have been introduced in [2] to give a sufficient condition for finiteness, portraits of automorphisms on a regular rooted tree (Section 3.3) come from geometric group theory and tensor closures (Section 3.4) are newly introduced in order to better control the structure of a Mealy automaton.

Let ${\mathcal {A}} = (A,{\Sigma },\delta ,\rho )$ be a Mealy automaton. A convenient and natural operation is to raise ${\mathcal {A}}$ to the power n, for some n>0: its n-th power is the Mealy automaton

$${\mathcal {A}}^{n} = \left( \ A^{n},{\Sigma}, (\delta_{i} : A^{n} \rightarrow A^{n})_{i\in {\Sigma}}, (\rho_{{\mathbf{u}}} : {\Sigma} \rightarrow {\Sigma} )_{{\mathbf{u}}\in A^{n}} \ \right)\:. $$

Note that the powers of a reversible Mealy automaton are reversible.

3.1 The Nerode Equivalence and the Minimization of a Mealy Automaton

Throughout this subsection, ${\mathcal A}=(A,{\Sigma },\delta ,\rho )$ denotes a Mealy automaton.

The Nerode equivalence ≡ on A is the limit of the sequence of increasingly finer equivalences (≡ _k ) recursively defined by:

$$\begin{array}{@{}rcl@{}} \forall x,y\in A,\qquad\qquad x\equiv_{0} y & \ \Longleftrightarrow \ \rho_{x}=\rho_{y}\:,\\ \forall k\geqslant 0,\ x\equiv_{k+1} y & \ \Longleftrightarrow\ \left(x\equiv_{k} y\quad \wedge\quad\forall i\in{\Sigma},\ \delta_{i}(x)\equiv_{k}\delta_{i}(y)\right)\:. \end{array} $$

Since the set A is finite, this sequence is ultimately constant; moreover if two consecutive equivalences are equal, the sequence remains constant from this point on. The limit is therefore computable.

For every element x in A, we denote by [x] (resp. [x] _k ) the class of x w.r.t. the Nerode equivalence (resp. the ≡ _k equivalence), called the Nerode class (resp. the k-class) of x. Extending to the n-th power of ${\mathcal {A}}$, we denote by [x] the Nerode class in A ⁿ of x∈A ⁿ.

The minimization of ${\mathcal {A}}$ is the Mealy automaton ${\mathfrak {m}}({\mathcal {A}})=(A/\mathord {\equiv },{\Sigma },\tilde {\delta },\tilde {\rho })$, where for every (x,i) in A×Σ, $\tilde {\delta }_{i}([x])=[\delta _{i}(x)]$ and $\tilde {\rho }_{[x]}=\rho _{x}$. This definition is consistent with the standard minimization of “deterministic finite automata” where instead of considering the mappings (ρ _x :Σ→Σ) _x , the computation is initiated by the separation between terminal and non-terminal states. Using the Hopcroft algorithm, the time complexity of minimization is ${\mathcal {O}}(\#{\Sigma } \#A\log {\#A})$, see [1].

Two states of a Mealy automaton belong to the same Nerode class if and only if they represent the same element in the generated semigroup, i.e. if and only if they have the same production function Σ^∗→Σ^∗. Two words on A of the same length n are equivalent if they belong to the same Nerode class in A ⁿ. By extension, any two words on A are equivalent if they have the same production function. The set of all words equivalent to x∈A ^∗, regardless of their length, is denoted by ⟦ x ⟧.

Two states of a Mealy automaton belong to the same k-class if and only if the restrictions of their production functions to Σ^k→Σ^k are equal.

The following remarks will be useful for the rest of the paper:

Remark 1

Let n be an integer. If each word of A ⁿ is equivalent to a strictly shorter word, then the semigroup $\langle {{\mathcal {A}}\rangle }_{+}$ is finite, its set of elements being {ρ _u ,u∈A ^≤n−1}.

Remark 2

If two words of A ^∗ are equivalent, so are their images under the action of each element of $\langle {{\mathfrak d}({{\mathcal A}})\rangle }_{+}$:

$$\begin{array}{@{}rcl@{}}\begin{array}{rcll} \rho_{{\mathbf{u}}} = \rho_{{\mathbf{v}}} & \,\Longleftrightarrow\, & \forall{\mathbf{s}},{\mathbf{t}}\in {\Sigma}^{*},\,& \rho_{{\mathbf{u}}}({\mathbf{st}}) = \rho_{{\mathbf{v}}}({\mathbf{st}})\\ & \,\Longleftrightarrow\, & & \rho_{{\mathbf{u}}}({\mathbf{s}})\rho_{\delta_{{\mathbf{s}}}({\mathbf{u}})}({\mathbf{t}}) = \rho_{{\mathbf{v}}}({\mathbf{s}})\rho_{\delta_{{\mathbf{s}}}({\mathbf{v}})}({\mathbf{t}})\\ & \,\Longrightarrow\, & & \rho_{\delta_{{\mathbf{s}}}({\mathbf{u}})}({\mathbf{t}}) = \rho_{\delta_{{\mathbf{s}}}({\mathbf{v}})}({\mathbf{t}})\\ & \,\Longleftrightarrow\, & \forall{\mathbf{s}}\in {\Sigma}^{*},\,& \delta_{{\mathbf{s}}}({\mathbf{u}}) = \delta_{{\mathbf{s}}}({\mathbf{v}})\\ \end{array}\end{array} $$

3.2 The ${\mathfrak {m}}{\mathfrak {d}}$-reduction and the ${\mathfrak {m}}{\mathfrak {d}}$-triviality

The ${\mathfrak {m}}{\mathfrak {d}}$-reduction and the ${\mathfrak {m}}{\mathfrak {d}}$-triviality were introduced in [2] to give a sufficient but not necessary condition of finiteness. We show in Section 5 that, in the case of a two-state or two-letter invertible-reversible Mealy automaton, this condition is actually necessary.

A pair of dual Mealy automata is reduced if both automata are minimal. The ${\mathfrak {m}}{\mathfrak {d}}$-reduction of a Mealy automaton consists in minimizing the automaton or its dual until the resulting pair of dual Mealy automata is reduced. It is well-defined: if both a Mealy automaton and its dual automaton are non-minimal, the reduction is confluent [2].

The trivial Mealy automaton represented in Fig. 2 generates the trivial (semi)group. If the ${\mathfrak {m}}{\mathfrak {d}}$-reduction of a Mealy automaton ${\mathcal A}$ leads to the trivial Mealy automaton, ${\mathcal {A}}$ is said to be ${\mathfrak {m}}{\mathfrak {d}}$ -trivial. It is decidable whether a Mealy automaton is ${\mathfrak {m}}{\mathfrak {d}}$-trivial. An ${\mathfrak {m}}{\mathfrak {d}}$-trivial Mealy automaton generates a finite semigroup, but in general the converse is false [2].

Fig. 2

The trivial Mealy automaton

A priori the sequence of minimization-dualization can be arbitrarily long: the minimization of a Mealy automaton with a minimal dual can make the dual automaton non-minimal. Nevertheless, if the automaton has two states, the ${\mathfrak {m}}{\mathfrak {d}}$-reduction can be shortened to ${\mathfrak {m}}{\mathfrak {d}}{\mathfrak {m}}{\mathfrak {d}}$. Hence, in this particular case, the time complexity of the ${\mathfrak {m}}{\mathfrak {d}}$-reduction is ${\mathcal {O}}(\#{\Sigma }\log {\#{\Sigma }})$.

3.3 Portrait of a Word

Throughout this subsection, ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ denotes an invertible Mealy automaton.

The set Σ^∗ can naturally be thought of as a regular rooted tree; its root is the empty word and two words are connected if and only if they are of the form s and s i, with s∈Σ^∗, i∈Σ. The set Σⁿ is the n th level of Σ^∗. A branch of the tree Σ^∗ is a sequence of words $({\mathbf {s}}_{k})_{k\in {\mathbb {N}}}$ such that, for each $k\in {\mathbb {N}}$, s _k is of length k and is a prefix of s _k+1.

An automorphism of Σ^∗ is a bijective map Σ^∗→Σ^∗ preserving the root and the adjacency of the vertices. Each state x of the automaton ${\mathcal A}$ acts on the regular rooted tree Σ^∗ by the production rule ρ _x . The constructions of this subsection are directly inspired by this view (see [23] and references therein for more details on automorphisms acting on regular rooted trees). Denote by A u t(Σ^∗) the set of automorphisms of Σ^∗.

An automorphism is level-transitive or spherically transitive if it acts transitively on each level of the regular rooted tree [17, 23]. Such an automorphism has an infinite order.

Let g be an automorphism on the regular rooted tree Σ^∗. For any word s∈Σ^∗, there exists a unique automorphism $g_{|{\mathbf {s}}}:{\Sigma }^{*} \to {\Sigma }^{*}$ called a section of g and defined, for all word t∈Σ^∗, by g(s t)=g(s)g _|s (t), see [23] for more details. The portrait of g is the tree Σ^∗ in which each vertex s∈Σ^∗ is labeled by g _|s :Σ→Σ. It is denoted by ${\mathfrak {p}}_{\infty }({g})$. The permutation of Σ associated to the empty word is the root permutation of g. A level (resp. branch) of a portrait is the labeled level (resp. branch) of the tree.

For a given integer k, the k-portrait of g is the restriction of ${\mathfrak {p}}_{\infty }({g})$ to levels 0 to k−1 and is denoted by ${\mathfrak {p}}_{k}({g})$, it represents the action of g on the partial regular rooted tree Σ^≤k.

Let u∈A ^∗. The portrait (or $\infty$ -portrait — resp. the k-portrait) of u is the portrait (resp. the k-portrait) of ρ _u : each vertex s∈Σ^∗ is labeled by $\rho _{\delta _{{\mathbf {s}}}({\mathbf {u}})}:{\Sigma }\to {\Sigma }$. It is denoted by ${\mathfrak {p}}_{\infty }[{\kern-2pt}[ {{\mathbf {u}}}]{\kern-2pt}]$ (resp. ${\mathfrak {p}}_{k}[{\kern-2pt}[ {{\mathbf {u}}}]{\kern-2pt}]$). This notation is completely justified by the fact that two equivalent words have the same production function, and hence the same portrait. An example is given in Fig. 3.

Fig. 3

Some portrait of a two-letter Mealy automaton; id = id_Σ and σ permutes i and j

The map from A u t(Σ^∗) to the set of portraits induces a monoid structure on the set of portraits. The neutral element of the product of portraits is the identity portrait: ${\mathcal {I}}_{\infty }={\mathfrak {p}}_{\infty }({\text {id}_{{\Sigma }^{*}}})$. The portraits of the automaton ${\mathcal {A}}$ are the portraits of the elements of $\langle {{\mathcal {A}}\rangle }_{+}$. The product of two k-portraits of ${\mathcal {A}}$ can be expressed in terms of words: ${\mathfrak {p}}_{k}[{\kern-2pt}[ {{\mathbf {u}}}]{\kern-2pt}] {\mathfrak {p}}_{k}[{\kern-2pt}[ {{\mathbf {v}}}]{\kern-2pt}] = {\mathfrak {p}}_{k}[{\kern-2pt}[ {{\mathbf {uv}}}]{\kern-2pt}]$. It provides a monoid structure to the set of k-portraits of ${\mathcal {A}}$, whose neutral element is the identity k-portrait ${\mathcal {I}}_{k}={\mathfrak {p}}_{k}({\text {id}_{{\Sigma }^{*}}})$.

A level of a portrait is homogeneous if all its vertices have the same label; a portrait is homogeneous if all its levels are homogeneous: the portrait ${\mathfrak {p}}_{3}[{\kern-2pt}[ {1}]{\kern-2pt}]$ of Fig. 3(b) has homogeneous levels 0 and 2, but is not homogeneous. For any integer k≥1, the k-portrait ${\mathfrak {p}}_{k}({g})$ is almost homogeneous if ${\mathfrak {p}}_{k-1}({g})$ and all the $\left ({\mathfrak {p}}_{k-1}({g_{|i}})\right )_{i\in {\Sigma }}$ are homogeneous.

An almost homogeneous (k+1)-portrait ${\mathcal {K}}$ is built in the following way from a homogeneous k-portrait ${\mathcal {J}}$ and a sequence τ=(τ _i ) _i∈Σ of permutations of Σ: the restriction of ${\mathcal {K}}$ to levels 0 to k−1 is ${\mathcal {J}}$ and the leaves of the subtree of the root corresponding to the letter i∈Σ have all label τ _i . This portrait is denoted by ${{\mathcal {J}}}\lfloor {\tau }\rfloor$, see Fig. 4.

Fig. 4

The almost homogeneous (k+1)-portrait ${{{\mathcal {J}}}}\lfloor {\tau }\rfloor$, τ=(τ _i ) _i∈Σ

Remark 3

The product of two homogeneous k-portraits is a homogeneous k-portrait.

Furthermore, if Σ={i,j}:

• the square of a homogeneous k-portrait is the identity k-portrait ${\mathcal {I}}_{k}$;

• the square of an almost homogeneous k-portrait whose root permutation is the identity on Σ is the identity k-portrait;

• the square of an almost homogeneous k-portrait ${{{\mathcal {J}}}}\lfloor {\tau _{i},\tau _{j}}\rfloor$ whose root permutation is the permutation of i and j is the identity k-portrait if and only if τ _i =τ _j .

3.4 Tensor Closure

When a Mealy automaton generates a finite semigroup, we may augment the alphabet on which it acts to gain a better control over its structure.

Let ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ be a Mealy automaton which generates a finite semigroup. Its tensor closure is the Mealy automaton ${\mathfrak {c}}(\mathcal {A})=(A,{\Xi },\bar \delta ,\bar \rho )$, where ${\Xi }=\{[{\kern-2pt}[ {{\mathbf {s}}}]{\kern-2pt}] \mid {\mathbf {s}}\in {\Sigma }^{*}\}=\langle {{\mathfrak d}({{\mathcal A}})\rangle }_{+}$ and $\bar \delta$ and $\bar \rho$ are the natural extensions of δ and ρ:

$$\begin{array}{@{}rcl@{}} \forall x\in A,\forall {\mathbf{s}}\in{\Sigma}^{*},\,\bar\delta_{[{\kern-2pt}[{{\mathbf{s}}}]{\kern-2pt}]}(x)=\delta_{{\mathbf{s}}}(x)\text{ and }\bar\rho_{x}([{\kern-2pt}[{{\mathbf{s}}}]{\kern-2pt}]) = [{\kern-2pt}[{\rho_{x}({\mathbf{s}})}]{\kern-2pt}]\:. \end{array} $$

A Mealy automaton is tensor closed if it is isomorphic to its tensor closure. Its dual is then minimal.

The following remark justifies the introduction of the tensor closures:

Remark 4

Let ${\mathcal A}$ be a two-state Mealy automaton which generates a finite semigroup. Then the automaton ${\mathfrak c}({\mathcal {A}})$ generates a finite semigroup. If ${\mathfrak {c}}({\mathcal {A}})$ is ${\mathfrak {m}}{\mathfrak {d}}$-trivial, then so is ${\mathcal {A}}$.

The first result is obtained by looking at the respective dual automata which generates the same semigroup. The second result is immediate since a two-state Mealy automaton ${\mathcal {A}}$ is ${\mathfrak {m}}{\mathfrak {d}}$-trivial if and only if ${\mathfrak {m}}{\mathfrak {d}}{\mathfrak {m}}{\mathfrak {d}}({\mathcal {A}})$ is trivial and the alphabet of ${\mathfrak {d}}{\mathfrak {m}}{\mathfrak {d}}({\mathcal {A}})$ can be injected into the alphabet of ${\mathfrak {c}}({\mathcal {A}})$.

Lemma 1

Let ${\mathcal {A}}$ be a two-state invertible-reversible tensor closed Mealy automaton. The connected components of the powers of ${\mathcal {A}}$ are complete graphs.

Proof

Set ${\mathcal {A}} =(A,{\Xi },\delta ,\rho )$ and let k be an integer. The connected components of ${\mathcal {A}}^{k}$ are strongly connected by reversibility. Hence any two words u and v in the same connected component are connected by a path with input label in Ξ^∗. The automaton ${\mathcal {A}}$ being tensor closed, any word over Ξ is equivalent to a one-length word over Ξ and so the connected component of u and v is a complete graph: any two states are connected by a transition. □

4 The Semigroup is Either Free or Finite

Recall that a semigroup S is free if there exists a subset X of S such that every element of S can be written uniquely as a word over X, its rank is then the cardinality of X.

Remark 5

A group G is free if there exists a subset X of G such that every element of G can be written uniquely as an irreducible word over X⊔X ⁻¹. An invertible automaton can generate a free semigroup and a non-free group; for example, the dual of Aleshin automaton (see Fig. 1(a)) generates a free semigroup, by Theorems 1 and 2, but not a free group: b a ⁻¹ b a ⁻¹=1.

Theorem 1

Let ${\mathcal {A}}$ be a reversible two-state Mealy automaton. If ${\mathcal {A}}$ admits a disconnected power, then it generates a finite semigroup, otherwise it generates a free semigroup of rank 2 with the states of ${\mathcal {A}}$ being free generators.

Theorem 1 is a corollary of Proposition 1 and the case p=2 in Proposition 2 below.

Let us look at the connected components of the powers of a Mealy automaton ${\mathcal {A}}$. For m>0, u,v∈A ^m, and x,y∈A, if there exists a path from u x to v y in ${\mathcal {A}}^{m+1}$, then there is a path from u to v in ${\mathcal {A}}^{m}$. Hence if ${\mathcal {A}}^{n}$ is disconnected, so are the ${\mathcal {A}}^{k}$, for all k>n. Thus there exists at most one integer n such that ${\mathcal {A}}^{n}$ is connected and ${\mathcal {A}}^{n+1}$ is disconnected. This integer is called the connection degree of ${\mathcal {A}}$. By convention, if ${\mathcal {A}}$ is disconnected, its connection degree is 0, and it has an infinite connection degree if no power of ${\mathcal {A}}$ is disconnected.

A Mealy automaton has an infinite connection degree if and only if its dual is spherically transitive.

4.1 Finite Connection Degree

In this section, we prove that a reversible two-state Mealy automaton has a finite connection degree if and only if it generates a finite semigroup. This result is already known [7, Lemma 3], but we present here a new proof which fully exploits the structure of the automaton; its main idea is to bound the sizes of the connected components of the powers of ${\mathcal {A}}$ once the connection degree has passed.

Lemma 2

Let ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ be a reversible Mealy automaton with at least two states, which generates a semigroup with torsion elements. Then its connection degree is finite.

Proof

Since $\langle {{\mathcal A}\rangle }_{+}$ has torsion elements, there exist a word u∈A ⁺ and two integers n≥0 and k>0 such that u ⁿ and u ^n+k are equivalent: $\rho _{{\mathbf {u}}^{n}}= \rho _{{\mathbf {u}}^{n+k}}$. Let s∈Σ^∗, we have:

$$\delta_{{\mathbf{s}}}({\mathbf{u}}^{n+2k}) = \delta_{{\mathbf{s}}}({\mathbf{u}}^{n}) \delta_{\rho_{{\mathbf{u}}^{n}}({\mathbf{s}})}({\mathbf{u}}^{k}) \delta_{\rho_{{\mathbf{u}}^{n+k}}({\mathbf{s}})}({\mathbf{u}}^{k}) = \delta_{{\mathbf{s}}}({\mathbf{u}}^{n}) \bigl(\delta_{\rho_{{\mathbf{u}}^{n}}({\mathbf{s}})}({\mathbf{u}}^{k})\bigr)^{2}\:. $$

Hence all the states of the connected component of u ^n+2k have form v w ² and ${\mathcal {A}}^{(n+2k)|{\mathbf {u}}|}$ is disconnected. □

In the remainder of this subsection, ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ denotes a reversible two-state Mealy automaton (A={x,y}) with finite connection degree n. If z∈A is a state of ${\mathcal {A}}$, $\bar {z}\in A$ denotes the other state: $z\neq \bar {z}$.

Lemma 3

Let ${\mathcal {C}}$ be a connected component of ${\mathcal {A}}^{m}$ for some m, and let u ∈A ^m be a state of ${\mathcal {C}}$ . The connected component (in ${\mathcal {A}}^{m+1}$ ) of u x has size $\#{\mathcal {C}}$ if it does not contain u y, and $2\#{\mathcal {C}}$ if it does contain u y.

Proof

Let ${\mathcal {D}}$ be the connected component of u x: v∈A ^m is a state of ${\mathcal {C}}$ if and only if there exists z∈A such that v z is a state of ${\mathcal {D}}$, hence: $N\leq \#{\mathcal D}\leq 2N$. Let v be a state of ${\mathcal {C}}$ and z∈A: u x and v z are in the same connected component if and only if so are u y and ${\mathbf {v}}\bar {z}$. The result follows. □

Recall that n is the connection degree of ${\mathcal {A}}$.

Lemma 4

For each m≥n, the connected components of ${\mathcal {A}}^{m}$ have size exactly 2 ⁿ.

Proof

By induction on m≥n. For m∈{n,n+1}, the property is true (using Lemma 3 for m=n+1).

Assume m>n+1. Suppose that the connected components of ${\mathcal {A}}^{m-1}$ and ${\mathcal {A}}^{m}$ have size 2ⁿ. Then let ${\mathcal {C}}$ be a connected component of ${\mathcal {A}}^{m+1}$ and u=u ₁⋯u _m+1 a state of ${\mathcal {C}}$. The word u ^∙=u ₁⋯u _m belongs to a connected component ${\mathcal {D}}$ of ${\mathcal {A}}^{m}$, of size 2ⁿ by the induction hypothesis. Hence ${\mathcal {C}}$ has size 2ⁿ or 2ⁿ⁺¹ according to Lemma 3.

Suppose that ${\mathcal {C}}$ has size 2ⁿ⁺¹: it means by Lemma 3 that both u and ${\mathbf {u}}^{\bullet }\overline {u_{m+1}}$ belong to ${\mathcal {C}}$. It follows that u ₂⋯u _m u _m+1 and $u_{2}{\cdots } u_{m}\overline {u_{m+1}}$ belong to the same connected component ${\mathcal {E}}$ of ${\mathcal {A}}^{m}$, of size 2ⁿ by the induction hypothesis. Hence Lemma 3 ensures the existence of a connected component of ${\mathcal {A}}^{m-1}$ of size 2ⁿ⁻¹, contradicting the induction hypothesis. □

Proposition 1

The connection degree of a reversible two-state Mealy automaton is finite if and only if it generates a finite semigroup.

Proof

Let ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ be a reversible two-state Mealy automaton. If the connection degree of ${\mathcal A}$ is 0, $\langle {{\mathfrak {d}}({\mathcal {A}})\rangle }_{+}$ is the trivial semigroup and $\langle {{\mathcal {A}}\rangle }_{+}$ is finite [2].

Otherwise, let n≥1 be the connection degree of ${\mathcal {A}}$: by Lemma 4, for m≥n, the connected components of ${\mathcal {A}}^{m}$ have size 2ⁿ. These connected components are reversible Mealy automata on the alphabet Σ. Up to state numbering, there are only a finite number of such automata and thus there exist p<q such that ${\mathfrak {m}}({\mathcal {A}}^{p}) = {\mathfrak {m}}({\mathcal {A}}^{q})$. It follows by Remark 1 that $\langle {{\mathcal { A}}\rangle }_{+}$ is finite.

The reciprocal property is a particular case of Lemma 2. □

4.2 Infinite Connection Degree

Here we prove that if a reversible p-state Mealy automaton, p prime, has infinite connection degree, then it generates a free semigroup, the states of the automaton being free generators. The idea is to bound the sizes of the Nerode classes in the powers of ${\mathcal {A}}$.

For the next three lemmas, let ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ be a reversible p-state Mealy automaton, p prime, with infinite connection degree ($A=\{x_{1},\dots , x_{p}\}$). By Lemma 2, ${\mathcal {A}}$ generates an infinite semigroup.

Lemma 5

There cannot exist two equivalent words of different length in A ^∗.

Proof

For each m, ${\mathcal {A}}^{m}$ is connected, and so any two words of length m are mapped one onto the other by an element of $\langle {{\mathfrak {d}}({{\mathcal A}})\rangle }_{+}$.

Let u and v be two equivalent words of different lengths, say |u|<|v|. Every word of length |v| is then equivalent to a word of length |u|: if w is of length |v|, then w=δ _t (v) for some t∈Σ^∗, and, by Remark 2, w is equivalent to δ _t (u) of length |u|. By Remark 1, the semigroup $\langle {{\mathcal {A}}\rangle }_{+}$ is finite, which is impossible. □

Lemma 6

All the Nerode classes of a given power A ^m have the same size, which happens to be a power of p.

Proof

Let u∈A ^m: $[{\mathbf {u}}]\subseteq A^{m}$ by definition. If [u]=A ^m, the result is clear. Otherwise, let v∈A ^m−[u]. Since ${\mathcal A}^{m}$ is connected, u is mapped onto v by an element of $\langle {{\mathfrak {d}}({{\mathcal A}})\rangle }_{+}$; that is there exists r∈Σ^∗ such that v=δ _r (u).

By Remark 2, any word equivalent to u is mapped by δ _r onto a word equivalent to v. Since the automaton ${\mathcal A}^{m}$ is reversible, δ _r is a permutation of A ^m, hence we find #[u]=#[v].

The stateset of ${\mathcal {A}}^{m}$ has size a power of p, where p is a prime number, and so has any Nerode equivalence class. □

Lemma 7

There cannot exist two equivalent words of the same length in A ^∗.

Proof

Let u and v be two different equivalent words of the same length n+1. Let us prove by induction on m>n that ${\mathfrak {m}}({\mathcal A}^{m})$ has at most p ⁿ states.

The automaton ${\mathcal {A}}^{n+1}$ has p ⁿ⁺¹ states. The words u and v are in the same Nerode class: by Lemma 6, all Nerode classes of A ⁿ⁺¹ have at least p elements and $\mathfrak m({\mathcal {A}}^{n+1})$ has at most p ⁿ states.

Suppose that ${\mathfrak {m}}({\mathcal {A}}^{m})$ has at most p ⁿ states. Then, since all Nerode classes have the same size by Lemma 6, the induction hypothesis implies that they have at least p ^m−n elements. Let us look at $[{x_{1}^{m}}]$: it contains

$$x_{1}^{m}, {\mathbf{u}}_{1}, {\mathbf{u}}_{2}, \dots, {\mathbf{u}}_{p^{m-n}-1}\:, $$

which are pairwise distinct. Among these words, there is at least one whose suffix in x ₁ is the shortest, say u ₁ without loss of generality: p ^m−n>1 and ${x_{1}^{m}}$ has the longest possible suffix in x ₁. Hence $[x_{1}^{m+1}]$ contains the following pairwise distinct p ^m−n+1 words

$$x_{1}^{m+1}, {\mathbf{u}}_{1}x_{1}, {\mathbf{u}}_{2}x_{1}, \dots, {\mathbf{u}}_{p^{m-n}-1}x_{1},x_{1}{\mathbf{u}}_{1}\:. $$

By Lemma 6, $\#[x_{1}^{m+1}]$ is a power of p, so $\#[x_{1}^{m+1}]\geq p^{m+1-n}$. As all Nerode classes of A ^m+1 have the same cardinality, we can conclude that ${\mathfrak {m}}({\mathcal {A}}^{m+1})$ has at most p ^m+1/p ^m+1−n=p ⁿ elements, ending the induction.

Consequently, since there is only a finite number of different Mealy automata with up to p ⁿ states, there exist k<ℓ such that ${\mathfrak {m}}({\mathcal {A}}^{k})$ and ${\mathfrak {m}}({\mathcal {A}}^{\ell })$ are equal up to state numbering. By Remark 1, the semigroup $\langle {{\mathcal {A}}\rangle }_{+}$ is finite, which is impossible. □

As a corollary of Proposition 1 and Lemmas 5, and 7 we can state the following proposition.

Proposition 2

Let ${\mathcal {A}}$ be a reversible p-state Mealy automaton, p prime. If the automaton ${\mathcal {A}}$ has infinite connection degree, then it generates a free semigroup of rank p with the states of ${\mathcal {A}}$ being free generators of the semigroup. The converse holds for p=2.

It is known that a group containing a free subsemigroup of rank at least 2 has exponential growth [11]. Thus it is useless to look for an intermediate growth group generated by a two-state invertible-reversible Mealy automaton.

Corollary 1

An infinite group generated by a two-state invertible-reversible Mealy automaton has exponential growth.

5 Decidability of Finiteness and of Freeness

This section is devoted to the decidability of finiteness and of freeness for semigroups generated by two-state invertible-reversible Mealy automata by linking Theorem 1 and the possible ${\mathfrak {m}}{\mathfrak {d}}$-triviality of such an automaton.

Lemma 8

Let ${\mathcal {A}}=(A,{\Sigma },\delta ,\rho )$ be a two-state invertible-reversible automaton of finite connection degree n. Two elements of Σ ^∗ which have the same action on a word of A ⁿ are equivalent.

Proof

It is sufficient to prove that $\text {id}_{A^{*}}$ is the only element of $\langle {{\mathfrak {d}}({{\mathcal {A}}})\rangle }_{+}$ which fixes a word of A ⁿ.

If n=0, $\langle {{\mathfrak {d}}({{\mathcal {A}}})\rangle }_{+}$ is the trivial semigroup and the result is true. Otherwise, let u∈A ⁿ and s∈Σ^∗ such that u is stable by δ _s : δ _s (u)=u.

By Lemma 3, ${\mathcal {A}}^{n+1}$ has two connected components: u x belongs to one of them and u y to the other one. Looking forward, a connected component ${\mathcal {C}}$ of ${\mathcal {A}}^{m}$, for m≥n, originates two connected components of ${\mathcal {A}}^{m+1}$: $\{{\mathbf {v}}z_{{\mathbf {v}}}\mid {\mathbf {v}}\in {\mathcal {C}}, z_{{\mathbf {v}}}\in A\}$ and $\{{\mathbf {v}}\overline {z_{{\mathbf {v}}}}\mid {\mathbf {v}}\in {\mathcal {C}}\}$. And all connected component of ${\mathcal {A}}^{m+1}$ are built this way. Hence if two different words of the same length m>n have the same prefix of length n, they belong to different connected components of ${\mathcal {A}}^{m}$.

Let t∈Σ^∗ satisfy ρ _u (s)=t, and let v,w∈A ^∗ such that t maps v onto w: δ _t (v)=w. The words u v and u w belong to the same connected component:

$$\delta_{{\mathbf{s}}}({\mathbf{uv}}) = \delta_{{\mathbf{s}}}({\mathbf{u}})\delta_{\rho_{{\mathbf{u}}}({\mathbf{s}})}({\mathbf{v}}) = {\mathbf{u}}\delta_{{\mathbf{t}}}({\mathbf{v}}) = {\mathbf{uw}}\:, $$

and have a common prefix of length n, so they are equal. Hence: $\delta _{{\mathbf {t}}}=\text {id}_{A^{*}}$. As ${\mathfrak {d}}({{\mathcal {A}}})$ is reversible, t is mapped onto s by an element of $\langle {{\mathcal {A}}\rangle }_{+}$ and $\delta _{{\mathbf {s}}}=\text {id}_{A^{*}}$. □

We have a similar (but weaker) result on shorter words for tensor closed Mealy automata. In the next three lemmas of this section, ${\mathcal {A}}=(A,{\Xi },\delta ,\rho )$ denotes a tensor closed two-state invertible-reversible automaton of finite connection degree n: A={x,y}. By Lemma 1, ${\mathcal {A}}^{n}$ is complete as a graph. Furthermore, a transition has a unique label: if a transition had several labels, they would coincide on a word of A ⁿ and by Lemma 8 they actually would be the same letter of Ξ.

Lemma 9

Let k be an integer, 1≤k≤n. Two elements of Ξ ^∗ which map a given word of A ^k into the same word have the same action on A ^k.

Proof

Each word of Ξ^∗ is equivalent to a letter of Ξ, hence it is sufficient to prove the result for letters.

The Mealy automaton ${\mathcal A}^{n}$ has 2ⁿ states, is complete as a graph and each transition has a unique label, so # Ξ=2ⁿ. By hypothesis, Ξ is the set of elements of $\langle {{\mathfrak {d}}({{\mathcal {A}}})\rangle }_{+}$, so $\#\langle {{\mathfrak {d}}({{\mathcal {A}}})\rangle }_{+}=2^{n}$.

Let us consider the minimization of ${\mathfrak {d}}({\mathcal {A}})$, using the sequence of increasingly finer equivalences (≡ _k ) introduced in Section 3.1. Each n-class of Ξ is a singleton by Lemma 8, hence the sequence (≡ _k ) remains constant at least from n on. So the Nerode equivalence produces 2ⁿ equivalence classes formed uniquely by singletons, by partitioning the stateset of ${\mathfrak {d}}({\mathcal {A}})$ of cardinality 2ⁿ in n steps, each step cutting each class of the previous one into at most two subsets as # A=2. Hence the equivalence ≡ _k cuts each (k−1)-class into two sets of the same cardinality: ∀k,0≤k≤n,∀s∈Ξ, #[s] _k =#[s] _k−1/2=2^n−k.

Let k, 1≤k≤n, u∈A ^k, and s∈Ξ. We have:

$$ [s]_{k}\subseteq \{t\in{\Xi}\mid t({\mathbf{u}})=s({\mathbf{u}})\}\:. $$

(1)

The left set in (1) has cardinality 2^n−k, it is the set of elements of Ξ which coincide with s on A ^k. Since two elements of Ξ whose actions coincide on a word of A ⁿ are equivalent, the right set of (1) has cardinality at most # A ^n−k=2^n−k, and so the two sets of (1) are equal, leading to the result. □

One consequence of Lemma 9 is that an element of Ξ^∗ which fixes a word of length k on A fixes completely A ^k.

Denote by id the identity of A and by σ the permutation of x and y. We can translate Lemma 9 in terms of portraits of ${\mathfrak {d}}({{\mathcal {A}}})$: whenever two k-portraits of ${\mathfrak {d}}({{\mathcal {A}}})$ have an identical branch, they are equal. In particular, ${\mathcal {I}}_{k}$ being a portrait of ${\mathfrak {d}}({{\mathcal {A}}})$, if a whole branch of a k-portrait of ${\mathfrak {d}({{\mathcal {A}}})}$ is labeled by id , this portrait is ${\mathcal {I}}_{k}$. Hence if in a k-portrait of ${\mathfrak {d}}({{\mathcal {A}}})$, all vertices at level less than k−1 are labeled by id , this portrait is either ${\mathcal {I}}_{k}$ or ${{{\mathcal {I}}_{k-1}}}\lfloor {\sigma ,\sigma }\rfloor$. Note that for k≤n, both ${\mathcal {I}}_{k}$ and ${{{\mathcal {I}}_{k-1}}}\lfloor {\sigma ,\sigma }\rfloor$ are portraits of ${\mathfrak {d}}({{\mathcal {A}}})$.

By Lemma 8, any element of $\langle {{\mathfrak {d}}({{\mathcal {A}}})\rangle }_{+}$ whose n-portrait is ${\mathcal {I}}_{n}$ acts trivially on A ^∗.

What are the possible portraits of ${\mathfrak {d}}({{\mathcal {A}}})$? Since ${\mathcal {A}}^{n}$ is connected and ${\mathcal {A}}$ is tensor closed, it is immediate that each finite sequence $(\pi _{i})_{1\leq i\leq n}\in \{\text {id}_{},\sigma \}^{n}$ labels a branch of an n-portrait of ${\mathfrak {d}}({{\mathcal {A}}})$: in ${\mathcal {A}}^{n}$, there is a transition with input s∈Ξ from x ⁿ to π ₁(x)⋯π _n (x) and the leftmost branch of ${\mathfrak {p}}_{n}[{\kern-2pt}[ {s}]{\kern-2pt}]$ is labeled by π.

Lemma 10

The portraits of ${\mathfrak d}({{\mathcal A}})$ are homogeneous.

Proof

Let us prove the result for k≤n, by induction on k≥1. A 1-portrait has a unique element, its root, and so is homogeneous.

Suppose that the ℓ-portraits of ${\mathfrak {d}}({{\mathcal {A}}})$ are all homogeneous, for ℓ≤k<n. Let us consider a letter s∈Ξ and ${\mathcal {S}}={\mathfrak {p}}_{k+1}[{\kern-2pt}[ {s}]{\kern-2pt}]$: it is almost homogeneous by the induction hypothesis. More precisely: ${\mathcal {S}} ={\mathfrak {p}}_{k}[{\kern-2pt}[ {s}]{\kern-2pt}] \lfloor {\tau _{1},\tau _{2}}\rfloor$ for τ ₁,τ ₂, some permutations of A.

First case: :

δ _s permutes x and y.

We consider the following (n+1)-portrait ${\mathcal {K}}$:

• the restriction of ${\mathcal {K}}$ to levels 0 to (n−k−1) is ${\mathcal {I}}_{n-k}$,

• in bottom-left of ${\mathcal {I}}_{n-k}$, we put ${\mathfrak {p}}_{k+1}[{\kern-2pt}[ {s}]{\kern-2pt}]$: the root of ${\mathfrak {p}}_{k+1}[{\kern-2pt}[ {s}]{\kern-2pt}]$ is the left child of the bottom-left leaf of ${\mathcal {I}}_{n-k}$ (it is possible since we can choose the left branch of a portrait, applying Lemma 9 and ${\mathfrak {p}}_{k+1}[{\kern-2pt}[ {s}]{\kern-2pt}]$ is actually a portrait of ${\mathfrak {d}}({{\mathcal {A}}})$),

• it is completed to be a portrait of ${\mathfrak {d}}({{\mathcal {A}}}$.

The leftmost branch of ${\mathcal {K}}^{2}$ starts with $\text {id}_{}^{n}$. Hence by Lemma 8, ${\mathcal {K}}^{2}$ is the identity (n+1)-portrait, which implies τ ₁=τ ₂ by Remark 3 and Lemma 8, that is ${\mathcal {S}}$ is homogeneous.

Second case: :

δ _s stabilizes A.

Let ${\mathcal {L}}$ be the (k+1)-portrait whose root permutation is σ and all other vertices are labeled by id: it is a portrait of ${\mathfrak {d}}({{\mathcal {A}}})$ since so are all homogeneous (k+1)-portraits with root permutation σ from first case. Then by multiplying ${\mathcal {S}}$ by ${\mathcal {L}}$, we obtain a non-homogeneous (k+1)-portrait with root permutation σ which has to be a portrait of ${\mathfrak d}({{\mathcal {A}}})$. That is impossible.

The proof is similar for k>n, considering the portrait ${\mathfrak {p}}_{k}[{\kern-2pt}[ {s}]{\kern-2pt}]$. □

Lemma 11

The states of ${\mathcal {A}}$ are equivalent.

Proof

By Lemma 10, all the portraits of ${\mathfrak {d}}({{\mathcal {A}}})$ are homogeneous. For any letter s∈Ξ, since its portrait is homogeneous, ρ _x (s) and ρ _y (s) are equivalent. The automaton being tensor closed, they are equal, and so ρ _x =ρ _y . □

Theorem 2

Let ${\mathcal {A}}$ be a two-state invertible-reversible Mealy automaton. It generates a finite group if and only if it is ${\mathfrak {m}}{\mathfrak {d}}$ -trivial.

Proof

By [2], if ${\mathcal {A}}$ is ${\mathfrak {m}}{\mathfrak {d}}$-trivial, it generates a finite group.

Suppose that ${\mathcal {A}}$ generates a finite group and consider its tensor closure ${\mathfrak {c}}({\mathcal {A}})$: ${\mathfrak {c}}({\mathcal {A}})$ generates a finite group by Remark 4. The connection degree of ${\mathfrak {c}}({\mathcal {A}})$ is finite by Proposition 1 and so ${\mathfrak {c}}({\mathcal {A}})$ is ${\mathfrak {m}}{\mathfrak {d}}$-trivial by Lemma 11. Hence ${\mathcal {A}}$ is ${\mathfrak {m}}{\mathfrak {d}}$-trivial by Remark 4. □

The last theorem summarizes all the decidability results arising from this article.

Theorem 3

It is decidable whether a two-state invertible-reversible Mealy automaton with alphabet Σ generates a finite group, in time ${\mathcal {O}}(\#{\Sigma }\log {\#{\Sigma }})$ . It is decidable whether it generates a free semigroup, in time ${\mathcal {O}}(\#{\Sigma }\log {\#{\Sigma }})$.

It is decidable whether a two-letter invertible-reversible Mealy automaton with stateset A generates a finite group, in time ${\mathcal {O}}(\#A\log {\#A})$.

Up to now, the only methods to conclude infiniteness of automaton groups were to prove the existence of an element of infinite order [5, SIZE_FR][22, FindElementOfInfiniteOrder], using Sidki’s fundamental work [8, 25], or to test level transitivity [5, IsLevelTransitive]. All these methods give sufficient but not necessary conditions.

To illustrate the actual efficiency of the ${\mathfrak {m}}{\mathfrak {d}}$-triviality as an algorithm to test finiteness, let us consider the 2-letter 6-state invertible-reversible Mealy automata. Bireversible Mealy automata are particular invertible-reversible Mealy automata and an invertible-reversible automaton generates a finite group only if it is bireversible [2]. Testing the ${\mathfrak {m}}{\mathfrak {d}}$-triviality of the 3446 bireversible 2-letter 6-states Mealy automata takes 751ms¹, while applying FindElementOfInfiniteOrder, SIZE_FR or IsLevelTransitive to determine the infinity of the group generated by the particular bireversible 2-letter 6-state Mealy automaton of Fig. 3(a) is unsuccessful after three weeks of computation.

6 (Im-)possible Extensions

All hypotheses are used to prove Theorems 1 and 2. This section is dedicated to see which hypothesis are mandatory for the results and how to possibly extend these results.

Theorem 1 (the semigroup is either finite or free)

It is quite clear that this theorem does not extend to more letters; for example the Baby Aleshin automaton (see Fig. 1(b)) is reversible, has three states, and generates an infinite non-free semigroup (its generators have order 2). Concerning the reversibility hypothesis, the automaton of Fig. 5 has two-state and is well-known to generate the semigroup ${\mathbb N}$, which is neither finite, nor free of rank 2.

Fig. 5

A Mealy automaton generating ${\mathbb N}$

An extension of Theorem 1 to bigger alphabets could be the following one:

Conjecture 1

An infinite semigroup generated by a reversible Mealy automaton admits a free non-abelian subsemigroup.

This conjecture is supported by the fact that all bireversible Mealy automata which appear in literature and generate infinite semigroups seem to have a non-abelian free subgroup. Of course, this subgroup is not necessary generated by the states of the automaton and finding its generators is surely the first difficulty to prove this conjecture.

Note that if this conjecture were true, it would follow that a group generated by an invertible-reversible Mealy automaton cannot answer to the Burnside problem and is of exponential growth, if infinite.

Theorem 2 (decidability of finiteness and freeness)

The article [2] gives two example of non-${\mathfrak {m}}{\mathfrak {d}}$-trivial automata which generate finite semigroups. One of these examples is a two-state non-reversible automaton, the other one an eight-state bireversible automaton and neither of them prove the necessity of the invertible hypothesis in Theorem 2. The automaton of Fig. 6 has two state, is reversible, non-invertible, and not ${\mathfrak {m}}{\mathfrak {d}}$-trivial. The semigroup generated by this automaton is not free: x ²=x y=y x=y ² maps any element of Σ^ω into a ^ω, and so this automaton generates a finite semigroup.

Fig. 6

A reversible non-invertible non-${\mathfrak {m}}{\mathfrak {d}}$-trivial automaton which generates a finite semigroup