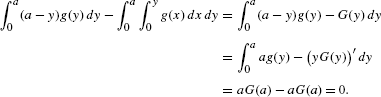Abstract
We consider mechanisms without payments for the problem of scheduling unrelated machines. Specifically, we consider truthful in expectation randomized mechanisms under the assumption that a machine (player) is bound by its reports: when a machine lies and reports value \(\tilde{t}_{ij}\) for a task instead of the actual one t ij , it will execute for time \(\tilde{t}_{ij}\) if it gets the task (unless the declared value \(\tilde{t}_{ij}\) is less than the actual value t ij , in which case, it will execute for time t ij ). Our main technical result is an optimal mechanism for one task and n players which has approximation ratio (n+1)/2. We also provide a matching lower bound, showing that no other truthful mechanism can achieve a better approximation ratio. This immediately gives an approximation ratio of (n+1)/2 and n(n+1)/2 for social cost and makespan minimization, respectively, for any number of tasks. We also study the price of anarchy of natural algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A major challenge today is to design algorithms that work well even when the input is reported by selfish agents or when the algorithm runs on a system with selfish components. The classical approach is to use mechanism design [18], that is, to design algorithms that use payments to convince the selfish agents to reveal the truth and then compute the outcome using the reported values. Central to the mechanism design approach is the use of dominant strategies as the equilibrium concept. Mechanism design is a very important framework with many unexpected results and it remains a very active research area trying to address some beautiful and challenging problems. Nevertheless, one major problem with mechanism design with payments is that in many situations, the use of payments may not be feasible.
Partly for this reason, there is a lot of recent interest in mechanisms that use no payments (mechanism design without payments) [18]. Given that in many problems we have obtained very poor results using mechanisms with payments, it will be really surprising if the substantially more restricted class of mechanisms without payments can achieve any positive results. For the general unrestricted domain with at least 3 outcomes and truthful mechanisms without payments, the Gibbard-Satterthwaite theorem [10, 24] states that only dictatorial mechanisms are truthful; dictatorial mechanisms are those in which a particular player determines the outcome. Contrast this to Roberts theorem [23], which states that if we allow payments, the truthful mechanisms are the affine maximizers, a much richer class than the dictatorial mechanisms (yet a very poor class in comparison to the set of all possible algorithms).
When we restrict the domain to scheduling unrelated machines, perhaps the most influential problem in algorithmic game theory, the results so far have also been disappointing. The best approximation ratio for the makespan that we know by truthful in expectation mechanisms is (n+1)/2 [7], where n is the number of players. The best known lower bound of 2 [7, 16] leaves the possibility open for improved mechanisms. The situation for deterministic mechanisms is similar: the upper bound is easily n [17], and the best known lower bound is 2.61 [13]. It may seem surprising that in this work we can achieve comparable results using mechanisms without payments if we assume that the players are bound by their declarations: Our main result, Theorem 2, is a truthful in expectation mechanism with approximation ratio n(n+1)/2. But a moments thought will reveal that we can get a slightly weaker bound (approximation ratio n for one task and hence approximation ratio n 2 for many tasks) with the natural mechanism which allocates each task independently and with probability inversely proportional to the execution times (Proposition 1). The assumption that the players are bound by their declarations plays a crucial role; without it, no positive result is possible. The main value of our main result is that it gives a definite answer (tight upper and lower bounds, albeit only for one task) for this fundamental problem.
Mechanism design without payments is a major topic in game theory [18], although it has not been studied as intensively as the variant with payments in algorithmic game theory. There are however many recent publications which study such mechanisms. Procaccia and Tennenholtz [22] proposed to study approximate mechanism design without payments for combinatorial problems and they studied facility location problems. This work was substantially extended (see for example [1, 14, 15]). Such mechanisms studied also by Dughmi and Ghosh [8] who consider mechanisms for assignment problems and by Guo and Conitzer [11] who consider selling items without payments to 2 buyers. Conceptually, closer to our approach of assuming that the players pay their declared values is the notion of impositions of Nissim, Smorodinsky, and Tennenholtz [19] which was further pursued by Fotakis and Tzamos [9].
2 Model
We study the problem of scheduling tasks when the machines are selfish. We formulate the problem in its more general form, the unrelated machines version: there are n selfish machines and m tasks; the machines are lazy and prefer not to execute any tasks. Machine i needs time t i,j to execute task j. The tasks are allocated to machines with the objective of minimizing the makespan (or the social welfare which is the negation of the sum of executing times of all machines). Let a be an (optimal) allocation for input t, where a i,j is an indicator variable about the event of allocating task j to machine i. The execution time of machine i is \(\sum_{j=1}^{m} a_{i,j}t_{i,j}\) and the makespan is \(\max_{i=1,\ldots,n} \sum_{j=1}^{m} a_{i,j}t_{i,j}\). For randomized algorithms, the allocation variables a i,j are not integral but real values in [0,1] which is the probability to allocate task j to machine i.Footnote 1
In this work, we consider direct revelation mechanisms; a mechanism is simply a randomized scheduling algorithm S which computes an allocation based on the declarations of the machines. There are no payments. More precisely, every machine i reports its private values \(\tilde{t}_{i,j}\), one for each task and we apply the algorithm S on this input. The notation \(\tilde{t}_{i,j}\) instead of t i,j is used because the machine may lie and not declare its true values t i,j . There is however a very important difference with the standard Nisan-Ronen framework [17] for this mechanism design problem. We assume that the machines are bound by their reports. More precisely, if a machine i declares a value \(\tilde{t}_{i,j}\geq t_{i,j}\) for task i and is allocated the task, its actual cost is the declared value \(\tilde{t}_{i,j}\) and not t i,j . One justification for this assumption is that in some environments the machines can be observed during the execution of the tasks and cannot afford to be caught lying about the execution times. Similar assumptions have been used for other problems. Our assumption is similar to the notion of imposition [9, 19]; for example, in the facility location problem, the players may be forced to use the facility which is closer to their declared position instead of letting them freely choose between the facilities. To complete our assumptions, we need to specify what happens when a machine declares a smaller value, i.e., \(\tilde{t}_{i,j} < t_{i,j}\). In this case, we make the simple assumption that the actual cost is the true value t i,j ; it would be simpler to assume that the machines are not allowed to lie in this direction, but we prefer the weakest assumption since it does not affect our results. To summarize, the cost of machine i for task j is \(\max(t_{i,j}, \tilde{t}_{i,j})\).
Our framework now is simple. We design a randomized scheduling algorithm S. The selfish machines report values \(\tilde{t}_{i,j}\) and we apply algorithm S to the reported values. This induces a game among the machines: the pure strategies of machine i are the vectors \((\tilde{t}_{i,j} )_{j=1}^{m}\) with \(\tilde{t}_{i,j}\geq 0\). The cost is the execution time computed by algorithm S on input \(\tilde{t}\). To be more precise, if \(a=S(\tilde{t})\) is the allocation computed by algorithm S on input \(\tilde{t}\), the cost of machine i is \(c_{i}=\sum_{j=1}^{m} a_{i,j}\max(t_{i,j},\tilde{t}_{i,j})\). We seek mechanisms which minimize the makespan max i=1,…,n c i or the social cost \(\sum_{i=1}^{n} c_{i}\).
Our assumption is related to mechanisms with verification [17], in which the mechanism learns the actual execution time of the machines and pays after the execution. Because of the delayed payments, these mechanisms are much more powerful than the mechanisms of our framework; for example, they can enforce that the machines are bound by their declarations by imposing a very high penalty for lying. A similar framework was proposed in [4], but in this case the power of the mechanism is limited: it can only deny payment at the end when a machine is caught lying by not being able to finish the tasks within the declared time. In this model, [20, 21] gave collusion-resistant mechanisms that are optimal. The power of this model is in some sense orthogonal to the power of the model of this work: on the one hand, the model of [4, 20, 21] is more powerful in that it can use payments as rewards for telling the truth, but on the other hand it is less powerful in that the players pay their actual cost, not their declared cost.
Mechanisms without money for the scheduling problem have been considered before: coordination mechanisms introduced in [5] are such mechanisms, but they differ substantially from the model of this work in that the players are the tasks, not the machines. This and subsequent work [2, 6] considered truthful mechanisms with the assumption, same with the assumption of this work, that the execution time of a task is the maximum of the declared and actual value, a condition which is more easily enforceable when the machines are controlled by the mechanism.
2.1 The Case of a Single Task
We focus on the simple case of one task and n machines. Let t 1,…,t n be the true values of the machines for the task and let \(\tilde{t}_{1},\ldots,\tilde{t}_{n}\) be the declared values; we drop the second subscript since there is only one task. Let \(p_{i}(\tilde{t})\) be the probability of allocating the task to player i. The expected cost of player i is \(c_{i}=c_{i}(t_{i},\tilde{t})=p_{i}(\tilde{t})\max(t_{i},\tilde{t}_{i})\), while the social cost of the algorithm is \(\sum_{i=1}^{n} c_{i}\) (in the case of the single task, the makespan and social cost are identical).
The mechanism is called truthful if for every t −i , the expected cost c i of player i is minimized when \(\tilde{t}_{i}=t_{i}\). This notion of truthfulness, truthful in expectation, is the weakest notion of truthfulness which contains a richer class of mechanisms than the standard notion of truthfulness or universal truthfulness. It is not ex post truthful, meaning that after the players see the outcome of the coins, they may want to change their declarations. In contrast, universal truthfulness is ex post truthfulness, and it is trivial to see that this stronger notion of truthfulness cannot achieve any positive result. Notice however, that for the fractional version of the scheduling problem, in which we can allocate parts of the same tasks to different machines, we can consider deterministic algorithms and consequently the strongest notion of truthfulness.
Lemma 1
An algorithm is truthful if and only if for every i and t −i , t i p i (t) is non-decreasing in t i and p i (t) is non-increasing in t i .
Proof
Indeed, if t i p i (t) is non-decreasing in t i , the player prefers t i to higher values, i.e., when \(\tilde{t}_{i}\geq t_{i}\), the cost \(c_{i}=p_{i}(\tilde{t}_{i}, t_{-i})\tilde{t}_{i}\) is minimized at \(\tilde{t}_{i}=t_{i}\). Similarly, if p i (t i ) is non-increasing, the player prefers t i to smaller values, i.e., when \(\tilde{t}_{i}\leq t_{i}\), the cost \(c_{i}=p_{i}(\tilde{t}_{i}, t_{-i})t_{i}\) is again minimized at \(\tilde{t}_{i}=t_{i}\).
Conversely, if there exist x<y with p i (t −i ,y)y<p i (t −i ,x)x, then player i gains by lying: when t i =x he prefers to declare y. Similarly, if there exist x>y with p i (t −i ,x)>p i (t −i ,y), the player would again prefer to declare y when t i =x. □
A mechanism is defined simply by the probability functions p i (t). The expected makespan is ∑ i c i and its approximating ratio is ∑ i c i /min i t i . We seek truthful mechanisms with small approximation ratio.
3 Truthful Mechanisms for One Task
In this section, we study the case of a single task. We first consider a natural mechanism, the proportional algorithm: It allocates the task to machine i with probability inversely proportional to the declared value t i , i.e., \(p_{i}(t)=t_{i}^{-1} / \sum_{k} t_{k}^{-1}\).
Proposition 1
The proportional algorithm is truthful and achieves approximation ratio n.
Proof
Indeed, to verify that the mechanism is truthful, it suffices to observe that p i (t) is non-increasing in t i and that t i p i (t) is non-decreasing it t i . The expected makespan of this mechanism is \(n/\sum_{i} t_{i}^{-1}\) while the optimal makespan is min i t i . It follows that the approximation ratio is at most n and that it can be arbitrarily close to n (when for example one value is 1 and the other n−1 values are arbitrarily high). □
It is natural to ask whether there are better mechanisms than the proportional mechanism. In the next subsection, we give a positive answer by designing an optimal mechanism, albeit with not substantially better approximation ratio.
3.1 An Optimal Truthful Mechanism
In this subsection, we study truthful algorithms that have optimal approximation ratio.
To find an optimal truthful mechanism, we want to find functions p i (t) such that for every t:
-
for every i: t i p i (t) is non-decreasing in t i ,
-
for every i: p i (t) is non-increasing in t i ,
-
∑ i p i (t)=1
and which minimize max t ∑ i t i p i (t)/min i t i . The first two conditions capture truthfulness and the third condition the natural property that the probabilities add to 1.
We will show the following theorem:
Theorem 1
There is a truthful in expectation mechanism without payments with approximation ratio (n+1)/2. Conversely, no truthful in expectation mechanism without payments can have approximation ratio better than (n+1)/2.
Before proceeding with the proof of the theorem, it is instructive to consider first the case of n=2 players. We will consider a symmetric mechanism, so it suffices to give the probabilities p i (t) of assigning the task to player i when t 1≤t 2. We claim that the mechanism with probabilities
is truthful and has approximation ratio 3/2. To clarify: these are the probabilities when t 1≤t 2; by symmetry, we can compute the probabilities when the declared value of the second player is smaller than the declared value of the first player.
Let us verify that this mechanism is truthful. Specifically we want to show that the expected cost of player i is minimized when he declares his true value; this must hold for every value t −i of the other player. Consider first player 1 (the one with true value less than the declared value of the other player).
-
He has no reason to declare something less than t 1, because p 1(t) is non-increasing in t 1, consequently \(t_{i} p_{i}(t)\leq t_{i} p_{i}(\tilde{t}_{i},t_{-i})\).
-
He has no reason to declare something in (t 1,t 2), because \(t_{1}p_{1}(t)=t_{1}-\frac{t_{1}^{2}}{2t_{2}}=\frac{t_{2}^{2}-(t_{2}-t_{1})^{2}}{2t_{2}}\) is increasing in t 1 for t 1<t 2.
-
Finally, he has no reason to declare something in [t 2,∞). In this case, his lie changes the order of the values, and, by the definition of the mechanism, the probability of getting the task will be \(p_{2}(t_{2},\tilde{t}_{1})\). Nevertheless, we still have
$$t_1p_1(t)=\frac{t_2^2-(t_2-t_1)^2}{2t_2}\leq \frac{t_2}{2}= \tilde{t}_1 \frac{t_2}{2\tilde{t}_1}=\tilde{t}_1p_2(t_2, \tilde{t}_1). $$
We work similarly for the second player (the one with true value greater than the declared value of the other player). If he declares his true value t 2, his expected cost is t 2 p 2(t)=t 1/2.
-
He has no reason to declare something less than t 1, because in this case the probability \(p_{1}(t_{1},\tilde{t}_{2})\) of getting the task is at least 1/2 and his cost will be at least t 2/2≥t 1/2.
-
He has no reason to declare any other value greater than t 1 because his cost is going to be \(\tilde{t}_{2} p_{2}(t_{1},\tilde{t}_{2})=t_{1}/2\), anyway.
The above mechanism has approximation ratio 3/2, because the cost is
Trivially, the approximation ratio tends to 3/2 as t 2 tends to ∞.
We proceed to generalize the above to more than two players. Again, we define a symmetric mechanism, so it suffices to describe it when t 1≤⋯≤t n :
For example, for n=2 we get the mechanism discussed above, and for n=3 the probabilities are
This definition is not arbitrary, but it is the natural solution to the requirements at the beginning of this subsection. This will become apparent as we proceed to show that this is an optimal algorithm for our problem.
First we verify that the mechanism is well-defined: We need to show that these probabilities are nonnegative and add up to 1. Indeed, consider the quantities q i inside the integrals

for which
Since the integral is for y≤t 1 and t 1 is the minimum among the t k ’s, all factors in these expressions are nonnegative. This shows that q i (y)≥0 for every i=1,…,n. We also observe that \(q_{1}'(y)=-\sum_{i=2}^{n} q_{k}'(y)\) which shows that \(\sum_{i=1}^{n} q_{i}(y)\) is constant; taking y=0, we see that this constant is 1. In summary the p i ’s are nonnegative and their sum is \(\frac{1}{t_{1}}\int_{0}^{t_{1}} \sum_{i=1}^{n} q_{i}(y) \, dy = \frac{1}{t_{1}}\int_{0}^{t_{1}} 1 \, dy =1\).
We also need to verify that (1) defines the probabilities consistently. More precisely, the definition of the probabilities is based on the order of the values; when these values are distinct, there is a unique order of the values t 1<t 2<⋯<t n , and there is no inconsistency. However, when some values are equal, there are many orders of the values and we need to guarantee that every such order gives the same probabilities. For all values except the minimum one, this follows directly from the symmetry of the algebraic expressions in (1). Thus we need only to verify consistency when the first two values are equal and specifically, we need to show that if t 1=t 2, then p 1=p 2. Indeed, it is straightforward to verify it by employing the following easy identity for every function g:Footnote 2
In this case, \(g(y)=\prod_{i=3}^{n} (1-\frac{y}{t_{i}} )\) and a=t 1.
We now proceed to establish that the mechanism is truthful.
Lemma 2
The symmetric mechanism defined by the probabilities in (1) is truthful.
Proof
To show that the algorithm is truthful, we observe that
-
The probabilities p i are non-increasing in t i . This is trivially true for i≠1 and it can be easily verified for i=1. The fact that the probabilities are non-increasing in t i shows that no player i has a reason to lie and declare a value \(\tilde{t}_{i} < t_{i}\). To see this, fix the values of the remaining players and assume that player i changes his value to \(\tilde{t}_{i}<t_{i}\). We will argue that the probability of getting the task with the new value is greater than or equal to the original probability; this suffices because the cost of the player is this probability times t i .
If, after the change, the order of the players remains the same, the probability does not decrease by this change because p i is non-increasing in t i . We need to show the same when the change affects the order of the players. This turns out to be easy but we note that we need to be careful, because the expressions that define the probabilities of the mechanism depend on the order of the values. However, we don’t need the expressions of the probabilities but a simpler argument: imagine that we lower the value from t i to \(\tilde{t}_{i}\) in stages: from t i to t i−1 to t i−2, and so on, to t i−k , and finally to \(\tilde{t}_{i}\). In each stage, the order of the values remains the same and therefore the probability can only increase. It follows that it does not decrease from the total change. The fact that the mechanism is symmetric is crucial in this argument because the algebraic expressions of the probability of the player may change from stage to stage, but the values at the boundaries t i−1,…,t i−k of successive stages are the same.
-
every player k for k≠1 is truthful since t k p k is independent of his value t k ; this holds even when the player reports a higher value which may change the order of the players
-
player 1 has no reason to lie and report a value in (t 1,t 2] because t 1 p 1 is increasing in t 1; furthermore, player 1 has no reason to report a higher value than t 2 which will change the order of the players because the cost will change from t 1 p 1 to \(t_{k}'p_{k}'=\frac{1}{t_{2}}\int_{0}^{t_{2}} \int_{0}^{y} \prod_{i=3}^{n} (1-\frac{x}{t_{i}} ) \, dx \, dy\) (because now the minimum value is t 2). It suffices therefore to show

The last holds because of Eq. (2).
Putting everything together, we see that the mechanism is indeed truthful. □
Lemma 3
The symmetric mechanism defined by the probabilities in (1) has approximation ratio (n+1)/2.
Proof
Now that we have established that the algorithm is truthful, we proceed to bound its approximation ratio. The approximation ratio is \(\sum_{i=1}^{n} t_{i}p_{i}/t_{1}\). Clearly, t 1 p 1≤t 1 and for k>1

Therefore, \(\sum_{i=1}^{n} t_{i}p_{i}\leq t_{1}+(n-1)t_{1}/2=t_{1}(n+1)/2\), which shows that the approximation ratio is at most (n+1)/2. It is trivial that if we fix the other values and let t 1 tend to 0, the above inequalities are almost tight, and therefore the approximation ratio can be arbitrarily close to (n+1)/2. □
We will show that no other truthful algorithm has a better approximation ratio. To do this, we first show that the optimal approximation ratio is achieved by a symmetric mechanism. By symmetric or anonymous, we mean a mechanism with the property that if we permute the indexes of the players, the allocation probabilities are permuted similarly. More formally, a mechanism is symmetric if for every t and every permutation π: p(π⋅t)=π⋅p(t), where π⋅t denotes \((t_{\pi_{1}},\ldots,t_{\pi_{n}})\). This in particular implies that if two players have equal values they have the same allocation probabilities, a property that we will use to establish the lower bound below.
Lemma 4
The optimal approximation ratio of the symmetric truthful mechanisms is the same with the approximation ratio of all truthful mechanisms.
Proof
Let p be the allocation probabilities of an arbitrary truthful mechanism. Consider the mechanism which selects a (uniformly) random permutation π of the values, computes the allocation probabilities using p, and then assigns the probabilities to the players by taking the inverse permutation π −1. More formally, the new mechanism has allocation probabilities p′(t)=E π [π −1⋅p(π⋅t)] and it is clearly symmetric.
We now establish that if p is truthful, then p′ is also truthful. The reason is simple: when we permute players and values by permutation π, player i plays the role of player π i ; since player π i is truthful in the original mechanism, player i has no reason to lie. More formally, \(p_{i}'(t)=E_{\pi}[p_{\pi_{i}^{-1}}(\pi\cdot t)]\). To establish the truthfulness of the new mechanism, we need to establish the monotonicity of \(p'_{i}(t)\) and \(t_{i} p'_{i}(t)\). Let t′=π⋅t. Since the original mechanism is truthful, \(p_{\pi_{i}^{-1}}(t')\) is monotone in \(t'_{\pi_{i}^{-1}}=t_{i}\) and therefore \(p_{i}'(t)\), being the expectation of monotone functions in t i , is also monotone. An almost identical argument establishes that \(t_{i} p'_{i}(t)\) is also monotone. In summary, p′ is a truthful mechanism.
We will now argue that the approximation ratio of the new symmetric mechanism is not higher than the approximation ratio of the original mechanism. Indeed, suppose that the original mechanism has approximation ratio ρ. This implies that for every t and every permutation π, the cost of the mechanism when the values are π⋅t is at most \(\rho \min_{i} t_{\pi_{i}} = \rho \min_{i} t_{i}\). It follows that if π is selected randomly, the expected cost of the original mechanism, which is equal to the cost of the new mechanism, is at most ρmin i t i ; this shows that the approximation ratio of the new mechanism is at most ρ. □
Lemma 5
No truthful in expectation mechanism without payments has approximation ratio smaller than (n+1)/2.
Proof
We will employ instances with values of the form (1,1,m,…,m) and (1,m,…,m) where m is some large value (which we will allow to tend to infinity to obtain the lower bound). By the previous lemma, we can assume without loss of generality that the mechanism is symmetric. Let p and p′ be the probabilities assigned by an algorithm to the above instances. For the instance (1,1,m,…,m), we have 2p 2+(n−2)p 3=1 and the approximation ratio is at least r≥2p 2+m(n−2)p 3=m−2p 2(m−1). Similarly for the other instance (1,m,…,m) we have \(p_{1}'+(n-1)p_{2}'=1\) and \(r\geq p_{1}'+(n-1)mp_{2}'=1+(m-1)(n-1)p_{2}'\).
The crucial step is to use the truthfulness of player 2 to connect the two instances. Specifically, the second player is truthful only when \(1\cdot p_{2}\leq m\cdot p_{2}'\). Substituting the value of \(p_{2}'\) in the bound of the second instance, we get that the approximation is at least 1+p 2(m−1)(n−1)/m.
In summary, the approximation ratio is at least max{m−2p 2(m−1),1+p 2(m−1)(n−1)/m}. The first expression is decreasing in p 2 while the second one is increasing in p 2; the minimum approximation ratio is achieved when the expressions are equal, that is, when p 2=m/(2m+n−1) which gives ratio at least (n+1)/2−(n 2−1)/(4m+2n−2). As m tends to infinity, the approximation ratio tends to (n+1)/2. □
4 Extension to Many Tasks and Discussion
In the previous section, we gave an optimal mechanism for one task. We can use it to get a mechanism for many tasks by running it independently for every task. Since the tasks are allocated independently, the resulting mechanism remains truthful. If the objective is the social cost (i.e., to minimize the sum of the cost of all players), the mechanism clearly retains its approximation ratio. If the objective however is the makespan, then the approximation ratio is at most n(n+1)/2, for the simple reason that max i c i ≤∑ i c i ≤nmax i c i . So we get
Theorem 2
There is a truthful in expectation mechanism without payments for the problem of scheduling unrelated machines with approximation ratio (n+1)/2 when the objective is the social cost and n(n+1)/2 when the objective is the makespan.
It follows from the case of one task that the approximation ratio (n+1)/2 is tight for the social cost. It is not clear that the pessimistic way we used to bound the approximation ratio of the makespan is tight. It remains open to estimate the approximation ratio of the given mechanism for many tasks. It is also open whether this is the best mechanism without payments for many tasks, that is, whether there are other (task-independent or not) mechanisms without payments for many tasks with better approximation ratio.
4.1 Mechanisms and the Price of Anarchy
So far, we have considered truthful mechanisms. It is however natural to ask whether there are non-truthful mechanisms with better performance. To formulate rigorously this question, we need first to agree on how to quantify the performance of non-truthful mechanisms, an issue that did not arise for truthful mechanisms because they have unique dominant equilibria. A natural way to evaluate non-truthful mechanism is to consider their price of anarchy (the performance of the worst Nash equilibrium) or their price of stability (the performance of the best Nash equilibrium) [3, 12].
To explain the issues of this approach, we analyze here the non-truthful natural greedy algorithm which gives the task to the machine with minimum reported time. Assume also that the ties are broken randomly (or in any deterministic way). We argue below that
Proposition 2
The price of stability of the greedy algorithm for one task is 1, while its price of anarchy is unbounded.
Proof
We will consider only the case of 2 players since it can be directly generalized to the case of more players. We assume that the actual values of the two players are t 1≤t 2.
For the price of stability, consider the Nash equilibrium in which the first player reports his true value t 1 while the second player declares any value x≥t 2 with cumulative distribution F 2(x)=1−t 2/x. The cost of the players is t 1 and 0 respectively, and the social cost is t 1, optimal. To see that this is indeed a Nash equilibrium, notice that the first player has no reason to switch: if he reports a value x in [t 2,∞) his expected cost would be xPr[t 2>x]=x(1−F 2(x))=t 2. Trivially the second player has no reason to switch since his cost is already 0.
For the price of anarchy, consider a similar Nash equilibrium in which the second player reports his true value t 2 and the first player reports a random value in [t 2,∞) with cumulative distribution F 1(x)=1−t 2/x. It is easy to check that this is indeed Nash equilibrium and that the social cost is t 2. The price of anarchy is t 2/t 1 which is unbounded. □
The optimal truthful mechanism of Sect. 3.1 for one task has price of anarchy (and stability) (n+1)/2. Because it is optimal, no other truthful mechanism has a better price of anarchy. Is there a non-truthful mechanism with better price of anarchy? If the answer is positive, it will perhaps be a challenging open problem to find an algorithm which achieves the minimum price of anarchy for the case of a single task, as well as the case of many tasks.
Notes
We may also interpret the probabilities as fractional allocations. Naturally, our results apply to the fractional allocations as well.
Proof: Let \(G(y)=\int_{0}^{y} g(x)\,dx\). Then
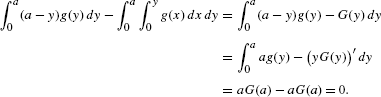
References
Alon, N., Feldman, M., Procaccia, A., Tennenholtz, M.: Strategy proof approximation of the minimax on networks. Math. Oper. Res. 35(3), 513–526 (2010)
Angel, E., Bampis, E., Pascual, F., Tchetgnia, A.: On truthfulness and approximation for scheduling selfish tasks. J. Sched. 12(5), 437–445 (2009)
Anshelevich, E., Dasgupta, A., Kleinberg, J., Tardos, E., Wexler, T., Roughgarden, T.: The price of stability for network design with fair cost allocation. In: Proceedings of 45th Annual IEEE Symposium on Foundations of Computer Science, pp. 295–304. IEEE Press, New York (2004)
Auletta, V., De Prisco, R., Penna, P., Persiano, G.: The power of verification for one-parameter agents. Autom. Lang. Program. 63–82 (2004)
Christodoulou, G., Koutsoupias, E., Nanavati, A.: Coordination mechanisms. Autom. Lang. Program. 45–56 (2004)
Christodoulou, G., Gourves, L., Pascual, F.: Scheduling selfish tasks: about the performance of truthful algorithms. In: Computing and Combinatorics, pp. 187–197 (2007)
Christodoulou, G., Koutsoupias, E., Kovács, A.: Mechanism design for fractional scheduling on unrelated machines. Autom. Lang. Program. 40–52 (2007)
Dughmi, S., Ghosh, A.: Truthful assignment without money. In: Proceedings of the 11th ACM Conference on Electronic Commerce, pp. 325–334. ACM, New York (2010)
Fotakis, D., Tzamos, C.: Winner-imposing strategy proof mechanisms for multiple facility location games. In: WINE, pp. 234–245 (2010)
Gibbard, A.: Manipulation of voting schemes: a general result. Econometrica 587–601 (1973)
Guo, M., Conitzer, V.: Strategy-proof allocation of multiple items between two agents without payments or priors. In: Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, vol. 1, pp. 881–888. International Foundation for Autonomous Agents and Multiagent Systems (2010)
Koutsoupias, E., Papadimitriou, C.H.: Worst-case equilibria. Comput. Sci. Rev. 3(2), 65–69 (2009). An earlier version appeared in STACS 1999
Koutsoupias, E., Vidali, A.: A lower bound of 1+φ for truthful scheduling mechanisms. Mat. Found. Comput. Sci. 454–464 (2007)
Lu, P., Wang, Y., Zhou, Y.: Tighter bounds for facility games. In: WINE, pp. 137–148 (2009)
Lu, P., Sun, X., Wang, Y., Zhu, Z.: Asymptotically optimal strategy-proof mechanisms for two-facility games. In: Proceedings of the 11th ACM Conference on Electronic Commerce, pp. 315–324. ACM, New York (2010)
Mu’alem, A., Schapira, M.: Setting lower bounds on truthfulness: extended abstract. In: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1143–1152. Society for Industrial and Applied Mathematics, Philadelphia (2007)
Nisan, N., Ronen, A.: Algorithmic mechanism design (extended abstract). In: Proceedings of the Thirty-First Annual ACM Symposium on Theory of Computing, pp. 129–140. ACM, New York (1999)
Nisan, N., Roughgarden, T., Tardos, E., Vazirani, V.: Algorithmic Game Theory. Cambridge Univ. Press, Cambridge (2007)
Nissim, K., Smorodinsky, R., Tennenholtz, M.: Approximately optimal mechanism design via differential privacy (2010). arXiv:1004.2888
Penna, P., Ventre, C.: Collusion-resistant mechanisms with verification yielding optimal solutions. In: Algorithms-ESA 2008, pp. 708–719 (2008)
Penna, P., Ventre, C.: Optimal collusion-resistant mechanisms with verification. Games Econ. Behav. (2012)
Procaccia, A., Tennenholtz, M.: Approximate mechanism design without money. In: Proceedings of the Tenth ACM Conference on Electronic Commerce, pp. 177–186. ACM, New York (2009)
Roberts, K.: The characterization of implementable choice rules. In: Aggregation and Revelation of Preferences, pp. 321–348 (1979)
Satterthwaite, M.: Strategy-proofness and Arrow’s conditions: existence and correspondence theorems for voting procedures and social welfare functions. J. Econ. Theory 10(2), 187–217 (1975)
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by the European Union Seventh Framework Programme FP7, grant 284731 (UaESMC), and by the ESF-NSRF research program Thales (AGT).
Rights and permissions
About this article
Cite this article
Koutsoupias, E. Scheduling Without Payments. Theory Comput Syst 54, 375–387 (2014). https://doi.org/10.1007/s00224-013-9473-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-013-9473-0