Abstract
We strengthen a previously known connection between the size complexity of two-way finite automata ( ) and the space complexity of Turing machines (tms). Specifically, we prove that
) and the space complexity of Turing machines (tms). Specifically, we prove that
-
every s-state
 has a poly(s)-state
has a poly(s)-state  that agrees with it on all inputs of length ≤s if and only if NL⊆L/poly, and
that agrees with it on all inputs of length ≤s if and only if NL⊆L/poly, and -
every s-state
 has a poly(s)-state
has a poly(s)-state  that agrees with it on all inputs of length ≤2s if and only if NLL⊆LL/polylog.
that agrees with it on all inputs of length ≤2s if and only if NLL⊆LL/polylog.
Here,  and
and  are the deterministic and nondeterministic
are the deterministic and nondeterministic  , NL and L/poly are the standard classes of languages recognizable in logarithmic space by nondeterministic tms and by deterministic tms with access to polynomially long advice, and NLL and LL/polylog are the corresponding complexity classes for space O(loglogn) and advice length poly(logn). Our arguments strengthen and extend an old theorem by Berman and Lingas and can be used to obtain variants of the above statements for other modes of computation or other combinations of bounds for the input length, the space usage, and the length of advice.
, NL and L/poly are the standard classes of languages recognizable in logarithmic space by nondeterministic tms and by deterministic tms with access to polynomially long advice, and NLL and LL/polylog are the corresponding complexity classes for space O(loglogn) and advice length poly(logn). Our arguments strengthen and extend an old theorem by Berman and Lingas and can be used to obtain variants of the above statements for other modes of computation or other combinations of bounds for the input length, the space usage, and the length of advice.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The question whether nondeterministic computations can be more powerful than deterministic ones is central in complexity theory. Numerous instantiations have been studied, for a variety of computational models under a variety of resource restrictions. This article investigates the relationship between two families of such instantiations, those for two-way finite automata under size restrictions and those for Turing machines under space restrictions. We start by introducing each of these two families separately, then continue to describe the relationship between them.
1.1 Size-Bounded Two-Way Finite Automata
The question whether nondeterminism makes a difference in two-way finite automata ( ) of bounded size was first studied by Seiferas in the early 70s [15]. Formally, this is the question whether every nondeterministic
) of bounded size was first studied by Seiferas in the early 70s [15]. Formally, this is the question whether every nondeterministic  (
( ) has an equivalent deterministic
) has an equivalent deterministic  (
( ) with only polynomially more states:
) with only polynomially more states:

The answer has long been conjectured to be negative [13, 15]. Indeed, this has been confirmed in several special cases: when the automata are single-pass (i.e., they halt upon reaching an end-marker [15]), or almost oblivious (i.e., they exhibit o(n) distinct input head trajectories over all n-long inputs [7]), or moles (i.e., they explore the configuration graph implied by the input [9]), or they perform few reversals (i.e., they reverse their input head only o(n) times on every n-long input [10]). For unary automata, however, a non-trivial upper bound is known: an equivalent  with only quasi-polynomially more states always exists [5].
with only quasi-polynomially more states always exists [5].
A robust theoretical framework was built around this question by Sakoda and Sipser in the late 70s [13]. Central in this framework are the complexity classes 2D and 2N. The former consists of every family of languages (L
h
)
h≥1 that can be recognized by a polynomial-size family (A
h
)
h≥1 of  , in the sense that every A
h
recognizes the corresponding L
h
and has ≤ p(h) states, for some polynomial p. The latter is the analogous class for
, in the sense that every A
h
recognizes the corresponding L
h
and has ≤ p(h) states, for some polynomial p. The latter is the analogous class for  . In these terms, the question becomes equivalent to the question:
. In these terms, the question becomes equivalent to the question:

and the long-standing conjecture becomes equivalent to 2D⊉2N.Footnote 1
In this article, we consider ‘bounded’ variants of (1). We replace the requirement that the  and
and  agree on all possible inputs with the requirement that they agree only on all ‘short’ inputs, for different interpretations of ‘short’. Could it be that under this relaxed requirement the
agree on all possible inputs with the requirement that they agree only on all ‘short’ inputs, for different interpretations of ‘short’. Could it be that under this relaxed requirement the  can now stay only polynomially larger?
can now stay only polynomially larger?
For the most part, we will focus only on two interpretations of ‘short’. Under the first one, an input is ‘short’ if its length is at most exponential in the size of the  :
:

Under the second interpretation, an input is ‘short’ if its length is at most linear in the size of the  :
:

We conjecture that neither relaxation makes the simulation easy. Namely, much like the answer to (1), we conjecture that the answers to (2) and (3) are still negative.
The new questions can be expressed in the Sakoda-Sipser framework, as well. To this end, we first extend the definitions of 2D and 2N so that they now consist of all families of promise problems (as opposed to just all families of languages) that admit polynomial-size families of  and
and  , respectively. Then, we introduce two new complexity classes, subclasses of the extended 2N, called 2N/exp and 2N/poly. The former consists of only those promise-problem families \((\mathfrak {L}_{h})_{h\geq1}\) in 2N where all instances of \(\mathfrak {L}_{h}\) are of length ≤ 2q(h), for some polynomial q and all h. Then (2) can be proved equivalent to:
, respectively. Then, we introduce two new complexity classes, subclasses of the extended 2N, called 2N/exp and 2N/poly. The former consists of only those promise-problem families \((\mathfrak {L}_{h})_{h\geq1}\) in 2N where all instances of \(\mathfrak {L}_{h}\) are of length ≤ 2q(h), for some polynomial q and all h. Then (2) can be proved equivalent to:

Similarly, 2N/poly consists of only those promise-problem families in 2N where every \(\mathfrak {L}_{h}\) has instances of length ≤ q(h). Then (3) can be proved equivalent to:

This way, our stronger conjectures are that even 2D⊉2N/exp and 2D⊉2N/poly.
We remark that other interpretations of ‘short’ are also possible, but not as crucial. In Sect. 2.1 (Lemma 2.1) we will see that restricting (1) to super-exponential lengths produces a question which is actually still equivalent to (1). Variants for quasi-polynomial lengths will be considered in Sect. 3 (Theorem 3.2).
1.2 Space-Bounded Turing Machines
The question whether nondeterminism makes a difference in Turing machines ( tms) of bounded space dates back to the work of Kuroda in the mid 60s [12]. Formally, this is the question whether every nondeterministic tm ( ntm) has an equivalent deterministic tm ( dtm) that uses the same space:
The answer has long been conjectured to be negative. We know, however, that we may restrict our attention to bounds outside o(loglogn), because for f(n)=o(loglogn) the inclusion follows trivially from the fact that both complexity classes contain only regular languages [1, 6, 17]. We also know that, if the inclusion is satisfied by any bound in Θ(loglogn)∪Ω(logn), then all greater bounds satisfy it, too [14, 18].
For the most part, we will focus on the two smallest natural bounds, loglogn and logn. The former gives rise to the complexity classes LL:=DSPACE(loglogn) and NLL:=NSPACE(loglogn), and to the respective question:
Similarly, the latter bound gives rise to the standard space complexity classes L=DSPACE(logn) and NL=NSPACE(logn), and to the question:
Once again, the answers to both questions are conjectured to be negative; i.e., most people believe that both LL⊉NLL and L⊉NL.
An early observation on (6) was that, even if L⊉NL, a deterministic logarithmic-space tm might still manage to simulate a nondeterministic one if it is allowed non-uniform behavior [2]. This led to the introduction of the class L/poly of all languages that can be recognized in space O(logn) by a dtm which has access to poly(n)≡n O(1) bits of non-uniform advice [11]. The new question was:

and the stronger conjecture was that even L/poly⊉NL. By a similar reasoning, we can introduce a corresponding class LL/polylog for space O(loglogn) and for poly(logn) bits of advice, then ask the question:

and conjecture that even LL/polylog⊉NLL.
We remark that other combinations of bounds for the space and the length of advice are also possible, but not as crucial. For example, if both the space and advice length are O(logn), then the resulting question whether L/log⊇NL is equivalent to (6) [11]. Combinations of sub-logarithmic space and sub-linear advice length will be considered in Sect. 3. Finally, we note that the classes DSPACE(f)/2O(f) for varying f have been studied in [8] under the names NUDSPACE(f).
1.3 Size-bounded  Versus Space-Bounded tms
Versus Space-Bounded tms
It has long been known, by a theorem of Berman and Lingas [3], that a simulation of nondeterministic logarithmic-space tms by deterministic ones would imply the simulation of nondeterministic polynomial-size  by deterministic ones on polynomially-long inputs, in our notation:
by deterministic ones on polynomially-long inputs, in our notation:
Our contribution is the tightening and deepening of this relationship.
We first show that 2D⊇2N/poly follows even from the weaker assumption that L/poly⊇NL, and that then the converse is also true:
Theorem 1.1
2D⊇2N/poly⇔L/poly⊇NL.
Next, we prove a similar relationship for the case where the bound for the input lengths increases to exponential while the bounds for the space and the advice length decrease to log-logarithmic and poly-logarithmic, respectively.
Theorem 1.3
2D⊇2N/exp⇔LL/polylog⊇NLL.
Finally, in between Theorems 1.1 and 1.3, we also relate the different levels of quasi-polynomial input lengths with different levels of sub-logarithmic space and sub-linear lengths of advice:
Theorem 1.2
For all k≥1 we have:
(See Sect. 2 for the precise definitions of the notations used in this statement.)
For the most part, the proofs of these theorems elaborate on standard, old ideas [3, 13, 18]. Perhaps their main value lies in what they imply for how we approach the questions on the two sides of the equivalences, as the next two paragraphs explain.
On the one hand, people interested in size-bounded  can use these theorems to extract evidence about how hard it is for various proof strategies towards 2D⊉2N to succeed. For example, suppose that we are exploring two strategies, the first of which promises to eventually establish that every deterministic simulation of
can use these theorems to extract evidence about how hard it is for various proof strategies towards 2D⊉2N to succeed. For example, suppose that we are exploring two strategies, the first of which promises to eventually establish that every deterministic simulation of  fails on at most exponentially long inputs, while the second strategy promises to prove failure only on super-exponentially long inputs. Then the first strategy is probably harder to succeed, because it implies an additional breakthrough in understanding nondeterminism in space-bounded tms (by Theorem 1.3), while the second strategy involves no such implications. (Incidentally, all proof techniques that have been successful on restricted
fails on at most exponentially long inputs, while the second strategy promises to prove failure only on super-exponentially long inputs. Then the first strategy is probably harder to succeed, because it implies an additional breakthrough in understanding nondeterminism in space-bounded tms (by Theorem 1.3), while the second strategy involves no such implications. (Incidentally, all proof techniques that have been successful on restricted  are of the latter kind.)
are of the latter kind.)
On the other hand, people interested in space-bounded tms can find in the 2D versus 2N question a single unifying setting in which to work. Separating polynomial-size  from polynomial-size
from polynomial-size  on super-exponentially long inputs can be seen as the first step in a gradual approach that sees ntms being separated from dtms for larger and larger space bounds as improved proof techniques separate polynomial-size
on super-exponentially long inputs can be seen as the first step in a gradual approach that sees ntms being separated from dtms for larger and larger space bounds as improved proof techniques separate polynomial-size  from polynomial-size
from polynomial-size  on shorter and shorter inputs.
on shorter and shorter inputs.
Another aspect of the proofs of Theorems 1.1, 1.2, and 1.3 is that they can be modified so as to work also for other modes of computation. For example, consider alternating
 and tms, and let 2A/poly and AL denote the alternating analogues of the complexity classes 2N/poly and NL, respectively. As with nondeterminism, the inclusions 2D⊇2A/poly and L⊇AL are open and conjectured to be false. Recalling that alternating logarithmic space equals deterministic polynomial time, namely
and tms, and let 2A/poly and AL denote the alternating analogues of the complexity classes 2N/poly and NL, respectively. As with nondeterminism, the inclusions 2D⊇2A/poly and L⊇AL are open and conjectured to be false. Recalling that alternating logarithmic space equals deterministic polynomial time, namely
we can state the following analogue of Theorem 1.1:
Theorem 1.4
2D⊇2A/poly⇔L/poly⊇P.
We claim that its proof is a straightforward modification of that of Theorem 1.1.
Concluding this introduction, we mention a different strengthening of the theorem of Berman and Lingas, by Geffert and Pighizzini [4]: if 2N/unary is the restriction of 2N to families of unary languages, then
where the inclusion on the left is independent of the lengths of the unary inputs. Our article has been largely motivated by this recent theorem—and our title reflects this.
2 Preparation
For n≥1, we let [n]:={0,…,n−1}. If S is a set, then \(\overline {S}\) and |S| are its complement and size. By ‘log(⋅)’ we always mean ‘log2(⋅)’, whereas lg(⋅):=max(1,⌈log2(⋅)⌉).
If Σ is an alphabet, then Σ ∗ is the set of all strings over Σ and ε is the empty string. If x is a string, then |x| is its length, x i is its ith symbol (for 1≤i≤|x|), x i is the concatenation of i copies of x (for i≥0), and 〈x〉 is the natural binary encoding of x into |x| blocks of lg|Σ| bits each (under a fixed ordering of Σ).
A (promise) problem over Σ is a pair \(\mathfrak {L}=(L,\tilde {L})\) of disjoint subsets of Σ ∗. An instance of \(\mathfrak {L}\) is any \(x\in L\cup \tilde {L}\), and is either positive, if x∈L, or negative, if \(x\in \tilde {L}\). A machine solves \(\mathfrak {L}\) if it accepts every positive instance but no negative one. If \(\tilde {L}=\overline {L}\) then every x∈Σ ∗ is an instance, and \(\mathfrak {L}\) is a language.
For  a family of problems and
a family of problems and  a class of functions on the natural numbers, we say that the problems of
a class of functions on the natural numbers, we say that the problems of  are
are  -long if there exists
-long if there exists  such that |x|≤g(h), for all \(x\in L_{h}\cup \tilde {L}_{h}\) and all h. In particular, if
such that |x|≤g(h), for all \(x\in L_{h}\cup \tilde {L}_{h}\) and all h. In particular, if  is the class poly(h) of all polynomial functions or the class 2poly(h) of all exponential functions, then the problems of
is the class poly(h) of all polynomial functions or the class 2poly(h) of all exponential functions, then the problems of  are respectively polynomially long or exponentially long. Note that, since every language has arbitrarily long instances, no member \(\mathfrak {L}_{h}\) of a
are respectively polynomially long or exponentially long. Note that, since every language has arbitrarily long instances, no member \(\mathfrak {L}_{h}\) of a  -long
-long  can be a language (irrespective of what
can be a language (irrespective of what  really is).
really is).
2.1 Two-Way Finite Automata
A two-way finite automaton ( ,
,  ,
,  ) consists of a finite control and an end-marked, read-only input tape, accessed via a two-way head (Fig. 1a). More carefully, a (s,σ)-
) consists of a finite control and an end-marked, read-only input tape, accessed via a two-way head (Fig. 1a). More carefully, a (s,σ)- is a tuple A=(S,Σ,δ,q
0,F) of a set of states S with |S|=s, an input alphabet Σ with |Σ|=σ, a designated start state q
0∈S, a set of designated final states F⊆S, and a set of transitions
is a tuple A=(S,Σ,δ,q
0,F) of a set of states S with |S|=s, an input alphabet Σ with |Σ|=σ, a designated start state q
0∈S, a set of designated final states F⊆S, and a set of transitions
where ⊢,⊣∉Σ are the two end-markers of the input tape, and l and r are the left and the right directions. An input x∈Σ
∗ is presented on the input tape surrounded by the end-markers, as ⊢x⊣, and is considered accepted if δ allows a computation that starts at q
0 on ⊢ and eventually falls off ⊣ into a state q∈F.Footnote 2 If δ allows at most one computation per input, then A is a  .
.
The behavior of A on a string x over Σ∪{⊢,⊣} is the set of tuples (p,d,p′,d′) of states p,p′ and sides d,d′∈{l,r} such that A can exhibit a computation that starts at p on the d-most symbol of x and eventually falls off the d′-most symbol of x into p′. Easily, the total number of all possible behaviors of A on all possible strings is at most \(2^{(2s)^{2}}\). If A is a  , then this number is at most (2s+1)2s=22slog(2s+1).
, then this number is at most (2s+1)2s=22slog(2s+1).
The language of A is the set L(A):={x∈Σ ∗∣A accepts x}.
The binary encoding of A is the binary string 〈A〉:=0 s 10 σ 1 uvw where u encodes δ with 2s 2(σ+2) bits (in the natural way, with 1 bit per possible transition, under some fixed ordering of the set of all possible transitions), whereas v encodes q 0 with lgs bits and w encodes F with s bits (again in natural ways, under some fixed ordering of S). Easily, |〈A〉|=O(s 2 σ).
For  a family of
a family of  and
and  a class of functions on the natural numbers, we say that the automata of
a class of functions on the natural numbers, we say that the automata of  are
are  -large if there exists
-large if there exists  such that every A
h
has ≤ f(h) states. In particular, if
such that every A
h
has ≤ f(h) states. In particular, if  is the class poly(h) of all polynomial functions, then the automata of
is the class poly(h) of all polynomial functions, then the automata of  are small. We say that
are small. We say that  solves a family of problems
solves a family of problems  if every A
h
solves the corresponding \(\mathfrak {L}_{h}\). The class of families of problems that admit
if every A
h
solves the corresponding \(\mathfrak {L}_{h}\). The class of families of problems that admit  -large
-large  is denoted by
is denoted by

Its subclass consisting only of families of  -long problems, for
-long problems, for  a class of functions, is denoted by
a class of functions, is denoted by  . (Note that no family in this subclass is a family of languages.) When we omit ‘
. (Note that no family in this subclass is a family of languages.) When we omit ‘ ’, we mean
’, we mean  . In particular,
. In particular,

We specifically let 2N/poly:=2N/poly(h) and 2N/exp:=2N/2poly(h). We also let  ,
,  , 2D, and
, 2D, and  be the respective classes for
be the respective classes for  .
.
As explained in Sect. 1.1, we are interested in the question whether 2D⊇2N and in its bounded variants for exponential or polynomial input lengths, namely the questions whether 2D⊇2N/exp or 2D⊇2N/poly. The next lemma explains why we are ignoring super-exponential bounds for the input lengths. The doubly-exponential function used in its statement is just a representative example; it can be replaced by any function that grows faster than every function in 2poly(h).
Lemma 2.1
\({ \textsf {2}\textsf {D}}\supseteq { \textsf {2}\textsf {N}}\iff { \textsf {2}\textsf {D}}\supseteq \mathsf{2N}/{\{2^{2^{h}}\}}\).
Proof
For the interesting direction, suppose \({ \textsf {2}\textsf {D}}\supseteq \mathsf{2N}/{\{2^{2^{h}}\} }\). Pick an arbitrary family of promise problems  . We will prove that
. We will prove that  , as well.
, as well.
Since  , we know some family of small
, we know some family of small 
 solves
solves  . For each h, consider the promise problem of checking that a string of at most doubly-exponential length is accepted by A
h
:
. For each h, consider the promise problem of checking that a string of at most doubly-exponential length is accepted by A
h
:
Then the family  is in \(\mathsf{2N}/{\{ 2^{2^{h}}\}}\), because its problems are doubly-exponentially long and are (obviously) solved by the small
is in \(\mathsf{2N}/{\{ 2^{2^{h}}\}}\), because its problems are doubly-exponentially long and are (obviously) solved by the small  of
of  . Therefore,
. Therefore,  (by our starting assumption). So, some family of small
(by our starting assumption). So, some family of small 
 solves
solves  . We will prove that (a modification of) this
. We will prove that (a modification of) this  solves
solves  , as well.
, as well.
Intuitively, the  of
of  correctly simulate the
correctly simulate the  of
of  on all inputs of at most doubly-exponential length. We will argue that, because the
on all inputs of at most doubly-exponential length. We will argue that, because the  of both families are small, it is impossible for this simulation to stay correct on inputs of such great length without actually being correct on all possible inputs. So, (a modification of)
of both families are small, it is impossible for this simulation to stay correct on inputs of such great length without actually being correct on all possible inputs. So, (a modification of)  cannot but simulate
cannot but simulate  correctly on all inputs, and thus solve
correctly on all inputs, and thus solve  , causing
, causing  .
.
For the argument, let us call an index h ‘failing’ if B h does not solve \(\mathfrak {L}_{h}\).
Claim
The number of failing h is finite.
Proof
Call an index h ‘conflicting’ if L(A h )≠L(B h ), namely some inputs are accepted by exactly one of A h and B h . Then every failing h is conflicting. Indeed, if h is failing, then B h does not solve \(\mathfrak {L}_{h}\); so B h errs on some instances x, namely
since A h solves \(\mathfrak {L}_{h}\), every such instance also satisfies
and is thus in the symmetric difference of L(A h ) and L(B h ), making h conflicting.
So, it suffices to prove finite the number of conflicting h. For this, let a and b be the degrees of the polynomials that bound the sizes of the automata in  and
and  , so that every A
h
has O(h
a) states and every B
h
has O(h
b) states. Then, every A
h
and B
h
exhibit respectively \(2^{O(h^{2a})}\) and \(2^{O(h^{b}\log h)}\) behaviors. So, the total number l
h
of pairs of behaviors of A
h
and B
h
is \(2^{O(h^{2a}+h^{b}\log h)}=2^{O(h^{c})}\), where c=max(2a,b+1).
, so that every A
h
has O(h
a) states and every B
h
has O(h
b) states. Then, every A
h
and B
h
exhibit respectively \(2^{O(h^{2a})}\) and \(2^{O(h^{b}\log h)}\) behaviors. So, the total number l
h
of pairs of behaviors of A
h
and B
h
is \(2^{O(h^{2a}+h^{b}\log h)}=2^{O(h^{c})}\), where c=max(2a,b+1).
Now pick any conflicting h, and let x h be a shortest string in the symmetric difference of L(A h ) and L(B h ). Since B h solves \(\mathfrak {L}_{h}'\), it is clear that the length of x h must exceed \(2^{2^{h}}\). Less obvious, but also true, is that it cannot exceed l h . Indeed, if |x h |>l h , then x h contains two prefixes on which A h behaves identically and B h behaves identically, too. Removing the infix of x h between the right boundaries of these two prefixes, we get a strictly shorter input y h that neither A h nor B h can distinguish from x h . Thus, A h and B h disagree on y h iff they disagree on x h . Given that they disagree on x h , they must also disagree on y h , contradicting the selection of x h as shortest.
Hence, for every conflicting h, our shortest witness of the disagreement satisfies
Since \(2^{O(h^{c})}=o(2^{2^{h}})\), only a finite number of h can satisfy these inequalities. □
Now consider the family  that differs from
that differs from  only at the failing h, where \(B_{h}'\) is any
only at the failing h, where \(B_{h}'\) is any  that solves \(\mathfrak {L}_{h}\) (e.g., the standard determinization of A
h
[16]). Obviously,
that solves \(\mathfrak {L}_{h}\) (e.g., the standard determinization of A
h
[16]). Obviously,  solves
solves  . Moreover, if p is a polynomial that bounds the size of the automata of
. Moreover, if p is a polynomial that bounds the size of the automata of  and if S is the maximum number of states of a \(B_{h}'\) that corresponds to a failing h, then every \(B_{h}'\) has ≤p(h) states, if it is identical to B
h
, or ≤S states, if h is failing. Hence, the polynomial p′(h)=p(h)+S bounds the size of the automata in
and if S is the maximum number of states of a \(B_{h}'\) that corresponds to a failing h, then every \(B_{h}'\) has ≤p(h) states, if it is identical to B
h
, or ≤S states, if h is failing. Hence, the polynomial p′(h)=p(h)+S bounds the size of the automata in  . Overall,
. Overall,  is a family of small
is a family of small  solving
solving  . Therefore
. Therefore  . □
. □
2.2 Turing Machines
A Turing machine ( tm, ntm, dtm) is a  with two extra tapes: a bi-infinite, read-write work tape and an end-marked, read-only advice tape, each of which is accessed via a dedicated two-way head (Fig. 1b). More carefully, a (s,σ,γ)- ntm is a tuple M=(S,Σ,Γ,Δ,δ,q
0,q
f
) of a set of states S with |S|=s, an input alphabet Σ with |Σ|=σ, a work alphabet Γ with |Γ|=γ, an advice alphabet Δ, two designated start and final states q
0,q
f
∈S, and a set of transitions
with two extra tapes: a bi-infinite, read-write work tape and an end-marked, read-only advice tape, each of which is accessed via a dedicated two-way head (Fig. 1b). More carefully, a (s,σ,γ)- ntm is a tuple M=(S,Σ,Γ,Δ,δ,q
0,q
f
) of a set of states S with |S|=s, an input alphabet Σ with |Σ|=σ, a work alphabet Γ with |Γ|=γ, an advice alphabet Δ, two designated start and final states q
0,q
f
∈S, and a set of transitions
where \({\vdash }{,}{\dashv }\not\in \varSigma \cup \varDelta \) are the two end-markers, ⊔∉Γ is the blank symbol, and l,r are the two directions. An input x∈Σ ∗ and an advice string y∈Δ ∗ are presented on the input and advice tapes surrounded by end-markers, as ⊢x⊣ and ⊢y⊣, and are considered accepted if δ allows a computation which starts at q 0, with blank work tape and with the input and advice heads on ⊢, and eventually falls off ⊣ on the input tape into q f . If δ allows at most one computation per input, then M is a dtm.
The internal configuration of M at a point in the course of its computation is the tuple (q,w,j,i) of its current state q, current non-blank content w∈Γ ∗ on the work tape, current head position j on ⊔w⊔, and current head position i on the advice tape.
The language of M under a family  of advice strings over Δ is the set
of advice strings over Δ is the set

If  is the empty advice (ε)
m≥0, then we just write L(M). The length of
is the empty advice (ε)
m≥0, then we just write L(M). The length of  is the function m↦|y
m
|. We say that
is the function m↦|y
m
|. We say that  is strong advice for M if every y
m
is valid not only for all inputs of length m but also for all shorter inputs:
is strong advice for M if every y
m
is valid not only for all inputs of length m but also for all shorter inputs:
This deviation from standard definitions of advice is unimportant if the advice length is at least polynomial in m (because then we can always replace y m with the concatenation of y 0,y 1,…,y m ). For shorter advice, though, it is not clear whether there is a difference. Our theorems need the strong variant.
A function f is a strong space bound for M under  if, for all m and all x with |x|≤m, every computation on x and y
m
visits at most f(m) work tape cells. If this is guaranteed just for the x and y
m
that are accepted and then just for at least one accepting computation, then f is only a weak space bound for M under
if, for all m and all x with |x|≤m, every computation on x and y
m
visits at most f(m) work tape cells. If this is guaranteed just for the x and y
m
that are accepted and then just for at least one accepting computation, then f is only a weak space bound for M under  .
.
For  and
and  two classes of functions, the class of languages that are solvable by ntms under strong
two classes of functions, the class of languages that are solvable by ntms under strong  -long advice in strongly
-long advice in strongly  -bounded space is denoted by
-bounded space is denoted by

When we just write  , we mean
, we mean  , so that the only possible advice is the empty one. In particular, we let
, so that the only possible advice is the empty one. In particular, we let
The respective classes for dtms, denoted by  ,
,  , L, and LL, are defined analogously. We specifically let L/poly:=DSPACE({logn})/poly(n) and LL/polylog:=DSPACE({loglogn})/poly(logn).
, L, and LL, are defined analogously. We specifically let L/poly:=DSPACE({logn})/poly(n) and LL/polylog:=DSPACE({loglogn})/poly(logn).
The next lemma lists the full details of the standard fact that every (advised) tm that computes on inputs of bounded length can be simulated by a  . In the statement, a function f is fully space constructible if there exists a dtm which, on any input x and any advice, halts after visiting exactly f(|x|) work tape cells. A transducer is a dtm without advice tape but with a write-only output tape, which is accessed via a one-way head (Fig. 1c).
. In the statement, a function f is fully space constructible if there exists a dtm which, on any input x and any advice, halts after visiting exactly f(|x|) work tape cells. A transducer is a dtm without advice tape but with a write-only output tape, which is accessed via a one-way head (Fig. 1c).
Lemma 2.2
Consider a
n
tm M under strong advice
 of length g, obeying a weak space bound f. For every length bound m, there exists a
of length g, obeying a weak space bound f. For every length bound m, there exists a
 A
m
with 2O(f(m)+logg(m))
states which agrees with M
under
A
m
with 2O(f(m)+logg(m))
states which agrees with M
under
 on every input of length at most m.
on every input of length at most m.
Moreover: (a) If
M
is deterministic, then so is A
m
. (b) If
 is empty, then
A
m
also agrees with M
under
is empty, then
A
m
also agrees with M
under
 on every non-accepted input (of any length). (c) If
f is fully space constructible, then there exists a transducer T
M
which, given m (in unary) and the corresponding y
m
, computes A
m
(in binary) in space
O(f(m)+logg(m)).
on every non-accepted input (of any length). (c) If
f is fully space constructible, then there exists a transducer T
M
which, given m (in unary) and the corresponding y
m
, computes A
m
(in binary) in space
O(f(m)+logg(m)).
Proof
Let M be a (s,σ,γ)- ntm and pick  and g and f as in the statement. Fix m and consider M working on any input (of any length) and on y
m
. Let S
m
be the set of all internal configurations of M with ≤ f(m) work tape cells when y
m
is on the advice tape. The number of such configurations is easily seen to satisfy:
and g and f as in the statement. Fix m and consider M working on any input (of any length) and on y
m
. Let S
m
be the set of all internal configurations of M with ≤ f(m) work tape cells when y
m
is on the advice tape. The number of such configurations is easily seen to satisfy:

We let A m :=(S m ,Σ,δ m ,q 0,F m ) where Σ is M’s input alphabet, q 0 and F m are the initial and the accepting internal configurations in S m , and δ m contains a transition (c,a,c′,d) iff M can change its internal configuration from c to c′ and move its input head in direction d when its current input cell contains a and its advice tape contains y m . (Note that y m is ‘embedded’ in δ m .) This concludes the definition of A m .
Now fix any input x (of any length). Let τ m and \(\tau _{m}'\) be respectively the computation tree of M on x and y m and the computation tree of A m on x. It should be clear that every branch β in τ m that uses ≤ f(m) work tape cells is fully simulated in \(\tau _{m}'\) by an equally long branch β′, which accepts iff β does. In contrast, every branch β in τ m that uses >f(m) work tape cells is only partially simulated in \(\tau _{m}'\), by a shorter branch β′ which hangs (at a rejecting state). Moreover, every branch of \(\tau _{m}'\) is the β′ of a branch β of τ m under the correspondence established by the above two cases.
Now suppose |x|=n≤m. We must prove that  iff A
m
accepts x. For this, let τ
n
be the computation tree of M on x and y
n
, and note that τ
n
accepts iff τ
m
does (because
iff A
m
accepts x. For this, let τ
n
be the computation tree of M on x and y
n
, and note that τ
n
accepts iff τ
m
does (because  is strong). We distinguish the natural two cases.
is strong). We distinguish the natural two cases.
-
If
 , then τ
n
accepts. Hence, τ
m
accepts as well. Therefore, some accepting branch β in τ
m
uses ≤ f(m) work tape cells (because f is a weak space bound). So, the corresponding branch β′ in \(\tau _{m}'\) completes the simulation and accepts, too. Hence, A
m
accepts x.
, then τ
n
accepts. Hence, τ
m
accepts as well. Therefore, some accepting branch β in τ
m
uses ≤ f(m) work tape cells (because f is a weak space bound). So, the corresponding branch β′ in \(\tau _{m}'\) completes the simulation and accepts, too. Hence, A
m
accepts x. -
If
 , then τ
n
does not accept. Hence, τ
m
does not accept either. Therefore, every branch in \(\tau _{m}'\) is non-accepting, either because it fully simulates a non-accepting branch of τ
m
or because it hangs after partially simulating one. Hence, A
m
does not accept x.
, then τ
n
does not accept. Hence, τ
m
does not accept either. Therefore, every branch in \(\tau _{m}'\) is non-accepting, either because it fully simulates a non-accepting branch of τ
m
or because it hangs after partially simulating one. Hence, A
m
does not accept x.
Overall, A
m
agrees with M under  on every x of length n≤m, as required. We continue with the remaining, special considerations of the lemma.
on every x of length n≤m, as required. We continue with the remaining, special considerations of the lemma.
-
(a)
If M is deterministic, then A m is clearly also deterministic.
-
(b)
If
 is empty, then the agreement between A
m
and M under
is empty, then the agreement between A
m
and M under  extends also to every
extends also to every 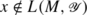 of length n>m. Indeed: Since
of length n>m. Indeed: Since  , we know τ
n
does not accept, hence τ
m
does not accept (because, since
, we know τ
n
does not accept, hence τ
m
does not accept (because, since  is empty, we have y
n
=y
m
and thus τ
n
=τ
m
), and thus \(\tau _{m}'\) does not accept (as in the second case above).Footnote 3
is empty, we have y
n
=y
m
and thus τ
n
=τ
m
), and thus \(\tau _{m}'\) does not accept (as in the second case above).Footnote 3
-
(c)
If f is fully space constructible, then the binary encoding 〈A m 〉 can be computed from 0 m and y m , as follows. We first mark exactly f(m) work tape cells, by running on 0 m the dtm that fully constructs f. Then, using these cells and y m , we mark another lgs+lg(f(m)+2)+lg(|y m |+2) cells. Now the marked region is as long as the longest description of an internal configuration c∈S m . This makes it possible to iterate over all c∈S m or pairs thereof (by lexicographically iterating over all possible strings and discarding those that are non-descriptions). From this point on, computing the bits of 〈A m 〉 is fairly straightforward. Overall, we will need no more than O(f(m)+logg(m)) work tape cells.
□
Corollary 2.1
-
(a)
For every n tm M (under empty advice) of weak space O(logn) and for every length bound m, there exists a poly(m)-state
 A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is. Moreover, there exists a logarithmic-space transducer T
M
which, given m (in unary), computes A
m
(in binary).
A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is. Moreover, there exists a logarithmic-space transducer T
M
which, given m (in unary), computes A
m
(in binary). -
(b)
For every n tm M (under empty advice) of weak space O(loglogn) and for every length bound m, there exists a poly(logm)-state
 A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is.
A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is.
Proof
-
(a)
Let T M be the transducer guaranteed by Lemma 2.2 for M under the empty advice and the fully space constructible space bound f(m)=logm. Since the advice is empty, we know that the second input to T M is always ε, that the advice length is g(m)=0, and that A m also agrees with M on every non-accepted input. Therefore, T M works on the single input 0 m, uses space O(f(m)+logg(m))=O(logm), and outputs a
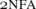 that has 2O(f(m)+logg(m))=poly(m) states and may disagree with M only on accepted inputs longer than m.
that has 2O(f(m)+logg(m))=poly(m) states and may disagree with M only on accepted inputs longer than m. -
(b)
Let A m be the
 guaranteed by Lemma 2.2 for m and for M under the empty advice and the weak space bound f(m)=O(loglogm). Since the advice is empty, we know that its length is g(m)=0 and that A
m
also agrees with M on all non-accepted inputs. Therefore, A
m
has 2O(f(m)+logg(m))=2O(loglogm)=poly(logm) states and may disagree with M only on accepted inputs longer than m.
guaranteed by Lemma 2.2 for m and for M under the empty advice and the weak space bound f(m)=O(loglogm). Since the advice is empty, we know that its length is g(m)=0 and that A
m
also agrees with M on all non-accepted inputs. Therefore, A
m
has 2O(f(m)+logg(m))=2O(loglogm)=poly(logm) states and may disagree with M only on accepted inputs longer than m.
□
2.3 Reductions
Let Σ 1 and Σ 2 be two alphabets, neither of which contains the end-markers ⊢ and ⊣. Every function \(r:\varSigma _{1}\cup\{{\vdash }{,}{\dashv }\}\to \varSigma _{2}^{*}\) extends naturally to the entire \({\vdash }\varSigma _{1}^{*}{\dashv }\) by the rule
for every \(x\in \varSigma _{1}^{*}\). Such a function is called a homomorphic reduction of a problem \(\mathfrak {L}_{1}=(L_{1},\tilde {L}_{1})\) over Σ 1 to a problem \(\mathfrak {L}_{2}=(L_{2},\tilde {L}_{2})\) over Σ 2 if it satisfies
for all x [13]. When such a reduction exists, we say that \(\mathfrak {L}_{1}\) homomorphically reduces to \(\mathfrak {L}_{2}\), and write \(\mathfrak {L}_{1}\leq _{\mathrm {h}}\mathfrak {L}_{2}\). The expansion of r is the function which maps every length bound m to the maximum length of the r-image of (the end-marked extension of) a string of length ≤m:
The ternary encoding of r, assuming a fixed ordering \(a_{1},\ldots ,a_{\sigma _{1}}\) of Σ 1, is
(On the right-hand side of this definition, 〈 ⋅ 〉 stands for the standard binary encoding of strings over Σ 2, as explained in the beginning of Sect. 2; so 〈r〉∈{0,1,#}∗.)
The next lemma lists the full details of the old fact that the class of problems that can be solved by small  is closed under homomorphic reductions [13].
is closed under homomorphic reductions [13].
Lemma 2.3
If
\(\mathfrak {L}_{1}\leq _{\mathrm {h}}\mathfrak {L}_{2}\)
and some
s-state
 A
2
solves
\(\mathfrak {L}_{2}\), then some 2s-state
A
2
solves
\(\mathfrak {L}_{2}\), then some 2s-state
 A
1
solves
\(\mathfrak {L}_{1}\).
A
1
solves
\(\mathfrak {L}_{1}\).
If A 2 is deterministic, then so is A 1. Moreover, there exists a logarithmic-space transducer T h which, given a homomorphic reduction of \(\mathfrak {L}_{1}\) to \(\mathfrak {L}_{2}\) (in ternary) and a deterministic A 2 (in binary), computes A 1 (in binary).
Proof
Suppose \(r:\varSigma _{1}\cup\{{\vdash }{,}{\dashv }\}\to \varSigma _{2}^{*}\) is a homomorphic reduction of \(\mathfrak {L}_{1}=(L_{1},\tilde {L}_{1})\) to \(\mathfrak {L}_{2}=(L_{2},\tilde {L}_{2})\), and the  A
2=(S
2,Σ
2,δ
2,q
2,F
2) solves \(\mathfrak {L}_{2}\) with |S
2|=s.
A
2=(S
2,Σ
2,δ
2,q
2,F
2) solves \(\mathfrak {L}_{2}\) with |S
2|=s.
On input \(x\in \varSigma _{1}^{*}\), the new automaton A 1 simulates A 2 on r(⊢x⊣) piece-by-piece: on each symbol a on its tape, A 1 does exactly what A 2 would eventually do on the corresponding infix r(a) on its own tape—except if a is ⊢ or ⊣, in which case the corresponding infix is respectively the prefix ⊢r(⊢) or the suffix r(⊣)⊣. This way, every branch β in the computation tree τ 2 of A 2 on r(⊢x⊣) is simulated by a branch in the computation tree τ 1 of A 1 on x, which is accepting iff β is; in addition, these simulating branches are the only branches in τ 1. Thus, τ 1 contains accepting branches iff τ 2 does, namely A 1 accepts x iff A 2 accepts r(⊢x⊣). Consequently, if x∈L 1, then r(⊢x⊣)∈L 2 (by the selection of r), hence A 2 accepts, and thus A 1 accepts as well. In contrast, if \(x\in \tilde {L}_{1}\), then \(r({\vdash }x{\dashv })\in \tilde {L}_{2}\) (again by the selection of r), hence A 2 does not accept, and thus A 1 does not accept either. Overall, A 1 solves \(\mathfrak {L}_{1}\).
To perform this simulation, A 1 keeps track of the current state of A 2 and the side (l or r) from which A 2 enters the current corresponding infix. Formally, A 1:=(S 2×{l,r},Σ 1,δ 1,(q 2,l),F 2×{l}), where δ 1 is fairly straightforward to derive from the above informal description. For example, ((p,l),a,(q,l),r)∈δ 1 iff δ 2 allows on r(a) a computation that starts at p on the leftmost symbol and eventually falls off the rightmost boundary into q (thus entering the subsequent infix from its left side). For another example, ((p,l),⊣,(q,r),l)∈δ 1 iff δ 2 allows on r(⊣)⊣ a computation that starts at p on the leftmost symbol and eventually falls off the leftmost boundary into q (thus entering the preceding infix from its right side).
If A 2 is deterministic, then clearly A 1 is also deterministic. Moreover, its encoding 〈A 1〉 can then be computed from the two encodings 〈r〉 and 〈A 2〉 in deterministic logarithmic space. To see how, let σ 1:=|Σ 1| and σ 2:=|Σ 2|, and recall that
where the u 1,v 1,w 1 and u 2,v 2,w 2 encode respectively the transition functions, the start states, and the sets of final states. Each part of 〈A 1〉 can be computed in a straightforward manner from the corresponding part of 〈A 2〉 (using no work tape at all), except for \(\texttt {0}^{\sigma _{1}}\) and u 1. For the former, we scan 〈r〉 and output a 0 for every occurrence of # after the first one. For the latter, we mark 2lgs+lg(σ 1+2)+3=O(log(σ 1 s)) work tape cells and use them to iterate over all encodings of tuples of the form
outputting 1 bit per tuple. To decide each bit, we locate 〈r(a)〉 in 〈r〉 and simulate A 2 on r(a) (or on ⊢r(a) if a=⊢, or on r(a)⊣ if a=⊣), starting at p on the d-most symbol and counting the simulated steps. We continue until either we fall off the string or the number of simulated steps exceeds s⋅|r(a)|=s⋅|〈r(a)〉|/lgσ 2 by 1 (or by s+1, if a=⊢ or ⊣). If we fall off the d″-most boundary into p′ and d′≠d″ then we output 1; in all other cases, we output 0. This simulation needs only a finite number of pointers into 〈r〉 and u 2, plus the aforementioned bounded counter. Overall, the space used is logarithmic in |〈r〉+〈A 2〉|. □
2.4 Two-Way Liveness
Central in our arguments in Sect. 3 are several variants of a computational problem that we call two-way liveness [13]. In this section we introduce these variants and study their properties.
Fix any h≥1. Let Γ h be the alphabet of all possible directed graphs consisting of two columns of h nodes each (Fig. 2a). Easily, \(|\varGamma _{h}|=2^{(2h)^{2}}\). Every string \(x\in\nolinebreak \varGamma _{h}^{*}\) of such graphs induces the multicolumn graph that we get when we identify adjacent columns (Fig. 2b). If this h-tall (|x|+1)-column graph contains a path from its leftmost to its rightmost column, we say that x is live; otherwise, no such path exists and we say that x is dead. The language

represents the computational problem of checking that a given string of h-tall two-column graphs is live. The family of languages

represents this computational task for all possible heights h.
The next lemma lists the full details of the old fact that every problem that can be solved by a  reduces homomorphically to the problem of checking two-way liveness on graphs of height twice the number of states in the automaton [13].
reduces homomorphically to the problem of checking two-way liveness on graphs of height twice the number of states in the automaton [13].
Lemma 2.4
If
\(\mathfrak {L}\)
can be solved by an
s-state
 A, then
A, then
 via a reduction which has expansion m+2 and is constructible from 〈A〉 in logarithmic space.
via a reduction which has expansion m+2 and is constructible from 〈A〉 in logarithmic space.
Proof
Let A=(S,Σ,δ,q 0,F) with |S|=s. We consider a reduction r which maps every a∈Σ∪{⊢,⊣} to a single symbol r(a)∈Γ 2s . This is the unique symbol that fully encodes the behavior of A on a, under the following scheme.
First, in each of the two columns of r(a) we distinguish the upper and the lower half. We thus get four half-columns (upper-left, lower-left, upper-right, and lower-right) of s nodes each, representing four copies of S. For every tuple (p,d,p′,d′) in the behavior of A on a we add an arrow with origin the p-th node of either the upper-left or the lower-right half-column, depending on whether d=l or r, and destination the p′-th node of the lower-left or the upper-right half-column, depending on whether d′=l or r. In the special case when a=⊢, an arrow with origin in the upper-left half-column is added only if p=q 0. In the special case when a=⊣, an arrow with destination in the upper-right half-column is added only if p′∈F.
With these definitions, it is not hard to see that the computation tree of A on a string x∈Σ ∗ contains an accepting branch iff r(⊢x⊣) contains a path from its leftmost to its rightmost column (see [13] for details). Hence, r is a correct reduction of the entire L(A) to twl 2s , and thus also of \(\mathfrak {L}\) to twl 2s . Obviously, |r(⊢x⊣)|=|⊢x⊣|=|x|+2 for every x∈Σ ∗, and thus the expansion is μ(m)=m+2. Finally, constructing 〈r〉 out of 〈A〉 reduces to computing the behavior of A on each a∈Σ∪{⊢,⊣}, which is straightforward to do with a finite number of pointers into 〈A〉. □
In order to establish Theorem 1.1, we will need a single language that can encode the problem of checking two-way liveness on every possible height. To introduce this language, we start with the binary encoding 〈a〉 of a single graph a∈Γ h , which is a string of (2h)2 bits that describes a in the natural way (with 1 bit per possible arrow, under a fixed ordering of the set of all possible arrows). Using this encoding scheme, we can “join” all languages of the family twl into the one binary language:

The interpretation is driven by the h leading 0s: the leftmost 1 and the rightmost 1 must be separated by 0 or more blocks of bits of length (2h)2 each (the “middle bits”); the multicolumn graph encoded by these blocks must contain a path from its leftmost to its rightmost column; and the number t of trailing 0s must be a multiple of h.Footnote 4
In order to establish Theorem 1.3, we will need a variant of twl join, called twl long-join. This differs only in the specification for the number of trailing 0s, which must now be a multiple of every positive j≤h, as opposed to just h:

Here, we are copying the padding scheme used by Szepietowski in [18]. In short, this scheme pads a string of length h with a string of 0s whose length is (i) at least exponential in h and (ii) checkable in space logarithmic in h—and thus log-logarithmic in the new total length, hence its usefulness for Theorem 1.3.
Finally, the proof of Theorem 1.2 requires yet more variants of twl join. For every k≥1, we let twl join k be the variant where the number of trailing 0s must be a multiple of every positive j≤⌊logh⌋k. This leads to a padding string whose length is (i) at least quasi-polynomial in h and (ii) checkable in space poly-logarithmic in h. (If k=1 then the length is at least polynomial and the space logarithmic, causing the properties of twl join 1 to be similar to those of twl join.)
The next two lemmas study the properties of these variants of two-way liveness. They also discuss another problem, the acceptance problem for  , with which it will be useful to compare in Sect. 3. This is the problem of checking whether a given
, with which it will be useful to compare in Sect. 3. This is the problem of checking whether a given  accepts a given input, formally the ternary language
accepts a given input, formally the ternary language

Note that the alphabet of the given automaton is not fixed: to solve this problem, one must also check that the binary string after # can indeed be interpreted as an input for the  that is encoded by the binary string before #. Finally, we also let
that is encoded by the binary string before #. Finally, we also let  be the corresponding problem for
be the corresponding problem for  .
.
Lemma 2.5
If
\(\mathfrak {L}\)
can be solved by a (s,σ)- A, then
\(\mathfrak {L}\)
homomorphically reduces to each of
A, then
\(\mathfrak {L}\)
homomorphically reduces to each of
 , twl join, twl join
k
, and
twl long-join
via reductions of expansion
O(s
2
σm), O(s
2
m), \(2^{O(\log^{k} s)}m\), and 2O(s)
m, respectively. The first two reductions are constructible from 〈A〉 in logarithmic space.Footnote 5
, twl join, twl join
k
, and
twl long-join
via reductions of expansion
O(s
2
σm), O(s
2
m), \(2^{O(\log^{k} s)}m\), and 2O(s)
m, respectively. The first two reductions are constructible from 〈A〉 in logarithmic space.Footnote 5
Proof
Let the alphabet of A be Σ={a 1,…,a σ }. We construct four homomorphic reductions of \(\mathfrak {L}\) to the four languages of the statement, and call them respectively
It will be straightforward to verify that each reduction is correct, and that 〈r 0〉 and 〈r 1〉 can be constructed from 〈A〉 in logarithmic space, so we will omit these discussions.
Reduction r 0 maps ⊢ to 〈A〉#, every a i to the lgσ-long binary representation of i−1, and ⊣ to the empty string. As a result, every string x of length n≤m is transformed into the string r 0(⊢x⊣)=〈A〉#〈x〉, of length (|〈A〉|+1)+nlgσ+0=O(s 2 σ)+nlgσ=O(s 2 σm).
Reduction r 1 uses the reduction r:Σ∪{⊢,⊣}→Γ 2s given by Lemma 2.4, along with the binary encoding 〈 ⋅ 〉 of the graphs of Γ 2s . It maps ⊢ to 0 2s 1〈r(⊢)〉, every a i to 〈r(a i )〉, and ⊣ to 〈r(⊣)〉10 2s. As a result, every string x of length n≤m is transformed into the string
which has length (2s+1)+(n+2)(4s)2+(1+2s)=O(s 2 m) and is in twl join iff r(⊢)r(x 1)⋯r(x n )r(⊣) is live (all other conditions in the definition of twl join are obviously satisfied), namely iff r(⊢x⊣)∈twl 2s .
The last two reductions, r 2 and r 3, use the function λ defined by
which is known to satisfy λ(l)=2Θ(l) [18, Lemma, part (b)]. The two reductions differ from r 1 only in that they map ⊣ respectively to
Hence, every string x of length n≤m is now mapped to the string r 2(⊢x⊣) of length
and to the string r 3(⊢x⊣) of length 2O(s) m (by a similar calculation). □
Lemma 2.6
The problems
 , twl join, twl join
k
and
twl long-join
are respectively
NL-complete, NL-complete, in
\(\textsf {NSPACE}(\sqrt[k]{\log n})\), and in
NLL.
, twl join, twl join
k
and
twl long-join
are respectively
NL-complete, NL-complete, in
\(\textsf {NSPACE}(\sqrt[k]{\log n})\), and in
NLL.
Proof
That  is NL-complete is well-known, so we focus on the other claims.
is NL-complete is well-known, so we focus on the other claims.
To prove that twl join is NL-hard, pick any L recognized by a ntm M in logarithmic space. Every instance x of L can be transformed into an instance of twl join by the following series of transductions, where m=|x|:
First, we append #0
m by running on x an obvious zero-space transducer. Then, we replace 0
m with the encoding of the  A
m
guaranteed by Corollary 2.1(a) for M and m, by running on 0
m the logarithmic-space transducer T
M
given by that corollary. Next, we replace 〈A
m
〉 with the encoding of the reduction r guaranteed by Lemma 2.5 for \(\mathfrak {L}=L(A_{m})\) and twl join, by running on 〈A
m
〉 the corresponding logarithmic-space transducer given by that lemma. Finally, we replace x
#〈r〉 with r(⊢x⊣) by running on it the obvious logarithmic-space transducer that applies r to every symbol of ⊢x⊣. By the transitivity of logarithmic-space transductions, it follows that the full transformation can also be implemented in logarithmic space. Moreover, by the selection of M, m, A
m
, and r, we have
A
m
guaranteed by Corollary 2.1(a) for M and m, by running on 0
m the logarithmic-space transducer T
M
given by that corollary. Next, we replace 〈A
m
〉 with the encoding of the reduction r guaranteed by Lemma 2.5 for \(\mathfrak {L}=L(A_{m})\) and twl join, by running on 〈A
m
〉 the corresponding logarithmic-space transducer given by that lemma. Finally, we replace x
#〈r〉 with r(⊢x⊣) by running on it the obvious logarithmic-space transducer that applies r to every symbol of ⊢x⊣. By the transitivity of logarithmic-space transductions, it follows that the full transformation can also be implemented in logarithmic space. Moreover, by the selection of M, m, A
m
, and r, we have

Therefore, L reduces to twl join in logarithmic space, as required.
To solve twl join by a ntm in logarithmic space, we work in two stages. First, we deterministically verify the format: we check that there are at least two 1s, compute the number h of leading 0s, and check that h divides the number of trailing 0s (by scanning and counting modulo h) and that (2h)2 divides the number of “middle bits” (similarly). Then, we nondeterministically verify liveness, by simulating on the “middle bits” the 2h-state  solving twl
h
[13]. Easily, each stage can be performed in space O(logh). Since h is obviously smaller than the total input length n, we conclude that the space usage is indeed O(logn). Thus twl join∈NL, completing the proof that twl join is NL-complete.
solving twl
h
[13]. Easily, each stage can be performed in space O(logh). Since h is obviously smaller than the total input length n, we conclude that the space usage is indeed O(logn). Thus twl join∈NL, completing the proof that twl join is NL-complete.
To solve twl long-join by a ntm in log-logarithmic space, we use the same algorithm as for twl join, but with a preliminary stage [18]. This starts by checking that there exist at least two 1s; if not, we reject. Then, we increment a counter from 1 up to the first number, t ∗, that does not divide the number t of trailing 0s (as above, divisibility is always tested by scan-and-count). On reaching t ∗, we compare it with the number h of leading 0s (scan-and-count, again). If t ∗≤h, we reject; otherwise we continue to the two main stages (omitting, however, the check that h divides t). We consider the correctness of this algorithm to be clear, and discuss only the space usage. First, in the preliminary stage the cost is clearly O(logt ∗). Then, as above, the two main stages cost O(logh), which is also O(logt ∗) because we get to them only if h<t ∗. Since t ∗=O(logt) [18, Lemma, part (d)] and t≤n (obviously), we conclude that the total space used is O(loglogn), as required.
To solve twl join k by a ntm in space \(O(\sqrt[k]{\log n})\), we use the same algorithm as for twl long-join, but with a modification. Instead of testing whether t ∗≤h, we test whether \(\sqrt[k]{t^{*}}\leq \lfloor \log h\rfloor \). If so, then t ∗≤⌊logh⌋k, hence the padding length is incorrect, and we reject; otherwise, the padding length is correct and we proceed to the two main stages. To test whether \(\sqrt[k]{t^{*}}\leq \lfloor \log h\rfloor \), we test the equivalent condition \(\bigl \lceil \sqrt[k]{t^{*}}\,\bigr \rceil \leq \lfloor \log h\rfloor \). For this, we first compute \(\tilde{t}:=\bigl \lceil \sqrt[k]{t^{*}}\,\bigr \rceil \) from t ∗ by standard methods in space O(logt ∗), then test \(\tilde{t}\leq \lfloor \log h\rfloor \). This last test can be performed using two counters α and β, as follows. After initializing \(\alpha :=\tilde{t}\) and β:=0, we start scanning the prefix 0 h 1 of the input, incrementing β at every step and decrementing α at every change of the length of β, until either α becomes 0 or we reach 1 on the input tape.
-
If the former condition is met first, then the initial value \(\tilde{t}\) of α equals the actual number of times that the length of β increased, and is thus bounded by the maximum number of times ⌊logh⌋ that the length of β can possibly increase (in the case when the latter condition is met first). That is, \(\tilde{t}\leq \lfloor \log h\rfloor \) and we reject. The space usage, for computing \(\tilde{t}\), for storing α, and for storing β, is respectively:
$$O\bigl(\log t^*\bigr) + O(\log\tilde{t}) + (\tilde{t}+1) = O\bigl(\sqrt[k]{t^*}\bigr) = O(\sqrt[k]{\log t}) = O(\sqrt[k]{\log n}). $$The first equality is clear, then we use that t ∗=O(logt) and t≤n (as above).
-
If the latter condition is met first, then \(\tilde{t}>\lfloor \log h\rfloor \) and we continue to the two main stages. The space usage is again \(O(\log t^{*}) + O(\log\tilde{t})\) for computing \(\tilde{t}\) and storing α, plus ⌊logh⌋+1 for storing β and O(logh) for the main stages. Overall:
$$O\bigl(\log t^*\bigr) + O(\log\tilde{t}) + \bigl(\lfloor \log h\rfloor {+}1\bigr) + O(\log h) = O\bigl(\sqrt[k]{t^*}\bigr) = O(\sqrt[k]{\log n}). $$The first equality uses the fact that \(\lfloor \log h\rfloor <\tilde{t}\), while the second one uses the fact that t ∗=O(logt) and t≤n (as above).
Overall, in both cases, the total space usage is \(O(\sqrt[k]{\log n})\), as required. □
3 The Berman-Lingas Theorem
The ‘Berman-Lingas Theorem’ is Theorem 6 of the old technical report [3]. It is usually cited as follows:

However, the full statement that was actually claimed in that report, via a remark a few pages after the statement of Theorem 6, is much stronger:Footnote 6

That is, the report also claimed that the promised  is constructible from the
is constructible from the  and the length bound in logarithmic space, and that then the converse is also true. The usual citation (8) is just a weak corollary of (\(8^{\scriptscriptstyle +}\)) for the case when m=poly(s).
and the length bound in logarithmic space, and that then the converse is also true. The usual citation (8) is just a weak corollary of (\(8^{\scriptscriptstyle +}\)) for the case when m=poly(s).
Unfortunately, the proofs of the above statements depend on the fact that |Σ| is constant. In cases where the alphabet grows with s (as is often true in the study of 2D versus 2N), the bound that is guaranteed by these proofs for the number of states in B may very well be exponential in s. To highlight this subtle point, we state and prove the theorem under no assumptions for the alphabet size.
Theorem 3.0
(Berman and Lingas [3])
The following statements are equivalent:
- (a) :
-
L⊇NL.
- (b) :
-
There exists a logarithmic-space transducer T which, on input a
 A (in binary) and a length bound m (in unary), outputs a
A (in binary) and a length bound m (in unary), outputs a
 B (in binary) that has at most poly(sσm) states, for s
and σ
the number of states and symbols in A, and may disagree with A
only on accepted inputs longer than m.
B (in binary) that has at most poly(sσm) states, for s
and σ
the number of states and symbols in A, and may disagree with A
only on accepted inputs longer than m.
Proof
- [(a)⇒(b)]:
-
Suppose L⊇NL. Then
 . Therefore, some dtm M under empty advice solves
. Therefore, some dtm M under empty advice solves  in space strongly bounded by logn.
in space strongly bounded by logn.To see the main idea behind the argument, consider any (s,σ)-
 A and any length bound m. Lemma 2.5 says that
A and any length bound m. Lemma 2.5 says that  via a reduction of expansion μ. Hence, Lemma 2.3 implies that constructing a
via a reduction of expansion μ. Hence, Lemma 2.3 implies that constructing a  B for L(A) and input lengths ≤ m reduces to constructing a
B for L(A) and input lengths ≤ m reduces to constructing a  \(\tilde{B}\) for
\(\tilde{B}\) for  and input lengths ≤ μ(m). This latter construction is indeed possible by Corollary 2.1(a).
and input lengths ≤ μ(m). This latter construction is indeed possible by Corollary 2.1(a).So, given A and m, we employ a series of logarithmic-space transductions:
$$\langle A\rangle \texttt {\#}\texttt {0}^m\longrightarrow \langle A\rangle \texttt {\#}\texttt {0}^{\mu (m)} \;\stackrel{T_M}{\longrightarrow}\; \langle A\rangle \texttt {\#}\langle \tilde{B}\rangle \;\stackrel{}{\longrightarrow}\; \langle r\rangle \texttt {\#}\langle \tilde{B}\rangle \;\stackrel{T_{\mathrm {h}}}{\longrightarrow}\; \langle B\rangle . $$First, we replace 0 m with 0 μ(m), by running on 〈A〉#0 m an obvious logarithmic-space transducer which performs the algebra for μ(m) on the parameters of A and on m. Then we replace 0 μ(m) with the encoding of the
 \(\tilde{B}\) guaranteed by Corollary 2.1(a) for M and for μ(m), by running on 0
μ(m) the logarithmic-space transducer T
M
given by that corollary. Then we replace 〈A〉 with the encoding of the homomorphism r guaranteed by Lemma 2.5 for
\(\tilde{B}\) guaranteed by Corollary 2.1(a) for M and for μ(m), by running on 0
μ(m) the logarithmic-space transducer T
M
given by that corollary. Then we replace 〈A〉 with the encoding of the homomorphism r guaranteed by Lemma 2.5 for  , by running on 〈A〉 the logarithmic-space transducer given by that lemma. Finally, we convert \(\langle r\rangle \texttt {\#}\langle \tilde{B}\rangle \) into the desired
, by running on 〈A〉 the logarithmic-space transducer given by that lemma. Finally, we convert \(\langle r\rangle \texttt {\#}\langle \tilde{B}\rangle \) into the desired  B, by running the logarithmic-space transducer T
h given by Lemma 2.3. By the transitivity of logarithmic-space transductions, we know that the full algorithm can also be implemented in logarithmic space. It remains to verify the properties of B.
B, by running the logarithmic-space transducer T
h given by Lemma 2.3. By the transitivity of logarithmic-space transductions, we know that the full algorithm can also be implemented in logarithmic space. It remains to verify the properties of B.If S and \(\tilde{S}\) are the sets of states in B and \(\tilde{B}\), then \(|S|=2|\tilde{S}|\) (by Lemma 2.3) and \(|\tilde{S}|=\mathrm {poly}\bigl(\mu (m)\bigr)\) (by Corollary 2.1(a)) and μ(m)=O(s 2 σm) (by Lemma 2.5). So,
$$|S| = 2|\tilde{S}| = 2\cdot \mathrm {poly}\bigl(\mu (m)\bigr) = 2\cdot \mathrm {poly}\bigl( O\bigl(s^2\sigma m\bigr) \bigr) = \mathrm {poly}(s\sigma m), $$as promised. Moreover, consider any input x to A. If y:=r(⊢x⊣) is its transformation under r, then clearly |y|≤μ(|x|) and the two cases of interest are as follows:
-
If \(x\not\in L(A)\), then
 , hence M does not accept y, so \(\tilde{B}\) does not accept y either, causing B not to accept x.
, hence M does not accept y, so \(\tilde{B}\) does not accept y either, causing B not to accept x. -
If x∈L(A) and |x|≤m, then
 , hence M accepts y, hence \(\tilde{B}\) also accepts y (since |y|≤μ(m)), causing B to accept x.
, hence M accepts y, hence \(\tilde{B}\) also accepts y (since |y|≤μ(m)), causing B to accept x.
Overall, B may disagree with A only on x∈L(A) with |x|>m, as promised.
-
- [(b)⇒(a)]:
-
Suppose the logarithmic-space transducer T of the statement exists. Then
 reduces to
reduces to  in logarithmic space, as follows. Given a
in logarithmic space, as follows. Given a  A and an input x, we apply the following two logarithmic-space transductions, where m=|x|: $$\langle A\rangle \texttt {\#}\langle x\rangle \longrightarrow \langle A\rangle \texttt {\#}\texttt {0}^m\texttt {\#}\langle x\rangle \;\stackrel{T}{\longrightarrow}\; \langle B\rangle \texttt {\#}\langle x\rangle . $$
A and an input x, we apply the following two logarithmic-space transductions, where m=|x|: $$\langle A\rangle \texttt {\#}\langle x\rangle \longrightarrow \langle A\rangle \texttt {\#}\texttt {0}^m\texttt {\#}\langle x\rangle \;\stackrel{T}{\longrightarrow}\; \langle B\rangle \texttt {\#}\langle x\rangle . $$First, we insert #0 m by running an obvious logarithmic-space transducer that performs the algebra for m=|〈x〉|/lgσ, where σ is the number of symbols in A. Then, we run T on 〈A〉#0 m to replace it with the encoding of a
 B that agrees with A on all inputs of length ≤m, including x. Clearly,
B that agrees with A on all inputs of length ≤m, including x. Clearly,  iff
iff  .
.Now, the NL-hardness of
 , the logarithmic-space reduction to
, the logarithmic-space reduction to  , the fact that
, the fact that 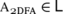 (easy, just simulate the
(easy, just simulate the  , being careful not to loop), and the closure of L under logarithmic-space reductions imply L⊇NL.
, being careful not to loop), and the closure of L under logarithmic-space reductions imply L⊇NL.
□
It is now clear that, when we restrict to inputs of length at most m=poly(s), the bound for the states in B is poly(sσ)—not poly(s). Hence, for a  A over an alphabet of size σ=2Ω(s) (e.g., a
A over an alphabet of size σ=2Ω(s) (e.g., a  for twl
s
), the bound of Theorem 3.0 for the number of states in a
for twl
s
), the bound of Theorem 3.0 for the number of states in a  simulating A on inputs of length poly(s) cannot be lower than 2O(s). We stress that this looseness is inherent in the Berman-Lingas argument, not just in our analysis of it: a larger alphabet for A implies a longer encoding 〈A〉, thus longer inputs to the alleged logarithmic-space dtm M for
simulating A on inputs of length poly(s) cannot be lower than 2O(s). We stress that this looseness is inherent in the Berman-Lingas argument, not just in our analysis of it: a larger alphabet for A implies a longer encoding 〈A〉, thus longer inputs to the alleged logarithmic-space dtm M for  , more work space for M when it computes on these inputs, more internal configurations, more states in the
, more work space for M when it computes on these inputs, more internal configurations, more states in the  \(\tilde{B}\) simulating M, and thus more states in the final
\(\tilde{B}\) simulating M, and thus more states in the final  B simulating \(\tilde{B}\).
B simulating \(\tilde{B}\).
It is also clear that the theorem’s equivalence requires that the relationship between the given A and m and the promised B is constructive. That is, if (b) were modified to state that for every  A and length bound m a fitting
A and length bound m a fitting  B simply exists (as opposed to it being logarithmic-space constructible), then the argument for (b)⇒(a) would not stand. This is an extra obstacle in connecting L versus NL with the purely existential question of 2D versus 2N (conceivably, a proof that 2D⊇2N needs no logarithmic-space conversion of s-state
B simply exists (as opposed to it being logarithmic-space constructible), then the argument for (b)⇒(a) would not stand. This is an extra obstacle in connecting L versus NL with the purely existential question of 2D versus 2N (conceivably, a proof that 2D⊇2N needs no logarithmic-space conversion of s-state  to poly(s)-state
to poly(s)-state  ).
).
Our Theorem 3.1 is a variant of Theorem 3.0 that removes both dependences above, on alphabet size and logarithmic-space constructibility. To remove the dependence on alphabet size, we switch to another NL-complete problem; to remove the dependence on constructibility, we switch to non-uniform L. The structure of the argument, however, is the same. Note that, of the six equivalences established among the four statements, (a)⇔(b) is the one closest to the statement of Theorem 3.0; (c)⇔(d) is the equivalence claimed in Sect. 1.1 between Questions (3) and (3′); and (d)⇔(a) is the statement in terms of complexity classes, as announced in Sect. 1.3.
Theorem 3.1
The following statements are equivalent:
- (a) :
-
L/poly⊇NL.
- (b) :
-
There exists a polynomial q such that for every
 A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
q(sm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m.
B
that has at most
q(sm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m. - (c) :
-
There exists a polynomial p such that every s-state
 has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length ≤ s.
with ≤ p(s) states that agrees with it on all inputs of length ≤ s. - (d) :
-
2D⊇2N/poly.
Proof
- [(a)⇒(b)]:
-
Suppose L/poly⊇NL. Then twl join∈L/poly. Therefore, some dtm M under strong advice
 of length g(m)=poly(m) solves twl join in space strongly bounded by f(m)=logm.
of length g(m)=poly(m) solves twl join in space strongly bounded by f(m)=logm.Pick any (s,σ)-
 A and length bound m. We know that L(A)≤h
twl join via a reduction of expansion μ(m)=O(s
2
m) (Lemma 2.5). Hence, finding a
A and length bound m. We know that L(A)≤h
twl join via a reduction of expansion μ(m)=O(s
2
m) (Lemma 2.5). Hence, finding a  B for L(A) and inputs of length ≤ m reduces to finding a
B for L(A) and inputs of length ≤ m reduces to finding a  \(\tilde{B}\) for
\(\tilde{B}\) for  and inputs of length ≤ μ(m) (Lemma 2.3). Indeed, such a \(\tilde{B}\) is guaranteed by Lemma 2.2, with a number of states at most exponential in f(μ(m))+logg(μ(m)). Calculating
and inputs of length ≤ μ(m) (Lemma 2.3). Indeed, such a \(\tilde{B}\) is guaranteed by Lemma 2.2, with a number of states at most exponential in f(μ(m))+logg(μ(m)). Calculating 
we see that the number of states in B is 2⋅poly(sm)=poly(sm), as required.
- [(b)⇒(c)]:
-
Applying (b) with m=s, we deduce (c) with p(s):=q(s 2).
- [(c)⇒(d)]:
-
Assume (c). Pick any family
 . Then every \(\mathfrak {L}_{h}\) has instances of length ≤q
1(h) and is solved by some
. Then every \(\mathfrak {L}_{h}\) has instances of length ≤q
1(h) and is solved by some  A
h
with ≤q
2(h) states, for q
1 and q
2 two polynomials. Let q:=q
1+q
2. Then clearly every \(\mathfrak {L}_{h}\) has instances of length ≤q(h) and is solved by some q(h)-state
A
h
with ≤q
2(h) states, for q
1 and q
2 two polynomials. Let q:=q
1+q
2. Then clearly every \(\mathfrak {L}_{h}\) has instances of length ≤q(h) and is solved by some q(h)-state  \(A_{h}'\). Now, (c) implies that every \(A_{h}'\) has a
\(A_{h}'\). Now, (c) implies that every \(A_{h}'\) has a  B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤q(h), and is thus correct on all instances of \(\mathfrak {L}_{h}\). Hence,
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤q(h), and is thus correct on all instances of \(\mathfrak {L}_{h}\). Hence,  is a family of small
is a family of small  that solve
that solve  . Therefore,
. Therefore,  .
. - [(d)⇒(a)]:
-
Suppose 2D⊇2N/poly. Pick any L∈NL. Let Σ be its alphabet and let M be a ntm solving it (under empty advice) in space strongly bounded by logn.
For each h≥1, consider the problem \(\mathfrak {L}_{h}\) that restricts L to inputs of length <h:
$$\mathfrak {L}_h := \bigl(\bigl\{x\in L \mid |x|< h\bigr\},\ \bigl\{x\in \overline {L} \mid |x|< h\bigr\} \bigr). $$By Corollary 2.1(a) for m=h−1, we know some
 A
h
with poly(h−1)=poly(h) states agrees with M on every input of length <h, and thus decides correctly on every instance of \(\mathfrak {L}_{h}\). So,
A
h
with poly(h−1)=poly(h) states agrees with M on every input of length <h, and thus decides correctly on every instance of \(\mathfrak {L}_{h}\). So,  is a family of polynomially long problems, solvable by the family of small
is a family of polynomially long problems, solvable by the family of small  (A
h
)
h≥1. Therefore
(A
h
)
h≥1. Therefore  is in 2N/poly, and thus also in 2D (by our starting assumption). So, there exists a
is in 2N/poly, and thus also in 2D (by our starting assumption). So, there exists a  family
family  and a polynomial p such that every B
h
solves \(\mathfrak {L}_{h}\) with ≤p(h) states.
and a polynomial p such that every B
h
solves \(\mathfrak {L}_{h}\) with ≤p(h) states.Now consider the binary encodings of the automata of
 as advice strings,
as advice strings, 
and let U be the dtm which, on input x∈Σ ∗ and advice y∈{0,1}∗, interprets y as the encoding of a
 and simulates it on x. Then
and simulates it on x. Then  , because
, because 
In addition,
 is strong advice for U, because every y
m
helps U treat an input x ‘correctly’ (namely, as it would under y
|x|) not only when |x|=m but also when |x|<m: Indeed, for all m and all x with |x|=n≤m, $$\begin{array}{@{}lll} \text{$U$ accepts $x$~and~$y_{m}$} &\iff&\text{$B_{m+1}$ accepts~$x$}\quad (\text{definition of $y_{m}$ and of $U$})\\[1mm] &\iff& x\in L\quad(\text{$B_{m+1}$ solves $\mathfrak {L}_{m+1}$, and $|x|<m{+}1$})\\[1mm] &\iff&\text{$B_{n+1}$ accepts~$x$}\quad (\text{$B_{n+1}$ solves $\mathfrak {L}_{n+1}$, and $|x|<n{+}1$})\\[1mm] &\iff&\text{$U$ accepts $x$~and~$y_{n}$}\quad (\text{definition of $y_{n}$ and of $U$}). \end{array} $$
is strong advice for U, because every y
m
helps U treat an input x ‘correctly’ (namely, as it would under y
|x|) not only when |x|=m but also when |x|<m: Indeed, for all m and all x with |x|=n≤m, $$\begin{array}{@{}lll} \text{$U$ accepts $x$~and~$y_{m}$} &\iff&\text{$B_{m+1}$ accepts~$x$}\quad (\text{definition of $y_{m}$ and of $U$})\\[1mm] &\iff& x\in L\quad(\text{$B_{m+1}$ solves $\mathfrak {L}_{m+1}$, and $|x|<m{+}1$})\\[1mm] &\iff&\text{$B_{n+1}$ accepts~$x$}\quad (\text{$B_{n+1}$ solves $\mathfrak {L}_{n+1}$, and $|x|<n{+}1$})\\[1mm] &\iff&\text{$U$ accepts $x$~and~$y_{n}$}\quad (\text{definition of $y_{n}$ and of $U$}). \end{array} $$Moreover, |y m |=|〈B m+1〉|=O(p(m+1)2⋅|Σ|)=poly(m), since Σ is constant in m. Finally, the space used by U for x and y m when |x|≤m is the space for storing the pointers into y m that are necessary for the simulation of B m+1, namely O(log|y m |)=O(logpoly(m))=O(logm). Overall, U and
 witness that L∈L/poly.
witness that L∈L/poly.
□
While Theorem 3.1 uncovers the full details of the Berman-Lingas connection between space-bounded tms and size-bounded  , our next two theorems reveal that this connection is only one aspect of a deeper relationship. Specifically, they show that the equivalences of Theorem 3.1 remain valid when we appropriately decrease the space usage and advice length on the tm side and increase the input lengths on the
, our next two theorems reveal that this connection is only one aspect of a deeper relationship. Specifically, they show that the equivalences of Theorem 3.1 remain valid when we appropriately decrease the space usage and advice length on the tm side and increase the input lengths on the  side. Theorem 3.2 is the case where the space usage and the advice length decrease respectively to sub-logarithmic and sub-linear, whereas the input length increases to quasi-polynomial. Theorem 3.3 is the case of log-logarithmic space usage, poly-logarithmic advice, and exponential input lengths.
side. Theorem 3.2 is the case where the space usage and the advice length decrease respectively to sub-logarithmic and sub-linear, whereas the input length increases to quasi-polynomial. Theorem 3.3 is the case of log-logarithmic space usage, poly-logarithmic advice, and exponential input lengths.
Because Theorem 3.3 is easier to compare to Theorem 3.1, we will state and prove it before Theorem 3.2. Both proofs use arguments very similar to those used for Theorem 3.1, so we will present them in less detail. The most important difference is that twl join is replaced respectively by twl long-join and by twl join k when we prove the implications (a)⇒(b). The remaining differences are in the calculations.
Theorem 3.3
The following statements are equivalent:
- (a) :
-
LL/polylog⊇NLL.
- (b) :
-
There exists a polynomial q such that for every
 A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
q(slogm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m.
B
that has at most
q(slogm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m. - (c) :
-
There exists a polynomial p such that every s-state
 has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length ≤ 2s.
with ≤ p(s) states that agrees with it on all inputs of length ≤ 2s. - (d) :
-
2D⊇2N/exp.
Proof
- [(a)⇒(b)]:
-
If LL/polylog⊇NLL then twl long-join is in LL/polylog, so it is solved by a dtm M under strong advice
 of length g(m)=poly(logm) and strong space bound f(m)=loglogm. As in Theorem 3.1, for every (s,σ)-
of length g(m)=poly(logm) and strong space bound f(m)=loglogm. As in Theorem 3.1, for every (s,σ)- A and length bound m, we know L(A)≤h
twl long-join via a reduction of expansion μ(m)=2O(s)
m (Lemma 2.5), so it suffices to find a
A and length bound m, we know L(A)≤h
twl long-join via a reduction of expansion μ(m)=2O(s)
m (Lemma 2.5), so it suffices to find a  \(\tilde{B}\) for
\(\tilde{B}\) for  on lengths ≤ μ(m) (Lemma 2.3), which indeed exists with 2O(f(μ(m))+logg(μ(m))) states (Lemma 2.2). Now,
on lengths ≤ μ(m) (Lemma 2.3), which indeed exists with 2O(f(μ(m))+logg(μ(m))) states (Lemma 2.2). Now, 
so our
 for L(A) on lengths ≤m has 2⋅poly(slogm)=poly(slogm) states.
for L(A) on lengths ≤m has 2⋅poly(slogm)=poly(slogm) states. - [(b)⇒(c)]:
-
Applying (b) with m=2s, we deduce (c) with p(s):=q(s 2).
- [(c)⇒(d)]:
-
Assume (c), and let
 . Then every \(\mathfrak {L}_{h}\) has instances of length \(\leq2^{q_{1}(h)}\) and is solved by a
. Then every \(\mathfrak {L}_{h}\) has instances of length \(\leq2^{q_{1}(h)}\) and is solved by a  A
h
with ≤q
2(h) states, for q
1,q
2 two polynomials. So, q:=q
1+q
2 is such that every \(\mathfrak {L}_{h}\) has instances of length ≤2q(h) and is solved by a q(h)-state
A
h
with ≤q
2(h) states, for q
1,q
2 two polynomials. So, q:=q
1+q
2 is such that every \(\mathfrak {L}_{h}\) has instances of length ≤2q(h) and is solved by a q(h)-state  \(A_{h}'\). By (c), every \(A_{h}'\) has a
\(A_{h}'\). By (c), every \(A_{h}'\) has a 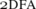 B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤2q(h), including the instances of \(\mathfrak {L}_{h}\). So, the small automata
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤2q(h), including the instances of \(\mathfrak {L}_{h}\). So, the small automata  solve
solve  , causing
, causing  .
. - [(d)⇒(a)]:
-
Suppose 2D⊇2N/exp. Pick any L∈NLL. Let Σ be its alphabet, and M a ntm solving L (under empty advice) in space strongly bounded by loglogn. As in Theorem 3.1, consider for each h≥1 the problem \(\mathfrak {L}_{h}\) that restricts L to instances of bounded length, this time exponential in h:
$$\mathfrak {L}_h := \bigl(\bigl\{ x\in L \mid|x| < 2^{h-1} \bigr\},\ \bigl\{ x\in \overline {L} \mid|x| < 2^{h-1} \bigr\}\bigr). $$By Corollary 2.1(b) for m=2h−1−1, we know some
 A
h
with poly(log(2h−1−1))=poly(h) states agrees with M on every input of length <2h−1, and thus decides correctly on every instance of \(\mathfrak {L}_{h}\). So, the family
A
h
with poly(log(2h−1−1))=poly(h) states agrees with M on every input of length <2h−1, and thus decides correctly on every instance of \(\mathfrak {L}_{h}\). So, the family  of exponentially long problems is solved by the family (A
h
)
h≥1 of small
of exponentially long problems is solved by the family (A
h
)
h≥1 of small  . Hence,
. Hence,  , and thus also
, and thus also 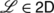 (by our starting assumption). So, some
(by our starting assumption). So, some  family
family  and polynomial p are such that every B
h
solves \(\mathfrak {L}_{h}\) with p(h) states.
and polynomial p are such that every B
h
solves \(\mathfrak {L}_{h}\) with p(h) states.We now continue with the same dtm U as in the proof of Theorem 3.1, advised by the encodings of the
 of
of  , this time ‘spread out’ exponentially:
, this time ‘spread out’ exponentially: 
So, U under
 decides whether to accept an input x by simulating B
h(|x|). Since this
decides whether to accept an input x by simulating B
h(|x|). Since this 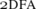 solves \(\mathfrak {L}_{h(|x|)}\), it decides L correctly on all inputs strictly shorter than $$2^{h(|x|)-1} =2^{\lceil \log(|x|+1)\rceil } \geq 2^{\log(|x|+1)} = |x|+1, $$
solves \(\mathfrak {L}_{h(|x|)}\), it decides L correctly on all inputs strictly shorter than $$2^{h(|x|)-1} =2^{\lceil \log(|x|+1)\rceil } \geq 2^{\log(|x|+1)} = |x|+1, $$and thus also on x. Therefore, U under
 decides L correctly on all inputs, namely
decides L correctly on all inputs, namely  . It is also easy to verify that every B
h(m) helps U decide correctly not only on all inputs of length exactly m but also on all inputs of length <m, namely
. It is also easy to verify that every B
h(m) helps U decide correctly not only on all inputs of length exactly m but also on all inputs of length <m, namely  is strong advice for U. Finally, $$|y_m|=\bigl|\langle B_{h(m)}\rangle \bigr| = O\bigl( p\bigl(h(m)\bigr)^2\cdot|\varSigma | \bigr) = O\bigl( p\bigl(h(m)\bigr)^2 \bigr) = \mathrm {poly}(\log m) $$
is strong advice for U. Finally, $$|y_m|=\bigl|\langle B_{h(m)}\rangle \bigr| = O\bigl( p\bigl(h(m)\bigr)^2\cdot|\varSigma | \bigr) = O\bigl( p\bigl(h(m)\bigr)^2 \bigr) = \mathrm {poly}(\log m) $$and the space used by U for the pointers into y m that are necessary to simulate B h(m) is O(log|y m |)=O(logpoly(logm))=O(loglogm). Overall, L∈LL/polylog.
□
Theorem 3.2
For any k≥1, the following statements are equivalent:
- (a) :
-
\(\textsf {DSPACE}(\sqrt[k]{\log n})/2^{O(\sqrt[k]{\log n})}\supseteq \textsf {NSPACE}(\sqrt[k]{\log n})\).
- (b) :
-
There exists a polynomial q such that for every
 A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
\(q(s\, 2^{\sqrt [k]{\log m}})\)
states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m.
B
that has at most
\(q(s\, 2^{\sqrt [k]{\log m}})\)
states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m. - (c) :
-
There exists a polynomial p such that every s-state
 has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length
\({\leq }\,2^{\log^{k} s}\).
with ≤ p(s) states that agrees with it on all inputs of length
\({\leq }\,2^{\log^{k} s}\). - (d) :
-
\({ \textsf {2}\textsf {D}}\supseteq \mathsf{2N}/{2^{O(\log^{k} h)}}\).
Proof
- [(a)⇒(b)]:
-
If (a) holds, then a dtm M under strong advice of length \(2^{O(\sqrt[k]{\log m})}\) solves twl join k in space strongly bounded by \(\sqrt[k]{\log m}\). Given a (s,σ)-
 A and length bound m, we now have a reduction of L(A) to twl join
k
with expansion \(\mu (m)=2^{O(\log^{k} s)}m\), and a
A and length bound m, we now have a reduction of L(A) to twl join
k
with expansion \(\mu (m)=2^{O(\log^{k} s)}m\), and a  \(\tilde{B}\) that solves twl join
k
on lengths ≤μ(m) with a number of states at most exponential in
\(\tilde{B}\) that solves twl join
k
on lengths ≤μ(m) with a number of states at most exponential in 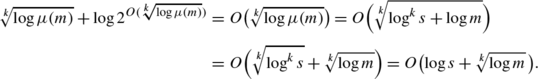
So, some
 B solves L(A) on lengths ≤m with a number of states at most $$2\cdot2^{O(\log s + \sqrt[k]{\log m})} = 2\cdot \mathrm {poly}\bigl( 2^{\log s + \sqrt[k]{\log m}} \bigr) = \mathrm {poly}\bigl( s \, 2^{\sqrt[k]{\log m}} \bigr). $$
B solves L(A) on lengths ≤m with a number of states at most $$2\cdot2^{O(\log s + \sqrt[k]{\log m})} = 2\cdot \mathrm {poly}\bigl( 2^{\log s + \sqrt[k]{\log m}} \bigr) = \mathrm {poly}\bigl( s \, 2^{\sqrt[k]{\log m}} \bigr). $$ - [(b)⇒(c)]:
-
Applying (b) with \(m=2^{\log^{k} s}\), we deduce (c) with p(s):=q(s 2).
- [(c)⇒(d)]:
-
Assuming (c), we let
 and pick q such that every \(\mathfrak {L}_{h}\) has instances of length \(\leq2^{\log^{k} q(h)}\) and is solved by a q(h)-state
and pick q such that every \(\mathfrak {L}_{h}\) has instances of length \(\leq2^{\log^{k} q(h)}\) and is solved by a q(h)-state  \(A_{h}'\). By (c), every \(A_{h}'\) has a
\(A_{h}'\). By (c), every \(A_{h}'\) has a  B
h
with ≤p(q(h)) states that agrees with it on all inputs of length \(\leq2^{\log ^{k} q(h)}\), and thus solves \(\mathfrak {L}_{h}\). Hence
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length \(\leq2^{\log ^{k} q(h)}\), and thus solves \(\mathfrak {L}_{h}\). Hence  .
. - [(d)⇒(a)]:
-
Suppose \({ \textsf {2}\textsf {D}}\supseteq \mathsf{2N}/{2^{O(\log^{k} h)}}\) and some ntm solves L under empty advice in space strongly bounded by \(\sqrt [k]{\log n}\). For every h≥1, we consider the restriction \(\mathfrak {L}_{h}\) of L to instances of length \(<2^{\lceil \log h\rceil ^{k}}\). Applying Lemma 2.2 for \(m=2^{\lceil \log h\rceil ^{k}}{-}1\) and \(f(m)=\sqrt[k]{\log m}\) and g(m)=0, we see that \(\mathfrak {L}_{h}\) is solved by a
 with a number of states exponential in $$f(m) = \sqrt[k]{\log m} = \sqrt[k]{\log\bigl( 2^{\lceil \log h\rceil ^k}{-}1\bigr)} = O(\log h) $$
with a number of states exponential in $$f(m) = \sqrt[k]{\log m} = \sqrt[k]{\log\bigl( 2^{\lceil \log h\rceil ^k}{-}1\bigr)} = O(\log h) $$and thus polynomial in h. Hence, \((\mathfrak {L}_{h})_{h\geq1}\) is in \({\textsf {2}\textsf {N}}/2^{O(\log^{k} h)}\subseteq { \textsf {2}\textsf {D}}\), and thus solvable by a family (B h ) h≥1 of small
 . Using the encodings of these
. Using the encodings of these  as advice
as advice 
to the dtm U from the proof of Theorem 3.1, we again verify that
 , that
, that  is strong advice of length \(2^{O(\sqrt [k]{\log m})}\), and that the space usage is \(O(\sqrt[k]{\log m})\).
is strong advice of length \(2^{O(\sqrt [k]{\log m})}\), and that the space usage is \(O(\sqrt[k]{\log m})\).
□
4 Conclusion
We strengthened and deepened an old theorem of Berman and Lingas (Theorem 3.0), which connected the comparison between determinism and nondeterminism in size-bounded two-way finite automata to the comparison between determinism and nondeterminism in space-bounded Turing machines. We proved three variants of that theorem, one which elaborated directly on it and tightened its statement (Theorem 3.1), and two more which extended this tightened statement to other combinations of bounds for the relevant resources (Theorems 3.2 and 3.3).
Our arguments suggest a more general proof scheme, applicable not only in the comparison between determinism and nondeterminism, but also in the comparison of other modes of computation. As evidence for this generality, we stated without proof a variant of the Berman-Lingas Theorem for the comparison between determinism and alternation (Theorem 1.4). We expect that several theorems of this kind will strengthen the connection between the size complexity of two-way finite automata and the space complexity of Turing machines, for the benefit of both theories.
In light of our arguments, it would also be interesting to explore possible improvements of the implication (7), the recent theorem of Geffert and Pighizzini from [4]. It is not hard to see that this can be strengthened by replacing its assumption that L⊇NL with the weaker assumption that L/poly⊇NL. It is then likely that the converse becomes true as well, but proving it appears not to be as straightforward.
Notes
Note the unusual forms ‘A⊇B’ and ‘A⊉B’. In cases where A⊆B (e.g., when A=2D & B=2N), these are of course equivalent to the more usual ‘A=B’ and ‘A⊆̷B’. However, we will encounter cases where A⊆B is not true (e.g., when A=2D & B=2N/poly or when A=L/poly & B=NL—see below) and hence ‘A⊇B’ and ‘A⊉B’ are appropriate. We thus use these forms throughout the article, so that all statements are easy to compare. We read and think of these forms as ‘A covers/does not cover B’.
Note that a set of designated final states F is not really necessary in this definition. Since the
 accepts by falling off ⊣, designating all states as accepting or just one state as accepting (e.g., q
0) would have had the same effect. With F, our definition stays comparable to other standard finite automata definitions.
accepts by falling off ⊣, designating all states as accepting or just one state as accepting (e.g., q
0) would have had the same effect. With F, our definition stays comparable to other standard finite automata definitions.Note that, in contrast, for an
 with n>m we have no guarantee that A
m
agrees with M under
with n>m we have no guarantee that A
m
agrees with M under  . It may be that the computation tree τ
n
of M on input x and advice y
n
=ε uses f(n) work tape cells on every accepting branch. Hence, if f(n)>f(m), our A
m
will be missing some of the states necessary to simulate these accepting branches in its computation tree \(\tau _{m}'\) on x. Therefore, τ
n
will be accepting but \(\tau _{m}'\) will be rejecting—despite the fact that y
n
=y
m
=ε.
. It may be that the computation tree τ
n
of M on input x and advice y
n
=ε uses f(n) work tape cells on every accepting branch. Hence, if f(n)>f(m), our A
m
will be missing some of the states necessary to simulate these accepting branches in its computation tree \(\tau _{m}'\) on x. Therefore, τ
n
will be accepting but \(\tau _{m}'\) will be rejecting—despite the fact that y
n
=y
m
=ε.These trailing 0s are, in fact, redundant. They are included in the definition just for symmetry with the definitions of the variants in the next two paragraphs.
More tightly, the expansion of the first reduction is O(s 2 σ)+mlgσ. But the looser O(s 2 σm) is simpler and does not harm our conclusions, since it is later (Theorem 3.0, forward direction) fed to an unspecified polynomial. Similar looseness is adopted elsewhere, too.
The actual statement of [3, Theorem 6] is very close to the usual citation (8); however, it also includes a pointer to a Remark a few pages later (p. 17), which explains that the promised
 can be constructed in logarithmic space and that with this observation the theorem becomes an equivalence. We also note that the actual statement of [3, Theorem 6] uses s⋅m as the length bound, for s the number of states in the
can be constructed in logarithmic space and that with this observation the theorem becomes an equivalence. We also note that the actual statement of [3, Theorem 6] uses s⋅m as the length bound, for s the number of states in the  , whereas the full statement (\(8^{\scriptscriptstyle +}\)) uses just m; the two statements are equivalent, but (\(8^{\scriptscriptstyle +}\)) is simpler and facilitates comparison with subsequent statements.
, whereas the full statement (\(8^{\scriptscriptstyle +}\)) uses just m; the two statements are equivalent, but (\(8^{\scriptscriptstyle +}\)) is simpler and facilitates comparison with subsequent statements.
References
Alberts, M.: Space complexity of alternating Turing machines. In: Proceedings of FCT, pp. 1–7 (1985)
Aleliunas, R., Karp, R.M., Lipton, R.J., Lovász, L., Rackoff, C.: Random walks, universal traversal sequences, and the complexity of maze problems. In: Proceedings of FOCS, pp. 218–223 (1979)
Berman, P., Lingas, A.: On complexity of regular languages in terms of finite automata. Report 304, Institute of Computer Science, Polish Academy of Sciences, Warsaw (1977)
Geffert, V., Pighizzini, G.: Two-way unary automata versus logarithmic space. Inf. Comput. 209(7), 1016–1025 (2011)
Geffert, V., Mereghetti, C., Pighizzini, G.: Converting two-way nondeterministic unary automata into simpler automata. Theor. Comput. Sci. 295, 189–203 (2003)
Hopcroft, J.E., Ullman, J.D.: Some results on tape-bounded Turing machines. J. ACM 16(1), 168–177 (1967)
Hromkovič, J., Schnitger, G.: Nondeterminism versus determinism for two-way finite automata: generalizations of Sipser’s separation. In: Proceedings of ICALP, pp. 439–451 (2003)
Ibarra, O.H., Ravikumar, B.: Sublogarithmic-space Turing machines, nonuniform space complexity, and closure properties. Math. Syst. Theory 21, 1–17 (1988)
Kapoutsis, C.: Deterministic moles cannot solve liveness. J. Autom. Lang. Comb. 12(1–2), 215–235 (2007)
Kapoutsis, C.: Nondeterminism is essential in small 2FAs with few reversals. In: Proceedings of ICALP, vol. 2, pp. 192–209 (2011)
Karp, R.M., Lipton, R.J.: Some connections between nonuniform and uniform complexity classes. In: Proceedings of STOC, pp. 302–309 (1980)
Kuroda, S.: Classes of languages and linear-bounded automata. Inf. Control 7, 207–223 (1964)
Sakoda, W.J., Sipser, M.: Nondeterminism and the size of two-way finite automata. In: Proceedings of STOC, pp. 275–286 (1978)
Savitch, W.J.: Relationships between nondeterministic and deterministic tape complexities. J. Comput. Syst. Sci. 4, 177–192 (1970)
Seiferas, J.I.: Untitled manuscript, communicated to M. Sipser (1973)
Shepherdson, J.C.: The reduction of two-way automata to one-way automata. IBM J. Res. Dev. 3, 198–200 (1959)
Stearns, R.E., Hartmanis, J., Lewis, P.M. II: Hierarchies of memory limited computations. In: Proceedings of SWCT, pp. 179–190 (1965)
Szepietowski, A.: If deterministic and nondeterministic space complexities are equal for loglogn then they are also equal for logn. In: Proceedings of STACS, pp. 251–255 (1989)
Author information
Authors and Affiliations
Corresponding author
Additional information
Research funded by a Marie Curie Intra-European Fellowship (pief-ga-2009-253368) within the European Union Seventh Framework Programme (fp7/2007-2013).
Rights and permissions
About this article
Cite this article
Kapoutsis, C.A. Two-Way Automata Versus Logarithmic Space. Theory Comput Syst 55, 421–447 (2014). https://doi.org/10.1007/s00224-013-9465-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-013-9465-0


 has a poly(s)-state
has a poly(s)-state  that agrees with it on all inputs of length ≤s if and only if
that agrees with it on all inputs of length ≤s if and only if  has a poly(s)-state
has a poly(s)-state  that agrees with it on all inputs of length ≤2s if and only if
that agrees with it on all inputs of length ≤2s if and only if 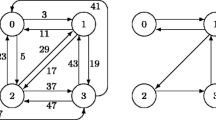

 Versus Space-Bounded
Versus Space-Bounded 
 , then τ
n
accepts. Hence, τ
m
accepts as well. Therefore, some accepting branch β in τ
m
uses ≤ f(m) work tape cells (because f is a weak space bound). So, the corresponding branch β′ in
, then τ
n
accepts. Hence, τ
m
accepts as well. Therefore, some accepting branch β in τ
m
uses ≤ f(m) work tape cells (because f is a weak space bound). So, the corresponding branch β′ in  , then τ
n
does not accept. Hence, τ
m
does not accept either. Therefore, every branch in
, then τ
n
does not accept. Hence, τ
m
does not accept either. Therefore, every branch in  is empty, then the agreement between A
m
and M under
is empty, then the agreement between A
m
and M under  extends also to every
extends also to every 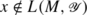 of length n>m. Indeed: Since
of length n>m. Indeed: Since  , we know τ
n
does not accept, hence τ
m
does not accept (because, since
, we know τ
n
does not accept, hence τ
m
does not accept (because, since  is empty, we have y
n
=y
m
and thus τ
n
=τ
m
), and thus
is empty, we have y
n
=y
m
and thus τ
n
=τ
m
), and thus  A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is. Moreover, there exists a logarithmic-space transducer T
M
which, given m (in unary), computes A
m
(in binary).
A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is. Moreover, there exists a logarithmic-space transducer T
M
which, given m (in unary), computes A
m
(in binary). A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is.
A
m
that may disagree with M
only on accepted inputs longer than m—and is deterministic, if
M is.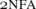 that has 2O(f(m)+logg(m))=poly(m) states and may disagree with M only on accepted inputs longer than m.
that has 2O(f(m)+logg(m))=poly(m) states and may disagree with M only on accepted inputs longer than m. guaranteed by Lemma 2.2 for m and for M under the empty advice and the weak space bound f(m)=O(loglogm). Since the advice is empty, we know that its length is g(m)=0 and that A
m
also agrees with M on all non-accepted inputs. Therefore, A
m
has 2O(f(m)+logg(m))=2O(loglogm)=poly(logm) states and may disagree with M only on accepted inputs longer than m.
guaranteed by Lemma 2.2 for m and for M under the empty advice and the weak space bound f(m)=O(loglogm). Since the advice is empty, we know that its length is g(m)=0 and that A
m
also agrees with M on all non-accepted inputs. Therefore, A
m
has 2O(f(m)+logg(m))=2O(loglogm)=poly(logm) states and may disagree with M only on accepted inputs longer than m.
 A (in binary) and a length bound m (in unary), outputs a
A (in binary) and a length bound m (in unary), outputs a
 B (in binary) that has at most poly(sσm) states, for s
and σ
the number of states and symbols in A, and may disagree with A
only on accepted inputs longer than m.
B (in binary) that has at most poly(sσm) states, for s
and σ
the number of states and symbols in A, and may disagree with A
only on accepted inputs longer than m. . Therefore, some
. Therefore, some  in space strongly bounded by logn.
in space strongly bounded by logn. A and any length bound m. Lemma 2.5 says that
A and any length bound m. Lemma 2.5 says that  via a reduction of expansion μ. Hence, Lemma 2.3 implies that constructing a
via a reduction of expansion μ. Hence, Lemma 2.3 implies that constructing a  B for L(A) and input lengths ≤ m reduces to constructing a
B for L(A) and input lengths ≤ m reduces to constructing a 
 and input lengths ≤ μ(m). This latter construction is indeed possible by Corollary 2.1(a).
and input lengths ≤ μ(m). This latter construction is indeed possible by Corollary 2.1(a).
 , by running on 〈A〉 the logarithmic-space transducer given by that lemma. Finally, we convert
, by running on 〈A〉 the logarithmic-space transducer given by that lemma. Finally, we convert  B, by running the logarithmic-space transducer T
h given by Lemma 2.3. By the transitivity of logarithmic-space transductions, we know that the full algorithm can also be implemented in logarithmic space. It remains to verify the properties of B.
B, by running the logarithmic-space transducer T
h given by Lemma 2.3. By the transitivity of logarithmic-space transductions, we know that the full algorithm can also be implemented in logarithmic space. It remains to verify the properties of B. , hence M does not accept y, so
, hence M does not accept y, so  , hence M accepts y, hence
, hence M accepts y, hence  reduces to
reduces to  in logarithmic space, as follows. Given a
in logarithmic space, as follows. Given a  A and an input x, we apply the following two logarithmic-space transductions, where m=|x|:
A and an input x, we apply the following two logarithmic-space transductions, where m=|x|:  B that agrees with A on all inputs of length ≤m, including x. Clearly,
B that agrees with A on all inputs of length ≤m, including x. Clearly,  iff
iff  .
. , the logarithmic-space reduction to
, the logarithmic-space reduction to  , the fact that
, the fact that 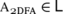 (easy, just simulate the
(easy, just simulate the  , being careful not to loop), and the closure of
, being careful not to loop), and the closure of  A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
q(sm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m.
B
that has at most
q(sm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m. has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length ≤ s.
with ≤ p(s) states that agrees with it on all inputs of length ≤ s. of length g(m)=poly(m) solves
of length g(m)=poly(m) solves  A and length bound m. We know that L(A)≤h
A and length bound m. We know that L(A)≤h
 B for L(A) and inputs of length ≤ m reduces to finding a
B for L(A) and inputs of length ≤ m reduces to finding a 
 and inputs of length ≤ μ(m) (Lemma 2.3). Indeed, such a
and inputs of length ≤ μ(m) (Lemma 2.3). Indeed, such a 
 . Then every
. Then every  A
h
with ≤q
2(h) states, for q
1 and q
2 two polynomials. Let q:=q
1+q
2. Then clearly every
A
h
with ≤q
2(h) states, for q
1 and q
2 two polynomials. Let q:=q
1+q
2. Then clearly every 
 B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤q(h), and is thus correct on all instances of
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤q(h), and is thus correct on all instances of  is a family of small
is a family of small  that solve
that solve  . Therefore,
. Therefore,  .
. A
h
with poly(h−1)=poly(h) states agrees with M on every input of length <h, and thus decides correctly on every instance of
A
h
with poly(h−1)=poly(h) states agrees with M on every input of length <h, and thus decides correctly on every instance of  is a family of polynomially long problems, solvable by the family of small
is a family of polynomially long problems, solvable by the family of small  (A
h
)
h≥1. Therefore
(A
h
)
h≥1. Therefore  is in
is in  family
family  and a polynomial p such that every B
h
solves
and a polynomial p such that every B
h
solves  as advice strings,
as advice strings, 
 and simulates it on x. Then
and simulates it on x. Then  , because
, because 
 is strong advice for U, because every y
m
helps U treat an input x ‘correctly’ (namely, as it would under y
|x|) not only when |x|=m but also when |x|<m: Indeed, for all m and all x with |x|=n≤m,
is strong advice for U, because every y
m
helps U treat an input x ‘correctly’ (namely, as it would under y
|x|) not only when |x|=m but also when |x|<m: Indeed, for all m and all x with |x|=n≤m,  witness that L∈
witness that L∈ A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
q(slogm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m.
B
that has at most
q(slogm) states, for
s
the number of states in A, and agrees with A
on all inputs of length at most m. has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length ≤ 2s.
with ≤ p(s) states that agrees with it on all inputs of length ≤ 2s. of length g(m)=poly(logm) and strong space bound f(m)=loglogm. As in Theorem 3.1, for every (s,σ)-
of length g(m)=poly(logm) and strong space bound f(m)=loglogm. As in Theorem 3.1, for every (s,σ)- A and length bound m, we know L(A)≤h
A and length bound m, we know L(A)≤h

 on lengths ≤ μ(m) (Lemma 2.3), which indeed exists with 2O(f(μ(m))+logg(μ(m))) states (Lemma 2.2). Now,
on lengths ≤ μ(m) (Lemma 2.3), which indeed exists with 2O(f(μ(m))+logg(μ(m))) states (Lemma 2.2). Now, 
 for L(A) on lengths ≤m has 2⋅poly(slogm)=poly(slogm) states.
for L(A) on lengths ≤m has 2⋅poly(slogm)=poly(slogm) states. . Then every
. Then every  A
h
with ≤q
2(h) states, for q
1,q
2 two polynomials. So, q:=q
1+q
2 is such that every
A
h
with ≤q
2(h) states, for q
1,q
2 two polynomials. So, q:=q
1+q
2 is such that every 
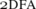 B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤2q(h), including the instances of
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length ≤2q(h), including the instances of  solve
solve  , causing
, causing  .
. A
h
with poly(log(2h−1−1))=poly(h) states agrees with M on every input of length <2h−1, and thus decides correctly on every instance of
A
h
with poly(log(2h−1−1))=poly(h) states agrees with M on every input of length <2h−1, and thus decides correctly on every instance of  of exponentially long problems is solved by the family (A
h
)
h≥1 of small
of exponentially long problems is solved by the family (A
h
)
h≥1 of small  . Hence,
. Hence,  , and thus also
, and thus also 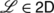 (by our starting assumption). So, some
(by our starting assumption). So, some  family
family  and polynomial p are such that every B
h
solves
and polynomial p are such that every B
h
solves  of
of  , this time ‘spread out’ exponentially:
, this time ‘spread out’ exponentially: 
 decides whether to accept an input x by simulating B
h(|x|). Since this
decides whether to accept an input x by simulating B
h(|x|). Since this 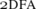 solves
solves  decides L correctly on all inputs, namely
decides L correctly on all inputs, namely  . It is also easy to verify that every B
h(m) helps U decide correctly not only on all inputs of length exactly m but also on all inputs of length <m, namely
. It is also easy to verify that every B
h(m) helps U decide correctly not only on all inputs of length exactly m but also on all inputs of length <m, namely  is strong advice for U. Finally,
is strong advice for U. Finally,  A
and length bound m
there exists a
A
and length bound m
there exists a
 B
that has at most
B
that has at most
 has a
has a
 with ≤ p(s) states that agrees with it on all inputs of length
with ≤ p(s) states that agrees with it on all inputs of length
 A and length bound m, we now have a reduction of L(A) to
A and length bound m, we now have a reduction of L(A) to 
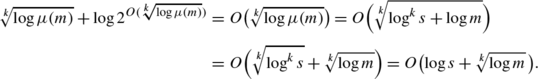
 B solves L(A) on lengths ≤m with a number of states at most
B solves L(A) on lengths ≤m with a number of states at most  and pick q such that every
and pick q such that every 
 B
h
with ≤p(q(h)) states that agrees with it on all inputs of length
B
h
with ≤p(q(h)) states that agrees with it on all inputs of length  .
. with a number of states exponential in
with a number of states exponential in  . Using the encodings of these
. Using the encodings of these  as advice
as advice 
 , that
, that  is strong advice of length
is strong advice of length  accepts by falling off ⊣, designating all states as accepting or just one state as accepting (e.g., q
0) would have had the same effect. With F, our definition stays comparable to other standard finite automata definitions.
accepts by falling off ⊣, designating all states as accepting or just one state as accepting (e.g., q
0) would have had the same effect. With F, our definition stays comparable to other standard finite automata definitions. with n>m we have no guarantee that A
m
agrees with M under
with n>m we have no guarantee that A
m
agrees with M under  . It may be that the computation tree τ
n
of M on input x and advice y
n
=ε uses f(n) work tape cells on every accepting branch. Hence, if f(n)>f(m), our A
m
will be missing some of the states necessary to simulate these accepting branches in its computation tree
. It may be that the computation tree τ
n
of M on input x and advice y
n
=ε uses f(n) work tape cells on every accepting branch. Hence, if f(n)>f(m), our A
m
will be missing some of the states necessary to simulate these accepting branches in its computation tree  can be constructed in logarithmic space and that with this observation the theorem becomes an equivalence. We also note that the actual statement of [
can be constructed in logarithmic space and that with this observation the theorem becomes an equivalence. We also note that the actual statement of [ , whereas the full statement (
, whereas the full statement (