Nonpreemptive Coordination Mechanisms for Identical Machines

Abstract

We focus on the problem of scheduling n weighted selfish tasks on m identical parallel machines and we study the performance of nonpreemptive coordination mechanisms. A nonpreemptive coordination mechanism consists of m local scheduling policies that decide the processing order of the tasks on each machine without delays or interruptions. We discuss the existence of Nash equilibria for this setting and show that it is not a guaranteed property of all nonpreemptive coordination mechanisms. Next, we focus on the wider class of randomized Nash equilibria and prove lower bounds on the price of anarchy. Our lower bounds are presented in comparison to the currently best known coordination mechanism (which uses delays) and lead to the conclusion that preemption or delays are required in order to improve on the currently best known solution.

1 Introduction

The advent of networking had a huge impact on the landscape of computer science and gave rise to environments where several self-interested entities share computational and communication resources. The rapid growth of the Internet has drawn attention to such settings and tools from game theory have been widely applied to model the interactions among selfish agents [26, 31].

In this framework, selfish entities are considered rational players who wish to minimize some defined personal cost (e.g. the time required for the processing of a task requested by the entity) and are expected to reach a solution state from which they are not willing to deviate. The most famous such concept is the Nash equilibrium, which is an outcome such that no player benefits by switching to a different choice unilaterally. The performance of the whole system is measured by a social cost (e.g. the maximum or the average of the players’ costs) and, in general, Nash equilibria are not optimal from this perspective. This inefficiency is captured by the price of anarchy [18, 27, 30]. More specifically, the price of anarchy measures the worst case ratio of the social cost in a Nash equilibrium to the optimal social cost.

A natural question that arises is whether and how this inefficiency might be contained. In distributed settings, such as those encountered in networked environments, imposing a centralized control upon the users and forcing them to coordinate and produce a socially desirable outcome is not an available alternative. Instead, the designer is restricted to defining system-wide rules and protocols a priori. This idea is traditional in game theory and is known as mechanism design [24, 25]. In this framework various approaches have been proposed such as applying economic incentives [4, 7, 11] or the Stackelberg strategy [3, 16, 29, 33]. One fundamental characteristic of these approaches is that global knowledge is required and the communication costs involved are heavy. In such settings where communication is impossible or the communication costs involved are too high, coordination mechanisms [6, 17] remedy the situation. Coordination mechanisms define local rules that do not require any information other than the state on a specific shared resource of the system.

In the described framework consider a selfish task scheduling game (in literature one may also encounter the names selfish task allocation, selfish load balancing, and selfish routing on parallel links). The game consists of n selfish tasks expecting to be processed on a system of m machines. The objective of each task is to minimize its completion time by selecting, as a strategy, the machine that will process it. The coordination mechanism for this game defines the scheduling policies of the m machines. The scheduling policies are strictly local and have no knowledge about the state of other machines. We are interested in the performance of the system which is measured by the total makespan, i.e. the completion time of all tasks. Tasks may select a probability distribution among the available machines as a strategy and, in this case, the social cost will be the expected makespan. The price of anarchy of a coordination mechanism is, among all possible sets of selfish tasks, the worst case ratio of the expected makespan in a Nash equilibrium to the optimal makespan.

In this paper we will study selfish scheduling games where all tasks are allowed to select any machine, all tasks have complete information about the weights of the other tasks and about the scheduling policies, all machines have identical processing speed and all machines have nonpreemptive policies. A policy is nonpreemptive if no task is delayed or interrupted while it is being processed.

1.1 Related Work

The price of anarchy and the existence of Nash equilibria for selfish scheduling on identical machines have received significant attention. The study of selfish scheduling was initiated in [18] by Koutsoupias and Papadimitriou. The model there is equivalent to a specific coordination mechanism, the one where every machine completes all tasks simultaneously at time equal to the sum of their processing times. This coordination mechanism, which we will call the KP mechanism has been studied extensively. For m=2, the authors in [18] proved that the price of anarchy of the KP mechanism is $\frac{3}{2}$ and for general m, they showed that it is $\varOmega(\frac{\log m}{\log \log m})$. In [22], Mavronicolas and Spirakis managed to prove a tight upper bound for the KP mechanism regarding the fully mixed case, where all tasks play all machines with positive probability. The price of anarchy of the KP mechanism for general m was settled independently in [10] and [19] and was shown to be $\varTheta(\frac{\log m}{\log \log m})$. In [12], Fotakis et al. show that the KP mechanism admits at least one pure strategy Nash equilibrium for any set of tasks. In [22], Mavronicolas and Spirakis show that the randomized Nash equilibrium, in which all tasks assign positive probability to all machines, is unique.

Subsequently attention was driven to coordination mechanisms other than the KP mechanism. In [6], Christodoulou et al. propose and study several coordination mechanisms for machines with identical processing speed. For 2 machines they propose the Largest First–Shortest First coordination mechanism. The policies of the mechanism are as follows. The first machine schedules the tasks it receives in decreasing weight order, while the second machine schedules the tasks in increasing weight order. The price of anarchy of this mechanism is $\frac{4}{3}$. For m≥2, Christodoulou et al. propose the Largest First coordination mechanism, where all machines schedule the tasks in decreasing weight order and each machine j imposes a delay jϵ, with ϵ infinitesimal. The price of anarchy of Largest First is $\frac{4}{3}-\frac{1}{3m}$ and is the best known among coordination mechanisms for selfish scheduling on machines with identical speed. Note that this mechanism does not fall in the nonpreemptive category since it uses delays. The mechanisms described above have a unique pure strategy Nash equilibrium for every set of tasks. The Largest First–Shortest First mechanism may also admit randomized Nash equilibria with social cost equal to that of the unique pure strategy Nash equilibrium.

We conclude this subsection by providing pointers to earlier work in the area of selfish scheduling, in settings other than that of machines with identical speed. Several such extensions of selfish scheduling have been studied, such as the case of machines with different processing speed [10, 18] and the restricted assignment model, where tasks are restricted to subsets of the machines [2]. In [15], Immorlica et al. study several coordination mechanisms, focusing on pure strategy Nash equilibria. Truthful coordination mechanisms, i.e., mechanisms such that no task benefits from declaring a false weight, are considered in [1, 6]. More general cases are studied in [5, 9, 20, 21] and different social costs, such as the average task cost, are studied in [5, 13, 14, 34]. Results in the area of selfish scheduling are surveyed in [8, 32].

1.2 Our Contributions

We focus on coordination mechanisms whose local scheduling policies simply decide the order in which the received tasks will be processed, i.e., nonpreemptive coordination mechanisms. We study the existence of Nash equilibria in games defined by a nonpreemptive coordination mechanism and a set of tasks. We prove that there exist identical machine scheduling games with nonpreemptive coordination mechanisms that do not accept any pure strategy Nash equilibrium, so naturally we turn our discussion to the broader class of randomized Nash equilibria.

We compare the performance of nonpreemptive coordination mechanisms, under the price of anarchy metric, with the $\frac{4}{3}-\frac{1}{3m}$ price of anarchy achieved by Largest First, which is the best known coordination mechanism. We prove constant lower bounds $\frac{7}{6}$ for m=2 and $\frac{3}{2}$ for m>2 and, this way, establish that we can’t produce a nonpreemptive coordination mechanism that outperforms the Largest First mechanism. We also extend the lower bound on the price of anarchy of every nonpreemptive coordination mechanism to $\varOmega(\frac{\log \log m}{\log \log \log m})$.

Combining our lower bounds with upper bounds from earlier work, we derive that the price of anarchy of the best nonpreemptive coordination mechanism for m=2 is between $\frac{4}{3}$ and $\frac{7}{6}$. For general m the price of anarchy of the best nonpreemptive coordination mechanism is $O(\frac{\log m}{\log \log m})$ and $\varOmega(\frac{\log \log m}{\log \log \log m})$.

2 The Model

A game of scheduling n weighted tasks on m parallel machines with identical speed is fully described by (c,w), where c and w are as follows:

• 1. c is a coordination mechanism, i.e., a set of m local scheduling policies. The scheduling policy of each machine j observes the weights of the tasks allocated to j and decides the completion time of each task.

• 2. w={w ₁,w ₂,…,w _n } is a vector of n task weights, with w _i being the weight of task i. We will assume that the tasks will be given in increasing weight order and that tasks with the same weight can be ordered from smallest to largest in a predefined manner.

The set of pure strategies of every task is the set of machines {1,2,…,m}. A randomized strategy is naturally a probability distribution over the set {1,2,…,m}. If p _i,j is the probability that task i assigns to machine j, then the n×m array p={p _i,j } describes an outcome of the game. For the game (c,w) and outcome p, we denote as t _i,j (c,w,p _−i ) the expected completion time of task i if all other tasks play their strategies as in p and i plays purely machine j. Outcome p is a Nash equilibrium in (c,w) if and only if for all i=1,…,n and for all j=1,…,m:

$$p_{i,j}>0\quad \Rightarrow\quad t_{i,j}(c,w,p_{-i}) \le t_{i,k}(c,w,p_{-i}) \quad\text{for all } k=1,\ldots,m . $$

This means that every task assigns positive probability only to machines that minimize its expected completion time. Thus, no task can improve its completion time by changing its selected probability distribution in p.

The social cost of the system will be the expected maximum among the task completion times, i.e., the expected makespan. We will write s(c,w,p) for the expected makespan of outcome p in the game (c,w). The price of anarchy of a coordination mechanism c is defined as the worst case ratio of the expected makespan in a Nash equilibrium to the optimal makespan, for all possible sets w. We will write $\operatorname{opt}(w,m)$ for the optimal makespan, which is given by the optimal allocation of the n tasks to the m machines, independent of the behavioral model. Summarizing we get that

$$\operatorname{PoA}(c) = \max_{w} \max_{\mathrm{Nash}\ p} \frac{s(c,w,p)}{\operatorname{opt}(w,m)} $$

2.1 Nonpreemptive Coordination Mechanisms

In this subsection, we will define nonpreemptive coordination mechanisms and introduce some notation. A nonpreemptive coordination mechanism is a coordination mechanism that consists of m nonpreemptive policies. A nonpreemptive policy for some machine j is one that, given a set of task weights (the weights of the tasks allocated to machine j), decides the processing order of the tasks. Such a policy is described by an infinite set c _j of task weight orderings, such that c _j includes exactly one ordering for every possible set of task weights received. The task whose weight has the k-th position in the ordering, is served k-th in order. Assume that c _j contains the ordering $(w_{a_{1}}, w_{a_{2}}, \ldots, w_{a_{k}})$. The task with weight $w_{a_{i}}$ has completion time $w_{a_{1}}+w_{a_{2}}+\cdots+w_{a_{i}}$. Obviously, c _j can’t contain any other ordering of the set $\{w_{a_{1}}, w_{a_{2}}, \ldots, w_{a_{k}}\}$. Now consider the following example:

$$c_j = \bigl\{(1,2),(5,9,3),(2,4,5),(4,1,2),\ldots\bigr\} . $$

This policy means that if machine j receives tasks 1, 2, and 3 with weights w ₁=1, w ₂=2, and w ₃=4, then task 3 is processed first with completion time 4, task 1 is processed second with completion time 5, and task 2 is processed last with completion time 7.

If there are weights with equal value, the ordering makes them distinct by assigning subscripts from assumed smallest to assumed largest. This means that the ordering for weights 4, 4, and 3, could be (4₂,3,4₁), where 4₁ is the weight of the task that is considered smaller among the two with weight 4. Note that the game might include more than two tasks with weight 4 but in case a machine receives any two of them it will name them 4₁ and 4₂ depending on which one is considered smaller (4₁) and which one is considered larger (4₂). Regarding the tie breaking rule, recall that the tasks are given in assumed increasing weight order. So if w _i =w _j and j>i, then w _j is the one considered larger by the scheduling policy. We will write, for example, that a policy includes (4,3,4) if it includes (4₁,3,4₂) or (4₂,3,4₁).

We write c={c ₁,c ₂,…,c _m }, with c _j , j=1,…,m, the policy of machine j, for an m-machine nonpreemptive coordination mechanism.

3 Equilibria and Nonpreemptive Coordination Mechanisms

Task scheduling games with coordination mechanisms can be thought of as variations of congestion games [17, 23, 28]. Congestion games consist of n players and m resources, with each player wishing to use a subset of the resources. The cost of each player on any resource is a function of the number of players using it. Thus, all players on a resource j suffer the same cost. The total cost of a player i is the sum of the costs of the resources that i uses. In the task scheduling model, studied in this paper, we have n players, m resources and each player wishing to use exactly one resource. The difference with congestion games is that the cost of player i on resource j does not only depend on the number of players using j. It also depends on their weights. Moreover, the costs assigned to the players by resource j are not symmetrical and depend on the order in which the tasks will be processed. Thus, task scheduling games share many similarities with congestion games but they are not a subclass of them.

What is of interest to us in this section is that congestion games have been shown to possess at least one pure strategy Nash equilibrium [28]. Moreover, the coordination mechanisms for selfish scheduling that have been studied so far, also possess at least one pure strategy Nash equilibrium for every set of task weights w (see Sect. 1.1). Thus, it is natural to ask whether this is a rule for nonpreemptive coordination mechanisms. We get the following result.

Theorem 1

A game (c,w), with c a nonpreemptive coordination mechanism and w a set of task weights, does not necessarily possess a pure strategy Nash equilibrium.

Proof

We prove this by presenting an example. Consider a game with n=4 tasks with weights w ₁=1, w ₂=1, w ₃=2, and w ₄=2. Note that the tasks are always given in (assumed) increasing weight order. Now suppose that the policies c ₁, c ₂ of the coordination mechanism c are as follows.

$$c_1 = c_2 = \bigl\{ (2,1), (2_1,2_2), (1_1,2,1_2), (2_1,2_2,1), \ldots \bigr\}. $$

This game does not admit a pure strategy Nash equilibrium. Our reasoning is as follows:

• 1. For the case where all tasks select the same machine, it is trivial to see that there will be 3 tasks (all but the one served first) with incentive to switch to the other machine.

• 2. For the case where 3 tasks select one machine and 1 task the other one.

  • (a) In case the task that is alone has weight 1, the other task with weight 1 has an incentive to join it, since its completion time drops from 5 to at most 2.

  • (b) In case the task that is alone has weight 2, the task with weight 1₂ (task 2—remember that they are given in increasing weight order) has an incentive to join it, since its cost drops from 4 to 3.

• 3. For the case where each machine is assigned 2 tasks.

  • (a) In case the tasks with weight 2 go to the same machine, then the task with weight 2₂ (task 4) has an incentive to switch to the other machine, since its cost drops from 4 to 3.

  • (b) In case each machine receives tasks with weight 1 and 2, then the task with weight 1₁ (task 1) has an incentive to switch to the other machine, since its completion time drops from 3 to 1.

This exhausts all possibilities. □

The existence of at least one randomized Nash equilibrium follows directly from Nash’s Theorem, since the number of players and the number of strategies are finite.

4 Lower Bounds on the Price of Anarchy of Nonpreemptive Coordination Mechanisms

In this section we focus on the price of anarchy of nonpreemptive coordination mechanisms. First we examine nonpreemptive coordination mechanisms for m>2 machines. The following theorem gives an interesting preliminary result.

Theorem 2

The price of anarchy of every nonpreemptive coordination mechanism for m>2 machines is at least $\frac{3}{2}$.

Proof

The main idea behind the proof is that for every coordination mechanism c for m>2, the game with n=m tasks with weight w ₁=w ₂=⋯=w _m =1 has a Nash equilibrium with expected makespan $\frac{3}{2}$. Here we describe how this equilibrium is reached. Players observe each policy c _j and are interested in whether it includes (1₁,1₂) or (1₂,1₁). If (1₂,1₁)∈c _j we will call j a big-first machine. Otherwise we will call j a small-first machine.

It is certain that we can find either two big-first machines, or two small-first machines, since the machines are at least 3 and the possible orderings for {1₁,1₂} are 2. Let these two machines be j ₁ and j ₂. Suppose that tasks start making their selections ignoring j ₁ and j ₂. Assume that there are k _b big-first machines and k _s small-first machines, other than j ₁ and j ₂. This means that k _b +k _s +2=m. The k _b tasks that are considered larger are allocated to the k _b big-first machines, one task per machine. The k _s tasks that are considered smaller are allocated to the k _s small-first machines, one task per machine. Since there are m tasks, there are 2 tasks i ₁ and i ₂ that have not selected their strategies. These two tasks play j ₁ and j ₂ with probability $\frac{1}{2}$ each. Without loss of generality we may assume that i ₁ is the task that is processed first if it ends up in the same machine with i ₂. This means that either it is considered larger and j ₁, j ₂ are big-first or it is considered smaller and j ₁, j ₂ are small-first.

This allocation has expected makespan $\frac{3}{2}$ due to the possible event that i ₁ and i ₂ end up on the same machine. The optimal allocation is obviously one task per machine with makespan 1. We claim that the allocation of the previous paragraph is a Nash equilibrium, something that would prove the theorem. Our reasoning is as follows:

• 1. All tasks outside j ₁ and j ₂ are alone in a machine and have optimal cost.

• 2. Task i ₁ is processed first no matter what happens, so it also has optimal cost.

• 3. Task i ₂ has expected completion time $\frac{3}{2}$ on both j ₁ and j ₂. It will not benefit by switching to some other big-first machine, since all such machines have another task that is considered larger than i ₂ and it will have to wait for its processing for a total cost of 2. For a similar reason it will not benefit by switching to some other small-first machine.

So, it follows that no task can improve its cost by a unilateral move, thus, the outcome is a Nash equilibrium. This proves the theorem. □

This provides a constant lower bound that will prove useful in our discussion on the power of nonpreemptive coordination mechanisms. However this result is only preliminary and can be extended as the next theorem shows.

Theorem 3

The price of anarchy of every nonpreemptive coordination mechanism for m machines is $\varOmega(\frac{\log \log m}{\log \log \log m})$.

Proof

Consider a coordination mechanism c for m machines and a game with n=m tasks, such that all tasks have weight 1. The proof is similar to the one of Theorem 2. The idea is that we do not find 2 machines with identical policy for 2 tasks with weight 1, but k machines with identical policy for 1,2,…,k−1, and k tasks with weight 1, for some k that depends on m as described in the next paragraph. The number of possible policies in Theorem 2 were just 2, namely {(1),(1₁,1₂),…} and {(1),(1₂,1₁),…}. The number of orderings for j tasks of length 1 is j!. Hence, the number of possible policies for 1,2,…,k−1, and k tasks with weight is l _k =1!2!…k!.

With m≥l _k (k−1)+1, we are certain we can find k machines j ₁,j ₂,…,j _k , that have the same policy for up to k tasks with weight 1. Now, tasks start making their selections ignoring j ₁,j ₂,…,j _k . Again assume that there are k _b big-first machines (as defined in the proof of Theorem 2) and k _s small-first machines, other than j ₁,j ₂,…,j _k . This means that k _b +k _s +k=m. The k _b tasks that are considered larger are allocated to the k _b big-first machines, one task per machine. The k _s tasks that are considered smaller are allocated to the k _s small-first machines, one task per machine. Since there are m tasks in total, there are k tasks i ₁,i ₂,…,i _k that have not selected their strategies. These tasks play j ₁,j ₂,…,j _k with probability $\frac{1}{k}$ each. We claim that this is a Nash equilibrium. This is verified as follows:

• 1. The tasks outside j ₁,j ₂,…,j _k are alone in a machine and have optimal cost.

• 2. Consider a task i among the ones that play j ₁,j ₂,…,j _k , with uniform probability. Assume that it is always processed last, in the purpose of obtaining an upper bound on the completion time of this task on any of the machines j ₁,j ₂,…,j _k . Then there is probability $\frac{1}{k}$ that it will have to wait for each of the k−1 other tasks on the machine. Then its expected completion time would be $1+\frac{k-1}{k}$, which is an upper bound on its actual completion time. Applying the same reasoning as the one used in the proof of Theorem 2, we get that there is no benefit for i in switching to any of the other machines, since its completion time will rise to 2.

• 3. Again consider a task i among the ones that play j ₁,j ₂,…,j _k , with uniform probability. All these machines have the exact same policy for up to k tasks with weight 1 and all k tasks play each of them with probability $\frac{1}{k}$. So everything is symmetric and task i has the same expected completion time on each of the k machines.

So this is a Nash equilibrium and we need to calculate its expected makespan. This setting, where k tasks play k machines with uniform probability, is identical to the setting where k balls are thrown to k bins at random. It is known that the expected maximum number of balls in a bin is $\varTheta(\frac{\log k}{\log \log k})$. This directly gives an $\varOmega(\frac{\log k}{\log \log k})$ lower bound on the price of anarchy of c, since the optimal makespan of the game is 1. From m=l _k (k−1)+1=1!2!…k!(k−1)+1, we get

$$\log m = \varTheta\Biggl(\sum_{j=1}^{k}j \log j\Biggr) = \varTheta\bigl(k^2 \log k\bigr)\quad \Rightarrow\quad k^2 \log k = \varTheta(\log m) . $$

This gives logk=Θ(loglogm). Combining this with the $\varOmega(\frac{\log k}{\log \log k})$ lower bound on the price of anarchy of c, we prove the theorem. □

Next, we focus on the case of m=2 machines. We will prove that the price of anarchy of every nonpreemptive coordination mechanism for m=2 is at least $\frac{7}{6}$ by following an extensive case analysis. We begin with the following lemma.

Lemma 1

Suppose c={c ₁,c ₂} is a nonpreemptive coordination mechanism such that both machines have the same policy for two tasks with weights w ₁,w ₂∈{2,3} and w ₁≤w ₂. Then $\operatorname{PoA}(c)\ge \frac{4}{3}$.

Proof

For the described c, consider the game (c,{w ₁,w ₂}). There always exists the Nash equilibrium p, where both tasks play both machines with probability $\frac{1}{2}$. Noting that w ₁≤w ₂, we get that

$$s(c,w,p) = \frac{1}{2}(w_1+w_2) + \frac{1}{2}w_2\quad \Rightarrow\quad \operatorname{PoA}(c)\ge 1 + \frac{w_1}{2w_2} . $$

For w ₁,w ₂∈{2,3}, this last inequality proves the lemma. □

Next, we need to examine mechanisms with the following property. One policy includes (2,3) and the other includes (3,2), one policy includes (2₁,2₂) and the other includes (2₂,2₁), and one policy includes (3₁,3₂) and the other includes (3₂,3₁). We will refer to this as the Mirror Property. Without loss of generality we may assume that (2,3)∈c ₁ which gives the following cases.

• 1. c ₁={(2,3),(2₂,2₁),(3₁,3₂),…} and c ₂={(3,2),(2₁,2₂),(3₂,3₁),…}.

• 2. c ₁={(2,3),(2₁,2₂),(3₁,3₂),…} and c ₂={(3,2),(2₂,2₁),(3₂,3₁),…}.

• 3. c ₁={(2,3),(2₂,2₁),(3₂,3₁),…} and c ₂={(3,2),(2₁,2₂),(3₁,3₂),…}.

• 4. c ₁={(2,3),(2₁,2₂),(3₂,3₁),…} and c ₂={(3,2),(2₂,2₁),(3₁,3₂),…}.

In the remainder of the section we will only examine mechanisms of the first form. We will prove that the price of anarchy of every one of them is at least $\frac{7}{6}$ and we will show that the other 3 cases are symmetric. We will say that mechanisms that match the first case satisfy the Specific Mirror Property.

At this point we proceed as follows. We present and prove several lemmata, which lead to the conclusion that for any ordering of {2₁,2₂,3} in c ₁, the price of anarchy of c is at least $\frac{7}{6}$. The next lemma examines the case where c ₁ includes (3,2₂,2₁) and the ones that follow examine the remaining 5 cases.

Lemma 2

If c satisfies the Specific Mirror Property and (3,2₂,2₁)∈c ₁ then $\operatorname{PoA}(c)\ge \frac{7}{6}$.

Proof

We examine 3 cases for the described c.

• 1. Case where c ₂ includes (3,2,2). In this case the game (c,{2,2,3,3}) has the Nash equilibrium

  

  Confirmation that this is indeed a Nash equilibrium comes from computing all values t _i,j (c,w,p _−i ). For this outcome we have

  • (a) $t_{1,1}(c,w,p_{-1})=\frac{1}{2}7+\frac{1}{2}2 =\frac{9}{2}$ and $t_{1,2}(c,w,p_{-1})\ge \frac{1}{2}5 + \frac{1}{2}5 = 5$.

  • (b) t _2,1(c,w,p ₋₂)=5 and t _2,2(c,w,p ₋₂)=5.

  • (c) $t_{3,1}(c,w,p_{-3}) = \frac{1}{2}3 + \frac{1}{2}5 = 4$ and $t_{3,2}(c,w,p_{-3})\ge \frac{1}{2}6 + \frac{1}{2}3 = \frac{9}{2}$.

  • (d) t _4,2(c,w,p ₋₄)=3, which is the optimal cost for task 4.

  These values verify that every task assigns positive probability only to machines that minimize its expected completion time. So, this outcome is a Nash equilibrium with expected makespan 6, while the optimal makespan is 5. Thus, in this case the price of anarchy of c is at least $\frac{6}{5}$.

• 2. Case where c ₂ includes (2,3,2). In this case the game (c,{2,2,2,3}) has the Nash equilibrium

  

  with expected makespan 6, while the optimal makespan is 5. So, also in this case $\operatorname{PoA}(c)\ge \frac{6}{5}$.

• 3. Case where c ₂ includes (2,2,3). In this case the game (c,{2,2,3}) has the Nash equilibrium

  

  with expected makespan $\frac{14}{3}$, while the optimal makespan is 4. This proves that the price of anarchy of c, in this case, is at least $\frac{7}{6}$.

These 3 cases prove the lemma. □

Lemma 3

If c satisfies the Specific Mirror Property and (3,2₁,2₂)∈c ₁ then $\operatorname{PoA}(c)>\frac{7}{6}$.

Proof

For the described c, the game (c,{2,2,3}) has the Nash equilibrium

with expected social cost $\frac{19}{4}$, while the optimal is 4. Thus, we get that $\operatorname{PoA}(c)\ge \frac{19}{16}>\frac{7}{6}$. □

Lemma 4

If c satisfies the Specific Mirror Property and (2,2,3)∈c ₁, then $\operatorname{PoA}(c)>\frac{6}{5}$.

Proof

Assume c is such that (3,2,3)∈c ₂ or (3,3,2)∈c ₂. Then (c,{2,2,3,3}) has the equilibrium

with makespan 6, while the optimal makespan is 5. This proves that the price of anarchy of c, in this case, is at least $\frac{6}{5}$. So, we need to prove that the same holds when (2,3,3)∈c ₂. Since c ₁ contains (2₁,2₂,3) or (2₁,2₂,3) and c ₂ contains (2,3₁,3₂) or (2,3₂,3₁), there are 4 cases we need to examine. For each one of them, we will give an equilibrium of the game (c,{2,2,3,3}) with expected makespan greater than 6. This will complete the proof.

• 1. When (2₂,2₁,3)∈c ₁ and (2,3₂,3₁)∈c ₂ the equilibrium is

  

• 2. When (2₂,2₁,3)∈c ₁ and (2,3₁,3₂)∈c ₂ the equilibrium is

  

• 3. When (2₁,2₂,3)∈c ₁ and (2,3₂,3₁)∈c ₂ the equilibrium is

  

• 4. When (2₁,2₂,3)∈c ₁ and (2,3₁,3₂)∈c ₂ the equilibrium is

  

 □

Lemma 5

If c satisfies the Specific Mirror Property, with (2,3,2)∈c ₁ and (3,2,2)∈c ₂, then $\operatorname{PoA}(c)\ge \frac{7}{6}$.

Proof

For such c, the game (c,{2,2,2,3,3}) always has a Nash equilibrium, in which machine 1 has load 5 (one task with weight 2 and one with weight 3) and machine 2 has load 7 (the remaining 3 tasks). Such an equilibrium has makespan 7, while the optimal is 6. We now present how to construct such an equilibrium.

• 1. We first decide which task with weight 3 will be allocated to machine 1 (with completion time 5). It must be selected such that it does not have incentive to switch to machine 2 in an allocation such as described above. So, we select the task that would have completion time at least 6 if it were on machine 2 together with 3 other tasks with weights 2, 2, and 3. So, this task is in a best response state. The other task with weight 3 is processed first in the allocation examined, so it is also in a best response.

• 2. Now we decide which task with weight 2 to allocate to machine 1. If (2₂,3,2₁)∈c ₁, then we allocate task 3, while if (2₁,3,2₂)∈c ₁, then we allocate task 1. We can easily confirm that they are in best response in both cases.

This completes the proof. □

Lemma 6

If c satisfies the Specific Mirror Property, with (2₁,3,2₂)∈c ₁ and (3,2,2)∉c ₂, then $\operatorname{PoA}(c)> \frac{7}{6}$.

Proof

For the described c, the game (c,{2,2,3}) has the equilibrium

with social cost $\frac{327}{70}$, while the optimal is 4. This competes the proof. □

The final case that remains to be examined is when (2₂,3,2₁)∈c ₁, (3,2₂,2₁)∉c ₂, and (3,2₁,2₂)∉c ₂. This will be done in Lemma 9, which makes use of the results presented in Lemma 7 and Lemma 8 below.

Lemma 7

If c satisfies the Specific Mirror Property, with (2₁,2₂,2₃)∈c ₁, then $\operatorname{PoA}(c)\ge \frac{5}{4}$.

Proof

For the described c, the game (c,{2,2,2,2}) always has a Nash equilibrium with expected makespan 5, while the optimal is 4. We examine all possible cases and give a Nash equilibrium with expected makespan 5 for each one.

• 1. If (2₃,2₁,2₂)∈c ₂, then the Nash equilibrium is the following.

  

• 2. If (2₃,2₂,2₁)∈c ₂, then the Nash equilibrium is the following.

  

• 3. For any other c ₂, the Nash equilibrium is the following.

  

This completes the proof. □

Lemma 8

If c satisfies the Specific Mirror Property, with (2₁,2₃,2₂)∈c ₁, then $\operatorname{PoA}(c)\ge \frac{5}{4}$.

Proof

For the described c, the game (c,{2,2,2,2}) always has a Nash equilibrium with expected makespan 5, while the optimal is 4. We examine all possible cases and give a Nash equilibrium with expected makespan 5 for each one.

• 1. If (2₂,2₁,2₃)∈c ₂, then the Nash equilibrium is the following.

  

• 2. If (2₂,2₃,2₁)∈c ₂, then the Nash equilibrium is the following.

  

• 3. For any other c ₂, the Nash equilibrium is the following.

  

This completes the proof. □

Lemma 9

If c satisfies the Specific Mirror Property, with (2₂,3,2₁)∈c ₁, (3,2₂,2₁)∉c ₂, and (3,2₁,2₂)∉c ₂, then $\operatorname{PoA}(c)\ge \frac{6}{5}$.

Proof

For the described c, we will examine all possible cases for the scheduling policy of c ₂.

• 1. If (2₁,3,2₂)∈c ₂, then the game (c,{2,2,2,3}) has the following Nash equilibrium.

  

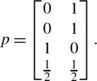
  The expected social cost in this case is 6, while the optimal would be 5.

• 2. If (2₂,3,2₁)∈c ₂, then the game (c,{2,2,2,3}) has the following Nash equilibrium.

  

  The expected social cost in this case is $\frac{25}{4}$, while the optimal would be 5.

• 3. If (2₂,2₁,3)∈c ₂, then the game c,{2,2,3,3} either

  

  is a Nash equilibrium, depending on the ordering of {2,3₁,3₂} that is included in c ₂. In both cases, the expected social cost is 6, while the optimal would be 5.

• 4. Finally, if (2₁,2₂,3)∈c ₂, and under the assumption that c ₁ does not include (2₁,2₂,2₃) or (2₁,2₃,2₂), then the game (c,{2,2,2,3}) has the following Nash equilibrium.

  

  The expected social cost in this case is 6, while the optimal would be 5. Removing the assumption, we would get from Lemma 7 and Lemma 8 that the mechanism would have price of anarchy at least $\frac{6}{5}$.

This completes the proof. □

Now, we can see that Lemmas 2 through 9 cover all possible cases of mechanisms that satisfy the Specific Mirror Property, i.e., c ₁={(2,3),(2₂,2₁),(3₁,3₂),…} and c ₂={(3,2),(2₁,2₂),(3₂,3₁),…}. We observe that the case analysis of Lemmas 2 through 9 can be modified to prove the remaining 3 cases of mechanisms that satisfy the Mirror Property, mentioned earlier. If instead of (2₂,2₁)∈c ₁ and (2₁,2₂)∈c ₂, we have (2₁,2₂)∈c ₁ and (2₂,2₁)∈c ₂, we adjust the case analysis as follows. We reverse the “direction” of the tasks with weight 2 in all orderings of the mechanism. For example, if an ordering of a policy in our case analysis is (…,2₃,…,2₁,…,2₂,…), we turn it into (…,2₁,…,2₃,…,2₂,…), or if it is (…,2₁,…,2₂,…), we turn it into (…,2₂,…,2₁,…). We also change the strategies of the tasks with weight 2 as follows. The task which is placed last in the increasing order switches strategies with the task which is placed first, the task which is placed second to last switches with the task which is placed second and so on. This produces a case analysis that is symmetric to the one we followed previously and proves the same result. The same idea is applied if instead of (3₁,3₂)∈c ₁ and (3₂,3₁)∈c ₂, we have (3₂,3₁)∈c ₁ and (3₁,3₂)∈c ₂. This proves that all mechanisms which satisfy the Mirror Property have price of anarchy at least $\frac{7}{6}$. Combining this with Lemma 1, we get the following theorem.

Theorem 4

The price of anarchy of every nonpreemptive coordination mechanism for m=2 machines is at least $\frac{7}{6}$.

5 Discussion

The results presented in this paper, derive two key properties. The first one is that games defined by nonpreemptive coordination mechanisms, do not necessarily possess pure Nash equilibria. The second property is tied to the performance of these mechanisms, with respect to randomized Nash equilibria, regarding the price of anarchy metric. We established constant lower bounds $\frac{7}{6}$ for 2 machines and $\frac{3}{2}$ for 3 or more machines. These lower bounds lead to the following corollary.

Corollary 1

The price of anarchy of every nonpreemptive coordination mechanism is at least $\frac{4}{3}-\frac{1}{3m}$. As a consequence, we are not able to design a nonpreemptive coordination mechanism that performs better than the preemptive Largest First coordination mechanism of [6].

This suggests that if there exists a coordination mechanism that has price of anarchy better than $\frac{4}{3}-\frac{1}{3m}$, which is the best known, it must use preemption or task delays.

Regarding the case of general m, we provide an $\varOmega(\frac{\log \log m}{\log \log \log m})$ lower bound, on the price of anarchy of nonpreemptive coordination mechanisms, in this paper. It is trivial to design a nonpreemptive coordination mechanism that has price of anarchy $O(\frac{\log m}{\log \log m})$ by just setting the same scheduling policy to all machines. Then, the bound follows directly as discussed by Christodoulou et al. in [6]. Combining this with the $\frac{4}{3}$ price of anarchy of the Largest First–Shortest First nonpreemptive coordination mechanism of [6], we conclude our discussion with the following corollary.

Corollary 2

The price of anarchy of the best nonpreemptive coordination mechanism for 2 machines is at least $\frac{7}{6}$ and at most $\frac{4}{3}$. For general m it is $\varOmega(\frac{\log \log m}{\log \log \log m})$ and $O(\frac{\log m}{\log \log m})$.