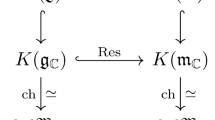Kirwan surjectivity for quiver varieties

Abstract

For algebraic varieties defined by hyperkähler or, more generally, algebraic symplectic reduction, it is a long-standing question whether the “hyperkähler Kirwan map” on cohomology is surjective. We resolve this question in the affirmative for Nakajima quiver varieties. We also establish similar results for other cohomology theories and for the derived category. Our proofs use only classical topological and geometric arguments.

1 Introduction

Suppose M is a complex algebraic variety with the action of a complex algebraic group G, yielding a quotient stack/equivariant space $\mathfrak {X}= M/G$; or more generally $\mathfrak {X}$ is any complex algebraic stack. Often $\mathfrak {X}$ has one or more natural open sets $\mathfrak {X}^{{\text {ss}}}$—typically defined via geometric invariant theory (GIT)—that are smooth algebraic varieties; thus, when $\mathfrak {X}= M/G$, we have $\mathfrak {X}^{{\text {ss}}} = M^{{\text {ss}}}/G$ where G acts freely on $M^{{\text {ss}}}$. Fixing such an open subset $i: \mathfrak {X}^{{\text {ss}}}\hookrightarrow \mathfrak {X}$, one has the following problem.

Kirwan Surjectivity Problem

When is the pullback map

$$\begin{aligned} H^*(\mathfrak {X}) \xrightarrow {i^*} H^*(\mathfrak {X}^{{\text {ss}}}) \end{aligned}$$

(1.1)

surjective?

Convention 1.1

Except when noted otherwise, $H^*$ means singular cohomology with ${\mathbb Z}$ coefficients.

When $\mathfrak {X}$ itself is smooth and $\mathfrak {X}^{{\text {ss}}}$ is defined by GIT, classical Morse-theoretic results of Atiyah-Bott and Kirwan show that the “Kirwan map” (1.1) is surjective. Significant recent attention focuses on the case when $\mathfrak {X}$ is a singular, but algebraic symplectic or even hyperkähler, stack: typically, letting Z be a smooth G-variety with algebraic moment map $\mu : T^*Z\rightarrow \mathfrak {g}^* = {\text {Lie}}(G)^*$, we have $\mathfrak {X}= \mu ^{-1}(0)/G$ and $\mathfrak {X}^{{\text {ss}}} = \mu ^{-1}(0)^{{\text {ss}}}/G$ for a choice of GIT stability.

This paper resolves the Kirwan Surjectivity Problem when $\mathfrak {X}^{{\text {ss}}}$ is a Nakajima quiver variety.

Thus, let $Q= (I,\Omega )$ be a quiver and $\mathbf v, \mathbf w \in \mathbb {Z}_{\ge 0}^I$ vectors with $\mathbf {w}\ne \mathbf 0$. Following Nakajima [18, 19], these data yield (notation as in Section 3.1):

• (1) a finite-dimensional complex vector space $\mathbb {M} = \mathbb {M}({\mathbf v},{\mathbf w})$, with

• (2) the linear action of the complex group $\mathbb {G} = \prod _i GL_{v_i}$, and

• (3) a (complex) moment map $\mu : \mathbb {M} \longrightarrow {\text {Lie}}(\mathbb {G})^*$.

Fix a nondegenerate stability condition $\theta$ (Definition 3.1) in the sense of GIT—for example the one used in [18, 19]—with stable locus $\mu ^{-1}(0)^{{\text {ss}}} = \mu ^{-1}(0)^s \subset \mathbb {M}^s$. The $\mathbb {G}$-action on $\mathbb {M}^s$ is free, and the quotient $\mathfrak M= \mathfrak M(\mathbf v, \mathbf w) := \mu ^{-1}(0)^s/\mathbb {G}$ is the Nakajima quiver variety associated to $Q, \mathbf {v}, \mathbf {w}, \theta$.

Theorem 1.2

Let $\mathfrak M(\mathbf v, \mathbf w)$ be a smooth Nakajima quiver variety. Then the Kirwan map

$$\begin{aligned} H^*_{\mathbb {G}}({\text {pt}}) \cong H^*_{\mathbb {G}}(\mu ^{-1}(0))\longrightarrow H^*_{\mathbb {G}}(\mu ^{-1}(0)^s) = H^*\big (\mathfrak M(\mathbf v, \mathbf w)\big ) \end{aligned}$$

is surjective. Thus, $H^*\big (\mathfrak M(\mathbf v, \mathbf w)\big )$ is generated by tautological classes.

We note that $H^*_{\mathbb {G}}({\text {pt}})$ is a polynomial ring (in the tautological classes of the theorem). Theorem 1.2 extends to many other cohomology theories, including complex K-theory and elliptic cohomology.¹

Theorem 1.3

Assume that $E^*({\text {pt}})$ is concentrated in even degrees.

• (1) The map $E^*(B\mathbb {G})\rightarrow E^*(\mathfrak M)$ is surjective.

• (2) If E is complex-oriented, then $E^*(\mathfrak M)$ is generated as an $E^*({\text {pt}})$-algebra by Chern classes of tautological bundles.

Corollary 1.4

The natural maps $K_{\mathbb {G}}^*({\text {pt}})\rightarrow K^*(\mathfrak M)$ and ${\text {Ell}}_{\mathbb {G}}^*({\text {pt}}) \rightarrow {\text {Ell}}^*(\mathfrak M)$ are surjective.

Furthermore, if $\mathbb {T}$ is an algebraic torus acting on $\mathfrak M$, then, because $H^*(\mathfrak M)$ is evenly graded, the Leray spectral sequence for $H^*_{\mathbb {T}}(\mathfrak M)$ degenerates, showing that $H^*(\mathfrak M) = H^*_{\mathbb {T}}(\mathfrak M) \otimes _{H^*_{\mathbb {T}}({\text {pt}})} H^*({\text {pt}})$. Via Theorem 1.2 and the Nakayama Lemma for graded rings, we conclude:

Corollary 1.5

For a torus $\mathbb {T}$ acting on $\mathfrak M$, the map $H^*_{\mathbb {G}\times \mathbb {T}}({\text {pt}})\rightarrow H^*_{\mathbb {T}}(\mathfrak M)$ is surjective.

In particular, the expectation expressed in Section 2.2.2 of [1]—that their map (9) is an embedding near the origin of $\mathscr {E}_{\mathsf {T}}$—follows. We note the applicability of the above results in other, similar contexts (cf. [17]). Analogues of Corollary 1.5 can also be proven for K-theory and elliptic cohomology equivariant with respect to a torus $\mathbb {T}$ or more general “flavor symmetries” of $\mathfrak M$: see Sect. 3.4 for more discussion of such symmetry groups.

Our method also yields the following.

Theorem 1.6

Let $D(\mathfrak M)$ denote the unbounded quasicoherent derived category of $\mathfrak M$, and $D_{{\text {coh}}}(\mathfrak M)$ its bounded coherent subcategory.

• (1) The category $D(\mathfrak M)$ is generated by tautological bundles.

• (2) There is a finite list of tautological bundles from which every object of $D_{{\text {coh}}}(\mathfrak M)$ is obtained by finitely many applications of (i) direct sum, (ii) cohomological shift, and (iii) cone.

We note that the second assertion of Theorem 1.6 is not simply a formal consequence of the first, since we do not include taking direct summands (i.e., retracts) among the operations (i–iii). Results related to Theorem 1.6 appear in [10].

We mention one further application of Theorem 1.2 (that will be readily apparent to experts).

Corollary 1.7

(Assumption 5.13 of [2]) Let $\mathfrak {g} = {\text {Lie}}(\mathbb {G})$, and $Z:= Z(\mathfrak {g})^*\subset \mathfrak {g}^*$ denote the dual of the center. Consider the family $\mathfrak {M} = \mu ^{-1}(Z)^{{\text {ss}}}/\mathbb {G}\longrightarrow Z$ of Hamiltonian reductions. Then the Duistermaat-Heckman map for this family is surjective. In particular, the family of Hamiltonian reductions $\mathfrak {M}\rightarrow Z$ provides a versal Poisson deformation of the Nakajima quiver variety $\mathfrak M$.

Cases of Kirwan surjectivity for quivers of finite and affine Dynkin type, and for star-shaped quivers, have previously been established (see [7, 15, 20, 22, 23]) by different techniques; and for moduli of $GL_n$-Higgs bundles by Markman [16].

Here is a sketch of the strategy used to prove Theorem 1.2.

• (1) We compactify $\mathfrak M$ to a projective variety $\overline{\mathfrak M}$ by an explicit quiver construction.

• (2) We identify the class of the graph $\Gamma$ of the inclusion $i: \mathfrak M\hookrightarrow \overline{\mathfrak M}$ in $H^*(\mathfrak M\times \overline{\mathfrak M})$ as a Chern class of a complex built from external tensor products of tautological bundles on $\mathfrak M\times \overline{\mathfrak M}$.

• (3) Purely topological arguments allow us to conclude (Sect. 2) that the Chern classes of the tautological bundles generate the cohomology of $\mathfrak M$.

We emphasize that the overall strategy is not new: see [18] (and [16]). The new ingredient here is the particular choice of modular compactification $\overline{\mathfrak M}$. Hiding behind our approach to Theorem 1.2 and our other results is, in fact, a general pattern (that experts may already discern here) for moduli spaces in noncommutative geometry—that is, moduli of objects in certain categories. The general story will be worked out in a forthcoming paper. Nonetheless, it seemed desirable to us to present the results for quiver varieties separately. Indeed, on the one hand, the proof of Theorem 1.2 can be made completely classical and explicit for quivers, in a way that avoids any categorical yoga or abstraction (and thus will be of independent interest to some readers). On the other hand, we also obtain sharper results for quiver varieties than seem to be easily achievable in a completely general context.

Convention 1.8

Throughout the paper, all varieties, groups, etc. are defined over $\mathbb {C}$.

2 Topology of compactifications

Throughout the paper, we use $H^*(X)$, with no further decorations indicating coefficients, to denote cohomology with $\mathbb {Z}$-coefficients, and $H^{{\text {BM}}}_*(X)$ to denote Borel-Moore homology with $\mathbb {Z}$-coefficients; if X is smooth with $D = \dim _{\mathbb {R}}(X)$, there is a canonical isomorphism $H^*(X) \cong H^{{\text {BM}}}_{D-*}(X)$.

2.1 Pushforwards and the projection formula

Suppose $f: X\rightarrow Y$ is a proper morphism of relative dimension d of smooth, connected varieties (or Deligne–Mumford stacks). Then there is a pushforward, or Gysin, map $f_*: H^*(X)\rightarrow H^{*-d}(Y)$.

The Gysin map satisfies the projection formula [5]: for classes $c\in H^*(X), c'\in H^*(Y)$, we have

$$\begin{aligned} f_*(c\cup f^*c') = f_*(c)\cup c'. \end{aligned}$$

(2.1)

Moreover, if $f: X\rightarrow Y$ is a closed immersion, then

$$\begin{aligned} f_*f^*c = c\cup [X], \end{aligned}$$

(2.2)

where [X] denotes the fundamental class of X in Borel-Moore homology (which is canonically isomorphic to cohomology since Y is smooth).

2.2 Künneth components and images under pullback

Suppose $C\in H^*(X\times Y)$ is a cohomology class and that the Künneth formula $H^*(X\times Y)\cong H^*(X)\otimes H^*(Y)$ holds.² We may write

$$\begin{aligned} C = \sum x_i \otimes y_i \; \text {with}\;x_i \in H^*(X), y_i \in H^*(Y). \end{aligned}$$

(2.3)

The classes $x_i$, $y_i$ are the left-hand, respectively right-hand, Künneth components of C with respect to the decomposition (2.3); they are not independent of the choice of decomposition (2.3).

Now suppose that $f: X\rightarrow Y$ is a morphism from a smooth variety X to a smooth, proper variety Y. Let $\Gamma _f\subset X\times Y$ be the graph of the map.

Proposition 2.1

The image of $f^*: H^*(Y)\rightarrow H^*(X)$ is contained in the span of the Künneth components of $[\Gamma _f]$ with respect to X (and any decomposition as in (2.3)).

Proof

Write for the projections and, abusively, $\Gamma _f: X\rightarrow X \times Y$ for both the graph immersion and its image. Write $p_*: Y\rightarrow {\text {Spec}}(\mathbb {C})$ for the projection to a point. Then $(p_X)_*$ exists since Y is proper, and

$$\begin{aligned} f^*d= & {} (p_X)_* (\Gamma _f)_*\Gamma _f^*p_Y^* d = (p_X)_*([\Gamma _f]\cup p_Y^*d) \\= & {} \sum _i (p_X)_*\big [(p_X^* x_i\cup p_Y^*y_i)\cup p_Y^*d\big ]\\= & {} \sum _i x_i \cup p_*(y_i\cup d). \end{aligned}$$

This proves the claim. $\square$

2.3 Resolution of a graph

Again suppose that $f: X\rightarrow Y$ is a morphism from a smooth variety to an irreducible projective variety, with graph $\Gamma \subset X\times Y$. We assume $f(X)\subset Y^{{\text {sm}}}$, the smooth locus of Y. We consider the situation in which $f^*: H^*(Y)\rightarrow H^*(X)$ is surjective.

Example 2.2

If $H^{{\text {BM}}}_*(X,\mathbb {Z})\cong H^*(X,\mathbb {Z})$ is generated by algebraic cycles and $X\rightarrow Y$ is an open immersion, then $H^*(Y, \mathbb {Z})\rightarrow H^*(X,\mathbb {Z})$ is surjective.

Remark 2.3

For a Nakajima quiver variety $\mathfrak M$, $H^*(\mathfrak M,\mathbb {Z})$ is generated by algebraic cycles by Theorem 7.3.5 of [19].

Continuing with the above situation, let $\widetilde{Y}$ be a resolution of singularities; since f(X) does not intersect the singular locus of Y, f lifts canonically to a morphism $\widetilde{f}: X\rightarrow \widetilde{Y}$ and the preimage of $\Gamma _f$ in $X\times \widetilde{Y}$ is $\Gamma _{\widetilde{f}}$.

Proposition 2.4

Suppose that

$$\begin{aligned} R: \bigoplus _j{\mathcal E}_j^{-1}\boxtimes {\mathcal F}_j^{-1} \longrightarrow \bigoplus _j{\mathcal E}_j^0\boxtimes {\mathcal F}_j^0\longrightarrow \bigoplus _j{\mathcal E}_j^1\boxtimes {\mathcal F}_j^1 \end{aligned}$$

(2.4)

is a complex of vector bundles on $X\times Y$ with the following properties.

• (1) $\mathcal {H}^1(R) = 0$, $\mathcal {H}^{-1}(R)=0$, and $\mathcal {H}:= \mathcal {H}^0(R)$ is a vector bundle on $X\times Y$.

• (2) ${\text {rk}}(\mathcal {H}) = d:=\dim (Y)$.

• (3) $s\in H^0(X\times Y, \mathcal {H})$ is a section with scheme-theoretic zero locus $Z(s) = \Gamma$.

Letting $\widetilde{Y}\rightarrow Y$ be a resolution of singularities, write

$$\begin{aligned} \widetilde{R}: \bigoplus _j{\mathcal E}_j^{-1}\boxtimes \widetilde{{\mathcal F}}_j^{-1} \longrightarrow \bigoplus _j{\mathcal E}_j^0\boxtimes \widetilde{{\mathcal F}}_j^0\longrightarrow \bigoplus _j{\mathcal E}_j^1\boxtimes \widetilde{{\mathcal F}}_j^1 \end{aligned}$$

for the pullback of R to $X\times \widetilde{Y}$ and $\widetilde{\mathcal {H}} = \mathcal {H}^0(\widetilde{R})$. Then:

• (i) $c_d(\widetilde{\mathcal {H}}) = [\Gamma _{\widetilde{f}}]$ in $X\times \widetilde{Y}$.

• (ii) The Chern classes of $\widetilde{\mathcal {H}}$ are polynomials, with integer coefficients, in the Chern classes of the bundles ${\mathcal E}_j^{\ell }$ and $\widetilde{{\mathcal F}}_j^{\ell }$.

• (iii) The image of the map $H^*(\widetilde{Y},\mathbb {Z}) \rightarrow H^*(X,\mathbb {Z})$ is contained in the span of the Chern classes of the bundles ${\mathcal E}_j^\ell$.

Proof

• (i) It is standard that if the zero locus of a section of a vector bundle $\widetilde{\mathcal {H}}$ of rank d has codimension d—in which case it is a local complete intersection subscheme—then its fundamental class equals $c_d(\widetilde{\mathcal {H}})$.

• (ii) By the additivity of Chern classes, we have

  $$\begin{aligned} c(\widetilde{\mathcal {H}}) = \prod _j c({\mathcal E}_j^0\boxtimes \widetilde{{\mathcal F}}_j^0) \prod _j c({\mathcal E}_j^{-1}\boxtimes \widetilde{{\mathcal F}}_j^{-1})^{-1}\prod _j c({\mathcal E}_j^1\boxtimes \widetilde{{\mathcal F}}_j^1)^{-1}. \end{aligned}$$

  The inverses of the total Chern classes are the total Segre classes, which are known to be polynomials, with integer coefficients, in the Chern classes: see Chapter 5 of [8]. Moreover, the Chern classes of ${\mathcal E}_j^\ell \boxtimes \widetilde{{\mathcal F}}_j^\ell$ are also polynomials (with integer coefficients) in the Chern classes of ${\mathcal E}_j^\ell$ and $\widetilde{{\mathcal F}}_j^\ell$: see Example 14.5.2 of [8].³

• (iii) By parts (i) and (ii), the class $[\Gamma _{\widetilde{f}}]$ has a Künneth decomposition (2.3) whose left-hand components are integer polynomials in the Chern classes of the bundles ${\mathcal E}_j^\ell$. Assertion (iii) is now immediate from Proposition 2.1.

$\square$

Corollary 2.5

Suppose that $\mathfrak M$ is a smooth Nakajima quiver variety and $\mathfrak M\hookrightarrow \overline{\mathfrak M}$ is an open immersion in a projective variety. If the graph $\Gamma$ of the immersion can be written as the zero locus Z(s) of a section $s\in H^0(\mathfrak M\times \overline{\mathfrak M},\mathcal {H})$ of a vector bundle $\mathcal {H}$ as in Proposition 2.4, then $H^*(\mathfrak M,\mathbb {Z})$ is generated by the Chern classes of the bundles ${\mathcal E}_j^\ell$.

Proof

As explained above, $H^*(\mathfrak M,\mathbb {Z})$ is known to be generated by algebraic cycles; hence (cf. Proposition 1.8 of [8]) for any projective compactification $\overline{\mathfrak M}$ the restriction map $H^*(\overline{\mathfrak M},\mathbb {Z})\rightarrow H^*(\mathfrak M,\mathbb {Z})$ is surjective. The assertion is now immediate from Proposition 2.4. $\square$

3 Quiver varieties

3.1 Basics of quivers

Let (I, E) be an undirected graph with with vertex set I and edge set E. Following Nakajima [18, 19], we let H denote the set of pairs of an edge with an orientation; thus H comes with source and target maps $s,t: H\rightarrow I$. Given $h\in H$, we let $\overline{h}$ denote the same edge with opposite orientation, so $s(\overline{h})= t(h)$ and $t(\overline{h}) = s(h)$.

Next, fix a preferred orientation for each edge: in other words, fix a decomposition $H = \Omega \sqcup \overline{\Omega }$ where $\overline{\Omega } = \{\overline{h}\; |\; h\in \Omega \}$. We let $Q = (I,\Omega )$ denote the quiver, i.e., the finite directed graph, with vertices I and arrows $\Omega$; then $Q^{{\text {dbl}}} = (I, H)$ is the associated doubled quiver. We define a function

$$\begin{aligned} \epsilon : H\longrightarrow \{\pm 1\} \,\,\,\text {by}\,\,\,\epsilon (h) ={\left\{ \begin{array}{ll} 1 &{} \text {if}\,h\in \Omega ,\\ -1 &{} \text {if} \,h\in \overline{\Omega }.\end{array}\right. } \end{aligned}$$

(3.1)

The preprojective algebra is the quotient $\Pi ^0(Q) = kQ^{{\text {dbl}}}/ \big (\sum _{h\in H} \epsilon (h)\overline{h}h\big )$ of the path algebra $kQ^{{\text {dbl}}}$ of the doubled quiver. The relation $\sum _{h\in H} \epsilon (h)\overline{h}h = 0$ is the preprojective relation.

If $V_\bullet$ is an I-graded vector space, then ${\text {Rep}}(Q,V_\bullet ) = \bigoplus _{h\in \Omega } {\text {Hom}}(V_{s(h)}, V_{t(h)})$. When $\mathbf {v}\in \mathbb {Z}_{\ge 0}^I$ and $V_i = \mathbb {C}^{\mathbf {v}_i}$ for all $i\in I$, we write ${\text {Rep}}(Q,\mathbf {v}) = {\text {Rep}}(Q,V_\bullet )$.

Let $\mathbf v = (v_i)_{i\in I}, \mathbf w = (w_i)_{i\in I}$ be dimension vectors, and $V_i, W_i (i\in I)$ be complex vector spaces with ${\text {dim}}(V_i) = v_i, \dim (W_i) = w_i$; here $W_i$ are the framing vector spaces. Given pairs ${\mathbf v}^1, {\mathbf w}^1$ and ${\mathbf v}^2, {\mathbf w}^2$ and vector spaces $V_i^j, W_i^j$ ($j=1,2$) as above, let

$$\begin{aligned} L(V^1, V^2) = \bigoplus _{i\in I} {\text {Hom}}(V_i^1, V_i^2), \quad E(V^1, V^2) = \bigoplus _{h\in H} {\text {Hom}}(V^1_{s(h)}, V^2_{t(h)}). \end{aligned}$$

One has obvious “compositions” of $L(V^1,V^2)$ with $L(V^2,V^3)$, $L(V^3,V^1)$, $E(V^2,V^3)$, and $E(V^3,V^1)$.

On p. 520 of [18], Nakajima defines a bilinear map

$$\begin{aligned} E(V^2, V^3)\times E(V^1, V^2) \rightarrow L(V^1, V^3), \text {by} \end{aligned}$$

$$\begin{aligned} \displaystyle (C,B)\mapsto CB = \left( \sum _{t(h) = k} C_hB_{\overline{h}}\right) _k \in L(V^1, V^3). \end{aligned}$$

(3.2)

We note that, for any (C, B), we have

$$\begin{aligned} (\epsilon C)B + C(\epsilon B) = 0. \end{aligned}$$

(3.3)

Now, fixing $\mathbf {v}, \mathbf {w}$ and collections of vector spaces $(V_i), (W_i)$ as above, let

$$\begin{aligned} \mathbb {M} = \mathbb {M}(\mathbf {v},\mathbf {w}) = E(V,V)\oplus L(W,V)\oplus L(V,W). \end{aligned}$$

We write [B, i, j] for an element of $\mathbb {M}$. The group

$$\begin{aligned} \mathbb {G} = \mathbb {G}(\mathbf {v})= \prod _i GL(V_i)\cong \prod _i GL_{v_i} \end{aligned}$$

acts linearly on $\mathbb {M}$ in the obvious way. There is a canonical moment map $\mu : \mathbb {M}\longrightarrow {\text {Lie}}(\mathbb {G})^*$, coming from the identification of $\mathbb {M}$ as a cotangent bundle to a linear space, defined by:

$$\begin{aligned} \mu (B,i,j) = \epsilon BB + ij \in L(V,V) \cong {\text {Lie}}(\mathbb {G})^*. \end{aligned}$$

3.2 Crawley-Boevey’s construction

Suppose $Q=(I,\Omega )$ is a quiver with dimension vectors $\mathbf {v}, \mathbf {w}$ as above. To such data, Crawley-Boevey associates [4, Section 1] a new quiver, that we will denote by $Q^{{\text {CB}}}$. It has vertex set $I^{{\text {CB}}} = I\cup \{\infty \}$, and oriented arrows

$$\begin{aligned} \Omega ^{{\text {CB}}} = \Omega \cup \big \{a_{(i,j)} \; |\; s(a_{i,j}) = \infty , t(a_{i,j}) = i,\; i\in I, j\in \{1,\dots , \mathbf {w}_i\}\big \}. \end{aligned}$$

In other words, we add $\mathbf {w}_i$-many arrows from $\infty$ to i. Let $\alpha \in {\mathbb Z}_{\ge 0}^{I^{{\text {CB}}}}$ be the dimension vector for $Q^{{\text {CB}}}$ that equals $\mathbf {v}_i$ at $i\in I$ and 1 at the vertex $\infty$. Then $\mathbb {M}(\mathbf {v},\mathbf {w}) = T^*{\text {Rep}}(Q^{{\text {CB}}},\alpha )$. Also the natural homomorphism $\mathbb {G}\rightarrow G(\alpha ) := \prod _{i\in I^{{\text {CB}}}} GL(\alpha _i) / {\mathbb G}_m$ (where ${\mathbb G}_m$ is the diagonal multiplicative group) is an isomorphism, making the identification of $\mathbb {M}(\mathbf {v},\mathbf {w})$ with $T^*{\text {Rep}}(Q^{{\text {CB}}},\alpha )$ equivariant. It is immediate that the two canonical moment maps coincide.

3.3 Semistability and stability for quiver representations

Fix a quiver $Q= (I,\Omega )$ with dimension vector $\alpha$. Let $\mathbb {G} = \prod _i GL(\alpha _i)$ denote the group determined by Q. We write $\beta \le \alpha$ for a dimension vector $\beta$ if $\beta _i\le \alpha _i$ for all $i\in I$, and $\beta <\alpha$ if $\beta \le \alpha$ and $\beta \ne \alpha$.

Following [14], given a character $\chi :\mathbb {G}\rightarrow {\mathbb G}_m$, write

$$\begin{aligned} \chi \big ((g_i)_{i\in I}\big ) = \prod _{i\in I} \det (g_i)^{\theta _i} \text {and} \theta = (\theta _i)_{i\in I} \in \mathbb {Z}^I. \end{aligned}$$

Given an I-graded vector space $(M_i)_{i\in I}$, we define $\delta _i(M) =\dim (M_i)$, and thus abusively write

$$\begin{aligned} \theta : K^0(kQ{\text {-mod}})\rightarrow \mathbb {Z}, \theta = \sum _i \theta _i \delta _i \text {so that} \theta (M) = \sum _i\theta _i\dim (M_i). \end{aligned}$$

Associated to $\chi$ one gets a corresponding notion of GIT semistability as in [14]. In particular, by Proposition 3.1 of [14], if V is a representation of Q for which $\theta (V) = 0$, then V is $\chi$-semistable, respectively stable, if and only if for every nonzero proper subrepresentation $M\subset V$, we have

$$\begin{aligned} \theta (M) \ge 0,\quad \text {respectively} \theta (M)>0. \end{aligned}$$

Definition 3.1

We will call the semistability condition $\theta$ a nondegenerate stability (with respect to $\alpha$) if, for every nonzero dimension vector $\beta < \alpha$ we have $\theta (\beta )\ne 0$.

Remark 3.2

If $\theta$ is a nondegenerate stability condition, then semistability and stability coincide. The converse is treated in [18, Theorem 2.8].

Now suppose that $Q_0 = (I_0,\Omega _0)$ is a quiver with dimension vector $\mathbf {v}$ and framing vector $\mathbf {w}$ and that $Q = Q_0^{{\text {CB}}} = (I,\Omega )$ is the associated Crawley-Boevey quiver, with dimension vector $\alpha$ so that $\alpha _\infty = 1$ and $\alpha |_{I_0} = \mathbf {v}$. Write $\mathbb {G}_0 = \prod _{i\in I_0}GL(\mathbf {v}_i)$ and $\mathbb {G} = \prod _i GL(\alpha _i)$, so that $\mathbb {G} = \mathbb {G}_0\times {\mathbb G}_m$. Given any character $\chi _0: \mathbb {G}_0\rightarrow {\mathbb G}_m$, $\chi _0(g_i) = \prod _{i\in I_0} \det (g_i)^{\theta _i}$, let $\delta : {\mathbb G}_m\rightarrow \mathbb {G}_0$ be the diagonal ${\mathbb G}_m$ and write $\chi _0(\delta (z)) = z^d$. We get a character $\chi : \mathbb {G} \rightarrow {\mathbb G}_m$ by $\chi (g, z) = \chi _0(g)z^{-d}$; we slightly abusively write $\theta = \sum _{i\in I_0}(\theta _0)_i\delta _i -d \delta _{\infty }$. Then $\chi$ is trivial on the diagonal ${\mathbb G}_m$ in $\mathbb {G}_0\times {\mathbb G}_m$, and thus $\chi$ factors through a character of $G(\alpha ): = \mathbb {G}/{\mathbb G}_m$, which obviously agrees with $\chi _0$ under the isomorphism $\mathbb {G}_0\rightarrow G(\alpha )$.

Recalling the moment map

$$\begin{aligned} \mu : \mathbb {M}(\mathbf {v},\mathbf {w})\rightarrow {\text {Lie}}(\mathbb {G}_0)^* \end{aligned}$$

above, the Nakajima quiver variety associated to dimension vector $\mathbf {v}$ and framing vector $\mathbf {w}$ is

$$\begin{aligned} \mathfrak M= \mathfrak M_\theta (\mathbf {v},\mathbf {w}) := \mu ^{-1}(0)/\!\!/_{\chi _0}\mathbb {G}_0. \end{aligned}$$

When $\theta$ is understood, we suppress the subscript $\theta$ in the rest of the paper. Crawley-Boevey [4, p. 261] shows that $\mathbb {M}(\mathbf {v},\mathbf {w})\cong T^*{\text {Rep}}(Q,\alpha )$, intertwining the $\mathbb {G}_0$ and $\mathbb {G}$-actions, and identifying $\chi _0$-(semi)stability with $\chi$-(semi)stability. Thus we may take the Hamiltonian reduction of $T^*{\text {Rep}}(Q,\alpha )$ with respect to $G(\alpha )$, using the stability condition determined by $\chi$ or equivalently $\theta$, and obtain $\mathfrak M$ as the GIT quotient.

The quiver variety $\mathfrak M$ comes equipped, by its construction, with a map $\mathfrak M\rightarrow B\mathbb {G}$ where $B\mathbb {G}$ is the classifying space of the group $\mathbb {G}$. The induced homomorphism $H^*(BG(\alpha )) = H^*_{G(\alpha )}({\text {pt}})\rightarrow H^*(\mathfrak M)$ is the Kirwan map appearing in Theorem 1.2.

3.4 Symmetries of $\mathfrak M$

As noted in the introduction, it is common (in enumerative geometry and in quantum field-theoretic contexts) to study equivariant cohomology of $\mathfrak M$ with respect to a “flavor symmetry” group.

We review a standard construction of such a group acting on $\mathfrak M$. Fix the quiver $Q = Q_0^{{\text {CB}}}$ and a dimension vector $\alpha$ with $\alpha _\infty = 1$. First, supposing i, j are distinct vertices of Q, we note that $T^*{\text {Hom}}(\mathbb {C}^{\alpha _i}, \mathbb {C}^{\alpha _j}) \cong {\text {Hom}}(\mathbb {C}^{\alpha _i}, \mathbb {C}^{\alpha _j}) \times {\text {Hom}}(\mathbb {C}^{\alpha _j}, \mathbb {C}^{\alpha _i})$ is $GL(\alpha _j)\times GL(\alpha _i)$-equivariantly and symplectically isomorphic to $T^*{\text {Hom}}(\mathbb {C}^{\alpha _j}, \mathbb {C}^{\alpha _i})$ via

$$\begin{aligned}&{\text {Hom}}(\mathbb {C}^{\alpha _i}, \mathbb {C}^{\alpha _j})\times {\text {Hom}}(\mathbb {C}^{\alpha _j}, \mathbb {C}^{\alpha _i})\ni (X,Y)\mapsto (-Y,X)\\&\in {\text {Hom}}(\mathbb {C}^{\alpha _j}, \mathbb {C}^{\alpha _i}) \times {\text {Hom}}(\mathbb {C}^{\alpha _i}, \mathbb {C}^{\alpha _j}). \end{aligned}$$

Thus, without loss of generality we will replace Q by a quiver in which, for every pair of distinct vertices i, j, all arrows between i and j are oriented in the same direction.

For distinct i, j, write $n_{ij}$ for the number of arrows of Q between i and j, and write $n_i$ for the number of loops at the vertex i. Then we have a $\mathbb {G}$-equivariant and symplectic identification

$$\begin{aligned} \mathbb {M}(\mathbf {v},\mathbf {w}) \cong \left( \prod _{\exists (i\rightarrow j)} T^*{\text {Hom}}(\mathbb {C}^{\alpha _i}, \mathbb {C}^{\alpha _j})\otimes \mathbb {C}^{n_{ij}}\right) \times \left( \prod _i {\text {End}}(\mathbb {C}^{\alpha _i})\otimes \mathbb {C}^{2n_i}\right) . \end{aligned}$$

(3.4)

Here the first product ranges over those pairs (i, j) of distinct vertices for which there exists an arrow in Q from i to j. Letting

$$\begin{aligned} \mathbb {K} = \left( \prod _{i\ne j} GL(n_{ij})\right) \times \left( \prod _i Sp(n_i)\right) , \end{aligned}$$

we see immediately from (3.4) that $\mathbb {K}$ acts by $\mathbb {G}$-equivariant symplectomorphisms on $\mathbb {M}(\mathbf {v},\mathbf {w})$, and thus acts on the quiver variety $\mathfrak M$. Because $\mathbb {K}$ commutes with $\mathbb {G}$, its action automatically lifts to an equivariant structure on every tautological bundle, and we obtain:

Theorem 3.3

The Kirwan map $H^*_{\mathbb {G}\times \mathbb {K}}({\text {pt}}) \rightarrow H^*_{\mathbb {K}}(\mathfrak M)$ is surjective.

The full symplectomorphism group of $\mathfrak M$ is in general larger than $\mathbb {K}$. For example, it is known (cf. [12] and the discussion in [13]) that the “affine Cremona group” of automorphisms of $\mathbb {A}^2$ is generated by GL(2) and the subgroup B of automorphisms of the form $(x,y) \mapsto (x+f(y), y)$ for polynomials f(y); the group ${\text {Aut}}(\mathbb {A}^2)$ also acts on the Hilbert scheme $(\mathbb {A}^2)^{[n]}$ and the moduli spaces of higher-rank framed sheaves, both of which appear as quiver varieties associated to the (framed) Jordan quiver, and the subgroup ${\text {Sympl}}(\mathbb {A}^2)$ generated by SL(2) and B acts by symplectomorphisms. More generally, there is a product of groups of “tame automorphisms” (a review of the terminology, some relevant literature, and illuminating results can be found in [21]) of the auxiliary spaces $\mathbb {C}^{n_{ij}}$, $\mathbb {C}^{2n_i}$ that can be seen to act on $\mathbb {M}(\mathbf {v},\mathbf {w})$ compatibly with $\mathbb {G}$.

In light of the previous paragraph, it is perhaps natural to restrict attention to the group ${\text {Aut}}_{{\mathbb G}_m}(\mathfrak M)$ of those automorphisms (or ${\text {Sympl}}_{{\mathbb G}_m}(\mathfrak M)$ of those symplectomorphisms) that are compatible with a suitable conical ${\mathbb G}_m$-action on $\mathfrak M$. This reduces ${\text {Aut}}(\mathbb {A}^2)$ to GL(2), or ${\text {Sympl}}(\mathbb {A}^2)$ to SL(2) for symplectomorphisms, i.e., to the group $\mathbb {K}$ for $(\mathbb {A}^2)^{[n]}$; in general, we are unsure whether this group is reductive, and one may want to restrict attention further to a “reductive part” of ${\text {Aut}}_{{\mathbb G}_m}(\mathfrak M)$ or ${\text {Sympl}}_{{\mathbb G}_m}(\mathfrak M)$.

Finally, we note that one knows that automorphisms of a quiver can induce finite groups of automorphisms of associated quiver varieties: for example, minimal resolutions $\widetilde{\mathbb {A}^2/\mu _r}$ of type A Kleinian singularities (for $r\ge 3$) admit $\mathbb {Z}/2$ symmetries that act nontrivially on $H^2(\widetilde{\mathbb {A}^2/\mu _r})$; the nontriviality of the action on cohomology shows that such a $\mathbb {Z}/2$-action cannot be the restriction of the action on $\widetilde{\mathbb {A}^2/\mu _r}$ of any connected group. We do not know how close $\mathbb {K}\rightarrow {\text {Sympl}}_{{\mathbb G}_m}(\mathfrak M)^\circ$ is to being surjective in general.

3.5 Tautological bundles and Nakajima’s section

We continue with a quiver $Q = (I,\Omega )$. Let $V^1$ and $V^2$ be I-graded vector spaces of dimension $\mathbf v$, and W an I-graded vector space of dimension $\mathbf w$. One defines functors from $\mathbb {G}$-representations, respectively $\mathbb {G}\times \mathbb {G}$-representations, to $\mathbb {G}$-equivariant vector bundles on a $\mathbb {G}$-variety Z, respectively to $\mathbb {G}\times \mathbb {G}$-equivariant vector bundles on a $\mathbb {G}\times \mathbb {G}$-variety, by $R\mapsto \mathscr {R} := \mathcal {O}\otimes _{\mathbb {C}} R$.

In particular, each $V^j_i$ defines a $\mathbb {G}$-equivariant vector bundle $\mathscr {V}^j_i$ on $\mathbb {M}$, and the $\mathbb {G}\times \mathbb {G}$-representations $L(V^1, V^2), E(V^1, V^2), L(W,V^2), L(V^1, W)$ define $\mathbb {G}\times \mathbb {G}$-equivariant vector bundles

$$\begin{aligned} \mathscr {L}(V^1, V^2), \mathscr {E}(V^1, V^2), \mathscr {L}(W,V^2), \mathscr {L}(V^1, W) \end{aligned}$$

on $\mathbb {M}\times \mathbb {M}$ (where $\mathbb {G}\times \mathbb {G}$ acts on $V^1$ via the first factor and on $V^2$ via the second factor).

Remark 3.4

In the language of stacks, these bundles are pullbacks along $\mathbb {M}/\mathbb {G}\times \mathbb {M}/\mathbb {G}\rightarrow B\mathbb {G}\times B\mathbb {G}$.

Nakajima defines $\mathbb {G}\times \mathbb {G}$-equivariant homomorphisms,

(3.5)

where at a point $([B,i,j],[B',i',j'])\in \mathbb {M}\times \mathbb {M}$ the maps $\sigma$, $\tau$ are given by

$$\begin{aligned} \sigma (\xi ) = (B'\xi - \xi B,-\xi i, j' \xi ),\quad \tau (C,a,b) = \epsilon B'C+\epsilon CB + i'b + aj. \end{aligned}$$

(3.6)

Fix a nondegenerate stability condition $\theta$ as in Sect. 3.3 and write $\mathbb {M}^{{\text {s}}}$ for the GIT stable locus of $\mathbb {M}$ with respect to $\theta$ and $\mu ^{-1}(0)^{{\text {s}}} = \mu ^{-1}(0)\cap \mathbb {M}^{{\text {s}}}$.

Proposition 3.5

Suppose $[B,i,j], [B',i',j']\in \mathbb {M}$.

• (1) If $[B',i',j']\in \mathbb {M}^{{\text {s}}}$ then $\sigma$ is injective in the fiber over $\big ([B,i,j], [B',i',j']\big )$.

• (2) If $[B,i,j]\in \mathbb {M}^{{\text {s}}}$ then $\tau$ is surjective in the fiber over $\big ([B,i,j], [B',i',j']\big )$.

• (3) $\tau \circ \sigma = 0$ in the fiber over $\big ([B,i,j], [B',i',j']\big )\in \mu ^{-1}(0)\times \mu ^{-1}(0)$.

Now define a section s of $\mathscr {E}(V^1,V^2)\oplus \mathscr {L}(W,V^2)\oplus \mathscr {L}(V^1,W)$ by

$$\begin{aligned} s([B,i,j],[B',i',j']) = (0,-i',j). \end{aligned}$$

(3.7)

Proposition 3.6

• (1) Over $\mathbb {M}\times \mathbb {M}$, we have $\tau (s)= 0$.

• (2) Viewing $s|_{\mu ^{-1}(0)\times \mu ^{-1}(0)^{{\text {s}}}}$ as a section of ${\text {coker}}(\sigma )$, its vanishing locus Z(s) in $\mu ^{-1}(0)^{{\text {s}}}\times \mu ^{-1}(0)^{{\text {s}}}$ is smooth and equals the locus of pairs $\big ([B,i,j], [B',i',j']\big )$ for which

  $$\begin{aligned} \mathbb {G}\cdot [B,i,j] = \mathbb {G}\cdot [B',i',j']. \end{aligned}$$

For the proofs of these propositions when the character is the one used in [18], see [18, p. 537 and Lemma 5.2]. We reprove the assertions in general in Proposition 5.4 and Theorem 6.2.

We now want to translate the above in terms of the Crawley-Boevey quiver $Q^{{\text {CB}}}$. Consider framed representations $[B,i,j], [B',i',j'] \in \mu ^{-1}(0)^{{\text {s}}}\times \mu ^{-1}(0)^{{\text {s}}}$, acting on the vector spaces $(V^1, W)$ and $(V^2, W)$ (both with associated dimensions $\mathbf {v}, \mathbf {w}$). We write $B^{{\text {CB}}}$, $(B')^{{\text {CB}}}$ for the associated representations of the preprojective algebra $\Pi ^0(Q^{{\text {CB}}})$, and $(V^\ell )^{{\text {CB}}}$ for their underlying vector spaces. Thus, one has

$$\begin{aligned} (V^\ell )^{{\text {CB}}}_j = {\left\{ \begin{array}{ll} V^\ell _i &{} \text {if}\,j=i\in I;\\ \mathbb {C} &{} \text {if}\,j=\infty .\end{array}\right. } \end{aligned}$$

Now

$$\begin{aligned} L\big ((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}\big )&= L(V^1, V^2) \oplus {\text {Hom}}(\mathbb {C},\mathbb {C}),\end{aligned}$$

(3.8)

$$\begin{aligned} E((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}})&= E(V^1, V^2)\oplus L(W, V^2)\oplus L(V^1, W). \end{aligned}$$

(3.9)

The following is immediate from (3.8), (3.9), and Proposition 3.6:

Proposition 3.7

• (1) Under the identifications of (3.8), (3.9), the map

  $$\begin{aligned} L\big ((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}\big )= & {} L(V^1,V^2)\oplus \mathbb {C} \xrightarrow {\sigma \oplus s} E(V^1,V^2)\\&\oplus L(W,V^2)\oplus L(V^1,W)\\= & {} E((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}) \end{aligned}$$

  is identified with the map

  $$\begin{aligned} \partial _0: L\big ((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}\big )\longrightarrow E((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}) \end{aligned}$$

  defined by $\partial _0(\phi ) = (B')^{{\text {CB}}}\phi - \phi B^{{\text {CB}}}$.

• (2) Thus, for the dual map

  $$\begin{aligned} \partial _0^\vee : \mathscr {E}((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}) \longrightarrow \mathscr {L}\big ((V^1)^{{\text {CB}}}, (V^2)^{{\text {CB}}}\big ) \end{aligned}$$

  we have that ${\text {coker}}(\partial _0^\vee )$ is the direct image to $\mu ^{-1}(0)^{{\text {s}}}\times \mu ^{-1}(0)^{{\text {s}}}$ of a line bundle on the smooth subvariety of part (2) of Proposition 3.6.

4 Graded tripled quivers and their moduli spaces

The present section is intended to provide a compactification of the moduli space of representations of the preprojective algebra $\Pi ^0(Q)$ associated to a quiver Q. For applications to Nakajima quiver varieties associated to a quiver $Q_0$, set $Q = Q_0^{{\text {CB}}}$, the Crawley-Boevey quiver associated to $Q_0$.

4.1 Graded tripling of a quiver

Let (I, E) be a graph, $\alpha \in \mathbb {Z}^I_{\ge 0}$ a dimension vector for I. Fix an orientation $\Omega$ defining a quiver $Q = (I,\Omega )$ as in Sect. 3.1. Fixing a closed interval $[a,b]\subset \mathbb {Z}$, we define a new quiver associated to $(I,\Omega )$, the graded-tripled quiver, denoted $Q^{{\text {gtr}}}$, as follows. We give $Q^{{\text {gtr}}}$ the vertex set $I\times [a,b]$ where I is the vertex set of Q. If E is the edge set of Q and H the associated set of pairs of an edge together with an orientation, we give $Q^{{\text {gtr}}}$ the arrow set

$$\begin{aligned} \big (H\times [a,b-1]\big ) \cup \big (I\times [a,b-1]). \end{aligned}$$

Thus:

• (1) for each $h\in H$, $n\in [a,b-1]$ we have arrows (h, n) with

  $$\begin{aligned} s(h,n) = (s(h), n) \text {and} t(h,n) = (t(h), n+1); \end{aligned}$$

• (2) for each $i\in I$, $n\in [a,b-1]$ we have arrows (i, n) with

  $$\begin{aligned} s(i,n) = (i,n) \text {and} t(i,n) = (i,n+1). \end{aligned}$$

For example, taking $[a,b] = [0,1]$:

Remark 4.1

Letting $b\rightarrow \infty$, the constructions extend mutatis mutandis to the case $[a,\infty )\subset \mathbb {Z}$.

Given a dimension vector $\alpha$ for Q, we define a “constant dimension vector” $\alpha ^{{\text {gtr}}}$ for $Q^{{\text {gtr}}}$ by $\alpha ^{{\text {gtr}}}_{i,n} = \alpha _i$ for all $i\in I, n\in [a,b]$.

4.2 Relations and representations

We will consider $Q^{{\text {gtr}}}$ as a quiver with relations. Many of the relations are derived from those for the preprojective algebra $\Pi ^0(Q)$.

Throughout the remainder of the paper, we assume $b-a\ge 2$ in the definition of $Q^{{\text {gtr}}}$. We fix a decomposition $H = \Omega \sqcup \overline{\Omega }$ as in Sect. 3.1, determining a function $\epsilon$.

Notation 4.2

We write:

• (1) $a_{h,n}$ for the generators of $kQ^{{\text {gtr}}}$ corresponding to arrows (h, n) (where $h\in H, n\in [a,b-1]$);

• (2) $e_{i,n}$ for the generators of $kQ^{{\text {gtr}}}$ corresponding to arrows (i, n) (where $i\in I, n\in [a,b-1]$).

Definition 4.3

We write $A := kQ^{{\text {gtr}}}/I$, where I is the two-sided ideal in the path algebra $kQ^{{\text {gtr}}}$ generated by the following relations:

• (1) $\sum _{h\in H} \epsilon (h)a_{\overline{h},n+1}a_{h,n}$, $n\in [a,b-2]$ (“preprojective relations”).

• (2) $e_{t(h),n+1}a_{h,n} - a_{h,n+1}e_{s(h),n}$ for all $n\in [a,b-2]$, $h\in H$.

We note that it is immediate from condition (2) that the element $e:= \sum _ne_{n} := \sum _n\sum _{i\in I}e_{i,n}$ is central in A.

We write ${\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$ for the space of representations of $Q^{{\text {gtr}}}$ with dimension vector $\alpha ^{{\text {gtr}}}$: thus, fixing an $I\times [a,b]$-graded vector space $V_{\bullet ,\bullet } = \bigoplus _{i\in I, n\in [a,b]} V_{i,n}$ with dimension vector $\alpha ^{{\text {gtr}}}$, we set

$$\begin{aligned} {\text {Rep}}(Q^{{\text {gtr}}},V_{\bullet ,\bullet })&= \left( \bigoplus _{h\in H, n\in [a,b-1]} {\text {Hom}}(V_{s(h),n}, V_{t(h),n+1})\right) \\&\qquad \bigoplus \left( \bigoplus _{i\in I, n\in [a,b-1]}{\text {Hom}}(V_{i,n}, V_{i,n+1})\right) . \end{aligned}$$

We write ${\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$ when $V_{i,n} = \mathbb {C}^{\alpha ^{{\text {gtr}}}_{i,n}}$. We also write

$$\begin{aligned} {\text {Rep}}(A,V_{\bullet ,\bullet })\subseteq {\text {Rep}}(Q^{{\text {gtr}}},V_{\bullet ,\bullet }), \quad \text {respectively}\quad {\text {Rep}}(A,\alpha ^{{\text {gtr}}})\subseteq {\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}}) \end{aligned}$$

for the closed affine subscheme of representations of A (that is, representations of $Q^{{\text {gtr}}}$ satisfying the relations generating I). We will write $\mathbb {G} = \prod _{i\in I} GL(\alpha _i)$ for the group associated to Q and dimension vector $\alpha$; then $\mathbb {G}^{{\text {gtr}}}\cong \mathbb {G}\times [a,b]$ naturally acts on the affine schemes ${\text {Rep}}(A,\alpha ^{{\text {gtr}}})\subseteq {\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$.

Remark 4.4

We note that this choice of notation is not entirely consistent with our earlier notation in the context of Nakajima quiver varieties. When $Q = Q_0^{{\text {CB}}}$ is the Crawley-Boevey quiver associated to $Q_0$, we will write $\mathbb {G}_0 = \prod _{i\in I_0}GL(\alpha _i)$.

Consider $\Pi ^0 = \Pi ^0(Q)$ as a graded algebra (with all generators corresponding to arrows $h\in H$ in degree 1). Let $\Pi ^0[e]$ be the graded polynomial extension with $\deg (e)=1$.

Lemma 4.5

Suppose $V_{\bullet ,\bullet }$ is an $I\times [a,b]$-graded vector space. Letting $h\in \Pi ^0$ act via $\sum _n a_{h,n}\in {\text {Rep}}(Q^{{\text {gtr}}},V_{\bullet ,\bullet })$ and $e$ act via $\sum _{i,n} e_{i,n}\in {\text {Rep}}(Q^{{\text {gtr}}},V_{\bullet ,\bullet })$, the space of graded $\Pi ^0[e]$-module structures on $V_{\bullet ,\bullet }$ is naturally identified with ${\text {Rep}}(A,V_{\bullet ,\bullet })$.

4.3 From $\Pi ^0$-modules to $Q^{{\text {gtr}}}$-representations

Suppose we have a finite-dimensional representation $V = (V_i)_{i \in I}$ of the preprojective algebra $\Pi ^0$ of dimension vector $\alpha$.

Construction 4.6

We obtain a representation of A on a vector space $V_{\bullet , \bullet }$ of dimension vector $\alpha ^{{\text {gtr}}}$ defined by:

• (1) setting $V_{i,n} := V_i$ for all $n\in [a,b]$;

• (2) defining each $e_{i,n}: V_{i,n} = V_i \xrightarrow {{\text {id}}} V_i = V_{i,n+1}$ to act by shift of $\mathbb {Z}$-grading; and

• (3) defining each generator of A corresponding to $h\in H$ to act via $\Pi ^0$ followed by grading shift.

The construction determines a morphism of algebraic varieties (“induction”)

$$\begin{aligned} \mathsf {Ind}^\circ : {\text {Rep}}(\Pi ^0,V)\longrightarrow {\text {Rep}}(A, V_{\bullet ,\bullet }). \end{aligned}$$

$$\begin{aligned} \text {Write } \mathbb {G}= \prod _i GL(V_{i})\,\text {and}\,\mathbb {G}^\mathrm{gtr} = \prod _{(i,n)\in I\times [a,b]} GL(V_{i,n}) \cong \prod _{n\in [a,b]}\mathbb {G}\text { as above,} \end{aligned}$$

with the diagonal homomorphism ${\text {diag}}: \mathbb {G}\rightarrow \mathbb {G}^{{\text {gtr}}}\cong \prod _{n\in [a,b]} \mathbb {G}$. Then the morphism $\mathsf {Ind}^\circ$ is $(\mathbb {G}, \mathbb {G}^{{\text {gtr}}})$-equivariant. We thus get a natural $\mathbb {G}^{{\text {gtr}}}$-equivariant morphism

$$\begin{aligned} \mathsf {Ind}: \mathbb {G}^{{\text {gtr}}}\times _{\mathbb {G}} {\text {Rep}}(\Pi ^0,V)\longrightarrow {\text {Rep}}(A, V_{\bullet ,\bullet }). \end{aligned}$$

(4.1)

Thus, given a representation $(a_h: V_{s(h)}\rightarrow V_{t(h)})_{h \in H}$ of $\Pi ^0$ on V, and $(g_{i,n})\in \mathbb {G}^{{\text {gtr}}}$, we have

$$\begin{aligned} \mathsf {Ind}\big ((g_{i,n}), a_h\big )= & {} (a_{h,n}, e_{i,n}) \, \text {where} \, a_{h,n} = g_{t(h),n+1}a_h g_{s(h),n}^{-1}\, \text {and}\\ e_{i,n}= & {} g_{i,n+1} g_{i,n}^{-1}. \end{aligned}$$

Proposition 4.7

The map $\mathsf {Ind}$ of (4.1) defines an open immersion of $\mathbb {G}^{{\text {gtr}}}\times _{\mathbb {G}} {\text {Rep}}(\Pi ^0,V)$ in ${\text {Rep}}(A,V_{\bullet ,\bullet })$, whose image consists of those $(a_{h,n}, e_{i,n})$ for which:

$$\begin{aligned} e_{i,n}\, \mathrm{is\, an\, isomorphism\, for\, all } \, n\in [a,b-1]. \end{aligned}$$

(4.2)

Proof

The condition (4.2) is clearly an open condition. Given $(a_{h,n}, e_{i,n})$ satisfying (4.2), define

$$\begin{aligned} a_h := e_{t(h),a}^{-1}a_{h,a}, g_{i,a} := {\text {Id}}_i, g_{i,n} := e_{i,n-1}e_{i,n-2}\dots e_{i,a} \, \text {for}\,\, n\ge a+1. \end{aligned}$$

Inductively applying the identity $e_{t(h), a+1} a_{h,a} = a_{h,a+1}e_{s(h),a}$, one calculates that $(g_{i,n})\cdot \mathsf {Ind}^\circ (a_h) = (a_{h,n}, e_{i,n})$. This construction $(a_{h,n}, e_{i,n})\mapsto ((g_{i,n}), a_h)\in \mathbb {G}^{{\text {gtr}}}\times _{\mathbb {G}} {\text {Rep}}(\Pi ^0,V)$ is evidently inverse to $\mathsf {Ind}$ on the locus of those $(a_{h,n}, e_{i,n})$ that satisfy the condition (4.2). $\square$

Corollary 4.8

The morphism of quotient stacks

$$\begin{aligned} \mathsf {Ind}^\circ : {\text {Rep}}(\Pi ^0,V)/\mathbb {G}\longrightarrow {\text {Rep}}(A,V_{\bullet ,\bullet })/\mathbb {G}^{{\text {gtr}}}\end{aligned}$$

is an open immersion.

Remark 4.9

We note that if $V_{\bullet ,\bullet }$ lies in the open image of $\mathsf {Ind}$, then it uniquely determines an $I\times \mathbb {Z}$-graded $\Pi ^0[e]$-module $\widetilde{V}_{\bullet ,\bullet }$ with $\widetilde{V}_{i,n} = \alpha _i$ for all $n\in \mathbb {Z}$ and $i\in I$. In other words, $V_{\bullet ,\bullet }$ uniquely extends “upwards and downwards” to all graded degrees compatibly with the $\Pi ^0[e]$-action.

4.4 Stability for Crawley-Boevey quivers

Suppose that $Q_0 = (I_0,\Omega _0)$ is a quiver with dimension vector $\mathbf {v}$ and framing vector $\mathbf {w}$ and that $Q = Q_0^{{\text {CB}}} = (I,\Omega )$ is the associated Crawley-Boevey quiver, with dimension vector $\alpha$ so that $\alpha _\infty = 1$ and $\alpha |_{I_0} = \mathbf {v}$. We fix $[a,b] \subset \mathbb {Z}$ and let $Q^{{\text {gtr}}}$ denote the quiver constructed above from Q. We write $\alpha ^{{\text {gtr}}}$ for the associated dimension vector: thus,

$$\begin{aligned} \alpha ^{{\text {gtr}}}_{i,n} = \alpha _i = {\left\{ \begin{array}{ll} \mathbf {v}_i &{} i\in I_0\\ 1 &{} i=\infty .\end{array}\right. } \end{aligned}$$

Assume given a nondegenerate stability condition $\theta = \sum \theta _i \delta _i$ for Q with respect to $\alpha$.

Remark 4.10

In particular, we have $\theta _\infty \ne 0$.

We want to choose a stability condition $\theta ^{{\text {gtr}}}$ for $Q^{{\text {gtr}}}$ with the following properties:

• (1) $\theta ^{{\text {gtr}}}$ is nondegenerate with respect to $\alpha ^{{\text {gtr}}}$. In particular, the semistable and stable points of ${\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$ coincide.

• (2) If V is a representation associated to a representation of the preprojective algebra $\Pi ^0(Q)$, then V is $\theta ^{{\text {gtr}}}$-stable if and only if the corresponding $\Pi ^0(Q)$-representation is $\theta$-stable.

We first remind the reader that $\delta _{i,n}(M) := \dim (M_{i,n})$; we will write $\theta$ as a linear combination of the $\delta _{i,n}$. Also, we note that it suffices to construct a rational linear functional $\theta ^{{\text {gtr}}}$, since any positive integer multiple of $\theta ^{{\text {gtr}}}$ evidently defines the same stable and semistable loci.

In our construction of $\theta ^{{\text {gtr}}}$, we will want to fix a positive integer

$$\begin{aligned} \displaystyle T \gg 0. \end{aligned}$$

(4.3)

We fix an ordering on the vertices of $Q_0$, identifying $I = \{1, \dots , r\}$. We write $\theta ^{{\text {gtr}}}$ as a sum of terms:

$$\begin{aligned} \theta ^{{\text {lg}}}= & {} T^{r+1}\big [\delta _{\infty ,b}-\delta _{\infty ,a}\big ] + \sum _{i=1}^r T^i\big [\delta _{i,b}-\delta _{i,a}\big ], \quad \theta ^{{\text {mid}}} = \sum _{i\in I} \theta _i \delta _{i,a}\\ \text {and}\; \theta ^{{\text {sm}}}= & {} -\sum _{i=1}^r T^{-i}\delta _{i,a} + T^{-r-1} \sum _{(i,n)\in I\times (a,b)} \delta _{i,n}. \end{aligned}$$

Finally, we write $C := \theta ^{{\text {lg}}}(\alpha ^{{\text {gtr}}}) + \theta ^{{\text {mid}}}(\alpha ^{{\text {gtr}}}) + \theta ^{{\text {sm}}}(\alpha ^{{\text {gtr}}})$ and write

$$\begin{aligned} \theta ^{{\text {gtr}}}:= \theta ^{{\text {lg}}} + \theta ^{{\text {mid}}} + \theta ^{{\text {sm}}} - C\delta _{\infty ,a}. \end{aligned}$$

We note that $\theta ^{{\text {lg}}}(\alpha ^{{\text {gtr}}}) =0$, so C is bounded independent of T. Also, since $\delta _{\infty , a}(\alpha ^{{\text {gtr}}}) = 1$, we get $\theta ^{{\text {gtr}}}(\alpha ^{{\text {gtr}}})=0$.

Lemma 4.11

For fixed dimension vector $\alpha$ (and thus $\alpha ^{{\text {gtr}}}$) and choices as in (4.3),

$$\begin{aligned} \theta ^{{\text {gtr}}}(M)\ne 0 \,\,\,\text {for}\,\,\, 0\not \subseteq M\not \subseteq V. \end{aligned}$$

Proof

Assume that $\theta ^{{\text {gtr}}}(M) = 0$. Write $m_{i,n}:= \delta _{i,n}(M) = \dim (M_{i,n})$. Since the coefficients of T in $\theta ^{{\text {gtr}}}$ are bounded independent of T, we conclude that each T-coefficient of $\theta ^{{\text {gtr}}}(M)$ must vanish. In particular, $\theta ^{{\text {lg}}}(M) = 0$ and thus $m_{i,b}= m_{i,a}$ for all $i\in I$.

Since $m_{\infty ,a} \in \{0,1\}$, we consider the two cases:

Case 1 :

$m_{\infty , a} = m_{\infty ,b} = 0$. In this case $0 = \theta ^{{\text {gtr}}}(M) = \theta ^{{\text {mid}}}(M) +\theta ^{{\text {sm}}}(M)$, and again for $T\gg 0$ each coefficient of T must vanish. From $\theta ^{{\text {sm}}}(M) = 0$ we get $m_{i,a}= 0$ for all $i\in I_0$, and $\sum _{(i,n)\in I\times (a,b)} m_{i,n} =0$ implying $m_{i,n} = 0$ for $(i,n)\in I\times (a,b)$. Combined with the equality $m_{i,b}= m_{i,a}$ for all $i\in I$ from above, we conclude $M=0$.

Case 2 :

$m_{\infty , a} = m_{\infty ,b} = 1$. Then

$$\begin{aligned} 0 =\theta ^{{\text {gtr}}}(M) = \theta ^{{\text {mid}}}(M) + \theta ^{{\text {sm}}}(M) - \big [\theta ^{{\text {mid}}}(\alpha ^{{\text {gtr}}}) +\theta ^{{\text {sm}}}(\alpha ^{{\text {gtr}}})]. \end{aligned}$$

Again, considering term-by-term in powers of T, we find that $m_{i,a} = \alpha _{i,a}$ for $i\in I_0$; and then $\sum _{(i,n)\in I\times (a,b)} m_{i,n} = \sum _{(i,n)\in I\times (a,b)} \alpha ^{{\text {gtr}}}_{i,n}$ implying (since $m_{i,n}\le \alpha ^{{\text {gtr}}}_{i,n}$) that $m_{i,n} = \alpha ^{{\text {gtr}}}_{i,n}$ for $(i,n)\in I\times (a,b)$. Combined with the equality $m_{i,b}= m_{i,a}$ for all $i\in I$, we conclude that $m_{i,n} = \alpha ^{{\text {gtr}}}_{i,n}$ for all $(i,n)\in I\times [a,b]$, i.e. $M=V$. $\square$

Proposition 4.12

With respect to $\theta ^{{\text {gtr}}}$ as above, we have:

• (1) The semistable and stable loci of ${\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$ coincide, as do those of ${\text {Rep}}(A,\alpha ^{{\text {gtr}}})$.

• (2) Every stable point of ${\text {Rep}}(Q^{{\text {gtr}}},\alpha ^{{\text {gtr}}})$ is generated as a $kQ^{{\text {gtr}}}$-module in degree a.

• (3) If $V_{\bullet ,\bullet }$, $W_{\bullet ,\bullet }$ are vector spaces with dimension vector $\alpha ^{{\text {gtr}}}$, equipped with A-module structures making them stable, then ${\text {Hom}}_{A}(V_{\bullet ,\bullet }, W_{\bullet ,\bullet })$ is 1-dimensional if $V_{\bullet ,\bullet }$ and $W_{\bullet ,\bullet }$ are isomorphic as A-modules and is 0-dimensional otherwise.

• (4) For a representation V of $\Pi ^0$ of dimension vector $\alpha$, V is stable with respect to $\theta$ if and only if $\mathsf {Ind}^\circ (V) \in {\text {Rep}}(A,\alpha ^{{\text {gtr}}})$ is stable with respect to $\theta ^{{\text {gtr}}}$.

Proof

• (1) This is the content of Lemma 4.11.

• (2) Supposing V is stable, let M be the subrepresentation generated by $V_{I\times \{a\}}$. Arguing as in the proof of Lemma 4.11, we have that $\theta ^{{\text {lg}}}(M) < 0$, and therefore V is unstable, unless $m_{i,b} = m_{i,a}$ for all $i\in I$. We conclude that $m_{i,b} = m_{i,a}$ for all $i\in I$ and hence that

  $$\begin{aligned} \theta ^{{\text {gtr}}}(M) = \theta ^{{\text {mid}}}(M) + \theta ^{{\text {sm}}}(M) - \big [\theta ^{{\text {mid}}}(\alpha ^{{\text {gtr}}}) +\theta ^{{\text {sm}}}(\alpha ^{{\text {gtr}}})]. \end{aligned}$$

  Noting that $\theta ^{{\text {mid}}}(M) = \theta ^{{\text {mid}}}(V)$ by definition and analyzing $\theta ^{{\text {sm}}}(M) -\theta ^{{\text {sm}}}(V)$ term-by-term in powers of T, we find that $\theta ^{{\text {gtr}}}(M)<0$ unless $m_{i,n} = \alpha ^{{\text {gtr}}}_{i,n}$ for all $(i,n)\in I\times (a,b)$, and thus stability of V implies $M=V$.

• (3) is standard.

• (4) Consider a representation V of $\Pi ^0(Q)$. As before, we write $\alpha ^{{\text {gtr}}}$ for the dimension vector of $\mathsf {Ind}^\circ (V)$ where V has dimension vector $\alpha$. For any sub-representation $M\subseteq \mathsf {Ind}^\circ (V)$, write $m_{i,n} = \dim (M_{i,n})$.

Because $e_{i,n}: \mathsf {Ind}^\circ (V)_{i,n} \rightarrow \mathsf {Ind}^\circ (V)_{i,n+1}$ is an isomorphism for each $n\in [a,b-1]$, we have, for any sub-representation M, that $m_{i,n+1}\ge m_{i,n}$ for all $(i, n)\in I\times [a,b-1]$. Analyzing $\theta ^{{\text {gtr}}}(M)$ term-by-term in powers of T, we conclude that $\theta ^{{\text {gtr}}}(M)>0$, and thus M is irrelevant to the stability of $\mathsf {Ind}^\circ (V)$, unless $m_{i,b} = m_{i,a}$ for all $i\in I$, i.e., unless $M = \mathsf {Ind}^\circ (V')$ for some $\Pi ^0(Q)$-submodule $V'\subseteq V$.

Thus, suppose $M = \mathsf {Ind}^\circ (V')$ for some $\Pi ^0(Q)$-submodule $V'\subseteq V$. Write $\alpha '$ for the dimension vector of $V'$. Then $\theta ^{{\text {gtr}}}(M) = \theta (\alpha ') + \theta ^{{\text {sm}}}(M) -\big [\theta (\alpha ) + \theta ^{{\text {sm}}}(\alpha ^{{\text {gtr}}})]\alpha '_\infty .$

Case 1 :

$\alpha '_\infty = 0$. In this case, $\theta ^{{\text {gtr}}}(M) = \theta (\alpha ') + \theta ^{{\text {sm}}}(M)$. If $\theta (\alpha ')<0$, so $V'$ destablizes V, then we see that $\theta ^{{\text {gtr}}}(M)<0$, so M destabilizes $\mathsf {Ind}^\circ (V)$. On the other hand if $\theta (\alpha ')>0$ then $\theta ^{{\text {gtr}}}(M)>0$ as well. Thus in this case, $V'$ destabilizes V if and only if $\mathsf {Ind}^\circ (V')$ destabilizes $\mathsf {Ind}^\circ (V)$.

Case 2 :

$\alpha '_\infty = 1$. Then, as in Case 2 of Lemma 4.11,

$$\begin{aligned} \theta ^{{\text {gtr}}}(M) = \theta ^{{\text {mid}}}(M) + \theta ^{{\text {sm}}}(M) - \big [\theta ^{{\text {mid}}}(\alpha ^{{\text {gtr}}}) +\theta ^{{\text {sm}}}(\alpha ^{{\text {gtr}}})]. \end{aligned}$$

The leading term in T is $\theta ^{{\text {mid}}}(M)-\theta ^{{\text {mid}}}(\alpha ^{{\text {gtr}}}) = \theta (\alpha ')$. Thus $\theta ^{{\text {gtr}}}(M)<0$ if and only if $\theta (\alpha ')<0$, and so $V'$ destabilizes V if and only if $\mathsf {Ind}^\circ (V')$ destabilizes $\mathsf {Ind}^\circ (V)$. This completes the proof. $\square$

As in [14, Proposition 4.3], since $Q^{{\text {gtr}}}$ has no oriented cycles we obtain a projective quotient

$$\begin{aligned} \overline{\mathfrak M} := {\text {Rep}}(A,\alpha ^{{\text {gtr}}})/\!\!/_{\chi ^{{\text {gtr}}}}\mathbb {G}^{{\text {gtr}}}. \end{aligned}$$

Corollary 4.13

The natural map $\mathsf {Ind}: \mathfrak M\rightarrow \overline{\mathfrak M}$ is an open immersion of the quiver variety $\mathfrak M$ in a projective scheme.

Remark 4.14

Although we expect that for sufficiently large interval [a, b] and sufficiently generic $\theta ^{{\text {gtr}}}$ the compactification $\overline{\mathfrak M}$ is nonsingular and connected, we do not need this. Instead, we may replace $\overline{\mathfrak M}$ by the closure of $\mathfrak M$ in $\overline{\mathfrak M}$ and give that closure the reduced scheme structure. Thus, in what follows we always assume without comment that $\overline{\mathfrak M}$ is integral and projective.

5 A perfect complex on $\mathfrak M\times \overline{\mathfrak M}$

We note that the construction in this section is similar to the one in Section 5 of [18]. However, we wish to emphasize that Nakajima’s framings are not explicitly present in this section: for applications to Nakajima quiver varieties with nonzero framing, one should take $Q = (Q_0)^{{\text {CB}}}$ to be the Crawley-Boevey quiver associated to the quiver $Q_0$ used in Nakajima’s constructions.

Fix a quiver Q and a dimension vector $\alpha$. Let $V_{\bullet ,\bullet }$, $W_{\bullet ,\bullet }$ be two $I\times [a,b]$-graded vector spaces with dimension vector $\alpha ^{{\text {gtr}}}$.

Remark 5.1

We again emphasize that $V_{\bullet ,\bullet }$, $W_{\bullet ,\bullet }$ will be endowed with the structure of representations of $Q^{{\text {gtr}}}$ satisfying the relations of A. Our choice of notation for the space $W_{\bullet ,\bullet }$ is not meant to indicate any relationship to Nakajima’s framing vector space $(W_i)_{i\in I}$.

Convention 5.2

We now fix an $N\ge 2$ and set $[a,b]=[0,N]$ in the definitions of $Q^{{\text {gtr}}}$, $\alpha ^{{\text {gtr}}}$, A.

Suppose that we choose representations of A in $V_{\bullet ,\bullet }, W_{\bullet ,\bullet }$; we write $(a^V, e^V) = (a^V_{h,n}, e^V_{i,n})$, respectively $(a^W, e^W) = (a^W_{h,n}, e^W_{i,n})$ to denote these two structures. We also write

$$\begin{aligned} \displaystyle a^V_n = \sum _{h\in H}a^V_{h,n} \text {and} e^V_n = \sum _{i\in I} e^V_{i,n}, \text {and similarly for { W}. } \end{aligned}$$

In terms of the sign function (3.1) and the pairing (3.2), the preprojective relations become

$$\begin{aligned} (\epsilon a^V_{n+1})a_n^V = 0 = a^V_{n+1}(\epsilon a^V_n). \end{aligned}$$

(5.1)

Assumption 5.3

We assume that the representation $V_{\bullet ,\bullet }$ lies in the image of $\mathsf {Ind}$: in other words, the linear operators $e^V_{i,n}$ are invertible for $n\in [0,N-1]$.

Consider the vector spaces and maps, graded so $E(V_{\bullet , 0}, W_{\bullet , 1})$ lies in cohomological degree 0,

$$\begin{aligned} L(V_{\bullet , 0},W_{\bullet , 0}) \xrightarrow {\partial _0} E(V_{\bullet , 0}, W_{\bullet , 1})\xrightarrow {\partial _1} L(V_{\bullet , 0}, W_{\bullet , 2}), \end{aligned}$$

(5.2)

defined as follows: given $\phi \in L(V_{\bullet , 0}, W_{\bullet , 0})$ and $\psi \in E(V_{\bullet , 0},W_{\bullet , 1})$, we let

$$\begin{aligned} \partial _0(\phi )= & {} a^W_0\phi - e^W_0\circ \phi \circ (e^V_0)^{-1}a^V_0, \nonumber \\ \partial _1(\psi )= & {} (\epsilon a^W_1)\psi - e^W_1\circ \psi \circ (e^V_0)^{-1}(\epsilon a^V_0). \end{aligned}$$

(5.3)

Proposition 5.4

• (1) The kernel of $\partial _0$ is naturally identified with a subspace of ${\text {Hom}}_{A}(V_{\bullet , \bullet }, W_{\bullet , \bullet })$.

• (2) The composite $\partial _1\circ \partial _0$ is zero.

• (3) If $[a,b]=[0,2]$, the cokernel of $\partial _1$ is naturally identified with ${\text {Hom}}_{A}(W_{\bullet , \bullet }, V_{\bullet , \bullet })^*$.

We note that for assertion (3), we use in a fundamental way that Remark 4.9 applies to $V_{\bullet , \bullet }$.

Proof

If $\partial _0(\phi ) = 0$, then we may define a linear map $\Phi _\bullet : V_{\bullet , \bullet }\rightarrow W_{\bullet , \bullet }$ by $\Phi _n = e^W_{n-1}\dots e^W_0\circ \phi \circ (e^V_{n-1}\dots e^V_0)^{-1}$. It is immediate from the construction that $\Phi _\bullet$ is compatible with the operators $e_n$ in the obvious sense. Similarly, since $\partial _0(\phi )= 0$ we get that $a^W_0\Phi _0 = \Phi _1a^V_0$; it is immediate by induction that $\Phi _\bullet$ is compatible with all operators a in the obvious sense. Thus $\Phi _\bullet \in {\text {Hom}}_{A}(V_{\bullet , \bullet }, W_{\bullet , \bullet })$. Since $e\in A$ acts invertibly on $V_{\bullet , \bullet }$ in the appropriate range, any such $\Phi _\bullet$ is determined uniquely by $\Phi _0 = \phi$ by the above construction, proving assertion (1).

For assertion (2), we calculate:

$$\begin{aligned} \partial _1\partial _0(\phi ) = (\epsilon a^W_1) a^W_0\phi - (\epsilon a^W_1)e^W_0\phi (e^V_0)^{-1}a^V_0 \\ -e^W_1 a^W_0\phi (e^V_0)^{-1}(\epsilon a^V_0) + e^W_1 e^W_0\phi (e^V_0)^{-1}a^V_0 (e^V_0)^{-1}(\epsilon a^V_0). \end{aligned}$$

(5.4)

Now

$$\begin{aligned}&- (\epsilon a^W_1)e^W_0\phi (e^V_0)^{-1}a^V_0 - e^W_1 a^W_0\phi (e^V_0)^{-1}(\epsilon a^V_0) \\&\quad = - e^W_1 (\epsilon a^W_1)\phi (e^V_0)^{-1}a^V_0 - e^W_1 a^W_0\phi (e^V_0)^{-1}(\epsilon a^V_0), \end{aligned}$$

which vanishes by (3.3). Thus to prove (2) it suffices to show that

$$\begin{aligned}&(\epsilon a^W_1) a^W_0\phi + e^W_1 e^W_0\phi (e^V_0)^{-1}a^V_0 (e^V_0)^{-1}(\epsilon a^V_0) \\&\quad = (\epsilon a^W_1) a^W_0\phi + e^W_1 e^W_0\phi (e^V_0)^{-1}(e^V_1)^{-1}a^V_1 (\epsilon a^V_0) =0. \end{aligned}$$

However, $(\epsilon a^W_1) a^W_0 = 0 = a^V_1 (\epsilon a^V_0)$ is immediate from the preprojective relations (5.1).

We now turn to assertion (3). Suppose $\lambda : W^2\rightarrow V^0$ is an I-graded linear map. We have that ${\text {tr}}\big (\lambda \partial _1(\psi )\big ) = 0$ for all $\psi \in E(V^0,W^1)$ if and only if

$$\begin{aligned} 0= & {} {\text {tr}}\big [\lambda \big ((\epsilon a^W_1)\psi - e^W_1\circ \psi \circ (e^V_0)^{-1}(\epsilon a^V_0)\big )\big ]\\= & {} {\text {tr}}\big [\big (\lambda (\epsilon a^W_1) - (e^V_0)^{-1}(\epsilon a^V_0)\lambda e^W_1\big )\circ \psi \big ] \end{aligned}$$

for all $\psi$, if and only if

$$\begin{aligned} \lambda (\epsilon a^W_1) - (e^V_0)^{-1}(\epsilon a^V_0)\lambda e^W_1 = 0. \end{aligned}$$

(5.5)

By the nondegeneracy of the trace pairing, we obtain:

Lemma 5.5

The cokernel of $\partial _1$ is naturally dual to the space of those $\lambda$ satisfying (5.5).

We now use Assumption 5.3 and Remark 4.9 to see that $V_{\bullet , \bullet }$ lifts to an $I\times \mathbb {Z}$-graded $\Pi ^0[e]$-module $\widetilde{V}_{\bullet , \bullet }$ with $\dim (V_{i,n}) = \alpha _i$ for all $i \in I$ and $n\in \mathbb {Z}$, in such a way that $\widetilde{V}_{\bullet , \bullet +1} \cong \widetilde{V}_{\bullet ,\bullet }$ via multiplication by $e$. In particular, we use $\lambda$ to define a graded linear map $\Lambda _\bullet : W_{\bullet , \bullet }\rightarrow V_{\bullet , \bullet }$ by taking

$$\begin{aligned} \Lambda _2 = e_1^V e_0^V\lambda , \Lambda _1 = e_0^V \lambda e^W_1, \Lambda _0 = \lambda e^W_1 e^W_0, \end{aligned}$$

(5.6)

similarly to our construction of $\Phi _\bullet$ above. It is immediate from the definitions of the $\Lambda _i$ that

$$\begin{aligned} \Lambda _2 e_1^W = e_1^V \Lambda _1, \Lambda _1 e_0^W = e_0^V \Lambda _0. \end{aligned}$$

As in our construction of $\Phi _\bullet$, it follows from Equation (5.5) that $\Lambda _\bullet$ is indeed a graded A-module homomorphism: it remains only to observe that

$$\begin{aligned} \Lambda _2(\epsilon a_1^W) = e_1^V e_0^V \lambda (\epsilon a_1^W) = e_1^V (\epsilon a_0^V)\lambda e_1^W = \epsilon a_0^V e_0^V \lambda e_1^W = \epsilon a_0^V \Lambda _1, \end{aligned}$$

where the second equality follows from (5.5); and

$$\begin{aligned} \Lambda _1(\epsilon a_0^W)= & {} e_0^V \lambda e_1^W(\epsilon a_0^W) = e_0^V \lambda (\epsilon a_1^W) e_0^W\\= & {} e^V_0(e^V_0)^{-1}(\epsilon a^V_0)\lambda e^W_1e^W_0 = \epsilon a^V_0\Lambda _0, \end{aligned}$$

where the third equality follows from (5.5); and that any graded A-module homomorphism $\Lambda _\bullet : W_{\bullet , \bullet }\rightarrow V_{\bullet , \bullet }$ is uniquely determined by $\Lambda _2=e_1^V e_0^V\lambda$ by the formulas (5.6), completing the proof. $\square$

Corollary 5.6

When Q is a Crawley-Boevey quiver and $[a,b]=[0,2]$, then the complex (5.2) descends to a perfect complex C on $\mathfrak M\times \overline{\mathfrak M}$.

Proof

When $Q = (Q_0)^{{\text {CB}}}$ is a Crawley-Boevey quiver, we have $\mathbb {G} \cong \mathbb {G}_0\times {\mathbb G}_m$, where $\mathbb {G}_0 = \prod _{i\in I_0}GL(\mathbf {v}_i)$, ${\mathbb G}_m$ acts trivially on the stable locus, and $\mathbb {G}_0$ acts freely on the stable locus of ${\text {Rep}}(\Pi ^0(Q),\alpha )$ with quotient $\mathfrak M$. Similarly, $\mathbb {G}^{{\text {gtr}}}\cong (\mathbb {G}_0)^3\times {\mathbb G}_m^{3}$; the subgroup $(\mathbb {G}^{{\text {gtr}}})_0 = (\mathbb {G}_0)^3\times {\mathbb G}_m^2 \times \{1\}$ acts freely on ${\text {Rep}}(A,\alpha ^{{\text {gtr}}})^{{\text {s}}}$ with quotient $\overline{\mathfrak M}$. Since the complex defined by (5.2) is $(\mathbb {G}^{{\text {gtr}}})_0\times (\mathbb {G}^{{\text {gtr}}})_0$-equivariant, it descends to a perfect complex C on $\mathfrak M\times \overline{\mathfrak M}$. $\square$

6 Proofs of Theorems 1.2, 1.3, and 1.6

Let $Q_0$ be a quiver with dimension vector $\mathbf {v}$ and framing vector $\mathbf {w}$, and let $Q = Q_0^{{\text {CB}}}$ be the Crawley-Boevey quiver associated to $Q_0$ and $\mathbf {w}$.

We take $[a,b] = [0,2]$ in the definitions of $Q^{{\text {gtr}}}$, etc.

Let $\mathfrak M\hookrightarrow \overline{\mathfrak M}$ denote the compactification of the quiver variety constructed in Sect. 4.4. We wish to modify slightly the complex of (5.2) and Corollary 5.6. Thus, we consider the splitting

$$\begin{aligned} L(V_{\bullet , 0},W_{\bullet , 0})= & {} L(V_{\bullet , 0},W_{\bullet , 0})_{I_0} \oplus {\mathbb C} \\= & {} \left[ \bigoplus _{i\in I_0} {\text {Hom}}(V_{i, 0},W_{i, 0})\right] \oplus {\text {Hom}}(V_{\infty ,0}, W_{\infty , 0}). \end{aligned}$$

$$\begin{aligned} \text {We write}\quad \delta _0 = \partial _0|_{L(V_{\bullet , 0},W_{\bullet , 0})_{I_0}}: L(V_{\bullet , 0},W_{\bullet , 0})_{I_0} \rightarrow E(V_{\bullet ,0}, W_{\bullet , 1}). \end{aligned}$$

Similarly, we consider the splitting

$$\begin{aligned} L(V_{\bullet , 0},W_{\bullet , 2})= & {} L(V_{\bullet , 0},W_{\bullet , 2})_{I_0} \oplus {\mathbb C} \\= & {} \left[ \bigoplus _{i\in I_0} {\text {Hom}}(V_{i, 0},W_{i, 2})\right] \oplus {\text {Hom}}(V_{\infty ,0}, W_{\infty ,2}) \end{aligned}$$

and write $\delta _1 = \pi \circ \partial _1$ for the composite of $\partial _1$ followed by the projection

$$\begin{aligned} \pi : L(V_{\bullet , 0},W_{\bullet , 2}) \twoheadrightarrow L(V_{\bullet , 0},W_{\bullet , 2})_{I_0}. \end{aligned}$$

It is immediate from Corollary 5.6 that we obtain a complex on $\mathfrak M\times \overline{\mathfrak M}$, namely

$$\begin{aligned} R: \mathscr {L}(V_{\bullet , 0},W_{\bullet , 0})_{I_0} \xrightarrow {\delta _0} \mathscr {E}(V_{\bullet , 0}, W_{\bullet , 1})\xrightarrow {\delta _1} \mathscr {L}(V_{\bullet , 0}, W_{\bullet , 2})_{I_0}. \end{aligned}$$

(6.1)

Remark 6.1

The complex (6.1) is evidently of the form (2.4).

Theorem 6.2

For the complex R of (6.1), we have:

• (1) $\delta _0$ is injective and $\delta _1$ is surjective on each fiber. In particular, $\mathcal {H}^1(R) = 0 = \mathcal {H}^1(R^\vee )$, and $\mathcal {H}^0(R)$ is a vector bundle on $\mathfrak M\times \overline{\mathfrak M}$.

• (2) the map $\mathbb {C} = {\text {Hom}}(V_{\infty ,0}, W_{\infty ,0})\rightarrow E(V_{\bullet ,0},W_{\bullet , 1})$ defines a section s of $\mathcal {H}^0(R)$ whose scheme-theoretic zero locus is the graph $\Gamma$ of the inclusion $\mathfrak M\hookrightarrow \overline{\mathfrak M}$.

• (3) ${\text {rk}}(R) = \dim (\overline{\mathfrak M})$.

Proof

• (1) By Proposition 5.4, when $V_{\bullet , \bullet }$ and $W_{\bullet ,\bullet }$ are stable, ${\text {ker}}(\partial _0)$ is zero or consists of multiples of the identity endomorphism of $V_{\bullet ,\bullet } \cong W_{\bullet ,\bullet }$; in either case, we have ${\text {ker}}(\partial _0)\cap L(V_{\bullet , 0},W_{\bullet , 0})_{I_0} = 0$. Thus $\delta _0$ is injective on each fiber.

Similarly either ${\text {coker}}(\partial _1)$ is zero, or else $V_{\bullet ,\bullet }\cong W_{\bullet ,\bullet }$ and ${\text {coker}}(\partial _1)\cong {\text {Hom}}(W_{\bullet ,\bullet }, V_{\bullet ,\bullet })^* \cong \mathbb {C}$ by stability of $V_{\bullet ,\bullet }$ and $W_{\bullet ,\bullet }$; in the latter case, since ${\text {im}}(\partial _1)$ has codimension 1, its projection on $L(V_{\bullet , 0}, W_{\bullet , 2})_{I_0}$ must be surjective: otherwise ${\text {im}}(\partial _1)\cap {\text {Hom}}(V_{\infty ,0},W_{\infty ,2}) \ne 0$, but (by stability) every nonzero element of its dual ${\text {Hom}}(W_{\bullet ,\bullet }, V_{\bullet ,\bullet })$ is nonzero at the vertex $\infty$. We conclude that $\delta _1$ is surjective on each fiber, concluding the proof of assertion (1).

• (2) By Proposition 5.4, the cohomologies $H^1(C)$ and $H^1(C^\vee )$ are supported set-theoretically on the graph $\Gamma$ of the inclusion $\mathfrak M\hookrightarrow \overline{\mathfrak M}$. It follows that the set-theoretic zero locus of the section s of assertion (2) is $\Gamma$. Thus, to prove the scheme-theoretic assertion, we may restrict R to $\mathfrak M\times \mathfrak M$.

Supposing, then, that both $e^V_{i,n}$ and $e^W_{i,n}$ act invertibly for $n=0,1$, and applying appropriate automorphisms of $V_{\bullet ,\bullet }$ and $W_{\bullet ,\bullet }$, we may assume that $a^V = a^W$ and that all $e^V_{i,n}$ and $e^W_{i,n}$ are identity matrices. Let $\mathbb {C}[\hbar ]$ denote the ring of dual numbers and let $a^V + \hbar b^V$, $a^W + \hbar b^W$ be first-order deformations of $V_{\bullet , \bullet }$, $W_{\bullet ,\bullet }$. It is immediate from the formulas (5.3) that the linearization of the map $\partial _0$ of (5.2) is given by $\phi \mapsto b_0^W \phi - \phi b_0^V$. If the linearization is of less than full rank, then by Proposition 5.4(1) there is a homomorphism $0\ne \phi \in {\text {Hom}}(V_{\bullet ,\bullet }, W_{\bullet ,\bullet })$ with $b^W \phi = \phi b^V$. Then the map ${\text {Id}}+ \hbar \phi$ intertwines $a^V + \hbar b^V$ and $a^W + \hbar b^W$: in other words, the differential of $\partial _0$ is degenerate only in directions tangent to $\Gamma$, which implies the assertion about s.

• (3) The rank assertion is immediate by direct calculation as in [18]. $\square$

Proof of Theorem 1.2

Let $d= {\text {dim}}(\mathfrak M)$. By Theorem 6.2 and Remark 6.1, the hypotheses of Corollary 2.5 are satisfied. Theorem 1.2 follows. $\square$

Proof of Theorem 1.3

By Theorem 7.3.5 of [19], $H^*(\mathfrak M,\mathbb {Z})$ is known to be free abelian and concentrated in even degrees. By the universal coefficient theorem, it follows that for any graded ring $E^*({\text {pt}})$, $H^*(\mathfrak M,\mathbb {Z})\otimes _{\mathbb {Z}} E^*({\text {pt}}) = H^*\big (\mathfrak M,E^*({\text {pt}})\big )$ and $H^*(B\mathbb {G},\mathbb {Z})\otimes _{\mathbb {Z}} E^*({\text {pt}}) = H^*(B\mathbb {G},E^*({\text {pt}})\big )$.

The Atiyah-Hirzebruch spectral sequence for a cohomology theory E and space X has $E_2$-page $E_2^{p,q} = H^p\big (X, E^q({\text {pt}})\big ) \implies E^{p+q}(X).$ By the previous paragraph, if $E^*({\text {pt}})$ is evenly graded the spectral sequence degenerates at $E_2$ for both $E^*(\mathfrak M)$ and $E^*(B\mathbb {G})$. Assertion (1) of the theorem thus follows from Theorem 1.2.

To prove (2), we observe that all the ingredients of the proof of Proposition 2.4 hold in any complex-oriented cohomology theory E. In particular, there is a Gysin map for proper morphisms and one can calculate $f^*$ via pull–cup-with-graph–push; that $[\Gamma ] = c_d(R)$ and Chern classes of R depend polynomially on the Chern classes of the tautological bundles follow from explicit formulas as in Lemmas 2.1 and 2.3 of [11]. It remains to see that $E^*(\overline{\mathfrak M})\rightarrow E^*(\mathfrak M)$ is surjective; however, the natural map $\mathfrak M\rightarrow B\mathbb {G}$ factors through $\overline{\mathfrak M}\rightarrow B\mathbb {G}$ defined via projection of $\mathbb {G}^{{\text {gtr}}}$ on any factor $\mathbb {G}$, and surjectivity of $E^*(\overline{\mathfrak M})\rightarrow E^*(\mathfrak M)$ follows from that of $E^*(B\mathbb {G})\rightarrow E^*(\mathfrak M)$. $\square$

Proof of Theorem 1.6

We note that assertion (1) is immediate from assertion (2).

In light of Remark 6.1, we will use the notation of Proposition 2.4 for the complex R. The Koszul complex associated to the complex R and section s of $\mathcal {H} = \mathcal {H}^0(R)$ of Theorem 6.2 provides a resolution (Section B.3.4 of [8]) of $\mathcal {O}_{\Gamma }$,

$$\begin{aligned} \Big [\bigwedge ^d \mathcal {H}^* \rightarrow \dots \rightarrow \bigwedge ^2 \mathcal {H}^* \rightarrow \mathcal {H}^*\rightarrow \mathcal {O}_{\mathfrak M\times \overline{\mathfrak M}}\Big ] \simeq \mathcal {O}_{\Gamma }. \end{aligned}$$

(6.2)

For each k, consider the kth tensor power $T^k(R)$ of the complex R: it is a differential graded vector bundle whose terms are tensor products of ${\mathcal E}_j^\ell$s and ${\mathcal F}_j^\ell$s. The symmetric group $S_k$ naturally acts on $T^k(R)$ with the usual ${\mathbb Z}/2{\mathbb Z}$-graded sign conventions; we write $\bigwedge ^k(R) = T^k(R)^{S_k, {\text {sgn}}}$, the sign-isotypic part of $T^k(R)$. Both operations $T^k(-)$ and $(-)^{S_k,{\text {sgn}}}$ preserve quasi-isomorphism, hence $\bigwedge ^k(R) \simeq \bigwedge ^k(\mathcal {H})$. The Koszul complex thus writes $\mathcal {O}_\Gamma$ as an iterated cone on the complexes $\bigwedge ^k(R)^\vee$.

We remark that, viewing ${\mathcal E}^\bullet :=\oplus _j{\mathcal E}_j^\bullet$ and ${\mathcal F}^\bullet :=\oplus _j{\mathcal F}_j^\bullet$ as $\mathbb {Z}/2$-graded vector bundles, we find that $\bigwedge ^k(R)$ is a direct summand of $\bigwedge ^k({\mathcal E}^\bullet \boxtimes {\mathcal F}^\bullet )$ in a canonical way. Furthermore, following the work of [3]⁴ it is known that $\bigwedge ^k({\mathcal E}^\bullet \boxtimes {\mathcal F}^\bullet )$ is an iterated extension of tensor products of Schur functors applied to the $\mathbb {Z}/2$-graded vector bundles ${\mathcal E}^\bullet$ and ${\mathcal F}^\bullet$ (see Corollary 1.2 of [6] and the discussion preceeding it for more details). Moreover, the expression for $\bigwedge ^k({\mathcal E}^\bullet \boxtimes {\mathcal F}^\bullet )$ as an iterated extension of $\mathcal {S}_{\lambda }({\mathcal E}^\bullet )$ and $\mathcal {S}_{\lambda }({\mathcal F}^\bullet )$ is compatible with the expression for $\bigwedge ^k(R)$ as a direct summand of $\bigwedge ^k({\mathcal E}^\bullet \boxtimes {\mathcal F}^\bullet )$: in particular, $\bigwedge ^k(R)$ is an iterated cone on external tensor products of the objects $S_{\lambda }({\mathcal E}_j^\ell )$, $S_\lambda ({\mathcal F}_j^\ell )$ that are obtained by applying Schur functors to the various ${\mathcal E}_j^\ell$ and ${\mathcal F}_j^\ell$.

Suppose ${\mathcal G}$ is a coherent complex on $\overline{\mathfrak M}$. For any external tensor product $S_{\lambda }({\mathcal E}_j^\ell )^\vee \boxtimes N$, we have

$$\begin{aligned} \mathbb {R}(p_{\mathfrak M})_*\big ((S_{\lambda }({\mathcal E}^\ell )^\vee \boxtimes N)\otimes (p_{\overline{\mathfrak M}})^*{\mathcal G}\big ) \simeq S_{\lambda }({\mathcal E}_j^\ell )^\vee \otimes U^\bullet \end{aligned}$$

for some bounded complex $U^\bullet$ of finite-dimensional vector spaces. Using (6.2) and the conclusion of the previous paragraph, we find that ${\mathcal G}|_{\mathfrak M}$ lies in the subcategory of $D_{{\text {coh}}}(\mathfrak M)$ that is generated, under the operations (i–iii) of assertion (2) of Theorem 1.6, by the $S_{\lambda }({\mathcal E}_j^\ell )^\vee$, where the Schur functors that appear are exactly those used in writing all the $\bigwedge ^k(\mathcal {H})$ as above. $\square$