1 Introduction

Let \(Q\subset \mathbb {R}^{3}\) be a convex polyhedron, and \(K\subset \mathbb {R}^{3}\) be a strictly convex body with smooth boundary \(\partial K\). We call \(Q\) a \(K\)-midscribing polyhedron if all its edges are tangent to \(\partial K\). In addition, when \(K=\mathbb {B}^3\) is the unit ball in \(\mathbb {R}^{3}\), we often call \(Q\) a midscribable polyhedron for short.

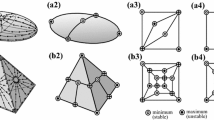
It follows from Koebe–Andreev–Thurston theorem (i.e. the Circle Packing Theorem) [2, 3, 19, 20] that: for any given convex polyhedron \(P\), there is a convex midscribable polyhedron \(Q\) combinatorially equivalent to \(P\). Moreover, the midscribable polyhedron is unique up to Möbius transformations which preserve the unit sphere. Indeed, it is a consequence of the simultaneous realization phenomenon of circle packings [5]. That is, any polyhedral graph (the \(1\)-skeleton of a polyhedron) and its dual graph can be simultaneously realized by two circle packings such that the two tangent circles corresponding to an edge in the primal graph and the two tangent circles corresponding to the dual of this edge are always orthogonal to each other at the same point of the Riemann sphere (Fig. 1).

Fig. 1
figure 1

A midscribable polyhedron

Full size image

Incidentally, Schulte [18] establishes that there is no higher dimensional analogue for the midscribability theorem: for every \(n\ge 3\) and any \(k\) with \(0\le k<n\), with the exception of \((n, k)=(3, 1)\), there exists a convex \(n\)-polytope \(P \subset {\mathbb {R}}^n\) such that no combinatorially isomorphic copy of \(P\) can have all of its \(k\)-dimensional faces tangent to the unit sphere. The case \(n=3\) is actually a classical result by Steiner (please see Grünbaum’s book [6]). The exceptional case \((n, k)=(3, 1)\) motivated the midscribability theorem and its generalizations.

A generalization of the midscribability theorem, also proposed by Schulte in [18], is the question of replacing the unit ball \(\mathbb {B}^3\) by any other smooth strictly convex body \(K \subset \mathbb {R}^3\). That is, given a convex body \(K \subset \mathbb R^3\), for any convex polyhedron \(P\), is there a \(K\)-midscribable polyhedron \(Q\) combinatorially equivalent to \(P\)?

In 1992, Schramm [15] proved the following generalization of the midscribability theorem:

Theorem 1.1

(Midscribability theorem) Given a strictly convex body \(K\subset \mathbb {R}^{3}\) with smooth boundary and a convex polyhedron \(P,\) there exists a convex \(P\)-type \(K\)-midscribing polyhedron \(Q\subset \mathbb R^3\).

Furthermore, Schramm proved that the space of all such \(K\)-midscribable \(Q\) is a \(6\)-manifold. In particular, if \(K\) is the closed unit ball, then the Circle Packing Theorem implies that the solution space can be identified with the Möbius group \(\textit{PSL}(2;{\mathbb {C}})\). Note that the rigidity property for the closed unit ball could be restated as the uniqueness of circle packings with the centers of three distinct circles fixed. The Circle Packing Theorem then immediately implies that the midscribable polyhedron is unique under this normalization condition.

Analogously, it remains to consider the solution space and the rigidity result for general convex bodies. This will be the main purpose of this paper. To reach this goal, let us introduce proper normalization conditions. Then we shall treat the midscribability theorem for general convex bodies by using a similar method.

Given a convex polyhedron \(P\subset \mathbb R^3\), we write \(P\equiv P({\mathcal {V}},{\mathcal {E}},{\mathcal {F}})\), where \({\mathcal {V}}\) (resp. \({\mathcal {E}},{\mathcal {F}}\)) denotes the set of vertices (resp. edges, faces). Denote by \(G(P)=({\mathcal {V}}, {\mathcal {E}}, {\mathcal {F}})\). Choosing \(f_{0}\in {\mathcal {F}}\) and three ordered sequential edges \(e_1,e_2,e_3\) of \(f_0\), we call such \(4\)-quadruple \({\fancyscript{O}}=\{f_0,e_1,e_2,e_3\}\) a combinatorial frame associated to \(P\). Suppose that \(Q\subset \mathbb R^3\) is a \(K\)-midscribable polyhedron combinatorially equivalent to \(P\). The midscribability implies that there exist three tangent points \(p_1,p_2,p_3\) corresponding to the edges \(e_1,e_2,e_3\) respectively. Under this convention, we call the polyhedron \(Q\) a normalized polyhedron with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\).

Then the question becomes: given a convex polyhedron \(P\) with a combinatorial frame \({\fancyscript{O}}\), for any triple \((p_1,p_2,p_3)\) with distinct points, \(p_i \in \partial K\), is there a convex \(K\)-midscribing polyhedron combinatorially equivalent to \(P\) with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\)? In addition, if the answer is yes, could the uniqueness hold?

For the close unit ball, from the Circle Packing Theorem, it follows that there exists a convex midscribable polyhedron in \(\mathbb R^3\). Moreover, all the other midscribable polyhedra can be transformed from the original one by using Möbius transformations. It is now possible that a Möbius transformation turns a convex polyhedron of \(\mathbb R^3\) into a non-convex one, or a degenerate one (some points go to infinity). That is, the resulted polyhedron could lose convexity or become degenerate.

To overcome these difficulties, in what follows let us use the \(3\)-dimensional real projective space \(\mathbb {RP}^3\) instead of the Euclidean space \(\mathbb R^3\). By viewing \(\mathbb R^3\) as a subset of \(\mathbb {RP}^3\), one can regard each polyhedron in \(\mathbb R^3\) as a polyhedron in \(\mathbb {RP}^3\). Note that a convex spherical polyhedron (or just a polyhedron) is a subset of \(\mathbb S^3\) obtained as the intersection of finitely many hemispheres and such that the interior \({P}^o \ne \emptyset \) and \(P \cap (-P)=\emptyset \) (that is, the polyhedron \(P\) does not contain any antipodal points). Using the covering \(\pi : \mathbb S^3 \rightarrow \mathbb {RP}^3\), then any closed set \(P \subset \mathbb {RP}^3\) is called a convex polyhedron in \(\mathbb {RP}^3\) if and only if either of the components of \(\pi ^{-1}(P)\) is a convex spherical polyhedron in \(\mathbb S^3\).

The following is our main result.

Theorem 1.2

Let \(K\subset \mathbb {R}^{3}\) be a given strictly convex body with smooth boundary. Given a convex polyhedron \(P\) with a combinatorial frame \({\fancyscript{O}},\) for any triple \((p_1,p_2,p_3)\) with distinct points on \(\partial K,\) then there exists a unique convex \(K\)-midscribing \(P\)-type polyhedron \(Q \subset \mathbb {RP}^3\) with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\).

Denote by \(\mathfrak {U}_{P,K}\) the space of all \(P\)-type polyhedra in \(\mathbb {RP}^3\) which midscribes \(K\). Due to the above theorem, we could identify \(\mathfrak {U}_{P,K}\) with the set of all distinct points triples \(\{(p_1,p_2,p_3)\}\), which is homeomorphic to the Möbius group. Namely,

$$\begin{aligned} \mathfrak {U}_{P,K}\cong \textit{PSL}(2;{\mathbb {C}})=\textit{Iso}^{+}(\mathbb {B}^{3}). \end{aligned}$$

It is a 6-dimensional manifold. Denote by \(\mathfrak {U}_{P,K}^{c} \subset \mathfrak {U}_{P,K}\) the subset which consists of all convex \(P\)-type \(K\)-midscribing polyhedra in \(\mathbb R^3\). We have:

Theorem 1.3

\(\mathfrak {U}_{P,K}^{c}\) is a non-empty open subset of \(\mathfrak {U}_{P,K}\).

Equivalently, we now give an alternative proof of the midscribability theorem (Theorem 1.1). Also, we prove that the space of all such \(P\)-type polyhedra which midscribe \(K\) is a smooth \(6\)-manifold.

The proof of Theorem 1.2 is briefly sketched as follows.

Recall that \(K\) is a convex body and \(P\) is the given convex polyhedron. Given an affine half space \(H^+ \subset \mathbb {RP}^3\) intersecting the interior of the convex body \(K\), then the intersection \(H^+\cap \partial K\) is a smooth topological disk in the boundary \(\partial K\). We call it a \(K\)-disk, and call its boundary a \(K\)-circle.

Now we associate every face of \(P\) with an affine half space. Let \(Z\) denote the space of all configurations; where a configuration is defined to be an indexed collection of affine half space and points in \(\mathbb {RP}^3\). The points are indexed by the vertices of \(P\), and the planes are indexed by the faces of \(P\).

We are interested in two subspaces \(Z_P, Z_K\) of \(Z\). The subspace \(Z_P\) is the space of all polyhedra combinatorially equivalent to \(P\). The subspace \(Z_K\) consists of all configurations corresponding to \(K\)-circle packings with contact graph \(G^{*}(P)\) (the dual graph of the \(1\)-skeleton of \(P\)).

With these notions, to find a \(K\)-midscribable polyhedron is equivalent to find a point in the intersection \(Z_P\cap Z_K\). By combining the intersection number theory with a homotopy method, we will obtain the desired result.

Notational conventions Through this paper, for any set \(A\), we use the notation \(|A|\) to denote the cardinality of \(A\). Also, for any triple \((p_1,p_2,p_3)\), we always assume that \(p_i, 1\le i\le 3\), are distinct.

2 Preliminaries

Differential topology, especially transversality and intersection number theory, will play an important role in this paper. In this section let us give a simple introduction to them. The reader is referred to [7, 10] for a detailed exposition of the general theory of differential topology.

The first topic is transversality. According to H. E. Winkelnkemper, it is said that transversality unlocks the secrets of the manifolds (see Chap. 3 in [10]). Indeed, it plays a significant role throughout the paper [15].

Suppose that \(M,N\) are two oriented smooth manifold, and suppose \(S\subset N\) is a submanifold.

Definition 2.1

Assume that \(f:M\rightarrow N\) is a \({C}^{1}\) map. Given \(A\subset M\), we say \(f\) is transverse to \(S\) along \(A\), denoted by , if

$$\begin{aligned} Im(df_{x})+T_{f(x)}S=T_{f(x)}N \end{aligned}$$

whenever \(x\in A\cap f^{-1}(S)\). When \(A=M\), we simply denote .

The other notion is the intersection number. Let \(S\subset N\) be a closed submanifold such that

$$\begin{aligned} \textit{dim} M + \textit{dim} S = \textit{dim} N. \end{aligned}$$

Suppose \(\Lambda \subset M\) is an open subset with compact closure \(\bar{\Lambda }\). Given a continuous map \(f:M\rightarrow N\) with \(f(\partial \Lambda )\cap S=\emptyset \), where \(\partial \Lambda =\bar{\Lambda }{\setminus }\Lambda \), we will define a topological invariant \(I(f,\Lambda ,S)\), the intersection number between \(f\) and \(S\) in \(\Lambda \). Supposing that \(f\in C^{0}(\bar{\Lambda },N)\cap C^{\infty }(\Lambda ,N)\) such that , then \(\Lambda \cap f^{-1}(S)\) consists of finite points. For each \(x \in \Lambda \cap f^{-1}(S)\), the \(sgn(f,S)_{x}\) at \(x\) is \(+1\), if the orientations on \(Im(df_{x_{j}})\) and \(T_{f(x_j)}S\) ”add up” to preserve the prescribed orientation on \(N\), and \(-1\) if not.

Definition 2.2

If \(\Lambda \cap f^{-1}(S)=\{x_1,x_2,\ldots ,x_m\}\), then we define the intersection number of the map \(f\) with \(S\) to be

$$\begin{aligned} I(f,\Lambda ,S){:=}\sum \nolimits _{j=1}^m sgn(f,S)_{x_j}. \end{aligned}$$

The following proposition tells us that homotopic maps always have the same intersection numbers. Its proof is in the same style as that of the homotopy invariance of Brouwer degree. Please see Milnor’s book [12].

Proposition 2.3

Suppose that \(f_{i}\in C^{0}(\bar{\Lambda },N)\cap C^{\infty }(\Lambda ,N),\) and \(f_{i}(\partial \Lambda )\cap S=\emptyset , \,i=0,1\). If there exists a homotopy \(H \in C^{0}({I\times \bar{\Lambda }},N)\) such that \(H(0, \cdot )=f_0(\cdot ), \,\, H(1, \cdot )=f_1(\cdot ),\) and \(H(I\times \partial \Lambda )\cap S=\emptyset ,\) then

$$\begin{aligned} I(f_{0},\Lambda ,S)=I(f_{1},\Lambda ,S). \end{aligned}$$

The next lemma, which helps us to manipulate the intersection number for general mappings, is a consequence of Sard’s theorem [7, 10].

Lemma 2.4

For any \(f\in C^{0}(\bar{\Lambda },N)\) with \(f(\partial \Lambda )\cap S=\emptyset ,\) there exists \(g\in C^{0}(\bar{\Lambda },N)\cap C^{\infty }(\Lambda ,N)\) and \(H\in C^{0}(I\times \bar{\Lambda },N)\) such that

  1. 1.
  2. 2.

    \(H(0,\cdot )=f(\cdot ),H(1,\cdot )=g(\cdot );\)

  3. 3.

    \(H(I\times \partial \Lambda )\cap S=\emptyset .\)

The above lemma, together with Proposition 2.3, allows one to define the intersection numbers for general continuous mappings.

Definition 2.5

For any \(f\in C^{0}(\bar{\Lambda },N)\) with \(f(\partial \Lambda )\cap S=\emptyset \), we define the intersection number

$$\begin{aligned} I(f,\Lambda ,S)=I(g,\Lambda ,S), \end{aligned}$$

where \(g\) is defined in Lemma 2.4.

From Proposition 2.3, it follows \(I(f,\Lambda ,S)\) is well-defined. Furthermore, the following theorem implies that the number \(I(f,\Lambda ,S)\) is a homotopy invariant.

Theorem 2.6

For \(i=0,1,\) suppose that \(f_{i}\in C^{0}(\bar{\Lambda },N)\) such that \(f_{i}(\partial \Lambda )\cap S=\emptyset \). If there exists \(H\in C^{0}(I\times \bar{\Lambda },N)\) such that

  1. 1.

    \(H(0,\cdot )=f_{0}(\cdot ),H(1,\cdot )=f_{1}(\cdot );\)

  2. 2.

    \(H(I\times \partial \Lambda )\cap S=\emptyset \).

Then \(I(f_{0},\Lambda ,S)=I(f_{1},\Lambda ,S)\).

In particular, it immediately follows from the definition that:

Theorem 2.7

If \(I(f,\Lambda ,S)\ne 0,\) then we have \(\Lambda \cap f^{-1}(S)\ne \emptyset \).

3 Teichmüller theory of packings

A disk (or circle) packing \(\mathcal {P}\), as its name suggests, is a configuration of topological disks (or circles) \(\{D_{v}:v\in V\}\) with specified patterns of tangency. The contact graph (or nerve) of \(\mathcal {P}\) is a graph \(G_{\mathcal {P}}\), whose vertex set is \(V\) and an edge appears if and only if the corresponding disks (or circles) touch.

Recall that a \(K\)-disk is defined to be the intersection \(H^+\cap \partial K\), where \(H^+\) is an affine half space which intersects the interior of the convex body \(K\). Naturally, we call \(\{D_{v}:v\in V\}\) a \(K\)-disk packing, if all \(D_{v}\) are \(K\)-disks.

In this section, we shall investigate the Teichmüller space of such packings, which characterizes the subspace \(Z_K\) of \(K\)-disk packings with the same contact graph. To reach the purpose, a main step is to extend the Circle Packing Theorem.

Given the convex body \(K\subset \mathbb {R}^3\), without loss of generality, we assume that it lies below the plane \(\{(x,y,z)\in {\mathbb {R}}^3: z=1\}\) and it is tangent to the plane at the point \(N=(0,0,1)\). The point \(N\) is regarded as the “North Pole” of \(\partial K\). Let \(h: \partial K \rightarrow {\mathbb {C}} \cup \{\infty \}\) denote the “stereographic projections” with \(h(N)=\infty \). Since \(h\) can be extended to a diffeomorphism between \(\partial K\) and \(\hat{\mathbb {C}}\), we endow \(\partial K\) with a complex structure by pulling back the standard complex structure of \(\hat{\mathbb {C}}\). Sometimes we identify \(\partial K\) with the Riemann sphere \(\hat{\mathbb {C}}\). Therefore it is plausible to introduce the following terminology.

Definition 3.1

A \(K\)-circle domain in the Riemann sphere \(\hat{\mathbb {C}}\) (or \(\partial K\)) is a domain, whose complement’s connected components are all closed \(K\)-disks or points.

Let \(\Omega _{n} \subset \hat{\mathbb {C}}\) be a finitely connected domain with \(n\) boundary components. A marked domain \(\Omega _{n}(z_1,z_2,z_3)\) is the domain \(\Omega _{n}\) together with three different ordered points \(z_1,z_2,z_3\) in the same boundary component of \(\Omega _{n}\). In [16], Schramm proved the following result, which generalizes Koebe’s Uniformization [9] of finitely connected domains:

Lemma 3.2

Let \(\Omega _{n}(z_1,z_2,z_3)\) be a marked \(n\)-connected domain in \(\hat{\mathbb {C}}.\) For any given triple \(\{p_1,p_2,p_3\}, p_i \in \partial K,\) there exist a marked \(K\)-circle domain \(\Omega _{n}^{K}(p_1,p_2,p_3)\) and a conformal mapping \(f:\Omega _{n}(z_1,z_2,z_3)\rightarrow \Omega _{n}^{K}(p_1,p_2,p_3)\) such that \(f(z_i)=p_i, \, i=1,2,3.\)

Given any polyhedral graph (the \(1\)-skeleton of a polyhedron) \(G\), let us fix a vertex \(v_{0}\) of \(G\) and three ordered edges \(e_1,e_2,e_3\) emanating from \(v_0\). Similarly, we call the \(4\)-quadruple \(\fancyscript{O}=\{v_0,e_1,e_2,e_3\}\) the combinatorial frame associated to the graph \(G\). Suppose that \(\mathcal {P}=\{D_{v}\}\) is a packing with the contact graph \(G\). Supposing that \(p_1,p_2,p_3\) are the three tangent points corresponding to the edges \(e_1,e_2,e_3\), we call \(\mathcal {P}\) a normalized packing with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\).

Under these conventions, by turning to the limiting case of Lemma 3.2, we have:

Corollary 3.3

Let \(G\) be a polyhedral graph with a combinatorial frame \(\fancyscript{O}\). If \((p_1,p_2,p_3)\) is any triple in \(\partial K,\) then there exists a normalized \(K\)-circle packing \(\mathcal {P}_{K}=\{D_v:v\in V\}\) with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\) which realizes the contact graph \(G\).

If \(G\) is a triangular graph of the Riemann sphere, Schramm [14] proved that such packing is unique. While \(G\) isn’t a triangular graph of \(\hat{{\mathbb C}}\), the uniqueness wouldn’t hold any more. In fact, there exist uncountable normalized \(K\)-circle packings with the same contact graph. To resolve this problem, He–Liu [8] developed the Teichmüller theory of circle patterns (packings). Recalling their method, it has little hard to extend similar results to \(K\)-circle packings.

We will give the notion of conformal polygons, which are considered as analogs of the conformal quadrangles. It is defined as pairs \(h:I\rightarrow \hat{\mathbb {C}}\), where \(I\subset \hat{\mathbb {C}}\) is a given topological polygon and \(h\) is a quasiconformal embedding. Please refer to [1] for details of quasiconformal mappings. Say two such conformal polygons \(h_1,h_2: I\rightarrow \hat{\mathbb {C}}\) are Teichmüller equivalent, if the composition mapping \(h_2\circ (h_{1})^{-1}: h_1(I)\rightarrow h_2(I)\) is isotopic to a conformal homeomorphism \(f\) such that, for each side \(e\subset \partial I\), \(f\) maps \(h_1(e)\) onto \(h_2(e)\).

Definition 3.4

The Teichmüller space of \(I\), denoted by \(\mathcal {T}_I\), is the space of all equivalence classes of conformal polygons \(h:I\rightarrow \hat{\mathbb {C}}\).

Remark 3.5

If the polygon \(I\) is \(k-\)sided, it follows from the classical Teichmüller theory that \(\mathcal {T}_I\) is diffeomorphic to the Euclidean space \(\mathbb {R}^{k-3}\). See e.g. [11].

Note that \(G(P)=({\mathcal {V}}, {\mathcal {E}}, {\mathcal {F}})\) and \(G^*(P)=(V, E)\) is the dual graph of the \(1\)-skeleton of \(G(P)\). Fix a disk packing \(\mathcal {P}_0=\{D_{0,v}\}_{v \in V}\) on the Riemann sphere \(\hat{{\mathbb C}}\) with the contact graph \(G^*(P)\). The closure of any component of \({\hat{\mathbb {C}}}-\cup _{v\in V}D_{0,v}\) is called an interstice. Evidently, it is also a topological polygon.

Denote \(\mathcal {T}_{G^*(P)}=\prod _{i=1}^{m}\mathcal {T}_{I_i}\), where \(\{I_1,I_2,\ldots , I_m\}\) are all interstices of the disk packing \({\mathcal {P}}_{0}\). Then \(m=|F|\), where \(F\) is the face set of the contact graph \(G^*(P)\). In view of Remark 3.5, we easily check that

$$\begin{aligned} \mathcal {T}_{G^*(P)}\cong \mathbb {R}^{2|E|-3|F|}=\mathbb {R}^{2|{\mathcal {E}}|-3|{\mathcal {V}}|}. \end{aligned}$$

Analogous to [8], we can now establish the following theorem.

Theorem 3.6

Let \(K,P,G^*(P)\) and \(\mathcal {T}_{G^*(P)}\) be as above. Suppose \(p_1, p_2, p_3\) are three different points in \(\partial K\). For any

$$\begin{aligned} \big [\tau \big ]=([\tau _{1}],[\tau _{2}],\ldots ,[\tau _{m}]) \in \mathcal {T}_{G^*(P)}, \end{aligned}$$

there exists a unique \(K\)-disk packing \(\mathcal {P}_{K}([\tau ])\) realizing the contact graph \(G^*(P)\) with mark \(\{\fancyscript{O},p_1,p_2,p_3\}\). Moreover\(,\) the interstice of \(\mathcal {P}_{K}([\tau ])\) corresponding to \(I_i\) is endowed with the given complex structure \([\tau _{i}],\,1\le i\le m\).

Proof

We will prove the theorem by two steps.

Existence part Indeed, it is straightforward as a limiting case of Lemma 3.2. However, in this paper we will pursue an alternative approach to this result. The ideal is similar to the method used by He–Liu in [8] or Schramm in [17], which is a combination of the Packing Theorem [14, 16] and Rodin–Sullivan method [13].

For each interstice \(I \in \{I_1,I_2,\ldots , I_m\}\) and complex structure \([\tau ]:I \rightarrow \hat{\mathbb {C}}\), for convenience, we assume that the region \([\tau ](I)\) is a bounded domain in \(\mathbb {C}\). Lay down a regular hexagonal packing of circles in \(\mathbb {C}\), say each of radius \(1/n\). By using the boundary components of \(\partial [\tau ](I)\) like a cookie-cutter, we have a circle packing \(\mathcal {Q}_{I,n}\) which consists of all the circles intersecting the closed region \([\tau ](I)\). Denote by \(\mathcal {G}_{I,n}\) the contact graph of \(\mathcal {Q}_{I,n}\). Glue the contact graphs \(\{\mathcal {G}_{I_i, n}\}_{1\le i\le m}\) and the contact graph \(G^*(P)\) along the corresponding edges to form a triangular graph \(G_n\) in \(\hat{{\mathbb C}}\). For each newly vertex of \(G_n \backslash G^*(P)\), we associate it with standard round disks. According to the general Packing Theorem [14, 16], there exists a normalized packing \({\mathcal {P}}_{n}\) realizing the contact graph \(G_{n}\).

It is easy to verify that there exists a subsequence (still denoted by \(\{{\mathcal {P}}_{n}\}\)) such that \({\mathcal {P}}_{n}\) convergent to a packing \({\mathcal {P}}_{\infty }\). According to the following Proposition 3.7, this packing doesn’t degenerate. Therefore \({\mathcal {P}}_{\infty }\) is actually a \(K\)-disk packing with the contact graph \(G^*(P)\). Setting \(\mathcal {P}_{K}([\tau ])=\mathcal {P}_{\infty }\), and by using Rodin–Sullivan’s method [13], it is not hard to verify that the interstices of \(\mathcal {P}_{K}([\tau ])\) are endowed with the given complex structures.

Uniqueness part Suppose that there are two normalized packings \(\mathcal {P}_{K}\) and \(\mathcal {P'}_{K}\) with the same contact graph \(G^*(P)\) such that there exists conformal maps between the corresponding interstices. We shall prove the uniqueness part in Appendix. \(\square \)

Proposition 3.7

The packing \(\mathcal {P}_{\infty }=\{D_{\infty ,v}:v\in V\}\) isn’t degenerating.

Proof

Suppose it is not true. Then there exists at least one vertex \(v \in V\) such that the disks \(\{D_{n}(v)\}_{n=1,2,\ldots }\) tends to a point. Note that any three \(K\)-disks with disjoint interiors in \({\mathcal {P}}_\infty \) can not meet at a common point. Therefore, except for at most two \(K\)-disks, all other \(K\)-disks in \({\mathcal {P}}_\infty \) degenerate to points, which contradicts to our normalized condition. \(\square \)

4 Proof of the main theorems

The \(3\)-dimensional real projective space \(\mathbb {RP}^3\) is the space of all lines through \(0\) in \(\mathbb R^4\). More precisely, we can define \(x\thicksim x'\) in \(\mathbb R^4\backslash \{0\}\) if and only if there is a real number \(\lambda \ne 0\) such that \(x'=\lambda x\). Let

$$\begin{aligned} \Pi : {\mathbb {R}}^4\backslash \{0\}\rightarrow {\mathbb {RP}}^3 \end{aligned}$$

denote the projection. Denote by \([x_0, x_1,x_2,x_3]\) the point \(\Pi ((x_0, x_1,x_2,x_3))\), which is the homogeneous coordinates in \(\mathbb {RP}^3\). We then have the projection

$$\begin{aligned} \Pi : \mathbb S^3 \rightarrow \mathbb {RP}^3, \end{aligned}$$

where \(\mathbb S^3\subset \mathbb R^4\backslash \{0\}\) is the unit sphere. Thus \(\mathbb {RP}^3\) can be regarded as the quotient of \(\mathbb S^3\) obtained by identifying antipodal points. Moreover, we can regard \(\mathbb R^3\) as a subset of \(\mathbb {RP}^3\) by identify the point \([1, x_1,x_2,x_3] \in \mathbb {RP}^3\) with \(( x_1,x_2,x_3) \in \mathbb R^3\). Namely, \(\mathbb {RP}^3=\mathbb R^3 \cup \mathbb {RP}^2\).

Each plane of \(\mathbb {RP}^3\) can be defined as

$$\begin{aligned} \{[x_0,x_1,x_2,x_3]: A x_0+B x_1+C x_2+D x_3=0\}. \end{aligned}$$

Therefore, each plane in \(\mathbb {RP}^3\) is uniquely determined by a point \([A,B,C,D] \in \mathbb {RP}^3\).

Recall that \(G(P)=({\mathcal {V}}, {\mathcal {E}}, {\mathcal {F}})\) and \(G^*(P)=(V, E)\) is the dual graph of the \(1\)-skeleton of \(G(P)\). Let \(Z\) denote the configurations space \((\mathbb {RP}^3)^{|{\mathcal {F}}|}\). That is, each point \(z\in Z\) gives rise to a half space (or an oriented plane) for each \(f\in {\mathcal {F}}\), which is called a configuration. For any configuration \(z\in Z\), we denote by \(z_f\) the plane corresponding to the face \(f\in {\mathcal {F}}\).

For any \(v\in {\mathcal {V}}\), let \(lk(v)\) be the number of faces linking to this vertex \(v\). Denote by \(\{f_1,f_2,\ldots , f_{lk(v)}\}\subset {\mathcal {F}}\) all faces linking to the vertex \(v\). Let \(Z_{vo}\subset Z\) be the set of configurations such that, for at least one triple \(\{i_1,i_2,i_3\} \subset \{1,2,\ldots , lk(v)\}\), the intersection

$$\begin{aligned} z_{f_{i_1}}\cap z_{f_{i_2}} \cap z_{f_{i_3}} \end{aligned}$$

contains more than one points. Evidently, \(Z_{vo}\subset Z\) is a closed set, which implies that

$$\begin{aligned} Z_{oc}=Z{\setminus }(\cup _{v\in {\mathcal {V}}}Z_{vo}) \end{aligned}$$

is open in \(Z\). That is, \(Z_{oc}\) is a manifold with the same dimension \(3|{\mathcal {F}}|\) as \(Z\). On the other hand, let \(Z_{vc}\subset Z_{oc}\) be the set of configurations such that \( \cap _{i=1}^{lk(v)} z_{f_i}\ne \emptyset \), where \(f_1,f_2,\ldots ,f_{lk(v)}\) are all faces in \({\mathcal {F}}\) linking to the vertex \(v\). We then define

$$\begin{aligned} Z_P=\cap _{v\in {\mathcal {V}}}Z_{vc}. \end{aligned}$$

It is obvious that any configuration in \(Z_P\) corresponds to a polyhedron of \(\mathbb {RP}^3\) combinatorially equivalent to \(P\). Moreover, we have:

Lemma 4.1

\(Z_P\) is a closed submanifold of \(Z_{oc}\) with real dimension \(\dim Z_{P}=|{\mathcal {E}}|+6.\)

Proof

Recall that \(f_1,f_2,\ldots ,f_{lk(v)}\) are all faces of the polyhedron \(P\) linking to \(v\). For each \(i=1,2,\ldots , lk(v)\), suppose that the plane \(z_{f_{i}}\) is defined by the equation

$$\begin{aligned} z_{f_{i}}=\{[x_0,x_1,x_2,x_3]: A_{i}x_0+B_{i}x_1+C_{i}x_2+D_{i}x_3=0\}. \end{aligned}$$

Then \(\cap _{i=1}^{lk(v)} z_{f_i}\ne \emptyset \) if and only if the rank of the matrix

$$\begin{aligned} \begin{pmatrix} A_1&{}B_1&{}C_1&{}D_1\\ A_2&{}B_2&{}C_2&{}D_2\\ A_3&{}B_3&{}C_3&{}D_4\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ A_{lk(v)}&{}B_{lk(v)}&{}C_{lk(v)}&{}D_{lk(v)} \end{pmatrix}, \end{aligned}$$

is less than \(4\). Equivalently, the determinant

$$\begin{aligned} R(f_{i_1},f_{i_2},f_{i_3},f_{i_4})= \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} A_{i_1}&{}B_{i_1}&{}C_{i_1}&{}D_{i_1}\\ A_{i_2}&{}B_{i_2}&{}C_{i_2}&{}D_{i_2}\\ A_{i_3}&{}B_{i_3}&{}C_{i_3}&{}D_{i_3}\\ A_{i_4}&{}B_{i_4}&{}C_{i_4}&{}D_{i_4} \end{array}\right| =0, \end{aligned}$$

for each subset \(\{i_1,i_2,i_3,i_4\} \subset \{1,2,\ldots , lk(v)\}\). In virtue of the definition of \(Z_{oc}\), \(0\) is a regular value of the smooth function \(R\). It follows from the regular value theorem that \(Z_P\) is a closed sub-manifold of \(Z_{oc}\). Please refer to [10]. Therefore,

$$\begin{aligned} \textit{dim} Z_{P}=3|{\mathcal {F}}|-\left( \sum \nolimits _{v\in {\mathcal {V}}} lk(v)-3\right) =3|{\mathcal {F}}|-(2|{\mathcal {E}}|-3|{\mathcal {V}}|)=|{\mathcal {E}}|+6, \end{aligned}$$

where the last identity follows from Euler’s formula. \(\square \)

Fix a combinatorial frame \(\fancyscript{O}\) for \(G^{*}(P)\) and three distinct points \(p_1,p_2,p_3\) in \(\partial K\). For each \([\tau ]\in \mathcal {T}_{G^{*}(P)}\), from Theorem 3.6, it follows that there is a unique normalized \(K\)-disk packing \(\mathcal {P}_{K}([\tau ])\) with the mark \(\{\fancyscript{O},p_1,p_2,p_3\}\) which realizes the graph \(G^{*}(P)\). As a result, it gives rise to the following mapping

$$\begin{aligned} f_{K}:\mathcal {T}_{G^{*}(P)}\longrightarrow Z_{oc}\hookrightarrow Z. \end{aligned}$$

In addition, a simple computation shows that:

$$\begin{aligned} \begin{aligned}&\textit{dim} Z_{P}=3|{\mathcal {F}}|-(2|{\mathcal {E}}|-3|{\mathcal {V}}|)=|{\mathcal {E}}|+6,\\&\textit{dim} \mathcal {T}_{G^{*}(P)}=2|{\mathcal {E}}|-3|{\mathcal {V}}|,\\&\textit{dim} \mathcal {T}_{G^{*}(P)}+\textit{dim} Z_{P}=3|{\mathcal {F}}|=\textit{dim} Z_{oc}.\\ \end{aligned} \end{aligned}$$

These identities remind us of the intersection number theory. However, in order to apply this tool, it is necessary to find a suitable compact set \(\Lambda \subset \mathcal {T}_{G^{*}(P)}\) and determine the intersection number \(I(f_{K},\Lambda ,Z_{P})\). In fact, the following lemma guarantees the existence of such a compact set.

Lemma 4.2

For any given strictly convex body \(K,\) there exists a compact set \(\Lambda \subset \mathcal {T}_{G^{*}(P)}\) such that \(f_K(\partial \Lambda )\cap Z_P=\emptyset .\)

Proof

We assume, by contradiction, that there is not such a compact set \(\Lambda \). Then there is a sequence of \([\tau ]_{n}\in f_{K}^{-1}(Z_P)\) such that the corresponding normalized packings \(\mathcal {P}_{n}\) satisfy one of the following two possibilities:

  • There is a fixing vertex \(v\in V\) such that the corresponding disks \({D}_{n}(v) \subset \mathcal {P}_{K}([\tau ]_n)\) tend to a point, as \(n\rightarrow \infty \);

  • As \(n\rightarrow \infty \), the distance of two non-adjacent arcs of the interstices \(\{I_{0,n}\}\) which face to the vertex (say \(v_0)\), tends to zero.

Using a similar argument as in Proposition 3.7, we rule out the first possibility.

In the second case, for each given \(n\), since \([\tau ]_{n}\in f_{K}^{-1}(Z_P)\), the normalized packing \(\mathcal {P}_{n}\) corresponds to a \(K\)-midscribing polyhedron \(P_{n}\). Hence the corresponding tangent edges of \(P_{n}\) will separate the non-adjacent arcs. On the other hand, we have known that the sizes of all disks in \(\mathcal {P}_{K}([\tau ]_{n})\) have positive infimum. These facts together tell us that the distance of any pair of non-adjacent arcs can not tend to zero, which implies the second case is also impossible. \(\square \)

If we could prove \(I(f_{K},\Lambda ,Z_{P})\ne 0\), then Theorem 2.7 implies that \(f^{-1}_{K}(Z_P)\cap \Lambda \ne \emptyset \), which leads to the existence part of Theorem 1.2. To obtain the desired result, we need the following transversality theorem, which is a modified version of Schramm’s result in [15].

Lemma 4.3

(Transversality theorem) Given any strictly convex body \(K\subset \mathbb {R}^{3}\) with smooth boundary\(,\) then we have .

Remark 4.4

It is worthwhile pointing out that the distinction between Schramm’s theorem and ours lies in the description of configuration spaces, which is far from essential. In other words, the above lemma could be deduced by using an analogous way as long as we do little modifications to our definitions.

With the help of the preceding results, and by using the homotopy method, now we can compute the intersection number.

Noting \(\mathbb {B}^3\subset \mathbb {R}^3\) is the close unit ball and \(K\) is the given convex body in \(\mathbb {R}^3\), for convenience, we assume that the diameter of \(K\) is greater than \(1\) and \(\mathbb {B}^3 \subset K\). We also assume that the boundary \(\partial K\) is tangent to the unit sphere \(\partial {\mathbb {B}^3}\) at the point \(N=(0,0,1)\). Then \(N=(0,0,1)\) could be considered as the common “North Pole” of \(\partial \mathbb {B}^3\) and \(\partial K\).

Let \(h_0\) (resp. \(h_1\)) be the “stereographic projection” for \(\mathbb {S}^{2}=\partial \mathbb {B}^3\) (resp. \(\partial K\)). Define a one parameter family of closed surfaces by

$$\begin{aligned} \left\{ s \cdot h_1^{-1}(z)+(1-s) \cdot h_0^{-1}(z): z \in \hat{\mathbb {C}}\right\} \!. \end{aligned}$$

For each \(s \in [0,1]\), the above set is a compact strictly convex surface in \({\mathbb {R}}^3\). Denote by \(K_s\) the convex body bounded by this surface. Then \(\{K_s\}_{1\le s \le 1}\) is a family of strictly convex bodies joining \({\mathbb {B}}^3\) and \(K\). Each convex body \(K_s\) is tangent to the plane \(\{(x,y,z)\in {\mathbb {R}}^3: z=1\}\) at \(N=(0,0,1)\) from the same side of \({\mathbb {B}}^3\). By the “stereographic projection”, we can also identify \(\partial K_s\) with \(\hat{\mathbb {C}}\) for each \(s \in [0,1]\). Moreover, the curve \(s \rightarrow K_s\) is continuous in the Hausdorff metric.

For each \(K_s\), Theorem 3.6 implies that we can construct a mapping

$$\begin{aligned} f_{s}=f_{K_s}:\mathcal {T}_{G^{*}(P)}\rightarrow Z_{oc}. \end{aligned}$$

Moreover, from Lemma 4.2, it immediately follows that there exists a common \(\Lambda \subset \mathcal {T}_{G^{*}(P)}\) such that \(f_s(\partial \Lambda )\cap Z_P=\emptyset \) for all \(s \in [0,1] \). Denoting \(K_0=\mathbb B^3\) and \(K_1=K\), since \(f_{s}\) is a homotopy from \(f_{K_0}\) to \(f_{K}\), then we have

Theorem 4.5

Given \(P,K,\Lambda ,\) and \(f_{K}\) as above\(,\) then \(I(f_{K},\Lambda ,Z_{P})=1\)

Proof

According to Theorem 2.6, we need only to calculate \(I(f_{K_0},\Lambda ,Z_{P})\). From the Circle Packing Theorem [2, 3, 19, 20], it follows that there is only one point in \(f_{K_0}^{-1}(Z_P)\cap \Lambda \). On the other hand, the preceding Transversality theorem tells us that the map \(f_{K_0}\) is transverse to \(Z_P\) at the intersection point, which implies \(I(f_{K_0},\Lambda ,Z_{P})=1\). Hence it proves \(I(f_{K},\Lambda ,Z_{P})=1\). \(\square \)

Remark 4.6

Although the Transversality theorem (Lemma 4.3) is a powerful result, its proof [15] is a little technically involved. On account of this fact, in next section we will pursue another approach to Theorem 4.5, which is independent of Lemma 4.3.

Up to now, we have made the necessary preparations for our purpose. It is ready to prove the main results of this paper.

Proof of Theorem 1.2

The existence part is an immediate consequence of Theorem 2.7 and Theorem 4.5. From , it follows that the cardinality \(|f_{s}^{-1}(Z_P)\cap \Lambda |\) is constant for \(0\le s\le 1\). Since \(|f_{K_0}^{-1}(Z_P)\cap \Lambda |=1\), we prove the uniqueness part of the theorem.

Proof of Theorem 1.3

The openness is an immediate consequence of the Transversality theorem.

It remains to treat the existence part. Since the arguments are technical, the proof will be sketchy. For any point \(x \in \mathbb {RP}^3 \backslash K\), let \(O_x\) be the set of points on \(\partial K\) which are visible from \(x\). Then \(O_x\) consists of all \(p\in \partial K\) such that the ray \(\overrightarrow{xp}\) and \(\vec {n}_p\) form an angle \(\theta _p \in [0,\pi /2]\), where \(\vec {n}_p\) is the inner normal vector of the smooth surface \(\partial K\) at the point \(p\). Obviously, \(O_x\) is a topological disk.

We have proved that, for any triple \((p_1,p_2,p_3)\), there is a unique \(K\)-midscribing \(P\)-type polyhedron \(Q=Q(p_1,p_2,p_3) \subset \mathbb {RP}^3\). For every \(v\in {\mathcal {V}}\), let \(x(v)\) denote the apex of \(Q\) corresponding to \(v\). Then \(\{O_{x(v)}\}_{v \in {\mathcal {V}}}\) forms a packing on \(\partial K\) with the contact graph \(G(P)\), where \(G(P)\) is the \(1\)-skeleton of \(P\).

Choose some triple \((p_1,p_2,p_3)\) such that the vertex \(x(v_0)\) of \(Q=Q(p_1,p_2,p_3)\) is at \(\mathbb {RP}^3 \backslash \mathbb R^3\). Since the points \(p_1, p_2, p_3\) uniquely determine a \(K\)-disk \(D_0\), for convenience, suppose that the vertex \(x(v_0)\) is the intersection of the two lines tangent to \(D_0\) at \(p_1\) and \(p_2\). Thus

$$\begin{aligned} O_{x(v)} \varsubsetneqq \partial K{\setminus } O_{x(v_0)},\quad v \ne v_0, \end{aligned}$$

which implies the remaining vertices \(x(v) \in \mathbb R^3,\,v_0\ne v \in {\mathcal {V}}\). We now move \(p_2\) a sufficiently small distance along the arc \(\widehat{p_1p_2}\subset \partial D_0\). Denote by \(p'_2\) the resulted point. Then \((p_1, p'_2, p_3)\) uniquely determines a convex \(K\)-midscribing polyhedron \(Q(p_1,p'_2,p_3) \subset \mathbb R^3\), which implies that \(\mathfrak {U}_{P,K}^{c}\ne \emptyset \). The proof is complete. \(\square \)

5 Further discussion

Consider the Klein model of the closed unit ball \(\mathbb {B}^{3}\) in \(\mathbb {R}\mathbb {P}^{3}\). A hyperideal polyhedron \(P_{hi}\) is defined to be a compact convex polyhedron in \( \mathbb {R}\mathbb {P}^{3}\) whose vertices locate outside of the closed unit ball \(\mathbb B^3\) and whose edges all meet \(\mathbb {B}^3\). In terms of the combinatorial type and dihedral angles, in 2002 Bao–Bonahon [4] classified the hyperideal polyhedron, up to isometries of \(\mathbb {B}^{3}\).

Recall that \(G^*(P)=(V, E)\) is the dual graph of the polyhedral graph of \(P\). They prove the following result.

Lemma 5.1

Let \(\theta _{e}\in (0,\pi ]\) be a weigh attached to each edge of \(e \in E\) with the following properties\(:\)

  1. (i)

    If a simple closed curve formed by edges \(e_0,e_1,\ldots ,e_n\) of \(E,\) then \(\sum \nolimits _{i=1}^{n}\theta _{e_i}> 2\pi ;\)

  2. (ii)

    If a simple arc \(\gamma \) of \(G^{*}(P)\) formed by edges \(e_0,e_1,\ldots ,e_n\) joining two distinct vertices \(v_1, v_2\) which are in the closure of the same component \(A\) of \(\mathbb {S}^{2}-G^{*}(P),\) and if \(\gamma \) is not contained in the boundary of \(A,\) then\(\sum \nolimits _{i=1}^{n}\theta _{e_i}>\pi \).

Then there exists a hyperideal polyhedron \(P_{hi}\) combinatorially to \(P\) and with external dihedral angle \(\theta _{e}, e\in E\). Moreover\(,\) such a hyperideal polyhedron \(P_{hi}\) is unique up to hyperbolic isometries of \(\mathbb {B}^{3}\).

In particular, Lemma 5.1 implies there exists an injection

$$\begin{aligned} \Psi :\textit{Iso}^{+}(\mathbb {B}^{3})\times U\rightarrow Z_{P}, \end{aligned}$$

where \(U\) is the relatively open set of \((\pi /2,\pi ]^{|E|}\) defined by the constraint conditions (i) and (ii). \(U\) is a convex set. Noting that \(\textit{dim} Z_P=|{\mathcal {E}}|+6=|E|+6\), Brouwer’s theorem on invariance of domains shows \(\Psi :\textit{Iso}^{+}(\mathbb {B}^{3})\times U^\circ \rightarrow \Psi (\textit{Iso}^{+}(\mathbb {B}^{3})\times U^\circ )\) is a homeomorphism, where \(U^\circ \) is the interior of \(U\). An elementary computation shows that this map is actually a diffeomorphism. Denoting \(\Theta =(\theta _{1},\theta _{2},\ldots ,\theta _{E})\), the injection tells us that there exist \((m_1,\Theta _1)\in \textit{Iso}^{+}(\mathbb {B}^{3})\times U\) such that the tangent map

$$\begin{aligned} \Psi _{*}:T_{m_1}\textit{Iso}^{+}(\mathbb {B}^{3})\times T_{\Theta _1}U \rightarrow T_{z_1}Z_{P} \end{aligned}$$

is a linear isomorphism, where \(z_1=\Psi (m_1,\Theta _1)\).

The tangent space \(T_{\Theta _1}U\) is expanded by vectors \(\frac{\partial }{\partial \theta _{1}},\frac{\partial }{\partial \theta _{2}},\ldots ,\frac{\partial }{\partial \theta _{|{\mathcal {E}}|}}\). Noting that

$$\begin{aligned} \textit{dim} Z_P=\textit{dim} T_{\Theta _1}U + \textit{dim} T_{m_1}\textit{Iso}^{+}(\mathbb {B}^{3})=|{\mathcal {E}}|+6, \end{aligned}$$

which gives us a geometric insight into the tangent space of \(Z_P\). In order to provide an alternative approach to Theorem 4.5, we need the following theorem concerning the Teichmüller theory of circle patterns [8].

Lemma 5.2

Let \(\Theta : E\rightarrow [\pi /2,\pi ]\) be a weight function satisfying the above conditions \((i)\) and \((ii)\). For any

$$\begin{aligned} \big [\tau \big ]=\big ([\tau _{{1}}],[\tau _{{1}}],\ldots ,[\tau _{{m}}]\big ) \in {\mathcal {T}}_{G^{*}(P)}, \end{aligned}$$

there exists a unique normalized circle pattern \({\mathcal {P}}(\Theta , [\tau ])\) with contact graph \(G^{*}(P)\) and with external dihedral angle \(\Theta (e), \,e\in E\). Moreover\(,\) the interstice corresponding to \(I_i\) is endowed with the given complex structure \([\tau _{i}], 1\le i\le m\).

Lemma 5.2 implies that one can define, for each \(\Theta \in U\cap (\pi /2,\pi ]^{|E|}\), a mapping \(f_{\Theta }:\mathcal {T}_{G^{*}(P)}\rightarrow Z_{oc}\) via associating every \([\tau ]\in \mathcal {T}_{G^{*}(P)}\) with the unique normalize circle pattern realizing the complex structure \([\tau ]\). Denoting \(\Theta _0=(\pi ,\pi ,\ldots ,\pi )\), since \(\Theta _1 \in U\cap (\pi /2,\pi ]^{|E|}\), we have \(\Theta _s=s\Theta _1+(1-s)\Theta _0 \in U\cap (\pi /2,\pi ]^{|E|}, \, s\in [0,1]\). Therefore \(f_{\Theta _s}\) is a homotopy from \(f_{\Theta _0}\) to \(f_{\Theta _1}\).

By using an argument similar to Lemma 4.2, it follows that there exists a common compact subset \(\Lambda \subset \mathcal {T}_{G^{*}(P)}\) such that \(f_{\Theta _s}(\partial \Lambda )\cap Z_{P}=\emptyset \) for \(s\in [0,1]\). Since the preceding tangent map \(\Psi _{*}\) is a linear isomorphism, it is easy to see that:

Proposition 5.3

.

To some extent, the above proposition could be considered as a substitution of the Transversality theorem (Lemma 4.3). By using an almost repeated procedure as in Sect. 4, we obtain that:

Corollary 5.4

Let \(P\) be the given polyhedron. Then

$$\begin{aligned} I (f_{K_0}, \Lambda ,Z_P)=I (f_{\Theta _0}, \Lambda ,Z_P)=I (f_{\Theta _1}, \Lambda ,Z_P)=1. \end{aligned}$$

As a result, we are able to obtain a new proof of Theorem 4.5, which implies the existence part of Theorem 1.2.

Since the Transversality theorem (Lemma 4.3) has been proved by Schramm independently, by combining it with the above discussion, conversely we could obtain a new proof of the existence part of Lemma 5.1.