Abstract
The Riemann–Hilbert problem for the coupled nonlinear Schrödinger equation is formulated on the basis of the corresponding \(3\times 3\) matrix spectral problem. Using the nonlinear steepest descent method, we obtain leading-order asymptotics for the Cauchy problem of the coupled nonlinear Schrödinger equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The nonlinear steepest descent method for oscillatory Riemann–Hilbert (RH) problems is developed by Deift and Zhou (1993) (also called Deift–Zhou method) based on earlier work of Manakov (1974b) and Its (1981), from which the long-time asymptotic behavior of the solution for the MKdV equation is obtained rigorously. Subsequently, the long-time asymptotic behaviors for a number of integrable nonlinear evolution equations associated with \(2\times 2\) matrix spectral problems have been studied by using the nonlinear steepest descent method, for example, the KdV equation, the nonfocusing nonlinear Schrödinger equation, the sine-Gordon equation, the derivative nonlinear Schrödinger equation, the Camassa–Holm equation and others (Deift and Zhou 1993; Deift et al. 1993; Cheng et al. 1999; Kitaev and Vartanian 1997, 1999, 2000; Grunert and Teschl 2009; Boutet de Monvel et al. 2009; Xu and Fan 2015).
The principal subject of this paper concerns the long-time asymptotic behavior for the Cauchy problem of the coupled nonlinear Schrödinger (CNLS) equation,
by means of the nonlinear steepest descent method, where u(x, t) and v(x, t) are complex-valued, \(u_0(x)\) and \(v_0(x)\) lie in the Sobolev space \(H^{1,1}(\mathbb {R})=\{f(x)\in \mathscr {L}^2(\mathbb {R}): f'(x),xf(x)\in \mathscr {L}^2(\mathbb {R})\}\). Moreover, \(u_0(x)\) and \(v_0(x)\) are assumed to be generic so that \(\det a(k)\) defined in the following context is nonzero in \(\mathbb {C}_-\). The set of such generic functions is an open dense subset of \(H^{1,1}(\mathbb {R})\) (Beals et al. 1988; Zhou 1998; Deift and Park 2011), which we denote by \(\mathcal {G}\). To our knowledge, there have been no results about the long-time asymptotic behavior for the Cauchy problem of the CNLS equation. Here there are two reasons for choosing the CNLS equation as a model problem: firstly, due to its physical interest. Equation (1), also called Manakov model, describes the propagation of an optical pulse in a birefringent optical fiber (Manakov 1974a) and arises in the context of multicomponent Bose–Einstein condensates (Busch and Anglin 2001). The adjoint symmetry constraints of the CNLS equation and its algebro-geometric solutions have been studied in Ma and Zhou (2002a), Ma and Zhou (2002b), Wu et al. (2016), Ma (2017). Secondly, the spectral problem of the CNLS equation is a \(3\times 3\) matrix case (Manakov 1974a). Although the asymptotic behaviors for a number of integrable nonlinear evolution equations associated with \(2\times 2\) matrix spectral problems have been derived, there is just a little of literature (Boutet de Monvel and Shepelsky 2013; Boutet de Monvel et al. 2015) about integrable nonlinear evolution equations associated with \(3\times 3\) matrix spectral problems. Therefore, it is very important to study the long-time asymptotics of integrable nonlinear evolution equations associated with \(3\times 3\) matrix spectral problems.
In this paper, our main purpose is to extend the nonlinear steepest descent method to studying multicomponent integrable nonlinear evolution equations. The analysis here presents for a few novelties: (a) Similar to Ablowitz et al. (2004), Geng et al. (2015), Liu and Geng (2016), all the \(3\times 3\) matrices in this paper can be rewritten as \(2\times 2\) block ones. Thus we can directly formulate the \(3\times 3\) matrix RH problem by the combinations of the entries in matrix-valued eigenfunctions. Compared with the idea of constructing the \(3\times 3\) matrix RH problem by the Fredholm integral equation in Boutet de Monvel and Shepelsky (2013), this procedure is more convenient for analyzing the multicomponent nonlinear evolution equations. (b) A function \(\delta (k)\) is always introduced in the context of nonlinear steepest descent method. In Deift and Zhou (1993), Deift et al. (1993), Cheng et al. (1999), Kitaev and Vartanian (1997), Kitaev and Vartanian (1999), Kitaev and Vartanian (2000), Grunert and Teschl (2009), Boutet de Monvel et al. (2009), Xu and Fan (2015), the function \(\delta \) can be solved explicitly by the Plemelj formula because the function \(\delta \) satisfies a scalar RH problem. However, the function \(\delta (k)\) in this paper satisfies a \(2\times 2\) matrix RH problem. The unsolvability of the \(2\times 2\) matrix function \(\delta (k)\) is a challenge for us. Noticing that our aim is to study the asymptotic behavior for solution of the CNLS equation, a nature idea is using the available function \(\det \delta (k)\) to approximate \(\delta (k)\) by error control.
The main result of this paper is expressed as follows:
Theorem 1
Let (u(x, t), v(x, t)) be the solution for the Cauchy problem of CNLS equation (1) with \(u_0,v_0\in \mathcal {G} \). Then, for \(\left| \frac{x}{t}\right| \leqslant C\), the leading asymptotics of (u(x, t), v(x, t)) has the form
where \(k_0=-\frac{x}{4t}\), C is a constant, \(\Gamma (\cdot )\) is a Gamma function, the vector-valued function \(\gamma (k)\) is defined by (14), and
The outline of this paper is as follows: In Sect. 2, we transform the solution of the Cauchy problem for the CNLS equation to that of a matrix RH problem. In Sect. 3, we use the nonlinear steepest descent method for RH problem to prove Theorem 1.
2 The Riemann–Hilbert Problem
In this section, we shall derive the Volterra integral equations which the Jost solutions satisfy and a scattering matrix from the Lax pair of CNLS equation (1). Then the Cauchy problem of the CNLS equation turns into a RH problem.
Let us consider a \(3\times 3\) matrix Lax pair of CNLS equation (1):
where \(\psi \) is a matrix-valued function and k is the spectral parameter,
and the superscript “\(\dag \)” denotes Hermitian conjugate of a matrix. It is necessary to introduce a new eigenfunction \(\mu \) by \(\mu =\psi \mathrm {e}^{-i(kx+2k^2t)\sigma }\). Then Eq. (3a) becomes
where \([\sigma ,\mu ]=\sigma \mu -\mu \sigma \). The matrix Jost solutions \(\mu _{\pm }\) of Eq. (5) are defined by the following Volterra integral equations:
where \(\hat{\sigma }\) acts on a \(3\times 3\) matrix X by \(\hat{\sigma }X=[\sigma , X]\), and \(\mathrm {e}^{\hat{\sigma }}X=\mathrm {e}^{\sigma }X\mathrm {e}^{-\sigma }\). We write \(\mu _{\pm }=(\mu _{\pm L},\mu _{\pm R})\), where \(\mu _{\pm L}\) denote the first column of \(\mu _\pm \), and \(\mu _{\pm R}\) denote the last two columns. Based on the exponential factor in the integral equations, it is easy to see that \(\mu _{-L}\) and \(\mu _{+R}\) are analytic in the upper complex k-plane \(\mathbb {C}_+\), while \(\mu _{+L}\) and \(\mu _{-R}\) are analytic in the lower complex k-plane \(\mathbb {C}_-\). Moreover, we have
Noticing the fact that U is traceless implies \(\det \mu _{\pm }\) are independent of x, then the evaluation of \(\det \mu _\pm \) at \(x=\pm \infty \) deduces that \(\det \mu _\pm =1\). In addition, since \(\mu _{\pm }\mathrm {e}^{i(kx+2k^2t)\sigma }\) are two solutions of linear equation (3), they are not independent but linearly related, that is, there exists a scattering matrix s(k) such that
Resorting to the symmetry property \(U^{\dag }=-U\), functions \(\mu ^{\dag }(k^*;x,t)\) and \(\mu ^{-1}(k;x,t)\) satisfy the same differential equation, where the superscript “\(*\)” represents complex conjugate. The initial conditions \(\mu _\pm ^{\dag }(k^*;\pm \infty ,t)=\mu _\pm ^{-1}(k;\pm \infty ,t)=I\) together with the above argument imply that
Let a \(3\times 3\) matrix A be rewritten as a block form
where \(A_{11}\) is scalar. It follows from Eqs. (7) and (8) that
where \(\mathrm {adj} (A)\) denotes the adjoint matrix of A in the context of linear algebra. Thus s(k) can be rewritten as the following block form:
where a(k) is a \(2\times 2\) matrix-valued function and b(k) is a row vector-valued function. The evaluation of Eq. (7) at \(t=0\) shows that
Thus a(k) and b(k) satisfy the integral equations
from which it is easy to see that a(k) is analytic for \(k\in \mathbb {C}_-\).
Theorem 2
Let M(k; x, t) be analytic for \(k\in \mathbb {C}\backslash \mathbb {R}\) and satisfy the RH problem:
where
with \(\gamma (k)\in H^{1,1}(\mathbb {R})\) and \(\sup _{k\in \mathbb {R}}\gamma (k)<\infty \). Then the solution of this RH problem exists and is unique. Define
which solves the Cauchy problem of CNLS equation (1).
Proof
The existence and uniqueness for the solution of RH problem (13) follow by the fact that J(k; x, t) is positive definite [see pp. 590–591 in Ablowitz and Fokas (2003)].
Based on the symmetry property of jump matrix J(k; x, t), one obtains that M(k; x, t) and \((M^\dag )^{-1}(k^*;x,t)\) satisfy the same RH problem (13). Taking into account the uniqueness for the solution of the RH problem, we arrive at \(M(k;x,t)=(M^\dag )^{-1}(k^*;x,t)\). Notice that the asymptotic expansion of M(k; x, t)
which implies that \((M_1)_{12}=-(M_1)_{21}\).
In the following, we shall prove that (u(x, t), v(x, t)) defined by (15) solves the Cauchy problem of CNLS equation (1) with the help of the dressing method (Fokas 2008). Set
where U and \(\tilde{U}\) are defined by (4). Therefore we have
If (u, v) is defined by (15), then \(\mathscr {L} M\) satisfies the homogeneous RH problem
which gives rise to
Furthermore, comparing the coefficients of \(O(\frac{1}{k})\) in the asymptotic expansion of (17), we can obtain \(M_1^{(O)}=\frac{i}{2}\sigma U\), \(\partial _x M_1^{(D)}=-\frac{i}{2}\sigma U^2\), where superscripts “(O)” and “(D)” denote the off-diagonal and diagonal parts of block matrix, respectively. Therefore \(\mathscr {N} M\) satisfies the homogeneous RH problem
which means that
The compatibility condition of Eqs. (17) and (18) yields CNLS equation (1). As a consequence, one obtains that the function (u, v) defined by Eq. (15) solves the CNLS equation. Moreover, it is not difficult to verify that the resulting (u, v) at \(t=0\) satisfies the initial conditions in a way similar to the arguments in Fokas (2008) and Fokas et al. (2005). \(\square \)
3 The Long-Time Asymptotics
In this section, we make the following basic notations:
-
1.
For any matrix M define \(|M|=(\mathrm {tr}M^\dag M)^{\frac{1}{2}}\) and for any matrix function \(A(\cdot )\) define \(\Vert A(\cdot )\Vert _p=\Vert |A(\cdot )|\Vert _p\).
-
2.
For two quantities A and B define \(A\lesssim B\) if there exists a constant \(C>0\) such that \(|A|\leqslant CB\). If C depends on the parameter \(\alpha \), we shall say that \(A\lesssim _{\alpha } B\).
-
3.
For any oriented contour \(\Sigma \), we say that the left side is “\(+\)” and the right side is “−”.
3.1 Factorization of the Jump Matrix
An analogue of the classical steepest descent method for Riemann–Hilbert problems was invented by Deift and Zhou (1993). The key idea is to notice that the jump matrix involves the same phase function as appeared in the Fourier integral, but the approach is slightly complicated by the fact that both exponential factors \(\mathrm {e}^{\pm 2i\theta }\) appear in the jump matrix. To see how to deal with this, note that the jump matrix enjoys two distinct factorizations:

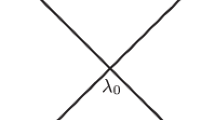
The stationary point of \(\theta (k)\) is denoted by \( k_0\), i.e., \(\left. \frac{\text {d} \theta }{\text {d} k}\right| _{k= k_0}=0\), where \(k_0=-\frac{x}{4t}\), thus \(\theta =2(k^2-2k_0k)\). In this paper, we focus on the physically interesting region \(|k_0|\leqslant C\), where C is a constant.
Let \(\delta (k)\) be the solution of the matrix Riemann–Hilbert problem
Then we have
In terms of the positive definiteness of the jump matrix \(I+\gamma ^\dag (k)\gamma (k)\) and the vanishing lemma (Ablowitz and Fokas 2003), one infers that \(\delta \) exists and is unique. A direct calculation shows that \(\det \delta \) is solved by the Plemelj formula (Ablowitz and Fokas 2003)
where
Indeed, the above integral is singular as \(k\rightarrow k_0\). In fact, we write the integral in the form
which implies that all the terms with the exception of the term \(\log (k-k_0)\) are analytic for k in a neighborhood of \(k_0\). Therefore, \(\det \delta \) can be written in the form
where
As \(k<k_0\), it follows from (19) that
Let \(f(k)=(\delta ^\dag (k^*))^{-1}\), then we have
Noticing the uniqueness of the solution for the matrix RH problem, we arrive at
Inserting Eq. (22) in Eq. (19), we obtain
for fixed \(k\in \mathbb {R}\). Hence, by the maximum principle, we have
for all \(k\in \mathbb {C}\).
Let
and
Define \(M^{\Delta }\) by
and reverse the orientation for \(k>k_0\) as shown in Fig. 1. Then \(M^{\Delta }\) satisfies the RH problem on \(\mathbb {R}\) oriented as in Fig. 1,
where
In what follows, we deform the contour. It is convenient to introduce analytic approximations of \(\rho (k)\).
3.2 Decomposition of \(\rho (k)\)
Let L denote the contour
Lemma 3
The vector-valued function \(\rho (k)\) has a decomposition
where R(k) is piecewise rational and \(h_2(k)\) has an analytic continuation to L satisfying
for an arbitrary positive integer l. Taking Schwartz conjugate
leads to the same estimate for \(\mathrm {e}^{2it\theta (k)}h_1^\dag (k^*)\), \(\mathrm {e}^{2it\theta (k)}h_2^\dag (k^*)\), and \(\mathrm {e}^{2it\theta (k)}R^\dag (k^*)\) on \(\mathbb {R}\cup L^*\).
Proof
It is enough to consider \(k\geqslant k_0\), the case \(k\leqslant k_0\) is similar. As \(k\geqslant k_0\), \(\rho (k)=\gamma (k)\). By using the Taylor’s expansion, we have
and define
Then the following result is straightforward:
In what follows, for fixed \(m\in \mathbb {Z}_+\), we assume that m is of the form
for convenience. As the map \(k\mapsto \theta (k)=2(k^2-2k_0k)\) is one-to-one in \(k\geqslant k_0\), we define
where
which implies that
By the Fourier transform, we have
where
Thus, as \(0\leqslant j\leqslant p+1\),
Resorting to the Plancherel theorem, we have
Now we give the decomposition of h(k) as follows
For \(k\geqslant k_0\), we obtain
where \(0\leqslant r\leqslant p+1.\) For k on the line \(\{k:k_0+\varepsilon \mathrm {e}^{\frac{3\pi i}{4}}\},\varepsilon <0\), we have
Here l is an arbitrary positive integer and \(m=3p+1\) is sufficiently large such that \(p-\frac{1}{2}>\frac{p}{2}\) are greater than l. The proof is completed. \(\square \)
3.3 First Contour Deformation
In this subsection, the original RH problem turns into an equivalent RH problem formulated on an augmented contour \(\Sigma \), where \(\Sigma =L\cup L^*\cup \mathbb {R}\) is oriented in Fig. 2.
Note that \(J^\Delta (k;x,t)\) can be rewritten as
where \(b_\pm =I\pm \omega _\pm \),

Lemma 4
Define
Then \(M^\sharp (k;x,t)\) solves the following RH problem on \(\Sigma \),
where
In the following, we construct the solution of the above RH problem (32) by using the approach in Beals and Coifman (1984). Assume that
and let
where \(C_+f\ (C_-f)\) denotes the left (right) boundary value for the oriented contour \(\Sigma \). Define the operator \(C_{\omega ^\sharp }: {\mathscr {L}}^2(\Sigma )+{\mathscr {L}}^\infty (\Sigma )\rightarrow {\mathscr {L}}^2(\Sigma ) \) by
for any \(3\times 3\) matrix-valued function f.
Theorem 5
(Beals and Coifman 1984) If \(\mu ^\sharp (k;x,t)\in {\mathscr {L}}^2(\Sigma )+{\mathscr {L}}^\infty (\Sigma )\) is the solution of the singular integral equation
Then
solves RH problem (32).
Theorem 6
The solution (u(x, t), v(x, t)) of the Cauchy problem for CNLS equation (1) is expressed by
Proof
It is easy to verify that the result of this theorem holds with the aid of Eqs. (23), (24), (31), Theorem 2, and the following fact
\(\square \)
3.4 Second Contour Deformation
In this subsection, we shall reduce the RH problem \(M^\sharp \) on \(\Sigma \) to the RH problem \(M'\) on \(\Sigma '\), where \(\Sigma '=\Sigma \backslash \mathbb {R}=L\cup L^*\) is orientated as in Fig. 2. Further, we estimate the error between the RH problems on \(\Sigma \) and \(\Sigma '\). Then it is proved that the solution of CNLS equation (1) can be expressed in terms of \(M'\) by adding an error term.
Let \(\omega ^e=\omega ^a+\omega ^b\), where
-
(1)
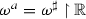 is supported on \(\mathbb {R}\) and composed of terms of type \(h_1(k)\) and \(h_1^\dag (k^*)\);
is supported on \(\mathbb {R}\) and composed of terms of type \(h_1(k)\) and \(h_1^\dag (k^*)\); -
(2)
\(\omega ^b\) is supported on \(L\cup L^*\) and composed of the contribution to \(\omega ^\sharp \) from terms of type \(h_2(k)\) and \(h_2^\dag (k^*)\).
Define \(\omega '=\omega ^\sharp -\omega ^e\), then \(\omega '=0\) on \(\mathbb {R}\). Thus, \(\omega '\) is supported on \(\Sigma '\) with contribution to \(\omega ^\sharp \) from R(k) and \(R^\dag (k^*)\).
Lemma 7
For arbitrary positive integer l, as \(t\rightarrow \infty \), then
Proof
Using Lemma 3, a direct calculation shows that Eqs. (36) and (37) hold. From the definition of R(k), we have
on the contour \(\{k=k_0+\alpha \mathrm {e}^{\frac{3\pi i}{4}}:-\infty<\alpha <+\infty \}\). By means of inequality (23), we have
from which estimate (38) follows by simple computations. \(\square \)
Lemma 8
As \(t\rightarrow \infty \), \((1-C_{\omega '})^{-1}: {\mathscr {L}}^2(\Sigma )\rightarrow {\mathscr {L}}^2(\Sigma )\) exists and is uniformly bounded:
Furthermore, \(\Vert (1-C_{\omega ^\sharp })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\lesssim 1\).
Proof
See Deift and Zhou (1993) and references therein. \(\square \)
Lemma 9
As \(t\rightarrow \infty \),
Proof
A direct computation shows that
It follows from Lemma 7 that
This completes the proof of the theorem. \(\square \)
Note As \(k\in \Sigma \backslash \Sigma '\), \(\omega '(k)=0\), let \(C_{\omega '}|_{{\mathscr {L}}^2(\Sigma ')}\) denote the restriction of \(C_{\omega '}\) to \({\mathscr {L}}^2(\Sigma ')\). For simplicity, we write \(C_{\omega '}|_{{\mathscr {L}}^2(\Sigma ')}\) as \(C_{\omega '}\). Then
Lemma 10
As \(t\rightarrow \infty \),
Proof
A direct consequence of Theorem 6 and Lemma 9. \(\square \)
Corollary 11
As \(t\rightarrow \infty \),
where \(M'(k;x,t)\) satisfies the RH problem
where

Proof
Set \(\mu '=(1-C_{\omega '} )^{-1}I\) and
In a way similar to Theorem 6, we can prove this corollary in terms of (40). \(\square \)
3.5 Rescaling and Further Reduction of the RH Problems
In this subsection, we localize the jump matrix of the RH problem to the neighborhood of the stationary phase point \(k_0\). Under suitable scaling of the spectral parameter, the RH problem is reduced to a RH problem with constant jump matrix which can be solved explicitly.
Let \(\Sigma _0\) denote the contour \(\{k=\alpha \mathrm {e}^{\pm i\frac{\pi }{4}}:\alpha \in \mathbb {R}\}\) oriented as in Fig. 3. Define the scaling operator
and set \(\hat{\omega }=N\omega '\). A simple change-of-variable argument shows that
where the operator \(C_{\hat{\omega }}\) is a bounded map from \({\mathscr {L}}^2(\Sigma _0)\) into \({\mathscr {L}}^2(\Sigma _0)\).
One infers that
on \(\hat{L}=\{k=\alpha \mathrm {e}^{\frac{3\pi i}{4}}:-\infty<\alpha < +\infty \}\), and
on \(\hat{L}^*\), where
Lemma 12
As \(t\rightarrow \infty \), and \(k\in \hat{L}\), for an arbitrary positive integer l, then
where \(\tilde{\delta }(k)=\mathrm {e}^{-2it\theta (k)} R(k)[\delta (k) -(\det \delta )(k) I]\).
Proof
It follows from Eqs. (19) and (20) that \(\tilde{\delta }\) satisfies the following RH problem:
where \(f(k)=[R(\gamma ^\dag \gamma -|\gamma |^2I)\delta _-](k)\).
The solution for the above RH problem can be expressed by
Observe that
thus \(f(k)=O((k-k_0)^l)\). Similar to Lemma 3, f(k) can be decomposed into two parts: \(f_1(k)\) and \(f_2(k)\), where \(f_2(k)\) has an analytic continuation to \(L_t\) satisfying
where
(see Fig. 4).
As \(k\in \hat{L}\), we have
As a consequence of Cauchy’s theorem, we can evaluate \(I_3\) along the contour \(L_t\) instead of the interval \((-\infty ,k_0-\frac{1}{t})\) and obtain \(|I_3|\lesssim t^{-l+1}\) in a similar way. Therefore, it is easy to see that (43) holds. \(\square \)
Note There is a similar estimate
where \(\hat{\delta }(k)=\mathrm {e}^{2it\theta (k)} [\delta ^{-1}(k)- (\det \delta )^{-1}(k)I]R^\dag (k^*)\).
Theorem 13
As \(t\rightarrow \infty \),
where \(M^0(k;x,t)\) satisfies the RH problem
Here \(J^{0}=(I-\omega ^0_-)^{-1}(I+\omega ^0_+)\) and

Proof
It follows from (43) and Lemma 3.35 in Deift and Zhou (1993) that
Thus,
For \(k\in \mathbb {C}\backslash \Sigma ^0\), let
Then \(M^0\) solves the above RH problem. From above arguments and Lemma 10, it is straightforward to prove this theorem. \(\square \)
Note In particular, if
then
3.6 Solving the Model Problem
In this subsection, we shall discuss the leading asymptotics of solution for the Cauchy problem of the CNLS equation. In order to give \((M^0_1)_{12}\) explicitly, it is convenient to introduce the following transformation
which implies that
Because the jump matrix is constant along each ray, we have
from which it follows that \(\frac{\text {d}\Psi (k)}{\text {d}k}\Psi ^{-1}(k)\) has no jump discontinuity along any of the rays. Moreover, from the relation between H(k) and \(\Psi (k)\), we have
It follows by the Liouville’s theorem that
where
In particular,
It is further possible to show that the solution of the RH problem for \(M^0(k)\) is unique, and therefore we have an identity:
which implies that \(\beta _{12}=-\beta ^\dag _{21}\).
Let
From (55) we obtain
As is well known, the Weber’s equation
has the solution
where \(D_a(\cdot )\) denotes the standard parabolic-cylinder function and satisfies
As \(\zeta \rightarrow \infty \), from Whittaker and Watson (1927) we have
where \(\varGamma \) is the Gamma function.
Set \(a=i\beta _{12}\beta _{21}\),
As \(\arg k\in (-\frac{\pi }{4},\frac{\pi }{4})\) and \(k\rightarrow \infty \), we arrive at
then
Consequently,
For \(\arg k\in (-\frac{3\pi }{4},-\frac{\pi }{4})\) and \(k\rightarrow \infty \), we have
then
Consequently,
Along the ray \(\arg k=-\frac{\pi }{4}\),
It follows from Eq. (58) that
Then we separate the coefficients of the two independent functions and obtain
In conclusion, main Theorem 1 is the consequence of Theorem 13 and Eqs. (51), (56), and (60).
References
Ablowitz, M.J., Fokas, A.S.: Complex Analysis: Introduction and Applications, 2nd edn. Cambridge University Press, Cambridge (2003)
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrodinger Systems. Cambridge University Press, Cambridge (2004)
Beals, R., Coifman, R.: Scattering and inverse scattering for first order systems. Commun. Pure Appl. Math. 37, 39–90 (1984)
Beals, R., Deift, P.A., Tomei, C.: Direct and Inverse Scattering on the Line, Mathematical Surveys and Monographs, vol. 28. American Mathematical Society, Providence (1988)
Boutet de Monvel, A., Shepelsky, D.: A Riemann–Hilbert approach for the Degasperis–Procesi equation. Nonlinearity 26, 2081–2107 (2013)
Boutet de Monvel, A., Kostenko, A., Shepelsky, D., Teschl, G.: Long-time asymptotics for the Camassa–Holm equation. SIAM J. Math. Anal. 41, 1559–1588 (2009)
Boutet de Monvel, A., Lenells, J., Shepelsky, D.: Long-time asymptotics for the Degasperis–Procesi equation on the half-line. arXiv preprint arXiv:1508.04097 (2015)
Busch, Th, Anglin, J.R.: Dark–bright solitons in inhomogeneous Bose–Einstein condensates. Phys. Rev. Lett. 87, 010401 (2001)
Cheng, P.J., Venakides, S., Zhou, X.: Long-time asymptotics for the pure radiation solution of the sine-Gordon equation. Commun. Partial Differ. Equ. 24, 1195–1262 (1999)
Deift, P.A., Park, J.: Long-time asymptotics for solutions of the NLS equation with a delta potential and even initial data. Int. Math. Res. Not. 24, 5505–5624 (2011)
Deift, P., Zhou, X.: A steepest descent method for oscillatory Riemann–Hilbert problems. Ann. Math. 137, 295–368 (1993)
Deift, P.A., Its, A.R., Zhou, X.: Long-time asymptotics for integrable nonlinear wave equations. In: Fokas, A.S., Zakharov, V.E. (eds.) Important Developments in Soliton Theory. Springer Series in Nonlinear Dynamics, pp. 181–204. Springer, Berlin (1993)
Fokas, A.S.: A unified approach to boundary value problems. In: CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM (2008)
Fokas, A.S., Its, A.R., Sung, L.Y.: The nonlinear Schrödinger equation on the half-line. Nonlinearity 18, 1771 (2005)
Geng, X.G., Liu, H., Zhu, J.Y.: Initial-boundary value problems for the coupled nonlinear Schrödinger equation on the half-line. Stud. Appl. Math. 135, 310–346 (2015)
Grunert, K., Teschl, G.: Long-time asymptotics for the Korteweg–de Vries equation via nonlinear steepest descent. Math. Phys. Anal. Geom. 12, 287–324 (2009)
Its, A.R.: Asymptotic behavior of the solutions to the nonlinear Schrödinger equation, and isomonodromic deformations of systems of linear differential equations. Sov. Math. Dokl. 24, 452–456 (1981)
Kitaev, A.V., Vartanian, A.H.: Leading-order temporal asymptotics of the modified nonlinear Schrödinger equation: solitonless sector. Inverse Probl. 13, 1311–1339 (1997)
Kitaev, A.V., Vartanian, A.H.: Asymptotics of solutions to the modified nonlinear Schrödinger equation: solution on a nonvanishing continuous background. SIAM J. Math. Anal. 30, 787–832 (1999)
Kitaev, A.V., Vartanian, A.H.: Higher order asymptotics of the modified nonlinear Schrödinger equation. Commun. Partial Differ. Equ. 25, 1043–1098 (2000)
Liu, H., Geng, X.G.: Initial-boundary problems for the vector modified Korteweg–de Vries equation via Fokas unified transform method. J. Math. Anal. Appl. 440, 578–596 (2016)
Ma, W.X.: Trigonal curves and algebro-geometric solutions to soliton hierarchies. Proc. A 473, 20170232–20170233 (2017)
Ma, W.X., Zhou, R.G.: Adjoint symmetry constraints of multicomponent AKNS equations. Chin. Ann. Math. Ser. B 23, 373–384 (2002a)
Ma, W.X., Zhou, R.G.: Adjoint symmetry constraints leading to binary nonlinearization. J. Nonlinear Math. Phys. 9, 106–126 (2002b)
Manakov, S.V.: On the theory of two-dimensional stationary self focussing of electromagnetic waves. Sov. Phys. JETP 38, 248–253 (1974a)
Manakov, S.V.: Nonlinear Fraunhofer diffraction. Sov. Phys. JETP 38, 693–696 (1974b)
Whittaker, E.T., Watson, G.N.: A Course of Modern Analysis, 4th edn. Cambridge University Press, Cambridge (1927)
Wu, L.H., Geng, X.G., He, G.L.: Algebro-geometric solutions to the Manakov hierarchy. Appl. Anal. 95, 769–800 (2016)
Xu, J., Fan, E.G.: Long-time asymptotics for the Fokas–Lenells equation with decaying initial value problem: without solitons. J. Differ. Equ. 259, 1098–1148 (2015)
Zhou, X.: \(L^2\)-Sobolev space bijectivity of the scattering and inverse scattering transforms. Commun. Pure Appl. Math. 51, 697–731 (1998)
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 11331008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Anthony Bloch.
Rights and permissions
About this article
Cite this article
Geng, X., Liu, H. The Nonlinear Steepest Descent Method to Long-Time Asymptotics of the Coupled Nonlinear Schrödinger Equation. J Nonlinear Sci 28, 739–763 (2018). https://doi.org/10.1007/s00332-017-9426-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-017-9426-x





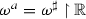 is supported on
is supported on 
