Introduction

Compared to other particle or polymer separation techniques, such as size exclusion or gel permeation chromatography, the field-flow fractionation (FFF) techniques tend to give greater relative differences in elution time for small relative differences in particle size or molecular weight. In the terminology of separation science, they exhibit higher selectivity. While this can be advantageous for the separation of a small number of slightly different species, it can lead to difficulties in the analysis of widely polydisperse samples. Conditions suitable for sufficient retention and resolution of the smaller components can result in excessive retention of the larger components. In the case of sedimentation FFF (SdFFF), the selectivity is so high that there may also be difficulty in detection of the larger components as they are eluted over extended periods of time with consequent dilution in the outlet stream. It is also possible that conditions giving sufficient retention for the smaller components result in the interference of steric inversion in the elution of the larger components. The continuous programmed reduction of field strength during sample elution takes care of these problems by effectively reducing the selectivity in a controlled manner [1, 2].

The technique of symmetrical flow field-flow fractionation (Sym-FlFFF) was introduced in 1976 [3–5] and the asymmetrical form (As-FlFFF) in 1986 [6, 7]. The selectivity of FlFFF is not as high as that of SdFFF, but it was confirmed using Sym-FlFFF that a programmed decay of cross flow rate is advantageous for the analysis of samples consisting of components having widely differing sizes [8, 9]. The nature of Sym-FlFFF allowed the cross flow rate to be programmed independently of the channel flow rate, which was usually held constant. It also allowed the channel flow rate to be programmed, if desired. Dual programming of cross flow and channel flow was demonstrated to be advantageous for sample analysis in the hyperlayer mode of operation [10], for example. Hyperlayer and steric modes of operation are not of concern here. In this publication, attention is confined to the normal or Brownian mode, applicable to submicron particles and macromolecules. The independence of the cross flow rate and the channel flow rate in Sym-FlFFF allows not only freedom in the selection of flow rate conditions but also the relatively simple prediction of elution time and fractionating power as a function of particle size or molecular weight for various programmed cross flow decay functions of time [11–14]. This is not the case for As-FlFFF.

In As-FlFFF, only the accumulation wall is permeable and the fluid flowing through the membrane-covered accumulation wall and channel outlet originates at the channel inlet. It follows that, when some of the fluid exits through the membrane, and it is assumed to exit with uniform membrane flux, the volumetric flow rate must decrease along the length of the channel. This form of FlFFF was named asymmetrical FlFFF because of its characteristic flow configuration—the flow-through the membrane is not matched by an equal flow through an opposite permeable wall, and the inlet and outlet flow rates are not equal. The interdependence of the channel inlet and outlet flow rates and the cross flow rate make the selection of suitable experimental conditions more complicated than for Sym-FlFFF. This is particularly true for programmed conditions where even the prediction of elution times becomes non-trivial. In spite of these difficulties, it has become the dominant form of FlFFF because it eliminates problems associated with the permeable frit that serves as the depletion wall in Sym-FlFFF. The flow through the frit may be non-uniform due to variations in its porosity and due to the pressure drop along the length of the channel under elution conditions. The ultrafiltration membrane, offering a much higher hydraulic resistance than the frit, requires a greater pressure drop across its thickness to maintain the cross flow. The much lower pressure drop along the channel length therefore has relatively little effect on the uniformity of membrane flux. However, the variation in frit flow due to the decreasing pressure along the channel can result in reduced channel flow rate and higher retention times than expected. The effect is related to that described by Martin and Hoyos for the “no-field method” for void time determination in FlFFF [15].

For an As-FlFFF channel of constant breadth, the flow velocity along the channel length necessarily decreases from the inlet to the outlet as fluid is lost through the accumulation wall. This can lead to problems in particle elution due to non-idealities such as particle interactions with the membrane surface. These interactions may increase as channel flow velocity decreases, and some of the more retained particles may not elute. The loss of volumetric flow rate along the channel length may be partially compensated by gradually reducing the channel breadth along its length. In 1991, Wahlund and Litzén introduced the trapezoidal channel in which the channel breadth decreases linearly [16], and in 1997 an exponentially decreasing channel breadth was proposed for use in As-FlFFF [17]. The variation in mean channel flow velocity along the length of these channels can be greatly reduced compared to a rectangular channel. Under conditions of programmed cross flow rate, the ratio of inlet to outlet flow rate is continuously changing. The ratio, initially high, approaches unity as cross flow rate approaches zero. A decreasing channel breadth remains advantageous for programmed operation as the ratio of inlet to outlet flow rate is likely to be considerably greater than unity for much of the time.

It was mentioned above that in Sym-FlFFF, the cross flow rate may be programmed independently of the channel flow rate which may be held constant or programmed as desired. This is not the case for As-FlFFF. The sum of the volumetric flow rates through the membrane and the channel outlet at any instant must equal the volumetric flow rate at the inlet. The programmed reduction of flow rate through the membrane may be carried out while maintaining a constant channel outlet flow rate, in which case the flow rate at the channel inlet must decrease at the same quantitative rate as the cross flow. This approach has the advantage of not requiring detector signal baseline adjustment, compensation for flow rate change through concentration-sensitive detectors, or compensation for change in delay times between multiple detectors. The programmed decay of cross flow rate may alternatively be carried out while maintaining constant channel inlet flow rate, which would result in an increasing channel outlet flow rate. It is also possible to program either the inlet or outlet flow rate along with the cross flow rate, the non-programmed flow being consistent with the difference or sum of the other two, respectively.

The programming of flow rates in rectangular-channel As-FlFFF was first carried out by Litzén and Wahlund in 1989 for the separation of human serum albumin from its dimer and trimer [18]. They used a multistep program where the ratio of cross flow rate to outlet flow rate was reduced in six abrupt steps while the channel inlet flow rate was held constant. The outlet flow rate therefore increased in stepwise fashion during programming. The first peak, corresponding to the monomer, did not elute until the cross flow program was completed and baseline correction was not therefore required. They also used a simple single-step program to separate two plasmid fragments of 700 and 4600 bp. In this case, the cross flow rate was reduced to zero following elution of the first peak.

In 1992, Kirkland et al. [19] used an exponential decay of cross flow rate in rectangular-channel As-FlFFF to separate a mixture of proteins and nucleic acids, a bacteria sample, and a mixture of submicron silica particles. They elected to hold the channel outlet flow rate constant to avoid baseline drift and to maintain constant detector response for quantification purposes. They were able to derive an analytical expression for elution time as a function of diffusion coefficient based on a simple high retention approximation for retention ratio (this is discussed later in this manuscript).

In 2001, Moon and Hwang [20] gave an example of a separation of four proteins obtained under linearly programmed decay of cross flow rate with the outlet flow rate held constant. Also in 2001, Moon [21] showed two more examples of separations obtained under linear decay of cross flow. In 2002, Moon et al. [22] applied a variety of flow programs to As-FlFFF using a trapezoidal channel. They were able to show how approximate analytical solutions were derivable for retention times with exponentially programmed cross flow rate and constant or exponentially programmed outlet flow rate, and that the solutions were independent of the channel breadth profile. A mixture of polystyrene sulfonate standards was separated under a variety of conditions, including isocratic, linear decay of cross flow rate with constant outlet flow rate, linear decay of cross flow rate with linearly increasing outlet flow rate (and linearly decreasing inlet flow rate), and power programmed decay of cross flow rate with constant, linearly increasing, and linearly decreasing outlet flow rate. In cases where outlet flow rate varied, a baseline correction was applied. The programming of outlet flow rate was seen to influence sample elution to a much smaller extent than the decay of cross flow rate.

In 2004, Andersson et al. [23] used successive intervals of decreasing gradients of linear decay of cross flow rate to fractionate ethyl hydroxyethyl cellulose samples. In 2006, Leeman et al. [24] published a comparison of various linear and exponential cross flow decay functions for the separation of mixtures of pullulan standards, paying particular attention to the effect of the rate of decay on the observed selectivity.

Since these early studies, the implementation of programmed decay of cross flow rate in As-FlFFF has become very common. The conditions are generally selected by trial and error or by reference to previous analyses, and the characterization of the fractionated samples commonly relies on a secondary technique, such as flow-through multi-angle light scattering (MALS) or dynamic light scattering (DLS) applied to the eluent, rather than on fundamental FFF theory. While the use of these secondary techniques for characterizing the fractionated samples compensates for uncertainties in effective channel void volume as well as various non-idealities, such as those due to sample–membrane interactions, the quality of the separation depends on the selected flow conditions. The capacity of a separation system to resolve the components of a polydisperse sample can be quantified in terms of the fractionating power. It provides a measure of the relative resolution that can be obtained across the breadth of the sample [11]. A modeling of elution time and fractionating power in As-FlFFF is therefore necessary for a logical and systematic optimization of separation conditions. This objective was accomplished for constant flow conditions in part I [25] and is accomplished for programmed cross flow rate conditions in the work presented here.

It was shown in part I [25] that, in the case of isocratic analysis of a polydisperse sample by As-FlFFF, the residual channel outlet polydispersity is inversely related to the predicted fractionating power. This relationship supports the use of predicted fractionating power as a criterion for the selection of optimum flow rate conditions because the return of reliable particle size or molecular weight by light scattering detection software depends upon low outlet polydispersity across the full range of the sample. It will be shown in this manuscript that the relationship between outlet polydispersity and fractionating power is also valid for conditions of programmed cross flow rate. The predicted fractionating power is therefore key to the optimization of programmed conditions in As-FlFFF. The consideration of fractionating power is particularly important for programmed decay of cross flow rate as the cross flow may be programmed in any number of ways, as may be seen from the earlier discussion. The selection of the optimum type of cross flow decay program (mathematical function of time) as well as the rate of decay and the magnitude of the channel flow rate may be made based upon the predicted relationship between fractionating power and particle size or molecular weight. It will be shown in this manuscript how fractionating power may be calculated for any programmed decay of cross flow or, in fact, for any arbitrary decrease of cross flow rate with time during sample elution.

Fractionating power

As mentioned above, the fractionating power is used to quantify the relative resolving power of the FFF system for polydisperse samples. If ϕ represents a selective sample property, such as particle diameter d or molecular weight M, then the ϕ-based fractionating power is defined by [11]

$$ {F}_{\phi }=\frac{R_s}{\delta \phi /\phi }=\frac{\phi }{4{\sigma}_t}\frac{\delta {t}_r}{\delta \phi } $$
(1)

where R s is the resolution, δt r /4σ t , between sample components having ϕ that differ by the small relative amount δϕ/ϕ, whose retention times consequently differ by δt r , and have a mean standard deviation in retention time of σ t . In the limit of δϕ/ϕ → 0, Eq. 1 reduces to

$$ {F}_{\phi }=\frac{\phi }{4{\sigma}_t}\frac{\boldsymbol{d}{t}_r}{\boldsymbol{d}\phi }=\frac{t_r}{4{\sigma}_t}{S}_{\phi } $$
(2)

where S ϕ is the ϕ-based selectivity given by

$$ {S}_{\phi }=\frac{\phi }{t_r}\frac{\boldsymbol{d}{t}_r}{\boldsymbol{d}\phi }=\frac{\boldsymbol{d} \ln {t}_r}{\boldsymbol{d} \ln \phi } $$
(3)

For isocratic operation, Eq. 2 may also be written in the form \( {F}_{\phi }=\sqrt{N}{S}_{\phi }/4 \), where N is the number of theoretical plates (= t r 2/σ t 2); this is not the case for programmed operation. The fractionating power F ϕ is therefore a continuous function of ϕ. In order to predict fractionating power, it is necessary to predict both t r and σ t as functions of ϕ. When particles or molecules are negligibly small, and when particle–particle and particle–membrane interactions are also negligible, the fundamental theory of FFF allows accurate prediction of the retention ratio R, the ratio of mean particle migration velocity to mean fluid velocity at any point in the channel [7]. Finite particle or molecular size can also be approximately accounted for using a first-order steric exclusion correction [26, 27]. For isocratic conditions, a knowledge of the void time then allows prediction of t r . The method for predicting t r under programmed conditions is described below.

There are two dominant contributions to bandspreading in As-FlFFF: the nonequilibrium and the multipath contributions. The nonequilibrium contribution is predictable using fundamental FFF theory [27–29], which may also include a steric exclusion correction for finite particle or molecular size [26, 27, 30]. The multipath contribution is the result of small variations in membrane permeability and channel thickness [25] and must be experimentally determined for each assembled channel. It is described below how the contributions to variance in retention time due to these effects may be predicted for programmed conditions.

Volumetric flow rates and mean channel flow velocities along channel length

The same assumptions and approximations regarding the uniformity of fluid flow in the channel are made here as were made in part I [25]. Particle–particle and particle–membrane interactions are also assumed to be negligible. In addition, the secondary relaxation effect due to the changing cross flow rate during sample elution [31–34] is not considered in this manuscript.

In programmed operation, the flow rate through the accumulation wall \( {\overset{.}{V}}_{\boldsymbol{c}} \) is a function of time. It may be held constant for a certain initial period, after which it is generally reduced according to some continuous function of time. It may alternatively be reduced in stepwise fashion or in a series of function segments. When the cross flow rate is being reduced, either the channel inlet or outlet flow rate, or possibly both, may vary. Conservation of mass will always demand that

$$ {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)=\overset{\cdot }{V}\left(0,t\right)-\overset{\cdot }{V}\left(L,t\right) $$
(4)

where \( {\overset{.}{V}}_{\boldsymbol{c}}(t) \) is the cross flow rate at time t and \( \overset{\cdot }{V}\left(0,t\right) \) and \( \overset{\cdot }{V}\left(L,t\right) \) are the flow rates at the channel inlet (at z = 0, where z is the distance measured from the channel inlet) and outlet (at z = L) at time t, respectively. The local volumetric channel flow rate \( \overset{\cdot }{V} \) will be a function of both the distance z from the channel inlet and time t and is given by

$$ \overset{\cdot }{V}\left(z,t\right)=\overset{\cdot }{V}\left(0,t\right)-\frac{{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\kern0.28em w}{V_{\boldsymbol{C}}^0}{\displaystyle \underset{0}{\overset{z}{\int }}{b}_z\kern0.28em \boldsymbol{d}z}=\overset{\cdot }{V}\left(L,t\right)+{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\left(1-\frac{w}{V_{\boldsymbol{C}}^0}{\displaystyle \underset{0}{\overset{z}{\int }}{b}_z\kern0.5em \boldsymbol{d}z}\right) $$
(5)

in which w is the channel thickness, V 0 C is the channel volume, and b z is the channel breadth at distance z from the inlet. Note that Eq. 5 assumes that the membrane flux is uniform throughout the channel. The local mean channel flow velocity 〈v〉 is then given by

$$ \left\langle v\left(z,t\right)\right\rangle =\frac{\overset{\cdot }{V}\left(z,t\right)}{w{b}_z} $$
(6)

Local volumetric channel flow rate can also be given as a function of channel volume V measured from the inlet to distance z from the inlet, such that \( V=w{\displaystyle \underset{0}{\overset{z}{\int }}{b}_z\;\boldsymbol{d}z} \), and expressed in the form

$$ \overset{\cdot }{V}\left(V,t\right)=\overset{\cdot }{V}\left(0,t\right)-{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\frac{V}{V_{\boldsymbol{C}}^0}=\overset{\cdot }{V}\left(L,t\right)+{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\left(1-\frac{V}{V_{\boldsymbol{C}}^0}\right) $$
(7)

It will be shown below how the use of Eq. 7 holds certain advantages over that of Eq. 5.

Approximate analytical solutions for retention time

It was shown by Kirkland et al. [19] that an approximate analytical solution for retention time is obtainable in the case of As-FlFFF using constant breadth channels with constant channel outlet flow rate and exponential decay of cross flow rate. They considered only the time-delayed exponential (TDE) program, where the initial constant cross flow period t 1 is equal to the exponential decay constant τ, and the simple exponential decay program with t 1 = 0. It was later shown by Moon et al. [22] that an approximate analytical solution could be obtained for As-FlFFF with channels of arbitrary breadth profile, exponential decay of cross flow rate with arbitrary t 1, and outlet volumetric flow rate held constant or exponentially programmed. This was shown to be the case by considering the progress of a zone in terms of the fraction of the channel volume that has been passed through rather than the distance covered, as considered by Kirkland et al. [19]. The local rate at which channel volume is passed through by the center of mass of a monodisperse zone is given by

$$ \frac{\boldsymbol{d}V}{\boldsymbol{d}t}=R(t)\overset{\cdot }{V}\left(V,t\right)=R(t)\kern0.28em \left(\overset{\cdot }{V}\left(L,t\right)+{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\left(1-\frac{V}{V_{\boldsymbol{C}}^0}\right)\right) $$
(8)

where R(t) is the time-dependent retention ratio. The strong retention approximation for retention ratio is given by

$$ R(t)=6{\lambda}_0(t)+6\alpha =\frac{6D{V}_{\boldsymbol{C}}^0}{w^2\kern0.28em {\overset{.}{V}}_{\boldsymbol{c}}(t)}+6\alpha $$
(9)

in which λ 0(t) is the \( {\overset{.}{V}}_{\boldsymbol{c}}(t) \)-dependent and therefore time-dependent retention parameter (equal to \( D{V}_{\boldsymbol{C}}^0/{w}^2{\overset{.}{V}}_{\boldsymbol{c}}(t) \)), D is the particle or molecule diffusion coefficient, and α is the ratio of the exclusion distance for the particle or molecule center from the wall to the channel thickness. Substituting Eq. 9 into Eq. 8, and rearranging, results in the ordinary differential equation

$$ \frac{\boldsymbol{d}V}{\boldsymbol{d}t}+\left(\frac{6D}{w^2}+\frac{6\alpha {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}{V_{\boldsymbol{C}}^0}\right)V=\left(\frac{6D{V}_{\boldsymbol{C}}^0}{w^2}+6\alpha {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\right)\left(\frac{\overset{\cdot }{V}\left(L,t\right)}{{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}+1\right) $$
(10)

and the solution of this equation is given by

$$ \begin{array}{l}V= \exp \left(-{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{6D}{w^2}+\frac{6\alpha {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}{V_{\boldsymbol{C}}^0}\right)\boldsymbol{d}t}\right)\\ {}\times \left\{{V}_{\boldsymbol{C}}^0-{V}^0+{\displaystyle \underset{0}{\overset{t}{\int }} \exp \left({\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{6D}{w^2}+\frac{6\alpha {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}{V_{\boldsymbol{C}}^0}\right)\boldsymbol{d}t}\right)\left(\frac{6D{V}_{\boldsymbol{C}}^0}{w^2}+6\alpha {\overset{\cdot }{V}}_{\boldsymbol{c}}(t)\right)\left(\frac{\overset{\cdot }{V}\left(L,t\right)}{{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}+1\right)\boldsymbol{d}t}\right\}\end{array} $$
(11)

In this equation, V 0 is the effective void volume for particle elution measured from the initial sample focusing point to the channel outlet. The initial V corresponding to t = 0 is therefore equal to V 0 C  − V 0. It has been shown [25] that V 0 is given by

$$ {V}^0=\frac{{\overset{.}{V}}_{\mathrm{B}}}{{\overset{.}{V}}_{\mathrm{F}}+{\overset{.}{V}}_{\mathrm{B}}}{V}_{\boldsymbol{C}}^0 $$
(12)

where \( {\overset{\cdot }{V}}_{\mathrm{F}} \) and \( {\overset{\cdot }{V}}_{\mathrm{B}} \) are the forward and backward flow rates during sample introduction and focusing, respectively. Equation 11 does not yield an analytical solution for any simple cross flow decay functions. The result is considerably simplified, however, if α is negligibly small:

$$ V= \exp \left(-\frac{6Dt}{w^2}\right)\left\{{V}_{\boldsymbol{C}}^0-{V}^0+\frac{6D{V}_{\boldsymbol{C}}^0}{w^2}{\displaystyle \underset{0}{\overset{t}{\int }} \exp \left(\frac{6Dt}{w^2}\right)\left(\frac{\overset{\cdot }{V}\left(L,t\right)}{{\overset{\cdot }{V}}_{\boldsymbol{c}}(t)}+1\right)\boldsymbol{d}t}\right\} $$
(13)

Equation 13 may be solved for elution time t r corresponding to the time at which V = V 0 C for certain programmed flow conditions. For example, it may be solved for the case of constant channel outlet flow rate \( {\overset{.}{V}}_L \) and exponential decay of channel cross flow rate described by

$$ {\overset{.}{V}}_{\boldsymbol{c}}(t)={\overset{.}{V}}_{\boldsymbol{c}0} \exp \left(-\frac{\left(t-{t}_1\right)}{\tau}\right) $$
(14)

in which t 1 is a pre-decay time period during which the cross flow rate is held constant at the initial rate of \( {\overset{.}{V}}_{\boldsymbol{c}0} \) and τ is the exponential decay constant. When t r  ≤ t 1, elution takes place under constant cross flow conditions, and the solution for t r is given by

$$ {t}_{\boldsymbol{r}}=\frac{w^2}{6D} \ln \left(1+\frac{V^0{\overset{.}{V}}_{\boldsymbol{c}0}}{V_{\boldsymbol{C}}^0{\overset{.}{V}}_L}\right) $$
(15)

When t r  > t 1, the solution is given by

$$ {t}_{\boldsymbol{r}}={t}_1+\frac{\tau }{\left(1+6D\tau /{w}^2\right)} \ln \left\{\left(1+\frac{V^0}{V_{\boldsymbol{C}}^0}\frac{{\overset{.}{V}}_{\boldsymbol{c}0}}{{\overset{.}{V}}_L}\right)\left(1+\frac{w^2}{6D\tau}\right) \exp \left(-\frac{6D{t}_1}{w^2}\right)-\frac{w^2}{6D\tau}\right\} $$
(16)

Note that this equation corrects an error in the final line of the derivation given in the appendix of Kirkland et al. [19] and is also more general in allowing t 1 to differ from τ. The corrected result for TDE programming of cross flow rate (for which t 1 = τ) at constant outlet flow rate, as considered by Kirkland et al. [19], is given in the Electronic supplementary materials (ESM). For exponential decay of \( {\overset{.}{V}}_{\boldsymbol{c}} \) and constant \( {\overset{.}{V}}_L \), Eq. 16 yields a good estimate of elution times for particles that are well retained but are also eluted well before the projected steric inversion. Equations 15 and 16 show how t r is related to diffusion coefficient D, and therefore to particle hydrodynamic diameter or to molecular weight. It will be shown later that the determination of nonequilibrium bandspreading under programmed flow conditions requires a numerical approach. The parallel determination of elution time using a more accurate calculation of R(t), as described below, is recommended for exponential decay of cross flow rate and is necessary for other mathematical forms of programmed cross flow rate.

Numerical determination of retention time

As mentioned above, the retention ratio R, being a function of λ 0, and therefore of \( {\overset{.}{V}}_{\boldsymbol{c}} \), is a function of time. It has long been known that the retention ratio in As-FlFFF deviates from that for symmetrical FlFFF due to the variation in cross flow velocity across the channel thickness [7]. The deviation is most significant for weakly retained sample components, and accurate determination of elution time should take this into account. The expression for retention ratio in As-FlFFF with correction for steric exclusion was recently presented [27]. ESM Table S1 shows numerically calculated values of R, the nonequilibrium parameter χ, and the product χR over a wide range of λ 0 from 0.0001 to 1024. The tabulated values do not include a steric exclusion correction. The incorporation of the steric exclusion correction into the calculation of R in As-FlFFF requires the integration of concentration profiles over the region of the channel thickness that is accessible to the particle or molecule centers. The core-channel approach taken by Giddings [26] to derive an expression for R in conventional FFF, where field-induced transverse velocity is constant across the channel, is not strictly valid for As-FlFFF. However, when particles or molecules are small in comparison to channel thickness, the errors associated with this approach are negligible while the savings in computation are considerable, which is particularly important for the modeling of programmed operation which requires repeated calculations at incrementally different conditions. The core-channel retention ratio R c is calculated for the fraction of the channel thickness accessible to the particle or molecule centers. This region has a thickness of (1 − 2α)w, and at the exclusion distance from the membrane, the transverse fluid velocity is (1 − 3α 2 + 2α 3)|u 0| [7, 27]. The core-channel retention parameter λ c is therefore given by λ 0/((1 − 2α)(1 − 3α 2 + 2α 3)). Rather than numerically evaluating R c for every λ c corresponding to each interval in time and each interval in ϕ, it is far more efficient to use a cubic spline interpolation [35] from tabulated values such as those of ESM Table S1. The estimate of R is then obtained using the relationship [26]

$$ R=6\alpha \left(1-\alpha \right)+{\left(1-2\alpha \right)}^2{R}_{\boldsymbol{c}} $$
(17)

ESM Figure S1 shows the error associated with the use of Eq. 17 for the relatively large values of α of 0.0005, 0.001, 0.002, and 0.005, corresponding to spherical particle diameters of 0.25, 0.5, 1.0, and 2.5 μm for a channel thickness of 250 μm. In each case, R is underestimated with the maximum error given at λ 0 of about 0.075, corresponding to accurate R values of 0.415, 0.418, 0.423, and 0.439 and errors for Eq. 17 of 0.0203, 0.0403, 0.0792, and 0.188 %, respectively. Errors are even smaller for both smaller α and smaller λ 0. The large saving in computational time is therefore justified.

Local sample zone velocity is expressed as

$$ \frac{\boldsymbol{d}z}{\boldsymbol{d}t}=R(t)\kern0.5em \left\langle v\left(z,t\right)\right\rangle =\frac{R(t)\overset{\cdot }{V}\left(z,t\right)}{w{b}_z} $$
(18)

A rearrangement of Eq. 18 shows that

$$ \delta z=\frac{R(t)\kern0.24em \overset{\cdot }{V}\left(z,t\right)}{w\;{b}_z}\delta t $$
(19)

The distance δz migrated in the small time interval δt depends on both the time t and the position of the particles z. The migration of a monodisperse sample component may be followed by summing increments in δz from the focusing position to the outlet in order to determine its elution time. The time t at any point is simply the sum of the intervals δt so far considered, and the position z is the summation of the corresponding intervals δz from the initial position z′. Using a simple Euler approach, successive intervals may be calculated using the conditions at the previous position:

$$ \delta {z}_{j+1}=\frac{R\left({t}_j\right)\kern0.24em \overset{\cdot }{V}\left({z}_j,{t}_j\right)}{w\;b\left({z}_j\right)}\delta t $$
(20)

where t j  = jδt and \( {z}_j=z^{\prime }+{\displaystyle \sum_{k=1}^j\delta {z}_k} \), so that t 0 = 0, z 0 = z ′, and z j + 1 = z j  + δz j + 1. This approach first necessitates the calculation of the focusing point z ′. The local volumetric flow rate is given by

$$ \overset{\cdot }{V}\left({z}_j,{t}_j\right)=\overset{\cdot }{V}\left(0,{t}_j\right)-\frac{{\overset{.}{V}}_{\boldsymbol{c}}\left({t}_j\right)w}{V_{\boldsymbol{C}}^0}{\displaystyle \underset{0}{\overset{z_j}{\int }}{b}_z\kern0.5em \boldsymbol{d}z} $$
(21)

or, alternatively, by

$$ \overset{\cdot }{V}\left({z}_j,{t}_j\right)=\overset{\cdot }{V}\left(L,{t}_j\right)+{\overset{\cdot }{V}}_{\boldsymbol{c}}\left({t}_j\right)\left(1-\frac{w}{V_{\boldsymbol{C}}^0}{\displaystyle \underset{0}{\overset{z_j}{\int }}{b}_z\boldsymbol{d}z}\right) $$
(22)

where the appropriate channel breadth function b z is used. Successive δz j are summed until z j + 1 just equals or exceeds L. Such an approach was followed by Nilsson et al. [36] for exponential decay of cross flow rate. A possible advantage of carrying out the summation in δz j is that the shear rate at the membrane surface can be calculated for the center of mass of each zone as it migrates along the channel. This might be of interest if particle–membrane interactions are suspected to influence retention. For example, there may be some critical ratio of shear rate to flow velocity through the membrane below which the particles or molecules become immobilized. The influence of local conditions on the elution of a sample component zone is complicated by the variation of conditions across the breadth of the zone, however; part of the zone may be adversely affected while other parts are not.

If particle–membrane interactions are not an issue, an alternative approach to that considered above is possible. The rate that channel volume is swept through by the position of the center of mass of the sample zone may be considered:

$$ \frac{\boldsymbol{d}V}{\boldsymbol{d}t}=R(t)\overset{\cdot }{V}\left(V,t\right) $$
(23)

Successive intervals in channel volume passed through in time intervals δt can be calculated using an equation analogous to Eq. 20:

$$ \delta {V}_{j+1}=R\left({t}_j\right)\overset{\cdot }{V}\left({V}_j,{t}_j\right)\delta t $$
(24)

where local channel volumetric flow rate is written as a function of V j , the volume of the channel from the inlet to the local position, and discrete time t j . Following Eq. 7, it is apparent that

$$ \overset{\cdot }{V}\left({V}_j,{t}_j\right)=\overset{\cdot }{V}\left(0,{t}_j\right)-{\overset{\cdot }{V}}_{\boldsymbol{c}}\left({t}_j\right)\frac{V_j}{V_{\boldsymbol{C}}^0}=\overset{\cdot }{V}\left(L,{t}_j\right)+{\overset{\cdot }{V}}_{\boldsymbol{c}}\left({t}_j\right)\left(1-\frac{V_j}{V_{\boldsymbol{C}}^0}\right) $$
(25)

The current V j is obtained via the summation of previous increments to channel volume

$$ {V}_j={V}_{\boldsymbol{C}}^0-{V}^0+{\displaystyle \sum_{k=1}^j\delta {V}_k} $$
(26)

where the channel volume up to the initial point V 0 is given by V 0 = V 0 C  − V 0, and it is not necessary to determine z′. It also follows that V j + 1 = V j  + δV j + 1. Equation 24 can now be written in the form

$$ \delta {V}_{j+1}=R\left({t}_j\right)\left(\overset{\cdot }{V}\left(0,{t}_j\right)-\frac{{\overset{\cdot }{V}}_{\boldsymbol{c}}\left({t}_j\right)}{V_{\boldsymbol{C}}^0}\left({V}_{\boldsymbol{C}}^0-{V}^0+{\displaystyle \sum_{k=1}^j\delta {V}_k}\right)\right)\delta t $$
(27)

or, alternatively, in the form

$$ \delta {V}_{j+1}=R\left({t}_j\right)\left(\overset{.}{V}\left(L,{t}_j\right)+\frac{{\overset{.}{V}}_{\boldsymbol{c}}\left({t}_j\right)}{V_{\boldsymbol{C}}^0}\left({V}^0-{\displaystyle \sum_{k=1}^j\delta {V}_k}\right)\right)\delta t $$
(28)

The summation of successive δV j is carried out until V j + 1 just equals or exceeds V 0 C . The number of required intervals δt then indicates the elution time (of course, the final interval will invariably be some fraction of δt consistent with the final increment to channel volume necessary to exactly obtain V 0 C ). For these numerical calculations, \( {\overset{.}{V}}_{\boldsymbol{c}}\left({t}_j\right) \), which also influences R(t j ), can follow any smooth mathematical function of time, or it can be a discontinuous function or series of functions, or indeed have an arbitrary variation with time. It is apparent from Eqs. 27 and 28 that, for any variation of \( {\overset{.}{V}}_{\boldsymbol{c}} \) with time, provided non-idealities are insignificant and the elution adheres to the expression used for the retention ratio, the increments to channel volume are independent of the breadth profile of the channel. This means that, provided the retention ratio is not influenced by local channel flow velocity, elution times will also be independent of the channel breadth profile.

The equations and discussion above imply that a simple application of Euler’s method may be used for summation of δz j or δV j . In practice, to better represent the gradually changing conditions across the intervals, a fourth-order Runge–Kutta summation may be carried out (see [37]). This involves the consideration of conditions at half time intervals. In fact, Nilsson et al. [36] used a similar approach. For the small time intervals typically considered, the improvement is modest, and very often negligible.

It is important to emphasize that Eqs. 27 and 28 are perfectly general. The values for \( {\overset{.}{V}}_{\boldsymbol{c}}\left({t}_j\right) \) and either\( \overset{\cdot }{V}\left(0,{t}_j\right) \) or \( \overset{\cdot }{V}\left(L,{t}_j\right) \) may correspond to a defined set of programmed conditions, or they may be quantities that are experimentally monitored during a sample analysis. The monitoring of flow rates can account for deviation from nominal set conditions or for flow rates that are arbitrarily varied as opposed to following precise functions of time. In any case, the mean elution time may be determined for any assumed ϕ, provided it is known how D and α are related to ϕ. The calculation of elution times for a series of discrete ϕ allows the use of interpolation to associate a value of ϕ i to every discrete elution time t i . This is the basis of the integral approach to FFF data reduction (transformation of fractogram to size or molecular weight distribution) [38]. The approach is here shown to be applicable to As-FlFFF.

Bandspreading

As a monodisperse zone passes along the channel, its breadth is influenced by the loss of carrier solution through the membrane and by the changing channel breadth. It was explained in part I [25] that the loss of carrier solution tends to reduce the zone breadth while the reduction in channel breadth tends to increase the zone breadth. For the calculation of the contributions to bandspreading, the channel may be considered to be divided into a series of small intervals, with each contributing to the breadth of the zone as it migrates through it. The conditions across the breadth of a zone can vary significantly, but it was explained in part I [25] that a projected standard deviation in breadth of the zone can be considered as corresponding to the standard deviation expected when conditions at the center of mass are assumed to apply across the full zone. Then as the center of mass passes from one interval to the next, the zone variance must be adjusted for the changing volumetric flow rate and channel breadth before the next contribution to variance is added. In the case of programmed operation, this adjustment must take into account the change in flow rates with time as well as position. The variance in zone breadth σ z 2 for center of mass at position and time (z i − 1, t i − 1) must therefore be adjusted by the ratio \( {\left({b}_{i-1}\overset{\cdot }{V}\left({z}_i,{t}_i\right)/{b}_i\overset{\cdot }{V}\left({z}_{i-1},{t}_{i-1}\right)\right)}^2 \), or equivalently (〈v(z i , t i )〉/〈v(z i − 1, t i − 1)〉)2, as the center of mass passes to (z i , t i ), where the next contribution δσ z,i 2 is added. The summation of successive contributions to variance can be written as

$$ {\sigma_{z,i}}^2={\displaystyle \sum_{j=1}^i{}_{\boldsymbol{C}}\delta {\sigma_{z,j}}^2}=\delta {\sigma_{z,i}}^2+{\left(\frac{\left\langle v\left({z}_i,{t}_i\right)\right\rangle }{\left\langle v\left({z}_{i-1},{t}_{i-1}\right)\right\rangle}\right)}^2{\displaystyle \sum_{j=1}^{i-1}{}_{\boldsymbol{C}}\delta {\sigma_{z,j}}^2} $$
(29)

where the subscript C on the summation signs indicates that they do not represent simple summations but mean velocity-corrected summations. In the same way as shown in part I [25] for isocratic operation, the expansion of successive terms in Eq. 29 shows that the mean velocity-corrected summation reduces to the simple summation:

$$ {\sigma_{z,i}}^2={\left\langle v\left({z}_i,{t}_i\right)\right\rangle}^2{\displaystyle \sum_{j=1}^i\frac{\delta {\sigma_{z,j}}^2}{{\left\langle v\left({z}_j,{t}_j\right)\right\rangle}^2}} $$
(30)

The variances represented in Eqs. 29 and 30 correspond to the projected variances where the conditions at the center of mass are imagined to extend across the whole breadth of the zone. As mentioned above, the conditions can vary significantly across a zone, distorting the distribution along the length or volume of the channel. The contributions to variance in the time of elution may alternatively be considered, but they are not simply summed as in isocratic operation, however; the change of retention ratio from interval to interval must be taken into account. An increase in R, as seen under programmed decay of cross flow rate, will reduce the variance in elution time simply because the zone velocity increases. Every fraction of the zone is influenced simultaneously by an instantaneous change in R. The progress of the center of mass of the zone in the time domain may be considered and the variance in elution time adjusted for the change in R from the previous interval to the current before adding the current contribution:

$$ {\sigma_{t,i}}^2={\displaystyle \sum_{j=1}^i{}_{\boldsymbol{C}}\delta {\sigma_{t,j}}^2}=\delta {\sigma_{t,i}}^2+{\left(\frac{R\left({t}_{i-1}\right)}{R\left({t}_i\right)}\right)}^2{\displaystyle \sum_{j=1}^{i-1}{}_{\boldsymbol{C}}\delta {\sigma_{t,j}}^2} $$
(31)

The subscript C on the summation signs again indicates that they are not simple summations. By expanding successive terms, this may be shown to be equivalent to the simple summation given by

$$ {\sigma_{t,i}}^2=\frac{1}{R{\left({t}_i\right)}^2}{\displaystyle \sum_{j=1}^iR{\left({t}_j\right)}^2\delta {\sigma_{t,j}}^2} $$
(32)

The comments made with regard to the calculation of elution times using Eq. 27 or Eq. 28 are equally applicable to the calculation of σ t 2 using Eq. 32. If δσ t,j 2 may be calculated for local conditions for a zone migrating along the channel, then the zone variance in elution time may be predicted for any given variation in channel and cross flow rates. This allows the calculation of F ϕ (by interpolation) for every discrete elution time t i and corresponding ϕ i . The integral approach to FFF data reduction [38] not only performs the transformation of the fractogram to a size or molecular weight distribution, it also provides the important knowledge of F ϕ across the distribution.

Nonequilibrium bandspreading

As for the retention ratio, the core-channel approach can be taken to obtain the nonequilibrium bandspreading parameter χ in order to save computational time. The core-channel λ c is calculated as before. The core-channel value of the product R c χ c can then be efficiently obtained using cubic spline interpolation of the tabulated data (ESM Table S1) and the product Rχ calculated via the relationship [14, 26]

$$ R\chi ={R}_{\boldsymbol{c}}{\chi}_{\boldsymbol{c}}{\left(1-2\alpha \right)}^6 $$
(33)

ESM Figure S1 shows the error associated with this approach, again for the examples of α of 0.0005, 0.001, 0.002, and 0.005. Equation 33 slightly underestimates the correct value, with maximum error occurring at λ 0 of about 0.045. A λ 0 of 0.045 corresponds to R values of 0.256, 0.259, 0.265, and 0.281, and the errors given by Eq. 33 are 0.105, 0.210, 0.417, and 1.028 %, respectively. For both smaller α and stronger retention, the errors are smaller, justifying the approach. The savings in computational time are considerable for calculations related to programmed cross flow rate conditions.

The local nonequilibrium plate height is given by [29]

$$ {H}_{\boldsymbol{neq}}\left({z}_j,{t}_j\right)=\frac{w^2}{D}\chi \left({t}_j\right)\;\left\langle v\left({z}_j,{t}_j\right)\right\rangle $$
(34)

where χ is the nonequilibrium parameter that is a function of λ 0, and therefore of time, and of α when the steric exclusion correction is included [26, 27, 30]. The local contribution to zone variance on migrating a small distance δz is then given by

$$ \delta {\sigma_{z,j}}^2={H}_{\boldsymbol{neq}}\left({z}_j,{t}_j\right)\kern0.5em \delta z=\frac{w^2}{D}\chi \left({t}_j\right)\;\left\langle v\left({z}_j,{t}_j\right)\right\rangle \kern0.5em \delta z $$
(35)

Local zone velocity is given by

$$ \frac{\delta z}{\delta t}=R\left({t}_j\right)\;\left\langle v\left({z}_j,{t}_j\right)\right\rangle $$
(36)

and therefore

$$ \delta {\sigma_{z,j}}^2=\frac{w^2}{D}\chi \left({t}_j\right)\;R\left({t}_j\right){\left\langle v\left({z}_j,{t}_j\right)\right\rangle}^2\delta t $$
(37)

This can be converted to an increment in variance of retention time by dividing by the square of the local zone velocity R(t j )2〈v(z j , t j )〉2

$$ \delta {\sigma_{t,j}}^2=\frac{w^2}{D}\frac{\chi \left({t}_j\right)}{R\left({t}_j\right)}\delta t $$
(38)

Summing the contributions to variance in retention time according to Eq. 32 shows that

$$ {\sigma_{t,i}}^2=\frac{w^2}{DR{\left({t}_i\right)}^2}{\displaystyle \sum_{j=1}^i\chi \left({t}_j\right)R\left({t}_j\right)\delta t} $$
(39)

Suppose that t r  = (i + f)δt, where f is the final fraction of a time interval δt required for the center of mass to reach the channel outlet, then

$$ {\sigma_{t,\boldsymbol{n}\boldsymbol{e}\boldsymbol{q}}}^2=\frac{w^2\delta t}{D\kern0.5em R{\left({t}_{\boldsymbol{r}}\right)}^2}{\displaystyle \sum_{j=1}^{i+\mathrm{f}}\chi \left({t}_j\right)R\left({t}_j\right)} $$
(40)

The calculation of elution time and variance in elution time due to nonequilibrium bandspreading may therefore be calculated by summations over small time intervals δt without specifying a channel breadth profile. They are in fact independent of the channel breadth profile. In practice, the summation represented by Eq. 40 is carried out using Simpson’s 1/3 rule, taking values of the product of χ and R at j and j + 0.5 intervals. Again, the improvement over a simple interval summation is generally modest for small time intervals.

Multipath bandspreading

It was explained in part I [25] how slight unevenness in the membrane surface and small variations in membrane permeability must contribute to bandspreading. Different fractions of the sample follow different paths along the channel having different mean fluid velocities and different mean transverse fluid velocities through the membrane. The fractions consequently reach the channel outlet at slightly different times, thereby contributing to bandspreading. Under isocratic conditions, this multipath contribution is not expected to be a strong function of retention ratio as the relative variation in mean fluid velocity and relative variation in retention ratio should be similar for all components. There should not be a significant change in the multipath effect with change of cross flow rate as the fractions of a component following different paths should show the same relative change in R. It is possible that the membrane may be forced into better contact with the supporting frit at high cross flow rate, but this supposes that the membrane draws away from the frit at a low cross flow rate, which would result in very poor efficiency or even split peaks. This possibility will therefore be discounted, and it will be assumed that the membrane remains in good contact with the frit at all cross flow rates.

It was also pointed out in part I [25] that the scale of the multipath effect in As-FlFFF as well as its two-dimensional nature do not allow lateral diffusional exchange of material between streams, as may occur in packed bed chromatographic columns [39]. The flow pattern along the channel can be assumed to be fixed and independent of the channel and cross flow rates. The multipath bandspreading is therefore the result of the distribution of sample across several independent streams having slightly different mean channel flow velocities and slightly different mean cross flow velocities, the relative differences between streams remaining constant under programmed conditions. To model the contribution to multipath bandspreading under programmed conditions, it will also be assumed that the relative differences in mean velocities and membrane permeabilities between different paths are fairly constant along the channel length. It is not necessary to make this assumption for isocratic conditions.

Consider a path for which the elution time for a monodisperse material is one standard deviation σ t,m lower than the mean elution time t r . The difference is due to the fact that, for this elution path, the increments δV j + 1 are attained in slightly less time than would material eluting at the mean migration rate from the same V j and t j , in time intervals of (1 − ε)δt, where ε is a small positive correction factor. Therefore, δV j + 1 is calculated using Eq. 24 or its equivalent, but the cumulative elution time is incremented by (1 − ε)δt.

For the special case of isocratic elution, this gives the simple result

$$ {t}_{\boldsymbol{r}}-{\sigma}_{t,\boldsymbol{m}}=\left(1-\varepsilon \right){t}_{\boldsymbol{r}} $$
(41)

For isocratic elution, the limiting multipath plate number N m has been defined as (t r /σ t,m )2 [25], and it follows from Eq. 41 that \( \varepsilon =1/\sqrt{N_{\boldsymbol{m}}} \). For N m  = 3000, for example, ε = 0.0183. It is now apparent that σ t,m may be obtained for any sample component eluting under programmed conditions by first solving for t r and then for t r  − σ t,m by applying the multiplicative factor (1 − ε) = (1 − N m − 0.5) to successive δt, with δV j + 1 as calculated using Eq. 24 or its equivalent. The value for N m depends on each assembled channel and membrane and can be determined experimentally as explained in the ESM of part I [25]. It may be found in practice that N m varies to some extent with particle size, molecular weight, or flow conditions. Such variation could be taken into account, but for the purposes of this work, N m will be assumed to be constant.

Other contributions to bandspreading

Other contributions are relatively minor or can be made minor by suitable selection of conditions, as in isocratic operation. These are discussed in the ESM.

Comparison of programmed and isocratic elution

Typical parameters of channel thickness w = 0.025 cm, channel volume V 0 C  = 0.75 mL, carrier fluid viscosity η = 0.01 P, and temperature T = 298 K were assumed, together with Boltzmann constant k = 1.38065 × 10− 23 J/K. A polydisperse nanoparticle sample was assumed to be initially focused at the inlet (so that V 0 = V 0 C ). This initial position was also considered in part I [25], where it was explained that focusing of the sample at some other position could have been considered, but this would not have contributed to the discussion. The nanoparticles were assumed to be spherical so that a simple steric exclusion correction could be taken into account. To show the influence of F d on the outlet polydispersity (see the next section), two sets of conditions involving exponential decay of cross flow rate were considered. Condition I corresponds to an initial cross flow rate \( {\overset{.}{V}}_{\boldsymbol{c}0}=2.0\mathrm{mL}/ \min \), constant outlet flow rate \( {\overset{.}{V}}_L=0.2\mathrm{mL}/ \min \), pre-decay time t 1 = 1.0 min, and exponential time constant τ = 5.0 min. Condition II corresponds to \( {\overset{.}{V}}_{\boldsymbol{c}0}=6.0\mathrm{mL}/ \min \), \( {\overset{.}{V}}_L=0.6\mathrm{mL}/ \min \), and the same time constants. These conditions were selected to obtain almost identical elution times (see approximate Eq. 16, valid for α < < λ 0 < < 1), and therefore selectivity, but different levels of F d . In each case, a multipath bandspreading equivalent to a limiting plate number N m of 3000 under isocratic conditions was assumed.

Figure 1 shows the predicted F d as a function of d (on a log scale) for programmed condition I (full black curve). Also included for comparison are the predicted F d curves for isocratic elution at \( {\overset{.}{V}}_{\boldsymbol{c}} \) values of 2.0, 1.0, 0.5, and 0.25 mL/min, with \( {\overset{.}{V}}_L \) held at 0.2 mL/min (full red, green, blue, and purple curves, respectively). All full curves were calculated using the equations for R and χR for As-FlFFF taking the core-channel approximation for steric exclusion as explained above. (It should be pointed out that the lower limit on particle size for retention and fractionation is ultimately determined by the membrane size cutoff. Particles smaller than the cutoff will not be retained in the channel by the membrane and will be lost. This aspect is not specifically considered in this work as the focus is on illustrating the predictions made by the equations derived to model the system.)

Fig. 1
figure 1

Fractionating power F d as a function of d (log scale) for programmed condition I (black curves) and isocratic conditions with \( {\overset{.}{V}}_{\boldsymbol{c}} \) values of 2.0, 1.0, 0.5, and 0.25 mL/min (red, green, blue, and purple curves, and as labeled) and \( {\overset{.}{V}}_L=0.2\mathrm{mL}/ \min \) in all cases. Full curves calculated using As-FlFFF equations and dashed curves using Sym-FlFFF equations

Full size image

For condition I, a maximum F d of 1.98 is predicted for d = 0.0094 μm. For d values of 0.001, 0.01, and 0.1 μm, F d is predicted to be 0.545, 1.98, and 0.490, respectively. For comparison, the dashed curves were calculated using the equations for conventional FFF in which field-induced transverse velocity is constant across the channel thickness. These equations are valid for Sym-FlFFF where the transverse fluid velocity component is assumed to be constant across the thickness. These equations are therefore referred to as the Sym-FlFFF equations in the following discussion. For the programmed condition I, the Sym-FlFFF equations result in a slightly higher predicted F d than the As-FlFFF equations across the full diameter range. A slightly higher F d for smaller diameters (weak retention) is predicted for isocratic conditions. Under the programmed condition I, the F d values predicted using the Sym-FlFFF equations were 34, 14, and 27 % higher at d values of 0.001, 0.01, and 0.1 μm, respectively, which is quite significant.

For programmed condition I, the projected steric inversion diameter d i  > 1.0 μm, whereas under the different isocratic conditions, the projected d i (where F d falls to zero) values are smaller than 1.0 μm and inversely related to \( {\overset{.}{V}}_{\boldsymbol{c}}^{0.5} \) (see Eq. 32 of part I [25], valid for isocratic conditions). The F d for isocratic elution may be much higher over some limited range of d than for programmed conditions, but the range of diameters eluted in the normal mode is reduced. For example, isocratic elution at \( {\overset{.}{V}}_{\boldsymbol{c}} \) of 2.0 mL/min shows no loss of F d at low d, a much higher maximum F d of 11.4 at 0.058 μm, but a projected d i of about 0.28 μm. Isocratic elution at a lower cross flow rate predicts higher projected d i , but considerably lower F d for the smaller particle diameters.

The elution times for the larger d are greatly reduced by the programmed decay of cross flow rate, which is, of course, one of the objectives of programming. ESM Figure S2 shows the predicted elution times as functions of log d for the same set of programmed and isocratic conditions. The maxima in the isocratic curves correspond to the projected inversion diameters. The differences between the elution times predicted using the As-FlFFF and Sym-FlFFF equations are too small to distinguish on the scale of the time axis, and only a single set of curves is included in the figure. Relative differences are significant, however.

Figure 2 shows the variation of selectivity S d with log d for the different conditions. In isocratic operation, S d approaches but does not quite attain a level of unity and remains fairly constant until steric effects start to influence elution and S d begins to fall, approaching zero at the projected d i . The range of d where S d is close to unity moves to higher diameters as \( {\overset{.}{V}}_{\boldsymbol{c}} \) is reduced, and the range is also reduced to some degree. In part I [25], an approximate equation for S d for isocratic operation was presented which is valid for the range of d where λ 0 < < 1 and α < < 1; it is not valid for the range of d over which S d rises to the plateau. The plateau is attained when λ 0 falls to about 0.07 in As-FlFFF, corresponding to R = 0.387 (results for S M were plotted on a linear scale in M in Fig. S1 of the ESM of part I [25], where this rise to the plateau was not made evident). Under the programmed condition I, S d is predicted to rise over the region of d where λ 0 decreases toward 0.07 and then to fall steadily over a wide range of d as \( {\overset{.}{V}}_{\boldsymbol{c}} \) decays. This shows the desired effect of programmed decay of cross flow rate on selectivity mentioned in the introduction and reflects the reduced elution times predicted for the larger particles. Note that S d does not rise to the level attained for isocratic conditions with \( {\overset{.}{V}}_{\boldsymbol{c}}=2.0\mathrm{mL}/ \min \) before falling. This is because the cross flow rate starts to decay at t 1 = 1.0 min, which is very close to the void time of 0.899 min. Those particles for which λ 0 = 0.07 at \( {\overset{.}{V}}_{\boldsymbol{c}}=2.0\mathrm{mL}/ \min \) are eluted after the start of the cross flow decay. In Fig. 2, the full curves were again predicted using the As-FlFFF equations, and the dashed curves the Sym-FlFFF equations. Note that the rise of S d to the plateau for isocratic operation is not so abrupt for the Sym-FlFFF equations, and the range of d for each plateau is consequently reduced. This is also true in the case of programmed operation, but the solutions for Sym-FlFFF and As-FlFFF equations converge as \( {\overset{\cdot }{V}}_{\boldsymbol{c}} \) decays. The differences in predicted S d are a consequence of the slightly different dependence of asymmetrical R As and symmetrical R Sym on λ 0. For FlFFF of spherical nanoparticles where λ 0 ∝ 1/d, it can be shown from Eq. 3 that

Fig. 2
figure 2

Selectivity S d as a function of d (log scale) for programmed condition I (black curves) and isocratic conditions as given in the caption to Fig. 1. Full curves calculated using As-FlFFF equations and dashed curves using Sym-FlFFF equations

Full size image
$$ {S}_d=\frac{\lambda_0}{R}\frac{\boldsymbol{d}R}{\boldsymbol{d}{\lambda}_0} $$
(42)

It is also interesting to compare the predicted contributions to bandspreading as functions of d for the different conditions. Figure 3 shows the nonequilibrium contribution σ t,neq as a function of log d for programmed condition I and the same isocratic conditions. In the case of isocratic elution, the nonequilibrium contribution rises to a relatively constant level before decreasing as the projected steric inversion is approached. This is as expected and is consistent with the approximate Eq. 36 of part I [25]. For the assumptions made here, this may be written as

$$ {\sigma}_{t,\boldsymbol{n}\boldsymbol{e}\boldsymbol{q}}=\frac{V_{\boldsymbol{C}}^0}{{\overset{.}{V}}_{\boldsymbol{c}}}{\left(\frac{2}{3} \ln \left(\frac{{\overset{.}{V}}_{\boldsymbol{c}}}{{\overset{.}{V}}_L}+1\right)\right)}^{0.5}{\left(1+{f}^2\right)}^{-1.5} $$
(43)

in which f is the ratio of d to the projected d i . Consistent with Eq. 43, the level of each plateau in σ t,neq increases with reduction of \( {\overset{.}{V}}_{\boldsymbol{c}} \). The final factor in Eq. 43 involving f accounts for the roll-off in σ t,neq from each plateau toward d i and beyond. In Fig. 3, the full curves were predicted using the equations for As-FlFFF and the dashed curves using the Sym-FlFFF equations. The As-FlFFF equations predict a steeper climb and some overshoot before reaching the plateau in σ t,neq , while the Sym-FlFFF equations predict a more gradual rise. There is therefore a significant difference in behavior in the lower region of the plateau. Under programmed condition I, σ t,neq increases with d for the range plotted, and the Sym-FlFFF equations predict a considerably lower contribution to bandspreading than the As-FlFFF equations. For example, the Sym-FlFFF equations predict 6.6, 12, 20, and 21 % lower σ t,neq at d values of 0.001, 0.01, 0.1, and 1.0 μm, respectively.

Fig. 3
figure 3

Predicted nonequilibrium contribution to bandspreading σ t,neq as a function of d (log scale) for programmed condition I (black curves) and isocratic conditions as given in the caption to Fig. 1. Full curves calculated using equations for As-FlFFF and dashed curves using Sym-FlFFF equations

Full size image

Figure 4 shows the multipath contributions σ t,m as functions of log d. Under isocratic conditions, σ t,m is seen to increase with d, rising to some maximum at the steric inversion point before falling again. Of course, under isocratic conditions it is assumed that \( {\sigma}_{t,\boldsymbol{m}}={t}_{\boldsymbol{r}}/\sqrt{N_{\boldsymbol{m}}} \) and in the region before inversion, and σ t,m is expected to increase with t r and therefore with \( {\overset{.}{V}}_{\boldsymbol{c}} \). Programmed condition I is predicted to give a relatively small contribution to σ t,m across the full range of d plotted; multipath bandspreading is therefore suppressed under programmed conditions. Equation 8 may be modified to take into account the (1 − ε) factor for δt, as shown in ESM Eq. S2. This may then be solved for the case of exponential decay of \( {\overset{.}{V}}_{\boldsymbol{c}} \), constant \( {\overset{.}{V}}_L \), and the R ≈ 6λ 0 approximation to obtain an approximate solution for t r  − σ t,m in the form of Eq. 16. The result, valid for α < < λ 0 < < 1, is shown in ESM Eq. S3. It is also pointed out in the ESM that a crude estimate of σ t,m  ≈ τ ln(1/(1 − ε)) is obtained when Dτ/w 2 → 0, and α remains negligible. For condition I, approximate σ t,m values of 0.100 and 0.093 min are obtained using Eqs. 16 and S3 for d values of 0.01 and 0.1 μm, respectively. These compare with the values obtained numerically, and as plotted in Fig. 4, of 0.092 and 0.122 min, respectively, and the σ t,m  ≈ τ ln(1/(1 − ε)) estimate of 0.092 min. As expected, there is no observable difference between predictions of σ t,m based on the As-FlFFF and Sym-FlFFF equations on the scale of the σ t,m axis, and only one set of curves is included in the figure. Relative differences are significant at low retention, however. Finally, Fig. 5 shows the results of summing the contributions to variance due to nonequilibrium and multipath effects for the different conditions. Again, full curves correspond to As-FlFFF equations and dashed curves to Sym-FlFFF equations.

Fig. 4
figure 4

Predicted multipath contribution to bandspreading σ t,m as a function of d (log scale) for programmed condition I (black curve) and isocratic conditions as given in the caption to Fig. 1. The curves calculated using As-FlFFF and Sym-FlFFF equations are indistinguishable on the scale of the σ t,m axis, as mentioned in the text

Full size image
Fig. 5
figure 5

Predicted σ t , calculated by summing the contributions to variance due to nonequilibrium and multipath effects, as functions of d (log scale) for programmed condition I (black curves) and isocratic conditions as given in the caption to Fig. 1. Full curves calculated using As-FlFFF equations and dashed curves using Sym-FlFFF equations

Full size image

The results for programmed condition II are shown in ESM Figs. S3 to S8, and they are also briefly discussed in the ESM. In these figures, the programmed condition II is compared with isocratic elution with \( {\overset{.}{V}}_{\boldsymbol{c}} \) values of 6.0, 3.0, 1.5, and 0.75 mL/min and \( {\overset{.}{V}}_L=0.6\mathrm{mL}/ \min \). The maximum F d for condition II is predicted to be 5.81, almost three times higher than for condition I, and at the same particle diameter d = 0.0094 μ m as for condition I. For d values of 0.001, 0.01, and 0.1 μm, F d values were predicted to be 1.43, 5.80, and 1.61, respectively. At this higher level of F d , the Sym-FlFFF equations for predicting F d do not deviate so strongly from the As-FlFFF equations. The Sym-FlFFF equations predict F d values just 18, 1, and 3 % higher than the As-FlFFF equations at d values of 0.001, 0.01, and 0.1 μm, respectively. While the predicted F d is almost three times higher for programmed condition II than for condition I, the elution times are very similar when the steric perturbation remains small. The elution times for conditions I and II are within 5 % of one another for d between 0.002 and 0.4 μm. This is as expected and is consistent with Eq. 16. For smaller particles, the difference is greater because initial void times differ, and for larger particles, the difference increases because of the lower projected d i for condition II. The elution times for the isocratic conditions shown in Figs. S2 and S4 (see ESM) are also very similar when α < < λ 0. This is because both the void times and the values of λ 0 for the conditions shown in ESM Fig. S4 are one third of those for the respective conditions of ESM Fig. S2. Their influence on t r therefore approximately cancels when α < < λ 0.

Relation of fractionating power to channel outlet polydispersity

The method of predicting outlet polydispersity for any given set of experimental conditions was explained in part I [25]. It is based on the approach taken by Schure [40]. A log-normal number distribution in particle diameter was assumed for the sample with number average diameter \( {\overline{d}}_{\boldsymbol{n}} \) of 0.01 μm and standard deviation σ d of 0.0075 μm. The normalized number distribution is given by

$$ N(d)=\frac{1}{\sqrt{2\pi }d\sigma } \exp \left(-\frac{{\left( \ln d-\mu \right)}^2}{2{\sigma}^2}\right) $$
(44)

in which

$$ \mu = \ln \left(\frac{{\overline{d}}_{\boldsymbol{n}}}{{\left(1+{\left({\sigma}_d/{\overline{d}}_{\boldsymbol{n}}\right)}^2\right)}^{0.5}}\right) $$
(45)

and

$$ \sigma ={\left( \ln \left(1+{\left({\sigma}_d/{\overline{d}}_{\boldsymbol{n}}\right)}^2\right)\right)}^{0.5} $$
(46)

For each of the programmed conditions I and II described earlier, a retention time–particle diameter matrix was set up with 10,000 equal intervals in diameter up to 0.5 μm (so that δd = 5 × 10− 5 μ m) across the horizontal and 1740 equal intervals in time up to 21.75 min (δt = 0.0125 min) in the vertical direction. For each discrete d, a Gaussian elution curve was assumed with mean elution time given by summing contributions to channel volume given by Eq. 28 until the outlet is reached and standard deviation in elution time calculated by summing contributions to variance due to nonequilibrium and multipath contributions. The Gaussian was weighted by the diameter number distribution function and put into the respective column of the matrix. The number distribution in particle size eluting at any discrete time is then given by the values across the row corresponding to that time.

Figure 6 shows the predicted outlet number distributions in particle diameter at elution times of 2, 4, 6, 8, 10, and 12 min for the fractionation of the log-normal sample (full black curves) under programmed condition I as determined using the time–diameter matrix. The normalized log-normal distribution assumed for the sample is also shown as a dash-dotted blue curve, referring to the right-hand axis. Also included are what Schure [40] referred to as the predicted apparent number distributions calculated as Gaussians with standard deviations in particle diameter given by

$$ {\sigma}_{\operatorname{d},\boldsymbol{app}}=\frac{\sigma_t}{\boldsymbol{d}{t}_{\boldsymbol{r}}/\boldsymbol{d}d}=\frac{d}{4{F}_d} $$
(47)

with d corresponding to the monodisperse particle diameters predicted to elute at mean elution times of 2, 4, 6, 8, 10, and 12 min. The latter are plotted as dashed red curves.

Fig. 6
figure 6

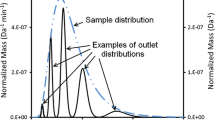
Predicted outlet particle diameter number distributions at 2, 4, 6, 8, 10, and 12 min for programmed condition I for a sample having a log-normal number distribution in particle diameter with \( {\overline{d}}_{\boldsymbol{n}}=0.01\ \upmu \mathrm{m} \) and σ d  = 0.0075 μm. Nonequilibrium bandspreading and multipath bandspreading consistent with a limiting overall system efficiency of 3000 plates under isocratic conditions were taken into account. Full black curves correspond to data in respective rows of the t r –d matrix. Dashed red curves correspond to Gaussians with mean d corresponding to monodisperse d predicted to elute at respective t r and σ d corresponding to apparent σ d, app calculated using Eq. 47. Dash-dotted blue curve shows the sample particle diameter number distribution referring to the right-hand axis

Full size image

There is fairly good agreement between the two sets of distribution curves for all but the lowest elution time of 2 min. The poorer agreement at 2 min is attributable to two factors: (1) the F d is low (0.917) at this time so that the relative polydispersity is high, and (2) the diameter d coincides with the steep front of the sample size distribution. The number distribution obtained from the row of the time–diameter matrix corresponding to 2 min will therefore be correctly skewed toward the sample distribution maximum. The predicted apparent number distribution (dashed red curve) is a symmetrical Gaussian and cannot account for this effect. This effect leads to a discrepancy of almost 14 % between the monodisperse particle diameter predicted to elute at a mean t r of 2 min and the \( {\overline{d}}_{\boldsymbol{n}} \) predicted at an elution time of 2 min. The approximation to σ d as calculated using Eq. 47 is also 8 % in error. The skewing of the outlet distributions at 8, 10, and 12 min is also apparent in Fig. 6, although consequent errors are far less significant. Numerical data describing the outlet distributions and discrepancies between the approaches are listed in ESM Table S2.

The same exercise was carried out for programmed condition II. Figure 7 shows the predicted F d (full curves, left axis) and S d (dashed curves, right axis) for conditions I and II (red and black curves, respectively) as functions of log(d). The F d for condition II is predicted to rise to a maximum of 5.81 at d = 0.0094 μ m as compared to a maximum of 1.98 at the same particle size for condition I, as mentioned earlier. The S d curves for the two conditions are very close for d between approximately 0.002 and 0.2 μm, as expected. In the case of condition I, S d decreases below 0.002 μm, whereas for condition II S d continues to increase until d falls to about 0.0008 μm, a result of the stronger retention of these smaller particles at the higher \( {\overset{.}{V}}_{\boldsymbol{c}0} \) of condition II. Figure 8 shows the predicted outlet distribution curves at 2, 4, 6, 8, 10, and 12 min for condition II. As in Fig. 6, the distributions obtained using the time–diameter matrix approach are shown as full black curves and the predicted apparent Gaussian number distributions as dashed red curves. The outlet distributions in Fig. 8 are much narrower than those in Fig. 6 due to the higher F d . Also, the agreement between the sets of curves in Fig. 8 is much better than in Fig. 6. The numerical data describing the outlet distributions of Fig. 8 are listed in ESM Table S3. Again, the greatest discrepancy between the approaches occurs at t r  = 2 min, but at the higher F d of condition II, the monodisperse d eluting at mean t r of 2 min differs only 1.5 % from \( {\overline{d}}_{\boldsymbol{n}} \), and σ d,app differs only 0.5 % from σ d .

Fig. 7
figure 7

Predicted F d (full curves) and S d (dashed curves, right-hand axis) as functions of d (log scale) for programmed conditions I and II (red and black curves, respectively)

Full size image
Fig. 8
figure 8

Predicted outlet particle diameter number distributions at 2, 4, 6, 8, 10, and 12 min for programmed condition II for the same log-normal sample considered for Fig. 6. Remaining details correspond to the caption for Fig. 6

Full size image

Finally, Fig. 9 shows plots of outlet polydispersities \( {\sigma}_d/{\overline{d}}_{\mathrm{n}} \) as functions of elution time, calculated using the data in rows of the respective t r –d matrices for conditions I and II (full black curves). Plots of 1/4F d for the two programmed conditions are shown as dashed red curves. Also included are the predicted normalized particle elution curves for conditions I and II shown as the dash-dotted green and dashed blue curves, respectively. These were obtained by summing the numbers of particles eluted across rows of the t r –d matrices corresponding to the discrete elution times. These elution curves do not represent predicted fractograms of detector response versus time. To predict such a fractogram, contributions for each discrete particle size would have to be adjusted by the detector response function before summation at each discrete elution time. The particle elution curve for condition I is only very slightly broader than that for condition II. This is because the breadth is dominated by the assumed polydispersity of the sample. The values for 1/4F d may be seen to serve very well as estimated upper bounds to outlet polydispersity for the two programmed conditions. For condition I, the 1/4F d approximation slightly underestimates outlet polydispersity on the tail of the distribution, but for condition II the agreement is excellent across the full size distribution. Some discrepancy in the 1/4F d approximation may be expected at the extremities of the distribution where the predicted F d are lower. The effects described earlier associated with the skew of outlet distributions predicted by the t r –d matrix are exacerbated at low F d on the front and tail of the sample distribution.

Fig. 9
figure 9

Predicted outlet number polydispersities \( {\sigma}_d/{\overline{d}}_{\boldsymbol{n}} \) as functions of t r for programmed conditions I and II. Full black curves calculated from data in rows of t r –d matrices. Dashed red curves correspond to 1/4F d . The upper pair of curves correspond to condition I and the lower pair to condition II. Predicted particle elution curves for conditions I and II are shown as dash-dotted green and dashed blue curves, respectively

Full size image

Conclusions

The theory has been presented for predicting t r and F ϕ as functions of selective parameter ϕ for As-FlFFF where the cross flow rate as well as the inlet and outlet flow rates are allowed to vary with time. An estimation for the contribution to multipath bandspreading under programmed conditions was included where it was assumed that the multipath effect did not vary strongly along the channel length. It was shown that, under exponentially programmed decay of cross flow rate and constant outlet flow rate, the residual outlet polydispersity is very well approximated by 1/4F ϕ . This confirms the importance of basing the optimization of programmed flow rate conditions on the predicted fractionating power. This is especially true when online MALS or DLS detection is used to extract particle size or molecular weight information from the eluent. The use of online MALS or DLS detection in combination with guidance in the selection of programmed conditions firmly based on fundamental FFF theory is recommended. The quantitative information provided by light scattering can correct for small perturbations from ideal FFF theory and uncertainties in instrumental parameters (channel thickness, channel volume, carrier fluid temperature and viscosity, etc.), while the maximization of fractionating power ensures that the light scattering information is obtained under optimum conditions. A variety of cross flow decay programs have been employed for sample analyses. It will now be possible to examine the utility of these different programs by a comparison of the predicted F ϕ as functions of ϕ.