Introduction

Fourier-transform infrared spectroscopy (FTIR) is important in biomedical research and applications [1–6]. In addition to increasing FTIR-imaging activity, in particular for characterization of tissues, mid-infrared spectroscopy of biological fluids has been shown to reveal disease-specific changes in spectral signature, e.g. for bovine spongiform encephalopathy [7], diabetes mellitus [8], or rheumatoid arthritis [9].

In contrast with other diagnostic tests, in which the presence or absence of, for example, the characteristic immunological reaction of a biomarker can easily be recognized, detection of such a characteristic change in high-dimensional spectral data remains in the realm of multivariate data analysis and pattern recognition. Consequently, diagnostic tests which combine the spectroscopy, e.g. of molecular vibrations, with subsequent multivariate classification are often referred to as “disease pattern recognition” or “diagnostic pattern recognition” [8–10].

To ensure the high performance of such a test, the robustness of this diagnostic decision rule is of crucial importance. In chemometrics, popular means of removing irrelevant variation from the data and regularizing the classifier in ill-posed learning problems include subset selection of relevant spectral regions and use of linear models.

In this manuscript a hierarchical design of a classifier is proposed which combines these two concepts for detection of evidence of bovine spongiform encephalopathy (BSE) in infrared spectra of biofilms of bovine serum (Data section). A hierarchical decision rule is introduced which explicitly considers covariates in the data set, and which is based on random forests—a recently proposed ensemble classifier [11]—and its entropy-related measure of feature importance, the Gini importance (Classification section). We will illustrate how this algorithm differs from other feature-selection strategies and discuss the relevance of our findings to the given diagnostic task. Finally, we will compare the performance with results from other chemometric approaches using the same data set (Results and discussion section). We would like to point out that one strength of this manuscript is that feature selection and classification are judged by comparison with other methods on the basis of an identical data set.

Experiments and data

Six-hundred and forty-one serum samples were acquired from confirmed BSE-positive (210) or BSE-negative (211) cattle from the Veterinary Laboratory Agency (VLA),Weybridge, UK, and from BSE-negative cattle from a commercial abattoir in southern Germany (220). All BSE-positive samples originated from cattle in the clinical stage, i.e. the animals had clinical signs of BSE and were subsequently shown to be BSE-positive by histopathological examination. To the extent to which this information was available (approx. 1/3 of the samples), all the BSE-negative samples originated from animals which were neither suspected to suffer from BSE nor did they originate from a farm at which a BSE-infection had previously occurred. With 641 samples originating from 641 cows this data set is one of the largest ever studied by biomedical vibrational spectroscopy.

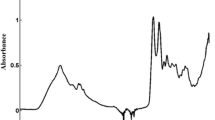
After thawing, 3 μL of each sample was pipetted on to each of three disposable silicon sample carriers using a modified Cobas Integra 400 instrumentFootnote 1 and left to dry, to reduce the strong infrared absorption of water. On drying, the serum samples formed homogenous films 6 mm in diameter and a few micrometers thick. Transmission spectra were measured using a Matrix HTS/XT spectrometer (Bruker Optics, Ettlingen, Germany) equipped with a DLATGS detector. Each spectrum was recorded in the wavenumber range 500–4000 cm−1, sampled at a resolution of 4 cm−1 (Fig. 1). Blackman–Harris three-term apodization was used and a zero-filling factor of 4 was chosen. Finally, a spectrum was represented by vector of length 3629. The three absorbance spectra from measurement of each sample were corrected individually for sample carrier background; further details are given elsewhere [12]. Subsequently the spectra were normalized to constant area (L1 normalization) in the region between 850 and 1500 cm−1 and the mean spectrum was calculated for each group of three. Final smoothing and subsampling by “binning” (averaging) over adjacent channels was subject to hyperparameter tuning on each binary subset of the data (using a single bin-width “bw” for the whole spectrum—see below). In contrast with other procedures in IR data processing, band and high-pass filters (for example Savitzky–Golay) were not applied.

Fig. 1
figure 1

Spectral data as a function of wavenumber; median (line) and quartiles (dots) of the two classes are indicated. Top: diseased (gray) and normal (black) groups. Bottom: Groups after channel-wise removal of the mean and a normalization to unit variance of the whole data set, as implicitly performed by most chemometric regression methods

Full size image

For teachingFootnote 2 of the classifier, 126 BSE-positive samples (from the VLA) and 355 BSE-negative samples (135 from the VLA, 220 from the German abattoir) were selected. Most of the teaching data were measured on a system at Roche Diagnostics, but 60 of the samples were measured on a second system located at the VLA, Weybridge [12]. A second, independent, data set, comprising the spectra of another 160 serum samples (84 positive, 76 negative, as randomly selected by the study site (the VLA), was reserved for validation; all of these were acquired and measured at the VLA). This validation data set was retained at Roche Diagnostic until teaching of the classifier was finalized. The classifier was then applied to the validation data and the classification results were reported to Roche Diagnostics, where final comparison with true (post-mortem) diagnosis of the validation data was conducted.

Classification

For the given data we defined eight binary subproblems, contrasting BSE-positive and negative samples that varied in one known covariate only (Fig. 2) such that each split between diseased and non-diseased specimens also represented a split over a maximum of one covariate within the data sets. On each binary subset we optimized preprocessing, feature selection (using Gini importance), and linear classification individually, and finally induced the decisions on the subsets in a second decision level (Fig. 3).

Fig. 2
figure 2

Scheme for the identification of binary subgroups. A classifier is trained to discriminate between pairs of “positives” and “negatives” which also differ by a maximum of one covariate (similarity in covariates is expressed by symbol or color)

Full size image
Fig. 3
figure 3

Architecture of the hierarchical classifier. For prediction a series of binary classification procedures is applied to each spectrum as a first step. The single classifiers of each subgroup (from left to right) are individually optimized in respect of preprocessing, feature extraction, and classification. To induce the final decision about the state of disease, a nonlinear classifier is applied to the binary output of all classifiers of the first level

Full size image

Concepts of both feature selection by random forests and the hierarchical classification scheme are presented first, followed by details of implementation and tuning procedures.

Feature selection by random forests

Decision trees are a very popular classifier in both biometry and machine learning, and have also found application in chemometric tasks (Ref. [13] and references cited therein). A decision tree splits the feature space recursively until each split holds training samples of one class only. A monothetic decision tree thus represents a sequence of binary decisions on single variables.

The pooled predictions of a large number of classifiers, trained on slightly different subsets of the teaching data, often outperform the decision of a single classification algorithm optimally tuned on the full data set. This is the idea behind ensemble classifiers. “Bootstrapping”, random sampling with replacement of the teaching data, is one way of generating such slightly differing training sets. “Random forest” is a recently proposed ensemble classifier that relies on decision trees trained on such subsets [11, 14]. In addition to bootstrapping, random forests also use another source of randomization to increase the “diversity” of the classifier ensemble: “random splits” [11] are used in the training of each single decision tree, restricting the search for the optimum split to a random subset of all features or spectral channels.

Random forests are a popular multivariate classifier which is benevolent to train, i.e. which yields results close to the optimum without extensive tuning of its parameters, and for which the classification performance is comparable with that of other algorithms, for example support vector machines, neural networks, or boosting trees, on several data sets [15]. Superior behavior on micro-array data, often resembling spectral data in sample size and feature dimensionality, has been reported [16–18]. This superior classification performance was not observed for our data set, however, and the initial training of a random forest on the binary subproblems of the hierarchical classification procedure serves a different purpose—it reveals information about the relevance of the spectral channels.

During training, the next split at the node of a decision tree (and thus the next feature) is chosen to minimize a cost function which rates the purity of the two subgroups arising from the split. Popular choices are the decrease in misclassification or, alternatively, in the Gini impurity, an empirical entropy criterion [19]. Both favor splits that separate the two classes completely—or at least result in one pure subgroup—and assign maximum costs, if a possible split cannot unmix the two classes at all (Fig. 4). Gini impurity and (cross-) entropy can be expressed formally in the two-class case as:

$$ \begin{array}{*{20}l} {{{\text{Gini}}\quad {\sum\nolimits_{i = 0,1} {p_{i} {\left( {1 - p_{i} } \right)}} }} \hfill} \\ {{{\text{Entropy}}\quad {\sum\nolimits_{i = 0,1} { - p_{i} \log {\left( {p_{i} } \right)}} }} \hfill} \\ \end{array} $$

with proportions p 0 and p 1 of samples from class 0 and class 1 within a separated subgroup.

Fig. 4
figure 4

Cost functions for an optimum split within a decision tree: Gini importance (circles), entropy (triangles), and classification error (boxes) as a function of the proportion of samples p from one of the two classes. Pure subsets which (after the splitting) contain one class only (p 1 = 0 and p 0 = 1) are assigned minimum costs and are favored, whereas splits which result in an evenly mixed situation (p 1 = p 0 = 0.5) are assigned the highest costs and, consequently, are avoided. As visible from the graph, the Gini importance is an approximation to the entropy which can be calculated without recourse to the computationally expensive logarithm (Ref. [19], p. 271)

Full size image

Recording the discriminative value of any variable chosen for a split during the classification process by the decrease in Gini impurity, and accumulating this quantity over all splits in all trees in the forest, leads to the Gini importance [11], a measure indicating which spectral channels were important at any stage during the teaching of the multivariate classifier. The Gini importance differs from the standard Gini gain, because it does not report the conditional importance of a feature at a certain node in the decision tree, but the contribution of a variable to all binary splits in all trees of the forest.

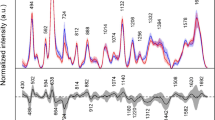
In practical terms, to obtain the Gini importance for a particular classification problem, a random forest is trained, and returns a vector which assigns an importance to each channel of the spectrum. This importance vector often resembles a spectrum itself (Fig. 5) and can be inspected and checked for plausibility. More importantly, it enables ranking of the spectral channels in a feature selection. In our hierarchical classification scheme (Fig. 3), the Gini importance is used to obtain an explicit feature selection on each binary subset in a wrapper approach together with a subsequent linear classification, e.g. by a (discriminative) partial least-squares regression or principal-component regression.

Fig. 5
figure 5

Importance measures on binary subset of the training data. Top: univariate tests for group differences, probabilities from T-test (black) and Wilcoxon–Mann–Whitney test (gray). Shown is the negative logarithm of the p-value—low entries indicate irrelevance, high values report high importance. Middle: random forest Gini importance (arbitrary units). Bottom: direct comparison of ranked Gini importance (black) and ranked T-score (gray). Horizontal dotted lines indicate optimum threshold on the Gini importance

Full size image

So, rather than using random forests as a classifier, we advocate the use of its feature importance to “upgrade” standard chemometric learners by feature selection according to the Gini importance measure.

Design of the hierarchical classifier

When a classifier is learned and its parameters are optimized on the training data, statistical learning often assumes independent and identically distributed samples. Experimental data do not, unfortunately, necessarily justify these ideal assumptions. Variations in the data and changes of the spectral pattern do not always correlate with the state of disease only. For the particular case under investigation, covariates such as breed of cattle or instrumental system-to-system variation also often result in notable changes of the spectrum.

As a consequence, differentiation between inter-class and intra-class variation becomes difficult for standard models which implicitly assume homogenous distributions of the two classes, e.g. as in linear discriminant analysis. Effects of covariates and external factors on the data and their characteristic changes of the spectra can be considered explicitly, however. If information about these confounding factors is available both during teaching and validation, and these factors can be used as input features to the classifier, a multilayered or stacked classification rule [20] can be designed to evaluate the combined information from spectra and factors appropriately (examples are given elsewhere [21, 22]). If information on covariates is available only during teaching, this information can still be leveraged in the design of the classifier. A mixture discriminant analysis (MDA) [19], for example, provides means of extending linear discriminant analysis to a nonlinear classifier. By introducing additional Gaussian probability distributions in the feature space, MDA enables one to explicitly model subgroups which are distinguished by different levels of the (discrete) external factors. The final decision is induced from the assessed probabilities, so—in a two-level architecture—the MDA is often also referred to as a “hierarchical mixture of experts” [19].

In the approach presented here, a similar hierarchical strategy is pursued. Instead of modeling probability distributions of subgroups, however, the decision boundaries between positive and negative (diseased and non-diseased) samples of the subgroups are taught directly (Fig. 2). In the feature space, this procedure generates several decision planes which partition the space into several high-dimensional regions. Samples within a certain region are coded by a specific binary sequence, according to the outcome of all binary classifiers of this first step. A second classifier, assigning a class label to each of these volumes, is trained on these binary codes and provides a final decision about the state of the disease. Two-layer-perceptrons are based on similar concepts. In the hierarchical rule presented here the binary decisions of the first level are, nevertheless, explicitly adapted to interclass differences of subgroups defined by the covariates and, in the second level, a nonlinear classifier is employed (Fig. 3) to ensure separability of nonlinear problems in a two-level design also. To this end, we used a method which is particularly suited to inducing decisions on categorical and binary data, namely binary decision trees. Considering the high variability of single-decision trees, we have also preferred to use the random forests ensemble at this stage. Thus we have obtained an approximation to the posterior probability, rather than the dichotomous decision of the single decision tree, as the final decision of our hierarchical classifier.

Overall, compared with the generative MDA and the discriminative perceptron, both of which enable sound optimization of the classification algorithm in a global manner, the hierarchical approach presented here is a mere ad-hoc rule. The hierarchical design, however, enables the tuning of all three steps of the data processing—preprocessing, feature selection, and classification—individually and explicit consideration of knowledge about the covariates in the data.

Implementation and training

The origin of the samples and the two instrumental systems in England and Germany were regarded as covariates within the data set. The subgroups comprised between 40 and 421 samples, with a median of 130.5.

For each binary subproblem, a number of factors in preprocessing, feature selection and classification were tested and optimized individually, in a global tuning procedure. The performance was assessed by tenfold cross-validation of the classification error using the teaching set only. The following factors (bw, P sel, Cl meth) were considered: in preprocessing, binning was tested from one to ten channels (bw = 1, 3, 5, 10) to obtain downsampled and smoothed feature vectors. In the feature selection, random forests learned on all binary subsets (using the implementation of Ref. [23] with the values: mtry = 60, nodesize = 1, 3000 trees). Data sets were defined which comprised the top 5%, 10%, and 15% of the input features, ranked according to the Gini importance obtained (resulting in a test set comprising between 19 and 544 spectral features P sel, depending on the preceding binning). For classification, partial least-squares (PLS), principal-component regression (PCR), ridge regression (also termed penalized or robust discriminant analysis), and standard linear discriminant analysis (LDA) were tested (Cl meth=PLS, PCR, ridge, LDA). For these classifiers, the optimum split parameter was adapted according to the least fit error on the training set and the respective hyperparameters (PLS and PCA dimensionality λ=1...12, ridge penalty λ = 2−5...5 [19]) were tuned by additional internal tenfold crossvalidation.

After the optimum parametrization was found in the first level, all binary classifiers were trained on their respective subsets and their binary predictions on the rest of the data set were recorded. Predictions for the samples of the subsets themselves were determined by tenfold cross-validation. The outcome of this procedure was a set of binary vectors of length eight as compact representations for each spectrum of the teaching data. A nonlinear classifier was trained on these vectors (random forest, initial experiments with bagging trees yielded similar results) and optimized according to the out-of-bag classification error.

All computing was performed using the programming language R [24] and libraries which are freely available from cran.r-project.org, in particular the randomForest package [23]. On a standard PC training of the random forest was performed within seconds. Tuning of all 8*4*3*4 combinations of the predefined factor levels was performed in hours. When the design of the hierarchical classifier was fixed, the training was done in minutes and final classification of the blinded validation data was performed (nearly) instantaneously.

Results and discussion

Feature selection

To compare the Gini importance with standard measures, univariate statistical tests were also applied to the data of the binary subproblems (Fig. 5). Differences between the model-based T-test and a nonparametric Wilcoxon–Mann–Whitney test are hardly noticeable (a representative example is given in Fig. 5, top). Spectral channels with an obvious separation between diseased and non-diseased channels (Fig. 1, bottom) usually also score high in multivariate Gini importance. Differences become easily visible, however, when ranking the spectral channels according to multivariate Gini importance and p-values of the univariate tests (Fig. 5, bottom). Regions which had a complete overlap between the two classes (Fig. 1, bottom), and therefore no importance at all according to the univariate tests, were often considered to be highly relevant by the multivariate measure (compare Figs. 1 and 5: e.g. 1300 cm−1, 3000 cm−1), indicating higher-order dependencies between variables. Conversely, regions for which there were only slight drifts in the baseline were assigned modest to high importance by the rank-ordered univariate measures, although known to be irrelevant biochemically (Fig. 5, 1800–2700 cm−1). Compared with the selection of the multivariate classifiers from Ref. [12], as obtained on the same data set, similarities between the optimum selections from the Gini importance and the earlier results could be observed (Fig. 6, bottom).

Fig. 6
figure 6

Spectral regions chosen by the different classification strategies, along the frequency axis. Top: Histogram (frequency, see bar on the right) of channel selection by random forest importance on one of the eight subproblems (RF). Bottom: selection of classifiers from Ref. [12], linear discriminant analysis (LDA), robust discriminant analysis (R-LDA), support vector machines (SVM), artificial neural networks (ANN)

Full size image

All linear classifiers in the first level of the hierarchical rule differed in the effect of the covariates on their respective subproblem. All were optimized to separate diseased and non-diseased samples, however. So, inspecting the regions that were chosen by most (≥50%) of the binary subgroup classifiers should primarily reveal disease-specific differences (Fig. 6). Highly relevant regions are found around 1030 cm−1, which is known to be a characteristic absorption of carbohydrates, and at 2955 cm−1, i.e. the asymmetric C−H stretch vibration of −CH3 in fatty acids, in agreement with earlier studies [3, 12, 25, 6]. Other major contributions can be found at 1120, 1280, 1310, 1350, 1460, 1500, 1560, and 1720 cm−1 (Fig. 6).

Classifier

Ridge regression yielded the best results for most of the binary classification subproblems during teaching of the classifiers. On average it performed 1–2% better than PLS, PCR, and LDA (usually in this order). The comparably poor performance of LDA, i.e. the unregularized version of the ridge in a binary classification, indicates that even after binning and random forest selection, the data were still highly correlated. To keep the architecture of the hierarchical classifier as simple as possible, ridge regression was fixed for all binary class separations in the first level.

Parameters for binning and feature selection were chosen individually for each subproblem, comprising 5–10% percent of the features after a binning by five or ten channels. The high level of binning reflects the impact of apodization and zero-filling, spectrometer resolution, and, in particular, the typical linewidths of the spectral signatures of ∼10 cm−1. This reduced the dimensionality of the classification problem by up to two orders of magnitude for all subproblems (19 to 106 features, median 69), compared with 3629 data points in each original spectrum.

The final training yielded a sensitivity of 92% and a specificity of 96% within the training set (out-of-bag error of the random forest in the second level).

Validation

After having applied the classifier to the pristine validation data set, unblinding revealed that 77 of 84 serum samples originating from BSE-positive cattle and 72 of 76 samples originating from BSE-negative cattle were identified correctly. Numerically, these numbers correspond to sensitivity of 92% and specificity of 95%. A slight improvement can be found compared with two of the four individual classifiers in Ref. [12], i.e. linear discriminant analysis with features selected by genetic optimization and robust linear discriminant analysis (Table 1). Results are comparable with or slightly better than those from the neural network or the support vector machine. Preliminary results from a subsequent test of all five classifiers on a larger data set (220 BSE-positive samples, 194 BSE-negatives) confirm this tendency of the random forest-based classifier.

Table 1 Sensitivity and specificity of classifiers from Ref. [12] and from random forest-based hierarchical rule (RF), when applied to the independent validation set (84 BSE-positive, 76 BSE-negative)
Full size table

On this data set the hierarchical classifier performs nearly as well as the meta classifier from Ref. [12] which combines the decisions of all four classifiers (Table 1). When extending the meta rule by the decisions of the classifier presented in this manuscript, the diagnostic pattern recognition approach achieved specificity of 93.4% and sensitivity of 96.4%. Comparing these numbers with the results presented in Ref. [12] we find an increase in sensitivity at the expense of a decrease in specificity. Of course, this desirable exchange of sensitivity and specificity depends on the particular choice of the decision rule and we had stringently followed the rule set up in Ref. [12] to enable unbiased comparison.

Conclusions

A hierarchical classification architecture is presented as part of serum-based diagnostic pattern-recognition testing for BSE. The classification process is separated in decisions on subproblems arising from the effect of covariates on the data. In a first step, all procedures in data processing—preprocessing, feature selection, linear classification—are optimized individually for each subproblem. In a second step, a nonlinear classifier induces the final decision from the outcome of these sub-classifiers. Compared with other established chemometric classification methods, this approach performed comparably or better on the given data.

The use of the random forest Gini importance as a measure of the contribution of each variable to a multivariate classification process enables feature ranking which is rapid and computationally efficient compared with other global optimization schemes. Beside its value in diagnostic interpretation of the importance of certain spectral regions, the methods readily allow for an additional regularization of any standard chemometric regression method by a multivariate feature selection.