Unconditional stability and convergence of Crank–Nicolson Galerkin FEMs for a nonlinear Schrödinger–Helmholtz system

Abstract

The paper is concerned with the unconditional stability and optimal $L^2$ error estimates of linearized Crank–Nicolson Galerkin FEMs for a nonlinear Schrödinger–Helmholtz system in ${\mathbb {R}}^d$ ($d=2,3$). By introducing a corresponding time-discrete system, we separate the error into two parts, i.e., the temporal error and the spatial error. Since the latter is $\tau$-independent, the uniform boundedness of numerical solutions in $L^{\infty }$-norm follows an inverse inequality immediately without any restrictions on time stepsize. Then, optimal error estimates are obtained in a routine way. Numerical examples in both two and three dimensional spaces are given to illustrate our theoretical results.

1 Introduction

A generalized nonlinear Schrödinger type system is defined by

$$\begin{aligned}&\text {i}u_t+\Delta u+\psi f(|u|)u+l(|u|)u=0, \end{aligned}$$

(1.1)

$$\begin{aligned}&\alpha \psi -\beta ^2 \Delta \psi =f(|u|)|u|^2, \end{aligned}$$

(1.2)

for $t\in [0,T]$, with the initial condition

$$\begin{aligned}&u(x,0)=u_0(x), \end{aligned}$$

(1.3)

where $\text {i}=\sqrt{-1}$, $\alpha$, $\beta$ are real nonnegative constants with $\alpha +\beta \ne 0$, and f, l are two given real-valued continuous functions. The above system may describe many different physical phenomena in optics, quantum mechanics, and plasma physics. The system defines the Schrödinger–Poisson–Slater model [4, 36, 45] when $\alpha =0$, $f(|u|)=c$, and the Schrödinger–Poisson model if $l=0$ and $\alpha =0$ [6, 16, 20, 27,28,29]. When $\beta =0$, the system reduces to a generalized nonlinear Schrödinger (GNLS) equation [1, 31, 32, 35]. Besides, the system (1.1)–(1.3) was called a Schrödinger–Helmholtz system in [10] when $l=0$.

Mathematical analysis for various Schrödinger type equations has been well studied, e.g., see [5, 37] and references therein. In [4, 20, 29, 36], the Schrödinger–Poisson type equations were analyzed by several authors and the existence and uniqueness of solutions in ${\mathbb {R}}^d$ ($d=1,2,3$) were proved. Cao et al. introduced a Schrödinger–Helmholtz system in [10] as a regularization of the generalized nonlinear Schrödinger equation, and studied local and global existence of a unique solution of the system. On the other hand, numerical methods and analysis for nonlinear Schrödinger type equations (system) have also been investigated extensively, e.g., see [8, 25, 33, 39] for finite difference methods, [2, 6, 19, 34, 42, 47] for finite element methods, [4, 7, 13, 28] for spectral methods and [1, 24, 27] for others. Akrivis et al. [2] presented several Crank–Nicolson Galerkin FEMs for the GNLS equation. To obtain optimal $L^2$ error estimates, the authors studied a truncated system with a classical energy method, which required to estimate the numerical solution of the truncated system in $L^{\infty }$-norm. A time-step condition $\tau =o(h^{d/4})$ ($d=2,3$) arose immediately for both nonlinear schemes and linearized schemes when an inverse inequality was used as usual, where $\tau$ and h were the stepsize in the temporal direction and the spatial direction, respectively. Later, Tourigny [42] proved optimal $H^1$ error estimates of both implicit backward Euler and Crank–Nicolson Galerkin finite element schemes for the GNLS equation. The work was based on a nonlinear stability theory introduced in [26], which resulted in time-step conditions $\tau =o(h^{d/2})$ and $\tau =o(h^{d/4})$ ($\ d=1,2,3$) for backward Euler and Crank–Nicolson schemes, respectively. Similarly, the optimal error estimates of finite difference methods have been done in [3, 34, 43] under certain time-step conditions. Chang et al. [11] presented systematic numerical investigations of several frequently-used finite difference schemes for the GNLS equation. Numerical results indicated that a linearized Crank–Nicolson scheme was more efficient. Wang et al. [43] studied this linearized scheme for a coupled cubic Schrödinger system. They obtained optimal $L^2$ error estimates by an energy method in one dimensional space when $\tau =o(h^{1/4})$. The stronger restriction $\tau =o(h^{d/4})$ is needed when applying their method in ${\mathbb {R}}^d,\ d=2,3$. More recently in [38], we studied two linearized Crank–Nicolson finite difference schemes for the coupled cubic Schrödinger system in three dimensional space. We established optimal $L^2$ error estimates of schemes unconditionally by making good use of both imaginary and real parts of the error equations.

Linearized schemes usually show better performance to deal with nonlinear partial differential equations, since one only needs to solve a linear system at each time step. The analysis of linearized schemes for a variety of nonlinear physical equations (system) can be found in the literatures, e.g., see [9, 12, 14, 17, 18, 30, 40, 44] and references therein. In these previous works, optimal error estimates were obtained with certain time-step restrictive conditions, which make practical computation extremely time-consuming, especially for a non-uniform mesh. Recently, Li and Sun studied a linearized backward Euler Galerkin FEM for a nonlinear thermistor system in [22]. They proposed an error splitting technique based on the corresponding time-discrete system. With a priori estimates of solutions for the time-discrete system, optimal error estimates of the method were obtained unconditionally. Moreover, the method was used in [23] for a nonlinear equation from incompressible miscible flows in porous media, in which, the same backward Euler scheme as in [22] and a low-order Galerkin-mixed FEM was used. Analysis presented in [23] required a strong regularity for the domain.

In this paper, we present two linearized Crank–Nicolson Galerkin FEMs for the complex Schrödinger type equations (1.1)–(1.3) and provide unconditionally optimal $L^2$ error estimates in both two and three dimensional spaces. For nonlinear complex PDEs, analysis for Crank–Nicolson schemes is usually much more complicated than that for Euler schemes, since the error in an energy-norm in Crank–Nicolson schemes is defined by an average of those at two consecutive time levels. Thus, the nonlinear term which is often defined in terms of classical extrapolation may not be easily controlled. The key to theoretical analysis is the boundedness of numerical solutions in $L^{\infty }$-norm. Following the splitting technique proposed in [22], also see [21], we introduce a time-discrete system. With the required regularity for solutions ($U^n$) of the time-discrete system, the fully discrete Galerkin FEM solution is bounded by

$$\begin{aligned} \Vert U^n_h \Vert _{L^{\infty }}&\le \Vert R_h U^n \Vert _{L^\infty } + \Vert U^n_h - R_h U^n \Vert _{L^\infty }\nonumber \\&\le \Vert R_h U^n \Vert _{L^\infty } + C h^{-d/2} \Vert U_h^n-R_h U^n\Vert _{L^2}\nonumber \\&\le C + C h^{-d/2} h^2\nonumber \\&\le C \, , \end{aligned}$$

(1.4)

where $U_h^n$ is the finite element solution of (1.1) and $R_h$ is a Ritz projection operator. With the boundedness, unconditionally optimal $L^2$ error estimates of fully discrete Galerkin FEMs of degree r ($r\ge 1$) can be obtained in a routine way.

The rest of the paper is organized as follows. In Sect. 2, we present two linearized Crank–Nicolson finite element schemes for the Schrödinger type equations (1.1)–(1.3) and our main results. The corresponding time-discrete scheme is then introduced, with which, the error function is separated into two parts: the temporal error function and the spatial error function. In Sect. 3, we obtain the uniform boundedness of numerical solutions in $L^{\infty }$-norm and establish optimal $L^2$ error estimates unconditionally. Finally, three numerical examples are given in Sect. 4 to illustrate our theoretical results, i.e. the optimal convergence rate and unconditional stability (convergence).

2 The main results

In this paper, we study the Schrödinger type equations (1.1)–(1.3) defined in a bounded and convex (or smooth) polygon $\Omega \in {\mathbb {R}}^2$ (or polyhedron in ${\mathbb {R}}^3$), with homogenous boundary conditions $u=\psi =0$ on $\partial \Omega$. Some remarks for problems in an infinite domain will be given in the conclusion part. For simplicity, we only consider the case $l(|u|)=0$, since this term will not add any further difficulty in the analysis. For this case, the system reduces to the Schrödinger–Helmholtz system [10].

In this section, we present two linearized Crank–Nicolson schemes with r-order ($r\ge 1$) Galerkin FEM approximation in the spatial direction. Some notations are introduced below.

Following classical FEM theory [41, 46], we define ${\mathcal {T}}_h$ to be a quasiuniform partition of $\Omega$ into triangles in ${\mathbb {R}}^2$ or tetrahedrons in ${\mathbb {R}}^3$, and $h=\max _{\pi _h\in {\mathcal {T}}_h}\{\text {diam}\pi _h\}$ denotes the mesh size. Let $V_h$ be the finite-dimensional subspace of $H_0^1(\Omega )$, which consists of continuous piecewise polynomials of degree r ($r\ge 1$) on ${\mathcal {T}}_h$. We define $\Omega _\tau =\{t_n|t_n=n\tau ;0\le n\le N \}$ to be a uniform partition of [0, T] with the time step $\tau =T/N$, and $t_{n-\frac{1}{2}}=\frac{1}{2}(t_n+t_{n-1})$. Let $u^m=u(x,t_m),\ \psi ^m=\psi (x,t_m)$. For a sequence of functions $\{\omega ^n \}_{n=0}^N$, we denote

$$\begin{aligned} D_{\tau }\omega ^n&=\frac{\omega ^n-\omega ^{n-1}}{\tau },\quad {{\overline{\omega }}}^{n-\frac{1}{2}}=\frac{1}{2}\left( \omega ^n+\omega ^{n-1}\right) ,\quad n=1,2,\ldots ,N, \\ {{\widehat{\omega }}}^{n-\frac{1}{2}}&= \frac{1}{2}\left( 3\omega ^{n-1}-\omega ^{n-2}\right) ,\quad n=2,\ldots ,N. \end{aligned}$$

We define the $L^2(\Omega )$ inner product by

$$\begin{aligned} (u,v)=\int _{\Omega } u(x)\left( {v(x)}\right) ^{*}\text {d}x, \end{aligned}$$

where $u,\ v$ are any two complex functions in $L^2(\Omega )$, and $v^*$ denotes the conjugate of v.

With these notations, a semi-implicit linearized Crank–Nicolson Galerkin FEM is: to seek $U_h^n,\ \Psi _h^{n-\frac{1}{2}}\in V_h$ such that

$$\begin{aligned}&\text {i}\left( D_{\tau }U_h^n, v \right) -\left( \nabla {{\overline{U}}}_h^{n-\frac{1}{2}},\nabla v \right) +\left( \Psi _h^{n-\frac{1}{2}}f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) {{\overline{U}}}_h^{n-\frac{1}{2}},v \right) =0, \end{aligned}$$

(2.1)

$$\begin{aligned}&\alpha \left( \Psi _h^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla \Psi _h^{n-\frac{1}{2}},\nabla \varphi \right) =\left( f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| ^2,\varphi \right) \end{aligned}$$

(2.2)

for any $v,\varphi \in V_h$ and $n=1,2,\ldots ,N$, where a standard extrapolation [15] is used for the nonlinear terms. ${{\widehat{U}}}_h^{\frac{1}{2}}$ is defined to be the solution of the following equation

$$\begin{aligned} \text {i}\left( \frac{{{\widehat{U}}}_h^{\frac{1}{2}}-U_h^0}{\tau /2},v \right) -\left( \nabla {{\widehat{U}}}_h^{\frac{1}{2}},\nabla v \right) +\left( \Phi _h^0f(|U_h^0|){{\widehat{U}}}_h^{\frac{1}{2}},v \right) =0 \end{aligned}$$

(2.3)

where $U_h^0=\Pi _h u_0$, $\Psi _h^0$ satisfies

$$\begin{aligned} \alpha \left( \Phi _h^0,\varphi \right) +\beta ^2\left( \nabla \Phi _h^0,\nabla \varphi \right) =\left( f(|u_0|)|u_0|^2,\varphi \right) . \end{aligned}$$

(2.4)

Here, $\Pi _h$ is an interpolation operator. It is easy to see that $U_h^n$ satisfies the mass conservation, i.e.,

$$\begin{aligned} \Vert U_h^n\Vert _{L^2}\equiv \Vert U_h^0\Vert _{L^2},\quad 1\le n\le N. \end{aligned}$$

(2.5)

With an explicit treatment of the nonlinear terms, an alternative linearized Crank–Nicolson Galerkin scheme can be defined by

$$\begin{aligned}&\text {i}\left( D_{\tau }U_h^n, v \right) -\left( \nabla {{\overline{U}}}_h^{n-\frac{1}{2}},\nabla v \right) +\left( {{\widehat{\Psi }}}_h^{n-\frac{1}{2}} f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) {{\widehat{U}}}_h^{n-\frac{1}{2}}, v \right) =0, \end{aligned}$$

(2.6)

$$\begin{aligned}&\alpha \left( {{\overline{\Psi }}}_h^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla {{\overline{\Psi }}}_h^{n-\frac{1}{2}},\nabla \varphi \right) =\left( f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| ^2, \varphi \right) \end{aligned}$$

(2.7)

for any $v,\varphi \in V_h$, where ${{\widehat{U}}}_h^{\frac{1}{2}}$ is the solution of (2.3) and ${{\widehat{\Psi }}}_h^{\frac{1}{2}}$ satisfies

$$\begin{aligned} \alpha \left( {{\widehat{\Psi }}}_h^{\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla {{\widehat{\Psi }}}_h^{\frac{1}{2}},\nabla \varphi \right) =\left( f\left( \left| {{\widehat{U}}}_h^{\frac{1}{2}}\right| \right) \left| {{\widehat{U}}}_h^{\frac{1}{2}}\right| ^2,\varphi \right) . \end{aligned}$$

(2.8)

At each time step of the scheme (2.1)–(2.2), one has to solve (2.2) for $\Psi _h^{n-\frac{1}{2}}$ first, and then (2.1) for $U_h^n$. However, for the second scheme (2.6)–(2.7), one only needs to solve the two equations simultaneously for $U_h^n$ and $\Psi _h^n$ at each time step. In this paper, we only present the theoretical analysis for the first linearized scheme (2.1)–(2.3). The analysis of the second linearized scheme (2.6)–(2.7) can be obtained analogously.

Here, we assume that $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is locally Lipschitz continuous, i.e., for any $s_1,s_2\in [-K^*,K^*]$,

$$\begin{aligned} |f(s_1)-f(s_2)| \le L_{K^*} |s_1-s_2|, \end{aligned}$$

(2.9)

where $L_{K^*}$ is the Lipschitz constant dependent on $K^*$. We also assume that the solution to the problem (1.1)–(1.3) exists and satisfies

$$\begin{aligned}&\Vert u_0 \Vert _{H^{r+1}} +\Vert u\Vert _{L^{\infty }((0,T);H^{r+1})}+ \Vert u_t\Vert _{L^{2}((0,T);H^{r+1})} +\Vert u_{tt}\Vert _{L^2((0,T);H^2)}\nonumber \\&\quad +\Vert u_{ttt}\Vert _{L^2((0,T);L^2)} +\Vert \psi \Vert _{L^{\infty }((0,T);H^{r+1})} \le K. \end{aligned}$$

(2.10)

We present our main results in the following theorem and the proof will be given in Sect. 3.

Theorem 2.1

Suppose that the system (1.1)–(1.3) has unique solutions u, $\psi$ satisfying (2.10). Then the finite element system defined in (2.1)–(2.3) has unique solutions $U_h^m$ and $\Psi _h^{m-\frac{1}{2}}$, $m=1,\ldots ,N$. Moreover, there exists $\tau _0>0$ such that when $\tau \le \tau _0$,

$$\begin{aligned} \Vert u^{m}-U_h^m\Vert _{L^2} +\left\| \psi ^{m-\frac{1}{2}}-\Psi _h^{m-\frac{1}{2}}\right\| _{L^2} \le C_0\left( \tau ^2+h^{r+1}\right) . \end{aligned}$$

(2.11)

where $C_0$ is a positive constant dependent on K and independent of $\tau$, h and N.

In our proof, the following lemma is useful.

Lemma 2.1

Let $\{ \omega ^n\}_{n=0}^N$ and $\{v^n \}_{n=0}^N$ be two sequences of functions in $\Omega$. Then

$$\begin{aligned}&\Vert \omega ^n\Vert \le 2 \sum _{m=1}^n \Vert {{\overline{\omega }}}^{m -\frac{1}{2}} \Vert +\Vert \omega ^0\Vert , \end{aligned}$$

(2.12)

for any norm $\Vert \cdot \Vert$, and

$$\begin{aligned} \sum _{m=1}^n \omega ^m {{\overline{v}}}^{m -\frac{1}{2}} =\frac{1}{2}\omega ^1 v^0 +\sum _{m=2}^n {{\overline{\omega }}}^{m -\frac{1}{2}} v^{m-1} +\frac{1}{2} \omega ^n v^n. \end{aligned}$$

(2.13)

To prove Theorem 2.1, we introduce a time-discrete system

$$\begin{aligned}&\alpha \Psi ^{n-\frac{1}{2}}-\beta ^2\Delta \Psi ^{n-\frac{1}{2}} =f(|{{\widehat{U}}}^{n-\frac{1}{2}}|) |{{\widehat{U}}}^{n-\frac{1}{2}}|^2, \end{aligned}$$

(2.14)

$$\begin{aligned}&\text {i}D_{\tau }U^{n}+\Delta {{\overline{U}}}^{n-\frac{1}{2}} +\Psi ^{n-\frac{1}{2}}f(|{{\widehat{U}}}^{n-\frac{1}{2}}|) {{\overline{U}}}^{n-\frac{1}{2}}=0, \end{aligned}$$

(2.15)

with the initial and boundary conditions

$$\begin{aligned} U^0(x)&=u_0(x),\quad \text {in}\ \Omega ,\nonumber \\ U^n(x)&=0,\quad \Psi ^{n-\frac{1}{2}}(x)=0, \quad \text {on}\ \partial \Omega , \end{aligned}$$

(2.16)

for $n=1,2,\ldots ,N$, where ${{\widehat{U}}}^{\frac{1}{2}}$ is the solution of the following system

$$\begin{aligned}&\text {i}\frac{{{\widehat{U}}}^{\frac{1}{2}}-U^0}{\tau /2} +\Delta {{\widehat{U}}}^{\frac{1}{2}} +\Psi ^0f(|U^0|){{\widehat{U}}}^{\frac{1}{2}}=0, \end{aligned}$$

(2.17)

$$\begin{aligned}&{{\widehat{U}}}^{\frac{1}{2}}(x)=0 , \quad \text {on}\ \partial \Omega , \end{aligned}$$

(2.18)

and $\Psi ^0=\psi ^0$ satisfies the Eq. (1.2) at $t=t_0$. By the homogeneous Dirichlet boundary condition $\psi =0$ on $\partial \Omega$, the classical theory of PDEs shows the boundedness of $\Vert \Psi ^0\Vert _{L^\infty }$. Also, it is easy to see that $U^n$ satisfies the mass conservation, i.e.

$$\begin{aligned} \Vert U^n\Vert _{L^2}\equiv \Vert U^0\Vert _{L^2}, \end{aligned}$$

(2.19)

for $1\le n\le N$, and ${{\widehat{U}}}^{\frac{1}{2}}$ satisfies $\Vert {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^2}\le \Vert U^0\Vert _{L^2}$. As proposed in [22, 23], we separate the errors into two parts

$$\begin{aligned} \Vert u^n-U_h^n\Vert _{L^2}&\le \Vert u^n-U^n\Vert _{L^2}+\Vert U^n-U_h^n\Vert _{L^2}, \end{aligned}$$

(2.20)

$$\begin{aligned} \left\| \psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2}&\le \left\| \psi ^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}}\right\| _{L^2} +\left\| \Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2} \, . \end{aligned}$$

(2.21)

Under the splitting, we will prove that the first term in the right-hand side of each above inequality is bounded by $O(\tau ^2)$ and the second term is bounded by $O(h^{2})$, with which, classical inverse inequality and induction assumption, we can obtain the uniform boundedness of numerical solution $U_h^n$ in $L^{\infty }$-norm. Then, the optimal error estimates can be easily proved by a routine method.

For the simplicity of notations, we denote by $C_K$ a generic positive constant, which is independent of $n,\ h,\ \tau$ and $C_0$ and dependent upon $\alpha$, $\beta$, f and K given in (2.10), and which could be different in different places. Also we denote by C a generic positive constant involved in some classical inequalities, such as Gagliardo–Nirenberg inequality and inequalities for standard interpolation and Ritz projection, which depend only upon the domain $\Omega$ and the partition ${\mathcal {T}}_h$ in general.

3 The proof of Theorem 2.1

We analyze the error functions $u^n-U^n$ and $\psi ^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}}$, $U^n-U_h^n$ and $\Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}$, respectively, in the following two subsections.

3.1 Temporal error analysis

Under the regularity assumption (2.10), we define

$$\begin{aligned} K_0:=\max _{0\le n\le N}\Vert u^n\Vert _{L^{\infty }} +\Vert {{\widehat{u}}}^{\frac{1}{2}}\Vert _{L^{\infty }} +1, \end{aligned}$$

(3.1)

where ${{\widehat{u}}}^{\frac{1}{2}}:=u^{\frac{1}{2}}=u(x,t_{\frac{1}{2}})$, and $K_0$ is a positive constant dependent on K and independent of $\tau$, h and n. Let

$$\begin{aligned} e^n=u^n-U^n,\quad \theta ^{n-\frac{1}{2}} =\psi ^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}}. \end{aligned}$$

From (2.14)–(2.15) and (1.1)–(1.2), we can derive the error equations of $e^n$ and $\theta ^{n-\frac{1}{2}}$:

$$\begin{aligned}&\alpha \theta ^{n-\frac{1}{2}}-\beta ^2\Delta \theta ^{n-\frac{1}{2}} =G_1^{n-\frac{1}{2}}+Q^{n-\frac{1}{2}}, \end{aligned}$$

(3.2)

$$\begin{aligned}&\text {i}D_{\tau }e^{n}+\Delta {{\overline{e}}}^{n-\frac{1}{2}} +R_1^{n-\frac{1}{2}} =P^{n-\frac{1}{2}}, \end{aligned}$$

(3.3)

for $n=1,2,\ldots ,N$, where

$$\begin{aligned} G_1^{n-\frac{1}{2}}&=f\left( |{{\widehat{u}}}^{n-\frac{1}{2}}|\right) |{{\widehat{u}}}^{n-\frac{1}{2}}|^2 -f\left( |{{\widehat{U}}}^{n-\frac{1}{2}}|\right) |{{\widehat{U}}}^{n-\frac{1}{2}}|^2, \end{aligned}$$

(3.4)

$$\begin{aligned} R_1^{n-\frac{1}{2}}&=\psi ^{n-\frac{1}{2}}f\left( |{{\widehat{u}}}^{n-\frac{1}{2}}|\right) {{\overline{u}}}^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}} f\left( |{{\widehat{U}}}^{n-\frac{1}{2}}|\right) {{\overline{U}}}^{n-\frac{1}{2}}, \end{aligned}$$

(3.5)

and $Q^{n-\frac{1}{2}}$, $P^{n-\frac{1}{2}}$ are truncation errors. Moreover, ${{\widehat{e}}}^{\frac{1}{2}}:= {{\widehat{u}}}^{\frac{1}{2}}-{{\widehat{U}}}^{\frac{1}{2}}$ satisfies

$$\begin{aligned} \text {i}\frac{{{\widehat{e}}}^{\frac{1}{2}}}{\tau /2} +\Delta {{\widehat{e}}}^{\frac{1}{2}} +\Psi ^0f(|u^0|){{\widehat{e}}}^{\frac{1}{2}} ={{\widehat{P}}}^{\frac{1}{2}}, \end{aligned}$$

(3.6)

where ${{\widehat{P}}}^{\frac{1}{2}}$ is the truncation error at the initial step (2.3). By Taylor expansion, we have

$$\begin{aligned} \Vert {{\widehat{P}}}^{\frac{1}{2}}\Vert _{L^2}&\le C\tau \Vert u_{tt}\Vert _{L^\infty ((0,T);L^2)}, \end{aligned}$$

(3.7)

$$\begin{aligned} \Vert Q^{n-\frac{1}{2}}\Vert _{L^2} +\left( \sum _{n=1}^N \tau \Vert P^{n-\frac{1}{2}}\Vert _{L^2}^2\right) ^{\frac{1}{2}}&\le C\tau ^2(\Vert u_{ttt}\Vert _{L^2((0,T);L^2)}+\Vert u_{tt}\Vert _{L^2((0,T);H^2)}). \end{aligned}$$

(3.8)

Theorem 3.1

Suppose that the system (1.1)–(1.3) has unique solutions u, $\psi$ satisfying (2.10). Then, there exists $\tau _0^*>0$ such that when $\tau \le \tau _0^*$, the time-discrete system (2.14)–(2.15) has unique solutions $U^m$ and $\Psi ^{m-\frac{1}{2}}$, $m=1,\ldots ,N$, satisfying

$$\begin{aligned}&\Vert e^m\Vert _{L^2} +\Vert \theta ^{m-\frac{1}{2}}\Vert _{L^2}\le C_0^* \tau ^2, \end{aligned}$$

(3.9)

$$\begin{aligned}&\tau \Vert D_{\tau } U^m\Vert _{H^2} + \Vert D_{\tau } {{\overline{U}}}^{m-\frac{1}{2}}\Vert _{H^2} +\Vert U^m\Vert _{H^2} +\Vert \Psi ^{m-\frac{1}{2}}\Vert _{H^2} \le C_0^+, \end{aligned}$$

(3.10)

where $C_0^*$ and $C_0^+$ are positive constants dependent on K and independent of $\tau$, h, N and $C_0$.

Proof

The time-discrete Eqs. (2.14)–(2.15) are actually linear elliptic equations, and the existence and uniqueness of solutions follow the classical theory of elliptic PDEs and the mass conservation (2.19). Before studying (3.9)–(3.10), we use mathematical induction to prove the following estimate

$$\begin{aligned} \Vert e^m\Vert _{L^\infty }\le \tau ^{\frac{1}{4}} \end{aligned}$$

(3.11)

for $m=1,2,\dots ,N$.

First we estimate the initial error. We multiply (3.6) by $({{\widehat{e}}}^{\frac{1}{2}})^*$, integrate it over $\Omega$ and then, take the imaginary part of the resulting equation to get

$$\begin{aligned} \Vert {{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^2} \le \frac{\tau }{2}\Vert {{\widehat{P}}}^{\frac{1}{2}}\Vert _{L^2} \le C_K\tau ^2, \end{aligned}$$

where we have used (3.7). From (3.6), we see that

$$\begin{aligned} \Vert \Delta {{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^2} \le \frac{2}{\tau }\Vert {{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^2} +\Vert \Psi ^0f(|u^0|){{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^2} +\Vert {{\widehat{P}}}^{\frac{1}{2}}\Vert _{L^2} \le C_K\tau . \end{aligned}$$

(3.12)

The above result implies

$$\begin{aligned} \Vert {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^{\infty }}&\le \Vert {{\widehat{u}}}^{\frac{1}{2}}\Vert _{L^{\infty }} +\Vert {{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^{\infty }} \le \Vert {{\widehat{u}}}^{\frac{1}{2}}\Vert _{L^{\infty }} + C \Vert {{\widehat{e}}}^{\frac{1}{2}}\Vert _{H^2} \nonumber \\&\le \Vert {{\widehat{u}}}^{\frac{1}{2}}\Vert _{L^{\infty }} +CC_K\tau \le K_0, \end{aligned}$$

(3.13)

when $\tau \le \tau _1=\frac{1}{CC_K}$. From (2.14), it is easy to see that

$$\begin{aligned} \Vert \Psi ^{\frac{1}{2}}\Vert _{L^\infty } \le C\Vert f(|{{\widehat{U}}}^{\frac{1}{2}}|)|{{\widehat{U}}}^{\frac{1}{2}}|^2\Vert _{L^\infty } \le C_{K}. \end{aligned}$$

(3.14)

Then, from (3.2) and (3.5), we have

$$\begin{aligned} \Vert \theta ^{\frac{1}{2}}\Vert _{L^2}&\le C\Vert G_1^{\frac{1}{2}}\Vert _{L^2}+C\Vert Q^{\frac{1}{2}}\Vert _{L^2} \le C_{K}\Vert {{\widehat{e}}}^{\frac{1}{2}}\Vert _{L^2}+C_K\tau ^2 \le C_K\tau ^2, \end{aligned}$$

(3.15)

$$\begin{aligned} \Vert R_1^{\frac{1}{2}}\Vert _{L^2}&\le C_{K}\left( \Vert e^1\Vert _{L^2} +\Vert {{\widehat{e}}}^{\frac{1}{2}} \Vert _{L^2} +\Vert \theta ^{\frac{1}{2}}\Vert _{L^2}\right) \le C_K\left( \Vert e^1\Vert _{L^2}+\tau ^2\right) , \end{aligned}$$

(3.16)

where we have noted $e^0=0$.

Furthermore, multiplying (3.3) by $(e^1)^*$, integrating it over $\Omega$ and taking the imaginary part of the resulting equation leads to

$$\begin{aligned} \frac{\text {i}}{\tau }\Vert e^1\Vert _{L^2}^2 +\text {Im}\left( R_1^{\frac{1}{2}},e^1 \right) =\text {Im}\left( P^{\frac{1}{2}},e^{1} \right) . \end{aligned}$$

(3.17)

By (3.8) and (3.16), we get

$$\begin{aligned} \Vert e^1\Vert _{L^2} \le C_K\tau ^2. \end{aligned}$$

(3.18)

From (3.3), we have

$$\begin{aligned} \Vert \Delta e^1\Vert _{L^2} \le \frac{1}{\tau }\Vert e^1\Vert _{L^2} +\left\| R_1^{\frac{1}{2}}\right\| _{L^2} +\Vert P^{\frac{1}{2}}\Vert _{L^2} \le C_K\tau . \end{aligned}$$

(3.19)

The above estimate implies that

$$\begin{aligned} \Vert e^1\Vert _{L^\infty } \le C\Vert e^1\Vert _{H^2} \le CC_K\tau \le \tau ^{\frac{1}{4}}, \end{aligned}$$

(3.20)

when $\tau \le \tau _2=(CC_K)^{-\frac{4}{3}}$. Thus (3.11) holds for $m=1$.

Secondly, by mathematical induction, we assume (3.11) holds for $m \le n-1$. Then

$$\begin{aligned} \Vert U^m \Vert _{L^\infty } \le \Vert u^m \Vert _{L^\infty } + \Vert e^m \Vert _{L^\infty } \le \Vert u^m\Vert _{L^\infty }+\tau ^{\frac{1}{4}} \le K_0. \end{aligned}$$

(3.21)

From the Eq. (2.14), we know that

$$\begin{aligned} \Vert \Psi ^{n-\frac{1}{2}}\Vert _{L^\infty } \le C\Vert f\left( |{{\widehat{U}}}^{n-\frac{1}{2}}|\right) |{{\widehat{U}}}^{n-\frac{1}{2}}|^2\Vert _{L^\infty } \le C_{K}. \end{aligned}$$

(3.22)

Then, from (3.2) and (3.5), we have

$$\begin{aligned} \Vert \theta ^{n-\frac{1}{2}}\Vert _{L^2}&\le C\left\| G_1^{n-\frac{1}{2}}\right\| _{L^2}+C\Vert Q^{n-\frac{1}{2}}\Vert _{L^2} \le C_{K}\Vert {{\widehat{e}}}^{n-\frac{1}{2}}\Vert _{L^2} +C_K\tau ^2, \end{aligned}$$

(3.23)

$$\begin{aligned} \Vert R_1^{n-\frac{1}{2}}\Vert _{L^2}&\le C_{K}\left( \Vert {\overline{e}}^{n-\frac{1}{2}}\Vert _{L^2}+\Vert {{\widehat{e}}}^{n-\frac{1}{2}}\Vert _{L^2} +\Vert \theta ^{n-\frac{1}{2}}\Vert _{L^2}\right) \nonumber \\&\le C_{K}\left( \Vert {\overline{e}}^{n-\frac{1}{2}}\Vert _{L^2} +\Vert {{\widehat{e}}}^{n-\frac{1}{2}}\Vert _{L^2}\right) +C_K\tau ^2. \end{aligned}$$

(3.24)

Now we prove that (3.11) also holds for $m = n$. We multiply (3.3) by $({{\overline{e}}}^{n-\frac{1}{2}})^*$, integrate it over $\Omega$ and take the imaginary part of the resulting equation to get

$$\begin{aligned} \frac{1}{2\tau }\left( \Vert e^{n}\Vert _{L^2}^2-\Vert e^{n-1}\Vert _{L^2}^2\right)&= -\text {Im}\left( R_1^{n-\frac{1}{2}}, {{\overline{e}}}^{n-\frac{1}{2}}\right) + \text {Im}\left( P^{n-\frac{1}{2}},{{\overline{e}}}^{n-\frac{1}{2}}\right) \nonumber \\&\le C_{K}(\Vert {\overline{e}}^{n-\frac{1}{2}}\Vert _{L^2}^2 +\Vert {{\widehat{e}}}^{n-\frac{1}{2}}\Vert _{L^2}^2)+C_K\tau ^4+\Vert P^{n-\frac{1}{2}}\Vert _{L^2}^2, \end{aligned}$$

(3.25)

where we have used (3.24). By Gronwall’s inequality and (3.8), there exists $\tau _3>0$ such that

$$\begin{aligned} \Vert e^n\Vert _{L^2}\le C_K\tau ^2 \end{aligned}$$

(3.26)

when $\tau \le \tau _3$. The above estimate further shows that

$$\begin{aligned} \Vert D_\tau e^n\Vert _{L^2} \le C_K\, \tau , \end{aligned}$$

(3.27)

with which and (3.3), we obtain

$$\begin{aligned} \Vert \Delta {{\overline{e}}}^{n-\frac{1}{2}}\Vert _{L^2} \le \Vert D_\tau e^n\Vert _{L^2} +\left\| R_1^{n-\frac{1}{2}}\right\| _{L^2} +\Vert P^{n-\frac{1}{2}}\Vert _{L^2} \le C_K\tau . \end{aligned}$$

(3.28)

By Lemma 2.1,

$$\begin{aligned} \Vert \Delta e^n\Vert _{L^2} \le 2\sum _{m=1}^n\Vert \Delta {{\overline{e}}}^{m-\frac{1}{2}}\Vert _{L^2} +\Vert \Delta e^0\Vert _{L^2} \le 2C _K. \end{aligned}$$

By using Gagliardo–Nirenberg inequality, we have

$$\begin{aligned} \Vert e^n\Vert _{L^\infty } \le C\Vert e^n\Vert _{H^2}^{\frac{3}{4}}\Vert e^n\Vert _{L^2}^{\frac{1}{4}}+C\Vert e^n\Vert _{L^2} \le CC_K\tau ^{\frac{1}{2}} \le \tau ^{\frac{1}{4}}, \end{aligned}$$

(3.29)

when $\tau \le \tau _4=\frac{1}{C^4C_K^4}$. Thus, (3.11) holds for $m=n$. The induction is closed. From (3.23) and (3.26), we can easily get

$$\begin{aligned} \Vert e^n\Vert _{L^2}+\Vert \theta ^{n-\frac{1}{2}}\Vert _{L^2} \le C_K\tau ^2 \le C_0^*\tau ^2. \end{aligned}$$

(3.30)

Furthermore, we arrive at

$$\begin{aligned} \Vert U^n\Vert _{L^{\infty }}&\le \Vert u^n\Vert _{L^{\infty }} +\Vert e^n\Vert _{L^\infty } \le \Vert u^n\Vert _{L^\infty }+\tau ^{\frac{1}{4}} \le K_0,\\ \Vert U^n\Vert _{H^2}&\le \Vert u^n\Vert _{H^2} +\Vert e^n\Vert _{H^2} \le \Vert u^n\Vert _{H^2} +C\Vert \Delta e^n\Vert _{L^2} \le C_0^+,\\ \Vert \Psi ^{n-\frac{1}{2}}\Vert _{H^2}&\le C_K\Vert {{\widehat{U}}}^{n-\frac{1}{2}}\Vert _{H^2} \le C_0^+,\\ \Vert D_{\tau } {{\overline{U}}}^{n-\frac{1}{2}}\Vert _{H^2}&\le \Vert D_{\tau } {{\overline{u}}}^{n-\frac{1}{2}}\Vert _{H^2}+ \Vert D_{\tau } {{\overline{e}}}^{n-\frac{1}{2}}\Vert _{H^2} \le C_0^+,\\ \tau \Vert D_{\tau } U^{n}\Vert _{H^2}&\le \tau \Vert D_{\tau } u^{n}\Vert _{H^2} +\tau \Vert D_{\tau } e^{n}\Vert _{H^2} \le C_0^+, \end{aligned}$$

for $n=1,2,\ldots ,N$. Taking $\tau _0^*\le \min _{1\le i\le 4} \tau _i$, the Proof of Theorem 3.1 is complete. $\square$

3.2 Spatial error analysis

In this subsection, we derive $\tau$-independent estimates for $U^n-U_h^n$ and $\Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}$. Let $R_h: H_0^1(\Omega )\rightarrow V_h$ be a Ritz projection operator defined by

$$\begin{aligned} \left( \nabla (v-R_h v),\nabla \omega \right) =0,\quad \text {for all } \omega \in V_h. \end{aligned}$$

(3.31)

By classical FEM theory [15, 41], it is easy to see that

$$\begin{aligned}&\Vert v-R_h v\Vert _{L^2}+h\Vert \nabla (v-R_h v)\Vert _{L^2}\le Ch^{s}\Vert v\Vert _{H^s}, \quad 1\le s\le r+1, \end{aligned}$$

(3.32)

for any $v\in H_0^1(\Omega )$. By classical interpolation theory [41], we further have

$$\begin{aligned} \Vert v-\Pi _h v\Vert _{L^2}+h\Vert \nabla (v-\Pi _h v)\Vert _{L^2}\le Ch^{s}\Vert v\Vert _{H^{s}}, \quad 1\le s\le r+1. \end{aligned}$$

(3.33)

Moreover, since $\Vert R_h U^n\Vert _{L^{\infty }} \le C\Vert U^n\Vert _{H^2}$ and $\Vert \Pi _h \Psi ^{n-\frac{1}{2}}\Vert _{L^\infty }\le C\Vert \Psi ^{n-\frac{1}{2}}\Vert _{H^2}$, by Theorem 3.1, we can define

$$\begin{aligned} K_1&= \max _{0\le n\le N}\Vert R_h U^n\Vert _{L^{\infty }} +\Vert R_h {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^{\infty }}+1, \end{aligned}$$

(3.34)

$$\begin{aligned} K_2&= \max _{1\le n\le N}\Vert \Pi _h \Psi ^{n-\frac{1}{2}}\Vert _{L^{\infty }} +\Vert \Pi _h \Psi ^0\Vert _{L^{\infty }}+1, \end{aligned}$$

(3.35)

where $K_1$ and $K_2$ are positive constants dependent on K and independent on $\tau$, h and n. The following inverse inequality will be always used in our proof:

$$\begin{aligned} \Vert v\Vert _{L^{\infty }}\le Ch^{-\frac{d}{2}} \Vert v\Vert _{L^2} \end{aligned}$$

(3.36)

for any $v\in V_h$ and $d=2,3$.

Let

$$\begin{aligned} e^n_h =R_h U^n-U_h^n,\quad \theta _h^{n-\frac{1}{2}} =\Pi _h\Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}. \end{aligned}$$

With (2.1)–(2.2) and (2.14)–(2.15), $e_h^n$ and $\theta _h^{n-\frac{1}{2}}$ satisfy

$$\begin{aligned}&\alpha \left( \theta _h^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla \theta _h^{n-\frac{1}{2}},\nabla \varphi \right) \nonumber \\&\quad = \left( G_2^{n-\frac{1}{2}},\varphi \right) +\alpha \left( \Pi _h\Psi ^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla (\Pi _h\Psi ^{n-\frac{1}{2}}-\Psi ^{n-\frac{1}{2}}), \nabla \varphi \right) , \end{aligned}$$

(3.37)

$$\begin{aligned}&\text {i}\left( D_{\tau } e^n_h,v \right) -\left( \nabla {{\overline{e}}}_h^{n-\frac{1}{2}},\nabla v \right) +\left( R_2^{n-\frac{1}{2}},v\right) = -\text {i}\left( D_{\tau }(U^n-R_h U^n),v \right) , \end{aligned}$$

(3.38)

for $v,\varphi \in V_h$, where

$$\begin{aligned} G_2^{n-\frac{1}{2}}&=f(|{{\widehat{U}}}^{n-\frac{1}{2}}|) |{{\widehat{U}}}^{n-\frac{1}{2}}|^2-f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}} \right| \right) \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| ^2, \end{aligned}$$

(3.39)

$$\begin{aligned} R_2^{n-\frac{1}{2}}&= \Psi ^{n-\frac{1}{2}}f\left( \left| {{\widehat{U}}}^{n-\frac{1}{2}}\right| \right) {{\overline{U}}}^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}} f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) {{\overline{U}}}_h^{n-\frac{1}{2}}. \end{aligned}$$

(3.40)

Similarly, let ${{\widehat{e}}}_h^{\frac{1}{2}}= R_h{{\widehat{U}}}^{\frac{1}{2}}-{{\widehat{U}}}_h^{\frac{1}{2}}.$ By (2.3) and (2.17), ${{\widehat{e}}}^{\frac{1}{2}}_h$ satisfies

$$\begin{aligned}&\frac{2\text {i}}{\tau }\left( {{\widehat{e}}}_h^{\frac{1}{2}},v \right) -\left( \nabla {{\widehat{e}}}_h^{\frac{1}{2}},\nabla v \right) +\left( \Psi ^0f(|U^0|){{\widehat{U}}}^{\frac{1}{2}} -\Psi _h^0f(|U_h^0|){{\widehat{U}}}_h^{\frac{1}{2}},v \right) \nonumber \\&\quad = -\frac{2\text {i}}{\tau }\left( {{\widehat{U}}}^{\frac{1}{2}}- R_h{{\widehat{U}}}^{\frac{1}{2}},v \right) +\frac{2\text {i}}{\tau }\left( U^0-U_h^0,v \right) . \end{aligned}$$

(3.41)

In this subsection, we prove the following theorem

Theorem 3.2

Suppose that the system (1.1)–(1.3) has unique solutions u, $\psi$ satisfying (2.10). Then the finite element system defined in (2.1)–(2.3) has unique solutions $U_h^m$ and $\Psi _h^{m-\frac{1}{2}}$, $m=1,\ldots ,N$, and there exists $\tau _0'>0$, $h_0'>0$ such that when $\tau \le \tau _0'$, $h\le h_0'$,

$$\begin{aligned} \Vert e_h^m\Vert _{L^2}+\left\| \theta ^{m-\frac{1}{2}}_h\right\| _{L^2} \le C_0' h^2 \end{aligned}$$

(3.42)

where $C_0'$ is a positive constant dependent on $C_0^*$, $C_0^+$, K, and independent of $\tau$, h, N and $C_0$.

Proof

The existence and uniqueness of solutions for Eqs. (2.1) and (2.3) follow the mass conservation (2.5) and $\Vert {{\widehat{U}}}_h^{1/2}\Vert _{L^2}\le \Vert U_h^0\Vert _{L^2}$. For the Eq. (2.2), the coefficient matrix is symmetric and positive definite, which leads to the existence and uniqueness of solutions immediately. Now, we prove the error estimate (3.42) by mathematical induction. Since $U_h^0=\Pi _h u_0$, by (2.10) and (3.32)–(3.33), we have

$$\begin{aligned} \Vert e^0_h\Vert _{L^2}\le \Vert u_0-U_h^0\Vert _{L^2}+\Vert u^0-R_hu_0\Vert _{L^2} \le Ch^{2}\Vert u_0\Vert _{H^2}\le C_Kh^2. \end{aligned}$$

(3.43)

From (2.4), it is easy to get

$$\begin{aligned} \Vert \Psi _h^0-\Pi _h\Psi ^0\Vert _{L^2} \le C_Kh^2. \end{aligned}$$

(3.44)

By using the inverse inequality (3.36), we obtain

$$\begin{aligned} \Vert U_h^0\Vert _{L^{\infty }}&\le \Vert R_h U^0\Vert _{L^{\infty }}+\Vert R_h U^0-U_h^0\Vert _{L^{\infty }} \le \Vert R_h U^0\Vert _{L^{\infty }} +Ch^{-\frac{d}{2}}C_Kh^2 \le K_1, \\ \Vert \Psi _h^0\Vert _{L^\infty }&\le \Vert \Pi _h\Psi ^0\Vert _{L^\infty }+\Vert \Pi _h\Psi ^0-\Psi _h^0\Vert _{L^\infty } \le \Vert \Pi _h\Psi ^0\Vert _{L^\infty }+Ch^{-\frac{d}{2}}C_Kh^2 \le K_2, \end{aligned}$$

for $d=2,3$, when $h\le h_1= (CC_K)^{-\frac{2}{4-d}}$.

We substitute $v={{\widehat{e}}}_h^{\frac{1}{2}}$ into (3.41) and take the imaginary part of the resulting equation to get

$$\begin{aligned} \Vert {{\widehat{e}}}_h^{\frac{1}{2}}\Vert _{L^2}^2&=-\frac{\tau }{2}\text {Im}\left( \Psi ^0f(|U^0|){{\widehat{U}}}^{\frac{1}{2}} -\Psi _h^0f(|U_h^0|){{\widehat{U}}}_h^{\frac{1}{2}}, {{\widehat{e}}}_h^{\frac{1}{2}} \right) \nonumber \\&\qquad -\text {Re}\left( {{\widehat{U}}}^{\frac{1}{2}} -R_h {{\widehat{U}}}^{\frac{1}{2}}, {{\widehat{e}}}_h^{\frac{1}{2}} \right) +\text {Re}\left( U^0-U_h^0, {{\widehat{e}}}_h^{\frac{1}{2}} \right) \nonumber \\&\quad \le C_K\tau \Big (\Big \Vert {{\widehat{U}}}^{\frac{1}{2}} -{{\widehat{U}}}_h^{\frac{1}{2}}\Big \Vert _{L^2}+\Vert U^0-U_h^0\Vert _{L^2} +\Vert \Psi ^0-\Psi _h^0\Vert _{L^2}\Big )\left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}\nonumber \\&\qquad +\Vert {{\widehat{U}}}^{\frac{1}{2}}-R_h{{\widehat{U}}}^{\frac{1}{2}} \Vert _{L^2}\left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}+\Vert U^0-U_h^0\Vert _{L^2}\left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2} \nonumber \\&\quad \le \frac{1}{2}\left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}^2 +C_K h^4, \end{aligned}$$

(3.45)

when $\tau \le \tau _5=\frac{1}{4C_K}$. Then, we have

$$\begin{aligned} \left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2} \le C_Kh^2. \end{aligned}$$

(3.46)

Then, we can derive from (3.34) that

$$\begin{aligned} \left\| {{\widehat{U}}}_h^{\frac{1}{2}}\right\| _{L^\infty }&\le \Vert R_h {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^\infty } +\left\| R_h {{\widehat{U}}}^{\frac{1}{2}}-{{\widehat{U}}}_h^{\frac{1}{2}} \right\| _{L^\infty } \nonumber \\&\le \Vert R_h {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^\infty } +Ch^{-\frac{d}{2}}\left\| R_h {{\widehat{U}}}^{\frac{1}{2}} -{{\widehat{U}}}_h^{\frac{1}{2}}\right\| _{L^2} \nonumber \\&\le \Vert R_h {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^\infty } +CC_Kh^{-\frac{d}{2}}h^2 \nonumber \\&\le K_1 \end{aligned}$$

(3.47)

for $d=2,3$, when $h\le h_2=(CC_K)^{-\frac{2}{4-d}}$. If $\beta \ne 0$, we substitute $\varphi =\theta _h^{\frac{1}{2}}$ into (3.37) and use (3.33) to arrive at

$$\begin{aligned} \left\| \nabla \left( \Psi ^{\frac{1}{2}}-\Psi _h^{\frac{1}{2}}\right) \right\| _{L^2} \le C_K\left( \left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}+h\right) . \end{aligned}$$

Furthermore, the difference of the Eqs. (2.14) and (2.2) gives

$$\begin{aligned} \alpha \Big (\Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h,\varphi \Big ) +\beta ^2\Big (\nabla \Big (\Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\Big ),\nabla \varphi \Big ) =\Big (G_2^{\frac{1}{2}},\varphi \Big ) \end{aligned}$$

for $\varphi \in V_h$. Let g be arbitrary in $L^2(\Omega )$, take $\phi \in H^2(\Omega )\cap H^1_0(\Omega )$ as the solution of

$$\begin{aligned} \alpha \phi -\beta ^2\Delta \phi =g\ \text {in }\Omega ,\quad \text {with }\phi =0\ \text {on }\partial \Omega , \end{aligned}$$

so that $\Vert \phi \Vert _{H^2}\le C\Vert g\Vert _{L^2}$. Taking $g=\Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h$, we have

$$\begin{aligned}&\left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2}^2 \\&\quad =\alpha \Big (\Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h,\phi -P_h\phi \Big ) +\beta ^2\Big (\nabla \left( \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right) ,\nabla (\phi -P_h\phi )\Big )\\&\qquad +\Big (G_2^{\frac{1}{2}},P_h\phi -\phi \Big )+\Big (G_2^{\frac{1}{2}},\phi \Big ) \\&\quad \le Ch^2\left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2}\Vert \phi \Vert _{H^2} +Ch\left\| \nabla \left( \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right) \right\| _{L^2}\Vert \phi \Vert _{H^2}\\&\qquad +Ch^2\left\| G_2^{\frac{1}{2}}\right\| _{L^2}\Vert \phi \Vert _{H^2} +\left\| G_2^{\frac{1}{2}}\right\| _{L^2}\Vert \phi \Vert _{L^2} \\&\quad \le Ch^2\left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2}^2 +C\left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2} \big (h\big \Vert \nabla \big (\Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\big ) \big \Vert _{L^2}+\big \Vert G_2^{\frac{1}{2}}\big \Vert _{L^2} \big ), \end{aligned}$$

where $P_h\phi$ denotes the elliptic projection of $\phi$. When $h\le h_3=(2C)^{-\frac{1}{2}}$, the above results further show that

$$\begin{aligned} \left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2}&\le Ch\left\| \nabla \left( \Psi ^{\frac{1}{2}}-\Psi _h^{\frac{1}{2}}\right) \right\| _{L^2} +C\left\| G_2^{\frac{1}{2}}\right\| _{L^2} \le C_K\left( \left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}+h^2\right) \nonumber \\&\le C_Kh^2. \end{aligned}$$

(3.48)

If $\beta =0$, from (3.37), it is straightforward to obtain

$$\begin{aligned} \left\| \Psi ^{\frac{1}{2}}-\Psi ^{\frac{1}{2}}_h\right\| _{L^2}^2 \le C_K\left( \left\| {{\widehat{e}}}_h^{\frac{1}{2}}\right\| _{L^2}^2+h^4\right) \le C_K h^4. \end{aligned}$$

(3.49)

Then, we derive from (3.35) that

$$\begin{aligned} \left\| \Psi _h^{\frac{1}{2}}\right\| _{L^\infty }&\le \Vert \Pi _h\Psi ^{\frac{1}{2}}\Vert _{L^\infty } +\left\| \Pi _h\Psi ^{\frac{1}{2}}-\Psi _h^{\frac{1}{2}}\right\| _{L^\infty } \nonumber \\&\le \Vert \Pi _h\Psi ^{\frac{1}{2}}\Vert _{L^\infty } +Ch^{-\frac{d}{2}}\left\| \Pi _h\Psi ^{\frac{1}{2}}-\Psi _h^{\frac{1}{2}}\right\| _{L^2} \nonumber \\&\le \Vert \Pi _h\Psi ^{\frac{1}{2}}\Vert _{L^\infty }+CC_Kh^{-\frac{d}{2}}h^2 \nonumber \\&\le K_2 \, , \end{aligned}$$

(3.50)

for $d=2,3$, when $h\le h_4=(CC_K)^{-\frac{2}{4-d}}$, and

$$\begin{aligned} \left\| R_2^{\frac{1}{2}}\right\| _{L^2} \le C_K\left( \left\| {{\overline{e}}}_h^{\frac{1}{2}}\right\| _{L^2} +\left\| {{\widehat{e}}}_h^{\frac{1}{2}} \right\| _{L^2}+\left\| \Psi ^{\frac{1}{2}}-\Psi _h^{\frac{1}{2}}\right\| _{L^2}\right) . \end{aligned}$$

(3.51)

Again we substitute $v={{\overline{e}}}_h^\frac{1}{2}$ into (3.38) and take the imaginary part of the resulting equation to arrive at

$$\begin{aligned}&\Vert e_h^1\Vert _{L^2}^2 +\tau \text {Im}\left( R_2^{\frac{1}{2}}, {{\overline{e}}}_h^\frac{1}{2}\right) = \Vert e_h^0\Vert _{L^2}^2 -\text {Re}\left( U^1-R_h U^1,{{\overline{e}}}_h^\frac{1}{2}\right) \!+\!\text {Re}\left( U^0-U_h^0,{{\overline{e}}}_h^\frac{1}{2}\right) . \end{aligned}$$

By (3.32)–(3.33), (3.48)–(3.49) and (3.51), we get

$$\begin{aligned} \Vert e^1_h\Vert _{L^2}+\left\| \theta _h^{\frac{1}{2}}\right\| _{L^2}\le C_Kh^2. \end{aligned}$$

(3.52)

Now, we assume that

$$\begin{aligned} \Vert e_h^m\Vert _{L^2} \le C_0' h^2, \end{aligned}$$

(3.53)

holds for $m\le n-1$, By (3.34),

$$\begin{aligned} \Vert U_h^m\Vert _{L^{\infty }}&\le \Vert R_h U^m\Vert _{L^{\infty }}+\Vert R_h U^m-U_h^m\Vert _{L^{\infty }}\nonumber \\&\le \Vert R_h U^m\Vert _{L^{\infty }}+Ch^{-\frac{d}{2}} \Vert R_h U^m-U_h^m\Vert _{L^2}\nonumber \\&\le \Vert R_h U^m\Vert _{L^{\infty }}+CC_0' h^{ -\frac{d}{2}}h^2\nonumber \\&\le K_1, \end{aligned}$$

(3.54)

for $d=2,3$, and $h\le h_5=(C C_0')^{-\frac{2}{4-d}}$. With a similar approach used in (3.48)–(3.49), we can get

$$\begin{aligned} \left\| \Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2} \le C_K\left( \left\| {{\widehat{e}}}_h^{n-\frac{1}{2}}\right\| _{L^2}+Ch^2\right) , \end{aligned}$$

(3.55)

from the Eq. (3.37). By (3.35), (3.53) and (3.55),

$$\begin{aligned} \left\| \Psi _h^{n-\frac{1}{2}}\right\| _{L^{\infty }}&\le \Vert \Pi _h \Psi ^{n-\frac{1}{2}}\Vert _{L^{\infty }}+\left\| \Pi _h\Psi ^{n-\frac{1}{2}} -\Psi _h^{n-\frac{1}{2}}\right\| _{L^{\infty }}\nonumber \\&\le \Vert \Pi _h\Psi ^{n-\frac{1}{2}}\Vert _{L^{\infty }}+Ch^{-\frac{d}{2}} \left\| \Pi _h\Psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2}\nonumber \\&\le \Vert \Pi _h \Psi ^{n-\frac{1}{2}}\Vert _{L^{\infty }} +C h^{ -\frac{d}{2}}C_KC_0'h^2\nonumber \\&\le K_2, \end{aligned}$$

(3.56)

for $d=2,3$, and $h\le h_6=(CC_K C_0')^{-\frac{2}{4-d}}$. With (3.54)–(3.56), we have

$$\begin{aligned} \left\| R_2^{n-\frac{1}{2}}\right\| _{L^2}&\le C_K\left( \left\| {{\overline{e}}}_h^{n-\frac{1}{2}}\right\| _{L^2} +\left\| {{\widehat{e}}}_h^{n-\frac{1}{2}}\right\| _{L^2}+\left\| \Psi ^{n-\frac{1}{2}} -\Psi _h^{n-\frac{1}{2}}\right\| _{L^2}+h^2\right) \nonumber \\&\le C_K\left( \left\| {{\overline{e}}}_h^{n-\frac{1}{2}}\right\| _{L^2} +\left\| {{\widehat{e}}}_h^{n-\frac{1}{2}}\right\| _{L^2} +h^2\right) . \end{aligned}$$

(3.57)

We need to prove that (3.53) also holds for $m=n$. Let $v={{\overline{e}}}_h^{n-\frac{1}{2}}$ in (3.38). Taking the imaginary part of the resulting equation gives

$$\begin{aligned} \frac{\Vert e^n_h\Vert _{L^2}^2-\Vert e^{n-1}_h\Vert _{L^2}^2}{2\tau } +\text {Im}\left( R_2^{n-\frac{1}{2}}, {{\overline{e}}}_h^{n-\frac{1}{2}}\right) = -\text {Re}\left( D_{\tau }(U^n-R_h U^n), {{\overline{e}}}_h^{n-\frac{1}{2}}\right) . \end{aligned}$$

(3.58)

By (3.57), summing up (3.58) leads to

$$\begin{aligned} \Vert e^n_h\Vert _{L^2}^2&\le C_K\tau \sum _{m=1}^{n } \Vert e^m_h\Vert _{L^2}^2 -\tau \sum _{m=1}^n \text {Re}\left( D_{\tau }\left( U^m-R_h U^m \right) ,{{\overline{e}}}^{m-\frac{1}{2}}_h \right) +C_Kh^4, \end{aligned}$$

(3.59)

where we have used (3.43). By Lemma 2.1, (3.10) and (3.52),

$$\begin{aligned}&\left| \tau \sum _{m=1}^n\left( D_{\tau }(U^m-R_h U^m), {{\overline{e}}}^{m-\frac{1}{2}}_h \right) \right| \nonumber \\&\quad \le \left| \frac{\tau }{2}\left( D_{\tau }(U^1-R_h U^1),e^0_h \right) \right| +\left| \tau \sum _{m=2}^n\left( D_{\tau }({{\overline{U}}}^{m-\frac{1}{2}} -R_h {{\overline{U}}}^{m-\frac{1}{2}}), e^{m-1}_h \right) \right| \nonumber \\&\qquad +\left| \frac{\tau }{2}\left( D_{\tau }(U^n-R_hU^n), e^n_h \right) \right| \nonumber \\&\quad \le C\tau ^2 h^4\Vert D_{\tau }U^1\Vert _{H^2}^2+\Vert e^0_h\Vert _{L^2}^2 +C\tau h^4\sum _{m=2}^n \Vert D_{\tau }{{\overline{U}}}^{m-\frac{1}{2}}\Vert _{H^2}^2 +C\tau \sum _{m=2}^n \Vert e^{m-1}_h\Vert _{L^2}^2\nonumber \\&\qquad +C\tau ^2 h^4\Vert D_{\tau }U^n\Vert _{H^2}^2 +\frac{1}{4}\Vert e^n_h\Vert _{L^2}^2\nonumber \\&\quad \le \frac{1}{4} \Vert e^n_h\Vert _{L^2}^2 +C\tau \sum _{m=1}^{n-1}\Vert e^m_h\Vert _{L^2}^2 +C_Kh^4. \end{aligned}$$

Applying Gronwall’s inequality to (3.59), there exists $\tau _6>0$, such that

$$\begin{aligned} \Vert e^n_h\Vert _{L^2}\le C_Kh^{2}. \end{aligned}$$

(3.60)

With (3.33) and (3.55), we have

$$\begin{aligned} \Vert e_h^n\Vert _{L^2}+\left\| \theta _h^{n-\frac{1}{2}}\right\| _{L^2}\le C_0' h^2. \end{aligned}$$

Thus, (3.53) holds for $m=n$. Taking $h_0' \le \min _{1\le i\le 6} h_i$ and $\tau _0'\le \min \{\tau _5,\tau _6,\tau _0^*\}$, the induction is closed. This completes the proof of Theorem 3.2. $\square$

Remark

Clearly, the error estimate obtained in Theorem 3.2 is optimal in $L^2$-norm for linear Galerkin FEM. Since the estimate (3.42) is $\tau$-independent, we have the optimal $H^1$ error estimate

$$\begin{aligned} \Vert \nabla e_h^n\Vert _{L^2}+\left\| \nabla \theta _h^{n-\frac{1}{2}}\right\| _{L^2}\le C_0' h, \quad n=1,2,\ldots , N, \end{aligned}$$

immediately by the inverse inequality. By (3.9), (3.32)–(3.33) and (3.42), we have the optimal error estimates for the linear Galerkin FEM ($r=1$) below.

Corollary 3.1

Under the assumption of Theorem 3.1, the finite element system defined in (2.1)–(2.3) with $r=1$ has unique solutions $U_h^m$, $\Psi _h^{m-\frac{1}{2}}$, $m=1,\ldots ,N$, and there exist $\tau _0'>0$ and $h_0'>0$ such that when $\tau \le \tau _0'$, $h\le h_0'$,

$$\begin{aligned} \Vert u^m-U_h^m\Vert _{L^2} +\left\| \psi ^{m-\frac{1}{2}}-\Psi _h^{m-\frac{1}{2}}\right\| _{L^2}&\le {{\widetilde{C}}}_0(\tau ^2+h^2), \end{aligned}$$

(3.61)

$$\begin{aligned} \Vert \nabla (u^m-U_h^m)\Vert _{L^2}+ \left\| \nabla \left( \psi ^{m-\frac{1}{2}}-\Psi _h^{m-\frac{1}{2}}\right) \right\| _{L^2}&\le {{\widetilde{C}}}_0(\tau ^2+h), \end{aligned}$$

(3.62)

where ${{\widetilde{C}}}_0$ is a positive constant dependent on $C_0^*, C_0^+,C_0'$, and independent of $\tau$, h, N and $C_0$.

When $r>1$, the above results are not optimal for the r-order Galerkin FEM. However, by Theorem 3.2, we see immediately the uniform boundedness of numerical solutions in $L^{\infty }$-norm:

$$\begin{aligned} \Vert {{\widehat{U}}}_h^{\frac{1}{2}}\Vert _{L^{\infty }}&\le \Vert R_h {{\widehat{U}}}^{\frac{1}{2}}\Vert _{L^{\infty }} +Ch^{-\frac{d}{2}}\left\| R_h {{\widehat{U}}}^{\frac{1}{2}} -{{\widehat{U}}}_h^{\frac{1}{2}}\right\| _{L^2} \le K_1, \end{aligned}$$

(3.63)

$$\begin{aligned} \Vert U_h^n\Vert _{L^{\infty }}&\le \Vert R_h U^n\Vert _{L^{\infty }}+Ch^{-\frac{d}{2}}\Vert R_h U^n-U_h^n\Vert _{L^2} \le K_1, \end{aligned}$$

(3.64)

$$\begin{aligned} \left\| \Psi _h^{n-\frac{1}{2}}\right\| _{L^\infty }&\le \Vert \Pi _h\Psi ^{n-\frac{1}{2}}\Vert _{L^\infty } +Ch^{-\frac{d}{2}}\left\| \Pi _h\Psi ^{n-\frac{1}{2}} -\Psi _h^{n-\frac{1}{2}}\right\| _{L^2} \le K_2, \end{aligned}$$

(3.65)

for $n=1,2,\ldots ,N$ when $\tau \le \tau _0'$ and $h\le h_0'$, with which and in a routine way, we can derive the optimal $L^2$ error estimate as given in Theorem 2.1.

3.3 The proof of Theorem 2.1

At the time step $t=\frac{t_1}{2}$, let ${{\widetilde{e}}}_h^{1/2}=R_h {{\widehat{u}}}^{1/2}-{{\widehat{U}}}_h^{1/2}$. When $\tau \le \tau _0'$ and $h\le h_0'$, with (3.32), (3.63) and $\Vert \Psi ^0-\Psi _h^0\Vert \le C_Kh^{r+1}$, we can easily get $\Vert {{\widetilde{e}}}_h^{1/2}\Vert \le C_K(\tau ^2+h^{r+1})$ from the Eqs. (1.1) and (2.3). Thus, in the following, we only analyze the errors $u^n-U_h^n$, $\psi ^{n-1/2}-\Psi _h^{n-1/2}$ for $1\le n\le N$.

Let ${{\widetilde{e}}}^n_h=R_h u^n-U_h^n,\ {{\widetilde{\theta }}}_h^{n-\frac{1}{2}} =\Pi _h\psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}.$ At $t=t_{n-\frac{1}{2}}$, the exact solutions u and $\psi$ satisfy

$$\begin{aligned}&\alpha \left( \psi ^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla \psi ^{n-\frac{1}{2}},\nabla \varphi \right) =\left( f(|u^{n-\frac{1}{2}}|)|u^{n-\frac{1}{2}}|^2,\varphi \right) , \\&\text {i}\left( u_t^{n-\frac{1}{2}},v\right) -\left( \nabla u^{n-\frac{1}{2}},\nabla v \right) +\left( \psi ^{n-\frac{1}{2}}f(|u^{n-\frac{1}{2}}|)u^{n-\frac{1}{2}},v \right) =0, \end{aligned}$$

for any $v,\varphi \in V_h$. With (2.1)–(2.2) and the above two equations, the error functions ${{\widetilde{e}}}_h^n$, ${{\widetilde{\theta }}}_h^{n-\frac{1}{2}}$ satisfy

$$\begin{aligned}&\alpha \left( {{\widetilde{\theta }}}_h^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla {{\widetilde{\theta }}}_h^{n-\frac{1}{2}},\nabla \varphi \right) \nonumber \\&\quad = \left( G^{n-\frac{1}{2}},\varphi \right) +\alpha \left( \Pi _h\psi ^{n-\frac{1}{2}}--\psi ^{n-\frac{1}{2}},\varphi \right) +\beta ^2\left( \nabla (\Pi _h\psi ^{n-\frac{1}{2}}-\psi ^{n-\frac{1}{2}}), \nabla \varphi \right) , \end{aligned}$$

(3.66)

$$\begin{aligned}&\quad \text {i}\left( D_{\tau }{{\widetilde{e}}}_h^n,v \right) -\left( \nabla \overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}},\nabla v \right) +\left( R^{n-\frac{1}{2}},v \right) \nonumber \\&\quad = \text {i}\left( D_{\tau }R_h u^n-u_t^{n-\frac{1}{2}},v \right) +\left( \Delta ({{\overline{u}}}^{n-\frac{1}{2}}-u^{n-\frac{1}{2}}), v \right) , \end{aligned}$$

(3.67)

for $n=1,2,\ldots ,N$, where

$$\begin{aligned} G^{n-\frac{1}{2}}&=f(|u^{n-\frac{1}{2}}|)|u^{n-\frac{1}{2}}|^2 -f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| ^2, \\ R^{n-\frac{1}{2}}&=\psi ^{n-\frac{1}{2}}f(|u^{n-\frac{1}{2}}|)u^{n-\frac{1}{2}} -\Psi _h^{n-\frac{1}{2}}f\left( \left| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right| \right) {{\overline{U}}}_h^{n-\frac{1}{2}}. \end{aligned}$$

Applying the same approach used in (3.48)–(3.49) to the error Eq. (3.66) and with (3.65), we obtain

$$\begin{aligned} \left\| \psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2}^2 \le C_K\left\| \widehat{{{\tilde{e}}}}_h^{n-\frac{1}{2}}\right\| _{L^2}^2+C_K(\tau ^2+h^{r+1})^2. \end{aligned}$$

(3.68)

Moreover, by (3.63)–(3.65), we further have

$$\begin{aligned} \Vert R^{n-\frac{1}{2}}\Vert _{L^2} \le C_K\left( \left\| \overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}}\right\| _{L^2} +\left\| \widehat{{{\tilde{e}}}}_h^{n-\frac{1}{2}}\right\| _{L^2} +\tau ^2+h^{r+1}\right) . \end{aligned}$$

(3.69)

We substitute $v=\overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}}$ into (3.67) and take the imaginary part to obtain

$$\begin{aligned}&\frac{\Vert {{\widetilde{e}}}^n_h\Vert _{L^2}^2- \Vert {{\widetilde{e}}}^{n-1}_h\Vert _{L^2}^2}{2\tau } +\text {Im}\left( R^{n-\frac{1}{2}}, \overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}} \right) \nonumber \\&\quad = \text {Re}\left( D_{\tau }R_h u^n-u_t^{n-\frac{1}{2}}, \overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}} \right) +\text {Im}\left( \Delta ({{\overline{u}}}^{n-\frac{1}{2}} -u^{n-\frac{1}{2}}), \overline{{{\tilde{e}}}}_h^{n-\frac{1}{2}} \right) . \end{aligned}$$

(3.70)

By Gronwall’s inequality, (3.69) and

$$\begin{aligned} \sum _{m=1}^n \tau \Vert \Delta ({{\overline{u}}}^{m-\frac{1}{2}} -u^{m-\frac{1}{2}})\Vert _{L^2}^2 \le&C\tau ^4\Vert u_{tt}\Vert _{L^2((0,T);H^2)}^2, \\ \sum _{m=1}^n\tau \Vert D_{\tau }R_h u^m-u_t^{m-\frac{1}{2}}\Vert _{L^2}^2 \le&\sum _{m=1}^n\tau \Vert D_\tau R_hu^m-D_{\tau }u^m\Vert _{L^2}^2\\&+\sum _{m=1}^n\tau \Vert D_{\tau }u^m-u_t^{m-\frac{1}{2}}\Vert _{L^2}^2 \\ \le&C(h^{2(r+1)}\Vert u_t\Vert _{L^2((0,T);H^{r+1})}^2 +\tau ^4\Vert u_{ttt}\Vert _{L^2((0,T);L^2)}^2), \end{aligned}$$

there exists a positive constant $\tau _7$ such that when $\tau \le \tau _7$, we get $\Vert {{\widetilde{e}}}^n_h\Vert _{L^2}\le C_{K}(\tau ^2+h^{r+1}).$ With (3.32) and (3.68), we have

$$\begin{aligned}&\Vert u^n-U_h^n\Vert _{L^2} +\left\| \psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2} \le C_{0}\left( \tau ^2+h^{r+1}\right) . \end{aligned}$$

(3.71)

Up to now, we have proved Theorem 2.1 when $\tau \le \tau _0:=\min \{\tau _0',\tau _7\}$ and $h\le h_0:=h_0'$. When $h\ge h_0$, by the mass conservation (2.5) and $\Vert {{\widehat{U}}}_h^{\frac{1}{2}}\Vert \le \Vert U_h^0\Vert _{L^2}$,

$$\begin{aligned} \left\| {{\widehat{U}}}_h^{\frac{1}{2}}\right\| _{L^{\infty }}&\le Ch_0^{-\frac{d}{2}}\left\| {{\widehat{U}}}_h^{\frac{1}{2}}\right\| _{L^2} \le Ch_0^{-\frac{d}{2}}\Vert u_0\Vert _{H^2} \le C_K, \end{aligned}$$

(3.72)

$$\begin{aligned} \Vert U_h^n\Vert _{L^{\infty }}&\le Ch_0^{-\frac{d}{2}}\Vert U_h^n\Vert _{L^2} \le Ch_0^{-\frac{d}{2}}\Vert u_0\Vert _{H^2} \le C_K. \end{aligned}$$

(3.73)

Together with (1.2), (2.2) and mass conservation, we have

$$\begin{aligned} \Vert u^n-U_h^n\Vert _{L^2}&\le \Vert u_0\Vert _{L^2}+\Vert U_h^0\Vert _{L^2} \le C\Vert u_0\Vert _{H^2} \le \frac{C_0}{2} \left( \tau ^2+h^{r+1}\right) , \end{aligned}$$

(3.74)

$$\begin{aligned} \left\| \psi ^{n-\frac{1}{2}}-\Psi _h^{n-\frac{1}{2}}\right\| _{L^2}&\le C_K\left( \Vert u^{n-\frac{1}{2}}\Vert _{L^2} +\left\| {{\widehat{U}}}_h^{n-\frac{1}{2}}\right\| _{L^2}\right) \nonumber \\&\le C_K\Vert u_0\Vert _{H^2} \le \frac{C_0}{2}\left( \tau ^2+h^{r+1}\right) , \end{aligned}$$

(3.75)

for $C_0\ge \frac{2(C+C_K)\Vert u_0\Vert _{H^2}}{h_0^{r+1}}$. The proof of Theorem 2.1 is complete. $\square$

4 Numerical results

In this section, three numerical examples are presented to confirm our theoretical analysis. All computations are performed by FreeFem++, where the finite element meshes are generated by a uniform triangular partition with $M+1$ nodes in each direction and $h=\frac{\sqrt{2}}{M}$.

Example 4.1

First, we consider the Schrödinger–Poisson system

$$\begin{aligned}&\text {i}u_t+\Delta u+\psi u=g_1, \end{aligned}$$

(4.1)

$$\begin{aligned}&-\Delta \psi =|u|^2+g_2, \end{aligned}$$

(4.2)

in $\Omega =[0,1]\times [0,1]$, with the initial condition $u(x,0)=u_0(x)$ and the homogeneous boundary condition $u=\psi =0$ on $\partial \Omega$, where $g_1$ and $g_2$ are chosen correspondingly to the exact solutions

$$\begin{aligned} u&=e^{(\text {i}+1)t}\sin (x)\sin (y)\sin (\pi x)\sin (\pi y), \end{aligned}$$

(4.3)

$$\begin{aligned} \psi&=e^{t+x+y}(1-x)(1-y)\sin (x)\sin (y). \end{aligned}$$

(4.4)

We solve the above system by the linearized Crank–Nicolson Galerkin schemes (2.1)–(2.2), and (2.6)–(2.7), respectively, with a linear finite element approximation. Here, we choose $\tau =\frac{1}{M}$ to confirm the optimal $L^2$ convergence rate $O(\tau ^2+h^2)=O(\frac{1}{M^2})$. Numerical results are presented in Tables 1 and 2 at time $t=0.5,\, 1.0,\, 1.5,\, 2.0$. We can observe from both tables that the errors in $L^2$-norm are proportional to $h^2$, which confirm our theoretical results and illustrates that the semi-implicit or explicit treatment of the nonlinear term in the Eq. (1.1) has little impact on the convergence of the whole scheme.

Table 1 $L^2$ errors of the first scheme (2.6)–(2.7) (Example 4.1)

Table 2 $L^2$ errors of the second scheme (2.1)–(2.2) (Example 4.1)

Example 4.2

Secondly, we consider a high order Schrödinger–Poisson–Slater system

$$\begin{aligned}&\text {i}u_t+\Delta u+\psi u+|u|^4 u=g_1, \end{aligned}$$

(4.5)

$$\begin{aligned}&-\Delta \psi =|u|^2+g_2, \end{aligned}$$

(4.6)

in $\Omega =[0,1]\times [0,1]$, with the initial condition $u(x,0)=u_0(x)$ and the homogenous Dirichlet boundary conditions for both u and $\psi$, where $g_1$, $g_2$ are chosen correspondingly to the exact solutions

$$\begin{aligned} u&=2e^{\text {i}t+(x+y)/5}(1+5t^3)x(1-x)y(1-y), \end{aligned}$$

(4.7)

$$\begin{aligned} \psi&=5(1+3t^2+\sin (t))\sin \left( \frac{x}{2}\right) \sin \left( \frac{y}{2}\right) (1-x)(1-y). \end{aligned}$$

(4.8)

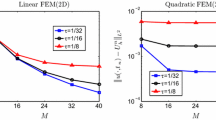
We solve the problem by the two Crank–Nicolson Galerkin schemes given in Sect. 2 with a quadratic FEM. To show the unconditional stability of schemes, we take meshes with $M=10,20,30,40,50$ for each $\tau =\frac{1}{10}, \frac{1}{20}, \frac{1}{40}$ and present in Figs. 1 and 2 the numerical results at $t=1.0$. We observe that, the $L^2$-errors converge to $O(\tau ^2)$ as $\tau /h\rightarrow \infty$ for each fixed time stepsize, which imply that the schemes are stable and the restriction on time step is unnecessary.

Fig. 1

Stability of the first linearized scheme (Example 4.2)

Fig. 2

Stability of the second linearized scheme (Example 4.2)

Example 4.3

Finally, we consider the high order Schrödinger–Poisson–Slater system (4.5)–(4.6) in three-dimensional space with $\Omega =[0,1]\times [0,1]\times [0,1]$ and homogenous Dirichlet boundary conditions. The exact solutions are given by

$$\begin{aligned} u&=10e^{\text {i}t+(x+y+z)/5}(1+5t^3)x(1-x)y(1-y)z(1-z), \end{aligned}$$

(4.9)

$$\begin{aligned} \psi&=10(1+3t^2+\sin (t))\sin \left( \frac{x}{2}\right) \sin \left( \frac{y}{2}\right) \sin \left( \frac{z}{2}\right) (1-x)(1-y)(1-z). \end{aligned}$$

(4.10)

Here, we use the first linearized Crank–Nicolson Galerkin FEM (2.1)–(2.2) with a quadratic FEM to solve the problem. Numerical results are obtained with several different meshes for each $\tau =\frac{1}{10}, \frac{1}{20}, \frac{1}{40}$ at $t=1.0$, and presented in Fig. 3. In previous works, the error estimates in 3-D often required stronger time stepsize conditions than that in 2-D. However, the results in Fig. 3 indicate that the scheme (2.1)–(2.2) is unconditionally stable for the three-dimensional model.

Fig. 3

Stability of the first linearized scheme (Example 4.3)

5 Conclusion

We have proved the optimal $L^2$ error estimates of a linearized Crank–Nicolson Galerkin FEM for a nonlinear Schrödinger–Helmholtz system unconditionally. The theoretical analysis has been confirmed by numerical results obtained in both two and three dimensional spaces. In some other works [10, 28, 29], people often rewrote $\psi$ explicitly from the Eq. (1.2) in terms of a Green function by

$$\begin{aligned} \psi =G(x)*\left( f(|u|)|u|^2\right) , \end{aligned}$$

(5.1)

where G(x) is the Green’s function of the elliptic equation (1.2) and $*$ denotes the convolution. With the formula (5.1), the system (1.1)–(1.3) reduces to a generalized Schrödinger equation with a nonlinear and nonlocal source. Then, the resulting equation was solved by Galerkin FEMs or spectral methods. Clearly, our approach is applicable for such a nonlinear and nonlocal Schrödinger equation to obtain unconditionally optimal error estimates.