Superconvergence analysis of Yee scheme for metamaterial Maxwell’s equations on non-uniform rectangular meshes

Abstract

Since the development of Yee scheme back in 1966, it has become one of the most popular simulation tools for modeling electromagnetic wave propagation in various situations. However, its rigorous error analysis on nonuniform rectangular type grids was carried out until 1994 by Monk and Süli. They showed that the Yee scheme is still second-order convergent on a nonuniform mesh even though the local truncation error is only of first order. In this paper, we extend their results to Maxwell’s equations in metamaterials by a simpler proof, and show the second-order superconvergence in space for the true Yee scheme instead of the only semi-discrete form discussed in Monk and Süli’s original work. Numerical results supporting our analysis are presented.

1 Introduction

The superconvergence study of finite element methods (FEMs) started in the early 1970s, over the years many interesting results have been proved mainly for a variety of equations such as elliptic [3, 4, 6, 7, 25], parabolic [9], hyperbolic [1, 16], KdV [2], and Stokes equations [36]. More details on superconvergence can be found in classic books such as [8, 21, 29, 35]. As for Maxwell’s equations in vacuum, until 1994 Monk carried out the first superconvergence analysis for FEMs [30], and for finite difference method together with Süli [31]. Later more superconvergence results have been obtained on Cartesian grids solved by edge elements [27, 28], nonconforming FEMs [33, 34], discontinuous Galerkin methods [11], and finite volume methods [12, 32].

Inspired by the many exotic potential applications of metamaterials (cf. [13, 14, 24] and references therein), in 2006 we [22] initiated the mathematical study of Maxwell’s equations in metamaterials. In [23], we developed a finite element time-domain (FETD) method for solving the metamaterial model (1)–(4) shown below, and proved that the scheme has an optimal error estimate $O(h)+O(\tau ^2)$ in the $L^2$-norm for the lowest-order edge element, i.e., converges first order in space, and second order in time. But numerical results of [23] showed the superconvergence rate $O(h^2)$ on non-uniform rectangular grids. The observed superconvergence phenomena were proved later for both 2D and 3D models solved by the FETD method on non-uniform rectangular and cubic grids in [18] and [20], respectively.

Compared to the superconvergence results obtained for Maxwell’s equations by FEMs, some superconvergences have also proved for the finite difference time-domain (FDTD) methods (cf. [5, 10, 15, 17, 26]). However, all papers except Monk and Süli [31] are restricted to uniform rectangular grids. In this paper, we extend Monk and Süli’s technique to the more complicated Maxwell’s equations in metamaterials. First, we prove that similar superconvergence results hold true for the metamaterial Maxwell’s equations solved by the FDTD method on staggered non-uniform rectangular grids. Our proof is more succinct than [31]. Second, we present the complete proofs for both the semi- and fully-discrete schemes (i.e, the true Yee scheme), while [31] only showed the proof for the semi-discrete scheme. To our best knowledge, this is the first superconvergence result obtained on Yee scheme for Maxwell’s equations in metamaterial.

The rest of the paper is organized as follows. In Sect. 2, we first derive a semi-discrete finite difference scheme on non-uniform rectangular meshes from a variational form, which will be used late in the error analysis. Then we prove the discrete stability, and the second order convergence rate in space (which is superconvergent) for all field variables in the discrete $L_2$ norm. In Sect. 3, we consider the fully-discrete scheme on non-uniform rectangular meshes. Detailed analysis is present for the discrete stability, and the error estimate which is second order in both time and spatial variables. Numerical results are presented in Sect. 4 to support our theoretical analysis. We conclude the paper in Sect. 5.

2 The semi-discrete scheme

Consider the metamaterial model [22]:

$$\begin{aligned}&\epsilon _0\frac{\partial \varvec{E}}{\partial t} = \nabla \times \varvec{H}- \varvec{J} \end{aligned}$$

(1)

$$\begin{aligned}&\mu _0\frac{\partial \varvec{H}}{\partial t} = -\nabla \times \varvec{E}- \varvec{K} \end{aligned}$$

(2)

$$\begin{aligned}&\frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial \varvec{J}}{\partial t} + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\varvec{J}= \varvec{E} \end{aligned}$$

(3)

$$\begin{aligned}&\frac{1}{\mu _0\omega _{pm}^2}\frac{\partial \varvec{K}}{\partial t} + \frac{\Gamma _m}{\mu _0\omega _{pm}^2}\varvec{K}= \varvec{H} \end{aligned}$$

(4)

supplemented with the perfect conduct (PEC) boundary condition

$$\begin{aligned} \varvec{n}\times \varvec{E}= \mathbf{0} \quad \text{ on }~~\partial \Omega , \end{aligned}$$

(5)

and the initial conditions

$$\begin{aligned} \varvec{E}(\varvec{x},0) = \varvec{E}_0(\varvec{x}), ~~ \varvec{H}(\varvec{x},0) = \varvec{H}_0(\varvec{x}), ~~ \varvec{J}(\varvec{x},0) = \varvec{J}_0(\varvec{x}),~~ \varvec{K}(\varvec{x},0) = \varvec{K}_0(\varvec{x}), \end{aligned}$$

(6)

where $\varvec{n}$ denotes the outward unit normal vector, $\varvec{E}_0(\varvec{x}), \varvec{H}_0(\varvec{x}), \varvec{J}_0(\varvec{x})$ and $\varvec{K}_0(\varvec{x})$ are some given proper functions.

To avoid the technicality of the proof for 3D problems, below we only consider the 2D case of (1)–(6), in which $\varvec{E}=(E_x,E_y), \varvec{H}=H_z:=H, \varvec{J}=(J_x,J_y), \varvec{K}=K_z$, and the curls $\nabla \times \varvec{E}=\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}$ and $\nabla \times H=(\frac{\partial H}{\partial y}, -\frac{\partial H}{\partial x})'$. Here the subindices x, y and z denote the components in the x, y and z directions, respectively. For simplicity, we consider the rectangular domain $\Omega =[a,b]\times [c,d]$, which is discretized by a non-uniform grid

$$\begin{aligned} a=x_0 < x_1 < \cdots < x_{N_x}=b, ~~ c=y_0 < y_1 < \cdots < y_{N_y}=d. \end{aligned}$$

We like to emphasize that our proof and the obtained results can be similarly extend to 3D problem.

Following the classic FDTD scheme, we choose the unknowns $E_x$ (and $J_x$) at the mid-points of the horizontal edges, $E_y$ (and $J_y$) at the mid-points of the vertical edges, and H (and K) at the element centers (cf. Fig. 1). Hence we can denote the corresponding approximate solutions (we suppress the explicit dependence on time t):

$$\begin{aligned}&E_{x,i+\frac{1}{2},j},~~ J_{x,i+\frac{1}{2},j}, ~~i=0, \ldots , N_x-1,~j=0, \ldots , N_y, \\&E_{y,i, j+\frac{1}{2}},~~ J_{y,i,j+\frac{1}{2}}, ~~j=0, \ldots , N_y-1,~i=0, \ldots , N_x, \\&H_{i+\frac{1}{2},j+\frac{1}{2}}, ~~K_{i+\frac{1}{2},j+\frac{1}{2}}, ~~i=0, \ldots , N_x-1,~ j=0, \ldots , N_y-1. \end{aligned}$$

For convenience, we denote the following three types of rectangles

$$\begin{aligned} T_{ij}= & {} (x_i,x_{i+1})\times (y_j,y_{j+1}), ~ T_{i-\frac{1}{2},j}=\left( x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}\right) \times (y_j,y_{j+1}), ~ T_{i,j-\frac{1}{2}}\\= & {} (x_i,x_{i+1}) \times \left( y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}\right) , \end{aligned}$$

and the corresponding areas $|T_{ij}|, |T_{i-\frac{1}{2},j}|$ and $|T_{i,j-\frac{1}{2}}|$, respectively. To distinguish the role of non-uniform mesh, we denote $h_x=\max _{0\le i\le N_x-1}(x_{i+1}-x_i)$ and $h_y=\max _{0\le j\le N_y-1}(y_{j+1}-y_j)$ for the maximal mesh sizes in the x and y directions, respectively. The global mesh size $h=\max (h_x,h_y).$

Fig. 1

The exemplary grid for solving 2D Maxwell’s equations

Integrating the x-component of (1) on $T_{i,j-\frac{1}{2}}$ (for any $0\le i\le N_x-1, 1\le j\le N_y-1$), we obtain

$$\begin{aligned} \int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\epsilon _0\frac{\partial E_x}{\partial t}= & {} \int _{x_i}^{x_{i+1}}\left[ H\left( x,y_{j+\frac{1}{2}},t\right) - H\left( x,y_{j-\frac{1}{2}},t\right) \right] dx\nonumber \\&-\int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}J_x. \end{aligned}$$

(7)

Approximating those integrals in (7) by the mid-point quadrature rule, we have

$$\begin{aligned} \epsilon _0\left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{\partial E_x}{\partial t}\bigg |_{i+\frac{1}{2},j} =(x_{i+1}-x_i)\left( H_{i+\frac{1}{2},j+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}\right) - \left| T_{i,j-\frac{1}{2}}\right| J_{x,i+\frac{1}{2},j}. \end{aligned}$$

(8)

Similarly, integrating the y-component of (1) on $T_{i-\frac{1}{2},j}$ (for any $1\le i\le N_x-1, 0\le j\le N_y-1$) yields

$$\begin{aligned} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\int _{y_j}^{y_{j+1}}\epsilon _0\frac{\partial E_y}{\partial t}= & {} -\int _{y_j}^{y_{j+1}}\left[ H\left( x_{i+\frac{1}{2}},y,t\right) -H\left( x_{i-\frac{1}{2}},y,t\right) \right] dy\nonumber \\&-\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\int _{y_j}^{y_{j+1}}J_y. \end{aligned}$$

(9)

Approximating those integrals in (9) by the mid-point quadrature rule, we have

$$\begin{aligned} \epsilon _0\left| T_{i-\frac{1}{2},j}\right| \cdot \frac{\partial E_y}{\partial t}\bigg |_{i,j+\frac{1}{2}} =-(y_{j+1}-y_j) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}-H_{i-\frac{1}{2},j +\frac{1}{2}}\right) - \left| T_{i-\frac{1}{2},j}\right| J_{y,i,j+\frac{1}{2}}. \end{aligned}$$

(10)

By the same technique, integrating (2) on $T_{ij}$ (for any $0\le i\le N_x-1, 0\le j\le N_y-1$) yields

$$\begin{aligned} \int _{x_i}^{x_{i+1}}\int _{y_j}^{y_{j+1}}\mu _0\frac{\partial H}{\partial t} =-\int _{x_i}^{x_{i+1}}\int _{y_j}^{y_{j+1}}\left( \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right) -\int _{x_i}^{x_{i+1}}\int _{y_j}^{y_{j+1}}K. \end{aligned}$$

(11)

Further application of the mid-point quadrature rule leads to

$$\begin{aligned} \mu _0|T_{ij}|\cdot \frac{\partial H}{\partial t}\bigg |_{i+\frac{1}{2},j+\frac{1}{2}}= & {} -(y_{j+1}-y_j) \left( E_{y,i+1,j+\frac{1}{2}}-E_{y,i,j+\frac{1}{2}}\right) \nonumber \\&+\,(x_{i+1}-x_i)\left( E_{x,i+\frac{1}{2},j+1}-E_{x,i+\frac{1}{2},j}\right) - |T_{ij}|\cdot K_{i+\frac{1}{2},j+\frac{1}{2}}. \nonumber \\ \end{aligned}$$

(12)

Integrating the x-component of (3) on $T_{i,j-\frac{1}{2}}$ (for any $0\le i\le N_x-1, 1\le j\le N_y-1$), we obtain

$$\begin{aligned} \int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial J_x}{\partial t} +\int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}J_x = \int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}E_x. \end{aligned}$$

(13)

Approximating (13) by the mid-point quadrature rule, we have

$$\begin{aligned} \left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial J_x}{\partial t}\bigg |_{i+\frac{1}{2},j} + \left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}J_{x,i+\frac{1}{2},j} = \left| T_{i,j-\frac{1}{2}}\right| \cdot E_{x,i+\frac{1}{2},j}. \nonumber \\ \end{aligned}$$

(14)

Integrating the y-component of (3) on $T_{i-\frac{1}{2},j}$ (for any $1\le i\le N_x-1, 0\le j\le N_y-1$), and using the mid-point quadrature rule, we obtain

$$\begin{aligned} \left| T_{i-\frac{1}{2},j}\right| \cdot \frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial J_y}{\partial t}\bigg |_{i,j+\frac{1}{2}} + \left| T_{i-\frac{1}{2},j}\right| \cdot \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}J_{y,i,j+\frac{1}{2}} = \left| T_{i-\frac{1}{2},j}\right| \cdot E_{y,i,j+\frac{1}{2}}. \qquad \end{aligned}$$

(15)

Similarly, integrating (4) on $T_{ij}$ (for any $0\le i\le N_x-1, 0\le j\le N_y-1$), and using the mid-point quadrature rule, we obtain

$$\begin{aligned} |T_{ij}|\cdot \frac{1}{\mu _0\omega _{pm}^2}\frac{\partial K}{\partial t}\bigg |_{i+\frac{1}{2},j+\frac{1}{2}} + |T_{ij}|\cdot \frac{\Gamma _m}{\mu _0\omega _{pm}^2}K_{i+\frac{1}{2},j+\frac{1}{2}} = |T_{ij}|\cdot H_{i+\frac{1}{2},j+\frac{1}{2}}. \end{aligned}$$

(16)

2.1 The stability analysis

We define the following mesh-dependent energy norms

$$\begin{aligned}&||E_x||^2_E =\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \cdot |E_{x,i+\frac{1}{2},j}|^2, \\&||E_y||^2_E =\sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \cdot \left| E_{y,i,j+\frac{1}{2}}\right| ^2, \\&||H||^2_H =\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot \left| H_{i+\frac{1}{2},j+\frac{1}{2}}\right| ^2, \\&||J_x||^2_J =\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}} \left| T_{i,j-\frac{1}{2}}\right| \cdot \left| J_{x,i+\frac{1}{2},j}\right| ^2, \\&||J_y||^2_J =\sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} \left| T_{i-\frac{1}{2},j}\right| \cdot \left| J_{y,i,j+\frac{1}{2}}\right| ^2, \\&||K||^2_K =\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot \left| K_{i+\frac{1}{2},j+\frac{1}{2}}\right| ^2. \end{aligned}$$

First, we can prove the following energy conservation for our semi-discrete scheme.

Theorem 2.1

The solution of the semi-discrete scheme (8)–(16) satisfies the global energy identity:

$$\begin{aligned}&\frac{1}{2}\bigg [\epsilon _0\left( ||E_x||^2_E+||E_y||^2_E\right) +\mu _0||H||^2_H\nonumber \\&\qquad + \frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}||K||^2_K \bigg ](t) \nonumber \\&\qquad +\int _0^t\left[ \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) +\frac{\Gamma _m}{\mu _0\omega _{pm}^2}||K||^2_K\right] dt \nonumber \\&\quad = \frac{1}{2}\bigg [\epsilon _0\left( ||E_x||^2_E+||E_y||^2_E\right) +\mu _0||H||^2_H + \frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) \nonumber \\&\qquad +\frac{1}{\mu _0\omega _{pm}^2}||K||^2_K\bigg ](0) \end{aligned}$$

(17)

holds true for any $t\in [0,T]$.

Proof

Multiplying (8) by $E_{x,i+\frac{1}{2},j}$, (10) by $E_{y,i,j+\frac{1}{2}}$, (12) by $H_{i+\frac{1}{2},j+\frac{1}{2}}$, (14) by $J_{x,i+\frac{1}{2},j}$, (15) by $J_{y,i,j+\frac{1}{2}}$, and (16) by $K_{i+\frac{1}{2},j+\frac{1}{2}}$, summing up each over its corresponding rectangular elements, then adding all results together, we obtain the sum of the right hand side as

$$\begin{aligned} RHS= & {} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}(x_{i+1}-x_i) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}\right) E_{x,i+\frac{1}{2},j} \nonumber \\&-\sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}(y_{j+1}-y_j) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}-H_{i-\frac{1}{2},j+\frac{1}{2}}\right) E_{y,i,j+\frac{1}{2}} \nonumber \\&-\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}(y_{j+1}-y_j) \left( E_{y,i+1,j+\frac{1}{2}}-E_{y,i,j+\frac{1}{2}}\right) H_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\&+\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}(x_{i+1}-x_i) \left( E_{x,i+\frac{1}{2},j+1}-E_{x,i+\frac{1}{2},j}\right) H_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\= & {} \sum _{0\le i \le N_x-1}(x_{i+1}-x_i)\sum _{0\le j \le N_y-1} \left[ H_{i+\frac{1}{2},j+\frac{1}{2}}E_{x,i+\frac{1}{2},j+1} -H_{i+\frac{1}{2},j-\frac{1}{2}}E_{x,i+\frac{1}{2},j}\right] \nonumber \\&-\sum _{0\le j \le N_y-1}(y_{j+1}-y_j)\sum _{0\le i \le N_x-1} \left[ H_{i+\frac{1}{2},j+\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}} -H_{i-\frac{1}{2},j+\frac{1}{2}}E_{y,i,j+\frac{1}{2}}\right] \nonumber \\= & {} \sum _{0\le i \le N_x-1}(x_{i+1}-x_i) \left[ H_{i+\frac{1}{2},N_y-\frac{1}{2}}E_{x,i+\frac{1}{2},N_y} -H_{i+\frac{1}{2},-\frac{1}{2}}E_{x,i+\frac{1}{2},0}\right] \nonumber \\&-\sum _{0\le j \le N_y-1}(y_{j+1}-y_j) \left[ H_{N_x-\frac{1}{2},j+\frac{1}{2}}E_{y,N_x,j+\frac{1}{2}} -H_{-\frac{1}{2},j+\frac{1}{2}}E_{y,0,j+\frac{1}{2}}\right] =0, \nonumber \\ \end{aligned}$$

(18)

where we used the PEC boundary condition (5), which in our 2D case is equivalent to

$$\begin{aligned} E_{x,i+\frac{1}{2},N_y}=E_{x,i+\frac{1}{2},0}=0, ~~E_{y,N_x,j+\frac{1}{2}}=E_{y,0,j+\frac{1}{2}}=0, \end{aligned}$$

(19)

for all i and j.

Using the above defined energy norms, the sum of the left hand side corresponding to the above operation is given as

$$\begin{aligned} LHS= & {} \frac{1}{2}\frac{d}{dt}\bigg [\epsilon _0\left( ||E_x||^2_E+||E_y||^2_E\right) +\mu _0||H||^2_H\nonumber \\&+\frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}||K||^2_K\bigg ] \nonumber \\&+ \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) + \frac{\Gamma _m}{\mu _0\omega _{pm}^2}||K||^2_K. \end{aligned}$$

(20)

Equating (18) and (20), and integrating the resultant leads to the global conservation identity. $\square$

Dropping the non-negative terms on the left hand side of (17), we can easily obtain the stability for our semi-discrete scheme.

Lemma 2.1

For any $t\in [0,T]$, the solution of the semi-discrete scheme (8)–(16) satisfies the following stability:

$$\begin{aligned}&\left[ \epsilon _0\left( ||E_x||^2_E+||E_y||^2_E\right) +\mu _0||H||^2_H + \frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) \right. \nonumber \\&\qquad \left. +\frac{1}{\mu _0\omega _{pm}^2}||K||^2_K\right] (t) \nonumber \\&\quad \le \left[ \epsilon _0\left( ||E_x||^2_E+||E_y||^2_E\right) +\mu _0||H||^2_H + \frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x||^2_J+||J_y||^2_J\right) \right. \nonumber \\&\qquad \left. +\frac{1}{\mu _0\omega _{pm}^2}||K||^2_K\right] (0). \end{aligned}$$

(21)

2.2 The error estimate

To make the error analysis easy to follow, we denote the errors by their corresponding script letters. For example, the error of $E_x$ at point $(x_{i+\frac{1}{2}},y_j,t)$ is denoted by $\mathcal {E}_{x,i+\frac{1}{2},j}=E_x(x_{i+\frac{1}{2}},y_j,t)-E_{x,i+\frac{1}{2},j}$, where $E_x(x_{i+\frac{1}{2}},y_j,t)$ and $E_{x,i+\frac{1}{2},j}$ denote the exact and numerical solutions of $E_x$ at point $(x_{i+\frac{1}{2}},y_j,t)$, respectively. Similarly, we denote errors

$$\begin{aligned}&\mathcal {E}_{y,i,j+\frac{1}{2}}= E_y\left( x_i,y_{j+\frac{1}{2}},t\right) -E_{y,i,j+\frac{1}{2}},\nonumber \\&\mathcal {H}_{i+\frac{1}{2},j+ \frac{1}{2}}=H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) -H_{i+\frac{1}{2},j+\frac{1}{2}}, \\&\mathcal {J}_{x,i+\frac{1}{2},j}= J_x\left( x_{i+\frac{1}{2}},y_j,t\right) -J_{x,i+\frac{1}{2},j}, \quad \mathcal {J}_{y,i,j+\frac{1}{2}} =J_y\left( x_i,y_{j+\frac{1}{2}},t\right) -J_{y,i,j+\frac{1}{2}},\\&\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}} =K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - K_{i+\frac{1}{2},j+\frac{1}{2}}. \end{aligned}$$

By the definition of errors, and from (7) and (8), we obtain

$$\begin{aligned}&\epsilon _0\left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{\partial \mathcal {E}_x}{\partial t}\bigg |_{i+\frac{1}{2},j} = \epsilon _0\left( \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \frac{\partial E_x}{\partial t}\left( x_{i+\frac{1}{2}},y_j,t\right) -\left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{\partial E_x}{\partial t}\bigg |_{i+\frac{1}{2},j}\right) \\&\quad = \epsilon _0\left( \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \frac{\partial E_x}{\partial t} \left( x_{i+\frac{1}{2}},y_j,t\right) - \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \frac{\partial E_x}{\partial t}(x,y,t)\right) \\&\qquad +\int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) -H\left( x,y_{j-\frac{1}{2}},t\right) \right) dx -\int \!\!\! \int _{T_{i,j-\frac{1}{2}}} J_x(x,y,t) \\&\qquad -\,(x_{i+1}-x_i) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}\right) + \left| T_{i,j-\frac{1}{2}}\right| \cdot J_{x,i+\frac{1}{2},j} \\&\quad = \epsilon _0\left( \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \frac{\partial E_x}{\partial t}\left( x_{i+\frac{1}{2}},y_j,t\right) - \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \frac{\partial E_x}{\partial t}(x,y,t)\right) \\&\qquad +\,(x_{i+1}-x_i)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} - \mathcal {H}_{i+\frac{1}{2},j-\frac{1}{2}}\right) +\int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) \right. \\&\qquad \left. -\,H\left( x,y_{j-\frac{1}{2}},t\right) \right) dx \\&\qquad -\,(x_{i+1}-x_i)\left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) -H\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}},t\right) \right) -\left| T_{i,j-\frac{1}{2}}\right| \cdot \mathcal {J}_{x,i+\frac{1}{2},j} \\&\qquad + \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} J_x\left( x_{i+\frac{1}{2}},y_j,t\right) - \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} J_x(x,y,t), \end{aligned}$$

which leads to the error equation for $E_x$:

$$\begin{aligned}&\epsilon _0\left| T_{i,j-\frac{1}{2}}\right| {\cdot } \frac{\partial \mathcal {E}_x}{\partial t}\bigg |_{i+\frac{1}{2},j} =(x_{i+1}-x_i)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} - \mathcal {H}_{i+\frac{1}{2},j-\frac{1}{2}}\right) -\left| T_{i,j-\frac{1}{2}}\right| {\cdot } \mathcal {J}_{x,i+\frac{1}{2},j} \nonumber \\&\qquad +\,\epsilon _0(\int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \left( \frac{\partial E_x}{\partial t}\left( x_{i+\frac{1}{2}},y_j,t\right) -\frac{\partial E_x}{\partial t}(x,y,t)\right) \nonumber \\&\qquad +\left[ \int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) - H\left( x,y_{j-\frac{1}{2}},t\right) \right) dx\right. \nonumber \\&\qquad \left. -\int _{x_i}^{x_{i+1}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) -H\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}},t\right) \right) dx\right] \nonumber \\&\qquad + \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \left( J_x\left( x_{i+\frac{1}{2}},y_j,t\right) - J_x(x,y,t)\right) \nonumber \\&\quad := (x_{i+1}-x_i)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} - \mathcal {H}_{i+\frac{1}{2},j-\frac{1}{2}}\right) -\left| T_{i,j-\frac{1}{2}}\right| \cdot \mathcal {J}_{x,i+\frac{1}{2},j}\nonumber \\&\qquad \quad + r_{1,ij}+r_{2,ij}+r_{3,ij}. \end{aligned}$$

(22)

Similarly, we can obtain the error equation for $E_y$:

$$\begin{aligned}&\epsilon _0\left| T_{i-\frac{1}{2},j}\right| \cdot \frac{\partial \mathcal {E}_y}{\partial t}\bigg |_{i,j+\frac{1}{2}} =-(y_{j+1}-y_j)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} - \mathcal {H}_{i-\frac{1}{2},j+\frac{1}{2}}\right) \nonumber \\&\qquad \quad -\left| T_{i-\frac{1}{2},j}\right| \cdot \mathcal {J}_{y,i,j+\frac{1}{2}} \nonumber \\&\qquad \qquad +\,\epsilon _0\int \!\!\! \int _{T_{i-\frac{1}{2},j}} \left( \frac{\partial E_y}{\partial t}\left( x_i,y_{j+\frac{1}{2}},t\right) - \frac{\partial E_y}{\partial t}(x,y,t)\right) \nonumber \\&\qquad -\left[ \int _{y_j}^{y_{j+1}} \left( H\left( x_{i+\frac{1}{2}},y,t\right) - H\left( x_{i-\frac{1}{2}},y,t\right) \right) dy\right. \nonumber \\&\qquad \left. -\int _{y_j}^{y_{j+1}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) -H\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}},t\right) \right) dy\right] \nonumber \\&\qquad + \int \!\!\! \int _{T_{i-\frac{1}{2},j}} \left( J_y\left( x_i,y_{j+\frac{1}{2}},t\right) - J_y(x,y,t)\right) \nonumber \\&\quad := -(y_{j+1}-y_j)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} - \mathcal {H}_{i-\frac{1}{2},j+\frac{1}{2}}\right) \nonumber \\&\qquad -\left| T_{i-\frac{1}{2},j}\right| \cdot \mathcal {J}_{y,i,j+\frac{1}{2}} + r_{4,ij}+r_{5,ij}+r_{6,ij}. \end{aligned}$$

(23)

By the same technique, we can obtain the error equation for H:

$$\begin{aligned}&\mu _0|T_{ij}|\cdot \frac{\partial \mathcal {H}}{\partial t}\bigg |_{i+\frac{1}{2},j+\frac{1}{2}} =-(y_{j+1}-y_j)\left( \mathcal {E}_{y,i+1,j+\frac{1}{2}} - \mathcal {E}_{y,i,j+\frac{1}{2}}\right) \nonumber \\&\qquad +\, (x_{i+1}-x_i)\left( \mathcal {E}_{x,i+\frac{1}{2},j+1} - \mathcal {E}_{x,i+\frac{1}{2},j}\right) -|T_{ij}|\cdot \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\qquad +\,\mu _0\int \!\!\! \int _{T_{ij}} \left( \frac{\partial H}{\partial t}\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - \frac{\partial H}{\partial t}(x,y,t)\right) \nonumber \\&\qquad -\left[ \int _{y_j}^{y_{j+1}}(E_y(x_{i+1},y,t)-E_y(x_i,y,t))dy\right. \nonumber \\&\qquad \left. -\int _{y_j}^{y_{j+1}} \left( E_y(x_{i+1},y_{j+\frac{1}{2}},t)-E_y(x_i,y_{j+\frac{1}{2}},t)\right) dy\right] \nonumber \\&\qquad + \int \!\!\! \int _{T_{ij}} \left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - K(x,y,t)\right) \nonumber \\&\quad := -(y_{j+1}-y_j)\left( \mathcal {E}_{y,i+1,j+\frac{1}{2}} - \mathcal {E}_{y,i,j+\frac{1}{2}}\right) \nonumber \\&\qquad + \,(x_{i+1}-x_i)\left( \mathcal {E}_{x,i+\frac{1}{2},j+1} - \mathcal {E}_{x,i+\frac{1}{2},j}\right) -|T_{ij}|{\cdot } \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}} + r_{7,ij}+r_{8,ij}+r_{9,ij}. \nonumber \\ \end{aligned}$$

(24)

The error equations for $\varvec{J}$ and K are easily obtained and given respectively by:

$$\begin{aligned}&\left| T_{i,j-\frac{1}{2}}\right| \cdot \frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial \mathcal {J}_x}{\partial t} \bigg |_{i+\frac{1}{2},j} + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\left| T_{i,j-\frac{1}{2}}\right| \cdot \mathcal {J}_{x,i+\frac{1}{2},j} \nonumber \\&\quad = \left| T_{i,j-\frac{1}{2}}\right| \cdot \mathcal {E}_{x,i+\frac{1}{2},j} + \frac{1}{\epsilon _0\omega _{pe}^2} \int \!\!\! \int _{T_{i,j-\frac{1}{2}}}\left( \frac{\partial J_x}{\partial t} \left( x_{i+\frac{1}{2}},y_j,t\right) - \frac{\partial J_x}{\partial t}(x,y,t)\right) \nonumber \\&\qquad + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \left( J_x\left( x_{i+\frac{1}{2}},y_j,t\right) - J_x(x,y,t)\right) \nonumber \\&\qquad -\int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \left( E_x\left( x_{i+\frac{1}{2}},y_j,t\right) - E_x(x,y,t)\right) \nonumber \\&\quad := \left| T_{i,j-\frac{1}{2}}\right| \cdot \mathcal {E}_{x,i+\frac{1}{2},j} + r_{10,ij}+r_{11,ij}+r_{12,ij}, \end{aligned}$$

(25)

$$\begin{aligned}&\left| T_{i-\frac{1}{2},j}\right| \cdot \frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial \mathcal {J}_y}{\partial t}\bigg |_{i,j+\frac{1}{2}} + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\left| T_{i-\frac{1}{2},j}\right| \cdot \mathcal {J}_{y,i,j+\frac{1}{2}} \nonumber \\&\quad = \left| T_{i-\frac{1}{2},j}\right| \cdot \mathcal {E}_{y,i,j+\frac{1}{2}} + \frac{1}{\epsilon _0\omega _{pe}^2} \int \!\!\! \int _{T_{i-\frac{1}{2},j}} \left( \frac{\partial J_y}{\partial t}\left( x_i, y_{j+\frac{1}{2}},t\right) - \frac{\partial J_y}{\partial t}(x,y,t)\right) \nonumber \\&\qquad + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \int \!\!\! \int _{T_{i-\frac{1}{2},j}} \left( J_y\left( x_i, y_{j+\frac{1}{2}},t\right) - J_y(x,y,t)\right) \nonumber \\&\qquad -\int \!\!\! \int _{T_{i-\frac{1}{2},j}} \left( E_y\left( x_i,y_{j+\frac{1}{2}},t\right) - E_y(x,y,t)\right) \nonumber \\&\quad := \left| T_{i-\frac{1}{2},j}\right| \cdot \mathcal {E}_{y,i,j+\frac{1}{2}} + r_{13,ij}+r_{14,ij}+r_{15,ij}, \end{aligned}$$

(26)

and

$$\begin{aligned}&|T_{ij}|\cdot \frac{1}{\mu _0\omega _{pm}^2}\frac{\partial \mathcal {K}}{\partial t}\bigg |_{i+\frac{1}{2},j+\frac{1}{2}} + \frac{\Gamma _m}{\mu _0\omega _{pm}^2}|T_{ij}|\cdot \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}} \nonumber \\&\quad = |T_{ij}|\cdot \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} + \frac{1}{\mu _0\omega _{pm}^2} \int \!\!\! \int _{T_{ij}} \left( \frac{\partial K}{\partial t}\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - \frac{\partial K}{\partial t}(x,y,t)\right) \nonumber \\&\qquad + \frac{\Gamma _m}{\mu _0\omega _{pm}^2} \int \!\!\! \int _{T_{ij}} \left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - K(x,y,t)\right) \nonumber \\&\qquad +\int \!\!\! \int _{T_{ij}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - H(x,y,t)\right) \nonumber \\&\quad := |T_{ij}|\cdot \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}} + r_{16,ij}+r_{17,ij}+r_{18,ij}. \end{aligned}$$

(27)

With the above preparations, we can obtain the following superconvergence result.

Theorem 2.2

Suppose that the solution of the model problem (1)–(6) possesses the following regularity property:

$$\begin{aligned}&E_x, E_y, H \in C([0,T]; C^3(\overline{\Omega }))\cap C^1([0,T]; C^2(\overline{\Omega })), \\&J_x, J_y, K \in C([0,T]; C^2(\overline{\Omega }))\cap C^1([0,T]; C^2(\overline{\Omega })). \end{aligned}$$

Under the assumption that if the following initial error

$$\begin{aligned}&\bigg [\epsilon _0\left( ||\mathcal {E}_x||^2_E+||\mathcal {E}_y||^2_E\right) + \mu _0||\mathcal {H}||^2_H +\frac{1}{\epsilon _0\omega _{pe}^2} \left( ||\mathcal {J}_x||^2_J+||\mathcal {J}_y||^2_J\right) \nonumber \\&\quad +\frac{1}{\mu _0\omega _{pm}^2}||\mathcal {K}||^2_K\bigg ](0) \le C\left( h_x^2+h_y^2\right) ^2, \end{aligned}$$

(28)

holds true, then we have

$$\begin{aligned}&\max _{0\le t\le T}\left[ \epsilon _0\left( ||\mathcal {E}_x||^2_E+||\mathcal {E}_y||^2_E\right) +\mu _0||\mathcal {H}||^2_H +\frac{1}{\epsilon _0\omega _{pe}^2}\left( ||\mathcal {J}_x||^2_J+||\mathcal {J}_y||^2_J\right) \right. \\&\quad \left. +\frac{1}{\mu _0\omega _{pm}^2}||\mathcal {K}||^2_K(t)\right] \le CT\left( h_x^2+h_y^2\right) ^2. \end{aligned}$$

Proof

By the Taylor expansion, for any function f we can easily prove that

$$\begin{aligned}&\int \!\!\! \int _{T_{i,j -\frac{1}{2}}}\left( f(x,y,t)-f\left( x_{i+\frac{1}{2}},y_j,t\right) \right) dxdy \nonumber \\&\quad = \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} \left[ \left( x-x_{i+\frac{1}{2}}\right) \frac{\partial f}{\partial x}(p_*) + (y-y_j)\frac{\partial f}{\partial y}(p_*) +\frac{1}{2}\left( x-x_{i+\frac{1}{2}}\right) ^2\frac{\partial ^2 f}{\partial x^2}(p_1) \right. \nonumber \\&\qquad \left. + \left( x-x_{i+\frac{1}{2}}\right) (y-y_j)\frac{\partial ^2 f}{\partial x\partial y}(p_2) + \frac{1}{2}(y-y_j)^2\frac{\partial ^2 f}{\partial y^2}(p_3)\right] \nonumber \\&\quad \le \int \!\!\! \int _{T_{i,j-\frac{1}{2}}} C\left[ h_x^2\left| \frac{\partial ^2 f}{\partial x^2}\right| _{\infty } +h_y^2\left| \frac{\partial ^2 f}{\partial y^2}\right| _{\infty }\right] , \end{aligned}$$

(29)

where we denote $p_*=(x_{i+\frac{1}{2}},y_j,t)$, and $p_1, p_2$ and $p_3$ for some midpoints between $p_*$ and (x, y, t).

Applying (29) to $f=\frac{\partial E_x}{\partial t}$, we obtain

$$\begin{aligned} r_{1,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 E_x}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 E_x}{\partial t\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

It is easy to see that for any function f, we have

$$\begin{aligned}&\left| \int _{y_j}^{y_{j+1}}(f(y)-f\left( y_{j+\frac{1}{2}}\right) dy\right| \nonumber \\&\quad =\left| \int _{y_j}^{y_{j+1}} \left[ \left( y-y_{j+\frac{1}{2}}\right) \frac{\partial f}{\partial y}\left( y_{j+\frac{1}{2}}\right) +\int _{y_{j+\frac{1}{2}}}^y(y-\eta ) \frac{\partial ^2 f}{\partial y^2}(\eta )d\eta \right] dy\right| \nonumber \\&\quad = \left| \int _{y_j}^{y_{j+1}} \left[ \int _{y_{j+\frac{1}{2}}}^y(y-\eta ) \frac{\partial ^2 f}{\partial y^2}(\eta )d\eta \right] dy\right| \le Ch_y^2 \int _{y_j}^{y_{j+1}}\left| \frac{\partial ^2 f}{\partial y^2}(\eta ) \left| d\eta \right. \right. \nonumber \\&\quad \left. \left. \le Ch_y^3\right| \frac{\partial ^2 f}{\partial y^2}(\eta )\right| _{\infty }, \end{aligned}$$

(30)

which leads to

$$\begin{aligned} \sum _{0\le i\le N_x-1}\sum _{0\le j\le N_y-1}\left| \int _{y_j}^{y_{j+1}}(f(y)-f\left( y_{j+\frac{1}{2}}\right) dy\right| \le Ch\left| \frac{\partial ^2 f}{\partial y^2}(\eta )\right| _{\infty }. \end{aligned}$$

(31)

Applying (31) to each single integral in (22)–(27), we will only obtain O(h) convergence rate. This was pointed out by Monk and Süli in [31]. They managed to prove the $O(h^2)$ rate by using a special structure of the local errors. Here we will use a simpler method to prove $O(h^2)$ error estimate.

Note that

$$\begin{aligned}&\int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) -H(x,y_{j-\frac{1}{2}},t)\right) dx\\&\qquad -\int _{x_i}^{x_{i+1}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t\right) - H\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}},t\right) \right) dx \nonumber \\&\quad =\int _{x_i}^{x_{i+1}} \left[ \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( \frac{\partial H}{\partial y}(x,y,t) - \frac{\partial H}{\partial y}\left( x_{i+\frac{1}{2}},y,t\right) \right) dy\right] dx\nonumber \\&\quad =O\left( h_x^2\right) \left| \frac{\partial ^3 H}{\partial y \partial x^2}\right| _{\infty }\left| T_{i,j-\frac{1}{2}}\right| , \end{aligned}$$

which leads to

$$\begin{aligned} r_{2,ij}=O\left( h_x^2\right) \left| \frac{\partial ^3 H}{\partial y\partial x^2}\right| _{\infty }\cdot \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

We like to remark that we can reduce the regularity requirement if we use the integral residue as shown in (29).

Applying (29) to $f=J_x$, we obtain

$$\begin{aligned} r_{3,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_x}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 J_x}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

By carrying out the above technique to the $E_y$ error equation, we have

$$\begin{aligned}&r_{4,ij}= \left( O\left( h_x^2\right) \left| \frac{\partial ^3 E_y}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 E_y}{\partial t\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i-\frac{1}{2},j}\right| , \\&r_{5,ij}=-\int \!\!\! \int _{T_{i-\frac{1}{2},j}}\left( \frac{\partial H}{\partial x}(x,y,t) -\frac{\partial H}{\partial x}\left( x,y_{j+\frac{1}{2}},t\right) \right) \\&\quad \quad =O\left( h_y^2\right) \left| \frac{\partial ^3 H}{\partial x\partial y^2}\right| _{\infty }\left| T_{i-\frac{1}{2},j}\right| , \\&r_{6,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_y}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 J_y}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i-\frac{1}{2},j}\right| . \end{aligned}$$

Using the same technique to the H error equation, we have

$$\begin{aligned}&r_{7,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 H}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 H}{\partial t\partial y^2}\right| _{\infty }\right) \cdot |T_{ij}|, \\&r_{8,ij}=-\int \!\!\! \int _{T_{ij}}\left( \frac{\partial E_y}{\partial x}(x,y,t) -\frac{\partial E_y}{\partial x} \left( x,y_{j+\frac{1}{2}},t\right) \right) =O\left( h_y^2\right) \left| \frac{\partial ^3 E_y}{\partial x\partial y^2}\right| _{\infty }|T_{ij}|, \\&r_{9,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 K}{\partial x^2}\right| _{\infty } +O\left( h_y^2\right) \left| \frac{\partial ^2 K}{\partial y^2}\right| _{\infty }\right) \cdot |T_{ij}|. \end{aligned}$$

Similarly, we can obtain the following estimates for the $J_x, J_y$ and K error equations, respectively,

$$\begin{aligned}&r_{10,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 J_x}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 J_x}{\partial t\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i,j-\frac{1}{2}}\right| , \\&r_{11,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_x}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 J_x}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i,j-\frac{1}{2}}\right| , \\&r_{12,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 E_x}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 E_x}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i,j-\frac{1}{2}}\right| ,\\&r_{13,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 J_y}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 J_y}{\partial t\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i-\frac{1}{2},j}\right| , \\&r_{14,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_y}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 J_y}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i-\frac{1}{2},j}\right| , \\&r_{15,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 E_y}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 E_y}{\partial y^2}\right| _{\infty }\right) \cdot \left| T_{i-\frac{1}{2},j}\right| , \end{aligned}$$

and

$$\begin{aligned}&r_{16,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 K}{\partial t\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^3 K}{\partial t\partial y^2}\right| _{\infty }\right) \cdot |T_{ij}|, \\&r_{17,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 K}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 K}{\partial y^2}\right| _{\infty }\right) \cdot |T_{ij}|, \\&r_{18,ij}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 H}{\partial x^2}\right| _{\infty }+O\left( h_y^2\right) \left| \frac{\partial ^2 H}{\partial y^2}\right| _{\infty }\right) \cdot |T_{ij}|. \end{aligned}$$

Denote the error energy

$$\begin{aligned} Q(t)= & {} [\epsilon _0\left( ||\mathcal {E}_x||^2_E+||\mathcal {E}_y||^2_E\right) +\mu _0||\mathcal {H}||^2_H\\&+\,\frac{1}{\epsilon _0\omega _{pe}^2} \left( ||\mathcal {J}_x||^2_J+||\mathcal {J}_y||^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}||\mathcal {K}||^2_K](t). \end{aligned}$$

Multiplying $\mathcal {E}_{x,i+\frac{1}{2},j}$ to (22), $\mathcal {E}_{y,i,j+\frac{1}{2}}$ to (23), $\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}$ to (24), $\mathcal {J}_{x,i+\frac{1}{2},j}$ to (25), $\mathcal {J}_{y,i,j+\frac{1}{2}}$ to (26), $\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}$ to (27), summing up the results for all i and j, using estimates such as the following:

$$\begin{aligned} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}r_{1,ij}\mathcal {E}_{x,i+\frac{1}{2},j}\le & {} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}} \left[ \delta \left| T_{i,j-\frac{1}{2}}\right| \cdot \left| \mathcal {E}_{x,i+\frac{1}{2},j}\right| ^2\right. \\&\left. + \frac{1}{4\delta }\left( O\left( h_x^2\right) +O\left( h_y^2\right) \right) ^2 \left| T_{i,j-\frac{1}{2}}\right| \right] \\\le & {} \delta ||\mathcal {E}_x||^2_E + \frac{1}{4\delta }(O\left( h_x^2\right) +O\left( h_y^2\right) )^2, \end{aligned}$$

and using the estimate (18) with E and H replaced by $\mathcal {E}$ and $\mathcal {H}$, respectively, we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}Q(t) + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \left( ||\mathcal {J}_x||^2_J+||\mathcal {J}_y||^2_J\right) +\frac{\Gamma _m}{\mu _0\omega _{pm}^2}||\mathcal {K}||^2_K \le C\left( h_x^2+h_y^2\right) ^2+\frac{\delta }{2}Q(t), \end{aligned}$$

where $\delta >0$ is a small constant.

Integrating the above inequality from 0 to t, we have

$$\begin{aligned} Q(t) \le Q(0) + C\left( h_x^2+h_y^2\right) ^2t +\delta \int _0^tQ(s)ds. \end{aligned}$$

(32)

Suppose that $t_*$ achieves the maximum of Q(s) on the interval [0, t], i.e., $\max _{0\le s\le t}Q(s)=Q(t_*)$. Using $t=t_*$ in (32), we obtain

$$\begin{aligned} Q(t_*) \le Q(0) + C\left( h_x^2+h_y^2\right) ^2t_*+\delta t_*Q(t_*). \end{aligned}$$

(33)

Choosing $\delta$ small enough such that $\delta t_*<1$, and using the assumption (80), we complete the proof. $\square$

3 The fully discrete scheme

To construct a fully discrete scheme, we divide the time interval [0, T] into $N_t+2$ uniform intervals, i.e., we have discrete times $0=t_0<t_1<\cdots < t_{N_t+2}=T.$

Approximating those time directives properly in the semi-discrete schemes (8), (10), (12), (14), (15), and (16), we can obtain the following fully-discrete scheme: Given initial approximations $E_{x,i+\frac{1}{2},j}^{0},E_{y,i,j+\frac{1}{2}}^{0}$, $H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}, J_{x,i+\frac{1}{2},j}^{\frac{1}{2}},J_{y,i,j+\frac{1}{2}}^{\frac{1}{2}}$, $K_{i+\frac{1}{2},j+\frac{1}{2}}^{1},$ for any $0\le n\le N_t$, solve $E_{x,i+\frac{1}{2},j}^{n+1},E_{y,i,j+\frac{1}{2}}^{n+1}$, $H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}, J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}},J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}}$, $K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2}$ from:

$$\begin{aligned}&\epsilon _0\frac{E_{x,i+\frac{1}{2},j}^{n+1}-E_{x,i+\frac{1}{2},j}^{n}}{\tau } =\frac{H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} -J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}, \end{aligned}$$

(34)

$$\begin{aligned}&\epsilon _0\frac{E_{y,i,j+\frac{1}{2}}^{n+1}-E_{y,i,j+\frac{1}{2}}^{n}}{\tau } =-\frac{H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} -J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}, \end{aligned}$$

(35)

$$\begin{aligned}&\mu _0\frac{H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}}{\tau } =-\frac{E_{y,i+1,j+\frac{1}{2}}^{n+1}-E_{y,i,j+\frac{1}{2}}^{n+1}}{x_{i+1}-x_i}\nonumber \\&\quad +\frac{E_{x,i+\frac{1}{2},j+1}^{n+1}-E_{x,i+\frac{1}{2},j}^{n+1}}{y_{j+1}-y_j} -K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}, \end{aligned}$$

(36)

$$\begin{aligned}&\frac{1}{\epsilon _0\omega _{pe}^2}\frac{J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} -J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}}{\tau } + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\frac{J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} +J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}}{2} =E_{x,i+\frac{1}{2},j}^{n+1}, \end{aligned}$$

(37)

$$\begin{aligned}&\frac{1}{\epsilon _0\omega _{pe}^2}\frac{J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}} -J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}}{\tau } + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}\frac{J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}} +J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}}{2} =E_{y,i,j+\frac{1}{2}}^{n+1}, \end{aligned}$$

(38)

$$\begin{aligned}&\frac{1}{\mu _0\omega _{pm}^2} \frac{K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2}-K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}}{\tau } + \frac{\Gamma _m}{\mu _0\omega _{pm}^2}\frac{K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} +K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}}{2} =H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}. \nonumber \\ \end{aligned}$$

(39)

Let $C_v=1/\sqrt{\epsilon _0\mu _0}$ be the wave propagation speed in free space. For any grid function $u_{i,j}$, let us denote the backward difference operators $\nabla _x$ and $\nabla _y$:

$$\begin{aligned} \nabla _x u_{i+1,j}=\frac{u_{i+1,j}-u_{i,j}}{x_{i+1}-x_i}, \quad \nabla _y u_{i,j+1}=\frac{u_{i,j+1}-u_{i,j}}{y_{j+1}-y_j}. \end{aligned}$$

Furthermore, we denote the constant $C_{inv}>0$ satisfying the inverse inequality

$$\begin{aligned} ||\nabla _x u|| \le C_{inv}h_x^{-1}||u||, \quad ||\nabla _y u|| \le C_{inv}h_y^{-1}||u||, \end{aligned}$$

(40)

for any energy norm defined earlier.

3.1 The stability analysis

Theorem 3.1

Assume that the time step size $\tau$ satisfies the constraint

$$\begin{aligned} \tau \le \min \left( \frac{C_{inv}h_y}{2C_v}, \frac{C_{inv}h_x}{2C_v}, \frac{1}{2\omega _{pe}}, \frac{1}{2\omega _{pm}}\right) , \end{aligned}$$

(41)

then the solution of the fully discrete scheme (34)–(39) satisfies the following stability: For any $1\le n\le N_t$,

$$\begin{aligned}&\epsilon _0\left( ||E_x^{n+1}||_E^2+||E_y^{n+1}||_E^2\right) +\mu _0||H^{n+\frac{3}{2}}||^2_H\nonumber \\&\qquad +\frac{1}{\epsilon _0\omega _{pe}^2} \left( \left| \left| J_x^{n+\frac{3}{2}}\right| \right| ^2_J +\left| \left| J_y^{n+\frac{3}{2}}\right| \right| ^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}||K^{n+2}||^2_K \nonumber \\&\quad \le C\bigg [\epsilon _0 \left( \left| \left| E_x^{0}\right| \right| _E^2 +\left| \left| E_y^{0}\right| \right| _E^2\right) +\mu _0||H^{\frac{1}{2}}||^2_H\nonumber \\&\qquad +\frac{1}{\epsilon _0\omega _{pe}^2}\left( ||J_x^{\frac{1}{2}}||^2_J +\left| \left| J_y^{\frac{1}{2}}\right| \right| ^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}||K^{1}||^2_K\bigg ], \end{aligned}$$

(42)

where the constant $C>0$ is independent of $\tau , h_x$ and $h_y.$

Proof

Multiplying (34) by $\tau |T_{i,j-\frac{1}{2}}|(E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n})$, (35) by $\tau |T_{i-\frac{1}{2},j}|(E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n})$, (36) by $\tau |T_{ij}|(H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}})$, (37) by $\tau |T_{i,j-\frac{1}{2}}|(J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} +J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}})$, (38) by $\tau |T_{i-\frac{1}{2},j}|(J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}} +J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}})$, (39) by $\tau |T_{ij}|(K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} +K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1})$, then summing up the results, we obtain the sum of the right hand side as

$$\begin{aligned} RHS= & {} \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}\left[ (x_{i+1}-x_i)\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \\&\left. -\,J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\left| T_{i,j-\frac{1}{2}}\right| \right] \left( E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n}\right) \nonumber \\&+\,\tau \sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} \left[ -(y_{j+1}-y_j)\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}-H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \\&\left. -\,J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\left| T_{i-\frac{1}{2},j}\right| \right] \left( E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n}\right) \nonumber \\&+\, \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} \left[ -(y_{j+1}-y_j)\left( E_{y,i+1,j+\frac{1}{2}}^{n+1}-E_{y,i,j+\frac{1}{2}}^{n+1}\right) \right. \\&+\,(x_{i+1}-x_i)\left( E_{x,i+\frac{1}{2},j+1}^{n+1}-E_{x,i+\frac{1}{2},j}^{n+1}\right) \nonumber \\&\left. -\,K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}|T_{ij}|\right] \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}+H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&+\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}E_{x,i+\frac{1}{2},j}^{n+1} \cdot \left| T_{i,j-\frac{1}{2}}\right| \left( J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}}+J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) \nonumber \\&+\,\tau \sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}E_{y,i,j+\frac{1}{2}}^{n+1} \cdot \left| T_{i-\frac{1}{2},j}\right| \left( J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}}+J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&+\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} \cdot |T_{ij}|\left( K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2}+K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) . \end{aligned}$$

Regrouping those terms in RHS, we rewrite RHS as

$$\begin{aligned} RHS= & {} \tau \sum _{0\le i \le N_x-1}(x_{i+1}-x_i)\sum _{1\le j \le N_y-1} \left[ \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \nonumber \\&\times \left. \left( E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n}\right) +\left( E_{x,i+\frac{1}{2},j+1}^{n+1} -E_{x,i+\frac{1}{2},j}^{n+1}\right) \right. \nonumber \\&\left. \times \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right] \nonumber \\ \end{aligned}$$

$$\begin{aligned}&+\,\tau \sum _{0\le j \le N_y-1}(y_{j+1}-y_j)\sum _{1\le i \le N_x-1} \left[ \left( H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \nonumber \\&\times \left. \left( E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n}\right) +\left( E_{y,i,j+\frac{1}{2}}^{n+1}-E_{y,i+1,j+\frac{1}{2}}^{n+1}\right) \right. \nonumber \\&\times \left. \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}+H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right] \nonumber \\&+\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}} \left| T_{i,j-\frac{1}{2}}\right| \left[ -J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}} \left( E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n}\right) \right. \nonumber \\&\left. +\,\left( J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} +J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) E_{x,i+\frac{1}{2},j}^{n+1}\right] \nonumber \\&+\,\tau \sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \left[ -J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}} \left( E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n}\right) \right. \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\left. +\,\left( J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}} +J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\right) E_{y,i,j+\frac{1}{2}}^{n+1}\right] \nonumber \\&+\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left[ -K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1} \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\left. +\,H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} \left( K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} +K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) \right] \nonumber \\:= & {} \tau \left[ \sum _{0\le i \le N_x-1}(x_{i+1}-x_i)R_1 + \sum _{0\le j \le N_y-1}(y_{j+1}-y_j)R_2 + R_3 +R_4 +R_5 \right] . \nonumber \\ \end{aligned}$$

(43)

To evaluate the above RHS, below we evaluate each term separately. First, note that

$$\begin{aligned} \sum _{n=0}^{N_t}R_1= & {} \sum _{n=0}^{N_t}\sum _{0\le j\le N_y-1} \left[ \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}-H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}})(E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n}\right) \right. \nonumber \\&\left. +\left( E_{x,i+\frac{1}{2},j+1}^{n+1}-E_{x,i+\frac{1}{2},j}^{n+1}\right) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}+H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right] \nonumber \\= & {} \sum _{n=0}^{N_t}\sum _{0\le j\le N_y-1}\left[ \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{n}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{n+1}\right) \right. \nonumber \\&\left. +\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j+1}^{n+1} -H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{n+1}\right) \right] \nonumber \\&+\sum _{n=0}^{N_t}\sum _{0\le j\le N_y-1} \left[ \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}E_{x,i+\frac{1}{2},j+1}^{n+1}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j+1}^{n}\right) \right. \nonumber \\&\left. + \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j+1}^{n}-H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{n}\right) \right] \nonumber \\ \end{aligned}$$

$$\begin{aligned}= & {} \sum _{0\le j\le N_y-1} \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{0} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{N_t+1}\right) \nonumber \\&+\sum _{n=0}^{N_t}\left( H_{i+\frac{1}{2},N_y+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},N_y}^{n+1} -H_{i+\frac{1}{2},-\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},0}^{n+1}\right) \nonumber \\&+ \sum _{0\le j\le N_y-1} \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j+1}^{N_t+1}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j+1}^{0}\right) \nonumber \\&+ \sum _{n=0}^{N_t}(H_{i+\frac{1}{2},N_y+\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},N_y}^{n}) -H_{i+\frac{1}{2},-\frac{1}{2}}^{n+\frac{1}{2}}E_{x,i+\frac{1}{2},0}^{n}) \nonumber \\ \end{aligned}$$

$$\begin{aligned}= & {} \sum _{0\le j\le N_y-1} \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{0} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{N_t+1}\right) \nonumber \\&+ \sum _{0\le j\le N_y-1} \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j+1}^{N_t+1}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j+1}^{0}\right) \nonumber \\= & {} \sum _{0\le j\le N_y-1}(y_{j+1}-y_j) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}\nabla _yE_{x,i+\frac{1}{2},j+1}^{N_t+1} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\nabla _yE_{x,i+\frac{1}{2},j+1}^{0}\right) , \nonumber \\ \end{aligned}$$

(44)

where we used the PEC boundary condition (19) in the second last step, and the backward difference operator $\nabla _y$ in the last step. Note that in the first step, we extended the original sum of $1\le j\le N_y-1$ to $0\le j\le N_y-1$. Even though $H_{i+\frac{1}{2},-\frac{1}{2}}^{n+\frac{1}{2}}$ has subindex out of the original bound, its product with $E_{x,i+\frac{1}{2},0}^{n+1}+E_{x,i+\frac{1}{2},0}^{n}=0$ (by the PEC boundary condition (19)) is still zero.

The term $R_2$ can be evaluated as follows:

$$\begin{aligned} \sum _{n=0}^{N_t}R_2= & {} \sum _{n=0}^{N_t}\sum _{0\le i\le N_x-1} \left[ \left( H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \left( E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n}\right) \right. \nonumber \\&\left. +\left( E_{y,i,j+\frac{1}{2}}^{n+1}-E_{y,i+1,j+\frac{1}{2}}^{n+1}\right) \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}+H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right] \nonumber \\= & {} \sum _{n=0}^{N_t}\sum _{0\le i\le N_x-1} \left[ \left( H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{n+1}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}}^{n+1}\right) \right. \nonumber \\&\left. + \left( -H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{n} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{n+1}\right) \right] \nonumber \\&+ \sum _{n=0}^{N_t}\sum _{0\le i\le N_x-1}\left[ \left( H_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{n}-H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}}^{n}\right) \right. \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\left. + \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}}^{n} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}E_{y,i+1,j+\frac{1}{2}}^{n+1}\right) \right] \nonumber \\= & {} \sum _{n=0}^{N_t}\left( H_{-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,0,j+\frac{1}{2}}^{n+1} -H_{N_x-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,N_x,j+\frac{1}{2}}^{n+1}\right) \nonumber \\&+ \sum _{0\le i\le N_x-1}\left( -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{0} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{N_t+1}\right) \nonumber \\&+\sum _{n=0}^{N_t}\left( H_{-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,0,j+\frac{1}{2}}^{n} -H_{N_x+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}E_{y,N_x,j+\frac{1}{2}}^{n}\right) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&+ \sum _{0\le i\le N_x-1}\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}}^{0} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i+1,j+\frac{1}{2}}^{N_t+1}\right) \nonumber \\= & {} \sum _{0\le i\le N_x-1}\left( -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{0} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{N_t+1}\right) \nonumber \\&+ \sum _{0\le i\le N_x-1}\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i+1,j+\frac{1}{2}}^{0} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i+1,j+\frac{1}{2}}^{N_t+1}\right) \nonumber \\= & {} \sum _{0\le i\le N_x-1}(x_{i+1}-x_i)\left( -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}} \nabla _xE_{y,i+1,j+\frac{1}{2}}^{N_t+1} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\nabla _xE_{y,i+1,j+\frac{1}{2}}^{0}\right) , \nonumber \\ \end{aligned}$$

(45)

where the PEC boundary condition (19) was used in the second last step, and the backward difference operator $\nabla _x$ was used in the last step. Here similarly to $R_1$, in the first step we extended the original sum of $1\le i\le N_x-1$ to $0\le i\le N_x-1$. Even though $H_{-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}$ has subindex out of the original bound, its product with $E_{y,0,j+\frac{1}{2}}^{n+1}+E_{y,0,j+\frac{1}{2}}^{n}=0$ (by the PEC boundary condition (19)) is still zero.

Similarly, we can evaluate the rest terms in RHS (43) as follows.

$$\begin{aligned} \sum _{n=0}^{N_t}R_3= & {} \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \left[ -J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\left( E_{x,i+\frac{1}{2},j}^{n+1}+E_{x,i+\frac{1}{2},j}^{n}\right) \right. \nonumber \\&\left. +\left( J_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}}+J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) E_{x,i+\frac{1}{2},j}^{n+1}\right] \nonumber \\= & {} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \left( J_{x,i+\frac{1}{2},j}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{N_t+1} -J_{x,i+\frac{1}{2},j}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{0}\right) , \end{aligned}$$

(46)

$$\begin{aligned} \sum _{n=0}^{N_t}R_4= & {} \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \left[ -J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\left( E_{y,i,j+\frac{1}{2}}^{n+1}+E_{y,i,j+\frac{1}{2}}^{n}\right) \right. \nonumber \\&\left. +\left( J_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}}+J_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\right) E_{y,i,j+\frac{1}{2}}^{n+1}\right] \nonumber \\= & {} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \left( J_{y,i,j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{N_t+1} -J_{y,i,j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{0}\right) , \end{aligned}$$

(47)

and

$$\begin{aligned} \sum _{n=0}^{N_t}R_5= & {} \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left[ -K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \nonumber \\&\left. +H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}\left( K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} +K_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) \right] \nonumber \\= & {} \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}K_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+2} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}K_{i+\frac{1}{2},j+\frac{1}{2}}^{1}\right) . \end{aligned}$$

(48)

Summing up (43) from $n=0$ to $N_t$, then substituting the estimates (44)–(48), and using the energy norm notations, we have

$$\begin{aligned}&\epsilon _0\left( \left| \left| E_x^{N_t+1}\right| \right| ^2_E-\left| \left| E_x^{0} \right| \right| ^2_E\right) +\epsilon _0\left( \left| \left| E_y^{N_t+1}\right| \right| ^2_E -\left| \left| E_y^{0}\right| \right| ^2_E\right) \nonumber \\&\qquad +\,\mu _0\left( ||H^{N_t+\frac{3}{2}}||^2_H-||H^{\frac{1}{2}}||^2_H\right) \nonumber \\&\qquad +\, \frac{1}{\epsilon _0\omega ^2_{pe}} \left( \left| \left| J_x^{N_t+\frac{3}{2}}\right| \right| ^2_J -\left| \left| J_x^{\frac{1}{2}}\right| \right| ^2_J\right) + \frac{1}{\epsilon _0\omega ^2_{pe}} \left( \left| \left| J_y^{N_t+\frac{3}{2}}\right| \right| ^2_J -\left| \left| J_y^{\frac{1}{2}}\right| \right| ^2_J\right) \nonumber \\&\qquad + \,\frac{1}{\mu _0\omega ^2_{pm}} \left( ||K^{N_t+2}||^2_K-||K^{1}||^2_K\right) \nonumber \\&\quad \le \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}\nabla _yE_{x,i+\frac{1}{2},j+1}^{N_t+1} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\nabla _yE_{x,i+\frac{1}{2},j+1}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( -H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}} \nabla _xE_{y,i+1,j+\frac{1}{2}}^{N_t+1} +H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\nabla _xE_{y,i+1,j+\frac{1}{2}}^{0}\right) \nonumber \\&\qquad +\, \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \left( J_{x,i+\frac{1}{2},j}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{N_t+1} -J_{x,i+\frac{1}{2},j}^{\frac{1}{2}}E_{x,i+\frac{1}{2},j}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \left( J_{y,i,j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{N_t+1} -J_{y,i,j+\frac{1}{2}}^{\frac{1}{2}}E_{y,i,j+\frac{1}{2}}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}K_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+2} -H_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}K_{i+\frac{1}{2},j+\frac{1}{2}}^{1}\right) . \end{aligned}$$

(49)

Now we just need to bound those right hand side terms of (49). Using the Cauchy–Schwarz inequality and the inverse estimate (40), we have

$$\begin{aligned}&\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}\nabla _yE_{x,i+\frac{1}{2},j+1}^{N_t+1} \nonumber \\&\quad \le \tau \left( \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot |H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}|^2\right) ^{1/2} \left( \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \cdot |\nabla _yE_{x,i+\frac{1}{2},j+1}^{N_t+1}|^2\right) ^{1/2} \nonumber \\&\quad = \tau ||H^{N_t+\frac{3}{2}}||_H||\nabla _yE_x^{N_t+1}||_E \le \delta \mu _0||H^{N_t+\frac{3}{2}}||_H^2\nonumber \\&\qquad +\frac{1}{4\delta }\cdot \frac{\left( \tau C_{inv}h_y^{-1}\right) ^2}{\mu _0\epsilon _0}\cdot \epsilon _0\left| \left| E_x^{N_t+1}\right| \right| _E^2. \end{aligned}$$

(50)

Similarly, we can obtain

$$\begin{aligned}&\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}\nabla _xE_{y,i+1,j+\frac{1}{2}}^{N_t+1} \le \delta \mu _0||H^{N_t+\frac{3}{2}}||_H^2\nonumber \\&\quad +\frac{1}{4\delta }\cdot \frac{(\tau C_{inv}h_x^{-1})^2}{\mu _0\epsilon _0}\cdot \epsilon _0||E_y^{N_t+1}||_E^2. \end{aligned}$$

(51)

By the similar technique, we can prove that

$$\begin{aligned}&\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 1\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \cdot J_{x,i+\frac{1}{2},j}^{N_t+\frac{3}{2}}E_{x,i+\frac{1}{2},j}^{N_t+1} \nonumber \\&\quad \le \tau ||J_x^{N_t+\frac{3}{2}}||_J||E_x^{N_t+1}||_E \le \frac{\tau \omega _{pe}}{2}\left( \frac{1}{\epsilon _0\omega ^2_{pe}}||J_x^{N_t+\frac{3}{2}}||_J^2 +\epsilon _0||E_x^{N_t+1}||_E^2\right) , \qquad \end{aligned}$$

(52)

$$\begin{aligned}&\tau \sum _{\begin{array}{c} 1\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \cdot J_{y,i,j+\frac{1}{2}}^{N_t+\frac{3}{2}}E_{y,i,j+\frac{1}{2}}^{N_t+1} \nonumber \\&\quad \le \tau ||J_y^{N_t+\frac{3}{2}}||_J||E_y^{N_t+1}||_E \le \frac{\tau \omega _{pe}}{2}\left( \frac{1}{\epsilon _0\omega ^2_{pe}}||J_y^{N_t+\frac{3}{2}}||_J^2 +\epsilon _0||E_y^{N_t+1}||_E^2\right) , \end{aligned}$$

(53)

and

$$\begin{aligned}&\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}|\cdot H_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}K_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+2} \nonumber \\&\quad \le \tau ||H^{N_t+\frac{3}{2}}||_H||K^{N_t+2}||_K \le \frac{\tau \omega _{pm}}{2}\left( \mu _0||H^{N_t+\frac{3}{2}}||_H^2 +\frac{1}{\mu _0\omega ^2_{pm}}||K^{N_t+2}||_K^2\right) . \nonumber \\ \end{aligned}$$

(54)

Substituting the estimates (50)–(54) into (49), then choosing $\delta$ and $\tau$ small enough so that the left hand side terms of (49) can control those corresponding terms on the right hand side. A specific choice can be

$$\begin{aligned} \delta =\frac{1}{4}, ~\tau \le \frac{C_{inv}h_y}{2C_v}, ~\tau \le \frac{C_{inv}h_x}{2C_v}, ~\tau \le \frac{1}{2\omega _{pe}},~\tau \le \frac{1}{2\omega _{pm}}. \end{aligned}$$

This completes the proof. $\square$

3.2 The error estimate

To make the error analysis easy to follow, we denote the errors by their corresponding script letters. For example, the error of $E_x$ at point $(x_{i+\frac{1}{2}},y_j,t_n)$ is denoted by $\mathcal {E}^n_{x,i+\frac{1}{2},j}=E_x(x_{i+\frac{1}{2}},y_j,t_n)-E^n_{x,i+\frac{1}{2},j}$, where $E_x(x_{i+\frac{1}{2}},y_j,t_n)$ and $E^n_{x,i+\frac{1}{2},j}$ denote the exact and numerical solutions of $E_x$ at point $(x_{i+\frac{1}{2}},y_j,t_n)$, respectively. Similar error notations given below will be used for other variables:

$$\begin{aligned} \mathcal {E}^n_{y,i,j+\frac{1}{2}},~~\mathcal {H}^{n+\frac{1}{2}}_{i+\frac{1}{2},j+\frac{1}{2}}, ~~\mathcal {J}^{n+\frac{1}{2}}_{x,i+\frac{1}{2},j},~~\mathcal {J}^{n+\frac{1}{2}}_{y,i,j+\frac{1}{2}},~~\mathcal {K}^{n+1}_{i+\frac{1}{2},j+\frac{1}{2}}. \end{aligned}$$

3.2.1 The error equation for $E_x$

Multiplying (34) by $|T_{i,j-\frac{1}{2}}|$ (the area of rectangle $T_{i,j-\frac{1}{2}}$), we can rewrite (34) as follows:

$$\begin{aligned} \frac{\epsilon _0\left| T_{i,j-\frac{1}{2}}\right| }{\tau } \left( E_{x,i+\frac{1}{2},j}^{n+1}-E_{x,i+\frac{1}{2},j}^{n}\right)= & {} (x_{i+1}-x_i)\left( H_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -H_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}\right) \\&-\left| T_{i,j-\frac{1}{2}}\right| J_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}, \end{aligned}$$

from which we can easily obtain the error equation for $E_x$:

$$\begin{aligned} \frac{\epsilon _0\left| T_{i,j-\frac{1}{2}}\right| }{\tau } \left( \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}-\mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right)= & {} (x_{i+1}-x_i)\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -\mathcal {H}_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&-\left| T_{i,j-\frac{1}{2}}\right| \mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}+R_1, \end{aligned}$$

(55)

where the local truncation error term $R_1$ is given by

$$\begin{aligned} R_1= & {} \frac{\epsilon _0\left| T_{i,j-\frac{1}{2}}\right| }{\tau } \left( E_x\left( x_{i+\frac{1}{2}},y_j,t_{n+1}\right) -E_x\left( x_{i+\frac{1}{2}},y_j,t_n\right) \right) \nonumber \\&-\,(x_{i+1}-x_i) \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) -H\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) \nonumber \\&+\left| T_{i,j-\frac{1}{2}}\right| J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) . \end{aligned}$$

(56)

Integrating (7) from $t=t_n$ to $t_{n+1}$ and dividing the resultant by $\tau$, we have

$$\begin{aligned}&\frac{\epsilon _0}{\tau }\iint _{T_{i,j-\frac{1}{2}}}(E_x(x,y,t_{n+1})-E_x(x,y,t_{n}))dxdy \nonumber \\&\quad =\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) -H\left( x,y_{j-\frac{1}{2}},t\right) \right) dxdt\nonumber \\&\qquad -\frac{1}{\tau }\int _{t_n}^{t_{n+1}} \iint _{T_{i,j-\frac{1}{2}}}J_x(x,y,t)dxdydt. \end{aligned}$$

(57)

Subtracting (57) from (56), we can rewrite $R_1$ as follows:

$$\begin{aligned} R_1= & {} \frac{\epsilon _0}{\tau }\iint _{T_{i,j-\frac{1}{2}}} \left[ \left( E_x\left( x_{i+\frac{1}{2}},y_j,t_{n+1}\right) -E_x(x,y,t_{n+1})\right) \right. \nonumber \\&\left. -\left( E_x\left( x_{i+\frac{1}{2}},y_j,t_n\right) -E_x(x,y,t_{n})\right) \right] dxdy \nonumber \\&-\left\{ \int _{x_i}^{x_{i+1}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) -H\left( x_{i+\frac{1}{2}},y_{j-\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) dx \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\int _{x_i}^{x_{i+1}} \left( H\left( x,y_{j+\frac{1}{2}},t\right) -H\left( x,y_{j-\frac{1}{2}},t\right) \right) dxdt \right\} \nonumber \\&+\left[ \iint _{T_{i,j-\frac{1}{2}}} J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) dxdy -\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\iint _{T_{i,j-\frac{1}{2}}}J_x(x,y,t)dxdydt\right] \nonumber \\= & {} R_{11} + R_{12} + R_{13}. \end{aligned}$$

(58)

Following the same technique used for deriving (29), for any function f we can prove that

$$\begin{aligned}&\iint _{T_{i,j-\frac{1}{2}}}\left( f(x,y,t_{n+1}) -f\left( x_{i+\frac{1}{2}},y_j,t_{n+1}\right) \right) dxdy\nonumber \\&\qquad -\iint _{T_{i,j-\frac{1}{2}}}\left( f(x,y,t_{n}) -f\left( x_{i+\frac{1}{2}},y_j,t_{n}\right) \right) dxdy \nonumber \\&\quad = \iint _{T_{i,j-\frac{1}{2}}}\left[ \frac{1}{2}\left( x-x_{i+\frac{1}{2}}\right) ^2\left( \frac{\partial ^2 f}{\partial x^2}(q_1,t_{n+1})-\frac{\partial ^2 f}{\partial x^2}(q_1,t_{n})\right) \right. \nonumber \\&\left. \qquad + \frac{1}{2}(y-y_j)^2\left( \frac{\partial ^2 f}{\partial y^2}(q_2,t_{n+1})-\frac{\partial ^2 f}{\partial y^2}(q_2,t_{n})\right) \right] dxdy \nonumber \\&\quad = \tau \iint _{T_{i,j-\frac{1}{2}}}\left[ \frac{1}{2} \left( x-x_{i+\frac{1}{2}}\right) ^2\frac{\partial ^3 f}{\partial t\partial x^2}(q_1,t_*) + \frac{1}{2}(y-y_j)^2\frac{\partial ^3 f}{\partial t\partial y^2}(q_2,t_*)\right] dxdy, \nonumber \\ \end{aligned}$$

(59)

where we denote $q_1$ and $q_2$ for some points between $(x_{i+\frac{1}{2}},y_j)$ and (x, y), and $t_*$ for some point between $t_n$ and $t_{n+1}$. In the last step we used the following Taylor expansion

$$\begin{aligned} g(t_{n+1})-g(t_n)=\tau \frac{\partial g}{\partial t}(t_*) \end{aligned}$$

with $g=\frac{\partial ^2 f}{\partial x^2}$ and $g=\frac{\partial ^2 f}{\partial y^2}$, respectively.

Applying (59) with $f=E_x$, we can bound $R_{11}$ as follows:

$$\begin{aligned} R_{11}= & {} \frac{\epsilon _0}{\tau }\iint _{T_{i,j -\frac{1}{2}}}\left[ \frac{1}{2} \left( x-x_{i+\frac{1}{2}}\right) ^2\tau \frac{\partial ^3 E_x}{\partial t\partial x^2}(q_1,t_*) + \frac{1}{2}(y-y_j)^2\tau \frac{\partial ^3 E_x}{\partial t\partial y^2}(q_2,t_*)\right] dxdy \\= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^3 E_x}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 E_x}{\partial t\partial y^2}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

Similarly, by the Taylor expansion, we can estimate $R_{12}$ as follows:

$$\begin{aligned} R_{12}= & {} -\int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\frac{\partial H}{\partial y}\left( x_{i+\frac{1}{2}},y,t_{n+\frac{1}{2}}\right) dydx\nonumber \\&+\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\frac{\partial H}{\partial y}(x,y,t)dydxdt \\= & {} -\int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left[ \frac{\partial H}{\partial y}\left( x_{i+\frac{1}{2}},y,t_{n+\frac{1}{2}}\right) -\frac{\partial H}{\partial y}(x,y,t_{n+\frac{1}{2}})\right] dydx \\&+ \int _{x_i}^{x_{i+1}}\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \frac{1}{\tau }\int _{t_n}^{t_{n+1}} \left[ \frac{\partial H}{\partial y}(x,y,t)-\frac{\partial H}{\partial y} \left( x,y,t_{n+\frac{1}{2}}\right) \right] dtdydx \\= & {} \iint _{T_{i,j-\frac{1}{2}}} \frac{1}{2} \left( x-x_{i+\frac{1}{2}}\right) ^2\frac{\partial ^3 H}{\partial x^2\partial y} \left( x_*,y,t_{n+\frac{1}{2}}\right) dxdy \\&+ \iint _{T_{i,j-\frac{1}{2}}}\frac{1}{\tau }\int _{t_n}^{t_{n+1}} \frac{1}{2}\left( t-t_{n+\frac{1}{2}}\right) ^2\frac{\partial ^3 H}{\partial t^2\partial y}(x,y,t_*)dtdydx \\= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^3 H}{\partial x^2\partial y}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^3 H}{\partial t^2\partial y}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| , \end{aligned}$$

where $x_*$ is some number between $x_{i+\frac{1}{2}}$ and x, and $t_*$ is some number between $t_{n+\frac{1}{2}}$ and t.

Using exactly the same argument, we can estimate $R_{13}$ as follows:

$$\begin{aligned} R_{13}= & {} \iint _{T_{i,j-\frac{1}{2}}} \left( J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) -J_x\left( x,y,t_{n+\frac{1}{2}}\right) \right) dxdy \\&+\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\iint _{T_{i,j-\frac{1}{2}}} \left( J_x\left( x,y,t_{n+\frac{1}{2}}\right) -J_x(x,y,t)\right) dxdydt \\= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_x}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 J_x}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 J_x}{\partial t^2}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

3.2.2 The error equation for $E_y$

Multiplying (35) by $|T_{i-\frac{1}{2},j}|$, we can easily derive the error equation for $E_y$:

$$\begin{aligned} \frac{\epsilon _0\left| T_{i-\frac{1}{2},j}\right| }{\tau } \left( \mathcal {E}_{y,i,j+\frac{1}{2}}^{n+1}-\mathcal {E}_{y,i,j+\frac{1}{2}}^{n}\right)= & {} -(y_{j+1}-y_j) \left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}} -\mathcal {H}_{i-\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&-\left| T_{i-\frac{1}{2},j}\right| \mathcal {J}_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}+R_2, \end{aligned}$$

(60)

where the local truncation error $R_2$ is given by

$$\begin{aligned} R_2= & {} \frac{\epsilon _0\left| T_{i-\frac{1}{2},j}\right| }{\tau } \left( E_y\left( x_i,y_{j+\frac{1}{2}},t_{n+1}\right) - E_y\left( x_i,y_{j+\frac{1}{2}},t_{n}\right) \right) \nonumber \\&+\,(y_{j+1}-y_j)\left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) -H\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) \nonumber \\&+\,\left| T_{i-\frac{1}{2},j}\right| J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) . \end{aligned}$$

(61)

Integrating (9) from $t=t_n$ to $t_{n+1}$ and dividing the resultant by $\tau$, we have

$$\begin{aligned}&\frac{\epsilon _0}{\tau }\iint _{T_{i-\frac{1}{2},j}} \left( E_y(x,y,t_{n+1})-E_y(x,y,t_{n})\right) dxdy \nonumber \\&\quad =-\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\int _{y_j}^{y_{j+1}} \left( H\left( x_{i+\frac{1}{2}},y,t\right) -H\left( x_{i-\frac{1}{2}},y,t\right) \right) dydt\nonumber \\&\qquad -\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\iint _{T_{i-\frac{1}{2}},j}J_y(x,y,t)dxdydt. \end{aligned}$$

(62)

Subtracting (62) from (61), we can rewrite $R_2$ as follows:

$$\begin{aligned} R_2= & {} \frac{\epsilon _0}{\tau }\iint _{T_{i-\frac{1}{2},j}} \left[ \left( E_y(x_i,y_{j+\frac{1}{2}},t_{n+1}) -E_y(x,y,t_{n+1})\right) \right. \nonumber \\&\left. -\left( E_y\left( x_i,y_{j+\frac{1}{2}},t_n\right) -E_y(x,y,t_{n})\right) \right] dxdy \nonumber \\&-\left\{ \int _{y_j}^{y_{j+1}} \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) -H\left( x_{i-\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) dy \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_n}^{t_{n+1}}\int _{y_j}^{y_{j+1}} \left( H\left( x_{i+\frac{1}{2}},y,t\right) -H\left( x_{i-\frac{1}{2}},y,t\right) \right) dydt \right\} \nonumber \\&+\left[ \iint _{T_{i-\frac{1}{2}},j} J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) dxdy -\frac{1}{\tau }\int _{t_n}^{t_{n+1}} \iint _{T_{i-\frac{1}{2},j}}J_y(x,y,t)dxdydt\right] \nonumber \\= & {} R_{21} + R_{22} + R_{23}. \end{aligned}$$

(63)

Following exactly the same technique developed above for $R_1$, we can show that

$$\begin{aligned}&R_{21}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 E_y}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 E_y}{\partial t\partial y^2}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| , \\&R_{22}= \left( O\left( h_y^2\right) \left| \frac{\partial ^3 H}{\partial y^2\partial x}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^3 H}{\partial t^2\partial x}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| , \\&R_{23}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_y}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 J_y}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 J_y}{\partial t^2}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| . \end{aligned}$$

3.2.3 The error equation for H

Multiplying (36) by $|T_{i,j}|$, we can easily obtain the error equation for H:

$$\begin{aligned}&\frac{\mu _0|T_{i,j}|}{\tau } \left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} -\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) =-(y_{j+1}-y_j) \left( \mathcal {E}_{y,i+1,j+\frac{1}{2}}^{n+1}-\mathcal {E}_{y,i,j+\frac{1}{2}}^{n+1}\right) \nonumber \\&\quad +\,(x_{i+1}-x_i) \left( \mathcal {E}_{x,i+\frac{1}{2},j+1}^{n+1}-\mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}\right) -|T_{i,j}|\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}+R_3, \end{aligned}$$

(64)

where the local truncation error $R_3$ is given by

$$\begin{aligned} R_3= & {} \frac{\mu _0|T_{i,j}|}{\tau } \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{3}{2}}\right) - H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) \nonumber \\&+\,(y_{j+1}-y_j)\left( E_y(x_{i+1},y_{j+\frac{1}{2}},t_{n+1}) - E_y\left( x_i,y_{j+\frac{1}{2}},t_{n+1}\right) \right) \\&-\,(x_{i+1}-x_i)\left( E_x(x_{i+\frac{1}{2}},y_{j+1},t_{n+1}) - E_x\left( x_{i+\frac{1}{2}},y_{j},t_{n+1}\right) \right) \nonumber \\&+\,|T_{i,j}|K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) . \nonumber \end{aligned}$$

(65)

Integrating (11) from $t=t_{n+\frac{1}{2}}$ to $t_{n+\frac{3}{2}}$ and dividing the resultant by $\tau$, we obtain

$$\begin{aligned}&\frac{\mu _0}{\tau }\iint _{T_{i,j}} \left( H\left( x,y,t_{n+\frac{3}{2}}\right) -H\left( x,y,t_{n+\frac{1}{2}}\right) \right) dxdy\nonumber \\&\quad =-\frac{1}{\tau } \int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i,j}}\left( \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right) (x,y,t)dxdydt \nonumber \\&\quad \quad -\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \iint _{T_{i,j}} K(x,y,t)dxdydt. \end{aligned}$$

(66)

Subtracting (66) from (65), we can rewrite $R_3$ as follows:

$$\begin{aligned} R_3= & {} \frac{\mu _0}{\tau }\iint _{T_{i,j}} \left\{ \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}, t_{n+\frac{3}{2}}\right) -H\left( x,y,t_{n+\frac{3}{2}}\right) \right) \right. \nonumber \\&\left. - \left( H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) -H\left( x,y,t_{n+\frac{1}{2}}\right) \right) \right\} dxdy \nonumber \\&+\left\{ \iint _{T_{i,j}} \left( \frac{\partial E_y}{\partial x}\left( x,y_{j+\frac{1}{2}},t_{n+1}\right) -\frac{\partial E_x}{\partial y}\left( x_{i+\frac{1}{2}},y,t_{n+1}\right) \right) dxdy \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \iint _{T_{i,j}} \left( \frac{\partial E_y}{\partial x}(x,y,t) -\frac{\partial E_x}{\partial y}(x,y,t)\right) dxdydt\right\} \nonumber \\&+\left\{ \iint _{T_{i,j}} K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) dxdy -\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \iint _{T_{i,j}} K(x,y,t)dxdydt\right\} \nonumber \\= & {} R_{31}+R_{32}+R_{33}. \end{aligned}$$

(67)

By the Taylor expansion, we can obtain

$$\begin{aligned} R_{31}= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^3 H}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 H}{\partial t\partial y^2}\right| _{\infty }\right) |T_{i,j}|, \\ R_{32}= & {} \left( O\left( h_y^2\right) \left| \frac{\partial ^3 E_y}{\partial y^2\partial x}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^3 E_y}{\partial t^2\partial x}\right| _{\infty }\right. \\&\left. +\, O\left( h_x^2\right) \left| \frac{\partial ^3 E_x}{\partial x^2\partial y}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^3 E_x}{\partial t^2\partial y}\right| _{\infty }\right) |T_{i,j}|, \\ R_{33}= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^2 K}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 K}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 K}{\partial t^2}\right| _{\infty }\right) |T_{i,j}|. \end{aligned}$$

3.2.4 The error equation for $J_x$

Multiplying (37) by $|T_{i,j-\frac{1}{2}}|$, we easily derive the error equation for $J_x$:

$$\begin{aligned}&\frac{\left| T_{i,j-\frac{1}{2}}\right| }{\tau \epsilon _0\omega _{pe}^2} \left( \mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} -\mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) + \frac{\Gamma _e\left| T_{i,j-\frac{1}{2}}\right| }{2\epsilon _0\omega _{pe}^2}\left( \mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}} +\mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) \nonumber \\&\quad =\left| T_{i,j-\frac{1}{2}}\right| \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1} + R_4, \end{aligned}$$

(68)

where the local truncation error $R_4$ is given by

$$\begin{aligned} R_4= & {} \frac{\left| T_{i,j-\frac{1}{2}}\right| }{\tau \epsilon _0\omega _{pe}^2}\left( J_x\left( x_{i+\frac{1}{2}},y_j, t_{n+\frac{3}{2}}\right) -J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) \right) \nonumber \\&+\frac{\Gamma _e\left| T_{i,j-\frac{1}{2}}\right| }{2\epsilon _0\omega _{pe}^2}\left( J_x\left( x_{i+\frac{1}{2}},y_j, t_{n+\frac{3}{2}}\right) +J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) \right) \nonumber \\&- \left| T_{i,j-\frac{1}{2}}\right| E_x\left( x_{i+\frac{1}{2}},y_j,t_{n+1}\right) . \end{aligned}$$

(69)

Integrating (13) from $t=t_{n+\frac{1}{2}}$ to $t_{n+\frac{3}{2}}$ and dividing the resultant by $\tau$, we have

$$\begin{aligned}&\frac{1}{\tau \epsilon _0\omega _{pe}^2} \iint _{T_{i,j-\frac{1}{2}}} \left( J_x\left( x,y,t_{n+\frac{3}{2}}\right) -J_x\left( x,y,t_{n+\frac{1}{2}}\right) \right) dxdy \nonumber \\&\qquad +\frac{\Gamma _e}{\tau \epsilon _0\omega _{pe}^2} \int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i,j-\frac{1}{2}}} J_x(x,y,t)dxdydt\nonumber \\&\quad =\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i,j-\frac{1}{2}}} E_x(x,y,t)dxdydt. \end{aligned}$$

(70)

Subtracting (70) from (69), we can rewrite $R_4$ as follows:

$$\begin{aligned} R_4= & {} \frac{1}{\tau \epsilon _0\omega _{pe}^2} \iint _{T_{i,j-\frac{1}{2}}} \left\{ \left( J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{3}{2}}\right) -J_x\left( x,y,t_{n+\frac{3}{2}}\right) \right) \right. \nonumber \\&\left. -\left( J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) -J_x\left( x,y,t_{n+\frac{1}{2}}\right) \right) \right\} dxdy \nonumber \\&+\frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \left\{ \iint _{T_{i,j-\frac{1}{2}}} \frac{1}{2}\left( J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{3}{2}}\right) +J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) \right) dxdy \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i,j-\frac{1}{2}}} J_x(x,y,t)dxdydt\right\} \nonumber \\&-\left\{ \iint _{T_{i,j-\frac{1}{2}}}E_x\left( x_{i+\frac{1}{2}},y_j,t_{n+1}\right) dxdy - \frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i,j-\frac{1}{2}}} E_x(x,y,t)dxdydt\right\} \nonumber \\= & {} R_{41}+R_{42}+R_{43}. \end{aligned}$$

(71)

By the Taylor expansion, we easily have

$$\begin{aligned} R_{41}= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^3 J_x}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 J_x}{\partial t\partial y^2}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| , \\ R_{42}= & {} \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \bigg \{\iint _{T_{i,j-\frac{1}{2}}} \frac{1}{2}\left( J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{3}{2}}\right) +J_x\left( x_{i+\frac{1}{2}},y_j,t_{n+\frac{1}{2}}\right) \right. \nonumber \\&\left. -\,J_x\left( x,y,t_{n+\frac{3}{2}}\right) -J_x\left( x,y,t_{n+\frac{1}{2}}\right) \right) dxdy\bigg \} \nonumber \\&+\,\iint _{T_{i,j-\frac{1}{2}}} \frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \left\{ \frac{1}{2}\left( J_x\left( x,y,t_{n+\frac{3}{2}}\right) +J_x\left( x,y,t_{n+\frac{1}{2}}\right) \right) -J_x(x,y,t)\right\} dtdxdy \nonumber \\= & {} \left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_x}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 J_x}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 J_x}{\partial t^2}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| , \end{aligned}$$

where in the last step we used the property: For any function $f\in C^2([0,T])$,

$$\begin{aligned} \frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \left\{ \frac{1}{2}\left( f\left( t_{n+\frac{3}{2}}\right) +f\left( t_{n+\frac{1}{2}}\right) \right) -f(t)\right\} dt=O(\tau ^2)\left| \frac{\partial ^2 f}{\partial t^2}\right| _{\infty }. \end{aligned}$$

Similarly, it is easy to show that

$$\begin{aligned} R_{43}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 E_x}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 E_x}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 E_x}{\partial t^2}\right| _{\infty }\right) \left| T_{i,j-\frac{1}{2}}\right| . \end{aligned}$$

3.2.5 The error equation for $J_y$

Following exactly the same technique used for the $J_x$ equation, we easily obtain the error equation for $J_y$ from (38):

$$\begin{aligned}&\frac{\left| T_{i-\frac{1}{2},j}\right| }{\tau \epsilon _0\omega _{pe}^2} \left( \mathcal {J}_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}} -\mathcal {J}_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\right) + \frac{\Gamma _e\left| T_{i-\frac{1}{2},j}\right| }{2\epsilon _0\omega _{pe}^2}\left( \mathcal {J}_{y,i,j +\frac{1}{2}}^{n+\frac{3}{2}} +\mathcal {J}_{y,i,j +\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&\quad =\left| T_{i-\frac{1}{2},j}\right| \mathcal {E}_{y,i,j+\frac{1}{2}}^{n+1} + R_5, \end{aligned}$$

(72)

where the local truncation error $R_5$ is given by

$$\begin{aligned} R_5= & {} \frac{\left| T_{i-\frac{1}{2},j}\right| }{\tau \epsilon _0\omega _{pe}^2}\left( J_y\left( x_i,y_{j+\frac{1}{2}}, t_{n+\frac{3}{2}}\right) -J_y\left( x_i,y_{j+\frac{1}{2}}, t_{n+\frac{1}{2}}\right) \right) \nonumber \\&+\,\frac{\Gamma _e\left| T_{i-\frac{1}{2},j}\right| }{2\epsilon _0\omega _{pe}^2}\left( J_y\left( x_i,y_{j+\frac{1}{2}}, t_{n+\frac{3}{2}}\right) +J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) \nonumber \\&-\, \left| T_{i-\frac{1}{2},j} \right| E_y\left( x_i,y_{j+\frac{1}{2}},t_{n+1}\right) . \end{aligned}$$

(73)

Integrating the y-component of (3) on $T_{i-\frac{1}{2},j}$, then integrating the resultant from $t=t_{n+\frac{1}{2}}$ to $t_{n+\frac{3}{2}}$ and dividing the resultant by $\tau$, we have

$$\begin{aligned}&\frac{1}{\tau \epsilon _0\omega _{pe}^2}\iint _{T_{i-\frac{1}{2},j}} \left( J_y\left( x,y,t_{n+\frac{3}{2}}\right) -J_y\left( x,y,t_{n+\frac{1}{2}}\right) \right) dxdy \nonumber \\&\qquad +\frac{\Gamma _e}{\tau \epsilon _0\omega _{pe}^2} \int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i-\frac{1}{2},j}} J_y(x,y,t)dxdydt\nonumber \\&\quad =\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i-\frac{1}{2},j}} E_y(x,y,t)dxdydt. \end{aligned}$$

(74)

Subtracting (74) from (73), we can rewrite $R_5$ as follows:

$$\begin{aligned} R_5= & {} \frac{1}{\tau \epsilon _0\omega _{pe}^2} \iint _{T_{i-\frac{1}{2},j}} \left\{ \left( J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{3}{2}}\right) -J_y\left( x,y,t_{n+\frac{3}{2}}\right) \right) \right. \nonumber \\&\left. -\left( J_y\left( x_i,y_{j+\frac{1}{2}}, t_{n+\frac{1}{2}}\right) -J_y\left( x,y,t_{n+\frac{1}{2}}\right) \right) \right\} dxdy \nonumber \\&+\frac{\Gamma _e}{\epsilon _0\omega _{pe}^2} \left\{ \iint _{T_{i-\frac{1}{2},j}} \frac{1}{2}\left( J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{3}{2}}\right) +J_y\left( x_i,y_{j+\frac{1}{2}},t_{n+\frac{1}{2}}\right) \right) dxdy \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}}\iint _{T_{i-\frac{1}{2},j}} J_y(x,y,t)dxdydt\right\} \nonumber \\&-\left\{ \iint _{T_{i-\frac{1}{2},j}} E_y\left( x_i,y_{j+\frac{1}{2}},t_{n+1}\right) dxdy - \frac{1}{\tau }\int _{t_{n+\frac{1}{2}}}^{t_{n+\frac{3}{2}}} \iint _{T_{i-\frac{1}{2},j}} E_y(x,y,t)dxdydt\right\} \nonumber \\= & {} R_{51}+R_{52}+R_{53}. \end{aligned}$$

(75)

By the Taylor expansion, we can obtain

$$\begin{aligned}&R_{51}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 J_y}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 J_y}{\partial t\partial y^2}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| , \\&R_{52}= \left( O\left( h_x^2\right) \left| \frac{\partial ^2 J_y}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 J_y}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 J_y}{\partial t^2}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| , \\&R_{53}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 E_y}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 E_y}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 E_y}{\partial t^2}\right| _{\infty }\right) \left| T_{i-\frac{1}{2},j}\right| . \end{aligned}$$

3.2.6 The error equation for K

Similarly, we can obtain the error equation for K from (39):

$$\begin{aligned}&\frac{|T_{i,j}|}{\tau \mu _0\omega _{pm}^2} \left( \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} -\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) + \frac{\Gamma _m|T_{i,j}|}{2\mu _0\omega _{pm}^2} \left( \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2} +\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) \nonumber \\&\quad =|T_{i,j}|\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}} + R_6, \end{aligned}$$

(76)

where the local truncation error $R_6$ is given by

$$\begin{aligned} R_6= & {} \frac{|T_{i,j}|}{\tau \mu _0\omega _{pm}^2} \left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}, t_{n+2}\right) -K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) \right) \nonumber \\&+\frac{\Gamma _m|T_{i,j}|}{2\mu _0\omega _{pm}^2} \left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}}, t_{n+2}\right) +K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) \right) \nonumber \\&- |T_{i,j}|H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{3}{2}}\right) . \end{aligned}$$

(77)

Integrating (4) on $T_{i,j}$, then integrating the resultant from $t=t_{n+1}$ to $t_{n+2}$ and dividing the resultant by $\tau$, we have

$$\begin{aligned}&\frac{1}{\tau \mu _0\omega _{pm}^2}\iint _{T_{i,j}} (K(x,y,t_{n+2})-K(x,y,t_{n+1}))dxdy \nonumber \\&\quad +\frac{\Gamma _m}{\tau \mu _0\omega _{pm}^2} \int _{t_{n+1}}^{t_{n+2}}\iint _{T_{i,j}}K(x,y,t)dxdydt =\frac{1}{\tau }\int _{t_{n+1}}^{t_{n+2}}\iint _{T_{i,j}} H(x,y,t)dxdydt. \nonumber \\ \end{aligned}$$

(78)

Subtracting (78) from (77), we can rewrite $R_6$ as follows:

$$\begin{aligned} R_6= & {} \frac{1}{\tau \mu _0\omega _{pm}^2}\iint _{T_{i,j}} \left\{ \left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+2}\right) -K\left( x,y,t_{n+2}\right) \right) \right. \nonumber \\&\left. -\left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) -K(x,y,t_{n+1})\right) \right\} dxdy \nonumber \\&+\frac{\Gamma _m}{\mu _0\omega _{pm}^2} \left\{ \iint _{T_{i,j}} \frac{1}{2}\left( K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+2}\right) +K\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+1}\right) \right) dxdy \right. \nonumber \\&\left. -\frac{1}{\tau }\int _{t_{n+1}}^{t_{n+2}}\iint _{T_{i,j}} K(x,y,t)dxdydt\right\} \nonumber \\&-\left\{ \iint _{T_{i,j}}H\left( x_{i+\frac{1}{2}},y_{j+\frac{1}{2}},t_{n+\frac{3}{2}}\right) dxdy - \frac{1}{\tau }\int _{t_{n+1}}^{t_{n+2}}\iint _{T_{i,j}} H(x,y,t)dxdydt\right\} \nonumber \\= & {} R_{61}+R_{62}+R_{63}. \end{aligned}$$

(79)

By the Taylor expansion, we can obtain

$$\begin{aligned}&R_{61}=\left( O\left( h_x^2\right) \left| \frac{\partial ^3 K}{\partial t\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^3 K}{\partial t\partial y^2}\right| _{\infty }\right) |T_{i,j}|, \\&R_{62}= \left( O\left( h_x^2\right) \left| \frac{\partial ^2 K}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 K}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 K}{\partial t^2}\right| _{\infty }\right) |T_{i,j}|, \\&R_{63}=\left( O\left( h_x^2\right) \left| \frac{\partial ^2 H}{\partial x^2}\right| _{\infty } + O\left( h_y^2\right) \left| \frac{\partial ^2 H}{\partial y^2}\right| _{\infty } + O(\tau ^2)\left| \frac{\partial ^2 H}{\partial t^2}\right| _{\infty }\right) |T_{i,j}|. \end{aligned}$$

3.2.7 The final error estimate

With the above preparations, we can now prove the major error estimate result.

Theorem 3.2

Suppose that the solution of (1)–(6) possesses the following regularity property:

$$\begin{aligned}&E_x, E_y, H \in C([0,T]; C^3(\overline{\Omega }))\cap C^1([0,T]; C^2(\overline{\Omega }))\cap C^2([0,T]; C^1(\overline{\Omega })), \\&J_x, J_y, K \in C([0,T]; C^2(\overline{\Omega }))\cap C^1([0,T]; C^2(\overline{\Omega }))\cap C^2([0,T]; C(\overline{\Omega })). \end{aligned}$$

If the initial error

$$\begin{aligned} \left| \left| \mathcal {E}_x^{0}\right| \right| _E +\left| \left| \mathcal {E}_y^{0}\right| \right| _E +\left| \left| \mathcal {H}^{\frac{1}{2}}\right| \right| _H +\left| \left| \mathcal {J}_x^{\frac{1}{2}}\right| \right| _J +\left| \left| \mathcal {J}_y^{\frac{1}{2}}\right| \right| _J +\left| \left| \mathcal {K}^{1}\right| \right| _K \le C\left( h_x^2+h_y^2+\tau ^2\right) , \end{aligned}$$

(80)

holds true, then for any $1\le n\le N_t$ we have

$$\begin{aligned}&\epsilon _0\left( \left| \left| \mathcal {E}_x^{n+1}\right| \right| _E^2 +\left| \left| \mathcal {E}_y^{n+1}\right| \right| _E^2\right) +\mu _0\left| \left| \mathcal {H}^{n+\frac{3}{2}}\right| \right| ^2_H\nonumber \\&\qquad +\frac{1}{\epsilon _0\omega _{pe}^2} \left( \left| \left| \mathcal {J}_x^{n+\frac{3}{2}}\right| \right| ^2_J +\left| \left| \mathcal {J}_y^{n+\frac{3}{2}}\right| \right| ^2_J\right) +\frac{1}{\mu _0\omega _{pm}^2}\left| \left| \mathcal {K}^{n+2}\right| \right| ^2_K \nonumber \\&\quad \le C\left( h_x^2+h_y^2+\tau ^2\right) ^2, \end{aligned}$$

(81)

where the constant $C>0$ is independent of $\tau , h_x$ and $h_y.$

Proof

Note that the error equations (55), (60), (64), (68), (72) and (76) have exactly the same form as (34)–(39) with extra right hand side terms representing the errors introduced by time discretization and space discretization. Hence we can follow exactly the same technique developed in the proof of Theorem 3.1 to obtain (cf. (49)):

$$\begin{aligned}&\epsilon _0\left( \left| \left| \mathcal {E}_x^{N_t+1}\right| \right| ^2_E -\left| \left| \mathcal {E}_x^{0}\right| \right| ^2_E\right) +\epsilon _0\left( \left| \left| \mathcal {E}_y^{N_t+1}\right| \right| ^2_E -\left| \left| \mathcal {E}_y^{0}\right| \right| ^2_E\right) \nonumber \\&\qquad +\,\mu _0\left( \left| \left| \mathcal {H}^{N_t+\frac{3}{2}}\right| \right| ^2_H -\left| \left| \mathcal {H}^{\frac{1}{2}}\right| \right| ^2_H\right) \nonumber \\&\qquad + \frac{1}{\epsilon _0\omega ^2_{pe}} \left( \left| \left| \mathcal {J}_x^{N_t+\frac{3}{2}}\right| \right| ^2_J -\left| \left| \mathcal {J}_x^{\frac{1}{2}}\right| \right| ^2_J\right) +\frac{1}{\epsilon _0\omega ^2_{pe}} \left( \left| \left| \mathcal {J}_y^{N_t+\frac{3}{2}}\right| \right| ^2_J -\left| \left| \mathcal {J}_y^{\frac{1}{2}}\right| \right| ^2_J\right) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\qquad + \frac{1}{\mu _0\omega ^2_{pm}}\left( \left| \left| \mathcal {K}^{N_t+2}\right| \right| ^2_K -\left| \left| \mathcal {K}^{1}\right| \right| ^2_K\right) \nonumber \\&\quad \le \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}} \nabla _y\mathcal {E}_{x,i+\frac{1}{2},j+1}^{N_t+1} -\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}} \nabla _y\mathcal {E}_{x,i+\frac{1}{2},j+1}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( -\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}} \nabla _x\mathcal {E}_{y,i+1,j+\frac{1}{2}}^{N_t+1} +\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\nabla _x\mathcal {E}_{y,i+1,j+\frac{1}{2}}^{0}\right) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\qquad +\, \tau \sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}}\left| T_{i,j-\frac{1}{2}}\right| \left( \mathcal {J}_{x,i+\frac{1}{2},j}^{N_t+\frac{3}{2}}\mathcal {E}_{x,i+\frac{1}{2},j}^{N_t+1} -\mathcal {J}_{x,i+\frac{1}{2},j}^{\frac{1}{2}}\mathcal {E}_{x,i+\frac{1}{2},j}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}}\left| T_{i-\frac{1}{2},j}\right| \left( \mathcal {J}_{y,i,j+\frac{1}{2}}^{N_t+\frac{3}{2}}\mathcal {E}_{y,i,j+\frac{1}{2}}^{N_t+1} -\mathcal {J}_{y,i,j+\frac{1}{2}}^{\frac{1}{2}}\mathcal {E}_{y,i,j+\frac{1}{2}}^{0}\right) \nonumber \\&\qquad +\,\tau \sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}}|T_{ij}| \left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+\frac{3}{2}}\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{N_t+2} -\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{\frac{1}{2}}\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{1}\right) \nonumber \\&\qquad +\, \tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_1\left( \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}+\mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right) \nonumber \\&\qquad +\,\tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_2\left( \mathcal {E}_{y,i,j+\frac{1}{2}}^{n+1}+\mathcal {E}_{y,i,j+\frac{1}{2}}^{n}\right) \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\qquad +\, \tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_3\left( \mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{3}{2}}+\mathcal {H}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&\qquad +\,\tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_4\left( \mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{3}{2}}+\mathcal {J}_{x,i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) \nonumber \\&\qquad +\,\tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_5\left( \mathcal {J}_{y,i,j+\frac{1}{2}}^{n+\frac{3}{2}}+\mathcal {J}_{y,i,j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \nonumber \\&\qquad +\,\tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 0\le j \le N_y-1 \end{array}} R_6\left( \mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+2}+\mathcal {K}_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) . \end{aligned}$$

(82)

All terms except those containing $R_i$ on the RHS of (82) can be bounded as in the proof of Theorem 3.1. The $R_i$ terms can be easily bounded by the Cauchy–Schwarz inequality. For example, we have

$$\begin{aligned}&\tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} R_1\left( \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}+\mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right) \\&\quad \le \tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} \left| T_{i,j-\frac{1}{2}}\right| C\left( h_x^2+h_y^2+\tau ^2\right) \left( \left| \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1} +\mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right| \right) \\&\quad \le \tau \sum _{n=0}^{N_t}\sum _{\begin{array}{c} 0\le i \le N_x-1 \\ 0\le j \le N_y-1 \end{array}} \left| T_{i,j-\frac{1}{2}}\right| \left[ \frac{C}{\delta } \left( h_x^2+h_y^2+\tau ^2\right) ^2 +\frac{\delta }{2} \left( \left| \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}|^2 +|\mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right| ^2\right) \right] \\&\quad \le \frac{CT}{\delta }\left( h_x^2+h_y^2+\tau ^2\right) ^2 +\tau \sum _{n=0}^{N_t}\frac{\delta }{2} \left( \left| \left| \mathcal {E}_{x,i+\frac{1}{2},j}^{n+1}\right| \right| _E^2 +\left| \left| \mathcal {E}_{x,i+\frac{1}{2},j}^{n}\right| \right| _E^2\right) , \end{aligned}$$

where we used the inequality $ab\le \frac{1}{\delta }a^2 + \frac{\delta }{4}b^2$, where the constant $\delta >0$.

Choosing $\delta$ small enough so that $||\mathcal {E}_{x,i+\frac{1}{2},j}^{N_t+1}||_E^2$ etc can be bounded by the corresponding terms on the left hand side of (82). The proof is completed by using the discrete Gronwall inequality. $\square$

4 Numerical results

In this section, we present two numerical examples. The first one is used to justify our theoretical analysis with an exact solution. The second one is a classic example showing the backward wave propagation phenomenon in metamaterial.

Example 1

In this example, we solve the 2D version of our model (1)–(4). More specifically, the governing equations are (with added source terms $g_x$, $g_y$, and f):

$$\begin{aligned}&\epsilon _0\frac{\partial E_x}{\partial t} = \frac{\partial H_z}{\partial y} - J_x + g_x, \end{aligned}$$

(83)

$$\begin{aligned}&\epsilon _0\frac{\partial E_y}{\partial t} = -\frac{\partial H_z}{\partial x} - J_y + g_y, \end{aligned}$$

(84)

$$\begin{aligned}&\mu _0\frac{\partial H_z}{\partial t} = -\frac{\partial E_y}{\partial x}+\frac{\partial E_x}{\partial y} - K_z + f, \end{aligned}$$

(85)

$$\begin{aligned}&\frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial J_x}{\partial t} + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}J_x = E_x, \end{aligned}$$

(86)

$$\begin{aligned}&\frac{1}{\epsilon _0\omega _{pe}^2}\frac{\partial J_y}{\partial t} + \frac{\Gamma _e}{\epsilon _0\omega _{pe}^2}J_y = E_y, \end{aligned}$$

(87)

$$\begin{aligned}&\frac{1}{\mu _0\omega _{pm}^2}\frac{\partial K_z}{\partial t} + \frac{\Gamma _m}{\mu _0\omega _{pm}^2}K_z = H_z. \end{aligned}$$

(88)

To rigorously check the convergence rate, we choose the physical domain $\Omega = [0,1]^2$, and coefficients as follows:

$$\begin{aligned} \epsilon _0 = \mu _0 = 1,\quad ~~\Gamma _m = \Gamma _e = \pi , \quad ~~\omega _{pm} = \omega _{pe} = \pi \end{aligned}$$

such that (83)–(88) has the exact solution:

$$\begin{aligned}&\mathbf E \equiv \left( \begin{array}{c} E_x \\ E_y \end{array} \right) = \left( \begin{array}{c} \cos (\pi x)\sin (\pi y)e^{-\pi t} \\ -\sin (\pi x)\cos (\pi y)e^{-\pi t} \end{array} \right) , \\&H_z = \cos (\pi x)\cos (\pi y)e^{-\pi t}, \\&\mathbf J \equiv \left( \begin{array}{c} J_x \\ J_y \end{array} \right) = \left( \begin{array}{c} \pi ^2 t \cos (\pi x)\sin (\pi y)e^{-\pi t} \\ -\pi ^2 t \sin (\pi x)\cos (\pi y)e^{-\pi t} \end{array} \right) , \\&K_z = \pi ^2 t \cos (\pi x)\cos (\pi y)e^{-\pi t}. \end{aligned}$$

The corresponding source terms are

$$\begin{aligned} g_x= & {} \pi ^2 t \cos (\pi x)\sin (\pi y)e^{-\pi t}, \\ g_y= & {} -\pi ^2 t \sin (\pi x)\cos (\pi y)e^{-\pi t}, \\ f= & {} (-3\pi + \pi ^2 t)\cos (\pi x)\cos (\pi y)e^{-\pi t}. \end{aligned}$$

We build the 1D non-uniform mesh in the X-direction as $[0:dx:0.5-dx, 0.5:dx2:1]$, where $dx2=dx/2$, and the 1D non-uniform mesh in the y-direction as $[0:dy:0.5-dy, 0.5:dy2:1]$, where $dy2=dy/2$. The 2D non-uniform mesh is obtained by extending both 1D meshes to cover the whole domain $\Omega$ (see Fig. 2).

Fig. 2

A non-uniform mesh with $dx=dy=1/32$

We solve the 2D problem (83)–(88) by our scheme (34)–(39) on a series of non-uniform meshes with $dx=dy=h$ varying from 1 / 4 to 1 / 128, a fixed time step $\tau =10^{-5}$, and runs total 1000 time steps. The obtained errors for the main fields $E_x, E_y$ and $H_z$ at the 1000th time step in discrete energy norms are presented in Table 1, which shows clearly that they all converges in $O(h^2)$. This confirms our theoretical superconvergence rates $O(h_x^2+h_y^2)$.

Table 1 The errors of $E_x, E_y, H_z$ obtained with $\tau =10^{-5}$ on non-uniform meshes

Fig. 3

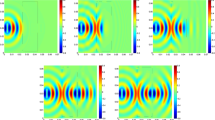
Example 2. A coarse mesh (the red rectangle shows the metamaterial slab), and contour plots of $|H_z|$ obtained with $\tau =0.1$ ps at 1000, 2000, 3000, 4000, and 5000 time steps

Example 2

In this example, we solve a classic example of wave propagation in metamaterial originally introduced by Ziolkowski [37] and late solved by us with edge elements [19]. This example assumes that a metamaterial slab of size $[0.024, 0.054]~\mathrm{m}\times [0.002,0.062]~\mathrm{m}$ is located inside a vacuum of size $[0, 0.07]~\mathrm{m}\times [0, 0.064]~\mathrm{m}$. An incident source wave is imposed as $H_z$ field and is excited at $x=0.004~\mathrm{m}$ and $y\in [0.025,0.035]~\mathrm{m}$. The source wave varies in space as $e^{-(x-0.03)^2/(50h)^2}$ and in time as:

$$\begin{aligned}f(t)=\left\{ \begin{array}{ll} 0, &{}\quad for \ \ t<0,\\ g_1(t)\sin (\omega _0t), &{}\quad for \ \ 0<t<mT_p, \\ \sin (\omega _0t), &{}\quad for \ \ mT_p<t<(m+k)T_p,\\ g_2(t)\sin (\omega _0t), &{}\quad for \ \ (m+k)T_p<t<(2m+k)T_p, \\ 0, &{}\quad for \ \ t>(2m+k)T_p,\\ \end{array} \right. \end{aligned}$$

where the functions $g_1$ and $g_2$ are

$$\begin{aligned}&g_1(t)=10x_1^3-15x_1^4+6x_1^5,~~~ x_1=t/mT_p, \\&g_2(t)=1-\left( 10x_2^3-15x_2^4+6x_2^5\right) ,~~~ x_2=\left( t-(m+k)T_p\right) /mT_p. \end{aligned}$$

Here we denote $T_p=1/f_0$ and $\omega _0=2\pi f_0$. In our simulation, we use $m=2, k=100, f_0=30$ GHz.

We solve this model with our scheme (34)–(39) on a non-uniform mesh uniformly refined from a coarse mesh demonstrated in Fig. 3 (top left). We used time step size $\tau =10^{-13}s=0.1$ ps (picosecond), and 12 perfectly matched layers (PML) around the physical domain (cf. [19]). The obtained $H_z$ fields at various time steps are presented in Fig. 3, which matches with what we obtained in [19]. The simulation shows that as wave enters into the metamaterial slab, the wave propagates backward due to the negative refractive index of the metamaterial.

5 Conclusions

In this paper, we first develop the Yee scheme for solving the Maxwell’s equations in metamaterials on nonuniform rectangular grids from the variational point of view. Then we show that the scheme achieves a second order superconvergence rate in space for both semi- and fully-discrete schemes. A numerical example supporting the theoretical analysis is presented first, then a popular backward wave propagation in metamaterial is simulated by Yee scheme on nonuniform rectangular grids. Similar techniques can be extended to more complicated metamaterial Maxwell’s equations [24], and detailed results will be presented in our future work.