Numerical solution of exterior Maxwell problems by Galerkin BEM and Runge–Kutta convolution quadrature

Abstract

In this paper we consider time-dependent electromagnetic scattering problems from conducting objects. We discretize the time-domain electric field integral equation using Runge–Kutta convolution quadrature in time and a Galerkin method in space. We analyze the involved operators in the Laplace domain and obtain convergence results for the fully discrete scheme. Numerical experiments indicate the sharpness of the theoretical estimates.

1 Introduction

Electromagnetic scattering problems in three dimensions have a wide range of practical applications in physics and engineering, prominent examples being magnetic resonance imaging, remote sensing systems or global positioning systems. The efficient and accurate numerical solution of such wave propagation phenomena in the time-domain has gained growing attention in the last years. Since such problems are typically formulated in unbounded domains the method of integral equations is an elegant tool to transform the underlying set of partial differential equations into time-domain boundary integral equations (TDBIEs) on the bounded surface of the scatterer.

Although the numerical solution of TDBIEs has been pursued since the 1960s (cf. [18]), their use was unpopular for a long time due to the need to deal with distributional fundamental solutions and due to stability problems of the resulting implementations. More recent numerical methods have overcome these stability issues. Important discretization techniques include Galerkin methods based on space-time variational formulations (cf. [1–3, 19, 33, 37, 40]) and methods based on bandlimited interpolation and extrapolation (cf. [44–47]).

An alternative approach to solve TDBIEs numerically is based on convolution quadrature. Developed more than 20 years ago (cf. [26, 27]), convolution quadrature based on linear multistep methods has been applied to numerous problems (cf. [8, 14, 28, 38, 39, 42, 43]); fast numerical implementations were developed in [20, 21, 23]. For a review on convolution quadrature and its applications we refer to [9, 29]. The advantages of this discretization scheme for TDBIEs include its excellent stability properties and the fact that only the Laplace transform of the time-domain fundamental solution is used and thus distributional kernels are avoided. An important assumption for the stability of convolution quadrature is the $A$-stability of the underlying time-discretization method. Since $A$-stable linear multistep methods cannot exceed a convergence order of 2, convolution quadratures based on Runge–Kutta methods have recently been considered and analyzed in order to obtain high order schemes (cf. [4–6, 30]). Most related to our work is [14] where multistep methods are considered for the time discretization and an error analysis is presented. Some of the stability estimates could be improved in our paper so that the regularity assumptions with respect to time are relaxed.

In this paper we are interested in the propagation of time-dependent electromagnetic fields in a homogeneous medium arising from the scattering of incoming waves at a perfectly conducting obstacle. In order to solve the resulting time-domain electric field integral equation (EFIE) numerically we use Runge–Kutta convolution quadrature for the time discretization and a Galerkin method for the discretization in space. The aim of this paper is, for the first time, to fully analyze this numerical method. We do this by first analyzing the Laplace domain EFIE operator $\mathcal V$ to show that the inverse operator can be polynomially bounded by

$$\begin{aligned} \left\Vert\mathcal V ^{-1}\left( s\right) \right\Vert\le C\left( \sigma _{0}\right) \frac{\left|s\right|}{\mathrm{Re}\,s}\end{aligned}$$

for $\mathrm{Re}\,s\ge \sigma _{0}>0$ and some $\sigma _{0}>0$. This allows us to use the analysis of Runge–Kutta convolution quadrature in [6] to obtain convergence estimates for the semi-discrete scheme. For the space discretization we use the classical Raviart–Thomas elements of lowest order. Using the results of the semi-discrete case we finally obtain convergence results for the fully discrete scheme. We perform numerical test with a spherical scatterer. The results indicate the sharpness of the derived convergence estimates.

2 Sobolev spaces and trace theorems

Let $\Omega _{-}$ be an open bounded set in $\mathbb R ^{3}$ with Lipschitz boundary $\Gamma$, unitary outer normal $\mathbf{n }$, and complement $\Omega _{+}:=\mathbb R ^{3}{\setminus }\overline{\Omega _{-}}$. The inner product of two vectors $\mathbf a ,\mathbf b \in \mathbb C ^{3}$ is denoted by $\mathbf a .\mathbf b ,\,\mathbf a \times \mathbf b$ is the usual vectorial product. Let $\Omega$ either be $\Omega _{-}$ or $\Omega _{+}$. For $u\in \text{ L}^{2}(\Omega )$ or $\mathbf v \in \mathbf L ^{2}(\Gamma ):=\text{ L}^{2}(\Omega )^{3}$, let

$$\begin{aligned} \Vert u\Vert _{0,\Omega }=\left( \int _{\Omega }|u(\mathbf{x })|^{2}\,d{\mathbf{x }}\right) ^{1/2} \text{ resp.} \Vert \mathbf v \Vert _{0,\Omega }=\left( \sum _{i=1}^{3}\Vert v_{i}\Vert _{0,\Omega }^{2}\right) ^{1/2}\end{aligned}$$

be the norms of $u,\mathbf v$ in these spaces. We define the following Hilbert spaces with their associated graph norms:

$$\begin{aligned}&{{\mathbf{H }}}(\text{ curl},\Omega ):=\left\{ \mathbf{v }\in \mathbf{L }^{2}(\Gamma ),\,\mathrm{curl}\,\mathbf v \in \mathbf L ^{2}(\Gamma )\right\} ,\\&\Vert \mathbf v \Vert _{\mathrm{curl},\Omega }=\left( \Vert \mathbf{v}\Vert _{0\text{,}\Omega }^{2}+\Vert \mathrm{curl}\,\mathbf v \Vert _{0\text{,}\Omega }^{2}\right) ^{1/2} \end{aligned}$$

and in a similar manner

$$\begin{aligned}&{{\mathbf{H }}}(\text{ div},\Omega ):=\left\{ \mathbf{v }\in \mathbf{L }^{2}(\Gamma ),\,\text{ div}\,\mathbf{v }\in \text{ L}^{2}(\Omega )\right\} ,\\&\Vert \mathbf{v }\Vert _{\mathrm{div,}\Omega }=\left( \Vert \mathbf{v } \Vert _{0,\Omega }^{2}+\Vert \text{ div}\,\mathbf{v }\Vert _{0,\Omega }^{2}\right) ^{1/2}. \end{aligned}$$

We will further require the $\mathbf L ^{2}(\Gamma )$ space of tangential fields,

$$\begin{aligned} \mathbf L _{t}^{2}(\Gamma ):=\left\{ \mathbf v \in \mathbf L ^{2}(\Gamma )|\mathbf{n }.\mathbf v =0 \ \text{ on}\ \Gamma \right\} \end{aligned}$$

and the following trace operators $\Pi _{\tau }$ and $\gamma _{\tau }$ mapping $\fancyscript{D}(\overline{\Omega })=\{\phi |_{\Omega }\;|\;\phi \in C_{{\text{ comp}} }^{\infty }(\mathbb R ^{3})\}$ to $\mathbf L _{t}^{2}(\Gamma )$

$$\begin{aligned} \Pi _{\tau }:\mathbf u \mapsto \mathbf{n }\times (\mathbf u \times \mathbf{n } )|_{\Gamma }\quad \text{ and}\quad \gamma _{\tau }:\mathbf u \mapsto \mathbf u |_{\Gamma }\times \mathbf{n }. \end{aligned}$$

Adhering to [13], we define the following Hilbert spaces

$$\begin{aligned} V:={\mathbf{H }}^{1/2}(\Gamma ),\qquad V_{\gamma }:=\gamma _{\tau }(V),\qquad V_{\Pi }:=\Pi _{\tau }(V), \end{aligned}$$

with norms that assure the continuity of the trace operators

$$\begin{aligned} \Vert \varvec{\lambda }\Vert _{V_{\gamma }}=\inf _{\mathbf{u }\in V}\{\Vert \mathbf{u }\Vert _{V}\;|\;\gamma _{\tau }(\mathbf{u })=\varvec{\lambda }\} \end{aligned}$$

and

$$\begin{aligned} \Vert \varvec{\lambda }\Vert _{V_{\Pi }}=\inf _{\mathbf{u }\in V}\{\Vert \mathbf{u } \Vert _{V}\;|\;\Pi _{\tau }(\mathbf{u })=\varvec{\lambda }\}. \end{aligned}$$

Further, we denote by $V_{\Pi }^{\prime }$ and $V_{\gamma }^{\prime }$ the respective dual spaces with $\mathbf{L }_{t}^{2}(\Gamma )$ as the pivot space and their natural norms. We are now ready, see [13], to introduce the following Hilbert spaces on $\Gamma$:

$$\begin{aligned} {{\mathbf{H }}}^{-1/2}(\text{ div}_{\Gamma },\Gamma )&:= \left\{ \mathbf{v }\in V_{\gamma }^{\prime }\;|\;\text{ div}_{\Gamma }\mathbf{v }\in H^{-1/2}(\Gamma )\right\} ,\\ {{\mathbf{H }}}^{-1/2}(\text{ curl}_{\Gamma },\Gamma )&:= \left\{ \mathbf{v }\in V_{\Pi }^{\prime }\;|\;\text{ curl}_{\Gamma }\mathbf{v }\in H^{-1/2} (\Gamma )\right\} \end{aligned}$$

with norms defined as

$$\begin{aligned} \begin{aligned} \left\Vert\mathbf{v }\right\Vert_{-1/2,\mathrm{div}_{\Gamma }}&:=\left\{ \left\Vert\mathbf{v }\right\Vert_{V_{\gamma }^{\prime }}^{2}+\left\Vert\text{ div}_{\Gamma }\mathbf v \right\Vert_{H^{-1/2}(\Gamma )} ^{2}\right\} ^{1/2},\\ \left\Vert\mathbf{v }\right\Vert_{-1/2,\mathrm{curl}_{\Gamma }}&:=\left\{ \left\Vert\mathbf{v }\right\Vert_{V_{\Pi }^{\prime }} ^{2}+\left\Vert\text{ curl}_{\Gamma }\mathbf{v }\right\Vert_{H^{-1/2}(\Gamma )}^{2}\right\} ^{1/2}. \end{aligned} \end{aligned}$$

(1)

The unknown densities which arise in the boundary integral equations for the Maxwell problem are traces of vector fields in ${\mathbf{H }}(\mathrm{curl},\Omega _{+})$. The following theorem shows that ${{\mathbf{H }}}^{-1/2} (\text{ div}_{\Gamma },\Gamma )$ and ${{\mathbf{H }}}^{-1/2} (\text{ curl}_{\Gamma },\Gamma )$ are the correct spaces for these densities.

Theorem 2.1

Let $\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\}$. The trace mappings

$$\begin{aligned} \Pi _{\tau }^{\Omega }:{{\mathbf{H }}}(\mathrm{curl},\Omega )\,\,\rightarrow \,\,{{\mathbf{H }}}^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma ) \end{aligned}$$

and

$$\begin{aligned} \gamma _{\tau }^{\Omega }:{{\mathbf{H }}}(\mathrm{curl},\Omega )\,\,\rightarrow \,\,{{\mathbf{H }}}^{-1/2}(\mathrm{div}_{\Gamma },\Gamma ) \end{aligned}$$

are continuous and surjective. Moreover, there exist continuous liftings for these trace operators in ${{\mathbf{H }}}(\mathrm{curl},\Omega )$.

For a proof we refer to [13, Theorem 4.1]. As an important consequence of Theorem 2.1 we get the following Green’s formula. For this, we put ${{\mathbf{H }}}^{-1/2}(\text{ curl}_{\Gamma },\Gamma )$ and ${{\mathbf{H }}}^{-1/2}(\text{ div}_{\Gamma },\Gamma )$ in duality when $\mathbf{L }_{t}^{2}(\Omega )$ is used as pivot space (cf. [13, Section 5]). More precisely, the usual $\mathbf{L }_{t} ^{2}(\Gamma )$ scalar product can be continuously extended to a sesqui-linear duality pairing

$$\begin{aligned} \left( \cdot ,\cdot \right) _{\Gamma }:{\mathbf{H }}^{-1/2}(\text{ div} _{\Gamma },\Gamma )\times {\mathbf{H }}^{-1/2}(\text{ curl}_{\Gamma } ,\Gamma )\rightarrow \mathbb C \end{aligned}$$

by means of Green’s formula: For all $\mathbf u,v \in {\mathbf{H }} (\mathrm{curl},\Omega )$

$$\begin{aligned}&\text{ sign}\left( \Omega \right) \int \limits _{\Omega }(\overline{\mathbf{u }}.\,\mathrm{curl}\,\mathbf v -\mathrm{curl}\,\overline{\mathbf{u }}.\,\mathbf v )\,d{\mathbf{x }} =\left( \gamma _{\tau }^{\Omega }\mathbf u ,\Pi _{\tau }^{\Omega }\mathbf v \right) _{\Gamma }\quad \nonumber \\&\quad \text{ with}\quad \text{ sign}\left( \Omega \right) :=\left\{ \begin{array} [c]{cc} -1,&\quad \Omega =\Omega _{+},\\ +1,&\quad \Omega =\Omega _{-}. \end{array} \right. \end{aligned}$$

(2)

Note that the complex conjugation in $(\cdot , \cdot )_\Gamma$ is on the first argument. This will be of importance in Sect. 4.4.

For bounded, smooth domains, Green’s formula is proved in [31] and for Lipschitz domains in [11, 13]. For exterior domains $\Omega _{+}$, this follows by employing a cutoff function and the dense embedding

$$\begin{aligned} \left\{ \left. u\right|_{\Omega _{+}}:u\in C_{\text{ comp}}^{\infty }(\mathbb R ^{3})\right\} \hookrightarrow {\mathbf{H }}\left( \mathrm{curl},\Omega \right) \end{aligned}$$

and applying Green’s formula for bounded domains.

Finally, as another consequence of the duality of the two trace spaces ${\mathbf{H }}^{-1/2}(\text{ div}_{\Gamma },\Gamma )$ and ${\mathbf{H }} ^{-1/2}(\text{ curl}_{\Gamma },\Gamma )$ with $\mathbf L _{t}^{2} (\Gamma )$ as the pivot space (see (36) in [13]) we have the identities

$$\begin{aligned} \Vert \mathbf u \Vert _{-1/2,\text{ div}}=\sup _{\varvec{\varphi }\in {\mathbf{H }}^{-1/2}(\text{ curl}_{\Gamma },\Gamma )}\,\frac{\left|\left(\mathbf u , \varvec{\varphi }\right)_\Gamma \right|}{\Vert \varvec{\varphi }\Vert _{-1/2,\text{ curl}}} \end{aligned}$$

(3a)

and

$$\begin{aligned} \Vert \mathbf v \Vert _{-1/2,\text{ curl}}=\sup _{\varvec{\varphi } \in {\mathbf{H }}^{-1/2}(\mathrm{div}_{\Gamma },\Gamma )}\,\frac{\left|\left(\mathbf v ,\varvec{\varphi }\right)_\Gamma \right|}{\Vert \varvec{\varphi }\Vert _{-1/2,\text{ div}}}. \end{aligned}$$

(3b)

Remark 2.2

In the remainder of the paper we may, in order to enhance readability, use both the classical notation $\mathbf{n } \times (\cdot \times \mathbf{n })$ and $\cdot \times \mathbf{n }$ and the notation $\Pi _\tau$ and $\gamma _\tau$, even though strictly speaking only the latter should be used.

3 Integral formulation for exterior scattering problems

In the following we will be concerned with the propagation of time-dependent electromagnetic fields near a perfectly conducting body. We consider three-dimensional exterior scattering problems in a homogeneous, isotropic medium with constant, positive electric permittivity $\varepsilon$ and constant, positive magnetic permeability $\mu$. Furthermore we assume that there are no external sources.

Let $\Omega _{-}$ be a three-dimensional perfectly conducting object with bounded Lipschitz surface $\Gamma$ and let $({\mathbf{E }}^{\text{ inc} },{\mathbf{H }}^{\text{ inc}})$ be an incident electromagnetic field. The scattered field $\left( {\mathbf{E }},{\mathbf{H }}\right)$ satisfies the time dependent Maxwell equations:

$$\begin{aligned} -\varepsilon \frac{\partial {\mathbf{E }}}{\partial t}+\mathrm{curl}\,{\mathbf{H }}&= \mathbf 0 \quad \text{ in}\,\mathbb R _{+}\times \Omega _{+},\end{aligned}$$

(4)

$$\begin{aligned} \mu \frac{\partial {\mathbf{H }}}{\partial t}+\mathrm{curl}\,{\mathbf{E }}&= \mathbf 0 \quad \text{ in}\,\mathbb R _{+}\times \Omega _{+}, \end{aligned}$$

(5)

$$\begin{aligned} \text{ div}\,{\mathbf{E }}=\text{ div}\,{\mathbf{H }}&= 0 \quad \text{ in}\,\mathbb R _{+}\times \Omega _{+}, \end{aligned}$$

(6)

with boundary conditions

$$\begin{aligned} ({\mathbf{E }}+{\mathbf{E }}^{\text{ inc}})\times \mathbf{n }=\mathbf 0 \quad \text{ on} \,\mathbb R _{+}\times \Gamma \end{aligned}$$

(7)

and initial conditions

$$\begin{aligned} {\mathbf{E }}(t,{\mathbf{x }})={\mathbf{H }}(t,{\mathbf{x }})=\mathbf 0 \quad \text{ for}\,t\le 0 \text{ and} {\mathbf{x }}\in \Omega _{+}. \end{aligned}$$

Since our problem is formulated in unbounded domains we use the method of integral equations to transform this set of partial differential equations to integral equations on the bounded surface of the scatterer. These can be derived by inverse Laplace transformation of the more widely known frequency domain integral representations, see (5.6.4–6) in [31], as we explain next. The application of the Laplace transform, i.e., $\hat{{\mathbf{E }} }:=\fancyscript{L}{\mathbf{E }}=\int _{0}^{t}\text{ e}^{-st}{\mathbf{E }} (\cdot ,t)dt$, to equations (4) and (5) leads to

$$\begin{aligned} -\varepsilon s\hat{{\mathbf{E }}}+\mathrm{curl}\,\hat{{\mathbf{H }}}&=\mathbf 0 \quad \text{ in}\;\Omega _{+},\\ \mu s\hat{{\mathbf{H }}}+\mathrm{curl}\,\hat{\mathbf{E }}&=\mathbf 0 \quad \text{ in}\,\Omega _{+}, \end{aligned}$$

with boundary condition

$$\begin{aligned} (\hat{\mathbf{E }}+\hat{\mathbf{E }}^{\text{ inc}})\times \mathbf{n } =\mathbf 0 \qquad \text{ on}\,\Gamma . \end{aligned}$$

The boundary integral representation for the solution of the above Laplace domain boundary value problem is given by

$$\begin{aligned} \hat{\mathbf{E }}(\mathbf{y })&= -s\mu \int _{\Gamma }K(s,\mathbf{x } -\mathbf{y }){\mathbf{j }}(\mathbf{x })d\Gamma _{\mathbf{x }}+\frac{1}{\varepsilon }\nabla \int _{\Gamma }K(s,\mathbf{x }-\mathbf{y })\frac{1}{s}\text{ div} _{\Gamma }{\mathbf{j }}(\mathbf{x })d\Gamma _{\mathbf{x }},\end{aligned}$$

(8)

$$\begin{aligned} \hat{{\mathbf{H }}}(\mathbf{y })&= \mathrm{curl}\int _{\Gamma }K(s,\mathbf{x }-\mathbf{y }){\mathbf{j }}(\mathbf{x })d\Gamma _{\mathbf{x }}, \end{aligned}$$

(9)

where the free space Green’s function for the Helmholtz operator is given by

$$\begin{aligned} K(s,{\mathbf{z }}):=\frac{\text{ e}^{-s\sqrt{\varepsilon \mu } \Vert {\mathbf{z }}\Vert }}{4\pi \Vert {\mathbf{z }}\Vert }. \end{aligned}$$

(10)

Taking the inverse Laplace transform of the above formulation gives the time-domain electric field integral equation (EFIE):

$$\begin{aligned} \mathbf{E }(t,\mathbf{y })&= -\mu \int _{0}^{t}\int _{\Gamma }k(t-\tau ,\mathbf{x }-\mathbf{y })\,\partial _{t}{\mathbf{j }}(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }}\,d\tau \nonumber \\&-\frac{1}{\varepsilon }\nabla \int _{0}^{t}\int _{\Gamma } k(t-\tau ,\mathbf{x }-\mathbf{y })\,q(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x } }\,d\tau \\ {\mathbf{H }}(t,\mathbf{y })&= \mathrm{curl}\int _{0}^{t}\int _{\Gamma }k(t-\tau ,\mathbf{x }-\mathbf{y })\,{\mathbf{j }}(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }}\,d\tau \nonumber \end{aligned}$$

(11)

for $\mathbf{y }\in \Omega _{+}{\setminus }\Gamma$, involving the electric surface current density ${\mathbf{j }}$, the charge density $q$

$$\begin{aligned} q(t,\mathbf{x })=-\int _{0}^{t}\text{ div}_{\Gamma }{\mathbf{j }} (\tau ,\mathbf{x })d\tau , \end{aligned}$$

(12)

and the time domain free space Green’s function

$$\begin{aligned} k(t,\mathbf{z }):=\fancyscript{L}^{-1}\{K(\cdot ,\mathbf{z })\}(t)=\frac{\delta (t-\sqrt{\varepsilon \mu }\Vert \mathbf{z }\Vert )}{4\pi \Vert \mathbf{z } \Vert } , \end{aligned}$$

(13)

where $\delta$ denotes the Dirac delta function. It can be easily checked that for any ${\mathbf{j }}$ and $q$ satisfying (12), $\mathbf{E }$ and ${\mathbf{H }}$ given by the representation formula (11) satisfy (4), (5), and (6). The initial conditions are also satisfied since we assume that ${\mathbf{j }} (\tau ,\mathbf{y })=\mathbf 0$ and $q(\tau ,\mathbf{y })=0$ for $\tau \le 0$ and $\mathbf{y }\in \Omega _{+}{\setminus }\Gamma$. The unknown density functions are now determined via the boundary condition (7). This requires the extension of $\mathbf{E }\times \mathbf{n }$ to the boundary $\Gamma$ which can be done continuously (cf. [31]). The resulting integral equation we have to solve reads

$$\begin{aligned}&-\mu \Pi _{\tau }\int _{0}^{t}\int _{\Gamma }k(t-\tau ,\mathbf{x }-\mathbf{y } ){\mathbf{j }}_{t}(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }}d\tau \nonumber \nonumber \\&\quad -\frac{1}{\varepsilon }\nabla _{\Gamma }\int _{0}^{t}\int _{\Gamma }k(t\!-\!\tau ,\mathbf{x }\!-\!\mathbf{y })q(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }} d\tau \!=\!\mathbf{n }\left( {\mathbf{y }}\right) \times \mathbf{g }\left( t,\mathbf{y }\right) \quad \text{ for} (t,\mathbf{y })\in \mathbb R \times \Gamma ,\nonumber \\ \end{aligned}$$

(14)

with

$$\begin{aligned} \mathbf{g }:=-\mathbf E^{\text{ inc}}\times n , \end{aligned}$$

(15)

${\mathbf{j }}_{t}=\partial _{t}{\mathbf{j }}$, and $\nabla _{\Gamma }$ the surface gradient.

In order to eliminate the unknown $q$ and for further reasons that will become apparent in the next section, see Remark 4.3, we differentiate both sides of the above equation with respect to time to obtain

$$\begin{aligned}&-\mu \Pi _{\tau } \int _{0}^{t}\int _{\Gamma }k(t-\tau ,\mathbf{x }-\mathbf{y } ){\mathbf{j }}_{tt}(\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }}d\tau \nonumber \\&\quad +\frac{1}{\varepsilon }\nabla _{\Gamma }\int _{0}^{t}\int _{\Gamma } k(t-\tau ,\mathbf{x }-\mathbf{y })\text{ div}_{\Gamma }{\mathbf{j }} (\tau ,\mathbf{x })\,d\Gamma _{\mathbf{x }}d\tau =\mathbf{n }\left( {\mathbf{y }} \right) \times \mathbf{g }_{t}\left( t,\mathbf{y }\right) \end{aligned}$$

(16)

which we have to solve for all $(t,\mathbf{y })\in \mathbb R \times \Gamma$. Note that this integral equation contains only the unknown electric surface current density ${\mathbf{j }}$.

4 Numerical discretization

4.1 Time discretization

For the time discretization we will make use of convolution quadrature based on a Runge–Kutta method. An $m$-stage Runge–Kutta method in the standard Butcher tableau notation can be described by the matrix $\mathbf A =(a_{ij})_{i,j=1}^{m}\in \mathbb R ^{m\times m}$ and the vectors $\mathbf b =(b_{1},b_{2},\dots ,b_{m})^{T}\in \mathbb R ^{m}$ and $\mathbf c =(c_{1} ,c_{2},\dots ,c_{m})^{T}$. The corresponding Runge–Kutta discretization of the initial value problem $y^{\prime }=f(t,y),y(0)=y_{0}$, is then given by

$$\begin{aligned} Y_{ni}&= y_{n}+\Delta t\sum _{j=1}^{m}a_{ij}f(t_{n}+c_{j}\Delta t,Y_{nj}),\qquad i=1,\dots ,m,\\ y_{n+1}&= y_{n}+\Delta t\sum _{j=1}^{m}b_{j}f(t_{n}+c_{j}\Delta t,Y_{nj}); \end{aligned}$$

here $\Delta t>0$ is the time-step and $t_{j}=j\Delta t$. The values $Y_{ni}$ and $y_{n}$ are approximations to $y(t_{n}+c_{i}\Delta t)$ and $y(t_{n})$, respectively. This Runge–Kutta method is said to be of (classical) order $p\ge 1$ and stage order $q$ if for sufficiently smooth right-hand sides $f$,

$$\begin{aligned} Y_{0i}-y(c_{i}\Delta t)=O(\Delta t^{q+1}), \text{ for}\,i=1,\dots ,m,\quad \text{ and}\quad y_{1}-y(t_{1})=O(\Delta t^{p+1}), \nonumber \\ \end{aligned}$$

(17)

as $\Delta t\rightarrow 0$. Using the notation

$$\begin{aligned} {\small 1}\!\!1=(1,1,\dots ,1)^{T}, \end{aligned}$$

the Runge–Kutta method is said to be $A$-stable if $\mathbf I -z\mathbf A$ is non-singular for $\text{ Re}\,z\le 0$ and the stability function

$$\begin{aligned} R(z)=1+z\mathbf b ^{T}(\mathbf I -z\mathbf A )^{-1}{\small 1}\!\!1\end{aligned}$$

(18)

satisfies $|R(z)|\le 1$ for $\text{ Re}\,z\le 0$. Note that if $\mathbf A ^{-1}$ exists, then $R(\infty )=1-\mathbf b ^{T}\mathbf A ^{-1}{\small 1}\!\!1$.

In order to use the convergence results proved in [6], we make the following assumptions on the Runge–Kutta methods.

Assumption 4.1

• a. The Runge–Kutta method is $A$-stable with (classical) order $p\ge 1$ and stage order $q\le p$.

• b. The stability function satisfies $|R(\text{ i}y)|<1$ for all real $y\ne 0$.

• c. $R(\infty )=0.$

• d. The Runge–Kutta coefficient matrix $\mathbf A$ is invertible.

Radau IIA and Lobatto IIIC are examples of methods satisfying all of the above assumptions with $q = m$ and $p = 2m-1$ for Radau IIA and $q = m-1$ and $p = 2m$ for Lobatto IIIC. For possible relaxation of these conditions and deeper meaning of them see [6].

Convolution quadrature is a method for the discretization of continuous convolutions

$$\begin{aligned} u(t)=K(\partial _{t})g:=\int _{0}^{t}k(t-\tau )g(\tau )d\tau \end{aligned}$$

(19)

that uses only the Laplace transformed kernel $K(s)=\left( \fancyscript{L}k\right) (s)$, the so-called transfer function. The importance of the transfer function is highlighted by the operational notation $K(\partial _{t})g$.

The Runge–Kutta based convolution quadrature approximation to $u(t_{n} +c_{\ell }\Delta t), \ell =1,\dots ,m$, is given by

$$\begin{aligned} \left( \begin{array}{c} u_{n1}\\ \vdots \\ u_{nm} \end{array} \ \ \right) =\left( K(\underline{\partial _{t}}^{\Delta t})g\right) _{n}:=\sum _{j=0}^{n}{\mathbf{W }}_{n-j}^{\Delta t}(K)\left( \begin{array}{c} g(t_{j}+c_{1}\Delta t)\\ \vdots \\ g(t_{j}+c_{m}\Delta t) \end{array} \ \ \right). \end{aligned}$$

(20)

Here, the matrix convolution weights ${\mathbf{W }}_{j}^{\Delta t}(K)$ are defined implicitly through a generating function

$$\begin{aligned} K\left( \frac{\chi \left( \zeta \right) }{\Delta t}\right) =\sum _{j=0}^{\infty }{\mathbf{W }}_{j}^{\Delta t}(K)\zeta ^{j}, \end{aligned}$$

(21)

with

$$\begin{aligned} \chi \left( \zeta \right) =\mathbf A ^{-1}-\zeta \mathbf A ^{-1} {\small 1}\!\!1\mathbf b ^{T}\mathbf A ^{-1}. \end{aligned}$$

(22)

The approximation at $t_{n+1}$ is given simply by $u_{n+1}=\mathbf b ^{T}\mathbf A ^{-1}(u_{n\ell })_{\ell =1}^{m}$, i.e.,

$$\begin{aligned} u_{n+1}:=\mathbf b ^{T}\mathbf A ^{-1}\left( K(\underline{\partial _{t} }^{\Delta t})g\right) _{n}. \end{aligned}$$

(23)

Note that for stiffly accurate Runge–Kutta methods like Radau IIA or Lobatto IIIC we have $\mathbf b ^{T}\mathbf A ^{-1}=(0,0,\ldots ,0,1)^{T}$ and therefore (23) simplifies to $u_{n+1}=u_{nm}$ in this case.

Applying this time-discretization to (16) we obtain the semi-discretized equations

$$\begin{aligned}&-\sum _{j=0}^{n}\mu \,\Pi _{\tau }\int _{\Gamma }{\mathbf{W }}_{n-j}^{(2)} (\mathbf{x }-\mathbf{y })\, \begin{pmatrix} {\mathbf{j }}(t_{j}+c_{1}\Delta t,\mathbf{x })\\ \vdots \\ {\mathbf{j }}(t_{j}+c_{m}\Delta t,\mathbf{x }) \end{pmatrix} \,d\Gamma _{\mathbf{x }}\nonumber \\&\quad +\sum _{j=0}^{n}\frac{1}{\varepsilon }\nabla _{\Gamma } \int _{\Gamma }{\mathbf{W }}_{n-j}(\mathbf{x }-\mathbf{y }) \begin{pmatrix} \text{ div}_{\Gamma }{\mathbf{j }}(t_{j}+c_{1}\Delta t,\mathbf{x })\\ \vdots \\ \text{ div}_{\Gamma }{\mathbf{j }}(t_{j}+c_{m}\Delta t,\mathbf{x }) \end{pmatrix} d\Gamma _{\mathbf{x }}=\left( {\mathbf{n }}\times {\mathbf{g }}_{t}\right) _{n}, \qquad \end{aligned}$$

(24)

with

$$\begin{aligned} \left( {\mathbf{n }}\times \mathbf{g }_{t}\right) _{n}\left( {\mathbf{y }}\right) := \begin{pmatrix} \mathbf{n }\left( {\mathbf{y }}\right) \times \mathbf{g }_{t}(t_{n}+c_{1}\Delta t,\mathbf{y })\\ \vdots \\ \mathbf{n }\left( {\mathbf{y }}\right) \times \mathbf{g }_{t}(t_{n}+c_{m}\Delta t,\mathbf{y }) \end{pmatrix} \end{aligned}$$

and the weights ${\mathbf{W }}_{j}=\left( w_{j,k,\ell }\right) _{1\le k,\ell \le m}$ and ${\mathbf{W }}_{j}^{\left( 2\right) }=\left( w_{j,k,\ell }^{\left( 2\right) }\right) _{1\le k,\ell \le m}$ defined by

$$\begin{aligned} K(\chi \left( \zeta \right) /\Delta t,\mathbf{z })\!=\!\sum _{j=0}^{\infty }{\mathbf{W }}_{j}(\mathbf{z })\zeta ^{j},\quad \left( \chi \left( \zeta \right) /\Delta t\right) ^{2}K(\chi \left( \zeta \right) /\Delta t,\mathbf{z } )\!=\!\sum _{j=0}^{\infty }{\mathbf{W }}_{j}^{(2)}(\mathbf{z })\zeta ^{j}, \nonumber \\ \end{aligned}$$

(25)

where $K$ is again as in (10). The importance of using the differentiated formulation (16) instead of (14) can be seen from the following proposition.

Proposition 4.2

Under the above assumptions on the Runge–Kutta method, there exists a constant $c>0$ such that for any $\epsilon >0$ and all $\mathbf{z }\in \mathbb R ^{3}$ with $\left\Vert{\mathbf{z }}\right\Vert<R$ it holds

$$\begin{aligned} \Vert {\mathbf{W }}_{j}(\mathbf{z })\Vert \le \epsilon ,\qquad \text{ for} \text{ all}\, j>\max \left( \frac{cR}{\Delta t},\log \frac{1}{\epsilon }\right) \end{aligned}$$

and

$$\begin{aligned} \Vert {\mathbf{W }}_{j}^{(2)}(\mathbf{z })\Vert \le \epsilon ,\qquad \text{ for} \text{ all}\,j>\max \left( \frac{cR}{\Delta t},\log \frac{1}{\epsilon }+\log \frac{1}{\Delta t}\right). \end{aligned}$$

Proof

By Cauchy’s integral formula it holds

$$\begin{aligned} {\mathbf{W }}_{j}(\mathbf{z })&= \frac{1}{4\pi \left\Vert{\mathbf{z }}\right\Vert}\frac{1}{2\pi \text{ i}}\oint _{C}\text{ e}^{-\chi (\zeta )\left\Vert\mathbf{z }\right\Vert/\Delta t}\zeta ^{-j-1}d\zeta \\&= \frac{1}{4\pi \left\Vert\mathbf{z }\right\Vert}\sum _{\ell =j}^{\infty } \frac{(\left\Vert\mathbf{z }\right\Vert/\Delta t)^{\ell }}{\ell !}\frac{1}{2\pi \text{ i}}\oint _{C}\left( -\chi (\zeta )\right) ^{\ell }\zeta ^{-j-1}d\zeta . \end{aligned}$$

For the contour $C$ we may use the unit circle and obtain the bound

$$\begin{aligned} \Vert {\mathbf{W }}_{j}(\mathbf{z })\Vert \le \frac{1}{4\pi \left\Vert\mathbf{z } \right\Vert}\sum _{\ell =j}^{\infty }\frac{(a\left\Vert\mathbf{z }\right\Vert/\Delta t)^{\ell }}{\ell !},\qquad \text{ with}\ a=\max _{|\zeta |=1}\Vert \chi (\zeta )\Vert . \end{aligned}$$

Using Stirling’s approximation finally we obtain a crude bound

$$\begin{aligned} \Vert {\mathbf{W }}_{j}(\mathbf{z })\Vert&\le \frac{1}{4\pi \left\Vert\mathbf{z }\right\Vert}\sum \limits _{\ell =j}^{\infty }\left( \frac{a\text{ e} \left\Vert\mathbf{z }\right\Vert}{\ell \Delta t}\right) ^{\ell }\\&\le \frac{1}{4\pi \left\Vert\mathbf{z }\right\Vert}\left( \frac{a\text{ e} \left\Vert\mathbf{z }\right\Vert}{j\Delta t}\right) ^{j}\frac{1}{1-(a\text{ e}\left\Vert\mathbf{z }\right\Vert/j\Delta t)}\\&= \frac{a\text{ e}}{4\pi j\Delta t}\left( \frac{a\text{ e}\left\Vert\mathbf{z }\right\Vert}{j\Delta t}\right) ^{j-1}\frac{1}{1-(a\text{ e}\left\Vert\mathbf{z }\right\Vert/j\Delta t)}. \end{aligned}$$

Assuming for example that $j>2a\text{ e}R/\Delta t$ we obtain that

$$\begin{aligned} \Vert {\mathbf{W }}_{j}(\mathbf{z })\Vert \le C\frac{1}{R}2^{-j} \end{aligned}$$

from which the first bound follows directly. Similar reasoning gives the result for ${\mathbf{W }}_{j}^{(2)}$.

$\square$

Remark 4.3

The above proposition shows that for large enough $j$, the weights ${\mathbf{W }}_{j}$ and ${\mathbf{W }}_{j}^{(2)}$ are exponentially close to zero. In order to eliminate $q$ from (14) we could have simply substituted for $q$ the conservation law (12). This would, however, have introduced the integration operator $1/s$ and since $(\chi \left( \zeta \right) )^{-1}=\mathbf A +\frac{\zeta }{1-\zeta } {\small 1}\!\!1\mathbf b ^{T}$ it is not difficult to see that weights for this operator do not converge to zero.

Standard algorithms for implementing convolution quadrature are listed in the recent review [9]. In this work we make use of the easiest to implement algorithm introduced in [8] and described in Section 3.3.1 of [9]. This approach does not require the explicit computation of convolution weights and its stability has been investigated theoretically and practically for acoustic problems in [8].

4.2 Convergence of the semi-discrete scheme

Let us define the Laplace domain EFIE operator on the boundary $\mathcal V (s)\!:{\mathbf{H }}^{-1/2}(\text{ div}_{\Gamma },\Gamma )\rightarrow {\mathbf{H }}^{-1/2}(\text{ curl}_{\Gamma },\Gamma )$ by

$$\begin{aligned} \left( \mathcal V (s)\hat{{\mathbf{j }}}\right) \left( \mathbf{y }\right)&:= -\mu \Pi _{\tau }\int _{\Gamma }s^{2}\,K(s,\mathbf{x }-\mathbf{y })\,\hat{{\mathbf{j }}}(\mathbf{x })\,d\Gamma _{\mathbf{x }}\nonumber \\&+ \frac{1}{\varepsilon }\nabla _{\Gamma }\int _{\Gamma }\,K(s,\mathbf{x } -\mathbf{y })\,\text{ div}_{\Gamma }\hat{{\mathbf{j }}}(\mathbf{x } )\,d\Gamma _{\mathbf{x }},\quad \quad \mathbf{y }\in \Gamma . \end{aligned}$$

(26)

Further denote by $\mathcal S (s):{\mathbf{H }}^{-1/2}(\text{ div}_{\Gamma },\Gamma )\rightarrow {\mathbf{H }}(\mathrm{curl},\Omega _{+})$ the operator

$$\begin{aligned} \left( \mathcal S (s)\hat{{\mathbf{j }}}\right) \left( \mathbf{y }\right)&:= -\mu \int _{\Gamma }s\,K(s,\mathbf{x }-\mathbf{y })\hat{{\mathbf{j }}} (\mathbf{x })\,d\Gamma _{\mathbf{x }}\nonumber \\&+ \frac{1}{\varepsilon }\nabla \int _{\Gamma }\,\frac{1}{s}K(s,\mathbf{x } -\mathbf{y })\,\text{ div}_{\Gamma }\hat{{\mathbf{j }}}(\mathbf{x } )\,d\Gamma _{\mathbf{x }},\qquad \mathbf{y }\in \Omega ^{+}. \end{aligned}$$

(27)

Note that $\mathcal V (s)$ is the tangential trace of the differentiated domain operator $\mathcal S (s)$:

$$\begin{aligned} \mathcal V (s)=s\Pi _{\tau }\mathcal S (s). \end{aligned}$$

Therefore, using the operational notation (19), the continuous system (16) can be written in short-hand as: Find ${\mathbf{j }}$ such that

$$\begin{aligned} \mathcal V (\partial _{t}){\mathbf{j }}=\mathbf{n }\times \mathbf{g }_{t}, \end{aligned}$$

(28)

and its Runge–Kutta discretization as: Find ${\mathbf{j }}^{\Delta t}$ such that

$$\begin{aligned} \left( \mathcal V (\underline{\partial _{t}}^{\Delta t}){\mathbf{j }}^{\Delta t}\right) _{n}=(\mathbf{n }\times \mathbf{g }_{t})_{n}. \end{aligned}$$

Using the composition rule

$$\begin{aligned} K_{2}K_{1}(\underline{\partial _{t}}^{\Delta t})g=K_{2}(\underline{\partial _{t}}^{\Delta t})K_{1}(\underline{\partial _{t}}^{\Delta t})g, \end{aligned}$$

(29)

see [5], we see that the unknown density is in fact given by

$$\begin{aligned} ({\mathbf{j }}^{\Delta t})_{n}= \begin{pmatrix} {\mathbf{j }}_{n1}^{\Delta t}\\ \vdots \\ {\mathbf{j }}_{nm}^{\Delta t}\\ \end{pmatrix} =\left( \mathcal V ^{-1}(\underline{\partial _{t}}^{\Delta t})\mathbf{n } \times \mathbf{g }_{t}\right) _{n} \end{aligned}$$

and

$$\begin{aligned} {\mathbf{j }}_{n+1}^{\Delta t}:=\mathbf b ^{T}\mathbf A ^{-1}\left( \mathcal V ^{-1}(\underline{\partial _{t}}^{\Delta t})\mathbf{n }\times \mathbf{g }_{t}\right) _{n}. \end{aligned}$$

Finally, using the definition of $\mathcal S (s)$ (recall that $\mathcal V (s)=s\Pi _{\tau }\mathcal S (s)$) we have that

$$\begin{aligned} \mathbf{E }=\mathcal S \mathcal V ^{-1}(\partial _{t})\,\mathbf{n } \times \mathbf{g }_{t} \end{aligned}$$

and the discrete approximation $\mathbf{E }_{n+1}^{\Delta t}\approx \mathbf{E }\left( t_{n+1},\cdot \right)$ of the electric field is given by

$$\begin{aligned} \mathbf{E }_{n+1}^{\Delta t}=\mathbf b ^{T}\mathbf A ^{-1}\left( \mathcal S \mathcal V ^{-1}(\underline{\partial _{t}}^{\Delta t})\mathbf{n } \times \mathbf{g }_{t}\right) _{n}. \end{aligned}$$

It is consequently possible to deduce convergence results just from properties of $\mathcal V ^{-1}(s)$ and $\mathcal S (s)$ in the Laplace domain.

Theorem 4.4

There exists $\sigma _{0}>0$ such that the following statements hold.

• (a) The inverse operator $\mathcal V ^{-1}(s):{\mathbf{H }}^{-1/2} (\mathrm{curl}_{\Gamma },\Gamma )\rightarrow {\mathbf{H }}^{-1/2} (\mathrm{div}_{\Gamma },\Gamma )$ is analytic for $\mathrm{Re}\, s>0$ and bounded in the operator norm as

  $$\begin{aligned} \left\Vert\mathcal V ^{-1}\left( s\right) \right\Vert\le C\left( \sigma _{0}\right) \frac{\left|s\right|}{\mathrm{Re}\,s} \qquad \text{ for} \mathrm{Re}\,s\ge \sigma _{0}>0. \end{aligned}$$

  (30)

• (b) An upper bound for the operator norm of $\mathcal V (s)\!:\!{\mathbf{H }} ^{-1/2}(\mathrm{div}_{\Gamma },\Gamma )\!\rightarrow \!\!{\mathbf{H }} ^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma )$ is given by

  $$\begin{aligned} \Vert \mathcal V (s)\Vert \le C\left( \sigma _{0}\right) \frac{|s|^{3} }{\mathrm{Re}\,s}. \end{aligned}$$

  (31)

• (c) For any $\mathbf{y }\in \Omega _{+}$, the field point evaluation $\delta _{\mathbf{y }}\mathcal S (s):{\mathbf{H }}^{-1/2}(\mathrm{div} _{\Gamma },\Gamma )\rightarrow \mathbb C ^{3}$ is analytic for $\mathrm{Re}\,s>0$ and bounded as

  $$\begin{aligned} \Vert \delta _{\mathbf{y }}\mathcal S (s)\Vert \le C(\sigma _{0} ,\mathrm{dist}(\mathbf{y },\Gamma ))\text{ e} ^{-\mathrm{Re}\,s\ \mathrm{dist}(\mathbf{y } ,\Gamma )}|s|^{2}\qquad \text{ for} \mathrm{Re}\,s\ge \sigma _{0}>0. \end{aligned}$$

Proof

We follow the ideas of [3] and extend them from the acoustic case to the present case of Maxwell operators. Similar arguments can be found in the master’s thesis of one of the authors [41, Prop. 3.5], see also the PhD theses [32] and [40]. The definitions of the single layer operators in these references differ slightly, for example $\mathcal V \left( s\right) =sR\left( s\right)$, where $R\left( s\right)$ is as in [41, (3.10)]. In our proof $C$ will denote a generic constant which is allowed to change from one line to the next.

For $\varvec{\varphi }\in {\mathbf{H }}^{-1/2}(\mathrm{div}_{\Gamma },\Gamma )$, we define $\varvec{\psi }:=\mathcal V (s)\varvec{\varphi }$. Let $\mathbf{h }\in {{\mathbf{H }}}(\mathrm{curl},\Omega )$ denote a lifting of $\varvec{\psi }\in {{\mathbf{H }}}^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma )$, i.e., $\varvec{\psi }=\Pi _{\tau }\mathbf h$; a proof of the existence of a continuous lifting operator can be found in [31, 40]. We relate this equation to the following exterior and interior, time-harmonic Maxwell problem. Let $\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\}$. Find $\left( \mathbf{E }_{\Omega },{\mathbf{H }}_{\Omega }\right) \in {\mathbf{H }} (\mathrm{curl},\Omega )\times {\mathbf{H }}(\mathrm{curl},\Omega )$ such that

$$\begin{aligned} -s\varepsilon \mathbf{E }_{\Omega }+\mathrm{curl}\,H_{\Omega }&= \mathbf 0 \quad \quad \text{ in}\,\Omega ,\nonumber \\ s\mu \mathbf{H }_{\Omega }+\mathrm{curl}\,\mathbf{E }_{\Omega }&= \mathbf 0 \quad \quad \text{ in}\,\Omega ,\\ \mathbf{E }_{\Omega }\times \mathbf{n }&= \frac{1}{s}\mathbf h \times \mathbf{n }\quad \quad \text{ on}\,\Gamma .\nonumber \end{aligned}$$

(32)

This problem admits a unique solution for all $\mathrm{Re}\,s>0$ as proved, e.g., in [40] and [41, Lemma 3.3].

In the following we will make use of the scaled norm

$$\begin{aligned} \left\Vert\mathbf{E }_{\Omega }\right\Vert^{2} _{\mathrm{curl},\Omega ,s}:=\int _{\Omega }\left|\mathrm{curl}\,\mathbf{E }_{\Omega }\right|^{2}+\left|\sqrt{\mu \varepsilon }s\mathbf{E }_{\Omega }\right|^{2}d\mathbf x. \end{aligned}$$

Then, we have, see [31, Theorem 5.5.1],

$$\begin{aligned} \Pi _{\tau }\mathbf h =s\Pi _{\tau }^{\Omega }\mathbf{E }_{\Omega }\quad \text{ and}\quad \varvec{\varphi }=\gamma _{\tau }^{\Omega _{-}}\mathbf{H } _{\Omega _{-}}-\gamma _{\tau }^{\Omega _{+}}\mathbf{H }_{\Omega _{+}}. \end{aligned}$$

(33)

Hence, by Green’s formula

$$\begin{aligned} \text{ Re}\left( -s\varvec{\varphi },\mathcal V (s)\varvec{\varphi }\right) _{\Gamma }&= \text{ Re}\left( -s\varvec{\varphi },\Pi _{\tau }\mathbf h \right) _{\Gamma }\end{aligned}$$

(34)

$$\begin{aligned}&= \text{ Re}\left[ \left( -s\gamma _{\tau }^{\Omega _{-}} \mathbf{H }_{\Omega _{-}},s\Pi _{\tau }^{\Omega _{-}}\mathbf{E }_{\Omega _{-} }\right) _{\Gamma }\right.\nonumber \\&\quad \left.-\left( -s\gamma _{\tau }^{\Omega _{+}}\mathbf{H }_{\Omega _{+}},s\Pi _{\tau }^{\Omega _{+}}\mathbf{E }_{\Omega _{+}}\right) _{\Gamma }\right] \nonumber \\&= -\text{ Re}\sum _{\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\} }\left|s\right|^{2}\int _{\Omega }(\overline{\mathbf{H }}_{\Omega }.\,\mathrm{curl}\,\mathbf{E }_{\Omega }-\mathrm{curl}\,\overline{\mathbf{H }}_{\Omega }.\,\mathbf{E }_{\Omega })\,d\mathbf{x }\nonumber \\&= \sum _{\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\} }\text{ Re} \int _{\Omega }\frac{s}{\mu }\left|\mathrm{curl}\,\mathbf{E }_{\Omega }\right|^{2}+\,\overline{s}\left|s\right|^{2}\varepsilon \left|\mathbf{E }_{\Omega }\right|^{2}\,d\mathbf{x }\nonumber \\&= \frac{\mathrm{Re}\,s}{\mu }\left\Vert{\mathbf{E }}\right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+},s}^{2}. \end{aligned}$$

(35)

To estimate $\varvec{\varphi }$ in terms of $\mathbf{E }$ we pick any $\varvec{\zeta }\in \mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma )$ and denote by $\mathbf u _{\Omega _{-}}\in \mathbf{H }(\mathrm{curl},\Omega _{-})$, resp. $\mathbf{u }_{\Omega _{+}}\in {\mathbf{H }} (\mathrm{curl},\Omega _{+})$ the interior and exterior lifting of $\varvec{\zeta }$, i.e., $\varvec{\zeta }=\Pi _{\tau }^{\Omega _{-} }\mathbf u _{\Omega _{-}}=\Pi _{\tau }^{\Omega _{+}}\mathbf u _{\Omega _{+}}$. The continuity of the lifting operator implies

$$\begin{aligned} \Vert \mathbf u _{\Omega _{\pm }}\Vert _{\text{ curl},\Omega _{\pm }}\le C\Vert \varvec{\zeta }\Vert _{-1/2,\text{ curl}}. \end{aligned}$$

We employ Green’s identity to obtain

$$\begin{aligned} \left|\,\left({\varvec{\varphi }},{\varvec{\zeta }}\right) _{\Gamma }\right|&= \left|\left(\gamma _{\tau }^{\Omega _{-}}{\mathbf{H }} _{\Omega _{-}}, \Pi _{\tau }^{\Omega _{-}}\mathbf{u }_{\Omega _{-}}\right)_{\Gamma }-\left( \gamma _{\tau }^{\Omega _{+}}{\mathbf{H }}_{\Omega _{+}}, \Pi _{\tau } ^{\Omega _{+}}\mathbf{u }_{\Omega _{+}}\right)_{\Gamma }\right|\\&= \left|\,\sum \limits _{\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\} } \int _{\Omega }(\overline{{\mathbf{H }}_{\Omega }}.\,\mathrm{curl}\,\mathbf{u }_{\Omega }-\mathrm{curl}\,\overline{{\mathbf{H }}_{\Omega } }.\,\mathbf{u }_{\Omega })\,d{\mathbf{x }}\right|\\&= \left|\,\sum \limits _{\Omega \in \left\{ \Omega _{-},\Omega _{+}\right\} } \int _{\Omega }\left( \frac{1}{\bar{s}\mu }\mathrm{curl}\,\overline{{\mathbf{E }}_{\Omega } }.\,\text{ curl}\mathbf{u }_{\Omega }+ \bar{s}\varepsilon \overline{{\mathbf{E }}_{\Omega }}.\,\mathbf{u }_{\Omega }\right) \,d{\mathbf{x }}\right|\\&\le \frac{1}{|s|\mu }\left\Vert\,{\mathbf{E }}\right\Vert_{\mathrm{curl} ,\Omega _{-}\cup \Omega _{+},s}\left\Vert\mathbf{u }\right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+},s}\\&\le \frac{1}{\mu }\max \left( \sqrt{\varepsilon \mu },\frac{1}{\mathrm{Re}\,s}\right) \left\Vert{\mathbf{E }}\right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+},s}\left\Vert\mathbf{u } \right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+}}\\&\le \frac{C}{\mu }\max \left( \sqrt{\varepsilon \mu },\frac{1}{\mathrm{Re}\,s}\right) \left\Vert{\mathbf{E }}\right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+},s}\Vert \varvec{\zeta } \Vert _{-1/2,\mathrm{curl}}. \end{aligned}$$

Hence, from (3a) we conclude that

$$\begin{aligned} \Vert \varvec{\varphi }\Vert _{-1/2,\mathrm{div}}\le \frac{C}{\mu } \max \left( \sqrt{\mu \varepsilon },\frac{1}{\sigma _{0}}\right) \left\Vert\mathbf{E }\right\Vert_{\mathrm{curl},\Omega _{-}\cup \Omega _{+},s} \end{aligned}$$

holds. The combination with (35) finally leads to

$$\begin{aligned} \text{ Re}\left( -s\varvec{\varphi },\mathcal V \left( s\right) \varvec{\varphi }\right) _{\Gamma }\ge C\min \left( \frac{1 }{\varepsilon },\mu \sigma _{0}^{2}\right) \mathrm{Re}\,s\left\Vert\varvec{\varphi }\right\Vert_{-1/2,\mathrm{div}}^{2}. \end{aligned}$$

(36)

The Lax-Milgram lemma in the form [36, Lemma 2.1.51 with the definition of ellipiticty as in (2.43)] gives

$$\begin{aligned} \left\Vert\left( s\mathcal V \left( s\right) \right) ^{-1}\right\Vert\le C \max \left( \varepsilon ,\frac{1}{\mu \sigma _{0}^{2} }\right) \frac{1}{\mathrm{Re}\,s}. \end{aligned}$$

Multiplying by $\left|s\right|$ leads to the asserted bound of $\mathcal V ^{-1}\left( s\right)$ in the operator norm.

Now, for any $\varvec{\psi }\in {\mathbf{H }}^{-1/2}(\mathrm{curl} _{\Gamma },\Gamma )$ we set $\varvec{\varphi }:=\mathcal V ^{-1}\left( s\right) \varvec{\psi }$. Let $\left( {\mathbf{E }}_{\Omega },{\mathbf{H }} _{\Omega }\right)$ denote the solution of (32) for this choice of $\varvec{\psi }$ and corresponding lifting $\mathbf h$. Note that the relations (33) also hold for this case. Again by Green’s formula and the continuity of the trace mapping $\Pi _{\tau }^{\Omega }:\mathbf{H }(\mathrm{curl},\Omega )\,\,\rightarrow \,\,\mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma )$ we get the estimate

$$\begin{aligned} \text{ Re}\left( -s\mathcal V ^{-1}\left( s\right) \varvec{\psi },\varvec{\psi }\right) _{\Gamma }&= \frac{\mathrm{Re}\,s}{\mu } \Vert \mathbf{E }\Vert _{\text{ curl},\Omega _{-}\cup \Omega _{+},s}^{2}\nonumber \\&\ge C \min \left( \frac{1}{\mu },\varepsilon \sigma _{0}^{2}\right) \mathrm{Re}\,s\,\Vert \mathbf{E }\Vert _{\text{ curl},\Omega _{-}\cup \Omega _{+}}^{2}\nonumber \\&\ge C\min \left( \frac{1}{\mu },\varepsilon \sigma _{0}^{2}\right) \mathrm{Re}\,s\,\Vert \Pi _{\tau }\mathbf{E }\Vert _{-1/2,\text{ curl}} ^{2}\nonumber \\&= C\min \left( \frac{1}{\mu },\varepsilon \sigma _{0}^{2}\right) \frac{\mathrm{Re}\,s}{|s|^2}\Vert \varvec{\psi }\Vert _{-1/2,\text{ curl} }^{2}. \end{aligned}$$

(37)

Similarly as for $\mathcal V ^{-1}(s)$, this now gives the required estimate for $\Vert \mathcal V (s)\Vert$.

To prove the third bound we can proceed as in the acoustic case discussed in [6, Lemma 5.1]:

$$\begin{aligned} \left|\mathcal S (s)\mathbf v (\mathbf{y })\right|&\le \mu |s|\left\Vert\frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}\Vert \mathbf v \Vert _{H^{-1/2}(\Gamma )}\\&+\frac{1}{|s|\varepsilon }\left\Vert\nabla \frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}\Vert \mathrm{div} _{\Gamma }\mathbf v \Vert _{H^{-1/2}(\Gamma )}\\&\le \left( \mu ^{2}|s|^{2}\left\Vert\frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}^{2}+\frac{1}{|s|^{2}\varepsilon ^{2}}\left\Vert\nabla \frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}^{2}\right) ^{1/2}\nonumber \\&\times \Vert \mathbf v \Vert _{-1/2,\mathrm{div}_{\Gamma }}. \end{aligned}$$

It is not difficult to show that, see [6, Lemma 5.1],

$$\begin{aligned} \left\Vert\frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}\le C(\sigma _{0},\text{ dist}(\mathbf{y },\Gamma ))|s|\text{ e} ^{-\text{ Re}\,s\, \mathrm{dist}(\mathbf{y },\Gamma )} \end{aligned}$$

and hence

$$\begin{aligned} \left\Vert\nabla \frac{\text{ e}^{-s\Vert \cdot -\mathbf{y }\Vert }}{4\pi \Vert \cdot -\mathbf{y }\Vert }\right\Vert_{H^{1/2}(\Gamma )}\le C(\sigma _{0},\text{ dist}(\mathbf{y },\Gamma ))|s|^{2}\text{ e} ^{-\text{ Re}\,s\,\mathrm{dist}(\mathbf{y },\Gamma )}. \end{aligned}$$

Combining the three estimates gives the required result. $\square$

In the following we will derive error estimates for the Runge–Kutta convolution quadrature approximation of the computation of the electric surface current density

$$\begin{aligned} {\mathbf{j }}=\mathcal V ^{-1}(\partial _{t})\left( \mathbf{n }\times \mathbf{g }_{t}\right) \end{aligned}$$

(38)

and the corresponding field point evaluation

$$\begin{aligned} \mathbf{E }\left( \mathbf{y }\right) =\delta _{\mathbf{y}}\mathcal S \mathcal V ^{-1}(\partial _{t})\mathbf{n }\times \mathbf{g}_{t} \end{aligned}$$

(39)

where $\mathbf{g }=-\mathbf{E }^{\text{ inc}} \times \mathbf{n }$. The transfer function for problem (38) is given (and estimated) by

$$\begin{aligned} \Vert \mathcal V ^{-1}(s)\Vert \le C\left( \sigma _{0}\right) \frac{|s|}{\mathrm{Re}\,s}, \end{aligned}$$

where for (39) it is

$$\begin{aligned} \left\Vert\delta _{\mathbf{y }}\mathcal S \left( s\right) \mathcal V ^{-1}(s)\right\Vert\le C(\sigma _{0},\text{ dist}(\mathbf{y } ,\Gamma ))\text{ e}^{-\text{ Re}\,s\,\mathrm{dist}(\mathbf{y },\Gamma )}\frac{|s|^{3}}{\text{ Re} s}. \end{aligned}$$

In [6] it has been proved that the Runge–Kutta convolution quadrature for a transfer function that is bounded by $C|s|^{\mu }/\left( \mathrm{Re}\,s\right) ^{\nu }$ for some real $\mu$ and $\nu \ge 0$ converges at the rate $O(\Delta t^{q+1-\mu +\nu })$. Hence, these estimates imply the following result.

Definition 4.5

Let $W_{0}^{r,1}\left( 0,T; X\right)$ denote the space of functions $g$ on $\left( 0,T\right)$ with values in the Banach space $X$ and the $r$-th weak derivative in $L^{1}\left( 0,T\right)$ and with $g\left( 0\right) =g^{\prime }\left( 0\right) =\cdots =g^{\left( r-1\right) }\left( 0\right) =0$ equipped with the norm

$$\begin{aligned} \left\Vert\,g^{\left( r\right)}\right\Vert_{L^{1}\left( 0,T\right)} = \int _0^T \Vert g^{(r)}(t)\Vert _X dt. \end{aligned}$$

Theorem 4.6

• (a) Let $r>p+3$ and $\mathbf{g }\in W_0^{r+1,1}([0,T];\mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma ))$. Then, under the above conditions on the Runge–Kutta method there exists $\bar{t}\ge 0$ such that for $0<\Delta t<\bar{t}$ and $t\in [0,T]$,

  $$\begin{aligned} \left\Vert{\mathbf{j }}_{n}^{\Delta t}(\cdot )-{\mathbf{j }}(t_{n},\cdot )\right\Vert_{-1/2,\mathrm{div}_{\Gamma }}\le C\Delta t^{\min (p,q+1)}\int _{0} ^{t}\Vert \partial _{t}^{r+1}\mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl}_{\Gamma }}d\tau . \end{aligned}$$

• (b) Let $r>p+5$ and assume further that $\mathbf{g }\in W_0^{r+1,1}([0,T];\mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma ))$. Then for any $\mathbf{y }\in \Omega ^{+}$

  $$\begin{aligned} \left\Vert\mathbf{E }_{n}^{\Delta t}(\mathbf{y })-\mathbf{E }(t_{n} ,\mathbf{y })\right\Vert\le C\Delta t^{p}\int _{0}^{t}\Vert \partial _{t} ^{r+1}\mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl}_{\Gamma }}d\tau . \end{aligned}$$

Remark 4.7

The statement of the theorem on convergence of Runge–Kutta based convolution quadrature as given in [6], requires the data $\mathbf{g }$ to be in the space $C^r([0,T])$ of $r$-times continuously differentiable functions. The proof is, however, easily seen to hold also for data $\mathbf{g }$ in spaces $W^{r,1}_0([0,T])$.

4.3 Spatial discretization

For the rest of the paper we we assume $\Omega _{-}$ to be a bounded polyhedron. In this case the spaces $V_{\Pi }$ and $V_{\gamma }$ can be explicitly characterized, see [11, 12]. We equip the boundary $\Gamma$ of $\Omega _{-}$ with a surface boundary element mesh $\mathcal G _{h}$ (in the sense of, e.g., [36]), where $h$ denotes the mesh width. We assume that the surface mesh is aligned with edges of $\Gamma$, i.e. the edges of $\Gamma$ are covered by a subset of triangle edges. Let

$$\begin{aligned} \mathcal G _{h}:=\left\{ \tau _{\ell }\right\} _{\ell =1}^{\tilde{M}} \end{aligned}$$

be such a triangulation with $\Gamma =\bigcup \nolimits _{\ell =1}^{\tilde{M}} \overline{\tau _{\ell }}$. The set of triangle edges is denoted by

$$\begin{aligned} \mathcal E _{h}:=\left\{ e_{i}\right\} _{i=1}^{M}. \end{aligned}$$

The triangulation is assumed to be conforming i.e. two panels $\overline{\tau _{\ell }}$ and $\overline{\tau _{k}}$ either coincide, they share a common edge, a common vertex or they are disjoint. In order to discretize our problem we have to define a suitable finite dimensional boundary element space

$$\begin{aligned} V_{h}\subset \mathbf{H }^{-1/2}(\mathrm{div}_{\Gamma },\Gamma ). \end{aligned}$$

We use here the classical Raviart–Thomas elements of lowest order, which we denote by $\mathcal{R T}_{0}(\mathcal G _{h})$, see [10, 34, 35].

Let a basis of $\mathcal RT _{0}(\mathcal{G }_{h})$ be given by $\left\{ \mathbf{b}_{1}, \mathbf b _{2},\ldots , \mathbf b _{M}\right\}$. We define the block matrices $\underline{\underline{\mathbf{W }}}_{k}\in \mathbb C ^{mM\times mM}$ for $1\le i,j\le m$ by

$$\begin{aligned} \left( \underline{\underline{\mathbf{W }}}_{k}\right) _{i,j}&:= \,\left( \mu \,\int _{\Gamma }\int _{\Gamma }\left( \mathbf{W }_{k}^{(2)}(\mathbf{x } -\mathbf{y })\right) _{i,j}\left( \mathbf b _{e}(\mathbf{x })\,,\,\mathbf b _{f}(\mathbf{y })\right) \,d\Gamma _{\mathbf{x }}d\Gamma _{\mathbf{y }}\right. \\&+\left. \frac{1}{\varepsilon }\int _{\Gamma }\int _{\Gamma }\left( \mathbf{W }_{k}(\mathbf{x }\!-\!\mathbf{y })\right) _{i,j} \mathrm{div}_{\Gamma }\mathbf b _{e}(\mathbf{x })\overline{\mathrm{div}_{\Gamma }\mathbf b _{f}(\mathbf{y })}d\Gamma _{\mathbf{x } }d\Gamma _{\mathbf{y }}\!\right) _{e,f =1}^M \!\in \!\mathbb C ^{M\times M}, \end{aligned}$$

where $(\cdot ,\cdot )$ refers to the standard inner product in $\mathbb C ^{3}$. For $1\le i\le m$, we define the right-hand sides $\mathbf r _{k,i} \in \mathbb C ^{M}$ by

$$\begin{aligned} \mathbf r _{k,i}:=\left( \int _{\Gamma }\left( \mathbf b _{f},\mathbf{E } _{t}^{\text{ inc}}(t_{k}+c_{i}\Delta t,\mathbf{y })\right) d\Gamma _{\mathbf{y } }\right) _{f=1}^M \end{aligned}$$

and form the block vectors $\underline{\mathbf{R }}_{k}:=\left( \mathbf r _{k,i}\right) _{i=1}^{m}\in \mathbb C ^{mM}$. Then, the Galerkin discretization of (24) is given by seeking, for $0\le k\le N$, the block vectors $\underline{\mathbf{J }}_{k}=\left( {\mathbf{j }}_{k,i}\right) _{i=1}^{m}$ with ${\mathbf{j }}_{k,i}=\left( j_{k,i,e}\right) _{e = 1}^M\in \mathbb C ^{M}$ such that

$$\begin{aligned} \sum _{j=0}^{n}\underline{\underline{\mathbf{W }}}_{n-j}\underline{\mathbf{J }}_{j}=\underline{\mathbf{R }}_{n}\qquad \forall 0\le n\le N. \end{aligned}$$

The temporal Runge–Kutta convolution quadrature, spatial Galerkin approximation to the electric surface current densities $\underline{{\mathbf{j }}}_{k}(\mathbf{x }):=\left( {\mathbf{j }}\left( t_{k}+c_{i}\Delta t,\mathbf{x }\right) \right) _{i=1}^{m}$ at time points $t_{k}+c_{i}\Delta t,\,1\le i\le m$, then is given by

$$\begin{aligned} \underline{{\mathbf{j }}}_{k}(\mathbf{x })\approx \underline{{\mathbf{j }}} _{k}^{\Delta t,h}(\mathbf{x }):=\left( \sum _{e = 1}^M j_{k,i,e}\mathbf b _{e}(\mathbf{x })\right) _{i=1}^{m}. \end{aligned}$$

(40)

In order to obtain approximations at $t_{k+1}$ and not only at stage values, under the assumption $R(\infty ) = 0$ on the Runge–Kutta method, note that

$$\begin{aligned} {\mathbf{j }}\left( t_{k+1},\mathbf{x }\right) \approx {\mathbf{j }}_{k+1}^{\Delta t,h}\left( \mathbf{x }\right) :=\mathbf b ^{T}\mathbf A ^{-1}\underline{{\mathbf{j }}}_{k}^{\Delta t,h}(\mathbf{x }) \end{aligned}$$

due to (23). For stiffly stable RK methods, such as the Radau IIA method, $b^{T}A^{-1} = (0,0,\dots ,0,1)^{T}$ and $c_m = 1$, so that

$$\begin{aligned} {\mathbf{j }}_{k+1}^{\Delta t,h} = {\mathbf{j }}_{km}^{\Delta t,h}. \end{aligned}$$

4.4 Convergence of the fully discrete scheme

The Galerkin discretization of the variational problem (28) in the Laplace domain is given by finding $\hat{{\mathbf{j }}}^{h}=\hat{{\mathbf{j }}} ^{h}\left( s\right) \in \mathcal RT _{0}(\mathcal G _{h})$ such that

$$\begin{aligned} \left( \varvec{\zeta },\mathcal V (s)\hat{{\mathbf{j }}}^{h}\right) _{\Gamma }=\left( \varvec{\zeta },s\,\mathbf{n }\times \hat{\mathbf{g } }\right) _{\Gamma }\qquad \forall \varvec{\zeta }\in \mathcal RT _{0}(\mathcal G _{h}). \end{aligned}$$

(41)

Let $P_{0,h}:\mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma ) \rightarrow \mathcal RT _{0}(\mathcal G _{h})$ be defined for all $\varvec{\psi }\in \mathbf{H }^{-1/2}(\mathrm{curl}_{\Gamma },\Gamma )$ by the relation

$$\begin{aligned} \left(P_{0,h}\varvec{\psi },\varvec{\varphi }\right)_\mathbf{L _{t}^{2}(\Gamma )} = \left( \varvec{\psi },\varvec{\varphi } \right)_\Gamma \quad \forall \varvec{\varphi }\in \mathcal RT _{0}(\mathcal G _{h}) \end{aligned}$$

and let $P_{0,h}^{\star }: \mathcal RT _{0}(\mathcal G _{h})\rightarrow \mathbf{H }^{-1/2}(\mathrm{div}_{\Gamma },\Gamma )$ denote its adjoint. Furthermore we denote by $P_{\mathrm{div},h}:\mathbf{H }^{-1/2} (\mathrm{div}_{\Gamma },\Gamma )\rightarrow \mathcal RT _{0} (\mathcal G _{h})$ the orthogonal projection. Then, the semi-discrete Galerkin discretization in the time domain can be written as

$$\begin{aligned} \mathcal V _{h}\left( \partial _{t}\right) {\mathbf{j }}^{h}=P_{0,h} \mathbf{n }\times \mathbf{g }_{t}, \end{aligned}$$

where

$$\begin{aligned} \mathcal V _{h}\left( s\right) :=P_{0,h}\mathcal V \left( s\right) P_{0,h}^{\star }:\mathcal RT _{0}(\mathcal G _{h})\rightarrow \mathcal RT _{0}(\mathcal G _{h}). \end{aligned}$$

The operator $\mathcal V _{h}\left( s\right)$ is invertible as we state in the next result.

Lemma 4.8

For $s\in \mathbb C$ with $\mathrm{Re}\,s\ge \sigma _{0}>0$, the discrete Laplace domain Galerkin variational problem (41) has a unique solution $\hat{{\mathbf{j }}}^{h}\left( s\right) \in \mathcal RT _{0}(\mathcal G _{h})$ with the stability estimate in the operator norm

$$\begin{aligned} \left\Vert\mathcal V _{h}^{-1}\left( s\right) \right\Vert\le C\left( \sigma _{0}\right) \frac{|s|}{\mathrm{Re}\,s}. \end{aligned}$$

(42)

Proof

Since $\mathcal V (s)$ is coercive, (36), the same estimate holds for $\Vert \mathcal V ^{-1}_{h}(s)\Vert$ as for $\Vert \mathcal V ^{-1}(s)\Vert$. $\square$

Hence,

$$\begin{aligned} \mathcal V _{h}\left( \partial _{t}\right) \left( {\mathbf{j }}^{h} -P_{\mathrm{div},h}{\mathbf{j }}\right) =P_{0,h}\mathcal V \left( \partial _{t}\right) \left( I-P_{\mathrm{div},h}\right) {\mathbf{j }} \end{aligned}$$

and the composition rule $K_{2}(\partial _{t})K_{1}(\partial _{t})g=K_{2} K_{1}(\partial _{t})g$ gives us

$$\begin{aligned} {\mathbf{j }}^{h}-P_{\mathrm{div},h}{\mathbf{j }}=\mathcal V _{h}^{-1}\left( \partial _{t}\right) P_{0,h}\mathcal V \left( \partial _{t}\right) \left( I-P_{\mathrm{div},h}\right) {\mathbf{j }}. \end{aligned}$$

(43)

The representation (43) along with the discrete stability estimate (42) allow to employ Parseval’s formula in the following form.

Lemma 4.9

Let $K\left( s\right)$ be analytic and bounded by $\left|K\left( s\right) \right|\le M\left|s\right|^{\mu }$ for all $s\in \mathbb C$ with $\text{ Re} s\ge \sigma _{0}>0$. Then, for $r>\mu$ the convolution operator $K\left( \partial _{t}\right)$ is a bounded linear operator

$$\begin{aligned} K\left( \partial _{t}\right) :W_{0}^{r,1}\left( 0,T\right) \rightarrow W_{0}^{r-\mu ,1}\left( 0,T\right). \end{aligned}$$

Further for any $r > \mu +1$

$$\begin{aligned} K\left( \partial _{t}\right) :W_{0}^{r,1}\left( 0,T\right) \rightarrow C\left( \left[ 0,T\right] \right) \end{aligned}$$

is also a bounded operator.

Proof

The first statement is a direct consequence of the definition of the spaces $W_{0}^{r,1}$, whereas the second statement is proved in [28, Lemma 2.2]. $\square$

In combination with both continuous stability estimates (30), (31), we obtain for $r>5$

$$\begin{aligned} \left\Vert{\mathbf{j }}^{h}\left( t\right) \!-\!P_{\mathrm{div},h} {\mathbf{j }}\left( t\right) \right\Vert_{-1/2,\mathrm{div}_{\Gamma } }\!\le \! C\left( \sigma _{0},T\right) \left\Vert\left( I\!-\!P_{\mathrm{div} ,h}\right) {\mathbf{j }}\right\Vert_{\mathbf{W }_{0}^{r,1}\left( \left[ 0,T\right] ;\mathbf{H }^{-1/2}\left(\mathrm{div}_{\Gamma } ,\Gamma \right) \right) }, \nonumber \\ \end{aligned}$$

(44)

i.e., quasi-optimality with respect to the space discretization.

Remark 4.10

Note that the regularity assumptions with respect to time are quite strong and larger than the order of the operator intuitively would suggest. Similar requirements are common in the literature (cf. [19, 28]) of retarded boundary integral equations and it is to the best of our knowledge an open problem whether this is a theoretical artefact. Numerical experiments (cf. [37]) typically indicate that the theoretical regularity assumptions are too strict.

Now, we can formulate the following theorem.

Theorem 4.11

Let a Runge–Kutta based convolution quadrature be applied in time and a Galerkin method with lowest order Raviart–Thomas elements be applied in space to the equation $\mathcal V (\partial _{t}){\mathbf{j }}=\mathbf{n }\times \mathbf{g }_{t}$. Under the conditions on the Runge–Kutta method stated in Assumption 4.1, the following hold:

• (a) Let $\mathbf{g } \in W_0^{r,1}((0,T); \mathbf{H }_{-1/2}(\mathrm{curl}_\Gamma ))$ with $r > p+4$, where $p$ is the (classical) order of the Runge–Kutta method. Then, the fully discrete method converges with

  $$\begin{aligned} \left\Vert{\mathbf{j }}\left( t_{k}\right) -{\mathbf{j }}_{k}^{\Delta t,h}\right\Vert_{-1/2,\mathrm{div}}&\le C\left( \Delta t\right) ^{\min \left\{ p,q+1\right\} }\int _{0}^{t}\Vert \partial _{t}^{r+1} \mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl}_{\Gamma }}d\tau \\&+C\left( \sigma _{0},T\right) \left\Vert\left( I-P_{\mathrm{div} ,h}\right) {\mathbf{j }}\right\Vert_{\mathbf{W }_{0}^{r,1}\left( \left[ 0,T\right] ;\mathbf{H }^{-1/2}\left( \mathrm{div}_{\Gamma } ,\Gamma \right) \right) }. \end{aligned}$$

• (b) Let $\mathbf{g } \in W_0^{r,1}((0,T); \mathbf{H }_{-1/2}(\mathrm{curl}_\Gamma ))$ with $r > p+5$, where $p$ is the (classical) order of the Runge–Kutta method. Further, let $\hat{\mathbf{w }}_\mathcal{S ,i}$ be the solution of the problem: Find $\hat{\mathbf{w }}_\mathcal{S ,i}\in \mathbf{H }^{-1/2}(\mathrm{div} _{\Gamma },\Gamma )$ such that

  $$\begin{aligned} \left(\hat{\mathbf{w }}_\mathcal{S ,i}, \mathcal V (s)\varvec{\zeta } \right)_{\Gamma }= \ell (\varvec{\zeta }) \qquad \forall \varvec{\zeta }\in \mathbf{H }^{-1/2}(\mathrm{div}_{\Gamma },\Gamma ), \end{aligned}$$

  where $\ell (\cdot )$ is the linear functional defined by

  $$\begin{aligned} \ell (\varvec{\zeta }) = \delta _{\mathbf{y }}\mathcal S _{i}(s) (\varvec{\zeta }). \end{aligned}$$

  If for some $-1/2 \le \kappa \le 1,\, \hat{\mathbf{w }}_\mathcal{S ,i}\in \mathbf{H }^{\kappa }(\mathrm{div}_{\Gamma },\Gamma )$ and $\Vert \hat{\mathbf{w }}_\mathcal{S ,i}\Vert _{\kappa ,\mathrm{div}_{\Gamma }} \le C |s|^{\alpha _\kappa }$ for $\mathrm{Re}\,s > \sigma _0$ and ${\mathbf{j }} \in W_0^{\alpha _\kappa +8,1}([0,T]; \mathbf{H }^{-1/2}(\mathrm{div}_{\Gamma },\Gamma ))$, then for any $\mathbf{y }\in \Omega ^{+}$ and $i=1,2,3$, it holds

  $$\begin{aligned} \left|\mathbf{E }_{i}(t_{k},\mathbf{y })-\mathbf{E }_{k,i}^{\Delta t,h}(\mathbf{y })\right|&\le C\Delta t^{p}\int _{0}^{t}\Vert \partial _{t}^{r+1}\mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl} _{\Gamma }}d\tau \\&+C\left( \sigma _{0},T\right) \left\Vert\left( I-P_{\mathrm{div} ,h}\right) {{\mathbf{j }}}\right\Vert_{{\mathbf{W }}_{0}^{\alpha _\kappa +8,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left( \mathrm{div}_{\Gamma } ,\Gamma \right) \right) }\\&\times \Vert I-P_{\mathrm{div},h}\Vert _{H^\kappa (\mathrm{div}_{\Gamma })\leftarrow H^{-1/2}(\mathrm{div}_{\Gamma })} \end{aligned}$$

Proof

Let us first remark that assumptions on $\mathbf{g }$ in both (a) and (b) together with Lemma 4.9 imply ${\mathbf{j }} \in W_0^{r,1}([0,T];\mathbf{H }^{-1/2}(\mathrm{curl}_\Gamma , \Gamma ))$, where $r > p+4 \ge 5$ so that (44) can be applied.

We employ a triangle inequality to obtain

$$\begin{aligned} \left\Vert{\mathbf{j }}\left( t_{k}\right) -{\mathbf{j }}_{k}^{\Delta t,h}\right\Vert_{-1/2,\mathrm{div}_{\Gamma }}\le \left\Vert{\mathbf{j }}\left( t_{k}\right) -{\mathbf{j }}^{h}\left( t_{k}\right) \right\Vert_{-1/2,\mathrm{div}_{\Gamma }}+\left\Vert{\mathbf{j }} ^{h}\left( t_{k}\right) -{\mathbf{j }}_{k}^{\Delta t,h}\right\Vert_{-1/2,\mathrm{div}_{\Gamma }}. \end{aligned}$$

The first term can be estimated by a best-approximation estimate in space by using (44):

$$\begin{aligned} \left\Vert{\mathbf{j }}\left( t_{k}\right) -{\mathbf{j }}^{h}\left( t_{k}\right) \right\Vert_{-1/2,\mathrm{div}_{\Gamma }}&\le \left\Vert{\mathbf{j }}\left( t_{k}\right) -P_{\mathrm{div} ,h}{\mathbf{j }}\left( t_{k}\right) \right\Vert_{-1/2,\mathrm{div} _{\Gamma }}\nonumber \\&+\left\Vert\,P_{\mathrm{div},h}{\mathbf{j }}\left( t_{k}\right) -{\mathbf{j }}^{h}\left(t_{k}\right) \right\Vert_{-1/2,\mathrm{div} _{\Gamma }}\\&\le \left( 1+C\left( \sigma _{0},T\right) \right) \left\Vert\left( I-P_{\mathrm{div},h}\right) {\mathbf{j }}\right\Vert_{{\mathbf{W }}_{0}^{r,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) }. \end{aligned}$$

Note that

$$\begin{aligned} {\mathbf{j }}^{h}-{\mathbf{j }}^{\Delta t,h}=\left( \mathcal V _{h}^{-1}\left( \partial _{t}\right) -\mathcal V _{h}^{-1}(\underline{\partial _{t}}^{\Delta t})\right) P_{0,h}\left( \mathbf n_{y} \times \partial _{t}\mathbf{g }\right) . \end{aligned}$$

Since $\mathcal V _{h}^{-1}\left( s\right)$ has the same analyticity and growth behaviour as $\mathcal V ^{-1}\left( s\right)$ with respect to $s\in \mathbb C$ with $\mathrm{Re}\,s\ge \sigma _{0}>0$ we can apply Theorem 4.6 verbatim for the operator $\mathcal V _{h} ^{-1}\left( s\right)$ to obtain

$$\begin{aligned} \left\Vert{\mathbf{j }}^{h}\left( t_{k}\right) -{\mathbf{j }}_{k}^{\Delta t,h}\right\Vert_{-1/2,\mathrm{div}_{\Gamma }}\le C\left( \Delta t\right) ^{\min \left\{ p,q+1\right\} }\int _{0}^{t}\Vert \partial _{t} ^{r+1}\mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl}_{\Gamma }}d\tau . \end{aligned}$$

For the estimate in b) we start again with a triangle inequality and denote

$$\begin{aligned} \left|\mathbf{E }_{i}(t_{k},\mathbf{y })-\mathbf{E }_{k,i}^{\Delta t,h}(\mathbf{y })\right|\le \left|\mathbf{E }_{i}(t_{k},\mathbf{y } )-\mathbf{E }_{i}^{h}(t_{k},\mathbf{y })\right|+\left|\mathbf{E } _{i}^{h}(t_{k},\mathbf{y })-\mathbf{E }_{k,i}^{\Delta t,h}(\mathbf{y } )\right|. \end{aligned}$$

(45)

The second difference can be written as

$$\begin{aligned} \mathbf{E }_{i}^{h}(t_{k},\mathbf{y })-\mathbf{E }_{k,i}^{\Delta t,h} (\mathbf{y })=\left( \delta _{\mathbf{y }}\mathcal S _{i}\mathcal V _{h} ^{-1}\left( \partial _{t}\right) -\delta _{\mathbf{y }}\mathcal S _{i}\mathcal V _{h}^{-1}\left( \underline{\partial _{t}}^{\Delta t}\right) \right) P_{0,h}\left( \mathbf n_{y} \times \mathbf{g }_{t}\right). \end{aligned}$$

From Theorem 4.6 we deduce

$$\begin{aligned} \left|\mathbf{E }_{i}^{h}(t_{k},\mathbf{y })-\mathbf{E }_{k,i}^{\Delta t,h}(\mathbf{y })\right|\le C\Delta t^{p}\int _{0}^{t}\Vert \partial _{t}^{r+1}\mathbf{g }(\tau ,\cdot )\Vert _{-1/2,\mathrm{curl}_{\Gamma }} d\tau . \end{aligned}$$

For the first term in the right-hand side of (45) we employ an Aubin-Nitsche type argument as, e.g., described in [36, Theorem 4.2.14]. We consider $\delta _{\mathbf{y }}\mathcal S _{i}\left( s\right)$ as a linear functional on $\mathbf{H }^{-1/2}(\mathrm{div}_{\Gamma },\Gamma )$. With the definition of $\hat{\mathbf{w }}_\mathcal{S ,i}\in \mathbf{H }^{-1/2} (\mathrm{div}_{\Gamma },\Gamma )$ above we have

$$\begin{aligned} \delta _{\mathbf{y }}\mathcal S _{i}\left( s\right) \left( \widehat{{\mathbf{j }}}-\widehat{{\mathbf{j }}}^{h}\right) =\left( \hat{\mathbf{w }}_\mathcal{S ,i}, \mathcal V (s)\left( \widehat{{\mathbf{j }}}-\widehat{{\mathbf{j }}}^{h}\right) \right)_{\Gamma }. \end{aligned}$$

By using Galerkin orthogonality and the assumptions $\hat{\mathbf{w }}_\mathcal{S ,i}\in \mathbf{H }^{\kappa }(\mathrm{div}_{\Gamma },\Gamma )$ and $\Vert \hat{\mathbf{w }}_\mathcal{S ,i}\Vert _{\kappa ,\mathrm{div}_{\Gamma }} \le C |s|^{\alpha _\kappa }$ we obtain

$$\begin{aligned}&\left|\delta _{{\mathbf{y }}}\mathcal{S }_{i}\left(s\right) \left( \widehat{{{\mathbf{j }}}}-\widehat{{{\mathbf{j }}}}^{h}\right)\right|\\&\quad = \left|\left(\left(I-P_{\mathrm{div},h}\right) \hat{\mathbf{w }}_{\mathcal{S },i}, \mathcal{V }(s)\left( \widehat{{{\mathbf{j }}}}-\widehat{{\mathbf{j }}}^{h}\right) \right)_{\Gamma }\right|\\&\quad \le C|s|^{\alpha _{\kappa }} \left\Vert\mathcal{V }\left(s\right)\left( \widehat{{\mathbf{j }}}-\widehat{{\mathbf{j }}}^{h}\right)\right\Vert_{-1/2,\mathrm{curl}_{\Gamma }}\left\Vert{I-P}_{\mathrm{div},h} \right\Vert_{H^\kappa (\mathrm{div}_{\Gamma })\leftarrow H^{-1/2}(\mathrm{div}_{\Gamma })}\\&\quad \le C|s|^{\alpha _{\kappa +3}} \left\Vert\widehat{{\mathbf{j }}}-\widehat{{\mathbf{j }}}^{h} \right\Vert_{-1/2,\mathrm{div}_{\Gamma }}\left\Vert{I-P}_{\mathrm{div},h} \right\Vert_{H^\kappa (\mathrm{div}_{\Gamma })\leftarrow H^{-1/2}(\mathrm{div}_{\Gamma })}. \end{aligned}$$

Taking into account that $\hat{\mathbf{E }}\left( s,\mathbf{y }\right) =\delta _{\mathbf{y }}\mathcal S \left( s\right) \widehat{\mathbf{j }}$ holds, we obtain

$$\begin{aligned} \left|{\mathbf{E }}_{i}(t_{k},{\mathbf{y }})-{\mathbf{E }}_{i}^{h}(t_{k} ,{\mathbf{y }})\right|&\le C\left( \sigma _{0},T\right) \left\Vert{\mathbf{j }}-{\mathbf{j }}^{h}\right\Vert_{{\mathbf{W }}_{0}^{\alpha _\kappa +4,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) }\\&\quad \times \Vert I-P_{\mathrm{div},h}\Vert _{H^\kappa (\mathrm{div}_{\Gamma })\leftarrow H^{-1/2}(\mathrm{div}_{\Gamma })}. \end{aligned}$$

Finally

$$\begin{aligned} \left\Vert\mathbf{j}-\mathbf{j}^{h}\right\Vert_{\mathbf{W}_{0}^{\alpha _\kappa +4,1}\left( \left[0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) }&\le \left\Vert{\mathbf{j }}^h-P_{\mathrm{div},h}{\mathbf{j }}\right\Vert_{{\mathbf{W }}_{0}^{\alpha _\kappa +4,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) }\\&+\left\Vert(I-P_{\mathrm{div},h}){\mathbf{j }}\right\Vert_{{\mathbf{W }}_{0}^{\alpha _\kappa +4,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) } \end{aligned}$$

and using (43)

$$\begin{aligned}&\left\Vert\mathbf{j}^h-P_{\mathrm{div},h}\mathbf{j}\right\Vert_{\mathbf{W}_{0}^{\alpha _\kappa +4,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right) }\\&\quad \le C \left\Vert(I-P_{\mathrm{div},h}){\mathbf{j }}\right\Vert_{{\mathbf{W }}_{0}^{\alpha _\kappa +8,1}\left( \left[ 0,T\right] ;{\mathbf{H }}^{-1/2}\left(\mathrm{div}_{\Gamma },\Gamma \right) \right)}. \end{aligned}$$

$\square$

Remark 4.12

In the case of full regularity, the term$\left\Vert\! \left(\! I\!-\!P_{\mathrm{div},h}\!\right) \mathbf{j}\right\Vert_{\mathbf{W} _{0}^{r,1}\left( \left[ 0,T\right] ;\mathbf{H }^{-1/2}\left( \mathrm{div}_{\Gamma },\Gamma \right)\!\right) }$ can be estimated by $\mathcal O \left( h^{3/2}\right)$. However, in the considered case of polyhedral surfaces, the regularity of the solution is typically reduced (cf. [13, 22]).

From Theorem 4.4, it follows that the assumption on the growth behaviour of $\hat{w}_{S,i}$ is satisfied with $\alpha _\kappa =3$ for $\kappa =-1/2$. In [7, Th. 9] it was proved for smooth surfaces that, for $1/2\le \kappa \le 1$, it holds $\alpha _\kappa \le \kappa +5/2$.

5 Numerical experiments

In all of the numerical experiments, we will consider scattering by a perfect conductor when the incident wave is given by

$$\begin{aligned} \mathbf{E }^{\text{ inc}}(t, \mathbf{x }) = \hat{\mathbf{p }} \cos \left( 2\pi f_{0} \left[ t- \mathbf{x } \cdot \hat{\mathbf{k }} /c\right] \right) \, \exp \left[ -\frac{(t-\mathbf{x } \cdot \hat{\mathbf{k }} /c-t_{p})^{2}}{2\sigma ^{2}}\right]. \end{aligned}$$

Here $f_{0}$ is the center frequency, $\hat{\mathbf{k }}$ the direction of travel, $\hat{\mathbf{p }}$ polarization, $\sigma = 6/(2\pi f_{bw})$, and $t_{p} = 6\sigma$. In all of the examples the scatterer will be the unit sphere. For a number of numerical experiments with the convolution quadrature applied to EFIE and CFIE on different scatterers, we refer the reader to [43].

5.1 Scattering by a spherical conductor

In the first example, we consider a spherical scatterer of radius $1$m and centered at the origin. The center frequency is chosen as $f_{0}=200$ MHz, bandwidth $f_{bw}=150$ MHz, polarization $\hat{\mathbf{p }}=(1,0,0)$, direction of travel $\hat{\mathbf{k }}=(0,0,1)$, and the length of time computation $T=6\times 10^{-8}s$. Due to the spherical shape of the scatterer, the problem can be approximated accurately and cheaply by Fourier transformation of frequency domain solutions obtained by Mie series [17]. After truncation, this series solution will play the role of the exact solution in the calculation of errors.

For the time discretization we have used the 3-stage Radau IIA convolution quadrature. In space, the lowest order Raviart–Thomas elements were used. The computation of the resulting matrices and their storage in $\mathcal H$-matrix format were done using a modification of the HLIBpro library written by Ronald Kriemann; see [24, 25] and the website www.hlibpro.org. The spatial discretization was chosen sufficiently fine so that no significant change in the error could be observed, the largest calculation had $M=12288$ spatial degrees of freedom. Since the operator $\mathcal V (s)$ satisfies the coercivity result (cf. (36)), an equivalent norm to $\Vert \cdot \Vert _{-1/2,\mathrm{div}}$ is given by

$$\begin{aligned} \Vert \varvec{\varphi }\Vert _{-1/2,\mathrm{div}}^{2}\sim \left( \varvec{\varphi },-\mathcal V (1)\varvec{\varphi }\right) _{L^{2}(\Gamma )}. \end{aligned}$$

The latter can then be estimated via a Galerkin discretization of the operator $\mathcal V (1)$. Finally, the error in time and space is computed as

$$\begin{aligned} e_{N,\Gamma }:=\left( \Delta t\sum _{j=0}^{N}\Vert \varvec{\varphi } _{e}(\cdot ,t_{j})-\varvec{\varphi }_{N}(\cdot ,t_{j})\Vert _{-1/2,\mathrm{div} }^{2}\right) ^{1/2}, \end{aligned}$$

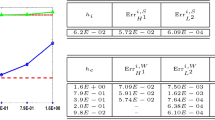
where $\varvec{\varphi }_{e}$ denotes the solution obtained by Mie series. The results thereby obtained are given in Table 1.

Table 1 Convergence of the 3-stage Radau IIA based convolution quadrature for the EFIE formulation of scattering by a spherical conductor

The 3-stage Radau IIA method has stage order $q=3$, therefore the theory stated in preceding sections predicts the order of convergence to be $O(\Delta t^{4})$. The results in Table 1 indeed suggest that this convergence order is obtained in the limit in this example.

Finally, let us note that the parameters defining the incident wave have been chosen so that interior resonances of the unit sphere can be excited, see [15]. Still, no adverse effect could be seen in using the EFIE instead of the CFIE.

5.2 Scattering by a spherical conductor: low frequency instability

In the previous example, the incident wave has a small low frequency component, in particular the Fourier transform of $\mathbf{E }^{\text{ inc}}$ at frequency zero is of size $\sim 10^{-22}$. In order to investigate possible instability induced by low-frequency breakdown, for the next computation we change the center frequency to $f_{0}=0$ thereby increasing the zero frequency component to magnitude ${\sim } 10^{-8}$. With a spatial discretization of 6,348 degrees of freedom, computational time interval increased to $1.8\times 10^{-7}$, and $400$ times steps of the three stage Radau IIA convolution quadrature, the magnitude of the current at a point on the sphere is shown in Fig. 2. For reference we also show the current for the previous example in Fig. 1. In Fig. 1 we see that after $t\approx 0.8\times 10^{-7}$ the current magnitude seems to stagnate. In reality the current should go to zero, but when implementing convolution quadrature as described in [4, 27], there is a limit in the accuracy that can be obtained. Therefore we do not expect the numerical current to go to zero, but in the second example the current increases. The convergence analysis allows for such an increase to happen since all the constants in the error estimates depend on the length of the computational time interval $T$, see [6]. Still, such increase has not been observed in the acoustic case, therefore we expect that the infinite dimensional kernel of the $\mathrm{curl} \mathrm{curl}$ operator is guilty for this instability.

Fig. 1

Magnitude of the current at a point on the perfectly conducting sphere induced by an incident wave with center frequency $f_{0} = 200$ MHz

Fig. 2

Magnitude of the current at a point on the perfectly conducting sphere induced by an incident wave with center frequency $f_{0} = 0$

The low frequency instability in time-domain calculations has been addressed in [43] by the use of loop-tree decomposition techniques, where the basis functions are split into solenoidal and non-solenoidal subspaces. Similar ideas are used in [16] for static problems at low frequency. These ideas promise to bring improvements to the results of our experiments as well, but at this stage we have not implemented them yet.

6 Conclusion

We described and analysed a numerical method for solving time-domain boundary integral equations arising in electromagnetic scattering which is based on Runge–Kutta convolution quadrature in time and Galerkin BEM for the spatial discretization. We obtained error estimates for the semi-discrete scheme by exploiting that the transfer function in the Laplace domain is bounded by $C |s|/(\text{ Re} s)$ and therefore the error analysis in [6] can be applied. For the spatial discretization we used the classical Raviart–Thomas elements of lowest order. Using the properties of the involved operators in the Laplace domain we derived convergence estimates for the fully discrete scheme. We performed numerical experiments in the case of a perfectly conducting spherical scatterer. The observed convergence behaviour of the method indicates that the derived error estimates are sharp. The numerical results also showed a possible instability developing if the incident wave excites low frequency modes. The current analysis does not fully describe this phenomenon.