Abstract
We consider a coupling of finite element (FEM) and boundary element (BEM) methods for the solution of the Poisson equation in unbounded domains. We propose a numerical method that approximates the solution using computations only in an interior finite domain, bounded by an artificial boundary \({{\mathcal {B}}}\). Transmission conditions between the interior domain, discretized by a FEM, and the exterior domain, which is reduced to the boundary \({{\mathcal {B}}}\) via a BEM, are imposed weakly on \({{\mathcal {B}}}\) using a mortar approach. The main advantage of this approach is that non matching grids can be used at the interface \({{\mathcal {B}}}\) of the interior and exterior domains. This allows to exploit the higher accuracy of the BEM with respect to the FEM, which justifies the choice of the discretization in space of the BEM coarser than the one inherited by the spatial discretization of the finite computational domain. We present the analysis of the method and numerical results which show the advantages with respect to the standard approach in terms of computational cost and memory saving.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many problems arising in different areas of science and engineering such as, for example, acoustics, aerodynamics, geophysics, electromagnetism lead to the study of scattering problems and to the solution of partial differential equations on exterior domains, whose unboundedness needs to be dealt within the numerical simulation.
Among the methods that directly deal with the unbounded domain we can count infinite element methods and the inverted elements method. The former are based on a polar decomposition of the solution with suitable shape functions which are integrable over elements that are extended towards infinity (see for example [9, 18]). In the latter, the infinite domain is described via a polygonal inversion mapping (see [6, 7]). Among the advantages of this approach is the possibility of treating partial differential equations with non constant coefficients and non local sources. However, as observed by the authors in [7], while the method yields optimal convergence rates, when the error is measured in the energy norm, it does not allow to obtain increased convergence rates, when the error is measured in the weaker \(L^2\) norms.
Problems defined in unbounded domains, with constant coefficients (or approaching constants at large distances) are usually solved by Boundary Element Methods (BEMs). The mathematics of the BE approximation, especially in the Galerkin version, is well established and the BEMs have been applied to a wide range of elliptic and time dependent problems. It is however known that the main drawback of the BEM is its cost related to the numerical computation of the matrix entries of the associated discrete boundary operators, which becomes expensive when large scale problems are considered. Moreover, once the solution of the corresponding boundary integral equation is retrieved, the solution of the original problem at any point of the exterior domain is obtained by computing boundary integrals. This procedure may not be efficient, especially when the solution is required at many points of the infinite domain.
Another approach to the solution of these problems is based on truncating the infinite domain to a finite one and applying the so-called Absorbing Boundary Conditions (ABCs) or Non reflecting Boundary Conditions (NRBCs) at a suitably chosen artificial boundary. In the engineering literature, the most commonly used NRBCs are of local type. While their cost is comparable to that required by the interior domain method associated to the discretization of the bounded computational domain, they provide only rough approximations of exact boundary conditions at the artificial boundary (for a review, see for example [19,20,21]). Therefore, when a high accuracy is required, the bounded domain must be chosen quite large, and consequently the total cost of the computation increases. In recent years the design of suitable boundary conditions with high accuracy on a given artificial boundary has attracted the attentions of many engineers and mathematicians. We refer to [1, 23, 24, 30] for recent works on NRBCs.
Alternatively, as proposed for some elliptic problems (see for instance [25, 29]) NRBCs can be defined by using Boundary Integral Equations (BIEs). Such conditions are of exact type (therefore more accurate than the local ones), they allow the use of curves of arbitrary shape and can be used also in situations of multiple scattering (see [23, 24]). The very recent one proposed in [11,12,13,14] for time dependent problems, allows the problem to have non trivial data, whose supports need not be included in the finite computational domain. The NRBC naturally includes the effects of far away data and is transparent for outgoing and incoming waves. The NRBC condition is expressed in terms of the single and double layer operators, associated to the BIE reformulation of PDE problem (see [15, 16]) . However, its non locality in space and time requires a high computational cost, in terms of CPU and memory occupation. Moreover, such NRBC needs to be coupled with the internal domain method. This is usually done by strongly imposing continuity of the solution and of its normal derivative along the artificial boundary. Therefore conforming meshes are required, and this can be a drawback especially when high accuracy is required, which implies using a fine mesh for the interior FEM, and, consequently, also for the mesh used in the discretization of the NRBC.
A possible remedy is to apply a mortar coupling strategy (see [3]), and relax the pointwise continuity of the solution and of the flux to a weak one, by using suitable Lagrange multipliers. Non conforming couplings between FEM and BEM have been proposed in several papers. We mention here the applications to elastic problems [28], wave propagation problems [27], acoustic-structure interaction [17] by using Lagrange multiplier approaches, or [22] where a three field method is used in elastostatics. In the above mentioned papers the mathematical analysis of the coupling strategies is not given. We have found a complete analysis and the proof of optimal error estimates in the work of [31], where a 2D elliptic problem is considered and a Dirichlet to Neumann map is proposed as NRBC on the artificial boundary, whose shape is limited to a circumference.
The aim of this paper is to provide a thorough analysis of the effect of using this kind of weak coupling between FEM and BEM. To fix the ideas we will focus on the 2D exterior Poisson problems, which is solved by using computations only in an interior finite domain, bounded by an artificial boundary \({{\mathcal {B}}}\). The transmission conditions between the interior domain and the exterior one, which is reduced to the boundary \({{\mathcal {B}}}\) via a BEM, are imposed weakly using a mortar approach. For the numerical discretization, we present a Galerkin approach based on a finite element approximation in the interior of the computational domain and on a piecewise linear approximation of the NRBC. In a quite general framework we will present the analysis of the new proposed approach, providing error estimates in the energy norm and in the \(L^2\) norm of the computational domain.
We will show that the proposed approach allows to use numerical grids on \({{\mathcal {B}}}\) coarser than the one inherited on it by the interior FEM, with a consequent strong reduction of the computational cost and the memory saving for the computation of the matrix entries associated to the boundary integral operators. Moreover, the possibility of choosing artificial boundaries of arbitrary shape (convex or non convex curves) further allows to reduce the computation due to the discretization of the physical domain. Finally, the approach proposed allows to automatically determine the farfield behavior of the solution, via the interior FEM.
2 The Model Problem
Let \({\mathcal {O}}^e= {\mathbb {R}}^2 {\setminus } {\overline{{\mathcal {O}}}}\) be the complement of a bounded rigid obstacle \({\mathcal {O}}\subset {\mathbb {R}}^2\), having a smooth boundary \({\varGamma }\). We consider the following exterior Dirichlet problem:
We assume that the support of f is bounded and that \(f \in L^2({\mathcal {O}}^e)\). It is known that Problem (1) admits a unique solution in the space
where \(\omega ({{\mathbf {x}}}) = \left( \sqrt{1+|{{\mathbf {x}}}|^2}\left( 1+\log \sqrt{1+|{{\mathbf {x}}}|^2}\right) \right) ^{-1}\) (see [25]). Such a solution displays the following asymptotic behaviour
where \(\alpha \) is a constant.
To solve (1) by means of a finite element method, we truncate the infinite external domain by an artificial boundary \({{\mathcal {B}}}\), defined by a smooth curve. This boundary divides \({\mathcal {O}}^e\) into two open sub-domains: a finite computational domain \({\varOmega }^i\), which is bounded internally by \({\varGamma }\) and externally by \({{\mathcal {B}}}\), and an unbounded domain \({\varOmega }^e= {\mathbb {R}}^2 {\setminus } \overline{{\varOmega }^i\cup {\mathcal {O}}}\). We assume that the artificial boundary \({{\mathcal {B}}}\) is chosen in such a way that the support of f is included in \({\varOmega }^i\) and that the function f is null in a whole neighborhood of the boundary \({{\mathcal {B}}}\). Then, Problem (1) can be split into two problems: a problem set on the interior domain
and a problem set on the exterior one
Denoting by \(\lambda ^i= \partial _{{{\mathbf {n}}}_i} u^i\) and \({\lambda ^e}= \partial _{{{\mathbf {n}}}_e} u^e\), \({{\mathbf {n}}}_i\) and \({{\mathbf {n}}}_e\) being the unit normal vectors on \({{\mathcal {B}}}\) pointing outward of \({\varOmega }^i\) and \({\varOmega }^e\), respectively, the two problems are coupled by the conditions
It is known that the solution \(u^e\) of (3) in \({\varOmega }^e\) can be represented by the Kirchhoff’s formula
where \({\mathcal {V}}: H^{-1/2}({{\mathcal {B}}}) \rightarrow H^{1/2}({{\mathcal {B}}})\),
and \({\mathcal {K}}: H^{1/2}({{\mathcal {B}}}) \rightarrow H^{1/2}({{\mathcal {B}}})\),
are the single and double layer integral operators. The function
is the fundamental solution of the Laplace equation \(-{\varDelta } u^e = 0\). We use the trace of (5) on \({{\mathcal {B}}}\) as NRBC, that reads
Furthermore, we know (see [25]) that the asymptotic conditions (2) coupled with (5) imply that \(\langle {\lambda ^e}, 1 \rangle = 0\), where \(\langle \cdot ,\cdot \rangle \) denotes the duality pairing between and \(H^{-1/2}({{\mathcal {B}}})\) and \(H^{1/2}({{\mathcal {B}}})\). We then introduce the spaces
and, for any \(w\in H^1({\varOmega }^i)\), we denote by \(\gamma _{_{{\mathcal {B}}}}(w)\) its trace on \({{\mathcal {B}}}\), which belongs to \(H^{1/2}({{\mathcal {B}}})\). Then, introducing the bilinear form \(a:H^1({\varOmega }^i)\times H^1({\varOmega }^i) \rightarrow {\mathbb {R}}\)
and denoting by \((v,w)_{{\varOmega }^i} = \int _{{\varOmega }^i} v({{\mathbf {x}}}) w({{\mathbf {x}}}) d{{\mathbf {x}}}\) the \(L^2({\varOmega }^i)\) scalar product, we write the weak formulation of the coupled problem as follows:
find \(u^i\in V^i_g\), \(\lambda ^i\in {\varLambda }^i\), \(u^e\in V^e\), \({\lambda ^e}\in {\varLambda }^e\) such that for all \(v^i\in V^i\), \(v^e\in V^e\), \(\mu ^i\in {\varLambda }^i\) and \(\mu ^e\in {\varLambda }^e\)
where the transmission conditions (4) are enforced in a weak form.
We remark that in Eq. (8) the solution in \({\varOmega }^e\) enters only via its trace on \({{\mathcal {B}}}\). Therefore, for the sake of notational simplicity, we denoted such a trace by the same symbol \(u^e\), as there is no need of distinguishing between functions in \(H^1({\varOmega }^e)\) and their traces on \({{\mathcal {B}}}\). Moreover observe that, as we test Eq. (5) with \(\mu ^e \in {\varLambda }^e\), satisfying by definition \(\langle \mu ^e,1 \rangle = 0\), the unknown constant \(\alpha \) does not appear in the formulation (8). Nevertheless, the asymptotic behavior \(\alpha \) will be automatically determined tanks to the coupling with the interior FEM method, since, contrary to \({\varLambda }^e\), the multiplier space \({\varLambda }^i\) contains the constant functions.
As usual we can reduce the non homogeneous boundary condition on \({\varGamma }\) to an homogeneous one by splitting \(u^i\) as the sum of a suitable fixed function in \(V^i_g\) and of an unknown function in \({V^i}\). We therefore from now on consider the case \(g=0\). Problem (8) is well posed, as stated by the following Theorem.
Theorem 1
For \(g = 0\), Problem (8) admits a unique solution \((u^i,u^e,\lambda ^i,\lambda ^e) \in {V^i}\times V^e\times {\varLambda }^i\times {\varLambda }^e\) satisfying
Proof
In order to analyze the method, we let \({\mathbb {V}}= {V^i}\times V^e\times {\varLambda }^e\), endowed with the norm
and we let \({{\mathbf {a}}}: {\mathbb {V}}\times {\mathbb {V}}\rightarrow {\mathbb {R}}\) be defined as
and \({\mathbf {b}}: {\mathbb {V}}\times {\varLambda }^i\rightarrow {\mathbb {R}}\) as
The problem can then be rewritten as: find \((u^i,u^e,\lambda ^e) \in {\mathbb {V}}\), \(\lambda ^i\in {\varLambda }^i\) such that for all \((v^i,v^e,\mu ^e) \in {\mathbb {V}}\), \(\mu ^i\in {\varLambda }^i\)
Following [8] (Theorem 1.1, Section II.1), in order to prove that such a problem is well posed we need to prove an inf-sup condition for \({\mathbf {b}}\) and a second inf-sup condition for \({{\mathbf {a}}}\) on the kernel of \({\mathbf {b}}\). The former is stated in the following proposition, which is an immediate consequence of the duality between \(\gamma _{{\mathcal {B}}}{V^i}\) and \({\varLambda }^i\).
Proposition 1
It holds that
Let us now consider the restriction of the bilinear form \({{\mathbf {a}}}\) to \(\ker {\mathbf {b}}\). We start by observing that
The two inf-sup conditions
reduce then to
and
These are not difficult to prove in view of Lemma 2 of [25]. The above mentioned theorem of [8] gives us the thesis. \(\square \)
Corollary 1
For all \(g \in H^{1/2}({\varGamma })\), Problem (8) admits a unique solution \((u^i,u^e,\lambda ^i,\lambda ^e)\) satisfying
Remark 1
We remark that, as the solution of (8) satisfies \(\langle \lambda ^i, 1 \rangle = - \langle {\lambda ^e}, 1 \rangle = 0\), we could also think of strongly embedding the zero average condition in the definition of \({\varLambda }^i\). However, it is not difficult to check that for such a choice we would not get a well posed problem, as Eq. (8) would only determine \(u^i\) up to a constant.
2.1 Galerkin Discretization
We present here a class of Galerkin type discretizations of Problem (8), which includes, but is not limited to, finite element methods. In Sect. 3 we will give an example of an order one discretization that falls in the framework considered. Once again we focus on the case of homogeneous boundary conditions on \({\varGamma }\). The results for the case of non homogeneous boundary conditions can then be obtained by standard arguments, under suitable standard assumptions on the discretization.
Let \(V^i_h\subset {V^i}\), \(V^e_h\subset V^e\), \({\varLambda }^i_h\subset {\varLambda }^i\) and \({\varLambda }^e_h\subset {\varLambda }^e\) denote finite dimensional subspaces, and let \(a_h : {V^i}\times {V^i}\rightarrow {\mathbb {R}}\) and \(\langle \cdot ,\cdot \rangle _h : {\varLambda }^i\times V^i_h\rightarrow {\mathbb {R}}\) denote two bounded bilinear forms, respectively approximating a and \(\langle \cdot , \gamma _{_{{\mathcal {B}}}}(\cdot ) \rangle \). We consider the following discrete problem: find \(u^i_h\in V^i_h\), \(u^e_h \in V^e_h\), \(\lambda ^i_h \in {\varLambda }^i_h\), \(\lambda ^e_h \in {\varLambda }^e_h\) such that for all \(v^i_h\in V^i_h\), \(v^e_h \in V^e_h\), \(\mu ^i_h \in {\varLambda }^i_h\), \(\mu ^e_h \in {\varLambda }^e_h\)
or, in compact form: find \({\mathbf {u}}_h= (u^i_h,u^e_h,\lambda ^e_h) \in {{\mathbb {V}}}_h = V^i_h\times V^e_h\times {\varLambda }^e_h\), \(\lambda ^i_h \in {\varLambda }^i_h\) such that for all \({\mathbf {v}}_h = (v^i_h,v^e_h,\mu ^e_h) \in {{\mathbb {V}}}_h\), \(\mu ^i_h \in {\varLambda }^i_h\) it holds
with
and
Remark that, for the sake of simplicity, we assumed that the couplings between \(V^e_h\) and \({\varLambda }^i_h\), \(V^e_h\) and \({\varLambda }^e_h\) as well as the right hand side and the integral operators are computed exactly, while the bilinear form a and the coupling between \(V^i_h\) and \({\varLambda }^i_h\) are only approximated. As we will see in Sect. 3, this is what happens when, for the interior problem, the geometry of the domain is approximated by a polygonal mesh, while the boundary \({{\mathcal {B}}}\) is described exactly via a parametrization. Of course one could choose to approximate also some of or all the other bilinear forms. The resulting method could be analyzed by the same approach, yielding similar results.
We assume that the discrete spaces and functionals satisfy the following assumptions.
-
A.1
The discretization is of order \(k \ge 1 \), that is, the following direct inequalities hold for all \(w \in {V^i}\cap H^{k+1}({\varOmega }^i)\), \(z \in H^{k+1}({{\mathcal {B}}})\), \(\eta \in H^{k}({{\mathcal {B}}})\)
$$\begin{aligned}&\inf _{{v^i_h}\in V^i_h} \Vert w - v^i_h\Vert _{1,{\varOmega }^i} \lesssim h_i^k \Vert w \Vert _{k+1,{\varOmega }^i}, \end{aligned}$$(11)$$\begin{aligned}&\inf _{v^e_h\in V^e_h} \Vert z - v^e_h\Vert _{1/2,{{\mathcal {B}}}} \lesssim h_e^{k+1/2} \Vert z \Vert _{k+1,{{\mathcal {B}}}} \end{aligned}$$(12)$$\begin{aligned}&\inf _{\mu ^i_h \in {\varLambda }^i_h} \Vert \eta - \mu ^i_h \Vert _{-1/2,{{\mathcal {B}}}} \lesssim h_i^{k} \Vert \eta \Vert _{k-1/2,{{\mathcal {B}}}}, \end{aligned}$$(13)$$\begin{aligned}&\inf _{\mu ^e_h \in {\varLambda }^e_h} \Vert \eta - \mu ^e_h \Vert _{-1/2,{{\mathcal {B}}}} \lesssim h_e^{k+1/2} \Vert \eta \Vert _{k,{{\mathcal {B}}}}. \end{aligned}$$(14) -
A.2
For all \(t < 3/2\), \(V_h^e \subset H^t({{\mathcal {B}}})\) and the following inverse inequality holds: for all \(u^e_h \in V^e_h\), and for all s with \(-1/2 \le s < t \) we have
$$\begin{aligned} \Vert u^e_h \Vert _{t,{{\mathcal {B}}}} \lesssim h_e^{s-t} \Vert u^e_h \Vert _{s,{{\mathcal {B}}}}. \end{aligned}$$(15) -
A.3
The spaces \(V^i_h\) and \({\varLambda }^i_h\) verify the following assumptions:
$$\begin{aligned}&\inf _{\lambda _h \in {\varLambda }^i_h} \sup _{v_h\in V^i_h} \frac{ \langle \lambda _h, v_h\rangle _h }{\Vert \lambda _h\Vert _{-1/2,{{\mathcal {B}}}} \Vert v_h \Vert _{1,{\varOmega }^i}} > rsim 1, \end{aligned}$$(16)$$\begin{aligned}&a_h(v_h,v_h) > rsim \Vert v_h \Vert ^2_{1,{\varOmega }^i}, \quad \text { for all }v_h \in V^i_h: \langle \mu _h,v_h \rangle _h = 0\quad \forall \mu _h \in {\varLambda }^i_h. \end{aligned}$$(17) -
A.4
For all \(u^i_h,v^i_h \in V^i_h\), \(\mu ^i_h \in {\varLambda }^i_h\) we have
$$\begin{aligned}&| a(u_h^i,v_h^i) - a_h(u_h^i, v_h^i) | \lesssim h_i^k \Vert u_h^i \Vert _{1,{\varOmega }^i} \Vert v_h^i \Vert _{1,{\varOmega }^i}, \end{aligned}$$(18)$$\begin{aligned}&| \langle \mu _h^i, v_h^i \rangle - \langle \mu _h^i, v_h^i \rangle _h | \lesssim h_i^k \Vert \mu _h^i \Vert _{-1/2,{{\mathcal {B}}}} \Vert v_h^i \Vert _{1,{\varOmega }^i}. \end{aligned}$$(19)
Under such assumptions, the following theorem holds.
Theorem 2
There exist \(h_0>0\) and \(\gamma >0\) such that if \(h_i,h_e< h_0\) and \(h_i/h_e< \gamma \), then the discrete problem (10) has a unique solution satisfying
Using [8] (Theorem 1.1, Section II.1) once again, in order to prove the well posedness of our problem it is sufficient to prove
-
1.
that an inf-sup condition of the form
$$\begin{aligned} \inf _{\mu ^i_h\in {\varLambda }^i_h} \sup _{{\mathbf {u}}_h\in {{\mathbb {V}}}_h} \frac{{\mathbf {b}}_h({\mathbf {u}}_h;\mu ^i_h)}{\Vert {\mathbf {u}}_h \Vert _{{\mathbb {V}}} \Vert \mu ^i_h \Vert _{-1/2,{{\mathcal {B}}}}} > rsim 1 \end{aligned}$$(20)holds;
-
2.
that, setting
$$\begin{aligned} \ker {\mathbf {b}}_h:=\{ {\mathbf {u}}_h \in {{\mathbb {V}}}_h: \ {\mathbf {b}}_h({\mathbf {u}}_h;\mu ^i_h) = 0\quad \forall \mu ^i_h \in {\varLambda }^i_h \}, \end{aligned}$$the problem of finding \({\mathbf {u}}_h \in \ker {\mathbf {b}}_h\) such that for all \({\mathbf {v}}_h \in \ker {\mathbf {b}}_h\)
$$\begin{aligned} {{\mathbf {a}}}_h ({\mathbf {u}}_h;{\mathbf {v}}_h) = L({\mathbf {v}}_h) \end{aligned}$$(21)is well posed for all \(L \in {{\mathbb {V}}}'\).
The inf-sup bound (20) derives easily from (16). Let us then concentrate on the well posedness of Problem (21). We start by characterizing \(\ker {\mathbf {b}}_h\). Let \({\mathcal {L}}^{{\mathcal {H}}}_h: H^{1/2}({{\mathcal {B}}}) \rightarrow V^i_h\) be a discrete harmonic lifting operator, defined as \({\mathcal {L}}^{{\mathcal {H}}}_hu^e = u_h^\star \), where \((u_h^\star ,\lambda _h^\star ) \in V^i_h\times {\varLambda }_h^i\) is the solution of the following saddle point problem:
It is easy to see that, thanks to Assumption A.4, Problem (22) is well posed and that for all \(v \in H^{1/2}({{\mathcal {B}}})\) we have
We have the following proposition.
Proposition 2
\({\mathbf {u}}_h = (u^i_h,u^e_h,\lambda ^e_h) \in \ker {\mathbf {b}}_h\) if and only if
with \(u_h^0 \in V_h^0 = \{u_h \in V^i_h: \langle \mu _h, u_h \rangle _h = 0,\ \forall \mu _h \in {\varLambda }^i_h\} \). Moreover, for all \({\mathbf {u}}_h \in \ker {\mathbf {b}}_h\) with \( u^i_h= u^0_h + {\mathcal {L}}^{{\mathcal {H}}}_h( u^e_h)\) it holds that
Proof
It is not difficult to verify that any triple \((u^i_h,u^e_h,\lambda ^e_h) \) with \(u^i_h\) and \(u^e_h\) satisfying (24) is in \(\ker {\mathbf {b}}_h\). On the other hand, \((u^i_h,u^e_h,\lambda ^e_h) \in \ker {\mathbf {b}}_h\) implies
Then \(u_h^0 = u^i_h- {\mathcal {L}}^{{\mathcal {H}}}_h( u^e_h) \in V_h^0 \), and, since it is not difficult to verify that
we get the thesis. \(\square \)
Proposition 2 states that \(\ker {\mathbf {b}}_h\) is isomorphic to \(V_h^0 \times V^e_h\times {\varLambda }_h^e\) uniformly in h. The isomorphism takes the form
Proving the well posedness of (21) reduces then to proving an inf-sup condition on the bilinear form \({{\hat{{{\mathbf {a}}}}}}: (V_h^0 \times V^e_h\times {\varLambda }_h^e) \times (V_h^0 \times V^e_h\times {\varLambda }_h^e) \rightarrow {\mathbb {R}}\) defined by
with
In order to take advantage of the characterization of \(\ker {\mathbf {b}}_h\) provided by Proposition 2, in the next lemma we study the approximation properties of the discrete harmonic extension operator.
Lemma 1
Letting \({\mathcal {H}}: H^{1/2}({{\mathcal {B}}}) \rightarrow H^1({\varOmega }^i)\) denote the harmonic lifting, \({\mathcal {L}}^{{\mathcal {H}}}_hv\) approximates \({\mathcal {H}}v\) and we have the following error bounds, the first one holding if \(v \in H^{1/2+t}({{\mathcal {B}}})\) with \(t >1/2\):
Proof
We observe that \({\mathcal {H}}v \) satisfies
Let us then assume that \(v \in H^{1/2+t}({{\mathcal {B}}})\). We can use [8, Proposition II.2.16], and we have that
The first two terms on the right hand side can be bound thanks to Assumption A.1, while we bound the third term by adding \( a({\mathcal {H}}v ,w_h) - \langle \partial _{{{\mathbf {n}}}_i}{\mathcal {H}}v,w_h \rangle \) which is null and using a triangular inequality, yielding
Now, letting \(v^I_h\in V^i_h\) denote the \(H^1({\varOmega }^i)\) projection of \({\mathcal {H}}v\), using (18), we can bound
Similarly, letting \(\mu _h^I\in {\varLambda }^i_h\) denote the \(H^{-1/2}({{\mathcal {B}}})\) projection of \(\partial _{{{\mathbf {n}}}_i} {\mathcal {H}}v\) and using (19), we can bound
where we used that for \( t > 1/2\), \(v \in H^{1/2+t}({{\mathcal {B}}})\) implies \(\nabla {\mathcal {H}}v \in H^t({\varOmega }^i)\) which admits a trace in \(H^{t - 1/2}({{\mathcal {B}}})\). By the same arguments we also have
Then, (25) easily follows.
We next need to bound
Let \(v^\phi \) be the solution to \(-{\varDelta } v^\phi = \phi \), \(v^\phi = 0\) on \(\partial {\varOmega }^i= {\varGamma } \cup {{\mathcal {B}}}\), and let \(v^i_h \in V^i_h\), \(\mu ^i_h \in {\varLambda }^i_h\) be the solution to
Observe that, with the same arguments used to prove (25), it is not difficult to prove that
Integrating by parts and using the definition of \({\mathcal {L}}^{{\mathcal {H}}}_h\) and of \(v^i_h\) and \(\mu ^i_h\), it is not difficult to check that we can write
with
and, since the definition of \(v^i_h\) and \(v^\phi \) yields \(\langle \lambda ^\star _h, v^i_h \rangle _h = 0\) and \( \langle \partial _{{{\mathbf {n}}}_i} {\mathcal {H}}v, v^\phi \rangle = 0\),
Combining the five bounds we easily obtain (26). As far as (27) is concerned, we have
We can write, for \(\phi _h \in {\varLambda }^i_h\) arbitrary
where we used the definition of \({\mathcal {L}}^{{\mathcal {H}}}_h\) and Assumption A.4. Choosing \(\phi _h \in {\varLambda }^i_h\) as the \(H^{-1/2}({{\mathcal {B}}})\) projection of \(\phi \), thanks to Assumption A.1 we easily see that (27) holds. \(\square \)
In order to prove the well posedness of the discrete problem, we start by proving the following lemma, which compares \(s_h\) to the bilinear form \(s: V^e\times V^e\rightarrow {{\mathbb {R}}}\) associated to the Steklov–Poincaré operator:
Lemma 2
For all t with \(1/2< t < 1\), there exists a positive constant \(c_t\) such that for all \(u^e_h,v^e_h \in V^e_h\) we have
Proof
We have
where we added and subtracted \({\mathcal {L}}^{{\mathcal {H}}}_hv^e_h\), and we used Lemma 1 and Assumption A.4. Finally, as \(h_i^k \lesssim (h_i/h_e)^t\), by using Assumption A.2, we have
\(\square \)
Let now
Lemma 4 of [25] yields the following Lemma.
Lemma 3
For all \((u^e_h,\lambda ^e_h) \in V^e_h\times {\varLambda }^e_h\) we have
Proof
Let \({\mathbf {s}}:(V^e \times {\varLambda }^e)\times (V^e \times {\varLambda }^e) \rightarrow {\mathbb {R}}\) be defind as
As a corollary to Lemma 2 in [25], it is easy to show that there exist \((v^e,\mu ^e) \in V^e\times {\varLambda }^e\) such that
Proceeding then as in the proof of Lemma 4 of the same paper, it is not difficult to prove the existence of \(({\hat{u}}^e_h,{\hat{\lambda }}^e_h) \in V^e_h\times {\varLambda }^e_h\) such that for some \(\alpha > 0\) independent of \(h_e\)
Without loss of generality, \({{\hat{u}}}_h^e\) and \({{\hat{\lambda }}}_h^e\) can be chosen in such a way that \(\Vert {{\hat{u}}}^e_h \Vert _{1/2,{{\mathcal {B}}}} + \Vert {\hat{\lambda }}^e_h \Vert _{-1/2,{{\mathcal {B}}}} =\Vert u^e_h \Vert _{1/2,{{\mathcal {B}}}} + \Vert \lambda ^e_h \Vert _{-1/2,{{\mathcal {B}}}}\).
Now we have:
Using Lemma 2, we can then write
Provided \((h_i/h_e) \le \rho \), with \(\rho \) chosen in such a way that \(\beta = c_t \rho ^{2t }< \alpha \), we get
The thesis easily follows. \(\square \)
Thanks to the coercivity of \(a_h\) on \(V_h^0\), we immediately have the following corollary.
Corollary 2
For all \({\mathbf {u}}_h \in \ker {\mathbf {b}}_h\) we have
Theorem 2 easily follows.
2.2 Error Estimates in the Energy Norm
Under the assumptions of the previous section, the method satisfies an error estimate with optimal order, as stated by the following theorem.
Theorem 3
Under assumptions A.1–4, if the solution of Problem (1) verifies \(u|_{{\varOmega }^i} \in H^{k+1}({\varOmega }^i)\), then the following error bounds hold true:
Proof
We start by observing that, in general, if the solution of Problem (1) verifies \(u|_{{\varOmega }^i} \in H^{k+1}({\varOmega }^i)\), we have that \(u^e \in H^{k+1/2}({{\mathcal {B}}})\) and that \(\lambda ^i= -\lambda ^e= \partial _{{{\mathbf {n}}}_i} u \in H^{k-1/2}({{\mathcal {B}}})\). However, under our assumptions, namely that f is supported away from \({{\mathcal {B}}}\), u is harmonic in a neighborhood of \({{\mathcal {B}}}\) and hence \(u^e\) and \(\lambda ^i= -\lambda ^e\) have a higher regularity. In particular we have that \(u^e\in H^{k+1}({{\mathcal {B}}})\) and \(\lambda ^e\in H^k({{\mathcal {B}}})\) with
Moreover we have that the right hand side \(f = -{\varDelta } u\) verifies \(f \in H^{k-1}({\varOmega }^i)\) (actually, with the assumptions we made on the domain \({\varOmega }^i\), \(f \in H^{k-1}({\varOmega }^i)\) if and only if \(u^i \in H^{k+1}({\varOmega }^i)\)).
Let us introduce the compact notation \({{\mathbf {u}}^e}= (u^e,\lambda ^e)\) and \({\mathbf {u}}^e_h = (u^e_h,\lambda ^e_h)\), and let \({\mathbf {w}}^e_h = (w_h^e,\eta _h^e)\), where \(w_h^e\in V^e_h\) and \(\eta _h^e\in {\varLambda }^e_h\) denote, respectively, the \(H^{1/2}({{\mathcal {B}}})\) projection of \(u^e\) onto \(V^e_h\) and the \(H^{-1/2}({{\mathcal {B}}})\) projection of \(\lambda ^e\) onto \({\varLambda }^e_h\). Setting \(v^i = {\mathcal {H}}v^e\) and \(v_h^i = {\mathcal {L}}^{{\mathcal {H}}}_hv_h^e\) in the first equation of, respectively, (8) and (10), it is not difficult to check that \({{\mathbf {u}}^e}\) and \({\mathbf {u}}^e_h\) satisfy, respectively
and
with
As in the proof of Lemma 3 [see (31)], there exists \(\hat{{\mathbf {v}}}^e_h = ({{\hat{v}}}_h^e,{{\hat{\mu }}}_h^e) \in V^e_h\times {\varLambda }_h^e\), which we can normalize in such a way that \(\Vert \hat{{\mathbf {v}}}^e_h \Vert _{\mathbb {V}}= \Vert {\mathbf {u}}^e_h - {\mathbf {w}}^e_h \Vert _{\mathbb {V}}\), such that
Now, adding and subtracting \({\mathbf {s}}({{\mathbf {u}}^e},\hat{{\mathbf {v}}}^e_h)\) and \({\mathbf {s}}({\mathbf {w}}^e_h,\hat{{\mathbf {v}}}^e_h)\), and using (35) and (36), we can write
Let us then separately bound the different components at the right hand side. We have:
Using (26) we can then write
Next, using A.1 and (34), we have
Finally, we have
where we used Assumption A.4. \( \Vert {\mathcal {H}}u^e- {\mathcal {L}}^{{\mathcal {H}}}_hu^e\Vert _{1,{\varOmega }^i}\) can be bound by using Lemma 1. Moreover, Assumption A.1 and (34) yield
Now, integrating by part, we can write
which, using Lemma 1 once again, finally yields
Bounding the right hand side of (37) by combining (38), (39) and (40), we get (32). Bound (33) is then not difficult to prove. In fact, observing that \(u^i\) and \(\lambda ^i\) are solution to
using [8, Proposition II.2.16] once again we can write
We bound the first two terms using Assumption A.1, which gives us
Using (41) and Assumption A.4, we have
Since \(u^e= \gamma _{{\mathcal {B}}}u^i\), and in view of the definition of \({\mathcal {L}}^{{\mathcal {H}}}_h\), we can write
and, using (32),
Then, (33) easily follows. \(\square \)
Remark 2
The higher regularity of the solution in a neighborhood of the boundary \({{\mathcal {B}}}\) allows us to obtain an error estimate where the meshsize \(h_e\) for the spaces used in the discretization of the integral operator appears with a higher exponent (namely \(k+1/2\) rather than k). As continuity is only imposed weakly, this allows to use a coarser mesh for discretizing \(V^e\) and \(\varLambda ^e\), with consequent savings both in CPU and storage requirements.
Remark 3
The assumption, made at the beginning of Sect. 2, that \({\varGamma }\) is smooth, is essentially needed only for the duality arguments à la Aubin–Nitsche used in deriving the error estimates. In particular, the smoothness of \({\varGamma }\) is needed to derive the bound on \( \Vert {\mathcal {L}}^{{\mathcal {H}}}_h{{\hat{v}}}_h^e - {\mathcal {H}}{{\hat{v}}}_h^e \Vert _{H^{k-1}({\varOmega }^i)'}\). However, such an assumption is not needed to prove the well posedness of both the continuous problem (8) and the discrete problem (10), results that hold, with unchanged proof, also in the more general case of a Lipschtiz boundary. Remark that, if \({\varGamma }\) is piecewise smooth, rather than globally smooth, the error estimate can still be proven, provided the discretization spaces are chosen in way well suited to deal with the pointwise lack of smoothness of \({\varGamma }\).
2.3 \(L^2\) Error Estimate
We want now to give an estimate on the error \(e^i_h= u^i- u^i_h\) in the weaker \(L^2({\varOmega }^i)\) norm. In order to do so, always assuming that A.1–4 hold, we make the following stronger assumption:
-
A.5
For \(v, w \in W^{1,\infty }({\varOmega }^i)\), \(\mu \in L^2({{\mathcal {B}}})\) it holds that
$$\begin{aligned} | a(v,w) - a_h(v,w) |\lesssim h_i^{k+1} \Vert \nabla v \Vert _{0,\infty ,{\varOmega }^i} \Vert \nabla w \Vert _{0,\infty ,{\varOmega }^i} \end{aligned}$$(42)as well as
$$\begin{aligned} | \langle \mu , w \rangle _h - \langle \mu , w \rangle | \le h_i^{k+1} \Vert \mu \Vert _{0,{{\mathcal {B}}}} \Vert \nabla w \Vert _{0,\infty ,{\varOmega }^i}. \end{aligned}$$(43)
Moreover, we assume that \(V^i_h\) and \({\varLambda }^i_h\) satisfy the following additional direct and inverse inequalities.
-
A.6
The spaces \({\varLambda }^i_h\) and \(V^i_h\) respectively satisfy \({\varLambda }^i_h\subseteq L^2({{\mathcal {B}}})\) and \(V^i_h\subseteq W^{1,\infty }({\varOmega }^i)\), and the following inverse bounds hold: for all \(\mu _h \in {\varLambda }^i_h\), \(v_h \in V^i_h\), and for all s, t with \(0 \le s < t \le 1\)
$$\begin{aligned}&\Vert \mu _h \Vert _{0,{{\mathcal {B}}}} \lesssim h_i^{-1/2} \Vert \mu _h \Vert _{-1/2,{{\mathcal {B}}}}, \end{aligned}$$(44)$$\begin{aligned}&\Vert v_h \Vert _{t,\infty ,{\varOmega }^i} \lesssim h_i^{s-t} \Vert v_h \Vert _{s,\infty ,{\varOmega }^i}, \qquad \Vert \nabla v_h \Vert _{0,\infty ,{\varOmega }^i} \lesssim h^{-1/2} | v_h |_{1,{\varOmega }^i}. \end{aligned}$$(45) -
A.7
For all \(u \in H^{m}({\varOmega }^i)\), \(2 \le m \le k+1\) there exists \(w_h\in V^i_h\) such that
$$\begin{aligned} \Vert u - w_h\Vert _{1,{\varOmega }^i} + \Vert u - w_h\Vert _{0,\infty ,{\varOmega }^i} + h_i\Vert \nabla ( u - w_h) \Vert _{0,\infty ,{\varOmega }^i} \lesssim h_i^{m-1} \Vert u \Vert _{m,{\varOmega }^i}. \end{aligned}$$
We start by proving some bounds on the discrete solutions in the stronger norms appearing in Assumption A.6. More precisely, we have the following Lemma.
Lemma 4
Let \(u^i,\lambda ^i,u^e,{\lambda ^e}\) and \(u^i_h,\lambda ^i_h,u^e_h,\lambda ^e_h\) be the solutions of (8) and (10). Then, under the additional Assumptions A.6–7, if \(h_e\lesssim h_i^{1/3}\) we have
the implicit constants in the first inequality depending on \(\varepsilon \).
Proof
Let \(w_h\) denote the approximation of u given by Assumption A.7 for \(m=2\). Adding and subtracting \(w_h\), using A.6 for \(w_h\) and subsequently adding and subtracting u we can write
We bound the first term using, once again, A.6, then adding and subtracting u, and using A.7 as well as Theorem 3:
We next bound the second term by using A.7, which, by space interpolation yields
Thanks to the injection of \(H^2({\varOmega }^i)\) in \(W^{1-\varepsilon ,\infty }({\varOmega }^i)\) we also have
finally yielding (46).
Letting now \(\mu ^I_h\) be the \(L^2({{\mathcal {B}}})\) projection of \(\lambda ^i\) onto \({\varLambda }^i_h\), and proceeding in a similar way as before, we can write
The bound (47) then follows from combining Theorem 3 with Assumption A.1, and using a standard Aubin–Nitsche’s duality argument to bound \(\Vert \lambda ^i- \mu _h^I \Vert _{-1/2,{{\mathcal {B}}}}\). \(\square \)
Observe that a bound similar to (46) can be proven for \(z \in H^2({\varOmega }^i)\) and \(z_h \in V^i_h\) its \(H^1({\varOmega }^i)\) projection. Then, letting now \(u^i,\lambda ^i,u^e,{\lambda ^e}\) and \(u^i_h,\lambda ^i_h,u^e_h,\lambda ^e_h\) be the solutions respectively of (8) and (10), under Assumptions A.5–7 we have the following corollaries, the implicit constant in both inequalities depending on \(\varepsilon \).
Corollary 3
For \(z \in H^2({\varOmega }^i)\), \(z_h \in {\varLambda }^i_h\) denoting its \(H^1({\varOmega }^i)\) projection, we have
Corollary 4
For \(\zeta \in L^2({{\mathcal {B}}})\) it holds that
We now introduce \(z \in {V^i}\), \(\zeta \in {\varLambda }^e\) such that for all \(w \in {V^i}\), \(\xi \in {\varLambda }^e\) it holds that
We have the following smoothness result (see [25, Lemma 3]): \(z \in H^2({\varOmega }^i)\)\(\zeta \in H^{1/2}({{\mathcal {B}}})\) and it holds that
We set: \(z^i = z\), \(z^e = \gamma _{{\mathcal {B}}}z\), \(\zeta ^i = - \zeta - 2{\mathcal {K}}^* \zeta \), where we denote by \({\mathcal {K}}^* : H^{-1/2}({{\mathcal {B}}}) \rightarrow H^{-1/2}({{\mathcal {B}}})\) the adjoint of \({\mathcal {K}}\). It is not difficult to check that we have, for all \(w^i \in {V^i}\), \(w^e \in V^e\), \(\xi ^i \in {\varLambda }^i\), \(\xi ^e \in {\varLambda }^e\),
which, using the compact notation introduced in Sect. 2, can be rewritten as
Let now \(\mathbf {w} = \mathbf {e} = (e^i_h,e^e_h,\delta ^e_h)\) and \(\xi ^i = \delta ^i_h\), with \(e^i_h= u^i - u^i_h\), \(e^e_h= u^e - u^e_h\), \(\delta ^i_h= \lambda ^i- \lambda ^i_h\) and \(\delta ^e_h= {\lambda ^e}- {\lambda ^e}_h\). Adding and subtracting \(\mathbf {z}_h = (z_h^i,z_h^e,\zeta _h^e)\) and \(\zeta _h^i\), where \(z_h^i \in V^i_h\)\(z_h^e\in V^e_h\), \(\zeta _h^i\in {\varLambda }^i_h\) and \(\zeta _h^e\in {\varLambda }^e_h\) are suitable interpolants to \(z^i\), \(z^e\), \(\zeta ^i\) and \(\zeta ^e\), which, thanks to Assumption A.1, we can choose in such a way that
we can write
Now it is easy to check that
where we used Corollaries 3 and 4. Combining with (50) we can then write
Dividing both sides by \(\Vert e_h^i \Vert _{0,{\varOmega }^i}\), as (48) holds, we finally get the quasi optimal estimate
3 The Discrete Scheme
We assume that \({\varOmega }^i\) is approximated by a polygonal domain \( {\varOmega }^i_{\varDelta } = \cup _{K\in {{\mathcal {T}}}_{h_i}} K\), union of the elements of a quasi uniform, shape regular triangular mesh \({{\mathcal {T}}}_{h_i}\), of mesh size \(h_i\), defined in such a way that all the nodes on \(\partial {\varOmega }^i_{\varDelta }\) lie on \(\partial {\varOmega }^i\). The boundary \(\partial {\varOmega }^i_{\varDelta }\) will be naturally split as \(\partial {\varOmega }^i_{\varDelta } = {\varGamma }_{\varDelta } \cup {{\mathcal {B}}}_{\varDelta }\), where \({\varGamma }_{\varDelta }\) and \({{\mathcal {B}}}_{\varDelta } \) respectively denote the piecewise linear curves interpolating \({\varGamma }\) and \({{\mathcal {B}}}\) at the boundary nodes of the triangulation. Observe that in general, we will neither have \({\varOmega }^i_{\varDelta } \subseteq {\varOmega }^i\) nor \({\varOmega }^i\subseteq {\varOmega }^i_{\varDelta }\). It will then be convenient to define the approximation spaces \(V_{g,h}^i\) and \(V_h^i\) as subspaces of \(H^1({\varOmega }^i\cup {\varOmega }^i_{\varDelta })\). In order to do so, we will extend to \(H^1({\varOmega }^i\cup {\varOmega }^i_{\varDelta })\) the standard P1 finite element approximation defined on \({\varOmega }^i_{\varDelta }\), by using the natural linear extension: the linear function defined on a triangle K with an edge e on \({{\mathcal {B}}}_{\varDelta }\) is prolongated linearly to the region \(\omega _h^K\) delineated by e and by the corresponding arc of \({{\mathcal {B}}}\). More precisely we introduce the finite dimensional spaces
where \({{\mathbb {P}}}^1\) denotes the space of polynomials of degree less than or equal to 1, and \({{\widetilde{g}}}_h \in V^i_h|_{{\varGamma }_{\varDelta }}\) denotes the piecewise linear function interpolating g at the triangulation nodes on \({\varGamma }_{\varDelta }\), and
By abuse of notation, we will also denote by \(V_{g,h}^i\) and \(V_h^i\) the restriction of such spaces to both \({\varOmega }^i\) and \({\varOmega }^i_{\varDelta }\). Observe that for all function \(v^i_h\) in \(V_{g,h}^i\) or in \(V_h^i\), we have that
This is easy to prove, by taking advantage of the fact that \(v^i_h\) is linear on \({{\widetilde{K}}}\).
The space \({\varLambda }^i_h\subseteq L^2({{\mathcal {B}}})\) is defined as the space of continuous functions which are piecewise linear in the curvilinear abscissa, on the decomposition \({{\mathcal {B}}}= \cup _{k=1}^{M^i} {{\mathcal {B}}}^i_k\) induced on \({{\mathcal {B}}}\) by the nodes of the mesh \({{\mathcal {T}}}_{h_i}\):
For approximating \(V^e\) and \({\varLambda }^e\), we consider a second, independent quasi uniform decomposition \({{\mathcal {B}}}= \cup _{k=1}^{M^e} {{\mathcal {B}}}^e_k\), of mesh size \(h_e\), and we define \(V^e_h\) and \({\varLambda }^e_h\) as
It is not difficult to check that the spaces thus defined satisfy assumptions A.1–2 as well as A.6–7 for \(k=1\). More in detail (13), (14) (12), and (44) can be obtained by duality from well known approximation and inverse inequality in a fairly standard way ([2], see also [4]). By smoothly extending \(w\in H^{k+1}({\varOmega }^i)\) to a function \({{\widetilde{w}}} \in H^{k+1}({{\widetilde{{\varOmega }}}}^i_{\varDelta })\), where \({\widetilde{{\varOmega }}}^i_{\varDelta }\) is a polygonal domain obtained extending all boundary triangles of \({{\mathcal {T}}}_h^i\) by a small strip of thickness \(\lesssim h_i\), in such a way that \( {\varOmega }^i \cup {\varOmega }^i_h \subseteq {{\widetilde{{\varOmega }}}}^i_{\varDelta }\), and applying the standard estimates for the finite element space defined on the resulting extended mesh, it is also easy to prove (11).
We now define the bilinear forms \(a_h\) and \(\langle \cdot ,\cdot \rangle _h\). We set:
where, for \(u \in C^0({\varOmega }^i\cup {\varOmega }^i_{\varDelta })\), \({{\widetilde{\gamma }}}_{{\mathcal {B}}}u \in H^{1/2}({{\mathcal {B}}})\) is defined as the piecewise linear (in the curvilinear abscissa) function interpolating u at the boundary nodes of \({{\mathcal {T}}}_{h_i}\). We need to prove that, with such a choice, Assumptions A.3-5 are satisfied. We have the following Lemma.
Proposition 3
The spaces \({\varLambda }^i_h\) and \(V^i_h\), and the bilinear form \(\langle \cdot ,\cdot \rangle _h\) defined by (54) satisfy Assumption A.3.
Proof
Letting \({{\varPhi }}: [0,|{{\mathcal {B}}}| ] \rightarrow {{\mathcal {B}}}\) denote the arc length parametrization of the curve \({{\mathcal {B}}}\), we let \(\psi : {\varOmega }^i_{\varDelta }\rightarrow {\varOmega }^i\) be defined as follows: for all triangles \(K \in {{\mathcal {T}}}_h^i\) with an edge \(e \subset \partial {\varOmega }^i_{\varDelta }\), letting \({{\mathbf {x}}}_0 = {\varPhi }(x_0)\), \({{\mathbf {x}}}_{1} = {\varPhi }(x_{1})\) denote the two vertices of e and \({{\mathbf {y}}}\) denote the third vertex of K, we define \(\psi \) by the relation
where, using barycentric coordinates, we express \({{\mathbf {x}}}\in K\) as \({{\mathbf {x}}}= \lambda _1 {{\mathbf {y}}}+ \lambda _2 {{\mathbf {x}}}_k + \lambda _3 {{\mathbf {x}}}_{k+1}\), with \(0\le \lambda _1, \lambda _2, \lambda _3 \le 1\), \(\lambda _1 + \lambda _2 + \lambda _3 = 1\). For triangles K which do not have any edge on \(\partial {\varOmega }^i_{\varDelta }\) (this includes interior triangles as well as triangles that have a single node on \(\partial {\varOmega }^i_{\varDelta }\)) we let \(\psi \) be the identity. We now observe that
satisfies
and that, for all \(\lambda _h^i \in {\varLambda }^i_h\) and \(u^i_h \in V^i_h\) we have
Moreover, is not difficult to verify that \(\Vert u^i_h \Vert _{1,{\varOmega }^i_{\varDelta }} \simeq \Vert u^i_h \circ \psi \Vert _{1,{\varOmega }^i}\). Letting \(\pi _h^0: L^2({{\mathcal {B}}}) \rightarrow {\widetilde{V}}_h^i |_{{\mathcal {B}}}= {\varLambda }^i_h\) denote the \(L^2\) projection operator, we can write
The thesis follows thanks to (52). \(\square \)
Proposition 4
The bilinear forms \(a_h\) and \(\langle \cdot , \cdot \rangle _{h}\) satisfy both Assumptions A.4 and A.5.
Proof
It is not difficult to prove that (42) holds. In fact, setting \(\omega _h= ({\varOmega }^i\cup {\varOmega }^i_{\varDelta }) {\setminus } ({\varOmega }^i\cap {\varOmega }^i_{\varDelta })\), it is easy to see that
Recalling that the area of \(\omega _h\) is of the order of \(h^2\) (see [25]), (42) follows easily. Let us now prove (43). For \(\mu \in L^2({{\mathcal {B}}})\) and \(v \in W^{1,\infty }({\varOmega }^i\cup {\varOmega }^i_{\varDelta })\) we have
Now, we can write, for \({{\mathbf {x}}}\in {{\mathcal {B}}}\) and \(\varvec{\xi }\) a point of the segment \([{{\mathbf {x}}},{{\widetilde{{{\mathbf {x}}}}}}]\)
whence we easily obtain
Then, (43) immediately follows. As already observed, the validity of Assumptions A.5 and A.6 together with A.2 finally entails the validity of A.4. \(\square \)
The spaces \(V^i_h\), \({\varLambda }^i_h\), \(V^e_h\), \({\varLambda }^e_h\) and the bilinear forms \(a_h\) and \(\langle \cdot ,\cdot \rangle _h\) satisfy then Assumptions A.1–7, and then we obtain an error bound both in the energy norms (as given by Theorem 3), and in the \(L^2({\varOmega }^i)\) norm, as given by (51).
4 Numerical Results
In this section we present some numerical examples to illustrate the application of the proposed method to some test problems. For a comparison with existing results, some of these are taken from [7, 26].
In the results we will show, we will compare our approach, in which the NRBC is imposed weakly, with that in which the NRBC is imposed strongly (see [25] for details on the corresponding formulation). These approaches, and whatever refers to them, will be labeled by the letters W and S, respectively.
We will test the accuracy of the approximate solutions \(u_h^{i,W}\) and \(u_h^{i,S}\) obtained by the two approaches in the interior finite computational domain \({\varOmega }^i_{\varDelta }\). To this aim, we will compute the relative \(H^1\) and \(L^2\) errors defined by
for \(*=\{W,S\}\). We will also compare the efficiency of the two approaches in terms of CPU and memory storage required by the discretization of the NRBC. With respect to this, we recall that the memory required to store the matrices \(\mathbf{V}\) and \(\mathbf{K}\) involved in the discretization of the NRBC is \(O((M^e)^2)\) and \(O((M^i)^2)\) in the approaches W and S, respectively. In the latter case \(M^i\) denotes the number of boundary points of \({{\mathcal {B}}}\) inherited by the triangulation of the interior domain \({\varOmega }^i\). In particular, we will report the quantities
that correspond to the memory and time saving to construct all the entries of the matrices \(\mathbf{V}\) and \(\mathbf{K}\) for the new approach with respect to the standard one.
Remark 4
When the boundary \({{\mathcal {B}}}\) is a circle and the mesh points chosen on it for the approximation of the NRBC in the approach W are equidistant, the matrices \(\mathbf{V}\) and \(\mathbf{K}\) have the particular Toeplitz structure. This means that only the first row of each matrix needs to be computed and stored, a property that allows to save significantly the CPU time and the memory storage requirement. We remark that the Toeplitz structure can not be obtained when the strong imposition of the NRBC is considered since the mesh grid inherited on \({{\mathcal {B}}}\) by the triangularization of \({\varOmega }^i\) is, in general, non uniform.
Example 1
In this first test, we perform a numerical study to investigate the accuracy of the solution \(u_h^{i,W}\) with respect to the choice of the discretization parameter \(h_e\). In particular, we aim at determining which choice of \(h_e\) guarantees that, for a fixed triangulation of the finite computational domain (hence for a fixed \(h_i\)) the new proposed method allows to compute the solution \(u_h^{i,W}\) with the same accuracy of the solution \(u_h^{i,S}\) in terms of the \(H^1\) and \(L^2\) errors.
To this aim, we consider Problem (1) where \({\mathcal {O}}^e\) is the unbounded region of \({\mathbb {R}}^2\), exterior to the unit disk, centered at the origin of the cartesian axis. We choose the artificial boundary
circumference centered at the origin and having radius \(R = 2\). The finite computational domain \({\varOmega }^i\) is bounded internally by \({\varGamma }\), the circumference of radius 1, and externally by \({{\mathcal {B}}}\). We denote by \(u({{\mathbf {x}}}) = u(x, y) = \frac{x}{x^2+y^2}\) the solution of (1), with \(g = u_{|{\varGamma }}\) and \(f=0\). We denote by \(n_T\) the number of triangles of the decomposition of \({\varOmega }^i\). We choose the parameter \(h_e\) by decomposing the boundary B into \(M^e\) sub-arcs of equal length, which corresponds to a uniform decomposition of the parametrization interval \([0,2\pi )\) into \(M^e\) subintervals. In Figs. 1 and 2 we show the behavior, in logarithmic scale, of the errors \({\text {Err}}_{H^1}^{i,*}\) and \({\text {Err}}_{L^2}^{i,*}\) for \(*=\{W,S\}\), with respect to decreasing values of \(h_e\), for the choices \(n_T = 3106\) and \(n_T = 12{,}874\), respectively, and we report the corresponding values in the associated tables. In the last two columns of the tables we report the CPU and memory saving. As we can see, the same order of accuracy for the \(H^1\) error is achieved when the parameter \(h_e\) is about ten times greater than \(h_i\), while for the \(L^2\) error when it is approximately four times greater than \(h_i\). We highlight the very high memory and CPU saving, which is due, in this case, to the particular choice of the artificial boundary and of its refinement (see Remark 4).
Example 1. Behavior of the \(H^1\) and \(L^2\) errors with respect to the artificial boundary refinement parameter \(h_e\). \(R=2\), \(n_T = 3106\)
Example 1. Behavior of the \(H^1\) and \(L^2\) errors with respect to the artificial boundary refinement parameter \(h_e\). \(R=2\), \(n_T = 12{,}874\)
In Tables 1, 2, 3 and 4 we report the study of the \(H^1\) and \(L^2\) errors behavior with respect to the refinement of the triangular mesh, and the associated expected orders of convergence (EOC), for the choices \(R=2\) and \(R=4\), respectively. Starting from an initial triangular mesh, the mesh refinement is obtained by halving the mesh size \(h_i\) (which implies that the number of triangles \(n_T\) is approximately multiplied by a factor 4 at each refinement). We point out that, based on the previous test, \(h_e\) has been chosen in such a way that the accuracy of the solution is preserved. In the last two columns of Tables 2 and 4 we report the percentage of the CPU and of the memory saving of the new approach with respect to the standard one.
From the results we have obtained, it is evident that the use of the weak FEM–BEM coupling strategy allows to reduce significantly the computational cost of the NRBC with respect to the approach where the strong coupling is considered, while preserving the accuracy of the approximate solution as well as the expected order of convergence, independently of the location of the artificial boundary \({{\mathcal {B}}}\).
Example 2
We consider here the example proposed in [26], for which \({\mathcal {O}}^e\) is the exterior of the unit disk, centered at the origin of the cartesian axis, \(f=0\) and g on \({\varGamma }\) is defined as
The artificial boundary
is the circumference of radius R centered at the origin. In Fig. 3 we show the behavior of the approximate solution \(u_h^{i,W}\) obtained by applying the new proposed approach in the bounded region \({\varOmega }^i\) delimited by the boundary \({\varGamma }\) and by \({{\mathcal {B}}}\) for the choices \(R =2\), \(R=4\), \(R=8\) and \(R=50\).
It is known that (see [26]) the asymptotic behavior of the solution u for \(|{{\mathbf {x}}}|\rightarrow \infty \) is \(\alpha =3/16\approx 1.87\mathrm{E}{-}01\). As remarked in the presentation of our method, and differently from the numerical approach proposed in [26], the value of the constant \(\alpha \) is determined by the interior FEM. In Fig. 4 we show the behavior of \(u_h^{i,S}(x,0)\) and \(u_h^{i,W}(x,0)\) for the values of \(x\in [-50,-1]\) (left plot) and for \(x\in [1,50]\) (right plot), obtained by choosing \(R=50\). In this case, the approximate solutions \(u_h^{i,S}\) and \(u_h^{i,W}\) have been obtained by decomposing the interior domain into \(n_T = 27{,}168\) triangles and by choosing \(M^e = 32\) for the approach W, which is definitely much smaller than the value \(M^i = 320\) inherited by the FEM triangulation of the domain \({\varOmega }^i\). Nevertheless, the two solutions perfectly match and tend to the asymptotic value \(\alpha \) which is represented by the dashed line. Moreover, the new approach allows to retrieve the solution with a \({\text {CPU}}\) saving of about \(98\%\) and with a memory saving \({\text {mem}} \approx 99\%\).
Example 2. Behavior of the solution \(u_h^{i,W}\) in \({\varOmega }^i\) for the choices \(R=2\) (top-left plot), \(R=4\) (top-right plot), \(R=8\) (bottom-left plot) and \(R=50\) (bottom-right plot)
Example 2. Behavior of the solutions \(u_h^{i,S}(x,0)\) and \(u_h^{i,W}(x,0)\) for \(x\in [-50,-1]\) (left plot) and for \(x\in [1,50]\) (right plot)
Example 3
For some geometries of the physical domain boundary \({\varGamma }\), or of the domain of interest \({\varOmega }^i\), the choice of a circular artificial boundary \({{\mathcal {B}}}\) can be wasteful both from the computational and space memory point of view. To show the feasibility in the choice of the geometry of the artificial boundary, we apply the proposed scheme to the problem presented in [26] where \({\mathcal {O}}^e\) is the unbounded region having the elliptic boundary \({\varGamma } = \{(x,y) \in {\mathbb {R}}^2: x^2/R^2 + y^2 = 1\}\) and the Dirichlet datum on \({\varGamma }\) is \(g(x,y) = x/R\). A natural choice for \({{\mathcal {B}}}\) in this case can be, for example, the ellipse
with \(R_1\) and \(R_2\) properly chosen. It has been shown in [26] that the expression of the solution to this problem along the positive real axis is
We consider the domain \({\varOmega }^i\) obtained by choosing the parameters \(R = 2\), \(R_1=4\) and \(R_2=2\) and two refinements of it: the first, labelled by \({\text {ref}}_1\), is obtained by a decomposition into \(n_T = 4010\) triangles, which induces \(M^i=158\) points on the artificial boundary \({{\mathcal {B}}}\); the second one, labelled by \({\text {ref}}_2\), obtained with \(n_T = 16{,}210\) and \(M^i = 312\). In Fig. 5, top-left and top-right plots, we show the behavior of the solution \(u_h^{i,W}\) in \({\varOmega }^i\). In the bottom-right plot, we compare \(u_h^{i,W}\) with the exact solution (58) for \(x\in [R,R_1]\) for the two choices of the refinements and we show, in the bottom-right plot, the corresponding absolute errors. In both cases, the weak NRBC has been computed by choosing \(M^e=40\). For the chosen discretization parameters, despite the fact that the matrices \(\mathbf{V}\) and \(\mathbf{K}\) do not have the special Toeplitz structure, because of the choice of the artificial boundary \({{\mathcal {B}}}\), the CPU and memory saving are \({\text {CPU}} \approx 91\%\) and \({\text {mem}}\approx 94\%\) for \({\text {ref}}_1\) and \({\text {CPU}}\approx 97\%\) and \({\text {mem}} \approx 98\%\) for \({\text {ref}}_2\). We remark that the maximum absolute error computed in the interval \([R,R_1]\) is approximately \(3.0\mathrm{E}{-}03\) for \({\text {ref}}_1\), and it does not improve for larger values of \(M^e\). For the refinement \({\text {ref}}_2\), by maintaining \(M^e=40\), the maximum error decreases to \(6.8\mathrm{E}{-}04\).
Example 3. The approximate solution \(u_h^{i,W}\) in \({\varOmega }^i\): 2D view (top-left plot) and 3D view (top-right plot). Comparison with the exact solution (bottom-left plot) and absolute error (bottom-right plot)
Example 4. The finite computational domain \({\varOmega }^i_{\varDelta }\) (top-left plot) for the choice \({{\mathcal {B}}}_1\). The 2D (top-right plot) and 3D (bottom plot) view of the solution \(u_h^{i,W}\)
Example 4
We consider here an example of multiple obstacles. Let \({\mathcal {O}}^e\) be the region exterior to five circles of radius 1 centred at \(C_1=(0,0)\), \(C_2=(-6,0)\), \(C_3=(6,0)\), \(C_4=(0,-6)\), \(C_5=(0,6)\). Aiming at determining the solution in a region close to the obstacles, we surround the circles by the curve
which determines the non convex finite computational domain \({\varOmega }^i\), represented in Fig. 6 (top-left plot) with a triangular decomposition. We prescribe the datum \(g(x,y) = x^4\) on the boundary \({\varGamma }\), which is the union of the boundary of the five circles. In Fig. 6, top-right and bottom plots, we show the 2D and 3D view of the solution \(u_h^{i,W}\) obtained by decomposing \({\varOmega }^i\) into \(n_T = 11{,}498\) triangles and by choosing \(M^e = 256\). Being the number of nodes inherited by the triangularization \(M^i = 535\), it results that the memory saving is \({\text {mem}} \approx 77\%\). In order to estimate the asymptotic value \(\alpha \) of the solution for \(|{{\mathbf {x}}}|\rightarrow \infty \), we enlarge the finite computational domain by choosing
In the top-left and top-right plots of Fig. 7 we show the 2D and 3D view of the solution \(u_h^{i,W}\), obtained by decomposing the resulting computational domain into \(n_T = 570{,}681\) triangles (\(M^i = 3075\)) and by choosing \(M^e = 512\). In the bottom plot we show the behaviour of the solution \(u_h^{i,W}(x,0)\) for \(x\in [7,360]\) (solid line) and of \(u_h^{i,W}(0,y)\) for \(y\in [7,360]\) (dashed line). The computed values \(u_h^{i,W}(360,0)\approx 775\) and \(u_h^{i,W}(0,360)\approx 774.5\) provide an approximation of the limit value \(\alpha \).
Example 4. The 2D (top-left plot) and 3D (top-right plot) view of the solution \(u_h^{i,W}\) for the choice \({{\mathcal {B}}}_2\). The asymptotic behavior of \(u_h^{i,W}\) (bottom plot)
Example 5
In this example we apply our method to a Poisson problem proposed in [7] with non null source f. We consider Eq. (1) with \(g=0\) on the elliptic boundary \({\varGamma } = \{(x,y) \in {\mathbb {R}}^2: b^2x^2 + a^2y^2 = a^2 b^2\}\), with \(a=1.5\) and \(b=1\). The source term \(f = f_1\) is chosen such that the exact solution is
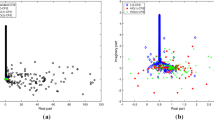
In Fig. 8, we show the graphic comparison between the exact solution (top-left plot) and the approximate one \(u_h^{i,W}\) (top-right plot) in the computational domain \({\varOmega }^i\) bounded externally by \({{\mathcal {B}}}\) circle of radius \(R=20\). The approximate solution has been obtained by decomposing \({\varOmega }^i\) into \(n_T = 276{,}480\) triangles (\(M^i = 1032\)) and choosing \(M^e = 32\). In the bottom plot we show the point-wise distribution of the absolute error in \([-5,5]^2\) (see [7] for a comparison). We remark that the source \(f_1\) does not have a local support, and thus contradicts one of our assumption. Indeed \(f_1\) assumes approximately values of the order \(1.0\mathrm{E}{-}05\) at the points belonging to the artificial boundary \({{\mathcal {B}}}\). This justifies the good agreement of the approximate solution with the exact one around the obstacle and the behavior of the error, that increases as the point moves away from \({\varGamma }\).
By modifying the source term, that is choosing \(f = f_2\) such that the exact solution is
it results that f decays exponentially fast to zero for \(|{{\mathbf {x}}}| \rightarrow \infty \), in such a way that from the computational point of view it can be regarded as supported in a disk of radius R (indeed \(f_2\) assumes approximately values of the order \(1.0\mathrm{E}{-}19\) at the points belonging to the artificial boundary \({{\mathcal {B}}}\)). With this choice, the approximate and the exact solution perfectly match in the whole domain \({\varOmega }^i\) and the pointwise error is bigger around the obstacle (see Fig. 9).
Example 5. Exact solution (top-left plot) and approximate solution \(u_h^{i,W}\) (top-right plot) in the domain \({\varOmega }^i\). Pointwise absolute error in \([-5,5]^2\) (bottom plot). \(f=f_1\)
Example 5. Exact solution (top-left plot) and approximate solution \(u_h^{i,W}\) (top-right plot) in the domain \({\varOmega }^i\). Pointwise absolute error in \([-5,5]^2\) (bottom plot). \(f=f_2\)
5 Conclusions
We proposed a weak FEM–BEM coupling method for the solution of elliptic problems on unbounded exterior domains, allowing to use two non-matching grids for the discretization of the non reflecting integral boundary condition and for the interior finite element solver. This allows to use a much coarser grid for the former, as compared to the grid induced on the artificial boundary by the finite element mesh, with a consequent reduction of the computational cost related to the numerical evaluation of the integral operators and with substantial saving in memory occupation. A theoretical analysis in an abstract framework is provided demonstrating the optimality of the method, under assumption that can, in principle, accommodate a variety of discretization spaces for both the boundary integral equation and the interior PDE. Numerical tests, confirming the validity of the theoretical estimates, are presented for a linear finite element discretization.
In allowing the discretization for the boundary integral operators to be chosen independently of the one for the interior PDE—only a mild compatibility condition between the two is required by the analysis—the proposed approach allows for a large flexibility in the choice of the approximation spaces, which in principle, do not need to be of finite element type. This can be exploited for designing efficient methods for the solution not only of elliptic problems but for a much wider class, including, for instance, wave propagation problems. This approach allows for instance the use of a wavelet discretization for the boundary integral operators, which we expect to yield a sparsification of the matrices relative to the integral operators, with a consequent further reduction of the storage requirement and computational cost of the overall procedure. In this case, special coupling strategies of the two methods will be required (see for instance [5, 10]).
References
Abboud, T., Joly, P., Rodríguez, J., Terrasse, I.: Coupling discontinuous Galerkin methods and retarded potentials for transient wave propagation on unbounded domains. J. Comput. Phys. 230(15), 5877–5907 (2011)
Babuška, I., Aziz, A.K.: Survey lectures on the mathematical foundation of the finite element method. In: Aziz, A.K. (ed.) The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations, pp. 5–359. Academic Press, New York (1972)
Bernardi, C., Maday, Y., Patera, A.T.: A new nonconforming approach to domain decomposition: the mortar element method. In: Brezis, H., Lions, J.-L. (eds.) Nonlinear Partial Differential Equations and Their Applications. Research Notes in Mathematics Series, Collège de France Seminar, vol. XI, pp. 13–51. Longman Sci. Tech, Harlow (1994)
Bertoluzza, S.: Wavelet stabilization of the Lagrange multiplier method. Numer. Math. 86, 1–28 (2000)
Bertoluzza, S., Falletta, S., Perrier, V.: Wavelet/FEM coupling by the mortar method. In: Pavarino, L.F., Toselli, A. (eds.) Recent Developments in Domain Decomposition Methods. Lecture Notes in Computational Science and Engineering, vol. 23, pp. 119–132. Springer, Berlin (2002)
Boulmezaoud, T.Z.: Inverted finite elements: a new method for solving elliptic problems in unbounded domains. M2AN Math. Model. Numer. Anal. 39(1), 109–145 (2005)
Bhowmik, S.K., Belbaki, R., Boulmezaoud, T.Z., Mziou, S.: Solving two dimensional second order elliptic equations in exterior domains using the inverted finite elements method. Comput. Math. Appl. 72(9), 2315–2333 (2016)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. Springer Series in Computational Mathematics. Springer, Berlin (1991)
Demkowicz, L., Ihlenburg, F.: Analysis of a coupled finite-infinite element method for exterior Helmholtz problems. Numer. Math. 88(1), 43–73 (2001)
Falletta, S.: The approximate integration in the mortar method constraint. In: Kornhuber, R., Hoppe, R.W., Périaux, J., Pironneau, O., Widlund, O., Xu, J. (eds.) Domain Decomposition Methods in Science and Engineering. Lecture Notes in Computational Science and Engineering, vol. 55, pp. 555–563. Springer, Berlin (2007)
Falletta, S.: BEM coupling with the FEM fictitious domain approach for the solution of the exterior Poisson problem and of wave scattering by rotating rigid bodies. IMA J. Numer. Anal. 38(2), 779–809 (2018)
Falletta, S., Monegato, G.: An exact non reflecting boundary condition for 2D time-dependent wave equation problems. Wave Motion 51(1), 168–192 (2014)
Falletta, S., Monegato, G.: Exact nonreflecting boundary conditions for exterior wave equation problems. Publ. Inst. Math. 96, 103–123 (2014)
Falletta, S., Monegato, G.: Exact non-reflecting boundary condition for 3D time-dependent multiple scattering-multiple sources problems. Wave Motion 58, 281–302 (2015)
Falletta, S., Monegato, G., Scuderi, L.: A space-time BIE method for nonhomogeneous exterior wave equation problems. The Dirichlet case. IMA J. Numer. Anal. 32(1), 202–226 (2012)
Falletta, S., Monegato, G., Scuderi, L.: A space-time BIE method for wave equation problems: the (two-dimensional) Neumann case. IMA J. Numer. Anal. 34(1), 390–434 (2014)
Fischer, M., Gaul, L.: Fast BEM–FEM mortar coupling for acoustic-structure interaction. Int. J. Numer. Methods Eng. 62, 1677–1690 (2005)
Gerdes, K., Demkowicz, L.: Solution of 3D-Laplace and Helmholtz equations in exterior domains using hp-infinite elements. Comput. Methods Appl. Mech. Eng. 137(3–4), 239–273 (1996)
Givoli, D.: Numerical Methods for Problems in Infinite Domains. Elsevier, Amsterdam (1992)
Givoli, D.: Recent advances in the DtN FE method. Arch. Comput. Methods Eng. 6, 71–116 (1999)
Givoli, D.: High-order local non-reflecting boundary conditions: a review. Wave Motion 39, 319–326 (2004)
Glowinski, R., Pan, T.W., Périaux, J.: FEM and BEM coupling in elastostatics using localized Lagrange multipliers. Int. J. Numer. Methods Eng. 69, 2058–2074 (2007)
Grote, M.J., Kirsch, C.: Nonreflecting boundary condition for time-dependent multiple scattering. J. Comput. Phys. 221, 41–62 (2007)
Grote, M.J., Sim, I.: Local nonreflecting boundary condition for time-dependent multiple scattering. J. Comput. Phys. 230, 3135–3154 (2011)
Johnson, C., Nédélec, J.C.: On the coupling of boundary integral and finite element methods. Math. Comput. 35(152), 1063–1079 (1980)
Le Roux, M.N.: Méthode d’éléments finis pour la résolution numérique de problémes extérieurs en dimension 2. R.A.I.R.O. Anal. Numer. 11, 27–60 (1977)
Rüberg, T., Schanz, M.: Non-conforming coupled time-domain boundary element analysis. In: C.A. Mota Soares et al. (ed.) III European Conference on Computational Mechanics Solids. Structures and Coupled Problems in Engineering, pp. 1–10 (2006)
Rüberg, T., Schanz, M.: Coupling finite and boundary element methods for static and dynamic elastic problems with non-conforming interfaces. Comput. Methods Appl. Mech. Eng. 198(3–4), 449–458 (2008)
Song, J., Kai-Tai, L.: The coupling of finite element method and boundary element method for two-dimensional Helmholtz equation in an exterior domain. J. Comput. Math. 5, 21–37 (1987)
Taflove, A., Hagness, S.C.: Computational Electrodynamics: The Finite-Difference Time-Domain Method. Hartech House, Boston (2005)
Yang, J., Yu, D.: Domain decomposition with nonmatching grids for exterior transmission problems via FEM and DTN mapping. J. Comput. Math. 24(3), 323–342 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the GNCS-INDAM 2016 research program: Accoppiamento FEM–BEM non conforme mediante tecniche di decomposizione di dominio di tipo mortar.
Rights and permissions
About this article
Cite this article
Bertoluzza, S., Falletta, S. FEM Solution of Exterior Elliptic Problems with Weakly Enforced Integral Non Reflecting Boundary Conditions. J Sci Comput 81, 1019–1049 (2019). https://doi.org/10.1007/s10915-019-01048-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-01048-4
Keywords
- Boundary element method
- Finite element method
- Non reflecting boundary conditions
- Non matching grids
- Numerical methods