Abstract
In this paper we propose and analyze a stochastic collocation method for solving the second order wave equation with a random wave speed and subjected to deterministic boundary and initial conditions. The speed is piecewise smooth in the physical space and depends on a finite number of random variables. The numerical scheme consists of a finite difference or finite element method in the physical space and a collocation in the zeros of suitable tensor product orthogonal polynomials (Gauss points) in the probability space. This approach leads to the solution of uncoupled deterministic problems as in the Monte Carlo method. We consider both full and sparse tensor product spaces of orthogonal polynomials. We provide a rigorous convergence analysis and demonstrate different types of convergence of the probability error with respect to the number of collocation points for full and sparse tensor product spaces and under some regularity assumptions on the data. In particular, we show that, unlike in elliptic and parabolic problems, the solution to hyperbolic problems is not in general analytic with respect to the random variables. Therefore, the rate of convergence may only be algebraic. An exponential/fast rate of convergence is still possible for some quantities of interest and for the wave solution with particular types of data. We present numerical examples, which confirm the analysis and show that the collocation method is a valid alternative to the more traditional Monte Carlo method for this class of problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Partial differential equations (PDEs) are important mathematical models for multidimensional physical systems. There is an increasing interest in including uncertainty in these models and quantifying its effects on the predicted solution or other quantities of physical interest. The uncertainty may be due to an intrinsic variability of the physical system. It may also reflect our ignorance or inability to accurately characterize all input data of the mathematical model. Examples include the variability of soil permeability in subsurface aquifers and heterogeneity of materials with microstructure.
Probability theory offers a natural framework to describe uncertainty by parametrizing the input data either in terms of a finite number of random variables or more generally by random fields. Random fields can in turn be accurately approximated by a finite number of random variables when the input data vary slowly in space, with a correlation length comparable to the size of the physical domain. A possible way to describe such random fields is to use the truncated Karhunen-Loéve [27, 28] or polynomial chaos expansion [42, 45].
There are different techniques for solving PDEs in probabilistic setting. The most popular one is the Monte Carlo sampling, see for instance [12]. It consists in generating independent realizations drawn from the input distribution and then computing sample statistics of the corresponding output values. This allows one to reuse available deterministic solvers. While being very flexible and easy to implement, this technique features a very slow convergence rate.
In the last few years, other approaches have been proposed, which in certain situations feature a much faster convergence rate. They exploit the possible regularity that the solution might have with respect to the input parameters, which opens up the possibility to use deterministic approximations of the response function (i.e. the solution of the problem as a function of the input parameters) based on global polynomials. Such approximations are expected to yield a very fast convergence. Stochastic Galerkin [4, 13, 29, 38, 44] and Stochastic Collocation [2, 31, 32, 43] are among these techniques.
Such new techniques have been successfully applied to stochastic elliptic and parabolic PDEs. In particular, we have shown in previous works [2, 30] that, under particular assumptions, the solution of these problems is analytic with respect to the input random variables. The convergence results are then derived from the regularity results. For stochastic hyperbolic problems, the analysis is not well developed. In the case of linear problems, there are a few works on the one-dimensional scalar advection equation with a time- and space-independent random wave speed [14, 37, 41]. Such problems also possess high regularity properties provided the data live in suitable spaces. The main difficulty arises when the coefficients vary in space or time. In this more general case, the solution of linear hyperbolic problems may have lower regularity than those of elliptic, parabolic and hyperbolic problems with constant random coefficients. There are also recent works on stochastic nonlinear conservation laws, see for instance [25, 26, 34, 39, 40].
In this paper, we consider the linear second order scalar wave equation with a piecewise smooth random wave speed. In many applications, such as seismology, acoustics, electromagnetism and general relativity, the underlying differential equations are systems of second order hyperbolic PDEs. In deterministic problems, these systems are often rewritten as first order systems and then discretized. This approach has the disadvantage of introducing auxiliary variables with their associated constraints and boundary conditions. This in turn reduces computational efficiency and accuracy [20, 21]. Here, we analyze the problem in the second order differential form, without reducing it to the first order form, and propose a numerical method that directly discretizes the second order PDE. The analysis of the first order and other types of second order hyperbolic systems with discontinuous random coefficients will be addressed elsewhere.
We propose a stochastic collocation method for solving the wave propagation problem in a medium consisting of non-overlapping sub-domains. In each sud-domain, the wave speed is smooth and is given in terms of one random variable. We assume that the interfaces of speed discontinuity are smooth. We derive a priori error estimates with respect to the number of collocation points. The main result is that unlike in elliptic and parabolic problems, the solution to hyperbolic problems is not in general analytic with respect to the random variables. Therefore, the convergence rate of error in the wave solution may only be algebraic. A fast spectral convergence is still possible for some linear quantities of interest with smooth mollifiers and for the wave solution with smooth data compactly supported within sub-domains. We also show that the semi-discrete solution is analytic with respect to the random variables with the radius of analyticity proportional to the mesh size \(h\). We therefore obtain an exponential rate of convergence which deteriorates as the quantity \(h \, p\) gets smaller, with \(p\) representing the polynomial degree in the stochastic space.
The outline of the paper is as follows: in Sect. 2 we formulate the mathematical problem, prove its well-posedness, and provide regularity results on the solution and a quantity of interest. The collocation method for solving the underlying stochastic PDE is described in Sect. 3. In Sect. 4 we give a complete error analysis for the collocation method and obtain convergence results. In Sect. 5 we perform some numerical examples to illustrate the accuracy and efficiency of the method. Finally, we present our conclusions in Sect. 6.
2 Mathematical setting
We consider the linear second order scalar wave equation with a discontinuous random wave speed and deterministic boundary and initial conditions. We study the well-posedness of the problem and regularity of the solution and a quantity of interest with respect to the input random parameters.
2.1 Problem statement
Let \(D\) be a convex bounded polygonal domain in \(\mathbb R ^d\) and \((\varOmega ,\mathcal F ,P)\) be a complete probability space. Here, \(\varOmega \) is the set of outcomes, \(\mathcal F \subset 2^{\varOmega }\) is the \(\sigma \)-algebra of events and \(P:\mathcal F \rightarrow [0,1]\) is a probability measure. Consider the stochastic initial boundary value problem (IBVP): find a random function \(u:[0,T] \times \bar{D} \times \varOmega \rightarrow \mathbb R \), such that \(P\)-almost everywhere in \(\Omega \), i.e. almost surely (a.s.), the following holds
where the data
are compatible. We assume that the random wave speed \(a\) is bounded and uniformly coercive,
In many wave propagation problems, the source of randomness can be described or approximated by using only a small number of uncorrelated random variables. For example, in seismic applications, a typical situation is the case of layered materials where the wave speeds in the layers are not perfectly known and therefore are described by uncorrelated random variables. The number of random variables corresponds therefore to the number of layers. In this case the randomness is described by a finite number of random variables. Another example is the approximation of the random speed by a truncated Karhunen-Loéve expansion [3]. In this case the number of random variables is the number of terms in the expansion. In this case the randomness is approximated by a finite number of random variables. This motivates us to make the following finite dimensional noise assumption on the form of the wave speed,
where \(N \in \mathbb{N }_+\) and \(Y=[Y_1,\ldots ,Y_N] \in \mathbb R ^N\) is a random vector. We denote by \(\varGamma _n \equiv Y_n(\varOmega )\) the image of \(Y_n\) and assume that \(Y_n\) is bounded. We let \(\varGamma = \prod _{n=1}^N \varGamma _n\) and assume further that the random vector \(Y\) has a bounded joint probability density function \(\rho : \varGamma \rightarrow \mathbb R _+\) with \(\rho \in L^{\infty }(\varGamma )\). We note that by using a similar approach to [2, 9] we can also treat unbounded random variables, such as Gaussian and exponential variables. Unbounded wave speeds could theoretically arise in the case of rigid materials. In this paper we consider only bounded random variables.
In this paper, in particular, we consider a heterogeneous medium consisting of \(N\) sub-domains. In each sub-domain, the wave speed is smooth and represented by one random variable. The boundaries of sub-domains, which are interfaces of speed discontinuity, are assumed to be smooth and do not overlap.
The random speed \(a\) can for instance be given by
where \(\mathcal X _n\) are indicator functions describing the geometry of each sub-domain, \(Y_n\) are independent and identically distributed random variables, and \(\alpha _n\) are smooth functions defined on each sub-domain. Note that the representation of the coefficient \(a\) in (5) is exact, and there is no truncation error as in the Karhunen-Loéve expansion. The more general case where the wave speed in each sub-domain \(a_n(\mathbf{x },\omega )\) is represented by a Karhunen-Loéve expansion can be treated in the same way. In this case the total number of random variables is \(\sum _{n=1}^N M_n\), where \(M_n\) is the number of terms in the truncated Karhunen-Loéve expansion in each sub-domain. The case where the geometry of sub-domains is also random will be addressed elsewhere. For elliptic equations, random boundaries have been studied, e.g., in [7, 15, 46].
The finite dimensional noise assumption implies that the solution of the stochastic IBVP (1) can be described by only \(N\) random variables, i.e., \(u(t,\mathbf{x},\omega ) = u(t,\mathbf{x},Y_1(\omega ),\ldots ,Y_N(\omega ))\). This turns the original stochastic problem into a deterministic IBVP for the wave equation with an \(N\)-dimensional parameter, which allows the use of standard finite difference and finite element methods to approximate the solution of the resulting deterministic problem \(u=u(t,\mathbf{x},Y)\), where \(t \in [0,T]\), \(\mathbf{x} \in D\), and \(Y \in \varGamma \). Note that the knowledge of \(u=u(t,\mathbf{x},Y)\) fully determines the law of the random field \(u=u(t,\mathbf{x},\omega )\). The ultimate goal is then the prediction of statistical moments of the solution \(u\) or statistics of some given quantities of physical interest.
Before studying the well-posedness and regularity in details, we start the discussion with two simple examples.
Example 1
A basic technique for studying the regularity of the solution of a PDE with respect to a parameter is based on analyzing the equation in the complex plane. In this approach, the parameter is first extended into the complex plane. Then, if the extended problem is well-posed and the first derivative of the resulting complex-valued solution with respect to the parameter satisfies the so called Cauchy–Riemann conditions, the solution can analytically be extended into the complex plane. This approach has been used in [30] to prove the analyticity of the solution of parabolic PDEs with stochastic parameters. As a first example, we therefore consider the Cauchy problem for the one-dimensional scalar wave equation with a complex-valued one-parameter wave speed
with a constant, complex-valued coefficient
Assume that \(g(x)\) is a smooth function that vanishes at infinity. We apply the Fourier transform with respect to \(x\) and get
where \({\hat{u}}(t,k) = \int _\mathbb{R } u(t,x) \, e^{-i \, k \, x} dx\) and \({\hat{g}}(k) = \int _\mathbb{R } g(x) \, e^{-i \, k \, x} dx\) are the Fourier transforms of \(u(t,x)\) and \(g(x)\) with respect to x, respectively. The solution of this linear, second order ordinary differential equation with parameter \(k\) is given by
When \(a_I = 0\), then \(r_{1,2} = \pm \, i \, a_R \, k\). Performing the inverse Fourier transform, we get the solution
and therefore the Cauchy problem is well-posed.
When \(a_I \ne 0\), then \({\text{ R}e}(r_1) = - {\text{ R}e}(r_2) = - a_I \, k \), and
Therefore, regardless of the sign of \({\text{ R}e}(a^2) = a_R^2 - a_I^2\), the Fourier transform of the solution \({\hat{u}}(t,k)\) grows exponentially fast, i.e., \(e^{|a_I| \, |k| \, t}\), unless the Fourier transform of the initial solution \({\hat{g}}(k)\) decays faster than \(e^{- |a_I| \, |k| \, t}\). The Cauchy problem is therefore well-posed only if \(g(x)\) is in a restricted class of Gevrey spaces [35].
Definition 1
A function \(g(x)\) is a Gevrey function of order \(q > 0\), i.e., \(g \in G^q(\mathbb{R })\), if \(g \in C^{\infty }(\mathbb{R })\) and for every compact subset \(D \subset \mathbb{R }\), there exists a positive constant \(C\) such that,
In particular, \(G^1(\mathbb{R })\) is the space of analytic functions [18]. For \(0< q< 1\), the class \(G^q(\mathbb{R })\) is a subclass of the analytic functions, while for \(1<q<\infty \) it contains the analytic functions.
We now state a known result on the decay of the Fourire transform of Gevrey functions [24, 35].
Lemma 1
A function \(g(x)\) belongs to the Gevrey space \(G^q(\mathbb{R })\) if and only if there exist positive constants \(C\) and \(\epsilon \) such that \(|{\hat{g}}(k)| \le C \, e^{- \epsilon \, |k|^{1/q}}\).
Therefore, for the Cauchy problem to be well-posed in the complex strip \(\Sigma _r = \{ (a_R + i \, a_I) \in \mathbb{C }: \, |a_I| \le r \}\), we need \(g \in G^q(\mathbb{R })\) with \(q < 1\). Note that for \(q=1\), the problem is well-posed only for a finite time interval when \(t \le \epsilon / r\). This shows that even if the initial solution \(g\) is analytic, i.e, \(g \in G^1(\mathbb{R })\), the solution is not analytic for all times in \(\Sigma _r\). Reversing the argument, we can say that, starting from an analytic initial solution \(g\), with \(|{\hat{g}}(k)| \le C \, e^{- \epsilon \, |k|}\), the solution at time \(t\) will be analytic only in the strip \(\Sigma _{\epsilon /t}\), and the analyticity region becomes smaller and smaller as time increases.
Example 2
An important characteristic of waves in a heterogeneous medium in which the wave speed is piecewise smooth, is scattering by discontinuity interfaces. As a simple scattering problem, we consider the Cauchy problem for the second order scalar wave equation in a one-dimensional domain consisting of two homogeneous half-spaces separated by an interface at \(x=0\),
with a piecewise constant wave speed
In this setting, the wave speed contains two positive parameters, \(a_-\) and \(a_+\). We choose the initial conditions such that the initial wave pulse is smooth, compactly supported, lies in the left half-space, and travels to the right. That is
By d’Alembert’s formula, the solution reads
Note that when \(x< - a_- \, t\), the solution is purely right-going, \(u=g(a_- \, t - x)\), and when \(x>a_+ \, t\), the solution is zero, \(u=0\).
The functions \(\varPhi _1\) and \(\varPhi _2\) are obtained by the interface jump conditions at \(x=0\),
After some manipulation, we get the solution
The interpretation of this solution is that the initial pulse \(g(-x)\) inside the left half-space moves to the right with speed \(a_-\) until it reaches the interface. At the interface it is partially reflected (\(\varPhi _1\)) with speed \(a_-\) and partially transmitted (\(\varPhi _2\)) with speed \(a_+\). The interface between two layers generates no reflections if the speeds are equal, \(a_- = a_+\). From the closed form of the solution (7), we note that the solution \(u(t,x)\) is infinitely differentiable with respect to both parameters \(a_-\) and \(a_+\) in \((0, + \infty )\). Note that the smooth initial solution \(u(0,x)\), which is contained in one layer with zero value at the interface, automatically satisfies the interface conditions (6) at time zero. Otherwise, if for instance the initial solution crosses the interface without satisfying (6), a singularity is introduced in the solution, and the high regularity result does no longer hold.
In the more general case of multi-dimensional heterogeneous media consisting of sub-domains, the interface jump conditions on a smooth interface \(\Upsilon \) between two sub-domains \(D_{I}\) and \(D_{II}\) are given by
Here, the subscript \(n\) represents the normal derivative, and \([v(.)]_{\Upsilon }\) is the jump in the function \(v\) across the interface \(\Upsilon \). In this general case, the high regularity with respect to parameters holds provided the smooth initial solution satisfies (8). The jump conditions are satisfied for instance when the initial data are contained within sub-domains. This result for Cauchy problems can easily be extended to IBVPs by splitting the problem to one pure Cauchy and two half-space problems. See Sect. 2.3.2 for more details.
Remark 1
Immediate results of the above two examples are the following:
-
1.
For the solution of the Cauchy problem for the one-dimensional wave equation to be analytic with respect to the random wave speed at all times in a given complex strip \(\Sigma _r\) with \(r>0\), the initial datum needs to live in a space strictly contained in the space of analytic functions, which is the Gevrey space \(G^q(\mathbb{R })\) with \(0<q < 1\). Moreover, if the problem is well-posed and the data are analytic, the solution may be analytic with respect to the parameter in \(\Sigma _r\) only for a short time interval. Problems in higher physical dimensions with constant random wave speeds can be studied similarly by the Fourier transform and the generalization of univariate Gevrey functions to the case of multivariate functions.
-
2.
In a one-dimensional heterogeneous medium with piecewise smooth wave speeds, if the data are smooth and the initial solution satisfies the interface jump conditions (8), the solution to the Cauchy problem is smooth with respect to the wave speeds. If the initial solution does not satisfy (8), the solution is not smooth with respect to the wave speeds. We refer to the proof of Theorem 3 where a more general one-dimensional problem, i.e. problem (14), with smooth data is considered. We also refer to Conjecture 1 for problems in two dimensions.
We note that the above high regularity results with respect to parameters are valid only for particular types of smooth data. In real applications, the data are not smooth. We therefore study the well-posedness and regularity properties in the more general case when the data satisfy the minimal assumptions (2).
2.2 Well-posedness
We now show that the problem (1) with the data satisfying (2) and the assumption (3) is well-posed. For a function of the random vector \(Y\), we introduce the space of square integrable functions:
with the inner product
We also introduce the mapping \(\mathbf{u} : [0,T] \rightarrow H_0^1(D) \otimes L_{\rho }^2(\varGamma )\), defined by
Similarly, we introduce the function \(\mathbf{f} : [0,T] \rightarrow L^2(D)\), defined by
Finally, for a real Hilbert space \(X\) with norm \(||.||_X\), we introduce the time-involving space
consisting of all measurable functions \(v\) with
Examples of \(X\) include the \(L^2(D)\) space and the Sobolev space \(H_0^1(D)\) and its dual space \(H^{-1}(D)\).
We now recall the notion of weak solutions for the IBVP (1).
Definition 2
The function \(\mathbf{u} \in H_{H_0^1(D)}\) with \({\mathbf{u}}^{\prime } \in H_{L^2(D)}\) and \(\mathbf{u}^{\prime \prime } \in H_{H^{-1}(D)}\) is a weak solution to the IBVP (1) provided the following hold:
-
(i)
\(\mathbf{u}(0)=g_1\) and \({\mathbf{u}}^{\prime } (0)= g_2\),
-
(ii)
for a.e. time \(0 \le t \le T\) and \(\forall v \in H_0^1(D) \otimes L_{\rho }^2(\varGamma )\):
$$\begin{aligned} \int _{D \times \varGamma } \mathbf{u}^{\prime \prime } (t) \, v \, \rho \, d\mathbf{x} \, dY + \int _{\varGamma } B(\mathbf{u}(t),v) \, \rho \, dY = \int _{D \times \varGamma } \mathbf{f}(t) \, v \, \rho \, d\mathbf{x} \, dY, \end{aligned}$$(9)where
$$\begin{aligned} B(v_1,v_2) (Y){=}\!\!\int _D a^2(\mathbf{x},Y) \, (\nabla v_1(\mathbf{x},Y){\cdot }\nabla v_2(\mathbf{x},Y)) \, d\mathbf{x}, \, \quad \forall v_1, v_2{\in }H_0^1(D) \otimes L_{\rho }^2(\varGamma ). \end{aligned}$$
Theorem 1
Under the assumptions (2) and (3), there is a unique weak solution \(\mathbf{u} \in H_{H_0^1(D)}\) to the IBVP (1). Moreover, it satisfies the energy estimate
Proof
The proof is an easy extension of the proof for deterministic problems, see e.g. [11]. \(\square \)
2.3 Regularity
In this section we study the regularity of the solution and of a quantity of interest with respect to the random input variable \(Y\). The main result is that under the minimal assumptions (2) and (3) the solution, which is in \(L_{\rho }^2(\varGamma )\), has in general only one bounded derivative with respect to \(Y\), while the considered quantity of interest may have many bounded derivatives. The available regularity is then used to estimate the convergence rate of the error for the stochastic collocation method.
2.3.1 Regularity of the solution
We first investigate the regularity of the solution with respect to the random variable \(Y\). For deterministic problems, for instance when \(Y\) is a fixed constant, it is well known that in the case of \(\mathbf{x}\)-discontinuous wave speed, with the data satisfying (2) and under the assumption (3), the solution of (1) is in general only \(\mathbf{u} \in C^0(0,T; H_0^1(D))\), see for instance [33, 36]. In other words, in the presence of discontinuous wave speed, one should not expect higher spatial regularity than \(H^1(D)\).
To investigate the \(Y\)-regularity of the solution in the stochastic space, we differentiate the IBVP (1) with respect to \(Y\) and obtain
with homogeneous initial and boundary conditions. The force term in the above IBVP is \(f_1 := \nabla \cdot \bigl ( 2 \, a \, a_Y \, \nabla u \bigr ) \in L^1(0,T;H^{-1}(D))\) for every \(Y \in \varGamma \). In fact if \(v \in L^1(0,T;H_0^1(D))\), then
We now state an important result which is a generalization of a result given by Hörmander [16].
Lemma 2
For arbitrary \(f \in L^1(0,T; H^k(D))\), \(g_1 \in H^{k+1}(D)\) and \(g_2 \in H^k(D)\), with \(k \in \mathbb R \), for every \(Y \in \varGamma \), there is a unique weak solution \(\mathbf{u} \in C^0(0,T;H^{k+1}(D)) \cap C^1(0,T; H^k(D))\) of the IBVP (1) with the \(\mathbf{x}\)-smooth wave speed (4) satisfying (3). Moreover, it satisfies the energy estimate
Proof
The proof is an easy extension of the proof of Lemma 23.2.1 and Theorem 23.2.2 in [16]. \(\square \)
We note that Lemma 2 holds for \(\mathbf{x}\)-smooth wave speeds. When the wave speed is non-smooth, it holds only for \(k=-1\) and \(k=0\) [36]. We apply Lemma 2 to (11) with \(k=-1\) (which is valid also for non-smooth coefficients) and obtain
Moreover, the solution (7) of Example 2 with \(g \in H_0^1(\mathbb R )\) shows that the second and higher \(Y\)-derivatives do not exist. Therefore, under the minimal assumptions (2), the solution has at most one bounded \(Y\)-derivative in \(L^2(D)\). We have proved the following result,
Theorem 2
For the solution of the second order wave propagation problem (1) with data given by (2) and a random piecewise smooth wave speed satisfying (3) and (5), we have \(\partial _Y u \in C^0(0,T;L^2(D))\) for every \(Y \in \varGamma \).
2.3.2 Regularity of quantities of interest
We now consider the quantity of interest
where \(u\) solves (1) and the mollifiers \(\phi \) and \(\psi \) are given functions of \(\mathbf{x}\). As a corollary of Theorem 2, we can write,
Corollary 1
With the assumptions of Theorem 2 and \(\phi \in L^1(D)\) and \(\psi \in L^1(D)\), we have \(\frac{d}{dY}\mathcal Q \in L^{\infty }(\varGamma )\).
We now assume that the mollifiers \(\phi (\mathbf{x}) \in C_0^{\infty }(D)\) and \(\psi (\mathbf{x}) \in C_0^{\infty }(D)\) are smooth functions and analytic in the interior of their supports. We further assume that their supports does not cross the speed discontinuity interfaces. We will show that the resulting quantity of interest (13) may have higher \(Y\)-regularity, without any higher regularity assumptions on the data than those in (2). For this purpose, we introduce the influence function (or dual solution) \(\varphi \) associated to the quantity of interest, \(\mathcal{Q }\), as the solution of the dual problem
Note that this is a well-posed backward wave equation with smooth initial data at the final time \(T\) and a smooth force term.
We can write
The last equality follows from the initial condition in (1) and in the dual problem (14). This shows that the regularity of the quantity of interest depends only on \(Y\)-regularity of the dual solution.
To investigate the \(Y\)-regularity of dual solution, we first note that the finite speed of wave propagation and the superposition principle due to the linearity of the dual problem (14) makes it possible to split the IBVP in \(\mathbb{R }^d\) into two half-space problems and a pure Cauchy problem [19]. To clarify this, consider a one-dimensional strip problem (\(d=1\)) for (14) on the physical domain \(D=[0,1]\) with \(N=2\) layers with widths \(d_1\) and \(d_2\). Let \(\vartheta _j \in C^{\infty }(D)\), \(j=1,2,3\), be monotone functions with
and \(\quad \vartheta _3(x) = 1- \vartheta _1(x) - \vartheta _2(x)\). Set \(\varphi = \varphi _1 + \varphi _2 + \varphi _3\), where each \(\varphi _j\) solves
The finite speed of propagation implies that there is a time \(0 < T_1 \le T\) where \(\varphi _1 = 0\) for \(x \in [d_1,1]\) and \(t \in [T-T_1,T]\). Therefore, we can consider \(\varphi _1\) as the solution of the right half-space problem
Note that here we redefine the wave speed \(a\) by extending the speed corresponding to the left layer to the whole half space \(0 \le x < \infty \). Similarly, \(\varphi _2\) and \(\varphi _3\) locally solve a left half-space and a pure Cauchy problem, respectively. These considerations are valid in the time interval \([T-T_1,T]\). At time \(t=T-T_1\), we obtain a new final dual solution and can restart.
The \(Y\)-regularity of the dual solution \(\varphi \) is therefore obtained by the regularity of \(\varphi _1, \varphi _2\) and \(\varphi _3\). The first two functions, \(\varphi _1\) and \(\varphi _2\), which solve two half-space problems with smooth data and coefficients, are smooth [11] and have bounded \(Y\)-derivatives of any order \(s \ge 1\). The third function \(\varphi _3\), which solves a single interface Cauchy problem with smooth data whose support does not cross the interface and with a piecewise smooth wave speed, has again bounded \(Y\)-derivatives of any order \(s \ge 1\). In one dimension (\(d=1\)), when the wave speed is piecewise constant, we can solve the Cauchy wave equation by d’Alembert’s formula and explicitly obtain the solution \(\varphi _3\) which is smooth with respect to the wave speed and therefore is \(Y\)-smooth, see Example 2 as a simple illustration. When the wave speed is variable, we can employ the energy method to show \(Y\)-regularity, see Theorem 7 in the Appendix. Note that the same result holds also for a multiple interface Cauchy problem. Therefore the dual solution \(\varphi \) and consequently the quantity of interest \(\mathcal{Q }\) have bounded \(Y\)-derivatives of any order \(s \ge 1\). We note that for \(0 \le t \le T-T_1\), although the new final dual solution \(\varphi (T-T_1,x,Y)\) may not be contained in one layer, but since it naturally satisfies the correct jump conditions at the interface, the \(Y\)-regularity of the dual solution holds in the time interval \([0,T]\). We have therefore proved the following result in a one-dimensional physical space,
Theorem 3
Let \(D \subset \mathbb{R }\). With the assumptions of Theorem 2 and if \(\phi \in C_0^{\infty }(D)\) and \(\psi \in C_0^{\infty }(D)\) and their supports do not cross the discontinuity interfaces, the quantity of interest (13) satisfies \(\frac{d^s}{d Y^s}\mathcal{Q } \in L^{\infty }(\varGamma )\) with any order \(s \ge 1\).
In a more general case of two-dimensional physical space (\(d=2\)), \(\varphi _1\) and \(\varphi _2\) are again smooth [11] and have bounded \(Y\)-derivatives of any order \(s \ge 1\). The proof of smoothness for \(\varphi _3\) is more complicated. However, noting that the discontinuity occurs in the normal direction to the interfaces, we can employ a localization argument and build a two-dimensional result by generalizing the one-dimensional ones. Based on this and numerical results, we therefore make the following conjecture,
Conjecture 1
Let \(D \subset \mathbb{R }^2\). With the assumptions of Theorem 2 and if \(\phi \in C_0^{\infty }(D)\) and \(\psi \in C_0^{\infty }(D)\) and their supports do not cross the discontinuity interfaces, the quantity of interest (13) satisfies \(\frac{d^s}{d Y^s}\mathcal{Q } \in L^{\infty }(\varGamma )\) with any order \(s \ge 1\).
Remark 2
For quantities of interest which are nonlinear in \(u\) the high \(Y\)-regularity property does not hold in general. In fact, the corresponding dual problems have non-smooth forcing terms and data (assuming \(u\) is not smooth), and therefore the dual solutions are not smooth with respect to \(Y\). In Sect. 5, we numerically study the Arias intensity [1] which is a nonlinear quantity of interest and show that it is not regular with respect to \(Y\).
3 A stochastic collocation method
In this section, we review the stochastic collocation method for computing the statistical moments of the solution \(u\) to the problem (1), see for example [2, 43]. We first discretize the problem in space and time, using a deterministic numerical method, such as the finite element or the finite difference method, and obtain a semi-discrete problem. We next collocate the semi-discrete problem in a set of \(\eta \) collocation points \(\{ Y^{(k)} \}_{k=1}^{\eta } \in \varGamma \) and compute the approximate solutions \(u_h(t,\mathbf{x},Y^{(k)})\). Finally, we build a global polynomial approximation \(u_{h,p}\) upon those evaluations
for suitable multivariate polynomials \(\{ L_k \}_{k=1}^{\eta }\) such as Lagrange polynomials. Here, \(h\) and \(p\) represent the discretization mesh size and the polynomial degree, respectively.
In what follows, we address in more details the choice of collocation points.
We seek a numerical approximation to \(u\) in a finite-dimensional subspace \(H_{h,\ell }\) of the space \(H_{H_0^1(D)} \equiv L^2(0,T;H_0^1(D)) \otimes L_{\rho }^2(\varGamma )\) in which the function \(u\) lives. We define the subspace based on a tensor product \(H_{h,\ell } = H_h \otimes H_{\ell }\), where
-
\(H_h ([0,T] \times D) \subset L^2(0,T;H_0^1(D))\) is the space of the semi-discrete solution in time and space for a constant \(Y\). The subscript \(h\) denotes the spatial grid-lengths and the time step-size. stability of the numerical scheme.
-
\(H_{\ell } (\varGamma ) \subset L_{\rho }^2(\varGamma )\) is a tensor product space which is the span of the tensor product of orthogonal polynomials with degree at most \(\mathbf{p} = [p_1(\ell ),\ldots ,p_N(\ell )]\). The positive integer \(\ell \) is called the level, and \(p_n(\ell )\) is the maximum degree of polynomials in the \(n\)-th direction, with \(n=1, \ldots , N\), given as a function of the level \(\ell \). For each \(Y_n, \, n=1, \ldots , N\), with the density \(\rho _n\), let \(H_{p_n}(\varGamma _n)\) be the span of \(\rho _n\)-orthogonal polynomials \(V_0^{(n)}, V_1^{(n)}, \ldots , V_{p_n}^{(n)}\). The tensor product space is then \(H_{\ell }(\varGamma ) = \bigotimes \nolimits _{n=1}^N H_{p_n}(\varGamma _n)\). The dimension of \(H_{\ell }\) is \(\text{ dim}(H_{\ell }) = \prod _{n=1}^N (p_n + 1)\). Without loss of generality, for bounded random variables, we assume \(\varGamma = [-1, 1]^N\).
Having the finite-dimensional subspace \(H_{h,\ell }\) constructed, we can use Lagrange interpolation to build an approximate solution \(u\).
The ultimate goal of the computations is the prediction of statistical moments of the solution \(u\) (such as the mean value and variance) or statistics of some given quantities of interest \(\mathcal{Q }(Y)\). For a linear bounded operator \(\varPsi (u)\),using the Gauss quadrature formula for approximating integrals, we write
where the weights are
and the collocation points \(Y^{(k)} = [Y_1^{(k_1)}, \ldots , Y_N^{(k_N)}] \in \Gamma \) are tensorized Gauss points with \(Y_n^{(k_n)}, \, k_n=0,1,\ldots ,p_n\), being the zeros of the \(\rho _n\)-orthogonal polynomial of degree \(p_n + 1\). Here, for any vector of indices \([k_1, \ldots , k_N]\) with \(0 \le k_n \le p_n\) the associated global index reads \(k = 1+k_1+(p_1+1) \, k_2 + (p_1+1) \, (p_2+1) \, k_3 + \cdots \).
Remark 3
The choice of orthogonal polynomials depends on the density function \(\rho \). For instance, for uniform random variables \(Y_n \sim \mathcal U (-1,1)\), Legendre polynomials are used,
Other well known orthogonal polynomials include Hermite polynomials for Gaussian random variables and Laguerre polynomials for exponential random variables [45].
Remark 4
There are other choices for the approximation space \(H_{\ell }\). For example, instead of orthogonal polynomials, we can choose a piecewise constant approximation using the Haar-wavelet basis. We can also choose a piecewise polynomial approximation. The choice of the approximating space may depend on the smoothness of the function with respect to \(Y\). In general, for smooth functions, we choose a polynomial approximation, while for non-smooth functions, we choose a low-degree piecewise polynomial or wavelet-type approximation [22, 23].
We now consider two possible approaches for constructing the tensor product space \(H_{\ell }\) and briefly review the Lagrange interpolation.
3.1 Full tensor product space and interpolation
For a given multi-index \(\mathbf{j} = [j_1, \ldots , j_N] \in \mathbb{Z }_+^N\), containing \(N\) non-negative integers, we define
Given an index \(j\), we calculate the polynomial degree \(p(j)\) either by
or by
The isotropic full tensor product space is then chosen as
In other words, in each direction we take all polynomials of degree at most \(p(\ell )\), and therefore \(\text{ dim}(H_{\ell }^T) = (p(\ell ) + 1)^N\). Since the dimension of the space grows exponentially fast with \(N\) (curse of dimensionality), the full tensor product approximation can be used only when the number of random variables \(N\) is small.
The multi-dimensional Lagrange interpolation corresponding to a multi-index \(\mathbf{j}\) is
where, for each value of a non-negative index \(j_n\) in the multi-index \(\mathbf{j}\), \(\mathcal{U }^{j_n}\) is the one-dimensional Lagrange interpolation operator, the set \(\{Y_{n,k_n}^{j_n}\}_{k_n=0}^{p(j_n)}\) is a sequence of abscissas for Lagrange interpolation on \(\Gamma _n\), and \(\{ L_{n,k_n}^{j_n} (y) \}_{k_n=0}^{p(j_n)}\) are Lagrange polynomials of degree \(p(j_n)\),
The set of points where the function \(u_h\) is evaluated to construct (17) is the tensor grid
The isotropic full tensor interpolation is obtained when we take \(\mathbf{j} = [\ell ,\ell ,\ldots ,\ell ]\) in (17), and the corresponding operator is denoted by \(\mathcal{I }_{\ell ,N}\),
3.2 Sparse tensor product space and interpolation
Here, we briefly describe the isotropic Smolyak formulas [5]. The sparse tensor product space is chosen as
The dimension of the sparse space is much smaller than that of the full space for large \(N\). For example, when \(p(j) = j\), we have \(\text{ dim}(H_{\ell ,N}^S) = \sum _{|\mathbf{j}| \le \ell } 1 = \frac{(N+\ell )!}{ N! \, \ell !}\), which helps reducing the curse of dimensionality. This space corresponds to the space of polynomials of total degree at most \(p(\ell )\).
The sparse interpolation formula can be written as a linear combination of Lagrange interpolations (17) on all tensor grids \(\mathcal{H }_\mathbf{j,N}\). With \(\mathcal{U }^{-1} = 0\), and for an index \(j_n \ge 0\), define
The isotropic Smolyak formula is then given by
Equivalently, the formula (19) can be written as
The collection of all tensor grids used in the sparse interpolation formula is called the sparse grid,
Sparse interpolation implies evaluating \(u_h(t,\mathbf{x},.)\) in all points of the sparse grid, known as collocation points. By construction, we have \(\mathcal{A }_{\ell ,N} \, [u](t,\mathbf{x},.) \in H_{\ell ,N}^S\). Note that the number of collocation points is larger than the dimension of the approximating space \(H_{\ell ,N}^S\).
Example 3
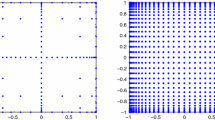
Let \(N=2\) and \(\ell =5\), and consider \(p(j) = j\). Moreover, let \(Y=[Y_1,Y_2]\) be a random vector with independent and uniformly distributed random variables \(Y_n \sim \mathcal U (-1,1)\). For a full tensor space, there are \((5+1)^2 = 36\) collocation points in the grid, shown in Fig. 1a. For a sparse tensor space, there are \(\frac{(2+5)!}{ 2! \, 5!}=21\) admissible sets of indices \(\mathbf{j}\) and \(89\) collocation points in the grid shown in Fig. 1b. Observe that the number of points in the full tensor grid grows much faster with the dimension \(N\) than the number of points in the sparse grid.
3.3 Choice of interpolation abscissas
We propose two different abscissas in the construction of the Smolyak formula.
Gaussian abscissas In this case, for a given index \(j_n\), the sequence of abscissas \(\{Y_{n,k_n}^{j_n}\}_{k_n=0}^{p(j_n)}\) are \(p(j_n)+1\) zeros of the orthogonal polynomial \(V_{p(j_n)+1}\). As the choice of the polynomial degree, we can use either the formula (15) or (16).
Clenshaw-Courtis abscissas These abscissas are the extrema of Chebyshev polynomials and are given by
It is recommended to use the formula (16) for the polynomial degree. In this case, one obtains nested sets of abscissas and thereby \(\mathcal{H }_{\ell ,N}^S \subset \mathcal{H }_{\ell +1,N}^S\).
We note that the structure of the stochastic collocation method, which involves solving \(\eta \) independent problems, allows us to use and perform parallel computations in a straight forward way.
4 Convergence analysis for stochastic collocation
In this section, we consider a linear bounded operator \(\varPsi (u)\) and give a priori estimates for the total error \(\varPsi (u) - \varPsi (u_{h,\ell })\) in the norm \(L^2(0,T;L^2(D)) \otimes L_{\rho }^2(\Gamma )\) when \(\varPsi (u) = u\), and in the norm \(L_{\rho }^2(\Gamma )\) when \(\varPsi (u) =\mathcal{Q }(Y)\) with \(\mathcal{Q }\) given in (13). We split the error into two parts and write
The first term in the right hand side \(\varepsilon _I\) controls the convergence of the deterministic numerical scheme with respect to the mesh size \(h\) and is of order \(\mathcal{O }(h^{r})\), where \(r\) is the minimum between the order of accuracy of the finite element or finite difference method used and the regularity of the solution. Notice that the constant in the term \(\mathcal{O }(h^{r})\) is uniform with respect to \(Y\).
Here, we focus on the second term \(\varepsilon _{II}\) which is an interpolation error in the stochastic space. We first consider the case when \(h \rightarrow 0\). We show that the error decays algebraically with respect to the number of collocation points \(\eta \) with an exponent proportional to \(- s\), provided there are \(s\) bounded \(Y\)-derivatives (i.e., \(\partial _{Y_n}^s \varPsi < \infty \) with \(n=1,\ldots ,N\)) when the full tensor interpolation is used, and if the mixed \(Y\)-drivatives (i.e., \(\partial _{Y_1}^s \, \partial _{Y_2}^s \cdots \partial _{Y_N}^s \varPsi < \infty \)) are bounded when the Smolyak interpolation is used. We next consider the case when \(h^{\beta } \, \ell \), with \(1\le \beta \le 2\), is large. In this case, we show that the approximate solution \(u_h\) is \(Y\)-analytic with the radius of analyticity proportional to \(h^{\beta }\). We therefore obtain a “fast” exponential rate of convergence which deteriorates as the quantity \(h^{\beta } \, \ell \) gets smaller. The effective error \(\varepsilon _{II}\) will then be the minimum of the two errors corresponding to the case when \(h \rightarrow 0\) and when \(h^{\beta } \, \ell \) is large.
4.1 The case when \(h \rightarrow 0\)
We only consider the operator \(\varPsi (u_h) = u_h\) and let \(h \rightarrow 0\). The discrete solution \(u_h\) has then a \(Y\)-regularity of order \(s=1\) as the continuous solution \(u\), i.e. \(\partial _Y u_h \in C^0(\Gamma ; W)\), where \(W := L^2(0,T; L^2(D))\), see Sec. 2. The second term of the error \(\varepsilon _{II}\) will then be in the norm \(L^2(0,T;L^2(D)) \otimes L_{\rho }^2(\Gamma )\). We notice that for the case \(\varPsi (u) =\mathcal{Q }(Y)\), where \(\mathcal{Q }\) is the quantity of interest in (13) with compactly supported smooth mollifiers whose supports does not cross the interfaces, the corresponding error estimates are obtained by replacing \(s=1\) with \(s \ge 1\).
The technique for obtaining error bounds for multivariate functions (when \(N>1\)) is based on one-dimensional results. We first quote a useful result from Erdös and Turán [10] for univariate functions.
Lemma 3
Let \(N=1\) and \(\Gamma \subset \mathbb{R }\) be bounded. Let \(W\) be a Hilbert space. For every function \(v \in C^0(\Gamma ; W)\) the interpolation error with Lagrange polynomials based on Gaussian abscissas satisfies
We then recall a Jackson-type theorem on the error of the best approximation of univariate functions with bounded derivatives by algebraic polynomials, see [5] for instance.
Lemma 4
Let \(N=1\) and \(\Gamma \subset \mathbb{R }\) be bounded. Set \(W := L^2(0,T;L^2(D))\). Given a function \(v \in C^0(\Gamma ; W)\) with \(s \ge 0\) bounded derivatives in \(Y\), there holds
where the constant \(C_s\) depends only on \(s\).
We consider one random variable \(Y_n \in \Gamma _n\) with density \(\rho _n\) and denote by \({\hat{Y}}_n \in {\hat{\Gamma }}_n\) the remainder \(N-1\) variables with density \({\hat{\rho }}_n = \Pi _{k=1, k \ne n}^N \rho _k\). We can now consider \(u_h^{(n)}:=u_h(., Y_n, {\hat{Y}}_n) : \Gamma _n \rightarrow W_n\) as a univariate function of \(Y_n\) with values in the Hilbert space \(W_n = W \otimes L^2_{{\hat{\rho }}_n}\). We are ready to prove the following result.
Theorem 4
Consider the isotropic full tensor product interpolation formula (18), and let \(u_{h,\ell } = \mathcal{I }_{\ell ,N} [u_h]\). Then the interpolation error \(\varepsilon _{II}\) defined in (21) satisfies
where the constant \(C= C_s \, \sum _{n=1}^N \max _{k=0, \ldots , s} || D_{Y_n}^k u_{h,\ell } ||_{L^{\infty }(\Gamma ; W)}\) does not depend on \(\ell \). Here, \(p(\ell )\) is either \(\ell \) or \(2^{\ell }\) depending on the choice of formula (15) or (16) for the polynomial degree, respectively.
Moreover, let \(\eta \) be the total number of collocation points, then
Proof
We consider the first random variable \(Y_1\) and the corresponding one-dimensional Lagrange interpolation operator \({\mathcal{I }}_{{\ell },1} = \mathcal{U }^{\ell }: \, C^0(\Gamma _{1} ; W_1) \rightarrow L_{\rho _1}^2(\Gamma _{1}; W_1)\). The global interpolation \(\mathcal{I }_{{\ell },N}\) can be written as the composition of two interpolations operators, \({\mathcal{I }}_{{\ell },N} = {\mathcal{I }}_{{\ell },1} \circ {\hat{\mathcal{I }}}_{{\ell },1}\), where \({\hat{\mathcal{I }}}_{{\ell },1}: \, C^0({\hat{\Gamma }}_1 ; W) \rightarrow L_{\rho _{1}}^2({\hat{\Gamma }}_{1}; W)\) is the interpolation operator in all directions \(Y_{2}, \ldots , Y_{N}\) except \(Y_{1}\). We have,
By (22) and (23), we can bound the first term,
To bound the second term we use the inequality (see Lemma 4.2 in [2]), \(|| \mathcal{I }_{\ell ,1}[v] ||_{L_{\rho }^2(\Gamma ; W)} \le {\tilde{C}} \, || v ||_{L^{\infty }(\Gamma ; W)}\), with \(v \in C^0(\Gamma ; W), \) for \(v = u_h - {\hat{\mathcal{I }}}_{\ell ,1}[u_h]\) and write
The right hand side is again an interpolation error in the remainder \(N-1\) directions \(Y_2, \ldots , Y_N\). We can proceed iteratively and define an interpolation operator in direction \(Y_2\) and so forth. Finally we arrive at
Note that \(C_s\) denotes a positive constant depending on \(s\) whose value may change from one expression to another expression. This proves the first inequality. The second inequality follows noting that the total number of collocation points is \(\eta = \bigl ( p(\ell )+1 \bigr )^N\).
\(\square \)
Remark 5
If the anisotropic full tensor interpolation [31] is used, the number of collocation points is \(\eta = \prod _{n=1}^N (p(\ell _n)+1)\), where \(\ell _n\) is the level in the \(n\)-th direction. In this case the error satisfies
In order to minimize the computational work \(\eta \) subject to the constraint \(\varepsilon _{II} \le TOL\), we introduce the Lagrange function \(\mathcal{L } = \eta + \lambda \, (C_s \, \sum _{n=1}^N D_n \, p(\ell _n)^{-s} -TOL)\), with the Lagrange multiplier \(\lambda \). By equating the partial derivative of \(\mathcal{L }\) with respect to \(p(\ell _n)\) to zero, we obtain \(p(\ell _n) \propto D_n^{1/s}\). Noting that \(D_n\) can be computed easily using just a few samples of \(Y_n\), we can quickly build a fast way on how to choose polynomial degrees in different directions and build the anisotropic full tensor grid.
To obtain error estimates using the isotropic Smolyak interpolation, we first recall another Jackson-type theorem on the error of the best approximation of univariate functions with bounded derivatives by algebraic polynomials, see [8] for instance.
Lemma 5
Let \(N=1\) and \(\Gamma \subset \mathbb{R }\) be bounded. Let \(W\) be a Hilbert space. For every function \(v \in L_{\rho }^2(\Gamma ; W)\) with \(s \ge 1\) square integrable \(Y\)-derivatives, the interpolation error with Lagrange polynomials based on Gauss-Legendre abscissas satisfies
where the constant \(C_s\) depends only on \(s\).
We also need the following lemma,
Lemma 6
In the isotropic Smolyak formula (19), with \(p(j)\) given by (16), if
then
Proof
We write
If we repeat the process, we finally arrive at (26). \(\square \)
We can now prove the following result,
Theorem 5
Consider the sparse tensor product interpolation formula (20) based on Gauss-Legendre abscissas when the formula (16) is used, and let \(u_{h,\ell } = \mathcal{A }_{\ell ,N} [u_h]\). Then for the discrete solution \(u_h\) with \(s \ge 1\) bounded mixed derivatives in \(Y\), the interpolation error \(\varepsilon _{II}\) defined in (21) satisfies
with \({\hat{C}} = \frac{C_0}{2} \, \frac{1-C_0^N}{1-C_0} \, || \rho ||_{\infty }^{1/2} \, \max _{d=1,\ldots ,N} D_d(u_h)\), where \(C_0 =2^{s+1} \, C_s\) and
Here, the constant \({\hat{C}}\) depends on the solution, \(s\) and \(N\), but not on \(\ell \).
Moreover, let \(\eta \) be the total number of collocation points, then
with \(\xi = 1 + \log 2 \, (1 + \log _2 1.5) \approx 2.1\).
Proof
We follow [5] and start with rewriting the isotropic Smolyak formula (19) as
Let \(I_N: \Gamma \rightarrow \Gamma \) be the identity operator on an \(N\)-dimensional space and \(I_1^{(n)}: \Gamma _n \rightarrow \Gamma _n\) be a one-dimensional identity operator for \(n=1, \ldots ,N\). We can compute the error operator recursively,
Noting that \(\sum _{\sum _{n=1}^{N-1} j_n \le \ell } \bigotimes _{n=1}^{N-1} \Delta ^{j_n} = \mathcal{A }_{\ell ,N-1}\) and that \(I_N = I_{N-1} \otimes I_1^{(N)}\), we can write
If we repeat the process, we arrive at
where
Then,
where the norms are in \({L^2_{\rho }(\Gamma ; W)}\). We first bound \({\tilde{R}}\). By (25), we have
and therefore,
By Lemma 6 and (29) and (31), we then have
with \(D_d(u_h)\) given by (27). Moreover, since
then by (30), we get
The first inequality stated in Theorem 5 follows noting that \(\genfrac(){0.0pt}{}{\ell +d-1}{\ell } \le (\ell +1)^{2 \, N}\) for \(d=1,\ldots ,N\).
To show the second inequality (28), we note that the number of collocation points \(\eta \) at level \(\ell \) using the Smolyak formula with Gaussian abscissas and the polynomial degree (16) satisfies (see Lemma 3.17 in [32])
with \(\xi = 1 + \log 2 \, (1 + \log _2 1.5) \approx 2.1\). From the first inequality we have
This completes the proof. \(\square \)
Remark 6
We note that the above estimates are uniform with respect to \(h\) in the case of smooth quantity of interest. For the solution, we have one \(Y\)-derivative uniformly bounded with respect to \(h\) in \(L^2(0,T; H_0^1(D))\).
Remark 7
(algebraic rate of convergence) In full tensor interpolation, with the minimal assumptions (2) on the data, by (24) we have an upper error bound of order \(\mathcal{O }(\eta ^{- s/N})\) with \(s=1\) when \(\varPsi (u) = u\) and with any order \(s \ge 1\) when \(\varPsi (u) =\mathcal{Q }(Y)\). In Smolyak interpolation, with the minimal assumptions (2), when \(\varPsi (u) = u\), then (28) implies an upper error bound of order \(\mathcal{O }(\eta ^{-\delta \, s})\) with \(s=1\) and some \(0<\delta <1\) only when \(N= 1\) for which \(D_d(u_h)\) is bounded. As we showed in Sect. 2, \(D_d(u_h)\), which involves mixed \(Y\)-derivatives of the solution for \(N \ge 2\), is not bounded. This gives an algebraic error convergence for the solution when \(N = 1\). When \(\varPsi (u) =\mathcal{Q }(Y)\), with the minimal assumptions (2), \(\mathcal{Q }(Y)\) has bounded mixed \(Y\)-derivatives of any order \(s \ge 1\) for \(N \ge 1\), as shown in Sect. 2. We obtain an upper error bound of order \(\mathcal{O }(\eta ^{- \delta \, s})\) with \(s \ge 1\) and some \(0<\delta <1\). This gives a faster error convergence for the quantity of interest (13).
Remark 8
(full tensor versus sparse tensor) The slowdown effect that the dimension \(N\) has on the error convergence (24) when a full tensor product is employed is known as the curse of dimensionality. This is the main reason for not using isotropic full tensor interpolation when \(N\) is large. On the other hand, the isotropic Smolyak approximation has a larger exponent \(\mathcal{O } (\frac{1}{\log N})\) in (28) compared to \(\mathcal{O } (\frac{1}{ N})\) in (24). This is a clear advantage of the isotropic Smolyak method over the full tensor method when bounded mixed \(Y\)-derivatives exist.
Remark 9
(computational cost versus error) In order to find the optimal choice of the mesh size \(h\), we need to minimize the computational complexity of the stochastic collocation method, \(\eta / h^{d+1}\), subject to the total error constraint \(\varepsilon _{F} \propto h^r + \eta ^{-s/ N} = TOL\) for the isotropic full tensor interpolation and \(\varepsilon _{S} \propto h^r + \eta ^{-s/ \log N} = TOL\) for the isotropic Smolyak interpolation. We introduce the Lagrange functions \(\mathcal{L }_F = \eta / h^{d+1} + \lambda \, ( h^r + \eta ^{-s/ N} -TOL)\) and \(\mathcal{L }_S = \eta / h^{d+1} + \lambda \, ( h^r + \eta ^{-s/ \log N} -TOL)\), with the Lagrange multiplier \(\lambda \). By equating the partial derivatives of the Lagrange functions with respect to \(\eta , h\), and \(\lambda \) to zero, we obtain \(h^r \approx TOL / (1+ \frac{r \, N}{s \, (d+1)})\) and \(h^r \approx TOL / (1+ \frac{r \, \log N}{s \, (d+1)})\), making the computational works of order \({TOL}^{- N / s-(d+1) / r}\) and \({TOL}^{- \log N / s-(d+1) / r}\) for the full tensor and Smolyak interpolations, respectively.
4.2 The case when \(h^{\beta } \, \ell \) is large with \(1 \le \beta \le 2\)
We consider a finite element approximation of (1) using a quasi-uniform triangulation of the physical domain. Let \(h\) denote the size of the largest triangle in the triangulation and \(u_h\) be the semi-discrete solution. We leave \(t\in [0,T]\) and \(Y \in \Gamma \) continuous and discretize only the spatial variables. The semi-discrete problem reads
We differentiate the semi-discrete equation (33) with respect to the random variable \(Y_n\). We then set \({\tilde{u}} := \partial _{Y_n} u_h\) and let \(v = {\tilde{u}}_t\) to obtain
where
We observe that \(({\tilde{u}}_{tt},{\tilde{u}}_{t}) = \frac{1}{2} \frac{d}{dt} \Vert {\tilde{u}}_{t} \Vert _{L^2(D)}^2\). Moreover, since \(a\) is time-independent, then \(B[{\tilde{u}},{\tilde{u}}_{t}] = \frac{1}{2} \frac{d}{dt} B[{\tilde{u}},{\tilde{u}}] = \frac{1}{2} \frac{d}{dt} \Vert a \, \nabla {\tilde{u}} \Vert _{L^2(D)}^2\). Furthermore, by Hölder, inverse and Cauchy inequalities [11], we have
where \(C_n := 2 \, \Vert a \, a_{Y_n} \Vert _{L^{\infty }(D_n \times \Gamma _n)} \), and \(C_{inv}\) is the constant in the inverse inequality. From (34) we therefore get
Now write
From the inequality (35), we have \(y_1^{\prime }(t) \le \frac{1}{T} \, y_1(t) + y_2(t)\). By the Gronwall’s inequality [11] and noting that \(y_1(0)=0\), we obtain
We now define the energy norm
and the Sobolev norm
We consider two different cases. One case is when the uniform coercivity assumption (3) holds. The other case is when the wave speed \(a(\mathbf{x},Y)\) may be zero or negative due to possible negative values in the random vector \(Y\), and therefore (3) does not hold.
4.2.1 The case of uniformly coercive wave speed
Under the uniform coercivity assumption (3), we have
Moreover, by (36), we obtain
Therefore,
We now obtain the estimate on the growth of all mixed \(Y\)-derivatives of \(u_h\). Let \(\mathbf{k} \in \mathbb{Z }_+^N\) be a multi-index and \(\partial _Y^\mathbf{k} u_h:= \frac{\partial ^{|\mathbf{k}|} u_h}{\partial _{Y_1}^{k_1} \cdots \partial _{Y_N}^{k_N}}\). In order to find an upper bound for the \(|\mathbf{k}|\)-th order mixed \(Y\)-derivative \(\partial _Y^\mathbf{k} u_h\), we follow [6] and introduce a set \(\mathcal{K }\) of indices with cardinality \(n_\mathcal{K }\) such that \(\partial _Y^\mathcal{K } u_h := \frac{\partial ^{n_\mathcal{K }} u_h}{\Pi _{k \in \mathcal{K }} \partial _{Y_k}} = \partial _Y^\mathbf{k} u_h\). As an example, let \(N=5\) and consider the set \(\mathcal{K } = \{ 1,1,2,3,5,5,5\}\) with \(n_\mathcal{K } = 7\). Then the corresponding multi-index is \(\mathbf{k} = [2 \, 1 \, 1 \, 0 \, 3]\) with \(|\mathbf{k}| = 7\), and we have
Before deriving the estimates, we need the following two lemmas.
Lemma 7
(generalized Leibniz rule) Given a set of indices \(\mathcal{K }\) with cardinality \(n_{\mathcal{K }}\) and two functions \(f, g \in \mathcal{C }^\mathcal{K }(\Gamma )\),
where \(\mathcal P (\mathcal{K })\) represents the power set of \(\mathcal{K }\).
Lemma 8
Let \(C \in \mathbb{R }_+\) and \(n \in \mathbb{Z }_+ \). Then we have
Proof
The left hand side of (38) can be written as
The right hand side of (38) can be written as
We now show that
from which the inequality (38) follows. We prove (39) by induction on \(n \ge j+1\).
Case \(n=j+1\). In this case (39) reads \(1 \le 1\) which is true.
General case. We assume that (39) holds for \(n \ge j+1\) and show that
We can use the induction hypothesis (39) and write
where the last equality is the Pascal’s rule. Therefore, by induction the proof is complete. \(\square \)
We are now ready to prove the following result,
Theorem 6
The \(Y\)-derivatives of the semi-discrete solution \(u_h\) which solves (33) can be bounded as
where \(\mathbf{k} \in \mathbb{Z }_+^N\) is a multi-index, and \({\hat{C}}\) is independent of \(h\).
Proof
Let \(\mathcal{K }\) be the index set corresponding to the multi-index \(\mathbf{k}\). Then, according to Lemma 7, the \(\partial _Y^\mathcal{K }\) derivative of the semi-discrete equation (33) is
Noting that \(\mathcal P (\mathcal{K }) = \mathcal{K } \cup \bigl ( \mathcal P (\mathcal{K }) \setminus \mathcal{K } \bigr )\), we write
Now let \(v = \partial _Y^\mathcal{K } \partial _{t} u_h\) and obtain
where
As before, by Hölder, inverse and Cauchy inequalities [11], we have
where \({\tilde{C}} := \max _{\mathcal{S } \in \mathcal P (\mathcal{K })} \Vert \partial _Y^\mathcal{S } a^2 \Vert _{L^{\infty }(D \times \Gamma )} \), and \(C_{inv}\) is the constant in the inverse inequality. From (41) we therefore get
Now we write
From the inequality (42), we have \(y_1^{\prime }(t) \le \frac{1}{T} \, y_1(t) + y_2(t)\). By the Gronwall’s inequality [11] and noting that \(y_1(0)=0\), we obtain
and therefore,
We finally obtain the formula
We now by induction show that
which is equivalent to the corresponding multi-index formulation (40).
Case \(n_\mathcal{K } =0\). In this case the set \(\mathcal{K }\) is empty, and (44) reads \(\Vert u_h \Vert _S \le \Vert u_h \Vert _S\), which is true.
Case \(n_\mathcal{K } =1\). In this case \(\mathcal{K } = \{k\}, 1 \le k \le N\), and (44) reads
which follows from (37).
General case. We now assume that (44) holds for all sets \(\mathcal{S }\) with cardinality \(0 \le n_\mathcal{S } \le n_\mathcal{K } -1\). We have then the induction hypothesis,
From (43) we have
Note that the number of subsets \(\mathcal{S }\) of \(\mathcal P (\mathcal{K })\) with cardinality \(i\) is \(\genfrac(){0.0pt}{}{n_\mathcal{K }}{i}\). Then
where the last inequality follows from Lemma 8. This completes the proof. \(\square \)
Remark 10
We note that the optimal choice of the mesh size \(h\) in Remark 9 in Sect. 4.1 is obtained by assuming that the \(Y\)-derivatives of the solution up to order \(s\), which appear in the coefficients \(C\) and \({\hat{C}}\) in the error estimates (24) and (28), are uniformly bounded with respect to \(h\). In the absence of such assumption, we can employ the estimate (40) and find the coefficients in the error bounds. For instance, for the full tensor interpolation, the coefficient \(C\) in the interpolation error (24) is \(C\propto N \, h^{-s}\). The total error is then \(\varepsilon _{F} \propto h^r +N \, h^{-s} \, \eta ^{-s/ N} = TOL\). By introducing the Lagrange function \(\mathcal{L }_F = \eta / h^{d+1} + \lambda \, ( h^r + N \, h^{-s} \, \eta ^{-s/ N} -TOL)\) and equating its partial derivatives with respect to \(\eta , h\), and \(\lambda \) to zero, we obtain \(h^r \approx TOL / (1+ \frac{r \, N}{s \, (N+d+1)})\), making the computational work of order \({TOL}^{- N / s-(N+d+1) / r}\).
We now define for every \(Y \in \Gamma \) the power series \(u_h:\mathbb{C }^N \rightarrow L^{\infty }(0,T;H_0^1(D))\) as
where \(\mathbf{k}! = \Pi _{n=1}^N (k_n!)\) and \(Y^\mathbf{k}=\Pi _{n=1}^N Y_n^{k_n}\). By (40) we get
We exploit the generalized Newton binomial formula for \(\mathbf{v} = [v_1,\ldots ,v_N] \in \mathbb{R }_+^N\) and \(k \in \mathbb{Z }_+\),
and obtain
Therefore, the series (46) converges for all \(Z \in \mathbb{C }^N\) such that \(|Z_n-Y_n| \le \tau < \frac{1}{N} \, (C + 1)^{-1} = \mathcal{O }(h)\). By a continuation argument, the function \(u_h\) can analytically be extended on the whole region \(\Sigma (\Gamma , \tau ) = \{ Z \in \mathbb{C }^N, \, {\text{ d}ist}(\Gamma _n , Z_n) \le \tau , \, n =1, \ldots , N\}\). We note that the radius of analyticity is proportional to \(h\).
We now build an approximate solution \(u_{h,\ell }\) to \(u_h\) based on Lagrange interpolation in \(Y\). We investigate only the case of a tensor product interpolation on Gauss-Legendre points as described in Sect. 3. We recall a result on the error of the best approximation of univariate analytic functions by polynomials [2].
Lemma 9
Let \(N=1\) and \(\Gamma \subset \mathbb{R }\) be bounded. Set \(W := L^2(0,T;L^2(D))\). Then, given a function \(v(Y) \in L^{\infty }(\Gamma ; W)\) which admits an analytic extension in the region of the complex plane \(\Sigma (\Gamma , \tau ) = \{ Z \in \mathbb{C }, \, {\text{ d}ist}(\Gamma , Z) \le \tau \}\), for some \(\tau > 0\), there holds
where \(0 < \sigma = \log \bigl ( \frac{2 \tau }{|\Gamma |} + \sqrt{1+\frac{4 \tau ^2}{|\Gamma |^2}} \bigr )\).
In the above lemma, \(\tau \) is smaller than the distance between \(\Gamma \) and the closest singularity of the extended function \(v(z): \mathbb{C } \rightarrow W\) in the complex plane.
In the multidimensional case when \(N \ge 2\), we note that \(\sigma _n = \log \bigl ( \frac{2 \tau }{|\Gamma _n|} + \sqrt{1+\frac{4 \tau ^2}{|\Gamma _n|^2}} \bigr )\) depends on the direction \(n\). We therefore set
Similar to the proof of Theorem 4, using (22) and (47), we can show that for the isotropic full tensor product interpolation formula (18), with \(u_{h,\ell } = \mathcal{I }_{\ell ,N} [u_h]\), the interpolation error \(\varepsilon _{II}\) defined in (21) satisfies
We now consider the Smolyak interpolation formula (20) based on Gaussian abscissas when the formula (16) is used and let \(u_{h,\ell } = \mathcal{A }_{\ell ,N} [u_h]\). Similar to the proof of Lemma 3.16 in [32], we can show that the interpolation error \(\varepsilon _{II}\) defined in (21) satisfies
with \({\hat{C}} = \frac{C_0}{2} \, \frac{1-C_0^N}{1-C_0}\) and \(C_0 =\frac{16 \, M^*(u_h)}{e^{4 \, \sigma ^*}-e^{2 \, \sigma ^*}} \, \large ( 1+\frac{1}{\log 2} \, \sqrt{\frac{\pi }{2 \, \sigma ^*}} \large )\).
From (48) and (49), we note that for both full tensor and Smolyak interpolations, since \(\sigma ^* = \mathcal{O }(h)\), we will have a fast exponential decay in the error when the product \(h \, \ell \) is large. As a result, with a fixed \(h\), the error convergence is slow (algebraic) for a small \(\ell \) and fast (exponential) for a large \(\ell \). Moreover, the rate of convergence deteriorates as \(h\) gets smaller. These results are precisely what we observe in the numerical experiments presented in Sect. 5.
4.2.2 The case of non-coercive wave speed
We now relax the uniform coercivity assumption (3) and instead assume that
We apply the inverse inequality to (36) and write
In the last inequality, we assume for simplicity that \(u_h(0)=0\). Similar to Sect. 4.2.1, we obtain
Therefore, the series (46) converges for all \(Z \in \mathbb{C }^N\) such that \(|Z_n-Y_n| \le \tau < \frac{1}{N} \, (C_0 + 1)^{-1} = \mathcal{O }(h^2)\). Comparing this with the case when the coercivity assumption (3) holds, we observe that as \(h\) decreases the radius of analyticity shrinks faster (proportional to \(h^2\)) for the non-coercive case than for the coercive case (proportional to \(h\)). We obtain the same estimates as (48) and (49) with \(\sigma ^* = \mathcal{O }(h^2)\). We will therefore have a fast exponential decay in the error when the product \(h^2 \, p(\ell )\) is large. Note that these estimates may not be sharp, as the numerical test 2 in Sect. 5 suggests that \(\sigma ^* \approx \mathcal{O }(h^{1.2})\). This may be related to the use of inverse inequality (which is not sharp) twice while obtaining (50).
5 Numerical examples
In this section, we consider the IBVP (1) in a two dimensional layered medium. We numerically simulate the problem by the stochastic collocation method and study the convergence of the statistical moments of the solution \(u\), the linear quantity of interest (13) and a nonlinear quantity of interest called the Arias intensity [1]
where, \(S\) is a sub-domain of the physical domain \(D\), and \(T\) is a positive final time. We show that the computational results are in accordance with the convergence rates predicted by the theory.
We consider a rectangular physical domain \(D = [-L_x,L_x] \times [-L_z,0]\) and a random wave speed \(a\) of form (5) for a two-layered medium (\(N=2\)). The computational domain containing two layers with widths \(d_1\) and \(d_2\) is shown in Fig. 2.
The deterministic solver employs a finite difference scheme based on second-order central difference approximation. Let \(\Delta x = \frac{2 \, L_x}{N_x}\) and \(\Delta z = \frac{L_z}{N_z}\) denote the spatial grid-lengths, where \(N_x\) and \(N_z\) are natural numbers. For \(i=0,1,\ldots , N_x\) and \(j=0,1,\ldots , N_z\), let \((x_i,z_j) =(-L_x+ i \, \Delta x, -L_z+j \, \Delta z)\) and \(u_{i,j}(t)\) denote the corresponding grid point and the grid function approximating \(u(t,x_i,z_j)\), respectively. On this spatial grid, we discretize the PDE in (1) and obtain the semi-discretization,
Here, \(D_+\) and \(D_-\) are forward and backward first-order difference operators, respectively. We then use the second-order central difference approximation in time to obtain the fully discrete deterministic scheme. In the stochastic space, we use the isotropic Smolyak formula (20) based on Gaussian abscissas, described in Sect. 3.
We perform four numerical tests. In the first test, we consider a zero force term and smooth initial data and study the mean and standard deviation of the solution \(u\). In the second test, we consider the same data as in the first test and select random variables so that the uniform coercivity assumption (3) is not satisfied, and we have \(a_{min}^2=0\). We study the expected value of the solution \(u\) in this case and compare it with the case when \(a_{min}^2 > 0\). In the third test, we consider zero initial data and a discontinuous time-independent forcing term and study the quantity of interest (13). Finally, in the fourth test, we study the Arias intensity (51) on the free surface due to a Ricker wavelet [17]. In all computations, we use a time step-size \(\Delta t = \Delta x / 5\) which guarantees the stability of the deterministic numerical solver. We use homogeneous Neumann boundary conditions in all tests.
5.1 Numerical test 1
In the first test, we choose a computational domain \(D = [-2,2] \times [-3.5,0]\) with two layers with widths \(d_1=0.5\) and \(d_2=3\). We consider a wave speed of form (5) with \(a_0=0\), \(\alpha _1= 2\) and \(\alpha _2 =3\), and let \(Y_n \sim \mathcal U (0.1,0.5)\), \(n=1,2\), be two independent and uniformly distributed random variables. We set \(f=g_2=0\) and consider an initial Gaussian wave pulse,
For computing the convergence rate of error, we consider a set of spatial grid-lengths \(\Delta x = \Delta z = 0.1, 0.05, 0.025, 0.0125\). For each grid-length \(\Delta x = h\), we consider different levels \(\ell \ge 1\) and compute the \(L^2\)-norm of error in the expected value of the solution at a fixed time \(t=T\) by
Here, the reference solution \(u_\mathrm{ref}\) is computed with a high level \(\ell _\mathrm{ref}\) for a fixed \(\Delta x = h\).
5.1.1 An irregular solution
We first put the center of the initial pulse at \((x_c,z_c)=(0,-1)\) and let \(\sigma _x = \sigma _z = 0.2\). The initial solution is then in both layers and does not vanishes on the interface. In this case, since the smooth initial solution does not satisfy the interface jump conditions (8), the solution is not highly regular in \(Y\). In fact, we only have \(u_Y \in L^{\infty }(\Gamma ; C^0(0,T;L^2(D)))\), and therefore, the solution has only one bounded \(Y\)-derivative and no bounded mixed derivatives in \(Y\). Figure 3 shows the initial solution and the expected value and standard deviation of the solution at time \(t=1\), computed with level \(\ell =5\) and \(\Delta x = \Delta z = 0.0125\).
Figure 4 shows the \(L^2\)-norm of error in the expected value of the solution at \(T=1\) versus the number of collocation points \(\eta (\ell )\).
Test 1. The \(L^2\)-norm of error in the expected value of the solution, \(\varepsilon _h(\ell )\), at time \(T=1\) versus the number of collocation points \(\eta (\ell )\). The smooth initial wave pulse is in both layers and does not vanish on the interface. The solution has only one bounded \(Y\)-derivative and no mixed derivatives in \(Y\)
We observe a slow convergence of order \(\mathcal{O }(\eta ^{-\delta })\) with \(0 <\delta < 1\), as expected due to low \(Y\)-regularity of the solution. We also note that for large values of \(h \, \eta \), we observe exponential decay in the error, and as \(h\) decreases, more collocation points are needed to maintain a fixed accuracy (as predicted in Sect. 4.2).
5.1.2 A regular solution
We next put the center of the initial pulse at \((x_c,z_c)=(0,-1.5)\) and let \(\sigma _x = \sigma _z = 0.11\). The initial solution is then essentially contained only in the bottom layer. In this case, since the smooth initial solution is zero at the interface, the interface conditions (8) are automatically satisfied. The solution remains smooth within each layer and satisfies the interface conditions. The solution is therefore highly regular in \(Y\), see Sect. 2. Figure 5 shows the \(L^2\)-norm of error in the expected value of the solution at \(T=1\) versus the number of collocation points \(\eta (\ell )\).
Test 1. The \(L^2\)-norm of error in the expected value of the solution, \(\varepsilon _h(\ell )\), at time \(T=1\) versus the number of collocation points \(\eta (\ell )\). The smooth initial wave pulse is contained only in one layer, and the solution remains smooth within that layer and has high \(Y\)-regularity
We observe a fast exponential rate of convergence in the error due to high regularity of the solution in \(Y\).
5.2 Numerical test 2
In this test, we consider the same problem as the previous test in Sec. 5.1.1, except that we choose \(Y_n \sim \mathcal U (-0.2,0.5)\) so that the coercivity assumption (3) does not hold and we have \(a_{min}^2=0\). Figure 6 shows the \(L^2\)-norm of error in the expected value of the solution at \(T=1\) versus the level \(\ell \). For the sake of comparison, we also plot the error for the coercive wave speed in the numerical test 1.
Test 2. The \(L^2\)-norm of error in the expected value of the solution, \(\varepsilon _h(\ell )\), at time \(T=1\) versus the level \(\ell \) for non-coercive (top) and coercive (bottom) wave speeds. The smooth initial wave pulse is in both layers and does not vanish on the interface. The solution has only one bounded \(Y\)-derivative and no mixed derivatives in \(Y\)
In Table 1 we give the values of the spatial grid-lengths \(\Delta x =h\) and the level \(\ell \) at the knee point where the transition from slow to fast error convergence occurs. The values are given in both non-coercive and coercive cases, where \(a_{min}^2 \ge 0\) and \(a_{min}^2 > 0\), respectively.
In the coercive case, when \(h=0.05\), the fast convergence starts at \(h \, \ell = 0.05 \times 10 = 0.5\), and when \(h=0.025\), the fast convergence starts at \(h \, \ell = 0.025 \times 20 = 0.5\). In the non-coercive case, to obtain the same threshold \(0.5\), when \(h=0.05\) we need \(h^{\alpha } \times \ell = 0.05^{\alpha } \times 20 = 0.5\), which gives \(\alpha \approx 1.23\), and when \(h=0.025\) we need \(h^{\alpha } \times \ell = 0.025^{\alpha } \times 40 = 0.5\), which gives \(\alpha \approx 1.19\). This suggests that \(\sigma ^* \approx \mathcal{O }(h^{1.2})\) and shows that the estimates (48) and (49) with \(\sigma ^* = \mathcal{O }(h^2)\), derived in Sect. 4.2.2, may not be sharp.
5.3 Numerical test 3
In the third test, we choose a computational domain \(D = [-1.5,1.5] \times [-3,0]\) with two layers with equal widths \(d_1=d_2=1.5\). Let \(a_0 = 0\), \(\alpha _1= 2\), \(\alpha _2 =3\) and \(Y_n \sim \mathcal U (0.1,0.5)\), \(n=1,2\) in (5). We consider zero initial data \(g_1=g_2=0\) and a time-independent forcing term on \(C=[-0.3,0.3] \times [-1.8,-1.2]\) contained in \(D\),
We note that since \(f \in C^0(0,T; L^2(D))\), we will have \(u_Y{\in } L^{\infty }(\Gamma ; C^0(0,T;L^2(D)))\), and therefore, the solution has only one bounded \(Y\)-derivative and no bounded mixed derivatives in \(Y\). Figure 7 shows the convergence of the \(L^2\)-norm of error in the expected value of the solution \(\varepsilon _h(\ell )\) at \(T=1\) versus the number of collocation points \(\eta (\ell )\). We observe a slow convergence of order \(\mathcal{O }(\eta ^{-\delta })\) with \(0 < \delta < 1\), as expected.
Next we consider a quantity of interest of form (13) with \(T=1\), \(\psi = 0\) and a smooth mollifier
with the support \(D_{\phi } = [-0.5,0.5] \times [-2.75,-1.75]\) contained in the bottom layer. Figure 8 shows the error in the expected value of the quantity of interest, computed by
We note that since the smooth mollifiers \(\psi = 0\) and \(\phi \in C_0^{\infty }(D)\) do no cross the interface, the quantity of interest (13) has high \(Y\)-regularity. We therefore expect a convergence rate faster than any polynomial rate. However, for the small values of \(\ell \) tested here, we observe an algebraic rate of order about \(\mathcal O (\eta ^{-3})\).
5.4 Numerical test 4
In this test, we study the Arias intensity (51) due to a Ricker wavelet [17]. Arias Intensity is an important quantity of interest in seismology which describes earthquake shaking that triggers landslides. It determines the intensity of shaking by measuring the acceleration of transient seismic waves. The Ricker wavelet, which is the negative normalized second derivative of a Gaussian function, is used to model the generation of seismic waves.
We choose a computational domain \(D = [-10,10] \times [-10,0]\) with two layers with widths \(d_1=1\) and \(d_2=9\). Let \(a_0 = 0\), \(\alpha _1= 2\), \(\alpha _2 =3\) and \(Y_n \sim \mathcal U (0.1,0.5)\), \(n=1,2\) in (5). We consider zero initial data \(g_1=g_2=0\) and a forcing term consisting of a Ricker wavelet on a small region \(R_c = [-0.1,0.1] \times [-1.2,-1.1]\),
We compute the Arias intensity on a part of the free surface \(S=\{(x,z) \, \, | \, \, x \in [0,1], \, \, z=0 \}\). Figure 9 shows the mean plus minus the standard deviation of the Arias intensity on \(S\) as a function of time, computed with the level \(\ell =15\) and the spatial grid-length \(\Delta x = \Delta z = 0.0125\).
Figure 10 shows the response surface of the Arias intensity on \(S\) at the final time \(T=4\) computed using sparse interpolation.
We note that due to the nonlinearity of the Arias intensity in \(u_{tt}\), we do not expect high \(Y\)-regularity. See Remark 3 in Sect. 2.3. This is also observable from the response surface of the Arias intensity in Fig. 10. Figure 11 shows the error \(\varepsilon _\mathcal{I _A,h}\) in the expected value of the Arias intensity at final time \(T=4\). We observe a slow rate of convergence \(\mathcal O (\eta ^{-\delta })\) with \(0 <\delta <\frac{1}{2}\) as expected.
6 Conclusion
We have proposed a stochastic collocation method for solving the second order wave equation in a heterogeneous random medium with a piecewise smooth random wave speed. The medium consists of non-overlapping sub-domains. In each sud-domain, the wave speed is smooth and is given in terms of one random variable. We assume that the interfaces of speed discontinuity are smooth. One important example is wave propagation in multi-layered media with smooth interfaces. We have derived a priori error estimates with respect to the number of collocation points for the stochastic collocation method based on full and sparse tensor interpolations.
The main result is that unlike in elliptic and parabolic problems, the solution to hyperbolic problems is not in general analytic with respect to the random variables. Therefore, the convergence rate of error in the wave solution is only algebraic. A fast spectral convergence is still possible for some linear quantities of interest with smooth mollifiers and for the wave solution with smooth data compactly supported within sub-domains. We also show that the semi-discrete solution is analytic with respect to the random variables with the radius of analyticity proportional to the mesh size \(h\). We therefore obtain an exponential rate of convergence which deteriorates as the quantity \(h \, p\) gets smaller, with \(p\) representing the polynomial degree in the stochastic space. We have shown that analytical results and numerical examples are consistent and that the stochastic collocation method may be a valid alternative to the more traditional Monte Carlo method.
Future directions will include the analysis of other types of second order hyperbolic problems such as elastic wave equation and the case where the position of discontinuity interfaces is also stochastic.
References
Arias, A.: A measure of earthquake intensity. In: Hansen, R.J. (ed.) Seismic Design for Nuclear Plants, pp. 438–483. The MIT Press, Cambridge (1970)
Babuska, I.M., Nobile, F., Tempone, R.: A stochastic collocation method for elliptic partial differential equations with random input data. SIAM J. Numer. Anal. 45, 1005–1034 (2007)
Babuska, I., Tempone, R., Zouraris, G.E.: Galerkin finite element approximations of stochastic elliptic partial differential equations. SIAM J. Numer. Anal. 42, 800–825 (2004)
Babuska, I., Tempone, R., Zouraris, G.E.: Solving elliptic boundary value problems with uncertain coefficients by the finite element method: the stochastic formulation. Comput. Methods Appl. Mech. Eng. 194(1216), 1251–1294 (2005)
Barthelmann, V., Novak, E., Ritter, K.: High dimensional polynomial interpolation on sparse grids. Adv. Comput. Math. 12, 273–288 (2000)
Beck, J., Tempone, R., Nobile, F., Tamellini, L.: On the optimal approximation of stochastic PDEs by Galerkin and collocation methods. Math. Model. Meth. Appl. Sci. (2011, to appear)
Canuto, C., Kozubek, T.: A fictitious domain approach to the numerical solution of PDEs in stochastic domains. Numer. Math. 107(2), 257–293 (2007)
Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods: Fundamentals in Single Domains. Springer, Berlin (2006)
Charrier, J.: Strong and weak error estimates for elliptic partial differential equations with random coefficients. SIAM J. Numer. Anal. 50(1), 216–246 (2012)
Erdös, P., Turán, P.: On interpolation I. Quadrature- and mean-convergence in the Lagrange-interpolation. Ann. Math. (2) 38, 142–155 (1937)
Evans, L.C.: Partial differential equations. Graduate Studies in Mathematics, vol. 19. AMS (1998)
Fishman, G.S.: Monte Carlo: Concepts, Algorithms, and Applications. Springer Series Operation Research. Springer, New York (1996)
Ghanem, R.G., Spanos, P.D.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (1991)
Gottlieb, D., Xiu, D.: Galerkin method for wave equations with uncertain coefficients. Commun. Comput. Phys. 3(2), 505–518 (2008)
Harbrecht, H., Schneider, R., Schwab, C.: Sparse second moment analysis for elliptic problems in stochastic domains. Numer. Math. 109, 385–414 (2008)
Hörmander, L.: The analysis of linear partial differential operators III, pseudo-differential operators. Classics in Mathematics. Springer, Berlin (1994)
Hosken, J.W.J.: Ricker wavelets in their various guises. First Break 6, 24–33 (1988)
John, F.: Partial Differential Equations. Springer, New York (1982)
Kreiss, H.-O., Lorenz, J.: Initial-boundary value problems and the Navier-Stokes equations. Classics in Applied Mathematics, vol. 47. SIAM, Philadelphia (2004)
Kreiss, H.-O., Ortiz, O.E.: Some mathematical and numerical questions connected with first and second order time-dependent systems of partial differential equations. Lect. Notes Phys. 604, 359–370 (2002)
Kreiss, H.-O., Petersson, N.A., Yström, J.: Difference approximations for the second order wave equation. SIAM J. Numer. Anal. 40, 1940–1967 (2002)
Le Maitre, O.P., Knio, O.M., Najm, H.N., Ghanem, R.G.: Uncertainty propagation using Wiener-Haar expansions. J. Comput. Phys. 197(1), 28–57 (2004)
Le Maitre, O.P., Najm, H.N., Ghanem, R.G., Knio, O.M.: Multi-resolution analysis of Wiener-type uncertainty propagation schemes. J. Comput. Phys. 197(2), 502–531 (2004)
Levermore, C.D., Oliver, M.: Analyticity of solutions for a generalized Euler equation. J. Differ. Equ. 133, 321–339 (1997)
Lin, G., Su, C.-H., Karniadakis, G.E.: Predicting shock dynamics in the presence of uncertainties. J. Comput. Phys. 217(1), 260–276 (2006)
Lin, G., Su, C.-H., Karniadakis, G.E.: Stochastic modeling of random roughness in shock scattering problems: theory and simulations. Comput. Methods Appl. Mech. Eng. 197(43–44), 3420–3434 (2006)
Loéve, M.: Probability Theory I. Graduate Texts in Mathematics, vol. 45. Springer, New York (1977)
Loéve, M.: Probability Theory II. Graduate Texts in Mathematics, vol. 46. Springer, New York (1978)
Matthies, H.G., Keese, A.: Galerkin methods for linear and nonlinear elliptic stochastic partial differential equations. Comput. Methods Appl. Mech. Eng. 194(1216), 1295–1331 (2005)
Nobile, F., Tempone, R.: Analysis and implementation issues for the numerical approximation of parabolic equations with random coefficients. Int. J. Numer. Meth. Eng. 80, 979–1006 (2009)
Nobile, F., Tempone, R., Webster, C.G.: An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Numer. Anal. 46, 2411–2442 (2008)
Nobile, F., Tempone, R., Webster, C.G.: A sparse grid stochastic collocation method for partial differential equations with random input data. SIAM J. Numer. Anal. 46, 2309–2345 (2008)
Owhadi, H., Zhang, L.: Numerical homogenization of the acoustic wave equations with a continuum of scales. Comput. Methods Appl. Mech. Eng. 198, 397–406 (2008)
Poette, G., Després, B., Lucor, D.: Uncertainty quantification for systems of conservation laws. J. Comput. Phys. 228(7), 2443–2467 (2009)
Rodino, L.: Linear Partial Differential Operators in Gevrey Spaces. World Scientific, Singapore (1993)
Stolk, C.C.: On the modeling and inversion of seismic data. PhD Thesis, Utrecht University (2000)
Tang, T., Zhou, T.: Convergence analysis for stochastic collocation methods to scalar hyperbolic equations with a random wave speed. Commun. Comput. Phys. 8(1), 226–248 (2010)
Todor, R.A., Schwab, C.: Convergence rates for sparse chaos approximations of elliptic problems with stochastic coefficients. IMA J. Numer. Anal. 27(2), 232–261 (2007)
Tryoen, J., Le Maitre, O., Ndjinga, M., Ern, A.: Intrusive projection methods with upwinding for uncertain nonlinear hyperbolic systems. J. Comput. Phys. 229, 6485–6511 (2010)
Tryoen, J., Le Maitre, O., Ndjinga, M., Ern, A.: Roe solver with entropy corrector for uncertain hyperbolic systems. J. Comput. Appl. Math. 235(2), 491–506 (2010)
Wang, X., Karniadakis, G.E.: Long-term behavior of ploynomial chaos in stochastic flow simulations. Comput. Methods Appl. Mech. Eng. 195, 5582–5596 (2006)
Wiener, N.: The homogeneous chaos. Am. J. Math. 60, 897–936 (1938)
Xiu, D., Hesthaven, J.S.: High-order collocation methods for differential equations with random inputs. SIAM J. Sci. Comput. 27(3), 1118–1139 (2005)
Xiu, D., Karniadakis, G.E.: Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos. Comput. Methods Appl. Mech. Eng. 191(43), 4927–4948 (2002)
Xiu, D., Karniadakis, G.E.: The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 24, 619–644 (2002)
Xiu, D., Tartakovsky, D.M.: Numerical methods for differential equations in random domains. SIAM J. Sci. Comput. 28(3), 1167–1185 (2006)
Acknowledgments
The authors would like to thank Olof Runborg and Georgios Zouraris for stimulating discussions and Lorenzo Tamellini for providing parts of source codes for implementing the stochastic collocation algorithm. The first author would also like to thank the MOX center in Politecnico di Milano for a two month visit funded by the Italian grant FIRB-IDEAS (Project n. RBID08223Z) “Advanced numerical techniques for uncertainty quantification in engineering and life science problems”.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the King Abdullah University of Science and Technology (AEA project “Bayesian earthquake source validation for ground motion simulation”), the VR project “Effektiva numeriska metoder för stokastiska differentialekvationer med tillämpningar”, and the PECOS center at ICES, University of Texas at Austin (Project Number 024550, Center for Predictive Computational Science). The second author was partially supported by the Italian grant FIRB-IDEAS (Project no. RBID08223Z) “Advanced numerical techniques for uncertainty quantification in engineering and life science problems”.
Appendix
Appendix
Lemma 10
Consider the 1D Cauchy problem for the scalar wave equation in the conservative form
and in the non-conservative form
subjected to the initial conditions
Suppose that
-
\(c(x)\) is positive bounded away from zero and smooth everywhere except at \(x=0\) where it has a discontinuity,
-
\(g(x)\) and \(h(x)\) are smooth, compactly supported functions and \(0 \notin \text{ supp} \, g \cup \text{ supp} \, h\),
-
\(\partial _t^k f \in L^2(\mathbb{R })\) for each fixed \(t\), and \(\partial _t^k f = 0\) at \(t=0\) for all \(k \ge 0\).
Then, for each fixed \(t\), for solutions \(u\) to any of the two wave equations (52) and (53),
Proof
Let \(v := \partial _t^k u\). Then, for the conservative form, \(v\) solves the Cauchy problem
with the initial conditions
and
For the non-conservative form, \(v\) solves the Cauchy problem
with the initial conditions
and
Since the functions \(g\) and \(h\) are smooth and their support does not include the discontinuity point of \(c(x)\), the initial data for \(v\) in both problems are smooth for all \(k\). It is well known that for the wave equations (54) and (55) with smooth initial data and \(L^2\) forcing term [11],
This completes the proof. \(\square \)
Theorem 7
Consider the 1D Cauchy problem for the scalar wave equation in the conservative form
subjected to the initial conditions
Let \(z_{k,l} := \partial _y^k \partial _t^l c u_x\), and assume that the assumptions of Lemma 10 hold. If \(\partial _y^k c \in L^{\infty }(\mathbb{R }), \forall k \ge 0\), then for each fixed \(t\) and \(y\),
Proof
We show the result by induction on \(k\).
Case \(k=0\). We have \(\partial _t z_{0,l} = c \, \partial _t^{l+1} u_x\) which belongs to \(L^2(\mathbb{R })\) by Lemma A2 for all \(l \ge 0\). Moreover, differentiating (56) \(l\) times with respect to \(t\) and once with respect to \(x\) and multiplying by \(c\), we obtain
Therefore, \(\partial _{xx} z_{0,l} \in L^2(\mathbb{R })\) for all \(l \ge 0\), because \(\partial _t z_{0,l+1} \in L^2(\mathbb{R })\).
General case. We assume that (58) holds with \(k < K\). Differentiating (59) \(K\) times with respect to \(y\) gives us
Since the right hand side belongs to \(L^2(\mathbb{R })\) by the induction hypothesis, Lemma 10 tells us that \(\partial _t z_{K,l} \in L^2(\mathbb{R })\) for all \(l \ge 0\). Moreover,
where the right hand side is in \(L^2(\mathbb{R })\). This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Motamed, M., Nobile, F. & Tempone, R. A stochastic collocation method for the second order wave equation with a discontinuous random speed. Numer. Math. 123, 493–536 (2013). https://doi.org/10.1007/s00211-012-0493-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-012-0493-5