On dual pairs in Dirac geometry

Abstract

In this note we discuss (weak) dual pairs in Dirac geometry. We show that this notion appears naturally when studying the problem of pushing forward a Dirac structure along a surjective submersion, and we prove a Dirac-theoretic version of Libermann’s theorem from Poisson geometry. Our main result is an explicit construction of self-dual pairs for Dirac structures. This theorem not only recovers the global construction of symplectic realizations from Crainic and Mărcuţ (J Symplectic Geom 9(4):435–444, 2011), but allows for a more conceptual understanding of it, yielding a simpler and more natural proof. As an application of the main theorem, we present a different approach to the recent normal form theorem around Dirac transversals from Bursztyn et al. (J für die reine und angewandte Mathematik (Crelles J), doi:10.1515/crelle-2017-0014, 2017).

1 Introduction

A symplectic realization

$$\begin{aligned} \mathbf {s}: (\Sigma ,\omega ^{-1}) \longrightarrow (M,\pi ) \end{aligned}$$

of a Poisson manifold $(M,\pi )$ is a surjective and submersive Poisson map $\mathbf {s}$ from a symplectic manifold $(\Sigma ,\omega )$.¹ The importance of symplectic realizations had been manifest since the early days of Poisson geometry (see [20, 26, 38]).

Our main result concerns one of the possible Dirac-theoretic² incarnations of the notion of symplectic realizations. Namely, we consider the following:

Problem

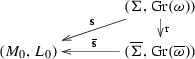
Given a Dirac structure $L \subset TM\oplus T^*M$ on a manifold M, find a surjective submersion $\mathbf {s}:\Sigma \rightarrow M$ and a closed two-form $\omega$ on $\Sigma$ such that

$$\begin{aligned} \mathbf {s}: (\Sigma ,\mathrm {Gr}(\omega )) \longrightarrow (M,L), \end{aligned}$$

is a forward Dirac map (where $\mathrm {Gr}(\omega )$ denotes the graph of $\omega$).

In the Poisson case, a global, direct proof of the existence of symplectic realizations was presented in [19]. Our result is a natural extension of this construction to the Dirac setting. Moreover, our construction produces a dual pair, which is one of the main notions introduced in this paper, which generalizes to the Dirac setting the classical notion of dual pair in Poisson geometry:

Definition

A dual pair consists of surjective, forward Dirac submersions

$$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}), \end{aligned}$$

where $\omega$ is a closed two-form on $\Sigma$, such that the following hold:

$$\begin{aligned} \omega (V,W)=0,\quad V\cap \ker \omega \cap W=0,\ \quad \mathrm {dim}(\Sigma )=\mathrm {dim}(M_0)+\mathrm {dim}(M_1), \end{aligned}$$

where $V:=\ker \mathbf {s}_*$ and $W:=\ker \mathbf {t}_*$.

The prototypical example of a dual pair is given by the presymplectic groupoid of an integrable Dirac structure [10].

We present the following solution to the Problem above (for a full statement of the result, including the explicit construction, see Sect. 6):

Main Theorem

Any Dirac manifold (M, L) fits into a self-dual pair

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M,-L). \end{aligned}$$

Here is an outline of the main results of the paper, and of its organization:

Section  2 establishes the notation and conventions used in the paper. Throughout, the symbol § refers to this Section.

Section 3 discusses in detail the problem of pushing forward a Dirac structure L on $\Sigma$ to a Dirac structure on M via a surjective submersion $\mathbf {s}: \Sigma \rightarrow M$ with connected fibres. The prototypical statement is Libermann’s theorem [29], which states that a non-degenerate Poisson structure $\omega ^{-1}\in \mathfrak {X}^2(\Sigma )$, corresponding to a symplectic structure $\omega \in \Omega ^2(\Sigma )$, can be pushed forward through $\mathbf {s}$ to a Poisson structure on M if and only if the symplectic orthogonal to the vertical foliation $\ker \mathbf {s}_*$ is involutive. We prove a general Dirac version of Libermann’s theorem:

Proposition

(Dirac–Libermann) A Dirac structure L on $\Sigma$ can be pushed forward via $\mathbf {s}$ to a Dirac structure on M if and only if the Lagrangian family (see §5)

$$\begin{aligned} p \mapsto L^{\mathbf {s}}_p:=\mathbf {s}^!(\mathbf {s}_!(L_p))\subset T_p\Sigma \oplus T_p^*\Sigma \end{aligned}$$

is a Dirac structure on $\Sigma$ – i.e. iff it forms a smooth, involutive subbundle of $\mathbb {T}\Sigma$.

Several criteria are discussed regarding smoothness and involutivity of $L^{\mathbf {s}}$.

Section 4 first discusses the above proposition in the case when $L = \mathrm {Gr}(\omega )$ is the graph of a closed two-form $\omega \in \Omega ^2(\Sigma )$. In particular, we show that a sufficient condition for a surjective submersion with connected fibres $\mathbf {s}: \Sigma \rightarrow M$ to push forward a closed two-form $\omega \in \Omega ^2(\Sigma )$ is the existence of an involutive subbundle $W \subset T\Sigma$ such that $L^{\mathbf {s}}=V+\mathcal {R}_{\omega }(W)$, where $V:=\ker \mathbf {s}_*$ and $\mathcal {R}_{\omega }(W)$ stands for the gauge-transformation of W under $\omega$ (see §10). This leads naturally to the notions of weak dual pairs and dual pairs of Dirac structures, which we discuss in this section. Next, we give several equivalent descriptions of these notions, and present several illustrative examples.

Section  5 discusses natural operations on weak dual pairs:

• composition of two weak dual pairs with one common leg,

• pullback of a weak dual pair through a surjective submersion,

• reduction of a weak dual pair to a dual pair,

• pullback of a (weak) dual pair via transverse maps,

the latter to be used in the proof of the Main Theorem.

Section 6 presents the complete statement and the proof of the Main Theorem. This result generalizes the construction of symplectic realization for Poisson structures from [19]; however, the proof presented here is completely conceptual, and bypasses all the unilluminating calculations in loc. cit., relying on natural Dirac geometric operators (like pullback, gauge transformations) which are not generally available in the Poisson setting.

Section 7 provides, as an application of the Main Theorem, an alternative proof of the normal form theorem around Dirac transversals from [13]. In fact, the initial motivation for undertaking this project had been to prove a Dirac version of the normal form theorem of [21] by extending the techniques from the Poisson setting; the outcome is the result stated below. In [13], this theorem is obtained through a completely different approach, by using a result on linearization of vector fields around submanifolds, which applies to other geometric settings (such as Lie algebroids, singular foliations, generalized complex structures etc.).

A Dirac transversal in a Dirac manifold (M, L) is an embedded submanifold $i:X \hookrightarrow M$ which is transverse to every presymplectic leaf of (M, L). Such submanifolds inherit a Dirac structure $i^!(L)$.

Theorem

(Normal form around Dirac transversals) Let $i:X \hookrightarrow M$ be a Dirac transversal in a Dirac manifold (M, L), and let $p:NX \rightarrow X$ denote its normal bundle. Then, up to a diffeomorphism extending i and an exact gauge-transformation, L and $p^!i^!(L)$ are isomorphic around X.

We refer the reader to Sect. 7 for the detailed statement.

Section  8 indicates connections with other results from the literature, and presents possible implications and extensions of our work. The origin of the formula from the Main Theorem is explained in terms of the path-space approach to integrability of Dirac structures [10, 17]; we explain that our Main Theorem can be used to find explicit models for local presymplectic groupoids; we give the necessary ingredients to extend our results to twisted Dirac structures; and finally, we discuss the relation between dual pairs and Morita equivalence in Poisson geometry.

2 Conventions and notation

• §1. The standard Courant algebroid of a smooth manifold M is denoted by $\mathbb {T}M$, and $\mathrm {pr}_T,\mathrm {pr}_{T^*}$ denote the canonical projections:

  

• §2. $\mathbb {T}M$ comes equipped with a nondegenerate, symmetric bilinear pairing

  $$\begin{aligned} \langle \cdot ,\cdot \rangle :\mathbb {T}M \times \mathbb {T}M \longrightarrow \mathbb {R}, \quad \langle u+\xi ,v+\eta \rangle :=\iota _v\xi +\iota _u\eta , \end{aligned}$$

  and the Dorfman bracket at the level of sections:

  $$\begin{aligned}{}[\cdot ,\cdot ] : \Gamma (\mathbb {T} M) \times \Gamma (\mathbb {T} M) \longrightarrow \Gamma (\mathbb {T} M), \quad [u+\xi ,v+\eta ]:=[u,v]+\mathscr {L}_u\eta - \iota _v\mathrm {d}\xi . \end{aligned}$$

• §3. For a smooth map $\varphi : M_0 \rightarrow M_1$, the elements $a_0=u_0+\xi _0 \in \mathbb {T}_{x_0}M_0$ and $a_1=u_1+\xi _1 \in \mathbb {T}_{x_1}M_1$ are $\varphi$-related [31, Definition 2.12], denoted $a_0 \sim _{\varphi } a_1$, if

  $$\begin{aligned} \varphi (x_0) = x_1, \quad \varphi _*(u_0)=u_1, \quad \xi _0 = \varphi ^*\xi _1. \end{aligned}$$

  The notion of being $\varphi$-related applies to sections $a_0 \in \Gamma (\mathbb {T}M_0)$ and $a_1 \in \Gamma (\mathbb {T}M_1)$ as well, meaning that $a_{0,x_0} \sim _{\varphi } a_{1,\varphi (x_0)}$ for every $x_0 \in M_0$. Note that if $a_0,b_0 \in \Gamma (\mathbb {T}M_0)$ and $a_1,b_1 \in \Gamma (\mathbb {T}M_1)$ are such that

  $$\begin{aligned} a_0 \sim _{\varphi } a_1, \quad b_0 \sim _{\varphi } b_1, \end{aligned}$$

  then also $[a_0,b_0] \sim _{\varphi } [a_1,b_1]$ (see e.g. the proof of [31, Proposition 2.13]).

• §4. A subset $E \subset \mathbb {T}M$ which meets each fibre $\mathbb {T}_xM$ in a linear subspace $E_x:=E \cap \mathbb {T}_xM$ is called a linear family. Note that no continuity is assumed for the assignment $x \mapsto E_x$. The $\langle \cdot ,\cdot \rangle$-orthogonal of a linear family E is denoted by $E^{\perp } \subset \mathbb {T}M$. If $E \subset E^{\perp }$, then E is called an isotropic family.

• §5. A linear family satisfying $E=E^{\perp }$ is called a Lagrangian family; equivalently, if each $E_x \subset (\mathbb {T}_xM,\langle \cdot ,\cdot \rangle )$ is a maximal isotropic subspace. The set of maximal isotropic linear subspaces of $\mathbb {T}_xM$ is denoted by $\mathrm {Lag}(\mathbb {T}_x M)$.

• §6. A linear family $E \subset \mathbb {T}M$ which is a smooth subbundle of $\mathbb {T}M$ is called smooth; if in addition E is Lagrangian, then it is called a Lagrangian subbundle.

  The graph of a two-form $\omega \in \Omega ^2(M)$ and the graph of a bivector field $\pi \in \mathfrak {X}^2(M)$ are the following Lagrangian subbundles, respectively,

  $$\begin{aligned} \mathrm {Gr}(\omega ) := \{ u+\iota _u\omega \ | \ u \in TM\}, \quad \mathrm {Gr}(\pi ) := \{ \pi ^{\sharp }\xi +\xi \ | \ \xi \in T^*M\}. \end{aligned}$$

• §7. An arbitrary linear family $E \subset \mathbb {T}M$ is called involutive if $[a,b] \in \Gamma (E)$ whenever $a,b \in \Gamma (E)$.

• §8. A Dirac structure is an involutive Lagrangian subbundle. For instance, the Lagrangian subbundle $\mathrm {Gr}(\omega )$ defined by a two-form $\omega \in \Omega ^2(M)$ is a Dirac structure iff $\omega$ is closed, whereas the Lagrangian subbundle $\mathrm {Gr}(\pi )$ defined by a bivector $\pi \in \mathfrak {X}^2(M)$ is a Dirac structure iff $\pi$ is Poisson.

• §9. The Courant tensor of a Lagrangian subbundle L is defined by

  $$\begin{aligned} \Upsilon \in \Gamma (\wedge ^3L^*), \quad \Upsilon (a_1,a_2,a_3):=\langle [a_1,a_2],a_3\rangle , \end{aligned}$$

  and it vanishes exactly when L is a Dirac structure [16, Proposition 2.3.3].

• §10. The following operations on Dirac structures will be used:

  • rescaling a Dirac structure $L \subset \mathbb {T}M$ by a scalar $\lambda \ne 0$:

    $$\begin{aligned} \lambda L := \{ u+\lambda \xi \ | \ u+\xi \in L\}; \end{aligned}$$

    in particular, $-L=(-1)L$ denotes the opposite Dirac structure;

  • gauge-transformation by a closed two-form $\omega \in \Omega ^2(M)$:

    $$\begin{aligned} \mathcal {R}_{\omega }(L) := \{ u+\xi +\iota _u\omega \ | \ u+\xi \in L\}; \end{aligned}$$

  • pullbacks through submersions: the pullback of a Dirac structure $L \subset \mathbb {T}M$ through a submersion $\mathbf {s}: \Sigma \rightarrow M$ is given by

    $$\begin{aligned} \mathbf {s}^!(L) \subset \mathbb {T}\Sigma , \quad \mathbf {s}^!(L)_p = \{ u+\mathbf {s}^*(\xi ) \in \mathbb {T}_p\Sigma \ | \ \mathbf {s}_*(u)+\xi \in L_{\mathbf {s}(p)}\}. \end{aligned}$$

• §11. A smooth map $\varphi : M_0 \rightarrow M_1$ gives rise to pointwise operations of pullback and push-forward:

  $$\begin{aligned}&\varphi ^!: \mathrm {Lag}(\mathbb {T}_{\varphi (x_0)} M_1) \longrightarrow \mathrm {Lag}(\mathbb {T}_{x_0} M_0), \quad \varphi ^!(L_{1,x_1}):=\{a_0 \ | \ a_0 \sim _{\varphi } a_1 \in L_{1,\varphi (x_0)}\}\\&\varphi _!: \mathrm {Lag}(\mathbb {T}_{x_0} M_0) \longrightarrow \mathrm {Lag}(\mathbb {T}_{\varphi (x_0)} M_1), \quad \varphi _!(L_{0,x_0}):=\{a_1 \ | \ L_{0,x_0} \ni a_0 \sim _{\varphi } a_1\}. \end{aligned}$$

  A smooth map between Dirac manifolds $\varphi : (M_0,L_0) \rightarrow (M_1,L_1)$ is called

  • forward if $\varphi _!(L_{0,x_0}) = L_{1,\varphi (x_0)}$ for all $x_0 \in M_0$;

  • backward if $L_{0,x_0}=\varphi ^!(L_{1,\varphi (x_0)})$ for all $x_0 \in M_0$.

• §12. In general, for a smooth map $\varphi : M_0 \rightarrow M_1$ and a Lagrangian subbundle $L_1$ on $M_1$, $\varphi ^!(L_1)$ need not be smooth. However (see e.g. [11, Proposition 5.6]):

  • (a) A sufficient criterion ensuring smoothness of $\varphi ^!(L_1)$ is that $L_1 \cap \ker (\varphi ^*)$ have constant rank;

  • (b) In particular, $\varphi ^!(L_1)$ is smooth when $\varphi$ is transverse to $L_1$, i.e., when either of the equivalent conditions holds:

    • (i) $L_1 \cap \ker (\varphi ^*) = 0$;

    • (ii) for all $x_0 \in M_0$, we have that $\varphi _*(T_{x_0}M_0) + \mathrm {pr}_T(L_{1,\varphi (x_0)}) = T_{\varphi (x_0)}M_1$;

  • (c) When $L_1$ is a Dirac structure and $\varphi ^!(L_1)$ is smooth, then it is automatically a Dirac structure.

• §13. Let $A_1 \rightarrow M_1$ be a vector bundle, and let $\varphi : M_0 \rightarrow M_1$ be a smooth map. Denote by $\varphi ^*(A_1):=M_0 \times _{M_1}A_1 \rightarrow M_0$ the pullback vector bundle. If $A_0 \rightarrow M_0$ is another vector bundle, a vector bundle map $\Phi : \varphi ^*(A_1) \rightarrow A_0$ over $\mathrm {id}_{M_0}$ is called a comorphism of vector bundles.

  A comorphism of vector bundles $\Phi : \varphi ^*(A_1) \rightarrow A_0$ induces a map on sections

  $$\begin{aligned} \Phi ^{\dagger } : \Gamma (A_1) \rightarrow \Gamma (A_0),\quad a_1\mapsto \Phi \circ a_1\circ \varphi . \end{aligned}$$

  If $A_i \rightarrow M_i$ are Lie algebroids, with anchor maps $\varrho _i:A_i \rightarrow TM_i$, a comorphism of vector bundles $\Phi :\varphi ^*(A_1) \rightarrow A_0$ is called a comorphism of Lie algebroids if it is compatible with anchors, $\varphi _* \circ \varrho _0 \circ \Phi = \varrho _1$, and the induced map of sections $\Phi ^{\dagger }$ is a Lie algebra homomorphism. A comorphism of Lie algebroids $\Phi$ is called complete if the following condition is met: if $a_1 \in \Gamma (A_1)$ is such that $\varrho _1(a_1) \in \mathfrak {X}(M_1)$ is a complete vector field, then $\varrho _0(\Phi ^{\dagger }a_1) \in \mathfrak {X}(M_0)$ is also a complete vector field. See e.g. [15] for more details on comorphisms.

3 Pushing forward Dirac structures

In this section, we discuss the following problem: given a Dirac structure $L \subset \mathbb {T}\Sigma$, when does a surjective submersion with connected fibres

$$\begin{aligned} \mathbf {s}: \Sigma \longrightarrow M \end{aligned}$$

push L forward to a Dirac structure $L_M \subset \mathbb {T}M$, i.e. when is there a Dirac structure $L_M$ for which $\mathbf {s}: (\Sigma ,L) \rightarrow (M,L_M)$ is a forward Dirac submersion?

First observe that, for a given $L_M \subset \mathbb {T}M$, there exists a canonical Dirac structure on $\Sigma$ for which $\mathbf {s}: (\Sigma ,L) \rightarrow (M,L_M)$ is forward Dirac—namely, the basic Dirac structure $L=\mathbf {s}^!(L_M)$:

Definition 1

Let $\mathbf {s}: \Sigma \rightarrow M$ be a surjective submersion. A Dirac structure L on $\Sigma$ is called basic if there exists a Dirac structure $L_M$ on M such that $L=\mathbf {s}^!(L_M)$, i.e., for which

$$\begin{aligned} \mathbf {s}: (\Sigma ,L) \longrightarrow (M,L_M) \end{aligned}$$

is a backward Dirac submersion.

The following proposition describes those Dirac structures on $\Sigma$ which are basic:

Proposition 1

(Basic criterion) Let $\mathbf {s}:\Sigma \rightarrow M$ be a surjective submersion with connected fibres, and denote by $V:=\ker \mathbf {s}_*\subset T\Sigma$. A Dirac structure L on $\Sigma$ is basic, $L=\mathbf {s}^!(L_M)$, if and only if $V\subset L$. In this case, we also have that $\mathbf {s}:(\Sigma ,L)\rightarrow (M,L_M)$ is a forward Dirac map.

Proof

If L is basic, $L=\mathbf {s}^!(L_M)$, then clearly $V\subset L$ and, since $\mathbf {s}$ is a submersion, we also have that $\mathbf {s}_!\mathbf {s}^!(L_M)=L_M$.

Conversely, assume that $V\subset L$. Then the flow of vector fields in V preserves L. Since the fibres of $\mathbf {s}$ are connected, this implies that, for every $p,q\in \mathbf {s}^{-1}(x)$, we can find a diffeomorphism $\varphi :\Sigma \rightarrow \Sigma$ such that $\varphi (p)=q$, $\varphi _!(L_p)=L_q$, and which is vertical: $\mathbf {s}\circ \varphi =\mathbf {s}$. So $\mathbf {s}_!(L_q)=\mathbf {s}_!\varphi _!(L_p)=\mathbf {s}_!(L_p)$. Thus, there is a well-defined Lagrangian family $x\mapsto L_{M,x}\in \mathbb {T}_xM$ such that $\mathbf {s}_!(L_p)=L_{M,\mathbf {s}(p)}$ for all $p\in \Sigma$.

Smoothness and involutivity of $L_M$ (in the sense of §6, §7) are proven as follows. First, remark that the submersion $\mathbf {s}$ admits local sections $\sigma :U\rightarrow \Sigma$, $U \subset M$, and that any such local section $\sigma$ is transverse to L, i.e. it satisfies:

$$\begin{aligned} \sigma _{*}(T_xM)+\mathrm {pr}_{T}(L_{\sigma (x)})=T_{\sigma (x)}\Sigma , \ \ \forall \ x\in U, \end{aligned}$$

and this condition implies that $\sigma ^!(L)$ is a Dirac structure on U (see §12). Second, note that $V\subset L$ implies that $L\subset T\Sigma \oplus {\text {im}}\mathbf {s}^*$. Now, if $v+\sigma ^{*}\alpha \in \sigma ^!(L)$, then $\sigma _*v+\alpha \in L\subset T\Sigma \oplus {\text {im}}\mathbf {s}^*$, and so $\alpha =\mathbf {s}^*\beta$ for some $\beta \in T^*M$; hence $\mathbf {s}_*\sigma _*v+\beta =v+\beta \in L_M$. Thus, $\sigma ^!(L)\subset L_M|_U$, and since these spaces have equal dimension, we conclude that $L_M|_U=\sigma ^!(L)$. This proves that $L_M$ is a Dirac structure.

Let us conclude by showing that $\mathbf {s}^!(L_M)=L$. An element in $\mathbf {s}^!(L_M)$ has the form $v+\mathbf {s}^*\alpha$, where $\mathbf {s}_*v+\alpha \in L_M$. Since $L_M=\mathbf {s}_!(L)$, there exists $w\in T\Sigma$ such that $\mathbf {s}_*w=\mathbf {s}_*v$ and $w+\mathbf {s}^*\alpha \in L$. But then $w-v\in V\subset L$; hence $v+\mathbf {s}^*\alpha =(w+\mathbf {s}^*\alpha )+(v-w)\in L$. $\square$

Given a surjective submersion $\mathbf {s}: \Sigma \rightarrow M$ from a Dirac manifold $(\Sigma ,L)$, there is a canonical Lagrangian family (see §5)

$$\begin{aligned} L^{\mathbf {s}} \subset \mathbb {T}\Sigma , \quad L^{\mathbf {s}}_p:=\mathbf {s}^!(\mathbf {s}_!(L_p)) \subset \mathbb {T}_p \Sigma , \quad p \in \Sigma , \end{aligned}$$

which one can view as the Lagrangian family closest to L among Lagrangian families which contain $V:=\ker \mathbf {s}_*$ [14, Section 3], since it satisfies

$$\begin{aligned} L^{\mathbf {s}} = L \cap V^{\perp } + V. \end{aligned}$$

(1)

Whether or not the Lagrangian family $L^{\mathbf {s}}$ is a Dirac structure (see §6–§8) plays a key role in the following Dirac-geometric version of Libermann’s theorem.

Proposition 2

(Dirac–Libermann) Let $\mathbf {s}:\Sigma \rightarrow M$ be a surjective submersion with connected fibres. A Dirac structure L on $\Sigma$ can be pushed forward via $\mathbf {s}$ to a Dirac structure on M if and only if the Lagrangian family:

$$\begin{aligned} L^{\mathbf {s}}=\mathbf {s}^!\mathbf {s}_!(L)\subset \mathbb {T}\Sigma \end{aligned}$$

is a Dirac structure on $\Sigma$, i.e., if $L^{\mathbf {s}}$ is a smooth, involutive subbundle of $\mathbb {T}\Sigma$.

Proof

First, if L can be pushed forward to a Dirac structure $L_M$ on M, then $L^{\mathbf {s}}=\mathbf {s}^!(L_M)$ is a Dirac structure on $\Sigma$, as it is the pullback of a Dirac structure through a surjective submersion (see §10).

Conversely, assume that $L^{\mathbf {s}}$ is a Dirac structure. Note that $\mathbf {s}_!(L^{\mathbf {s}}_p)=\mathbf {s}_!(L_p)$ for all $p\in \Sigma$ (see §11); hence it suffices to check that $L^{\mathbf {s}}$ can be pushed forward. Since $V\subset L^{\mathbf {s}}$, this follows from Proposition 1. $\square$

The purpose of the next two examples is to highlight that, under the hypotheses of Proposition 2, neither smoothness nor involutivity of $L^{\mathbf {s}}$ is ensured.

Example 1

Consider $\mathbf {s}:\mathbb {R}^2\rightarrow \mathbb {R}$, $\mathbf {s}(x,y)=x$, and let $L=\mathrm {Gr}(x \mathrm {d}x \wedge \mathrm {d}y)$. Then the Lagrangian family $L^{\mathbf {s}}$ is not smooth; explicitly, it is given by

$$\begin{aligned} L^{\mathbf {s}}_{(x,y)} = {\left\{ \begin{array}{ll} \mathbb {R}\partial _y+\mathbb {R}x\mathrm {d}x &{}\quad \text {if} \ x \ne 0,\\ \mathbb {R}\partial _x+\mathbb {R}\partial _y &{}\quad \text {if} \ x = 0. \end{array}\right. } \end{aligned}$$

In particular, $\mathbf {s}$ does not push L forward to a Dirac structure on $\mathbb {R}$.

Example 2

Consider $\mathbf {s}:\mathbb {R}^3\rightarrow \mathbb {R}^2$, $\mathbf {s}(x,y,z)=(x,y)$, and let $L=\mathrm {Gr}(z \partial _x \wedge \partial _y)$. In this case the smooth sections $s_i \in \Gamma (\mathbb {T}\mathbb {R}^3)$ given by

$$\begin{aligned} s_1 = z\partial _x-\mathrm {d}y, \quad s_2=z\partial _y+\mathrm {d}x, \quad s_3=\partial _z \end{aligned}$$

span $L^{\mathbf {s}}$; hence $L^{\mathbf {s}}$ is a smooth bundle. However, it is not involutive; e.g., $[s_3,s_1] =\partial _x \notin \Gamma (L^{\mathbf {s}})$. In particular, $\mathbf {s}$ does not push L forward to a Dirac structure on $\mathbb {R}^2$.

3.1 Sufficient criteria

Next, we give sufficient criteria for $L^{\mathbf {s}}$ to be a Dirac structure.

Proposition 3

(Bundle criterion) Let $(\Sigma ,L)$ be a Dirac manifold and let $\mathbf {s}: \Sigma \rightarrow M$ be a surjective submersion.

• (i) If a vector subbundle $E \subset \mathbb {T}\Sigma$ exists, such that

  $$\begin{aligned} L^{\mathbf {s}}=E+V, \end{aligned}$$

  then $L^{\mathbf {s}}$ is smooth. This condition is also necessary for $L^{\mathbf {s}}$ to be smooth.

• (ii) If in addition E is involutive, then also $L^{\mathbf {s}}$ is involutive. Hence, if $\mathbf {s}$ has connected fibres, then there is a Dirac structure $L_M$ on M for which $\mathbf {s}:(\Sigma ,L)\rightarrow (M,L_M)$ is a forward Dirac map.

Proof

Note that $L^{\mathbf {s}}$ is the image of the vector bundle map

$$\begin{aligned} F:E\oplus V\longrightarrow \mathbb {T}\Sigma ,\ \ \ F(e,v):= e+v. \end{aligned}$$

Since $L^{\mathbf {s}}$ is a family of Lagrangian subspaces, we conclude that F has constant rank, and therefore $L^{\mathbf {s}}$ is smooth. Conversely, if $L^{\mathbf {s}}$ is smooth, then one can take E to be any smooth complement of V in $L^{\mathbf {s}}$. This proves (i).

By choosing a smooth splitting of the vector bundle map F, note that any section $s\in \Gamma (L^{\mathbf {s}})$ can be represented as $s=v+e$, where $v\in \Gamma (V)$ and $e\in \Gamma (E)$. Assume now that E is involutive. Recall that the smooth Lagrangian subbundle $L^{\mathbf {s}}=E+V$ is Dirac iff the Courant tensor $\Upsilon \in \Gamma (\bigwedge ^3 (L^{\mathbf {s}})^*\big )$, $\Upsilon (s_1,s_2,s_3)=\langle [s_1,s_2],s_3\rangle$ vanishes identically (see §9). So to check that $\Upsilon =0$, it suffices to show that it vanishes on sections which are either in $\Gamma (V)$ or in $\Gamma (E)$. For $i=1,2,3$, let $v_i\in \Gamma (V)$ and $e_i\in \Gamma (E)$. Because V and E are involutive and $E+V$ is isotropic, we have

$$\begin{aligned} \Upsilon (v_1,v_2,v_3)=0, \quad \Upsilon (v_1,v_2,e_1)=0, \quad \Upsilon (e_1,e_2,v_3)=0, \quad \Upsilon (e_1,e_2,e_3)=0. \end{aligned}$$

Thus, $\Upsilon =0$, and therefore $L^{\mathbf {s}}$ is Dirac. Hence if $\mathbf {s}$ has connected fibres, we can invoke Proposition 2 to conclude that $\mathbf {s}$ pushes L forward. This proves (ii). $\square$

Since $L^{\mathbf {s}}=L\cap V^{\perp }+V$ (1), a candidate for the vector bundle E in Proposition 3 is the isotropic family $L\cap V^{\perp }$—which need not be smooth. The next criterion shows that, if $L^{\mathbf {s}}$ is smooth, then its involutivity is controlled by that of $L\cap V^{\perp }$.

Proposition 4

($L\cap V^{\perp }$ criterion) Let $(\Sigma ,L)$ be a Dirac manifold and let $\mathbf {s}: \Sigma \rightarrow M$ be a surjective submersion.

• (i) If $L\cap V^{\perp }$ (or equivalently, if $L\cap V$) is smooth, then $L^{\mathbf {s}}$ is smooth.

• (ii) If $L^{\mathbf {s}}$ is smooth, then $L^{\mathbf {s}}$ is involutive if and only if $L\cap V^{\perp }$ is involutive in the sense of §7.

Proof

Note that $L \cap V$ has constant rank iff $L+V$ has constant rank iff $(L+V)^{\perp }=L\cap V^{\perp }$ has constant rank. Thus (i) follows from Proposition 3(i).

Note that $L\cap V^{\perp }=L \cap L^{\mathbf {s}}$. Thus, if $L^{\mathbf {s}}$ is involutive, then, being the intersection of two involutive subbundles, so is $L\cap V^{\perp }$. Conversely, suppose that $L\cap V^{\perp }$ is involutive. Note that the isotropic family $L\cap V^{\perp }$ restricts on an open, dense subset $U \subset \Sigma$ to a vector bundle $E=L\cap V^{\perp }|_U$; hence Proposition 3(ii) applies, showing that $L^{\mathbf {s}}|_U$ is a Dirac structure on U. Hence the Courant tensor $\Upsilon$ of $L^{\mathbf {s}}$ (see §9) vanishes on an open, dense subset, whence it vanishes on the whole $\Sigma$. Thus, $L^{\mathbf {s}}$ is a Dirac structure. $\square$

Remark 1

When $L^{\mathbf {s}}$ is a Dirac structure, and $\mathbf {s}$ has connected fibres, $L^{\mathbf {s}}$ is a basic Dirac structure, i.e., $L^{\mathbf {s}}=\mathbf {s}^!(L_M)$ for a Dirac structure $L_M$ on M. In this case, there is an induced bundle map $\mathbf {s}_! : L^{\mathbf {s}} \rightarrow L_M$ covering $\mathbf {s}:\Sigma \rightarrow M$, where $s_!(a) = b$ iff $a \in L^{\mathbf {s}}_{p}$ and $b \in L_{M,\mathbf {s}(p)}$ are $\mathbf {s}$-related: $a \sim _{\mathbf {s}} b$ (see §3). Note that this gives rise to an exact sequence of Lie algebroids

$$\begin{aligned} 0 \longrightarrow V \longrightarrow L^{\mathbf {s}} {\mathop {\longrightarrow }\limits ^{\mathbf {s}_{!}}} L_M \longrightarrow 0. \end{aligned}$$

The next criterion concerns the existence of a splitting of this sequence.

Proposition 5

(Comorphism criterion) Let $\mathbf {s}: \Sigma \rightarrow M$ be a surjective submersion with connected fibres from the Dirac manifold $(\Sigma ,L)$. If an involutive subbundle $E \subset \mathbb {T}\Sigma$ exists such that

$$\begin{aligned} L^{\mathbf {s}}=E \oplus V, \end{aligned}$$

then there is an induced comorphism of Lie algebroids $\Phi :\mathbf {s}^*(L_M) \rightarrow E$, where $L_M$ is the push-forward Dirac structure on M, $L_M=\mathbf {s}_{!}(L)$.

Proof

By Proposition 3(ii), $\mathbf {s}$ pushes L forward to a Dirac structure $L_M$ on M. The surjective vector bundle map $\mathbf {s}_!: L^{\mathbf {s}} \rightarrow L_M$ covering $\mathbf {s}$ induces an exact sequence of vector bundles over $\Sigma$

$$\begin{aligned} 0 \longrightarrow V \longrightarrow L^{\mathbf {s}} \longrightarrow \mathbf {s}^*(L_M) \longrightarrow 0 \end{aligned}$$

which restricts to a vector bundle isomorphism on (see Remark 1). Denote by $\Phi : \mathbf {s}^*(L_M) \rightarrow E$ the inverse isomorphism, which is a vector bundle comorphism. By definition of $\Phi$, we have that, for each $a \in \Gamma (L_M)$, $\Phi ^{\dagger }(a) \in \Gamma (E)$ is the unique section such that $\Phi ^{\dagger }(a) \sim _{\mathbf {s}} a$; in particular, it is compatible with anchors. Moreover (see §3) $\Phi ^{\dagger }([a,b]) \sim _{\mathbf {s}} [a,b]$, and $[\Phi ^{\dagger }(a),\Phi ^{\dagger }(b)] \sim _{\mathbf {s}} [a,b]$ imply that $\Phi ^{\dagger }([a,b])=[\Phi ^{\dagger }(a),\Phi ^{\dagger }(b)]$; hence $\Phi :\mathbf {s}^*(L_M) \rightarrow E$ is a comorphism of Lie algebroids. $\square$

3.2 Coupling Dirac structures

As an application of Proposition 2, we consider the case of when a surjective submersion $\mathbf {s}: \Sigma \rightarrow M$ pushes forward a coupling Dirac structure $L \subset \mathbb {T}\Sigma$, i.e., a Dirac structure satisfying:

$$\begin{aligned} L\cap (V\oplus V^{\circ })=0, \quad \text {where} \ V=\ker \mathbf {s}_*,\ V^{\circ }=\mathrm {im}\phantom {l}\mathbf {s}^*. \end{aligned}$$

Such Dirac structures are also called horizontally nondegenerate [37].

A Lagrangian subbundle $L \subset \mathbb {T}\Sigma$ satisfying the condition above can be described by a Vorobjev triple $(H,\omega ,\pi )$, where $H\subset T\Sigma$ is an Ehresmann connection for $\mathbf {s}:\Sigma \rightarrow M$, $\omega$ is a two-form on H, and $\pi$ is a vertical bivector field:

$$\begin{aligned} T\Sigma =H\oplus V, \ \ \omega \in \Gamma (\wedge ^2 V^{\circ })\subset \Omega ^2(\Sigma ), \ \ \pi \in \Gamma (\wedge ^2 V )\subset \mathfrak {X}^2(\Sigma ), \end{aligned}$$

in terms of which L has the direct sum decomposition:

$$\begin{aligned} L=\{v+\iota _v\omega \ | \ v\in H\}\oplus \{\xi +\pi ^{\sharp }\xi \ | \ \xi \in H^{\circ }\}. \end{aligned}$$

Involutivity of L is equivalent to the following conditions (see e.g. [37]):

• (a) $\pi$ is a Poisson structure: $[\pi ,\pi ]=0$,

• (b) $\mathscr {L}_{u_1}\pi \in \Gamma (H\wedge T\Sigma )$,

• (c) $[u_1,u_2]+\pi ^{\sharp }\iota _{u_1}\iota _{u_2}\mathrm {d}\omega \in \Gamma (H)$,

• (d) $\mathrm {d}\omega (u_1,u_2,u_3)=0$,

for all $u_1,u_2,u_3\in \Gamma (H)$.

In this situation, Proposition 2 specializes to:

Corollary 1

(Coupling Dirac structures) Let $\mathbf {s}:\Sigma \rightarrow M$ be a surjective submersion with connected fibres, and let L be a coupling Dirac structure on $\Sigma$, with corresponding Vorobjev triple $(H,\omega ,\pi )$. Then L can be pushed forward via $\mathbf {s}$ to a Dirac structure on M if and only if $\omega$ is closed. In this case, $\omega =\mathbf {s}^*\eta$, where $\eta$ is a closed two-form on M, $\mathbf {s}_{!}(L)=\mathrm {Gr}(\eta )$, and moreover, H is involutive.

Proof

It is easy to check that $L^{\mathbf {s}}=\mathrm {Gr}(\omega )$. This is always a smooth bundle, and it is a Dirac structure iff $\omega$ is closed. Thus, the first part follows from Proposition 2. By Proposition 1, $\mathrm {Gr}(\omega )$ is a basic Dirac structure, and hence $\omega$ is a basic two-form, i.e. $\omega =\mathbf {s}^*\eta$, where $\eta$ is a closed two-form on M, and $\mathbf {s}:(\Sigma ,L)\rightarrow (M,\mathrm {Gr}(\eta ))$ is a forward Dirac map. By (c) above, $\mathrm {d}\omega =0$ implies that H is involutive. $\square$

4 Weak dual pairs and dual pairs

In this section we discuss the notions of weak dual pairs and dual pairs in Dirac geometry. In the setting of Lie groupoids endowed with multiplicative two-forms, these notions correspond to over-presymplectic groupoids [10, Definition 4.6] and presymplectic groupoids [10, Definition 2.1], respectively.

4.1 Pushing forward two-forms

In order to motivate the notion of weak dual pairs, we begin by specializing Proposition 2 to the case of closed two-forms. Given a closed two-form $\omega \in \Omega ^2(\Sigma )$, denote the corresponding gauge transformation by

$$\begin{aligned} \mathcal {R}_{\omega }:\mathbb {T}\Sigma \longrightarrow \mathbb {T}\Sigma , \quad \mathcal {R}_{\omega }(u+\xi ):=u+\xi +\iota _u\omega . \end{aligned}$$

The $\omega$-orthogonal of a linear space $E\subset T\Sigma$ will be denoted by

$$\begin{aligned} E^{\omega }:=T\Sigma \cap \mathcal {R}_{\omega }(E)^{\perp }\subset T\Sigma . \end{aligned}$$

Given a surjective submersion $\mathbf {s}:\Sigma \rightarrow M$ and denoting $V:=\ker \mathbf {s}_*$, we have that

$$\begin{aligned} \mathrm {Gr}(\omega )\cap V^{\perp }=\mathcal {R}_{\omega }(V^{\omega }), \end{aligned}$$

and so the Lagrangian family $\mathrm {Gr}(\omega )^{\mathbf {s}}$ becomes

$$\begin{aligned} \mathrm {Gr}(\omega )^{\mathbf {s}}=V+\mathrm {Gr}(\omega ) \cap V^{\perp }=V+\mathcal {R}_{\omega }(V^{\omega }). \end{aligned}$$

(2)

The criteria from Sect. 3 specialize to the following:

Corollary 2

Let $\mathbf {s}: \Sigma \rightarrow M$ be a surjective submersion with connected fibres, $\omega \in \Omega ^2(\Sigma )$ be a closed two-form, and let $V:=\ker \mathbf {s}_*$.

• (i) $\mathbf {s}$ pushes $\mathrm {Gr}(\omega )$ to a Dirac structure $L_M$ on M if and only if the Lagrangian family $\mathrm {Gr}(\omega )^{\mathbf {s}}=V+\mathcal {R}_{\omega }(V^{\omega })$ is a Dirac structure on $\Sigma$. In this case,

  $$\begin{aligned} L_M \ \ \text {is Poisson} \quad \iff \quad \ker \omega \subset V. \end{aligned}$$

• (ii) If $V^{\omega }$ is smooth then also $\mathrm {Gr}(\omega )^{\mathbf {s}}$ is smooth. On the other hand, if $\mathrm {Gr}(\omega )^{\mathbf {s}}$ is smooth then it is a Dirac structure exactly when the linear family $V^{\omega }$ is involutive.

• (iii) If there exists a smooth subbundle $W\subset T\Sigma$ such that

  $$\begin{aligned} \mathrm {Gr}(\omega )^{\mathbf {s}}=V+\mathcal {R}_{\omega }(W), \end{aligned}$$

  (3)

  then $\mathrm {Gr}(\omega )^{\mathbf {s}}$ is smooth. If W is also involutive, then $\mathrm {Gr}(\omega )^{\mathbf {s}}$ is a Dirac structure, and so $\mathbf {s}$ pushes $\mathrm {Gr}(\omega )$ forward to a Dirac structure $L_M$ on M. Moreover, if the decomposition above is a direct sum

  $$\begin{aligned} \mathrm {Gr}(\omega )^{\mathbf {s}}=V\oplus \mathcal {R}_{\omega }(W) \end{aligned}$$

  then there is an induced Lie algebroid comorphism $\Phi :\mathbf {s}^*(L_M) \rightarrow W$.

Proof

Proposition 2 implies the first part of i); for the second part, note that

$$\begin{aligned} \mathbf {s}_!(L_{p})\cap T_{\mathbf {s}(p)}M=\mathbf {s}_*(\ker \omega _p), \end{aligned}$$

and therefore the induced Dirac structure is Poisson if and only if this space is trivial, which is equivalent to $\ker \omega \subset V$. Item (ii) is implied by Proposition 4. The first part of item (iii) follows from Propositions 3 and the second from Proposition 5. $\square$

Thus the condition that there be an involutive $W \subset T\Sigma$ satisfying (3) is sufficient to ensure that a surjective submersion $\mathbf {s}:\Sigma \rightarrow M$ pushes $\mathrm {Gr}(\omega )$ forward, but it is certainly not necessary, as the following example illustrates:

Example 3

Consider $\mathbf {s}:\mathbb {R}^3\rightarrow \mathbb {R}$, $\mathbf {s}(x,y,z)=x$ and $\omega =\mathrm {d}(x^2 y)\wedge \mathrm {d}z$. Then

$$\begin{aligned} \mathbf {s}:(\mathbb {R}^3,\mathrm {Gr}(\omega ))\longrightarrow (\mathbb {R},T\mathbb {R}) \end{aligned}$$

is a forward Dirac map.

Note that there cannot be a smooth subbundle $W \subset T\Sigma$ satisfying $\mathrm {Gr}(\omega )^{\mathbf {s}}=V+\mathcal {R}_{\omega }(W)$. Indeed, such a subbundle would have to be spanned by the vector field $v:=x\partial _x-2y\partial _y$ on $x \ne 0$, yet this cannot be extended smoothly (as a line bundle) over points of the form (0, 0, z), since:

$$\begin{aligned} \lim _{y\rightarrow 0}\lim _{x\rightarrow 0}\langle v\rangle =\langle \partial _y\rangle \quad \text {and} \quad \lim _{x\rightarrow 0}\lim _{y\rightarrow 0}\langle v\rangle =\langle \partial _x\rangle . \end{aligned}$$

Remark 2

Part (ii) of Corollary 2 resembles the most Libermann’s theorem in Poisson geometry. Namely, assuming that $\mathrm {Gr}(\omega )^{\mathbf {s}}$ is smooth, $\mathbf {s}$ pushes $\mathrm {Gr}(\omega )$ forward if and only if $V^{\omega }$ is involutive. However, note that even if this is the case, the rank of $V^{\omega }$ need not be lower semicontinuous (see Example 3); thus, even if it is involutive, it need not be a singular foliation (in the sense of [36]).

4.2 Weak dual pairs

The key ingredient in defining weak dual pairs is condition (3) of Corollary 2(iii). First, we give several algebraic reformulations of this condition, which, in particular, show that V and W play a symmetric role (note that condition (a) in Lemma 1 below is the pointwise version of (3)).

Lemma 1

Consider a finite dimensional vector space A, vector subspaces $B\subset A$ and $C\subset A$, and a 2-form $\omega \in \wedge ^2A^*$. Denote $\ker \omega \subset A$ by K. Then the following are equivalent:

• (a) $B+\mathcal {R}_{\omega }(B^{\omega })=B+\mathcal {R}_{\omega }(C)\subset A\oplus A^*$;

• (b) $C+\mathcal {R}_{-\omega }(C^{\omega })=C+\mathcal {R}_{-\omega }(B)\subset A\oplus A^*$;

• (c) $B^{\omega }=C+B\cap K$;

• (d) $C^{\omega }=B+C\cap K$;

• (e) $\omega (B,C)=0$ and $\mathrm {dim}(B\cap K \cap C)=\mathrm {dim}(B)+\mathrm {dim}(C)-\mathrm {dim}(A)$.

Proof

Note first that all conditions imply $\omega (B,C)=0$. Next, note that:

$$\begin{aligned} \mathrm {dim}(B^{\omega })= & {} \dim (A)-\mathrm {dim}(B)+\mathrm {dim}(B\cap K),\\ \mathrm {dim}(C+B\cap K)= & {} \mathrm {dim}(C)+\mathrm {dim}(B\cap K)-\mathrm {dim}(B\cap K\cap C). \end{aligned}$$

Clearly, $C+B\cap K\subset B^{\omega }$; thus the two are equal iff they have the same dimension. This shows that $(c)\Leftrightarrow (e)$. Similarly, $(d)\Leftrightarrow (e)$.

On the other hand, $B+\mathcal {R}_{\omega }(C)\subset B+\mathcal {R}_{\omega }(B^{\omega })$. The latter is a Lagrangian subspace of $A\oplus A^*$, thus (a) holds iff

$$\begin{aligned} \mathrm {dim}(B+\mathcal {R}_{\omega }(C))=\mathrm {dim}(A), \end{aligned}$$

which is equivalent to (e), because

$$\begin{aligned} \mathrm {dim}(B+\mathcal {R}_{\omega }(C))=\mathrm {dim}(B)+\mathrm {dim}(C)-\mathrm {dim}(B\cap K\cap C). \end{aligned}$$

Hence $(a)\Leftrightarrow (e)$. Similarly, $(b)\Leftrightarrow (e)$. $\square$

Motivated by Corollary 2(iii) and Lemma 1, we introduce:

Definition 2

A weak dual pair consists of surjective, forward Dirac submersions

$$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}), \end{aligned}$$

(4)

where $\omega$ is a closed two-form on $\Sigma$, satisfying

$$\begin{aligned} \omega (V,W)=0\quad \text {and}\quad \mathrm {rank}(V\cap K\cap W)=\mathrm {dim}(\Sigma )-\mathrm {dim}(M_0)-\mathrm {dim}(M_1), \end{aligned}$$

(*)

where $V:=\ker \mathbf {s}_*$, $W:=\ker \mathbf {t}_*$, and $K:=\ker \omega$.

A first consequence of this definition is that

Lemma 2

For a weak dual pair, we have that $V\cap K\cap W$ is a smooth, involutive subbundle of $T\Sigma$, where we used the notation of Definition 2.

Proof

Note that the kernel of the vector bundle map

$$\begin{aligned} V\oplus W\longrightarrow \mathbb {T}\Sigma , \ \ v\oplus w\mapsto v+\mathcal {R}_{\omega }(w) \end{aligned}$$

can be identified with $V\cap K\cap W$. This map has constant rank, because its image is $V+\mathcal {R}_{\omega }(W)$, which, by Lemma 1(a) is Lagrangian. Therefore $V\cap K\cap W$ is smooth. The bundles V and W are involutive, and since $\omega$ is closed, also K is involutive in the sense of §7. Thus $V\cap K\cap W$ is involutive. $\square$

By Lemma 1, condition ($*$) in Definition 2 is the same as condition (3) in Corollary 2. Due to the symmetric role played by V and W, we may apply Corollary 2(iii) and obtain an intrinsic description of weak dual pairs:

Corollary 3

Let $\omega \in \Omega ^2(\Sigma )$ be a closed two-form, and let $\mathbf {s}:\Sigma \rightarrow M_0$ and $\mathbf {t}:\Sigma \rightarrow M_1$ be surjective submersions with connected fibres. If $V:=\ker \mathbf {s}_*$ and $W:=\ker \mathbf {t}_*$ satisfy $(*)$, then $M_0$ and $M_1$ carry Dirac structures $L_0$ and $L_1$ respectively, which yield a weak dual pair

$$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}). \end{aligned}$$

Next we give some alternative descriptions of weak dual pairs.

Proposition 6

Let $\omega \in \Omega ^2(\Sigma )$ be a closed two-form, $(M_0,L_0)$ and $(M_1,L_1)$ be Dirac manifolds and $\mathbf {s}:\Sigma \rightarrow M_0$ and $\mathbf {t}:\Sigma \rightarrow M_1$ be surjective submersions. The following are equivalent:

• (i) the diagram below is a weak dual pair:

  $$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}); \end{aligned}$$

• (ii) $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ and $\mathrm {rank}(V\cap K\cap W)=\mathrm {dim}(\Sigma )-\mathrm {dim}(M_0)-\mathrm {dim}(M_1)$;

• (iii) $(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M_0,L_0) \times (M_1,-L_1)$ is a forward Dirac map and either $\mathrm {rank}(V\cap K\cap W)=\mathrm {dim}(\Sigma )-\mathrm {dim}(M_0)-\mathrm {dim}(M_1)$ or $\omega (V,W)=0$ holds;

• (iv) $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ and $(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M_0,L_0) \times (M_1,-L_1)$ is a forward Dirac map,

where $V:=\ker \mathbf {s}_*$, $W:=\ker \mathbf {t}_*$, and $K:=\ker \omega$.

Proof

First, we claim that $(\mathbf {s},\mathbf {t})$ being forward Dirac is equivalent to the inclusions:

$$\begin{aligned} \mathbf {s}^!(L_0) \subset V+\mathcal {R}_{\omega }(W), \quad \mathbf {t}^!(L_1) \subset \mathcal {R}_{-\omega }(V)+W. \end{aligned}$$

(5)

Assume that $(\mathbf {s},\mathbf {t})$ is a forward Dirac map. Let $\widetilde{u}_0+\mathbf {s}^*(\xi _0) \in \mathbf {s}^!(L_0)_p$ be $\mathbf {s}$-related to $u_0+\xi _0 \in L_{0,\mathbf {s}(p)}$. By assumption, for all $(u_0+\xi _0,u_1-\xi _1) \in L_{0,\mathbf {s}(p)} \times -L_{1,\mathbf {t}(p)}$, there is $u \in T_p\Sigma$ such that $u+\iota _u\omega \sim _{(\mathbf {s},\mathbf {t})} (u_0+\xi _0,u_1-\xi _1)$. Applying this to $(u_0+\xi _0,0)$, we deduce the existence of $w \in W_p$ such that $w+\iota _w\omega \sim _{\mathbf {s}} u_0+\xi _0$; hence

$$\begin{aligned} \widetilde{u}_0 = w+v, \quad \iota _w\omega = \mathbf {s}^*(\xi _0) \end{aligned}$$

for some $v \in V_p$. Therefore

$$\begin{aligned} \widetilde{u}_0+\mathbf {s}^*(\xi _0) = v+w+\iota _w\omega \in V+\mathcal {R}_{\omega }(W), \end{aligned}$$

which shows that $\mathbf {s}^!(L_0) \subset V+\mathcal {R}_{\omega }(W)$. The inclusion $\mathbf {t}^!(L_1) \subset \mathcal {R}_{-\omega }(V)+W$ is proved similarly. Hence (5) holds.

Conversely, assume that (5) holds. Then for $(u_0+\xi _0,u_1-\xi _1) \in L_{0,\mathbf {s}(p)} \times -L_{1,\mathbf {t}(p)}$ there exist $v_0,v_1 \in V_p$ and $w_0,w_1 \in W_p$, such that

$$\begin{aligned} v_0+w_0+\iota _{w_0}\omega \sim _{\mathbf {s}} u_0+\xi _0, \quad v_1+w_1+\iota _{v_1}\omega \sim _{\mathbf {t}} u_1-\xi _1; \end{aligned}$$

this implies that

$$\begin{aligned} w_0+\iota _{w_0}\omega \sim _{\mathbf {s}} u_0+\xi _0, \quad v_1+\iota _{v_1}\omega \sim _{\mathbf {t}} u_1-\xi _1, \end{aligned}$$

and so $v_1+w_0+\iota _{v_1+w_0}\omega \sim _{(\mathbf {s},\mathbf {t})} (u_0+\xi _0,u_1-\xi _1)$; hence $(\mathbf {s},\mathbf {t})$ is forward Dirac.

Assume now that (i) holds. Then by Lemma 1, the following equalities below

$$\begin{aligned} \mathbf {s}^!(L_0) =(\mathrm {Gr}(\omega ))^{\mathbf {s}} = V+\mathcal {R}_{\omega }(W), \quad \mathbf {t}^!(L_1) = (\mathrm {Gr}(\omega ))^{\mathbf {t}}= \mathcal {R}_{-\omega }(V)+W, \end{aligned}$$

hold, and imply both the condition $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ and the inclusions (5). Since condition $(*)$ is implied by (i), we conclude that (i) implies both (ii) and (iii).

Assume now that (ii) holds. Since $V\subset \mathbf {s}^!(L_0)$ and $W\subset \mathbf {t}^{!}(L_1)$, (ii) yields

$$\begin{aligned} V+\mathcal {R}_{\omega }(W) \subset \mathbf {s}^!(L_0)=\mathcal {R}_{\omega }(\mathbf {t}^!(L_1)). \end{aligned}$$

The rank condition in (ii) implies that $\mathrm {rank}(V+\mathcal {R}_{\omega }(W))=\mathrm {dim}(\Sigma )$, and so the above must hold with equality

$$\begin{aligned} V+\mathcal {R}_{\omega }(W) = \mathbf {s}^!(L_0)=\mathcal {R}_{\omega }(\mathbf {t}^!(L_1)). \end{aligned}$$

The fact that this space is isotropic gives $\omega (V,W)=0$, hence $V+\mathcal {R}_{\omega }(W)\subset V+\mathcal {R}_{\omega }(V^{\omega })\subset \mathrm {Gr}(\omega )^{\mathbf {s}}$. Again, since both spaces are Lagrangian, we conclude that

$$\begin{aligned} V+\mathcal {R}_{\omega }(W)=\mathrm {Gr}(\omega )^{\mathbf {s}}=\mathbf {s}^!(L_0). \end{aligned}$$

This implies that $\mathbf {s}$ is forward Dirac, and similarly, one shows that $\mathbf {t}$ is forward Dirac. Thus (ii) implies (i).

Assume now that (iii) holds. By the claim, (5) holds. The condition $\omega (V,W)=0$ implies that $V+\mathcal {R}_{\omega }(W)$ is isotropic, so $\mathrm {rank}(V+\mathcal {R}_{\omega }(W))\le \mathrm {dim}(\Sigma )$, and the rank condition from (iii) implies that $\mathrm {rank}(V+\mathcal {R}_{\omega }(W))= \mathrm {dim}(\Sigma )$. Assuming that either $\mathrm {rank}(V\cap K\cap W)=\mathrm {dim}(\Sigma )-\mathrm {dim}(M_0)-\mathrm {dim}(M_1)$ or $\omega (V,W)=0$ yields equalities in (5), and so $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ and $\mathrm {rank}(V+\mathcal {R}_{\omega }(W))= \mathrm {dim}(\Sigma )$, which is equivalent to the rank condition in (ii). Hence, (iii) implies (ii).

Clearly, by the discussion above, (i) implies (iv). Finally, assume that (iv) holds. Note that $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ implies that $V+\mathcal {R}_{\omega }(W)\subset \mathbf {s}^!(L_0)$; hence $V+\mathcal {R}_{\omega }(W)$ is isotropic, and so $\omega (V,W)=0$. Thus (iii) holds. $\square$

Remark 3

In [7] (see also [10, Lemma 4.2]), a different version of weak dual pairs is considered. Namely, the diagram (4) from Definition 2 is called a pre-dual pair if instead of $(*)$ it satisfies (see [7, Definition 3.1]):

$$\begin{aligned} V^{\omega } = W+K\ \ \text {and}\ \ W^{\omega }=V+K. \end{aligned}$$

(**)

Note that these two conditions are equivalent: by taking the $\omega$-orthogonal of the first relation one obtains the second. Weak dual pairs satisfy $(**)$ (see (c) in Lemma 1), but not conversely (see Example 1 with $W=V=\ker \mathbf {s}_*$, and also Example 5).

That condition $(**)$ is not sufficient for $\mathbf {s}$ to push the Dirac structure $\mathrm {Gr}(\omega )$ forward should be contrasted to the setting in [10, Lemma 4.2]—where $(**)$ is enough to ensure that a multiplicative two-form on a Lie groupoid pushes forward via the source map.

Below are two examples of diagrams of surjective, forward Dirac submersions, as in 4, which are not weak dual pairs.

Example 4

Let $\mathbf {s}:(\mathbb {R}^3,\mathrm {Gr}(\omega ))\longrightarrow (\mathbb {R},T\mathbb {R})$ be as in Example 3, and consider $\mathbf {t}:(\mathbb {R}^3,\mathrm {Gr}(\omega )) \rightarrow (\mathbb {R}^0,0)$, which is trivially a forward map into the trivial Dirac structure on $\mathbb {R}^0$. Then

$$\begin{aligned}(\mathbb {R},T\mathbb {R}) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (\mathbb {R}^0,0)\end{aligned}$$

is a diagram of surjective, forward Dirac submersions, in which

$$\begin{aligned}(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (\mathbb {R},T\mathbb {R}) \times (\mathbb {R}^0,0)\end{aligned}$$

is forward Dirac. However, $\mathbf {s}^!(L_0) \ne \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$. Clearly, the fibres of $\mathbf {s}$ and $\mathbf {t}$ are not $\omega$-orthogonal.

Example 5

Consider the forward Dirac submersions

$$\begin{aligned} (\mathbb {R}^2,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\mathbb {R}^3,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (\mathbb {R}^2,-L_1), \end{aligned}$$

where $\mathbf {s}(x,y,z):=(x,y)$, $\mathbf {t}(x,y,z):=(y,z)$, $\omega := \mathrm {d}x \wedge \mathrm {d}y + \mathrm {d}y \wedge \mathrm {d}z$, $L_0:=\langle \partial _x, \mathrm {d}y \rangle$ and $L_1:=\langle \partial _z, \mathrm {d}y \rangle$. In this case, $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))=\langle \partial _x, \partial _z, \mathrm {d}y \rangle$. However, $(\mathbf {s},\mathbf {t}):(\mathbb {R}^3,\mathrm {Gr}(\omega )) \rightarrow (\mathbb {R}^2,L_0) \times (\mathbb {R}^2,-L_1)$ is not forward Dirac. Moreover, the fibres of $\mathbf {s}$ and $\mathbf {t}$ are $\omega$-orthogonal.

This is also an example of a pre-dual pair (see Remark 3) which is not a weak dual pair, i.e. condition $(**)$ holds, but condition $(*)$ (Lemma 1(c)) fails:

$$\begin{aligned} V^{\omega } = W + K\ne W + V \cap K. \end{aligned}$$

4.3 Dual pairs

Next, we introduce the main notion of this paper:

Definition 3

A dual pair is a weak dual pair

$$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}), \end{aligned}$$

satisfying the condition

where $V:=\ker \mathbf {s}_*$, $W:=\ker \mathbf {t}_*$ and $K:=\ker \omega$.

Equivalently, by $(*)$, a dual pair is weak dual pair satisfying:

$$\begin{aligned} \mathrm {dim}(\Sigma )=\mathrm {dim}(M_0)+\mathrm {dim}(M_1). \end{aligned}$$

Analogously to Lemma 1, the algebraic conditions appearing in the definition of dual pairs can be reformulated as follows:

Lemma 3

In the setting of Lemma 1, the following are equivalent

• (a) $B+\mathcal {R}_{\omega }(B^{\omega })=B\oplus \mathcal {R}_{\omega }(C)$;

• (b) $C+\mathcal {R}_{-\omega }(C^{\omega })=C\oplus \mathcal {R}_{-\omega }(B)$;

• (c) $B^{\omega }=C\oplus B\cap K$;

• (d) $C^{\omega }=B\oplus C\cap K$;

• (e) $\omega (B,C)=0$ and $B\cap K\cap C=0$ and $\mathrm {dim}(A)=\mathrm {dim}(B)+\mathrm {dim}(C)$.

Before giving further descriptions of dual pairs, we recall the following notion:

Definition 4

A forward Dirac map

$$\begin{aligned} \varphi : (M_0,L_0) \rightarrow (M_1,L_1) \end{aligned}$$

is called strong if $L_0 \cap \ker \varphi _* = 0$ [2]. When $L_0$ is the graph of a closed two-form $\omega _0 \in \Omega ^2(M_0)$, we call it a presymplectic realization [10, Definition 7.1].

Proposition 7

Consider a diagram of surjective submersions

$$\begin{aligned} M_0 {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} \Sigma {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} M_1, \ \ \ \ \ \text {where} \ \ \dim \Sigma = \dim M_0 + \dim M_1. \end{aligned}$$

Let $\omega \in \Omega ^2(\Sigma )$ be a closed two-form, and let $L_i \subset \mathbb {T}M_i$ be Dirac structures. Then the following conditions are equivalent:

• (i) the diagram below is a dual pair:

  $$\begin{aligned} (M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1}); \end{aligned}$$

• (ii) $\mathbf {s}^!(L_0) = \mathcal {R}_{\omega }(\mathbf {t}^!(L_1))$ and $V\cap K\cap W=0$;

• (iii) $(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M_0,L_0) \times (M_1,-L_1)$ is a presymplectic realization;

where $V:=\ker \mathbf {s}_*$, $W:=\ker \mathbf {t}_*$, and $K:=\ker \omega$.

Proof

Note that, under the assumption $\dim \Sigma =\dim M_0+\dim M_1$, the first two items are equivalent to the corresponding items of Proposition 6. Similarly, item (iii) is equivalent to $(\mathbf {s},\mathbf {t})$ being a forward Dirac map, and to $V\cap W\cap K=0$; thus it is equivalent to the first version of the corresponding item in Proposition 6. Thus, the result follows from Proposition 6. $\square$

Example 6

A foliation $\mathscr {F}$ on a smooth manifold M admits a presymplectic realization. Indeed, let $L \subset \mathbb {T}M$ be the Dirac structure corresponding to $\mathscr {F}$. Denote the conormal bundle of $\mathscr {F}$ by $N^*\mathscr {F} \subset T^*M$, the bundle projection by $\mathbf {s}: N^*\mathscr {F} \rightarrow M$, and by $\omega \in \Omega ^2(N^*\mathscr {F})$ the restriction of the canonical symplectic form on $T^*M$. Then

$$\begin{aligned} \mathbf {s}: (N^*\mathscr {F},\mathrm {Gr}(\omega )) \longrightarrow (M,L) \end{aligned}$$

is a presymplectic realization.

Assume that the foliation $\mathscr {F}$ is given by the fibres of a surjective submersion $p:M \rightarrow B$. Then the above presymplectic realization is part of a dual pair

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (N^*\mathscr {F},\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (B,T^*B), \quad \mathbf {t}:=p \circ \mathbf {s}. \end{aligned}$$

Example 7

If $(M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1})$ is a dual pair, and $\sigma _0 \in \Omega ^2(M_0)$, $\sigma _1 \in \Omega ^2(M_1)$ are closed two-forms, then

$$\begin{aligned} (M_0,\mathcal {R}_{\sigma _0}(L_0)){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega +\mathbf {s}^*(\sigma _0)-\mathbf {t}^*(\sigma _1))) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-\mathcal {R}_{\sigma _1}(L_{1})) \end{aligned}$$

is again a dual pair, as follows by the description provided in Proposition 7(iii).

The main property of strong forward Dirac maps is contained in the following result from [2, Proposition 2.8] (see also [10, Lemma 7.3]):

Lemma 4

(Strong forward Dirac maps) A strong, forward Dirac map $\varphi : (\Sigma ,L_{\Sigma }) \rightarrow (M,L)$ induces a comorphism of Lie algebroids $\Phi :\varphi ^*(L) \rightarrow L_{\Sigma }$.

A presymplectic realization $\varphi : (\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M,L)$ induces a comorphism of Lie algebroids $\Psi :\varphi ^*(L) \rightarrow T\Sigma$.

Proof

The forward condition on $\varphi$ means that, for each $x \in \Sigma$ and $a\in L_{\varphi (x)}$, there is at least one $b \in L_{\Sigma ,x}$ such that $b \sim _{\varphi } a$, and the strong condition means that at most one such b exists. This defines a comorphism of vector bundles $\Phi :\varphi ^*(L) \rightarrow L_{\Sigma }$ by setting $b=:\Phi _x(a)$. If now $a_1,a_2 \in \Gamma (L)$, then $\Phi ^{\dagger }(a_1) \sim _{\varphi } a_1$ and $\Phi ^{\dagger }(a_2) \sim _{\varphi } a_2$; therefore $\Phi ^{\dagger }([a_1,a_2]) \sim _{\varphi } [a_1,a_2]$; by uniqueness, it follows that $\Phi ^{\dagger }([a_1,a_2])=[\Phi ^{\dagger }(a_1),\Phi ^{\dagger }(a_2)]$ and hence $\Phi ^{\dagger }$ is a homomorphism of Lie algebras. This proves the first assertion, and the second follows by composing $\Phi$ with the anchor map $\mathrm {pr}_T:\mathrm {Gr}(\omega ) \rightarrow T\Sigma$. $\square$

Remark 4

Let $(M_0,L_0){\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_{1})$ be a dual pair. By Proposition 7(iii) and Lemma 4 above, we obtain a comorphism of Lie algebroids

$$\begin{aligned} \Psi :(\mathbf {s}, \mathbf {t})^*(L_0\times -L_1)\longrightarrow T\Sigma . \end{aligned}$$

Restricting this to the first and second components, we obtain induced comorphisms of Lie algebroids:

$$\begin{aligned} \Psi _0 : \mathbf {s}^*(L_0) \longrightarrow W = \ker \mathbf {t}_*, \quad \Psi _1 : \mathbf {t}^*(L_1) \longrightarrow V= \ker \mathbf {s}_*. \end{aligned}$$

For sections $a_i \in \Gamma (L_i)$, $w:=\Psi _0^{\dagger }(a_0) \in \Gamma (W)$ is the unique vector field tangent to the fibres of $\mathbf {t}$, satisfying $w+\iota _w\omega \sim _{\mathbf {s}} a_0$; similarly, $v:=\Psi _1^{\dagger }(a_1)$ is the unique vector field tangent to the fibres of $\mathbf {s}$ satisfying $v-\iota _v\omega \sim _{\mathbf {t}} a_1$. Note also that any two such vector fields $\Psi _0^{\dagger }(a_0),\Psi _1^{\dagger }(a_1)$ are $\omega$-orthogonal and commute, since

$$\begin{aligned}{}[\Psi _0^{\dagger }(a_0),\Psi _1^{\dagger }(a_1)]+\iota _{[\Psi _0^{\dagger }(a_0),\Psi _1^{\dagger }(a_1)]}\omega \sim _{(\mathbf {s},\mathbf {t})} [(a_0,0),(0,\overline{a_1})] = 0, \end{aligned}$$

where for a section $a=u+\xi$, $\overline{a}$ denotes the section $u-\xi$.

The main example of dual pairs is the following:

Example 8

If a Dirac manifold (M, L) is integrable by a (Hausdorff) presymplectic groupoid $(G,\omega )\rightrightarrows (M,L)$, then

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (G,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M,-L) \end{aligned}$$

forms a dual pair [10]. In this case, the induced comorphism of Lie algebroids $\mathbf {s}^*(L) \rightarrow W$ is the canonical action by left-invariant vector fields of the Lie algebroid L on its Lie groupoid G, and is automatically complete (in the sense of §13). Our Main Theorem is strongly related to this example (see Sect. 8).

It was proven in [18, Theorem 8] that the existence of a complete symplectic realization of a Poisson manifold implies its integrability; but, as pointed out in [18, Corollary 7], the proof depends only upon the existence of a complete action of the corresponding Lie algebroid. Applying these results in the same way as in the case of presymplectic realizations [10, Remark 7.5], one obtains the following:

Corollary 4

(Integrability criterion) Consider a surjective, forward Dirac submersion $\mathbf {s}: (\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M,L)$. Assume that there is an involutive subbundle $W\subset T\Sigma$ such that:

$$\begin{aligned} \mathrm {Gr}(\omega )^{\mathbf {s}}=V\oplus \mathcal {R}_{\omega }(W), \ \ \text {where}\ V:=\ker s_*. \end{aligned}$$

If the induced comorphism of Lie algebroids $\mathbf {s}^*(L) \rightarrow W$ (see Corollary 2(iii)) is complete (see §13), then (M, L) is integrable by a (not necessarily Hausdorff) presymplectic groupoid. In that case, the source-simply connected Lie groupoid integrating (M, L) is Hausdorff if and only if the holonomy groupoid $\mathrm {Hol}(W)\rightrightarrows \Sigma$ of the foliation W is Hausdorff.

5 Operations with weak dual pairs

In this section we discuss operations that can be performed with weak dual pairs: the operation of composition of weak dual pairs, the operation of pullback along a surjective submersion, and its partial inverse, called the reduction procedure (which, under certain assumptions, allows one to reduce a weak dual pair to a dual pair), and finally the pullback procedure along transverse maps.

5.1 Composition

Weak dual pairs can be composed. Namely, suppose

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{01}}} (\Sigma _{01},\mathrm {Gr}(\omega _{01})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{01}}} (M_1,-L_1), \\ (M_1,L_1) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{12}}} (\Sigma _{12},\mathrm {Gr}(\omega _{12})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{12}}} (M_2,-L_2)\end{aligned}$$

are weak dual pairs. Their composition is

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{02}}}&(\Sigma _{02},\mathrm {Gr}(\omega _{02})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{02}}} (M_2,-L_2), \end{aligned}$$

where

$$\begin{aligned}&\Sigma _{02}:=\Sigma _{01} \times _{M_1} \Sigma _{12}, \quad \omega _{02}:=\mathrm {pr}_1^*(\omega _{01})+\mathrm {pr}_2^*(\omega _{12}),\\&M_0 {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{02}}} \Sigma _{02} {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{02}}} M_2, \quad \mathbf {s}_{02}:=\mathbf {s}_{01} \circ \mathrm {pr}_1, \ \ \mathbf {t}_{02}:=\mathbf {t}_{12} \circ \mathrm {pr}_2. \end{aligned}$$

Pictorially:

Proposition 8

The composition of weak dual pairs is again a weak dual pair.

Proof

We must check that

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{02}}} (\Sigma _{02},\mathrm {Gr}(\omega _{02})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{02}}} (M_2,-L_2) \end{aligned}$$

is again a weak dual pair. First, since $\mathbf {s}_{12}$ is a submersion, the map $\mathrm {pr}_1:\Sigma _{02}\rightarrow \Sigma _{01}$ is a submersion. Similarly, $\mathrm {pr}_2:\Sigma _{02}\rightarrow \Sigma _{12}$ is a submersion. Hence, $\mathbf {s}_{02},\mathbf {t}_{02}$ are compositions of submersions. The same sequence of implications shows that these maps are also surjective.

We turn next to the characterization provided by item (iv) of Proposition 6. From

$$\begin{aligned} \mathcal {R}_{-\omega _{01}}(\mathbf {s}_{01}^!(L_0)) = \mathbf {t}_{01}^!(L_1), \quad \mathbf {s}_{12}^!(L_1) = \mathcal {R}_{\omega _{12}}(\mathbf {t}_{12}^!(L_2)), \end{aligned}$$

and from the equality $\mathbf {t}_{01}\circ \mathrm {pr}_1=\mathbf {s}_{12}\circ \mathrm {pr}_2$ on $\Sigma _{02}$, it follows that

$$\begin{aligned} \mathcal {R}_{-\mathrm {pr}_1^*(\omega _{01})}(\mathbf {s}_{02}^!(L_0)) = \mathcal {R}_{\mathrm {pr}_2^*(\omega _{12})}(\mathbf {t}_{12}^!(L_2)) \quad \iff \quad \mathbf {s}_{02}^!(L_0) = \mathcal {R}_{\omega _{02}}(\mathbf {t}_{02}^!(L_2)). \end{aligned}$$

Thus the first condition of Proposition 6(iv) holds. We conclude the proof by showing that also the second condition in Proposition 6(iv) hold. Let $a_0 \in L_0$. Then there is $w_{01} \in W_{01}:=\ker (\mathbf {t}_{01*})$ such that $w_{01}+\iota _{w_{01}}\omega _{01} \sim _{\mathbf {s}_{01}} a_0$. Then $w_{02}:=(w_{01},0) \in T\Sigma _{01} \times _{TM_1} T\Sigma _{12}$ lies in $W_{02}:=\ker (\mathbf {t}_{02*})$, and $w_{02} + \iota _{w_{02}}\omega _{02} \sim _{\mathbf {s}_{02}} a_0$. Similarly, for all $a_1 \in -L_1$, there is $v_{02} \in V_{02}:=\ker (\mathbf {s}_{02*})$ such that $v_{02} + \iota _{v_{02}}\omega _{02} \sim _{\mathbf {t}_{02}} a_1$. Hence

$$\begin{aligned} w_{02}+v_{02}+\iota _{w_{02}+v_{02}}\omega _{02} \sim _{(\mathbf {s}_{02},\mathbf {t}_{02})} (a_0,a_1). \end{aligned}$$

This concludes the proof. $\square$

Remark 5

Given dual pairs

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{01}}} (\Sigma _{01},\mathrm {Gr}(\omega _{01})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{01}}} (M_1,-L_1)\\ (M_1,L_1) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_{12}}} (\Sigma _{12},\mathrm {Gr}(\omega _{12})) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_{12}}} (M_2,-L_2), \end{aligned}$$

their composition (in the sense of Proposition 8) is not a dual pair, unless $\dim M_1 =0$, simply because

$$\begin{aligned} \dim \Sigma _{02} = \dim M_0 + \dim M_1 + \dim M_2. \end{aligned}$$

and hence the dimension condition of Definition 3 is violated.

When the foliation $\ker \mathbf {s}_{02*}\,\cap \,\ker \omega _{02}\,\cap \,\ker \mathbf {t}_{02*} \subset T\Sigma _{02}$ is simple, the reduction procedure of Proposition 9(ii) below, applied to their composition, yields again a dual pair. Note however that this requirement is not always met, as illustrated in Example 9 below.

5.2 Reduction to dual pairs

In the following, we describe how weak dual pairs can be pulled back via surjective submersions, and how, under certain assumptions (which hold locally), weak dual pairs can be reduced to dual pairs.

Proposition 9

(Reduction to dual pairs) Consider a weak dual pair diagram

$$\begin{aligned}(M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_1).\end{aligned}$$

• (i) If $\mathrm {r}:\widetilde{\Sigma } \rightarrow \Sigma$ is a surjective submersion, then

  $$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}\circ \mathrm {r}}} (\widetilde{\Sigma },\mathrm {Gr}(\mathrm {r}^*(\omega ))) {\mathop {\longrightarrow }\limits ^{\mathbf {t}\circ \mathrm {r}}} (M_1,-L_1) \end{aligned}$$

  is again a weak dual pair.

• (ii) Assume that the foliation $V\cap K\cap W$ is simple, i.e., that there exists a surjective submersion $\mathrm {r}:\Sigma \rightarrow \overline{\Sigma }$ whose fibres are the leaves of $V\cap K\cap W$. Then there is an induced commutative diagram of surjective, forward Dirac submersions:

  

  where $\overline{\omega }$ is a closed two-form on $\overline{\Sigma }$ such that $\omega =\mathrm {r}^*(\overline{\omega })$, and where the bottom line is a dual pair.

Proof

We use the description of weak dual pairs provided by item (iv) of Proposition 6. The first condition of (iv) holds, since

$$\begin{aligned} (\mathbf {s}\circ \mathrm {r})^!(L_0) = \mathrm {r}^!(\mathbf {s}^!(L_0)) = \mathrm {r}^!(\mathcal {R}_{\omega }(\mathbf {t}^!(L_1))) = \mathcal {R}_{\mathrm {r}^*(\omega )}((\mathbf {t}\circ \mathrm {r})^!(L_1)), \end{aligned}$$

whereas the second holds because, for any surjective submersion $\mathrm {r}:\widetilde{\Sigma } \rightarrow \Sigma$, we have that $\mathrm {r}:(\widetilde{\Sigma },\mathrm {Gr}(\mathrm {r}^*\omega )) \rightarrow (\Sigma ,\mathrm {Gr}(\omega ))$ is forward Dirac. This proves (i).

By Lemma 2, $V\cap K\cap W$ is a smooth, involutive distribution. For (ii), assume the existence of a surjective submersion $\mathrm {r}:\Sigma \rightarrow \overline{\Sigma }$ whose fibres are the leaves of $V\cap K\cap W$. By applying Proposition 1 to the three Dirac structures corresponding to the foliations V and W and to the closed two-form $\omega$, we deduce that there are foliations $\overline{V}$ and $\overline{W}$, and a closed two-form $\overline{\omega }$ on $\overline{\Sigma }$, such that

$$\begin{aligned} V=\mathrm {r}^{-1}_*\overline{V}, \quad W=\mathrm {r}_*^{-1}\overline{W}, \quad \omega =\mathrm {r}^*\overline{\omega }. \end{aligned}$$

Since $\ker \mathrm {r}_*\subset V\cap W$, and the fibres of $\mathrm {r}$ are connected, it follows that $\mathbf {s}$ and $\mathbf {t}$ are constant along the fibres of $\mathrm {r}$; hence they factor as in the diagram, $\mathbf {s}=\overline{\mathbf {s}}\circ \mathrm {r}$, $\mathbf {t}=\overline{\mathbf {t}}\circ \mathrm {r}$, and these equalities imply that the maps $\overline{\mathbf {s}}$ and $\overline{\mathbf {t}}$ are surjective submersions. Note next that both these maps push forward the Dirac structure $\overline{L}:=\mathrm {Gr}(\overline{\omega })$:

$$\begin{aligned} \overline{\mathbf {s}}_{!}(\overline{L})=\overline{\mathbf {s}}_{!}\mathrm {r}_!(L)=\mathbf {s}_{!}(L)=L_0, \quad \overline{\mathbf {t}}_{!}(\overline{L})=\overline{\mathbf {t}}_{!}\mathrm {r}_!(L)=\mathbf {t}_{!}(L)=-L_1, \end{aligned}$$

where $L:=\mathrm {Gr}(\omega )$. Moreover, the equalities:

$$\begin{aligned} \overline{K}=\ker \overline{\omega }=\mathrm {r}_*K, \ \ \overline{V}=\mathrm {r}_*V, \ \ \overline{W}=\mathrm {r}_{*}W, \end{aligned}$$

imply that

$$\begin{aligned}&\displaystyle \overline{\omega }(\overline{V},\overline{W})=\overline{\omega }(\mathrm {r}_*V,\mathrm {r}_*W) =\omega (V,W)=0,\\&\displaystyle \overline{V}\cap \overline{K}\cap \overline{W}=0. \end{aligned}$$

Since

$$\begin{aligned} \dim (\overline{\Sigma })=\dim (\Sigma )-\mathrm {rank}(V\cap K\cap W)=\dim (M_0)+\dim (M_1), \end{aligned}$$

all the conditions from Definition 3 are met, hence the diagram is a dual pair. $\square$

Example 9

Consider the dual pairs

$$\begin{aligned}&(\mathbb {S}^1,T^*\mathbb {S}^1) {\mathop {\longleftarrow }\limits ^{\mathrm {pr}_2}} (\mathbb {S}^1 \times \mathbb {S}^1,\mathrm {Gr}(\omega _{01})) {\mathop {\longrightarrow }\limits ^{\mathrm {pr}_1}} (\mathbb {S}^1,T^*\mathbb {S}^1), \\&(\mathbb {S}^1,T^*\mathbb {S}^1) {\mathop {\longleftarrow }\limits ^{\mathrm {pr}_2}} (\mathbb {S}^1 \times \mathbb {S}^1,\mathrm {Gr}(\omega _{12})) {\mathop {\longrightarrow }\limits ^{\mathrm {pr}_1}} (\mathbb {S}^1,T^*\mathbb {S}^1) \\&\omega _{01} = \mathrm {pr}_1^*(\mathrm {d}\theta ) \wedge \mathrm {pr}_2^*(\mathrm {d}\theta ), \quad \omega _{12} = \lambda \mathrm {pr}_1^*(\mathrm {d}\theta ) \wedge \mathrm {pr}_2^*(\mathrm {d}\theta ), \end{aligned}$$

where $\lambda \in \mathbb {R} \diagdown \mathbb {Q}$ and where $\mathrm {d}\theta \in \Omega ^1(\mathbb {S}^1)$ denotes a volume form. Their composition as weak dual pairs is isomorphic with the diagram

$$\begin{aligned} (\mathbb {S}^1,T^*\mathbb {S}^1) {\mathop {\longleftarrow }\limits ^{\mathrm {pr}_2}} (\mathbb {S}^1 \times \mathbb {S}^1 \times \mathbb {S}^1,\mathrm {Gr}(\omega _{02})) {\mathop {\longrightarrow }\limits ^{\mathrm {pr}_1}} (\mathbb {S}^1,T^*\mathbb {S}^1). \end{aligned}$$

The leaves of the foliation $\ker \mathbf {s}_{02*} \cap \ker \omega _{02} \cap \ker \mathbf {t}_{02*} = \langle \lambda \partial _{\theta _1}+\partial _{\theta _3}\rangle$ on $\mathbb {S}^1 \times \mathbb {S}^1 \times \mathbb {S}^1$ are not closed; in particular, the foliation is not simple, and therefore the weak dual pair above does not reduce to a dual pair. (See also [9, p. 39]).

Let us give a simple characterization of the situation when one of the legs of a weak dual pair is a Poisson structure.

Lemma 5

Let $(M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_1)$ be a weak dual pair.

• i) Then $L_1$ is a Poisson structure if and only if $W=V^{\omega }$.

• ii) If $L_1$ is a Poisson structure, then $\mathbf {s}$ is a presymplectic realization iff the weak dual pair is a dual pair.

Proof

$L_1$ is a Poisson structure exactly when $L_1 \cap TM_1 = 0$; but note that

$$\begin{aligned} L_1 \cap TM_1&= \mathbf {t}_!\mathbf {t}^!(L_1) \cap TM_1 = \mathbf {t}_!(\mathcal {R}_{-\omega }(V)+W) \cap TM_1 \\&= \mathbf {t}_!(\mathcal {R}_{-\omega }(V)) \cap TM_1= \mathbf {t}_*(V \cap K). \end{aligned}$$

Hence, $L_1$ is Poisson iff $V \cap K \subset W$. By Lemma 1, we have $V^{\omega }=W+V\cap K$. Therefore, $V \cap K \subset W$ iff $V^{\omega } = W$. This proves (i).

Let us prove now (ii). By (i) we have that $V\cap K\subset W$. Therefore $V \cap K \cap W=0$ iff $V\cap K=0$. The first condition is equivalent to the diagram being a dual pair, while the second is equivalent to $\mathbf {s}$ being a presymplectic realization. $\square$

Proposition 9 and Lemma 5 give a procedure for reducing to presymplectic realizations:

Corollary 5

(Reduction to presymplectic realizations) Let

$$\begin{aligned}\mathbf {s}:(\Sigma ,\mathrm {Gr}(\omega ))\longrightarrow (M_0,L_0)\end{aligned}$$

be a surjective, forward Dirac submersion. Assume that $V^{\omega }$ is a smooth distribution. Then $V^{\omega }$ and $V\cap K$ are both smooth, involutive distributions, and:

• (i) if the foliation $V\cap K$ is simple, i.e. if its leaves are the fibres of a surjective submersion $\mathrm {r}:\Sigma \rightarrow \overline{\Sigma }$, then $\omega =\mathrm {r}^*(\overline{\omega })$, where $\overline{\omega }$ is a closed 2-form on $\overline{\Sigma }$, and $\mathbf {s}$ factors as $\mathbf {s}=\overline{\mathbf {s}}\circ \mathrm {r}$, where $\overline{\mathbf {s}}$ is a presymplectic realization

  

• (ii) if the foliation $V^{\omega }$ is simple, i.e. if its leaves are the fibres of a surjective submersion $\mathbf {t}:\Sigma \rightarrow M_1$, then there exists a Poisson structure $\pi _1$ on $M_1$ which fits into the weak dual pair

  $$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,\mathrm {Gr}(-\pi _1)) \end{aligned}$$

• (iii) if both (i) and (ii) are assumed, then $\mathbf {t}$ factors as $\mathbf {t}=\overline{\mathbf {t}}\circ \mathrm {r}$, and the weak dual pair from (ii) reduces to a dual pair:

  

Example 10

Consider the forward Dirac map $\mathbf {s}:(\mathbb {R}^3,\mathrm {Gr}(\omega ))\rightarrow (\mathbb {R}^2,L_0)$ from Example 5. Then $\mathbf {s}$ is a presymplectic realization, i.e. $V\cap K=0$, and $V^{\omega }$ is the simple foliation corresponding to the fibres of $\overline{\mathbf {t}}:\mathbb {R}^3\rightarrow \mathbb {R}$, $\overline{\mathbf {t}}(x,y,z):=y$. By Corollary 5, we obtain the dual pair (compare with the pre-dual pair of Example 5):

$$\begin{aligned} (\mathbb {R}^2,L_1) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\mathbb {R}^3,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\overline{\mathbf {t}}}} (\mathbb {R},T^*\mathbb {R}). \end{aligned}$$

5.3 Pullback along transverse maps

In the Poisson setting, the procedure of pullback of a dual pair to small transversals to the symplectic leaves goes back to [38, Theorem 8.1], where it is shown that the induced transverse Poisson structures are anti-isomorphic. Here we discuss the procedure in the general Dirac setting.

We will use the following result.

Lemma 6

Let $f:(M,L_M)\rightarrow (N,L_N)$ be a forward Dirac map, and let $g:X\rightarrow N$ be a smooth map that is transverse to $L_N$ (see §12). Then the following hold:

• (i) f and g are transverse maps, so that $M\times _{N}X$, i.e. the pullback of f and g, is a smooth manifold;

• (ii) $\mathrm {pr}_1:M\times _{N}X\rightarrow M$ is transverse to $L_M$, so that $\mathrm {pr}_1^{!}(L_M)$ is a Dirac structure on $M\times _{N}X$;

• (iii) $\mathrm {pr}_2:(M\times _{N}X,\mathrm {pr}_1^{!}(L_M))\rightarrow (X,g^{!}(L_N))$ is forward Dirac. Moreover, if f is a strong map, then also $\mathrm {pr}_2$ is a strong map.

Proof

Throughout, (m, x) will denote a point in $M\times _NX$, so that $n:=f(m)=g(x)$. Using that g is transverse to $L_N$ and that f is forward Dirac, for , we obtain:

$$\begin{aligned} T_nN=g_*(T_xX)+\mathrm {pr}_T(L_{N,n})=g_*(T_xX)+\mathrm {pr}_T(f_{!}L_{M,m})\subset g_*(T_xX)+f_*(T_mM), \end{aligned}$$

which proves (i).

For (ii), let $v\in T_mM$. By item (i) above, we can decompose $f_*(v)=g_*(u)+f_*(w)$, with $u\in T_xX$ and $w+\alpha \in L_{M,m}$ for some $\alpha \in T^*_mM$. Then $(v-w,u)\in T_{(m,x)}(M\times _NX)$ and $v=\mathrm {pr}_1(v-w,u)+\mathrm {pr}_T(w+\alpha )$. This proves (ii).

The first part of (iii) is proven in [22, Lemma 3a)]. Finally, assume that f is a strong forward Dirac map. Consider $(v,0)\in T_{(m,x)}(M\times _NX)\cap \mathrm {pr}_1^!(L_M)$. Then $f_*(v)=g_*(0)=0$. Since $\mathrm {pr}_1$ is backward Dirac, there is $\alpha \in \ker \mathrm {pr}_1^*$ such that $v+\alpha \in L_{M,m}$. By transversality of f and g, we have the short exact sequence:

$$\begin{aligned} 0\longrightarrow T^*_nN{\mathop {\longrightarrow }\limits ^{f^*-g^*}}T^*_mM\oplus T^*_xX{\mathop {\longrightarrow }\limits ^{(\mathrm {pr}_1^*,\mathrm {pr}_2^*)}}T^*_{(m,x)}(M\times _NX)\longrightarrow 0. \end{aligned}$$

Hence, there is $\beta \in T^*_nN$ such that $f^*(\beta )=\alpha$ and $g^*(\beta )=0$. Since f is forward Dirac, we have that $f_*(v)+\beta =\beta \in L_{N,n} \cap \ker g^*$. Since g is transverse to $L_N$, this yields $\beta =0$, and so $\alpha =0$. So $v\in L_{M,m}\cap \ker f_*$, and since f is a strong map, $v=0$. We have shown that $\ker \mathrm {pr}_{2*}\cap \mathrm {pr}_1^!(L_M)=0$, i.e. $\mathrm {pr}_2$ is a strong map. $\square$

Next, we present the general procedure of pulling back along transverse maps.

Proposition 10

(Transverse pullback) Consider a weak dual pair

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_1). \end{aligned}$$

For $j=0,1$, consider a smooth map $i_j:X_j\rightarrow M_j$ that is transverse to $L_j$. Denote

$$\begin{aligned} \Sigma _X:= & {} X_0\times _{M_0}\Sigma \times _{M_1}X_1,\ \ \ \omega _X:=\mathrm {pr}_2^*\omega \\ \mathbf {s}_X= & {} \mathrm {pr}_1:\Sigma _X\rightarrow X_0,\ \ \ \mathbf {t}_X=\mathrm {pr}_3:\Sigma _X\rightarrow X_1. \end{aligned}$$

Then the diagram

$$\begin{aligned} (X_0,i_0^!(L_0)) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_X}} (\Sigma _X,\mathrm {Gr}(\omega _X)) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_X}} (X_1,-i_1^!(L_1)) \end{aligned}$$

satisfies all axioms of a weak dual pair, except maybe for the surjectivity of the maps $\mathbf {s}_X$ and $\mathbf {t}_X$. The same holds for dual pairs instead of weak dual pairs.

Proof

We apply Lemma 6 to the pair of maps:

$$\begin{aligned}&(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega ))\longrightarrow (M_0,L_0)\times (M_1,-L_1),\\&i_0\times i_1:X_0\times X_1\longrightarrow M_0\times M_1. \end{aligned}$$

We conclude that $\Sigma _X$ is a smooth manifold, and that

$$\begin{aligned} (\mathbf {s}_X,\mathbf {t}_X):(\Sigma _X,\mathrm {Gr}(\omega _X))\longrightarrow (X_0,i_0^!(L_0))\times (X_1,-i_1^!(L_1)) \end{aligned}$$

is a forward Dirac map.

Next, we show that $\mathbf {s}_X$ and $\mathbf {t}_X$ are submersions. We use the notation $V:=\ker \mathbf {s}_*$, $W:=\ker \mathbf {t}_*$ and $K:=\ker \omega$. Let $(x_0,z,x_1)\in \Sigma _{X}$, and let $v_0\in T_{x_0}X_0$. Since $\mathbf {s}$ is a submersion, there is $w_0\in T_{z}\Sigma$ such that $\mathbf {s}_*(w_0)=i_{0*}(v_0)$. Since $i_1$ and $L_1$ are transverse, we can decompose $\mathbf {t}_*(w_0)=i_{1*}(v_1)+u$, where $u+\alpha \in L_{1,m_1}$ and $m_1=i_1(x_1)$. Since $\mathbf {t}$ is forward Dirac, there is $w_1\in T_{z}\Sigma$ such that $\mathbf {t}_*(w_1)=u$ and $\iota _{w_1}\omega =-\mathbf {t}^*(\alpha )$. This implies that $w_1\in W^{\omega }$. By Lemma 1(c), $W^{\omega }=V+W\cap K$, so we can decompose $w_1=w_2+w_3$ with $w_2\in V$ and $w_3\in W$. Hence $\mathbf {t}_*(w_2)=\mathbf {t}_*(w_1)=u$ and $\mathbf {s}_*(w_2)=0$. So the element $w=w_0-w_2$ satisfies $\mathbf {s}_*(w)=i_{0*}(v_0)$ and $\mathbf {t}_*(w)=i_{1*}(v_1)$, thus $(v_0,w,v_1)\in T_{(x_0,z,x_1)}\Sigma _X$. This shows that $\mathbf {s}_X$ is a submersion, and similarly, one shows that also $\mathbf {t}_X$ is a submersion.

Since the fibres of $\mathbf {s}$ and $\mathbf {t}$ are $\omega$-orthogonal, by construction it follows that also the fibres of $\mathbf {s}_X$ and $\mathbf {t}_X$ are $\omega _X$-orthogonal; hence it follows from Proposition 6(iii) that the transverse pullback

$$\begin{aligned} (X_0,i_0^!(L_0)) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_X}} (\Sigma _X,\mathrm {Gr}(\omega _X)) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_X}} (X_1,-i_1^!(L_1)) \end{aligned}$$

is a weak dual pair.

Assume now that the weak dual pair in the statement is a dual pair. This is equivalent by Proposition 7(iii) to $(\mathbf {s},\mathbf {t})$ being a presymplectic realization and $\dim \Sigma = \dim M_0+\dim M_1$. In that case, it follows from Lemma 6 that $(\mathbf {s}_X,\mathbf {t}_X)$ is also a presymplectic realization, and transversality yields the dimension condition

$$\begin{aligned} \mathrm {dim}(\Sigma _X)&=\mathrm {dim}(\Sigma )+\mathrm {dim}(X_0)+\mathrm {dim}(X_1)-\mathrm {dim}(M_0)-\mathrm {dim}(M_1)\\&=\mathrm {dim}(X_0)+\mathrm {dim}(X_1). \end{aligned}$$

Invoking Proposition 7(iii) once again, we conclude that the transverse pullback of a dual pair is again a dual pair. $\square$

6 On the existence of self-dual pairs

An important ingredient of our Main Theorem is the following notion:

Definition 5

Let $L \subset \mathbb {T}M$ be a Dirac structure on M, and let $\mathbf {s}:L \rightarrow M$ denote the bundle projection. A spray for L is a vector field $\mathcal {V} \in \mathfrak {X}(L)$, satisfying:

• (Spr1) $\mathbf {s}_{*}\mathcal {V}_a = \mathrm {pr}_{T}(a)$, for all $a \in L$;

• (Spr2) $m_t^{*}\mathcal {V}=t\mathcal {V}$, where $m_t:L\rightarrow L$ denotes multiplication by $t\ne 0$.

For example, given a linear connection on L with horizontal lift h, the vector field $\mathcal {V}_a:=h_a(\mathrm {pr}_{T}(a))$ is a spray for L.

Given a spray $\mathcal {V}$ for L, note that (Spr2) implies that $\mathcal {V}$ vanishes along M, identified with the zero-section of L. Therefore, there exists a small enough neighborhood $\mathcal {U}\subset L$ of M on which the flow $\varphi _{\epsilon }:\mathcal {U} \rightarrow L$ of $\mathcal {V}$ is defined for $0\le \epsilon \le 1$, and consider

$$\begin{aligned} \omega :=\int _0^1\varphi _{\epsilon }^{*}\omega _L \mathrm {d}\epsilon \ \in \ \Omega ^2(\mathcal {U}), \quad \mathbf {t}:=\mathbf {s}\circ \varphi _1:\mathcal {U} \rightarrow M, \end{aligned}$$

where $\omega _L \in \Omega ^2(L)$ denotes the pullback of the canonical two-form on $T^*M$ under $\mathrm {pr}_{T^*}:L \rightarrow T^*M$. With this notation, we state:

Main Theorem

There is an open set $\Sigma \subset \mathcal {U}$ containing M, such that the diagram

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M,-L) \end{aligned}$$

forms a dual pair.

The proof will make use of the following

Lemma 7

• (i) The flow $\varphi _{\epsilon }$ is the identity along M, and in the canonical decomposition $TL|_M=TM \oplus L$, its differential reads

  

• (ii) We have that $(\ker \mathbf {s}_* \cap \ker \omega \cap \ker \mathbf {t}_*)|_M = 0$.

Proof

$\mathrm{(i)}$ Since $\mathcal {V}$ vanishes along M, we have $\varphi _{\epsilon }|_M=\mathrm {id}_M$. Let $\mathcal {V}_T \in \mathfrak {X}(TL)$ be the vector field generating the flow (also called the tangent lift of $\mathcal {V}$). Due to (Spr2), $\mathcal {V}_T$ is tangent to $T_{x}L\subset TL$ for each $x \in M$, and $\mathcal {V}_T|_{T_{x}L} \in \mathfrak {X}(T_{x}L)$ is a linear vector field. By (Spr1), this vector field corresponds to the endomorphism

$$\begin{aligned} T_xM \oplus L_x \rightarrow T_xM \oplus L_x, \quad (u,a) \mapsto (\mathrm {pr}_T(a),0); \end{aligned}$$

the exponential of this map, i.e. $\varphi _{\epsilon *}$ on $T_xM\oplus L_x$, is given by the formula in the statement. For a different proof, see [3, Lemma 3.21].

$\mathrm{(ii)}$ Along the zero section $M \subset L$, the two-form $\omega _L \in \Omega ^2(L)$ reads:

$$\begin{aligned} \omega _L\left( (u,v+\eta ),(u',v'+\eta ')\right) =\eta '(u)-\eta (u'). \end{aligned}$$

On the other hand, by item i), we have

$$\begin{aligned} \varphi _{\epsilon *}(u,v+\eta )= (u+\epsilon v,v+\eta ), \ \ (u,v+\eta )\in TL|_M = TM\oplus L; \end{aligned}$$

hence

$$\begin{aligned} \omega \left( (u,v+\eta ),(u',v'+\eta ')\right) =\eta '(u+1/2v)-\eta (u'+1/2v'). \end{aligned}$$

(6)

Let $(u,v+\eta )\in \ker \mathbf {s}_* \cap \ker \omega \cap \ker \mathbf {t}_*|_M$. Since $\mathbf {s}_{*}(u,v+\eta )=u$ and

$$\begin{aligned} \mathbf {t}_{*}(u,v+\eta )=\mathbf {s}_{*}\varphi _{1*}(u,v+\eta )=\mathbf {s}_{*}(u+v,v+\eta )=u+v, \end{aligned}$$

it follows that $u=0$ and $v=0$. By formula (6),

$$\begin{aligned} 0=\omega ((u,v+\eta ),(u',0))=-\eta (u') \end{aligned}$$

for all $u'$; thus, also $\eta =0$. $\square$

Proof of Main Theorem

Let $\mathcal {U}\subset L$ be a neighborhood of M on which $\varphi _{\epsilon }$ is defined for $0\le \epsilon \le 1$, and so also $\mathbf {t}=\mathbf {s}\circ \varphi _1$ and $\omega =\int _0^1\varphi _{\epsilon }^*\omega _{L} \mathrm {d}\epsilon$ are defined on $\mathcal {U}$. Write $V,W,K \subset T\mathcal {U}$ for $\ker \mathbf {s}_*,\ker \mathbf {t}_*$ and $\ker \omega$, respectively. By Lemma 7(ii), $(V\cap K \cap W)|_M=0$. Sine this condition is open, we may assume that

$$\begin{aligned} (V\cap K \cap W)|_{\Sigma }=0, \end{aligned}$$

(7)

where $\Sigma \subset \mathcal {U}$ is an open neighborhood of M.

Consider the pullback to L of the tautological one-form $\lambda _{\mathrm {can}}$ on $T^*M$:

$$\begin{aligned} \lambda _L:=(\mathrm {pr}_{T})^*\lambda _{\mathrm {can}}\in \Omega ^1(L). \end{aligned}$$

Note that condition (Spr1) in the definition of a spray $\mathcal {V}$ implies that $\mathcal {V}+\lambda _L$ is a section of the Dirac structure $\mathbf {s}^!(L)$. The local flow $\Phi _{\epsilon }$ of the section $\mathcal {V}+\lambda _L$ on $\mathbf {s}^!(L)$ covers the local flow $\varphi _{\epsilon }:L \rightarrow L$ and, on its domain of definition, it is given by (e.g. [23, Proposition 2.3]):

$$\begin{aligned} \Phi _{\epsilon }=\varphi _{\epsilon *}\circ \mathcal {R}_{B_{\epsilon }}:\mathbf {s}^!(L)\longrightarrow \mathbf {s}^!(L), \end{aligned}$$

where $B_{\epsilon }=\int _0^{\epsilon } \varphi _{s}^{*}\mathrm {d}\lambda _L \mathrm {d}s=-\int _0^{\epsilon } \varphi _{s}^{*}\omega _L \mathrm {d}s$. Since $B_1=-\omega$, we have that:

$$\begin{aligned} \mathbf {s}^!(L)|_{\varphi _{1}(\Sigma )}=\Phi _{1}\left( \mathbf {s}^!(L)|_{\Sigma }\right) =\varphi _{1!}(\mathcal {R}_{-\omega }(\mathbf {s}^!(L)|_{\Sigma })), \end{aligned}$$

and therefore

$$\begin{aligned} \mathcal {R}_{-\omega }(\mathbf {s}^!(L)|_{\Sigma })=\varphi _1^!(\mathbf {s}^!(L)|_{\varphi _1(\Sigma )})=\mathbf {t}^!(L)|_{\Sigma }. \end{aligned}$$

(8)

Since $\dim \Sigma = 2 \dim M$ and Eqs. (7) and (8) hold, Proposition 7 $(ii)\Rightarrow (i)$ yields the conclusion. $\square$

7 Application: normal forms around Dirac transversals

In this section, we use the Main Theorem to prove the normal form theorem around Dirac transversals (from [13]) The same strategy is already present in [21] in the context of Poisson geometry.

Definition 6

An embedded submanifold X of a Dirac manifold (M, L) is called a Dirac transversal if the inclusion $i:X\rightarrow M$ is transverse to L.

The normal form theorem around Dirac transversals states that, up to diffeomorphisms and exact gauge transformations, the induced Dirac structure on the transversal determines the Dirac structure around the transversal. The Poisson geometric version of this result appeared in [21]; a local version for Dirac structures occurs in [5]; a version for generalized complex structures was described in [3]. Moreover, the same statement as the one below, but with a different proof, appeared in [13]:

Theorem

(Normal form around Dirac transversals) Let $i:X \rightarrow (M,L)$ be a Dirac transversal, and let $p:NX\rightarrow X$ be the normal bundle of X. Then there exist an embedding $\varphi : U \rightarrow M$ of an open neighborhood $U \subset NX$ of X extending i, and an exact two-form $\alpha \in \Omega ^2(U)$, such that

$$\begin{aligned} \varphi ^!(L) = \mathcal {R}_{\alpha }(p^!i^!(L)). \end{aligned}$$

Proof

Consider the dual pair given by the Main Theorem:

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M,-L). \end{aligned}$$

We apply the pullback procedure of Proposition 10, and obtain the diagram

$$\begin{aligned} (X,i^!(L)) {\mathop {\longleftarrow }\limits ^{\mathbf {s}_0}} (\Sigma _0,\mathrm {Gr}(\omega _0)) {\mathop {\longrightarrow }\limits ^{\mathbf {t}_0}} (M,-L), \end{aligned}$$

(9)

where

$$\begin{aligned} \Sigma _{0}:=\mathbf {s}^{-1}(X), \ \ \omega _0:=\omega |_{\Sigma _0},\ \ \mathbf {s}_0:=\mathbf {s}|_{\Sigma _0}, \ \ \mathbf {t}_0:=\mathbf {t}|_{\Sigma _0}. \end{aligned}$$

Note that $\mathbf {s}_0$ is surjective. By construction, the image of $\mathbf {t}_0$ contains X and it is open, because $\mathbf {t}_0$ is a submersion. Therefore, by replacing M by $\mathbf {t}_0(\Sigma _0)$, we may assume that also $\mathbf {t}_0$ is onto, and so, by Proposition 10, we may assume that the diagram (9) is a dual pair.

The fact that X is a Dirac transversal implies that

$$\begin{aligned} \widetilde{i}: i^!(L) \longrightarrow L|_X, \quad \widetilde{i}(u+i^*\xi ):=i_{*}(u)+\xi \end{aligned}$$

is a well-defined bundle map which fits into the exact sequence:

$$\begin{aligned} 0 \longrightarrow i^!(L) {\mathop {\longrightarrow }\limits ^{\widetilde{i}}} L|_X \longrightarrow NX \longrightarrow 0. \end{aligned}$$

Let $\rho :NX \rightarrow i^*(L)$ be a splitting of this sequence. By Lemma 7(i), we have that

$$\begin{aligned} \mathbf {t}_{0_*} : T\Sigma _0|_X = TX \oplus L \longrightarrow TM, \quad \mathbf {t}_{0_*}(u,a) = u+\mathrm {pr}_T(a), \end{aligned}$$

and therefore there exists an open set $X \subset U \subset NX$ such that

is an open embedding extending the inclusion i. Since $\mathbf {s}_0 \circ \rho = p$ and $\varphi = \mathbf {t}_0 \circ \rho$,

$$\begin{aligned} p^!(i^!(L)) = \rho ^!(\mathbf {s}_0^!(i^!(L))) = \rho ^!\left( \mathcal {R}_{\omega _0}(\mathbf {t}_0^!(L))\right) = \mathcal {R}_{\rho ^*\omega _0}(\varphi ^!(L)), \end{aligned}$$

where we have used the relation $\mathbf {s}_0^!(i^!(L)) = \mathcal {R}_{\omega _0}(\mathbf {t}_0^!(L))$ from Proposition 7(ii). This implies the conclusion:

$$\begin{aligned} \varphi ^!(L) = \mathcal {R}_{\alpha }(p^!(i^!(L))), \ \ \text {where} \ \ \alpha :=-\rho ^*\omega _0 \in \Omega ^2(U). \end{aligned}$$

$\square$

8 Further remarks

8.1 The origin of the formula

The formula for the two-form $\omega$ from the Main Theorem originates in the path-space approach to integrability of Lie algebroids, developed in [17]. In a nutshell, given a Lie algebroid A over a manifold M, the space P(A) of A-paths carries a canonical homotopy foliation, of finite codimension. The leaf space of this foliation has a canonical structure of topological groupoid $G(A) \rightrightarrows M$ (the so-called Weinstein groupoid of A), which is smooth exactly when A is integrable by a Lie groupoid. If the Lie algebroid is a Dirac structure $A=L$ on M, and moreover, if it is integrable, then G(L) carries a canonical, multiplicative, closed two-form $\omega _{G(L)}$, for which the source and target maps $\mathbf {s},\mathbf {t}:(G(L),\mathrm {Gr}(\omega _{G(L)}))\rightarrow (M,L)$ give a dual pair [10]. However, even if L is not integrable, the Banach manifold P(L) of L-paths carries a canonical two-form $\omega _{P(L)}$ which is basic for the homotopy foliation, and, in the integrable case, it is the pullback of $\omega _{G(L)}$. Using the language developed in Sect. 5, in the integrable case the passage from P(L) to G(L) can be viewed as a reduction of an infinite dimensional weak dual pair to a finite dimensional dual pair:

Now, a spray $\mathcal {V}$ on L induces an exponential map $\exp _{\mathcal {V}}:\Sigma \rightarrow P(L)$ on a neighborhood $\Sigma \subset L$ of the zero-section, which is transverse to the homotopy foliation, and of complementary dimension. The two-form $\omega$ from our main result is the precisely the pullback of $\omega _{P(L)}$ via $\exp _{\mathcal {V}}$ (see the explicit formula of $\omega _{P(L)}$ from [10, Section 5]). In fact, along these lines, one can use results of loc.cit. to give an alternative proof of our Main Theorem; however, such a proof is bound to be less elementary.

8.2 Local presymplectic groupoids

Closely related to the dual pair constructed in our Main Theorem is the notion of local presymplectic groupoid. First, by [17, Corollary 5.1], any Lie algebroid is integrable by a local Lie groupoid, and second, by extending the results of [10] to the setting of such local objects, one can prove the existence of a local presymplectic groupoid integrating a given Dirac manifold; and in particular, the existence of a self-dual pair.

However, the converse construction seems of more significance: one can endow the self-dual pair constructed in the Main Theorem with the structure of a local presymplectic groupoid, yielding a rather explicit construction of a local integration of a Dirac manifold; a simple version of this construction was shown to us by Eckhard Meinrenken [31], which uses the comorphism $\Psi$ from Remark 4 to construct an action of $L\times -L$ of $\Sigma$, which corresponds to the left and right invariant vector fields on the local Lie groupoid $\Sigma \rightrightarrows M$. This is very much in the spirit of [20], where a local symplectic groupoid integrating a Poisson manifold is constructed by using a symplectic realization. For a general construction of local Lie groupoids using Lie algebroid sprays, see [4].

8.3 The twisted case

Courant algebroids may be twisted by closed three-forms. Specifically, let $\phi \in \Omega ^3(M)$ be closed, and consider the $\phi$-twisted Dorfman bracket

$$\begin{aligned}{}[u+\xi ,v+\eta ]_{\phi }:=[u+\xi ,v+\eta ]+\iota _u\iota _v\phi , \quad u+\xi , \ v+\eta \in \Gamma (\mathbb {T}M), \end{aligned}$$

and where $[u+\xi ,v+\eta ]$ stands for the Dorfman bracket of §2. A Lagrangian subbundle $L \subset \mathbb {T}M$ (in the sense of §6) is called a $\phi$-twisted Dirac structure if its space of sections is involutive under the $\phi$-twisted Dorfman bracket.

Twisted Dirac structures go back, in one form or another, to [27, 32, 34, 35]. A crucial example of such structures is given by Cartan-Dirac structures associated to nondegenerate, invariant inner products on the Lie algebra $\mathfrak {g}$ of a Lie group G [35, Example 4.2], and whose presymplectic realizations correspond to the quasi-Hamiltonian $\mathfrak {g}$-spaces of [1] (see [10]).

Twisted Dirac structures are in particular Lie algebroids, whose global objects correspond (in the integrable case) to the twisted presymplectic groupoids of [10], or quasi-symplectic groupoids in the language of [41].

Our Main Theorem can be adapted to the twisted setting in a straightforward way [30] (see also the comments in [19, Section 4]). We briefly indicate here the necessary modifications. The notions of forward/backward Dirac maps, and of sprays make sense for general Lagrangian subbundles (as pointwise conditions), and retain their meaning from the untwisted case. For example, if $L \subset \mathbb {T}M$ is a $\phi$-twisted Dirac structure, and $\mathbf {s}:\Sigma \rightarrow M$ is a submersion, then $\mathbf {s}^!(L):=\{u+\mathbf {s}^*(\xi ) \ | \ \mathbf {s}_*(u)+\xi \in L\}$ is a $\mathbf {s}^*(\phi )$-twisted Dirac structure on $\Sigma$. The notion of dual pair, however, needs to be adapted: if $(M_i,L_i,\phi _i)$ are twisted Dirac structures, a twisted dual pair is a diagram of surjective, forward Dirac submersions

$$\begin{aligned} (M_0,L_0) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\omega ) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-L_1) \end{aligned}$$

as in Definition 3, but where now $\omega \in \Omega ^2(\Sigma )$ is a two-form satisfying

$$\begin{aligned} \mathrm {d}\omega = \mathbf {s}^*(\phi _0) - \mathbf {t}^*(\phi _1). \end{aligned}$$

Lemma 7 remains valid ipsis litteris in the twisted case, and if $\mathcal {V} \in \mathfrak {X}(L)$ is a spray for L (in the sense that it satisfies conditions (Spr1) and (Spr2) of Definition 5), then $\mathcal {V}+\lambda _L$ is a section of the $\mathbf {s}^*(\phi )$-twisted Dirac structure $\mathbf {s}^!(L)$ (where $\lambda _L$ is, as before, the pullback of the tautological one-form on M via the projection $\mathrm {pr}_{T^*}:L \rightarrow T^*M$). Then $D=[\mathcal {V}+\lambda _L,\cdot ]_{\mathbf {s}^*(\phi )}$ corresponds to the derivation

$$\begin{aligned} D=(\mathcal {V},b) \in \mathfrak {X}(L) \oplus \Omega ^2(L), \quad b:=\mathrm {d}\lambda _L+\iota _{\mathcal {V}}\mathbf {s}^*(\phi ), \quad \mathscr {L}_\mathcal {V}\mathbf {s}^*(\phi ) = \mathrm {d}b, \end{aligned}$$

that is, it integrates to a linear automorphism

$$\begin{aligned} \Phi _{\epsilon }:\mathbb {T}\mathcal {U}\longrightarrow \mathbb {T}\mathcal {U}, \ \ \Phi _{\epsilon }(u+\eta )=\varphi _{\epsilon *}(u)+\varphi _{\epsilon }^{*-1}(\iota _uB_{\epsilon }+\eta ), \end{aligned}$$

which is orthogonal for the inner product of §2, and preserves the $\mathbf {s}^*(\phi )$-twisted bracket; here $\mathcal {U} \subset L$ denotes (as before) an open neighborhood of M on which the flow of $\mathcal {V}$ is defined up to time one, and $B_{\epsilon }$ denotes the two-form $B_{\epsilon }:=\int _0^{\epsilon } \varphi _s^*(b) \mathrm {d}s$, which satisfies $\mathrm {d}B_{\epsilon }=\varphi _{\epsilon }^*\mathbf {s}^*(\phi ) - \mathbf {s}^*(\phi )$.

The condition that $[\Gamma (\mathbf {s}^!(L)),\Gamma (\mathbf {s}^!(L))]_{\mathbf {s}^*(\phi )} \subset \Gamma (\mathbf {s}^!(L))$ implies that $D\Gamma (\mathbf {s}^!(L)) \subset \Gamma (\mathbf {s}^!(L))$, and so $\Phi _{\epsilon }$ restricts to a Lie algebroid automorphism of $\mathbf {s}^!(L)$. As in the proof of the Main Theorem, this implies that

$$\begin{aligned} \mathbf {s}^!(L) = \ker \mathbf {s}_* \oplus \mathcal {R}_{\omega }(\ker \mathbf {t}_*), \quad \mathbf {t}^!(L) = \mathcal {R}_{-\omega }(\ker \mathbf {s}_*) \oplus \ker \mathbf {t}_*, \end{aligned}$$

where $\omega :=-B_1$, $\mathbf {t}:=\mathbf {s}\circ \varphi _1$. The twisted version of Proposition 7 allows us to deduce that, on an open neighborhood $\Sigma \subset \mathcal {U}$ of M, the map $(\mathbf {s},\mathbf {t}):(\Sigma ,\mathrm {Gr}(\omega )) \rightarrow (M,L) \times (M,-L)$ is a presymplectic realization; we obtain a twisted dual pair:

$$\begin{aligned} (M,L) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M,-L), \quad \mathrm {d}\omega = \mathbf {s}^*(\phi )-\mathbf {t}^*(\phi ). \end{aligned}$$

8.4 Morita equivalence

Closely related to the notion of dual pairs above is that of Morita equivalences. This notion of equivalence was first introduced by Xu [39, 40] in the context of Poisson manifolds as a classical analogue of the algebraic notion for $C^*$-algebras developed by Rieffel [33].

Two Poisson manifolds $(M_0,\pi _0)$, $(M_1,\pi _1)$ are called Morita equivalent if there exists a dual pair

$$\begin{aligned} (M_0,\mathrm {Gr}(\pi _0)) {\mathop {\longleftarrow }\limits ^{\mathbf {s}}} (\Sigma ,\mathrm {Gr}(\omega )) {\mathop {\longrightarrow }\limits ^{\mathbf {t}}} (M_1,-\mathrm {Gr}(\pi _1)) \end{aligned}$$

with simply-connected fibres, in which the induced comorphisms

$$\begin{aligned} \mathbf {s}^*(\mathrm {Gr}(\pi _0)) \rightarrow T\Sigma , \quad \mathbf {t}^*(\mathrm {Gr}(\pi _1)) \rightarrow T\Sigma \end{aligned}$$

are complete [40, Definition 2.1]. This ensures that the Poisson manifolds are integrable (see Corollary 4), that the symplectic leaves of $(M_0,\pi _0)$ and $(M_1,\pi _1)$ are in bijection (with the same first homology), that they have anti-isomorphic transverse Poisson structures, isomorphic algebras of Casimirs and modules of first Poisson cohomology [24, 38]. More importantly, it ensures that Morita equivalent Poisson manifolds have equivalent ’categories’ of complete symplectic realizations [40, Theorem 3.3].

Morita equivalence of Poisson manifolds can also be approached through symplectic groupoids: two (integrable) Poisson manifolds are Morita equivalent if their source-simply connected symplectic groupoids $(G_0,\omega _0) \rightrightarrows (M_0,\pi _0)$, $(G_1,\omega _1) \rightrightarrows (M_1,\pi _1)$ admit a symplectic $(G_0,G_1)$-bibundle which is biprincipal [9, 28, 39, 40]. This line of thought was greatly extended in [41], which introduces Morita equivalence for quasi-symplectic groupoids (or twisted presymplectic groupoids in the sense of [10]), which plays an analogous role for twisted Dirac manifolds as Morita equivalence of symplectic groupoids in Poisson geometry. As in the Poisson case, this notion only makes sense in the integrable case, but some recent ’stacky’ versions of Morita equivalence forgo the integrability hypothesis [8, 9, 12] (cf. also the weaker notion of Morita equivalence discussed in [25, Section 6]).