Abstract
Given a generic family \(Q\) of 2-dimensional quadrics over a smooth 3-dimensional base \(Y\) we consider the relative Fano scheme \(M\) of lines of it. The scheme \(M\) has a structure of a generically conic bundle \(M \rightarrow X\) over a double covering \(X \rightarrow Y\) ramified in the degeneration locus of \(Q \rightarrow Y\). The double covering \(X \rightarrow Y\) is singular in a finite number of points (corresponding to the points \(y \in Y\) such that the quadric \(Q_y\) degenerates to a union of two planes), the fibers of \(M\) over such points are unions of two planes intersecting in a point. The main result of the paper is a construction of a semiorthogonal decomposition for the derived category of coherent sheaves on \(M\). This decomposition has three components, the first is the derived category of a small resolution \(X^+\) of singularities of the double covering \(X \rightarrow Y\), the second is a twisted resolution of singularities of \(X\) (given by the sheaf of even parts of Clifford algebras on \(Y\)), and the third is generated by a completely orthogonal exceptional collection.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The subject of this note is a description of the structure of the derived category of coherent sheaves on the relative scheme of lines for a family of 2-dimensional quadrics. We had two motivations for the investigation of this category. First of all it has an interesting structure and exhibits some interesting features. For example, it combines the minimal resolution of singularities and the twisted resolution of singularities of the double covering of the base naturally associated with the family.
The second, and the most important motivation, comes from investigation of the derived categories of so-called nodal Enrique surfaces. These surfaces can be associated with families of 2-dimensional quadrics parameterized by \({\mathbb{P }}^3\) (webs of quadrics). The relative scheme of lines in this case can be identified with the blowup of the Grassmannian \(\mathsf{Gr }(2,4)\) in the corresponding Enriques surface. Consequently, its derived category contains the derived category of the Enriques surface as a semiorthogonal component. So, another description of the derived category of the relative scheme of lines, provided by the present paper, gives a link between the derived categories of nodal Enriques surfaces and of the associated double coverings of \({\mathbb{P }}^3\), which in this case are nothing but the Artin–Mumford quartic double solids, appeared in the famous paper [2] as examples of unirational but nonrational threefolds. See the companion paper [6] for more details.
The precise formulation of the main result of the paper is the following. Consider a family of 2-dimensional quadrics \(q:Q \rightarrow Y\). This means that we are given a projectivization of a rank 4 vector bundle \({\fancyscript{V}}\) on \(Y\) and a divisor \(Q \subset {\mathbb{P }}_{Y}({\fancyscript{V}})\) of relative degree 2 which is flat over \(Y\). Such divisor is given by a line subbundle \(\mathcal{L }\subset S^2{\fancyscript{V}}^\vee \).
Given this we consider the relative Fano scheme of lines of \(Q\) over \(Y\). By definition this is the zero locus on the relative Grassmannian \(\mathsf{Gr }_{Y}(2,{\fancyscript{V}})\) of the global section
where \({\fancyscript{U}}\subset {\fancyscript{V}}\) is the tautological subbundle on the Grassmannian. We denote this relative Fano scheme by \(M\). The fibers \(M_y\) of the projection \(\rho :M \rightarrow Y\) are the Fano schemes of lines on quadrics \(Q_y\), and so they have the following structure
-
\(M_y\) is a disjoint union of two smooth conics, if the quadric \(Q_y\) is smooth;
-
\(M_y\) is a single smooth conic (with a nonreduced scheme structure), if the quadric \(Q_y\) has corank 1;
-
\(M_y\) is a union of two planes intersecting in a point, if the quadric \(Q_y\) has corank 2;
-
\(M_y\) is a single plane (with a nonreduced structure), if the quadric \(Q_y\) has corank 3.
The main result of this paper is a description of the derived category of \(M\) when \(\dim Y = 3\) under the following genericity assumptions: we assume that
-
the generic fiber of \(Q\) over \(Y\) is smooth, and
-
the codimension of the locus \(D_r \subset Y\) of quadrics of corank \(r\) equals \(r(r+1)/2\).
As \(\dim Y = 3\), the second assumtion implies that \(D_3 = \emptyset \) and \(D_2\) consists of a finite number \(N\) of isolated points \(y_1,\dots ,y_N\). Additionally we assume that
-
\(D_1\) has an ordinary double point (an ODP or a node for short) in each of \(y_i\).
The last assumption is equivalent to smoothness of \(M\) if \(Q\) is smooth (see Lemma 2.4 below).
To state the answer we need the following ingredients. First, consider the Stein factorization for the morphism \(\rho :M \rightarrow Y\):

where \(f:X \rightarrow Y\) is the double covering ramified in the divisor \(D_1\), and \(\mu :M \rightarrow X\) is generically a conic bundle. Note that \(X\) is smooth away from \(N\) points \(x_i = f^{-1}(y_i)\) which are isolated ordinary double points. So being 3-dimensional it has \(2^N\) small resolutions of singularities in the category of Moishezon varieties. To fix one of these resolutions we should choose for each point \(y_i \in D_2\) one of the planes in the corank 2 quadric \(Q_{y_i}\), or equivalently one of the planes in the fiber \(M_{y_i}\) of \(M\) over \(Y\). Let us pick one of these resolutions and denote it by \(\sigma _+:X^+ \rightarrow X\). Let us denote the planes in \(M_{y_i}\) corresponding to this choice by \(\Sigma _i^+\), and the complementary planes by \(\Sigma _i^-\), so that \(M_{y_i} = \Sigma _i^+ \cup \Sigma _i^-\).
Second, consider the sheaf of even parts of Clifford algebras \(\mathcal{B }_0\) on \(Y\) associated with the family of quadrics \(Q \rightarrow Y\) (see Sect. 3 or [10] for details). If \(Q\) is smooth then the category \(\mathcal{D }^b(Y,\mathcal{B }_0)\) is also smooth and can be thought of as a twisted noncommutative resolution of the double covering \(X\).
The main result of this paper is the following
Theorem 1.1
Assume that \(Q \rightarrow Y\) is a family of quadrics, \(Y\) and \(Q\) are smooth, \(\dim Y = 3\), and the degeneration locus \(D_1\) has a finite number of ordinary double points \(\{y_1,\dots ,y_N\} = D_2\). Then the relative Fano scheme \(M\) of lines of \(Q\) over \(Y\) is smooth and there is a semiorthogonal decomposition
Here the third component is a completely orthogonal exceptional collection.
It is natural to ask, whether one can remove some of the assumptions and prove a similar result. It seems that indeed, there are some ways of a generalization of this decomposition. For example, if the dimension of \(Y\) is higher than \(3\) (but still \(Y\) and \(Q\) are smooth, \(D_1\) has ordinary double points (in the transversal slice) along \(D_2\), and \(D_3 = \emptyset \)), then probably one can construct a semiorthogonal decomposition with the first component being a categorical crepant resolution of \(X\), the same second component, and the third component equal to the derived category of the stratum \(D_2\). See Sect. 6 for a discussion of further perspectives of the question.
The proof of the Theorem goes as follows. In Sect. 2 we prove smoothness of \(M\) and investigate the local structure of \(M\) around the planes \(\Sigma _i^\pm \). In particular, we check that the sheaves \(\mathcal{O }_{\Sigma _i^+}\) form a completely orthogonal exceptional collection in \(\mathcal{D }^b(M)\). In Sect. 3 we recall some facts about the sheaf of even parts of Clifford algebras \(\mathcal{B }_0\) and construct a fully faithful embedding \(\mathcal{D }^b(Y,\mathcal{B }_0) \rightarrow \mathcal{D }^b(M)\). In Sect. 4 we show that there is a birational transformation of \(M\), known as a flip in \(N\) planes \(\Sigma _i^+\), transforming it into a \({\mathbb{P }}^1\)-fibration \(\mu _+:M^+ \rightarrow X^+\) over a small resolution \(X^+ \rightarrow X\). This gives an identification of the orthogonal to the collection \(\{ \mathcal{O }_{\Sigma _i^+} \}_{i=1}^N\) in \(\mathcal{D }^b(M)\) with \(\mathcal{D }^b(M^+)\). In Sect. 5 we construct a fully faithful embedding \(\mathcal{D }^b(X^+) \rightarrow \mathcal{D }^b(M^+)\) and identify the complement with \(\mathcal{D }^b(Y,\mathcal{B }_0)\). In the last Sect. 6 we discuss another way of proving Theorem 1.1 and suggest some further directions of investigation.
2 Geometry of \(M\)
For each quadric \(Q_y\) in the family \(Q \rightarrow Y\) denote by \(K_y \subset {\fancyscript{V}}_y\) the kernel of the corresponding quadratic form (thus \({\mathbb{P }}(K_{y})\) is the singular locus of the quadric \(Q_y\)). Note that the differential of the section \(s \in \Gamma (Y,\mathcal{L }^{-1}\otimes S^2{\fancyscript{V}}^\vee )\) at \(y\) gives a linear map \(T_yY \rightarrow S^2{\fancyscript{V}}_y^\vee \) (depending on a choice of trivializations on the bundles \(\mathcal V \) and \(\mathcal L \) near \(y\)). Composing it with the natural projection \(S^2{\fancyscript{V}}_y^\vee \rightarrow S^2K_y^\vee \) we obtain a map
which does not depend on the choices of the trivializations.
In terms of these maps one can check the smoothness of \(Q\) and \(M\).
Proposition 2.1
Assume that \(Y\) is smooth. Then
-
1.
\(Q\) is smooth if and only if for any \(y \in Y\) and any subspace \(K \subset K_y\) with \(\dim K \le 1\), the composition
 is surjective;
is surjective; -
2.
\(M\) is smooth if and only if for any \(y \in Y\) and any embedding \(K \rightarrow K_y\) with \(\dim K \le 2\), the composition
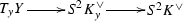 is surjective.
is surjective.
Proof
The question is local in \(Y\) so we can assume that \({\fancyscript{V}}\) is a trivial bundle, \({\fancyscript{V}}\cong V\otimes \mathcal{O }_Y\), and so \({\mathbb{P }}_{Y}({{\fancyscript{V}}}) = Y \times {\mathbb{P }}(V)\). Let \((y,K)\) be an arbitrary point of \(Q\), where \(K \subset V\) is a 1-dimensional subspace of \(V\). Then the smoothness of \(Q\) at the point \((y,K)\) is equivalent to the surjectivity of the differential \(ds:T_{y}Y {\oplus } {\mathop {\mathsf{Hom }}\nolimits }(K,V/K) {\rightarrow } S^{2}K^{\vee }\). If \(K \not \subset K_y\) then the second summand maps surjectively. If, on a contrary, \(K \subset K_y\) then the second summand maps trivially, while the map of the first summand is the map in the statement of the Lemma. This proves the first part.
For the second part, let \((y,K)\) be an arbitrary point of \(M\), where \(K \subset V\) is a 2-dimensional subspace of \(V\). Then the smoothness of \(M\) at the point \((y,K)\) is equivalent to the surjectivity of the differential \(ds:T_{y}Y {\oplus } {\mathop {\mathsf{Hom }}\nolimits }(K,V/K) {\rightarrow } S^{2}K^{\vee }\). If \(K \cap K_y = 0\) then the second summand maps surjectively. Further, if the space \(K_{1} := K \cap K_{y}\) is 1-dimensional, then the cokernel of the map of the second summand is equal to \(S^{2}K_{1}^{\vee }\) and the map of the first summand is the map in the statement of the Lemma for \(K_{1}\). Finally, if \(K \subset K_{y}\), then the second summand maps trivially, while the map of the first summand is the map in the statement of the Lemma. This proves the second part. \(\square \)
Remark 2.2
This result generalizes to arbitrary relative isotropic Grassmannians of families of quadrics of arbitrary dimension. The smoothness of the Grassmannian of \(k\)-dimensional subspaces is equivalent to the surjectivity of the corresponding map for all \(K\) with \(\dim K \le k\).
Corollary 2.3
Assume that \(Y\) is smooth and \(D_3 = \emptyset \). Then \(M\) is smooth if and only if \(Q\) is smooth and for any \(y \in D_2\) the map \(\kappa _y:T_yY \rightarrow S^2K_y^\vee \) is surjective.
Another consequence of the smoothness of \(Q\) is the smoothness of \(D_1{\setminus } D_2\). On the other hand, the points of \(D_2\) are always singular on \(D_1\). In fact they are ordinary double points if \(M\) is smooth.
Lemma 2.4
Assume that \(Q\) is smooth and \(\dim Y = 3\). Then \(M\) is smooth if and only if \(D_2\) is a finite number of points and any point of \(D_2\) is an ordinary double point of \(D_1\).
Proof
Take any \(y \in D_2\), so that \(\dim K_y = 2\). The map \(T_yY \rightarrow S^2K_y^\vee \) can be thought of as a net of quadrics on \(K_y\) parameterized by \(T_yY\). Its degeneration locus in \({\mathbb{P }}(T_{y}Y)\) is a conic, either nondegenerate (if the map \(T_yY \rightarrow S^2K_y^\vee \) is surjective) or singular (since the kernel of the map lies in the singular locus). But on the other hand, this degeneration locus is the base of the tangent cone to \(D_1\) at \(y_i\). So, if \(y_i\) is an ODP of \(D_1\), the conic should be nondegenerate, hence the map should be surjective. \(\square \)
Remark 2.5
Note also that if the map \(\kappa _y\) for \(y\in D_2\) is surjective, then it is an isomorphism (since \(\dim T_yY = \dim S^2K_y^\vee = 3\)).
For each point \(y_i \in D_2\) we have \(Q_{y_i} = {\mathbb{P }}(W_i^+) \cup {\mathbb{P }}(W_{i}^{-})\), both \(W_i^+\) and \(W_i^-\) being 3-dimensional subspaces in \({\fancyscript{V}}_{y_i}\), the fiber of \({\fancyscript{V}}\) over \(y_i\). The planes \({\mathbb{P }}(W_{i}^{+})\) and \({\mathbb{P }}(W_{i}^{-})\) intersect along the line \({\mathbb{P }}(K_{y_{i}})\). In these terms the fiber \(M_{y_i}\) of \(M\) over the point \(y_i\) can be written as
where both \(\Sigma _i^+\) and \(\Sigma _i^-\) are isomorphic to projective planes, intersecting transversally in the point \(P_i = \mathsf{Gr }(2,K_{y_i})\).
Choose an arbitrary point \(y = y_i \in D_2\) and one of the planes \(\Sigma = \Sigma _i^\pm \). The following Proposition computes its normal bundle in \(M\).
Proposition 2.6
If a point \(y \in D_2\) is an ODP of \(D_1\) then \(\mathcal{N }_{\Sigma /M} \cong \mathcal{O }_\Sigma (-1) \oplus \mathcal{O }_\Sigma (-1)\).
Proof
Choosing a local trivialization of the bundles \({\fancyscript{V}}\) and \(\mathcal{L }\) we obtain an isomorphism
On the other hand, \(\mathcal{N }_{M/\mathsf{Gr }_Y(2,{\fancyscript{V}})} \cong S^2{\fancyscript{U}}^\vee \). Hence the standard exact sequence
gives
Since \(\Sigma = \mathsf{Gr }(2,W), W\subset {\fancyscript{V}}_y\), the cohomology exact sequence looks like
Consider the map \(W^{*} \oplus T_yY \rightarrow S^2W^{*}\). Its first component is the multiplication by the equation of the line \(K_y \subset W\). Hence the sequence can be rewritten as
The middle map here is just the map \(\kappa _y\), hence by Remark 2.5 it is an isomorphism. Thus the bundle \(\mathcal{N }_{\Sigma /M}\) is acyclic. Moreover, it is easy to see that the bundle \(\mathcal N _{\Sigma /M}(-1)\) is acyclic as well. It follows that \(\mathcal N _{\Sigma /M}\) is isomorphic to \(\mathcal O _\Sigma (-1) \oplus \mathcal O _\Sigma (-1)\). \(\square \)
From now on we assume that every point \(y_i \in D_2\) is an ODP of \(D_1\).
Corollary 2.7
We have \((\omega _{M})_{|\Sigma ^\pm _i} \cong \mathcal{O }_{\Sigma ^\pm _i}(-1)\).
Proof
By adjunction formula \(\mathcal{O }_{\Sigma }(-3) \cong \omega _{\Sigma } \cong \omega _{M|\Sigma } \otimes \det \mathcal{N }_{\Sigma /M} \cong \omega _{M|\Sigma } \otimes \mathcal{O }_{\Sigma }(-2)\), hence the claim. \(\square \)
The most important corollary is the following
Corollary 2.8
The structure sheaf \(\mathcal{O }_\Sigma \in \mathcal{D }^b(M)\) is exceptional.
Proof
We have an isomorphism \(\mathop {\mathcal{E } xt }\nolimits ^{t}({\mathcal{O }}_{\Sigma },{\mathcal{O }}_{\Sigma }) \cong {\Lambda }^{t}{\mathcal{N }}_{\Sigma /M} \cong {\Lambda }^{t}({\mathcal{O }}_{\Sigma }(-1) \oplus {\mathcal{O }}_{\Sigma }(-1))\). Note that for \(t = 1\), and \(t = 2\) this sheaf on \(\Sigma = {\mathbb{P }}^{2}\) is acyclic. Hence \({\mathop {\mathsf{Ext }}\nolimits }^{\bullet }({\mathcal{O }}_{\Sigma },{\mathcal{O }}_{\Sigma }) \cong H^{\bullet }({\Sigma },{\mathop {\mathcal{H } om }\nolimits }({\mathcal{O }}_{\Sigma },{\mathcal{O }}_{\Sigma })) \cong H^{\bullet }({\Sigma },{\mathcal{O }}_{\Sigma })\) implies exceptionality of \({\mathcal{O }}_{\Sigma }\). \(\square \)
Another simple observation is that \(\Sigma _i^\pm \) with different \(i\) are completely orthogonal.
Lemma 2.9
If \(i {\ne } j\) then \({\mathop {\mathsf{Ext }}\nolimits }^{\bullet }({\mathcal{O }}_{{\Sigma _{i}}^{\pm }},{\mathcal{O }}_{{\Sigma _{j}}^{\pm }}) = 0\).
Proof
The planes \(\Sigma _i^\pm \) and \(\Sigma _j^\pm \) are contained in fibers of \(M\) over different points \(y_i,y_j \in Y\), hence there is no local \({\mathop {\mathsf{Ext }}\nolimits }\)’s between their structure sheaves. Hence global \({\mathop {\mathsf{Ext }}\nolimits }\)’s also vanish. \(\square \)
Thus choosing one plane for each \(y_i\) we obtain a completely orthogonal exceptional collection.
Corollary 2.10
The collection \(\{ \mathcal{O }_{\Sigma _i^+} \}_{i=1}^N\) is a completely orthogonal exceptional collection in \(\mathcal{D }^b(M)\).
3 The Clifford algebra
For the precise definition and basic results about the sheaves of even parts of Clifford algebras, see [10]. Here we remind some of their properties. Recall that the Clifford multiplication is the composition
where the first map is the partial polarization; the second map is the iterated application of the map \(s:{\fancyscript{V}}\otimes {\fancyscript{V}}\rightarrow \mathcal{L }^{-1}\), first to the two copies of \({\fancyscript{V}}\) in the middle, then to the next two, and so on; and the third map is the wedge product. The Clifford multiplication provides the sheaf
with a structure of a sheaf of \(\mathcal{O }_Y\)-algebras, called the even part of the Clifford algebra, and the sheaf
(the odd part of the Clifford algebra) with a structure of a \(\mathcal{B }_0\)-bimodule. It is convenient to extend this pair of sheaves to a sequence defined by
This sequence can be thought of as a sequence of powers of a line bundle. In particular, by [10] the functors \(-\otimes _{{\mathcal{B }}_{0}}{\mathcal{B }}_{l}\) and \({\mathop {\mathcal{H } om }\nolimits }_{{\mathcal{B }_{0}}}({\mathcal{B }}_{l},{-})\) are exact and we have
Remark 3.1
It follows that for any coherent sheaves \(\mathcal{F }\) and \(\mathcal{F }'\) on \(Y\) there is an isomorphism between the space of maps of \(\mathcal{B }_0\)-modules \(\mathcal{F }\otimes \mathcal{B }_k \rightarrow \mathcal{F }' \otimes \mathcal{B }_l\) and the space of maps of \(\mathcal{O }\)-modules \(\mathcal{F }\rightarrow \mathcal{F }'\otimes \mathcal{B }_{l-k}\). In fact the corresponding map of \(\mathcal{B }_0\)-modules is given by the composition \(\mathcal{F }\otimes \mathcal{B }_k \rightarrow \mathcal{F }' \otimes \mathcal{B }_{l-k} \otimes \mathcal{B }_k \rightarrow \mathcal{F }' \otimes \mathcal{B }_l\), where the second map is the Clifford multiplication. We will use frequently this observation to define and compare such maps.
Let \(\alpha \) denote the embedding \(M \rightarrow \mathsf{Gr }_Y(2,{\fancyscript{V}})\). Let
be the positive generator of the relative Picard group. Since the scheme \(M\) is the zero locus of the section \(s \in \Gamma (\mathsf{Gr }_Y(2,V),\mathcal{L }^\vee \otimes S^2{\fancyscript{U}}^\vee )\) we have the Koszul resolution for its structure sheaf
Now we will show that \(M\) also comes with a sequence of naturally defined \(\mathcal{B }_0\)-modules. To unburden the notation we denote the pullbacks of the sheaves \(\mathcal{B }_k\) to \(\mathsf{Gr }_Y(2,{\fancyscript{V}})\) by the same letters. For each \(k \in \mathbb{Z }\) consider the morphism \({\fancyscript{U}}\otimes \mathcal{B }_{k-1} \rightarrow \mathcal{B }_k\) of sheaves of \(\mathcal{B }_0\)-modules on \(\mathsf{Gr }_Y(2,{\fancyscript{V}})\) induced by the embedding \({\fancyscript{U}}\subset {\fancyscript{V}}\subset \mathcal{B }_1\) (see Remark 3.1).
Proposition 3.2
There are isomorphisms \({\mathop {\mathsf{Coker }}\nolimits }({{\fancyscript{U}}}{\otimes }{\mathcal{B }}_{k-1} \rightarrow {\mathcal{B }}_{k}) \cong {\alpha }_{*}{\mathcal{S }}_{k}\), where
and there is an exact sequence
Moreover, the sheaves \({\mathcal{S }}_{k}\) have a structure of right \({\mathcal{B }}_{0}\)-modules such that
Finally, for each \(k\) there is an exact sequence of right \(\mathcal{B }_0\)-modules on \(\mathsf{Gr }_Y(2,{\fancyscript{V}})\)
Proof
First let us check that the cokernels are supported on \(M\) scheme-theoretically. For this we note that the composition of the maps \(S^2{\fancyscript{U}}\otimes \mathcal{B }_{k-2} \rightarrow {\fancyscript{U}}\otimes \mathcal{B }_{k-1} \rightarrow \mathcal{B }_k\) (both of which are induced by the Clifford multiplication) coincides with the map \(S^2{\fancyscript{U}}\otimes \mathcal{B }_{k-2} \cong S^2{\fancyscript{U}}\otimes \mathcal{B }_k\otimes \mathcal{L }\rightarrow \mathcal{B }_k\) induced by the section \(s\) defining the family \(Q\). Indeed, by Remark 3.1 it is enough to compare the corresponding maps \(S^2{\fancyscript{U}}\rightarrow \mathcal{B }_2\). The first map is the composition
of the natural embeddings and of the Clifford multiplication. The first component of the composition is zero since the wedge product vanishes on symmetric tensors, and the second component coincides with the second map.
Thus, the cokernel of the map \({\fancyscript{U}}\otimes \mathcal{B }_{k-1} \rightarrow \mathcal{B }_k\) is a quotient of \(\alpha _*\alpha ^{*}\mathcal{B }_k\), hence it can be written as \(\alpha _*\mathcal{S }_k\), where \(\mathcal{S }_k\) is a sheaf of \(\mathcal{B }_0\)-modules on \(M\). Note also that the formulas (5) follow from the definition of \({\mathcal{S }}_{k}\) combined with Eqs. (1) and exactness of functors \({-}{\otimes _{\mathcal{B }_{0}}}{\mathcal{B }}_{l}\) and \({\mathop {\mathcal{H } om }\nolimits _{\mathcal{B }_{0}}}({\mathcal{B }}_{l},{-})\). So, it remains to verify (3), (4) and (6).
For this let us construct the first two maps in (6) using Remark 3.1. The first map is induced by the embedding
and the second is induced by the composition
(where the map \(\wedge _{23}\) is the wedge product of the second and the third factors, and the map \(s_{23}\) is the map \(s\) again applied to the second and the third factors of the tensor product \({\fancyscript{U}}\otimes {\fancyscript{U}}\otimes {\fancyscript{U}}\)).
Now let us check that the constructed sequence
is a complex. Indeed, to check that the composition of the second and the third arrow is zero we use Remark 3.1. It says that it is enough to compute the corresponding map \(\Lambda ^2{\fancyscript{U}}\otimes {\fancyscript{U}}\rightarrow \mathcal{B }_3\). The map is the composition

It takes a vector \((u_1\wedge u_2) \otimes u_3\) to \(u_1 \otimes u_2 \otimes u_3 - u_2 \otimes u_1 \otimes u_3\), then to
and then to
The first component is zero since the rank of \({\fancyscript{U}}\) is 2, and in the second component all summands cancel out. This proves that the composition of the second and the third arrows in (6) is zero. A similar computation shows that the composition of the first two arrows is zero as well.
Note that each term of the complex is naturally filtered. Consider the spectral sequence of the filtered complex in case \(k = 0\). The first term looks like

The rows are natural complexes with maps corresponding to the wedge multiplication. Their cohomology are easy to compute, so it is not difficult to see that the second term looks like

The arrows here are induced by \(s\). So, it is easy to see that the bottom chain is the Koszul complex of \(s\), while the top chain is the same complex twisted by \(\det {\fancyscript{V}}\otimes \mathcal{L }(g)\). Hence the spectral sequence degenerates in the third term and shows that the cohomology of the above complex is supported in degree zero and is an extension of \(\alpha _*\alpha ^{*}(\det {\fancyscript{V}}\otimes \mathcal{L }(g))\) by \(\alpha _*\alpha ^{*}\mathcal{O }\). Since we already know that it is supported on \(M\), we conclude that it can be written as \(\alpha _*\mathcal{S }_0\), where \(\mathcal{S }_0\) is an extension of \(\det {\fancyscript{V}}\otimes \mathcal{L }(g)\) by \(\mathcal{O }\) on \(M\). This gives (4) and (6) for \(\mathcal{S }_0\).
Analogously, consider the complex for \(k = 1\). The first term of the spectral sequence looks like

The maps are induced by the wedge multiplication, so one can check that the second term looks like

The maps are induced by \(s\), so it is the Koszul complex of \(s\) tensored with \({\fancyscript{V}}/{\fancyscript{U}}\), hence \(\mathcal{S }_1 \cong {\fancyscript{V}}/{\fancyscript{U}}\). This gives (3) and (6) for \(\mathcal{S }_1\). For other \(\mathcal{S }_k\) we deduce (3), (4) and (6) by a suitable twist. \(\square \)
Applying the functor \(\rho _*\) to the resolutions (6) twisted by \(\mathcal{O }(-g)\) and using the projection formula and the Borel–Bott–Weil Theorem to compute the pushforwards of \(\mathcal{O }(-kg)\) and \({\fancyscript{U}}(-kg)\) for \(0 \le k \le 3\), we deduce the following
Corollary 3.3
We have \(\rho _*(\mathcal{S }_k) \cong \mathcal{B }_k, \rho _*(\mathcal{S }_k(-g)) = 0\).
This gives an easy proof of the fact that
Lemma 3.4
The extension in (4) is nontrivial.
Proof
Assume that \(\mathcal{S }_0 \cong \mathcal{O }_M \oplus \det {\fancyscript{V}}\otimes \mathcal{L }(g)\). Then
By the projection formula we have \(\rho _*(\det {\fancyscript{V}}\otimes \mathcal{L }) = \det {\fancyscript{V}}\otimes \mathcal{L }\), so we deduce that \(\rho _* \mathcal{S }_0(-g) \ne 0\), which contradicts to Corollary 3.3. \(\square \)
Now we can also compute the pushforwards of the duals of \(\mathcal{S }_k\).
Corollary 3.5
We have \(\rho _*(\mathcal{S }_k^\vee ) = 0\).
Proof
Indeed, since \(\mathcal{S }_k\) is of rank 2 and \(\det \mathcal{S }_k = \det {\fancyscript{V}}\otimes \mathcal{L }^{1-k}(g)\) [this follows from (3) and (4)], we have \(\mathcal{S }_k^\vee \cong \mathcal{S }_k(-g)\otimes \det {\fancyscript{V}}^\vee \otimes \mathcal{L }^{k-1}\), hence its pushforward is a twist of \(\rho _*(\mathcal{S }_k(-g))\) which is zero. \(\square \)
Another consequence is the following
Corollary 3.6
We have \(\rho _*(\mathcal{S }_l^\vee \otimes \mathcal{S }_k) \cong \mathcal{B }_{k-l}\).
Proof
First of all consider the case \(l = 0\). Then dualizing (4) we obtain an exact triple
Tensoring it by \(\mathcal{S }_k\), pushing forward and using Corollary 3.3, we obtain the claim. Now for arbitrary \(l\) the formula follows by tensoring with \(\mathcal{B }_{-l}\) and using (5). \(\square \)
Now we can describe the embedding \(\mathcal{D }^b(Y,\mathcal{B }_0) \rightarrow \mathcal{D }^b(M)\).
Theorem 3.7
The functor \(\Phi :\mathcal{D }^b(Y,\mathcal{B }_0) \rightarrow \mathcal{D }^b(M), \mathcal{F }\mapsto \mathcal{S }_0\otimes _{\mathcal{B }_0} \rho ^{*}\mathcal{F }\) is fully faithful. Moreover,
Proof
First, note that
Thus the right adjoint functor \(\Phi ^!:\mathcal{D }^b(M) \rightarrow \mathcal{D }^b(Y,\mathcal{B }_0)\) is given by
(the structure of \(\mathcal{B }_0\)-module is induced by that of \(\mathcal{S }_0^\vee \)). So, to check the full faithfulness of \(\Phi \) it suffices to compute \(\Phi ^!\circ \Phi \). For this we note that by the projection formula abd Corollary 3.6 we have
Thus \({\Phi }^{!}{\circ }{\Phi } \cong {\mathsf{id }}\), so \(\Phi \) is fully faithful. Finally, \({\Phi }({\mathcal{B }_{k}}) = {\mathcal{S }}_{0}\otimes _{{\mathcal{B }_{0}}}{\mathcal{B }}_{k} \cong {\mathcal{S }}_{k}\) by (5). \(\square \)
We conclude the section with the following simple calculation.
Lemma 3.8
For each \(i\) and each \(k\) we have \((\mathcal{S }_k)_{|\Sigma _i^\pm } \cong \mathcal{O }_{\Sigma _i^\pm } \oplus \mathcal{O }_{\Sigma _i^\pm }(1)\).
Proof
Restrict (3) and (4) to \(\Sigma = \Sigma _i^\pm \). Since \(\mathcal{O }(g)\) restricts to \(\Sigma \) as \(\mathcal{O }_\Sigma (1)\) we obtain the claim for even \(k\). For odd \(k\) we have to describe the restriction of \({\fancyscript{V}}_y/{\fancyscript{U}}\) to \(\Sigma \). Since \(\Sigma = \mathsf{Gr }(2,W) \subset \mathsf{Gr }(2,{\fancyscript{V}}_y)\), we have on \(\Sigma \) an exact sequence of vector bundles
The first term is \(\mathcal{O }_\Sigma (1)\) and the third is \(\mathcal{O }_\Sigma \). Hence \(({\fancyscript{V}}_y/{\fancyscript{U}})_{|\Sigma } \cong \mathcal{O }_\Sigma \oplus \mathcal{O }_\Sigma (1)\). \(\square \)
4 The flip
A flip is a very important operation in the birational geometry. The definition and examples of flips can be found, e.g. in [5], or in [8]. In our situation we will meet the simplest example of a flip.
From now on we choose one of the planes \({\mathbb{P }}(W_i^\pm ) \subset Q_{y_i}\) for each point \(y_i\), say \({\mathbb{P }}(W_{i}^{+})\), and the corresponding plane \(\Sigma _i^+ = \mathsf{Gr }(2,W_i^+) \subset M\). Recall that by Proposition 2.6 the normal bundles of \(\Sigma _i^+\) in \(M\) are \(\mathcal{O }(-1) \oplus \mathcal{O }(-1)\). Let us apply the composition of flips in all these planes and denote by \(M^+\) the resulting Moishezon variety. More precisely, consider the blowup \(\xi :{\widetilde{M}}\rightarrow M\) of \(M\) in the union of all \(\Sigma _i^+\). Then each of the exceptional divisors \(E_i = \xi ^{-1}(\Sigma _i^+)\) is isomorphic to \(\Sigma _i^+\times {\mathbb{P }}^{1}\) and its normal bundle is \(\mathcal{O }(-1,-1)\). Hence in the category of Moishezon varieties it can be blown down onto a line \(L_i \cong {\mathbb{P }}^1 \subset M^+\). Thus we have a diagram

By a result of Bondal and Orlov we have the following
Proposition 4.1
([4]) The functor \(\xi _*(\xi ^+)^{*}:\mathcal{D }^b(M^+) \rightarrow \mathcal{D }^b(M)\) is fully faithful. Moreover, there is a semiorthogonal decomposition
Further we will need a detailed description of the fibers of \(M^+\) over \(X\). Let \(x_i = f^{-1}(y_i)\) be the nodal points of \(X\) and \(X_{sm} = X \!\setminus \! \{ x_i \}_{i=1}^N\) be the smooth locus of \(X\).
Since the plane \(\Sigma _i^-\) intersects \(\Sigma _i^+\) transversally at point \(P_i\) and does not intersect other planes \(\Sigma _j^+\), the proper preimage of \(\Sigma _i^-\) with respect to the map \(\xi \) is the blowup \({\tilde{\Sigma }}_i^-\) of \(\Sigma _i^-\) at \(P_i\), i.e. a Hirzebruch surface \(F_1\). Moreover, \({\tilde{\Sigma }}_i^-\) intersects the exceptional divisor \(E_i = \Sigma _i^+\times {\mathbb{P }}^1\) of the blowup \(\xi \) along the line \(P_i\times {\mathbb{P }}^1\), which is the exceptional line of the Hirzebruch surface. It follows that the contraction \(\xi _+\) maps \({\tilde{\Sigma }}_i^-\) into \(M^+\) isomorphically, and its exceptional line maps onto \(L_i := \xi _+(E_i)\).
Lemma 4.2
There is a regular morphism \(M^+ \rightarrow X\) such that the diagram

commutes. Moreover, over the smooth locus \(X_{sm}\) the maps \(M \rightarrow X\) and \(M^+ \rightarrow X\) coincide. Finally, the fiber \(M^+_{x_i}\) of \(M^+\) over \(x_i\) is the blowup \({\tilde{\Sigma }}_i^-\) of \(\Sigma _i^-\) in the point \(P_i\) and the line \(L_i = \xi _+(E_i)\) is the \((-1)\)-curve on \({\tilde{\Sigma }}_i^-\).
Proof
The first claim is evident—since the map \(\xi _+:{\widetilde{M}}\rightarrow M^+\) is a contraction of divisors \(E_i\), and the map \(\mu \circ \xi :{\widetilde{M}}\rightarrow X\) contracts each of these divisors to a point, we conclude that \(\mu \circ \xi \) factors through \(\xi _+\). Moreover, since \(\xi \) and \(\xi _+\) are identities over \(X_{sm}\), it follows that the morphisms \(M \rightarrow X\) and \(M^+ \rightarrow X\) coincide over \(X_{sm}\). Finally, note that the fiber of \({\widetilde{M}}\) over \(x_i\) is the union of \(E_i\) and the proper preimage of \(\Sigma _i^-\). Since the map \(\xi _+\) contracts \(\Sigma _i^+\) onto the line \(L_i\) which is contained in the image of the embedding \({\tilde{\Sigma }}_i^- \subset M^+\), we conclude that \(M_{x_i}^+ = {\tilde{\Sigma }}_i^-\). The fact that \(L_i\) is the exceptional line of the Hirzebruch surface \({\tilde{\Sigma }}_i^- \cong F_1\) was already explained above. \(\square \)
As we already have seen, \({\tilde{\Sigma }}_i^-\) is isomorphic to a Hirzebruch surface \(F_1\). In particular, it has a canonical contraction \({\tilde{\Sigma }}_i^- \rightarrow {\mathbb{P }}^1\) which induces an isomorphism of the exceptional line \(L_i \subset {\tilde{\Sigma }}_i^-\) onto \({\mathbb{P }}^1\). Denote (the pullback to \({\tilde{\Sigma }}^-_i\) of) the generator of the Picard group of \(\Sigma _i\) by \(h\) and the class of the exceptional line \(L_i \subset {\tilde{\Sigma }}^-_i\) by \(l\). Then the class of the fiber of the projection \({\tilde{\Sigma }}_i^- \rightarrow {\mathbb{P }}^1\) is \(h-l\).
Lemma 4.3
We have \(\omega _{M^+|{\tilde{\Sigma }}^-_i} \cong \mathcal{O }_{{\tilde{\Sigma }}^-_i}(-h-l)\).
Proof
Note that \(\omega _{{\widetilde{M}}} \!=\! \xi ^{*}\omega _M(\sum E_i) \!=\! \xi _+^{*}\omega _{M^+}(2\sum E_i)\). Hence \(\xi _+^{*}\omega _{M^+} \!=\! \xi ^{*}\omega _M(-\!\sum E_i)\). Using Corollary 2.7 we obtain
But \(\xi _+\) is an isomorphism on \({\tilde{\Sigma }}^-_i\), hence the claim. \(\square \)
It turns out that \(M^+\) has a very simple structure—it is a \({\mathbb{P }}^1\)-fibration over a small resolution of \(X\).
Proposition 4.4
The map \(M^+ \rightarrow X\) factors as a composition  , where the map \(\mu _+:M^+ \rightarrow X^+\) is a \({\mathbb{P }}^1\)-fibration and \(\sigma ^+:X^+ \rightarrow X\) is a small resolution of singularities. The restriction of the map \(\mu _+\) to the fiber \(M^+_{x_i} = {\tilde{\Sigma }}_i^-\) coincides with the projection \({\tilde{\Sigma }}_i^- \rightarrow {\mathbb{P }}^1\). The curve \(C_i = \mu _+({\tilde{\Sigma }}_i^-) \cong {\mathbb{P }}^1\) is the exceptional locus of \(X^+\) over \(x_i \in X\).
, where the map \(\mu _+:M^+ \rightarrow X^+\) is a \({\mathbb{P }}^1\)-fibration and \(\sigma ^+:X^+ \rightarrow X\) is a small resolution of singularities. The restriction of the map \(\mu _+\) to the fiber \(M^+_{x_i} = {\tilde{\Sigma }}_i^-\) coincides with the projection \({\tilde{\Sigma }}_i^- \rightarrow {\mathbb{P }}^1\). The curve \(C_i = \mu _+({\tilde{\Sigma }}_i^-) \cong {\mathbb{P }}^1\) is the exceptional locus of \(X^+\) over \(x_i \in X\).
Proof
We apply to \(M^+\) the relative Minimal Model Program over \(X\), see [12]. Since the relative MMP commutes with the base change, let us first look at \(M^+ {\setminus } \bigsqcup {\tilde{\Sigma }}_i^-\) which is the preimage of \(X_{sm}\). The map \(M^+{\setminus } \bigsqcup {\tilde{\Sigma }}_i^- \rightarrow X_{sm}\) is a \({\mathbb{P }}^1\)-fibration, so its relative Picard group is \(\mathbb{Z }\), and the relative canonical class is ample, hence the first (and the last) step of the MMP for \(M^+ {\setminus } \bigsqcup {\tilde{\Sigma }}_i^-\) is the \({\mathbb{P }}^1\)-fibration \(M^+ {\setminus }\bigsqcup {\tilde{\Sigma }}_i^- \rightarrow X_{sm}\).
Now consider what happens over analytic neighborhoods of singular points. Let \(x = x_i\) be one of singular points. Consider an analytic neighborhood \(U\) of \(x\) in \(X\) and its preimage \(M^+_U \subset M^+\). Then the relative (over \(U\)) effective cone of \(M^+_U\) is generated by curves in the special fiber \(M^+_x = {\tilde{\Sigma }}^-\), that is by the \((-1)\)-curve \(L\) and by the fiber of the projection \({\tilde{\Sigma }}^- \rightarrow {\mathbb{P }}^1\). By Lemma 4.3 the canonical class \(K_{M^+/X}\) restricts to \({\tilde{\Sigma }}^-\) as \(-h-l\), hence \(L\) is \(K\)-positive, while the fiber is \(K\)-negative. Hence the first step in MMP is the contraction of the ray generated by the fiber of the projection \({\tilde{\Sigma }}^- \rightarrow {\mathbb{P }}^1\). By MMP this contraction should be either
-
1.
a flip, or
-
2.
a divisorial contraction, or
-
3.
a conic bundle.
By a result of Kawamata [7] the case of a flip is impossible, since the center of a flip in dimension 4 is always a \({\mathbb{P }}^2\), while in our case the only compact surface in \(M^+_U\) is \(M^+_x = {\tilde{\Sigma }}^-\) which is a Hirzebruch surface \(F_1\). Similarly, a divisorial contraction is impossible, since then one of the steps of MMP on \(M^+_U {\setminus } {\tilde{\Sigma }}_i^-\) would also be a divisorial contraction, while as we have shown above the only nontrivial step of this MMP is a \({\mathbb{P }}^1\)-fibration.
Thus the first step of MMP for \(M^+_U\) is a conic bundle \(M^+_U \rightarrow X^+_U\). Once again, over \(U \setminus \{x\}\) this conic bundle should coincide with the \({\mathbb{P }}^1\)-fibration \(M^+ \setminus \bigsqcup {\tilde{\Sigma }}_i^- \rightarrow X_{sm}\), hence gluing all these conic bundles for all singular points \(x_i\), we obtain a global conic bundle structure on \(M^+\), that is a global map \(\mu _+:M^+ \rightarrow X^+\) for some Moishezon variety \(X^+\). Now we apply [13] and conclude that \(X^+\) is necessarily smooth, hence \(X^+\) is a resolution of singularities of \(X\). Further, the restriction of the map \(\mu _+\) to \({\tilde{\Sigma }}^-_i\) is a conic bundle which contracts all the fibers of the projection \({\tilde{\Sigma }}_i^- \rightarrow {\mathbb{P }}^1\), hence the fiber of \(X_+\) over \(x_i\) is the image \(C_i\) of \({\tilde{\Sigma }}_i^-\). Since \(X^+\) is smooth and the fiber of \(X^+\) over \(x_i\) is \(C_i \cong {\mathbb{P }}^1\), the map \(\sigma _+:X^+ \rightarrow X\) is a small resolution of singularities. So, it remains to check that \(\mu _+:M^+ \rightarrow X^+\) is a \({\mathbb{P }}^1\)-fibration.
Since we already know that \(\mu _+\) is a conic bundle, we should check that its degeneration locus is empty. But the degeneration locus of a conic bundle is a divisor, while \(M^+ \rightarrow X^+\) is nondegenerate over the complement \(X_{sm} = X^+ {\setminus }(\sqcup C_i)\) of a finite number of curves, hence the degeneration locus is empty. \(\square \)
Denoting \(f_+ = f\circ \sigma _+, \rho _+ = f_+\circ \mu _+\), we obtain a commutative diagram

Since the map \(\mu _+:\mathcal{D }^b(M^+) \rightarrow \mathcal{D }^b(X^+)\) is a \({\mathbb{P }}^1\)-fibration, the pullback functor \(\mu _+^{*}:\mathcal{D }^b(X^+) \rightarrow \mathcal{D }^b(M^+)\) is fully faithful. Composing with the functor given by the flip we obtain
Corollary 4.5
The functor \(\xi _*\xi _+^{*}\mu _+^{*}:\mathcal{D }^b(X^+) \rightarrow \mathcal{D }^b(M)\) is fully faithful.
Thus we have constructed all the required components in \(\mathcal{D }^b(M)\). It remains to check that they generate the whole category. This is done in the next section.
5 Derived category of \(M^+\)
As it was shown in the previous section, \(M^+\) is a \({\mathbb{P }}^1\)-bundle over \(X^+\), that is a Severi–Brauer variety, see [1, 11]. It is well known that Severi-Brauer varieties over a scheme \(S\) are in bijection with Morita-equivalence classes of Azumaya algebras over \(S\) (recall that an Azumaya algebra on \(S\) is a sheaf of \(\mathcal{O }_S\)-algebras which étale locally is isomorphic to the endomorphism algebra of a vector bundle). One of the ways to construct an Azumaya algebra from a \({\mathbb{P }}^1\)-bundle \(T \rightarrow S\) is to find a vector bundle \(\mathcal{E }\) on \(T\) which restricts to any fiber of \(T\rightarrow S\) as \(\mathcal{O }(1)^{\oplus n}\) for some \(n\). Then the sheaf of algebras \({\mathcal{A }}_{T} = {\mathop {\mathcal{E } nd }\nolimits }({\mathcal{E }})\) restricts trivially to any fiber of \(T \rightarrow S\), hence it is the pullback of a sheaf of algebras \(\mathcal{A }\) on \(S\). This is the corresponding Azumaya algebra.
To construct such a vector bundle for the \({\mathbb{P }}^1\)-bundle \(M^+ \rightarrow X^+\) we modify the vector bundle \(\mathcal{S }_k\) defined in Proposition 3.2. Recall that the exceptional divisors of the blowups \(\xi :{\widetilde{M}}\rightarrow M\) and \(\xi _+:{\widetilde{M}}\rightarrow M^+\) are \(E_i \cong \Sigma _i^+ \times L_i \cong {\mathbb{P }}^2\times {\mathbb{P }}^1\).
Lemma 5.1
There are vector bundles \(\mathcal{R }_k\) of rank \(2\) on \(M^+\) such that there is a short exact sequence
Proof
By Lemma 3.8 we have an isomorphism \((\xi ^{*}\mathcal{S }_k^\vee )_{|E_i} \cong \mathcal{O }_{E_i} \oplus \mathcal{O }_{E_i}(-1,0)\). Consider the composition \(\xi ^{*}\mathcal{S }_k^\vee \rightarrow (\xi ^{*}\mathcal{S }_k^\vee )_{|E_i} \rightarrow \mathcal{O }_{E_i}(-1,0)\), where the second map is the unique projection. This map is clearly surjective. Denote the kernel of the sum of these maps over \(i\) by \(F\), so that we have an exact triple
Let us check that \(F\) is a pullback of a vector bundle from \(M^+\). Since \(\xi _+:{\widetilde{M}}\rightarrow M^+\) is a smooth blowup, it suffices to check that \(F_{|E_i}\) is a pullback of a vector bundle from \(L_i\). Let us restrict the above exact sequence to \(E_i\). Since \(\mathcal{N }_{E_i/{\widetilde{M}}} \cong \mathcal{O }_{E_i}(-1,-1)\) we obtain an exact sequence
The last map is the projection to the second summand, hence we have an exact triple
Since \({{\mathop {\mathsf{Ext }}\nolimits }_{\mathcal{D }^{b}(E_i)}^{1}}({\mathcal{O }}_{{E_{i}}},{\mathcal{O }}_{{E_{i}}}(0,1)) \cong {H}^{1}({E}_{i},{\mathcal{O }}_{{E_{i}}}(0,1)) = 0\), we see that there is a decomposition \(F_{{|E_{i}}} \cong {\mathcal{O }}_{{E_{i}}} \oplus {\mathcal{O }}_{{E_{i}}}(0,1)\). So, the bundle \(F_{{|E_{i}}}\) is a pullback of \(\mathcal{O }_{L_i} \oplus \mathcal{O }_{L_i}(1)\), hence the bundle \(F\) is a pullback of a vector bundle on \(M^+\) which restricts to \(L_i\) as \(\mathcal{O }_{L_i} \oplus \mathcal{O }_{L_i}(1)\). Now we define \(\mathcal{R }_k\) as the dual of this vector bundle. So, by definition we have the following exact sequence
Dualizing this sequence and taking into account that
we obtain (8). \(\square \)
Remark 5.2
Note that we also proved an isomorphism \(\mathcal{R }_{k|E_i} \cong \mathcal{O }_{E_i} \oplus \mathcal{O }_{E_i}(0,-1)\).
The bundles \(\mathcal{R }_k\) enjoy a lot of interesting properties.
Lemma 5.3
We have \((\rho _+)_*\mathcal{R }_k^\vee = 0\).
Proof
Indeed, using commutativity of (7) we deduce
Applying the functor \(\rho _*\xi _*\) to (9) we obtain a triangle
The second term equals to \(\rho _*\mathcal{S }_k^\vee \) which is zero by Corollary 3.5. Since \(\rho \circ \xi \) contracts \(E_i\) to the point \(y_i\), the third term is \(\oplus H^\bullet (E_i,\mathcal{O }_{E_i}(-1,0))\otimes \mathcal{O }_{y_i}\), so it is also zero. Hence \((\rho _+)_*\mathcal{R }_k^\vee = 0\). \(\square \)
Proposition 5.4
The bundle \(\mathcal{R }_k\) restricts to any fiber of \(\mu _+:M^+ \rightarrow X^+\) as \(\mathcal{O }(1) \oplus \mathcal{O }(1)\). Moreover
Proof
We are going to prove instead that \(\mathcal{R }_k^\vee \) restricts to all fibers as \(\mathcal{O }(-1)\oplus \mathcal{O }(-1)\). For fibers of \(\mu ^+:M^+\!\setminus \! \bigsqcup {\tilde{\Sigma }}^-_i \rightarrow X^+ \!\setminus \! \bigsqcup C_i\) this follows from Lemma 5.3. So it remains to investigate the restriction of \({\mathcal{R }}_{k}^{\vee }\) to \({{\tilde{\Sigma }}}_{i}^{-}\). For this we restrict (9) to \({{{\tilde{\Sigma }}}_{i}^{-}}\) and taking into account that by Lemma 3.8 we have \({{\mathcal{S }}_{k}^{\vee }}_{|{{\tilde{\Sigma }}}_{i}^{-}} \cong {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}} \oplus {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}(-h)\), we obtain
It follows that either (10) holds, or \((\mathcal{R }_k^\vee )_{|{\tilde{\Sigma }}^-_i} \cong \mathcal{O }_{{\tilde{\Sigma }}^-_i}(-h-l) \oplus \mathcal{O }_{{\tilde{\Sigma }}^-_i}\). In the former case we are done since both \(\mathcal{O }_{{\tilde{\Sigma }}^-_i}(h)\) and \(\mathcal{O }_{{\tilde{\Sigma }}^-_i}(l)\) restrict as \(\mathcal{O }(1)\) to any fiber of \({\tilde{\Sigma }}^-_i\) over \(C_i\). Let us check that the case \((\mathcal{R }_k^\vee )_{|{\tilde{\Sigma }}^-_i} \cong \mathcal{O }_{{\tilde{\Sigma }}^-_i}(-h-l) \oplus \mathcal{O }_{{\tilde{\Sigma }}^-_i}\) is impossible.
For this we note that by Lemma 5.3
On the other hand, the cohomology sheaves \(\mathcal{H }^l = {\mathcal{H }}^{l}({\rho }_{+}^{*}{\mathcal{O }}_{{y_{i}}})\) are supported on \({{\tilde{\Sigma }}}_{i}^{-}\). Moreover, \({\mathcal{H }}^{l} = 0\) for \(l > 0\) (since \({\rho }_{+}^{*}\) is right exact) and \({\mathcal{H }}^{0} \cong {\mathcal{O }}_{{\tilde{\Sigma }}_{i}^{-}}\). Consider the spectral sequence
Note that by Serre duality on \(M^+\) we have
The right-hand side vanishes for \(q \not \in \{2,3,4\}\) since the sheaf \(\mathcal{H }^i\) is supported on \({\tilde{\Sigma }}_i^-\) and \(\dim {\tilde{\Sigma }}_i^- = 2\). Hence the line \(q = 3\) does not change in the spectral sequence. But if \(({\mathcal{R }}_{k}^{\vee })_{|{{\tilde{\Sigma }}}_{i}^{-}} \cong {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}({-h-l}) \oplus {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}\) then
gives a nontrivial element in \({\mathop {\mathsf{Ext }}\nolimits }^{3}({\rho }_{+}^{*}{\mathcal{O }}_{{y_{i}}},{\mathcal{R }}_{k}^{\vee })\), which is impossible. \(\square \)
As we mentioned at the beginning of the section, the bundle \(\mathcal{R }_0\) allows to construct the Azumaya algebra on \(X^+\) corresponding to the \({\mathbb{P }}^1\)-bundle \(M^+ \rightarrow X^+\).
Proposition 5.5
([11]) The Brauer class of the \({\mathbb{P }}^{1}\)-fibration \(M^{+} \rightarrow {X}^{+}\) is given by an Azumaya algebra \({\mathcal{B }}^{+}\) on \({X}^{+}\) such that \({\mu }_{+}^{*}{\mathcal{B }}^{+} \cong {\mathop {\mathcal{E } nd }\nolimits }({\mathcal{R }}_{0})\).
The Azumaya algebra \(\mathcal{B }^+\) in its turn provides a description of the derived category of \(M^+\) due to the following result of Bernardara.
Proposition 5.6
([3]) There is a semiorthogonal decomposition
with the embedding functors of the components given by \(F \mapsto \mu _+^{*}F\) and \(F \mapsto \mu _+^{*}F \otimes _{\mathcal{B }^+} \mathcal{R }_0\) respectively.
Combining this with Proposition 4.1 we see, that to prove Theorem 1.1 it remains to check that the functor \(\xi _*\xi _+^{*}\) identifies \(\mathcal{D }^b(X^+,\mathcal{B }^+)\) with the subcategory \(\Phi (\mathcal{D }^b(Y,\mathcal{B }_0)) \subset \mathcal{D }^b(M)\). For this we find a relation between the algebras \(\mathcal{B }^+\) on \(X^+\) and \(\mathcal{B }_0\) on \(Y\).
Lemma 5.7
We have \((f_+)_*\mathcal{B }^+ \cong \mathcal{B }_0\), an isomorphism of sheaves of algebras.
Proof
First of all
On the other hand, tensoring (8) with \(\xi ^{*}\mathcal{S }_0^\vee \) and (9) with \(\xi _+^{*}\mathcal{R }_0\) and using Lemma 3.8 and Remark 5.2 we obtain exact sequences
Pushing these sequences along \(\rho \circ \xi \) and noting that \(E_i\) is contracted to a point we conclude that
On the other hand \({\rho }_{*}{\xi }_{*}{\xi }^{*}{\mathop {\mathcal{E } nd }\nolimits }({\mathcal{S }}_{0}) \cong {\rho }_{*}{\mathop {\mathcal{E } nd }\nolimits }({\mathcal{S }}_{0}) \cong {\mathcal{B }}_{0}\) (see Corollary 3.6 for the last isomorphism). \(\square \)
Now we are ready to prove our main result.
Proof of Theorem 1.1
As we already mentioned, by Proposition 4.1 and Proposition 5.6 we only have to identify the image of \(\mathcal{D }^b(X^+,\mathcal{B }^+)\) under the functor \(\xi _*\xi _+^{*}\) with the subcategory \(\Phi (\mathcal{D }^b(Y,\mathcal{B }_0))\).
The isomorphism \((f_+)_*\mathcal{B }^+ \cong \mathcal{B }_0\) of Lemma 5.7 gives by adjunction a morphism \(f_+^{*}\mathcal{B }_0 \rightarrow \mathcal{B }^+\) which equips \(\mathcal{B }^+\) with a structure of a \(\mathcal{B }_0\)-module. Now we define the functor \(\mathcal{D }^b(Y,\mathcal{B }_0) \rightarrow \mathcal{D }^b(X^+,\mathcal{B }^+)\) by \(F \mapsto f_{+}^{*} F\otimes _{\mathcal{B }_0}\mathcal{B }^+\). The right adjoint functor then is \((f_+)_*:\mathcal{D }^b(X^+,\mathcal{B }^+) \rightarrow \mathcal{D }^b(Y,\mathcal{B }_0)\). Their composition takes \(F\) to
This implies that this functor is fully faithful, and the orthogonal to its image consists of all objects \(G\) such that \((f_+)_*G = 0\). Since \(f_+\) is the contraction of \((-1,-1)\) curves \(C_i\), any object \(G\) in \(\mathcal{D }^b(X^+)\) such that \((f_+)_*G = 0\) is a complex with cohomology supported on the union of curves \(C_i\) and being the direct sums of sheaves \(\mathcal{O }_{C_i}(-1)\). Since \(\mathcal{B }^+\) is an Azumaya algebra, the forgetful functor \(\mathcal{D }^b(X^+,\mathcal{B }^+) \rightarrow \mathcal{D }^b(X^+)\) commutes with sheaf cohomology, hence each of these direct sums of \(\mathcal{O }_{C_i}(-1)\) should be a \(\mathcal{B }^+\)-module. So, it remains to check that there is no such \(\mathcal{B }^+\)-modules.
For this we note that (10) implies \({\mathop {\mathcal{E } nd }\nolimits }({\mathcal{R }_{0}})_{|{{\tilde{\Sigma }}}_{i}^{-}} \cong {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}} \oplus {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}(h-l) \oplus {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}(l-h) \oplus {\mathcal{O }}_{{{\tilde{\Sigma }}}_{i}^{-}}\). Therefore we have \({\mathcal{B }}^{+}_{|C_{i}} \cong {\mathcal{O }}_{{C_{i}}} \oplus {\mathcal{O }}_{{C_{i}}}(1) \oplus {\mathcal{O }}_{{C_{i}}}(-1) \oplus {\mathcal{O }}_{{C_{i}}} \cong {\mathop {\mathcal{E } nd }\nolimits }({\mathcal{O }}_{{C_{i}}} \oplus {\mathcal{O }}_{{C_{i}}}(-1))\), hence the category of \(\mathcal{B }^+\)-modules supported on \(C_i\) is equivalent to the category of sheaves on \(C_i\), the equivalence taking a sheaf \(F\) to \(F\otimes (\mathcal{O }_{C_i} \oplus \mathcal{O }_{C_i}(-1)) \cong F \oplus F(-1)\). It is clear that if \(F \oplus F(-1)\) is a direct sum of \(\mathcal{O }(-1)\) then \(F = 0\). Thus we have checked that \(\mathcal{D }^b(Y,\mathcal{B }_0) \cong \mathcal{D }^b(X^+,\mathcal{B }^+)\).
Finally, we compute the composition of the equivalence \(\mathcal{D }^b(Y,\mathcal{B }_0) \cong \mathcal{D }^b(X^+,\mathcal{B }^+)\), and embeddings \(\mathcal{D }^b(X^+,\mathcal{B }^+) \rightarrow \mathcal{D }^b(M^+) \rightarrow \mathcal{D }^b(M)\). It acts on \(F \in \mathcal{D }^b(Y,\mathcal{B }_0)\) as
Note that \(\xi _+^{*}\rho _+^{*}F \cong \xi ^{*}\rho ^{*}F\), so tensoring (8) by it we obtain
Since \(\xi _*\mathcal{O }_{E_i}(0,-1) = 0\), applying \(\xi _*\) we see that
which gives the required isomorphism of functors and finishes the proof of Theorem 1.1. \(\square \)
6 Concluding remarks and further questions
Remark 6.1
There is another way of proving Theorem 1.1, avoiding use of Moishezon varieties. For this one has to perform another birational modification of \(M\). First, consider the blowup \(M' \rightarrow M\) in the \(N\) points \(P_i = \Sigma _i^+ \cap \Sigma _i^-\). Let \(E'_i \cong {\mathbb{P }}^3\) be the exceptional divisors of this blowup. Then the proper preimages of the planes \(\Sigma _i^+\) and \(\Sigma _i^-\) are Hirzebruch surfaces \({\tilde{\Sigma }}_i^-,{\tilde{\Sigma }}_i^+ \subset M'\) which do not intersect. Moreover, the \((-1)\)-curves \(L_i^\pm \) on \({\tilde{\Sigma }}_i^\pm \) are skew-lines in \(E'_i\). One can check that the normal bundle to \({\tilde{\Sigma }}_i^\pm \) in \(M'\) restricts as \(\mathcal{O }(-1)\oplus \mathcal{O }(-1)\) to any fiber of \({\tilde{\Sigma }}_i^\pm \) over \({\mathbb{P }}^1\). Hence one can make a (relative over \({\mathbb{P }}^1\)) flop in all \(2N\) surfaces \({\tilde{\Sigma }}_i^\pm \) simultaneously. We will obtain an algebraic variety \(M''\) over \(X\). The special fibers \(M''_{x_i}\) will coincide with blowups \(E''_i\) of \(E'_i\) in the lines \(L_i^\pm \) (and each of the surfaces \({\tilde{\Sigma }}_i^\pm \) will be replaced by \({\mathbb{P }}^1\times {\mathbb{P }}^1\), coinciding with the exceptional divisor of \(E''_i\) over \(L_i^\pm \)). Then by the same arguments as in Proposition 4.4 one can show that the map \(M'' \rightarrow X\) factors as a \({\mathbb{P }}^1\)-fibration \(M'' \rightarrow X'\), where \(X'\) is the blowup of \(X\) in all points \(x_i\). Then a careful analysis of the relation of the categories \(\mathcal{D }^b(M'')\) and \(\mathcal{D }^b(M)\) allows to prove Theorem 1.1.
An interesting question for the further investigation is to describe the category \(\mathcal{D }^b(M)\) without restrictions on the dimension of \(Y\). A natural approach would be to consider first the universal family of quadrics and then to apply a base change argument (see [9]) to obtain a decomposition in general case. Unfortunately, the approach of this paper does not work in this general setup because of the following effect — assume for simplicity that \(D_3 = \emptyset \), but \(\dim D_2 > 0\). Since the fibers of \(M\) over \(D_2\) are the unions of two planes, we have an unramified double covering \({\tilde{D_{2}}} \rightarrow D_{2}\). This covering in general is connected. Therefore, we cannot pick up one of the planes \({\Sigma }^{+}\) in all the fibers over \(D_2\) and make a flip in them. However, the approach suggested in Remark 6.1 may work, and I guess that in case \(D_3 = \emptyset \) should work without big changes. As for the case of nonempty \(D_3\), a deeper analysis of the behavior of \(M\) over \(D_3\) (and possibly more birational transformations) is required.
Another question which may prove interesting is investigation of the derived category of the relative scheme of lines (or other isotropic Grassmannians) of a family of quadrics of dimension bigger than 2.
References
Artin, M.: Brauer-Severi varieties. In: van Oystaeyen, F.M.J., Verschoren, A.H.M.J. (eds.) Brauer Groups in Ring Theory and Algebraic Geometry, pp. 194–210. Springer, Berlin (1982)
Artin, M., Mumford, D.: Some elementary examples of unirational varieties which are not rational. Proc. Lond. Math. Soc. 25(3), 75–95 (1972)
Bernardara, M.: A semiorthogonal decomposition for Brauer-Severi schemes. Math. Nach. 282(10), 1406–1413 (2009)
Bondal, A., Orlov, D.: Semiorthogonal decomposition for algebraic varieties. preprint math.AG/9506012
Debarre, O.: Higher-Dimensional Algebraic Geometry, Universitext, vol. 4. Springer, New York (2001)
Ingalls, C., Kuznetsov, A.: On nodal Enriques surfaces and quartic double solids, preprint math.AG/1012.3530
Kawamata, Yu.: Small contractions of four-dimensional algebraic manifolds. Math. Ann. 284, 595–600 (1989)
Kollár, J., Mori, S.: Birational Geometry of Algebraic Varieties, vol. 134. Cambridge University Press, Cambridge (2008)
Kuznetsov, A.: Base change for semiorthogonal decompositions. Compos. Math. 147(3), 852–876 (2011)
Kuznetsov, A.: Derived categories of quadric fibrations and intersections of quadrics. Adv. Math. 218(5), 1340–1369 (2008)
Milne, J.: Étale Cohomology, vol. 33. Princeton university press, Princeton (1980)
Nakayama, N.: The lower semicontinuity of the plurigenera of complex varieties. In: Algebraic Geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, vol. 10, pp. 551–590. North-Holland, Amsterdam (1987)
Tetsuya, A.: On extremal rays of the higher dimensional varieties. Invent. math. 81, 347–357 (1985)
Acknowledgments
I would like to thank L.Katzarkov, D.Orlov, and Yu.Prokhorov for helpful discussions. I am also grateful to the referee for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
I was partially supported by RFFI grants 11-01-00393, 11-01-00568, 12-01-33024, NSh-5139.2012.1, the grant of the Simons foundation, and by AG Laboratory SU-HSE, RF government grant, ag.11.G34.31.0023.
Rights and permissions
About this article
Cite this article
Kuznetsov, A. Scheme of lines on a family of 2-dimensional quadrics: geometry and derived category. Math. Z. 276, 655–672 (2014). https://doi.org/10.1007/s00209-013-1217-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-013-1217-y





 is surjective;
is surjective;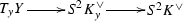 is surjective.
is surjective.