Abstract
In this article, we study the long-time behaviour of a system describing the coupled motion of a rigid body and of a viscous incompressible fluid in which the rigid body is contained. We assume that the system formed by the rigid body and the fluid fills the entire space \({\mathbb {R}}^3\). In the case in which the rigid body is a ball, we prove the local existence of mild solutions and, when the initial data are small, the global existence of solutions for this system with a precise description of their large time behavior. Our main result asserts, in particular, that if the initial datum is small enough in suitable norms then the position of the center of the rigid ball converges to some \(h_\infty \in {\mathbb {R}}^3\) as time goes to infinity. This result contrasts with those known for the analogues of our system in 2 or 1 space dimensions, where it has been proved that the body quits any bounded set, provided that we wait long enough. To achieve this result, we use a “monolithic” type approach, which means that we consider a linearized problem in which the equations of the solid and of the fluid are still coupled. An essential role is played by the properties of the semigroup, called fluid-structure semigroup, associated to this coupled linearized problem. The generator of this semigroup is called the fluid-structure operator. Our main tools are new \(L^p - L^q\) estimates for the fluid-structure semigroup. Note that these estimates are proved for bodies of arbitrary shape. The main ingredients used to study the fluid-structure semigroup and its generator are resolvent estimates which provide both the analyticity of the fluid-structure semigroup (in the spirit of a classical work of Borchers and Sohr) and \(L^p- L^q\) decay estimates (by adapting a strategy due to Iwashita).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
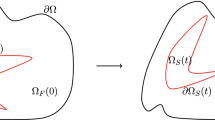
We consider a homogeneous rigid body which occupies at instant \(t=0\) a ball B of radius \(R >0\) and centered at the origin and we study the motion of this body in a viscous incompressible fluid which fills the remaining part of \({\mathbb {R}}^{3}\). We denote by h(t), \({\mathcal {S}}(t),\) \({\mathcal {F}}(t)\) the position of the centre of the ball, the domain occupied by the solid, which coincides with the ball of radius R centered at h, and the domain filled by the fluid, respectively, at instant \(t > 0.\) Moreover, the velocity and pressure fields in the fluid are denoted by u and p, respectively. With the above notation, the system describing the motion of the rigid ball in the fluid is

In the above equations, \(\omega (t)\) represents the angular velocity of the ball (with respect to its centre) and the fluid is supposed to be homogeneous with density equal to 1 and of constant viscosity \(\mu >0\). Moreover, the unit vector field normal to \(\partial S(t)\) and directed towards the interior of \({\mathcal {S}}(t)\) is denoted by \(\nu (t,\cdot )\). The constant \(m>0\) and the matrix J stand for the mass and the inertia tensor of the rigid body. Since in the above equations the rigid body is a homogeneous ball of radius R, the inertia tensor is independent of time and
Finally, the Cauchy stress tensor field in the fluid is given by the constitutive law
where \(\delta _{k\ell }\) stands for the Kronecker symbol.
The system (1.1) can be easily transformed into a system in which the fluid equation is written in a fixed spatial domain. Indeed, using the change of frame \(x \mapsto y(t,x) := x + h(t)\) and setting
and \(E: ={\mathcal {F}}(0) = {\mathbb {R}}^3 {\setminus } B\), Eq. (1.1) can be written in the form of the following system of unknowns v, \(\pi \), \(\ell \) and \(\omega \):

As far as we know, the initial and boundary value problem (1.2) has been first studied in Serre [24], where it is proved, in particular, that (1.2) admits global in time weak solutions (of Leray type). The existence and uniqueness of strong solutions, with initial velocity supposed to be small (in the Sobolev space \(W^{1,2}\)) has been first established in Cumsille and Takahashi [4]. For the \(L^p\) theory for the local in time existence and uniqueness of strong solutions of (1.2), we refer to Geissert et al. [9]. Let us also mention that the analogue of (1.2) when the fluid–rigid body system fills a bounded cavity \(\Omega \) (instead of the whole \({\mathbb {R}}^3\)) has also been studied in a quite important number of papers (see, for instance, Maity and Tucsnak [20] and references therein).
A natural question when considering (1.2) is the large time behaviour of the position of the mass centre of the ball, i.e., of the function h defined by
It is, in particular, important to establish whether the centre of the rigid ball stabilizes around some position in \({\mathbb {R}}^3\) or its distance to the origin tends to infinity when \(t\rightarrow \infty \). As far as we know, this question is open in the three dimensional context of (1.2). However, if one replaces the rigid ball by an infinite cylinder (so that the fluid can be modeled by the Navier–Stokes equations in two space dimensions) the question is studied in Ervedoza et al. [6], where it is established that the norm of \(\ell (t)\) behaves like \(\frac{1}{t}\) when \(t\rightarrow \infty \), thus not excluding the possibility of an unbounded trajectory of the rigid ball. Other results in the same spirit concern Burgers type models for the fluid, like Vázquez and Zuazua [29], or one dimensional viscous compressible fluids, like Koike [17].
The main novelty brought in by our work is twofold. Firstly, we prove that (1.2) is well-posed (globally in time) for initial data which are small in appropriate \(L^q\) type spaces. Secondly, by appropriately choosing q, we prove that there exists \(h_\infty \in {\mathbb {R}}^3\) such that \(\lim _{t\rightarrow \infty } h(t)=h_\infty \), i.e., that the rigid body “stops” as \(t \rightarrow \infty \).
To state our main result we first recall that if \(G\subset {\mathbb {R}}^3\) is an open set, \(q>1\) and \(s \in {\mathbb {R}}\), the notation \(L^q(G)\) and \(W^{s,q}(G)\) stands for the standard Lebesgue and Sobolev–Slobodeckij spaces, respectively. Our main result can be stated as follows:
Theorem 1.1
With the above notation for the set E. There exists \(\varepsilon _0>0\) such that for every \(v_0\in \left[ L^3(E)\right] ^3\) and \(\ell _0,\ \omega _0\in {\mathbb {R}}^3\) with
there exists a unique solution \((v, \ell , \omega )\) of (1.2) in \({C}^0([0,\infty ); \left[ L^{3}(E) \right] ^3\times {\mathbb {R}}^3 \times {\mathbb {R}}^3)\) such that
with
Moreover, for \(q \in (1, 3],\) there exists \(\varepsilon _0(q) \in (0, \varepsilon _0]\) such that if \(v_0 \in \left[ L^{q}(E)\right] ^3 \cap \left[ L^{3}(E)\right] ^3\) satisfies (1.3) and
then, for every \(p \in \left[ \max \left\{ \frac{3}{2},q\right\} , \infty \right] \) the solution \((v, \ell , \omega )\) of (1.2) satisfies
In particular, if \(q < 3/2,\) taking \(p = \infty \) in (1.6) we have that \(\ell \in L^1([0, \infty ); {\mathbb {R}}^3 ),\) hence that the position of the centre of the moving rigid ball converges to some point at finite distance \(h_\infty \in {\mathbb {R}}^3\) as \(t \rightarrow \infty \).
Remark 1.2
In fact, one can prove that, for every \(v_0\in \left[ L^3(E)\right] ^3\) and \(\ell _0,\ \omega _0\in {\mathbb {R}}^3\) satisfying (1.3) and (1.4), the solution \((v, \ell , \omega )\) of (1.2) provided by Theorem 1.1 satisfies, for all \(\theta \in [0,1/2)\),
see Theorem 8.2 afterwards.
As precisely stated in Theorem 8.2 below, the results in Theorem 1.1 can be completed to include a local in time existence result without any smallness assumption on the initial data, see Sect. 8 for more precise statements.
The proof of Theorem 1.1 is based on decay estimates for the solutions of the linearized version of (1.2). Therefore, an important part of this work is devoted to the study of the semigroup associated to the linearized problem. As shown in the forthcoming sections, this semigroup called the fluid-structure semigroup, and its generator (called the fluid-structure operator) share several important properties of the Stokes semigroup and Stokes operator in an exterior domain. To establish this fact, an essential step consists in proving that the resolvent estimates derived in Iwashita [15] and Giga–Sohr [10] for the Stokes operator also hold for the fluid-structure operator (see also the corresponding estimates for the non-autonomous system describing the Navier–Stokes flow around a rotating obstacle, which have been obtained in Hishida [13, 14]). Our results on the linearized problem will be derived for a solid of arbitrary shape, opening the way to a generalization of Theorem 1.1 for solids of arbitrary shape. However, the fixed point methodology used in the present paper to pass from the linearized equations to the full nonlinear problem is strongly using the fact that the rigid body is a ball (see the comments in Sect. 9 below concerning some tracks towards the modification of this procedure for tackling rigid bodies of arbitrary shape).
Note that Theorem 1.1 refers to mild solutions of (1.2), i.e., satisfying the integral equation
where
\({\mathbb {T}}=\left( {\mathbb {T}}_t\right) _{t\geqslant 0}\) is the fluid-structure semigroup and \({\mathbb {P}}\) is a Leray type projector on the space of free divergence vector fields on \({\mathbb {R}}^3\) which coincide with a rigid velocity field on B. A precise definition of these objects requires some preparation and notation, so it is postponed to Sect. 3. However, we mention here that the roles of the projector \({\mathbb {P}}\) and of the fluid-structure semigroup in this paper are very close to those played by the Leray projector and the Stokes semigroup in the analysis of the Navier–Stokes equations. Consequently, the construction and study of the fluid-structure semigroup and of its generator are essential steps of our analysis, which are detailed in Sects. 4–7.
The outline of the paper is as follows. In Sect. 2, we introduce the notation (in particular several function spaces) that will be used throughout the article and we recall several results on the Stokes system in exterior domains. In Sect. 3 we introduce the fluid-structure operator and we give some of its basic properties. Section 4 is devoted to resolvent estimates for the fluid-structure operator. We use existing results on the Stokes system in exterior domains to derive our results. In Sects. 5 and 6 we show that the fluid-structure operator generates a bounded analytic semigroup on a suitable Banach space. We prove, in particular, \(L^{p}-L^{q}\) decay estimates for the fluid-structure semigroup in Sect. 7. Section 8 is devoted to the proof of Theorem 1.1. In Sect. 9, we formulate some open problems. Some technical results are collected in Appendix A and Appendix B.
2 Notation and preliminaries
Throughout this paper, the notation
stands for the sets of natural numbers (starting with 1), integers, real numbers and complex numbers, respectively. For \(n\in {\mathbb {N}}\), the euclidian norm on \({\mathbb {C}}^n\) will be simply denoted by \(|\cdot |\). For \(\theta \in (0,\pi )\) we define the sector \(\Sigma _{\theta }\) in the complex plane by
Moreover, \({\mathbb {Z}}_+\) stands for \({\mathbb {N}}\cup \{0\}\). For \(n,\ m\in {\mathbb {N}}\), \(u:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m\) and \(\alpha \in {\mathbb {Z}}_+^n\) we set \(|\alpha |=\sum _{k=1}^n \alpha _k\) and we use the notation \(\partial ^\alpha u\) for the partial derivative \(\frac{\partial ^{|\alpha |}u}{\partial x_1^{\alpha _1}\dots x_n^{\alpha _n}}\).
If \(G\subset {\mathbb {R}}^3\) is an open set, \(q>1\) and \(k \in {\mathbb {N}}\), we denote the standard Lebesgue and Sobolev spaces by \(L^q(G)\) and by \(W^{k,q} (G)\), respectively. For \(s \in {\mathbb {R}},\) \(W^{s,q}(G)\) denotes the Sobolev–Slobodeckij spaces. The norms on \([L^q(G)]^n\) and \(\left[ W^{k,q} (G)\right] ^n\) with \(n\in {\mathbb {N}}\), will be denoted by \(\Vert \cdot \Vert _{q, G}\) and \(\Vert \cdot \Vert _{k,q,G}\), respectively. When \(G = {\mathbb {R}}^{3},\) these norms will be simply denoted by \(\Vert \cdot \Vert _{q}\) and \(\Vert \cdot \Vert _{k,q}\), respectively. Moreover, the space \(W^{k,q}_{0}(G)\) is the completion of \(C_{0}^{\infty }(G)\) with respect to the \(W^{k,q}(G)\) norm.
We use repeatedly below the following well known result due to Bogovskiĭ [1]:
Lemma 2.1
Let G be a smooth bounded domain in \({\mathbb {R}}^{3},\) \(q\in (1,\infty )\) and \(k \in {\mathbb {Z}}_+\) and let
Then there exists a linear bounded operator \({\mathbb {B}}_{G}\) from \(\left[ W^{k,q}_{0} (G)\right] ^3 \cap \left[ L^{q}_{0}(G)\right] ^3\) to \([W^{k+1,q}_{0} (G)]^{3}\) such that
We also introduce the homogeneous Sobolev spaces
with the norm
where we identify elements differing by a constant.
Moreover, the function space
will often appear in the remaining part of this work.
For \(k \in {\mathbb {N}},\) and \(s, q \in {\mathbb {R}}\) with \(1< q < \infty ,\) we define the weighted Sobolev spaces \(W^{k,q,s}(G)\) by
and we set \(L^{q,s}(G) = W^{0,q,s}(G).\) For \(\varphi \in [W^{1,q}(G)]^3\) we denote by \(D(\varphi )\) the associated strain field defined by
To end this section, we recall several results due to Borchers and Sohr [2] and Iwashita [15], on the Stokes system in the exterior domain \(E={\mathbb {R}}^3{\setminus } \overline{{\mathcal {O}}}\), where \({\mathcal {O}}\subset {\mathbb {R}}^3\) is an open bounded set with \(\partial {\mathcal {O}}\) of class \(C^2\). More precisely, we consider the stationary Stokes problem:

By combining Theorem 1.2 in [2] and Corollary 3.2 in [15] we have:
Theorem 2.2
Let \(\theta \in \left( \frac{\pi }{2},\pi \right) \) and let \(\Sigma _\theta \) be the set defined in (2.1). Then
-
1.
Then there exist two families of operators \((R(\lambda ))_{\lambda \in \Sigma _\theta }\) and \((P(\lambda ))_{\lambda \in \Sigma _\theta }\) such that for every \( \lambda \in \Sigma _\theta \) we have
$$\begin{aligned}&R(\lambda )\in {\mathcal {L}}\left( \left[ L^q(E)\right] ^3, \left[ W^{2,q}(E)\right] ^3\right) , \\&\quad P(\lambda )\in {\mathcal {L}}\left( \left[ L^q(E)\right] ^3,\widehat{W}^{1,q}(E)\right) , \qquad (q >1), \end{aligned}$$and the functions \(v=R(\lambda ) f\) and \(p=P(\lambda ) f\) satisfy (2.5). Moreover, there exists a positive constant M, depending only on \({\mathcal {O}},\ q\) and \(\theta \) such that for every \(\lambda \in \Sigma _\theta \) we have
$$\begin{aligned}&|\lambda | \Vert R(\lambda ) f\Vert _{q,E} + \left\| \mu \Delta R(\lambda ) f - \nabla P(\lambda ) f\right\| _{q,E} \leqslant M \Vert f\Vert _{q,E}\nonumber \\&\quad \left( q>1,\ f\in \left[ L^q(E)\right] ^3\right) . \end{aligned}$$(2.6) -
2.
For every \(q>1,\) \(\lambda \in \Sigma _\theta ,\) \(m\in {\mathbb {Z}}_+,\) \(s>3\left( 1-\frac{1}{q}\right) \) and \(s'<-\frac{3}{q},\) we have
$$\begin{aligned}&R(\lambda )\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, \left[ W^{m+2,q,s'}(E)\right] ^3\right) , \\&\quad P(\lambda )\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3,{W}^{m+1,q,s'}(E)\right) . \end{aligned}$$Moreover, the functions \(\lambda \mapsto R(\lambda )\) and \(\lambda \mapsto P(\lambda )\) are holomorphic from \(\Sigma _\theta \) to \({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, \left[ W^{m+2,q,s'}(E)\right] ^3\right) \) and \({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3,{W}^{m+1,q,s'}(E)\right) ,\) respectively. Finally, there exist
$$\begin{aligned}&R_0\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, \left[ W^{m+2,q,s'}(E)\right] ^3\right) ,\\&\quad P_0\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, W^{m+1,q,s'}(E)\right) \end{aligned}$$such that
$$\begin{aligned}&\limsup _{\lambda \in \Sigma _\theta ,\lambda \rightarrow 0}\ |\lambda |^{-\frac{1}{2}}\, \left\| R(\lambda )-R_0\right\| _{{\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, \left[ W^{m+2,q,s'}(E)\right] ^3\right) } < \infty , \end{aligned}$$(2.7)$$\begin{aligned}&\limsup _{\lambda \in \Sigma _\theta ,\lambda \rightarrow 0}\ |\lambda |^{-\frac{1}{2}}\, \left\| P(\lambda )-P_0\right\| _{{\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, W^{m+1,q,s'}(E)\right) }< \infty . \end{aligned}$$(2.8)
Remark 2.3
Setting \(R(0):=R_0\) and \(P(0):=P_0\), estimates (2.7) and (2.8) imply that the functions \(\lambda \mapsto R(\lambda )\) and \(\lambda \mapsto P(\lambda )\) extend to continuous functions from \(\Sigma _\theta \cup \{0\}\) to
\({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3, \left[ W^{m+2,q,s'}(E)\right] ^3\right) \) and \({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3,W^{m+1,q,s'}(E)\right) \), respectively.
3 Some background on the fluid-structure operator
3.1 Definition and first properties
In this section, we introduce the fluid-structure operator and the fluid-structure semigroup and we remind some of their properties, as established in the existing literature. For the remaining part of this section the notation \(\Omega \) designs either an open, connected and bounded subset of \({\mathbb {R}}^3\), with \(\partial \Omega \) of class \(C^2\), or we have \(\Omega ={\mathbb {R}}^3\). Let \({\mathcal {O}}\) be an open bounded set with smooth boundary such that \(\overline{{\mathcal {O}}}\subset \Omega \) and such that 0 is its center of mass. We denote \(E_\Omega =\Omega {\setminus } \overline{{\mathcal {O}}}\) and we set \(E_{{\mathbb {R}}^3}:=E\). Moreover, we denote by \(\nu \) the unit normal vector on \(\partial {\mathcal {O}}\) oriented towards the interior of \({\mathcal {O}}\).
Reminding notation (2.4) for the tensor field D, we introduce the function space
associated to the sets \(\Omega \) and \({\mathcal {O}}\), which plays an important role in this work. Note that, for every \(q\in (1,\infty )\) the dual \(({\mathbb {X}}^{q}(\Omega ))^{*}\) of \({\mathbb {X}}^{q}(\Omega )\) can be identified with \({\mathbb {X}}^{q'}(\Omega ),\) where \(\displaystyle \frac{1}{q} + \frac{1}{q'} = 1\), with the duality pairing
where \(\rho \) is the constant density of the rigid body. Our notation is making explicit only the dependence of \({\mathbb {X}}^{q}\) on \(\Omega \) since these spaces will be used later on for various \(\Omega \) and with fixed \({\mathcal {O}}\). For \(\Omega ={\mathbb {R}}^3\), we simply set
Since every \(\Phi \) in \({\mathbb {X}}^q(\Omega )\) satisfies \(D (\Phi ) = 0\) in \({\mathcal {O}}\), there exist a unique couple \(\begin{bmatrix}\ell \\ \, \omega \end{bmatrix} \in {\mathbb {C}}^3\times {\mathbb {C}}^3\) and \(\varphi \in L^q_\sigma (E_\Omega )\) such that
where \(\mathbb {1}_U\) stands for the characteristic function of the set U (see for instance [27, Lemma 1.1]). We can thus use the identification:
with
The two results below will allow us to precisely introduce the projection operator \({\mathbb {P}}_{q,\Omega }\) from \(\left[ L^q(\Omega )\right] ^3\) onto \({\mathbb {X}}^q(\Omega )\) which will be used in the following, and which will be denoted by \({\mathbb {P}}_q\) when \(\Omega = {\mathbb {R}}^3\).
Proposition 3.1
Let \({\mathcal {O}}\) be an open bounded set of \({\mathbb {R}}^3\) with \(\partial {\mathcal {O}}\) of class \(C^2\). For \(q>1\) let \(G_1^q\) and \(G_2^q\) be the spaces

Then for every \(u\in \left[ L^q({\mathbb {R}}^3)\right] ^3\) there exists a unique triple \(\begin{bmatrix} v\\ w_1\\ w_2\end{bmatrix}\in {\mathbb {X}}^q\times G_1^q\times G_2^q\) with
The map \(u\mapsto v,\) denoted \({\mathbb {P}}_{q},\) is a projection operator form \(\left[ L^q(\Omega )\right] ^3\) onto \({\mathbb {X}}^q(\Omega )\). Moreover, the dual of the operator \({\mathbb {P}}_{q}\) is \({\mathbb {P}}_{q'},\) where \(\displaystyle \frac{1}{q} + \frac{1}{q'} =1.\)
For the proof of Proposition 3.1 we refer to Wang and Xin [30, Theorem 2.2].
Proposition 3.2
Let \(\Omega \subset {\mathbb {R}}^3\) be an open bounded set with \(\partial \Omega \) of class \(C^2\) . Let \({\mathcal {O}}\) be an open bounded set with \(\partial {\mathcal {O}}\) of class \(C^2\) such that \(\overline{{\mathcal {O}}}\subset \Omega \). For \(q>1\) let \(G_1^q(\Omega )\) and \(G_2^q(\Omega )\) be the spaces

Then for every \(u\in \left[ L^q(\Omega )\right] ^3\) there exists a unique triple \((v, w_1, w_2) \in {\mathbb {X}}^q(\Omega )\times G_1^q(\Omega )\times G_2^q(\Omega )\) with
The map \(u\mapsto v,\) denoted \({\mathbb {P}}_{q,\Omega },\) is a projection operator form \(\left[ L^q(\Omega )\right] ^3\) onto \({\mathbb {X}}^q(\Omega )\). Furthermore, the dual of the operator \({\mathbb {P}}_{q,\Omega }\) is \({\mathbb {P}}_{q',\Omega },\) where \(\displaystyle \frac{1}{q} + \frac{1}{q'} =1.\)
The proof of Proposition 3.2 is similar to the proof of [30, Theorem 2.2]. However, for the sake of completeness we provide a short proof in Appendix A.
We also need some density results. Let us define
As before, for \(\Omega = {\mathbb {R}}^{3},\) we simply set
Using Propositions 3.1 and 3.2, we have the following result
Proposition 3.3
We have \({\mathbb {X}}^{q}(\Omega ) = {\mathbb {Y}}^{q}(\Omega )\) and \({\mathbb {X}}^{q} = {\mathbb {Y}}^{q}.\)
The proof of this proposition is similar to [7, Theorem 2] and [23, Theorem 1.6]. We provide a short proof in Appendix A.
The fluid-structure operator on \(\Omega \) is the operator \({\mathbb {A}}_{q,\Omega }:{\mathcal {D}}({\mathbb {A}}_{q,\Omega })\rightarrow {\mathbb {X}}^q(\Omega )\) defined, for every \(q>1\), by
where \({\mathbb {P}}_{q,\Omega }\) is the projector introduced in Proposition 3.1, and the operator \({\mathcal {A}}_{q,\Omega }: {\mathcal {D}}({\mathcal {A}}_{q,\Omega }) \rightarrow \left[ L^q(\Omega )\right] ^3\) is defined by \({\mathcal {D}}({\mathcal {A}}_{q,\Omega })={\mathcal {D}}({\mathbb {A}}_{q,\Omega })\) and for every \(\varphi \in {\mathcal {D}}({\mathcal {A}}_{q,\Omega })\),
where m and J are given in terms of the constant density \(\rho \) of the body by
Note that the tensor of inertia \({\mathcal {J}}\) is positive. Also note that in the following, the density \(\rho \) of the homogeneous body will not intervene anymore directly: it will only appear through the constants m and \({\mathcal {J}}\) defined above.
In the case \(\Omega ={\mathbb {R}}^3\), the operators \({\mathbb {P}}_{q,\Omega }, {\mathcal {A}}_{q,\Omega }\) and \({\mathbb {A}}_{q,\Omega }\) are denoted by \({\mathbb {P}}_{q}, {\mathcal {A}}_{q}\) and \({\mathbb {A}}_{q}\), respectively and \({\mathbb {A}}_{q}:{\mathcal {D}}({\mathbb {A}}_{q})\rightarrow {\mathbb {X}}^q\) is defined, for every \(q>1\), by
In the case \(q=2\) and when \({\mathcal {O}}\) is a ball, the fluid-structure operator \(\mathbb {A}_q\) has been introduced in Takahashi and Tucsnak [26], where it has been proven that this operator generates an analytic semigroup on \({\mathbb {X}}^{2}\). Later, Wang and Xin [30] proved that the operator \({\mathbb {A}}_{q}\) generates an analytic semigroup on \({\mathbb {X}}^{6/5}\cap {\mathbb {X}}^{q}\) if \(q \geqslant 2\) and that if the solid is a ball in \({\mathbb {R}}^3\) the operator \({\mathbb {A}}_{q}\) generates an analytic semigroup (not necessarily bounded) on \({\mathbb {X}}^{2} \cap {\mathbb {X}}^{q}\) if \(q \geqslant 6.\) One of our main result improves the result of Wang and Xin [30]. Actually, in Theorem 6.1 we will prove that \({\mathbb {A}}_{q}\) generates a bounded analytic semigroup on \({\mathbb {X}}^{q}\) for any \(q > 1.\) Moreover, this result is true for bodies of arbitrary shape.
It is important for future use to rephrase the resolvent equation for \({\mathbb {A}}_{q,\Omega }\) in a form involving only PDEs and algebraic constraints. To this aim, for \(\lambda \in {\mathbb {C}}\), we consider the system

In the above system the unknowns are \(v,\ \pi ,\ \ell \) and \(\omega \), whereas
By slightly adapting the methodology used in [25, 26] for the case \(q=2\), it can be checked that we have the following equivalence:
Proposition 3.4
Let \(\Omega \subset {\mathbb {R}}^3\) be an open, connected and bounded set with \(\partial \Omega \) of class \(C^2\) or \(\Omega ={\mathbb {R}}^3\). Let \(1< q < \infty \) and \(\lambda \in {\mathbb {C}}\). Assume that \(f \in \left[ L^{q}(E_\Omega )\right] ^3\) and \(f_\ell ,f_\omega \in {\mathbb {C}}^3\). If \((v,\pi ,\ell ,\omega ) \in \left[ W^{2,q} (E_\Omega )\right] ^3 \times {{\widehat{W}}}^{1,q}(E_\Omega ) \times {\mathbb {C}}^3 \times {\mathbb {C}}^3\) satisfies (3.14) then
where
Conversely, assume that \(F \in {\mathbb {X}}^{q}(\Omega )\) and \(V \in {\mathcal {D}}({\mathbb {A}}_{q, \Omega })\) satisfy (3.15). Then there exists \(\pi \in {{\widehat{W}}}^{1,q}(E_\Omega )\) such that \((v,\ell , \omega ) \in \left[ W^{2,q} (E_\Omega )\right] ^3 \times {\mathbb {C}}^3 \times {\mathbb {C}}^3\) satisfies (3.14) where
and
3.2 The fluid-structure semigroup on bounded domains
In this subsection we assume that \(\Omega \) is an open bounded set in \({\mathbb {R}}^3\) with boundary of class \(C^2\). In this case the operator \({\mathbb {A}}_{q, \Omega }\) has been extensively studied in Maity and Tucsnak [20]. In particular, by combining the density result from Proposition 3.3 with Theorem 1.3 and Theorem 4.1 from [20], we have
Theorem 3.5
With the above notation, let \(q>1\) and assume that \(\Omega \subset {\mathbb {R}}^3\) is bounded, with \(\partial \Omega \) of class \(C^2\). Then the operator \({\mathbb {A}}_{q,\Omega },\) defined in (3.8) and (3.9), generates an analytic and exponentially stable \(C^0\)-semigroup, denoted \({\mathbb {T}}^{q,\Omega }=\left( {\mathbb {T}}_{t}^{q,\Omega }\right) _{t\geqslant 0}\), on \({\mathbb {X}}^q(\Omega )\).
The above result has the following consequence, which follows by standard analytic semigroups theory:
Corollary 3.6
With the notation and under the assumptions in Theorem 3.5, for every \(\theta \in \left( \frac{\pi }{2},\pi \right) \) the exists a constant M, possibly depending on \(q,\ \theta ,\ {\mathcal {O}}\) and \(\Omega ,\) such that
By combining Corollary 3.6 and Proposition 3.4 we obtain the following result:
Proposition 3.7
Let \(\theta \in (\pi /2, \pi ),\) \(q \in (1, \infty )\) and assume that \(\Omega \subset {\mathbb {R}}^3\) is bounded, with \(\partial \Omega \) of class \(C^2\). Then there exists a constant \(C>0,\) possibly depending on \(\theta ,\ q,\) \(\Omega \) and \({\mathcal {O}},\) such that for all \(\lambda \in \Sigma _\theta ,\) \(f\in \left[ L^q(E_\Omega )\right] ^3\) and \(f_\ell ,\ f_\omega \in {\mathbb {C}}^3,\) there exists a unique solution \((v, \pi ,\ell , \omega ) \in \left[ W^{2,q} (E_\Omega )\right] ^3 \times {{\widehat{W}}}^{1,q}(E_\Omega ) \times {\mathbb {C}}^3 \times {\mathbb {C}}^3\) of (3.14) satisfying
We need below the following slight generalization of Proposition 3.7:
Corollary 3.8
With the notation and assumptions in Proposition 3.7, let \(v\in \left[ W^{2,q}(E_\Omega )\right] ^3,\) \(\pi \in \widehat{W}^{1,q}(E_{\Omega }),\) \(\ell ,\ \omega \in {\mathbb {C}}^3\) be such that
Then for every \(\lambda _0>0\) there exists a constant \(C=C(\Omega ,p,\lambda _0,\theta )\) such that
for every \(\lambda \in \Sigma _\theta \) with \(|\lambda |\leqslant \lambda _0\).
Proof
According to Lemma 2.1 there exists \({{\tilde{v}}}\in \left[ W^{2,q}_0(E_\Omega )\right] ^3\) such that \(\mathrm{div}\, {{\tilde{v}}}=\mathrm{div}\, v\) on \(E_\Omega \) and
where C is a constant depending only on \(\Omega \) and on q. Setting \(u=v-{{\tilde{v}}}\) we see that \(u\in \left[ W^{2,q}(E_\Omega )\right] ^3\) and
By applying Proposition 3.7 and elementary inequalities, it follows that
The above estimate and (3.18) imply the conclusion (3.17). \(\square \)
4 From the Stokes operator in exterior domains to the fluid-structure operator in the whole space
In this section, we study the fluid structure operator \({\mathbb {A}}_{q,\Omega }\), defined in (3.12) and (3.13), in the case \(\Omega ={\mathbb {R}}^3\). As mentioned in Sects. 2 and 3, in this case the space \({\mathbb {X}}^q(\Omega )\), defined in (3.1), and the operators \({\mathbb {P}}_{q,\Omega }\), \({\mathbb {A}}_{q,\Omega }\) are simply denoted by \({\mathbb {X}}^q\), \({\mathbb {P}}_q\) and \({\mathbb {A}}_q\), respectively. The main idea developed in this section is that the resolvent of the fluid-structure operator can be expressed in terms of the resolvent of the Stokes operator with homogeneous Dirichlet conditions on the boundary of an obstacle of arbitrary shape \({\mathcal {O}}\). The connection between these two families of resolvents is then used to study the behaviour of the of \((\lambda I-{\mathbb {A}}_q)^{-1}\) for \(\lambda \) close to zero, in the spirit of the similar results for the Stokes operator in exterior domains obtained by Iwashita [15].
Let \({\mathcal {O}}\) be an open, bounded subset of \({\mathbb {R}}^3\) with \(\partial {\mathcal {O}}\) of class \(C^2\) and let \(E={\mathbb {R}}^3{\setminus } {\mathcal {O}}\). We consider the system

where \(f \in [L^{q}(E)]^{3},\) \(f_\ell , f_\omega \in {\mathbb {C}}^{3}\) and \(\lambda \in {\mathbb {C}}.\) In the above system the unknowns are \(u,\ \pi ,\ \ell \) and \(\omega \), whereas
To study the solvability of (4.1) we introduce several auxiliary operators.
Firstly, given \(\lambda \in {\mathbb {C}}\) and \(\ell ,\ \omega \in {\mathbb {C}}^3\), we consider the boundary value problem:
and we remind the notation (2.3) (and more generally the notation in Sect. 2) for the possibly weighted Sobolev spaces in unbounded domains.
Proposition 4.1
Assume that \(\theta \in (0,\pi )\). Then for all \(q >1,\) for every \(\lambda \in \Sigma _\theta \) and \(\ell , \omega \in {\mathbb {C}}^{3},\) the system (4.2) admits a unique solution \((w,\eta ) \in \left[ W^{2,q}(E)\right] ^3 \times \widehat{W}^{1,q}(E)\). Moreover, let \((D_\lambda )_{\lambda \in \Sigma _\theta }\) be the family of operators defined by
where \((w, \eta ) \in \left[ W^{2,q}(E)\right] ^3 \times \widehat{W}^{1,q}(E)\) is the solution of (4.2). Then for every \(\lambda \in \Sigma _\theta \) and \(m\in {\mathbb {N}},\) we have
Finally, there exists
such that
for every \(m\in {\mathbb {N}}\), \(q>1\) and \(s'<-\frac{3}{q}\).
Proof
We choose two balls \(B_{1}\) and \(B_{2}\) in \({\mathbb {R}}^{3}\) such that \(\overline{{\mathcal {O}}} \subset B_{1} \subset {\overline{B}}_{1} \subset B_{2}.\) We define a cut-off function \(\chi \in C^{\infty }({\mathbb {R}}^{3})\) such that \(\chi (x)\in [0,1]\) for every \(x\in {\mathbb {R}}^3\) and

We set
where \({\mathbb {B}}_{B_{2}{\setminus } {\overline{B}}_1}\) is the Bogovskii operator as introduced in Lemma 2.1. It is easy to see that, \({\mathrm {div}} \ {\overline{w}} = 0\) in E, \({\overline{w}}(x) = \ell + \omega \times x\) for \(x \in \partial E\) and \({\overline{w}} \in W^{k,q}(E),\) for any \(k \in {\mathbb {N}}.\) Since \( w = {{\widetilde{w}}} + {\overline{w}},\) where \({{\widetilde{w}}}\) satisfies
We can apply classical regularity results for Stokes (e.g. [15, Proposition 2.7(i)]) to get (4.4) and Theorem 2.2 to obtain (4.5) and (4.6). \(\square \)
The above result allows us to introduce the family of operators \(({\mathcal {T}}_\lambda )_{\lambda \in \Sigma _\theta }\subset {\mathcal {L}}({\mathbb {C}}^6)\) defined by
where \((w,\eta )\) is the solution of (4.2), given by \(D_\lambda \) according to (4.3).
Proposition 4.2
Let \(\theta \in (0,\pi )\). For every \(\lambda \in \Sigma _\theta \) let \(({\mathcal {T}}_\lambda )_{\lambda \in \Sigma _\theta }\) be the operators defined in (4.7) and let \(({\mathcal {K}}_\lambda )_{\lambda \in \Sigma _\theta }\) be the family of operators defined by
Then there exists \({\mathcal {K}}_0\in {\mathcal {L}}({\mathbb {C}}^6)\) invertible such that
Moreover, \({\mathcal {K}}_\lambda \) is invertible for every \(\lambda \in \Sigma _\theta \) and
Proof
For \(\ell ,\ \omega \in {\mathbb {C}}^3\) we set
where \(D_0\) is the operator introduced in Proposition 4.1. Applying Proposition 4.1 and a standard trace theorem it follows that (4.9) holds. The fact that \({\mathcal {K}}_0\) (which is called the resistance matrix of \({\mathcal {O}}\)) is invertible is a classical result (see, for instance, Happel and Brenner [11, Section 5.4], where it is shown that this matrix is strictly positive).
On the other hand, taking the inner product in \(\left[ L^2(E)\right] ^3\) of the first equation in (4.2) by w, integrating by parts and using the second equation in (4.2) it follows that
Assume now that \(\ell ,\ \omega \in {\mathbb {C}}^3\) and \(\lambda \in \Sigma _\theta \) are such that
Taking the inner product in \({\mathbb {C}}^6\) of the two sides of the above formula by \(\begin{bmatrix} \ell \\ \omega \end{bmatrix}\) and using (4.11) it follows that
If \(\lambda \in \Sigma _{\theta }\) with \(\mathrm{Im}\, \lambda \ne 0\) it follows that \(\ell =0\) and \(\omega =0\). On the other hand, if \(\lambda \in \Sigma _{\theta }\) and \({\mathrm {Im}} \lambda =0\) we have \({\mathrm {Re}} \lambda > 0.\) In this case, we obtain \(w = 0\) and consequently \(\ell =\omega =0.\) We have thus shown that the operator in (4.8) is invertible for every \(\lambda \in \Sigma _\theta \). This fact, (4.9) and the fact that \({\mathcal {K}}_0\) is invertible finally imply (4.10). \(\square \)
We are now in a position to state the main result in this section.
Theorem 4.3
Let \(q\in (1,\infty )\) and \(\theta \in \left( \frac{\pi }{2},\pi \right) \). Then
-
1.
For every \(\lambda \in \Sigma _\theta \) there exist operators
$$\begin{aligned}&{\mathcal {R}}(\lambda )\in {\mathcal {L}}\left( \left[ L^q(E)\right] ^3\times {\mathbb {C}}^6, \left[ W^{2,q}(E)\right] ^3\times {\mathbb {C}}^6\right) , \\&\quad {\mathcal {P}}(\lambda )\in {\mathcal {L}}\left( \left[ L^q(E)\right] ^3\times {\mathbb {C}}^6,\widehat{W}^{1,q}(E)\right) , \end{aligned}$$such that, for \(f\in \left[ L^q(E)\right] ^3,\) \(f_\ell ,\ f_\omega \in {\mathbb {C}}^3,\) setting
$$\begin{aligned} \begin{bmatrix} u\\ \ell \\ \omega \end{bmatrix} ={\mathcal {R}}(\lambda ) \begin{bmatrix} f \\ f_\ell \\ f_\omega \end{bmatrix},\quad \pi ={\mathcal {P}}(\lambda ) \begin{bmatrix} f \\ f_\ell \\ f_\omega \end{bmatrix} , \end{aligned}$$(4.12)then \(u,\ \ell ,\ \omega \) and \(\pi \) satisfy (4.1).
-
2.
For \(\lambda \in \Sigma _\theta ,\) \(m\in {\mathbb {Z}}_+,\) \(s>3\left( 1-\frac{1}{q}\right) \) and \(s'<-\frac{3}{q},\) we have
$$\begin{aligned}&{\mathcal {R}}(\lambda )\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, \left[ W^{m+2,q,s'}(E)\right] ^3\times {\mathbb {C}}^6\right) , \end{aligned}$$(4.13)$$\begin{aligned}&{\mathcal {P}}(\lambda )\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6,{W}^{m+1,q,s'}(E)\right) . \end{aligned}$$(4.14)Moreover, the functions \(\lambda \mapsto {\mathcal {R}}(\lambda )\) and \(\lambda \mapsto {\mathcal {P}}(\lambda )\) are holomorphic from \(\Sigma _\theta \) to
\({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, \left[ W^{m+2,q,s'}(E)\right] ^3\times {\mathbb {C}}^6\right) \) and \({\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, {W}^{m+1,q,s'}(E)\right) ,\) respectively. Finally, there exist
$$\begin{aligned}&{\mathcal {R}}_0\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, \left[ W^{m+2,q,s'}(E)\right] ^3\times {\mathbb {C}}^6\right) , \\&{\mathcal {P}}_0\in {\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, W^{m+1,q,s'}(E)\right) , \end{aligned}$$such that
$$\begin{aligned}&\limsup _{\lambda \in \Sigma _\theta ,\lambda \rightarrow 0}\ |\lambda |^{-\frac{1}{2}}\, \left\| {\mathcal {R}}(\lambda )-{\mathcal {R}}_0\right\| _{{\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, \left[ W^{m+2,q,s'}(E)\times {\mathbb {C}}^6\right] ^3\right) } < \infty ,\qquad \end{aligned}$$(4.15)$$\begin{aligned}&\limsup _{\lambda \in \Sigma _\theta ,\lambda \rightarrow 0}\ |\lambda |^{-\frac{1}{2}}\, \left\| {\mathcal {P}}(\lambda )-{\mathcal {P}}_0\right\| _{{\mathcal {L}}\left( \left[ W^{m,q,s}(E)\right] ^3\times {\mathbb {C}}^6, W^{m+1,q,s'}(E)\right) }< \infty .\nonumber \\ \end{aligned}$$(4.16)
Proof
Let \(m \in {\mathbb {Z}}_+,\) \(q>1\), \(s>0,\) \(f\in \left[ W^{m,q,s}(E)\right] ^3\) and \(f_\ell ,\ f_\omega \in {\mathbb {C}}^3\). For \(\lambda \in \Sigma _\theta \cup \{0\}\) we remind from Proposition 4.2 that the matrix \({\mathcal {K}}_\lambda \), defined in (4.8), is invertible and we set
where \((R(\lambda ))\) and \((P(\lambda ))\) are the families of operators introduced in Theorem 2.2 and Remark 2.3. The last formula implies, according to Proposition 4.2 and Theorem 2.2, that there exist \(\delta , c_\delta >0\) such that
For \(\lambda \in \Sigma _\theta \cup \{0\}\) we set \(\begin{bmatrix} v_\lambda \\ \eta _\lambda \end{bmatrix}=D_\lambda \begin{bmatrix}\ell _\lambda \\ \omega _\lambda \end{bmatrix}\), where \((D_\lambda )_{\lambda \in \Sigma _\theta \cup \{0\}}\) is the family of operators introduced in Proposition 4.1, and we define
where the operators \((R(\lambda ))_{\lambda \in \Sigma _\theta \cup \{0\}}\), \((P(\lambda ))_{\lambda \in \Sigma _\theta \cup \{0\}}\) have been introduced in Theorem 2.2 and Remark 2.3. By combining Theorem 2.2, Proposition 4.1 and (4.18) it follows that for every \(s>3\left( 1-\frac{1}{q}\right) ,\ s'<-\frac{3}{q}\) and \(\delta >0\) there exists \(d>0\) (possibly depending on s, \(s'\) and \(\delta \)) such that
By combining (4.17) and (4.19) it follows that for every \(\lambda \in \Sigma _\theta \) we have that \(u=u_\lambda \), \(\ell =\ell _\lambda \), \(\omega =\omega _\lambda \) and \(\pi =\pi _\lambda \) satisfy (4.1). Consequently, if we set
then for every \(\lambda \in \Sigma _\theta \) the operators \({\mathcal {R}}(\lambda )\), \({\mathcal {P}}(\lambda )\) satisfy (4.13), (4.14) and \(u,\ \ell ,\ \omega \) and \(\pi \) defined by (4.12) is indeed a solution of (4.1).
Finally the properties (4.15) and (4.16), with \({\mathcal {R}}_0:={\mathcal {R}}(0)\), follow now from (4.21), (4.22), together with (2.7), (2.8), (4.6) and (4.10). \(\square \)
5 Further properties of the fluid-structure semigroup in \({\mathbb {R}}^3\)
In this section we study the fluid structure operator \({\mathbb {A}}_{q,\Omega }\), defined in (3.12) and (3.13), in the case \(\Omega ={\mathbb {R}}^3\). More precisely, we give several results opening the way to the proofs of the facts that \({\mathbb {A}}_q\) generates a bounded analytic semigroup and of the decay estimates for the fluid-structure operator by collecting several results which follow quite easily from the existing literature. The first one is:
Proposition 5.1
Let \(1< q< \infty \) and let \(\theta \in \left( \frac{\pi }{2},\pi \right) .\) Then there exist \(\gamma >0\) and \(m_{q,\theta }>0\) such that
Consequently, \({\mathbb {A}}_{q}\) generates an analytic semigroup on \({\mathbb {X}}^{q}.\)
The proof of the above result can be obtained by a perturbation argument. Since this argument is a slight variation of the proof of Theorem 3.1 in [20], where the similar estimate is detailed for the case of fluid-structure system confined in a bounded domain, we omit the proof. We also note that by combining Proposition 3.4 and the first statement of Theorem 4.3, we have
Proposition 5.2
For every \(\lambda \in \Sigma _{\theta }\) and \(F \in {\mathbb {X}}^{q},\) setting
where the family \(({\mathcal {R}}(\lambda ))\) has been introduced in (4.12) and
we have
The result below provides some simple but important properties of the fluid-structure operator \({\mathbb {A}}_{q}.\)
Proposition 5.3
For every \(1< q < \infty ,\) the dual \({\mathbb {A}}_{q}^{*}\) of \({\mathbb {A}}_{q}\) is given by \({\mathbb {A}}_{q}^{*} = {\mathbb {A}}_{q'},\) with \(\displaystyle \frac{1}{q} + \frac{1}{q'} = 1.\)
Proof
For \(G \in {\mathbb {X}}^{q'},\) we set
We consider the equation
which according to Proposition 3.4 is equivalent to the system

where
Assume that \(u \in \left[ W^{2,q}(E)\right] ^3, \pi \in \widehat{W}^{1,q}(E), \ell \in {\mathbb {C}}^{3}\) and \( \omega \in {\mathbb {C}}^{3} \) satisfy the system (4.1). Taking the inner product in \({\mathbb {C}}^{3},\) of (5.6\(_{1}\)) by u and of (4.1) by \(\varphi ,\) integrating by parts and summing up the two formulas we obtain
Using the boundary conditions, the above relation can be written as
In terms of the operator \({\mathbb {A}}_{q}\) and \({\mathbb {A}}_{q'},\) the above equality reads as
with \(U = u \mathbb {1}_{E} + (\ell + \omega \times y) {\mathbb {1}}_{{\mathcal {O}}}.\) Therefore from the above identity we deduce \({\mathcal {D}}({\mathbb {A}}_{q'}) \subset {\mathcal {D}}({\mathbb {A}}_{q}^{*}).\) In order to prove the reverse inclusion, we first note that, for \(\lambda _{0} > 0\) large enough the operator \((\lambda _{0} I - {\mathbb {A}}_{q'})\) is invertible (see Proposition 5.1). Take \(\lambda _{0}\) as above and \(W \in {\mathcal {D}}((\lambda _{0} I -{\mathbb {A}}_{q})^{*}).\) Since \({\mathbb {X}}_{q}^{*} = {\mathbb {X}}_{q'},\) there exists \({\widetilde{U}} \in {\mathcal {D}}({\mathbb {A}}_{q'})\) such that
Let \(U \in {\mathcal {D}}({\mathbb {A}}_{q}).\) Then using the last two formulas, we obtain
In particular, we have
Therefore \(W = {\widetilde{U}}\) and this completes the proof. \(\square \)
The last result in this section provides some information on the resolvent equation associated to \({\mathbb {A}}_q\).
Proposition 5.4
Let \(\lambda \in {\mathbb {C}},\) such that \( \lambda \notin (-\infty ,0)\). Then for every \(q \in (1,\infty )\) we have
-
(i)
\(\displaystyle {\mathrm {Ker}} \left( \lambda I - {\mathbb {A}}_{q} \right) = \{ 0 \}. \)
-
(ii)
\(\displaystyle \overline{{\mathrm {Range}}\left( \lambda I - {\mathbb {A}}_{q} \right) } = {\mathbb {X}}^{q}.\)
Proof
Due to Proposition 3.4, it is enough to show that if \((u,\pi , \ell , \omega ) \in \left[ W^{2,q}(E)\right] ^{3} \times \widehat{W}^{1,q}(E) \times {\mathbb {C}}^{3} \times {\mathbb {C}}^{3}\) satisfies the system (4.1) with \((f, f_{\ell }, f_{\omega }) = 0\), then \(u = \pi = \ell = \omega =0.\)
We first consider the case \(q = 2.\) Multiplying, (4.1\(_{1}\)) by u, (4.1\(_{4}\)) by \({\ell }\) and (4.1\(_{5}\)) by \(\omega \), we obtain after integration by parts:
Note that, to justify properly these computations, we should multiply (4.1\(_{1}\)) by \(\varphi _R {u},\) where \(\varphi _R = \varphi ( x/R)\), \(\varphi \) being a smooth cut-off function taking value one close to the unit ball and vanishing outside the ball of radius 2, and R being a large positive parameter. One should then prove the following convergences,
the first limit coming from Lebesgue dominated convergence theorem and the second from the fact that \(u \in L^2(E)\) and \(\nabla u \in L^2(E)\). The last limit is more delicate and is based on the fact that, since \(\nabla \pi \in L^2(E)\), there exists a constant \(c_\pi \) such that \(\pi + c_\pi \in L^6(E)\). Then we can write
To conclude (5.13), it then remains to check that \(\Vert \nabla \varphi _R\Vert _{3,{\mathbb {R}}^3}\) is bounded uniformly in R, while \(\Vert u\Vert _{2,{\mathbb {R}}^3 {\setminus } B(R)} \) goes to 0 as \(R \rightarrow \infty \).
If \({\mathrm {Im}} \lambda \ne 0\), we take the imaginary part of identity (5.10) and obtain that \( u = \pi = \ell =\omega =0.\) If \({\mathrm {Im}} \lambda = 0\), then \({\mathrm {Re}} \lambda \geqslant 0,\) hence using the above identity and the boundary conditions we also obtain \( u = \pi = \ell =\omega =0.\)
Let us then consider the case \(q > 2\) and \(\lambda \ne 0.\) Let \(B_1\) and \(B_2\) be two open balls in \({\mathbb {R}}^3\) such that
and let \(\varphi _1,\ \varphi _2\in C^\infty ({\mathbb {R}}^3)\) be such that \(\varphi _1(x)\geqslant 0\), \(\varphi _2(x)\geqslant 0\), \(\varphi _1(x)+\varphi _2(x)=1\) for every \(x\in {\mathbb {R}}^3\), \(\varphi _1=1\) on \(\overline{B_1}\), \(\varphi _1=0\) on \({\mathbb {R}}^3{\setminus } B_2\), \(\varphi _2=1\) on \({\mathbb {R}}^3{\setminus } B_2\) and \(\varphi _2=0\) on some open neighbourhood of \(\overline{B_1}\). Then \(\varphi _{1} u\) satisfies the following system

Note that \(-2(\nabla u)(\nabla \varphi _1)-(\Delta \varphi _1)u +\pi \nabla \varphi _1 \in \left[ L^{2}(B_{2} {\setminus } \overline{{\mathscr {O}}})\right] ^3.\) Therefore, by using Corollary 3.8 we obtain \((\varphi _{1} u, \varphi _{1} \pi ) \in \left[ W^{2,2}(B_{2} {\setminus } \overline{{\mathscr {O}}})\right] ^3 \times W^{1,2}(B_{2} {\setminus } \overline{{\mathscr {O}}}).\) Similarly, \((\varphi _{2}u, \varphi _{2} \pi )\) satisfies the following system

We also have \(2(\nabla u)(\nabla \varphi _2)-(\Delta \varphi _2)u+\pi \nabla \varphi _2 \in \left[ L^{2}({\mathbb {R}}^{3})\right] ^3.\) By standard results on Stokes operator in the whole space, we also get \((\varphi _{2}u, \varphi _{2} \pi ) \in \left[ W^{2,2}({\mathbb {R}}^{3}) \right] ^3 \times \widehat{W}^{1,2}({\mathbb {R}}^{3}).\) Combining the above results we obtain \(u \in \left[ W^{2,2}(E)\right] ^3\) and \(\pi \in \widehat{W}^{1,2}(E).\)
Let us consider the case \( 1< q < 2\) and \(\lambda \ne 0.\) We use a bootstrap argument here. Let us set \({\bar{f}}_{i} = -2(\nabla u)(\nabla \varphi _i)-(\Delta \varphi _i)u +\pi \nabla \varphi _i.\) By Sobolev imbedding theorem we obtain \({\bar{f}}_{1}, \, {\bar{f}}_2 \in \left[ L^{r}(B_{2} {\setminus } \overline{{\mathscr {O}}})\right] ^3,\) for \(r > q,\) with \(\displaystyle \frac{1}{3}+\frac{1}{r} = \frac{1}{q}.\) This implies that \(\varphi _{1} u \in \left[ W^{2,r}(B_{2} {\setminus } \overline{{\mathscr {O}}})\right] ^3\) and \(\varphi _{2} u \in \left[ W^{2,r}({\mathbb {R}}^{3})\right] ^3\), hence \( u \in \left[ W^{2,r}(E)\right] ^3\). If \(r \geqslant 2,\) we are reduced to the previous case. Otherwise, we continue the process until we get \( u \in \left[ W^{2,2}(E)\right] ^3.\)
We next consider the case \(\lambda = 0\), which only consists in justifying identity (5.10) in that case, since \(u = \pi = \ell = \omega =0\) would then follow immediately.
According to [8, Lemma V.4.1], we have that for all \(p \in (1, \infty )\), \(D^2 u \in L^p(E)\) and \(\nabla \pi \in L^p(E)\). Consequently, using [3, Theorem 2.1], for all \(r >3/2\), \(\nabla u \in L^r(E)\). In particular, \(\nabla u \in L^2(E)\) and we then get the convergence (5.11). We also have, again from [3, Theorem 2.1], for all \({{\tilde{q}}} >3\), \( u \in L^{{{\tilde{q}}}}(E)\). Taking \({{\tilde{q}}} >3\) close to 3 and \(r>3/2\) close to 3/2 so that \(1- 1/{{\tilde{q}}} - 1/ r < 1/3\), choosing \(s >3\) such that \(1/s + 1/{{\tilde{q}}} + 1/r = 1\), we get
Using then that \( \Vert \nabla \varphi _R \Vert _{s,E}\) goes to 0 as R goes to infinity since \(s >3\), the convergence (5.12) also holds.
Similarly, using that for all \(p \in (1, \infty )\), \(\nabla \pi \in L^p(E)\), we get that there exists \(c_\pi \in {\mathbb {R}}\) such that \(\pi + c_\pi \in L^r(E)\) for all \(r > 3/2\), and we then get, with the choices of \({{\tilde{q}}}>3\), \(r>3/2\) and \(s>3\) above, satisfying \(1/s + 1/{{\tilde{q}}} + 1/r =1\), that
Using again that \( \Vert \nabla \varphi _R \Vert _{s,E}\) goes to 0 as R goes to infinity since \(s >3\), the convergence (5.13) also holds. \(\square \)
6 Analyticity of the fluid-structure semigroup
We begin by stating the main result in this section, which, besides being of independent interest, is an important ingredient in the proof of our main results. In fact, as mentioned earlier, this result improves the existing result of [30, Theorem 2.5, Theorem 2.9].
Theorem 6.1
For every \(1< q< \infty \) and \(\theta \in \left( \frac{\pi }{2},\pi \right) \) there exists \(M_{q,\theta }>0\) such that the operator \({\mathbb {A}}_q\) satisfies
Consequently, \({\mathbb {A}}_{q}\) generates a bounded analytic semigroup \({\mathbb {T}}^{q} = ({\mathbb {T}}_{t}^{q})_{t\geqslant 0}\) on \({\mathbb {X}}^{q}.\)
The guiding idea in proving the above result is borrowed from Borchers and Sohr [2] and it consists in using a contradiction argument and appropriate cut-off functions, combined with Proposition 3.7 and classical results for the Stokes operator in the whole space.
A first step towards the proof of Theorem 6.1 is the following result, concerning the case \(q \in (1,3/2)\):
Proposition 6.2
Let \(q\in \left( 1,\frac{3}{2} \right) \) and \(\theta \in (\frac{\pi }{2}, \pi ).\) Let \(({\mathcal {R}}(\lambda ))\) and \((\mathcal {P}(\lambda ))\) be the family of the operators introduced in Theorem 4.3. For \((f, f_{\ell }, f_{\omega }) \in \left[ L^{q}(E)\right] ^{3} \times {\mathbb {C}}^{3} \times {\mathbb {C}}^3,\) we set
Then there exists a constant \(M_{q,\theta } > 0\) such that, for every \((f, f_{\ell }, f_{\omega }) \in \left[ L^{q}(E)\right] ^{3} \times {\mathbb {C}}^{3} \times {\mathbb {C}}^3\) and for every \(\lambda \in \Sigma _{\theta },\)
Proof
First remark that Proposition 5.1 easily implies (6.3) for \(\lambda \in \Sigma _\theta \) with \(|\lambda | \geqslant \gamma \). We thus focus on the proof of the estimate (6.3) for \(\lambda \in \Sigma _\theta \) with \(|\lambda | \leqslant \gamma \). Assume that (6.3) is false for some \(q\in \left( 1,\frac{3}{2} \right) \) for \(\lambda \in \Sigma _\theta \) with \(|\lambda | \leqslant \gamma \). Then there exists a sequence of complex numbers \((\lambda _n)_{n\in {\mathbb {N}}}\), together with a sequence \((u_n, \ell _n, \omega _n)\) in \({\mathbb {X}}^q \cap (\left[ W^{2,q}(E)\right] ^{3}\cap \times {\mathbb {C}}^{3} \times {\mathbb {C}}^{3})\) and \((\pi _n)\) in \(\widehat{W}^{1,q}(E)\) such that
To obtain the desired contradiction we proceed, following [2], in several steps.
Step 1: Localization.
Let \(B_1\) and \(B_2\) be two open balls in \({\mathbb {R}}^3\) such that
and let \(\varphi _1,\ \varphi _2\in C^\infty ({\mathbb {R}}^3)\) be such that \(\varphi _1(x)\geqslant 0\), \(\varphi _2(x)\geqslant 0\), \(\varphi _1(x)+\varphi _2(x)=1\) for every \(x\in {\mathbb {R}}^3\), \(\varphi _1=1\) on \(\overline{B_1}\), \(\varphi _1=0\) on \({\mathbb {R}}^3{\setminus } B_2\), \(\varphi _2=1\) on \({\mathbb {R}}^3{\setminus } B_2\) and \(\varphi _2=0\) on some open neighbourhood of \(\overline{B_1}\). After some calculations, we see that for each \(n\in {\mathbb {N}}\) we have

By applying Corollary 3.8 and using the fact that \(\varphi _1\) vanishes outside \(B_2\), it follows that there exists \(c > 0\) such that for every \(n\in {\mathbb {N}}\) we have
On the other hand, using the fact that \(\varphi _2=0\) on some open neighbourhood of \(\overline{B_1}\), for each \(n\in {\mathbb {N}}\) we have:

Using classical results for the Stokes operator in \({\mathbb {R}}^3\) (see, for instance, McCracken [22]), it follows that, for every \(n\in {\mathbb {N}}\) we have
By combining (6.10) and (6.12) it follows that for every \(n\in {\mathbb {N}}\) we have
where
Step 2. Passage to the limit.
Let \(r, s > 1\) be defined by
so that
By Theorem 2.1 and Lemma 3.1 in Crispo and Maremonti [3] and (6.5), we have
Thus, there exist a subsequence, still denoted by \((u_{n}),\) \((\pi _{n}),\) \((\ell _{n})\), \((\omega _{n})\) and \(u \in \left[ L^{r}(E)\right] ^3,\) \(\pi \in L^{s}(E)\), \((\ell , \omega ) \in {\mathbb {C}}^{3} \times {\mathbb {C}}^3 \) and \(\lambda \in \overline{\Sigma _\theta }\) such that
where \(\rightharpoonup _{X}\) stands for the weak convergence in a Banach space X. Let us set
Then \(U_{n} \in {\mathbb {X}}^{r}\) and the sequence \((U_{n})\) weakly converges to U in \({\mathbb {X}}^{r}.\) According to (6.6)–(6.8) and by the definition of the operator \({\mathbb {A}}_{q},\) we have that
Let \(W \in {\mathcal {D}}({\mathbb {A}}_{q'}) \cap {\mathcal {D}}({\mathbb {A}}_{r'}).\) By Proposition 5.3,
Since the set \(\left\{ (\lambda I - {\mathbb {A}}_{r'}) W \mid W \in {\mathcal {D}}({\mathbb {A}}_{q'}) \cap {\mathcal {D}}({\mathbb {A}}_{r'}) \right\} \subseteq {\mathbb {X}}^{q'} \cap {\mathbb {X}}^{r'}\) is dense in \({\mathbb {X}}^{r'}\) (see Proposition 5.4), the last formula implies that \(U = 0.\) Consequently, using (6.5) and (6.6),
Next using the fact that \(\sup _n \Vert \pi _{n}\Vert _{L^{s}(\Omega )} < \infty \) (see (6.17)) we deduce that \(\pi = 0.\)
Now we consider the expression \(W(u_n,\nabla u_n,\pi _n)\) defined in (6.14). We claim that
To shorten the proof, since all the terms in \(W(u_n, \nabla u_n ,\pi _n)\) are the same as in [2], we consider only one term of \(W(u_n,\nabla u_n,\pi _n),\) say \(f_{j,n} = \nabla (\nabla \varphi _j\cdot u_n)\) for \(j \in \{1, 2\}\), since the other terms can be estimated in a similar manner. Note that, \(f_{j,n} \in \left[ W^{1,q}_{0}(B_{2} {\setminus } {\overline{B}}_{1})\right] ^3\) for every \(n \in {\mathbb {N}}\) and using (6.16), (6.18) and the fact that \(u = 0\) we also have \((f_{j,n})\) converges weakly to 0 in \(\left[ L^{q}(B_{2} {\setminus } {\overline{B}}_{1})\right] ^3.\) Moreover, using (6.17)
Thus, \(f_{j,n}\) converges strongly to 0 in \(\left[ L^{q}(B_{2} {\setminus } {\overline{B}}_{1})\right] ^3\) as \(n \rightarrow \infty .\) Consequently, we obtain (6.20). This, together with (6.5), contradicts the estimate (6.13), which ends the proof. \(\square \)
We are now in position to prove the main result in this section.
Proof of Theorem 6.1
We first note that from Proposition 3.4, Theorem 4.3 and Proposition 6.2, we obtain (6.1) for \(1< q < \frac{3}{2}.\) In the case \(\frac{3}{2} \leqslant q \leqslant 2\) we take \(q_{0} \in (1,\frac{3}{2}).\) We define \(0 \leqslant s \leqslant 1\) by
Since (6.1) holds for \(q_{0}\), there exists a constant \(M_{\theta , q_{0}} > 0\) such that
On the other hand, \({\mathbb {A}}_{2}\) is a self-adjoint operator on \({\mathbb {X}}^{2}\) (see [26]). Therefore, we also have
for some \(M_{\theta ,2}\) depending only on \(\theta .\) Then by Riesz–Thorin interpolation theorem (see for instance [28, Theorem 1, Section 1.18.7]), we obtain
This ends the proof of (6.1) for \(\displaystyle \frac{3}{2} \leqslant q \leqslant 2.\)
In the case \(2< q < \infty \), we take \(1 < q' \leqslant 2\) such that \(\displaystyle \frac{1}{q} + \frac{1}{q'} = 1.\) By Proposition 5.3, we have \(\lambda (\lambda I - {\mathbb {A}}_{q})^{-1} = [\lambda (\lambda I - {\mathbb {A}}_{q'})^{-1}]^{*},\) so that
We have already seen that (6.1) holds for \(1 < q\leqslant 2.\) Thus from the above identity we infer that, (6.1) holds for any \(2<q < \infty ,\) which ends the proof. \(\square \)
We end this section with the result below, whose proof can be easily obtained by combining Theorem 6.1 and the results from Lunardi [19, Chapter 3]:
Corollary 6.3
With the assumptions and notations of Theorem 6.1, for any \(\varepsilon >0\) and \(k \in \mathbb {N}\), there exists \(C_\varepsilon >0\) such that
7 Decay estimates for the fluid-structure semigroup
Based on Theorem 6.1, we consider the fluid-structure semigroup which is, for each \(q \in (1,\infty )\), the bounded analytic semigroup \({\mathbb {T}}^{q}\) introduced in Theorem 6.1. Our main result in this section is:
Theorem 7.1
-
(i)
Let \(1< q < \infty .\) Let \(R_{0} > 0\) be such that \(\overline{{\mathcal {O}}} \subset B_{R_{0}}.\) Then for any \(R > R_{0},\) there exists a constant \(C > 0,\) depending on q and R, such that
$$\begin{aligned} \left\| {\mathbb {T}}_{t}^{q} U\right\| _{q,B_{R}} \leqslant C t^{-\frac{3}{2q}} \left\| U\right\| _{{\mathbb {X}}^{q}} \quad (t > 1,\ U \in {\mathbb {X}}^{q}). \end{aligned}$$(7.1) -
(ii)
Let \(1<q\leqslant r<\infty \) and \(\sigma =\frac{3}{2} \left( \frac{1}{q}-\frac{1}{r}\right) \). Then there exists a constant \(C > 0,\) depending on q and r, such that
$$\begin{aligned} \left\| {\mathbb {T}}_{t}^{q} U\right\| _{{\mathbb {X}}^{r}} \leqslant C t^{-\sigma } \left\| U\right\| _{{\mathbb {X}}^{q}} \quad ( t> 0,\ U \in {\mathbb {X}}^{q}). \end{aligned}$$(7.2) -
(iii)
Let \(1 < q \leqslant r \leqslant 3.\) Then there exists a constant \(C > 0,\) depending on q and r, such that
$$\begin{aligned} \left\| \nabla {\mathbb {T}}_{t}^{q} U\right\| _{r,E} \leqslant C t^{-\sigma -1/2} \left\| U\right\| _{{\mathbb {X}}^{q}} \quad ( t> 0,\ U \in {\mathbb {X}}^{q}). \end{aligned}$$(7.3) -
(iv)
Estimate (7.2) also holds for \(1< q <\infty \) and \(r =\infty \).
Let us emphasize that Theorem 7.1 holds for the linearized fluid-structure equations for bodies \({\mathcal {O}}\) of arbitrary shapes. It seems thus likely that these properties can be used to derive the well-posedness for solids of arbitrary shape, see the discussion in Sect. 9 below.
Let us also mention that, Maremonti and Solonnikov in [21] proved that, while considering Stokes equation in the exterior domain, the same decay estimates hold, and the estimate (7.2) are sharp for \(3/2 \leqslant q \leqslant r \leqslant \infty \). It is then expected that same holds for the fluid-structure operator also. This is indeed the case, at least in the case of the ball, see Theorem B.1 in the appendix for more details.
Our methodology to prove the above result is inspired by [15] and it consists in using the resolvent estimates developed in Sects. 4–6. However, applying the strategy proposed in [15] requires several adaptations which are described below.
To start with, we state the following regularity result of the projection operator \({\mathbb {P}}_q\).
Proposition 7.2
Let \(k \in {\mathbb {N}}.\) Assume that \(1< r \leqslant q< \infty .\) Let \(u \in \left[ L^{q}({\mathbb {R}}^{3})\right] ^{3}\) be such that \({\mathrm {div}} \; u =0\) in \({\mathcal {D}}'({\mathbb {R}}^{3})\) and \(\partial ^\alpha u \in \left[ L^{r}(E)\right] ^3\) for every multi-index \(\alpha \in {\mathbb {Z}}_+^3\) with \(|\alpha |=k\). Then \(\partial ^\alpha ({\mathbb {P}}_{q} u)\in \left[ L^{r}(E)\right] ^3\) for every multi-index \(\alpha \in {\mathbb {Z}}_+^3\) with \(|\alpha |=k\). Moreover, there exists a constant C independent of the choice of u with the above properties, such that
Proof
Let \(v = {\mathbb {P}}_{q} u.\) Then
where
Moreover, there exists a positive constant C, depending only on q and on \({\mathcal {O}}\), such that (see for instance [30, Proof of Theorem 2.2, Eq. (3.14)])
Since \({\mathrm {div}}\; u =0,\) we have that \(w_1\) from the decomposition (3.4) of u vanishes and, according to [30, Proof of Theorem 2.2, Eq. (3.15)], \(w_2\) from the same decomposition satisfies \(w_{2} =\nabla \pi _{2}\), with \(\pi _{2}\) satisfying
Then estimate (7.4) follows from (7.7) and from Giga and Sohr [10, proof of Lemma 2.3]. \(\square \)
results characterising the graph norm of \({\mathbb {A}}_q^m\) in terms of Sobolev spaces.
Proposition 7.3
Let \(1< q < \infty .\)
-
(i)
Assume that \(U \in {\mathcal {D}}({\mathbb {A}}_{q})\) and \({\mathbb {A}}_q U|_E \in \left[ W^{m,q}(E)\right] ^{3}\) for some \(m \in {\mathbb {Z}}_+.\) Then \(U|_{E} \in \left[ W^{m+2,q}(E)\right] ^3\) and there exists a constant \(C_{m} > 0\) such that
$$\begin{aligned} \left\| U\right\| _{m+2,q,E} \leqslant C_{m} \left( \left\| {\mathbb {A}}_{q} U\right\| _{m,q,E} + \left\| U\right\| _{{\mathbb {X}}^{q}}\right) . \end{aligned}$$(7.9) -
(ii)
For every \(m \in {\mathbb {N}},\) if \(U \in {\mathcal {D}}({\mathbb {A}}_{q}^{m}),\) then \(U|_{E} \in W^{2m,q}(E)\) and there exists a constant \(C_m>0\) such that
$$\begin{aligned} \left\| U\right\| _{2m, q, E} \leqslant C_m \left( \left\| {\mathbb {A}}_{q}^{m} U\right\| _{{\mathbb {X}}^{q}} + \left\| U\right\| _{{\mathbb {X}}^{q}}\right) \quad (U \in {\mathcal {D}}({\mathbb {A}}_{q}^{m})). \end{aligned}$$(7.10)
Proof
Let us set \({\mathbb {A}}_{q} U =- F\), so that \(F|_{E} \in \left[ W^{m,q}(E)\right] ^{3}\). Moreover, we denote
Then according to Proposition 5.2 there exists \(\pi \in \widehat{W}^{1,q}(E)\) such that \(u, \pi , \ell \) and \(\omega \) satisfy

Let \(\displaystyle \begin{bmatrix} w_{1} \\ \eta _{1} \end{bmatrix} = D_{1} \begin{bmatrix} \ell \\ \omega \end{bmatrix}, \) where \(D_{1}\) is the Dirichlet map introduced in Proposition 4.1. According to Proposition 4.1, for every \(k \in {\mathbb {N}}\) there exists positive constants \(C_{1,k}\), \(C_{2,k}\) such that
We denote \({{\widetilde{u}}} = u - w_{1}\) and \(\widetilde{\pi } = \pi - \eta _{1}.\) Then \({\widetilde{u}}\) and \(\widetilde{\pi }\) satisfy

According to [15, Proposition 2.7(i)], for every \(m \in {\mathbb {N}}\) there exists a positive constant \(C_{3,m}\) such that
The above estimate together with (7.11) implies the estimate (7.9).
To prove (7.10), we use an induction argument. We first note that (7.10) is true for \(m=1,\) since it is nothing else but the estimate (7.9) for \(m =0.\) Let us assume that (7.10) is true for some \(m \in {\mathbb {N}}\) and \(U \in {\mathcal {D}}({\mathbb {A}}_{q}^{m+1}).\) Then by (7.9) and induction hypothesis, there exists a positive constant \(C_{m} > 0\) such that
Then the assertion (7.10) holds for m replaced by \(m+1\) by applying Corollary 6.3 repeatedly and (7.12). This completes the proof of the proposition. \(\square \)
Proposition 7.4
Let \(q \in (1,\infty )\). Then :
-
(i)
For any \(m \in {\mathbb {N}},\) there exists a positive constant \(C_{m} > 0\) such that
$$\begin{aligned} \left\| {\mathbb {A}}_{q}^{m} U\right\| _{{\mathbb {X}}^{q}} \leqslant C_{m} \left( \left\| U\right\| _{2m,q,E} + \left\| U\right\| _{{\mathbb {X}}^{q}}\right) \quad \left( U \in {\mathcal {D}}({\mathbb {A}}^{m}_{q})\right) . \end{aligned}$$(7.13) -
(ii)
Let \(\theta \in \displaystyle \left( \frac{\pi }{2}, \pi \right) \) and \(m \in {\mathbb {N}}.\) Then there exists a positive constant \(C_{m} > 0\) such that
$$\begin{aligned} \left\| (\lambda I - {\mathbb {A}}_{q})^{-1} F\right\| _{2m+2,q,E}\leqslant & {} C_{m} \left( \left\| F\right\| _{2m,q,E} + \left\| F\right\| _{{\mathbb {X}}^{q}}\right) , \nonumber \\&\left( F \in {\mathcal {D}}({\mathbb {A}}^{m}_{q}), \lambda \in \Sigma _{\theta }, |\lambda | \geqslant 1\right) . \end{aligned}$$(7.14)
Proof
We use an induction argument to prove (7.13). Using Proposition 3.1, (3.9) and (3.10) 111 note that the estimate (7.13) is true for \(m=1.\) Assume that (7.13) holds for some \(m \in {\mathbb {N}}\) and \(\displaystyle U \in {\mathcal {D}}({\mathbb {A}}^{m+1}_{q}).\) By the induction hypothesis, we have
By applying Proposition 7.2 and Corollary 6.3, the above estimate implies that
Thus (7.13) also holds when m is replaced by \(m+1.\)
Finally (7.14) follows from the facts that
together with the estimates (7.10) and (7.13). \(\square \)
Remark 7.5
Putting together (7.10) and (7.13), it follows that, for every \(m \in {\mathbb {N}},\) the graph norm of \({\mathbb {A}}_{q}^{m}\) is equivalent to \(\left\| \cdot \right\| _{2m,q,E} + \left\| \cdot \right\| _{{\mathbb {X}}^{q}}.\) We also note that this equivalence also holds for the bounded domain version of the fluid-structure operator, i.e., \(\Omega \subset {\mathbb {R}}^{3}\) open and bounded, and the operator \({\mathbb {A}}_{q, \Omega }\) defined in (3.9). Moreover, elements \(\varphi \) of \({\mathcal {D}}({\mathbb {A}}_{q}^{m})\) belong to \(\left[ W^{1,q}({\mathbb {R}}^{3})\right] ^{3}\cap {\mathbb {X}}^q ({\mathbb {R}}^{3})\) and satisfy \(\varphi _{|E} \in \left[ W^{2m,q}(E)\right] ^{3}\).
To state the next results, which yield decay estimates for the fluid-structure semigroup in weighted \(L^p\) spaces, we remind from Sect. 2 the notation \(L^{q,s}\) for the weighted Lebesgue spaces introduced in (2.3).
Theorem 7.6
Let \(1< q< \infty .\) Let s and \(s'\) be real numbers such that \(s > 3(1 - 1/q)\) and \(s' < - 3/q.\) Then there exists a positive constant C, depending only on q, s and \(s',\) such that
Proof
We first note that Theorem 4.3 is a complete analogue of Corollary 3.2 in [15], and Theorem 6.1 is the analogue of the main result in [2]. We can thus complete the proof following line by line the proof of Theorem 1.1 in [15]. \(\square \)
Remark 7.7
For \(U_{0} \in {\mathcal {D}}({\mathbb {A}}_{q}),\) we denote by
Moreover for every \(t \geqslant 0,\) we set \(U(t) = {\mathbb {T}}_{t}^{q} U_{0}\) and
Then there exists \(\pi \in C([0,\infty );\widehat{W}^{1,q}(E))\) such that \((u, \pi , \ell , \omega )\) satisfies the following system

Our next result in this section provides \(L^{q}-L^{r}\) smoothing estimates for the fluid-structure semigroup \({\mathbb {T}}^{q}\) for small time:
Theorem 7.8
Let \(1<q \leqslant r<\infty \) and \(\sigma =\frac{3}{2} \left( \frac{1}{q}-\frac{1}{r}\right) \). Then for each \(\tau \in (0,\infty ),\) there exists a constant \(C > 0,\) depending on \(\tau ,\) q and r, such that
Proof
Let \(N = [2\sigma ]\), where \([ \cdot ]\) denotes the integer part function. Let us assume that N is even. Then by (7.10), there exists a constant \(C > 0\) depending on \(\tau ,\) q and r, such that
In a similar manner, we also obtain
Thus by Sobolev embedding, interpolation and using (7.22)-(7.23), we obtain
If N is odd then we replace N by \(N-1.\) This completes the proof of (7.20). The proof of (7.21) is completely similar, thus omitted here. \(\square \)
The next step towards the proof of Theorem 7.1 is the following result:
Lemma 7.9
With the notations and assumptions of Theorem 7.1, let \(d > R_{0}\) and let \(m \in {\mathbb {N}}.\) Moreover, denote \(E_{d} := \{x\in E\ \ | \ \ |x| < d\}\). Then
-
(i)
There exists a constant \(C > 0\) depending on d and m such that for all \(t >0,\)
$$\begin{aligned} \left\| {\mathbb {T}}_{t}^{q} U\right\| _{q,B_{d}} + \left\| {\mathbb {T}}_{t}^{q} U\right\| _{2m, q, E_{d}} \leqslant C (1 + t)^{-\frac{3}{2}} \left( \left\| U\right\| _{2m, q, E_{d}} + \left\| U\right\| _{{\mathbb {X}}^{q}} \right) , \end{aligned}$$(7.24)for every \(U \in {\mathcal {D}}({\mathbb {A}}_{q}^{m})\) with \(U =0\) for \(|x| > d.\)
-
(ii)
There exists a constant \(C > 0\) depending on d and m such that for all \(t>0,\)
$$\begin{aligned} \left\| \partial _{t} {\mathbb {T}}_{t}^{q} U\right\| _{q,B_{d}} + \left\| \partial _{t} {\mathbb {T}}_{t}^{q} U\right\| _{2m, q, E_{d}} \leqslant C (1 + t)^{-\frac{5}{2}} \left( \left\| U\right\| _{2m+2, q, E_{d}} + \left\| U\right\| _{{\mathbb {X}}^{q}} \right) ,\nonumber \\ \end{aligned}$$(7.25)for every \(U \in {\mathcal {D}}({\mathbb {A}}_{q}^{m+1})\) with \(U =0\) for \(|x| > d.\)
Proof
The proof can be obtained following line by line the proof Lemma 5.2 from Iwashita [15]. More precisely, it suffices to use instead of Proposition 2.7 and Lemma 2.8 in [15] our results in Proposition 7.3 and Proposition 7.4 above, respectively, and to replace expansion (3.2) in [15] by (4.15) above. \(\square \)
Proposition 7.10
With the notation and assumptions of Remark 7.7 and Theorem 7.1, let \(d > R_{0} + 5\) and \(m \in {\mathbb {N}}.\) Moreover, assume that \(U_{0} \in {\mathrm {Ran}}({\mathbb {T}}_{1}^{q}).\) Then there exists a positive constant C, depending only on E, d, m and q, such that, for every \(t \geqslant 0\) we have
where [s] denotes the integer part of \(s \in {\mathbb {R}}\).
Proof
We follow with minor modifications the steps of the proof of Lemma 5.3 in [15].
Step 1. Since \(U_{0} \in {\mathrm {Ran}}({\mathbb {T}}_{1}^{q}),\) we have \(U_{0} \in {\mathcal {D}}({\mathbb {A}}_{q}^{k})\) for all \(k \in {\mathbb {N}}.\) Let \({\widetilde{u}}_{0}\) be an extension of \(u_{0}\) to \({\mathbb {R}}^{3}\) such that \({\widetilde{u}}_{0} \in \left[ W^{2m,q}({\mathbb {R}}^{3})\right] ^3\) and \(\left\| {\widetilde{u}}_{0}\right\| _{2m, q} \leqslant C \left\| U_{0}\right\| _{{\mathcal {D}}({\mathbb {A}}_{q}^{m})}\), where C is a constant independent of \(U_{0}.\) Then \({\mathrm {div}} \; {\widetilde{u}}_{0} \in W^{2m -1,q}_{0}({\mathcal {O}})\) and \(\displaystyle \int _{ {\mathcal {O}}} {\mathrm {div}} \; {\widetilde{u}}_{0} = \int _{\partial {\mathcal {O}}} (\ell _{0} + \omega _{0} \times x) \cdot \nu \ \mathrm{d}s = 0.\) Then by Lemma 2.1 we have that \({\mathbb {B}}_{{\mathcal {O}}} \left( {\mathrm {div}} {\widetilde{u}}_{0} \right) \in W^{2m,q}_{0}({\mathcal {O}}).\) Let us set
where \({\mathbb {B}}_{{\mathcal {O}}} \left( {\mathrm {div}} {\widetilde{u}}_{0} \right) \) is seen as a function in \(\left[ W^{2m,q}({\mathbb {R}}^{3})\right] ^3\) after its extension by 0 in E. Then \(\psi \in \left[ W^{2m,q}({\mathbb {R}}^{3})\right] ^3\) has the following properties
Step 2. We consider the following Stokes system in \({\mathbb {R}}^{3}\)

Let q and r be such that \(1 < q\leqslant r \leqslant \infty \) and define \(\sigma = \frac{3}{2} (\frac{1}{q} - \frac{1}{r}).\) According to classical estimates (see, for instance, [15, Lemma 5.1]) for the heat kernel, for every \(m \in {\mathbb {Z}}_+,\) there exists a constant \(C_{m} >0,\) depending on q and r, with
Let \(\varphi \in C_{0}^{\infty }({\mathbb {R}}^{3})\) be such that \(\varphi (x) = 1\) for \(|x| \leqslant d-2\) and \(\varphi (x) = 0\) for \(|x| > d-1.\) Denote \(\Omega _{d} = \left\{ x \in {\mathbb {R}}^{3} \mid d-2 \leqslant |x| \leqslant d-1\right\} \) and let \({\mathbb {B}}_{d} : {\mathcal {D}}(\Omega _{d}) \rightarrow \left[ {\mathcal {D}}(\Omega _{d})\right] ^{3}\) be the Bogovskii operator such that \({\mathrm {div}}( {\mathbb {B}}_{d} h )= h\) if \(\displaystyle \int _{\Omega _{d}} h = 0.\) We define
By applying (7.32) and (7.34), it follows that there exists a constant \(C_{m} >0,\) depending on q, such that
Step 3. We now set
Then \(v_{2},\pi , \ell \) and \(\omega \) satisfy

where
Moreover, we have
Denote
and
Recall that \(U_{0} \in {\mathrm {Ran}}({\mathbb {T}}_{1}^{q}),\) in particular \(U_{0} \in {\mathcal {D}}({\mathbb {A}}_{q}^{m})\) for every \(m \in {\mathbb {N}}.\) Therefore \(V_{20} \in {\mathcal {D}}({\mathbb {A}}_{q}^{m})\) for every \(m \in {\mathbb {N}}\) and there exists a constant \(C > 0\), depending on m and q, such that
Using (7.31), (7.32), (7.36) and (7.37), we infer that there exists a constant \(C > 0\), depending only on m and q, such that
On the other hand, applying the variation of the constants formula to (7.39), we have
The last estimate, combined with Lemma 7.9, can be used, following line by line the end of the third step of the proof of Lemma 5.3 in [15], to obtain the existence of a constant C (depending only on d, m and q), such that for every \(t>0\) we have
Final step. Estimates (7.26) easily follow by combining (7.38) with the estimates (7.31)–(7.33), (7.36), (7.37), (7.47) and (7.48). The estimate (7.27) can be obtained similarly. Putting together (7.26) and (7.27), from (7.19\(_{1}\)) we obtain
Then the estimate (7.28) follows from the above estimate after redefining \(\pi \) as \(\displaystyle \pi - \int _{E_{d}} \pi \ \mathrm{d}x\) and applying Poincaré type inequalities. \(\square \)
The results in Lemma 7.9 and Proposition 7.10 provide decay estimates for the restrictions to bounded sets of the solution u of the linearized problem. The result below provides decay estimates for the restriction of \(u(t,\cdot )\) to the exterior of the bounded set \(E_{d}\) introduced in Lemma 7.9.
Proposition 7.11
With the notation and assumptions of Remark 7.7 and Theorem 7.1, let \(d > R_{0} + 5\). Moreover, assume that \(U_{0} \in {\mathrm {Ran}}({\mathbb {T}}_{1}^{q}).\) Then, for \(q \in (1, \infty )\) and \(r \in [q, \infty )\), there exists a positive constant C, depending only on E, d, q and r such that,
and for \(q \in (1, 3]\) and \(r \in [q, 3]\), there exists a positive constant C, depending only on E, d, q and r, such that
where [s] denotes the integer part of \(s \in {\mathbb {R}}\).
Proof
Let \(\chi \in C^{\infty }({\mathbb {R}}^{3})\) be such that \(\chi (x)= 1\) for \(|x| > d\) and \(\chi (x)= 0\) for \(|x| < d-1\). It follows that for every \(t\geqslant 0\) we have that \({\mathrm {supp}} \; {\mathrm {div}}(\chi u(t, \cdot )) \subset \left\{ d -1< |x| < d \right\} .\) Then there exists \(v_{3}(t,\cdot )\) such that \({\mathrm {div}}\; v_{3} = {\mathrm {div}}(\chi u),\) \({\mathrm {supp}} \; v_{3}(t,\cdot ) \subset \left\{ d -1< |x| < d \right\} \) and for every \(m \in {\mathbb {N}},\) we have
for some constant \(C > 0\) depending on m and q. To derive the last two estimates we have used Bogovskii Lemma, (7.26) and (7.27). We now define
Note that \({\mathrm {div}} \; v_{4} = 0\) so that \(v_{4}\) satisfies

where
and
Note that, since all the functions appearing in (7.54) are supported away from \({\mathcal {O}},\) the function \(v_{4}\) shares all the properties derived in Lemma 5.5 and proofs of Theorems 1.2 and 1.3 of [15]. In particular,
and
By combining (7.57), (7.51) (with \(m = [2\sigma ] + 1\)) and Sobolev’s embedding theorem we conclude that
This completes the proof of (7.49).
Finally, the proof of (7.50) is obtained similarly from (7.58), together with (7.51) (with \(m = [2\sigma ] +2\)). \(\square \)
We are now in a position to prove the main result in this section.
Proof of Theorem 7.1, items (i)–(iii)
For small times, Theorem 7.1 items (i)–(iii) simply is Theorem 7.8, and we thus only focus on the estimates of Theorem 7.1 items (i)–(iii) for times larger than 1.
To prove (7.1), it suffices to note that, for every \(U \in {\mathbb {X}}^{q}\) we have \({\mathbb {T}}_{1}^{q} U \in {\mathcal {D}}({\mathbb {A}}_{q}^{k})\) for any \(k \in {\mathbb {N}},\) so that applying (7.26) with \(m =0\) we obtain
Concerning (7.2), we first note that this estimate holds for \(t \in (0,1]\) (see (7.20)). Again applying (7.26) with \(m =[2\sigma ] + 1,\) we get
and by (7.49)
The above two estimates give (7.2) for \(t \geqslant 1.\)
The proof of (7.3) follows analogously by combining (7.21), (7.26) and (7.50). \(\square \)
To complete the proof of Theorem 7.1, it remains to show that (7.2) holds for \(r =\infty \) and \(1< q < \infty .\) To this aim, we first prove the following result
Proposition 7.12
With the notation and assumptions of Remark 7.7 and Theorem 7.1, let \(d > R_{0} + 5\). Moreover, assume that \(1< q < \infty \) and \(U_{0} \in {\mathrm {Ran}}({\mathbb {T}}_{1}^{q}).\) Then, for \(q \in (1, \infty )\), there exists a positive constant C, depending only on E, d and q, such that for every \(t \geqslant 0\), we have
where [s] denotes the integer part of \(s \in {\mathbb {R}}\).
Proof
Combining (7.38) together with the estimates (7.32)(with \(m=0, r =\infty \)), (7.36)(with \(m =3\)) and (7.47) (with \(m=2\)), we deduce that
where the set \(E_d\) has been defined in Lemma 7.9. Moreover, using (7.51) with \(m =3\) we also have
where \(v_{3}\) is defined as in Proposition 7.11. Therefore, by virtue of the decomposition (7.53), it remains to show the \(L^{\infty }\) estimate of \(v_{4},\) where \(v_{4}\) is defined by (7.54). Recall the definition of h from (7.55). Using (7.26), (7.28), (7.51) and (7.52), we obtain for any \(m \in {\mathbb {N}} \cup \{0\}\)
Let us take \(q_{0} = \min \{5/4, q\}\). Then using (7.32) and the above estimate, we evaluate
Note that, in the above estimate, we have used the fact that h has compact support, which comes from its definition in (7.55) and the fact that \(v_3\) is compactly supported. The above estimate together with (7.61) and (7.62) implies (7.60). \(\square \)
(7.2) for \(q \in (1, \infty ) \) and \(r =\infty \).
Note that, for every \(U \in {\mathbb {X}}^{q}\) we have \({\mathbb {T}}_{1}^{q} U \in {\mathcal {D}}({\mathbb {A}}_{q}^{k})\) for any \(k \in {\mathbb {N}}.\) Thus applying (7.60) we have
This proves (7.2) for \(q \in (1, \infty )\), \(r =\infty \), and \(t \geqslant 1.\)
For \(t \in (0,1)\), \(1< q < \infty \), and \(q_{0} > \max \{ 3,q\}\), we apply Theorem 7.8 to obtain
where the constant C is independent of t. This completes the proof of item (iv) of Theorem 7.1. \(\square \)
8 Proof of the main results
In this section, we focus on the analysis of the non-linear fluid-structure model, assuming that the rigid body is a ball. Note that this assumption has been already used when fixing the frame via a simple translation, which drastically simplifies the structure of the non-linear terms. Given \(q>1\) we continue to use the notation \({\mathbb {X}}^q\) for the space defined in Eq. (3.1) and \({\mathbb {T}}^q\) for the fluid structure semigroup introduced in the previous sections. However, to simplify the notation and when there is no risk of confusion, the fluid-structure semigroup will be simply denoted by \({\mathbb {T}}\). Similarly, if the appropriate value of q is clear from the context, the projector \({\mathbb {P}}_q\), introduced in Proposition 3.2, is simply denoted by \({\mathbb {P}}\).
The arguments we are using are close to those in Kato [16], with several adaptations necessary to tackle the extra term coming from the motion of the rigid body, in a spirit close to [6], and with the extensive use of the results obtained in the previous sections on the fluid-structure semigroup, and in particular Theorem 7.1.
We rely, in particular, on the following lemma, which is a rather straightforward consequence of Theorem 7.1:
Lemma 8.1
Let \(p_{0}\) and \(q_{0}\) be such that \( q_{0}\in [3/2, \infty )\) and \( p_{0} \in [q_0, \infty ]\). Then there exists \(C>0\) such that for every \(F \in L^{q_{0}}({\mathbb {R}}^3; {\mathbb {R}}^{3\times 3})\) satisfying \(F = 0\) in B and \(\mathrm{div}\,F \in \left[ L^r({\mathbb {R}}^3)\right] ^3\) for some \(r \in (1, p_{0}]{\setminus } \{\infty \}\) we have
Proof
The proof follows the same steps as those appearing in [6, Proof of Corollary 3.10]. More precisely, for \(F \in L^{q_{0}}({\mathbb {R}}^3; {\mathbb {R}}^{3\times 3})\) satisfying \(F = 0\) in B and \(\mathrm{div}\,F \in \left[ L^r({\mathbb {R}}^3)\right] ^3\) for some \(r \in (1, p_{0}] {\setminus } \{\infty \}\), we necessarily have \(F\cdot \nu = 0\) on \(\partial B\) and for \(t>0\), \({\mathbb {T}}_t^r {\mathbb {P}}_r \mathrm{div}\,F\) is a well-defined element of \({\mathbb {X}}^{r} \cap {\mathbb {X}}^\infty \) (see Theorem 7.1).
Setting \(r_0 = \max \{r, q_0\}\), we thus have that
Finally, using (7.3), we obtain
Now, for \(p_0 \in [ r_0, \infty ]\), we use
where the last estimate comes from (7.2). \(\square \)
We state below a result which, taking in consideration the notation recalled at the beginning of this section, clearly includes our main result in Theorem 1.1. More precisely, this result provides local in time existence of solutions for initial data in \({\mathbb {X}}^3\) and global existence of solutions of (1.2) for small data in \({\mathbb {X}}^3\), with a description of the long time behavior of the solutions when further assuming that the initial datum belongs to \({\mathbb {X}}^q\) for some \(q \in (1,3]\).
Theorem 8.2
Let \(V_0 \in {\mathbb {X}}^3\). Then there exists \(T_0 >0\) such that there exists a unique solution \(V = \begin{bmatrix} v\\ \ell \\ \omega \end{bmatrix} \in {C}^0([0,T_0]; {\mathbb {X}}^3)\) with \(t^{1/4} V(t) \in C^0([0,T_0]; {\mathbb {X}}^6)\), \(t^{1/2} V(t) \in C^0([0,T_0]; {\mathbb {X}}^\infty )\) and \(\min \{t^{1/2},1\} \nabla v(t) \in {C}^0([0,T_0]; \left[ L^{3}(E)\right] ^9)\) of (1.2), such that
Furthermore, this solution is such that for all \(p \in [3, \infty ],\) \(t^{3/2(1/3 - 1/p)} V \in C^0([0,T_0]; {\mathbb {X}}^p)\).
Besides, there exists \(\varepsilon _0 >0\) such that if \(\Vert V_0\Vert _3 \leqslant \varepsilon _0,\) \(T_0\) can be taken to be infinite, i.e. \(T_0 = \infty ,\) for all \(p \in [3, \infty ],\) \(t^{3/2(1/3 - 1/p)} V \in C_b^0([0,\infty ]; {\mathbb {X}}^p),\) and for all \(\theta \in [0,1/2),\) \(\min \{t^{1/2}, t^\theta \} \nabla v(t) \in L^\infty (0,\infty ; \left[ L^{3}(E)\right] ^9)\).
For \(q \in (1,3],\) there exists \(\varepsilon _0(q) \in (0, \varepsilon _0]\) such that if \(V_0 \) belongs to \({\mathbb {X}}^q \cap {\mathbb {X}}^3\) and satisfies \(\Vert V_0 \Vert _3 \leqslant \varepsilon _0(q),\) then the solution V also satisfies, for all \(p \in [\max \{q, 3/2\}, \infty ],\) \(t^{3/2(1/q - 1/p)} V \in C_b^0([0,\infty ]; {\mathbb {X}}^p)\).
Proof
Existence theory for \(V_0 \in {\mathbb {X}}^3\). We first focus on the existence of solutions V of (1.2).
As mentioned in the introduction, we are looking for mild solutions V of the non-linear problem (1.2), i.e. solutions of the Eq. (1.8). For each \(t>0\) we identify \(V(t,\cdot )\) with a triple \(\begin{bmatrix} v(t,\cdot )\\ \ell (t)\\ \omega (t)\end{bmatrix}\), where \(v(t,\cdot ):E\rightarrow {\mathbb {R}}^3\) and \(\ell (t),\ \omega (t)\in {\mathbb {R}}^3\), as described in (3.3).
We first remark that, since \((v - \ell ) \cdot \nu = 0\) on \(\partial B\), we have
where
In particular the triple \(V = \begin{bmatrix} v\\ \ell \\ \omega \end{bmatrix}\) is a mild solution of (1.2) iff it satisfies
where F is defined in (8.3). The above formulation will be intensively used in the remaining part of the section, in conjunction with Lemma 8.1.
For \(T>0\), we introduce the class
which we endow with the norm
Note in particular that, for \(V = \begin{bmatrix} v\\ \ell \\ \omega \end{bmatrix} \in {\mathscr {C}}(T)\), we have the estimate
We start by remarking that we are looking for a solution V of (1.8) or equivalently (8.4). We then define the map \(\Lambda _T: V \in {\mathscr {C}}(T) \mapsto \Lambda _{T} V\) defined for \(t \in [0,T]\) by
or, equivalently,
Next we claim the following lemma:
Lemma 8.3
There exists a constant \(C_0>0\) independent of T such that
Proof
Since estimate (8.6) can be easily deduced from (8.7) by taking \(V^a = 0\) and \(V^b = V\), we prove only (8.7).
Let \(V^a\) and \(V^b\) be in \({\mathscr {C}}(T)\). Then easy computations show that
where G is given by
Writing
we easily deduce that for all \(s \in (0,T)\),
Besides, for all \(s\in (0,T]\), \(\text {div\,} G(s)\) belongs to \([L^3({\mathbb {R}}^3)]^3\) since \(V^a\) and \(V^b\) belongs to \({\mathscr {C}}(T)\). Therefore, using Lemma 8.1, with \(p_{0} = q_{0} =6,\)
for some C independent of T, where we used that, by scaling, for all \(t>0\),
Similarly, using again Lemma 8.1, with \(p_{0} = \infty , q_{0} =6,\) we get, for some C independent of T,
To estimate \(\nabla (\Lambda _T V^a - \Lambda _T V^b)\), it is convenient to first write
where g is given
that we decompose as
with
We then bound \(g_\ell \) in \([L^3({\mathbb {R}}^3)]^9\): for \(s \in (0,T]\),
We also bound \(g_v\) in \([L^2({\mathbb {R}}^3)]^9\): for \(s \in (0,T]\),
Accordingly, estimate (7.3) yields
We then show that the supremum in \(t \in [0,T]\) can in fact be bounded by a constant independent of T. For \(t \in (0,1)\),
where \(c_{\alpha , \beta }\) is defined for \((\alpha , \beta ) \in (0,1)^2\) by
For \(t \geqslant 1\), we write
Consequently, there exists some C independent of \(T>0\) such that
Putting together estimates (8.8), (8.9) and (8.14), we conclude the estimate (8.7) and Lemma 8.3. \(\square \)
According to Lemma 8.3, for \(K >0\), the set \({\mathscr {C}}(T,K) = \{ V \in {\mathscr {C}}(T), \, \Vert V \Vert _{{\mathscr {C}}(T)} \leqslant K\}\) is such that for all \(V^a\) and \(V^b\) in \({\mathscr {C}}(T,K)\),
where \(C_0\) is the constant in Lemma 8.3. Therefore, for \(K \leqslant K_0 = 1/(4 C_0)\), the map \(\Lambda _T\) is 1/2-Lipschitz in \({\mathscr {C}}(T,K)\).
Now, for \(V_0 \in {\mathbb {X}}^3\), the map \(T \mapsto \Vert {\mathbb {T}}_t V_0 \Vert _{{\mathscr {C}}(T)} \) is a continuous increasing function of T, which is bounded by \(C \Vert V_0 \Vert _{{\mathbb {X}}^3}\) according to estimates (7.2)–(7.3), and which goes to 0 as T to 0 by density of \({\mathcal {D}}({\mathbb {A}}_3)\) in \({\mathbb {X}}^3\) and the decay estimates (7.2)–(7.3).
Therefore, for \(V_0 \in {\mathbb {X}}^3\), we can guarantee that there exists a time \(T_K>0\) such that
so that by (8.6), for \(K \leqslant K_0 = 1/(4C_0)\), the set \({\mathscr {C}}(T_K,K)\) is stable by \(\Lambda _{T_K}\), and \(\Lambda _{T_K}\) is strictly contractive in it. Therefore, by Banach–Picard fixed point theorem, there exists a fixed point \(V \in {\mathscr {C}}(T_K)\), which is by construction a mild solution of (1.2).
Besides, this solution is such that for all \(T < T_K\), \(V|_{(0,T)} \) is the fixed point of \(\Lambda _T\) in \({\mathscr {C}}(T,K)\). Therefore, for T such that \( \Vert {\mathbb {T}}_t V_0 \Vert _{{\mathscr {C}}(T)} \leqslant 1/(8C_0)\), it is easy to check from (8.6) that \(\Vert V|_{(0,T)} \Vert _{{\mathscr {C}}(T)} \leqslant 2 \Vert {\mathbb {T}}_t V_0 \Vert _{{\mathscr {C}}(T)} \), and thus goes to 0 as \(T \rightarrow 0\).
Furthermore, V can be constructed as the limit of the sequence \(V_{n+1} = \Lambda _{T_K} V_n\) for \(n \in {\mathbb {N}}\), \(V_1 = 0\), for which we have, for all \(n \in {\mathbb {N}}\), \(V_n \in {\mathscr {C}}(T_K,K)\). Elements of this sequence satisfies
In particular, using Lemma 8.1, we get
Therefore, taking K smaller if necessary to guarantee that \(CK < 1\), we get that the sequence \(V_n\) is also uniformly bounded in \(L^\infty (0,T_K; {\mathbb {X}}^3)\), so that its limit V is also bounded in \(L^\infty (0,T_K; {\mathbb {X}}^3)\). We then easily deduce by interpolation that, for all \(p \in [3, \infty ]\), \(t^{3/2(1/3 - 1/p)} V \in C^0([0,T_K]; {\mathbb {X}}^p)\).
Besides, since \( \Vert {\mathbb {T}}_t V_0 \Vert _{{\mathscr {C}}(\infty )} \leqslant C_1 \Vert V_0 \Vert _{{\mathbb {X}}^3}\) according to estimates (7.2)–(7.3) for some constant \(C_1\), if \(\Vert V_0\Vert _{{\mathbb {X}}^3}\) is small enough (namely \(\leqslant 1/(8 C_0 C_1)\)), we can take \(K = 2 C \Vert V_0 \Vert _{{\mathbb {X}}^3}\) and \(T_K = \infty \). In this case, we have from the above computations that the above sequence \(V_n\) stays in \({\mathscr {C}}(\infty , K)\) and stays bounded in \(L^\infty (0,\infty ; {\mathbb {X}}^3)\) with \( \Vert V_{n}\Vert _{L^\infty (0,\infty ; {\mathbb {X}}^3)} \leqslant C \Vert V_0 \Vert _{{\mathbb {X}}^3}\). Consequently, when \(\Vert V_0\Vert _{{\mathbb {X}}^3}\) is small enough, we can deduce by interpolation that there exists \(C >0\) such that for all \(n \in {\mathbb {N}}\),
and this also holds for the limit V of the sequence \(V_n\):
Now, we prove that we also have that for all \(\theta \in [0,1/2)\), \(\min \{t^{1/2}, t^\theta \} \nabla v \in L^\infty (0, \infty ; [L^3(E)]^{9})\), taking \(\Vert V_0 \Vert _{{\mathbb {X}}^3}\) smaller if needed. Indeed, starting from (8.16), that we rewrite
using (7.3) with \(r=3\) and \(q = 3\) and \(q = 3/2\), we have, for all \(t >0\) and \(n \in {\mathbb {N}}\),
where we used that the sequence \((V_n)\) satisfies (8.17), and
Now, arguing as in (8.10)–(8.13), one can easily check that there exists a constant C independent of t such that for all \(t >0\),
Consequently, combining the above estimates, we have, for all \(n \in {\mathbb {N}}\),
It follows that if \(\Vert V_0 \Vert _{{\mathbb {X}}^3}\) is small enough, then the sequence \((\min \{ t^{1/2}, t^\theta \} \nabla v_{n}(t))\) is bounded in \(L^\infty (0,\infty ; [L^3(E)]^9)\), and since \(v_n\) converges to v in \({\mathscr {C}}(\infty )\), we obtain \((\min \{ t^{1/2}, t^\theta \} \nabla v(t)) \in L^\infty (0,\infty ; [L^3(E)]^9)\).
Uniqueness. Let \(V^a\) and \(V^b\) be two mild solutions of (1.2) with the same initial datum \(V^0\) in the class \({\mathscr {C}}(T_0)\) such that for \(\left\| V^a\right\| _{{\mathscr {C}}(T)}\) and \(\left\| V^b\right\| _{{\mathscr {C}}(T)}\) go to 0 as \(T \rightarrow 0\).
Then, setting
according to (8.7), we have
Since \(\left\| V^a\right\| _{{\mathscr {C}}(T)}\) and \(\left\| V^b\right\| _{{\mathscr {C}}(T)}\) go to 0 as \(T \rightarrow 0\), there exists \(t_0 \in (0,T_0]\), such that
and thus \(e(t_0) = 0\), and \(V^a \) and \(V^b\) coincides on \([0,t_0]\). If \(t_0 < T_0\), it is easily seen that this argument can be repeated on time intervals of the form \([t_*,T]\) with \(t^*\geqslant t_0\): Using that for \(t \in (0,1)\) such that \(t+t_* \leqslant T_0\),
we immediately have that there exists \(t_1>0\) such that if \(V^a\) and \(V^b\) coincide in \([0,t_*]\) with \(t_* \geqslant t_0\), then they coincide on \([0, \min \{ t_*+t_1, T_0\}]\). This argument proves that \(V^a\) and \(V^b\) in fact coincide on the whole time interval \([0,T_0]\).
The case of an initial datum in \({\mathbb {X}}^q\) for \(q \in (1,3)\). Let \(q \in (1,3)\) and \(V_0 \in {\mathbb {X}}^q \cap {\mathbb {X}}^3\) with \(\Vert V_0\Vert _{{\mathbb {X}}^3} \leqslant \varepsilon _0\). Then we know that the solution V of (1.2) is global in time and belong to \({\mathscr {C}}(\infty )\), and we know that the sequence given by \(V_1 = 0\) and \(V_{n+1} = \Lambda _\infty (V_n)\), i.e.
converges to V in \({\mathscr {C}}(\infty )\), and we have the estimates (8.17).
To prove that V is bounded in some class, it is enough to check that the sequence \((V_n)_{n \in {\mathbb {N}}} \) is uniformly bounded in this class.
Let us start by proving that \(\min \{1, t^{1/2}\} \nabla v \in L^\infty (0,\infty ; \left[ L^{q}(E)\right] ^9)\). With \(p \in (3,\infty )\) such that \(1/p+ 1/q < 1\),
where we used that, according to (8.17),
We then use that
which can be proved along the same lines as in (8.10)–(8.11)–(8.12)–(8.13).
This allows to deduce
Accordingly, if \(\Vert V_0\Vert _{{\mathbb {X}}^3}\) is small enough, we have that
so that the sequence \((\min \{1, t^{1/2}\} \nabla v_{n})_{n\in {\mathbb {N}}}\) is uniformly bounded in \(L^\infty (0,\infty ; \left[ L^{q}(E)\right] ^9)\), and passing to the limit \( n \rightarrow \infty \), \(\min \{1, t^{1/2}\} \nabla v\) belongs to \(L^\infty (0,\infty ; \left[ L^{q}(E)\right] ^9)\).
Accordingly, \(\min \{ t^{1/2}, t\} (v_n - \ell _n) \cdot \nabla v_n\) belongs to \(L^\infty (0,\infty ; L^q({\mathbb {R}}^3))\) and we can use Lemma 8.1 for \(q_0 \geqslant \max \{q, 3/2\}\).
Then we set \(q_0 = \max \{q, 3/2\}\), and we next prove that \(t^{3/2(1/q - 1/q_0)}V \in L^\infty (0, \infty ; {\mathbb {X}}^{q_0})\) and \(t^{3/2(1/q - 1/6)}V\in L^\infty (0, \infty ; {\mathbb {X}}^{6})\). In order to do that, again we look at the sequence \((t^{3/2(1/q - 1/q_0)}V_n)_{n \in {\mathbb {N}}}\) in \(L^\infty (0, \infty ; {\mathbb {X}}^{q_0})\):
This implies that for \( \Vert V_0 \Vert _{{\mathbb {X}}^3}\) small enough, the sequence \((t^{3/2(1/q - 1/q_0)} V_{n})_{n \in {\mathbb {N}}}\) is uniformly bounded in \(L^\infty (0,\infty ; {\mathbb {X}}^{q_0})\) by \(C \Vert V_0\Vert _{{\mathbb {X}}^q}\).
Similarly, we consider the norm of \(t^{3/2(1/q - 1/6)}V_n\) in \(L^\infty (0, \infty ; {\mathbb {X}}^{6})\):
Accordingly, if \(\Vert V_0\Vert _{{\mathbb {X}}^3}\) is small enough, the sequence \((t^{3/2(1/q - 1/6)} V_{n})_{n\in {\mathbb {N}}} \) is bounded in \(L^\infty (0,\infty ; {\mathbb {X}}^{6})\) by \(C \Vert V_0\Vert _{{\mathbb {X}}^q} + C \Vert V_0 \Vert _{{\mathbb {X}}^3} \Vert V_0 \Vert _{{\mathbb {X}}^q} \).
Therefore, the limit V of the sequence \((V_n)_{n \in {\mathbb {N}}}\) satisfies \(t^{3/2(1/q - 1/q_0)} V \in L^\infty (0,\infty ; {\mathbb {X}}^{q_0})\) and \(t^{3/2(1/q - 1/6)} V \in L^\infty (0,\infty ; {\mathbb {X}}^{6})\).
Then, we use that V satisfies
and the fact that, from our previous computations, there exists \(C>0\) such that for all \(s >0\),
Next, using Lemma 8.1 with \(q_0\) and \(p_0 = \infty \) for \(s \in (0,t/2)\), and with 6 and \(p_0 = \infty \) for \(s \in (t/2, t)\), we have
Therefore, \(t^{3/(2q)} V(t) \in L^\infty (0,\infty ; {\mathbb {X}}^\infty )\). Since we have already proved that \(t^{3/2(1/q - 1/q_0)} V \in L^\infty (0,\infty ; {\mathbb {X}}^{q_0})\), we conclude by interpolation that for all \(p \in [q_0, \infty ]\), \(t^{3/2(1/q - 1/p)} V \in L^\infty (0,\infty ; {\mathbb {X}}^{p})\). \(\square \)
9 Concluding remarks and open questions
The main result in this paper, namely Theorem 1.1, concerns the wellposedness of the system modelling the motion of a rigid ball in a viscous incompressible fluid filling the remaining part of \({\mathbb {R}}^3\) and asserts that the position of the centre of the ball tends, when \(t\rightarrow \infty \), to some position \(h_\infty \in {\mathbb {R}}^3\). This result differs from those previously obtained in two space dimensions in [6], or for a simplified 1D model in [29], where it has been shown that the distance of the centre of the ball to the origin tends to \(+\infty \) when \(t\rightarrow \infty \). Several open questions seem natural in view of our results.
One of the most challenging ones, for which we have no track at this stage, is determining \(h_\infty \) from the initial data.
Another natural question is the generalization of Theorem 1.1 for a body of arbitrary shape. When the rigid body is not a ball, writing the equations in a fixed domain requires the use of more delicate changes of variables, since it has to include the rotation of the body. There are basically two ways of doing that: one consists in setting \(v (t,x) = Q^*(t) u(t, h(t) + Q(t) x )\) , where Q(t) is the rotation matrix of the body, that is the solution of \(\dot{Q}(t) Q^*(t) x = \omega (t) \times x\) starting from \(Q(0) = Id\). The problem is that such change of frame would induce in the fixed frame a term of the form \((\omega \times x) \cdot \nabla v\) which our estimate does not allow to handle since the identity mapping does not belong to \(L^\infty (E)\). The alternative approach proposed in [4], which consists in constructing a change of variable which follows the structure in a neighbourhood of it and equals the identity far from the body, seems more suitable to deal with the non-linear terms. However, this change of variable introduces a lot of delicate terms which we do not know how to handle in the above setting so far. In fact, even in two space dimensions, the existing results (see [6]) provide an analysis of the motion of a rigid body in a viscous incompressible fluid in \({\mathbb {R}}^2\) only in the case when the rigid body is a disk.
Finally, let us mention that the counterparts in two space dimensions of some of our results in Sects. 4–7 have been used in Takahashi and Lacave [18] to study the behaviour of solutions of (1.2) when the radius of the rigid ball tends to zero (see also He and Iftimie [12] and references therein). We believe that the approach in [18] can be adapted to the three dimensional case by using our results on the fluid structure-semigroup and its generator, but this deserves further work.
Availability of data and material
This manuscript has no associated data.
Code availability
Not applicable.
References
Bogovskiĭ, M.E.: Solution of the first boundary value problem for an equation of continuity of an incompressible medium. Dokl. Akad. Nauk SSSR 248, 1037–1040 (1979)
Borchers, W., Sohr, H.: On the semigroup of the Stokes operator for exterior domains in \(L^q\)-spaces. Math. Z. 196, 415–425 (1987)
Crispo, F., Maremonti, P.: An interpolation inequality in exterior domains. Rend. Sem. Mat. Univ. Padova 112, 11–39 (2004)
Cumsille, P., Takahashi, T.: Wellposedness for the system modelling the motion of a rigid body of arbitrary form in an incompressible viscous fluid. Czechoslov. Math. J. 58(133), 961–992 (2008)
Dashti, M., Robinson, J.C.: The motion of a fluid–rigid disc system at the zero limit of the rigid disc radius. Arch. Ration. Mech. Anal. 200, 285–312 (2011)
Ervedoza, S., Hillairet, M., Lacave, C.: Long-time behavior for the two-dimensional motion of a disk in a viscous fluid. Commun. Math. Phys. 329, 325–382 (2014)
Fujiwara, D., Morimoto, H.: An \(L_{r}\)-theorem of the Helmholtz decomposition of vector fields. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24, 685–700 (1977)
Galdi, G.P.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Vol. II. Nonlinear steady problems. Springer Tracts in Natural Philosophy, vol. 39. Springer, New York (1994)
Geissert, M., Götze, K., Hieber, M.: \(L^p\)-theory for strong solutions to fluid–rigid body interaction in Newtonian and generalized Newtonian fluids. Trans. Am. Math. Soc. 365, 1393–1439 (2013)
Giga, Y., Sohr, H.: On the Stokes operator in exterior domains. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 36, 103–130 (1989)
Happel, J., Brenner, H.: Low Reynolds Number Hydrodynamics with Special Applications to Particulate Media. Prentice-Hall, Inc., Englewood Cliffs (1965)
He, J., Iftimie, D.: On the small rigid body limit in 3D incompressible flows. J. Lond. Math. Soc. (2021)
Hishida, T.: Large time behavior of a generalized Oseen evolution operator, with applications to the Navier–Stokes flow past a rotating obstacle. Mathematische Annalen 372, 915–949 (2018)
Hishida, T.: Decay estimates of gradient of a generalized Oseen evolution operator arising from time-dependent rigid motions in exterior domains. Arch. Ration. Mech. Anal. 238, 215–254 (2020)
Iwashita, H.: \(L_q\)-\(L_r\) estimates for the solutions of the nonstationary Stokes equations in an exterior domain and the Navier–Stokes initial value problems in \({L}_q\) spaces. Math. Ann. 285, 265–288 (1989)
Kato, T.: Strong \(L^{p}\)-solutions of the Navier–Stokes equation in \({ R}^{m}\), with applications to weak solutions. Math. Z. 187, 471–480 (1984)
Koike, K.: Long-time behavior of a point mass in a one-dimensional viscous compressible fluid and pointwise estimates of solutions. J. Differ. Equ. 271, 356–413 (2021)
Lacave, C., Takahashi, T.: Small moving rigid body into a viscous incompressible fluid. Arch. Ration. Mech. Anal. 223, 1307–1335 (2017)
Lunardi, A.: Interpolation Theory, Appunti. Scuola Normale Superiore di Pisa (Nuova Serie). [Lecture Notes. Scuola Normale Superiore di Pisa (New Series)], Edizioni della Normale, Pisa, 2nd edn. (2009)
Maity, D., Tucsnak, M.: \(L^p\)-\(L^q\) maximal regularity for some operators associated with linearized incompressible fluid–rigid body problems. In: Mathematical Analysis in Fluid Mechanics—Selected Recent Results, vol. 710. Contemporary Mathematics, pp. 175–201. American Mathematical Society, Providence (2018)
Maremonti, P., Solonnikov, V.A.: On nonstationary Stokes problem in exterior domains. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 24, 395–449 (1997)
McCracken, M.: The resolvent problem for the Stokes equations on halfspace in \({L}^p\). SIAM J. Math. Anal. 12, 201–228 (1981)
Miyakawa, T.: On nonstationary solutions of the Navier–Stokes equations in an exterior domain. Hiroshima Math. J. 12, 115–140 (1982)
Serre, D.: Chute libre d’un solide dans un fluide visqueux incompressible. Existence. Jpn. J. Appl. Math. 4, 99–110 (1987)
Takahashi, T.: Analysis of strong solutions for the equations modeling the motion of a rigid–fluid system in a bounded domain. Adv. Differ. Equ. 8, 1499–1532 (2003)
Takahashi, T., Tucsnak, M.: Global strong solutions for the two dimensional motion of an infinite cylinder in a viscous fluid. J. Math. Fluid Mech. 6, 53–77 (2004)
Temam, R.: Problèmes mathématiques en plasticité. Méthodes Mathématiques de l’Informatique [Mathematical Methods of Information Science], vol. 12. Gauthier-Villars, Montrouge (1983)
Triebel, H.: Interpolation Theory, Function Spaces, Differential Operators, 2nd edn. Johann Ambrosius Barth, Heidelberg (1995)
Vázquez, J.L., Zuazua, E.: Large time behavior for a simplified 1D model of fluid–solid interaction. Commun. Partial Differ. Equ. 28, 1705–1738 (2003)
Wang, Y., Xin, Z.: Analyticity of the semigroup associated with the fluid–rigid body problem and local existence of strong solutions. J. Funct. Anal. 261, 2587–2616 (2011)
Acknowledgements
The authors are indebted to Toshiaki Hishida for his suggestions, which had led to many improvements of our work.
Funding
S. Ervedoza has been supported by the CIMI Labex, Toulouse, France, under Grant ANR-11-LABX-0040-CIMI. D. Maity is supported in part by INSPIRE faculty fellowship (IFA18-MA128) and by Department of Atomic Energy, Government of India, under Project no. 12-R & D-TFR-5.01-0520. D. Maity and M. Tucsnak are partially supported by the IFCAM project “Analysis, Control and Homogenization of Complex Systems”. M. Tucsnak has been supported by the SingFlows project, Grant ANR-18-CE40-0027 of the French National Research Agency (ANR). S. Ervedoza and M. Tucsnak have been partially supported by the Agence Nationale de la Recherche, Project IFSMACS, Grant ANR-15-CE40-0010 and Project TRECOS, Grant ANR-20-CE40-0009-01.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Communicated by Giga.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
1.1 Proof of Proposition 3.2
We first show that every \(u\in \left[ L^q(\Omega )\right] ^3\) can be written in the form \( u = v + w_{1} + w_{2},\) with \(v \in {\mathbb {X}}^q(\Omega ),\) \(w_{1} \in G_1^q(\Omega )\) and \(w_{2} \in G_2^q(\Omega )\).
To this aim, let \(q_{11}\) be the solution of the problem
Thus \(q_{11} \in W^{1,q}_{0}(\Omega )\) and we have \({\mathrm {div}}( u -\nabla q_{11}) = 0\) in \(\Omega \). Accordingly \((u- \nabla q_{11}) \cdot \nu \) is well-defined on \(\partial \Omega \), and we can solve
Setting then \(q_1 = q_{11} + q_{12}\), and \(w_1 = \nabla q_1\), \(w_1 \in G_1^q(\Omega )\), and \( {\mathrm {div}} \ (u -w_1) = 0 \) in \(\Omega \) and \((u - w_1) \cdot \nu = 0\) on \(\partial \Omega \).
Since we are looking for \(v \in {\mathbb {X}}^{q}(\Omega ),\) we know that
for some \(\ell _{v} \in {\mathbb {R}}^{3}\) and \(\omega _{v} \in {\mathbb {R}}^{3}\). We set
and

Since we are looking for \(w_{2} \in G_{2}^{q}(\Omega )\) we require
and
where m and \({\mathcal {J}}\) are defined in (3.11).
Now we define \(q_{2}\) as the solution of the Neumann problem

where \(\ell _{v}\) and \(\omega _{v}\) are defined in (A.4) and (A.5), respectively. Note that, \(q_{2}\) solves a Laplace equation with non-local boundary condition. As shown below, we have that \(q_{2} \in W^{1,q}(E_{\Omega })\) and there exists a constant C depending on q, \(\Omega \) and \({\mathcal {O}}\) such that
In this case we can determine \(\ell _{v}\) and \(\omega _{v}\) from (A.4) and (A.5) respectively. Consequently, we obtain \(\varphi \) and \(w_{2}\) from (A.2) and (A.3) respectively. In particular, we have that \(w_{2} \in G_{2}^{q}(\Omega )\) and by setting \(v = u - w_{1} - w_{2}\) we can verify that \(v \in {\mathbb {X}}^{q}(\Omega ).\)
We still have to prove that \(q_{2} \in W^{1,q}(\Omega )\) and (A.7) holds. If \(q=2,\) this is a consequence of Lax–Milgram Theorem (see for instance [5, Lemma 1]). If \(q \ne 2,\) we employ a density argument. Assume that \(u \in \left[ C_{0}^{\infty }(\Omega )\right] ^3\) and \(q_{2}\) solves (A.6). Then there exists a constant C depending only on \(q, \Omega \) and \({\mathcal {O}}\) such that
Next, by following the arguments of the proof of Theorem 2.2 in [30], we have
where C is a positive constant depending only on \(q, \Omega \) and \({\mathcal {O}}.\) The above two estimates yield that there exists a positive constant C, depending only on \(q, \Omega \) and \({\mathcal {O}}\), such that estimate (A.7) holds. Thus the conclusion follows by a density argument. This completes the proof of the existence of a decomposition with the required properties. The proof of uniqueness of the decomposition is similar to that of [30, Theorem 2.2].
1.2 Proof of Proposition 3.3
Let \({\mathbb {Y}}^{q}(\Omega )^{\perp }\) and \(({\mathbb {Y}}^{q})^{\perp }\) be the annihilators of \({\mathbb {Y}}^{q}(\Omega )\) and \({\mathbb {Y}}^{q}\) respectively, i.e.,
Let us set \(G^{q'}(\Omega ) = G_{1}^{q'}(\Omega ) \oplus G_{2}^{q'}(\Omega )\) and \(G^{q'} = G_{1}^{q'} \oplus G_{2}^{q'}.\)
Step 1. We claim that \({\mathbb {Y}}^{q}(\Omega )^{\perp } = G^{q'}(\Omega )\) and \(({\mathbb {Y}}^{q})^{\perp } = G^{q'}.\)
Let us assume that \(u \in G^{q'}(\Omega ) = G^{q'}_{1}(\Omega ) \oplus G^{q'}_{2}(\Omega ),\) i.e., \(u = u_{1}+u_{2}\) with \(u_{1} \in G^{q'}_{1}(\Omega )\) and \(u_{2} \in G^{q'}_{2}(\Omega ).\) Let us take \(v \in C_{c}^{\infty }(\Omega )\), \({\mathrm {div}}\, v = 0 \text{ in } \Omega \), and \(Dv = 0 \text{ in } {\mathcal {O}}.\) Then we have
and
Thus by density \(\int _{\Omega } u \cdot v = 0\) for all \(v \in {\mathbb {Y}}^{q}(\Omega ).\) This shows that \(u \in {\mathbb {Y}}^{q}(\Omega )^{\perp }\) and \( G^{q'}(\Omega ) \subset {\mathbb {Y}}^{q}(\Omega )^{\perp }.\) In a similar manner, we can show \( G^{q'} \subset ({\mathbb {Y}}^{q})^{\perp }.\)
Conversely, let us assume that \(u \in {\mathbb {Y}}^{q}(\Omega )^{\perp }.\) Then according to Proposition 3.2,
Since \(u \in {\mathbb {Y}}^{q}(\Omega )^{\perp },\) by similar calculation as above, we obtain for all \(v \in C_{c}^{\infty }(\Omega )\), with \({\mathrm {div}}\, v = 0 \text{ in } \Omega \) and \( Dv = 0 \text{ in } {\mathcal {O}},\)
We claim that \(w \in G^{q'}_{2}(\Omega ).\) By choosing, \(v \in C_{c}^{\infty }(E_{\Omega })\) with \( {\mathrm {div}}\, v = 0 \text{ in } E_{\Omega },\) we have
Then by de Rham’s theorem there is a distribution \(q_{2}\) such that \(w = \nabla q_{2}\) in \(E_{\Omega }.\) Further, from the fact that \(w \in {\mathbb {X}}^{q'}(\Omega )\) we have \(q_{2} \in L^{1}_{\text {loc}}(E_{\Omega }),\) and if \(\Omega \) is a bounded domain we have \(q_{2} \in W^{1,q'}(E_{\Omega }).\) Furthermore, we have \(w = \ell _{w} + \omega _{w} \times y\) in \({\mathcal {O}},\) and
In particular,
Now by choosing v as above with \(v = \ell _{v}\) in \({\mathcal {O}}\) we infer that
Similarly, by choosing \(v = \omega _{v} \times y\) in \({\mathcal {O}}\) we get
Therefore \(w \in G^{q'}(\Omega ).\) Since by construction, \(w = {\mathbb {P}}_{q', \Omega } u\) belongs to \({\mathbb {X}}^{q'}(\Omega )\), and \({\mathbb {X}}^{q'}(\Omega ) \cap G^{q'}(\Omega ) = \{0\}\), \(w = 0\) and \(u = w_0\) belongs to \(G^{q'}(\Omega )\). The proof is similar when \(\Omega = {\mathbb {R}}^{3}.\)
Step 2. By Proposition 3.2, we have \({\mathbb {X}}^{q'} = [L^{q'}(\Omega )]^{3}/G^{q'}(\Omega ).\) Then
The same also holds when \(\Omega ={\mathbb {R}}^{3}.\)
Appendix B Optimality of the decay estimates in (7.2) in the case of a ball
In this section, following [21, p.441], we prove the optimality of the decay estimates (7.2) when \({\mathcal {O}}\) is the unit ball (the extension to any ball can be done analogously and is left to the reader).
Theorem B.1
Let \({\mathcal {O}}\) be the unit ball, and \({\mathbb {T}}_t^q\) be the fluid-structure semigroup introduced in Theorem 6.1 for \(q \in (1, \infty )\).
There is no \(\varepsilon >0\) and \(r \geqslant q \geqslant 3/2\) with \(r \leqslant \infty \) such that the semigroup \({\mathbb {T}}_t= {\mathbb {T}}_t^q\) satisfies
where \(\sigma = \frac{3}{2} \left( \frac{1}{q} - \frac{1}{r} \right) \).
In other words, item (ii) and (iv) of Theorem 7.1 are sharp decay estimates.
Proof
First, using the semigroup property and the decay estimates (7.2), if (B.1) holds for some \(r \in [3/2, \infty ]\) and \(q \in [3/2,r]\), writing
the decay estimate (B.1) holds for \(r = \infty \) and \(q = 3/2\). Therefore, in the following, we suppose without loss of generality that (B.1) holds with \(r = \infty \) and \(q = 3/2\), i.e.
Following the arguments in [21, p.441], we will prove that if this estimate holds, then the Kirchhoff potential (see e.g. [11, p.163])
would belong to \(L^{3}(E)\), which is obviously not the case.
Indeed, recalling that we assumed that \({\mathcal {O}}\) is the unit ball. One can then check that (v, p) in (B.3) satisfies the equations
Also note that V given by \(V|_{E} = v\) and \(V|_{{\mathcal {O}}} = e_1\) belongs to all \({\mathbb {X}}^q\) with \(q >3\).
Next, let \( q \in (1, 3/2)\) and consider a datum \(U_0 \in {\mathbb {X}}^{q} \cap {\mathbb {X}}^{3/2}\). With the notations of Remark 7.7, \(U(t) = {\mathbb {T}}_t U_0\) corresponds to \((u(t), \pi (t), \ell (t), \omega (t))\) solving (7.19).
Multiplying then the equation (7.19)\(_{(1)}\) by v, integrating on E, doing integration by parts and using the boundary conditions, we get
and integrating in time on (0, T) for some \(T>0\),
On one hand, using the decay estimate (7.2), for \(s \in (q, 3/2)\), we have \(\Vert U(T)\Vert _{{\mathbb {X}}^{s}} \leqslant C T^{-\alpha _s} \Vert U_0\Vert _{{\mathbb {X}}^{q}}\) for some positive decay rate \(\alpha _s >0\), and since \(s' > 3\),
On the other hand, using (7.2) with \(r = 3/2\), we get that for all \(t \geqslant 0\), \(|\ell (t)| + |\omega (t)| \leqslant C \Vert U_0\Vert _{{\mathbb {X}}^{3/2}}\), while the estimate (B.2) implies that for all \(t >0\), \(|\ell (t)| + |\omega (t)| \leqslant C t^{-1- \varepsilon } \Vert U_0\Vert _{{\mathbb {X}}^{3/2}}\).
Accordingly, using identity (B.5), we get, for all \(U_0 \in {\mathbb {X}}^{q} \cap {\mathbb {X}}^{3/2}\) and \(T>0\),
Letting T go to infinity, we obtain that for all \(U_0 \in {\mathbb {X}}^{q} \cap {\mathbb {X}}^{3/2}\),
This implies that \(V \in {\mathbb {X}}^3\) from [21, Lemma 2.6], and from the explicit formula of V (recall (B.3)), we get a contradiction. \(\square \)
Rights and permissions
About this article
Cite this article
Ervedoza, S., Maity, D. & Tucsnak, M. Large time behaviour for the motion of a solid in a viscous incompressible fluid. Math. Ann. 385, 631–691 (2023). https://doi.org/10.1007/s00208-021-02351-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-021-02351-y