A backward $\lambda$-lemma for the forward heat flow

Abstract

The inclination or $\lambda$-lemma is a fundamental tool in finite dimensional hyperbolic dynamics. In contrast to finite dimension, we consider the forward semi-flow on the loop space of a closed Riemannian manifold $M$ provided by the heat flow. The main result is a backward $\lambda$-lemma for the heat flow near a hyperbolic fixed point $x$. There are the following novelties. Firstly, infinite versus finite dimension. Secondly, semi-flow versus flow. Thirdly, suitable adaption provides a new proof in the finite dimensional case. Fourthly and a priori most surprisingly, our $\lambda$-lemma moves the given disk transversal to the unstable manifold backward in time, although there is no backward flow. As a first application we propose a new method to calculate the Conley homotopy index of $x$.

1 Introduction and main results

Assume $M$ is a closed smooth manifold of dimension $n\ge 1$ equipped with a Riemannian metric $g$ and the Levi–Civita connection $\nabla$. Throughout smooth means $C^\infty$ smooth. The loop space is the Hilbert manifold $\varLambda M:=W^{1,2}(S^1,M)$ of absolutely continuous loops in $M$ with square integrable derivative. We identify $S^1={\mathbb {R}}/{\mathbb {Z}}$ and think of $\gamma \in \varLambda M$ as a map $\gamma :{\mathbb {R}}\rightarrow M$ that satisfies $\gamma (t+1)=\gamma (t)$. Pick a smooth function $V:S^1\times M\rightarrow {\mathbb {R}}$ and set $V_t(q):=V(t,q)$.

Consider the heat equation

$$\begin{aligned} {\partial }_su - \nabla {}_{t}{\partial }_tu - \mathrm{grad }V_t(u) = 0 \end{aligned}$$

(1)

for smooth maps ${\mathbb {R}}\times S^1\rightarrow M:(s,t)\mapsto u(s,t)$. It is well known that the corresponding Cauchy problem for the map $[0,\infty )\rightarrow \varLambda M:s\mapsto u_s:=u(s,\cdot )$ admits a unique solution. The associated forward semi-flow $\varphi$ on $\varLambda M$ is called the heat flow. It is a continuous map

$$\begin{aligned} \varphi :[0,\infty )\times \varLambda M\rightarrow \varLambda M \end{aligned}$$

which is of class $C^1$ on $(0,\infty )$; see (5) for its representative $\phi$ in local coordinates. For $\gamma \in \varLambda M$ abbreviate $\dot{\gamma }=\frac{d}{dt}\gamma$. Because (1) is the downward $L^2$ gradient equation of the action functional ${\fancyscript{S}}_V:\varLambda M\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} {\fancyscript{S}}_V(\gamma )=\int \limits _0^1\left( \frac{1}{2}\mathopen |\dot{\gamma }(t)\mathclose |^2 -V_t(\gamma (t))\right) dt, \end{aligned}$$

the fixed points of the heat flow are the critical points of the action. The latter are (perturbed) closed geodesics, that is solutions $x:S^1\rightarrow M$ to the second order ODE

$$\begin{aligned} -\nabla {}_{t}\dot{x}-\nabla V_t(x)=0. \end{aligned}$$

By $\mathrm{ind}(x)$ we denote the Morse index of $x$. Nondegeneracy of the critical point $x$, that is nondegeneracy of the Hessian of ${\fancyscript{S}}_V$ at $x$, corresponds to hyperbolicity of the fixed point $x$.

Fix a nondegenerate critical point $x$ of the action ${\fancyscript{S}}_V$. While the stable manifold $W^s(x)$ is defined in the usual way as the set of all points which flow in forward time asymptotically into $x$, it is of infinite dimension. The fact that $W^s(x)$ is globally embedded is, firstly, remarkable since the standard method of pulling back coordinates near $x$ using the backward flow is obviously not available. Secondly, except for [8, Theorem 6.1.9] this fact is usually not mentioned at all in the literature—unlike the widely known local submanifold property near $x$; see Sect. 2.5. In contrast, without a backward flow the definition of the unstable manifold $W^u(x)$ becomes somewhat awkward: It is the set of endpoints of all heat flow trajectories parametrized by $(-\infty ,0]$ and emanating at time $-\infty$ from $x$. On the other hand, this definition lends itself to define a backward flow on $W^u(x)$ which immediately implies that the unstable manifold is globally embedded. Most importantly, its dimension given by $\mathrm{ind}(x)$ is finite; see e.g. [18]. It is this finite dimensionality which is one of two pillars on which this paper is based. A key consequence is smoothness of every $\gamma \in W^u(x)$; see Remark 3.

1.1 Some history

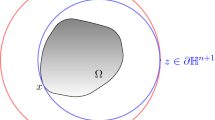
In finite dimensional hyperbolic dynamics there are two fundamental tools: The Grobman–Hartman Theorem [5, 7] and the $\lambda$-lemma [11]. While the first is powerful concerning topological questions the latter reigns in the differentiable world. It even implies the former. The $\lambda$-lemma asserts that the backward flow applied to any disk ${\fancyscript{D}}$ transversal to the unstable manifold and of complementary dimension converges in $C^1$ to the local stable manifold, see Fig. 1, and similarly for the forward flow. For a beautiful presentation see [12]. Since convergence is in $C^1$, the $\lambda$-lemma is also called inclination lemma.

Fig. 1

Preimage of disk ${\fancyscript{D}}_\gamma (x)$ converges in $C^1$ and locally near $x$ to the stable manifold $W^s(x)$

The second pillar on which this paper is based is the replacement of the absent backward flow on the loop space by the family of preimages $s\mapsto {\varphi _s}^{-1}{\fancyscript{D}}$. This idea was born when we attempted to construct a Morse filtration of the loop space using the method of Abbondandolo and Majer [1]. Their construction builds on open sets being mapped to open sets under a forward flow. But this is not true for $\varphi _s$—from a topological point of view the heat semi-flow is useless! The way out was the simple observation that preimages of open sets are open by continuity of $\varphi _s$. Unfortunately, still the Abbondandolo–Majer method would not apply, because things were moving in the wrong direction now. However, the definition given in [15, proof of Lemma 3.2] in finite dimensions carries over providing a Conley pair $(N,L)$ for the semi-flow invariant set given by the critical point $x$. Now the backward $\lambda$-lemma enters. In [19, 20] we use it to define an invariant stable foliation of $(N,L)$ which is a fundamental ingredient in our construction of a Morse filtration of $\varLambda M$ by open semi-flow invariant sets. In Sect. 1.4 we discuss the key calculation.

In other words, we were led to discover the backward $\lambda$-lemma through the attempt to solve a very different problem—thereby reconfirming a major principle advocated by Arnol’d throughout his mathematical life.

1.2 Main results

Assume ${\fancyscript{D}}_\gamma (x)$ is a disk in the Hilbert manifold $\varLambda M=W^{1,2}(S^1,M)$ which intersects the unstable manifold $W^u(x)$ transversally in a point $\gamma$ near $x$. Our main goal is to prove that the preimage ${\varphi _T}^{-1}{\fancyscript{D}}_\gamma (x)$ converges, as $T\rightarrow \infty$, uniformly in $C^1$ and locally near $x$ to the stable manifold $W^s(x)$; see Fig. 1. In fact, we prove right away a family version where ${\fancyscript{D}}$ is fibered over a descending sphere $S^u_{\varepsilon }(x)=W^u(x)\cap \{{\fancyscript{S}}_V={\fancyscript{S}}_V(x)-{\varepsilon }\}$.

Since the $\lambda$-lemma is a local result we choose a local parametrization

$$\begin{aligned} \varPhi :=\exp _x: X \rightarrow \varLambda M ,\qquad X=T_x \varLambda M=W^{1,2}(S^1,x^*TM), \end{aligned}$$

of an open neighborhood of $x$ in $\varLambda M$ in terms of the exponential map; here compactness of $M$ enters. The orthogonal splitting

$$\begin{aligned} X \simeq T_x W^u(x)\oplus T_x W^s(x) =X^-\oplus X^+ \end{aligned}$$

with associated orthogonal projections $\pi _\pm$ is a key ingredient to make the analysis work; at this stage take the final identity as a definition. By a standard graph argument we may assume without loss of generality that ${\fancyscript{U}}$ is of the form $W^u\times {\fancyscript{O}}^+$. Here $W^u\subset X^-$ represents a descending disk $W^u(x)\cap \{{\fancyscript{S}}_{\fancyscript{V}}>{\fancyscript{S}}_{\fancyscript{V}}(x)-\delta \}$ for some $\delta >0$ sufficiently small and ${\fancyscript{O}}^+\subset X^+$ is an open ball about $0$. By $\phi$ we denote the local semi-flow on ${\fancyscript{U}}$ which represents the heat flow $\varphi$ on $\varLambda M$ with respect to the local parametrization $\varPhi$; see (5).

Hypothesis 1

(Local setup—Fig. 4) Fix a perturbation $V\in C^\infty (S^1\times M)$ and a nondegenerate critical point $x$ of ${\fancyscript{S}}_V$ of Morse index $k$.

• (a) Consider the coordinates on $\varLambda M$ provided by $\varPhi$ and modelled on the open subset ${\fancyscript{U}}=W^u\times {\fancyscript{O}}^+$ of $X$. In these coordinates the origin $0\in X$ represents $x$ and ${\fancyscript{S}}:={\fancyscript{S}}_V\circ \varPhi ^{-1}$ represents the action. Denote closed radius $R$ balls about $0$ by

  $$\begin{aligned} {\fancyscript{B}}_R :=\{\left\| \cdot \right\| _X\le R\} ,\qquad {\fancyscript{B}}^+_R :=\{\left\| \cdot \right\| _{X^+}\le R\}. \end{aligned}$$

  Choose the constant $\rho _0>0$ in the Lipschitz Lemma 1 smaller, if necessary, such that ${\fancyscript{B}}_{\rho _0}\subset {\fancyscript{U}}$. Pick a sufficiently small constant ${\varepsilon }_0>0$ such that for each ${\varepsilon }\in (0,{\varepsilon }_0]$ the descending and ascending disks

  $$\begin{aligned}&W^u_{\varepsilon }(x) :=W^u(x)\cap \{{\fancyscript{S}}_V>{\fancyscript{S}}_V(x)-{\varepsilon }\} ,\\&W^s_{\varepsilon }(x) :=W^s(x)\cap \{{\fancyscript{S}}_V<{\fancyscript{S}}_V(x)+{\varepsilon }\}, \end{aligned}$$

  are contained in the coordinate patch $\varPhi ({\fancyscript{B}}_{\rho _0})$ and such that their closures are diffeomorphic to the closed unit disks in ${\mathbb {R}}^k$ and $X^+$, respectively. Existence of ${\varepsilon }_0$ follows by the Morse- and the Palais–Morse lemma.

• (b) Fix $\mu \in (0,d)$ in the spectral gap (4) of the Jacobi operator. Pick $\varkappa \in (0,\rho _0)$ so small that ${\fancyscript{D}}:=S^u_{\varepsilon }\times {\fancyscript{B}}^+_\varkappa$ is contained in ${\fancyscript{B}}_{\rho _0}$ and set ${\fancyscript{D}}_\gamma :=\{\gamma \}\times {\fancyscript{B}}^+_\varkappa$.

• (c) Our notation for objects expressed in coordinates will be the global notation with $x$ omitted, for example $W^s_{\varepsilon }$ and ${\fancyscript{D}}_\gamma$.

Theorem 1

(Backward $\lambda$-lemma) Assume the local setup of Hypothesis 1. In particular, consider the hyperbolic fixed point $0$ of the local semi-flow $\phi$ defined by (5) on ${\fancyscript{U}}\subset X$ and the hypersurface ${\fancyscript{D}}=S^u_{\varepsilon }\times {\fancyscript{B}}^+_\varkappa \subset {\fancyscript{B}}_{\rho _0}\subset {\fancyscript{U}}$; see Fig. 2. Then the following is true. There is a closed ball ${\fancyscript{B}}^+\subset X^+$ of radius $r>0$ about zero, a constant $T_0>0$, and a Lipschitz continuous map

$$\begin{aligned} {\fancyscript{G}}:(T_0,\infty )\times S^u_{\varepsilon }\times {\fancyscript{B}}^+&\rightarrow W^u\times {\fancyscript{B}}^+\subset {\fancyscript{U}}\\ (T,\gamma ,z_+)&\mapsto \left( G^T_\gamma (z_+),z_+\right) =:{\fancyscript{G}}^T_\gamma (z_+) \end{aligned}$$

of class $C^1$ and defined by (25). Each map ${\fancyscript{G}}^T_\gamma :{\fancyscript{B}}^+\rightarrow X$ is bi-Lipschitz, a diffeomorphism onto its image, and ${\fancyscript{G}}^T_\gamma (0)=\phi _{-T}\gamma =:\gamma _T$. The graph of $G^T_\gamma$ consists of those $z\in {\fancyscript{U}}$ which satisfy $\pi _+ z\in {\fancyscript{B}}^+$ and reach the fiber ${\fancyscript{D}}_\gamma =\{\gamma \}\times {\fancyscript{B}}^+_\varkappa$ at time $T$, that is

$$\begin{aligned} {\fancyscript{G}}^T_\gamma ({\fancyscript{B}}^+) ={\phi _T}^{-1} {\fancyscript{D}}_\gamma \cap \left( X^-\times {\fancyscript{B}}^+\right) . \end{aligned}$$

Furthermore, the graph map ${\fancyscript{G}}^T_\gamma$ converges uniformly, as $T\rightarrow \infty$, to the stable manifold graph map ${\fancyscript{G}}^\infty$ of Theorem 3. More precisely, it holds that ¹

$$\begin{aligned} \left\| {\fancyscript{G}}^T_\gamma (z_+)-{\fancyscript{G}}^\infty (z_+)\right\| _{C^1(S^1)} \le \rho _0 e^{-T\frac{\mu }{16}} \end{aligned}$$

for all $T>T_0$, $\gamma \in S^u_{\varepsilon }$, and $z_+\in {\fancyscript{B}}^+$.

Fig. 2

Backward $\lambda$-lemma

Theorem 2

(Uniform $C^1$ convergence on $X$) Under the assumptions of Theorem 1 the linearized graph maps $d{\fancyscript{G}}^T_\gamma (z_+):X^+\rightarrow X$ extend to bounded linear operators on the $L^2$ completions and their limit, as $T\rightarrow \infty$, is $d{\fancyscript{G}}^\infty (z_+)$, uniformly in $z_+\in {\fancyscript{B}}^+$. More precisely,

$$\begin{aligned} \left\| d{\fancyscript{G}}^T_\gamma (z_+) v\right\| _2 \le 2 \left\| v\right\| _2 \end{aligned}$$

and

$$\begin{aligned} \left\| d{\fancyscript{G}}^T_\gamma (z_+)v-d{\fancyscript{G}}^\infty (z_+)v\right\| _2 \le e^{-T\frac{\mu }{16}}\left\| v\right\| _2 \end{aligned}$$

for all $T>T_0, \gamma \in S^u_{\varepsilon }, z_+\in {\fancyscript{B}}^+$, and $v$ in the $L^2$ closure of $X^+$.

Remark 1

• (i) The reason why the $W^{1,2}$ norm has been replaced by $C^1$ ($\hookleftarrow W^{1,4}$) in Theorem 1 and by $L^2$ in Theorem 2 is the application in Sect. 1.4. Here the $L^2$ nature of (1) requires to estimate the nonlinearity $f$ in (5) in the $L^2$ norm. Observe that $f$ maps $W^{1,4}$ to $L^2$.

• (ii) All results in this paper extend to the more general class of perturbations satisfying axioms (V0–V3) in [16]; see [21].

Remark 2

• (a) Theorem 1 recovers the common case of a single disk intersecting the unstable manifold transversely in one point $\gamma$ near $0$. Apply the implicit function theorem to bring the disk into the normal form $\{\gamma \}\times {\fancyscript{B}}^+_\varkappa$. Observe that ${\fancyscript{G}}^T_\gamma$ is defined without reference to any neighbors of $\gamma$. To formally get a bundle ${\fancyscript{D}}=S^u_{\varepsilon }\times {\fancyscript{B}}^+_\varkappa$ as in the hypothesis just add disks artificially.

• (b) Theorem 1 for endpoint time $T=\infty$ and radius $\varkappa =0$ recovers two known results. These appear as extreme cases concerning the radius $0$ disk bundle ${\fancyscript{D}}=S^u_{\varepsilon }\times \{0\}$.

  • I Disk of radius 0 sitting at the origin: In this case $S^u_{\varepsilon }=\{0\}$, that is the disk bundle degenerates to just one radius $0$ disk sitting at the origin. This recovers the local stable manifold Theorem 3 and inspires the notation ${\fancyscript{G}}^\infty$ for the stable manifold graph map. The preimage ${\phi _T}^{-1}(0)$ for $T=\infty$ corresponds to the local stable manifold.

  • II Radius 0 disk bundle sitting at $\infty$: This recovers the stable foliation in [3]. Two points belong to the same leaf if under the semi-flow $\phi _s$ their difference converges exponentially to zero, as $s\rightarrow \infty$. The leaf over $0$ is the local stable manifold.

Remark 3

(Mixed Cauchy problem) We motivate why the map ${\fancyscript{G}}$ in the backward $\lambda$-lemma should exist. Assume the hypotheses of the backward $\lambda$-lemma and fix $T>0$. Each point $z$ in the preimage ${\phi _T}^{-1}{\fancyscript{D}}_\gamma$ corresponds to a unique semi-flow line $\xi$ such that $\xi (0)=z$ and $\xi$ hits the fiber ${\fancyscript{D}}_\gamma$ precisely at time $T$, say in the point $q:=\xi (T)$. Of course, we cannot change the order, i.e. first choosing an end point $q\in {\fancyscript{D}}_\gamma$ and then determining a semi-flow line $\xi$ with $\xi (T)=q$. This would amount to solve the Cauchy problem for the heat equation in backward time, a problem well known to be ill defined in general: Indeed any non-smooth element $q\in {\fancyscript{D}}_\gamma \subset W^{1,2}$ cannot be reached, since the point $\xi (T)$ on any heat flow trajectory $\xi$ is necessarily a smooth loop in $M$—due to the strongly regularizing effect of the heat flow for $T>0$; see e.g. [21]. However, consider the splitting $X=X^-\oplus X^+$ in unstable and stable tangent spaces. In Sect. 2.3 we will see that each element of $X^-$ is smooth. So specifying only the $X^-$ part of the endpoint does not contradict regularity to start with. The key idea is to introduce the notion of a mixed Cauchy problem: Apart from time $T$ only the stable part $z_+$ of the initial point is prescribed—in exchange of prescribing in addition the unstable part $q_u$ of the end point; see Fig. 3. Indeed the representation formula in Proposition 2 shows that the mixed Cauchy problem is equivalent to the usual Cauchy problem with initial value $z$. Since the latter admits a unique solution, so does the mixed Cauchy problem.

Fig. 3

Data $(T,q_u,z_+)$ for mixed Cauchy problem

1.3 Outlook

To put the backward $\lambda$-lemma and the associated stable foliations [20] in perspective recall the celebrated proof by Palis in his 1967 PhD thesis [10] of Andronov–Pontryagin structural stability of hyperbolic dynamical systems in small dimensions. Key innovations and tools in his proof were the notions of stable and unstable foliations which led to numerous applications ever since.

Another interesting perspective of the backward $\lambda$-lemma is that, to the best of our knowledge, it provides the first backward time information concerning the heat flow—apart from the obvious backward flow on the (finite dimensional) unstable manifolds. In fact the backward $\lambda$-lemma provides backward time information on open subsets.

Going from (1) and $W^{1,2}$ to general semilinear parabolic PDEs and $W^{k,p}$ will be investigated elsewhere.

1.4 Application

The method in [19, 20] to construct a Morse filtration of the loop space is inspired by Conley theory [4]. For reals ${\varepsilon },\tau >0$ denote by $N$ the path connected component of $x$ of the open set $\{\gamma \in \varLambda M\mid {\fancyscript{S}}_V(\gamma ) <{\fancyscript{S}}_V(x)+{\varepsilon }, {\fancyscript{S}}_V(\varphi _\tau \gamma )>{\fancyscript{S}}_V(x)-{\varepsilon }\}$. For ${\varepsilon }>0$ small and $\tau >0$ large the closed subset $L:=\{\gamma \in N\mid {\fancyscript{S}}_V(\varphi _{2\tau }\gamma ) \le {\fancyscript{S}}_V(x)-{\varepsilon }\}$ of $N$ is an exit set of $N$ and $(N,L)$ is a Conley pair for the semi-flow invariant set $\{x\}$; see [20, 21]. Concerning the Morse filtration a fundamental step is to prove that relative singular homology is given by

$$\begin{aligned} \mathrm{H}_\ell (N,L) \simeq \left\{ \begin{array}{l@{\quad }l} {\mathbb {Z}}, &{} \ell =k:=\mathrm{ind}(x),\\ 0, &{} \text {otherwise.} \end{array}\right. \end{aligned}$$

Because the part of $N$ in the unstable manifold is an open $k$ disk bounded by the (relatively) closed annulus $L\cap W^u(x)$, the relative homology of these parts has the required property and it suffices to show that $(N\cap W^u(x),L\cap W^u(x))$ is a deformation retract of $(N,L)$. Observe that $N$ contains the ascending disk $W^s_{\varepsilon }(x)$—from now on abbreviated $W^s_{\varepsilon }$—whose part in the unstable manifold is precisely the critical point $x$ itself. Thus on $W^s_{\varepsilon }$ the semi-flow $\varphi _s$ itself provides the desired deformation. Obviously this fails on the complement of the ascending disk. Now the backward $\lambda$-lemma comes in. It naturally endows $(N,L)$, as we show in [20], with the structure of a codimension $k$ foliation whose leaves $N(\gamma _u)$ are parametrized by $\gamma _u\in N\cap W^u(x)$. Furthermore, each leaf is diffeomorphic to a neighborhood $U_{\gamma _u}$ of $W^s_{\varepsilon }$ in $W^s(x)$. The leaf through $x$ is given by $N(x)=W^s_{\varepsilon }=U_x(W^s_{\varepsilon })$. These diffeomorphisms, denoted by

$$\begin{aligned} \varPsi _{\gamma _u}:U_{\gamma _u}(W^s_{\varepsilon }) \mathop {\longrightarrow }\limits ^{\simeq \,\,} N(\gamma _u) ,\qquad \varPsi _{\gamma _u}(x)=\gamma _u ,\qquad \varPsi _x=id_{W^s_{\varepsilon }}, \end{aligned}$$

allow to extend to all of $N$ the desirable deformation property provided by $\varphi _s$ on $W^s_{\varepsilon }$. Indeed pick $\gamma \in N$. By the foliation property $\gamma$ lies on some leaf, say on $N(\gamma _u)$. Now the map $\theta _s(\gamma ) :=\varPsi _{\gamma _u}\circ \varphi _s \circ {\varPsi _{\gamma _u}}^{-1}(\gamma )$ for $s\in [0,\infty ]$ deforms $N$ onto its part in the unstable manifold. So we are done. Well, note the subtlety arising due to the deformation having to take place entirely in $N$ which is equivalent to invariance of $U_{\gamma _u}(W^s_{\varepsilon })$ under $\varphi _s$. For $U_x(W^s_{\varepsilon })=W^s_{\varepsilon }$ this follows immediately from the fact that the action decreases along the heat flow. Since $\dim U_{\gamma _u}(W^s_{\varepsilon })=\infty$, the general case is non-trivial. Apart from the Palais–Smale condition, the analytic properties of the graph maps ${\fancyscript{G}}^T_\gamma$ provided by Theorems  and 2 enter heavily. We refer to [20] for details and to [19] for a survey.

2 Toolbox

Throughout we fix a nondegenerate critical point $x$ of ${\fancyscript{S}}_V:\varLambda M\rightarrow {\mathbb {R}}$. Representing the Hessian of ${\fancyscript{S}}_V$ at $x$ with respect to the $L^2$ inner product on the loop space gives rise to the Jacobi operator $A_x$ defined by

$$\begin{aligned} A_x\xi =-\nabla {}_{t}\nabla {}_{t}\xi -R(\xi ,\dot{x})\dot{x} -\nabla {}_{\xi }\nabla V_t(x) \end{aligned}$$

(2)

for every smooth vector field $\xi$ along the loop $x$. Here $R$ denotes the Riemannian curvature tensor. Viewed as unbounded operator on a general Sobolev space $W^{k,q}:=W^{k,q}(S^1,x^*TM)$ with dense domain $W^{k+2,q}$, where $k\in {\mathbb {N}}_0$ and $q\ge 1$, the spectrum of $A_x$ does not depend on $(k,q)$ and takes the form of a sequence of real eigenvalues (counting multiplicities)

$$\begin{aligned} \lambda _1\le \lambda _2\le \cdots \le \lambda _k<0< \lambda _{k+1}\le \lambda _{k+2}\le \cdots \end{aligned}$$

(3)

which converges to $\infty$. Calculation of the spectrum is standard: One picks the Hilbert space case $(k,q)=(0,2)$ and proves first that $A_x$ admits a compact self-adjoint resolvent. In the second step it remains to prove $C^\infty$ regularity of eigenfunctions. The spectral gap $(0,d)$ of $A_x$ is determined by

$$\begin{aligned} d:=dist\left( 0,\sigma (A)\right) =\min \{-\lambda _k,\lambda _{k+1}\}>0. \end{aligned}$$

(4)

By $\sigma _\pm$ we denote the positive and negative part of the spectrum of $A_x$. Note that nondegeneracy of the critical point $x$ means that zero is not in the spectrum of $A_x$. Equivalently $x$ is a hyperbolic fixed point of $\varphi _s$ whenever $s>0$, that is the spectrum of the linearized flow $d\varphi _s(x)$ does not contain $1$. The Morse index of $x$ is the number $k$ of negative eigenvalues of $A_x$ counted with multiplicities.

It is worthwhile to mention some of the useful properties enjoyed by the action functional: It strictly decreases along non-constant heat flow trajectories. It is bounded below and satisfies the Palais–Smale condition.

In the following subsections we provide the analytical tools required in the proof of the backward $\lambda$-lemma. Apart from Lemma 1 they are all well known, surely by the experts, and so we simply list them without proofs. On the other hand, some are difficult to find in the literature, e.g. sectoriality of $A_x$ in the relevant periodic case. So here is some good news for non-experts:

Convention The proof of any assertion attributed well known in Sect. 2 is given in [21]. The same holds for facts stated without reference.

2.1 Local semi-flow

Recall that ${\fancyscript{U}}=W^u\times {\fancyscript{O}}^+$ by Hypothesis 1. Any path $[0,T]\ni s\mapsto u_s$ in the neighborhood ${\fancyscript{U}}(x):=\varPhi ({\fancyscript{U}})$ of $x$ in the Hilbert manifold $\varLambda M$ corresponds to a path $\zeta :[0,T]\rightarrow {\fancyscript{U}}$, $s\mapsto \zeta (s)$, determined uniquely by the identity $u_s=\exp _{x}\zeta (s)=:\varPhi (\zeta (s))$ pointwise for $t\in S^1$. Applying the operators ${\partial }_s$ and $\nabla {}_{t}\nabla {}_{t}$ to this identity transforms the Cauchy problem on $\varLambda M$ associated to (1) into the equivalent Cauchy problem

$$\begin{aligned} \frac{d}{ds}\zeta (s)+A_x\zeta (s) =f(\zeta (s)),\qquad \zeta (0)=z:=\varPhi ^{-1}(\gamma )\in {\fancyscript{U}}, \end{aligned}$$

(5)

for maps $\zeta :[0,T]\rightarrow {\fancyscript{U}}\subset X=W^{1,2}(S^1,x^*TM)$ where $T$ depends on $z\in {\fancyscript{U}}$ and $A_x$ denotes the Jacobi operator (2) on $W^{1,2}$ with dense domain $W^{3,2}$. The solution to (5) defines the local semi-flow $\phi _sz:=\zeta (s)$ on ${\fancyscript{U}}$ that represents the heat flow. The nonlinearity

$$\begin{aligned} f:X\supset {\fancyscript{U}}\rightarrow Y ,\qquad X=W^{1,2} ,\qquad Y=L^1, \end{aligned}$$

actually maps $W^{1,2p}$ to $L^p$ for $p\ge 1$ and is given by the identity

$$\begin{aligned} f(\zeta )&= E_2(x,\zeta )^{-1} \Bigl ( E_{11}(x,\zeta )\bigl (\dot{x},\dot{x}\bigr ) +2E_{12}(x,\zeta ) \bigl (\dot{x},\nabla {}_{t}\zeta \bigr )\nonumber \\&\quad +E_{22}(x,\zeta ) \bigl (\nabla {}_{t}\zeta , \nabla {}_{t}\zeta \bigr ) +\nabla V_t(\exp _x\zeta ) -E_1(x,\zeta )\,\nabla V_t(x) \Bigr ) \nonumber \\&\quad -R(\zeta ,\dot{x})\dot{x}-\nabla {}_{\zeta }\nabla V_t(x) \end{aligned}$$

(6)

pointwise at $(s,t)$. To arrive at this form of $f$ we used the well known covariant partial derivatives of the exponential map $E(q,v):=\exp _q v$. These are multilinear maps

$$\begin{aligned} E_{i_1\ldots i_j}(q,v):\left( T_qM\right) ^{\times j} \rightarrow T_{\exp _q v}M \end{aligned}$$

which depend smoothly on $(q,v)\in TM$ for each $j\in {\mathbb {N}}$. Those up to order two are characterized by the identities

$$\begin{aligned} \tfrac{d}{dt}\exp _\gamma (\xi )&= E_1(\gamma ,\xi ){\partial }_t\gamma +E_2(\gamma ,\xi )\nabla {}_{t}\xi \\ \nabla {}_{t}\left( E_1(\gamma ,\xi )\eta \right)&= E_{11}(\gamma ,\xi )\left( \eta ,{\partial }_t \gamma \right) +E_{12}(\gamma ,\xi )\left( \eta ,\nabla {}_{t}\xi \right) +E_1(\gamma ,\xi )\nabla {}_{t}\eta \\ \nabla {}_{t}\left( E_2(\gamma ,\xi )\eta \right)&= E_{21}(\gamma ,\xi )\left( \eta ,{\partial }_t \gamma \right) +E_{22}(\gamma ,\xi )\left( \eta ,\nabla {}_{t}\xi \right) +E_2(\gamma ,\xi )\nabla {}_{t}\eta \end{aligned}$$

whenever $\gamma :{\mathbb {R}}\rightarrow M, t\mapsto \gamma (t)$, is a smooth curve in $M$ and $\xi ,\eta$ are smooth vector fields along $\gamma$. These covariant derivatives satisfy

$$\begin{aligned} E_1(q,0)=E_2(q,0)={\small 1}\!\!1 ,\quad E_{11}(q,0)=E_{21}(q,0)=E_{22}(q,0)=0, \end{aligned}$$

(7)

and admit symmetries

$$\begin{aligned} E_{12}(q,z)(v,w) =E_{21}(q,z)(w,v) ,\quad E_{22}(q,z)(v,w) =E_{22}(q,z)(w,v), \end{aligned}$$

and

$$\begin{aligned} E_{11}(q,z)(v,w) -E_{11}(q,z)(w,v) =E_{2}(q,z) R(v,w)z \end{aligned}$$

for all $q\in M$ and $z,v,w\in T_qM$. Furthermore, it holds that

$$\begin{aligned} E_{112}(\gamma ,0) (\dot{\gamma },\dot{\gamma },\xi ) :={\textstyle \left. \frac{D}{d\tau }\right| }_{\tau =0} E_{11}(\gamma ,\tau \xi )(\dot{\gamma },\dot{\gamma }) =R(\xi ,\dot{\gamma })\dot{\gamma }\end{aligned}$$

(8)

pointwise for every $t\in {\mathbb {R}}$. For more details see e.g. [21, Appendix].

After all what is the advantage of reformulating the Cauchy problem? Obviously the linear structure of $X$ to start with. However, the really great features are (a)  the spectral splitting $X\simeq X^-\oplus X^+$ induced by $A_x$ is preserved by the semigroups of Sect. 2.3 and (b) the part $X^-$ is of finite dimension $k$ and consists of smooth elements.

2.2 Lipschitz estimate for the nonlinearity

Lemma 1

(Locally Lipschitz) There are constants $\rho _0,\kappa _*>0$ and a continuous nondecreasing function $\kappa$ on the interval $[0,\rho _0]$ with $\kappa (0)=0$ such that the following is true for any constant $p\ge 1$. In the Sobolev space $W^{1,2p}(S^1,x^*TM)$ consider the closed ball ${\fancyscript{B}}^{1,2p}_{\rho _0}$ of radius $\rho _0$. Then ${\fancyscript{B}}^{1,2p}_{\rho _0}\subset {\fancyscript{U}}$ and the nonlinearity $f:{\fancyscript{B}}^{1,2p}_{\rho _0}\rightarrow L^p$ given by (6) is of class $C^1$ and satisfies $f(0)=0, df(0)=0$, and

$$\begin{aligned} \left\| f(\xi )-f(\eta )\right\| _p&\le \kappa (\rho ) \left\| \xi -\eta \right\| _{1,2p},\\ \left\| df(\xi )v-df(\eta )v\right\| _p&\le \kappa _* \left\| \xi -\eta \right\| _{1,2p} \left\| v\right\| _{1,2p}, \end{aligned}$$

whenever $\mathopen \Vert \xi \mathclose \Vert _{1,2p},\mathopen \Vert \eta \mathclose \Vert _{1,2p} \le \rho <\rho _0$ and $v\in W^{1,2p}$.

Corollary 1

The assumptions of Lemma  1 imply that $\mathopen \Vert df(\xi )v\mathclose \Vert _p \le \kappa (\rho ) \mathopen \Vert v\mathclose \Vert _{1,2p}$ whenever $v\in W^{1,2p}$ and $\mathopen \Vert \xi \mathclose \Vert _{1,2p}\le \rho <\rho _0$.

Proof

Use that $df(\xi )v =\lim _{\tau \rightarrow 0}\frac{f(\xi +\tau v)-f(\xi )}{\tau }$ and apply Lemma 1. $\square$

Remark 4

• (a) That $\kappa (\rho )$ is nondecreasing in $\rho$ is used to prove the assertion of Theorem 3 that at the fixed point $0$ the stable manifold is tangent to $X^+$.

• (b) The Lipschitz estimate for $df$ with constant $\kappa _*$ is required, firstly, to prove that the graph map ${\fancyscript{G}}^T_\gamma$ is of class $C^1$ in $T$ and, secondly, to prove uniform convergence of its derivative to the derivative of the stable manifold graph map, as $T\rightarrow \infty$; see proofs of Theorem 1 step 4 and Theorem 2 step II.

• (c) While Lemma 1 is used mainly in case $p=1$ the fundamental step in Sect. 1.4, carried out in [20], requires Lemma 1 for $p=2$.

Proof

(Lipschitz Lemma 1) Fix $p\ge 1$ and observe that $\mathopen \Vert \cdot \mathclose \Vert _\infty \le c_\infty \mathopen \Vert \cdot \mathclose \Vert _{1,2} \le c_\infty \mathopen \Vert \cdot \mathclose \Vert _{1,2p}$ for some constant $c_\infty >0$. The last step uses Hölder’s inequality and $\mathrm {vol}(S^1)=1$. By $\iota >0$ we denote the injectivity radius of the closed Riemannian manifold $M$. Fix $\rho _0\in (0,\iota /8c_\infty )$ sufficiently small such that the ball ${\fancyscript{B}}_{\rho _0}:={\fancyscript{B}}_{\rho _0}^{1,2}$ in $W^{1,2}$ of radius $\rho _0$ is contained in ${\fancyscript{U}}$. From now on assume that $\rho \in [0,\rho _0)$ and $\xi ,\eta \in W^{1,2p}$ satisfy $\mathopen \Vert \xi \mathclose \Vert _{1,2p},\mathopen \Vert \eta \mathclose \Vert _{1,2p}\le \rho$. Note that $\xi \in {\fancyscript{U}}$ and $\mathopen \Vert \xi \mathclose \Vert _\infty \le c_\infty \rho <\frac{\iota }{8}$ and similarly for $\eta$. So both $\xi$ and $\eta$ take values in the compact subset $D_\rho \subset TM$ consisting of all pairs $(q,v)$ such that $q\in M$ and $v\in T_qM$ satisfies $\mathopen |v\mathclose |\le 4c_\infty \rho$. Note that ${D}_0$ is the zero section.

To see that $f(0)=0$ use (6) and (7). Use in addition (8) to prove that $df(0)\zeta :=\frac{d}{d\tau }f(\tau \zeta )=0$. Abbreviate $X:=\eta -\xi$ to obtain that

$$\begin{aligned} f(\xi )-f(\eta )&= \left( E_2(x,\xi )^{-1} E_{11}(x,\xi ) -E_2(x,\eta )^{-1} E_{11}(x,\eta )\right) \bigl (\dot{x},\dot{x}\bigr ) +R(X,\dot{x})\dot{x}\\&+2\left( E_2(x,\xi )^{-1} E_{21}(x,\xi )\nabla {}_{t}\xi -E_2(x,\eta )^{-1} E_{21}(x,\eta )\nabla {}_{t} \eta \right) \dot{x}\\&+E_2(x,\xi )^{-1} E_{22}(x,\xi ) \bigl (\nabla {}_{t}\xi ,\nabla {}_{t} \xi \bigr ) -E_2(x,\eta )^{-1} E_{22}(x,\eta ) \bigl (\nabla {}_{t}\eta , \nabla {}_{t}\eta \bigr )\\&+E_2(x,\xi )^{-1} \nabla V_t(\exp _{x}\xi ) -E_2(x,\eta )^{-1} \nabla V_t(\exp _{x}\eta ) +\nabla {}_{X}\nabla V_t(x)\\&-\left( E_2(x,\xi )^{-1} E_1(x,\xi ) -E_2(x,\eta )^{-1} E_1(x,\eta )\right) \nabla V_t(x) \end{aligned}$$

pointwise at every $t\in S^1$. We denote the last five lines of the formula above by $I$ through $V$, respectively, and deal with each one separately. For now think of $\xi$ as a fixed parameter and view $\eta (X)=\xi +X$ as a function of $X$. Then each line becomes a (smooth) function of $X(t)$ depending on additional quantities such as certain derivatives of $\xi$, $X$, and $x$ all evaluated at $t$. For instance, term $I$ becomes the identity

$$\begin{aligned} I(X) =\left( E_2(x,\xi )^{-1}E_{11}(x,\xi ) -E_2(x,\eta (X))^{-1}E_{11}(x,\eta (X)) \right) \bigl (\dot{x},\dot{x}\bigr ) +R(X,\dot{x})\dot{x} \end{aligned}$$

pointwise at every $t\in S^1$. Straighforward calculation shows that

$$\begin{aligned} dI(X) Y&= \left. \tfrac{D}{d\tau }\right| _{\tau =0} I(X+\tau Y)\\&= \bigl (E_2(x,\eta (X))\, \bigr )^{-1} E_{22}(x,\eta (X)) \Bigl (E_2(x,\eta (X))^{-1} E_{11}(x,\eta (X)) \left( \dot{x},\dot{x}\right) , Y\Bigr )\\&-E_2(x,\eta (X))^{-1} E_{112}(x,\eta (X)) \left( \dot{x},\dot{x},Y\right) +R(Y,\dot{x})\dot{x} \end{aligned}$$

pointwise at every $t\in S^1$. Note that $\eta (\sigma X)=\sigma \eta +(1-\sigma )\xi$, for $\sigma \in [0,1]$ and pointwise in $t$, takes values in ${D}_{\rho /2}\subset {D}_\rho \subset {D}_{\rho _0}$. Note further that $I(0)=0$. Hence by Taylor’s theorem there is a constant $\sigma =\sigma (t)\in [0,1]$ such that

$$\begin{aligned} \left| I(X)\right| =\left| dI(\sigma X) X\right|&\le \left\| {E_2}^{-1}\right\| _{L^\infty ({D}_{\rho _0})}^2 \left\| E_{22}\right\| _{L^\infty ({D}_\rho )} \left\| E_{11}\right\| _{L^\infty ({D}_\rho )} \left| \dot{x}\right| ^2\left| X\right| \\&\quad +\left\| {E_2}^{-1} E_{112}\left( *,*,\cdot \right) -R(\cdot ,*) *\right\| _{L^\infty ({D}_\rho )} \left| \dot{x}\right| ^2\left| X\right| \\&=: \kappa _1(\rho )\left| \dot{x}\right| ^2\left| X\right| \end{aligned}$$

pointwise at every $t\in S^1$. The function $\kappa _1$ depends continuously on $\rho \in [0,\rho _0]$ and $\kappa _1(0)=0$ by the curvature identity (8) and since $E_{ij}(\cdot ,0)=0$ for $i,j\in \{1,2\}$ by (7). By the a priori estimate [18, Theorem 12] applied to the constant heat flow trajectory $u(s)\equiv x$ there is a constant $C=C(V,{\fancyscript{S}}_{\fancyscript{V}}(x))$ such that $\mathopen |\dot{x}(t)\mathclose |\le \mathopen \Vert \dot{x}\mathclose \Vert _\infty \le C$. By Hölder’s inequality $\mathopen \Vert gh\mathclose \Vert _p\le \mathopen \Vert g\mathclose \Vert _{2p}\mathopen \Vert h\mathclose \Vert _{2p}$ we obtain the desired Lipschitz estimate for term one, namely $\mathopen \Vert I(X)\mathclose \Vert _p \le \kappa _1(\rho )\mathopen \Vert \dot{x}\mathclose \Vert _{2p}^2 \mathopen \Vert X\mathclose \Vert _\infty \le c_\infty \kappa _1(\rho )\mathopen \Vert \dot{x}\mathclose \Vert _\infty ^2 \mathopen \Vert \xi -\eta \mathclose \Vert _{1,2p}$. Indeed the constant depends on $\rho$, but not on $p$. We did not pull out $\mathopen \Vert \dot{x}\mathclose \Vert _\infty$ right in the first step in order to illustrate how Hölder’s inequality serves to deal with first order squares. The argument for terms two through five is analogous; see [21] for details. Here first order squares of the form $\mathopen |\nabla {}_{t} X\mathclose |^2$ appear.

To see that $f$ is of class $C^1$ observe that $df(\xi ) X =-dI(0)X-\cdots -dV(0) X$. Careful inspection term by term then shows that each of the five terms in this sum depends continuously on $\xi$ with respect to the $W^{1,2p}$ topology.

It remains to prove the second Lipschitz estimate, that is the one for the difference of derivatives $df(\xi )-df(\eta )$. Unfortunately, the number of terms appearing during the calculation is rather large. Fortunately, we are only claiming existence of a constant $\kappa _*$. Straightforward calculation shows that

$$\begin{aligned} df(\xi )v&= -R(v,\dot{x})\dot{x} -E_2(x,\xi )^{-1} \Bigl [ E_{22}(x,\xi )\left( E_2(x,\xi )^{-1} E_{11}(x,\xi )\left( \dot{x},\dot{x}\right) \!, v\right) \\&\quad -E_{22}(x,\xi ) \bigl (E_2(x,\xi )^{-1} \bigl [ 2E_{12}(x,\xi )\left( \dot{x},\nabla {}_{t}\xi \right) +E_{22}(x,\xi )\left( \nabla {}_{t}\xi ,\nabla {}_{t}\xi \right) \bigr ] ,v\bigr )\\&\quad -E_{22}(x,\xi )\left( E_2(x,\xi )^{-1} \nabla V_t(\exp _x \xi ), v\right) +E_{22}(x,\xi )\left( \nabla V_t(x),v\right) \\&\quad +E_{112}(x,\xi )\left( \dot{x},\dot{x},v\right) +2E_{122}(x,\xi )\left( \dot{x},\nabla {}_{t}\xi ,v\right) +2E_{12}(x,\xi )\left( \dot{x},\nabla {}_{t} v\right) \\&\quad +E_{222}(x,\xi ) \left( \nabla {}_{t}\xi ,\nabla {}_{t}\xi ,v\right) +2E_{22}(x,\xi )\left( \nabla {}_{t}\xi ,\nabla {}_{t} v\right) \\&\quad +{\textstyle \left. \frac{D}{d\tau }\right| _{\tau =0}} \nabla V_t(\exp _x (\xi +\tau v)) -E_{12}(x,\xi )\left( \nabla V_t(x),v\right) \Bigr ] -\nabla {}_{v}\nabla V_t(x). \end{aligned}$$

Denote the 14 terms in this sum by $\sum _{j=1}^{14}H_j(\xi )v$. For $X:=\eta -\xi$ set $2F_j(X)v:=H_j(\xi )v-H_j(\xi +X)v$. For instance, consider $F_8$. We get that

$$\begin{aligned}&dF_8(X)( v,Y)\\&=\left. \tfrac{D}{d\tau }\right| _{\tau =0} \bigl [ E_2(x,\xi +X+\tau Y)^{-1} E_{122}(x,\xi +X+\tau Y) \left( \dot{x},\nabla {}_{t}\left( \xi +X+\tau Y\right) \!,v\right) \bigr ]\\&=-{E_2}^{-1}E_{22}\bigl ({E_2}^{-1}E_{122} \left( \dot{x},\nabla {}_{t}\xi +\nabla {}_{t} X,v\right) ,Y\bigr )\\&\quad +{E_2}^{-1}E_{1222} \left( \dot{x},\nabla {}_{t}\xi +\nabla {}_{t} X,v,Y\right) +{E_2}^{-1}E_{122} \left( \dot{x},\nabla {}_{t} Y,v\right) \end{aligned}$$

where the maps are evaluated at $(x,\xi +X)$. Since $F_8(0)=0$ there is by Taylor’s theorem, pointwise at every $t\in S^1$, a constant $\sigma =\sigma (t)\in [0,1]$ such that

$$\begin{aligned} \left\| 2F_8(X)v\right\| _p&= \left\| 2dF_8(\sigma X)\left( v,X\right) \right\| _p\\&\le \left\| {E_2}^{-1}\right\| _{L^\infty _{\rho _0}} \Bigl ( \left\| {E_2}^{-1}\right\| _{L^\infty _{\rho _0}} \left\| E_{22}\right\| _{L^\infty _{\rho }} \left\| E_{122}\right\| _{L^\infty _{\rho _0}} +\left\| E_{1222}\right\| _{L^\infty _{\rho _0}} \Bigr )\\&\quad \cdot \left\| \dot{x}\right\| _{2p} \Bigl (\sigma \left\| \eta \right\| _{1,2p} +(1-\sigma )\left\| \xi \right\| _{1,2p}\Bigr ) \left\| v\right\| _\infty \left\| \xi -\eta \right\| _\infty \\&\quad +\left\| {E_2}^{-1}\right\| _{L^\infty _{\rho _0}} \left\| E_{122}\right\| _{L^\infty _{\rho _0}} \left\| \dot{x}\right\| _{2p} \left\| \xi -\eta \right\| _{1,2p} \left\| v\right\| _\infty \end{aligned}$$

where we abbreviated $L^\infty _{\rho }:=L^\infty ({D}_{\rho })$. Since $\left\| \dot{x}\right\| _{2p}\le \left\| \dot{x}\right\| _\infty \le C$ this proves the Lipschitz estimate for term eight. Note that $F_1\equiv 0\equiv F_{14}$. The estimates for the other 11 $F$-terms follow similarly. This proves the Lipschitz Lemma 1. $\square$

2.3 Semigroups and splittings

For any $q\in [1,\infty )$ and $k\in {\mathbb {N}}_0$ the negative Jacobi operator $-A:=-A_x$ on $Z:=W^{k,q}$ with dense domain $W^{k+2,q}$ and given by (2) is sectorial and therefore generates the strongly continuous semigroup $e^{-sA}\in {\fancyscript{L}}(Z)$ given by

$$\begin{aligned} e^{-sA}:=\frac{1}{2\pi i} \int \limits _{\gamma } e^{s\varLambda } R(\lambda ,-A) \, d\lambda ,\qquad \forall s>0, \end{aligned}$$

(9)

and by $e^{0A}:={\small 1}\!\!1_Z$ for $s=0$. Here $R$ denotes the resolvent and $\gamma :{\mathbb {R}}\rightarrow {\mathbb {C}}\cup \{\infty \}$ is a suitable loop inside the resolvent set $\rho (-A)$. Sectoriality of $-A$ is well known, but a proof for the periodic domain $S^1$ is hard to find, unlike for the domain ${\mathbb {R}}$. So we provide the details in [21]. By nondegeneracy of $x$ the operator $-A$ is hyperbolic, that is its spectrum and the imaginary axis $i{\mathbb {R}}$ are disjoint. Pick a counter-clockwise oriented circle $\gamma ^+:S^1\rightarrow (0,\infty )\times i{\mathbb {R}}$ which encloses precisely the positive part $\{-\lambda _k,\ldots ,-\lambda _1\}$ of the spectrum of $-A$. The linear operators

$$\begin{aligned} {\pi _-} :=\frac{1}{2\pi i}\int \limits _{\gamma ^+} R(\lambda ,-A)\, d\lambda ,\qquad {\pi _+}:={\small 1}\!\!1-{\pi _-}, \end{aligned}$$

(10)

are elements of ${\fancyscript{L}}(Z)$ called spectral projections, because $(\pi _\pm )^2=\pi _\pm$.

We collect key facts of semigroup theory. By boundedness of $\pi _\pm$ the images

$$\begin{aligned} Z^\pm :=\mathrm{range\, }{\pi _\pm }, \end{aligned}$$

(11)

are closed (Banach) subspaces. As a vector space $Z^-$ is spanned by $k$ eigenfunctions corresponding to the $k=\mathrm{ind}(x)$ negative eigenvalues of $A$, in particular $Z^-\subset C^\infty (S^1,x^*TM)$. In contrast $Z^+$ is the $W^{k,q}$ closure of the sum of eigenspaces coresponding to positive eigenvectors of $A$. Thus $Z^+=Z^+(k,q)$. The obvious identity $\pi _-\pi _+=\pi _+\pi _-=0$ shows that

$$\begin{aligned} Z\simeq Z^-\oplus Z^+. \end{aligned}$$

Moreover, this splitting is preserved by $A$ and the restrictions of $A$ to the Banach subspaces $Z^\pm$ are denoted by $A^\pm$. Since the semigroup $e^{-sA}$ preserves both subspaces $Z^\pm$, the restrictions $e^{-sA}|_{Z^\pm }$ are semigroups as well. They are called subspace semigroups. On the other hand, the restrictions $-A^\pm$ themselves are sectorial operators on the Banach spaces $Z^\pm$ with dense domains $Z^\pm \cap D(A)$. Therefore they generate strongly continuous semigroups $e^{-sA^\pm }$ on $Z^\pm$. But these coincide with the subspace semigroups due to the resolvent identity $R(\lambda ,-A)|_{Z^\pm }=R(\lambda ,-A^\pm )$ which holds for every $\lambda$ in the resolvent set $\rho (-A)\subset \rho (-A^\pm )$. The upshot is the formula

$$\begin{aligned} e^{-sA} =e^{-sA^-}\oplus e^{-sA^+} ,\qquad s\ge 0. \end{aligned}$$

Note that $D(A)\cap Z^-=Z^-$ by smoothness. Thus $A^-\in {\fancyscript{L}}(Z^-)$ and the series

$$\begin{aligned} e^{-sA^-} :=\sum _{k=0}^\infty \frac{(-sA^-)^k}{k!}, \qquad \forall s\in {\mathbb {R}}, \end{aligned}$$

(12)

is well defined providing a norm continuous group which for $s\ge 0$ coincides with the subspace semigroup $e^{-sA}|_{Z^-}$. For negative times $s\le 0$ it decays exponentially $\mathopen \Vert e^{-sA^-}\mathclose \Vert _{{\fancyscript{L}}(Z^-)}\le ce^{-s\lambda _k}\le ce^{s\mu }$. The constructions above “commute” with Sobolev embeddings $W^{\ell ,r}\hookrightarrow W^{k,q}$. For $\pi _\pm$ this is again a consequence of a resolvent identity.

Proposition 1

Fix integers $\ell \ge k\ge 0$ and constants $r\ge q\ge 1$. Consider the Jacobi operator $A:=A_x$ on $Z:=W^{k,q}$ with dense domain $W^{k+2,q}$ and its restrictions $A^\pm$ to the closed subspaces $Z^\pm :=\pi _\pm (Z)$. Fix $\mu >0$ in the spectral gap (4) of $A$. Then there is a constant $c=c(\ell ,k,r,q,\mu )$ such that

• (a) The operator $-A$ on $L^1$ generates the strongly continuous semigroup $e^{-sA}$ on $L^1$ given by (9). Both commute with the spectral projections $\pi _\pm$ in (10).

• (b) The subspace semigroup $e^{-sA}|$ on $Z\subset L^1$ coincides with the strongly continuous semigroup $e^{-sA|}$ generated by the restriction $-A|$ of $-A$ to $Z\subset L^1$. Restricting the semigroup and restricting $A$ both commute with the spectral projections which themselves satisfy $\pi _\pm (-A|)=\pi _\pm (-A)|$. To simplify notation we omit from now on the slash sign $\mid$.

• (c) The restriction of $-A$ to $Z^-$ generates the norm continuous group $e^{-sA^-}$ on $Z^-$ given by the exponential series (12). For positive times this group is equal to the restriction of the semigroup $e^{-sA}$ to $Z^-$. For negative times it holds that

  $$\begin{aligned} \big \Vert e^{-sA^-}\pi _-\big \Vert _{{\fancyscript{L}}(W^{k,q},W^{\ell ,r})} \le ce^{s\mu } ,\quad s\le 0. \end{aligned}$$

  (13)

• (d) Restricting $e^{-sA}$ to $Z^+$ gives a strongly continuous semigroup on $Z^+$ and

  $$\begin{aligned} \left\| e^{-sA}\pi _+\right\| _{{\fancyscript{L}}(W^{k,q},W^{\ell ,r})} \le c s^{-\frac{1}{2}(\frac{1}{q}-\frac{1}{r}+\ell -k)} e^{-s\mu } ,\quad s>0. \end{aligned}$$

  (14)

2.4 The representation formula

Proposition 2

Consider the nonlinearity $f:X\supset {\fancyscript{U}}\rightarrow Y$ given by (6) and the constant $\rho _0$ provided by the Lipschitz Lemma 1. Pick $T>0$ and assume $\xi :[0,T]\rightarrow X$ is a map bounded by $\rho _0$, thus taking values in ${\fancyscript{U}}$. Then the following are equivalent.

• (a) The map $\xi :[0,T]\rightarrow Y$ is the (unique) solution of the Cauchy problem (5) with initial value $\xi (0)$.

• (b) The map $\xi :(0,T]\rightarrow X$ is continuous² and satisfies the integral equation, also called representation formula, given by

  $$\begin{aligned} \xi (s)&= e^{-sA}\pi _+ \xi (0) +\int \limits _0^s e^{-(s-\sigma )A} \pi _+f(\xi (\sigma ))\, d\sigma \nonumber \\&+\, e^{-(s-T)A^-}\pi _- \xi (T) -\int \limits _s^T e^{-(s-\sigma )A^-} \pi _-f(\xi (\sigma ))\, d\sigma \end{aligned}$$

  (15)

  for every $s\in [0,T]$. In the limit $T\rightarrow \infty$ the first term in line two disappears.

2.5 Local stable manifold theorem

Theorem 3

($C^1$ graph) Assume the local setup of Hypothesis 1; see Fig. 4. In particular, consider the hyperbolic fixed point $0$ of the local semi-flow $\phi$ defined by (5) on ${\fancyscript{U}}\subset X$. Then the following is true. There is a closed ball ${\fancyscript{B}}^+\subset X^+$ of radius $r>0$ about $0$ such that a neighborhood of $0$ in the local stable manifold

$$\begin{aligned} W^s(0,{\fancyscript{U}}) :=\left\{ z\in {\fancyscript{U}}\,\big |\, \phi (s,z)\in {\fancyscript{U}}\,\forall s>0 \,\,\,and\, \lim _{s\rightarrow \infty }\phi (s,z)=0 \right\} \end{aligned}$$

(16)

is a graph over ${\fancyscript{B}}^+$, tangent to $X^+$ at $0$. In fact, there is a Lipschitz continuous map

$$\begin{aligned} {\fancyscript{G}}^\infty =( G,id ) :{\fancyscript{B}}^+\rightarrow X^-\times {\fancyscript{B}}^+ ,\qquad G(0)=0 ,\qquad dG(0)=0, \end{aligned}$$

of class $C^1$ such that ${\fancyscript{G}}^\infty ({\fancyscript{B}}^+)$ is a neighborhood of $0$ in $W^s(0,{\fancyscript{U}})$; cf. Fig. 2.

Fig. 4

Local setup

Proposition 3

($L^2$ extension) Assume Theorem 3. Then the linearization $d{\fancyscript{G}}^\infty (z_+):X^+\rightarrow X$ extends to a bounded linear operator on the $L^2$ completions, uniformly in $z_+\in {\fancyscript{B}}^+$. More precisely, it holds that

$$\begin{aligned} \left\| d{\fancyscript{G}}^\infty (z_+) v\right\| _2 \le 2 \left\| v\right\| _2 ,\qquad \left\| d{\fancyscript{G}}^\infty (z_+) v-v\right\| _2 \le \frac{1}{4} \left\| v\right\| _2, \end{aligned}$$

for all $v\in \pi _+(L^2)$ and $z_+\in {\fancyscript{B}}^+$.

The local stable manifold Theorem 3 is well known; see e.g. [8, Theorem 5.2.1] for a proof by the contraction method. In finite dimensions the theorem is also called Hadamard–Perron Theorem [6, 13].

Observe that proofs of Theorem 3 and Proposition 3 arise as special cases of the proofs in Sect. 3, formally set $T=\infty$. Now we recall the contraction method for the stable manifold theorem. Pick a value for each parameter of interest, in our case $z_+\in X^+$. Our object of interest is a heat flow line $\eta :[0,\infty )\rightarrow {\fancyscript{U}}$ whose initial value projects to $z_+$ under $\pi _+$ and which converges to $0$, as $s\rightarrow \infty$. Find a complete metric space, namely

$$\begin{aligned} Z=Z^\rho _\mu :=\Bigl \{\eta \in C^0([0,\infty ),X)\,\,\Big |\,\, \left\| \eta \right\| _{\exp } :=\sup _{s\ge 0} e^{s\frac{\mu }{2}} \left\| \eta (s)\right\| _X \le \rho \Bigr \} \end{aligned}$$

(17)

for suitable constants $\rho$ and $\mu$, and a strict contraction on $Z$, namely

$$\begin{aligned} (\varPsi _{z_+}\eta )(s) = e^{-sA}z_+ +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ f(\eta (\sigma )) d\sigma -\int \limits _s^\infty e^{-(s-\sigma )A^-} \pi _-f(\eta (\sigma )) d\sigma \end{aligned}$$

such that the (unique) fixed point $\eta _{z_+}$ is the initial object of interest. Use the representation formula (15) for $T=\infty$ to see that this is indeed true. In fact this setup works for any $\mu$ in the spectral gap (4) of the Jacobi operator $A:=A_x$, see [21], and for all $\rho >0$ sufficiently small, that is whenever (20) holds. The map

$$\begin{aligned} G: {\fancyscript{B}}^+&\rightarrow X^-, \qquad \qquad \quad {\fancyscript{B}}^+ :=\left\{ z_+\in X^+: \left\| z_+\right\| _X\le \rho /2c \right\} ,\\ z_+&\mapsto \pi _-\left( \eta _{z_+}(0)\right) \end{aligned}$$

has the properties asserted by Theorem 3; here $c=c(\mu )$ is given by Proposition 1.

Remark 5

(Unstable manifold) The contraction method also serves to represent the elements of the local unstable manifold $W^u(0,{\fancyscript{U}})$; see e.g. [8, Theorem 5.2.1, proof of Theorem 5.1.3]. By definition this is the set of end points of all (backward) heat flow lines $\tilde{\eta }$ in ${\fancyscript{U}}$ parametrized by $(-\infty ,0]$ and emanating at time $-\infty$ from $0$. There is a ball ${\fancyscript{B}}^-\subset W^u\subset X^-$ of sufficiently small radius $r>0$ such that the following is true.

Pick $\gamma \in {\fancyscript{B}}^-$ and consider the backward heat flow trajectory $\tilde{\eta }$ which satisfies $\gamma =\tilde{\eta }(0)=\pi _-\tilde{\eta }(0)$. (Backward flow invariance of descending disks and $W^u\subset X^-$ imply that $\tilde{\eta }$ lies completely in $X^-$.) Note that $\tilde{\eta }$ is asymptotic to zero in infinite backward time since $\tilde{\eta }(0)$ lies in a descending disk. By (15) and the uniqueness Theorem 17 in [18] for action bounded backward heat flow solutions $\tilde{\eta }$ is equal to the unique fixed point of the map

$$\begin{aligned} (\varPhi _{\gamma }\tilde{\eta })(s) :=e^{-sA^-}\gamma -\int \limits _s^0 e^{-(s-\sigma )A^-}\pi _- f(\tilde{\eta }(\sigma )) d\sigma +\int \limits _{-\infty }^s e^{-(s-\sigma )A} \pi _+ f(\tilde{\eta }(\sigma )) d\sigma \end{aligned}$$

which acts as a strict contraction on the complete metric space

$$\begin{aligned} \tilde{Z}=\tilde{Z}_{\frac{\mu }{2},\rho } :=\Bigl \{\tilde{\eta }\in C^0((-\infty ,0],X)\,\,\Big |\,\, \left\| \tilde{\eta }\right\| _{\exp } :=\sup _{s\le 0} e^{-s\frac{\mu }{2}} \left\| \tilde{\eta }(s)\right\| _X \le \rho \Bigr \}. \end{aligned}$$

3 Proofs

3.1 Proof of the backward $\lambda$-lemma (Theorem 1)

Uniform exponential convergence in step 6 is the heart of the proof. It relies on a suitable time decomposition of trajectories. Throughout assume

Hypothesis 2

Assume the local setup of Hypothesis 1; see Fig. 4. Consider the constants $\rho _0>0$ and $\kappa _*\ge 1$ and the continuous function $\kappa (\rho )$ with $\kappa (0)=0$ provided by the Lipschitz Lemma 1. Note that ${\fancyscript{B}}_{\rho _0}\subset {\fancyscript{U}}$. Fix $\mu$ in the spectral gap $(0,d)$ given by (4) and a constant $c=c(\mu )\ge 1$ satisfying Proposition 1 for the (finitely many) choices of $(\ell ,k,r,q)$ that will be used in the present proof. We may assume that ³

$$\begin{aligned} \rho _0 c^2\kappa _* \left( \frac{1}{\mu } +\frac{8}{\mu ^\frac{1}{4}} +\frac{6}{\mu ^\frac{5}{4}} \right) \le \frac{1}{8}. \end{aligned}$$

(18)

In Hypothesis 1 (b) we picked $\varkappa \in (0,\rho _0)$ and so the constant ⁴

$$\begin{aligned} T_1=T_1(\varkappa ,\mu ,\rho _0) :=-\frac{2}{\mu }\ln \frac{\varkappa }{\rho _0}> 0 \end{aligned}$$

(19)

is well defined. Assume $\rho \in \left( 0,\frac{1}{2}\rho _0\right]$ is sufficiently small such that

$$\begin{aligned} c^2\kappa (\rho ) \left( \frac{9}{\mu ^\frac{1}{4}} +\frac{4}{3\mu } +\frac{3}{\mu ^\frac{5}{4}} \right) \le \frac{1}{8} \end{aligned}$$

(20)

and such that all points of ${\fancyscript{U}}$ of distance $\le \rho$ to the descending sphere $S^u_{\varepsilon }$ are contained in ${\fancyscript{B}}_{\rho _0}$. Fix a constant $T_2=T_2(c,\mu ,\rho ,{\varepsilon })\ge 0$ such that $8ce^{-\mu T_2/4}\le 1$ and $\phi _{-T_2/8}W^u_{\varepsilon }\subset {\fancyscript{B}}^-:={\fancyscript{B}}_{\rho /2c}\cap X^-$; see Remark 5. ⁵ Set $T_0 :=\max \{T_1,T_2\} > 0$.

Pick $T\ge T_0$ and $\gamma \in S^u_{\varepsilon }$ and consider the infinite dimensional disk ${\fancyscript{D}}_\gamma =\{\gamma \}\times {\fancyscript{B}}^+_\varkappa$. The key observation to represent the preimage ${\phi _T}^{-1}{\fancyscript{D}}_\gamma$ under the time-$T$-map $\phi _T$ as a graph over the stable subspace $X^+$ is the fact that to any pair $(q_u,z_+)\in X^-\oplus X^+$ sufficiently close to zero there corresponds a unique heat flow trajectory $\xi$ whose initial value $\xi (0)$ projects under $\pi _+$ to $z_+$ and whose endpoint at time $T$ projects under $\pi _-$ to $q_u$; see Remark 3. In particular, for $q_u:=\gamma$ any $z_+\in X^+$ near the origin corresponds to a unique heat flow line $\xi =\xi ^T_{\gamma ,z_+}$ which ends at time $T$ in ${\fancyscript{D}}_\gamma$. Because its initial value $\xi (0)$ is of the form $(\pi _-\xi (0),z_+)$, it is natural to define the map $G^T_\gamma (z_+):=\pi _-\xi (0)$ whose graph at $z_+$ reproduces $\xi (0)$. In fact, we prove that for any $z_+\in X^+$ with $\mathopen \Vert z_+\mathclose \Vert \le \rho /2c$ there is precisely one semi-flow line $\xi =\xi _{\gamma ,z_+}^T$ with initial condition $\pi _+ \xi (0)=z_+$ and endpoint condition $\xi (T)\in {\fancyscript{D}}_\gamma$. The latter is equivalent to

$$\begin{aligned} \pi _-\xi (T)=\gamma \quad \wedge \quad \left\| \xi (T)-\gamma \right\| _X\le \varkappa . \end{aligned}$$

(21)

We will see in step 2 that the definition of $T_1$ assures the second condition.

The key step to determine the unique semi-flow line $\xi$ associated to $(T,\gamma ,z_+)$ is to set up a strict contraction on a complete metric space $Z^T$ whose (unique) fixed point is $\xi$. Set

$$\begin{aligned} \left\| \xi \right\| _{\exp } =\left\| \xi \right\| _{\exp ,T} :=\max _{s\in [0,T]} e^{s\frac{\mu }{2}} \left\| \xi (s)\right\| _X \end{aligned}$$

(22)

and for $\gamma _T:=\phi _{-T}\gamma$ define

$$\begin{aligned} Z^T =Z^{T,\gamma }_{\mu /2,\rho } :=\left\{ \xi \in C^0([0,T],X)\,:\left\| \xi -\phi _\cdot \gamma _T\right\| _{\exp } \le \rho \right\} . \end{aligned}$$

(23)

Consider the map $\varPsi ^T=\varPsi ^T_{\gamma ,z_+}$ defined on $Z^T$ by

$$\begin{aligned} \left( \varPsi _{\gamma ,z_+}^T \xi \right) (s)&:= e^{-sA}z_+ +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ f(\xi (\sigma )) \, d\sigma \nonumber \\&+\,e^{-(s-T)A^-}\gamma -\int \limits _s^T e^{-(s-\sigma )A^-}\pi _- f(\xi (\sigma )) \, d\sigma \end{aligned}$$

(24)

for every $s\in [0,T]$. The fixed points of $\varPsi ^T$ correspond to the desired heat flow trajectories by Proposition 2. By step 1 and step 2 below $\varPsi ^T$ is a strict contraction on $Z^T$. Hence by the Banach fixed point theorem it admits a unique fixed point $\xi _{\gamma ,z_+}^T$ and for ${\fancyscript{B}}^+:={\fancyscript{B}}^+_{\rho /2c}\subset X^+$ we define the map

$$\begin{aligned} G^T:S^u_{\varepsilon }\times {\fancyscript{B}}^+\rightarrow W^u\subset X^- ,\qquad (\gamma ,z_+)\mapsto \pi _-\xi _{\gamma ,z_+}^T(0) =:G^T_\gamma (z_+). \end{aligned}$$

(25)

Actually ${\fancyscript{B}}^+$ is the same ball for which the stable manifold Theorem 3 holds true [21].

The proof takes six steps. Fix $\gamma \in S^u_{\varepsilon }$ and $z_+\in {\fancyscript{B}}^+$ and abbreviate $\varPsi ^T=\varPsi _{\gamma ,z_+}^T$.

Step 1

Fix $T\ge 0$. Then the set $Z^T$ equipped with the metric induced by the exp norm is a complete metric space, any $\xi \in Z^T$ takes values in ${\fancyscript{B}}_{\rho _0}$, and $\varPsi ^T$ acts on $Z^T$.

Proof

In case of the compact domain $[0,T]$ the space $C^0([0,T],X)$ is complete with respect to the supremum norm, hence with respect to the exp norm as both norms are equivalent by compactness of $[0,T]$. The subset $Z^T\subset C^0([0,T],X)$ is closed with respect to the exp norm. By the assumption which immediately follows (20) the elements of $Z^T$ take values in ${\fancyscript{B}}_{\rho _0}$, hence in ${\fancyscript{U}}$.

To see that $\varPsi ^T$ acts on $Z^T$ we need to verify that $\varPsi ^T\xi$ is continuous and satisfies the exponential decay condition in (23) whenever $\xi \in Z^T$. By definition $\varPsi ^T\xi$ is a sum of four terms. That each one is continuous as a map $[0,T]\rightarrow X$ is standard. For terms one, two, and four see step 1 (iii) in the proof of Theorem 3 given in [21]. For term three continuity follows from the definition of the exponential by the power series (12). For latter reference we sketch the argument for term two which we denote by $F(s)$: Continuity of $F:[0,T]\rightarrow X$ and the fact that $F(0)=0$ (used in steps 2 and 3 below) both follow by an analogue of [17, Lemma 9.7 a)] for $-A$ instead of $\Delta$ and with $p=2$; see also [8, Lemma 3.2.1]. The condition to be checked is that the map $\tilde{f} :=\pi _+ \circ f\circ \xi :[0,T]\rightarrow Y^+\hookrightarrow Y$ is continuous and bounded: This is true since $\xi :[0,T]\rightarrow X$ is continuous and bounded by definition of $Z^T$ and so is $f$ by Lemma 1.

We prove exponential decay. For $s\in [0,T]$ consider the heat flow trajectory given by $\phi _s\gamma _T$. By the representation formula of Proposition 2 it satisfies

$$\begin{aligned} \phi _s\gamma _T =\int \limits _0^s e^{-(s-\sigma )A}\pi _+ f(\phi _\sigma \gamma _T)\, d\sigma +e^{-(s-T)A^-}\gamma -\int \limits _s^T e^{-(s-\sigma )A^-}\pi _- f(\phi _\sigma \gamma _T)\, d\sigma . \end{aligned}$$

(26)

Here we used that $\pi _+\gamma _T=0$, because $\gamma$ and therefore $\gamma _T=\phi _{-T}\gamma$ lies in $W^u(0,{\fancyscript{U}})\subset X^-$ by backward flow invariance. By the same argument $\pi _-\phi _T\gamma _T=\pi _-\gamma =\gamma$. By definition (24) of $\varPsi ^T$ and (26) we get for $s\in [0,T]$ the estimate

$$\begin{aligned}&\left\| \left( \varPsi ^T\xi \right) (s)-\phi _s\gamma _T\right\| _X\nonumber \\&\quad \le \left\| e^{-sA}z_+\right\| _X +\int \limits _0^s \left\| e^{-(s-\sigma )A}\pi _+\right\| _{{\fancyscript{L}}(Y,X)} \left\| f(\xi (\sigma ))-f(\phi _\sigma \gamma _T)\right\| _Y d\sigma \nonumber \\&\quad \quad +\int \limits _s^T \left\| e^{-(s-\sigma )A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,X)} \left\| f(\xi (\sigma ))-f(\phi _\sigma \gamma _T)\right\| _Y d\sigma \nonumber \\&\quad \le ce^{-s\mu }\left\| z_+\right\| _X +c\kappa (\rho )e^{-s\frac{\mu }{2}} \left\| \xi -\phi _\cdot \gamma _T\right\| _{\exp }\int \limits _0^s \frac{e^{-(s-\sigma )\frac{\mu }{2}}}{(s-\sigma )^{\frac{3}{4}}}\, d\sigma \nonumber \\&\quad \quad +c\kappa (\rho )e^{-s\frac{\mu }{2}} \left\| \xi -\phi _\cdot \gamma _T\right\| _{\exp }\int \limits _s^Te^{(s-\sigma )\frac{3}{2}\mu }\, d\sigma \nonumber \\&\quad \le \frac{\rho }{2} e^{-s\mu } + c\kappa (\rho ) \left( \frac{8}{\mu ^{1/4}} +\frac{2}{3\mu }\right) \rho e^{-s\frac{\mu }{2}}\le \rho e^{-s\frac{\mu }{2}} \end{aligned}$$

(27)

where the last inequality is by smallness (20) of $\rho$. Inequality two follows by the exponential decay Proposition 1 with constant $c$ and the Lipschitz Lemma 1 for $f$ with Lipschitz constant $\kappa (\rho )$. We multiplied the integrands by $e^{-\sigma \frac{\mu }{2}} e^{\sigma \frac{\mu }{2}}$ to create the exp norms. Inequality three uses $\mathopen \Vert z_+\mathclose \Vert _X\le \frac{\rho }{2c}$ and boundedness of the exp norms by $\rho$ since $\xi \in Z^T$. We also used that

$$\begin{aligned} \int \limits _s^\infty e^{(s-\sigma )\frac{3}{2}\mu } \, d\sigma =\frac{2}{3\mu }. \end{aligned}$$

(28)

To estimate the other integral define $\varGamma (\alpha ):=\int _0^\infty e^{-\tau }\tau ^{\alpha -1}\, d\tau$ for $\alpha >0$. The $\varGamma$ function satisfies $\varGamma (\frac{1}{4}) =4\varGamma (\frac{5}{4})\le 4$ since $\varGamma \le 1$ on the interval $[1,2]$. Hence

$$\begin{aligned} \int \limits _0^s\frac{e^{-(s-\sigma )\frac{\mu }{2}}}{(s-\sigma )^{\frac{3}{4}}} \, d\sigma =\left( \frac{2}{\mu }\right) ^{\frac{1}{4}} \int \limits _0^{s\frac{\mu }{2}} e^{-\tau } \tau ^{\frac{1}{4}-1} \, d\tau \le \frac{2^{\frac{1}{4}}}{\mu ^{\frac{1}{4}}}\, \varGamma (\tfrac{1}{4}) \le \frac{8}{\mu ^{\frac{1}{4}}}. \end{aligned}$$

(29)

$\square$

Step 2

For $T\ge 0$ the map $\varPsi ^T$ acts as a strict contraction on $Z^T$. Each image point $\varPsi ^T\xi$ satisfies the initial condition $\pi _+\left( \varPsi ^T\xi \right) (0)=z_+$ and, if $T\ge T_1$, also the endpoint condition (21), that is $\left( \varPsi ^T\xi \right) (T) \in {\fancyscript{D}}_\gamma =\{\gamma \}\times {\fancyscript{B}}^+_\varkappa$.

Proof

Assume $T\ge 0$ and fix $\xi _1,\xi _2\in Z^T$. Similarly to (27) we obtain that

$$\begin{aligned}&\left\| \left( \varPsi ^T\xi _1\right) (s) -\left( \varPsi ^T\xi _2\right) (s)\right\| _X\nonumber \\&\quad \le \int \limits _0^s\left\| e^{-(s-\sigma )A} \pi _+\right\| _{{\fancyscript{L}}(Y,X)} \left\| f(\xi _1(\sigma )) -f(\xi _2(\sigma ))\right\| _Y d\sigma \nonumber \\&\quad \quad +\int \limits _s^T \left\| e^{-(s-\sigma )A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,X)} \left\| f(\xi _1(\sigma )) -f(\xi _2(\sigma ))\right\| _Y d\sigma \nonumber \\&\quad \le c\kappa (\rho ) \left( \frac{8}{\mu ^{1/4}} +\frac{2}{3\mu } \right) e^{-s\frac{\mu }{2}} \left\| \xi _1-\xi _2\right\| _{\exp } \end{aligned}$$

(30)

for every $s\in [0,T]$. Now use the smallness assumption (20) on $\rho$ to conclude that $\mathopen \Vert \varPsi ^T\xi _1-\varPsi ^T\xi _2\mathclose \Vert _{\exp } \le \frac{1}{2}\mathopen \Vert \xi _1-\xi _2\mathclose \Vert _{\exp }$.

The identities $\pi _+\left( \varPsi ^T\xi \right) (0)=z_+$ and $\pi _-\left( \varPsi ^T\xi \right) (T)=\gamma$ follow from definition (24) of $\varPsi ^T$, the identities $\pi _+\pi _-=\pi _-\pi _+=0$, strong continuity of the semigroups on $X^{-}$ and $X^{+}$ asserted by Proposition 1, continuity and boundedness of both integrands, and $F(0)=0$ by the proof of step 1. Concerning the second endpoint condition in (21) assume $T\ge T_1$ and evaluate (27) at $s=T$ to get

$$\begin{aligned} \left\| \left( \varPsi \xi \right) (T) -\gamma \right\| _X \le \rho e^{-T\frac{\mu }{2}} \le e^{-T_1\frac{\mu }{2}}\rho _0 =\varkappa \end{aligned}$$

where the last step is by definition of $T_1$ in (19). $\square$

Step 3

For $T\ge 0$ the map $G^T:S^u_{\varepsilon }\times {\fancyscript{B}}^+\rightarrow X^-$ defined by (25) is of class $C^1$ and, for each $\gamma \in S^u_{\varepsilon }$, the map $G^T_\gamma :=G^T(\gamma ,\cdot ):{\fancyscript{B}}^+\rightarrow X^-$ satisfies

$$\begin{aligned} G^T_\gamma (0) =\phi _{-T}\gamma =:\gamma _T ,\qquad \mathrm {graph}\, G^T_\gamma =\left\{ \xi _{\gamma ,z_+}^T(0) \,\big |\, z_+\in {\fancyscript{B}}^+\right\} . \end{aligned}$$

Proof

Assume $T\ge 0$. By step 2 and its proof the map

$$\begin{aligned} \varPsi ^T: S^u_{\varepsilon }\times {\fancyscript{B}}^+\times Z^T\rightarrow Z^T,\qquad (\gamma ,z_+,\xi )\mapsto \varPsi ^T_{\gamma ,z_+}\xi \end{aligned}$$

is a uniform contraction on $Z^T$ with contraction factor $\tfrac{1}{2}$. (Actually $Z^T$ depends on $\gamma$, but the complete metric spaces associated to different $\gamma$’s are quasi-isometric.) Observe that $\varPsi ^T$ is linear, hence smooth, in $\gamma$ and in $z_+$ and of class $C^1$ in $\xi$, because $f$ is of class $C^1$ by the Lipschitz Lemma 1. Hence by the uniform contraction principle, see e.g. [2], the map $\lambda :S^u_{\varepsilon }\times {\fancyscript{B}}^+\rightarrow Z^T$ assigning to $(\gamma ,z_+)$ the unique fixed point $\xi ^T_{\gamma ,z_+}$ of $\varPsi ^T_{\gamma ,z_+}$ is of class $C^1$. So is its composition with (linear) evaluation $ev_0:Z^T\rightarrow X$, $\xi \mapsto \xi (0)$, and (linear) projection $\pi _-:X\rightarrow X^-$. But overall this composition is $G^T$ by definition (25). This proves that $G^T$, thus ${\fancyscript{G}}$, is of class $C^1$ in $\gamma$ and $z_+$.

Consider the heat flow trajectory $\tilde{\eta }:[0,T]\rightarrow X$, $s\mapsto \phi _s\gamma _T=\phi _{s-T}\gamma$. By Remark 5 it takes values in $X^-$, because $\tilde{\eta }(T)=\gamma \in S^u_{\varepsilon }={\partial }W^u_{\varepsilon }\subset W^u$ lies in a descending disk. Hence $\pi _+\tilde{\eta }(0)=0$ and $\pi _-$ leaves $\tilde{\eta }$ pointwise invariant. An argument as in Remark 5 (using likewise forward uniqueness) shows that $\tilde{\eta }=\xi ^T_{\gamma ,0}$. Thus $G^T_\gamma (0) :=\pi _-\xi ^T_{\gamma ,0}(0) =\pi _-\tilde{\eta }(0) =\tilde{\eta }(0) =\gamma _T$. To get the desired representation of $\mathrm {graph}\, G^T_\gamma$ observe that

$$\begin{aligned} {\fancyscript{G}}^T_\gamma (z_+) :=\left( G^T_\gamma (z_+),z_+\right) =\left( \pi _-\xi ^T_{\gamma ,z_+}(0), \pi _+ \xi ^T_{\gamma ,z_+}(0)\right) = \xi ^T_{\gamma ,z_+}(0) \end{aligned}$$

(31)

by definition (25). The first identity also uses the fixed point property and the initial condition proved in step 2. The final identity is by $\pi _-\oplus \pi _+={\small 1}\!\!1_Y$. $\square$

Step 4

The map ${\fancyscript{G}}$ is of class $C^1$. The map $T\mapsto {\fancyscript{G}}(T,\gamma ,z_+)$ is Lipschitz continuous and its derivative is locally Hölder continuous with exponent $\alpha =\frac{1}{8}$. The map $\gamma \mapsto {\fancyscript{G}}(T,\gamma ,z_+)$ is Lipschitz continuous.

Proof

By step 3 the map ${\fancyscript{G}}$ is of class $C^1$ in the $\gamma$ and $z_+$ variables. By compactness of the $(k-1)$-dimensional sphere $S^u_{\varepsilon }$, the derivative of ${\fancyscript{G}}$ with respect to $\gamma$ is bounded. Thus ${\fancyscript{G}}$ is Lipschitz continuous in $\gamma$.

We prove that ${\fancyscript{G}}$ is Lipschitz continuous in T. Fix $T\ge T_0>0, \gamma \in S^u_{\varepsilon }$, and $z_+\in {\fancyscript{B}}^+$. The fixed point $\xi ^T:=\xi ^T_{\gamma ,z_+}$ of $\varPsi ^T$ is given by (24) and the one of $\varPsi ^{T+\tau }$ by

$$\begin{aligned} \xi ^{T+\tau }(s) :=\xi ^{T+\tau }_{\gamma ,z_+}(s)&= e^{-sA}z_+ +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ f(\xi ^{T+\tau }(\sigma )) \, d\sigma \\&+\, e^{-(s-T-\tau )A^-}\gamma -\int \limits _s^{T+\tau } e^{-(s-\sigma )A^-}\pi _- f(\xi ^{T+\tau }(\sigma )) \, d\sigma . \end{aligned}$$

For $s\in [0,T]$ and $\tau \ge 0$ we obtain, analogously to (27), the estimate

$$\begin{aligned}&\left\| \xi ^{T+\tau }(s)-\xi ^T(s)\right\| _X\\&\quad \le \int \limits _0^s\bigl \Vert e^{-(s-\sigma )A}\pi _+\bigr \Vert _{{\fancyscript{L}}(Y,X)} \left\| f(\xi ^{T+\tau }(\sigma ))-f(\xi ^T(\sigma ))\right\| _Y \, d\sigma \\&\quad \quad +\bigl \Vert \bigl (e^{\tau A^-}-{\small 1}\!\!1\bigr ) e^{-(s-T)A^-}\gamma \bigr \Vert _X+\int \limits _s^T\bigl \Vert e^{-(s-\sigma )A^-}\pi _-\bigr \Vert _{{\fancyscript{L}}(Y,X)} \\&\quad \quad \left\| f(\xi ^{T\!+\!\tau }(\sigma ))\!-\!f(\xi ^T(\sigma ))\right\| _Y\, d\sigma \!+\!\int \limits _T^{T+\tau } \bigl \Vert e^{-(s-\sigma )A^-}\pi _-\bigr \Vert _{{\fancyscript{L}}(Y,X)} \left\| f(\xi ^{T\!+\!\tau }(\sigma ))\right\| _Y\, d\sigma \\&\quad \le c\kappa (\rho ) \left\| \xi ^{T+\tau }-\xi ^T\right\| _{C^0([0,T],X)} \left( \int \limits _0^s\frac{e^{-(s-\sigma )\mu }}{(s-\sigma )^{\frac{3}{4}}}\, d\sigma +\int \limits _s^T e^{(s-\sigma )\mu }\, d\sigma \right) \\&\quad \quad +\tau c\mathopen |\lambda _1\mathclose |\cdot ce^{(s-T)\mu }\left\| \gamma \right\| _X +c\kappa (\rho )\rho _0\int \limits _T^{T+\tau } e^{(s-\sigma )\mu }\, d\sigma \\&\quad \le c\kappa (\rho ) \left( \frac{8}{\mu ^{1/4}}+\frac{1}{\mu }\right) \left\| \xi ^{T+\tau }-\xi ^T\right\| _{C^0([0,T],X)}+\tau \rho _0 c^2\mathopen |\lambda _1\mathclose | e^{(s-T)\mu }\\&\quad \quad + c\kappa (\rho )\rho _0\frac{e^{(s-T)\mu }}{\mu }\left( 1-e^{-\tau \mu }\right) \\&\quad \le \frac{1}{8}\left\| \xi ^{T+\tau }-\xi ^T\right\| _{C^0([0,T],X)}+\tau \rho _0\left( c^2\mathopen |\lambda _1\mathclose |+1\right) e^{(s-T)\mu }. \end{aligned}$$

Inequality two uses the Lipschitz Lemma 1 for $f$ and the exponential estimates of Proposition 1. To estimate the second of the four terms recall that $X^-$ is spanned by an orthonormal basis of eigenvectors of $A^-\in {\fancyscript{L}}(X^-)$ corresponding to the eigenvalues $\lambda _1\le \cdots \le \lambda _k<0$. Hence $\mathopen \Vert A^-\mathclose \Vert =-\lambda _1=\mathopen |\lambda _1\mathclose |$. Since $e^{-s\mu }\le 1$ we get that

$$\begin{aligned} \frac{1-e^{-\mu \tau }}{\mu } =\int \limits _0^\tau e^{-s\mu }\; ds \le \tau . \end{aligned}$$

(32)

Thus [9, Proposition 1.3.6. (ii)] implies the estimate

$$\begin{aligned} \mathopen \Vert e^{\tau A^-}-{\small 1}\!\!1\mathclose \Vert _{{\fancyscript{L}}(X^-)} =\left\| A^-\int \limits _0^\tau e^{\sigma A^-}\, d\sigma \right\| _{{\fancyscript{L}}(X^-)} \le \mathopen |\lambda _1\mathclose | \int \limits _0^\tau ce^{-\sigma \mu }\, d\sigma \le \tau c\mathopen |\lambda _1\mathclose |. \end{aligned}$$

(33)

Coming back to inequality two above, we used that $\xi ^{T+\tau }\in Z^{T+\tau }$ in term four takes values in ${\fancyscript{B}}_{\rho _0}$ by step 1. Inequality three uses (29) and (28) for the first two integrals and that $\gamma \in S^u_{\varepsilon }\subset {\fancyscript{B}}_{\rho _0}$. Inequality four uses (32) and smallness (20) of $\rho$ which also implies that $c\kappa (\rho )\le 1$. Now set $c_1=2(c^2\mathopen |\lambda _1\mathclose |+1)$ and take the supremum over $s\in [0,T]$ to get that

$$\begin{aligned} \left\| \xi ^{T+\tau }-\xi ^T\right\| _{C^0([0,T],X)} \le \rho _0 c_1\tau . \end{aligned}$$

(34)

Therefore by (31) we get $\mathopen \Vert {\fancyscript{G}}^{T+\tau }_\gamma (z_+)-{\fancyscript{G}}^T_\gamma (z_+)\mathclose \Vert _X =\mathopen \Vert \xi ^{T+\tau }(0)-\xi ^T(0)\mathclose \Vert _X \le \rho _0 c_1\tau$ and this proves that ${\fancyscript{G}}(T,\gamma ,z_+)={\fancyscript{G}}^T_\gamma (z_+)$ is Lipschitz continuous in $T$. The difference $\xi ^{T+\tau }-\xi ^T$ is illustrated by Fig. 5.

Fig. 5

The difference ${\fancyscript{G}}^{T+\tau }_\gamma (z_+)-{\fancyscript{G}}^T_\gamma (z_+)$

We prove that $T\mapsto \frac{d}{dT}{\fancyscript{G}}(T,\gamma ,z_+)$ is locally Hölder. Consider the derivative

$$\begin{aligned} \Theta ^T(s)&:= \left. \tfrac{d}{d\tau }\right| _{\tau =0} \xi ^{T+\tau }_{\gamma ,z_+}(s)\\&= \int \limits _0^s e^{-(s-\sigma )A}\pi _+ \bigl (df|_{\xi ^T(\sigma )}\circ \Theta ^T(\sigma )\bigr ) d\sigma \;+\; A^- e^{-(s-T)A^-}\gamma \\&-\, e^{-(s-T)A^-}\pi _- f(\xi ^T(T)) -\int \limits _s^T e^{-(s-\sigma )A^-}\pi _- \Bigl (df|_{\xi ^T(\sigma )}\circ \Theta ^T(\sigma )\Bigr )d\sigma . \end{aligned}$$

Since $\frac{d}{dT}{\fancyscript{G}}(T,\gamma ,z_+)=\Theta ^T(0)$ by (31), it remains to show that the map $T\mapsto \Theta ^T(0)\in X$ is locally Hölder continuous. By definition of $\Theta ^T$ we get the identity

$$\begin{aligned}&\Theta ^{T+\tau }(s)-\Theta ^T(s)\\&\quad =\int \limits _0^s e^{-(s-\sigma )A}\pi _+df|_{\xi ^{T+\tau }(\sigma )} \left( \Theta ^{T+\tau }(\sigma )-\Theta ^T(\sigma )\right) \, d\sigma \\&\quad \quad +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ \left( df|_{\xi ^{T+\tau }(\sigma )}-df|_{\xi ^T}(\sigma ) \right) \circ \Theta ^T(\sigma )\, d\sigma \\&\quad \quad +\bigl (e^{\tau A^-}-{\small 1}\!\!1\bigr ) A^- e^{-(s-T)A^-}\gamma -\bigl (e^{\tau A^-}-{\small 1}\!\!1\bigr )e^{-(s-T)A^-}\pi _- f(\xi ^{T+\tau }(T+\tau ))\\&\quad \quad -e^{-(s-T)A^-}\pi _-\left( f(\xi ^{T+\tau }(T+\tau ))-f(\xi ^T(T))\right) \\&\quad \quad -\int \limits _s^T e^{-(s-\sigma )A^-}\pi _-df|_{\xi ^{T+\tau }(\sigma )} \left( \Theta ^{T+\tau }(\sigma )-\Theta ^T(\sigma )\right) \, d\sigma \\&\quad \quad -\int \limits _s^T e^{-(s-\sigma )A^-}\pi _-\left( df|_{\xi ^{T+\tau }(\sigma )}-df|_{\xi ^T}(\sigma ) \right) \circ \Theta ^T(\sigma )\, d\sigma \\&\quad \quad -\int \limits _T^{T+\tau }e^{-(s-\sigma )A^-}\pi _-df|_{\xi ^{T+\tau }(\sigma )}\circ \Theta ^{T+\tau }(\sigma )\, d\sigma \end{aligned}$$

for all $s\in [0,T]$ and $\tau \ge 0$. To obtain terms one and two we added zero, similarly for terms four and five and terms six and seven. Abbreviate the norm of the Banach space $C^0([0,T],X)$ by $\mathopen \Vert \cdot \mathclose \Vert _{C^0_T}$ and combine terms one and six and terms two and seven to get that

$$\begin{aligned}&\left\| \Theta ^{T+\tau }(s)-\Theta ^T(s)\right\| _X\\&\quad \le c\kappa (\rho ) \left\| \Theta ^{T+\tau }-\Theta ^T\right\| _{C^0_T}\left( \int \limits _0^s\frac{e^{-(s-\sigma )\mu }}{(s-\sigma )^{\frac{3}{4}}}\, d\sigma +\int \limits _s^T e^{(s-\sigma )\mu }\, d\sigma \right) \\&\quad \quad +c\kappa _* \left\| \xi ^{T+\tau }-\xi ^T\right\| _{C^0_T}\left\| \Theta ^T\right\| _{C^0_T} \left( \int \limits _0^s\frac{e^{-(s-\sigma )\mu }}{(s-\sigma )^{\frac{3}{4}}}\, d\sigma +\int \limits _s^T e^{(s-\sigma )\mu }\, d\sigma \right) \\&\quad \quad +\tau c^2\mathopen |\lambda _1\mathclose |\left( \mathopen |\lambda _1\mathclose |\cdot \left\| \gamma \right\| _X +\kappa (\rho )\left\| \xi ^{T+\tau }(T\!+\!\tau )\right\| _X\right) e^{(s-T)\mu }\\&\quad \quad \!+\!c\kappa (\rho )\left\| \xi ^{T+\tau }(T\!+\!\tau )-\xi ^T(T)\right\| _X e^{(s-T)\mu } +c\kappa (\rho )\left\| \Theta ^{T+\tau }\right\| _{C^0_{T+\tau }} \int \limits _T^{T\!+\!\tau } e^{(s-\sigma )\mu }\, d\sigma \\&\quad \le c\kappa (\rho )\left( \frac{8}{\mu ^{1/4}}+\frac{1}{\mu }\right) \left\| \Theta ^{T+\tau }-\Theta ^T\right\| _{C^0_T}+\tau c\kappa _*\rho _0^2 c_1^2 \left( \frac{8}{\mu ^{1/4}}+\frac{1}{\mu }\right) \\&\quad \quad +\tau c\rho _0\mathopen |\lambda _1\mathclose |\left( c\mathopen |\lambda _1\mathclose |+1\right) +\tau ^{\frac{1}{8}}\rho _0\left( c_3T^{\frac{1}{8}}+c_4\tau ^{\frac{1}{8}} \right) +\frac{\rho _0 c_1}{\mu }\left( 1-e^{-\tau \mu }\right) \\&\quad \le \frac{1}{8}\left\| \Theta ^{T+\tau }-\Theta ^T\right\| _{C^0_T} +\rho _0\left( \tau c_1^2+\tau c\mathopen |\lambda _1\mathclose | c_1 +\tau ^{\frac{1}{8}}\left( c_3T^{\frac{1}{8}}+c_4\tau ^{\frac{1}{8}} \right) +\tau c_1\right) \end{aligned}$$

for $s\in [0,T]$ and $\tau \ge 0$. Inequality one uses the exponential decay Proposition 1, the Lipschitz Lemma 1 for $f$, and its Corollary 1. To obtain line three we used (33). In line five we used backward time exponential decay (13).

To see inequality two observe the following. Estimate the first integral in lines one and two by (29), the second one by (28). Recall that $\gamma \in {\fancyscript{B}}_{\rho _0}$ by our local setup. Apply estimate (34). In addition, use (34) to conclude that $\mathopen \Vert \Theta ^T(s)\mathclose \Vert _X\le \rho _0 c_1$ whenever $s\in [0,T]$. (Note that the same is true when $T$ is replaced by $T+\tau$.) The elements of $Z^T$ (and $Z^{T+\tau }$) take values in ${\fancyscript{B}}_{\rho _0}$ by step 1. Use that $c\kappa (\rho )\le 1$ by (20) and that $e^{(s-T)\mu }\le 1$. To estimate the difference $\xi ^{T+\tau }(T+\tau )-\xi ^T(T)\in X$ in line four is surprisingly subtle. This estimate will be carried out separately below; see (36) for the result used in inequality two and for the definition of $c_3$ and $c_4$.

To obtain inequality three we used smallness (18) and (20) of $\rho$ and estimate (32). Now take the supremum over $s\in [0,T]$ to get

$$\begin{aligned} \left\| \Theta ^{T+\tau }-\Theta ^T\right\| _{C^0([0,T],X)} \le c_T\rho _0 \tau ^{\frac{1}{8}} \end{aligned}$$

(35)

where $\frac{1}{2} c_T = c_3 T^{\frac{1}{8}} +\tau ^{\frac{7}{8}} \left( c_1^2 +c^2\lambda _1^2+c\mathopen |\lambda _1\mathclose | +c_1 \right) +c_4 \tau ^{\frac{1}{8}}$. Thus

$$\begin{aligned} \left\| \tfrac{d}{dT}{\fancyscript{G}}(T+\tau ,\gamma ,z_+) -\tfrac{d}{dT}{\fancyscript{G}}(T,\gamma ,z_+) \right\| _X =\left\| \Theta ^{T+\tau }(0)-\Theta ^T(0)\right\| _X \le c_T\rho _0\tau ^{\frac{1}{8}}, \end{aligned}$$

that is $T\mapsto \frac{d}{dT}{\fancyscript{G}}(T,\gamma ,z_+)$ is locally Hölder continuous with exponent $\alpha =\frac{1}{8}$.

As mentioned above it remains to estimate the $W^{1,2}$ norm of the difference:

$$\begin{aligned} \xi ^{T+\tau }(T+\tau )-\xi ^T(T)&= \left( e^{-\tau A}-{\small 1}\!\!1\right) e^{-T A}z_+\\&\quad +\int \limits _0^T e^{-(T+\tau -\sigma )A}\pi _+\left( f(\xi ^{T+\tau }(\sigma ))-f(\xi ^T(\sigma ))\right) \, d\sigma \\&\quad +\int \limits _0^T\left( e^{-\tau A}-{\small 1}\!\!1\right) e^{-(T-\sigma )A}\pi _+ f(\xi ^T(\sigma ))\, d\sigma \\&\quad +\int \limits _T^{T+\tau }e^{-(T+\tau -\sigma )A}\pi _+f(\xi ^{T+\tau }(\sigma ))\, d\sigma . \end{aligned}$$

We added zero to obtain terms II and III in this sum I + II + III + IV of four.

• I. Concerning term one we get

  $$\begin{aligned} \left\| \left( e^{-\tau A}-{\small 1}\!\!1\right) e^{-TA}z_+\right\| _X&= \left\| \int \limits _0^\tau -A e^{-sA} e^{-TA}z_+ \, ds \right\| _X\\&\le \int \limits _0^\tau \left\| e^{-sA}\pi _+\right\| _{{\fancyscript{L}}(X)} \left\| Ae^{-TA}\pi _+\right\| _{{\fancyscript{L}}(X)} \left\| z_+\right\| _X \, ds\\&\le \int \limits _0^\tau ce^{-s\mu } \left( \frac{c^\prime C}{T} e^{-T\mu }\right) \rho _0 \, ds\\&\le \frac{cc^\prime C\rho _0e^{-T_0\mu }}{T_0}\;\tau . \end{aligned}$$

  The first identity even without norms is standard; see e.g. [9, Proposition 1.3.6. (ii)]. To obtain inequality one we permuted $A$ and $e^{-sA}$; see e.g. [9, Theorem 1.3.3. (i)]. Here we used that $e^{-TA}z_+\in W^{2,1}=D(A)$ since $T>0$. Compare the above estimate on $X^+$ with the corresponding estimate (33) on the finite dimensional vector space $X^-$ and note how boundedness of $A^-$ simplifies (33). Inequality two uses that the norms $\mathopen \Vert A\cdot \mathclose \Vert _{1,2}$ and $\mathopen \Vert \cdot \mathclose \Vert _{3,2}$ are equivalent with constant $c^\prime$ by compactness of $S^1$ and $A$ being of second order. The regularity-for-singularity estimate (14) with constant $C=C(\mu )$ allows to get from $W^{3,2}$ back to $W^{1,2}$ catching a factor $CT^{-1}$. The final step uses (32).

• II. For term two use estimate (34) and the fact that $c\kappa (\rho )\le 1$ by (20) to get that

  $$\begin{aligned} \int \limits _0^T\left\| e^{-(T+\tau -\sigma )A}\pi _+\left( f(\xi ^{T+\tau }(\sigma ))-f(\xi ^T(\sigma )) \right) \right\| _X d\sigma&\le \frac{\rho _0 c_1\tau }{\mu ^\frac{1}{4}} \int \limits _{\tau \mu }^{\tau \mu +T\mu } \frac{e^{-s}}{s^{\frac{3}{4}}}ds\\&\le \frac{\rho _0 c_1\tau }{\mu ^\frac{1}{4}}\varGamma (\tfrac{1}{4})\\&\le \frac{4\rho _0 c_1}{\mu ^\frac{1}{4}}\;\tau . \end{aligned}$$

  We also used the definition of the $\varGamma$ function after (28) and its functional equation.

• III. Term three requires similar techniques as term one, but their application requires more care. Namely, it is crucial not to deal with the ${\fancyscript{L}}(L^1,W^{3,2})$ norm in one go, but to decompose it into a product involving ${\fancyscript{L}}(L^1,W^{1,q})$ and ${\fancyscript{L}}(W^{1,q},W^{3,2})$ norms where $q$ is any real strictly larger than the order (two) of the differential operator $A$. This way we avoid catching factors $s^{-\alpha }$ with $\alpha \ge 1$ when trading regularity for singularity via (14). Such factors would void our estimate, since they are not integrable locally near zero. As we will see below integrability requires $q > 2$ and $q < \infty$ and picking $q = 4$ leads to equal exponents. Similarly as in case of term one we obtain that

  $$\begin{aligned}&\int \limits _0^T \left\| \left( e^{-\tau A}-{\small 1}\!\!1\right) e^{-(T-\sigma )A}\pi _+ f(\xi ^T(\sigma )) \right\| _X \, d\sigma \\&\le \int \limits _0^T\int \limits _0^\tau \left\| Ae^{-sA}e^{-(T-\sigma )A}\pi _+ f(\xi ^T(\sigma )) \right\| _{W^{1,2}} \, ds\, d\sigma \\&\le \int \limits _0^T\int \limits _0^\tau c^\prime \left\| e^{-sA}e^{-(T-\sigma )A}\pi _+ f(\xi ^T(\sigma )) \right\| _{W^{3,2}} \, ds\, d\sigma \\&\le c^\prime \kappa (\rho )\rho _0 \int \limits _0^T\int \limits _0^\tau \left\| e^{-sA}\pi _+\right\| _{{\fancyscript{L}}(W^{1,q},W^{3,2})} \left\| e^{-(T-\sigma )A}\pi _+\right\| _{{\fancyscript{L}}(L^1,W^{1,q})} \, ds\, d\sigma \\&\le c^\prime C^\prime C^{\prime \prime }\rho _0 \int \limits _0^\tau e^{-s\mu } s^{-\frac{3}{4}-\frac{1}{2q}}\, ds\, \int \limits _0^T e^{-(T-\sigma )\mu } (T-\sigma )^{-1+\frac{1}{2q}}\, d\sigma \\&= c^\prime C^\prime C^{\prime \prime }\rho _0 \int \limits _0^\tau e^{-s\mu } s^{-\frac{7}{8}}\, ds\, \int \limits _0^T e^{-s\mu } s^{-\frac{7}{8}}\, ds\\&\le 64c^\prime C^\prime C^{\prime \prime }\rho _0 T^{\frac{1}{8}} \tau ^{\frac{1}{8}}. \end{aligned}$$

  Inequality three uses once more that $\mathopen \Vert \xi ^T(\sigma )\mathclose \Vert _X\le \rho _0$ by step 1. Note that $\kappa (\rho )\le 1$. Inequality four uses twice the regularity-for-singularity estimate (14) with constants $C^\prime$ and $C^{\prime \prime }$, respectively. In the final inequality we dropped the factors $e^{-s\mu }\le 1$ and carried out the integrals.

• IV. Concerning term four we get the estimate

  $$\begin{aligned} \int \limits _T^{T+\tau }\left\| e^{-(T+\tau -\sigma )A}\pi _+ f(\xi ^{T+\tau }(\sigma ))\right\| _X d\sigma \le \rho _0 \int \limits _0^{\tau } e^{-s\mu } s^{-\frac{3}{4}} \, ds \le 4\rho _0\tau ^{\frac{1}{4}} \end{aligned}$$

  by dropping the term $e^{-s\mu }\le 1$ under the integral.

Side remark concerning the estimate for term III: Unfortunately, we do not see any way to trade $\tau ^{1/8}$ for $\tau$ or, equivalently, to trade $T^{1/8}$ for $T$. This has the following consequences. The positive power of $T$ obstructs the conclusion that $\frac{d}{dT}{\fancyscript{G}}$ is uniformly continuous in $T$. The conclusion of local Lipschitz continuity is obstructed by the factor $\tau ^\alpha$ with $\alpha =1/8<1$. All we can say is that $\frac{d}{dT}{\fancyscript{G}}$ is locally Hölder continuous in $T$ with exponent $\alpha =1/8$.

To summarize, the above estimates show that

$$\begin{aligned} \left\| \xi ^{T+\tau }(T+\tau )-\xi ^T(T)\right\| _X \le \tau ^{\frac{1}{8}}\rho _0 \left( c_3T^{\frac{1}{8}} +c_4\tau ^{\frac{1}{8}}\right) \end{aligned}$$

(36)

for $\tau \ge 0$ and where

$$\begin{aligned} c_3:=64c^\prime C^\prime C^{\prime \prime } ,\qquad c_4:=4+\tau ^{\frac{7}{8}}\left( cc^\prime C T_0^{-1} +4c_1\mu ^{-\frac{1}{4}}\right) . \end{aligned}$$

This concludes the proof of (35) and therefore of step 4. $\square$

Step 5

For $T\ge 0$ the graph map ${\fancyscript{G}}^T_\gamma :{\fancyscript{B}}^+\rightarrow X^-\oplus X^+$, $z_+\mapsto \left( G^T_\gamma (z_+),z_+\right)$, and its inverse $\pi _+|_{{\fancyscript{G}}^T_\gamma ({\fancyscript{B}}^+)}$ are both Lipschitz continuous with respect to the $W^{1,2}$ norm. In fact, the graph map is a diffeomorphism onto its image.

Proof

For $j=1,2$ pick $z_j\in {\fancyscript{B}}^+$ and denote the fixed point $\xi ^T_{\gamma ,z_j}$ of $\varPsi ^T=\varPsi ^T_{\gamma ,z_j}$ by $\xi _j$. Similarly to the estimate in the proof of step 2 we obtain for each $s\in [0,T]$ that

$$\begin{aligned} \left\| \xi _1(s)-\xi _2(s)\right\| _X \le ce^{-s\mu } \left\| z_1-z_2\right\| _X +\frac{1}{2} \left\| \xi _1-\xi _2\right\| _{\exp }. \end{aligned}$$

Multiply by $e^{s\frac{\mu }{2}}$ and take the supremum over $s\in [0,T]$ to get

$$\begin{aligned} \left\| \xi _1-\xi _2\right\| _{\exp } \le 2 c \left\| z_1-z_2\right\| _X. \end{aligned}$$

(37)

By (31) this proves Lipschitz continuity of ${\fancyscript{G}}^T_\gamma$, namely

$$\begin{aligned} \left\| {\fancyscript{G}}^T_\gamma (z_1) -{\fancyscript{G}}^T_\gamma (z_2)\right\| _X =\left\| \xi _1(0)-\xi _2(0)\right\| _X \le \left\| \xi _1-\xi _2\right\| _{\exp } \le 2c\left\| z_1-z_2\right\| _X. \end{aligned}$$

Next use that $\pi _+$ vanishes on $X^-$ and acts as the identity on $X^+$ to see that $\pi _+$ is a left inverse of ${\fancyscript{G}}^T_\gamma$. Thus $\pi _+$ restricted to ${\fancyscript{G}}^T_\gamma ({\fancyscript{B}}^+)$ is its inverse. But this restriction is of class $C^1$, because it is of the form $\pi _+\circ {\fancyscript{G}}^T_\gamma (z_+)$ where $\pi _+$ is linear and the map $z_+\mapsto {\fancyscript{G}}^T_\gamma (z_+) :=\left( G^T_\gamma z_+, z_+\right)$ is of class $C^1$ by step 3.

To see that the restriction of $\pi _+$ to ${\fancyscript{G}}^T_\gamma ({\fancyscript{B}}^+)$ is Lipschitz continuous consider the difference $\xi _1(0)-\xi _2(0)=\varPsi ^T\xi _1(0)-\varPsi ^T\xi _2(0)$ whose right hand side is given by (24). Apply $\mathopen \Vert a-b\mathclose \Vert \ge \mathopen \Vert a\mathclose \Vert -\mathopen \Vert b\mathclose \Vert$ with $a=z_1-z_2$ and (30) for $s=0$ to get

$$\begin{aligned} \left\| \xi _1(0)-\xi _2(0)\right\| _X \ge \left\| z_1-z_2\right\| _X - c\kappa (\rho )\frac{2}{3\mu } \left\| \xi _1-\xi _2\right\| _{\exp }. \end{aligned}$$

By (37) and the smallness assumption (20) on $\rho$ this implies that

$$\begin{aligned} \left\| \xi _1(0)-\xi _2(0)\right\| _X \ge \left( 1-c\kappa (\rho ) \frac{2}{3\mu } 2c\right) \left\| z_1-z_2\right\| _X \ge \frac{1}{2}\left\| z_1-z_2\right\| _X \end{aligned}$$

which by (31) and the fact that $\pi _+$ left inverts ${\fancyscript{G}}^T_\gamma$ is equivalent to

$$\begin{aligned} \left\| {\fancyscript{G}}^T_\gamma (z_1) -{\fancyscript{G}}^T_\gamma (z_2)\right\| _X \ge \frac{1}{2} \left\| \pi _+{\fancyscript{G}}^T_\gamma (z_1) -\pi _+{\fancyscript{G}}^T_\gamma (z_2)\right\| _X. \end{aligned}$$

(38)

This proves that $\pi _+$ is Lipschitz continuous on the image of ${\fancyscript{G}}^T_\gamma$.

By estimate (38) and the estimate after (37) the map ${\fancyscript{G}}^T_\gamma$ is bi-Lipschitz and therefore a homeomorphism onto its image. Since the map and its inverse are both of class $C^1$, it is in fact a diffeomorphism onto its image. $\square$

Step 6

(Uniform convergence) $\mathopen \Vert {\fancyscript{G}}^\infty (z_+) -{\fancyscript{G}}_\gamma ^T(z_+)\mathclose \Vert _{W^{2,2}} \le \rho _0 e^{-T\frac{\mu }{16}}$ $\forall T\ge T_2$.

Proof

Assume $T\ge T_2$; see (39) below. Consider the fixed point $\xi ^T=\xi ^T_{\gamma ,z_+}$ of $\varPsi _{\gamma ,z_+}^T$ on $Z^T$ and the fixed point $\eta =\eta _{z_+}$ of $\varPsi _{z_+}$ on $Z$ defined by (17). Because ${\fancyscript{G}}^T_\gamma (z_+)=\xi ^T(0)$ by (31), similarly ${\fancyscript{G}}^\infty (z_+)=\eta (0)$, it remains to estimate the difference $\eta (0)-\xi ^T(0)$. Observe that, firstly, since the difference lies in $X^-\subset C^\infty$ application of the $W^{2,2}$ norm makes sense. Secondly, by the respective representation formulae, this difference depends on the whole trajectories $\eta$ and $\xi ^T$. But while $\eta$ runs into the origin, the trajectory $\xi ^T$ ends on the fiber ${\fancyscript{D}}_\gamma$ far away! So the difference $\eta -\xi ^T$ cannot converge to zero, as $T\rightarrow \infty$, uniformly on $[0,T]$. However, Fig. 5 suggests that this could be true on some initial part of the domain $[0,T]$, say on $\left[ 0,\frac{1}{2}T\right]$. So step A is to reduce the problem to the smaller interval $\left[ 0,\frac{1}{2}T\right]$. Step B is to solve the reduced problem. Here the key idea is to suitably partition both trajectories $\eta$ and $\xi ^T$ and compare due parts; see Fig. 6. The fact that $\eta$ is asymptotically well behaved, i.e. exponentially close to zero on $[T,\infty )$, enters frequently.

Fig. 6

Time partitions and exponentially decaying differences

We proceed as follows: In step A we estimate the (stronger) $W^{2,2}$ norm of the difference $\eta (0)-\xi ^T(0)$ by an exponentially decaying function of $T$ plus the supremum over $s\in \left[ 0,\frac{1}{2}T\right]$ of the (weaker) norm $\mathopen \Vert \eta (s)-\xi ^T(s)\mathclose \Vert _{X}$. This reduction of a stronger to a weaker norm is based on the key fact that the difference $\eta (0)-\xi ^T(0)$ only involves $\pi _-$ terms. Namely, these take values in $X^-$, hence in $C^\infty$. In step B we prove exponential decay of this sup norm. Here we encounter again the difference $\eta -\xi ^T$, unfortunately on the whole interval $[0,T]$. Now the key idea is to decompose this interval into three pieces, namely

$$\begin{aligned} I:=\left[ 0,\tfrac{1}{2}T\right] ,\qquad II:=\left[ \tfrac{1}{2}T,\tfrac{3}{4} T\right] ,\qquad III:=\left[ \tfrac{3}{4} T,T\right] , \end{aligned}$$

as shown in Fig. 6. In fact an extra piece $[T,\infty )$ is brought in by $\eta$. On interval $I$ we pull out the supremum norm and use smallness of the Lipschitz constant $\kappa (\rho )$ to get a coefficient less than one to throw the whole $(\eta -\xi ^T)$ term on the left hand side. Off $I$ we apply the triangle inequality to deal with each term $\eta$ and $\xi ^T$ separately. Exponential decay built into the definition (17) of $Z$ allows to handle $\eta$ on its whole remaining time interval $\left[ \frac{1}{2}T,\infty \right)$ in one go. It remains to deal with $\xi ^T$ on intervals $\textit{II}$ and $\textit{III}$. For $\sigma \in \textit{II}$ we exploit (after adding zero) that both terms $\xi ^T(\sigma )-\phi _\sigma (\gamma _T)$ and $\phi _\sigma (\gamma _T)$ individually decay exponentially in $T$, uniformly in $\sigma \in II$. For the first term this is simply true by definition (23) of $Z^T$. Concerning the second term we use that $\gamma$ lies in the unstable manifold. Hence $\phi _\sigma (\gamma _T)=\phi _t(\gamma )$ collapses exponentially fast into the origin, since $t:=\sigma -T\in \left[ -\frac{1}{2}T,-\frac{1}{4} T\right]$ and the whole interval sets off to $-\infty$ ⁶; cf. Remark 5. For interval $III$ the argument is analytic and cannot be guessed by Fig. 6. The figure even suggests trouble. Fortunately, we are not concerned with the image of the trajectory, but with the integral over its time parametrization. In fact due to an abundance of negative powers already the coarse estimate $\mathopen \Vert \xi ^T(\sigma )\mathclose \Vert _X\le \rho _0$ is fine: It leaves us with integrating $e^{(s-\sigma )\mu }$ over $III$. But $s\le \frac{1}{2} T$ by assumption and $\sigma \ge \frac{3}{4} T$ on $III$. ⁷

Our choice of time partitions and combinations of trajectory pieces which leads to exponential decay in $T$ is shown in Fig. 6 where the upper labels of points are time. It is instructive to figure out how the drawing changes as $T$ tends to infinity. How do $\eta$ and $\xi ^T$ change and how their time labels? What happens to the lengths of the four double arrows? Consider the pair of double arrows with common point $\xi ^T(T/2)$. What is the asymptotic behavior of this point?

• (A) Abbreviate ${\tilde{X}}:=W^{2,2}$. Note that by parabolic regularity the heat flow trajectories $\eta$ and $\xi ^T$ take values in $C^\infty$ at strictly positive times. Recall that $\gamma \in S^u_{\varepsilon }\subset (X^-\cap {\fancyscript{B}}_{\rho _0})$ by our local setup. Use formula (24) for $\xi ^T$ and the one for $\eta$, see formula after (17), together with the fact that the nonlinearity $f$ maps $X$ to $Y$ to obtain ⁸

  $$\begin{aligned}&\left\| \eta (0)-\xi ^T(0)\right\| _{\tilde{X}}\\&\quad \le \left( \int \limits _0^{T/2}+\int \limits _{T/2}^T\right) \left\| e^{\sigma A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,\tilde{X})} \left\| f\circ \eta (\sigma )-f\circ \xi ^T(\sigma )\right\| _Y\,d\sigma \\&\quad \quad +\left\| e^{TA^-}\pi _-\right\| _{{\fancyscript{L}}(X,\tilde{X})}\left\| \gamma \right\| _X +\int \limits _T^\infty \left\| e^{\sigma A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,\tilde{X})} \left\| f\circ \eta (\sigma )\right\| _Y\, d\sigma \\&\quad \le c\kappa (\rho )\left\| \eta -\xi ^T\right\| _{C^0\left( \left[ 0,\frac{T}{2}\right] ,X\right) } \int \limits _0^{T/2}e^{-\sigma \mu }\, d\sigma +c\kappa (\rho )\cdot 2\rho _0 \int \limits _{T/2}^T e^{-\sigma \mu }\, d\sigma \\&\quad \quad +c\rho _0 e^{-T\mu }+c\kappa (\rho )\rho _0\int \limits _T^\infty e^{-\sigma \mu }\,d\sigma .\\&\quad \le \frac{c\kappa (\rho )}{\mu }\left\| \eta -\xi ^T\right\| _{C^0\left( \left[ 0,\frac{T}{2}\right] ,X\right) } +\frac{2c\kappa (\rho )}{\mu }\rho _0 e^{-T\frac{\mu }{2}}+\frac{\rho _0}{8} e^{-T\frac{\mu }{2}} +\frac{c\kappa (\rho )}{\mu }\rho e^{-T\mu }\\&\quad \le \frac{1}{8}\left\| \eta -\xi ^T\right\| _{C^0\left( \left[ 0,\frac{T}{2}\right] ,X\right) } +\frac{1}{2} \rho _0 e^{-T\frac{\mu }{2}}. \end{aligned}$$

  Inequality two uses the exponential decay Proposition 1 (c) and the Lipschitz Lemma 1 for $f$ and $p=1$. We also used definition (22) of the exp-$T$ norm and the fact that the elements of $Z^T$ take values in ${\fancyscript{B}}_{\rho _0}$ by step 1 and those of $Z$ in ${\fancyscript{B}}_\rho \subset {\fancyscript{B}}_{\rho _0}$ by definition (17). Inequalities three is by calculation and definition of $T_2$. Now use (20).

• (B) Pick $s\in \left[ 0,\frac{T}{2}\right]$. Similarly as in (A) we get the estimate

  $$\begin{aligned}&\left\| \eta (s)-\xi ^T(s)\right\| _X\\&\le \int \limits _0^s\left\| e^{-(s-\sigma )A}\pi _+\right\| _{{\fancyscript{L}}(Y,X)} \left\| f\circ \eta (\sigma )-f\circ \xi ^T(\sigma )\right\| _Y\, d\sigma \\&\quad +\left( \int \limits _s^{\frac{T}{2}}+\int \limits _{\frac{T}{2}}^{\frac{3T}{4}} +\int \limits _{\frac{3T}{4}}^T\right) \left\| e^{-(s-\sigma )A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,X)} \left\| f\circ \eta (\sigma )-f\circ \xi ^T(\sigma )\right\| _Y d\sigma \\&\quad +ce^{(s-T)\mu }\left\| \gamma \right\| _X + \int \limits _T^\infty \left\| e^{-(s-\sigma )A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,X)} \left\| f\circ \eta (\sigma )\right\| _Y d\sigma \\&\le c\rho _0 e^{-T\frac{\mu }{2}}+c\kappa (\rho )\left\| \eta -\xi ^T\right\| _{C^0([0,\frac{T}{2}],X)} \left( \int \limits _0^s\frac{e^{-(s-\sigma )\mu }}{(s-\sigma )^{\frac{3}{4}}}\, d\sigma +\int \limits _s^{\frac{T}{2}}e^{(s-\sigma )\mu } d\sigma \right) \\&\quad +c\kappa (\rho )\int \limits _{\frac{T}{2}}^{\frac{3T}{4}}e^{(s-\sigma )\mu } \left( \left\| \xi ^T(\sigma )-\phi _\sigma (\gamma _T)\right\| _X +\left\| \phi _\sigma (\gamma _T)\right\| _X\right) d\sigma \\&\quad +c\kappa (\rho )\int \limits _{\frac{3T}{4}}^Te^{(s-\sigma )\mu } \left\| \xi ^T(\sigma )\right\| _X d\sigma + c\kappa (\rho )\left\| \eta \right\| _{\exp } \int \limits _{\frac{T}{2}}^\infty e^{(s-\frac{3}{2}\sigma )\mu } d\sigma . \end{aligned}$$

  To get overall exponential decay in $T$ we have split the domain of integration in three parts. The domain of integration $\int _{T/2}^\infty$ in the last line is not a misprint. To continue the estimate consider the last three lines. Now we explain how to get to the corresponding three lines in (40) below. Concerning line one use the definition of $T_2$ and recall that $s\in [0,T/2]$ and use (28) and (29). In line two we drop $e^{(s-\sigma )\mu }\le 1$ and use that $\mathopen \Vert \xi ^T(\sigma ) -\phi _\sigma (\gamma _T)\mathclose \Vert _X \le \rho e^{-\sigma \frac{\mu }{2}}$ by definition of $Z^T$ and that

  $$\begin{aligned} \int \limits _{\frac{T}{2}}^{\frac{3T}{4}} \left\| \phi _{\sigma -T}\gamma \right\| _X d\sigma = \int \limits _{\frac{T}{8}}^{\frac{3T}{8}} \left\| \phi _{-t-\frac{T}{8}}\gamma \right\| _X dt \le \int \limits _{\frac{T}{8}}^{\frac{3T}{8}} \rho e^{-t\frac{\mu }{2}}\, dt \le \frac{2\rho }{\mu } e^{-T\frac{\mu }{16}}. \end{aligned}$$

  (39)

  Here the identity is by change of variables $t=-\sigma +\frac{7}{8}T$ and the first inequality uses Remark 5 for the backward time trajectory $\tilde{\eta }(-t)=\phi _{-t-T/8}(\gamma )$ defined for $t\ge 0$. To see this note that $\tilde{\eta }(-t)\rightarrow 0$, as $t\rightarrow \infty$, because $\gamma$ lies in the descending sphere $S^u_{\varepsilon }$ by assumption. Observe that the image of $\tilde{\eta }$ is contained in the backward flow invariant set $\phi _{-T/8}\overline{W^u_{\varepsilon }}$ which by assumption on $T_2$ is itself contained in ${\fancyscript{B}}^-:={\fancyscript{B}}_{\rho /2c}\cap X^-\subset {\fancyscript{B}}_\rho$. By the argument in Remark 5 the solution $\tilde{\eta }$ is equal to the unique fixed point of the map $\varPhi _\gamma$. In particular, it holds that $\tilde{\eta }\in Z^u$ and therefore $\mathopen \Vert \tilde{\eta }(-t)\mathclose \Vert _X\le \rho e^{-t\mu /2}$ for every $t\ge 0$. To summarize, line two is bounded from above by

  $$\begin{aligned} c\kappa (\rho )\cdot \rho \left( \int \limits _{\frac{T}{2}}^{\frac{3T}{4}} e^{-\sigma \frac{\mu }{2}} \, d\sigma +\frac{2e^{-T\frac{\mu }{16}}}{\mu } \right) \le c\kappa (\rho )\cdot \frac{2\rho }{\mu } \left( e^{-T\frac{\mu }{4}} +e^{-T\frac{\mu }{16}} \right) . \end{aligned}$$

  In line three use $\mathopen \Vert \xi ^T(\sigma )\mathclose \Vert _X\le \rho _0$ for any $\xi ^T\in Z^T$ by step 1 and $\mathopen \Vert \eta \mathclose \Vert _{\exp }\le \rho$ by definition of $Z$. Carry out the integrals, in the second one drop $e^{(s-\sigma )\mu }\le 1$, to get

  $$\begin{aligned} \left\| \eta (s)-\xi ^T(s)\right\| _X&\le \frac{\rho _0}{8} e^{-T\frac{\mu }{4}} + c\kappa (\rho )\left( \frac{8}{\mu ^{1/4}}+\frac{1}{\mu }\right) \left\| \eta -\xi ^T\right\| _{C^0([0,\frac{T}{2}],X)}\nonumber \\&+\frac{4c\kappa (\rho )}{\mu }\rho e^{-T\frac{\mu }{16}} \!+\! \frac{c\kappa (\rho )}{\mu }\rho _0 e^{-T\frac{\mu }{4}} \!+\! \frac{2c\kappa (\rho )}{\mu }\rho e^{-T\frac{\mu }{4}}\nonumber \\&\le \frac{1}{8} \left\| \eta -\xi ^T\right\| _{C^0([0,\frac{T}{2}],X)} +\frac{1}{2}\rho _0 e^{-T\frac{\mu }{16}}. \end{aligned}$$

  (40)

  The last step uses smallness (20) of $\rho$. Take the sup over $s\in [0,\frac{T}{2}]$ to get

  $$\begin{aligned} \left\| \eta -\xi ^T\right\| _{C^0([0,\frac{T}{2}],X)} \le \frac{4}{7} \rho _0 e^{-T\frac{\mu }{16}}. \end{aligned}$$

  (41)

  Hence $\mathopen \Vert {\fancyscript{G}}^\infty (z_+)-{\fancyscript{G}}^T_\gamma (z_+)\mathclose \Vert _{\tilde{X}} =\mathopen \Vert \eta (0)-\xi ^T(0)\mathclose \Vert _{\tilde{X}} \le \rho _0 e^{-T\frac{\mu }{16}}$, for all $\gamma \in S^u_{\varepsilon }$, times $T\ge T_2$, and $z_+\in {\fancyscript{B}}^+$ and this proves step 6. $\square$

The Sobolev embedding $W^{2,2}(S^1)\hookrightarrow C^1(S^1)$ concludes the proof of Theorem 1.

3.2 Proof of uniform $C^1$ convergence (Theorem 2)

Theorem 2 builds on the backward $\lambda$-lemma, Theorem 1. So we may use any of the six steps of its proof. The proof at hand takes two steps. Fix $\gamma \in S^u_{\varepsilon }$ and $z_+\in {\fancyscript{B}}^+$.

Step I. ($L^2$ extension) $\mathopen \Vert d{\fancyscript{G}}^T_\gamma (z_+)v\mathclose \Vert _2 \le 2 \mathopen \Vert v\mathclose \Vert _2$ for all $v\in \pi _+(L^2)$ and $T\ge T_1$.

Proof

By the bounded linear transform theorem [14, Theorem I.7] it suffices to pick $v$ in the dense subspace $X^+=\pi _+(X)$ of $\pi _+(L^2)$. Pick $\tau \ge 0$ small. Consider the fixed point $\xi _{z_++\tau v}=\xi ^T_{\gamma ,z_++\tau v}\in Z^T$ of $\varPsi ^T_{\gamma ,z_++\tau v}$. By (24) the fixed point property means

$$\begin{aligned} \xi _{z_++\tau v}(s)&= e^{-sA}(z_++\tau v) +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ f(\xi _{z_++\tau v}(\sigma ))\, d\sigma \nonumber \\&+\, e^{-(s-T)A^-}\gamma -\int \limits _s^T e^{-(s-\sigma )A^-} \pi _-f(\xi _{z_++\tau v}(\sigma ))\,d\sigma \end{aligned}$$

(42)

for every $s\in [0,T]$. By the proof of step 3 the composition of maps $\tau \mapsto \xi _{z_++\tau v} \mapsto \xi _{z_++\tau v}(s)$ is of class $C^1$. Hence the linearization is well defined and satisfies

$$\begin{aligned} X_v(s)&:= \left. \tfrac{d}{d\tau }\right| _{\tau =0} \xi _{z_++\tau v}(s)\nonumber \\&= e^{-sA} v +\int \limits _0^s e^{-(s-\sigma )A}\pi _+ \left( df|_{\xi _{z_+}(\sigma )}\circ X_v(\sigma )\right) \, d\sigma \nonumber \\&-\, \int \limits _s^T e^{-(s-\sigma )A^-}\pi _- \left( df|_{\xi _{z_+}(\sigma )}\circ X_v(\sigma ) \right) \, d\sigma \end{aligned}$$

(43)

for each $s\in [0,T]$. Use (31) to see that $X_v(0) =\left. \frac{d}{d\tau }\right| _{\tau =0} \xi _{z_++\tau v}(0) =d{\fancyscript{G}}^T_\gamma (z_+) v$. To conclude the proof it remains to show that $\mathopen \Vert X_v(0)\mathclose \Vert _2\le 2\mathopen \Vert v\mathclose \Vert _2$. Recall the estimate

$$\begin{aligned} \left\| e^{-sA}\pi _+\right\| _{{\fancyscript{L}}(L^2,X)} \le c s^{-\frac{1}{2}}e^{-s\mu }, \qquad s>0, \end{aligned}$$

(44)

provided by Proposition 1. This motivates, cf. [8], to define the weighted exp norm

$$\begin{aligned} \left\| X_v\right\| _{\frac{1}{2},\exp }= \left\| X_v\right\| _{\frac{1}{2},\exp ,T} :=\sup _{s\in [0,T]} s^{\frac{1}{2}} e^{s\frac{\mu }{2}} \left\| X_v(s)\right\| _X. \end{aligned}$$

This choice allows to estimate $\mathopen \Vert X_v(s)\mathclose \Vert _X$ (up to a singular factor) in terms of $\mathopen \Vert v\mathclose \Vert _2$ instead of $\mathopen \Vert v\mathclose \Vert _X$. Namely, by (43) and since $v\in X^+\subset X\hookrightarrow L^2$ we obtain that

$$\begin{aligned} s^{\frac{1}{2}}e^{s\frac{\mu }{2}} \left\| X_v(s)\right\| _X&\le s^{\frac{1}{2}}e^{s\frac{\mu }{2}} \left\| e^{-sA}\pi _+\right\| _{{\fancyscript{L}}(L^2,X)} \left\| v\right\| _2\\&+ s^{\frac{1}{2}}e^{s\frac{\mu }{2}} \int \limits _0^s \left\| e^{-(s-\sigma )A}\pi _+\right\| _{{\fancyscript{L}}(Y,X)} \kappa (\rho ) \left\| X_v(\sigma )\right\| _X \, d\sigma \\&+ s^{\frac{1}{2}}e^{s\frac{\mu }{2}} \int \limits _s^T \left\| e^{-(s-\sigma )A^-}\pi _-\right\| _{{\fancyscript{L}}(Y,X)} \kappa (\rho ) \left\| X_v(\sigma )\right\| _X d\sigma \\&\le ce^{-s\frac{\mu }{2}}\left\| v\right\| _2 + c\kappa (\rho ) \left\| X_v\right\| _{\frac{1}{2},\exp } \int \limits _0^s \frac{e^{-(s-\sigma )\frac{\mu }{2}}}{(s-\sigma )^{\frac{3}{4}}} \left( \frac{s}{\sigma }\right) ^{\frac{1}{2}} d\sigma \\&+ c\kappa (\rho ) \left\| X_v\right\| _{\frac{1}{2},\exp } \int \limits _s^T e^{\frac{3}{2}(s-\sigma )\mu } \left( \frac{s}{\sigma }\right) ^{\frac{1}{2}} d\sigma \\&\le ce^{-s\frac{\mu }{2}}\left\| v\right\| _2 +c\kappa (\rho ) \left( \frac{18}{\mu ^{1/4}} +\frac{2}{3\mu }\right) \left\| X_v\right\| _{\frac{1}{2},\exp } \end{aligned}$$

for every $s\in [0,T]$. Inequality one uses that $\xi _{z_+}\in Z^T$ takes values in $B_{\rho _0}\subset {\fancyscript{U}}$ by step 1. Hence Corollary 1 applies and provides the estimate for $df$. In inequality two we used that $\mathopen \Vert X_v(\sigma )\mathclose \Vert _X \le \sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}} \mathopen \Vert X_v\mathclose \Vert _{\frac{1}{2},\exp }$ by definition of the exp norm. We used (44) to obtain the first term and Proposition 1 to obtain the other two terms of the sum. Inequality three will be proved below. Now use smallness (20) of $\rho$ and take the supremum over $s\in [0,T]$ to obtain

$$\begin{aligned} \left\| X_v\right\| _{\frac{1}{2},\exp } \le 2c \left\| v\right\| _2. \end{aligned}$$

(45)

Concerning inequality three we need to estimate the two integrals. Observe first of all that $\int _s^T e^{\frac{3}{2}(s-\sigma )\mu } \left( \frac{s}{\sigma }\right) ^\frac{1}{2} \, d\sigma \le \int _s^T e^{\frac{3}{2}(s-\sigma )\mu } \, d\sigma \le \frac{2}{3\mu }$ and

$$\begin{aligned}&\int \limits _0^s \frac{e^{-(s-\sigma )\frac{\mu }{2}}}{(s-\sigma )^{\frac{3}{4}}} \left( \frac{s}{\sigma } \right) ^{\frac{1}{2}} d\sigma \nonumber \\&= \int \limits _0^{s/2} \underbrace{ e^{-(s-\sigma )\frac{\mu }{2}}} _{\le e^{-s\mu /4}} (\underbrace{s-\sigma } _{\ge s/2})^{-\frac{3}{4}} s^{\frac{1}{2}} \sigma ^{-\frac{1}{2}} d\sigma + \int \limits _{s/2}^s \frac{e^{-(s-\sigma )\frac{\mu }{2}}}{(s-\sigma )^{\frac{3}{4}}} \,(\, \underbrace{s/\sigma } _{\le 2} \,)^{\frac{1}{2}} d\sigma \nonumber \\&\le 2^{\frac{3}{4}} s^{-\frac{1}{4}} e^{-s\frac{\mu }{4}} \int \limits _0^{s/2} \sigma ^{-\frac{1}{2}} d\sigma + \frac{2^{\frac{3}{4}}}{\mu ^{\frac{1}{4}}} \varGamma (\tfrac{1}{4})\nonumber \\&\le \frac{2}{\mu ^{\frac{1}{4}}} + \frac{8}{\mu ^{\frac{1}{4}}}. \end{aligned}$$

(46)

Here we used that the last integral is equal to $\sqrt{2s}$ and $h(s) :=2^{\frac{5}{4}}s^{\frac{1}{4}} e^{-s\frac{\mu }{4}}$ is bounded by $h(s_{max})=h(1/\mu ) =2(2/\mu e)^{1/4}$. Furthermore, we used (29).

We start over estimating $X_v(s)$, but now at $s=0$ and in the $L^2$ norm. Similarly as above, using that $\mathopen \Vert X_v(\sigma )\mathclose \Vert _X \le 2c\sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}}\mathopen \Vert v\mathclose \Vert _2$ by (45) we get

$$\begin{aligned} \left\| X_v(0)\right\| _2&\le \left\| v\right\| _2 + \int \limits _0^T \left\| e^{\sigma A^-}\pi _-\right\| _{{\fancyscript{L}}(L^1,L^2)} \kappa (\rho ) \left\| X_v(\sigma )\right\| _X d\sigma \\&\le \left\| v\right\| _2 +2c^2\kappa (\rho ) \left\| v\right\| _2 \int \limits _0^T e^{-\frac{3}{2}\sigma \mu } \sigma ^{-\frac{1}{2}} \, d\sigma \\&\le \left\| v\right\| _2 +c^2\kappa (\rho ) \left( \frac{6}{\mu ^{1/4}} +\frac{3}{\mu ^{5/4}}\right) \left\| v\right\| _2 \le 2\left\| v\right\| _2. \end{aligned}$$

Inequality one also uses that $e^{-sA}$ restricts to a strongly continuous semigroup on $L^2$ by Proposition 1 and that $\mathopen \Vert \cdot \mathclose \Vert _{{\fancyscript{L}}(L^1,L^2)} \le \mathopen \Vert \cdot \mathclose \Vert _{{\fancyscript{L}}(L^1,X)}$ by the embedding $X\hookrightarrow L^2$. Inequality four is by smallness (20) of $\rho$. Concerning inequality three we applied (for $s=0$) the following consequence of Hölder’s inequality on the domain $[s,\infty )$, namely

$$\begin{aligned} \int \limits _s^\infty e^{-\frac{3}{2}\sigma \mu } \sigma ^{-\frac{1}{2}} d\sigma \le \mathopen \Vert e^{-\sigma \mu } \mathclose \Vert _{L^4} \mathopen \Vert e^{-\sigma \frac{\mu }{2}} \sigma ^{-\frac{1}{2}} \mathclose \Vert _{L^{4/3}} \le \left( 3+\frac{3}{2\mu }\right) \frac{e^{-s\mu }}{\mu ^{\frac{1}{4}}} \end{aligned}$$

(47)

for $s\ge 0$. Here step two uses that $\mathopen \Vert e^{-\sigma \mu }\mathclose \Vert _{L^4} =(1/4\mu )^{1/4} e^{-s\mu }$ by calculation and that

$$\begin{aligned} \mathopen \Vert e^{-\sigma \frac{\mu }{2}} \sigma ^{-\frac{1}{2}}\mathclose \Vert _{L^{\frac{4}{3}}}^{\frac{4}{3}} = \int \limits _s^\infty e^{-\sigma \frac{2}{3}\mu } \sigma ^{-\frac{2}{3}} \, d\sigma \le \int \limits _0^1\sigma ^{-\frac{2}{3}} \, d\sigma + \int \limits _1^\infty e^{-\sigma \frac{2}{3}\mu } \, d\sigma = 3+\frac{3}{2\mu } e^{-\frac{2}{3}\mu }. \end{aligned}$$

This proves Step I. $\square$

Step II. $\mathopen \Vert d{\fancyscript{G}}^T_\gamma (z_+)v -d{\fancyscript{G}}^\infty (z_+)v\mathclose \Vert _2 \le e^{-T\frac{\mu }{16}} \mathopen \Vert v\mathclose \Vert _2 \;\forall T\ge T_0 \;\forall v\in \pi _+(L^2)$.

Proof

The proof of convergence of the linearized graph maps should use convergence of the graph maps themselves. Indeed (41) is a key ingredient. Another one is the Lipschitz estimate for $df$ provided by Lemma 1.

Pick $T\ge T_0$ and $v\in X^+$. Consider the fixed point $\xi _{z_+}=\xi ^T_{\gamma ,z_+}$ of the strict contraction $\varPsi ^T_{\gamma ,z_+}$ on $Z^T$ and the fixed point $\eta _{z_+}$ of $\varPsi _{z_+}$ on $Z$. It is a side remark that Theorem 3 is recovered by the present setup for $T=\infty$ and $\gamma :=0$. For $\tau \ge 0$ small $\xi _{z_++\tau v}$ satisfies the integral equation (42) and $\eta _{z_++\tau v}$ satisfies (42) with $T=\infty$; in particular, term three in that sum disappears. Consider the linearizations $X_v :=\left. \frac{d}{d\tau } \right| _{\tau =0} \xi ^T_{\gamma ,z_++\tau v}$ and $Y_v :=\left. \frac{d}{d\tau } \right| _{\tau =0} \eta _{z_++\tau v}$. Observe that $X_v$ satisfies the integral equation (43) and $Y_v$ satisfies (43) with $T=\infty$. We know that $d{\fancyscript{G}}^T_\gamma (z_+) v= X_v(0)$ by the identity following (43), similarly $d{\fancyscript{G}}^\infty (z_+) v=Y_v(0)$. It remains to estimate $\mathopen \Vert X_v(0)-Y_v(0)\mathclose \Vert _2$. Define

$$\begin{aligned} \left\| X_v\right\| _* :=\sup _{s\in [0,\frac{1}{2}T]} s^{\frac{1}{2}} \left\| X_v(s)\right\| _X \end{aligned}$$

and abbreviate $\xi :=\xi ^T_{\gamma ,z_+}$ and $\eta :=\eta _{z_+}$. Then we obtain the $L^2$ estimate

$$\begin{aligned}&\left\| X_v(0)-Y_v(0)\right\| _2\\&\le \left( \int \limits _0^{{\frac{T}{2}}} +\int \limits _{{\frac{T}{2}}}^T\right) \left\| e^{\sigma A^-}\pi _-\right\| _{{\fancyscript{L}}(L^1,L^2)} \left\| df|_{\xi (\sigma )} \circ X_v(\sigma ) -df|_{\eta (\sigma )} \circ Y_v(\sigma ) \right\| _Y \, d\sigma \\&\quad +\int \limits _T^\infty \left\| e^{\sigma A^-}\pi _-\right\| _{{\fancyscript{L}}(L^1,L^2)} \left\| df|_{\eta (\sigma )} \circ Y_v(\sigma ) \right\| _Y \, d\sigma \\&\le \int \limits _0^{{\frac{T}{2}}} ce^{-\sigma \mu } \left( \kappa _* \underbrace{ \left\| \xi (\sigma )-\eta (\sigma )\right\| _X }_{\le \frac{4}{7}\rho _0 e^{-T\frac{\mu }{16}}, (41)} \left\| X_v(\sigma )\right\| _X + \kappa (\rho ) \left\| X_v(\sigma )-Y_v(\sigma )\right\| _X \right) d\sigma \\&\quad +\int \limits _{{\frac{T}{2}}}^T ce^{-\sigma \mu } \kappa (\rho ) \underbrace{ \left\| X_v(\sigma )\right\| _X }_{\le 2c\sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}} \left\| v\right\| _2} \, d\sigma +\int \limits _{{\frac{T}{2}}}^\infty ce^{-\sigma \mu } \kappa (\rho ) \underbrace{ \left\| Y_v(\sigma )\right\| _X }_{\le 2c\sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}} \left\| v\right\| _2} \, d\sigma \\&\le \frac{8}{7}\rho _0 c^2\kappa _* e^{-T\frac{\mu }{16}}\left\| v\right\| _2 \int \limits _0^{{\frac{T}{2}}} e^{-\sigma \frac{3}{2}\mu } \sigma ^{-\frac{1}{2}} d\sigma +c\kappa (\rho ) \left\| X_v-Y_v\right\| _* \int \limits _0^{{\frac{T}{2}}} e^{-\sigma \mu } \sigma ^{-\frac{1}{2}} d\sigma \\&\quad + 4c^2\kappa (\rho ) \left\| v\right\| _2 \int \limits _{{\frac{T}{2}}}^\infty e^{-\sigma \frac{3}{2}\mu }\sigma ^{-\frac{1}{2}} d\sigma \\&\le \frac{1}{8} \left\| X_v-Y_v\right\| _* + \left( \frac{1}{4} e^{-T\frac{\mu }{16}} +\frac{1}{4} e^{-T\frac{\mu }{2}}\right) \left\| v\right\| _2. \end{aligned}$$

Inequality two uses that by the Lipschitz Lemma 1 for $df$ and its Corollary 1

$$\begin{aligned}&\left\| df|_{\xi (\sigma )} \circ X_v(\sigma ) -df|_{\eta (\sigma )} \circ Y_v(\sigma ) \right\| _Y\\&= \left\| \left( df|_{\xi (\sigma )} -df|_{\eta (\sigma )}\right) \circ X_v(\sigma ) + df|_{\eta (\sigma )}\circ \left( X_v(\sigma ) -Y_v(\sigma )\right) \right\| _Y\\&\le \kappa _* \left\| \xi (\sigma )-\eta (\sigma )\right\| _X \left\| X_v(\sigma )\right\| _X + \kappa (\rho ) \left\| X_v(\sigma )-Y_v(\sigma )\right\| _X \end{aligned}$$

and $\mathopen \Vert df|_{\eta (\sigma )} \circ Y_v(\sigma )\mathclose \Vert _Y \le \kappa (\rho ) \mathopen \Vert Y_v(\sigma )\mathclose \Vert _X$, respectively. We treated the integral over $[T/2,T]$ with the triangle inequality and incorporated its $\eta$ part into the integral over $[T/2,\infty )$. Furthermore, use that $\mathopen \Vert \cdot \mathclose \Vert _{{\fancyscript{L}}(L^1,L^2)} \le \mathopen \Vert \cdot \mathclose \Vert _{{\fancyscript{L}}(L^1,X)}$ by the embedding $X\hookrightarrow L^2$, then apply Proposition 1. Consider inequality three. In the calculation above we indicated how to estimate certain terms. The estimates used are (41) and (45). We also used (45) for $Y_v$ with $T=\infty$. In inequality four we applied the estimate (47) to deal with all integrals and we used the smallness assumption (18) on $\rho _0$ and (20) on $\rho$.

It remains to prove exponential decay of the weighted sup norm $\mathopen \Vert \cdot \mathclose \Vert _*$ over the domain $\left[ 0,\frac{1}{2} T\right]$. Fix $s\in \left[ 0,\frac{1}{2} T\right]$ and conclude similarly as above that

$$\begin{aligned}&s^{\frac{1}{2}} \left\| X_v(s)-Y_v(s)\right\| _X\\&\le s^{\frac{1}{2}} c \int \limits _0^s \frac{e^{-(s-\sigma )\mu }}{(s\!-\!\sigma )^{\frac{3}{4}}} \left( \kappa _* \underbrace{ \left\| \xi (\sigma ) \!-\!\eta (\sigma )\right\| _X }_{\le \frac{4}{7}\rho _0e^{-T\frac{\mu }{16}}} \left\| X_v(\sigma )\right\| _X +\kappa (\rho ) \left\| X_v(\sigma ) -Y_v(\sigma )\right\| _X \right) d\sigma \\&\quad + s^{\frac{1}{2}} c \int \limits _s^{{\frac{T}{2}}} e^{(s-\sigma )\mu } \Bigl (\kappa _* \left\| \xi (\sigma ) \!-\!\eta (\sigma )\right\| _X \left\| X_v(\sigma )\right\| _X \!+\!\kappa (\rho ) \left\| X_v(\sigma ) -Y_v(\sigma )\right\| _X \Bigr ) d\sigma \\&\quad + s^{\frac{1}{2}}c\kappa (\rho )\left( \int \limits _{\frac{T}{2}}^T e^{(s-\sigma )\mu } \underbrace{ \left\| X_v(\sigma )\right\| _X }_{\le 2c\sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}}\mathopen \Vert v\mathclose \Vert _2} d\sigma + \int \limits _{\frac{T}{2}}^\infty e^{(s-\sigma )\mu } \underbrace{ \left\| Y_v(\sigma )\right\| _X }_{\le 2c\sigma ^{-\frac{1}{2}} e^{-\sigma \frac{\mu }{2}}\mathopen \Vert v\mathclose \Vert _2} d\sigma \right) \\&\le \frac{8}{7}\rho _0 c^2\kappa _* e^{-T\frac{\mu }{16}}\left\| v\right\| _2 \left( \int \limits _0^s \frac{e^{-(s-\sigma )\mu } e^{-\sigma \frac{\mu }{2}} s^{\frac{1}{2}}}{(s-\sigma )^{\frac{3}{4}} \sigma ^{\frac{1}{2}}} \, d\sigma + \int \limits _s^{\frac{T}{2}} \frac{e^{(s-\sigma )\mu } e^{-\sigma \frac{\mu }{2}} s^{\frac{1}{2}}}{\sigma ^{\frac{1}{2}}} \, d\sigma \right) \\&\quad +c\kappa (\rho ) \left\| X_v-Y_v\right\| _* \left( \int \limits _0^s \frac{e^{-(s-\sigma )\mu } s^{\frac{1}{2}}}{(s-\sigma )^{\frac{3}{4}} \sigma ^{\frac{1}{2}}} \, d\sigma + \int \limits _s^{\frac{T}{2}} \frac{e^{(s-\sigma )\mu } s^{\frac{1}{2}}}{\sigma ^{\frac{1}{2}}} \, d\sigma \right) \\&\quad +4c^2\kappa (\rho ) \left\| v\right\| _2 \int \limits _{{\frac{T}{2}}}^\infty e^{(s-\frac{3}{2}\sigma )\mu } \left( \frac{s}{\sigma }\right) ^{\frac{1}{2}} d\sigma \\&\le \left( \frac{8}{7}\rho _0 c^2\kappa _* \left( \frac{10}{\mu ^{1/4}} +\frac{1}{\mu }\right) +\frac{8 c^2\kappa (\rho )}{3\mu }\right) \frac{\left\| v\right\| _2}{e^{T\frac{\mu }{16}}} +c\kappa (\rho )\left( \frac{10}{\mu ^{1/4}} +\frac{1}{\mu }\right) \left\| X_v-Y_v\right\| _*\\&\le \Bigl (\frac{1}{4}+\frac{1}{4}\Bigr ) \left\| v\right\| _2 e^{-T\frac{\mu }{16}} +\frac{1}{4}\left\| X_v-Y_v\right\| _*. \end{aligned}$$

It is a side remark that without the weight factor $s^{1/2}$ in the $\mathopen \Vert \cdot \mathclose \Vert _*$ norm the integrals involving $(s-\sigma )^{-3/4}$ cause trouble, concerning boundedness, for $s$ near zero. It is another side remark that due to the presence of the extra factor $\mathopen \Vert X_v(\sigma )\mathclose \Vert _X$ we do not have to cut the interval $[\frac{T}{2},T]$ into two pieces as we did in step 6 above. Inequality three uses the following estimates. By (46) and by calculation, respectively, we obtain

$$\begin{aligned} \int \limits _0^s \frac{e^{-(s-\sigma )\mu }}{(s-\sigma )^{3/4}} \left( \frac{s}{\sigma }\right) ^{1/2} d\sigma \le 10/\mu ^{\frac{1}{4}},\quad \int \limits _s^{\frac{T}{2}} e^{(s-\sigma )\mu } \left( \frac{s}{\sigma }\right) ^{1/2} d\sigma \le \frac{1}{\mu }. \end{aligned}$$

To get the second of these estimates we used $s/\sigma \le 1$. Again by calculation we get

$$\begin{aligned} \int \limits _{\frac{T}{2}}^\infty e^{(s-\frac{3}{2}\sigma )\mu } \left( \frac{s}{\sigma }\right) ^{\frac{1}{2}} d\sigma \le \int \limits _{\frac{T}{2}}^\infty e^{(s-\frac{3}{2}\sigma )\mu } d\sigma \le \frac{2}{3\mu } e^{(s-\frac{3}{4}T)\mu } \le \frac{2}{3\mu } e^{-T\frac{\mu }{4}} \end{aligned}$$

since $s\le T/2\le \sigma$. In the final inequality four use smallness (18) of $\rho _0$ and (20) of $\rho$. Now take the supremum over $s\in [0,\frac{1}{2}T]$ to obtain $\left\| X_v-Y_v\right\| _* \le e^{-T\mu /16}\left\| v\right\| _2$. Together with the estimate for $\mathopen \Vert X_v(0)-Y_v(0)\mathclose \Vert _2$ derived earlier this concludes the proof of Step II. $\square$

This concludes the proof of Theorem 2.