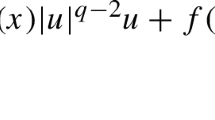Necessary condition for eigensolutions of the 1-Laplace operator by means of inner variations

Abstract

Eigenfunctions of the $p$-Laplace operator for $p>1$ are defined to be critical points of an associated variational problem or, equivalently, to be solutions of the corresponding Euler–Lagrange equation. In the highly degenerated limit case of the 1-Laplace operator eigenfunctions can also be defined to be critical points of the corresponding variational problem if critical points are understood on the basis of the weak slope. However, the associated Euler–Lagrange equation has many solutions that are not critical points and, thus, it cannot be used for an equivalent definition. The present paper provides a new necessary condition for eigenfunctions of the 1-Laplace operator by means of inner variations of the associated variational problem and it is shown that this condition rules out certain solutions of the Euler–Lagrange equation that are not eigenfunctions.

1 Introduction

For an open bounded $\Omega \subset {\mathbb R ^{n}}$ with Lipschitz boundary a solution of the variational problem

$$\begin{aligned} \int _\Omega |Du|^p\, dx \rightarrow \mathrm{Min!} \quad \text{ in}\ \mathcal W ^{1,p}_0(\Omega ) \quad \text{ with}\quad \int _\Omega |u|^p\, dx=1, \end{aligned}$$

(1.1)

$1<p<\infty$, has to satisfy the Euler–Lagrange equation

$$\begin{aligned} -\text{ div}|Du|^{p-2}Du = \lambda |u|^{p-2}u \quad \text{ on}\ \Omega . \end{aligned}$$

(1.2)

By definition, any solution $u\in \mathcal W ^{1,p}_0(\Omega )$ of this Euler–Lagrange equation is a critical point of the corresponding variational problem (1.1) and it is called an eigenfunction of the $p$-Laplace operator. In the limit case $p=1$ equation (1.2) becomes

$$\begin{aligned} -\text{ div}\frac{Du}{|Du|} = \lambda \frac{u}{|u|} \quad \text{ on}\ \Omega \end{aligned}$$

(1.3)

and, due to a number of difficulties, we cannot define eigenfunctions of the 1-Laplace operator as solutions of (1.3). First we observe that (1.1) for $p=1$ does not have a minimizer in $\mathcal W ^{1,1}_0(\Omega )$ but merely in $BV(\Omega )$ so that we have to consider

$$\begin{aligned} \int _\Omega d|Du| + \int _{\partial \Omega }|u| d\mathcal H ^{n-1} \rightarrow \mathrm{Min!} \quad \text{ in}\ BV(\Omega ) \quad \text{ with}\quad \int _\Omega |u|\, dx=1 \end{aligned}$$

(1.4)

instead of (1.1) where the surface integral replaces homogeneous boundary conditions (cf. Kawohl and Schuricht [21]). Since the characteristic function $u=\chi _C$ of a Cheeger set $C$ of $\Omega$, that is a strict subset of $\Omega$ in general, is always a minimizer of (1.4) (cf. [21]), Eq. (1.3) is highly degenerate and needs a suitable interpretation. In [21] it is shown that, as necessary condition for a minimizer of (1.4), in a first step (1.3) can be replaced with one equation, that we want to call single equation, containing well-defined substitutes for $Du/|Du|$ and $u/|u|$. But in the end, it turns out that (1.3) can be even replaced with infinitely many equations for $u$, a condition that we want to call multiple equation, cf. Sect. 2. Nevertheless, both interpretations of (1.3) seem to be inappropriate for a definition of eigenfunctions, since there are either too many solutions or, eventually, only minimizers solve it. While the definition of first eigenfunctions of the 1-Laplace operator as minimizers of the variational problem is clear, the definition of higher eigenfunctions as critical points of the variational problem is neither obvious nor unique. In Milbers and Schuricht [23] and Chang [6] eigenfunctions of the 1-Laplace operator are critical points of the variational problem in the sense that the weak or the strong slope of an assigned function vanishes. Here the different slopes and an interesting norm dependence may lead to different sets of eigenfunctions. Moreover, a completely different approach for defining higher eigenvalues of the 1-Laplace operator by means of multiple Cheeger sets is given by Parini [25]. It is still quite open how both approaches are related to each other.

The eigenfunctions that are critical points of (1.4) with vanishing weak or strong slope have to satisfy (1.3) in the sense of a single equation. However, this equation provides many solutions that are not expected to be critical points of the associated variational problem. Therefore further necessary conditions for critical points are needed to single out such solutions of (1.3) that are not critical. In calculus of variations perturbations of a solution $u$ of the form

$$\begin{aligned} v(x,t)=u(x)+t\xi (x) \quad \text{ for}\ \xi \in \mathcal C ^\infty _0(\Omega ), \end{aligned}$$

also called outer variations, are usually considered to derive the Euler–Lagrange equation as necessary condition. But, occasionally, also so called inner variations

$$\begin{aligned} v(x,t)=u(x+t\xi (x)) \quad \text{ for}\ \xi \in \mathcal C ^\infty _0(\Omega ,\mathbb R ^n) \end{aligned}$$

are used. However, the corresponding necessary condition is always satisfied for $\mathcal C ^2$-solutions of the Euler–Lagrange equation and, thus, it plays a minor role for many problems. But several examples show that inner variations might provide an additional information for nonsmooth minimizers, cf. Giaquinta and Hildebrandt [19, Chapter 3.1].

If one combines the method of inner variations with a Lagrange multiplier rule, a minimizer of problem (1.1) for $1<p<\infty$ has to satisfy

$$\begin{aligned}&\int _\Omega \left\langle |Du|^{p-2} Du, D\xi Du \right\rangle - |Du|^p \text{ div}\xi \,dx \nonumber \\&\quad = -\lambda \int _\Omega |u|^p \text{ div}\xi \,dx \quad \text{ for} \text{ all}\ \xi \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n). \end{aligned}$$

(1.5)

Since minimizers are merely in $\mathcal C ^{1,\alpha }_\mathrm{loc}(\Omega )$ (cf. DiBenedetto [14, Theorem 2]) but not in $\mathcal C ^2(\Omega )$, it is not clear whether (1.5) follows from (1.2) in general. But this fact is not disturbing, since eigenfunctions of the $p$-Laplace operator for $1<p<\infty$ are defined to be solutions of (1.2) and, by definition, they uniquely correspond to the critical points of the corresponding variational problem. However, in the limit case $p=1$ there is a completely different situation. Though also here the eigenfunctions are defined as critical points of the corresponding variational problem, this is done by means of a notion that is in some sense independent of the Euler–Lagrange equation. Thus it seems that eigenfunctions cannot be characterized as solutions of a reasonable version of (1.3).

Having in mind that eigenfunctions of the 1-Laplace operator might be piecewise constant and, thus, highly nonsmooth, one can expect that the evaluation of inner variations might provide an extra condition by giving meaning to the formal limit of (1.5)

$$\begin{aligned} \int _\Omega \left(\left\langle \frac{Du}{|Du|} , D\xi \frac{Du}{|Du|}\right\rangle -\text{ div}\xi \right) |Du| \,dx = -\lambda \int _\Omega |u| \text{ div}\xi \, dx. \end{aligned}$$

(1.6)

The derivation of a precise condition replacing (1.6) and the investigation of further consequences is the main purpose of the present paper. Here we have to extend the classical approach with inner variations, that had been used merely for minimizers before, to critical points of a highly degenerate variational problem. This way we provide a new condition that rules out many “artificial” solutions of the Euler–Lagrange equation (1.3) interpreted as single equation.

In Sect. 2 we briefly discuss difficulties in formulating the eigenvalue problem for the 1-Laplace operator and we present an example showing that the solutions of Eq. (1.3), interpreted as single equation, would provide a continuum of eigenvalues where “almost” each of them has a continuum of normalized eigenfunctions. Section 3 collects several tools from nonsmooth analysis. In particular we introduce the notions of weak and strong slope and we prove a new characterization of the weak slope for lower semicontinuous functions. Moreover we provide the convex subdifferentials for the nonsmooth functions occurring in problem (1.4). In Sect. 4 first higher eigenfunctions of the 1-Laplace operator are defined as critical points by means of the weak slope. Then we formulate a precise replacement for the formal limit equation (1.6) as necessary condition for eigenfunctions that is based on inner variations. The proof essentially rests on a proposition stated at the end of this section. Consequences of the new necessary condition are studied in Sect. 5. First it is shown that the “many” solutions of the single version of Eq. (1.3) that are not expected to be critical points do not satisfy the new condition. Then the one-dimensional case $n=1$ is investigated and all eigenfunctions are determined. At the end of Sect. 5 some general consequences of the new necessary condition for eigenfunctions are derived. The major proofs are collected in Sect. 6.

Notation

For a set $A$ let $\bar{A}$ denote its closure and $\partial A$ its boundary. Its indicator function $I_A$ and its characteristic function $\chi _A$ are defined by

$$\begin{aligned} I_A(x) := \left\{ \begin{array}{l@{\quad }l} 0&\text{ for}\ x\in A,\\ \infty&\text{ otherwise}, \end{array} \right. \quad \chi _A(x) := \left\{ \begin{array}{l@{\quad }l} 1&\text{ for}\ x\in A,\\ 0&\text{ otherwise}. \end{array} \right. \end{aligned}$$

The usual sign function on $\mathbb R$ is $\text{ sgn}(\cdot )$ and the set-valued sign function is

$$\begin{aligned} \text{ Sgn}(\alpha ):=\left\{ \begin{array}{l@{\quad }l} \{1\}&\text{ if}\ \alpha >0,\\ {[-1,1]}&\text{ if}\ \alpha =0,\\ \{-1\}&\text{ if}\ \alpha <0. \end{array} \right. \end{aligned}$$

The open $\delta$-neighborhood of $u$ is denoted by $B_\delta (u)$ and $\mathcal H ^k$ stands for the $k$-dimensional Hausdorff measure. We write $\mathcal L ^p(\Omega )$ for the $p$-integrable functions on $\Omega$ and $\mathcal L ^{p^{\prime }}(\Omega )$ with $\tfrac{1}{p}+\tfrac{1}{p^{\prime }}=1$ for its dual. The Sobolev space $\mathcal W ^{1,p}(\Omega )$ contains all $p$-integrable functions having $p$-integrable weak derivatives. $\mathcal C _0^\infty (\Omega )$ are the infinitely often differentiable functions with compact support. $BV(\Omega )$ denotes the space of functions of bounded variation where $|Du|$ is the total variation measure for these functions. $\text{ spt}f$ stands for the support of function $f$ and $f(x\pm )$ for its limit at $x$ from the right or left. For the Banach space $X$ its dual is $X^*$ and $\langle \cdot ,\cdot \rangle$ is the duality form on $X^*\times X$. The convex subdifferential of $F$ is $\partial F$ and we write $\text{ id}$ for the identity mapping.

2 Eigenvalue problem

Let $\Omega \subset \mathbb R ^n$ be an open bounded set with Lipschitz boundary. For $u\in BV(\Omega )$ we consider the variational problem

$$\begin{aligned} E(u):= \int _\Omega \,d|Du| + \int _{\partial \Omega } |u|\,d\mathcal H ^{n-1} \rightarrow \mathrm{Min!}, \quad u\in BV(\Omega ), \end{aligned}$$

(2.1)

with respect to the constraint

$$\begin{aligned} G(u):= \int _\Omega |u|\,dx = 1. \end{aligned}$$

(2.2)

Here the surface integral in (2.1) is a replacement for homogeneous boundary conditions in $BV(\Omega )$ (cf. [21]). Problem (2.1), (2.2) has always a solution $u\in BV(\Omega )$ which is not necessarily unique and which is called (first) eigenfunction of the 1-Laplace operator. In Kawohl and Schuricht [21] it is shown that any minimizer $u\in BV(\Omega )$ of (2.1), (2.2) satisfies the eigenvalue equation

$$\begin{aligned} -\text{ div}z = \lambda s { a.e.} \text{ on}\ \Omega , \quad \lambda =E(u) \end{aligned}$$

(2.3)

where $z\in \mathcal L ^\infty (\Omega ,\mathbb R ^n)$ and $s\in \mathcal L ^\infty (\Omega )$ are related to $u$ by the coupling conditions

$$\begin{aligned} \Vert z\Vert _{\mathcal L ^\infty }=1,\quad \text{ div}z\in \mathcal L ^{n}(\Omega ), \quad E(u)=-\int _\Omega u\,\text{ div}z\, dx \end{aligned}$$

(2.4)

and

$$\begin{aligned} s(x)\in \text{ Sgn}(u(x))\quad { a.e.} { on}\ \Omega . \end{aligned}$$

(2.5)

More precisely, adapting the usual direct methods of calculus of variations to the nonsmooth situation met in (2.1), (2.2), one obtains the existence of a vector field $z\in \mathcal L ^\infty (\Omega ,\mathbb R ^n)$ and a function $s\in \mathcal L ^\infty (\Omega )$ satisfying (2.4) and (2.5) such that (2.3) holds. In addition, it is shown in [21] by means of a new argument that for any $s\in \mathcal L ^\infty (\Omega )$ with (2.5) there is some $z\in \mathcal L ^\infty (\Omega ,\mathbb R ^n)$ with (2.4) such that the eigenvalue equation (2.3) is satisfied. Thus, since a typical minimizer vanishes on a set with positive measure, a minimizer $u$ has to satisfy infinitely many Euler–Lagrange equations in general. Let us call $u$ a solution of the single eigenvalue equation if it satisfies (2.3) for one selection $s$ satisfying (2.5) and a corresponding $z$ with (2.4) and let us call $u$ a solution of the multiple eigenvalue equation if it satisfies (2.3) for any selection $s$ satisfying (2.5) with corresponding vector fields $z$ satisfying (2.4).

Now a natural question is that of higher eigensolutions of the 1-Laplace operator. The eigenfunctions of the $p$-Laplace operator for $p>1$ are, by definition, the solutions of the Euler–Lagrange equation of the associated variational problem. But, by our previous arguments, it is not immediately clear how to define eigenfunctions in the limit case $p=1$. The multiple eigenvalue equation seems to be too restrictive for the definition of higher eigensolutions, since it is expected that merely minimizers of the variational problem might satisfy it. Alternatively one could consider eigenfunctions to be solutions of the single eigenvalue equation. But the example below demonstrates that also the single eigenvalue equation is inappropriate for the definition, since it possesses “too many” solutions providing a continuum of eigenvalues.

Example

Let $B = B_r(x_0) \subset \Omega$ be a ball with radius $r>0$ and center $x_0\in \Omega$ that is compactly contained in $\Omega$ (i.e. $\partial B$ does not touch $\partial \Omega$). We claim that the $BV$-function

$$\begin{aligned} v(x):= \frac{1}{|B|}\chi _B(x) \quad \text{ on}\ \Omega \end{aligned}$$

satisfies the single eigenvalue equation (2.3). Clearly,

$$\begin{aligned} \lambda = E(v)= \frac{|\partial B|}{|B|}= \frac{n}{r} . \end{aligned}$$

We choose the continuous vector field

$$\begin{aligned} z(x) := {\left\{ \begin{array}{ll} \frac{x_0-x}{r}&\text{ for}\ x \in B,\\ \frac{x_0-x}{|x_0-x|}&\text{ for}\ x\in \Omega \setminus B, \end{array}\right.} \end{aligned}$$

where all $z(x)$ point to the center $x_0$ of $B$. Obviously,

$$\begin{aligned} -\text{ div}z= \frac{n}{r} = \lambda \quad \text{ on}\ B. \end{aligned}$$

Since $z$ is the unit normal field to the foliation of $\Omega \setminus B$ by concentric spheres centered at $x_0$ and pointing to the center, we have that

$$\begin{aligned} -\text{ div}z(x) =\frac{n-1}{|x_0-x|} \quad \text{ on}\ \Omega \setminus B \end{aligned}$$

where the expression on the right hand side is just the mean curvature of the sphere containing point $x$ (notice that $\text{ div}z$ jumps across $\partial B$). We readily see that $\Vert z\Vert _{\mathcal L ^\infty }=1$, $z\in \mathcal L ^n(\Omega )$, and

$$\begin{aligned} -\int _\Omega v\,\text{ div}z\, dx = -\frac{1}{|B|}\int _B\text{ div}z\, dx = \frac{1}{|B|}\int _{\partial B}d\mathcal H ^{n-1} = \frac{|\partial B|}{|B|} = E(v), \end{aligned}$$

i.e. $z$ satisfies the coupling condition (2.4). Certainly

$$\begin{aligned} s(x) := {\left\{ \begin{array}{ll} 1&\text{ for}\ x \in B,\\ \frac{n-1}{n}\frac{r}{|x_0-x|}&\text{ for}\ x\in \Omega \setminus B, \end{array}\right.} \end{aligned}$$

satisfies the coupling condition (2.5) and we conclude that the eigenvalue equation

$$\begin{aligned} -\text{ div}z = \lambda s \quad \text{ a.e.} \text{ on} \Omega \text{ with}\ \lambda =\frac{n}{r} \end{aligned}$$

is satisfied. Consequently, $v$ satisfies the single eigenvalue equation.

Notice that we obtain “very many” solutions of the single eigenvalue equation by changing the center $x_0\in \Omega$ and the radius $r>0$ of the ball $B$. In particular there is a solution $v$ for any $\lambda \in (\tfrac{n}{r_0},\infty )$ where $r_0$ denotes the radius of the largest ball contained in $\Omega$. Moreover, for any $\lambda \in (\tfrac{n}{r_0},\infty )$ we have a continuum of normalized solutions $v$ by slightly moving the center $x_0$.

From the previous example we conclude that, in general, we would get a continuum of eigenvalues $\lambda$ with a continuum of normalized eigenfunctions $v$ for “most” eigenvalues if we would define eigenfunctions as solutions of the single eigenvalue equation. But this seems to be inappropriate. Thus it turns out that neither the single nor the multiple eigenvalue equation are suitable to define higher eigenfunctions of the 1-Laplace operator.

Alternatively we can consider to define higher eigenfunctions as critical points of $E$ subject to the constraint $G(v)=1$. But, in contrast to the classical case $p>1$, here we are confronted with the difficulty that both $E$ and $G$ are not differentiable and, therefore, the usual definition of critical points being solutions of the Euler–Lagrange equation is not available. However we can use a theory of critical points for nondifferentiable functionals that uses a notion of critical points independent of an Euler–Lagrange equation. Let us provide the necessary tools in the next section.

3 Tools of nonsmooth analysis

3.1 Weak slope

Let us introduce the notion of weak slope as formulated in Degiovanni and Marzocchi [12]. We assume $X$ to be a metric space endowed with metric $d$ and let $f : X \rightarrow \mathbb R$ be a continuous function. For every $u\in X$ we denote by $|df|(u)$ the supremum of all $\omega \in [0,\infty )$ for which there exist $\delta >0$ and a continuous map $\mathcal H : B_\delta (u) \times [0,\delta ] \rightarrow X$ such that for all $v\in B_\delta (u)$ and all $t\in [0,\delta ]$

$$\begin{aligned} d(\mathcal H (v,t),v)&\le t,\end{aligned}$$

(3.1)

$$\begin{aligned} f(\mathcal H (v,t))&\le f(v)-\omega t. \end{aligned}$$

(3.2)

The extended real number $|df|(u)$ is called the weak slope of $f$ at $u$. Note that for differentiable functions the weak slope corresponds to the norm of the gradient.

Now we consider a lower semicontinuous function $f:X\rightarrow \mathbb R \cup \{\infty \}$. We define the domain of $f$ by

$$\begin{aligned} \mathcal D (f) := \{u\in X \,|\, f(u)<\infty \} \end{aligned}$$

(3.3)

and the epigraph of $f$ by

$$\begin{aligned} \mathrm{epi} \,(f):= \{(u,\xi ) \in X\times \mathbb R \,|\, f(u)\le \xi \}. \end{aligned}$$

The set $X\times \mathbb R$ will be endowed with the metric

$$\begin{aligned} d((u,\xi ),(v,\mu )) = (d(u,v)^2 + (\xi -\mu )^2)^{1/2} \end{aligned}$$

(3.4)

and $\mathrm{epi} \,(f)$ with the induced metric. Using the continuous function

$$\begin{aligned} \mathcal G _f : \mathrm{epi} \,(f) \rightarrow \mathbb R , \quad \mathcal G _f(u,\xi )=\xi , \end{aligned}$$

(3.5)

we define the weak slope of $f$ at $u\in \mathcal D (f)$ as

$$\begin{aligned}|df|(u) := {\left\{ \begin{array}{ll} \frac{|d\mathcal G _f|(u,f(u))}{\sqrt{1-|d\mathcal G _f|(u,f(u))^2}}&\text{ for}\ |d\mathcal G _f|(u,f(u))<1,\\ \infty&\text{ for}\ |d\mathcal G _f|(u,f(u))=1. \end{array}\right.}\end{aligned}$$

The idea of this definition is to reduce the study of the lower semicontinuous function $f$ to that of the Lipschitz continuous function $\mathcal G _f$. When $f$ is finite and continuous on $X$ this definition is consistent with the first definition of the weak slope for continuous functions. Occasionally we denote the weak slope of $f$ at $u$ by $|df|^X(u)$ in order to indicate that it is taken in the metric space $X$.

We say that $u\in \mathcal D (f)$ is a critical point of $f$ if $|df|(u)=0$. The value $c\in \mathbb R$ is called a critical value of $f$ if there exists a critical point $u \in \mathcal D (f)$ of $f$ with $f(u)=c$. Note that if $(u,f(u)) \in \mathrm{epi} \,(f)$ is a critical point of $\mathcal G _f$ then $u$ is also a critical point of $f$. The bijective correspondence between the critical points of $f$ and those of $\mathcal G _f$ is given if

$$\begin{aligned} \inf \{|d\mathcal G _f|(u,\xi ) \,|\, f(u)<\xi \} >0, \end{aligned}$$

(3.6)

cf. Canino and Degiovanni [4, Theorem 1.5.5]. If $f$ is finite and continuous, we have $|d\mathcal G _f|(u,\xi )=1$ whenever $f(u)<\xi$. The same property holds for some important classes of lower semicontinuous functions (cf. Canino and Perri [5], Corvellec et al. [9], Degiovanni and Marzocchi [12]).

We are interested in critical points of $f$ under a constraint $g(u)=0$ where $g:X\rightarrow \mathbb R$ is a locally Lipschitz continuous function. We set

$$\begin{aligned} K:= \{ u\in X \,|\, g(u)=0 \} \end{aligned}$$

(3.7)

and call $u\in \mathcal D (f)\cap K$ a critical point of $f$ with respect to $K$ (or with respect to $g=0$) if $u$ is a critical point of $f$ on the metric space $K$ with induced metric $d$ of $X$, i.e. if $|df|^K(u)=0$. Using the indicator function $I_K$ we readily obtain the analytically useful fact that $|df|^K(u)=0$ if and only if $|d(f+I_K)|^X(u)=0$ (cf. Milbers and Schuricht [24]). Notice that this definition of critical points is independent of an associated Euler–Lagrange equation. But, in order to obtain such an equation as necessary condition for critical points let us formulate a special version of a Lagrange multiplier rule given in Degiovanni and Schuricht [13]. Here $X$ is assumed to be a Banach space, $\partial f(v),\,\partial g(v)\subset X^*$ denote the convex subdifferentials of $f$, $g$ at $v$, and $g^{\prime }(v;w)$ be the directional derivative of $g$ at $v$ in direction $w$.

Proposition 3.1

Let $f:X\rightarrow \mathbb R \cup \{\infty \}$ be convex and lower semicontinuous and let $g:X\rightarrow \mathbb R$ be convex and locally Lipschitz continuous. If $u\in \mathcal D (f)\cap K$ is a critical point of $f$ with respect to $K$ such that there exist $u_\pm \in \mathcal D (f)$ with $\pm g^{\prime }(u;u-u_\pm )<0$, then $\partial f(u)\ne \emptyset$ and there are $\lambda \in \mathbb R$, $f^*\in \partial f(u), g^*\in \partial g(u)$ such that $f^*+\lambda g^*=0$.

Notice that the property of $u\in X$ being critical depends on the metric on $X$ in general. We say $u$ is a critical point on $X$ if this uniquely refers to the corresponding metric $d$ on $X$.

For an upper estimate of the weak slope one can use the strong slope (cf. De Giorgi et al. [10]) defined for a lower semicontinuous function $f:X\rightarrow \mathbb R \cup \{\infty \}$ at $u\in \mathcal D (f)$ by

$$\begin{aligned} |\nabla f|(u) := \left\{ \begin{array}{l@{\quad }l} {\mathop {\text{ lim} \text{ sup}}\limits _{v\rightarrow u}\frac{f(u)-f(v)}{d(u,v)}}&\text{ if}\ u \text{ is} \text{ not} \text{ a} \text{ local} \text{ minimum,}\\ 0&\text{ if}\ u \text{ is} \text{ a} \text{ local} \text{ minimum.} \end{array} \right. \end{aligned}$$

It is easily seen that $|df|(u)\le |\nabla f|(u)$. Occasionally, we call $u\in X$ a strong critical point of $f$ on $X$ if $|\nabla f|(u)=0$ and, clearly, strong critical points are critical points. $|\nabla f|^X(u)$ indicates the underlying metric space $X$.

For analytical arguments the previous indirect definition of $|df|(u)$ for a lower semicontinuous function $f$ is not very convenient. Therefore, let us provide a more direct characterization where we use the notation

$$\begin{aligned} f^\beta := \{v\in X\,|\, f(v)\le \beta \} \end{aligned}$$

(cf. Chang [6] for a similar characterization).

Lemma 3.2

Let $f:X\rightarrow \mathbb R \cup \{\infty \}$ be lower semicontinuous and let $u\in \mathcal D (f)$. Then $|df|(u)$ is the supremum of all $\omega \in [0,\infty )$ for which there exist $\delta >0$, $\beta >f(u)$, and a continuous map $\mathcal H :(B_\delta (u)\cap f^\beta )\times [0,\delta ]\rightarrow X$ such that

$$\begin{aligned} d(\mathcal H (v,t),v)\le t, \quad f(\mathcal H (v,t))\le f(v)-\omega t \end{aligned}$$

(3.8)

for all $v\in B_\delta (u)\cap f^\beta$ and all $t\in [0,\delta ]$.

Proof

If for some $\omega \in [0,\infty )$ there exist $\delta$, $\beta$, $\mathcal H$ as in the lemma, then $|df|(u)\ge \omega$ according to [12, Proposition 2.5]. Hence $|df|(u)\ge {\tilde{\omega }}$ if $\tilde{\omega }$ denotes the supremum in the lemma.

If $|df|(u)=0$ the assertion is readily verified with $\mathcal H (v,t)=v$. Let us now assume that $|df|(u)>0$. According to [11], the weak slope $|df|(u)$ is the supremum of all $\omega \in [0,\infty )$ for which there exist ${\tilde{\delta }}>0$ and a continuous map $\tilde{\mathcal H }:(B_{\tilde{\delta }}(u,f(u))\cap \mathrm{epi} \,{f})\times [0,{\tilde{\delta }}]\rightarrow X$ such that

$$\begin{aligned} d(\tilde{\mathcal H }((v,\mu ),t),v)\le t, \quad f(\tilde{\mathcal H }((v,\mu ),t))\le \mu -\omega t \end{aligned}$$

(3.9)

for all $(v,\mu )\in B_{{\tilde{\delta }}}(u,f(u))\cap \mathrm{epi} \,(f)$ and all $t\in [0,{\tilde{\delta }}]$. Let us now fix some $\omega \in (0,|df|(u))$ and let us choose corresponding ${\tilde{\delta }}$ and $\tilde{\mathcal H }$ as above. Clearly, there is $\delta _1\in (0,{\tilde{\delta }})$ such that

$$\begin{aligned} B_{\delta _1}(u)\times (f(u)-\delta _1,f(u)+\delta _1) \subset B_{{\tilde{\delta }}}(u,f(u)). \end{aligned}$$

Since $f$ is lower semicontinuous, there is $\delta \in (0,\delta _1)$ such that

$$\begin{aligned} f(v) > f(u)-\delta _1 \quad \text{ for} \text{ all}\ v\in B_\delta (u). \end{aligned}$$

With $\beta :=\delta _1/2$ we readily get

$$\begin{aligned} (v,f(v))\in B_{{\tilde{\delta }}}(u,f(u))\cap \mathrm{epi} \,(f) \quad \text{ for} \text{ all}\ v\in B_\delta (u)\cap f^\beta . \end{aligned}$$

For the continuous map $\mathcal H :B_\delta (u)\cap f^\beta \times [0,\delta ]\rightarrow X$ with $\mathcal H (v,t):=\tilde{\mathcal H }((v,f(v)),t)$ we obtain (3.8) from (3.9). By the arbitrariness of $\omega$ we conclude that $|df|(u)\le {\tilde{\omega }}$ which yields the assertion. $\square$

3.2 Some special subdifferentials

Let $\Omega \subset \mathbb R ^n$ be an open bounded set with Lipschitz boundary and let us consider the convex functions $E,G:BV(\Omega )\rightarrow \mathbb R$ given by

$$\begin{aligned} E(u)= \int _\Omega \,d|Du|+\int _{\partial \Omega } |u|\,d\mathcal H ^{n-1}, \quad G(u)= \int _\Omega |u|\,dx = 1 \end{aligned}$$

as defined in (2.1), (2.2). Since the structure of the dual space $BV(\Omega )^*$ is not known very well, we cannot compute the subdifferentials $\partial E(u)$ and $\partial G(u)$ directly. Therefore, for $1\le q\le \tfrac{n}{n-1}$, let us first consider the extended function $E_q:\mathcal L ^q(\Omega )\rightarrow \mathbb R \cup \{\infty \}$ given by

$$\begin{aligned} E_q(u):= {\left\{ \begin{array}{ll} \int _\Omega \,d|Du| + \int _{\partial \Omega } |u|\,d\mathcal H ^{n-1}&\text{ for}\ u\in BV(\Omega ),\\ \infty&\text{ for}\ u\in \mathcal L ^q(\Omega )\setminus BV(\Omega ), \end{array}\right.} \end{aligned}$$

and the natural extension $G_q:\mathcal L ^q(\Omega )\rightarrow \mathbb R$ according to

$$\begin{aligned} G_q(u) := \int _\Omega |u|\,dx = 1. \end{aligned}$$

Proposition 3.3

Let $1\le q\le \tfrac{n}{n-1}$. Then:

• (1) The functional $E_q$ is convex and lower semicontinuous on $\mathcal L ^q(\Omega )$. Moreover, $E^*\in \partial E_q(u)$ for $u\in \mathcal L ^q(\Omega )\cap BV(\Omega )$ if and only if there exists a vector field $z\in \mathcal L ^\infty (\Omega ,\mathbb R ^n)$ with

  $$\begin{aligned} \Vert z\Vert _{\mathcal L ^\infty } \le 1, \quad E^*=-\text{ div}z\in \mathcal L ^{q^{\prime }}(\Omega ),\quad E_q(u)=\langle E^*,u\rangle = -\int _\Omega u\,\text{ div}z \,dx.\nonumber \\ \end{aligned}$$

  (3.10)

  If $E(u)>0$, then $\Vert z\Vert _{\mathcal L ^\infty }=1$.

• (2) The functional $G_q$ is convex and Lipschitz continuous on $\mathcal L ^q(\Omega )$. Moreover, $G^*\in \partial G_q(u)$ for $u\in \mathcal L ^q(\Omega )$ if and only if

  $$\begin{aligned} G^*(x)\in \text{ Sgn}(u(x)) \quad \text{ a.e.} \text{ on} \ \Omega . \end{aligned}$$

  (3.11)

Proof

This is shown in Kawohl and Schuricht [21], but without the case $q=1$ for (1) which remains to be shown.

First let $E^*\in \partial E_1(u)$ for $u\in BV(\Omega )$. Then $E_1(v)-E_1(u)\ge \langle E^*,v-u\rangle$ for all $v\in \mathcal L ^1(\Omega )$. Since $E_1=E_q$ on $\mathcal L ^q(\Omega )$ for $q>1$, the element $E^*\in \mathcal L ^\infty (\Omega )$ belongs also to $\partial E_q(u)$ and, thus, must have the structure as in (3.10). Now let $E^*=-\text{ div}z\in \mathcal L ^\infty (\Omega )$ as in (3.10) for $u\in BV(\Omega )$. Obviously $E^*\in \partial E_q(u)$ for any $q\in (1,\tfrac{n}{n-1}]$ and $E_q(v)-E_q(u)\ge \langle E^*,v-u\rangle$ for all $v\in \mathcal L ^q(\Omega )\supset BV(\Omega )$. Since $E_1=E_q$ on $BV(\Omega )$ and $E_1=\infty$ on $\mathcal L ^1(\Omega )\setminus BV(\Omega )$, the previous inequality remains true with $q=1$ for all $v\in \mathcal L ^1(\Omega )$ and, hence, $E^*\in \partial E_1(u)$. But this verifies the assertion. $\square$

Let us now consider an element $G^*\in \partial G(u)\subset BV(\Omega )^*$ for $u\in BV(\Omega )$. By definition,

$$\begin{aligned} G(v)-G(u)\ge \langle G^*,v-u\rangle \quad \text{ for} \text{ all}\ v\in BV(\Omega ). \end{aligned}$$

(3.12)

With $v=2u, v=0$ we get $G(u)=\langle G^*,u\rangle$ and, thus, $\langle G^*,v\rangle \le G_1(v)$ for all $v\in BV(\Omega )$. The Hahn–Banach theorem provides a continuous linear extension $G_1^*\in \mathcal L ^\infty (\Omega )$ of $G^*$ on $\mathcal L ^1(\Omega )$ that respects the inequality. Since (3.12) remains valid with $G_1$ and $G_1^*$ for all $v\in \mathcal L ^1(\Omega )$, we obtain $G_1^*\in \partial G_1(u)$ (cf. also Chang [6]).

Corollary 3.4

We have $\partial G(u)=\partial G_1(u)$ for $u\in BV(\Omega )$, i.e. $G^*\in \partial G(u)$ if and only if (3.11) is satisfied.

The next result describes the relation between the subdifferentials $\partial E_q(u)$ and $\partial E(u)$.

Lemma 3.5

Let $f:BV(\Omega )\rightarrow \mathbb R \cup \{\infty \}$ be convex and, for $1\le q\le \tfrac{n}{n-1}$, let $f_q:\mathcal L ^q(\Omega )\rightarrow \mathbb R \cup \{\infty \}$ be the extension of $f$ with $f(v)=\infty$ for all $v\in \mathcal L ^q(\Omega )\setminus BV(\Omega )$. Then

$$\begin{aligned} \partial f(u) \cap \mathcal L ^{q^{\prime }}(\Omega ) = \partial f_q(u) \quad \text{ for} \text{ all}\ u\in \mathcal D (f)\subset BV(\Omega ). \end{aligned}$$

This fact is already used in [6] but without proof. Thus let us briefly sketch it for completeness.

Proof

Let $f^*\in \partial f_q(u)\subset \mathcal L ^{q^{\prime }}(\Omega )$. By $BV(\Omega )\subset \mathcal L ^q(\Omega )$, we get $f(v)-f(u)\ge \langle f^*,v-u\rangle$ for all $v\in BV(\Omega )$. Then $\mathcal L ^{q^{\prime }}(\Omega )\subset BV(\Omega )^*$ implies $f^*\in \partial f(u)$. For $f^*\in \partial f(u) \cap \mathcal L ^{q^{\prime }}(\Omega )$ we have $f(v)-f(u)\ge \langle f^*,v-u\rangle$ for all $v\in BV(\Omega )$. This remains true for $f_q$ instead of $f$ and all $v\in \mathcal L ^q(\Omega )$ and, hence, $f^*\in \partial f_q(u)$. $\square$

4 Higher eigensolutions

Based on our preliminary discussion we define eigenfunctions of the 1-Laplace operator to be certain constrained critical points of the total variation where we distinguish different cases depending on the underlying norm. More precisely, $u\in BV(\Omega )$ is called $BV$-eigenfunction if it is a critical point of $E$ with respect to $G(v)=1$ on $BV(\Omega )$ (i.e., subject to the $BV$-norm) and $u\in BV(\Omega )$ is called ${\mathcal L }^{q}$-eigenfunction if it is a critical point of $E_q$ subject to $G_q(v)=1$ on $\mathcal L ^q(\Omega )$ (i.e., subject to the $\mathcal L ^q$-norm). Occasionally we use the notion of strong $BV$-eigenfunction or strong ${\mathcal L ^{q}}$-eigenfunction which refers to corresponding strong critical points. With

$$\begin{aligned} K := \{v\in BV(\Omega )\,|\, G(v)=1\}, \quad K_q := \{v\in \mathcal L ^q(\Omega )\,|\, G_q(v)=1\}, \end{aligned}$$

we readily see that $u\in BV(\Omega )$ is $BV$-eigenfunction if and only if $u$ is critical point of $E+I_K$ in $BV(\Omega )$ and it is $\mathcal L ^q$-eigenfunction if and only if it is critical point of $E_q+I_{K_q}$ in $\mathcal L ^q(\Omega )$.

Now let $u\in BV(\Omega )$ be $BV$-eigenfunction or $\mathcal L ^q$-eigenfunction, i.e. we have either $|d(E+I_K)|^{BV}(u)=0$ or $|d(E_q+I_{K_q})|^{\mathcal L ^q}(u)=0$. Then the assumptions of Proposition 3.1 are obviously satisfied for the functions $E$, $G$ on $BV(\Omega )$ or for $E_q$, $G_q$ on $\mathcal L ^q(\Omega )$, respectively, with $u_+=2u$, $u_-=0$. Thus, correspondingly, there are either $E^*\in \partial E(u)$, $G^*\in \partial G(u)$ or $E^*\in \partial E_q(u)$, $G^*\in \partial G_q(u)$ and $\lambda \in \mathbb R$ such that

$$\begin{aligned} E^* + \lambda G^* = 0 \quad \text{ in}\ BV(\Omega )^* \text{ or} \mathcal L ^{q^{\prime }}(\Omega ). \end{aligned}$$

We call $\lambda$ eigenvalue corresponding to eigenfunction $u$. By Proposition 3.3 and Corollary 3.4 we know that $G^*\in \mathcal L ^\infty (\Omega )$ in any case and, hence, also $E^*\in \mathcal L ^\infty (\Omega )$. Consequently, Proposition 3.3 combined with Lemma 3.5 provides the structure of $E^*$ and we obtain the next result (cf. also Milbers and Schuricht [24], Chang [6]).

Proposition 4.1

Let $u\in BV(\Omega )$ be $BV$-eigenfunction or $\mathcal L ^q$-eigenfunction, $q\in [1,\tfrac{n}{n-1}]$, of the 1-Laplace operator. Then there exists a measurable selection $s(x)\in \text{ Sgn}(u(x))$ for a.e. $x\in \Omega$ and a vector field $z\in \mathcal L ^\infty (\Omega ,\mathbb R ^n)$ with

$$\begin{aligned} \Vert z\Vert _{\mathcal L ^\infty } = 1, \quad \text{ div}z\in \mathcal L ^\infty (\Omega ),\quad E(u) = -\int _\Omega u \text{ div}z \,dx \end{aligned}$$

(4.1)

such that

$$\begin{aligned} -\text{ div}z = \lambda s \text{ a.e.} \text{ on}\ \Omega , \quad \lambda =E(u). \end{aligned}$$

(4.2)

This means that $BV$-eigenfunctions and $\mathcal L ^q$-eigenfunctions $u$ satisfy the single eigenvalue equation (2.3) and that the corresponding eigenvalue $\lambda$ equals $E(u)$.

In Milbers and Schuricht [24] the existence of a sequence of pairs $\pm u_k\in BV(\Omega )$ of critical points of $E_q+I_{K_q}$ on $\mathcal L ^q(\Omega )$ with $\lambda _k=E(u_k)\rightarrow \infty$ is shown for $1\le q<\tfrac{n}{n-1}$ (critical points $\pm u_k\in BV(\Omega )$ of $E_1+I_{K_1}$ on $\mathcal L ^1(\Omega )$ are verified in Chang [6] without analyzing the convergence of $\lambda _k$). Clearly, all these critical points are $\mathcal L ^q$-eigenfunctions and satisfy the single eigenvalue equation (2.3). Unfortunately that equation cannot identify the eigenfunctions, since it has too many solutions according to our previous example. Therefore it is reasonable to look for further necessary conditions eigensolutions have to satisfy. We deduce a new additional condition for $\mathcal L ^1$-eigenfunctions by means of inner variations that can be considered as precise interpretation of the formal equation (1.6).

For $u\in BV(\Omega )$ let $\sigma :\Omega \rightarrow \mathbb R ^n$ be a $|Du|$-measurable vector field such that

$$\begin{aligned} |\sigma (x)|=1 \quad |Du|\text{-a.e.} \text{ on} \Omega \quad \text{ and}\quad Du = \sigma |Du|, \end{aligned}$$

(4.3)

i.e. $Du=\sigma |Du|$ is the polar decomposition of the measure $Du$, cf. Ambrosio et al. [1, Corollary 1.29].

Theorem 4.2

Let $\Omega \subset \mathbb R ^n$ be an open bounded set with Lipschitz boundary, let $u\in BV(\Omega )$ be ${{\mathcal L }^{1}}$-eigenfunction of the 1-Laplace operator, and let $\sigma$ be the vector field from the polar decomposition $Du=\sigma |Du|$. Then for each $\xi \in C_0^\infty (\Omega ,\mathbb R ^n)$ we have

$$\begin{aligned} \int _\Omega \langle \sigma , D\xi \sigma \rangle - \text{ div}\xi \, d|Du|=-\lambda \int _\Omega |u| \text{ div}\xi \,dx \end{aligned}$$

(4.4)

with $\lambda =E(u)$ (notice that $D\xi \sigma =(D\xi )\sigma$).

As a direct consequence of the Gauss–Green formula for the BV-function $|u|$ and using the continuity of $\xi$ (cf. Milbers and Schuricht [23, Sect. 3]), we obtain an alternative expression for the right hand side in (4.4) by

$$\begin{aligned} -\lambda \int _\Omega |u| \text{ div}\xi \,dx = \lambda \int _\Omega \xi \cdot dD|u| \quad \text{ for} \text{ all}\ \xi \in C_0^\infty (\Omega ,\mathbb R ^n). \end{aligned}$$

(4.5)

The proof of the theorem will be carried out in several steps in Sect. 6 where the next observation is an essential ingredient.

Proposition 4.3

Let $X\subset \mathcal L ^1(\Omega )$ be a Banach space continuously embedded into $\mathcal L ^1(\Omega )$ and let $K^X:=\{v\in X|\, G(v)=1\}$. Then $u\in X$ is a critical point of $E$ with respect to $K^X$ on $X$ if and only if $u\in X$ is a critical point of $F:=E-\lambda G$ on $X$ with $\lambda =E(u)$.

The proof can be found in Sect. 6 below.

5 Consequences

5.1 Previous example

We demonstrate how the new necessary condition from Theorem 4.2 works for our example from Sect. 2 where we had constructed a continuum of solutions for the single Euler–Lagrange equation. In fact all these solutions are candidates for eigenfunctions of the 1-Laplace operator. Recall that for any ball $B=B_r(x_0)\in \mathbb R ^n$ with $\overline{B} \subset \Omega$ the function

$$\begin{aligned} v(x):= \frac{1}{|B|}\chi _B(x) \end{aligned}$$

satisfies the single eigenvalue equation (2.3). If $v$ would be an $\mathcal L ^1$-eigenfunction, then it has to satisfy condition (4.4)

$$\begin{aligned} \int _\Omega \langle \sigma ,D\xi \sigma \rangle -\text{ div}\xi \, d|Dv| = -\lambda \int _\Omega |v| \text{ div}\xi \,dx \end{aligned}$$

for any $\xi \!\in \! C_0^\infty (\Omega ,\mathbb R ^n)$ with $\lambda = E(v) = n/r$ (cf. Sect. 2). We pick a $\xi \!\in \! C_0^\infty (\Omega ,\mathbb R ^n)$ such that $\xi (x)= x$ on a set containing $\overline{B}$. Then we have

$$\begin{aligned} D\xi (x) = \text{ id}\quad \text{ and}\quad \text{ div}\xi (x)= n \text{ on}\ \overline{B}. \end{aligned}$$

Moreover, we know that $|Dv| = \frac{1}{|B|} \mathcal H ^{n-1} \lfloor \partial B$, cf. Evans and Gariepy [16, p. 169]. Thus we get for the left hand side

$$\begin{aligned} \int _\Omega \langle \sigma ,D\xi \sigma \rangle -\text{ div}\xi \, d|Dv|&= \frac{1}{|B|}\int _{\partial B} \langle \sigma , \sigma \rangle -n \, d\mathcal H ^{n-1} \\&= \frac{1}{|B|} \int _{\partial B} (1-n) \,d\mathcal H ^{n-1} = \frac{|\partial B|}{|B|} (1-n) \\&= \frac{n(1-n)}{r} \end{aligned}$$

and for the right hand side

$$\begin{aligned} -\lambda \int _\Omega |v| \text{ div}\xi \,dx = -\frac{n}{r} \frac{1}{|B|} \int _B n \,dx = -\frac{n^2}{r}, \end{aligned}$$

which implies the contradiction

$$\begin{aligned} n-1 = n. \end{aligned}$$

Consequently, the new condition (4.4) confirms our expectation and shows its ability by ruling out all these functions $v$ from being $\mathcal L ^1$-eigenfunctions of the 1-Laplace operator.

5.2 One-dimensional case $n=1$

Here we want to investigate eigensolutions of the 1-Laplace operator for the special case $\Omega \subset \mathbb R ^1$ where we can restrict our attention to the case $\Omega =(0,1)$. This case has been already investigated to some extend in Chang [6] where, however, the focus was on strong $\mathcal L ^1$-eigenfunctions $u$, i.e., the strong slope $|\nabla (E_1+I_{K_1})|(u)=0$ with respect to the $\mathcal L ^1$-norm, cf. Sect. 3. Notice that strong $\mathcal L ^1$-eigenfunctions are also $\mathcal L ^1$-eigenfunctions, since the strong slope is an upper bound for the weak slope, but the opposite is not clear in general.

Let us start with a necessary condition for solutions of the single eigenvalue equation (2.3) that reduces to

$$\begin{aligned} -z^{\prime }(x) = \lambda s(x) \quad \text{ a.e.} \text{ on}\ (0,1), \quad \lambda = E(u) \end{aligned}$$

(5.1)

where $s$ and $z$ are coupled with $u$ by

$$\begin{aligned}&s\in \mathcal L ^\infty (0,1) \quad \text{ with}\ s(x)\in \text{ Sgn}(u(x)) \quad \text{ a.e.} \text{ on}\ (0,1),\end{aligned}$$

(5.2)

$$\begin{aligned}&z\in \mathcal W ^{1,\infty }(0,1) \quad \text{(i.e.}\; z \text{ is} \text{ Lipschitz} \text{ continuous}), \quad \Vert z\Vert _{\mathcal L ^\infty } =1,\end{aligned}$$

(5.3)

$$\begin{aligned}&E(u)=-\int _0^1uz^{\prime }\,dx. \end{aligned}$$

(5.4)

For any $(a,b)\subset (0,1)$ we have the Gauss–Green formula

$$\begin{aligned} \int _a^b uz^{\prime }\, dx + \int _{(a,b)}z\, d(Du) = z(b)u(b-)-z(a)u(a+) \end{aligned}$$

(5.5)

(notice that $u(a+)$, $u(b-)$ agree with $u$ on the boundary of $(a,b)$ in the sense of trace) and we obtain a condition that is equivalent to (5.4)

$$\begin{aligned} z Du \!=\! |Du| \quad \text{(in} \text{ the} \text{ sense} \text{ of} \text{ measures),} \quad z(0)\!\in \!\text{ Sgn}(u(0+)), \; -z(1)\!\in \!\text{ Sgn}(u(1-))\nonumber \\ \end{aligned}$$

(5.6)

(cf. Milbers and Schuricht [23, Sect. 3]).

Proposition 5.1

Let $u\in BV(0,1)$ be a solution of the single eigenvalue equation (5.1). Then there are points $0=a_0<a_1<\cdots <a_k=1$, $\alpha _j\in \mathbb R$, $j=1,\dots ,k$, such that with $I_j:=(a_{j-1},a_j)$

$$\begin{aligned} u = \sum _{j=1}^k \alpha _j\chi _{I_j} \quad a.e. on (0,1). \end{aligned}$$

(5.7)

Though this is already shown in [6] let us provide a brief alternative proof.

Proof

Using the polar decomposition $Du=\sigma |Du|$ (here $\sigma (x)=\pm 1$ for all $x$) in (5.6), we get $z(x)=\sigma (x)$ for $|Du|$-a.e. $x\in (0,1)$. Thus,

$$\begin{aligned} z(x) \in \{\pm 1\} \quad |Du|\text{-a.e.} \text{ on}\ (0,1). \end{aligned}$$

(5.8)

Since $u\in BV(0,1)$, we have

$$\begin{aligned} u(y-)-u(x+) = Du((x,y)) = \int _{(x,y)}d(Du) \quad \text{ for} \text{ all}\ 0\le x<y\le 1 \end{aligned}$$

(5.9)

(cf. Ambrosio et al. [1, Theorem 3.28]).

Let $I\subset (0,1)$ be a nonempty open interval with length $|I|\le 1/\lambda$. If $|z(x)|<1$ on an open interval ${\tilde{I}}\subset I$, then $Du=0$ on ${\tilde{I}}$ by (5.8) and $u$ is constant on ${\tilde{I}}$ by (5.9). If $\{x\in I|\,|z(x)|=1\}\ne \emptyset$, then $z$ cannot change sign on $I$, since $|z^{\prime }|\le \lambda$ by (5.1). Assume that $z(a)=z(b)=1$ for some $a,b\in I$ with $a<b$. Then $zDu=Du$ on $I$ in the sense of measures. Hence, by (5.5), (5.1), and (5.9),

$$\begin{aligned} -\lambda \int _a^b |u|\, dx + u(b-)-u(a+) = u(b-)-u(a+). \end{aligned}$$

Consequently, $u=0$ a.e. on $(a,b)$ and we get the same result in the case $z(a)=z(b)=-1$. Summarizing we conclude that $I$ can be covered by at most three subintervals such that $u$ is constant on each subinterval. Since $(0,1)$ can be covered by finitely many intervals of length less than $1/\lambda$, we readily obtain the assertion. $\square$

Let us now consider the consequences of Theorem 4.2 for $\mathcal L ^1$-eigenfunctions.

Proposition 5.2

Let $u\in BV(0,1)$ be $\mathcal L ^1$-eigenfunction of the 1-Laplace operator with eigenvalue $\lambda$. Then there is some $k\in \mathbb N$ such that, up to sign of $u$,

$$\begin{aligned} u(x)= u_k(x):=\text{ sgn}(\sin (k\pi x)) \quad a.e. on (0,1) \quad and \quad \lambda =\lambda _k:=2k. \end{aligned}$$

(5.10)

Proof

Theorem 4.2 with the polar decomposition $Du=\sigma |Du|$ gives

$$\begin{aligned} \int _{(0,1)}(\sigma ^2\xi ^{\prime }-\xi ^{\prime })\, d|Du| = -\lambda \int _0^1|u| \xi ^{\prime }\, dx \quad \text{ for} \text{ all}\ \xi \in \mathcal C _0^\infty (0,1). \end{aligned}$$

Since $\sigma ^2=1$, the left hand side vanishes. Therefore, by the Lemma of Du Bois-Reymond and by $\Vert u\Vert _{\mathcal L ^1}=1$,

$$\begin{aligned} |u| = 1 \quad \text{ a.e.} \text{ on}\ (0,1). \end{aligned}$$

As $\mathcal L ^1$-eigenfunction $u$ has to satisfy the single eigenvalue equation (5.1) by Proposition 4.1 with corresponding functions $z$ and $s$. Moreover, $u$ must have the form (5.7) where, clearly, all $|\alpha _j|=1$. We get that $|s|=1$ a.e. on $(0,1)$ and, thus, $z^{\prime }(x)=-\lambda \text{ sgn}(u(x))$ a.e. on $(0,1)$. Since $u$ can only jump at points where $|z|=1$ by (5.8), since $|z|=1$ only at isolated points, and since $|z(0)|=|z(1)|=1$ by (5.6), the intervals $(a_j,a_{j+1})$ must all have the length $2/\lambda =1/k$ for some $k\in \mathbb N$ and the $\alpha _j$ have to alternate. But this gives the assertion. $\square$

Chang [6, Theorem 3.10] has shown that any strong $\mathcal L ^1$-eigenfunction must equal $\pm u_k$ from (5.10) for some $k\in \mathbb N$. Proposition 5.2 generalizes this result so far that already ${\mathcal L }^{1}$-eigenfunctions (i.e., with respect to the weak slope) have to meet that necessary condition. Since

$$\begin{aligned} |d(E_1+I_{K_1})|^{\mathcal L ^1}(\pm u_k)=|\nabla (E_1+I_{K_1})|^{\mathcal L ^1}(\pm u_k)=0 \end{aligned}$$

by Chang [6, Lemma 3.9], all $\pm u_k$ are really $\mathcal L ^1$-eigenfunctions. Thus, combined with Proposition 5.2, we obtain a precise characterization of all $\mathcal L ^1$-eigenfunctions.

Theorem 5.3

For $\Omega =(0,1)$ the $\mathcal L ^1$-eigenfunctions of the 1-Laplace operator are the functions $\pm u_k$, $k\in \mathbb N$, given in (5.10) with corresponding eigenvalues $\lambda _k=2k$.

The eigenvalues $\lambda _k$ can be characterized by a usual min-max principle and the eigenfunctions $u_k$ are the pointwise limit of the normalized eigenfunctions $u_k^p$ of the $p$-Laplace operator according to [6].

Interestingly, the $\mathcal L ^1$-eigenfunctions are exactly the same as the strong $\mathcal L ^1$-eigenfunctions in the case $n=1$ which might be wrong in higher dimensions. Notice that the existence of a sequence of eigenfunctions is shown in general merely for $\mathcal L ^1$-eigenfunctions and not for strong $\mathcal L ^1$-eigenfunctions. Moreover, it turns out that the case $\mathbb R ^1$ is somehow special, since, in contrast to higher dimensions, the selection $s(x)\in \text{ Sgn}(u(x))$ is uniquely determined (in the sense of $\mathcal L ^\infty$) and, thus, single and multiple eigenvalue equation agree.

The rich structure of the eigenvalue problem for the 1-Laplace operator also becomes visible in the case of $BV$-eigenfunctions. In Chang [6, Theorem 3.12], it is shown that all functions

$$\begin{aligned} u=\pm \sum _{j=1}^k (-1)^j\alpha _j\chi _{I_j} \text{ with}\ \alpha _j>0,I_j=\left(\tfrac{j-1}{k},\tfrac{j}{k}\right),j=1,\dots ,k,\sum _{j=1}^k \alpha _j=k \end{aligned}$$

are local minimizers of $E+I_K$ in $BV(\Omega )$. Hence $|d(E+I_K)|^{BV}(u)=|\nabla (E+I_K)|^{BV}(u)=0$, i.e., all these $u$ are $BV$-eigenfunctions and even strong $BV$-eigenfunctions on $\Omega =(0,1)$ with eigenvalue $\lambda =2k$. Consequently, the set of $BV$-eigenfunctions is strictly larger than that of $\mathcal L ^1$-eigenfunctions and the same is true for strong eigenfunctions. More general, let us consider

$$\begin{aligned} u=\pm \sum _{j=1}^k (-1)^j\alpha _j\chi _{I_j} \text{ with}\ \alpha _j\ge 0,I_j=\left(\tfrac{j-1}{k},\tfrac{j}{k}\right),j=1,\ldots ,k,\sum _{j=1}^k \alpha _j=k\nonumber \\ \end{aligned}$$

(5.11)

where we assume that $\alpha _j=0$ for at least one index $j$. For $\varepsilon >0$ we define $u^\pm _\varepsilon$ as in (5.11) with coefficients

$$\begin{aligned} \alpha ^\pm _{\varepsilon ,j}:=\left\{ \begin{array}{l@{\quad }l} \pm \varepsilon&\quad \text{ if}\ \alpha _j=0,\\ \alpha _j-c\varepsilon&\quad \text{ if}\ \alpha _j>0 \end{array} \right. \end{aligned}$$

where $c>0$ is a constant such that $\sum _{j=1}^k |\alpha ^\pm _{\varepsilon ,j}|=k$. Thus $u^\pm _\varepsilon \in K$ for all $\varepsilon >0$ and $u^{\pm }_\varepsilon \rightarrow u$ in $BV(\Omega )$ as $\varepsilon \rightarrow 0$. Clearly $\alpha ^+_{\varepsilon ,j}>0$ for all $j$ if $\varepsilon >0$ is sufficiently small. Hence, all $u^+_\varepsilon$ are local minimizers of $E+I_K$ in $BV(\Omega )$ and

$$\begin{aligned} |d(E+I_K)|^{BV}(u^+_\varepsilon )=0 \quad \text{ for} \text{ all} \text{ small}\ \varepsilon >0. \end{aligned}$$

Since the weak slope is lower semicontinuous, we have $|d(E+I_K)|^{BV}(u)=0$. Moreover, a simple computation shows that

$$\begin{aligned} |\nabla (E+I_K)|^{BV}(u)\ge {\mathop {\text{ lim} \text{ sup}}_{\varepsilon \rightarrow 0}} \frac{E(u)-E(u^-_\varepsilon )}{\Vert u-u^-_\varepsilon \Vert _{BV}} \ge {\tilde{c}} \end{aligned}$$

for some ${\tilde{c}}>0$. Consequently, $u$ according to (5.11) with $\alpha _j=0$ for at least one index $j$ is $BV$-eigenfunction but not strong $BV$-eigenfunction. This in particular means that, in contrast to the $\mathcal L ^1$-case, the set of $BV$-eigenfunctions is strictly larger than that of strong $BV$-eigenfunctions.

5.3 General case

Let us start with some generalization of the arguments from Sect. 5.1. Let $u\in BV(\Omega )$ and let $\Omega _0\subset \Omega$ be an open compactly contained subset with Lipschitz boundary such that $u=0$ on a neighborhood of $\partial \Omega _0$ (inside and outside). If $u$ were $\mathcal L ^1$-eigenfunction of the 1-Laplace operator, then we multiply the single eigenvalue equation (2.3) by $u$ and integrate to get

$$\begin{aligned} \lambda \int _{\Omega _0}|u|\, dx = -\int _{\Omega _0}u \text{ div}z\, dx = \int _{\Omega _0} d|Du| \end{aligned}$$

where the most right equality follows from the Gauss–Green formula with $(z,Du)=|Du|$ and $u=0$ on $\partial \Omega _0$ in the sense of trace (cf. Milbers and Schuricht [23, Sect. 3]). Now we consider (4.4) with $\xi (x)=x$ on $\Omega _0$ and $\text{ spt}\xi$ contained in a small neighborhood of $\Omega _0$ and obtain

$$\begin{aligned} \int _{\Omega _0} (1-n)\, d|Du| = -\lambda n\int _{\Omega _0}|u|\, dx \end{aligned}$$

which leads to the contradiction $1-n=-n$. Therefore a function $u\in BV(\Omega )$ of the kind described above cannot be $\mathcal L ^1$-eigenfunction.

If $u$ would be a smooth $\mathcal L ^1$-eigenfunction with $Du(x)\ne 0$ and $u(x)\ne 0$, then $z$ in the single eigenvalue equation (2.3) would coincide with $Du/|Du|$ in a neighborhood of $x$, i.e., $z$ were a unit normal field on the level sets of $u$ that must have the constant mean curvature $-\text{ div}z=\lambda \text{ sgn}(u)$. Therefore we expect $\mathcal L ^1$-eigenfunctions to be step functions in general though exceptions might be possible.

Let us consider an $\mathcal L ^1$-eigenfunction $u\in BV(\Omega )$ such that on an open ball $B\subset \Omega$

$$\begin{aligned} u=c_1\chi _{\Omega _1}+ c_2\chi _{\Omega _2} ,\quad \partial \Omega _1=\partial \Omega _2 \end{aligned}$$

with $\Omega _1,\Omega _2\subset \Omega$ being disjoint open subsets having smooth boundary and outer unit normals $\nu _1$, $\nu _2$. For the left hand side in (4.4) with $\text{ spt}\xi \subset B$ we get

$$\begin{aligned} \int _B \langle \sigma ,D\xi \, \sigma \rangle -\text{ div}\xi \, d|Du|&= -\int _B \text{ div}_{\partial \Omega _1}\xi \, d|Du| \\&= |c_1-c_2|\int _{B\cap \partial \Omega _1} H_{\partial \Omega _1}\langle \xi ,\nu _1\rangle - \text{ div}\!_g\xi _{\partial \Omega _1}\, d\mathcal H ^{n-1} \\&= |c_1-c_2| \int _{B\cap \partial \Omega _1} H_{\partial \Omega _1} \langle \xi ,\nu _1\rangle \, d\mathcal H ^{n-1} \end{aligned}$$

where $\text{ div}_{\partial \Omega _1}$ denotes the tangential part of the divergence, $\text{ div}\!_g$ the divergence in the manifold $\partial \Omega _1$, $\xi _{\partial \Omega _1}$ the tangential part of $\xi$, and $H_{\partial \Omega _1}$ the mean curvature of $\partial \Omega _1$ (with respect to the normal field $\nu _1$) while we have used the divergence theorem in the manifold $\partial \Omega _1$ for the last equality, cf. [22, Proposition 8.7]. Using (4.5) and $D|u|=\big (|c_2|-|c_1|\big )\nu _1\mathcal H ^{n-1}\lfloor \partial \Omega _1$, we derive from (4.4)

$$\begin{aligned} |c_1-c_2|\int _{B\cap \partial \Omega _1} H_{\partial \Omega _1} \langle \xi ,\nu _1\rangle \, d\mathcal H ^{n-1} = \lambda \big (|c_2|-|c_1|\big )\int _{B\cap \partial \Omega _1}\langle \xi ,\nu _1\rangle \, d\mathcal H ^{n-1} \end{aligned}$$

for all $\xi \in \mathcal C _0^\infty (B,\mathbb R ^n)$. Consequently,

$$\begin{aligned} H_{\partial \Omega _1} |c_1-c_2| = \lambda \big (|c_2|-|c_1|\big ) \quad \text{ on}\ B\cap \partial \Omega _1. \end{aligned}$$

Let us consider some special cases of that condition. First,

$$\begin{aligned} H_{\partial \Omega _1} = -\lambda \quad \text{ if}\ c_2=0, \end{aligned}$$

i.e. on a “free” part of $\partial \Omega _1$ we have a curvature condition as for the boundary of a Cheeger set. Notice that one obtains the same condition for the “free” parts of $\partial \Omega _2$. Next,

$$\begin{aligned} H_{\partial \Omega _1} = -\lambda \quad \text{ if}\ c_1>c_2>0 \quad \text{ or}\ c_1<c_2<0 . \end{aligned}$$

Finally,

$$\begin{aligned} H_{\partial \Omega _1} = - \lambda \, \frac{|c_1|-|c_2|}{|c_1-c_2|} \quad \text{ if}\ c_1>0>c_2 \quad \text{ or}\ c_2>0>c_1 . \end{aligned}$$

Notice that, in the last case, $H_{\partial \Omega _1}=0$ if and only if $|c_1|=|c_2|$. Summarizing we can say that the new necessary condition (4.4) provides additional information supplementing the single eigenvalue equation (2.3).

6 Proofs

In this section we first carry out the proof of Proposition 4.3 and then, in several steps, the proof of Theorem 4.2.

Proof of Proposition 4.3

In this proof $B_\delta (u)$ denotes the $\delta$-neighborhood with respect to $\Vert \cdot \Vert _X$ and $\Vert \cdot \Vert$ denotes the norm in $\mathcal L ^1(\Omega )$. By assumption there is some $c>0$ such that

$$\begin{aligned} \Vert v\Vert \le c\Vert v\Vert _X \quad \text{ for} \text{ all}\ v\in X. \end{aligned}$$

(6.1)

(a) Let $u\in X$ be a critical point of $E$ with respect to $K^X$ on $X$ and, by contradiction, let $|dF|^X(u)>0$. Hence, there is $\omega >0, \delta >0$, $\beta >F(u)$, and $\mathcal H :(B_\delta (u)\cap F^\beta )\times [0,\delta ]\rightarrow X$ continuous such that

$$\begin{aligned} \Vert \mathcal H (v,t)-v\Vert _X\le t, \quad F(\mathcal H (v,t))\le F(v)-\omega t \end{aligned}$$

(6.2)

for all $v\in B_\delta (u)\cap F^\beta$, $t\in [0,\delta ]$. With $F=E-\lambda G$ and the 1-homogeneity of $E$, $G$, the inequality on the right implies

$$\begin{aligned} \Vert \mathcal H (v,t)\Vert E\Big (\frac{\mathcal H (v,t)}{\Vert \mathcal H (v,t)\Vert }\Big ) - E(u)\Vert \mathcal H (v,t)\Vert \le \Vert v\Vert E\Big (\frac{v}{\Vert v\Vert }\Big ) - E(u)\Vert v\Vert - \omega t . \end{aligned}$$

Using $\tilde{\mathcal H }(v,t):=\mathcal H (v,t)/\Vert \mathcal H (v,t)\Vert$, ${\tilde{v}}:=v/\Vert v\Vert$ we get

$$\begin{aligned}&\Vert \mathcal H (v,t)\Vert \big ( E(\tilde{\mathcal H }(v,t))-E({\tilde{v}})\big ) + \big ( \Vert \mathcal H (v,t)\Vert -\Vert v\Vert \big )E({\tilde{v}}) \\&\qquad \qquad \le E(u)\big (\Vert \mathcal H (v,t)\Vert -\Vert v\Vert \big ) - \omega t \end{aligned}$$

and, thus,

$$\begin{aligned} \Vert \mathcal H (v,t)\Vert \big ( E(\tilde{\mathcal H }(v,t))-E({\tilde{v}})\big ) \le \big ( E(u)-E({\tilde{v}})\big )\big (\Vert \mathcal H (v,t)\Vert -\Vert v\Vert \big ) -\omega t\qquad \end{aligned}$$

(6.3)

for all $v\in B_\delta (u)\cap F^\beta$, $t\in [0,\delta ]$.

Since $E$ is lower semicontinuous (also on $X$), we can choose an eventually smaller $\delta >0$, denoted the same way, such that

$$\begin{aligned} E(u)-E\left(\tfrac{v}{\Vert v\Vert }\right)= E(u)-E({\tilde{v}}) \le \frac{\omega }{2c} \quad \text{ for} \text{ all}\ v\in B_\delta (u). \end{aligned}$$

(6.4)

Using (6.1), we get

$$\begin{aligned} \big |\Vert u\Vert -\Vert v\Vert \big | \le \Vert u-v\Vert \le c \Vert u-v\Vert _X\le c\delta \quad \text{ for}\ v\in B_\delta (u). \end{aligned}$$

(6.5)

With $\Vert u\Vert =1$ and since $\mathcal H$ is continuous (with respect to the norm on $X$), we can assume that $\delta >0$ is so small that

$$\begin{aligned} \Vert \mathcal H (v,t)\Vert \le 2, \quad \Vert \mathcal H (v,t)\Vert \,\Vert v\Vert \ge \frac{1}{2}, \quad \Vert v\Vert \ge \frac{1}{2} \quad \text{ for} \text{ all}\ v\in B_\delta (u), t\in [0,\delta ].\nonumber \\ \end{aligned}$$

(6.6)

Furthermore, with some eventually smaller $\beta >F(u)=0$, denoted the same way, and satisfying $2\beta \le \tfrac{\omega }{2c}$, we obtain for all $v\in B_\delta (u)\cap F^\beta$

$$\begin{aligned} E({\tilde{v}})-E(u) = \frac{1}{\Vert v\Vert } \big ( E(v)- \lambda G(v) \big ) = \frac{1}{\Vert v\Vert } F(v)\le 2\beta \le \frac{\omega }{2c}. \end{aligned}$$

By (6.1), (6.2)

$$\begin{aligned} \big |\, \Vert \mathcal H (v,t)\Vert -\Vert v\Vert \,\big | \le \Vert \mathcal H (v,t)-v\Vert \le c \Vert \mathcal H (v,t)-v\Vert _X \le ct. \end{aligned}$$

Consequently, by (6.3), (6.4),

$$\begin{aligned} \Vert \mathcal H (v,t)\Vert \big ( E(\tilde{\mathcal H }(v,t))-E({\tilde{v}})\big ) \le \frac{\omega }{2}t-\omega t = -\frac{\omega }{2} t \end{aligned}$$

and, moreover,

$$\begin{aligned} E(\tilde{\mathcal H }(v,t))-E({\tilde{v}}) \le -\frac{\omega }{2} \frac{t}{\Vert \mathcal H (v,t)\Vert } \le -\frac{\omega }{4} t \end{aligned}$$

for all $v\in B_\delta (u)\cap F^\beta$, $t\in [0,\delta ]$. Using (6.6) we can also estimate

$$\begin{aligned} \Vert \tilde{\mathcal H }(v,t)-{\tilde{v}}\Vert _{X}&= \Big \Vert \frac{\mathcal H (v,t)}{\Vert \mathcal H (v,t)\Vert } - \frac{v}{\Vert v\Vert } \Big \Vert _X \;\\&= \frac{1}{\Vert \mathcal H (v,t)\Vert \Vert v\Vert }\;\Big \Vert \Vert v\Vert \mathcal H (v,t)-\Vert \mathcal H (v,t)\Vert v \Big \Vert _X \\&\le 2\big (\Vert v\Vert \,\Vert \mathcal H (v,t)-v\Vert _X +\big |\,\Vert v\Vert - \Vert \mathcal H (v,t)\Vert \,\big |\,\Vert v\Vert _X \big ) \\&\le 2\big ( c\Vert v\Vert _X\, t + ct\Vert v\Vert _X\big ) \; \le \; 4ct(\delta +\Vert u\Vert _X) \end{aligned}$$

for all $v\in B_\delta (u)\cap F^\beta$, $t\in [0,\delta ]$.

For $v\in B_\delta (u)\cap (E+I_{K^X})^{E(u)+\beta }$ with $K^X:=\{v\in X|\, G(v)=1\}$ we get

$$\begin{aligned} F(v)=E(v)-\lambda G(v)=E(v)-E(u)\le \beta . \end{aligned}$$

Thus, with ${\tilde{\beta }}:=E(u)+\beta$,

$$\begin{aligned} B_\delta (u)\cap (E+I_{K^X})^{\tilde{\beta }} \subset B_\delta (u)\cap F^\beta . \end{aligned}$$

With $c_0:=4c(\delta +\Vert u\Vert _X)$ and $\hat{\mathcal H }(v,t):=\tilde{\mathcal H }(v,t/c_0)$ we finally get for all $v\in B_\delta (u)\cap (E+I_{K^X})^{{\tilde{\beta }}}$, $t\in [0,\delta ]$

$$\begin{aligned} \Vert \hat{\mathcal H }(v,t)- v\Vert _{X} = \Vert \tilde{\mathcal H }(v,t/c_0)- v\Vert _{X}\le t \end{aligned}$$

and

$$\begin{aligned} (E+I_{K^X})(\hat{\mathcal H }(v,t))-(E+I_{K^X})(v) = E(\tilde{\mathcal H }(v,t/c_0))-E(v) \le -\frac{\omega }{4c_0} t \end{aligned}$$

(notice that $v={\tilde{v}}\in K^X$ and $\hat{\mathcal H }(v,t)\in K^X$ in that case). But this implies that $u$ is not a critical point of $E$ with respect to $K^X$, which is a contradiction and verifies the assertion.

(b) Assume that $|d(E-\lambda G|^X(u)=0$ and, by contradiction, let $|d(E+I_{K^X})|^X(u)>0$. Then there exist $\omega >0$, $\delta >0$, $\beta >(E+I_{K^X})(u)=E(u)$, and $\mathcal H :B_\delta (u)\cap (E+I_K)^\beta \times [0,\delta ]\rightarrow X$ continuous such that

$$\begin{aligned} \Vert \mathcal H (v,t)-v\Vert _X\le t,\quad (E+I_{K^X})(\mathcal H (v,t))\le (E+I_{K^X})(v)-\omega t \end{aligned}$$

for all $v\in B_\delta (u)\cap (E+I_{K^X})^\beta$, $t\in [0,\delta ]$. Clearly, $(E+I_{K^X})^\beta =E^\beta \cap K^X$ and

$$\begin{aligned} \mathcal H (v,t)\in K^X \quad \text{ for} \text{ all}\ v\in B_\delta (u)\cap E^\beta \cap K^X, t\in [0,\delta ]. \end{aligned}$$

Hence,

$$\begin{aligned} E(\mathcal H (v,t))\le E(v)-\omega t \quad \text{ for} \text{ all}\ v\in B_\delta (u)\cap E^\beta \cap K^X,t\in [0,\delta ]. \end{aligned}$$

(6.7)

Using (6.5) we can choose ${\tilde{\delta }}\in (0,\delta )$ so small that

$$\begin{aligned} \frac{v}{\Vert v\Vert }\in B_\delta (u) \quad \text{ and}\quad \Vert v\Vert \ge \frac{1}{2} \quad \text{ for} \text{ all}\ v\in B_{{\tilde{\delta }}}(u). \end{aligned}$$

Then there is $c_1\ge 1$ with $\Vert v\Vert \le c\Vert v\Vert _{X}\le c(\Vert u\Vert _X+{\tilde{\delta }})\le c_1$ on $B_{\tilde{\delta }}(u)$. With $\tilde{\beta }:=\tfrac{\beta -E(u)}{2}$ we have for all $v\in B_{{\tilde{\delta }}}(u)\cap (E-\lambda G)^{{\tilde{\beta }}}$

$$\begin{aligned} E\big (\tfrac{v}{\Vert v\Vert }\big ) = \tfrac{1}{\Vert v\Vert } \big (E(v)-\lambda G(v)\big )+E(u) \le 2\tilde{\beta }+E(u) = \beta . \end{aligned}$$

Let us now define the continuous map

$$\begin{aligned} \tilde{\mathcal H }(v,t):=\Vert v\Vert \mathcal H \big (\tfrac{v}{\Vert v\Vert },\tfrac{t}{c_1}\big ) \quad \text{ on}\ \big (B_{\tilde{\delta }}(u)\cap (E-\lambda G)^{\tilde{\beta }}\big )\times [0,\tilde{\delta }]. \end{aligned}$$

We conclude,

$$\begin{aligned} \Vert \tilde{\mathcal H }(v,t)-v\Vert _{X}&= \Big \Vert \,\Vert v\Vert \mathcal H \Big (\frac{v}{\Vert v\Vert },\frac{t}{c_1}\Big )-v\,\Big \Vert _{X} =\Vert v\Vert \,\Big \Vert \,\mathcal H \Big (\frac{v}{\Vert v\Vert },\frac{t}{c_1}\Big )-\frac{v}{\Vert v\Vert }\, \Big \Vert _X \\&\le c_1\frac{t}{c_1} = t \end{aligned}$$

and, by (6.7) and $G(\mathcal H (\tfrac{v}{\Vert v\Vert },\tfrac{t}{c_1}))=1$,

$$\begin{aligned} E(\tilde{\mathcal H }(v,t))-\lambda G(\tilde{\mathcal H }(v,t))&= \Vert v\Vert E\left(\mathcal H \left(\tfrac{v}{\Vert v\Vert },\tfrac{t}{c_1}\right)\right) - \lambda \Vert v\Vert G\left(\mathcal H \left(\tfrac{v}{\Vert v\Vert },\tfrac{t}{c_1}\right)\right) \\&\le \Vert v\Vert E\left(\tfrac{v}{\Vert v\Vert }\right)-\omega \Vert v\Vert \tfrac{t}{c_1}-\lambda G(v) \\&\le E(v)-\lambda G(v)-\frac{\omega }{2c_1}t \end{aligned}$$

for all $v\in B_{\tilde{\delta }}(u)\cap (E-\lambda G)^{\tilde{\beta }}$, $t\in [0,\tilde{\delta }]$. Consequently, $|d(E-\lambda G)|^X(u)>0$. But this contradicts our assumption and yields the assertion. $\square$

Let us now start with preliminary considerations for the proof of Theorem 4.2. We set

$$\begin{aligned} \mathrm{Diff}_\Omega :=\{\eta \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n)| (\mathrm{id}+\eta ):\Omega \rightarrow \Omega \text{ is} \text{ a} \text{ diffeomorphism}\} \end{aligned}$$

and, clearly, $0\in \mathrm{Diff}_\Omega$. For $v\in BV(\Omega )$ and $\eta \in \mathrm{Diff}_\Omega$ we consider perturbations

$$\begin{aligned} v^\eta :\Omega \rightarrow \mathbb R \quad \text{ with}\ v^\eta (x) := v(x+\eta (x)) . \end{aligned}$$

For $v$ in a $\mathcal L ^1$-neighborhood of a critical point $u$ we claim to study the functions

$$\begin{aligned} \mathcal E _v: \mathrm{Diff}_\Omega \rightarrow \mathbb R \quad \text{ with}\ \mathcal E _v(\eta )&:= E(v^\eta )=\int _\Omega d|Dv^\eta |+\int _{\partial \Omega }|v^\eta |\, d\mathcal H ^{n-1},\\ \mathcal G _v: \mathrm{Diff}_\Omega \rightarrow \mathbb R \quad \text{ with}\ \mathcal G _v(\eta )&:= G(v^\eta )=\int _\Omega |v^\eta | \,dx \end{aligned}$$

near $\eta =0$. In particular, for $\xi \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n)$ we want to derive a first order expansion of the real functions $t\rightarrow \mathcal E _v(t\xi )$ and $t\rightarrow \mathcal G _v(t\xi )$ at $t=0$ by computing the directional derivatives $\delta \mathcal E _v(0,\xi )$ and $\delta \mathcal G _v(0,\xi )$. But first we have to clarify that $\mathcal E _v$, $\mathcal G _v$ are well defined.

Lemma 6.1

If $v\in BV(\Omega )$ and $\eta \in \mathrm{Diff}_\Omega$, then $v^\eta \in BV(\Omega )$. With $\tilde{y}(x):=x+\eta (x)$ and $\tilde{x}(\cdot )$ being the inverse of $\tilde{y}$ on $\Omega$, we have

$$\begin{aligned} \int _\Omega |v^\eta (x)|\,dx&= \int _\Omega |v(y)|\det D\tilde{x}(y)\,dy,\end{aligned}$$

(6.8)

$$\begin{aligned} \int _\Omega \, d|Dv^\eta |&= \int _\Omega | D\tilde{y}(\tilde{x}(y))^T \sigma (y)| \det D\tilde{x}(y)\,d|Dv| \end{aligned}$$

(6.9)

where $\sigma :\Omega \rightarrow \mathbb R ^n$ denotes the vector field according to the polar decomposition of $Dv=\sigma |Dv|$ (cf. (4.3)).

Proof

By the change of variables formula we have $v^\eta \in \mathcal L ^1(\Omega )$ with (6.8). Relation (6.9) is shown in Giusti [20, Lemma 10.1], and, since the integrand on the right hand side is bounded, $v^\eta \in BV(\Omega )$. $\square$

For an arbitrary but fixed $\xi \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n)$ we define

$$\begin{aligned} \tilde{y}(x,t):=x+t\xi (x), \quad D\tilde{y}(x,t):=\frac{\partial }{\partial x}\tilde{y}(x,t) \quad \text{ on}\ \Omega \times \mathbb R . \end{aligned}$$

Using the implicit function theorem we readily obtain the next lemma.

Lemma 6.2

There is $t_0>0$ such that $t\xi \in \mathrm{Diff}_\Omega$ and $\tilde{y}(\cdot ,t)$ is a $\mathcal C ^\infty$-diffeomorphism from $\Omega$ to $\Omega$ for all $t\in (-t_0,t_0)$. Moreover $D\tilde{y}(x,t)$ is regular for all $(x,t)\in \Omega \times (-t_0,t_0)$ and

$$\begin{aligned} \text{ det}D\tilde{y}(x,t)\ge \frac{1}{c} \quad \text{ for} \text{ all}\ x\in \Omega ,t\in (-t_0,t_0) \end{aligned}$$

for some constant $c>0$.

For any $t\in (-t_0,t_0)$ we denote the inverse of $\tilde{y}(\cdot ,t)$ on $\Omega$ by

$$\begin{aligned} \tilde{x}(\cdot ,t) \quad \text{ and} \text{ set}\ D\tilde{x}(y,t):= \frac{\partial }{\partial y}\tilde{x} (y,t). \end{aligned}$$

The next corollary summarizes standard results about inner variations (cf. Giaquinta and Hildebrandt [19, Chapter 3.1]).

Corollary 6.12

We have $\tilde{x} \in \mathcal C ^\infty \big (\Omega \times (-t_0,t_0),\Omega \big )$ and $\tilde{x}(\cdot ,t)$ is a $C^\infty$-diffeomorphism on $\Omega$ with

$$\begin{aligned} \tilde{x}(y,t) = y \quad \text{ for} \text{ all}\ y\in \Omega \setminus \text{ spt}\xi ,t\in (-t_0,t_0). \end{aligned}$$

Moreover, there are $\mathcal C ^\infty$-functions $r_j:\Omega \times (-t_0,t_0)\rightarrow \mathbb R , j=1,2$, such that

$$\begin{aligned} \tilde{x}(y,t) = \tilde{x}(y,0) - t \xi (y) + r_1(y,t), \quad \text{ det}D\tilde{x}(y,t) = 1 - t \text{ div}\xi (y) + r_2(y,t) \end{aligned}$$

for all $y\in \Omega$, $t\in (-t_0,t_0)$ and

$$\begin{aligned} r_j(y,t)=o(t) \quad \text{ as}\ t\rightarrow 0 \ \text{ uniformly} \text{ in}\ y\in \Omega ,\ j=1,2. \end{aligned}$$

We readily conclude that the real functions $t\rightarrow \mathcal E _v(t\xi )$, $t\rightarrow \mathcal G _v(t\xi )$ are well defined on $(-t_0,t_0)$ for any $v\in BV(\Omega )$. Notice that $t_0$ and the $r_j$ from Corollary  depend on $\xi$ but not on $v$. Moreover, the surface integral in the definition of $\mathcal E _v(t\xi )$ is independent of $t$.

Lemma 6.4

Let $v\in BV(\Omega )$ with polar decomposition $Dv=\sigma |Dv|$ (cf. (4.3)) and let $\xi \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n)$. Then we have the directional derivatives

$$\begin{aligned} \delta \mathcal E _v(0,\xi ):= \int _\Omega \langle \sigma , D\xi \sigma \rangle - \text{ div}\xi \,d|Dv|, \quad \delta \mathcal G _v(0,\xi ):= -\int _\Omega |v|\text{ div}\xi \,dx. \end{aligned}$$

Moreover, there are functions $r_{\mathcal E },r_{\mathcal G }:(-t_0,t_0)\rightarrow \mathbb R$ depending on $\xi$ but not on $v$ and satisfying

$$\begin{aligned} r_{\mathcal E }(t)=o(t), \quad r_{\mathcal G }(t)=o(t)\quad \text{ as}\ t\rightarrow 0 \end{aligned}$$

such that

$$\begin{aligned} \mathcal E _v(t\xi )&= \mathcal E _v(0)+\delta \mathcal E _v(0,\xi )t + r_{\mathcal E }(t)\mathcal E _v(0)\\ \mathcal G _v(t\xi )&= \mathcal G _v(0)+\delta \mathcal G _v(0,\xi )t + r_{\mathcal G }(t)\mathcal G _v(0) \end{aligned}$$

for all $t\in (-t_0,t_0)$.

Proof

For $v\in BV(\Omega )$, $\sigma$ from the corresponding polar decomposition, and $|t|$ small, we get by Lemma 6.1 and Corollary 6.3

$$\begin{aligned} \mathcal E _v(t\xi )&= \int _\Omega \,d|Dv^{t\xi }| + \int _{\partial \Omega } |v^{t\xi }|\, d\mathcal H ^{n-1}\nonumber \\&= \int _\Omega | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \det D\tilde{x}(y,t) \,d|Dv| + \int _{\partial \Omega } |v|\, d\mathcal H ^{n-1} \nonumber \\&= \int _\Omega | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| (1-t\,\text{ div}\xi (y)+r_2(y,t))\, d|Dv| + \int _{\partial \Omega } |v|\, d\mathcal H ^{n-1}\nonumber \\&= \int _\Omega | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \,d|Dv| \end{aligned}$$

(6.10)

$$\begin{aligned}&- \int _\Omega t\, | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)|\,\text{ div}\xi (y)\,d|Dv| \end{aligned}$$

(6.11)

$$\begin{aligned}&+ \int _\Omega | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)|\, r_2(y,t) \,d|Dv| + \int _{\partial \Omega } |v|\, d\mathcal H ^{n-1} . \end{aligned}$$

(6.12)

We calculate the directional derivative

$$\begin{aligned} \delta \mathcal E _v(0,\xi ) = \frac{\partial }{\partial t} \Big ( \int _\Omega \,d|Dv^{t\xi }| + \int _{\partial \Omega } |v^{t\xi }|\, d\mathcal H ^{n-1} \Big ) \,_{\big |_{t=0}} \end{aligned}$$

by treating the terms in (6.10), (6.11), (6.12) separately and using a majorizing result for the differentiability of parameter-dependent integrals, cf. Schilling [26, Theorem 11.5].

Let us calculate the derivatives of the integrands. For the first one, cf. (6.10), we obtain

$$\begin{aligned} \mathcal F (y,t)&:= \frac{\partial }{\partial t}\,|D\tilde{y}(\tilde{x}(y,t),t)^T\, \sigma (y)| \nonumber \\&= \bigg \langle \frac{D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)}{|D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)|}, \frac{\partial }{\partial t} D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y) \bigg \rangle \nonumber \\{}&= \!\bigg \langle \frac{D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)}{|D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)|}, \frac{\partial }{\partial t} \big (\text{ id}+ t\,D\xi (\tilde{x}(y,t))\big )^T \sigma (y) \bigg \rangle \nonumber \\&= \! \bigg \langle \frac{D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)}{|D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)|}, \Big (\! D\xi (\tilde{x}(y,t)) \!+\! t\, D^2\xi (\tilde{x}(y,t)) \frac{\partial }{\partial t}\tilde{x}(y,t) \!\Big )^T \sigma (y) \!\bigg \rangle .\nonumber \\ \end{aligned}$$

(6.13)

Since $D\tilde{y}(\tilde{x}(y,0),0)=\text{ id}$, $|\sigma (y)|=1$,

$$\begin{aligned} \mathcal F (y,0) = \langle \sigma (y),D\xi (y)\, \sigma (y)\rangle \quad \text{ for} \text{ all}\ y\in \Omega . \end{aligned}$$

For the second integrand, cf. (6.11),

$$\begin{aligned} \frac{\partial }{\partial t} \left( t\, | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \right) \text{ div}\xi (y) \!=\! \Big ( | D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \!+\! t \mathcal F (y,t) \!\Big ) \text{ div}\xi (y).\nonumber \\ \end{aligned}$$

(6.14)

Since $r_2$ is smooth, we get for the third part, cf. (6.12),

$$\begin{aligned} \frac{\partial }{\partial t} \Big (| D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \; r_2(y,t)\Big )&= \mathcal F (y,t) r_2(y,t) \nonumber \\&+ |D\tilde{y}(\tilde{x}(y,t),t)^T \sigma (y)| \, \frac{\partial }{\partial t}r_2(y,t).\nonumber \\ \end{aligned}$$

(6.15)

Notice that $r_2(y,0)= \tfrac{\partial }{\partial t} r_2(y,0)=0$ for all $y\in \Omega$ by Corollary 6.3. Since $r_2(\cdot ,t)$ has compact support on $\Omega$, the right hand sides in (6.13), (6.14), (6.15) are uniformly bounded by a constant for $y\in \Omega$ and $|t|$ small. Thus

$$\begin{aligned} \delta \mathcal E _v(0,\xi ) = \int _\Omega \langle \sigma (y),D\xi (y)\, \sigma (y)\rangle + \text{ div}D\xi (y)\,d|Dv|. \end{aligned}$$

Clearly all integrands in (6.10), (6.11), (6.12) are even twice continuously differentiable with respect to $t$ ($|t|$ small) and all second derivatives are uniformly bounded with respect to $y\in \Omega$ by a constant $\tilde{c}>0$. Therefore we find some function $r_{\mathcal E }:(-t_0,t_0)\rightarrow \mathbb R$ with $r_{\mathcal E }(t)=o(t)$ as $t\rightarrow 0$ such that

$$\begin{aligned} \mathcal E _v(t\xi ) = \mathcal E _v(0)+ \delta \mathcal E _v(0,\xi )t + r_{\mathcal E }(t)\int _\Omega \,d|Dv|. \end{aligned}$$

Notice that $r_{\mathcal E }$ depends on $\xi$ but not on $v$.

By Lemma 6.1,

$$\begin{aligned} \mathcal G _v(t\xi )= \int _\Omega |v^{t\xi }(x)|\,dx = \int _\Omega |v(y)|\det D\tilde{x}(y,t) \,dy. \end{aligned}$$

(6.16)

Using Lemma 6.3 we calculate the derivative of the integrand

$$\begin{aligned} \frac{\partial }{\partial t} \big (|v(y)| \det D\tilde{x}(y,t) \big )&= \frac{\partial }{\partial t} \big ( |v(y)| (1 - t\,\text{ div}\xi (y) + r_2(y,t))\big )\nonumber \\&= - |v(y)| \text{ div}\xi (y) + |v(y)| \frac{\partial }{\partial t}r_2(y,t) \end{aligned}$$

(6.17)

and, hence,

$$\begin{aligned} \frac{\partial }{\partial t}\big (|v(y)| \det D\tilde{x}(y,t)\big )\,\big |_{t=0} = - |v(y)|\text{ div}\xi (y) . \end{aligned}$$

Since the terms in (6.17) are uniformly bounded in $y$ and $t$, we get the directional derivative

$$\begin{aligned} \delta \mathcal G _v(0,\xi ) = -\int _\Omega |v(y)|\text{ div}\xi (y) \,dy . \end{aligned}$$

Again the function $t\rightarrow \det D\tilde{x}(y,t)$ is twice continuously differentiable and the second derivative is uniformly bounded with respect to $y\in \Omega$ and $|t|$ small. Therefore we find some function $r_{\mathcal G }:(-t_0,t_0)\rightarrow \mathbb R$ with $r_{\mathcal G }(t)=o(t)$ as $t\rightarrow 0$ such that

$$\begin{aligned} \mathcal G _v(t\xi ) = \mathcal G _v(0)+ \delta \mathcal G _v(0,\xi )t + r_{\mathcal G }(t)\int _\Omega |v|\,dy. \end{aligned}$$

Also $r_{\mathcal G }$ depends on $\xi$ but not on $v$. $\square$

Proof of Theorem 4.2

Notice that Eq. (4.4) is equivalent to

$$\begin{aligned} \delta \mathcal E _u(0,\xi ) -\lambda \delta \mathcal G _u(0,\xi )= 0 \quad \text{ for} \text{ all}\ \xi \in \mathcal C _0^\infty (\Omega ,\mathbb R ^n). \end{aligned}$$

By contradiction let us assume that the assertion is wrong, i.e., there is some $\xi \in \mathcal C _0^\infty (\Omega )$ such that

$$\begin{aligned} \delta \mathcal E _u(0,\xi ) -\lambda \delta \mathcal G _u(0,\xi ) < -\omega <0 \end{aligned}$$

(6.18)

for some $\omega >0$. We claim to show that $|d(E-\lambda G)|^{\mathcal L ^1}(u)>0$.

For the fixed $\xi$ from (6.18) we choose $t_0>0$ as in Lemma 6.2 and we fix $\delta$, $\beta$ with

$$\begin{aligned} \delta :=t_0, \quad \beta >F(u):=E(u)-\lambda G(u)=0 . \end{aligned}$$

By Lemma 6.2,

$$\begin{aligned} 0<\frac{1}{\det (\mathrm{id}+tD\xi (x))}\le c \quad \text{ for} \text{ all}\ |t|<\delta , x\in \Omega . \end{aligned}$$

Now we define a map $\mathcal H :(B_\delta (u)\cap F^\beta )\times [0,\delta ]\rightarrow \mathcal L ^1(\Omega )$, where $B_\delta (u)$ denotes the $\delta$-ball in $\mathcal L ^1(\Omega )$, with

$$\begin{aligned} \mathcal H (v,t) := v^{t\xi } = v(\cdot +t\xi (\cdot )) \end{aligned}$$

(recall $F^\beta =\{v\in \mathcal L ^1|\, F(v)<\beta \}$). Notice that $v\in F^\beta$ implies $v\in BV(\Omega )$ and, hence,

$$\begin{aligned} \mathcal H (v,t)\in BV(\Omega ) \quad \text{ for} \text{ all}\ v\in B_\delta (u)\cap F^\beta , t\in [0,\delta ] \end{aligned}$$

by Lemma 6.1.

Assume there is a sequence $v_k\rightarrow u$ in $\mathcal L ^1(\Omega )$ with $F(v_k)\rightarrow F(u)$ and

$$\begin{aligned} \delta \mathcal E _{v_k}(0,\xi ) -\lambda \delta \mathcal G _{v_k}(0,\xi ) \ge -\omega \quad \text{ for} \text{ all}\ k\in \mathbb N . \end{aligned}$$

Obviously $E(v_k)\rightarrow E(u)$ and, with the extensions $\bar{v}_k, \bar{u}$ of $v_k,u$ on $\mathbb R ^n$ by zero, $|D\bar{v}_k|(\Omega )\rightarrow |D\bar{u}|(\Omega )$. With the polar decompositions $Dv_k=\sigma _k|Dv_k|$ Reshetnyak’s theorem (cf. Ambrosio et al. [1, Theorem 2.39]) implies

$$\begin{aligned} \int _{\mathbb R ^n} \langle \sigma _k, D\xi \sigma _k\rangle - \text{ div}\xi \,d|D\bar{v}_k|\rightarrow \int _{\mathbb R ^n} \langle \sigma , D\xi \sigma \rangle - \text{ div}\xi \,d|D\bar{u}|. \end{aligned}$$

Since $\xi$ has compact support on $\Omega$ we obtain $\delta \mathcal E _{v_k}(0,\xi )\rightarrow \delta \mathcal E _u(0,\xi )$. Moreover, for some $c_1>0$,

$$\begin{aligned} |\delta \mathcal G _{v_k}(0,\xi )-\delta \mathcal G _u(0,\xi )|&\le \int _\Omega \big ||v_k|-|u|\big |\,|\text{ div}\xi |\, dx \le c_1\int _\Omega |v_k-u|\, dx\\&= c_1\Vert v_k-u\Vert _{\mathcal L ^1} \rightarrow 0. \end{aligned}$$

We derive $\delta \mathcal E _u(0,\xi )-\lambda \delta \mathcal G _u(0,\xi )\ge -\omega$ which contradicts (6.18). Therefore, with eventually smaller constants $\delta >0$ and $\beta >F(u)$,

$$\begin{aligned} \delta \mathcal E _v(0,\xi ) -\lambda \delta \mathcal G _v(0,\xi ) < -\omega \quad \text{ for} \text{ all}\ v\in B_\delta (u)\cap F^\beta . \end{aligned}$$

(6.19)

Let us now verify the continuity of $\mathcal H$ on $(B_\delta (u)\cap F^\beta )\times [0,\delta ]$ as mapping from $\mathcal L ^1(\Omega )\times [0,\delta ]$ to $\mathcal L ^1(\Omega )$ where the next lemma is a first step.

Lemma 6.5

We have for $v\in BV(\Omega )$, $t_1,t_2\in [0,\delta ]$

$$\begin{aligned} \Vert v(\cdot + t_2\xi (\cdot )) - v(\cdot + t_1 \xi (\cdot ))\Vert _{\mathcal L ^1} \le c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv|(\Omega )|t_2-t_1|. \end{aligned}$$

Proof

Notice that $t\xi \in \mathrm{Diff}_\Omega$ for all $t\in [0,\delta ]$ and, thus, all expressions in the lemma are well defined. Let $(v_k)_{k\in \mathbb N } \subset BV(\Omega )\cap C^\infty (\Omega )$ be such that $\Vert v_k-v\Vert _{\mathcal L ^1}\rightarrow 0$ and $|Dv_k|(\Omega ) \rightarrow |Dv|(\Omega )$. Note that we have $v_k^{t\xi }\in BV(\Omega )$ for all $k\in \mathbb N$, $t\in (-t_0,t_0)$ by Lemma 6.1. We get

$$\begin{aligned}&\int _\Omega |v_k(x+t_2\xi (x)) - v_k(x+t_1\xi (x))|\,dx \\&\quad = \int _\Omega \left| \int _{t_1}^{t_2} Dv_k(x+\tau \xi (x)) \xi (x) \,d\tau \right| \,dx \\&\quad \le \Vert \xi \Vert _{\mathcal L ^\infty } \int _{t_1}^{t_2} \int _\Omega | Dv_k(x+\tau \xi (x))| \,dx \,d\tau \\&\quad = \Vert \xi \Vert _{\mathcal L ^\infty } \int _{t_1}^{t_2} \int _\Omega | Dv_k(y)| \frac{1}{\det (\text{ id}+\tau D\xi (x(y)))}\,dy \,d\tau \\&\quad \le c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv_k|(\Omega )|t_2-t_1|\\&\quad \rightarrow c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv|(\Omega )|t_2-t_1|. \end{aligned}$$

For the left-hand side we have

$$\begin{aligned}&\!\!\!\int _\Omega \big | |v_k(x+t_2\xi (x))-v_k(x+t_1\xi (x))|-|v(x+t_2\xi (x))-v(x+t_1\xi (x))| \big |\,dx\\&\!\!\quad \le \int _\Omega |v_k(x+t_2\xi (x)) - v(x+t_2\xi (x))|+|v_k(x+t_1\xi (x)) - v(x+t_1\xi (x))|\,dx \\&\!\!\!\quad = \int _\Omega \!\!|v_k(y)\!-\!v(y)| \frac{1}{\det (\text{ id}+t_2D\xi (x(y)))} \,dy + \int _\Omega \!\!|v_k(y)\!-\!v(y)| \frac{1}{\det (\text{ id}+t_1D\xi (x(y)))} \,dy \\&\!\!\!\quad \le 2c \Vert v_k-v\Vert _{\mathcal L ^1} \rightarrow 0. \end{aligned}$$

Thus we get

$$\begin{aligned} \Vert v(\cdot + t_2\xi (\cdot )) - v(\cdot + t_1 \xi (\cdot ))\Vert _{\mathcal L ^1} \le c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv|(\Omega )|t_2-t_1|. \end{aligned}$$

$\square$

Lemma 6.6

The mapping $\mathcal H :(B_\delta (u)\cap F^\beta )\times [0,\delta ]\rightarrow BV(\Omega )$ with

$$\begin{aligned} \mathcal H (v,t)= v(\cdot + t\xi (\cdot )) \end{aligned}$$

is continuous as mapping from $\mathcal L ^1(\Omega )\times [0,\delta ]$ to $\mathcal L ^1(\Omega )$.

Proof

Let $v_1,v_2\in B_\delta (u)\cap F^\beta$, $t_1,t_2\in [0,\delta ]$. Then

$$\begin{aligned} |Dv_2|(\Omega )| \le E(v_2) = F(v_2)+\lambda G(v_2) \le \beta + \lambda (1+\delta ) \end{aligned}$$

and

$$\begin{aligned}&\int _\Omega |v_1(x+t_1\xi (x))-v_2(x+t_2\xi (x))| \,dx \\&\quad \le \int _\Omega |v_1(x+t_1\xi (x))-v_2(x+t_1\xi (x))| + |v_2(x+t_1\xi (x))-v_2(x+t_2\xi (x))|\,dx \\&\quad \le \int _\Omega |v_1(y)-v_2(y)|\frac{1}{\det (\text{ id}+t_1 D\xi (x(y)))} \,dx + c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv_2|(\Omega )|t_2-t_1|\\&\quad \le c\big (\Vert v_1-v_2\Vert _{\mathcal L ^1} + \Vert \xi \Vert _{\mathcal L ^\infty } |Dv_2|(\Omega )|t_2-t_1|\big )\\&\quad \le c\big (\Vert v_1-v_2\Vert _{\mathcal L ^1} + \Vert \xi \Vert _{\mathcal L ^\infty } (\beta +\lambda (1+\delta ))|t_2-t_1|\big ) \rightarrow 0 \end{aligned}$$

as $(v_1,t_1) \rightarrow (v_2,t_2)$ in $\mathcal L ^1(\Omega )\times (-t_0,t_0)$. $\square$

We continue the proof of Theorem 4.2 with estimates used in the definition of the weak slope $|dF|^{{\mathcal L }^1}(u)$. By Lemma 6.5 with $\tilde{c}:=c\Vert \xi \Vert _{{\mathcal L }^\infty }(\beta +\lambda (1+\delta ))$

$$\begin{aligned} \Vert \mathcal H (v,t)-v\Vert _{{\mathcal L }^1}\le c\Vert \xi \Vert _{\mathcal L ^\infty } |Dv|(\Omega )t \le c\Vert \xi \Vert _{{\mathcal L }^\infty } \big (F(v)+\lambda G(v)\big )t \le \tilde{c} t \end{aligned}$$

for all $v\in (B_\delta (u)\cap F^\beta )$, $t\in [0,\delta ]$. Hence, with $\tilde{\mathcal H }(v,t):=\mathcal H (v,t/\tilde{c})$ and $\tilde{\delta }:=\min \{\delta ,\tilde{c}\delta \}$

$$\begin{aligned} \Vert \tilde{\mathcal H }(v,t)-v\Vert _{{\mathcal L }^1}\le t \quad \text{ for} \text{ all}\ v\in B_{\tilde{\delta }}(u)\cap F^\beta ,t\in [0,\tilde{\delta }]. \end{aligned}$$

(6.20)

Moreover, by Lemma 6.4 and (6.19),

$$\begin{aligned} F(\mathcal H (v,t))-F(v)&= E(\mathcal H (v,t))-E(v) - \lambda \big ( G(\mathcal H (v,t)) - G(v)\big )\\&= \mathcal E _v(t\xi )-\mathcal E _v(0) - \lambda \big ( \mathcal G _v(t\xi )-\mathcal G _v(0) \big ) \\&= \big (\delta \mathcal E _v(0,\xi )-\lambda \delta \mathcal G _v(0,\xi )\big )t + r_{\mathcal E }(t)\mathcal E _v(0)-\lambda r_{\mathcal G }(t)\mathcal G _v(0) \\&< -\omega t + r_{\mathcal E }(t)E(v)-\lambda r_{\mathcal G }(t)G(v) \\&\le -\omega t + |r_{\mathcal E }(t)|(\beta +\lambda (1+\delta )) + \lambda |r_{\mathcal G }(t)|(1+\delta )\\&\le -\omega t + \frac{\omega }{2}t = - \frac{\omega }{2}t \end{aligned}$$

for all $v\in B_\delta (u)\cap F^\beta$, $t\in [0,\delta ]$. Consequently,

$$\begin{aligned} F(\tilde{\mathcal H }(v,t))-F(v) \le - \frac{\omega }{2\tilde{c}}t \quad \text{ for} \text{ all}\ v\in B_{\tilde{\delta }}(u)\cap F^\beta ,t\in [0,\tilde{\delta }]. \end{aligned}$$

With (6.20) we conclude that $|dF|^{{\mathcal L }^1}(u)>0$ by Lemma 3.2. Since $u$ is $\mathcal L ^1$-eigenfunction, it is also critical point of $F=E-\lambda G$ in $\mathcal L ^1$ by Proposition 4.3. Thus $|dF|^{{\mathcal L }^1}(u)=0$, a contradiction to the previous estimate. Hence (6.18) cannot be true and the assertion of Theorem 4.2 follows. $\square$