1 Introduction

With large-scale wind farms connected to the power system, the penetration of wind energy in modern power systems is increasing, and the impact on system stability is more complex [1]. Due to the inherent volatility and randomness of wind energy and the inability to predict and control it artificially and accurately, large-scale wind turbines connected to the grid have a negative impact on the stability of the system with small disturbances [2].

The additional damping control of traditional synchronous generators provides an important means for wind turbines to improve system damping characteristics. Different types of PSS have different suppression effects on low-frequency oscillations. Low-frequency oscillations may lead to instability in the power system and, in addition, a reduction in the ability to transmit power. Power system stabilizers (PSSs) have the potential to improve system damping and enhance system stability by introducing a stabilizing signal into the excitation system [3]. The reference [4] evaluates PSS2B and PSS4B in terms of their relative performance in handling a wide range of system problems. The reference [5] explores the capacity of PSS3B to offer phase compensation over a large frequency range, while the frequency domain response of the PSS is explored to validate its filtering features by evaluating alternative structural configurations. The results reveal that, like the PSS2B, the PSS3B may give great compensation, but it has certain limitations in its filtering characteristics that must be considered while utilizing it.

The current research on PSS can be divided into several categories, such as parameter tuning, controller design, etc. The reference [6] develops a control constraint-based PID–PSS using a nature-inspired search optimization technique, namely the search and rescue algorithm (SAR), to suppress low-frequency oscillations of the power system under various operating states. In addition, a multi-objective function has been developed to improve the operating effectiveness of the proposed PID–PSS under a wide range of operating states. The literature [7] describes a predictive optimal adaptive PSS (POA–PSS), which is capable of improving oscillations in single-machine infinite-bus (SMIB) power systems. By utilizing an optimal predictive algorithm that is responsive to changes in system inputs, the POA–PSS provides optimal design parameters for classic PSS systems. There are four types of PSS models studied in the literature [8]: conventional PSS (CPSS), single neuron-based PSS (SNPSS), adaptive PSS (APSS), and multifrequency PSS (MBPSS). Optimal PSS design parameters are determined using steep descent parameter optimization algorithms. The article in reference [9] proposes a nonlinear power system stabilizer that utilizes cooperative control theory. The studies on the effects of different types of PSS on power system low-frequency oscillation suppression in the above literature are all based on synchronous machine-attached PSS. With the integration of large-scale wind power into modern power systems, the impact of wind power on power systems is increasing, so research on DFIG to suppress low-frequency oscillations in power systems is getting hotter and hotter, and a large number of scholars have conducted research on the improvement of DFIG control methods and additional PSS. In the reference [10], the effect of wind power on the stability of small disturbances is elucidated in terms of the contribution of wind power to power system oscillations and the contribution of damped oscillations. According to reference [11], if power oscillation dampers (PODs) and PSS are installed on DFIG and synchronous generators, a coordinated control method can be used to improve their work performance. The literature [12] proposes that the shaft system oscillations occurring in doubly fed asynchronous motor (DFIG)-based wind power systems may lead to low-frequency oscillations in the grid, thus weakening the dynamic stability of the power system, and investigates the shaft system oscillation damping control of DFIG-based systems. Considering the dynamic properties of the phase-locked loop, reference [13] demonstrates the impact of the interaction between the DFIG and the grid on the low-frequency oscillations of the system. Particle swarm optimization is used to characterize the design of controller for a DFIG powered by a wind turbine in reference [14]. The open-loop subsystem formulas of DFIG with POD and power systems are derived in the literature [15] to describe their relationships. The reference [16] designs a two-input adaptive IEEE multiband PSS4B for power system oscillation damping control. Two additional loops based on MRAC are added to the PSS4B design. The designed PSS is applied to a 4-machine system. The simulation results show that the controller can present a robust and superior response effect. The reference [17] provides a robust composite broad-area control for dampening inter-region oscillations in a DFIG wind energy system. In the reference [18], state-space equations are given that include the DFIG–PSS transfer function. Using these equations, the functional feature sensitivity model can be expressed, and the eigenvalue increments are used to calculate the transfer function increments in an iterative way. The literature [19] clarifies that the addition of an appropriate power system stabilizer to a double-fed induction generator may significantly improve wind farm damping to the grid without diminishing the quality of the voltage control offered (DFIG–PSS). In the literature [20], a two-channel auxiliary damping controller coordinating DFIG and PSS to suppress inter-area power oscillations is proposed; a dynamic performance index for measuring conventional synchronous generators and DFIG during damping control is proposed; and a design method for PSS and a two-channel auxiliary damping controller with an objective function as the sum of weighted performance index and inter-area modal damping requirement constraints is proposed. In reference [21], the parameter adjustment problem of PSS is transformed into a multi-objective function optimization problem based on eigenvalues, and an improved version of non-dominated sorting genetic algorithms (NSGA-II) is presented to deal with this problem.

The MRAC method is applied in this paper to improve the application of PSS. Reference [22] investigated the adjustment mechanism of MRAC by applying the stability theory that contains the gradient function and the Lyapunov function. Reference [23] compared MRAC with cascaded PID controllers as a way to evaluate the performance of MRAC control. In the reference [24], the PSS is designed using the MRAC approach and virtual impedance (VI) control tactic, and the controller is retrofitted to the DFIG control loop for suppressing low-frequency oscillations in the power system.

After grid-connected wind power, low-frequency oscillation modes are introduced to the system, and more literature have investigated the DFIG with PSS attached to suppress low-frequency oscillations, but there is less research on different types of PSS linked to the DFIG. Based on this background, the following is a summary of the major contributions of this work:

  1. (a)

    An examination of the impacts of DFIG with various types of PSS on the low-frequency oscillations of power systems is presented;

  2. (b)

    Optimization of PSS4B control is performed using the MRAC method;

  3. (c)

    The MRAC is modeled according to the TLS-ESPRIT approach along with regional pole assignment;

  4. (d)

    To solve the adaptive law, the gradient method is employed;

  5. (e)

    The eigenvalue analysis and time-domain simulation approach are utilized to evaluate the effects of enhancing the stability when DFIG is equipped with MRAC–PSS4B.

2 DFIG additional different types of PSS analysis

2.1 DFIG model and power system stability analysis method

2.1.1 DFIG mathematical model

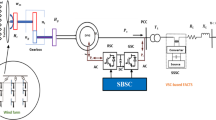
Figure 1 depicts the WTG system’s controller model. There are three components that make up the mechanical controller: a model of aerodynamics, a model of mechanical drive, and a model of pitch angle. An electrical controller is composed of two models: the DFIG and the converter.

Fig. 1
figure 1

DFIG control strategy and grid integration diagram

Full size image

Referring to Fig. 1, the DFIG scheme is described. The stator terminal is directly connected to the local AC power grid, whereas the slip-ring terminal of the rotor is incorporated into the same grid via a dual power converter and transformer. The respective names of the two converters are rotor-side converter (RSC) and grid-side converter (GSC). There are four models included in the wind generator model. These include a model of wind speed, a wind turbine, a mechanical drive, and a model of the DFIG with its control system.

RSC can be represented in Fig. 2; the equation is as follows:

$$ \left\{ \begin{gathered} \frac{{{\text{d}}x_{1} }}{{{\text{d}}t}} = P_{{{\text{s\_ref}}}} - P_{s} \hfill \\ i_{{q{\text{r\_ref}}}} = K_{{{\text{p1}}}} \left( {P_{{{\text{s\_ref}}}} - P_{s} } \right) + K_{{{\text{i1}}}} x_{1} \hfill \\ \frac{{{\text{d}}x_{2} }}{{{\text{d}}t}} = i_{{q{\text{r\_ref}}}} - i_{{q{\text{r}}}} = \left( {P_{{{\text{s\_ref}}}} - P_{s} } \right) + K_{{{\text{i1}}}} x_{1} - i_{{q{\text{r}}}} \hfill \\ \frac{{{\text{d}}x_{3} }}{{{\text{d}}t}} = v_{{{\text{s\_ref}}}} - v_{s} \hfill \\ i_{{d{\text{r\_ref}}}} = K_{{{\text{p3}}}} \left( {v_{{{\text{s\_ref}}}} - v_{s} } \right) + K_{{{\text{i3}}}} x_{3} \hfill \\ \frac{{{\text{d}}x_{4} }}{{{\text{d}}t}} = i_{{d{\text{r\_ref}}}} - i_{{d{\text{r}}}} = K_{{{\text{p3}}}} \left( {v_{{{\text{s\_ref}}}} - v_{s} } \right) + K_{{{\text{i3}}}} x_{3} - i_{{d{\text{r}}}} \hfill \\ v_{{q{\text{r}}}} = K_{{{\text{p2}}}} \left( {K_{{{\text{p1}}}} \Delta P + K_{{{\text{i1}}}} x_{1} - i_{{q{\text{r}}}} } \right) + K_{{{\text{i2}}}} x_{2} + s_{{\text{r}}} \omega_{{\text{s}}} L_{m} i_{{d{\text{s}}}} \hfill \\ \qquad\qquad + s_{{\text{r}}} \omega_{{\text{s}}} L_{{{\text{rr}}}} i_{{q{\text{r}}}} \hfill \\ v_{{d{\text{r}}}} = K_{{{\text{p2}}}} \left( {K_{{{\text{p3}}}} \Delta P + K_{{{\text{i3}}}} x_{1} - i_{{d{\text{r}}}} } \right) + K_{{{\text{i2}}}} x_{4} - s_{{\text{r}}} \omega_{{\text{s}}} L_{m} i_{{q{\text{s}}}} \hfill \\ \qquad\qquad- s_{{\text{r}}} \omega_{{\text{s}}} L_{{{\text{rr}}}} i_{{q{\text{r}}}} \hfill \\ \end{gathered} \right. $$
(1)

where the proportional and integral active power control coefficients are represented by Kp1 and Ki1, respectively; Kp2 and Ki2 denote the RSC current control proportional and integral coefficients; Kp3 and Ki3 are the voltage control proportional and integral coefficients; x1, x2, x3, and x4 are the intermediate variables in this equation.

Fig. 2
figure 2

Block diagram of RSC with additional MRAC–PSS-VI

Full size image

In this case, the stator and rotor windings are assumed to be three-phase sinusoidal and symmetrical. The voltage between the stator and rotor in a rotating reference frame with a random dq-axis and a speed of ωs is represented as follows:

$$ \left[ {\begin{array}{*{20}c} {v_{{d{\text{s}}}} } \\ {v_{{q{\text{s}}}} } \\ {v_{{d{\text{r}}}} } \\ {v_{{q{\text{r}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - r_{{\text{s}}} } & {\left( {x_{{\text{s}}} + x_{{\text{m}}} } \right)} & 0 & {x_{{\text{m}}} } \\ {\left( {x_{{\text{s}}} + x_{{\text{m}}} } \right)} & { - r_{{\text{s}}} } & {x_{{\text{m}}} } & 0 \\ 0 & {\left( {1 - \omega_{m} } \right)x_{{\text{m}}} } & { - r_{{\text{r}}} } & {\left( {1 - \omega_{m} } \right)\left( {x_{{\text{r}}} + x_{{\text{m}}} } \right)} \\ { - \left( {1 - \omega_{m} } \right)x_{{\text{m}}} } & 0 & { - \left( {1 - \omega_{m} } \right)\left( {x_{{\text{r}}} + x_{{\text{m}}} } \right)} & { - r_{{\text{r}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{d{\text{s}}}} } \\ {i_{{q{\text{s}}}} } \\ {i_{{d{\text{r}}}} } \\ {i_{{q{\text{r}}}} } \\ \end{array} } \right] $$
(2)

where ids, iqs and idr, iqr are stator and rotor currents in dq-axis; vds, vqs and vdr, vqr are stator and rotor voltages in dq-axis; xm is the magnetizing reactance; rs and xs are the stator resistance and reactance; rr and xr are the rotor resistance and reactance, and ωm is the rotor speed.

The stator output active and reactive power delivered to the grid is expressed as:

$$ \left[ {P\quad Q} \right]^{T} = \left[ {P_{s} + P_{c} \quad Q_{s} + Q_{c} } \right] $$
(3)

The stator output power transmitted to the grid is expressed as follows:

$$ \left[ {\begin{array}{*{20}c} {P_{s} } \\ {Q_{s} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{{d{\text{s}}}} } & {v_{{q{\text{s}}}} } \\ {v_{{q{\text{s}}}} } & { - v_{{d{\text{s}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{d{\text{s}}}} } \\ {i_{{q{\text{s}}}} } \\ \end{array} } \right] $$
(4)
$$ \left[ {\begin{array}{*{20}c} {P_{r} } \\ {Q_{r} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{{d{\text{r}}}} } & {v_{{q{\text{r}}}} } \\ {v_{{q{\text{r}}}} } & { - v_{{d{\text{r}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{d{\text{r}}}} } \\ {i_{{q{\text{r}}}} } \\ \end{array} } \right] $$
(5)

The output power of the grid-side converter is

$$ \left[ {\begin{array}{*{20}c} {P_{c} } \\ {Q_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{{d{\text{c}}}} } & {v_{{q{\text{c}}}} } \\ {v_{{q{\text{c}}}} } & { - v_{{d{\text{c}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{d{\text{c}}}} } \\ {i_{{q{\text{c}}}} } \\ \end{array} } \right] $$
(6)

Neglecting the power losses at GSC

$$ \left[ {\begin{array}{*{20}c} {P_{c} } & {Q_{c} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {P_{r} } & 0 \\ \end{array} } \right]^{T} $$
(7)

Accordingly, the power transmitted to the grid can be summarized as follows:

$$ \left[ {\begin{array}{*{20}c} P & Q \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {P_{s} + P_{r} } & {Q_{s} } \\ \end{array} } \right]^{T} $$
(8)

Modeling the generator as a single shaft

$$ \omega_{m} = \left( {T_{{\text{m}}} - T_{{\text{e}}} } \right)\left( {2H_{m} } \right)^{ - 1} $$
(9)

where ωm is the rotor speed, Te denotes the electrical torque, and Tm represents the mechanical torque. The inertia of the rotor is Hm.

After the MRAC–PSS4B is equipped in the RSC loop, the rotor-side power is provided as follows:

$$ \left[ {\begin{array}{*{20}c} {P_{r}^{\prime } } \\ {Q_{r}^{\prime } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {v_{{d{\text{r}}}} } & {v_{{q{\text{r}}}} + u_{p} } \\ {v_{{q{\text{r}}}} + u_{p} } & { - v_{{d{\text{r}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{d{\text{r}}}} } \\ {i_{{q{\text{r}}}} } \\ \end{array} } \right] $$
(10)

Similarly, power transmitted to the grid is shown again as

$$ \left[ {\begin{array}{*{20}c} {P^{\prime } } & Q \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {P_{s} + P_{r}^{\prime } } & {Q_{s} } \\ \end{array} } \right]^{T} $$
(11)

2.1.2 Small-signal stability analysis model

Typically, the Lyapunov linearization approach is employed to analyze the stability of small signals. In a sufficiently small motion range, it is demonstrated that the nonlinear system can exhibit properties similar to those of its linearization. A power system’s dynamic process can be characterized using DAEs and linearized as follows:

$$ \left[ {\begin{array}{*{20}c} {\Delta \dot{x}} \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\nabla_{x} f} & {\nabla_{y} f} \\ {\nabla_{x} g} & {\nabla_{y} g} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta x} \\ {\Delta y} \\ \end{array} } \right] = A_{C} \left[ {\begin{array}{*{20}c} {\Delta x} \\ {\Delta y} \\ \end{array} } \right] $$
(12)

where \(\nabla_{x} f = \partial f(x,y)/\partial x\) is the gradient of the function \(f(x,y)\). Other symbols and x have similar meanings.

Assuming that \(\nabla_{x} f\) is nonsingular, it can be obtained by Eq. (12)

$$ \Delta \dot{x} = \left[ {\nabla_{x} f - \nabla_{y} f(\nabla_{y} g)^{ - 1} \nabla_{x} g} \right]\Delta x = A\Delta x $$
(13)

where A is the state matrix of the system.

For the system described by the state equation, its small-signal stability is determined by the eigenvalues of the state matrix A. The analysis of the matrix A is mainly based on the calculation results of the eigenvalues. If the real part of all eigenvalues has a negative real component, the system is stable at this operating point; otherwise, as long as one eigenvalue has a positive real component or a double root with a real component of zero, the system is unstable. This paper mainly studies the low-frequency oscillation of the system; thus, the content of simulation analysis mainly gives the eigenvalue and damping ratio related to the electromechanical oscillation mode of the system.

In order to determine the eigenvalue of A, a small-signal stability analysis is used. For the complex eigenvalue \(\lambda = \sigma + j\Omega\), the frequency of the related oscillation is \(f = w/2\pi\), and the damping ratio is stated as follows:

$$ \xi = - \frac{\sigma }{{\sqrt {\sigma^{2} + \omega^{2} } }} $$
(14)

Using the related left and right eigenvectors v and w, it is feasible to calculate the participating factor pij, which represents the degree of correlation between state variables and modes of the i’th state variable of the j’th eigenvalue, where \(p_{ij} = w_{ij} v_{ji} /(w_{j}^{T} v_{j} )\). For any eigenvalue λi, the n-dimensional column vectors wi fulfilling \(Aw_{i} = \lambda_{i} w_{i} (i = 1,2, \ldots ,n)\) is defined the right eigenvector of λi; and the n-dimensional row vectors vi fulfilling \(v_{i} A = v_{i} \lambda_{i} (i = 1,2, \ldots ,n)\) is defined the left eigenvector of λi.

2.2 Four typical models of PSS

2.2.1 PSS1A

The basic block diagram of PSS1A is demonstrated in Fig. 3. It is a single-input PSS with two overrun hysteresis links, using generator power signal Pe as the input signal. The structure of PSS1A is simple, easy to set parameters, having a better stability, but is easy to “anti-tuning phenomenon.” When the excitation current of a generator increases and the active power of the unit increases, the PSS will make the reactive power of the unit decrease. When the excitation current of the generator decreases and the active power of the unit decreases, the PSS will make the reactive power of the unit increase. Therefore, it is necessary to overcome its anti-tuning phenomenon in order to effectively suppress the low-frequency oscillations of the power system.

Fig. 3
figure 3

The block diagram of PSS1A

Full size image

2.2.2 PSS2B

Figure 4 shows the block diagram of PSS2B, which is a dual-input PSS model proposed for the phenomenon of reactive power inversion in PSS1A, whose one input signal uses the generator speed ω, and the other input signal uses the generator electric power Pe. When the active power of the generator oscillates, the PSS will start to play a role in suppressing the power system’s low-frequency oscillation. However, PSS2B has a limited effect on suppressing multiple oscillation modes in a power system at the same time.

Fig. 4
figure 4

The block diagram of PSS2B

Full size image

2.2.3 PSS3B

The PSS3B structure block diagram is shown in Fig. 5, which is seldom used in China. PSS3B also has two input signals like PSS2B, but instead of combining the two signals into one acceleration power like PSS2B, it is equivalent to two independent PSS working in coordination, which not only improves the efficiency of PSS but also allows more flexible parameter setting. However, for slow excitation generators that require over-phase compensation of more than 90, the PSS3B cannot provide angular compensation.

Fig. 5
figure 5

The block diagram of PSS3B

Full size image

2.2.4 PSS4B

The block diagram of the PSS4B is shown in Fig. 6, which is improved from the PSS2B model. The biggest advantage of the PSS4B model over the other three is that it has three operating bands: high, medium, and low, which have non-interfering gain coefficients, center frequency filtering, phase compensation, and limiting links, which can meet the damping needs of different oscillation bands and suppress the low-frequency oscillation problem of a power system more effectively. The PSS4B model still adopts two input signals, respectively: the medium and low-frequency bands use rotational speed as the input signal, and the high-frequency band uses electric power as the input signal. The speed sensor classifies the PSS4B into low-frequency bands, intermediate frequency bands, and high-frequency bands according to the oscillation frequency of the input signal Δω. The low-frequency band corresponds to the oscillation frequency of low-frequency oscillation between units of the interconnected system at 0.04–0.1 Hz, the intermediate frequency band is 0.1–1 Hz, and the high-frequency band is 1–2.5 Hz. The PSS4B still provides sufficient damping to suppress oscillations when ultralow-frequency oscillations occur in the system, and the three operating bands of the model ensure that multiple oscillation modes at different frequencies occurring in the system can be suppressed simultaneously.

Fig. 6
figure 6

The block diagram of PSS4B

Full size image

The input signals ΔωL−I and ΔωH of PSS4B can be obtained from the sensor whose model is shown in Fig. 7.

Fig. 7
figure 7

The block diagram of sensor

Full size image

2.3 Simulation analysis

The purpose of this part was to analyze the improvement effect of DFIG connected to different types of PSS on the power system’s low-frequency oscillation. A model of DFIG with different types of PSS attached is built and simulated in DIGSILENT/PowerFactory simulation software in this paper. A brief description of the model is given below, and the values of some of the system characteristics for a contact line power of 400 MW are given in Table 1. The purpose of this part was to analyze the improvement effect of DFIG connected to different types of PSS on the power system’s low-frequency oscillation.

Table 1 Partial eigenvalue of system with DFIG additional different types of PSS
Full size table

According to Table 1, the eigenvalues of the system containing DFIG after the addition of PSS are slightly shifted to the right for intra-regional oscillation mode 2 and inter-regional oscillation mode 4, demonstrating that DFIG has no significant effect on the improvement of system damping after the addition of traditional PSS1A in the RSC control loop. The eigenvalues of intra-regional oscillation mode 2 remain virtually constant after adding PSS2B to the RSC control loop of DFIG; however, the eigenvalues of inter-regional oscillation mode 4 show a substantial leftward shift trend, and system stability is somewhat enhanced. The eigenvalues of intra-regional oscillation mode 2 do not significantly change from those of the extra PSS1A and PSS2B after installing PSS3B in the DFIG RSC control loop, while the eigenvalues of inter-regional oscillation mode 4 exhibit a strong leftward shift trend. While, after attaching PSS4B, the eigenvalues of inter-regional oscillation mode 2 have a lesser left-shift trend, and the eigenvalues of inter-regional oscillation mode 4 have a more evident left-shift trend, indicating that DFIG attaching PSS4B is more obvious for system resilience enhancement.

In this section, it is assumed that a load fluctuation fault occurs on the transmission line between buses 6 and 7, with a fault incidence time of 1 s and a duration of 0.5 s, to further highlight the system’s efficiency in suppressing low-frequency oscillations. The simulation lasts 20 s. When a load fluctuation fault occurs in the system, Fig. 8 shows the power angle of the generator G2 as well as the voltage and frequency waveforms of bus 9.

Fig. 8
figure 8

Load fluctuation response curve

Full size image

From Fig. 8, it can be seen that when the system is subjected to small disturbances, the RSC control loop of DFIG with different types of PSS attached to the system has a certain effect on the improvement of stability. It can be seen from the power angle curve of G2 that the amplitude of the first circumferential wave after the system is added to PSS4B is significantly suppressed compared to the first amplitude after the PSS is added. From the voltage curve of bus 9, it can be seen that the voltage dip of bus 9 is the smallest when the system is subjected to small disturbances after the DFIG is attached to PSS4B, while the voltage dip after the addition of other types of PSS is larger. From the frequency curve of bus 9, it can be seen that the DFIG additional PSS4B has the most obvious effect on the suppression of frequency fluctuation in the system when the system is subjected to small disturbances. Combined with the above analysis, it can be concluded that the DFIG additional PSS4B type has the most obvious improvement in the stability of the power system with small disturbances, which is consistent with the eigenvalue analysis above.

3 MRAC–PSS4B controller design

According to the conclusion in Sect. 2, PSS4B has three operating bands: high, medium, and low, and the three operating bands have non-interfering gain coefficients, center frequency filtering, phase compensation, and limiting links, which can meet the damping needs of different oscillation bands and suppress the low-frequency oscillation problem of a power system more effectively. Therefore, in this section, the PSS4B is selected for improvement based on MRAC control so that the PSS4B can provide more accurate damping in the corresponding frequency band, and the DFIG additional MRAC–PSS4B controller can present a better low-frequency oscillation suppression effect. To test the performance of the designed MRAC–PSS4B controller in the system, the MRAC–PSS4B model is built in this section, just as Fig. 9 shown. The designed controller is still added to the RSC control loop and the reactive power control link of DFIG, and the simulation is verified in the 4-machine, 2-area system.

Fig. 9
figure 9

The block diagram of MRAC–PSS4B

Full size image

3.1 Mathematical model of MRAC–PSS4B

By using rotational invariance techniques (TLS-ESPRITs) and the regional pole assignment approach, a reference model is developed on the basis of the common block diagram of MRAC. The PID controller is employed to reduce the error between up and uref by eliminating the trajectory tracking error due to its positive effect on eliminating the trajectory tracking error. Parameters in a PID controller can be adjusted automatically using the adaptive law. The reference model can be found from the Eq. (17).

3.2 Mathematical model of MRAC

To ensure system stability and convergence, the MRAC employs Lyapunov’s theory and Barbalat’s lemma. In order to meet the settling time, rising time, peak time, and overshoot criteria, the second-order system is used. On the basis of the reference model, general adaptive control laws are established. Dynamic uncertainties and modeling errors are significantly reduced by MRAC. Figure 10 illustrates the primary MRAC block diagram. K1(s) corresponds to the reference model as shown in Fig. 9.

Fig. 10
figure 10

General block diagram of MRAC

Full size image

3.2.1 Reference model design

As shown in Fig. 11, the TLS-ESPRIT is an improved estimation of signal parameters through rotational invariance technique (ESPRIT) that is used to estimate signal parameters from metrical data.where fk, σk, and ξk stand for the signal frequency, damping factor, and damping ratio, respectively, αk and θk represent the original amplitude and the initial phase, respectively.

Fig. 11
figure 11

The process of TLS-ESPRIT algorithm

Full size image

Based on the oscillation frequency band established by the TLS-ESPRIT, a 0.2–2.5 Hz Butterworth bandpass filter is applied. During the identification process, a 2% disturbance is provided to simulate the system’s minor disturbance, and the related eigenvalues are determined by the algorithm. The system mostly participates in the local oscillation modes of around 1.1–1.6 Hz. And the damping ratios are low. They all belong to the primary oscillation modes, which are the poorly damped oscillation modes to be inhibited. Additionally, the system participates in an inter-area mode with a frequency of around 0.5 Hz and a damping ratio that is a bit larger than the local mode. By adding a Butterworth bandpass filter with a frequency range of 0.2–1.7 Hz, these modes serve as the identification target. Using TLS-ESPRIT for identification once more, the system’s 4th-order transfer function G(s) is represented by Eq. (15):

$$ \begin{aligned} & G\left( s \right) \\ &\quad = \frac{{ - 6.89 \times 10^{ - 5} s^{4} - 1.1865s^{3} - 23.5649s^{2} - 29.564s - 13.5641}}{{s^{4} + 174532.7s^{3} + 5964.1s^{2} + 6638.9s + 138.9645}} \end{aligned} $$
(15)

For increased stability, a regional pole assignment method is used to design the controller. According to the designed controller, the transfer function is as follows:

$$ \begin{aligned} K\left( s \right) = & \frac{{ - 1.25s^{5} - 163.42s^{4} - 4.45 \times 10^{3} s^{3} }}{{s^{6} + 272.23s^{5} + 2.65 \times 10^{4} s^{4} + 1.65 \times 10^{6} s^{3} }} \\ & \to \frac{{ - 4.96 \times 10^{4} s^{2} - 4.32 \times 10^{4} s - 3.11 \times 10^{4} }}{{ + 1.45 \times 10^{7} s^{2} + 1.23 \times 10^{7} s + 2.36 \times 10^{5} }} \\ \end{aligned} $$
(16)

Equation (16) shows that the controller’s order is high, which makes it unsuitable for practical application. To reduce the controller’s order, the balanced truncation model based on Hankel SVD is employed in this paper. According to the reduced controller function, it is as follows:

$$ K_{1} \left( s \right) = \frac{{ - 3.18 \times 10^{ - 9} s - 2.45 \times 10^{ - 10} }}{{s^{2} + 0.43s + 11.25}} $$
(17)

3.2.2 Conventional PID controller

PID controllers are commonly used in control systems due to their simple construction and excellent robustness. The PID controller’s performance can be improved by tuning parameters, as shown in Fig. 12.

Fig. 12
figure 12

Block of PID controller. Where Kp1, Ki1, and Kd1 are the parameters of the PID controller

Full size image

The results caused by the changes in PID controller parameters are shown in Table 2. In order to reduce the differential link’s effect on the system, the differential link’s parameters are rounded down to an extremely low value.

Table 2 The parameter variation of PID controller
Full size table

3.2.3 Adaptive ratio controller

Assuming that the controlled system is a linear time-invariant system, the output amount is the default state variable, and the state and output equation is as follows:

$$ \left\{ \begin{aligned} \dot{x}\left( t \right) = & A_{1} x\left( t \right) + B_{1} u\left( t \right) \\ y\left( t \right) = & x\left( t \right) \\ \end{aligned} \right. $$
(18)

For the related equation, the reference model is expressed as:

$$ \left\{ \begin{aligned} \dot{x}_{m} \left( t \right) = & A_{m} x_{m} \left( t \right) + B_{m} c_{m} \left( t \right) \\ y_{m} \left( t \right) = & x_{m} \left( t \right) \\ \end{aligned} \right. $$
(19)

where xm(t) is the reference state equation, and c(t) is the model’s input signal.

The acquired controller transfer function is utilized as the MRAC reference model to build the MRAC–PSS4B controller, whose structure is depicted in Fig. 9. The adaptive law is used to resolve the parameters of the controller, whereas the gradient method is employed to handle the adaptive law. Using the gradient approach to solve the adaptive law is briefly presented below.

Assuming that the MRAC control includes an uncertain parameter θ, define the error in the state variables of the reference model and the controlled object as:

$$ e = x_{m} - x $$
(20)

In Eq. (24), the error e is designed to converge to zero by adjusting the parameter θ in MRAC, where a loss function is introduced:

$$ J = \frac{1}{2}e^{2} $$
(21)

When the error e tends to zero, the loss function J also tends to zero, and now J obtains the minimum value. Using the gradient descent algorithm:

$$ \Delta \theta = - k\frac{\partial J}{{\partial \theta }} = - ke\frac{\partial e}{{\partial \theta }} $$
$$ \dot{\theta } = - \gamma \frac{\partial J}{{\partial \theta }} = - \gamma e\frac{\partial e}{{\partial \theta }} $$
(22)

where \(\Delta \theta\) is the difference between two steps, and k is the learning step. The second line is obtained after the derivation of the first line of Eq. (22), γ is the adjustment rate, and Eq. (22) can be individually referred to as the MIT law.

First, assume the following controller equation: \(u(t) = ac(t) + bx(t)\) , where the parameters a and b are unknown, this part use the MIT law to determine the values of these parameters. The two unknown parameters are as follows:

$$ \dot{a}\left( t \right) = - \gamma e\left( t \right)\frac{\partial e\left( t \right)}{{\partial a}} $$
$$ \dot{b}\left( t \right) = - \gamma e\left( t \right)\frac{\partial e\left( t \right)}{{\partial b}} $$
(23)

where e(t) can be solved using Eq. (24)

$$ e\left( t \right) = x_{m} \left( t \right) - x\left( t \right) $$
$$ \dot{x}_{m} \left( t \right) = A_{m} x_{m} \left( t \right) + B_{m} c\left( t \right) $$
(24)

Substituting into the controller equation and combining with Eqs. (18) and (25) can be obtained:

$$ \dot{x}_{m} (t) = Ax\left( t \right) + B\left[ {ac\left( t \right) + bx\left( t \right)} \right] $$
(25)

Equation (23) can be solved for x(t) by substituting it into Eq. (20) and adding a differential operator p

$$ e\left( t \right) = x_{m} \left( t \right) - \frac{Ba}{{p - A - Bb}}c\left( t \right) $$
(26)

According to Eq. (23):

$$ \frac{\partial e\left( t \right)}{{\partial a}} = - \frac{Ba}{{p - A - Bb}}c\left( t \right) $$
$$ \frac{\partial e\left( t \right)}{{\partial b}} = - \frac{Ba}{{p - A - Bb}}x\left( t \right) $$
(27)

In Eq. (27) the parameters A and B are unknown, but they can be simplified by treating them as first-order inertia links:

$$ \frac{\partial e\left( t \right)}{{\partial a}} = - \frac{1}{p + Am}c\left( t \right) $$
$$ \frac{\partial e\left( t \right)}{{\partial b}} = - \frac{1}{p + Am}x\left( t \right) $$
(28)

As shown in Eq. (28), the parameters a and b can be calculated according to the MIT law. This section still uses a conventional PID controller.

3.3 3.3 Simulation analysis

3.3.1 System simulation of tie-line transmission power variation

In this section, simulation experiments are still conducted using the 4-machine, 2-area system, where power is set to be delivered from area 1 to area 2, and the transmission power of the contact line is adjusted by changing the output of the generator in area 1. The system’s characteristic values are examined under three distinct operating conditions:

Case a: The power transmitted on the tie line from region 1 to region 2 is 300 MW;

Case b: The power transmitted on the tie line from region 1 to region 2 is 450 MW;

Case c: The power transmitted on the tie line from region 1 to region 2 is 600 MW.

As shown in Tables 3 and 4, when PSS4B is attached to the DFIG, the eigenvalues of inter-regional oscillation mode 3 exhibit a slight leftward shift trend, which improves the system’s small disturbance stability. The corresponding eigenvalues of the system’s inter-regional oscillation mode 4 and intra-regional oscillation mode 2 have a large left-shift trend for the MRAC–PSS4B, and both show a significant improvement in the damping ratio. Furthermore, the eigenvalues of inter-regional oscillation mode 3 exhibit a small left-shift trend, which has an improving effect. Under three different operating conditions (a, b, and c), the damping ratio of inter-area oscillation mode 4 rises from 16.518, 16.524, and 16.387 to 20.560, 17.69, and 17.216%, respectively. The MRAC–PSS4B can further improve the damping characteristics of the system. The damping ratios of inter-area and intra-area oscillation modes are greatly improved, especially the damping ratios of inter-area oscillation mode 4 corresponding to different operating conditions, which are improved by 24.47%, 7.05%, and 5.06%, respectively. It can be seen that the stability and robustness of the system with small disturbances have greatly improved.

Table 3 The eigenvalues of system in different tie-line power condition
Full size table
Table 4 The eigenvalues of system with MRAC–PSS4B in different tie-line power condition
Full size table

Figure 13 shows the power angle, voltage, and frequency response curves of the system under different tie-line powers with the same conditions as shown in Sect. 2.3, assuming the same fault happened in the system. As the tie-line power grows, the power angle of generator G2 gradually increases, the voltage of bus 9 gradually lowers, and the frequency gradually decreases. The oscillation amplitude of the curve increases as the tie-line power increases, as does the time for the system to reach stability. From the power angle of the G2 response curves in the three operating conditions, the DFIG with PSS4B has a damping effect on the system oscillation, but the improvement effect on the system bus frequency and voltage is not satisfactory. As shown in Fig. 13, after attaching the MRAC–PSS4B controller to the RSC control loop, the amplitude of the power angle curve of G1 is further suppressed, the amplitude of the frequency response curve of bus 9 is obviously suppressed, and the voltage drop of bus 9 is very small under less interference conditions. It can be concluded that the system’s additional MRAC–PSS4B controller has a better damping impact on oscillations under different tie-line power situations, and the system’s robustness is greatly increased, which is consistent with the eigenvalue analysis results.

Fig. 13
figure 13

Response curves of small disturbances under different working conditions

Full size image

3.3.2 System simulation of DFIG access point changes

In this section, the effect of DFIG additional MRAC–PSS controller on system stability with small disturbances is investigated when the DFIG access location is changed. The effectiveness of the designed controller is verified in the following three cases:

Case d: DFIG access bus 6 in area 1;

Case e: DFIG access transmission line7–8 in area 1;

Case f: DFIG access bus 9 in area 2.

As shown in Tables 5 and 6, different eigenvalues of the system correspond to the same oscillation mode when the DFIG is at different access points. As a result, when the turbine access position changes, the system characteristic values change as well. After connecting the PSS4B to the DFIG, there is no clear leftward trend in the system’s eigenvalues for intra-regional oscillation mode 2. When the DFIG is attached to the PSS4B at different access points, the damping ratio of the system is affected in both positive and negative ways. However, when the DFIG connects the MRAC–PSS4B controller to intra-regional oscillation mode 2, the eigenvalues in the complex plane exhibit a significant leftward shift trend, and the system’s damping ratio improves significantly. There is a certain effect on the improvement of the damping ratio of the system after attaching the PSS4B to the DFIG for inter-regional oscillation mode 4, but it is not ideal. After attaching the MRAC–PSS4B at the same position in the DFIG control loop, the trend of the left shift of the system’s eigenvalues is significantly better than after adding the PSS4B, as is the improvement of the damping ratio for inter-regional oscillation.

Table 5 The eigenvalues of the system at different DFIG access locations
Full size table
Table 6 DFIG additional MRAC–PSS4B eigenvalues at different DFIG access locations
Full size table

A time-domain simulation analysis was performed in DIGSILENT/PowerFactory software to validate the damping impact of adding the MRAC–PSS4B controller in DFIG for different grid-connected locations of DFIG wind turbines on the system. Assuming different DFIG locations are linked to the 4-machine, 2-area system, and the load L2 is configured to have a 5% step at 1 s and 0.5 s later to recover, the generator G2 power angle curve with bus 9 voltage and frequency response curves is formed, as illustrated in Fig. 14.

Fig. 14
figure 14

Response curves for different access positions of DFIG

Full size image

According to Fig. 14, the varied access points of the DFIG wind turbine to the grid have an effect on the power angle characteristics of the system, and the relative power angle of the synchronous machine changes when the DFIG wind turbine is at different access points. The amplitude of the first pendulum of the power angle curve of generator G2 is reduced to a certain extent after DFIG is attached to PSS4B, which improves system stability, but the voltage and frequency response curves of bus 9 show that the DFIG is attached to PSS4B for the system voltage, and frequency fluctuation improvement effect is relatively weak. The amplitude of the power angle curve of G1 and the voltage curve of bus 9 are obviously weakened after attaching the MRAC–PSS4B at the same position in the DFIG control loop, as shown in Fig. 14, and the stabilization time required for oscillation is obviously shortened, indicating that the system’s stability is greatly improved. It can be shown that the RSC control loop of the MRAC–PSS4B controller retrofitted to the DFIG greatly enhances system stability at various DFIG access points and operation situations.

4 Conclusion

The MRAC–PSS4B controller is constructed in DigSILENT/PowerFactory simulation software to address the low-frequency oscillation problem of wind power systems. In this paper, a four-machine, two-area system is utilized as a simulation scenario to examine the improvement impact of comparing DFIG with four different PSS, and the MRAC–PSS4B controller is built to be put in DFIG’s RSC control loop. The developed controller’s improved impact on the system’s low-frequency oscillation is validated using both time-domain simulation and eigenvalue analysis.

The main conclusions are as follows:

  1. (1)

    Among the four types of power system stabilizers, PSS4B is the most successful in increasing the stability of power systems with minor disruptions.

  2. (2)

    The installation of MRAC–PSS4B in the DFIG rotor-side reactive power control loop decreases low-frequency oscillations in the system and is especially effective when the power of the contact line changes and the DFIG access position changes.

  3. (3)

    The MRAC–PSS4B has a greater influence on damping in systems where the primary participating units contain DFIG than in systems where the main participating units do not have DFIG.