A new robust tilt-PID controller based upon an automatic selection of adjustable fractional weights for permanent magnet synchronous motor drive control

Abstract

This paper focuses on achieving a good trade-off between performance and robustness for a class of uncertainty models including unstructured multiplicative uncertainties. In robust control, the simultaneous improvement of the two secure margins for nominal performances and robust stability using a standard controller structure represents two contradictory objectives and guaranteeing simultaneously of these goals represents therefore a major challenge for most researchers. In this context, a robust tilt-proportional integral derivative (T-PID) controller synthesized with an automatic selection of adjustable fractional weights (AFWs) is discussed in our work. Their parameters are optimized through solving a weighted-mixed sensitivity problem using an optimization tool which is based on the genetic algorithm. This problem is formulated from performance and robustness requirements where a fitness function is accordingly determined. Furthermore, thus its search space is built according to some guidelines for ensuring an automatic selection of adequate AFWs. The proposed constrained optimization problem is initialized by using arbitrary T-PID speed controller as well as through initial fixed integer weights (FIWs) which were chosen previously by the designer. To highlight the proposed control strategy, the synthesized robust T-PID speed controller is applied on the permanent magnet synchronous motor. Their performance and robustness are compared to those provided by an integer-order PID (IO-PID) and two conventional fractional-order PID (FO-PID) controllers. This comparison reveals superiority of the proposed robust T-PID controller over the remaining controllers in terms of robustness with reduced control energy.

1 Introduction

In general, reaching a good trade-off between two conflicting objectives such as (NP) and (RS) presents a critical issue for the PMSM speed control [10]. It is considered as a main objective of most synthesis methods, especially when some undesired effects such as neglected and unmodeled dynamics uncertainty, model parameter variation and sensor noise are considered [10, 31].

It is well known that satisfying the trade-off condition for the PMSM speed control leads systematically to ensuring simultaneously NP and RS conditions. On the other hand, meeting the two last conditions does not necessarily imply achieving a good trade-off between NP and RS [31]. Consequently, in mechanical speed regulation of the PMSM drive, several sensitivities can be derived from a closed-loop system such as direct sensitivity, complementary sensitivity, controller sensitivity and plant sensitivity. Analysis of these sensitivities in the frequency domain allows verifying the mentioned above robustness conditions. Moreover, from basic theories that are available in robust control strategies [29, 31], the singular value diagrams of direct sensitivity and complementary sensitivity functions provide information on the NP condition and RS condition, respectively. Accordingly, a suitable NP is achieved if the singular values of direct sensitivity modules exhibit very steep slopes at low frequency [29]. This property means in the time domain that the feedback control system of the PMSM speed control can ensure a good disturbance attenuation of the PMSM model uncertainties and a good reference tracking of the mechanical speed of the PMSM drive. On the other hand, a suitable RS can be achieved if singular values of the complementary sensitivity modules are provided by another steeper slopes at high frequency. This is explained in the time domain by ensuring a good sensor noise rejection, a less sensitivity against effects of unmodeled (usually high-frequency) dynamics, neglected nonlinearities in the modeling and effects of deliberate reduced-order of the PMSM models [29].

In the $H_{\infty }$ weighted-mixed sensitivity problem, all preceding properties are highly constrained by a good choice of two appropriate FIWs named performance weight and stability weight. Solving this problem leads often to an acceptable trade-off if the linearized model is well conditioned around the operating point and their parameters vary in a reasonable range. Usually, this kind of problems is solved using two synthesis methods: $H_{\infty }$ method based on two algebraic Riccati equations (AREs) [10, 29, 31] and $H_{\infty }$ method based on linear matrix inequality approach (LMI) [14]. Unfortunately, these methods lead to a high-order controller where its implementation in real-world applications is expensive and leads to difficult commissioning, poor reliability and potential problems in maintenance. To overcome these drawbacks, various synthesis methods based on optimization algorithms have been proposed since the end of the 90s, including methods from global optimization [5], matrix inequality constrained nonlinear programming [4], eigenvalue optimization [3] and others. Therefore, an optimal performance associated with an acceptable robustness not only requires a judicious choice of a suitable controller structure, but requires a careful choice of appropriate weights, including all the $H_{\infty }$ specifications [26, 29].

It should be noted that the inverse of an optimal performance weight presents the ideal shape (to be achieved) for the direct sensitivity function. Also, the inverse of an optimal stability weight presents the ideal form of the complementary sensitivity function [18, 26]. Furthermore, one of the major issues occurring in the design of robust controllers via conventional FIWs is the inability to achieve satisfactory closed-loop performance with good robustness, especially when model parameters vary in a wide range [28]. Instead of using FIWs in the weighted-mixed sensitivity problem, finding optimal AFWs leads to an acceptable trade-off. This avoids easily the above mentioned drawbacks [28].

According to several previously published works, a large number of researchers have demonstrated the advantage of controllers synthesized by the AFWs compared to those given by the FIWs in terms of time responses and ensured by reasonable control energies [1, 2, 27]. For this reason, several synthesis methods based on either adjustable integer weights (AIWs) or AFWs have been proposed in recent years, providing robust controllers, presented with a sufficient number of parameters. Among them, Hu [13] proposed a new procedure based on AIWs to the real-time control of a vertical take-off aircraft. This procedure allows updating the parameters of these weights during the design of the integer-order $H_{\infty }$ controller [13]. Kaitwanidvilai et al. [15] synthesized a fixed-structure of integer-order robust loop shaping controller for the power system control applications using AIWs. This technique used the particle swarm optimization (PSO) to find the optimal controller parameters and their corresponding weights so that the stability margin of controlled system was maximized [15]. Zang et al. [32] used the space vector model of PMSM to design the robust integer-order $H_{\infty }$ speed controller using the AIWs. The systematic selection of these weights and the controller parameters was determined through optimizing five fitness using the GA [32]. Kaur and Ohri [16] used the same preceding idea for the pneumatic servo regulation. The automatic selection of the AIWs and the tuning parameter of the corresponding $H_{\infty }$ controller have been ensured from minimizing the $H_{\infty }$ norm of the transfer function of the nominal closed loop [16]. Nair [21] controlled the active magnetic bearing system by the integer-order robust loop shaping controller where the corresponding weighted-mixed sensitivity problem including the AIWs has solved by the GA. Sedraoui et al. [27] proposed the cascade FO-PID controller synthesized with optimal AFWs to control the doubly fed induction generator DFIG. Bouiadjra et al. [7] proposed a variety of parallel FO-PID controllers synthesized with appropriate AFWs for the PMSM speed control. The used optimization process in these two preceding control strategies employs the min–max optimization algorithm to solve the weighted-mixed sensitivity problem. In the same context, several other controller structures, derived from fractional-order controllers, have been used by many scholars [8, 11, 19, 20]. Among the latter, Morsali et al. [20] proposed the TID-based damping controller where their parameters were determined by minimizing the integral time square error (ITSE) by the modified group search optimization (MGSO) algorithm. Behera et al. [6] synthesized the TID controller for hybrid power systems using differential evolution (DE) algorithm. Guessoum et al. [12] enhanced the robust performance of the PMSM speed drive control. This goal is ensured through robustifying the standard $H_{\infty }$ controller by the AFWs where its automatic selection is performed by the particle swarm optimization (PSO) algorithm [12].

It should be noted that the above-mentioned controllers have not been, so far, employed to achieve the trade-off. One of the novelties of this paper is to introduce the proposed T-PID speed controller and the AFWs in the weighted-mixed sensitivity problem. Their optimal parameters are ensured by the GA, enhancing therefore the given trade-off by the FO-PID controller. To highlight the proposed control strategy, the proposed robust T-PID speed controller based on the automatic selection of optimal AFWs is applied on the PMSM drive system. Their given performance and robustness are compared to those provided by IO-PID and FO-PID speed controllers. The main goal of the proposed control strategy is to ensure a good trade-off with reduced control energy while considering plant uncertainties, unmodeled dynamic and sensor noise effect.

2 Mathematical modeling of the PMSM system

The actual PMSM behavior is commonly modeled by a nonlinear model which is given, in stationary reference frame, by [7, 9, 17, 30]:

• Direct and quadrature axis voltages:

  $$\begin{aligned} {U_d}= & {} {R_s} \cdot {i_d} + \frac{{\text {d}{\phi _d}}}{{\text {d}t}} - {\omega _r} \cdot {\phi _q}\nonumber \\ {U_q}= & {} {R_s} \cdot {i_q} + \frac{{\text {d}{\phi _q}}}{{\text {d}t}} - {\omega _r} \cdot {\phi _d} \end{aligned}$$

  (1)

• Direct and quadrature axis flux linkages:

  $$\begin{aligned} {\phi _d}= & {} {L_d} \cdot {i_d} + {\phi _f}\nonumber \\ {\phi _q}= & {} {L_q} \cdot {i_q} \end{aligned}$$

  (2)

• Electromagnetic torque of the motor:

  $$\begin{aligned} {C_{em}} = \frac{3}{2}{n_p}\left( {{\phi _f} \cdot {i_q} + ({L_d} - {L_q}) \cdot {i_d} \cdot {i_q}} \right) \end{aligned}$$

  (3)

• Mechanical speed of the motor:

  $$\begin{aligned} J \cdot \frac{{\text {d}{\varOmega _m}}}{{\text {d}t}} + {f_c} \cdot {\varOmega _m} = {C_{em}} - {C_t} \end{aligned}$$

  (4)

Therefore, Table 1 summarizes the meaning and the corresponding nominal values of diverse PMSM components [7, 9, 17, 30].

Table 1 Values of diverse PMSM components

This paper focuses on the mechanical speed control of the PMSM system where the desired speed controller should satisfy some conflicting goals such as the tracking dynamic of the reference mechanical speed, the rejection of model uncertainties, the mitigation of undesirable effects caused by parametric variations of the linear PMSM model, sensor noise and nonlinear dynamics neglected during the linearization step of the actual PMSM system. In general, ensuring a good trade-off between all the preceding goals by a robust speed controller requires developing a suitable linear model where the field oriented control (FOC) principle, given in Fig. 1, is used.

Fig. 1

The used block diagram to illustrate the FOC strategy

2.1 Field oriented control of PMSM

The principle of the FOC strategy for the mechanical speed control of the PMSM system is depicted in Fig. 1. Accordingly, the mechanical speed $\varOmega _{m}$ is controlled by regulating the quadrature axis current $i_{q}^{*}$ while the direct axis $i_{d}^{*}$ current must be kept at zero [9]. According to the FOC strategy, the independent current regulator, incorporated in the direct axis, allows to attenuate as much as possible the discrepancy which is generated between the measured direct axis $i_{d}$ current and the corresponding reference current $i_{d}^{*}$. This enables decoupling of the nonlinear behavior of the PMSM system where the mechanical speed control is only carried out in the q-axis. It should be noted that the preceding target involves prior regulation of the electrical compartment of PMSM system in the q-axis. This requires the development of an adequate linear model describing the transfer function from the stator voltage $U_{q}$ to the stator current $i_{q}$.

2.1.1 Quadrature current controller design

Assuming that the direct current regulation in the d-axis is perfectly controlled by a corresponding current regulator in which the current $i_{d}$ is always kept at zero. Hence, from Eqs. 1–4, the linear PMSM model of the q-axis can be determined by [9, 30]:

$$\begin{aligned}&{U_q} = {R_s} \cdot {i_q} + {L_q} \cdot \frac{{\text {d}{i_q}}}{{\text {d}t}} + {\phi _f} \cdot {n_p} \cdot {\varOmega _m}\nonumber \\&{C_{em}} = \frac{3}{2} \cdot {\phi _f} \cdot {n_p} \cdot {i_q}\nonumber \\&J \cdot \frac{{\text {d}{\varOmega _m}}}{{\text {d}t}} + {f_c} \cdot {\varOmega _m} = {C_{em}} - {C_t} \end{aligned}$$

(5)

The synthesis of the quadrature current controller $K_{q}(s)$ requires maintaining the load torque $C_{t}$ at zero in Eq. 5, yielding thus the block diagram, given by Fig. 2. The transfer function $G_{q}(s)$ that associates the stator voltage input $U_{q}$ by the stator current output $i_{q}$ is computed by means of the Matlab®command linmod. Hence, $G_{q}(s)$ is given by the following zero-pole-gain format:

$$\begin{aligned} G_{q}(s)=\frac{117.65\cdot \left( s+0.05618\right) }{s^{2}+23.59\cdot s+972.9} \end{aligned}$$

(6)

Based on Eq. 6, the Matlab®command rltool is applied to design the desired quadrature current controller $K_{q}(s)$ using the following tuning parameters:

• Controller type: PID tuning

• Design mode: Frequency

• Desired bandwidth: 480 rad/s

• Desired phase margin: 60 degree

Therefore, the desired quadrature current controller is provided by:

$$\begin{aligned} K_{q}(s)=\frac{4557\cdot \left( s+45.74\right) }{s\cdot \left( s+972.9\right) } \end{aligned}$$

(7)

The given time response for unit-step excitation confirms the good stability of the closed-loop system where the reference tracking dynamic is characterized by:

• Rise time: $T_{r}=2.9502$ ms

• Overshoot: $D_{\max }=11.4011 \%$ provided at time $T_{D_{\max }}=2.9502$ ms

• Settling time: $T_{s}=17.7001$ ms

Fig. 2

The used block diagram for the quadrature current regulation

Fig. 3

The used block diagram for the mechanical speed regulation

2.1.2 Mechanical speed controller design

The used mechanical speed controller used in most industrial applications is usually given by the PID structure. Its parameters are often tuned according to the appropriate nominal model $G_{n}(s)$ developed through the zero-pole compensation system, performed in inner loop between the two preceding transfer functions $G_{q}(s)$ and $K_{q}(s)$. The corresponding closed-loop system is done by the block diagram, given in Fig. 3.

Similarly, the transfer function $G_{n}(s)$ which associates the reference stator current input $i_{q}^{*}$ by the mechanical speed output $\varOmega _m$ is computed using the Matlab®command linmod. Hence, $G_{n}(s)$ is given by the following zero-pole-gain format [19]:

$$\begin{aligned} G_{n}\left( s\right) =\frac{6.325\cdot 10^{6}\cdot \left( s+45.74\right) }{ \left( s+49.87\right) \left( s+0.054\right) \left( s^{2}+992.2\cdot s+5.1165\cdot 10^{5}\right) } \end{aligned}$$

(8)

The speed controller is synthesized from the linear model, given by Eq. 8, and depending on the control requirements, the desired controller is commonly chosen using either PI or PID structure. Indeed, the Matlab®command rltool is carried out to determine the controller parameters using the following tuning parameters:

• Controller type: PID tuning

• Design mode: Frequency

• Desired bandwidth: 144.7 rad/s

• Desired phase margin: 60 degree

For the PI structure case, the transfer function of the mechanical speed controller is given by:

$$\begin{aligned} K_{w0}(s)=\frac{11.61\cdot \left( s+38.46\right) }{ s} \end{aligned}$$

(9)

where the corresponding closed-loop response for a unit-step excitation is characterized by:

• Rise time: $T_{r}=7.0702$ ms

• Overshoot: $D_{\max }=29.109 \%$ provided at time $T_{D_{\max }}=22.801$ ms

• Settling time: $T_{s}=71.702$ ms

According to previous works carried on the PMSM system [7, 8, 11, 19, 20], when undesirable properties such as model uncertainties and cross-coupling between direct and quadrature currents are considered in the controller synthesis, the mechanical speed regulation based on simple PI structure often becomes insufficient to guarantee all imposed specifications. For example, when the corresponding closed-loop system is excited by the reference mechanical speed input $\varOmega _{m}^{*}=50$ r.p.m., the corresponding unit-step response provides the undesired speed threshold $\max \left( \varOmega _{m}\right) =64.558$ r.p.m., appearing in transient state. Consequently, the desired attenuation of the control error imposing the additional the electromagnetic torque $C_{em}=318.8058$ N m, causing thus the deterioration of the PMSM system. In this paper, the mechanical speed control based on the PI controller will be bypassed. It will be substituted by the PID structure where the corresponding transfer function:

$$\begin{aligned} K_{w1}(s)=\frac{109.27\cdot \left( s+1751\right) \left( s+26.54\right) }{ s\left( s+26.54\right) } \end{aligned}$$

(10)

Therefore, the given closed-loop step response is characterized by:

• Rise time: $T_{r}=8.4101$ ms

• Overshoot: $D_{\max }=11.501 \%$ provided at time $T_{D_{\max }}=27.501$ ms

• Settling time: $T_{s}=92.403$ ms

In general, the synthesis methods based on IO-PID speed controllers usually provide a good reference tracking dynamic. Nevertheless, when the effect of measurement noises is considered, the corresponding reference current in the q-axis often becomes highly fluctuating, degrading the secure margin of the closed-loop robustness. These control signals typically saturate the actuators installed in the feedback control system, leading thus to its failure in most real-world applications. This drawback can be overcome using the robust fractional-order controller instead of the IO-PI and IO-PID controllers. Accordingly, the trade-off between reference tracking dynamic and closed-loop robustness can be achieved independent of pole-zero compensation quality which is performed in the inner loop by quadrature current controller.

In general, the design of the robust fractional-order controller for PMSM speed control requires the resolution of a $H_{\infty }$ problem, also known as a weighted mixed sensitivity problem. Its structure can be imposed by a three-degree-of-freedom including the structure of the fractional-order Proportional-Integral $PI^{\lambda }$. Also, it can be imposed by a five-degree-of-freedom including the structure of the fractional-order proportional integral derivative $PI^{\lambda }D^{\mu }$ type. Usually, these structures improve significantly the response quality of the closed-loop system in terms of rapidity, overshoot and sensitivity to effect of sensor noise.

3 Proposed of the robust mechanical speed controller

In the design of the PMSM speed control, when the imposed control targets are becoming severe and the model parameters are varying within a wide range, the choice of one of the two preceding $PI^{\lambda }$ and $PI^{\lambda }D^{\mu }$ structures is still insufficient to achieve the desired trade-off. For this purpose, the T-PID structure including six degree-of-freedom is chosen in the synthesis of the desired speed controller where its transfer function is depicted in Fig. 4.

Fig. 4

Structure of the proposed T-PID speed controller

Here $K_{t}$, $K_{p}$ , $K_{i}$ and $K_{d}$ are four adjustable gains, referred to as tilt gain, proportional gain, integral gain and derivative gain. Furthermore, the adjustable filter coefficient $\tau _{d}$ represents the bandwidth of the low-pass filter carried on the derived part of the proposed T-PID speed controller. It should be added to prevent the amplification of sensor noise effect. In the T-PID structure, the tilt part includes the fractional-order transfer function $s^{\frac{-1}{N}}$ where the adjustable parameter N is preferably chosen between 2 and 3. The transfer function of the proposed T-PID speed controller is given by:

$$\begin{aligned} K(s,{x_c}) = \frac{{{K_t}}}{{{s^{\frac{1}{N}}}}} + \left( {{K_p} + \frac{{{K_i}}}{s} + {K_d} \cdot \frac{{{\tau _d}}}{{1 + {\tau _d} \cdot \frac{1}{s}}}} \right) \end{aligned}$$

(11)

Here, ${x_c} = {\left( {{K_p},{K_i},{K_d},{K_t},N,{\tau _d}} \right) ^\mathrm{T}}$ is the design vector to be optimized by an adequate optimization algorithm. The search space $\chi _{m}$ including the desired optimal parameters is defined as boundary or saturation constraints; it is expressed by:

$$\begin{aligned} \chi _{m}: \left\{ \begin{array}{c} K_{p_{\min }}\le K_{p}\le K_{p_{\max }} \\ K_{i_{\min }}\le K_{i}\le K_{i_{\max }} \\ K_{d_{\min }}\le K_{d}\le K_{d_{\max }} \\ K_{t_{\min }}\le K_{t}\le K_{t_{\max }} \\ 2\le N\le 3 \\ \tau _{d_{\min }}\le \tau _{d}\le \tau _{d_{\max }} \end{array} \right. \end{aligned}$$

(12)

It is well known that implementing the proposed the T-PID speed controller needs to approximate the fractional-order transfer function of power $\left( \gamma =-\frac{1}{N}\right)$ using usual integer-order transfer function with a similar behavior. In this study, the Oustaloup-based method is used to approximate the fractional-order operator ${s^v}$ by a rational transfer function of order $2\cdot q+1$ in the specified frequency range $\omega =\left( \omega _{h},\omega _{b}\right)$. This yields also [24, 25]:

$$\begin{aligned} {s^v} \simeq {k_w} \cdot \prod \limits _{k =- q}^{k = + q} {\frac{{s + {z_k}}}{{s + {p_k}}}} \end{aligned}$$

(13)

where $z_{k}$, $p_{k}$ and $k_{k}$ denote, respectively, zeros, poles and gain of the corresponding rational transfer function. They are defined by [24, 25]:

$$\begin{aligned} {z_k}= & {} {\omega _b}{\left( {\frac{{{\omega _h}}}{{{\omega _b}}}} \right) ^{\frac{{k + q + \frac{1}{2}(1 - v)}}{{2 \cdot q + 1}}}} \end{aligned}$$

(14)

$$\begin{aligned} {p_k}= & {} {\omega _b}{\left( {\frac{{{\omega _h}}}{{{\omega _b}}}} \right) ^{\frac{{k + q + \frac{1}{2}(1 + v)}}{{2 \cdot q + 1}}}} \end{aligned}$$

(15)

$$\begin{aligned} {k_k}= & {} {\left( {\frac{{{\omega _h}}}{{{\omega _b}}}} \right) ^{^{ - \frac{v}{2}}}} \cdot \prod \limits _{k = - q}^{ + q} {\left( {\frac{{{p_k}}}{{{z_k}}}} \right) } \end{aligned}$$

(16)

4 Formulation of the synthesis problem of the robust T-PID speed controller

4.1 Weighted-mixed sensitivity problem including FIWs

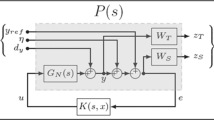
Consider the shown block diagram in Fig. 5, where u denotes the control signal, y denotes the measured output, r denotes the reference input (to be tracked), e denotes the control error, and $\eta$ denotes the sensor noise (to be rejected).

Supposing that the perturbed plan $G_{p}(s)$ is given by the form $G_{p}(s)=\left( I+\varDelta _{m}\left( s\right) \right) \cdot G_{n}(s)$ where $\varDelta _{m}\left( s\right)$ is a stable transfer function satisfying $\left\| \varDelta _{m}\left( s\right) \right\| _{\infty }\le 1$. All these transfer functions have appropriate dimensions. In this paper, the resulting effects from model uncertainties, parametric model variations and unmodeled dynamics are quantified as unstructured multiplicative uncertainties. They are described by the unknown signal $d_{y}$ that is carried on the output of the nominal model (see Fig. 5).

Fig. 5

Block diagram system based on unstructured multiplicative uncertain model

In this paper, the trade-off between NP and RS should be reached with a good secure margin. Here, the NP requirement includes the tracking dynamic of the reference mechanical speed as well as the rejection dynamic of the effect of model uncertainties. Note that the direct sensitivity function $S_{0}(s, x_{c})$, defined by Eq. 17, represents the transfer function between the control error e and the measured output y. It also represents the transfer function between the disturbance input $d_{y}$ and the measured output y.

$$\begin{aligned} {S_0}(s,{x_c}) = {\left[ {I + {G_n}(s) \cdot K(s,{x_c})} \right] ^{ - 1}} \end{aligned}$$

(17)

Therefore, ensuring a good NP needs limiting the evolution of the maximum singular values of the direct sensitivity function, i.e., $\bar{\sigma }\left( S_{0}\left( \omega ,x_{c}\right) \right)$ over the entire frequency range $\omega _{\min }\le \omega \le \omega _{\max }$. This goal is reached by selecting the suitable weighting function $W_{S_{0}}\left( s\right)$ such that the NP condition which is given by Eq. 18 is always satisfied.

$$\begin{aligned} \left\| W_{S_{0}}\left( s\right) \cdot S_{0}\left( s,x_{c}\right) \right\| _{\infty }\le 1 \end{aligned}$$

(18)

This condition may be translated into an upper bound $\left\| W_{S_{0}}\left( s\right) \right\|$ on the frequency plot of $\bar{\sigma }\left( S_{0}\left( \omega ,x_{c}\right) \right)$, yielding thus the inequality $\left\| S_{0}\left( {s,x_{c}})\right) \right\| _{\infty }\le \left\| W_{S_{0}}\left( s\right) \right\| _{\infty }^{-1}$.

On the other hand, the RS requirement includes the closed-loop stability against some effects caused by sensor noises, unmodeled and neglected nonlinear dynamics. Note that the complementary sensitivity function $T_{0}(s,x_{c})$, defined by Eq. 19, represents the transfer function between the reference input r and the measured output y. It also represents the transfer function between the sensor noise input $\eta$ and the measured output y.

$$\begin{aligned} {T_0}(s,{x_c}) = {{G_n}(s) \cdot K(s,{x_c}) \cdot \left[ {I + {G_n}(s) \cdot K(s,{x_c}} \right] ^{ - 1}} \end{aligned}$$

(19)

Therefore, ensuring a good RS needs limiting the evolution of the maximum singular values of the complementary sensitivity function, i.e., $\bar{\sigma }\left( T_{0}\left( \omega ,x_{c}\right) \right)$ over the entire frequency range $\omega _{\min }\le \omega \le \omega _{\max }$. This goal is reached by selecting the suitable weighting function $W_{T_{0}}\left( s\right)$ such that the RS condition which is given by Eq. 20 is always satisfied.

$$\begin{aligned} \left\| W_{T_{0}}\left( s\right) \cdot T_{0}\left( s,x_{c}\right) \right\| _{\infty }\le 1 \end{aligned}$$

(20)

Similarly, the preceding RS condition may be translated into an upper bound $\left\| W_{T_{0}}\left( s\right) \right\|$ on the frequency plot of $\bar{\sigma }\left( T_{0}\left( \omega ,x_{c}\right) \right)$, yielding thus the inequality $\left\| T_{0}\left( {s,x_{c}})\right) \right\| _{\infty }\le \left\| W_{T_{0}}\left( s\right) \right\| _{\infty }^{-1}$.

It should be noted that the two preceding requirements can be combined into a single one called the weighted mixed sensitivity criterion. Indeed, meeting this criterion achieves the desired trade-off between the two conflicting objectives NP and RS [26, 29]. It is defined by:

$$\begin{aligned} {J_{\infty }(s,x_{c})} = {\left\| \begin{array}{l} {W_{{S_0}}}(s) \cdot {S_0}(s,{x_c})\\ {W_{{T_0}}}(s) \cdot {T_0}(s,{x_c}) \end{array} \right\| _\infty } \le \gamma \end{aligned}$$

(21)

Equation 21 means that the desired controller must attenuate the worst case of the threshold appearing from either plot of $\bar{\sigma }\left( W_{S_{0}}\left( \omega \right) \cdot S_{0}\left( \omega ,x_{c}\right) \right)$ or $\bar{\sigma }\left( W_{T_{0}}\left( \omega \right) \cdot T_{0}\left( \omega ,x_{c}\right) \right)$. This last must be reduced less than the pre-specified attenuation level $\gamma \le 1$ at all frequencies, i.e.,

$\max \Big \{ {\mathop {max}\limits _\omega \bar{\sigma } \left( {{W_{{S_0}}}(\omega ) \cdot {S_0}(\omega ,{x_c})} \right) ,\mathop {max}\limits _\omega \bar{\sigma }\left( {{W_{{T_0}}}(\omega ) \cdot {T_0}(\omega ,{x_c})} \right) } \Big \} \le \gamma$.Knowing that, the preceding $H_{\infty }$ optimal control problem can be formulated as a $H_{\infty }$ suboptimal control problem. It yields also to the following min–max optimization problem [27]:

$$\begin{aligned} \mathop {\text {Min}}_{x_{c}}\left\{ {\mathop {\text {Max}}_{\omega } \bar{\sigma }\left( \begin{array}{l} {W_{{S_0}}}(\omega ) \cdot {S_0}(\omega ,{x_c})\\ {W_{{T_0}}}(\omega ) \cdot {T_0}(\omega ,{x_c}) \end{array} \right) } \right\} \end{aligned}$$

(22)

Fig. 6

Initial $\bar{\sigma }\left[ (W_{S_{0}}^{-1})\right]$, desired $\bar{\sigma }\left[ (W_{S}^{-1})\right]$, initial $\bar{\sigma }\left[ (W_{T_{0}}^{-1})\right]$ and desired $\bar{\sigma }\left[ (W_{T}^{-1})\right]$

4.2 Weighted-mixed sensitivity problem including AFWs

It should be noted that the choice of adequate FIWs in designing T-PID speed controller presents a difficult task, especially when the number of imposed frequency specifications becomes higher. To avoid this drawback, the use of AWFs instead of FIWs in the mixed-sensitivity problem becomes indispensable to enhance the trade-off between RS and NP. In general, the transfer function of the desired stability weight often takes the following form [21,22,23]:

(23)

where $A_{T}$ is a desired multiplicative error reached in steady-state, i.e., $A_{T} = W_{T}^{ - 1}(\infty ,x)$, $\omega _{BT}^*$ is a closed-loop bandwidth carried on the preferred complementary sensitivity function, $M_{T}$ is a desired $H_{\infty }$-norm to be reached by the preferred complementary sensitivity function, i.e., $M_{T} = {\left\| {T(s,x)} \right\| _\infty }$, $n\epsilon \mathbb {R}^{+}$ is a fractional order imposing the slope $- 20 \cdot n$ dB per decade on the maximal singular value plot of the preferred complementary sensitivity function at high frequency. On the other hand, the transfer function of the desired performance weight often takes the following form [21,22,23]:

(24)

where $A_{S}$ is a desired tracking error reached in steady state, i.e.,

$A_{S} = W_{S}^{ - 1}(\infty ,x)$, $\omega _{B}^*$ is a desired minimum bandwidth carried on preferred sensitivity function, $M_{S}$ is a desired $H_{\infty }$-norm to be reached by the preferred sensitivity function, i.e., $M_{S} = {\left\| {S(s,x)} \right\| _\infty }$, $m\epsilon \mathbb {R}^{+}$ is a desired fractional order imposing the slope of $- 20 \cdot m$ dB per decade on the maximal singular value plot of the preferred sensitivity function at low frequency. Now, from Eqs. 23 and 24, it can be seen that the appropriate $W_{S}\left( s\right)$ and $W_{T}\left( s\right)$ would heavily depend on a good choice of the weight parameter vector $x = \left( M_{S},A_{S},m,\omega _{B}^ {*} ,M_{T},A_{T},n,\omega _{BT}^ {*}\right) ^{T}$. In the next section, let us consider that the initial AFWs have the same structures that were given by Eqs. 23 and 24 where their parameters are given by $x_{0} = \left( M_{S_{0}},A_{S_{0}},m_{0},\omega _{B_{0}}^{*} ,M_{T_{0}},A_{T_{0}},n_{0},\omega _{BT_{0}}^ {*} \right) ^{T}$. Therefore, Fig. 6(a) gives the perfect template of desired performance weight $W_{S}(s,x)$ for increasing the NP margin. It is compared, in frequency domain, by the initial weight $W_{S_{0}}(s)$. Similarly, Fig. 6(b) gives the perfect template of desired performance weight $W_{T}(s,x)$ for increasing the RS margin. It is compared, in frequency domain, by the initial weight $W_{T_{0}}(s)$ [22]. It is worth noting that the safety margin of any trade-off can be increased against the undesired exogenous effects. This target can be met if the parameters of the two preceding adjustable weights are well chosen. In this paper, four guidelines will be scaled so that the two perfect templates can be automatically guaranteed using the GA. Consequently, the preceding threshold becoming always less than one.

4.3 Used Guidelines for the automatic selection of AFWs

In this section, some guidelines, available in the literature, are described to ensure proper parameter tuning of both robust T-PID speed controller and corresponding adequate AFWs. These rules are summarized as follows [22]:

• Rule 1: The general rule for limiting the singular values of desired sensitivity and desired complementary sensitivity is to reduce, as much as possible, the values of $M_{S}$ and $M_{T}$, respectively. It should be mentioned that larger values of $M_{S}$ and $M_{T}$ are always unavoidable. Typically, they are often chosen to be in the range 1.5–2 so that the two following bounded constraints are satisfied [22, 27]:

  $$\begin{aligned}&{\delta _{{M_S}}} \cdot {M_{{S_0}}}< {M_S}< {M_{{S_0}}}\nonumber \\&{\delta _{{M_T}}} \cdot {M_{{T_0}}}< {M_T} < {M_{{T_0}}} \end{aligned}$$

  (25)

  where $\delta _{M_{S}}$ and $\delta _{M_{T}}$ are often chosen to be in the range $\left] 0, 1\right[$ .

• Rule 2: The general rule to enlarge the NP margin (with respect to increase in the RS margin) is to increase, as much as possible the fractional-order m (with respect to increase in the fractional-order n). However, increasing m more than necessary affects the RS margin in high frequency, leading thus to violate the RS condition. By contrast, increasing the fractional order n more than necessary affects negatively the disturbance attenuation in low frequency, leading thus to violate the NP condition [25]. Consequently, these fractional orders are chosen so that the two following bounded constraints are satisfied [22, 27]:

  $$\begin{aligned} \left. \begin{array}{rll} m_{0}< &{} m &{}<\delta _{m}\cdot m_{0} \\ n_{0}< &{} n &{} <\delta _{n}\cdot n_{0} \end{array} \right. \end{aligned}$$

  (26)

  where $\delta _{m}$ and $\delta _{n}$ are often chosen to be in the range $\left] 1, 2\right[$ .

• Rule 3: The general rule to enhance the disturbance attenuation is to translate the bandwidth $\omega _{B}^{*}$, as much as possible, to the high-frequency range. In addition, to enhance the sensor noise rejection, the bandwidth $\omega _{BT}^{*}$ should be translated, as much as possible, toward the low-frequency range. Nevertheless, increasing the bandwidth $\omega _{B}^{*}$ more than necessary allows appearing an unsuitable overshoot in $\bar{\sigma }\left( S\left( \omega ,x_{c}\right) \right)$ while decreasing the bandwidth $\omega _{BT}^{*}$ more than necessary causes a reduction in the system bandwidth and to a poor tracking performance [25]. As a result, the choice of these bandwidths is ensured so that the two following bounded constraints are satisfied [22, 27]:

  $$\begin{aligned}&\omega _{{B_0}}^*< \omega _B^*< {\delta _{\omega _B^*}} \cdot \omega _{{B_0}}^*\nonumber \\&{\delta _{\omega _{BT}^*}} \cdot \omega _{B{T_0}}^*< \omega _{BT}^* < \omega _{B{T_0}}^* \end{aligned}$$

  (27)

  where $\delta _{\omega _{B}^{*}}$ is often chosen to be in the range $\left] 1, 2\right[$, whereas $\delta _{\omega _{BT}^{*}}$ is chosen to be in the range $\left] 0, 1\right[$.

• Rule 4: It should be noted that the ideal case for $A_{S}$ and $A_{T}$ is to set $A_{S}=A_{T}=0$. As a result, the $\bar{\sigma } \left( W_{S}^{-1}\left( \omega ,x_{c}\right) \right)$ and $\bar{\sigma }\left( W_{T}^{-1}\left( \omega ,x_{c}\right) \right)$ curves become maximally flat in the high- and low- frequency ranges, respectively. Actually, these parameters must be chosen very close to zero because of numerical difficulties [25]. This choice can be ensured by the following constraints [22, 27]:

  $$\begin{aligned}&{\delta _{{A_S}}} \cdot {A_{{S_0}}} \le {A_S} \le {A_{{S_0}}}\nonumber \\&{\delta _{{A_T}}} \cdot {A_{{T_0}}} \le {A_T} \le {A_{{T_0}}} \end{aligned}$$

  (28)

  where $\delta _{A_{S}}$ and $\delta _{A_{T}}$ are often chosen to be in the range $\left] 0, 1\right[$ .

4.4 GA-based solution of the weighted-mixed sensitivity problem including AFWs

The new design vector $x_{g}$ ensuring the simultaneous determination of transfer functions of the robust T-PID speed controller as well as their optimal AFWs is defined by:

$$\begin{aligned} {x_g} = \left( {\underbrace{{K_p},{K_i},{K_d},{K_t},N,{\tau _d}}_{{x_c}},\underbrace{{M_S},{A_S},m,\omega _B^ * ,{M_T},{A_T},n,\omega _{BT}^ * }_x} \right) \end{aligned}$$

(29)

where the fitness function which was given by Eq. 22 and the given corresponding search space, given by Eqs. 25–28, are parametrized by the augmented design vector $x_{g}$. If all these previous tuning rules are used in the optimization process, then 14 variables will be found by the GA where their setting parameters such as number of iterations, population size, bit size, crossing probability and mutation probability will be previously chosen by the designer. Indeed, if the optimization process properly respects the stopping criterion, then vector $x_{g}^\mathrm{{best}}$ represents the optimal solution of the following optimization problem:

$$\begin{aligned} \begin{array}{c} \mathop {\text {Min}}\limits _{{x_g}} \left\{ {\mathop {\text {Max}}\limits _\omega \bar{\sigma }\left( \begin{array}{l} {W_{{S_0}}}(\omega ,{x_g}) \cdot {S_0}(\omega ,{x_g})\\ {W_{{T_0}}}(\omega ,{x_g}) \cdot {T_0}(\omega ,{x_g}) \end{array} \right) } \right\} \\ \text {subject}\;\text {to}\;{\chi _m}:\left\{ \begin{array}{l} {\delta _{{M_T}}} \cdot {M_{{T_0}}}< {M_T}< {M_{{T_0}}}\\ {n_0}< n< {\delta _n} \cdot {n_0}\\ {\delta _{\omega _{BT}^*}} \cdot \omega _{B{T_0}}^*< \omega _{BT}^*< \omega _{B{T_0}}^*\\ {\delta _{{A_T}}} \cdot {A_{{T_0}}}< {A_T}< {A_{{T_0}}}\\ {\delta _{{M_S}}} \cdot {M_{{S_0}}}< {M_S}< {M_{{S_0}}}\\ {m_0}< m< {\delta _m} \cdot {m_0}\\ \omega _{{B_0}}^*< \omega _B^*< {\delta _{\omega _B^*}} \cdot \omega _{{B_0}}^*\\ {\delta _{{A_S}}} \cdot {A_{{S_0}}}< {A_S}< {A_{{S_0}}}\\ {K_{{p_{\min }}}}< {K_p}< {K_{{p_{\max }}}}\\ {K_{{i_{\min }}}}< {K_i}< {K_{{i_{\max }}}}\\ {K_{{d_{\min }}}}< {K_d}< {K_{{d_{\max }}}}\\ {K_{{t_{\min }}}}< {K_t}< {K_{{t_{\max }}}}\\ 2< N< 3\\ {\tau _{{d_{\min }}}}< {\tau _d} < {\tau _{{d_{\max }}}} \end{array} \right. \end{array} \end{aligned}$$

(30)

In this paper, to avoid all complex computations during the optimization process, only 2 rules among of the previous guidelines are used to increase the safety margin of the NP-RS trade-off. For this purpose, the size of the optimization problem is reduced to only 10 variables, distributed as follows: 2 variables for each AFW and 6 variables for the T-PID speed controller. Finally, the optimization process based on the GA is summarized by the flowchart, depicted in Fig. 7.

Fig. 7

The flowchart providing the robust T-PID speed controller given with automatic selection of AFWs

5 Simulation results and discussions

In this paper, it is assumed that each AFW has the two adjustable parameters, which are the desired bandwidth and the desired order of the descending slope, while their remaining parameters are assumed to be fixed. These adjustable parameters are optimized taking into account the respect of the two rules: Rule 2 and Rule 3. Also, the parameters of the two existing FIWs, described below, are used to define the search space and initialize the optimization process.

• Transfer function of the NP weight [7]: ${W_{{S_0}}}(s) = \frac{{8.33 \cdot s + 25}}{{s + 25 \cdot {{10}^{ - 4}}}}$, where ${m_0} = 1$, $\omega _{{B_0}}^* = 25$, ${M_{{S_0}}} = 1.2$ and ${A_{{S_0}}} = {10^{ - 4}}$.

• Transfer function of the RS weight [7]: ${W_{{T_0}}}(s) = \frac{{0.0025 \cdot s + 0.8}}{{25 \cdot {{10}^{ - 8}} \cdot s + 1}}$, where ${n_0} = 1$, $\omega _{{BT_0}}^* = 400$, ${M_{{T_0}}} = 1.25$ and ${A_{{T_0}}} = {10^{ - 4}}$.

The design problem is formulated as follows: in the set of all stabilizing fractional-order controllers as well as in the set of all AFWs, finding the optimal parameters of the robust T-PID speed controller and those of the two corresponding AFWs such that the NP-RS trade-off must be reached with a good secure margin over the entire frequency range. Therefore, the desired optimal solution $x_g^\mathrm{{best}}$ solves the following optimization problem:

$$\begin{aligned} \begin{array}{c} \mathop {\text {Min}}\limits _{{x_g}} \left\{ {\mathop {\text {Max}}\limits _\omega \bar{\sigma }\left( \begin{array}{l} {W_{{S_0}}}(\omega ,{x_g}) \cdot {S_0}(\omega ,{x_g})\\ {W_{{T_0}}}(\omega ,{x_g}) \cdot {T_0}(\omega ,{x_g}) \end{array} \right) } \right\} \\ \text {subject}\;\text {to}\;{\chi _m}:\left\{ \begin{array}{l} 0< {K_p}< 10\\ 0< {K_i},{K_d},{K_t}< 3\\ 0< {\tau _d}< 1\\ 2< N< 3\\ 1< m,n< 2\\ 25< \omega _B^*< 50\\ 200< \omega _{BT}^* < 400 \end{array} \right. \end{array} \end{aligned}$$

(31)

To reach the preceding goal, the tuning parameters of the GA are chosen by:

• $Generation number =30$;

• $Tolerance function =10^{-4}$;

• $Population size =30$;

• Plotfunction : @gaplotbestfun;

• $Reproducibility: rng (2,'twister')$.

Due to the probabilistic nature of the GA, the optimization process is run 20 times with different initial populations of ${x_g} \in \left( {{x_{{g_{\min }}}},{x_{{g_{\max }}}}} \right)$. Consequently, the best minimization yields the desired level $\gamma$ where the fitness function is attenuated below one just after the third iteration, i.e., ${\left\| {{T_{{z_\mathrm{in}} \rightarrow {z_\mathrm{out}}}}} \right\| _\infty } < \gamma = 0.9862$ (see Fig. 8).

Fig. 8

The best provided minimization using the GA of the weighted-mixed sensitivity problem

The performance level given above is acceptable; this means that both NP and RS conditions are well fulfilled over the frequency range $\omega \in \left( {{{10}^{ - 4}},\mathrm{{ }}{{10}^6}} \right)$ radians per sec. Furthermore, the given optimal solution $x_g^\mathrm{{best}}$ allows to determine the following AFWs:

• Optimal performance weight:

  $$\begin{aligned} {W_S}(s,x_g^\mathrm{{best}}) = {\left( {\frac{{\frac{s}{{\root 1.1351 \of {{1.2}}}} + 28.8308}}{{s + 28.8308 \cdot \root 1.1351 \of {{{{10}^{ - 4}}}}}}} \right) ^{1.1351}} \end{aligned}$$

  (32)

• Optimal stability weight:

  $$\begin{aligned} {W_T}(s,x_g^\mathrm{{best}}) = {\left( {\frac{{\frac{s}{{319.9517}} + \frac{1}{{\root 1.1910 \of {{1.25}}}}}}{{\frac{{\root 1.1910 \of {{{{10}^{ - 4}}}} \cdot s}}{{319.9517}} + 1}}} \right) ^{1.1910}} \end{aligned}$$

  (33)

where $\left\{ \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\omega _{{B_0}}^*< \omega _B^{*best} = 28.8308< 50}\\ {\begin{array}{*{20}{c}}{{m_0}< {m^\mathrm{{best}}} = 1.1351< 2}\\ {{n_0}< {n^\mathrm{{best}}} = 1.1910< 2}\end{array}}\end{array}}\\ {200< \omega _{BT}^{*\mathrm {best}} = 319.9517 < \omega _{B{T_0}}^*} \end{array} \right.$

Equations 31–33 show that the setting of the parameters for each desired fractional weight is done according to the guidelines described above. Indeed, the previous trade-off is well improved and the desired control objective is well achieved. Therefore, the automatic selection of these weights is also associated with the providing of the optimal parameters of the robust T-PID speed controller whose transfer function is given by:

(34)

where $\left\{ \begin{array}{l}0< K_p^\mathrm{{best}} = 7.8030< 10\\ 0< K_i^\mathrm{{best}} = 1.046< 3\\ 0< K_d^\mathrm{{best}} = 0.114< 3\\ 0< \tau _d^\mathrm{{best}} = 0.977 < 3\end{array} \right.$, and $\left\{ \begin{array}{l}0< K_t^\mathrm{{best}} = 1.189< 3\\ 2< {N^\mathrm{{best}}} = 2.437 < 3\end{array} \right.$

From Eqs. 31 and 34, it is easy to see that the search space ${\chi _m}$, which includes the optimal parameters of both T-PID speed controller and the two corresponding AFWs, is well chosen since the GA-based optimization process is not performed at the edge of ${\chi _m}$ and no relaxation of lower and upper bounds is carried out. This result confirms that the components of the resulting solution are not saturated at any upper or lower limit.

5.1 Frequency-domain analysis

It is important to note that frequency analysis based on the frequency response plotting of the sensitivity functions is not performed on the closed-loop system based on the preceding conventional IO-PID speed controller. Furthermore, it is only applied to robust controllers synthesized by solving the same mixed sensitivity problem. Indeed, the performances of the proposed T-PID speed controller are compared with those provided by two existing FO-PID speed controllers whose transfer functions are given [7]:

$$\begin{aligned} {K_{01}}(s)= & {} 0.0825 + \frac{{25.9816}}{{{s^{0.2144}}}} + 1.787 \cdot {s^{0.4049}} \end{aligned}$$

(35)

$$\begin{aligned} {K_{02}}(s)= & {} 3.8699 + \frac{{27.0594}}{{{s^{0.2233}}}} + 5.3577 \cdot {s^{0.0369}} \end{aligned}$$

(36)

The frequency-domain analysis is carried out in a frequency window whose lower limit is chosen so that the curve of $\bar{\sigma }\left( {W_S^{ - 1}(\omega ,x_g^\mathrm{{best}})} \right)$ becoming flat in low frequencies, in which no innovative evolution is observed in the frequency plot of $\bar{\sigma }\left( {S(\omega ,x_g^\mathrm{{best}})} \right)$. On the other hand, the upper limit of the preceding frequency window is chosen so that the curve of $\bar{\sigma }\left( {W_T^{ - 1}(\omega ,x_g^\mathrm{{best}})} \right)$ becomes flat in high frequencies, in which no innovative evolution is observed in the frequency plot of $\bar{\sigma }\left( {T(\omega ,x_g^\mathrm{{best}})} \right)$. As a result, the frequency range to be chosen for the frequency-domain analysis is given by $\omega \in \left( {{{10}^{ - 4}}{{,10}^6}} \right)$ radians per sec where the setpoint tracking dynamic and the rejection of the caused effect by model uncertainties becomes important in low frequency, particularly in the frequency range $\omega \in \left( {{{10}^{ - 4}}{{,10}^{ - 2}}} \right)$ radians per sec. Also, the closed-loop stability against unstructured multiplicative uncertainties and suppression dynamic of the effect of sensor noise and unmodeled dynamics uncertainties becomes important in high frequency, particularly in the frequency range $\omega \in \left( {{{10}^1}{{,10}^6}} \right)$radians per sec. Therefore, Fig. 9 presents the maximal singular value plots of direct sensitivity functions that are provided by $K(s,x_g^\mathrm{{best}})$, $K_{01}(s)$ and $K_{02}(s)$ controllers. These frequency plots are compared, at low-frequency range, by those provided by the inverse of initial and optimal performance weights.

According to Fig. 9, it is clear to see how automatic selection based on GA is carried out according to the two principles outlined in Rules 2 and 3, so that the optimization process starts with the initial FIW and ends with the achievement of the optimal AFW in which NP margin is well increased. Here, the optimal AFW has the steepest slope, i.e., $20 \times {m^\mathrm{{best}}} = 22.702$ dB per decade, compared to slope of the initial FIW, i.e., $20 \times {m_0} = 20$ dB per decade. Therefore, the proposed robust T-PID provides the better NP margin, especially below the frequency range $\omega \in \left( {{{10}^{ - 4}}{{,10}^{ - 2}}} \right)$ radians per sec, over the one provided the slopes of the two FO-PID speed controllers. This will be explained later, in time domain, by ensuring a good reference tracking dynamic and a good disturbance attenuation dynamic. Also, Fig. 9 shows also that all singular values of $S(s,x_g^\mathrm{{best}})$ are bounded by its template $\bar{\sigma }\left( {W_S^{ - 1}(\omega ,x_g^\mathrm{{best}})} \right)$. This statement means that the proposed robust T-PID can satisfy the NP condition for all frequencies $\omega$.

Fig. 9

Maximal singular value plots of the sensitivity functions compared by the initial and optimal performance weights

For the RS condition, Fig. 10 presents the maximal singular value plots of the complementary sensitivity functions that are provided by the three controllers $K(s,x_g^\mathrm{{best}})$, $K_{01}(s)$ and $K_{02}(s)$ . These sensitivities are compared, at high-frequency range, to those provided by the maximal singular value plots of the inverse of initial and optimal stability weights.

According to Fig. 10, it is easy to see that the inverse of the optimal stability weight has the steepest slope, i.e., $20 \times {n^\mathrm{{best}}} = 23.820$ dB per decade, compared to the slope of the initial stability weight, i.e., $20 \times {n_0} = 20$ dB per decade. Accordingly, the proposed robust T-PID offers better RS margin, compared to those of the two remaining FO-PID speed controllers. This will be explained later, in time domain, by ensuring the less sensitivity to sensor noise, neglected and unmodeled dynamics uncertainty. Figure 10 shows also that all singular values of $T(s,x_g^\mathrm{{best}})$ are bounded by their templates $\bar{\sigma }\left( {W_T^{ - 1}(\omega ,x_g^\mathrm{{best}})} \right)$. This means that the proposed robust T-PID can satisfy the RS condition for all $\omega$ frequencies.

5.2 Time-domain analysis

5.2.1 Time responses provided by Simulink software package

The feedback control system based on the linear nominal PMSM model for the classical IO-PID speed controller ${K_{{w_1}}}(s)$, the two robust FO-PID speed controllers $K_{01}(s)$ and $K_{02}(s)$ and the proposed robust T-PID speed controller $T(s,x_g^\mathrm{{best}})$ are depicted in Fig. 11.

Fig. 10

Maximal singular value plots of the complementary sensitivity functions compared by the initial and optimal stability weights

Fig. 11

Feedback control system based on three controllers and linear nominal PMSM model

According to Fig. 11, the three exogenous inputs, which are the mechanical speed reference, the disturbance and the sensor noise are used. The first input is assumed as a unit-step function applied until the time $t=0.1$ s. Afterward, it is increased to a gain equal 2 until the total simulation time $t=0.3$ s. On the other hand, the second input is assumed as a unit-step function with a gain equal to ${d_y}=-0.5$ ($50\%\,overshoot$) applies at the start time $t=0.2$ s 2 until the total simulation time $t=0.3$ s. Finally, the third input is assumed to be a random signal of zero mean and Gaussian distribution with a variance equal to $10^{-3}$ with the star time $t=0.25$ s. Therefore, the output signals given by $K(s,x_g^\mathrm{{best}})$ and ${K_{{w_1}}}(s)$ controllers are compared in Fig. 12, while their control signals are compared in Fig. 13. Also, the output signals given by $K(s,x_g^\mathrm{{best}})$ and ${K_{{w_1}}}(s)$ controllers are compared in Fig. 14, while their control signals are compared in Fig. 15. Finally, the output signals given by $K(s,x_g^\mathrm{{best}})$ and ${K_{{w_1}}}(s)$ controllers are compared in Fig. 16, while their control signals are compared in Fig. 17. As a result, all these time responses show the better performances of the proposed robust T-PID speed controller over those provided by the three remaining controllers in terms of exceedance, response time, settling time, time needed to reject the effect of the modeling uncertainty, the width of the control fluctuation range against the effect of measurement noise.

Fig. 12

The given output signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{w_1}}}(s)$ speed controllers

According to Fig. 12, it can be seen that steady-state tracking error of the ${K_{{w_1}}}(s)$ speed controller is ${\xi _S} = 0.032$ where the corresponding output signal has two overshoots ${D_{\max }}=12\%$, provided at time $t= 0.0284$ s and $t= 0.129$ s, respectively. On the other hand, the steady-state tracking error of the $K(s,x_g^\mathrm{{best}})$ speed controller is almost negligible, i.e., ${\xi _S} = 0.005$, involving an improvement of $84.375\%$. The corresponding time response is also ensured without overshoot. In addition, the maximum peak of the control, provided by the $K(s,x_g^\mathrm{{best}})$ speed controller, is ${u_{\max }}=7.994$ which also fluctuates within $- 0.75 \le u \le + 0.75$ in the steady state. For the ${K_{{w_1}}}(s)$ speed controller, the corresponding control which is signal fluctuates within $-15 \le u \le + 15$ where its maximum peak is ${u_{\max }}=109.211$. This last value means that the ${K_{{w_1}}}(s)$ speed controller requires almost 13 times more control effort than the $K(s,x_g^\mathrm{{best}})$ speed controller to ensure both performance and robustness of the closed-loop system (see Fig. 13). As a result, the above findings are a clear indication that the $K(s,x_g^\mathrm{{best}})$ controller has the potential to provide better trade-off with reduced control energy as compare to ${K_{{w_1}}}(s)$ controller.

Fig. 13

The provided control signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{w_1}}}(s)$ speed controllers

Fig. 14

The given output signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{0_1}}}(s)$ speed controllers

Fig. 15

The provided control signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{0_1}}}(s)$ speed controllers

According to Fig. 14 and Fig. 15, it can be noticed that the steady-state tracking error of the $K_{01}(s)$ speed controller is ${\xi _S} = 0.018$ , whereas for $K(s,x_g^\mathrm{{best}})$ controller, it is almost negligible, i.e., ${\xi _S} = 0.005$. This implies that there is an improvement of $72.22\%$ which can be provided by the proposed controller. Also, because of sensor noise effect, the control signal of the $K_{01}(s)$ speed controller fluctuates within $- 20 \le u \le + 20$ in the steady state, whereas for $K(s,x_g^\mathrm{{best}})$ controller, it fluctuates within $- 0.75 \le u \le + 0.75$. Moreover, for the $K_{01}(s)$ speed controller, the maximum amplitude of the control signal is ${u_{\max }}=150.411$, whereas for $K(s,x_g^\mathrm{{best}})$ controller, it is ${u_{\max }}=7.994$. This means that the $K_{01}(s)$ controller requires almost 20 times more control effort than the $K(s,x_g^\mathrm{{best}})$ controller to ensure both performance and robustness of the closed-loop system. As a result, the above findings are a clear indication that the $K(s,x_g^\mathrm{{best}})$ controller has the potential to provide better trade-off with reduced control energy as compared to $K_{01}(s)$ speed controller.

Similar comparison of output response of the $K(s,x_g^\mathrm{{best}})$ controller with that given by the $K_{01}(s)$controller is shown in Fig. 16, while their control signals are compared in Fig. 17.

Fig. 16

The given output signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{0_2}}}(s)$ speed controllers

Fig. 17

The provided control signals by the two $K(s,x_g^\mathrm{{best}})$ and ${K_{{0_2}}}(s)$ speed controllers

Fig. 18

Implementation of the four controllers using the Matlab/PowerSim software package

According to Figs. 14,  15,  16 and 17, it is easy to see that the time responses of the $K_{02}(s)$ speed controller are better enhanced, compared to those of the $K_{01}(s)$ speed controller, in terms of tracking error given in steady-state, amplitude of the control signal and sensitivity to sensor noise effect. However, by investigating the simulation time responses with $K(s,x_g^\mathrm{{best}})$ and $K_{02}(s)$ speed controllers, it can be found that:

• For $K_{02}(s)$ speed controller, the maximum overshoot is $12\%$, whereas for $K(s,x_g^\mathrm{{best}})$ controller the overshoot is almost negligible.

• The closed-loop system with $K(s,x_g^\mathrm{{best}})$ becomes less sensitive to the sensor noise effect than the one looped with $K_{02}(s)$.

• For $K_{02}(s)$ controller the maximum amplitude of control signal is ${u_{\max }}=15.301$ which means that the $K_{02}(s)$ speed controller requires almost a double control compared to the $K(s,x_g^\mathrm{{best}})$ controller.

5.2.2 Provided time responses by PowerSim software package

The feedback control systems based on the preceding four controllers are simulated in MATLAB/Simulink using blocks of PowerSim toolbox such as electrical IGBT inverter, PMSM system, DC link voltage source, three-phase I-V measurement and powergui solver (see Fig. 18). It is important to recall here that the preceding simulation has been carried out only on the basis of the simplified PMSM model (nominal model). However, the present simulation includes a PMSM model given with more extensive and more detailed behaviors over the preceding one. Furthermore, the used feedback control system, used in this simulation, contains other additional dynamics of some power electronic systems such as inverter block and I–V measurement block. All these dynamics have been neglected in the synthesis of the four previous controllers.

It should be pointed out that the different signals that are provided throughout this simulation are very close to the ones that an electric drive engineer might expect in real-world applications. It includes several signals types such as the low I–V control signals which are converted into high I–V signals and then used to drive the motor, trigger signals which are transmitted to the three-phase converter, I–V measurement signals which are used in the control and display parts, etc.

Fig. 19

The given mechanical speeds by the four controllers $K(s,x_g^\mathrm{{best}})$, $K_{01}(s)$, $K_{02}(s)$ and $K_{w1}(s)$

Here, the chosen PMSM system in this validation has a salient pole type rotor. It is fed by a three-phase IGBT inverter, and it is equipped with three bridge arms, infinite capacitance and a Snubber resistance of ${R_{sn}} = 5000\varOmega$. This inverter is connected to a 290VDC link voltage source where its trigger signal inputs are generated by the space-vector pulse width modulation PWM block given by the Simscape libraries Electrical$^\mathrm{TM}$. The digital implementation of PWM-based radio frequency (RF) transmitters is ensured by the frequency switching ${f_s} = 20$ KHz, and the pulse generator is ensured by three SR (set–reset ) flip-flop blocks using the sampling time ${T_e} = 0.02$ ms. Also, the fractional part of the robust T-PID and the two conventional FO-PID speed controllers are implemented using additional Simulink blocks of free ninteger Toolbox, downloaded through the website: https://www.mathworks.com/matlabcentral/fileexchange/8312-ninteger.

• (a) Case of no model uncertainties and no-load torque.

  In this section, no load torques and no changes in the parameters of the PMSM model are taken into account. Indeed, the two inputs such as the reference speed $\varOmega _m^*$ and sensor noise $\eta$ are used to excite the feedback control system. The first input is assumed by [7]:

  $$\begin{aligned} \varOmega _m^* = \left\{ \begin{array}{l} + 50: 0 \le t< 0.2\\ + 30: 0.2 \le t< 0.4\\ + 10: 0.4 \le t< 0.55\\ - 10: 0.55 \le t < 0.8 \end{array} \right. \end{aligned}$$

  (37)

  For practical consideration, a first-order lead–lag filter which is given by is added to make $\varOmega _m^*$ close to the one used in real-world applications. On the other hand, the second input is assumed to be a random signal of zero mean and Gaussian distribution with a variance equal to $0.1(\text {r.p.m.})^2$ with a star time $t=0.7$ s. Therefore, Fig. 19 compares the given mechanical speeds, whereas Fig. 20 compares their provided quadrature currents.

  According to Figs. 19 and 20, it can be stated that the proposed robust T-PID speed controller allows ensuring simultaneously, the better reference speed tracking, characterized by an almost negligible overshoot and reduced steady-state error. It also provides good suppression of the sensor effect where the corresponding quadrature current command is delivered with less sensitivity to measurement noise. Its amplitude becomes less fluctuating in steady state compared to those provided by the three remaining speed controllers.

• (b) Case of model uncertainties and no-load torque.

  The performances of the previous speed controllers are examined for 20 perturbed plants where the feedback control system of each one is excited using the same previous reference speed and sensor noise inputs. In fact, a parametric uncertainty of $20\%$ is assumed to be carried on the model parameters ${R_s}$, ${L_q}$, J and ${L_d}$. Furthermore, the set of the 20 perturbed plants is generated from a random selection of these parameters where each one is chosen within two limits that are given by a $\pm 20\%$ of deviation from its nominal value. As a result, Table 2 summarizes the numerical values of the used parameters used to compute the 20 different perturbed models ${G_{{p_j}}}(s)$. Furthermore, Table 3 summarizes the stable and unstable closed-loop system for 20 perturbed plants. The proposed T-PID speed controller has the ability to stabilize $100\%$ of the perturbed plants. Fourteen perturbed plants among 20 ones are stabilized by the speed controller $K_{w1}(s)$ which exhibits a success ratio of $70\%$. It is increased up to $75\%$ for the speed controller $K_{02}(s)$ and to $80\%$ for the speed controller $K_{01}(s)$.

• (c) Case of sinusoidal and triangular reference speed and load torque.

  In this section, among of the preceding four worst-case perturbed plants, that are $G_{p1}(s)$, $G_{p8}(s)$, $G_{p11}(s)$ and $G_{p17}(s)$, the delivered mechanical speed outputs by the feedback control systems based on the proposed T-PID speed controller are plotted only for the two perturbed plants $G_{p8}(s)$ and $G_{p17}(s)$. These time responses are given in the presence of the load torque input $C_{t}=20 N\cdot m$, applied at the starting time $t=0.5$ s. Also, for each perturbed plant, two reference speed type inputs are used to excite the feedback control system during the time range $\left[ 0, 1 \right]$ s. The first reference speed input is assumed to be a sinusoidal signal based sample type. It is given with the amplitude $a_m^* = 50$, where 100 samples per period are used. On the other hand, the second reference speed input is assumed to be a triangular signal with the amplitude $a_m^* = 50$ and the period $T_m^*=0.4$ s. Therefore, Fig. 21 shows the mechanical speed response of the perturbed plant $G_{p17}(s)$, given for the two preceding reference inputs. According to Fig. 21, the feedback control system provides a good speed tracking dynamic which is ensured with a good load attenuation dynamic where its effect is quickly attenuated within a short time range.

Fig. 20

The provided quadrature currents by the four controllers $K(s,x_g^\mathrm{{best}})$, $K_{01}(s)$, $K_{02}(s)$ and $K_{w1}(s)$

Table 2 The used numerical model parameters to compute the perturbed system

Table 3 Closed-loop stability of each controller for 20 perturbed plants

Fig. 21

The given mechanical speeds by the proposed T-PID controller for the perturbed plant $G_{p17}(s)$

6 Conclusion

In this paper, we have proposed a new robust fractional-order controller synthesized through combining the standard IO-PID and the tilt controller structures. The main goal is to achieve a good trade-off between NP and RS where the control energy would be ensured with reduced cost. This goal is reached by solving the weighted-mixed sensitivity problem, in which optimal AFWs are systematically selected by the GA and some existing rules are well satisfied. The validity of the proposed new controller structure was validated on the PMSM drive control which was modeled previously by unstructured multiplicative uncertainty. The given simulation results show the evident improvement in terms of good tracking dynamic of the set-point reference input, a good rejection of the model uncertainties, a good attenuation of the load torque input, a good suppression of the effects caused by sensor noise and unmodeled dynamics. These properties are ensured with less cost of the control energy. The performance and robustness analysis which is ensured by the proposed T-PID controller was performed in the frequency domain using the curves of both direct and complementary sensitivity functions. They are also performed in the time domain where the model parametric variations, the presence of load torque and the presence of various types of the reference speed are considered in the feedback control system using the Matlab/PowerSim software package. Finally, it is clear that the proposed controller structure will require further improvements to satisfy other hard condition such as the Robust Performance (RP) condition where other plant uncertainties types are taken into account. This requires a more general condition than the one mentioned in this work.